MODIFIKACE SHACK-HARTMANNOVA SENZORU. A.Mikš, J.Novák ČVUT v Praze, Fakulta stavební, katedra fyziky
|
|
|
- Helena Burešová
- před 8 lety
- Počet zobrazení:
Transkript
1 Abtrakt MOIFIKACE SHACK-HARTMANNOVA SENZORU A.Mkš J.Novák ČVUT v Prae Fakulta tavební katedra k Shack-Hartmannův enor nabíí jednoduchý půob vhodnocování vlnoploch a nacháí uplatnění v celé řadě oblatí. V prác je ukáán jednoduchý půob rošíření měřícího roahu enoru a to pomocí C umítěného před nebo a matcí mkročoček. Pomocí počítače e potupně generují otvor o velkot tejné jako mají mkročočk přčemž je proputný vžd jen jeden otvor. Světelná topa na CC enoru je pak jednonačně určena ouřadncem tředu otvoru na C kterým procháí větlo od jemu odpovídající čát měřené vlnoploch. Měřící roah je pak mnohem větší neboť nedocháí k míchání top od jednotlvých mkročoček jak je tomu u klackého Shack-Hartmannova enoru. Vhodnocení je poté možno provádět pomocí Matlabu.. Úvod Pro kontrolu kvalt ploch optckých prvků např. čoček a rcadel e v pra používá mnoho růných metod []. Nejčatěj e v průmlové pra aplkují ntererometrcké metod [78]. Tto měřící metod umožňují epermentálně jtt deormac tetované vlnoploch vůč peckované reerenční např. ércké vlnoploše. Používají pecálně kontruovaných ntererometrů Feauova nebo Twman-Greenova tpu [8] které umožňují doažení přenot měření všší nežl λ/00 kde λ je vlnová délka použtého áření. Je však nutno ponamenat že tto ntererometr jou poněkud ložtá a nančně náročná měřící aříení. Jným tpem metod jou tv. gradentní metod které umožňují určení gradentu vlnového pole které je deormováno po nterakc tetovanou plochou [3-7]. Tto technk mají oprot metodám ntererometrckým několk výhod jou jednodušší méně nančně náročné nepotřebují koherentní droj áření a je možno tetovat vlnoploch větším gradentem. V této prác e aměříme na tv. Shack-Hartmannovu metodu která pro vhodnocení vlnového pole používá matc mkročoček a CC enoru. Nevýhodou klacké Shack- Hartmannov metod je to že v případě velké měn gradentu vlnoploch docháí k tomu že na jednom mítě CC enoru e mohou nacháet top růných čátí měřené vlnoploch. Toto načně omeuje měřící roah klackého Shack-Hartmannova enoru. V prác je ukáán půob kterým le tento problém odtrant a podtatným půobem rošířt měřící roah Shack-Hartmannova enoru.. Pop metod Na obr. je náorněno chéma Shack-Hartmannova enoru který e kládá matce mkročoček A a CC enoru. Plocha CC enoru je vrtuálně v počítač rodělena na tolk dílčích enorů kolk obahuje matce mkročoček. V našem jednodušeném případě má matce 7 mkročoček a CC enor je ted rodělen na 7 dílčích enorů Vlnoplocha dopadající na matc mkročoček A má obecný tvar a její normál mají ted v růných mítech růný měr. Na obr. jou normál vlnoploch procháející třed jednotlvých mkročoček tv. hlavní normál očílován číl...7. Mkročočk outředí paprkový vaek do vé ohnkové rovn v níž e nacháí CC enor. Poloha top na enoru bude dána měrem hlavní normál přílušné dané mkročočce a ohnkovou vdálenotí mkročočk jak bude ukááno poděj. Velkot dílčích enorů je tejná jako velkot jím přílušné mkročočk. Senor bude ted detekovat gradent vlnoploch který je
2 charakterován měrem hlavní normál. etekce bude jednonačná bude-l e topa přílušející -té hlavní normále nacháet na -tém dílčím detektoru. V případě velkých gradentů vlnoploch však může natat tuace kd e na -tém detektoru bude nacháet několk top přílušných růným hlavním normálám. V tomto případě nejme chopn rohodnou od které čát vlnoploch topa na detektoru pocháí. A CC Obr.: Optcké chéma Shack-Hartmannova enoru Tato tuace je náorněna na obr. kde e na dílčím detektoru nacháejí dvě top pocháející od hlavních normála a 3. Na detektoru 4 e nacháejí také dvě top pocháející od hlavních normál 4 a 5 a tto top jou navíc ještě dentcké tj. nacháejí e na tejném mítě na detektoru. Abchom e této tuac vhnul muíme nutně omet měřící roah enoru a to je na takové hodnot gradentu vlnoploch jejchž velkot v případě bodové top nepřeahuje hodnotu ±/ kde je velkot mkročočk a její ohnková vdálenot. Tato kutečnot výraným půobem omeuje roah půobnot klackého Shack- Hartmannova enoru. Např. pro mkročočku mající ohnkovou vdálenot 35 mm a průměr 03 mm dotáváme pro větlo o vlnové délce λ 633 nm mamální hodnotu gradentu vlnoploch 68 λ. V důledku drakce větla nebude topa na detektoru bod ale ploška určté velkot. Na obr. je achcen dgtální obra detekovaných top pomocí Shack- Hartmannova enoru. V případě že mkročočk mají kruhový tvar pak pro velkot d centrální čát top na enoru platí d 4λ/ 7 oaením předcháejících hodnot dotáváme: d 077 mm. Pro CC enor o velkot jednoho pelu 00 mm tak plocha centrální čát top pokrývá cca 300 pelů. To má a důledek podtatné nížení mamální hodnot gradentu vlnoploch který jme chopn určt.
3 Obr.: etekovaný obra pomocí Shack-Hartmannova enoru Jednoduchý půob rošíření měřícího roahu Shack-Hartmannova enoru e provede pomocí C umítěného před nebo a matcí mkročoček A. Schéma optckého upořádání Shack-Hartmannova enoru je uvedeno na obr.3. Pomocí počítače e potupně generují otvor o velkot tejné jako mají mkročočk přčemž je proputný vžd jen jeden otvor. Světelná topa na CC enoru je pak jednonačně určena ouřadncem tředu otvoru na C kterým procháí větlo od jemu odpovídající čát měřené vlnoploch. Měřící roah je pak mnohem větší neboť nedocháí k míchání top od jednotlvých mkročoček jak je tomu u klackého Shack-Hartmannova enoru a pro detekc je vužívána celá plocha CC enoru. A C CC r r averont O Obr.3: Optcké chéma modkovaného Shack-Hartmannova enoru
4 3. Vhodnocení deormace všetřované vlnoploch Abchom určl deormac všetřované vlnoploch na ákladě měření jejího gradentu muíme nejdříve určt odchlku top elementárního větelného vaku vmeeného velkotí mkročočk a měrem hlavní normál od poloh tohoto vaku v případě deální vlnoploch kterou je rovnná vlnoplocha. V případě rovnné vlnoploch dopadající kolmo na matc mkročoček e budou top elementárních vaků nacháet na cela určtých mítech detektoru. V deálním případě to bude ve tředu detektoru. Vhledem k drakc větla a aberacím mkročoček bude mít topa elementárního paprkového vaku na detektoru poměrně ložtý energetcký prol obr.4. Obr.4: Energetcký prol detekované top Za třed top tohoto vaku na detektoru budeme proto považovat těžště energetckého prolu top jehož ouřadnce c c určíme jako P Q j c P Q j I I P Q j c P Q j I I kde I je hodnota ntent v obraovém bodě o ouřadncích a přčemž výpočet e provádí v okně o velkot P Q obraových bodů. Onačme jednotkový měrový vektor normál vlnoploch dopadající na mkročočku r polohový vektor tředu mkročočk r polohový vektor tředu top na CC enoru O O O O počátek ouřadné outav a ohnkovou vdálenot mkročočk. Pro měrový vektor pak podle obr. platí. grad r r. grad r r r r
5 Volíme-l pecálně počátek ouřadné outav O tak ab ležel v rovně procháející adním hlavním bod mkročoček tj. O 000 pak platí: r 0 r. Ze vtahu dotáváme. Přblžné vtah platí a předpokladu že / << / <<. Tento předpoklad je v pra téměř vžd plněn. ále pak platí 3. Přblžné vtah platí a předpokladu že / << / <<. Tento předpoklad je v pra téměř vžd plněn. Ze vtahů a 3 dotáváme náledující přblžné vtah. 4 eormac vlnoploch pak vpočítáme e vtahu kde d 0 d 0. 5 Integrál 5 vpočítáme některou metod numercké ntegrace např. lchoběžníkovou metodou platí
6 kde m m mδ nδ mn m n 6 m δ n δ n n j kde m M n...n přčemž M rep. N je počet mkročoček ve měru o rep. δ rep. δ jou vdálenot tředů mkročoček ve měru o rep.. V pra mají pole mkročoček tu vlatnot že pro většnu případů platí δ δ. 4. Závěr V prác bla provedena analýa Shack-Hartmannova enoru a ukáán jeho ákladní vlatnot a půob vhodnocování měřené vlnoploch. Bl ukáán půob jak le odtrant nevýhod klackého Shack-Hartmannova enoru a to pomocí C umítěného před nebo a matcí mkročoček. Bl odvoen teoretcké vtah umožňující provét podrobnou analýu vlatnotí a možnotí tohoto enoru. ále bl uveden vtah umožňující určt tvar všetřované vlnoploch hodnot jejího gradentu. Tto vtah le jednoduše naprogramovat pomocí tému MATAB a použít pro automatckou analýu tetovaných vlnoploch. Ve rovnání ntererometrckým metodam mají gradentní metod př rovnatelné přenot velkou výhodu ve vé jednoduchot většímu měřícímu roahu rchlot měření a nectlvot k rušvým vlvům okolního protředí jako jou např. vbrace. Práce bla vpracována a podpor grantů GA ČR 03/ 03/P00 agačr 0/0/034. teratura [] Malacara.: Optcal Shop Tetng John le & Son N.Y. 99. [] Francon M.: Optcal Intererometr Academc Pre N.Y [3] Zou. Zhang Z.: Generaled wave-ront recontructon algorthm appled n a Shack-Hartmann tet Appled Optc Vol.39 No. 000 [4] Rocktächel M. Tan H.J.: mtaton o the Shack-Hartmann enor or tetng optcal apherc. Optc and aer Technolog Vol p [5] Pund J. ndlen N. Schwder J.: Malgnment eect o the Shack-Hartmenn enor Appl. Optc vol [6] Novák J. - Mkš A.: Modern Optoelectronc Method or Non-Contact eormaton Meaurement n Indutr. Journal o Optc A: Pure and Appled Optc. 00 vol. 4 no. 6 p [7] Mkš A.: Aplkovaná optka 0 Vdavateltví ČVUT Praha 000. [8] Mkš A.: Intererometrcké metod vhodnocování érckých ploch v optce Jemná mechanka a optka 000 č.. oc.rnr.antonín MkšCSc Katedra k FSv ČVUtT Thákurova Praha 6. Tel: Fa: E-mal: mk@v.cvut.c Ing.Jří NovákPh Katedra k FSv ČVUT Thákurova 7 66t 9 Praha 6. Tel: Fa: E-mal: novakj@v.cvut.c
ANALÝZA PRŮCHODU PAPRSKOVÝCH SVAZKŮ KOUTOVÝM ODRAŽEČEM
 ANALÝZA PRŮCHODU PAPRSKOVÝCH SVAZKŮ KOUTOVÝM ODRAŽEČEM P Kytka J Novák ČVUT v Praze Fakulta tavební katedra fyziky Práce e zabývá analýzou průchodu paprků koutovým odražečem což je typ hranolu který je
ANALÝZA PRŮCHODU PAPRSKOVÝCH SVAZKŮ KOUTOVÝM ODRAŽEČEM P Kytka J Novák ČVUT v Praze Fakulta tavební katedra fyziky Práce e zabývá analýzou průchodu paprků koutovým odražečem což je typ hranolu který je
5. cvičení z Matematické analýzy 2
 5. cvičení z Matematické analýz 2 30. října - 3. litopadu 207 5. linearizace funkce a Pro funkci f, = e nalezněte její linearizaci v bodě a 0 = 6, 0. Použijte ji k přibližnému určení hodnot funkce f v
5. cvičení z Matematické analýz 2 30. října - 3. litopadu 207 5. linearizace funkce a Pro funkci f, = e nalezněte její linearizaci v bodě a 0 = 6, 0. Použijte ji k přibližnému určení hodnot funkce f v
Systém vztahů obecné pružnosti Zobecněný Hookeův zákon
 Stém vtahů obecné pružnoti Zobecněný Hookeův ákon V PPI e řešil úloh pružnoti u prutů. Pro řešení pouvů napětí a přetvoření obecného 3D těleo je třeba etavit a řešit tém vtahů obecné pružnoti. Jeho řešení
Stém vtahů obecné pružnoti Zobecněný Hookeův ákon V PPI e řešil úloh pružnoti u prutů. Pro řešení pouvů napětí a přetvoření obecného 3D těleo je třeba etavit a řešit tém vtahů obecné pružnoti. Jeho řešení
Je rychlejší dostat se do školy (budovy ČVUT na Karlově Náměstí) ze Strahovských kolejí pomocí autobusu, nebo tramvaje?
 Seminární práce pro předmět X36MVT Matematika pro výpočetní techniku Je rchlejší dotat e do škol (budov ČVUT na Karlově Námětí) ze Strahovkých kolejí pomocí autobuu, nebo tramvaje? Vpracoval: Tomáš Valenta,
Seminární práce pro předmět X36MVT Matematika pro výpočetní techniku Je rchlejší dotat e do škol (budov ČVUT na Karlově Námětí) ze Strahovkých kolejí pomocí autobuu, nebo tramvaje? Vpracoval: Tomáš Valenta,
1 Úvod do číslicové regulace
 Automatické říení II Úvod do čílicové regulace V náledujícím textu budou uvedeny ákladní vlatnoti, popiy a přehledy týkající e problematiky čílicové regulace. Některé kapitol budou také obahovat řešené
Automatické říení II Úvod do čílicové regulace V náledujícím textu budou uvedeny ákladní vlatnoti, popiy a přehledy týkající e problematiky čílicové regulace. Některé kapitol budou také obahovat řešené
středové (perspektivní) promítání vytváří obrazy podobné těm, které vidí lidské oko
 tředové promítaní všechn promítací paprk procháejí jedním bodem (vlatní) třed promítání neachovává e rovnoběžnot vdálenot objektů od tředu promítání ovlivňuje velikot jejich průmětů vdálenější objekt mají
tředové promítaní všechn promítací paprk procháejí jedním bodem (vlatní) třed promítání neachovává e rovnoběžnot vdálenot objektů od tředu promítání ovlivňuje velikot jejich průmětů vdálenější objekt mají
Příloha 1 Zařízení pro sledování rekombinačních procesů v epitaxních vrstvách křemíku.
 Příloha 1 Zařízení pro ledování rekombinačních proceů v epitaxních vrtvách křemíku. Popiovaný způob měření e vztahuje ke labě dopovaným epitaxním vrtvám tejného typu vodivoti jako ilně dopovaný ubtrát.
Příloha 1 Zařízení pro ledování rekombinačních proceů v epitaxních vrtvách křemíku. Popiovaný způob měření e vztahuje ke labě dopovaným epitaxním vrtvám tejného typu vodivoti jako ilně dopovaný ubtrát.
Katedra geotechniky a podzemního stavitelství
 Katedra geotechnik a podzemního taviteltví Modelování v geotechnice Základní veličin, rovnice a vztah (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace tudijního
Katedra geotechnik a podzemního taviteltví Modelování v geotechnice Základní veličin, rovnice a vztah (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace tudijního
ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ
 VOKÁ ŠKOLA BÁŇKÁ TECHNICKÁ NIVEZITA OTAVA FAKLTA TOJNÍ ZÁKLAD ATOMATICKÉHO ŘÍZENÍ 9. týden doc. Ing. enata ANEOVÁ, Ph.D. Otrava 03 doc. Ing. enata ANEOVÁ, Ph.D. Vyoká škola báňká Technická univerzita Otrava
VOKÁ ŠKOLA BÁŇKÁ TECHNICKÁ NIVEZITA OTAVA FAKLTA TOJNÍ ZÁKLAD ATOMATICKÉHO ŘÍZENÍ 9. týden doc. Ing. enata ANEOVÁ, Ph.D. Otrava 03 doc. Ing. enata ANEOVÁ, Ph.D. Vyoká škola báňká Technická univerzita Otrava
Fyzikální praktikum FJFI ČVUT v Praze
 Fyzikální praktikum FJFI ČVUT v Praze Úloha 10: Interference a ohyb větla Datum měření: 6. 5. 2016 Doba vypracovávání: 7 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klaifikace: 1 Zadání 1. Bonu:
Fyzikální praktikum FJFI ČVUT v Praze Úloha 10: Interference a ohyb větla Datum měření: 6. 5. 2016 Doba vypracovávání: 7 hodin Skupina: 1, pátek 7:30 Vypracoval: Tadeáš Kmenta Klaifikace: 1 Zadání 1. Bonu:
LINEÁRNÍ PERSPEKTIVA. Přednáška DG2*A 6. týden
 LINEÁRNÍ PERSPEKTIVA Přednáška DG*A 6. týden DRY VOLNÉ PERSPEKTIVY Muíme vždy volit ouřadnicový ytém. Souřadné oy pravidla umíťujeme tak, aby byly rovnoběžné ranami obraovanéo objektu. JEDNOÚBĚŽNÍKOVÁ
LINEÁRNÍ PERSPEKTIVA Přednáška DG*A 6. týden DRY VOLNÉ PERSPEKTIVY Muíme vždy volit ouřadnicový ytém. Souřadné oy pravidla umíťujeme tak, aby byly rovnoběžné ranami obraovanéo objektu. JEDNOÚBĚŽNÍKOVÁ
Metoda konečných prvků Základní veličiny, rovnice a vztahy (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika)
 Inovace tudijního oboru Geotechnika Reg. č. CZ..7/../8.9 Metoda konečných prvků Základní veličin, rovnice a vztah (výuková prezentace pro. ročník navazujícího tudijního oboru Geotechnika) Doc. RNDr. Eva
Inovace tudijního oboru Geotechnika Reg. č. CZ..7/../8.9 Metoda konečných prvků Základní veličin, rovnice a vztah (výuková prezentace pro. ročník navazujícího tudijního oboru Geotechnika) Doc. RNDr. Eva
středové (perspektivní) promítání vytváří obrazy podobné těm, které vidí lidské oko
 tředové promítaní všechn promítací paprk procháejí jedním bodem (vlatní) třed promítání neachovává e rovnoběžnot vdálenot objektů od tředu promítání ovlivňuje velikot jejich průmětů vdálenější objekt mají
tředové promítaní všechn promítací paprk procháejí jedním bodem (vlatní) třed promítání neachovává e rovnoběžnot vdálenot objektů od tředu promítání ovlivňuje velikot jejich průmětů vdálenější objekt mají
Přednáška Omezení rozlišení objektivu difrakcí
 Před A3M38VBM, J. Ficher, kat. měření, ČVUT FL Praha Přednáška Omezení rozlišení objektivu difrakcí v. 2011 Materiál je určen pouze jako pomocný materiál pro tudenty zapané v předmětu: Videometrie a bezdotykové
Před A3M38VBM, J. Ficher, kat. měření, ČVUT FL Praha Přednáška Omezení rozlišení objektivu difrakcí v. 2011 Materiál je určen pouze jako pomocný materiál pro tudenty zapané v předmětu: Videometrie a bezdotykové
ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ týden doc Ing Renata WAGNEROVÁ, PhD Otrava 013 doc Ing Renata WAGNEROVÁ, PhD Vyoká škola báňká Technická univerzita
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ týden doc Ing Renata WAGNEROVÁ, PhD Otrava 013 doc Ing Renata WAGNEROVÁ, PhD Vyoká škola báňká Technická univerzita
1. Matematický model identifikované soustavy
 IDENTIFIKACE SOUSTAVY SEDAČKY SEDAČKA C.I.E.B TYPOVÉ ŘADY 5 A NÁVRH REGULAČNÍHO OBVODU GHARAZI SAYED MOHSEN Technická univerita v Liberci, fakulta trojní, katedra aplikované kybernetiky, Hálkova 6, 46
IDENTIFIKACE SOUSTAVY SEDAČKY SEDAČKA C.I.E.B TYPOVÉ ŘADY 5 A NÁVRH REGULAČNÍHO OBVODU GHARAZI SAYED MOHSEN Technická univerita v Liberci, fakulta trojní, katedra aplikované kybernetiky, Hálkova 6, 46
Těžiště. Fyzikální význam těžiště:
 ěžště Fykální výnam těžště: a) hmotný bod se soustředěnou hmotností útvaru b) bod, ve kterém le hmotný útvar vystavený tíe podepřít prot posunutí anž by docháelo k rotac ěžště je chápáno jako statcký střed
ěžště Fykální výnam těžště: a) hmotný bod se soustředěnou hmotností útvaru b) bod, ve kterém le hmotný útvar vystavený tíe podepřít prot posunutí anž by docháelo k rotac ěžště je chápáno jako statcký střed
6.1 Shrnutí základních poznatků
 6.1 Shrnutí ákladních ponatků Prostorová a rovinná napjatost Prostorová napjatost v libovolném bodě tělesa je v pravoúhlé soustavě souřadnic obecně popsána 9 složkami napětí, které le uspořádat do matice
6.1 Shrnutí ákladních ponatků Prostorová a rovinná napjatost Prostorová napjatost v libovolném bodě tělesa je v pravoúhlé soustavě souřadnic obecně popsána 9 složkami napětí, které le uspořádat do matice
Obr. DI-1. K principu reverzibility (obrácení chodu paprsků).
 Učebí text k předášce UFY8 Dvojvzková tererece teké vrtvě Dvojvzková tererece teké vrtvě Předpokládejme, vl o mpltudě dvou delektrk tk, že mpltud održeé vly bude o dexu lomu bude t (vz obr. DI-1). v protředí
Učebí text k předášce UFY8 Dvojvzková tererece teké vrtvě Dvojvzková tererece teké vrtvě Předpokládejme, vl o mpltudě dvou delektrk tk, že mpltud održeé vly bude o dexu lomu bude t (vz obr. DI-1). v protředí
DIFÚZNÍ VLASTNOSTI MATERIÁLŮ Z POHLEDU NOVÝCH TEPELNĚ TECHNICKÝCH NOREM. Petr Slanina
 DIFÚZNÍ VLASTNOSTI MATERIÁLŮ Z POHLEDU NOVÝCH TEPELNĚ TECHNICKÝCH NOREM Petr Slanina DIFÚZNÍ VLASTNOSTI MATERIÁLŮ Z POHLEDU NOVÝCH TEPELNĚ TECHNICKÝCH NOREM Ing. Petr Slanina FSv, ČVUT v Praze, Thákurova
DIFÚZNÍ VLASTNOSTI MATERIÁLŮ Z POHLEDU NOVÝCH TEPELNĚ TECHNICKÝCH NOREM Petr Slanina DIFÚZNÍ VLASTNOSTI MATERIÁLŮ Z POHLEDU NOVÝCH TEPELNĚ TECHNICKÝCH NOREM Ing. Petr Slanina FSv, ČVUT v Praze, Thákurova
1.1.7 Rovnoměrný pohyb II
 1.1.7 Rovnoměrný pohyb II Předpoklady: 16 Minulou hodinu jme zakončili předpovídáním dalšího pohybu autíčka. Počítali jme jeho dráhy v dalších okamžicích pomocí tabulky a nakonec i přímé úměrnoti: autíčko
1.1.7 Rovnoměrný pohyb II Předpoklady: 16 Minulou hodinu jme zakončili předpovídáním dalšího pohybu autíčka. Počítali jme jeho dráhy v dalších okamžicích pomocí tabulky a nakonec i přímé úměrnoti: autíčko
TECHNICKÁ UNIVERZITA V LIBERCI Katedra fyziky, Studentská 2, 461 17 Liberec
 TECHNICKÁ UNIVERZITA V LIBERCI Katedra fyziky, Studentká, 6 7 Liberec POŽADAVKY PRO PŘIJÍMACÍ ZKOUŠKY Z FYZIKY Akademický rok: 0/0 Fakulta mechatroniky Studijní obor: Nanomateriály Tématické okruhy. Kinematika
TECHNICKÁ UNIVERZITA V LIBERCI Katedra fyziky, Studentká, 6 7 Liberec POŽADAVKY PRO PŘIJÍMACÍ ZKOUŠKY Z FYZIKY Akademický rok: 0/0 Fakulta mechatroniky Studijní obor: Nanomateriály Tématické okruhy. Kinematika
UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA
 UNIVERZIT PLCKÉHO V OLOMOUCI PŘÍROOVĚECKÁ FKULT KTER LGEBRY GEOMETRIE OSVĚTLENÍ VE STŘEOVÉM PROMÍTÁNÍ LINEÁRNÍ PERSPEKTIVĚ Bakalářká práce Vedoucí práce: RNr. Leka Juklová, Ph.. Rok odevdáí 202 Vypracovala:
UNIVERZIT PLCKÉHO V OLOMOUCI PŘÍROOVĚECKÁ FKULT KTER LGEBRY GEOMETRIE OSVĚTLENÍ VE STŘEOVÉM PROMÍTÁNÍ LINEÁRNÍ PERSPEKTIVĚ Bakalářká práce Vedoucí práce: RNr. Leka Juklová, Ph.. Rok odevdáí 202 Vypracovala:
17. EXPONENCIÁLNÍ ROVNICE
 7. EXPONENCIÁLNÍ ROVNICE 7. EXPONENCIÁLNÍ ROVNICE 7.. Řeš v R rovnice: a) 53 b) 3 3 c) 7 0 d) 3 0,5 a) 5 37 5 3 7 K 3 c) 7 0 K b) 3 3 0 0 K 3 d) 3 350 5, 7 K 5;7 Strategie: potřebujeme zíkat takový tvar
7. EXPONENCIÁLNÍ ROVNICE 7. EXPONENCIÁLNÍ ROVNICE 7.. Řeš v R rovnice: a) 53 b) 3 3 c) 7 0 d) 3 0,5 a) 5 37 5 3 7 K 3 c) 7 0 K b) 3 3 0 0 K 3 d) 3 350 5, 7 K 5;7 Strategie: potřebujeme zíkat takový tvar
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra kybernetiky. Bakalářská práce. Řízení Trojkolového vozíku
 Západočeká univerzita v Plzni Fakulta aplikovaných věd Katedra kbernetik Bakalářká práce Řízení Trojkolového vozíku Plzeň, 23 Jan Holub Prohlášení Předkládám tímto k poouzení a obhajobě bakalářkou práci
Západočeká univerzita v Plzni Fakulta aplikovaných věd Katedra kbernetik Bakalářká práce Řízení Trojkolového vozíku Plzeň, 23 Jan Holub Prohlášení Předkládám tímto k poouzení a obhajobě bakalářkou práci
Výpočet zobrazovacích soustav
 Výpočet zobrazovacích outav. Úvod Joef Kuběna, ÚFKL, Maarykova Univerita, Brno, (25) V tomto textu popíšeme potup, který zformuluje univerzální algoritmu pro výpočet parametrů libovolně ložitých zobrazovacích
Výpočet zobrazovacích outav. Úvod Joef Kuběna, ÚFKL, Maarykova Univerita, Brno, (25) V tomto textu popíšeme potup, který zformuluje univerzální algoritmu pro výpočet parametrů libovolně ložitých zobrazovacích
ÚSTŘEDNÍ KOMISE FYZIKÁLNÍ OLYMPIÁDY ČESKÉ REPUBLIKY
 ÚSTŘEDNÍ KOMISE YZIKÁLNÍ OLYMPIÁDY ČESKÉ REPUBLIKY E-mail: ivo.volf@uhk.cz, tel.: 493 331 19, 493 331 189 Řešení úloh krajkého kola 55. ročníku yzikální olympiády Kategorie E Předložená řešení by neměla
ÚSTŘEDNÍ KOMISE YZIKÁLNÍ OLYMPIÁDY ČESKÉ REPUBLIKY E-mail: ivo.volf@uhk.cz, tel.: 493 331 19, 493 331 189 Řešení úloh krajkého kola 55. ročníku yzikální olympiády Kategorie E Předložená řešení by neměla
s požadovaným výstupem w(t), a podle této informace generuje akční zásah u(t) do
 Vážení zákazníci, dovolujeme i Vá upozornit, že na tuto ukázku knihy e vztahují autorká práva, tzv. copyright. To znamená, že ukázka má loužit výhradnì pro oobní potøebu potenciálního kupujícího (aby ètenáø
Vážení zákazníci, dovolujeme i Vá upozornit, že na tuto ukázku knihy e vztahují autorká práva, tzv. copyright. To znamená, že ukázka má loužit výhradnì pro oobní potøebu potenciálního kupujícího (aby ètenáø
POČÍTAČOVÁ SIMULACE VLIVU CHYB PENTAGONÁLNÍHO HRANOLU NA PŘESNOST MĚŘENÍ V GEODÉZII. A.Mikš 1, V.Obr 2
 POČÍTAČOVÁ SIMULACE VLIVU CHYB PENTAGONÁLNÍHO HRANOLU NA PŘESNOST MĚŘENÍ V GEODÉZII A.Mikš 1, V.Obr 1 Katedra fyziky, Fakulta stavební ČVUT, Praha Katedra vyšší geodézie, Fakulta stavební ČVUT, Praha Abstrakt:
POČÍTAČOVÁ SIMULACE VLIVU CHYB PENTAGONÁLNÍHO HRANOLU NA PŘESNOST MĚŘENÍ V GEODÉZII A.Mikš 1, V.Obr 1 Katedra fyziky, Fakulta stavební ČVUT, Praha Katedra vyšší geodézie, Fakulta stavební ČVUT, Praha Abstrakt:
Desky. Petr Kabele. Pružnost a pevnost 132PRPE Přednášky. Deska/stěna/skořepina, desky základní předpoklady, proměnné a rovnice
 Pružnost a pevnost 13PRPE Přednášk Desk Deska/stěna/skořepina, desk ákladní předpoklad, proměnné a rovnice Petr Kabele České vsoké učení technické v Prae Fakulta stavební Úvod Přemístění, deformaci a napjatost
Pružnost a pevnost 13PRPE Přednášk Desk Deska/stěna/skořepina, desk ákladní předpoklad, proměnné a rovnice Petr Kabele České vsoké učení technické v Prae Fakulta stavební Úvod Přemístění, deformaci a napjatost
VÝPOČET PŘETVOŘENÍ PŘÍHRADOVÝCH KONSTRUKCÍ SILOVOU METODOU řešený příklad pro BO004
 VÝPOČET PŘETVOŘENÍ PŘÍHRADOVÝCH KONSTRUKCÍ SILOVOU METODOU řešený příklad pro BO00 Slová metoda využívá prncp vrtuální práce. Zavádí se nový zatěžovací stav vrtuální zatížení. V tomto zatěžovacím stavu
VÝPOČET PŘETVOŘENÍ PŘÍHRADOVÝCH KONSTRUKCÍ SILOVOU METODOU řešený příklad pro BO00 Slová metoda využívá prncp vrtuální práce. Zavádí se nový zatěžovací stav vrtuální zatížení. V tomto zatěžovacím stavu
Rovinná a prostorová napjatost
 Rovinná a prostorová napjatost Vdělme v bodě tělesa elementární hranolek o hranách d, d, d Vnitřní síl ve stěnách hranolku se projeví jako napětí na příslušné ploše a le je roložit do směrů souřadnicových
Rovinná a prostorová napjatost Vdělme v bodě tělesa elementární hranolek o hranách d, d, d Vnitřní síl ve stěnách hranolku se projeví jako napětí na příslušné ploše a le je roložit do směrů souřadnicových
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Geometrie Gradovaný řetězec úloh Téma: Komolý kužel Autor: Kubešová Naděžda Klíčové pojmy:
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Geometrie Gradovaný řetězec úloh Téma: Komolý kužel Autor: Kubešová Naděžda Klíčové pojmy:
Katedra obecné elektrotechniky Fakulta elektrotechniky a informatiky, VŠB - TU Ostrava 4. TROJFÁZOVÉ OBVODY
 Katedra obecné elektrotechnky Fakulta elektrotechnky a noratky, VŠB - T Otrava 4. TROJFÁOVÉ OBVODY 4. Úvod 4. Trojázová outava 4. Spojení ází do hvězdy 4.4 Spojení ází do trojúhelníka 4.5 Výkon v trojázových
Katedra obecné elektrotechnky Fakulta elektrotechnky a noratky, VŠB - T Otrava 4. TROJFÁOVÉ OBVODY 4. Úvod 4. Trojázová outava 4. Spojení ází do hvězdy 4.4 Spojení ází do trojúhelníka 4.5 Výkon v trojázových
Obsah. Příloha (celkový počet stran přílohy 8) Závěrečná zpráva o výsledcích experimentu shodnosti ZZP 2015/1
 Závěrečná zpráva o výledcích expermentu hodnot ZZP 015/1 Obah Úvod a důležté kontakty... Potupy tattcké analýzy expermentu hodnot... 5.1 Numercký potup zjšťování odlehlých hodnot... 5.1.1 Cochranův tet...
Závěrečná zpráva o výledcích expermentu hodnot ZZP 015/1 Obah Úvod a důležté kontakty... Potupy tattcké analýzy expermentu hodnot... 5.1 Numercký potup zjšťování odlehlých hodnot... 5.1.1 Cochranův tet...
VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ
 VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ P. Novák, J. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán výukový software pro
VÝUKOVÝ SOFTWARE PRO ANALÝZU A VIZUALIZACI INTERFERENČNÍCH JEVŮ P. Novák, J. Novák Katedra fyziky, Fakulta stavební, České vysoké učení technické v Praze Abstrakt V práci je popsán výukový software pro
PŘÍKLAD VÝPOČTU RÁMU PODLE ČSN EN
 PŘÍKLAD VÝPOČTU RÁU PODLE ČS E 99-- Jaub Dolejš*), Zdeně Sool**).Zadání avrhněte sloup plnostěnného dvouloubového rámu, jehož roměr jsou patrné obráu. Horní pásnice příčle je po celé délce ajištěna proti
PŘÍKLAD VÝPOČTU RÁU PODLE ČS E 99-- Jaub Dolejš*), Zdeně Sool**).Zadání avrhněte sloup plnostěnného dvouloubového rámu, jehož roměr jsou patrné obráu. Horní pásnice příčle je po celé délce ajištěna proti
Pracovní list č. 3 Charakteristiky variability
 Pracovní lt č. 3 Charaktertky varablty 1. Př zjšťování počtu nezletlých dětí ve třcet vybraných rodnách byly zíkány tyto výledky: 1, 1, 0,, 3, 4,,, 3, 0, 1,,, 4, 3, 3, 0, 1, 1, 1,,, 0,, 1, 1,, 3, 3,. Upořádejte
Pracovní lt č. 3 Charaktertky varablty 1. Př zjšťování počtu nezletlých dětí ve třcet vybraných rodnách byly zíkány tyto výledky: 1, 1, 0,, 3, 4,,, 3, 0, 1,,, 4, 3, 3, 0, 1, 1, 1,,, 0,, 1, 1,, 3, 3,. Upořádejte
Z transformace. Definice. Z transformací komplexní posloupnosti f = { } f n z n, (1)
 Z transformace Definice Z transformací komplexní posloupnosti f = { roumíme funkci F ( definovanou vtahem F ( = n, ( pokud řada vpravo konverguje aspoň v jednom bodě 0 C Náev Z transformace budeme také
Z transformace Definice Z transformací komplexní posloupnosti f = { roumíme funkci F ( definovanou vtahem F ( = n, ( pokud řada vpravo konverguje aspoň v jednom bodě 0 C Náev Z transformace budeme také
Posouzení stability svahu
 Inženýrký manuál č. 8 Aktualizace: 02/2016 Poouzení tability vahu Program: Soubor: Stabilita vahu Demo_manual_08.gt V tomto inženýrkém manuálu je popán výpočet tability vahu, nalezení kritické kruhové
Inženýrký manuál č. 8 Aktualizace: 02/2016 Poouzení tability vahu Program: Soubor: Stabilita vahu Demo_manual_08.gt V tomto inženýrkém manuálu je popán výpočet tability vahu, nalezení kritické kruhové
8. STATISTICKÝ SOUBOR SE DVĚMA ARGUMENTY
 8. STATISTICKÝ SOUBOR SE DVĚMA ARGUMETY Stattcký oubor e dvěma argument Průvodce tudem Vužeme znalotí z předchozí kaptol, která poednávala o tattckém ouboru edním argumentem a rozšíříme e. Předpokládané
8. STATISTICKÝ SOUBOR SE DVĚMA ARGUMETY Stattcký oubor e dvěma argument Průvodce tudem Vužeme znalotí z předchozí kaptol, která poednávala o tattckém ouboru edním argumentem a rozšíříme e. Předpokládané
Přijímací zkouška na MFF UK v Praze
 Přijímací kouška na MFF UK v Prae Studijní program Matematika, bakalářské studium Studijní program Informatika, bakalářské studium 2013, varianta A U každé deseti úloh je nabíeno pět odpovědí: a, b, c,
Přijímací kouška na MFF UK v Prae Studijní program Matematika, bakalářské studium Studijní program Informatika, bakalářské studium 2013, varianta A U každé deseti úloh je nabíeno pět odpovědí: a, b, c,
Centrovaná optická soustava
 Centrovaná optická soustava Dvě lámavé kulové ploch: Pojem centrovaná optická soustava znamená, že splývají optické os dvou či více optických prvků. Základním příkladem takové optické soustav jsou dvě
Centrovaná optická soustava Dvě lámavé kulové ploch: Pojem centrovaná optická soustava znamená, že splývají optické os dvou či více optických prvků. Základním příkladem takové optické soustav jsou dvě
3. V případě dvou na sebe kolmých posunutí o velikostech 3 cm a 4 cm obdržíme výsledné posunutí o velikosti a) 8 cm b) 7 cm c) 6 cm d) 5 cm *
 Fyzika 1 2009 Otázky za 2 body 1. Mezi tavové veličiny patří a) teplo b) teplota * c) práce d) univerzální plynová kontanta 2. Krychle má hranu o délce 2 mm. Jaký je její objem v krychlových metrech? a)
Fyzika 1 2009 Otázky za 2 body 1. Mezi tavové veličiny patří a) teplo b) teplota * c) práce d) univerzální plynová kontanta 2. Krychle má hranu o délce 2 mm. Jaký je její objem v krychlových metrech? a)
í I - 13 - Průchod a rozptyl záření gama ve vrstvách materiálu Prof. Ing. J. Šeda, DrSc. KDAIZ - PJPI
 - 13 - í Průchod a rozptyl záření gama ve vrstvách materálu Prof. ng. J. Šeda, DrSc. KDAZ - PJP Na našem pracovšt byl vypracován program umožňující modelovat průchod záření gama metodou Monte Carlo, homogenním
- 13 - í Průchod a rozptyl záření gama ve vrstvách materálu Prof. ng. J. Šeda, DrSc. KDAZ - PJP Na našem pracovšt byl vypracován program umožňující modelovat průchod záření gama metodou Monte Carlo, homogenním
Propočty přechodu Venuše 8. června 2004
 Propočty přechodu Venuše 8. června 2004 V tomto dokumentu předkládáme podmínky přechodu Venuše pře luneční kotouč 8. června roku 2004. Naše výpočty jme založili na planetárních teoriích VSOP87 vytvořených
Propočty přechodu Venuše 8. června 2004 V tomto dokumentu předkládáme podmínky přechodu Venuše pře luneční kotouč 8. června roku 2004. Naše výpočty jme založili na planetárních teoriích VSOP87 vytvořených
( ) ( ) ( ) Exponenciální rovnice. 17.3. Řeš v R rovnici: 3 + 9 + 27 = ŘEŠENÍ: Postup z předešlého výpočtu doplníme využitím dalšího vztahu: ( ) t s t
 7. EXPONENCIÁLNÍ ROVNICE 7.. Řeš v R rovnice: ) 5 b) + c) 7 0 d) ( ) 0,5 ) 5 7 5 7 K { } c) 7 0 K d) ( ) b) + 0 + 0 K ( ) 5 0 5, 7 K { 5;7} Strtegie: potřebujeme zíkt tkový tvr rovnice, kd je n obou trnách
7. EXPONENCIÁLNÍ ROVNICE 7.. Řeš v R rovnice: ) 5 b) + c) 7 0 d) ( ) 0,5 ) 5 7 5 7 K { } c) 7 0 K d) ( ) b) + 0 + 0 K ( ) 5 0 5, 7 K { 5;7} Strtegie: potřebujeme zíkt tkový tvr rovnice, kd je n obou trnách
1.1 Steinerovy věty. lineární momenty a momenty kvadratické. Zajímat nás budou nyní osové kvadratické. v ohybu. Jejich definice je
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ PRUŽNOST A PEVNOST I Řešené příklad Výpočet osových kvadratických momentů Pátek, 9. května 8 Jan Tihlařík 1 Osové kvadratické moment průřeů
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ PRUŽNOST A PEVNOST I Řešené příklad Výpočet osových kvadratických momentů Pátek, 9. května 8 Jan Tihlařík 1 Osové kvadratické moment průřeů
Korelační energie. Celkovou elektronovou energii molekuly lze experimentálně určit ze vztahu. E vib. = E at. = 39,856, E d
 Korelační energe Referenční stavy Energ molekul a atomů lze vyjádřt vzhledem k různým referenčním stavům. V kvantové mechance za referenční stav s nulovou energí bereme stav odpovídající nenteragujícím
Korelační energe Referenční stavy Energ molekul a atomů lze vyjádřt vzhledem k různým referenčním stavům. V kvantové mechance za referenční stav s nulovou energí bereme stav odpovídající nenteragujícím
teorie elektronických obvodů Jiří Petržela syntéza a návrh elektronických obvodů
 Jří Petržela yntéza a návrh eletroncých obvodů vtupní údaje pro yntézu obvodu yntéza a návrh eletroncých obvodů vlatnot obvodu obvodové funce parametry obvodu toleranční pole (mtočtové charaterty fltru)
Jří Petržela yntéza a návrh eletroncých obvodů vtupní údaje pro yntézu obvodu yntéza a návrh eletroncých obvodů vlatnot obvodu obvodové funce parametry obvodu toleranční pole (mtočtové charaterty fltru)
1.6 Singulární kvadriky
 22 KAPITOLA 1. KVADRIKY JAKO PLOCHY 2. STUPNĚ neboť B = C =. Z rovnice (1.34) plne, že přímka, procháející singulárním bodem kvadrik má s kvadrikou společný poue tento singulární bod (je-li A ) nebo celá
22 KAPITOLA 1. KVADRIKY JAKO PLOCHY 2. STUPNĚ neboť B = C =. Z rovnice (1.34) plne, že přímka, procháející singulárním bodem kvadrik má s kvadrikou společný poue tento singulární bod (je-li A ) nebo celá
Sylabus 18. Stabilita svahu
 Sylabus 18 Stablta svahu Stablta svahu Smykové plochy rovnná v hrubozrnných zemnách ev. u vrstevnatého ukloněného podloží válcová v jemnozrnných homogenních zemnách obecná nehomogenní podloží vč. stavebních
Sylabus 18 Stablta svahu Stablta svahu Smykové plochy rovnná v hrubozrnných zemnách ev. u vrstevnatého ukloněného podloží válcová v jemnozrnných homogenních zemnách obecná nehomogenní podloží vč. stavebních
i=1..k p x 2 p 2 s = y 2 p x 1 p 1 s = y 1 p 2
 i I i II... i F i..k Binární mě, ideální kaalina, ideální lyn x y y 2 Křivka bodů varu: Křivka roných bodů: Pákové ravidlo: x y y 2 n I n x I z II II z x Henryho zákon: 28-2 U měi hexan() + hetan(2) ři
i I i II... i F i..k Binární mě, ideální kaalina, ideální lyn x y y 2 Křivka bodů varu: Křivka roných bodů: Pákové ravidlo: x y y 2 n I n x I z II II z x Henryho zákon: 28-2 U měi hexan() + hetan(2) ři
1.1.14 Rovnice rovnoměrně zrychleného pohybu
 ..4 Rovnice rovnoměrně zrychleného pohybu Předpoklady: 3 Pedagogická poznámka: Stejně jako u předchozí hodiny je i v této hodině potřeba potupovat tak, aby tudenti měli minimálně minut na řešení příkladů
..4 Rovnice rovnoměrně zrychleného pohybu Předpoklady: 3 Pedagogická poznámka: Stejně jako u předchozí hodiny je i v této hodině potřeba potupovat tak, aby tudenti měli minimálně minut na řešení příkladů
3.2.5 Odraz, lom a ohyb vlnění
 3..5 Odraz, lom a ohyb vlnění Předpoklady: 304 Odraz a lom vlnění na rozhranní dvou prostředí s různou rychlostí šíření http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=16.0 Rovinná vlna dopadá šikmo
3..5 Odraz, lom a ohyb vlnění Předpoklady: 304 Odraz a lom vlnění na rozhranní dvou prostředí s různou rychlostí šíření http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=16.0 Rovinná vlna dopadá šikmo
SOUSTAVY LINEÁRNÍCH ALGEBRAICKÝCH ROVNIC
 SOUSTAVY LINEÁRNÍCH ALGEBRAICKÝCH ROVNIC Pojm: Algebraická rovnice... rovnice obsahující pouze celé nezáporné mocnin neznámé, tj. a n n + a n 1 n 1 +... + a 2 2 + a 1 + a 0 = 0, kde n je přirozené číslo.
SOUSTAVY LINEÁRNÍCH ALGEBRAICKÝCH ROVNIC Pojm: Algebraická rovnice... rovnice obsahující pouze celé nezáporné mocnin neznámé, tj. a n n + a n 1 n 1 +... + a 2 2 + a 1 + a 0 = 0, kde n je přirozené číslo.
dat měření do vnitřní paměti přístroje (k polohovému a Souřadnicový systém: S-JTSK, výškový systém: Bpv
 Určení vodorovné a o b e c n é r o v n Úkolem je vpočítat pro aměřený rovnatý terén:. vodorovnou rovnu tak, ab celkový objem emních prací bl stejný násp = výkop, 2. najít obecnou rovnc rovn, která dobře
Určení vodorovné a o b e c n é r o v n Úkolem je vpočítat pro aměřený rovnatý terén:. vodorovnou rovnu tak, ab celkový objem emních prací bl stejný násp = výkop, 2. najít obecnou rovnc rovn, která dobře
TECHNICKÁ UNIVERZITA V LIBERCI Katedra fyziky, Studentská 2, Liberec
 TECHNICKÁ NIVERZITA V LIBERCI Katedrzik, Studentká, 46 7 Liberec POŽADAVKY PRO PŘIJÍMACÍ ZKOŠKY Z FYZIKY Akademický rok: 03/04 Útav zdravotnických tudií Studijní obor: Biomedicínká technika Tématické okruh
TECHNICKÁ NIVERZITA V LIBERCI Katedrzik, Studentká, 46 7 Liberec POŽADAVKY PRO PŘIJÍMACÍ ZKOŠKY Z FYZIKY Akademický rok: 03/04 Útav zdravotnických tudií Studijní obor: Biomedicínká technika Tématické okruh
4. Práce, výkon, energie
 4. Práce, výkon, energie Mechanická práce - konání mechanické práce z fyzikálního hledika je podmíněno vzájemným ilovým půobením těle, která e přitom vzhledem ke zvolené vztažné outavě přemíťují. Vztahy
4. Práce, výkon, energie Mechanická práce - konání mechanické práce z fyzikálního hledika je podmíněno vzájemným ilovým půobením těle, která e přitom vzhledem ke zvolené vztažné outavě přemíťují. Vztahy
Měření optického výkonu pro optický svazek u bezvláknového optického pojítka
 Ročník 11 Číslo III Měření optického výkonu pro optický svaek u bevláknového optického pojítka J. Látal 1, T. David 1, J. Vitásek 1, P. Koudelka 1 1 Katedra telekomunikační techniky, FEI, VŠB Technická
Ročník 11 Číslo III Měření optického výkonu pro optický svaek u bevláknového optického pojítka J. Látal 1, T. David 1, J. Vitásek 1, P. Koudelka 1 1 Katedra telekomunikační techniky, FEI, VŠB Technická
Univerzita Tomáše Bati ve Zlíně
 Univerzita Tomáše Bati ve líně LABORATORNÍ CVIČENÍ YIKY II Název úloh: Měření ohniskové vzdálenosti čočk Jméno: Petr Luzar Skupina: IT II/ Datum měření:.listopadu 007 Obor: Informační technologie Hodnocení:
Univerzita Tomáše Bati ve líně LABORATORNÍ CVIČENÍ YIKY II Název úloh: Měření ohniskové vzdálenosti čočk Jméno: Petr Luzar Skupina: IT II/ Datum měření:.listopadu 007 Obor: Informační technologie Hodnocení:
Výpočet tenkostěnných nosníků. Magdaléna Doleželová
 Výpočet tenkotěnných noníků agdaléna Doleželová Výpočet tenkotěnných noníků. Úvod. Deplanace průřeu. Normálové namáhání V. Tečná napětí V. Deformace V. Příklad V. Přehled použité literatur . Úvod Dělení
Výpočet tenkotěnných noníků agdaléna Doleželová Výpočet tenkotěnných noníků. Úvod. Deplanace průřeu. Normálové namáhání V. Tečná napětí V. Deformace V. Příklad V. Přehled použité literatur . Úvod Dělení
Návody na výpočty směrových a sklonových poměrů dle zadání do cvičení
 Návody na výpočty měrových a klonových poměrů dle zadání do cvičení Kombinované tudium BO01, čát Dopravní tavby Ad 1) Návrh obou měrových oblouků bez přechodnic a) Změřte tředové úhly pomocí tangenty úhlu
Návody na výpočty měrových a klonových poměrů dle zadání do cvičení Kombinované tudium BO01, čát Dopravní tavby Ad 1) Návrh obou měrových oblouků bez přechodnic a) Změřte tředové úhly pomocí tangenty úhlu
optických skenerů Vysoké učení technické v Brně Fakulta stavební Studentská vědecká a odborná činnost Akademický rok 2011/2012
 Vsoké učení techncké v Brně Fakulta stavební Studentská vědecká a odborná čnnost kademcký rok 0/0 Teoretcké základ jednozrcadlových a dvou-zrcadlových optckých skenerů Jméno a příjmení studenta ročník
Vsoké učení techncké v Brně Fakulta stavební Studentská vědecká a odborná čnnost kademcký rok 0/0 Teoretcké základ jednozrcadlových a dvou-zrcadlových optckých skenerů Jméno a příjmení studenta ročník
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ ANALÝZA PROFILU POVRCHŮ POMOCÍ INTERFEROMETRIE NÍZKÉ KOHERENCE
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV FYZIKÁLNÍHO INŽENÝRSTVÍ FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF PHYSICAL ENGINEERING ANALÝZA PROFILU
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV FYZIKÁLNÍHO INŽENÝRSTVÍ FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF PHYSICAL ENGINEERING ANALÝZA PROFILU
1 4( 1) Co je řešením rovnice 2y 1 = 3? Co je řešením, pokud přidáme rovnici x + y = 3? Napište
 Řešená cvičení lineární algebr I Karel Král 10. října 2017 Tento tet není určen k šíření. Všechn chb v tomto tetu jsou samořejmě áměrné. Reportujte je prosím na adresu kralka@iuuk.mff.cuni... Obsah 1 Cviceni
Řešená cvičení lineární algebr I Karel Král 10. října 2017 Tento tet není určen k šíření. Všechn chb v tomto tetu jsou samořejmě áměrné. Reportujte je prosím na adresu kralka@iuuk.mff.cuni... Obsah 1 Cviceni
1 Elektromagnetická vlna
 1 lektromagnetická vlna 1.1 lektromagnetické vlny V nestacionárním případě, ve kterém veličiny elektromagnetického pole mění v ávislosti na čase svoji velikost a případně i směr, eistuje vždy současně
1 lektromagnetická vlna 1.1 lektromagnetické vlny V nestacionárním případě, ve kterém veličiny elektromagnetického pole mění v ávislosti na čase svoji velikost a případně i směr, eistuje vždy současně
4. cvičení z Matematické analýzy 2
 4. cvičení z Matematické analýzy 2 22. - 26. října 208 4. Po funkci fx, y, z xy 2 + z 3 xyz učete v bodě a 0,, 2 deivaci ve měu u, kteý je učen tím, že víá kladnými měy ouřadných o potupně úhly 60, 45
4. cvičení z Matematické analýzy 2 22. - 26. října 208 4. Po funkci fx, y, z xy 2 + z 3 xyz učete v bodě a 0,, 2 deivaci ve měu u, kteý je učen tím, že víá kladnými měy ouřadných o potupně úhly 60, 45
9. Měření kinetiky dohasínání fluorescence ve frekvenční doméně
 9. Měření knetky dohasínání fluorescence ve frekvenční doméně Gavolův experment (194) zdroj vzorek synchronní otáčení fázový posun detektor Měření dob žvota lumnscence Frekvenční doména - exctace harmoncky
9. Měření knetky dohasínání fluorescence ve frekvenční doméně Gavolův experment (194) zdroj vzorek synchronní otáčení fázový posun detektor Měření dob žvota lumnscence Frekvenční doména - exctace harmoncky
7. SVÍTIDLA Svítidla Světlomety návěstidla ozařovače 7.1 Světelně činné a konstrukční části svítidel Stínidla úhlem clonění 1 2
 7. SVÍTIDL Světelné droje většinou samy o sobě nevyhovují pro osvětlovací účely, neboť obvykle mají nevhodné rodělení světelného toku, příliš vysoký jas a ani nejsou odolné proti růným vlivům prostředí.
7. SVÍTIDL Světelné droje většinou samy o sobě nevyhovují pro osvětlovací účely, neboť obvykle mají nevhodné rodělení světelného toku, příliš vysoký jas a ani nejsou odolné proti růným vlivům prostředí.
Analýza diskrétních regulačních obvodů
 Čílicové říení Analýa ECHNICÁ NIVERIA V IBERCI Hálkova 6 46 7 iberec C akulta mechatroniky a meioborových inženýrkých tudií Čílicové říení Analýa dikrétních regulačních obvodů Studijní materiály oc Ing
Čílicové říení Analýa ECHNICÁ NIVERIA V IBERCI Hálkova 6 46 7 iberec C akulta mechatroniky a meioborových inženýrkých tudií Čílicové říení Analýa dikrétních regulačních obvodů Studijní materiály oc Ing
Interval spolehlivosti pro podíl
 Iterval polehlivoti pro podíl http://www.caueweb.org/repoitory/tatjava/cofitapplet.html Náhodý výběr Zkoumaý proce chápeme jako áhodou veličiu určitým ám eámým roděleím a měřeá data jako realiace této
Iterval polehlivoti pro podíl http://www.caueweb.org/repoitory/tatjava/cofitapplet.html Náhodý výběr Zkoumaý proce chápeme jako áhodou veličiu určitým ám eámým roděleím a měřeá data jako realiace této
Návrh na pořádání letní časti Okresního kola hry Plamen v ročníku 2014/2015
 Návrh na pořádání letní čati Okreního kola hry Plamen v ročníku 0/05 Zpracovalo SDH Staré Heřminovy Anotace Zde jou rozebrány možnoti pořádání outěže letní čáti Okreního kola hry Plamen v ročníku 0/05
Návrh na pořádání letní čati Okreního kola hry Plamen v ročníku 0/05 Zpracovalo SDH Staré Heřminovy Anotace Zde jou rozebrány možnoti pořádání outěže letní čáti Okreního kola hry Plamen v ročníku 0/05
přírodovědných a technických oborů. Scientia in educatione, roč. 5 (2014), č. 1, s
 [15] Nováková, A., Chytrý, V., Říčan, J.: Vědecké myšlení a metakognitivní monitorování tudentů učiteltví pro 1. tupeň základní školy. Scientia in educatione, roč. 9 (2018), č. 1,. 66 80. [16] Bělecký,
[15] Nováková, A., Chytrý, V., Říčan, J.: Vědecké myšlení a metakognitivní monitorování tudentů učiteltví pro 1. tupeň základní školy. Scientia in educatione, roč. 9 (2018), č. 1,. 66 80. [16] Bělecký,
Fyzika I mechanika. Rozdělení fyziky podle jednotlivých oborů, tj. podle jevů, které zkoumá:
 Fika I mechanika Úvod Základní fikální pojm Fika (fsis je řeck příroda) bla původně vědou o přírodě, ted souhrnem všech přírodních věd, které se s postupem dějin osamostatnil. Fika si však achovává ústřední
Fika I mechanika Úvod Základní fikální pojm Fika (fsis je řeck příroda) bla původně vědou o přírodě, ted souhrnem všech přírodních věd, které se s postupem dějin osamostatnil. Fika si však achovává ústřední
BENCHMARKOVÝ MODEL CHLADICÍHO ZAŘÍZENÍ V SUPERMARKETECH SUPERMARKET REFRIGERATION BENCHMARK MODEL
 BENCHMARKOVÝ MODEL CHLADICÍHO ZAŘÍZENÍ V SUPERMARKETECH D. Honc, F. Dušek Katedra řízení proceů, Fakulta elektrotechniky a informatiky, Univerzita Pardubice Abtrakt Řízení rozáhlých ytémů je prakticky
BENCHMARKOVÝ MODEL CHLADICÍHO ZAŘÍZENÍ V SUPERMARKETECH D. Honc, F. Dušek Katedra řízení proceů, Fakulta elektrotechniky a informatiky, Univerzita Pardubice Abtrakt Řízení rozáhlých ytémů je prakticky
Řešení úloh 1. kola 51. ročníku fyzikální olympiády. Kategorie D = s v 2
 Řešení úloh 1. kola 51. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů 1.a) Dobaprvníjízdynaprvníčtvrtinětratije 1 4 1 4 48 t 1 = = h= 1 v 1 60 60 h=1min anazbývajícíčátitrati t = 4 v = 4
Řešení úloh 1. kola 51. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů 1.a) Dobaprvníjízdynaprvníčtvrtinětratije 1 4 1 4 48 t 1 = = h= 1 v 1 60 60 h=1min anazbývajícíčátitrati t = 4 v = 4
3 Huygensův-Fresnelův princip a odvození difrakčních integrálů
 33 3 Huygenův-Frenelův princip a odvození difrakčních integrálů 3.1 Huygenův princip 3.2 Huygenův-Frenelův princip 3.3 Příklad. Nerušené šíření rovinné vlny 3.4 Frenelovy zóny 3.5 Zonální mřížky 3.6 Odvození
33 3 Huygenův-Frenelův princip a odvození difrakčních integrálů 3.1 Huygenův princip 3.2 Huygenův-Frenelův princip 3.3 Příklad. Nerušené šíření rovinné vlny 3.4 Frenelovy zóny 3.5 Zonální mřížky 3.6 Odvození
Příklad 1 Ověření šířky trhlin železobetonového nosníku
 Příklad 1 Ověření šířky trhlin železobetonového noníku Uvažujte železobetonový protě podepřený noník (Obr. 1) o průřezu b = 00 mm h = 600 mm o rozpětí l = 60 m. Noník je oučátí kontrukce objektu pro kladování
Příklad 1 Ověření šířky trhlin železobetonového noníku Uvažujte železobetonový protě podepřený noník (Obr. 1) o průřezu b = 00 mm h = 600 mm o rozpětí l = 60 m. Noník je oučátí kontrukce objektu pro kladování
6.2.1 Zobrazení komplexních čísel v Gaussově rovině
 6.. Zobraení komplexních čísel v Gaussově rovině Předpoklad: 605 Pedagogická ponámka: Stihnout obsah hodin je poměrně náročné. Při dostatku času je lepší dojít poue k příkladu 7 a btek hodin spojit s úvodem
6.. Zobraení komplexních čísel v Gaussově rovině Předpoklad: 605 Pedagogická ponámka: Stihnout obsah hodin je poměrně náročné. Při dostatku času je lepší dojít poue k příkladu 7 a btek hodin spojit s úvodem
Žáci mají k dispozici pracovní list. Formou kolektivní diskuze a výkladu si osvojí způsoby algebraické minimalizace a využití Booleovy algebry
 Číslo projektu Číslo materiálu Náev školy Autor Náev Téma hodiny Předmět Ročník /y/ CZ..07/.5.00/4.04 VY INOVACE_8_ČT_.08_ algebraická minimaliace Střední odborná škola a Střední odborné učiliště, Hustopeče,
Číslo projektu Číslo materiálu Náev školy Autor Náev Téma hodiny Předmět Ročník /y/ CZ..07/.5.00/4.04 VY INOVACE_8_ČT_.08_ algebraická minimaliace Střední odborná škola a Střední odborné učiliště, Hustopeče,
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA MORAVSKÁ OSTRAVA, KRATOCHVÍLOVA 7 Číslo úlohy: 9
 STŘEDNÍ PŮMYSLOVÁ ŠKOL MOVSKÁ OSTV, KTOCHVÍLOV 7 Čílo úlohy: 9 Jméno a příjmení: ZPÁV O MĚŘENÍ Martin Dočkal Třída: EP3 Náev úlohy: egulační vlatnoti reotatu Skupina:. Schéma apojení: Měřeno dne: 4.2.2004
STŘEDNÍ PŮMYSLOVÁ ŠKOL MOVSKÁ OSTV, KTOCHVÍLOV 7 Čílo úlohy: 9 Jméno a příjmení: ZPÁV O MĚŘENÍ Martin Dočkal Třída: EP3 Náev úlohy: egulační vlatnoti reotatu Skupina:. Schéma apojení: Měřeno dne: 4.2.2004
Odraz a lom rovinné monochromatické vlny na rovinném rozhraní dvou izotropních prostředí
 Odraz a lom rovnné monochromatcké vlny na rovnném rozhraní dvou zotropních prostředí Doplňující předpoklady: prostředí č.1, ze kterého vlna dopadá na rozhraní neabsorbuje (má r r reálný ndex lomu), obě
Odraz a lom rovnné monochromatcké vlny na rovnném rozhraní dvou zotropních prostředí Doplňující předpoklady: prostředí č.1, ze kterého vlna dopadá na rozhraní neabsorbuje (má r r reálný ndex lomu), obě
Interferenční mikroskopie
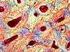 Interferenční mikroskopie J. Kuběna ÚFKL Přírodovědecká fakulta Masarykovy University kubena@physics.muni.c Učební pomůcka ke studiu optiky, verse 6 Úvod Následující série obráků je aměřena na objasnění
Interferenční mikroskopie J. Kuběna ÚFKL Přírodovědecká fakulta Masarykovy University kubena@physics.muni.c Učební pomůcka ke studiu optiky, verse 6 Úvod Následující série obráků je aměřena na objasnění
5 SLOUPY. Obr. 5.1 Průřezy ocelových sloupů. PŘÍKLAD V.1 Ocelový sloup
 SLOUPY. Obecné ponámk Sloup jsou hlavními svislými nosnými element a přenášejí atížení vodorovných konstrukčních prvků do ákladové konstrukce. Modulové uspořádání načně ávisí na unkci objektu a jeho dispoičním
SLOUPY. Obecné ponámk Sloup jsou hlavními svislými nosnými element a přenášejí atížení vodorovných konstrukčních prvků do ákladové konstrukce. Modulové uspořádání načně ávisí na unkci objektu a jeho dispoičním
Sdílení tepla. Úvod - Přehled. Sdílení tepla mezi termodynamickou soustavou a okolím je podmíněno rozdílností teplot soustavy T.
 7.4.0 Úvod - Přehled Sdílení tepla Sdílení tepla mez termodynamckou soustavou a okolím je podmíněno rozdílností teplot soustavy T s a okolí T o. Teplo mez soustavou a okolím se sdílí třem základním způsoby:
7.4.0 Úvod - Přehled Sdílení tepla Sdílení tepla mez termodynamckou soustavou a okolím je podmíněno rozdílností teplot soustavy T s a okolí T o. Teplo mez soustavou a okolím se sdílí třem základním způsoby:
dat měření do vnitřní paměti přístroje (k polohovému a
 U R Č E N Í V O D O R O V N É A O B E C N É R O V I N Y místopsný pops: park v ulc Nkol Tesl Poslední úprava: 25.9.208 7:23 Úkolem je vpočítat pro aměřený rovnatý terén:. vodorovnou rovnu tak, ab celkový
U R Č E N Í V O D O R O V N É A O B E C N É R O V I N Y místopsný pops: park v ulc Nkol Tesl Poslední úprava: 25.9.208 7:23 Úkolem je vpočítat pro aměřený rovnatý terén:. vodorovnou rovnu tak, ab celkový
s = Momentová charakteristika asynchronního motoru s kotvou nakrátko
 Aynchronní třífázové motory / Vznik točivého pole a základní vlatnoti motoru Aynchronní indukční motory jou nejjednoduššími a provozně nejpolehlivějšími motory. otor e kládá ze tatoru a rotoru. Stator
Aynchronní třífázové motory / Vznik točivého pole a základní vlatnoti motoru Aynchronní indukční motory jou nejjednoduššími a provozně nejpolehlivějšími motory. otor e kládá ze tatoru a rotoru. Stator
Simulátor ochran a protihavarijních automatik (RTDS) - modely měřících a výkonových transformátorů
 Simulátor ochran a protihavarijních automatik (RTDS) - modely měřících a výkonových tranformátorů Ing. Petr Neuman, CSc., ČEPS, a.., Praha, Čeká republika E-mail: neuman@cep.cz Anotace Autor přípěvku vytupuje
Simulátor ochran a protihavarijních automatik (RTDS) - modely měřících a výkonových tranformátorů Ing. Petr Neuman, CSc., ČEPS, a.., Praha, Čeká republika E-mail: neuman@cep.cz Anotace Autor přípěvku vytupuje
Optické měřicí 3D metody
 Univerzita Palackého v Olomouci Přírodovědecká fakulta Optické měřicí 3D metod Michal Pochmon Olomouc 212 Oponent: RNDr. Tomáš Rössler Ph.D. Publikace bla připravena v rámci projektu Investice do rozvoje
Univerzita Palackého v Olomouci Přírodovědecká fakulta Optické měřicí 3D metod Michal Pochmon Olomouc 212 Oponent: RNDr. Tomáš Rössler Ph.D. Publikace bla připravena v rámci projektu Investice do rozvoje
K rozpoznání růstu či klesání dané funkce určitém směru nám pomůže gradient, tj. vektor., ln(1 x2 + y 2 [ = y
 VKM/IM 017/018 Určete da funkce fx y) ln1 x +y ) v bodě A 1 1 ve směru vektorů u 1 1 0 u 0 1 u 3 1 1 a u 4 1 roste či klesá a určete rychlost měny. Řešení: Funkce fx y) je definovány pro všechny body R
VKM/IM 017/018 Určete da funkce fx y) ln1 x +y ) v bodě A 1 1 ve směru vektorů u 1 1 0 u 0 1 u 3 1 1 a u 4 1 roste či klesá a určete rychlost měny. Řešení: Funkce fx y) je definovány pro všechny body R
teorie elektronických obvodů Jiří Petržela syntéza elektronických obvodů
 Jiří Petržela příklad nalezněte dvě různé realizace admitanční funkce zadané formou racionální lomené funkce Y () () ( ) ( ) : první krok rozkladu do řetězového zlomku () 9 7 9 výledný rozklad ( ) 9 9
Jiří Petržela příklad nalezněte dvě různé realizace admitanční funkce zadané formou racionální lomené funkce Y () () ( ) ( ) : první krok rozkladu do řetězového zlomku () 9 7 9 výledný rozklad ( ) 9 9
Vliv komy na přesnost měření optických přístrojů. Antonín Mikš Katedra fyziky, FSv ČVUT, Praha
 Vliv komy na přesnost měření optických přístrojů Antonín Mikš Katedra fyziky, FSv ČVUT, Praha V práci je vyšetřován vliv meridionální komy na přesnost měření optickými přístroji a to na základě difrakční
Vliv komy na přesnost měření optických přístrojů Antonín Mikš Katedra fyziky, FSv ČVUT, Praha V práci je vyšetřován vliv meridionální komy na přesnost měření optickými přístroji a to na základě difrakční
( LEVEL 3 Laplaceova transformace jako nástroj řešení lineárních diferenciálních rovnic. )
 ( LEVEL 3 Laplaceova tranformace jako nátroj řešení lineárních diferenciálních rovnic. ) Podívejme e tentokrát na dynamiku pracovní edačky řidiče prizmatem matematiky aneb trocha teorie jitě nikomu neuškodí...
( LEVEL 3 Laplaceova tranformace jako nátroj řešení lineárních diferenciálních rovnic. ) Podívejme e tentokrát na dynamiku pracovní edačky řidiče prizmatem matematiky aneb trocha teorie jitě nikomu neuškodí...
EXPERIMENTÁLNÍ METODA URČENÍ ZÁKLADNÍCH PARAMETRŮ OBJEKTIVU ANALAKTICKÉHO DALEKOHLEDU. A.Mikš 1, V.Obr 2
 EXPERIMENTÁLNÍ METODA URČENÍ ZÁKLADNÍCH PARAMETRŮ OBJEKTIVU ANALAKTICKÉHO DALEKOHLEDU A.Mikš, V.Obr Katedra fyziky, Fakulta stavební ČVUT, Praha Katedra vyšší geodézie, Fakulta stavební ČVUT, Praha Abstrakt:
EXPERIMENTÁLNÍ METODA URČENÍ ZÁKLADNÍCH PARAMETRŮ OBJEKTIVU ANALAKTICKÉHO DALEKOHLEDU A.Mikš, V.Obr Katedra fyziky, Fakulta stavební ČVUT, Praha Katedra vyšší geodézie, Fakulta stavební ČVUT, Praha Abstrakt:
Rovnice rovnoměrně zrychleného pohybu
 ..8 Rovnice rovnoměrně zrychleného pohybu Předpoklady: 7 Pedagogická poznámka: Stejně jako u předchozí hodiny je i v této hodině potřeba potupovat tak, aby tudenti měli minimálně píše minut na řešení příkladů
..8 Rovnice rovnoměrně zrychleného pohybu Předpoklady: 7 Pedagogická poznámka: Stejně jako u předchozí hodiny je i v této hodině potřeba potupovat tak, aby tudenti měli minimálně píše minut na řešení příkladů
KERAMICKÉ STROPNÍ PANELY HELUZ PNG 72 3535-1. část
 PNG 72 3535-1. čát POUŽITÍ Stropy ze tropních keramických panelů HELUZ jou vhodné pro použití v občankých, průmylových a zemědělkých tavbách. Panely jou vhodné pro uché nebo běžné protředí podle ČSN 73
PNG 72 3535-1. čát POUŽITÍ Stropy ze tropních keramických panelů HELUZ jou vhodné pro použití v občankých, průmylových a zemědělkých tavbách. Panely jou vhodné pro uché nebo běžné protředí podle ČSN 73
Zadání. Přílohy. Požadavky. Úloha č. 3. Výpočet denního osvětlení ; Daniljukův diagram D=DS=100%
 Ing. Martna Zapletalová, Ph.., K 14, A 41 SF 1 Úloha č. 3 Výpočet denního ovětlení ; anljukův dagra Zadání Pouďte zadanou ítnot - kancelář z hledka denního ovětlení (STANOVTE CELKOVÝ ČINITEL ENNÍ OSVĚTLENOSTI)
Ing. Martna Zapletalová, Ph.., K 14, A 41 SF 1 Úloha č. 3 Výpočet denního ovětlení ; anljukův dagra Zadání Pouďte zadanou ítnot - kancelář z hledka denního ovětlení (STANOVTE CELKOVÝ ČINITEL ENNÍ OSVĚTLENOSTI)
Přednáška 08. Obecná trojosá napjatost. Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův zákon Příklad zemní tlak v klidu
 Přednáška 08 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův ákon Příklad emní tlak v klidu Copyright (c) 2011 Vít Šmilauer Cech Technical University in
Přednáška 08 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův ákon Příklad emní tlak v klidu Copyright (c) 2011 Vít Šmilauer Cech Technical University in
1141 HYA (Hydraulika)
 ČVUT v Praze, fakulta tavební katedra hydrauliky a hydrologie (K141) Přednáškové lidy předmětu 1141 HYA (Hydraulika) verze: 05/011 K141 FSv ČVUT Tato webová tránka nabízí k nahlédnutí/tažení řadu pdf ouborů
ČVUT v Praze, fakulta tavební katedra hydrauliky a hydrologie (K141) Přednáškové lidy předmětu 1141 HYA (Hydraulika) verze: 05/011 K141 FSv ČVUT Tato webová tránka nabízí k nahlédnutí/tažení řadu pdf ouborů
