Předmět studia klasické fyziky

Předmět studia klasické fyziky

Přemě sui klsiké fik mehnik, emonmik, elekonmik, opik klsiká fik eoeiká fik epeimenální fik eoie elii sisiká fik knoá fik moení fik Přemě sui klsiké fik Fik oeně koumá sukuu hmo její ákon, hoání přío se

Základy vektorového počtu

Zákl vekoového poču késká sousv souřná pvoúhlá pvoočivá veko je popsán svými řemi půmě o souřnýh os oogonálními veko áe veko i áe: veko: i j k j velikos vekou: k i k α γ β j Polohový veko: osα os i osβ

INTEGRÁLNÍ POČET. Primitivní funkce. Neurčitý integrál. Pravidla a vzorce pro integrování

INTEGRÁLNÍ POČET Primiivní unkce. Neurčiý inegrál Deinice. Jesliže pro unkce F einovné n oevřeném inervlu J plí F pro kžé J, říkáme, že F je primiivní unkcí k unkci n J. Vě. Je-li spojiá n J, pk k ní eisuje

VÝPOČET PŘETVOŘENÍ STATICKY URIČTÝCH KONSTRUKCÍCH KOMPLEXNÍ PŘÍKLAD

Miloš Hüne SMR neilové účink vičení 05 Zání VÝPOČET PŘETVOŘENÍ STATICKY URIČTÝCH KONSTRUKCÍCH KOMPLEXNÍ PŘÍKLAD Příkl č. Uvžje konki z O., vpočíeje vooovný pon v oě (znčený eploní ozžnoi vžje α 0 6 K -.

asi 1,5 hodiny seznámit studenty se základními zákonitostmi křivočarého pohybu bodu Dynamika I, 3. přednáška Obsah přednášky : Doba studia :

Dmk I, 3. předášk Obsh předášk : křočý pohb bodu, smě kemckých elč - chlos chleí, přoeý, késký, cldcký sfécký souřdý ssém, pohb bodu po kužc Dob sud : s 1,5 hod Cíl předášk : seám sude se ákldím ákoosm

Křivočarý pohyb bodu.

Křočý pohb bodu. Obsh předášk : křočý pohb bodu, smě kemckých elč - chlos chleí, přoeý, késký, cldcký sfécký souřdý ssém, pohb bodu po kužc Dob sud : s 1,5 hod Cíl předášk : seám sude se ákldím ákoosm

= = Řešení: Pro příspěvek k magnetické indukci v bodě A platí podle Biot-Savartova zákona. d 1

Mgntiké pol 8 Vypočtět mgntikou inuki B kuhové smyčky o poloměu 5 m n jjí os symti v válnosti 1 m o oviny smyčky, jstliž smyčkou potéká lktiký pou 1 A Řšní: Po příspěvk k mgntiké inuki v boě A pltí pol

Schéma podloží pod základem. Parametry podloží: c ef c d. třída tloušťka ɣ E def ν β ϕef

Příkla avrhněte záklaovou esku ze ŽB po sloupy o rozměru 0,6 x 0,6 m a stanovte max. provozní napětí záklaové půy. Zatížení a geometrie le orázku. Tloušťka esky hs = 0,4 m. Zatížení: rohové sloupy 1 =

( ) 1.7.8 Statika I. Předpoklady: 1707

.7.8 Sik I Přeokly: 707 Peoická oznámk: Hoinu rozěluji n vě čási. V rvní čási (5 minu) očíáme rvní čyři říkly, ve ruhé (0 minu) zývjící ři. Př. : N koncích yče o hmonosi 0 k élce m jsou zvěšen závží o

Elektromagnetické pole

Elekomagneické pole Zákon elekomagneické inukce pohybujeme-li uzařeným oičem honým způsobem magneickém poli, zniká e oiči elekický pou nachází-li se uzařený oič časoě poměnném magneickém poli, zniká e

DYNAMIKA časový účinek síly Impuls síly. 2. dráhový účinek síly mechanická práce W (skalární veličina)

DYNAMIKA 2 Působením síly na čásici se obecně mění její pohybový sav. Síla působí vždy v učiém časovém inevalu a záoveň na učiém úseku ajekoie s. 1. časový účinek síly Impuls síly 2. dáhový účinek síly

Zjednodušená styčníková metoda

Stvní sttik, 1.ročník klářského stui Rovinné nosníkové soustvy III Příhrový nosník Zjnoušná styčníková mto Rovinný klouový příhrový nosník Skl rovinného příhrového nosníku Pomínk sttiké určitosti příhrového

š š Ť ř ň š ú ř ý ž š ř ě Š ě š ř ň š ú ř ý ž ř ý ě ř š ř ň š ú ý ř ý ž ě ě š š ě ě ě ž ž š ě ř ý ěž ů ň ů ý š ř ý ř ě ž ř ě ž ý ž ý ř š ř š ě ř ý š ý ě ž ř ě ž ě ř ěž ř ž ř ň ř ý ý š ě ě ž ň ř ý ř ě ý

Ortogonalita ORTOGONALITA, KOEFICIENTY FOURIEROVY ŘADY, GIBBSŮV JEV X31EO2

OROGONALIA, KOEFICIENY FOURIEROVY ŘADY, GIBBSŮV JEV Orogoni X3EO Orogonání znmená omý. Orogoni e široý poem, používá se v různých oorech, nás ude zím memi. V memice zřemě nesnáze předsviený příd e omos

Rovinné nosníkové soustavy III Příhradový nosník

Stvení sttik,.ročník klářského stui Rovinné nosníkové soustvy III Příhrový nosník Rovinný klouový příhrový nosník Skl rovinného příhrového nosníku Pomínk sttiké určitosti příhrového nosníku Zjenoušená

Statika 1. Miroslav Vokáč ČVUT v Praze, Fakulta architektury. Statika 1. M. Vokáč. Plocha.

Saika 1 Saika 1 2. přednáška ové veličin Saický momen Těžišě Momen servačnosi Hlavní ěžiš ové os a hlavní cenrální momen servačnosi Elipsa servačnosi Miroslav Vokáč miroslav.vokac@klok.cvu.cz Konrolní

4.4.3 Další trigonometrické věty

443 Další trigonometriké věty Předpoklady: 440 Věty, které ojevíme v této hodině, mohou usnadnit některé výpočty, ale je možné se ez nih (na rozdíl od kosinové a sinové věty) oejít Pedagogiká poznámka:

Stavba atomu: Elektronový obal

Svb ou: Elkonový obl Nils Boh 885 96 Bohův ol ou Ewin Schöing 887 96 Schöingov vlnová ovnic Louis Bogli 89 987 uální vlnově-čásicový chk lnáních čásic M Bon 88 97 Bonov pvěpoobnosní inpc vlnové funkc Wn

Digitální učební materiál

Digiální učení meriál Číslo projeku CZ..7/../.8 Náev projeku Zkvlinění výuk prosřednicvím ICT Číslo náev šlon klíčové kivi III/ Inovce kvlinění výuk prosřednicvím ICT Příjemce podpor Gmnáium, Jevíčko,

VI. Nevlastní integrály

VI. Nevlsní inegrály Obsh 1 Inegrál jko funke horní meze 2 2 Nevlsní inegrály 2 2.1 Nevlsníinegrályvlivemmeze... 3 2.2 Nevlsníinegrályvlivemfunke... 3 2.3 Výpočeneurčiýhinegrálů.... 4 2.3.1 Nevlsníinegrályvlivemmeze...

- Ohybový moment zleva:

příkl 1 q = 10k/m =0 1) Ohněte směry rekí z pomínek rovnováhy určete jejih velikost, proveďte kontrolu ) ykreslete průěhy vnitřníh sil jejih honoty určete ve všeh vyznčenýh oeh,,. R z R Reke z pomínek

= μ. (NB.3.1) L kde bezrozměrný kritický moment μ cr je: Okrajové podmínky při kroucení Krouticí zatížení α β. (volná deplanace) obecné 3,7 1,08

Kroucení NB. Vniřní síl od kroucení Výsledk jednodušené analý pruů oevřeného průřeu se anedbáním účinku prosého kroucení ve smslu 6..7.(7) le upřesni na ákladě následující modifikované analogie ohbu a

2. ZÁKLADY KINEMATIKY

. ZÁKLDY KINEMTIKY Kinemaika se zabýá popisem pohbu čásice nebo ělesa, aniž sleduje příčinné souislosi. Jedním ze základních lasnosí pohbu je, že jeho popis záleží na olbě zažného ělesa ( souřadnicoého

Smíšený součin

7..14 Smíšený součin Předpokldy: 713 Je dán ronoěžnostěn LMNOPR. R O P N M L Jeho ojem umíme spočítt stereometrikým zorem: V = S. p Ronoěžnostěn je tké určen třemi ektory, : R O P N M L jeho ojem musí

Přednáška 7, ODM, prostorové a příčně zatížené prutové konstrukce

Sik sveníh konsrukí II.,.ročník kářského sudi Přednášk 7, ODM, prosorové příčně ížené pruové konsruke Výpočový mode prosorové konsruke Tvor výpočového modeu Aný pruu v prosoru Příkd řešení prosorového

Obvykle se používá stejná transformační matice pro napětí a proud.

Trnsformce do složkových sousv náhrd fázorů fyzikálních veličin složkmi V rojfázové sousvě plí I I I c Ic b bc b bc V rnsformovné sousvě plí o I o I I n In m omn m omn Definičně určíme pro npěí 1 bc u

Kinematika hmotného bodu

DOPLŇKOVÉ TEXTY BB1 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ Kinemik hmoného bodu Obsh Klsická mechnik... Vzžný sysém... Polohoý ekor... Trjekorie... Prmerické ronice rjekorie... 3 Příkld 1... 3

EI GI. bezrozměrný parametr působiště zatížení vzhledem ke středu smyku ζ g =

NB.3 NB.3.1 Rosah planosi Pružný kriický momen π I µ cr 1 + κ w + ζ k 诲诲쩎睃睅 睅 a s 5 s ( + ) I A 1 ψ f )I (hf / ) (1) Posup uvedený v éo příloe je vhodný pro výpoče kriického momenu nosníků konsanního dvojose

š č š ě Ú č ě ú š č Úň ě ž Ú ě ň ž ň ě Ý š ů š ž úč č Š ň ď Ž č š ě ň ů č Ž č Ž ú ň č š ž Ž ů č ů Š ú š ě č š ě ů š ů ě šť ě š š Ž č ě ě š ď Š ž ď ě š ě ě š ě ě š š ě Ě č ó ů ě ů ů ě š ě ů č ž š č Š ó

Odraz na kulové ploše

Odz n kulové ploše Duté zcdlo o.. os zcdl V.. vchol zcdl S.. střed zcdl (kul. ploch).. polomě zcdl (kul. ploch) Ppsek vchází z odu A n ose zcdl po odzu n zcdle dopdá do nějkého odu B n ose. tojúhelníků

Kinematika hmotného bodu. Petr Šidlof

et Šilof Úo Kinemtik popis pohybu (nezkoumá příčiny pohybu) Šiší souislosti: mechnik tuhých těles sttik kinemtik ynmik Mechnik mechnik poných těles sttik kinemtik ynmik mechnik tekutin hyosttik ynmik tekutin

4. Střední radiační teplota; poměr osálání,

Sálavé a průmyslové vyápění (60). Sřední radiační eploa; poměr osálání, operaivní a výsledná eploa.. 08 a.. 08 Ing. Jindřich Boháč TEPLOTY Sřední radiační eploa - r Sálavé vyápění = PŘEVÁŽNĚ sálavé vyápění

Pružnost a plasticita II

Pružnost a plasticita II. ročník bakalářskéo stuia oc. Ing. Martin Krejsa, P.. Katera stavební ecanik Plošné konstrukce, nosné esk Nosné esk Iealiují se jako rovinný obraec (nejčastěji ve voorovné rovině),

Rovinné nosníkové soustavy Gerberův nosník

Stvení sttik, 1.ročník klářského stui Rovinné nosníkové soustvy Gererův nosník Spojitý nosník s vloženými klouy - Gererův nosník Kter stvení mehniky Fkult stvení, VŠB - Tehniká univerzit Ostrv Sttiky neurčité

Přednáška 1. Elektrické zařízení vs Elektrický obvod. Obvodové veličiny. Časové průběhy obvodových veličin

Prof. Ing. Ivan Zemánek, CSc Přenáška 1 Elekrické zařízení vs Elekrický obvo Obvoové veličiny Časové průběhy obvoových veličin Charakerisické honoy perioických veličin 1 Prof. Ing. Ivan Zemánek, CSc Elekrické

1.3.4 Rovnoměrně zrychlený pohyb po kružnici

34 Rovnoměrně zrychlený pohyb po kružnici Předpoklady: 33 Opakování: K veličinám popisujícím posuvný pohyb exisují analogické veličiny popisující pohyb po kružnici: rovnoměrný pohyb pojíko rovnoměrný pohyb

Popis polohy tělesa. Robotika. Vladimír Smutný. Centrum strojového vnímání. České vysoké učení technické v Praze

Popis poloh těles 1 2 Robotik Popis poloh těles 3 4 5 6 7 8 9 10 11 12 Vldimír Smutný Centrum strojového vnímání České vsoké učení technické v Prze 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Hlavní body. Úvod do vlnění. Harmonické vlny. Energie a intenzita vlnění. Popis, periodicita v čase a prostoru Huygensův princip, odraz a lom vlnění

Vlnění Úvod do vlnění Hlavní bod Harmoniké vln Popis, periodiia v čase a prosoru Hugensův prinip, odraz a lom vlnění Energie a inenzia vlnění Inerferene vln, Dopplerův jev Vln přenos kmiů prosorem Prosředím

Vlastní čísla a vlastní vektory

5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi

Řešení testu 2b. Fyzika I (Mechanika a molekulová fyzika) NOFY ledna 2016

Řešení testu b Fika I (Mecanika a molekulová fika NOFY. ledna 6 Příklad Zadání: Po kouli o poloměu se be pokluovaní valí malá koule o poloměu. Jaká bude úlová clost otáčení malé koule v okamžiku kd se

10 Transformace 3D. 10.1 Transformace a jejich realizace. Studijní cíl. Doba nutná k nastudování. Průvodce studiem

Trnsformce 3D Sudijní cíl Teno blok je věnován rnsformcím 3D grfik. V eu budou popsán ákldní rnsformce v prosoru posunuí oočení kosení měn měřík používné při prcování 3D modelu. Jednolivé rnsformce budou

Derivace funkce více proměnných

Derivace funkce více proměnných Pro sudeny FP TUL Marina Šimůnková 21. prosince 2017 1. Parciální derivace. Ve výrazu f(x, y) považujeme za proměnnou jen x a proměnnou y považujeme za konsanu. Zderivujeme

4.2.1 Goniometrické funkce ostrého úhlu

.. Goniometriké funke ostrého úhlu Předpokldy: 7 Dnešní látku opkujeme už potřetí (poprvé n zčátku mtemtiky, podruhé ve fyzie) je to oprvdu důležité. C C C C C C Všehny prvoúhlé trojúhelníky s úhlem α

Í ř Á Á Č Č ř Š ó ř Č ř š ř ů ř ň ň ň ř Ž Ž Ž ň ř ť ň Ť ř ř ů ř ř Ž ř š ň É ó Ť š š ř ř ř š ř ř ř ř š ř š ř ř š ř š š ř ť ř ň š ř ř ť ř ř š Ť ř ř ř š ř Ť š ř ř ř š ř š ř ř ř š ů ř š ř ř š ř ř š ř ř ť š

Okruhy z učiva středoškolské matematiky pro přípravu ke studiu na Fakultě bezpečnostního inženýrství VŠB TU Ostrava

Okruhy z učiv sředoškolské memiky pro příprvu ke sudiu Fkulě ezpečosího ižeýrsví VŠB TU Osrv I Úprvy lgerických výrzů, zlomky, rozkld kvdrického rojčleu, mociy se záporým epoeem, mociy s rcioálím epoeem,

Odraz na kulové ploše Duté zrcadlo

Odz n kulové ploše Duté zcdlo o.. os zcdl V.. vchol zcdl S.. střed zcdl (kul. ploch).. polomě zcdl (kul. ploch) Ppsek vchází z odu A n ose zcdl po odzu n zcdle dopdá do nějkého odu B n ose. Podle oázku

Mechanická silová pole

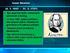Mechanická siloá pole siloé pole mechanice je ekooé pole chaakeizoané z. inenziou siloého pole (inenziou síly): E m [ms ] inenzia je oožná se zychlením, keé siloé pole aném mísě uělí liboolnému ělesu Siloé

Nadměrné daňové břemeno

Nměrné ňové břemeno Nměrné ňové břemeno je efinováno jko ztrát přebytku spotřebitele přebytku výrobe, ke kterému ohází v ůsleku znění. Něky se tož nzývá jko ztrát mrtvé váhy. Připomenutí: Přebytek spotřebitele:

Nakloněná rovina II

1215 Nkloněná rovin II Předokldy: 1214 Pomůcky: siloměr 2,5 N, sd n měření řecí síly Pedoická oznámk: V éo následující hodině se nerobírá žádná nová lák Přeso jde o oměrně důležié hodiny, roože žáci se

Seznámíte se s principem integrace substituční metodou a se základními typy integrálů, které lze touto metodou vypočítat.

4 Inegrace subsiucí 4 Inegrace subsiucí Průvodce sudiem Inegrály, keré nelze řeši pomocí základních vzorců, lze velmi časo řeši subsiuční meodou Vzorce pro derivace elemenárních funkcí a věy o derivaci

Dynamika hmotného bodu

Dynmik hmoného bou Dynmik - obo mechniky, yšeřující zájemné působení ěles, keé ee ke změně pohybu Síl - ekooá eličin, je míou zájemného působení ěles, keé ee ke změnám pohybu nebo efomci ěles Síly mohou

Statika 2. Kombinace namáhání N + M y + M z. Miroslav Vokáč 19. října ČVUT v Praze, Fakulta architektury.

2. přednáška N + M + M Jádro průřeu Šikmý ohb M + N M + N M + M + N Jádro průřeu Ecenrický lak a vloučeného ahu Konrolní oák Miroslav Vokáč miroslav.vokac@cvu.c ČVUT v Prae, Fakula archiekur 19. října

Příloha-výpočet motoru

Příloha-výpočet motoru 1.Zadané parametry motoru: vrtání d : 77mm zdvih z: 87mm kompresní poměr ε : 10.6 atmosférický tlak p 1 : 98000Pa teplota nasávaného vzduchu T 1 : 353.15K adiabatický exponent κ

Mechanika zemin a zakládání staveb, 2 ročník bakalářského studia. Zemní tlaky

Mechanika zemin a zakládání staveb, 2 ročník bakalářského studia Zemní tlaky Rozdělení, aktivizace Výpočet pro soudržné i nesoudržné zeminy Tlaky zemin a vody na pažení Katedra geotechniky a podzemního

Kinematika a dynamika soustavy těles

Knemaka a dynamka sousay ěles Vyšeřoání poybu mecansmů Analycké yšeřoání poybu mecansmu le poés pomocí doé funkce j. au me souřadncem popsujícím polou nacío a nanýc členů. Posup je paný níže uedenéo příkladu.

Á š Á ž Ý ř ě ř Č Č Č ú ě Č ř ř Č Č Č ř Č ú ř ž ě Ú ř ě Ú ř ú š ě ř ř ř ě ž ř ž ž ř ž ě ž ž ř ě ě ě ř š ž ě ř š ů š Á ž Ý ž ě ě ř ě ě ě ř ě š ů ř ř ě ě ř ě ě ů ř ě ě ě ě ě ž ž ř ž ú ě ě ě š ř š ě Ů ě š

29. PL Čtyřúhelníky, mnohoúhelníky Čtyřúhelník = rovinný útvar, je tvořen čtyřmi úsečkami, které se protínají ve čtyřech bodech (vrcholech).

.ročník 9. PL Čtyřúhlníky, mnohoúhlníky Čtyřúhlník = rovinný útvr, j tvořn čtyřmi úsčkmi, ktré s protínjí v čtyřh oh (vrholh). Pozn.: Njčstěji s používá znční,,, pro vrholy,,,, pro strny α, β, γ, δ pro

γ α β E k r r ρ ρ 0 θ θ G Θ G U( r, t) w(z) w 0 ω z R z U( r, t) 1 c 2 2 U( r, t) t 2 = 0, U( r, t) U( r, t) = E( r, t) U( r, t) = u( r)e iωt. u( r) + k 2 u( r) = 0, k = ω/c u( r) = A exp( i k r), k

Hodnoty pro trubkový vazník předpokládají styčníky s průniky trubek, v jiných případech budou vzpěrné délky stejné jako pro úhelníkové vazníky.

5. Vazník posuek pruů 5. Vzpěrné élky Tab.: Vzpěrné élky pruů příhraových vazníků Úhelníkový vazník v rovině vzálenos uzlů Horní pás z roviny vzálenos vaznic vzálenos svislého zužení Dolní pás z roviny

ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE. Fakulta strojní Ústav mechaniky DIPLOMOVÁ PRÁCE. Dynamický model poddajného mechanismu Trijointu s řízením

ČESKÉ VYSOKÉ UČENÍ EHNIKÉ V PRAZE ala sojní Úsav mehan DIPLOOVÁ PRÁE Dnamý moel poajného mehansm jon s řízením Obo: Inženýsá mehana a mehaona 005 omáš HEŘAN íle plomové páe Vvoření namého moel hého mehansm

Rovinné nosníkové soustavy II h=3

Stvní sttik,.ročník klářského stui Mimostyčníkové ztížní prutu V prutu č. vznikn v ůslku mimostyčníkového ztížní rovněž V M. q konst. Rovinné nosníkové soustvy II h Rovinný klouový příhrový nosník Mimostyčníkové

Řešený příklad - Nechráněný nosník zajištěný proti klopení

Řešený příl - Nehráněný nosní zjištěný proti lopení Nvrhněte prostý nosní s rozpětí 6,, viz obráze, ztížený rovnoěrný spojitý ztížení. Stálé ztížení je 3,8 N/, proěnné ztížení q 5,8 N/. Stbilitu tlčené

Pohyb po kružnici - shrnutí. ω = Předpoklady:

.3.3 Pohyb po kružnici - shrnuí Předpokldy: 3 Pomocí dou ě U kruhoého pohybu je ýhodnější měři úhel (kerý je pro šechny body sejný) než dráhu (kerá se pro body s různou zdálenosí od osy liší). Ke kždé

Měření momentu setrvačnosti z doby kmitu

Úloha č. 4 Měření momentu setrvačnosti z doby kmitu Úkoly měření:. Určete moment setrvačnosti vybraných těles, kruhové a obdélníkové desky.. Stanovení momentu setrvačnosti proveďte s využitím dvou rozdílných

Zakládání staveb 9 cvičení

Zakláání tave 9 včení Únonot áklaové půy Mení tavy Geotehnké kategore Mení tav únonot (.MS) MEZÍ STAVY I. Skupna mení tav únonot (hrouení kontruke, nepříputné aoření, naklonění) II. Skupna mení tav přetvoření

Stavební mechanika 1 (K132SM01)

Stní mnik 1 (K132SM01) Přnáší: o. ng. Mtěj Lpš, P.D. Ktr mniky K132 místnost D2034 konzult Čt 9:30-11:00 -mil: mtj.lps@fs.ut.z ttp://m.fs.ut.z/~lps/ting/inx.tml Řáný trmín zápočtoé písmky j ÚTERÝ 25. un

Obrázková matematika D. Šafránek Fakulta jaderná a fyzikálně inženýrská, Břehová 7, Praha 1

Orázková mtemtik D. Šfránek Fkult jerná fyzikálně inženýrská řehová 7 115 19 Prh 1.sfrnek@seznm.z strkt Názorná ovození záklníh geometrikýh vět známýh ze stření školy. 1 Úvo N stření škole se mehniky používjí

Mechanické vlnění. představuje šíření nějakého rozruchu prostorem (např.deformace pružného tělesa, změny teploty, tlaku, hustoty, intenzity silového

Mehaniké vlnění Vlnění předsavje šíření nějakého ozh posoem (např.deomae pžného ělesa, změny eploy, lak, hsoy, inenziy silového pole, ) Tyo veličiny se v dané vlnění přenáší enegii posoem mísě poso mění

A1M14PO2 - ELEKTRICKÉ POHONY A TRAKCE 2

Ing. Pvel Kole, Ph.D.. týen A114PO, 014/15 A114PO - ELEKTRICKÉ POHONY A TRAKCE Zenoušený návo e vičení ve. týnu temtiý moel ynhonního motou Po potřey vičení z přemětu Eletié pohony te potčí mtemtiý moel

F1040 Mechanika a molekulová fyzika

4 Mechnik molekuloá fzik Pe Šfřík 4 Přednášk 4 Mechnik molekuloá fzik Tped b Pe Šfřík 4 Mechnik molekuloá fzik... Zchlení:... 3 Pohb po kužnici... 4 Pohb z hledisk ůzných pozooelů... 6 Pohboé onice hmoného

( ) ( ) ( ) Vzdálenost bodu od přímky II. Předpoklady: 7312

.. Vzálenost bou o přímk II Přepokl: Pegogiká poznámk: Průběh hoin honě závisí n tom, jk oolní jsou stuenti v oszování o vzorů, které je nejtěžší částí hoin. Dlším problémem pk mohou být rovnie s bsolutní

Fyzika I mechanika. Rozdělení fyziky podle jednotlivých oborů, tj. podle jevů, které zkoumá:

Fika I mechanika Úvod Základní fikální pojm Fika (fsis je řeck příroda) bla původně vědou o přírodě, ted souhrnem všech přírodních věd, které se s postupem dějin osamostatnil. Fika si však achovává ústřední

Učební text k přednášce UFY102

Matematický popis vlnění vlna - ozuch šířící se postředím zachovávající svůj tva (pofil) Po jednoduchost začneme s jednodimenzionální vlnou potože ozuch se pohybuje ychlostí v, musí být funkcí jak polohy

Rotačně symetrické úlohy

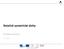Roačně symeické úlohy Pužnos a pevnos Napěí a defomace zaíženého pužného ělesa Základní úloha pužnosi - Posup řešení úlohy ) podmínky ovnováhy ) vzahy mezi posuvy a převořeními 3) vyloučení posuvů ovnice

Lineární algebra : Metrická geometrie

Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních

ŘEŠENÍ OBVODŮ S TRANSIMPEDANČNÍMI OPERAČNÍMI ZESILOVAČI POMOCÍ GRAFŮ SIGNÁLOVÝCH TOKŮ

ŘEŠENÍ OBVODŮ S ANSMPEDANČNÍM OPEAČNÍM ESLOVAČ POMOÍ AFŮ SNÁLOVÝH OŮ ÚVOD Dlior Biolek, VA Brno rnsimpenční operční zesilovče (O) jsou perspektivní tegrovné ovoy, které jsou svými přenosovými vlstnostmi

Řešení: uvolnění - volba reakcí, vnitřní síly řešené z levého tělesa: Ekvivalentní varianty prutu: Deformační podmínka: ΔL=0

Cvičení 4 k procvičení označeno vlevo červeno čaro P/4 až P4/4 osaní D/4 až D4/4, ožný doácí úkol P/4 Dána je soosá příá yč konsanních průřezů =00 s ěžiši T složená z ěděného úsek délky =00 a ocelového

2. ANALYTICKÁ GEOMETRIE V PROSTORU Vektory Úlohy k samostatnému řešení... 21

2 ANALYTICKÁ GEOMETRIE V PROSTORU 21 21 Vektory 21 Úlohy k samostatnému řešení 21 22 Přímka a rovina v prostoru 22 Úlohy k samostatnému řešení 22 23 Vzájemná poloha přímek a rovin 25 Úlohy k samostatnému

TERMOMECHANIKA 16. Přenos tepla vedením

FSI VU v Bně, Enegetický ústv Odbo temomechniky techniky postředí pof. Ing. Miln Pvelek, CSc. ERMOMECHANIKA 6. Přenos tepl vedením OSNOVA 6. KAPIOLY Difeenciální ovnice vedení tepl Počáteční okjové podmínky

X 3U U U. Skutečné hodnoty zkratových parametrů v pojmenovaných veličinách pak jsou: Průběh zkratového proudu: SKS =

11. Výpoče poměrů při zkraeh ve vlasní spořebě elekrárny Zkra má v obvodeh shémau smysl pouze v čáseh provozovanýh s účinně uzemněným sředem zdroje, čili mimo alernáor, vyvedení výkonu a přilehlá vinuí

Univerzita Tomáše Bati ve Zlíně

Univerzia omáše Bai ve Zlíně Úsav elekroechniky a měření Sřídavý proud Přednáška č. 5 Milan Adámek adamek@f.ub.cz U5 A711 +4057603551 Sřídavý proud 1 Obecná charakerisika periodických funkcí zákl. vlasnosí

1 Princip relativity.

Prinip relativit Prinip relativit íká, že fzikální zákon mají stejný tvar ve všeh ineriálníh sou anýh soustaváh Ineriální soustava je efinována tak, že se v ní volná ástie pohbuje rovnom rným p ímo arým

Posouzení únosnosti patky

Vrifikační manál č. Aktaliza 03/016 Posozní únosnosti patky Program: Soor: Patky Dmo_vm_0.gpa V tomto vrifikačním manál j vn rční výpočt posozní únosnosti patky na trvalo sitai při ovoněnýh ínkáh pro první

SPECIÁLNÍ TEORIE RELATIVITY

SPECIÁLNÍ TEORIE RELATIVITY GALILEO GALILEI (6.s.) pohbuje-li se ažná sousaa hlee k jiné onoěný příočaý pohbe, je s ní onoenná (pohb je ájený elainí) neeisuje žáná absoluní ažná sousaa, keou jeinou b ěl

Teplota. 3 kt. Boltzmanova konstanta k = J K -1. definice teploty. tlaky v obou částech se vyrovnají

Teploa laky obou čásech se yroají 1 m1 1 m rooáe budou sředí kieické eergie obou druhů molekul sejé: 1 1 m m 1 1 ěžší molekuly se pohybují pomaleji ež lehčí sejé musí edy bý i objemoé kocerace: 1 když

Příhradové konstrukce - průsečná metoda v Ritterově úpravě

Příhrové konstruk - průsčná mto v Rittrově úprvě vyřšt síly v pruth u soustvy n orázku. goniomtri os = /( + ) / = 0,6 γ β () sin = /( + ) / = 0,8 (h) β osβ = /[ + ] / sinβ = /[ + ] / = 0, 987 = 0, 6 γ

( ) ( ) Sinová věta II. β je úhel z intervalu ( 0;π ). Jak je vidět z jednotkové kružnice, úhly, pro které platí. Předpoklady:

4.4. Sinová vět II Předpokldy 44 Kde se stl hy? Námi nlezené řešení je správné, le nenšli jsme druhé hy ve hvíli, kdy jsme z hodnoty sin β určovli úhel β. β je úhel z intervlu ( ;π ). Jk je vidět z jednotkové

( ) Podmínka plasticity: σ σ 0. Podmínky plasticity. Podmínky plasticity. Podmínky plasticity. = σ = σ. f σ σ σ

Podmínka plasticit rovnice popisující všechn stav napětí, které vedou k plastickému přetváření materiálu. ednoosá napjatost charakteriovaná jedinou složkou normálového napětí. Podmínka plasticit: nebo

litinové dešťové svody

litinové ešťové svoy PAM-TYP R PAM-TYP R ANTIK PAM-SME PAM Estetik U letil mteriál trie itin PAM je tenikou referení Trouy rezienční řy typ R Kompletní ník pro jkákoliv uspořáání. 3 typy kruové, kruové

11. cvičení z Matematické analýzy 2

11. cvičení z Mtemtické nlýzy 1. - 1. prosince 18 11.1 (cylindrické souřdnice) Zpište integrály pomocí cylindrických souřdnic pk je spočítejte: () x x x +y (x + y ) dz dy dx. (b) 1 1 x 1 1 x x y (x + y

Vlny jsou podélné elementy ve a proti směru šíření rozruchu (tlaková vlna v plynovém či vodovodním potrubí)

Vlnění Mehaniké vlnění Je formo ohyb lákového rosředí Elemeny láky se ři růhod vlny vyhyljí ze svýh rovnovážnýh oloh a ohybjí se (kmiají) kolem nih věšino nearně Změna deformae a naěí (mehaniký rozrh)

Zada ní 2. Semina rní pra ce z pr edme tu Matematický software (KI/MSW)

Z ní. Semin ní p e z p eme u Memiý sofwe (KI/MSW) Dum zání.. 6 Pomín poání - Seminání páe se sláá z pogmoé čási (ó Mlbu) eoé čási (poool o poání). - Kžý suen oezáá pái sám z sebe. - Suen si bee nejméně

4. cvičení z Matematiky 2

4. cvičení z Mtemtiky 2 14.-18. březn 2016 4.1 Njděte ity (i (ii (iii (iv 2 +(y 1 2 +1 1 2 +(y 1 2 z 2 y 2 z yz 1 2 y 2 (,y (0,0 2 +y 2 2 y 2 (,y (0,0 2 +y 3 (i Pro funkci f(, y = 2 +(y 1 2 +1 1 2 +(y

Válcová momentová skořepina

Válcová momenová skořepina Momenová skořepina je enkosěnné ěleso, jež nesplňuje předpoklady o membánové napjaosi. Válcová skořepina je vlášním případem skořepiny oačně symeické, musí edy splňova podmínky

Tangens a kotangens

4.3.12 Tngens kotngens Předpokldy: 040311 Př. 1: Úhel, pod kterým je možné ze pozorovt vrhol věže ze vzdálenosti 19 m od její pty, yl změřen n 53 od vodorovné roviny. Jk je věž vysoká? h 53 19 m Z orázku

ě ž š Č Č Č úč č Á É ď Č Č úč ě ě ě č č š č č ž ž č č š š ý ň č ě ů ý ž ž č ý ě ů ž ž č ž Ť ú ý ž Ť Ž č č ž č ě č ě š ě ň ž č č š š ý ě č ě ů Ž Ů ď č ý ě ě č ě ě ž Š ž ů Ž ě č ó č Š úč Ť ž ž ě č š ě č

Upozornění: Dne: 12.10.2015

Objekt : Pod Haltýřem 5 Dne: 12.10.2015 Byty č. : 183,182,169,168 od 8:00 hod. do 9:00 hod. Byty č. : 167,149,148,147 od 9:00 hod. do 10:00 hod. Byty č. : 123,122,121,94 od 10:00 hod. do 11:00 hod. Byty

VZÁJEMNÉ SILOVÉ PŮSOBENÍ VODIČŮ S PROUDEM A MAGNETICKÉ POLE

Příklady: 1A. Jakou silou působí homogenní magnetické pole na přímý vodič o délce 15 cm, kterým prochází proud 4 A, a svírá s vektorem magnetické indukce úhel 60? Velikost vektoru magnetické indukce je

Í Č ú Č Š Í Á É Č Č ú š š Ž ž š Ť Ť Ž ž Ó ó Ž ž ž Í ú ž Ť ž ž š ň ž š š Í ž Í ň Ž ň š ó š Ž Ž Í Š ú Í ž ž Í š ž ž Ť š š Ž Ž Á ž ó ž Ť š ž ť š Í ň ť ž Ž ž Ž ž Ť ž šť š ž Ž ň ú ž š ž ú ú ť Ž ň ú š ú ž Ž