13. VLIV PARAMETRŮ NA TEORETICKOU A SKUTEČNOU DRSNOST POVRCHU

Transkript

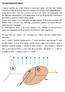
1 3 VLIV PAAMETŮ NA TEOETICKOU A SKUTEČNOU DSNOST POVCHU Po úspěšném a aktivním absovování této KAPITOLY Budete umět: Deinovat ákadní paamety kvaity obobené pochy Popsat mikogeometii obobené pochy Stanovit teoetickou dsnost v ávisosti na řené geometii a řených paametech nástoje Budete umět Budete schopni: Vypočítat teoetickou dsnost Budete schopni Čas ke studiu: 3 hodiny Výkad Kvaita obobeného povchu jako integovaná chaakteistika stojových součástí, je deinována: Geometií obobeného povchu Fyikáně-mechanickými vastnostmi povchové vstvy, ejména odchykami od ideáního tvau Fyikáně-chemickým stavem povchu 3 Mikogeometie obobeného povchu Stav a kvaita povchové vstvy obobeného kovu ovivňují únavovou pevnost, odonost poti opotřebení, potikooní stabiitu, kvaitu montáţe apod je námé, ţe dynamicky namáhané součástky se pavida ačnou poušovat na povchu Obobená pocha se tvoří jako obaová pocha tajektoií pacovního pohybu bodů řené hany nástoje a od ákadních geometických poch adaných výkesem, tedy od oviny, vácové pochy apod se ásadně iší Např podéně soustuţená pocha je šoubovitá, čeně soustuţená spiáová, hobovaná ţábkovitá Avšak i takové pojetí obobené pochy je ideaiací jejího skutečného stavu Geometický sed postupných pooh bodů řené hany je přetvořený v ávisosti od jednotivých yikáních pocesů, kteé ákonitě pováejí obábění Teoetický sed pooh řené části nástoje, daný kinematickým schématem se mění v důsedku násedujících aktoů: Puţnou a pastickou deomací v půběhu tvoření třísky Dynamickými jevy, tedy kmitáním technoogické soustavy Přesností výobního aříení

2 Viv pastické deomace na skutečný obobený povch se akádá ejména na adheních siách mei obobkem a nástojem a na tvoření náůstku Náůstek se odděuje od poch řeného nástoje, přiepuje se na obobený povch a vytváří na něm vyvýšeniny Ty se můţou v pocesu řeání odthávat a na povchu se objeví vythané pošky Při obábění itiny a kovů v křehkém stavu nevniká čisté řeání V důsedku napjatosti se někteá na odthávají od ákadního mateiáu, čím vnikají odchyky od teoetického povchu ve tvau nepavidených pohoubení Viv kmitání se pojevuje tím, ţe naůstá teoetický sed pohybů řené hany, jednak má viv na odděování náůstku od poch nástoje Viv tření hřbetu noţe o obobek se pojevuje i tím, ţe neovnosti řené hany se kopíují na obáběný povch Dsnost povchu, deinovanou na výkese, e povaţovat a imitní hodnotu, kteá se má v technoogickém pocesu dosáhnout Jednoduchý geometický přístup k identiikaci mikogeometie obobeného povchu vycháí postého kopíování tvau řeného kínu na obobený povch 3 Výpočet teoetické dsnosti povchu Mohou nastat tři případy: Hot nástoje není aobený, tedy ε = 0 (ob 3) Tento imitní případ namená, ţe posuv můţeme anedbat, potoţe je mnohem menší jako poomě aobení nástoje a odpovídá hubování vekými posuvy Neovnost povchu je vytvářena havní a vedejší řenou hanou Hot nože je aobený a poomě hotu je menší jako posuv: ε (ob 3) Neovnost povchu je vytvářena aobeným hotem i úseky havní a vedejší řené hany Le to povaţovat a poohubování Hot nože je aobený, přičemž poomě ε Poi povchu je vytvořený jen aobeným hotem nástoje Tento případ odpovídá dokončování povchu (ob 3), poto nás hediska kvaity povchu aujímají nejvíce Ob 3 Schéma po výpočet teoetické neovnosti obobeného povchu při obábění nástojem s minimáním pooměem hotu []

3 Ob 3 Schéma poohubování povchu [] Ob 33 Schéma dokončování povchu [] Sedujeme pvní případ Z ob 3 Patí [0, 3]: AD BD (3) Odtud: (3) Pode tohoto vtahu teda oste se většováním obou úhů nastavení (v čitatei je součin, ve jmenovatei součet) a ineání na posuvu 3

4 V případě nástoje s pooměem hotu (ob 3) bude: ED ED AO EC ED CO EO (33) Po dosaení: (34) Dostai jsme ovnici na výpočet teoetické výšky neovností poiu Po paktické pouţití se pouţívá jednodušší tva ovnice: Po úpavě: 4 Potoţe čen je vemi maý v poovnání s ε, e ho anedbat a dostáváme: 8 (35) (36) Tento často používaný vtah udává unkční ávisost mei teoetickou neovností povchu, posuvem a pooměem aobení hotu nástoje Vypývá něho, ţe s náůstem posuvu stoupá paaboicky Naopak, pode ákona hypeboy kesá s náůstem ε Na ob 34 je diagam, vytvořený tohoto vtahu Le vidět, ţe při vyšších posuvech pudce stoupá Poto cesta na menšování vede k pouţívání maých posuvů a větších pooměů hotu (pokud je to moţné hediska vniku kmitání soustavy) Ob 34 Teoetická ávisost mei posuvem a pooměem hotu nástoje -5, postupně 5mm [] 4

5 Skutečná výška neovností poiu je vyšší neţ teoetická Poces tvoření povchu je totiţ pováen vnikem někteých deektů na obobené poše, kteé jsou důsedkem pastické deomace V důsedku pastického většování šířky třísky b opoti šířce odřeávané vstvy b docháí na povchu obobené pochy ke vniku hřebínků, kteé jsou oientovány podé vedejší řené hany (ob 35) Ob 35 příčný ře obobeným povchem (ře ovinou P ) teoet sk - teoetická výška poiu [] - skutečná výška neovností poiu, Uvedené úvahy se týkay příčné neovnosti povchu (měřené komo na vekto řené ychosti) Mimo to existuje i podéná dsnost, kteá se měří ve směu vektou řené ychosti V případě vekých odíů mei příčnou a podénou neovností povchu chaakteiujeme takový povch jako oientovány Podéná neovnost vniká v důsedku vtáčení mateiáu pod aobenou řenou hanu, pode ob 36 Na ob 36c je pohed na řenou hanu eektoyticky ostřeného nástoje při většení 00x V daném případě je opsaný poomě hany 40µm V důsedku jeho existence docháí při maých h k vtačení mateiáu pod řený kín V důsedku puţné a pastické deomace spojené s přinutím na hřbetě nástoje, ůstávají na obobeném povchu šupinky, kteé tvoří podénou neovnost povchu (ob 36d) Teoetickou představu o mikoneovnosti obobeného povchu ískáme poiových křivek Jsou to půsečnice povchu s ovinami komými na povch Paamety neovnosti povchu ískané poiových křivek chaakteiuje noma STN ISO 487 Deinuje poi povchu a souřadnicovou soustavu na sedování povchu pode ob 37 5

6 Ob 36 a- pohyb mateiáu podé aobené řené hany, b - vnik mikotřísky na obobeném povchu, c - pohed na řenou hanu nástoje ostřeného eektoyticky, d- obobený povch s podénou mikoneovností [] Ob 37 Deinice poiu povchu [] 6

7 Na ob 38 je deinice největší výšky neovností poiu křivky, kteá se hodnotí v osahu ákadní déky eáného půběhu poiové Ob 38 Deinice největší výšky neovností poiu poiogau obobeného povchu [] Patí: p max v max (37) přří Neovnost, kteá je deinovaná na ob 37 můţeme povaţovat a příčnou ( ) Při oientovaných povších v případě podéného měření neovnosti povchu dostaneme podstatně odišnou pod veikost ( ),(ob 39) Ob 39 Deinice příčné a podéné neovnosti povchu [] Neoientované povchy, kteé vnikají při eektických metodách obábění, otyskávání, eptání, mají ve všech směech stejnou hodnotu Na ob 30 je příkad tyskaného povchu součástky Pocha je tvořená kátey, kteé mají ůnou houbku a jsou náhodně omístěny Podobné povchy vnikají při eektických metodách obábění 7

8 Ob 30 Otyskaný povch součástky [] Dašími chaakteistikami povchu, kteé se uvádí na výkese součástky jsou: střední aitmetická odchyka poiu střední kvadatická odchyka poiu a q Střední aitmetická odchyka poiu a je deinovaná jako střední hodnota absoutních odchyek poiu Z x : a Z x dx Střední kvadatická odchyka poiu q je deinovaná: q Z x dx (38) (39) V paxi se pouţívají ještě daší chaakteistiky povchu, např únosnost povchu, epeentovaná křivkou mateiáového podíu poiu (měna sumání déky dotyku povchu v ávisosti na houbce poiu) Pokud je na výkese součástky deinována, není pobém po technooga učit maximání posuv na jeho dosáhnutí odí mei teoetickou a skutečnou hodnotou je na ob 3 Ob 3 Deinice teoetické a skutečné poiogau povchu [] 8

9 Aby byo moţné stanovit potřebný posuv, povaţujeme maximání posuv teoetického vtahu po : t s Potom je moţné stanovit max 8 (30) V případě, ţe na výkese je adaná hodnota Běţně patí: 4 max a a a musíme nát vtah mei a a (3) Při přesnějším učování tohoto poměu však musíme vědět, o jaký tva poiu (anebo působ obábění) jde V tabuce 3 je tento pomě deinovaný po někteé případy poiu povchu Tab 3 Vtah mei a a při odíném tvau poiu [] Le vidět, ţe vtah mei a a se iší Současné poioměy umoţňují přímé vyhodnocení všech paametů poiu Na ob 3 a 33 je vo ánamu poioměu Mitutoyo Suest 30 9

10 Ob 33 Poi dsnosti soustuženého povchu [] Ob 33 Poi dsnosti boušeného povchu [] Shnutí kapitoy této kapitoe jsme se dověděi, co vše ahnuje kvaita obobené pochy a jaké paamety mají viv na teoetickou dsnost povchu Dáe jsme se naučii vypočítat teoetickou dsnost povchu, kdyţ hot nástoje není aobený, hot noţe je aobený a poomě hotu je menší jako posuv ε a hot noţe je aobený, přičemţ poomě ε Kontoní otáky Co namená a, q a? Jak se vypočítá střední aitmetická odchyka poiu? 3 Jak se vypočítá střední kvadatická odchyka poiu? 4 Jak se vypočítá teoetická dsnost? 5 Jaké případy mohou nastat při výpočtu teoetické dsnosti? 6 Kteému typu obábění odpovídá, kdyţ hot není aobený? 7 Kteému typu obábění odpovídá, kdyţ hot noţe je aobený a poomě hotu je menší jako posuv: ε? 8 Kteému typu obábění odpovídá, kdyţ hot noţe je aobený, přičemţ poomě ε? Daší doje VASILKO Kao Anaytická teóia tieskového obábania COFIN Pešov, 007 ISBN BUDA, J - SOUČEK, J - VASILKO, K: Teóia obábania, ALFA Batisava, MAŇKOVÁ, I - BEŇO, J: Technoogické a mateiáové činitee obábania, Vienaa Košice, 004, ISBN X 4 MAŇKOVÁ, I: Vybané aspekty monitoovania stavu nástoja v pocese eania, Košice, 004, ISBN NESLUŠAN, M TUEK, S BYCHTA, J ČEP, TABAČEK, M: 0

11 Expeimentáne metódy v tieskovom obábaní EDIS Ţiina, 007 ISBN MÁDL, J - SCHUBET, V: Expeimentání metody a optimaiace v teoii obábění Paha : ČVUT Paha, Biík, O Obábění II (Dí): Fyikáně mechanické áežitosti pocesu obábění Ostava: Vysoká škoa báňská TU Ostava, s ISBN Biík, O Obábění II (Dí) Ostava: Vysoká škoa báňská TU Ostava, 00 8 s ISBN BYCHTA, Jose; ČEP, obet; NOVÁKOVÁ, Jana, PETŘKOVSKÁ, Lenka Technoogie II dí Ostava : Ediční středisko VŠB TU Ostava ISBN BYCHTA, Jose; ČEP, obet; NOVÁKOVÁ, Jana, PETŘKOVSKÁ, Lenka Technoogie II dí Ostava : Ediční středisko VŠB TU Ostava ISBN CD-OM Na videu jsou obaeny dva případy obábění (pooměem nástoje dokončování a ineání částí ostří se aobením poodokončování) a měřena dsnost povchu při daných řených paametech Dáe je poovnána s teoetickou dsností, kteá je vypočítána de vtahů v kapitoe Kíč k řešení O 3 a střední aitmetická odchyka poiu, q střední kvadatická odchyka poiu, maximání výška neovností O 3 O 33 O 34 a q 8 Z x dx Z x dx O 35 Hot nástoje není aobený, tedy ε = 0 O 36 Hubování O 37 Poohubování O 38 Dokončování Hot noţe je aobený a poomě hotu je menší jako posuv: ε Hot noţe je aobený, přičemţ poomě ε