Je základní funkcionalitou autonomního robotu operujícího v reálném (vždy částečně neznámém) prostředí

Transkript

1 Předcházení koizím Je zákadní funkcionaitou autonomního obotu opeujícího v eáném (vždy částečně neznámém) postředí Jednoduché postupy detekují neočekávanou překážku a zastavují vykonávání pánu Sožitější postupy nad předchozí funkcionaitu eaizují autonomní objetí překážky (tzv. efexní předcházení sážkám nebo okání pánování) Zahnuje koky: Detekce překážky a stanovení jejího ozměu a tvau Výpočet a eaizace objízdné tajektoie s návatem na původní tajektoii k cíi Nevýhoda: Při nevyužítí apioní znaosti o postředí (modeu světa) může vést k eaizaci neoptimáních tajektoií

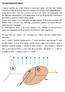
2 Metody Vecto Fied Histogam (Pus) ( VFH, VFH+) Úoha: Jako součást fyzické eaizace tajektoie Pánované bez úpného zohednění omezujících podmínek Překážky postředí, Kinematická omezení řízení obotu a Fyzické ozměy obotu Typické funkcionaity úoh: Umožní detekci neznámých objektů Koiguje aktuáně vykonávanou tajektoii obotu směem k cíi za současného předcházení sážkám s detekovanými objekty. Vstupem agoitmu je: D pavděpodobnostní mode světa - mřížku (Cetainty Gids) - snadná kontinuání údžba obsahu modeu z dákoměných senzoů (sona, ida) Aktuání měření houbky scény dákoměnými senzoy Poces zpacování (edukce) vstupních dat ve až 4 stupních (de metody, odišují se stupněm hadkosti tajektoie, přesností apoximace původní tajektoie a náočností nastavení paametů) Výstupem je okamžité řízení obotu (esp. jeho koekce) Apikace VFH pasivní sepecký původce

3 Vecto Fied Histogam Pus (VFH+) Odvozeno z oigináního postupu VHF Dosahuje vyššího stupně hadkosti tajektoie Zjednodušuje nastavení paametů metody (expicitní kompenzace fyzikáního ozměu obotu) Lepší apoximace oiginání takjektoie obotu vyšší spoehivost Vstupem VFH+ je mřížková mapa histogam gid (zaožená na předchozích postupech cetainty/occupancy gids) VHF+ eaizuje 4-stupňové zpacování vstupních dat Vstupní D mřížková mapa je zpacována do 1D poáních histogamů v (okamžitém) okoí obotu Posední kok postupu vybíá nejvýhodnější smě dašího postupu obotu na využitím maskovaného poáního histogamu a cenové funkce

4 VFH+, kok 1 Mějme mřížkovou mapu C obsahující objekt (aktivní obast) C a, jenž je tvořena kuhovým okoím obotu o půměu w s (pohybuje se s obotem) kok 1 mapuje C a na tzv. zákadní poání histogam H p Každá aktivní obast (pixe) je zpacovávána jako vekto přísušný překážce Smě β i,j a veikost m i,j vektou překážky jsou učeny aktivní obastí a středem obotu (Robot Position Cente RPC) : i, j tan 1 y x 0 i y x 0 j x 0, y 0 x i, y j značí souřadnice středu obotu souřadnice aktivní obasti m c a bd i, j i, j i, j c i,j značí hodnotu obsazenosti aktivní obasti C i,j d i,j vzdáenost aktivní obasti C i,j od středu obotu a paamety a, b jsou zvoeny tak, že spňují podmínku: (po souřadnou sosutavu viz. nás. ob.) a b ws 1 1

5 VFH+, kok1 - situace

6 VFH+, kok 1, poznámky c i, j Kvadatický čen zohedňuje násedující situace: Vysoké hodnoty c i,j značí opakovaně potvzená měření, tj. jistotu existence překážky Nízké hodnoty c i,j mohou být způsobeny přítomným šumem a poto je ve výsedku potačuje Veikost vektou je též kvadatickou fcí d i,j pefeuje bízké překážky vůči vzdáenějším Funkce veikosti vektou obasti je otačně symetická vzhedem ke středu obotu, tj. ve výsedku je chování VFH (obotu) invaiantní vzhedem ke směu ke překážce.

7 VFH+, kok 1, zákadní poání histogam Konstukce poáního histogamu H p s využitím vektoů překážek H p nechť má zvoené tangenciání ozišení α takové, že 360/ α je ceé číso (typická voba např. α=5 o, tj. obdžíme děení do 7 diskétních směů/sektoů) Každý takový smě epezentuje komponentu poáního histogamu poání hustotu překážky (mía jistoty existence překážky)

8 VFH+, kok 1, diatace překážek I Po zpacování poáního histogamu je nezbytné zohednit fyzický ozmě obotu Původní VFH metoda apikuje na hodnoty histogamu fit (donofekvenční popust) za účeem vyhazení tajektoií a zohednění šířky obotu (eiminuje úzké půchody mezi překážkami) nevýhodné, náočné empiické nastavování VFH+ apikuje teoeticky odvozenou fitaci ke kompenzaci ozměu obotu bez nutnosti nastavování expanzí (diatací) překážek. Překážky postředí jsou diatovány o ozmě obotu (tj. o největší vzdáenost jeho okaje od středu obotu, případně zvětšenou o bezpečnostní ádius d s ), tj. výsedné zvětšení překážek je: s Situace je násedně zpacována jako po obot s nuovým ozměem (bod) d s

9 VFH+, kok 1, diatace překážek II Fitace diatací objektů pacuje vemi dobře po oboty s kompaktním tvaem; asymetické oboty si vyžadují expanzi překážek s ohedem na okamžitou oientaci obotu. Diataci ze efektivně impementovat již ve fázi vytváření poáních histogamů Namísto update jediného koespondujícího sektou ke každé obasti ze povést update i po všechny okoní sektoy do úhové vzdáenosti γ i,j odpovídající veikosti požadované diatace

10 VFH+, kok 1, zákadní poání histogam - konstukce Konstukce poáního histogamu H p s využitím vektoů překážek H p nechť má zvoené tangenciání ozišení α takové, že 360/ α je ceé číso (typická voba např. α=5 o, tj. obdžíme děení do 7 diskétních směů/sektoů) Každý takový smě epezentuje komponentu poáního histogamu poání hustotu překážky (mía jistoty existence překážky) Po každý sekto k je hodnota poáního histogamu učena jako: 0 1,. ;, :. ', ',,,,,, ',, j i j i j i j i j i j i C j i j i j i P k h jinde h k k kde h m H a

11 VFH+, kok 1, zákadní poání histogam - vastnosti Vzniký poání histogam zohedňuje fyzikání ozmě obotu, esp. jeho šířku vyhedem ke směu pohybu. Funkce h má v důsedku viv jako donofekvenční popust, poání histogam vyhazuje, nevyžaduje žádné nastavení Poání histogam je konstuhován koem aktuání pozice obotu, což umožňuije efektivní impementaci, tipy: Repezentace okoí maticemi o ozměu w s x w s Hodnoty směu vektou překážky β i,j, tangenciání diatace γ i,j a hodnota výazu a-b i,j po každou aktivní buňku v obasti C a mohou být epezentovány efeenčními tabukami

12 VFH+, kok, binání poání histogam Riziko osciací a nekontoovaného chování v situacích kdy je veikost půchodů v postředí sovnatená (bízká) s ozměem obotu (peiodická změna ozhodnutí agoitmu v závisosti na změně pozoovacího úhu (vzokování) vede ke kývání a neřízené přibížení k hanicím objektů Pobém je edukován zavedením hysteeze po hodnoty histogamu Definice honí a doní pahové hodnoty τ ow a τ high Násednou tansfomací původního histogamu H p do binání fomy H b apikací pavide: H H p k, j p k, j high ow jinak : H H H p k, j b k, j b k, j H 0 b k, j 1 Poces nahazuje poání míu jistoty (jenž je spojitá veičina) bináními hodnotami 0 (voný posto) a 1 (nepřístupný posto)

13 VFH+, kok 3, maskovaný poání histogam I Původní VFH metoda uvažuje obot bez dynamiky obotu a kinematického modeu, tj. obot je schopen měnit svůj smě bez omezení a pynue. Uvedená podmínka je komě situace, kdy obot ve vzokovacím okamžiku zastaví a opaví svoji tajektoii, poušena. VFH+ metoda eiminuje předchozí užitím přesnější (eaističtější) apoximace tajektoie obotu - předpokádá pohyb po tajektoii s konstantní křívostí (kužnice, přímka) Křivost nechť je definována jako K=1/, poomě zatáčení může být snadno učen Křivost tajektoie je často funkcí dopředné ychosti obotu Čím ycheji se obot pohybuje, tím je dosažitená křivost menší Po difeenciání pohon může být poomě zatáčení oven nue po nuovou dopřednou ychost (!) Při znaosti dosažiteného pooměu zatáčení a mřířkové mapy postředí, esp. úhového/bináního histogamu, ze stanovit postupnost jednotivých úhových sektoů po daný obot. Dosažitené tajektoie bez dynamiky (a), se zohedněním dynamických omezení (b)

14 VFH+, kok 3, maskovaný poání histogam II Potíná-i se mezní tajektoie s diatovanou hanicí překážky, jsou všechny tajektoie od překážky směem k obotu nedostupné Středy tajektoií (L,R) de ob. jsou vztaženy k eativní pooze obotu a definovány jako: x y x y sin cos sin cos Vzdáenost(i) aktivní buňky C i,j ke středům tajektoií jsou dány vztahy: d d ( x ( x i x( j)) x( j)) ( y ( y y( i)) y( i)) Situace s bokovanou kuhovou tajektoií (překážka A) a vonou tajektoií (překážka B), ozděení bokovaných a voných sektoů

15 VFH+, kok 3, maskovaný poání histogam III Překážka bokuje směy po své pavé, esp. evé staně (viz. ob.) pávě když je spněna podmínka 1, esp. podmínka : d d s s Testování všech aktivních buněk na patnost podmínky 1 a podmínky obdžíme dvojici mezních úhů φ a φ dosupných sektoů po evý a pavý smě od obotu Přičtením úhu π k hodnotám úhů φ a φ obdžíme zpětné směy vzhedem k aktuánímu směu pohybu úhů: φ b = Θ+π Situace s bokovanou kuhovou tajektoií (překážka A) a vonou tajektoií (překážka B), ozděení bokovaných a voných sektoů

16 VFH+, kok 3, maskovaný poání histogam ag., vastnosti I Metodu ze snadno impementovat agoitmem, kteý uvažuje buňky mající viv na jeden z úhu úhů φ a φ : 1. Uči φ b, nastav φ a φ ovno φ b. Po každou buňku C i,j v aktivním okoí (okně) C a mající c i,j >τ Jestiže β i,j se nachází vpavo od Θ a vevo od φ, ověř spnění podmínky 1, je-i spněna, nastav φ = β i,j. Jestiže β i,j se nachází vevo od Θ a vpavo od φ, ověř spnění podmínky, je-i spněna, nastav φ = β i,j. Efektivní impementace po případ spoehivých senzoů. V případě vyšší četnosti chyb měření mohou být φ a φ učeny stochastickými postupy: Namísto poovnání míy jistoty obsazenosti buněk s pevným pahem ze sestavit poání histogam, jehož sektoové hodnoty epezentují míu jistoty s jakou je tento sekto zabokován z důvodů dynamiky obotu Hodnoty φ a φ jsou násedně stanoveny pahováním výše zmíněného histogamu Metoda je obustnějši ae méně výhodná k výpočtu

17 VFH+, kok 3, maskovaný poání histogam ag., vastnosti II Při znaosti φ a φ a bináního poáního histogamu ze učit maskovaný poání histogam jako: H H m k m k 0 1 jestiže jinak, H b k 0 k. {[, ],[, ]} úhe sektou. k n n Kde: α úhová šířka jednotivého sektou, k n pořadnice Maskovaný histogam ukazuje, jaké směy jsou přípustné po aktuání ychost obotu, jsou-i všechny bokované, obot nemůže na této ychosti naézt řešení, tj.: Je třeba učit novou sadu hodnot φ a φ po odišnou (nižší) ychost obotu; pokud neze naézt žádnou sadu hodnot φ a φ, po kteou existuje aspoň jedno přípustné řešení (nebokovaný smě pohybu) obot uvíznu (deadock)

18 VFH+, kok 3, poání histogamy iustace Binání poání histogam nespávně indikuje směy vevo od překážky A jako půchodné. Maskovaný histogam uvedenou chybu postihne a eiminuje Moduy vektoů přísušných překážce A jsou vyšší než po B neboť A je bíže obotu než B. Z téhož důvodu je po překážku A úhe obasti s nedostupností tajektoií větší. Výchozí situace Pvotní poání histogam po diskétní směy (a), binání poání histogam téhož (b) a maskovaný binání histogam (c)

19 VFH+, kok 4, výbě směu I Maskovaný poání histogam ukazuje všechny směy vhodné k neomezeného pohybu obotu Z množiny přípustných (nebokovaných) směů je vhodné zvoit nejvhodnější smě dašího pohybu obotu: V jednoduchém případe (původní VFH postup) ze zachovávat cíově oientovanou stategii (t.j. výbě směu nejbižšího původnímu směu k t směem k cíi... Postup VFH+ stanoví: Množinu kandidátských směů jako půchody v okoí překážek a Povede výbě optimání cesty užitím (minimaizací) obecnějšího kitéia (než je odchyka od původní tajektoie) nově zvoený smě pohybu je:. n k n Výbě směu je pováděn v kocích: 1. Výbě kajních směů (evého k a pavého k ) po všechny existující půchody v maskovaném poáním histogamu. Metoda ozišuje šioké a úzké půchody de ozdíu pořadnice přísušných haničních směů jako: k k smax šioký k k s úzký max (Typicky: s max ~ 16)

20 VFH+, kok 4, výbě směu II. Po úzké půchody je smě řízení obotu c n zvoen jednoznačně středem půchodu: k k cn 3. Po šioké půchody existuijí po smě řízení obotu cekem 3 kandidátské směy: Při evém a pavém okaji půchodu, směy k a k Smě k cíi k t, pokud se nachází mezi ostatními dvěma kandidátskými směy k a k Tedy: c k s max vpavo c k s max vevo ct kt pokt c, c k cíi

21 VFH+, kok 4, výbě směu III, vastnosti Kandidátské směy c a c vedou obot podé kontuy překážky (v bezpečné vzdáenosti, viz. diatace překážky), smě c t míří k cíi Po necíově oientovaná chování obotu mohou být kandidátské směy vybíány jinou stategií (např. náhodná pocházka může být eaizována zachováním (vobou) nového směu přednostně shodného s aktuáním/minuým směem): c c i k po i n, i1 po kn, i1 c, c Po situaci s cíově-oientovaným chováním obdžíme z maskovaného bináního histogamu 1 až 3 kandidátské směy po každý půchod. Vobu mezi nimi povádíme užitím cenové funkce g po kandidátský smě c. c, c c n k k

22 VFH+, kok 4, výbě směu IV, výbě fináního směu i Cenová funkce: g c). c, ki. 3 c 1,c kde učuje absoutní úhovou odchyku mezi sektoy c 1 a c, tj. její hodnota je vždy n/ Možná impementace je: c k ( 1, n, i1 c c min{ c c, c c n, c c } 1, n Pvní výaz cenové fce g(c) má význam ceny odvozené od úhové odchyky kandidátského směu a směu k cíi, větší odchyka vyšší cena, zajišťuje cíověoientované chování agoitmu Duhý výaz postihuje odchyku kandidátského směu od okamžitého natočení podvozku obotu, vyšší odchyka podvozku od kandidátského směu značí potřebu větší změny směu vyšší cena, přispívá k dosažení potřebného směu po daší činnost

23 VFH+, kok 4, výbě směu V, výbě fináního směu Třetí výaz značí cenu za změnu směu mezi kandidátským směem a směem zvoeným v předchozím koku, větší řídicí zásah vyšší cena, přispívá k dosažení potřebného směu po daší činnost Pozn.: Posední dva výazy eaizují kátkodobou pamět chováni - duhý výaz má význam mechanické paměti, třetí umoži obotu učit potřebný směu ještě před změnou jeho oientace. Váhové koeficienty μ, význam nemají absoutní hodnoty, nýbž jejich vzájemný pomě: μ 1 ovivňuje míu cíově oientovaného chování stiknost vykonávání cesty k danému cíi μ ovivňuje jakou měou se obot snaží eaizovat efektivní budoucí tajektoii s minimáními změnami směu. μ 3 ovivňuje snahu o zachování dříve zvoeného směu pohybu a tím zachování hadké tajektoie

24 VFH+, kok 4, výbě směu VI, výbě fináního směu K zachování cíově oientovaného chování obotu je nezbytné spnit podmínku: 1 3 Je-i získání efektivní tajektoie důežitější než změny v řízení směu obotu voba μ > μ 3 (pefeence hadkosti tajektoie se opíá o kompementání podmínku) Typická voba paametů μ 1 = 5, μ =, μ 3 =... K impementaci daších funkcionait je možné ozšířit cenovou funkci o daší čeny (např. k vyhýbání se úzkým půchodům, přidáním čenu. 4 k, k zohedńujícím šířku půchodu, popř. naézání úzkých míst (dveří) užitím výazu 4.1/ k, ) k Cenovou funkci je možné dočasně modifikovat v půběhu řešení...

25 VFH+, závě vastnosti Výhody Spoehivé řešení z důvodu páce s minuou tajetoií obotu (maskování bokovaných tajektoií) a jeho okamžitou ychostí a omezení. Minimání počet nastavovaných paametů: s max, n, μ 1, μ, μ 3... Použití cenové funkce k eaizaci stategie umožňuje vobu a dynamické přepínání chování Nevýhody: Nastavení, byť nevekého počtu, paametů může být kitické Metoda pacuje ze své podstaty okáně, t.j. existuje iziko uvíznutí při neznaosti potřebného okoí obotu/specifické stuktuře a sožitosti scény

26 Refeence: Boenstein J. et. a.: The Vecto Fied Histogam Fast Obstace Avoidance fo Mobie Robots, in: IEEE Jouna of Robotics and Automation, Vo.7, No.3, June 1991, pp Uich I., Boenstein J.: VFH+: eiabe Obstace Avoidance fo Fast Mobie Robots, in: Poceedings of the 1998 IEEE Intenationa Confeence on Robotics and Automation, Leuven, Begium, May 16-1, 1998, pp