Univerzita Pardubice Dopravní fakulta Jana Pernera Měření deformací na součásti pomocí tenzometrického měření a ověření výsledků metodou MKP
|
|
|
- Radomír Němeček
- před 8 lety
- Počet zobrazení:
Transkript
1 niverzita Pardubice Dopravní fakuta Jana Pernera ěření deformací na součásti pomocí tenzometrického měření a ověření výsedků metodou KP Jan Doutnáč Bakaářská práce 00
2
3
4 Prohášení autora Prohašuji: Tuto práci jsem vypracova samostatně. Veškeré iterární prameny a informace, které jsem v práci využi, jsou uvedeny v seznamu použité iteratury. By jsem seznámen s tím, že se na moji práci vztahují práva a povinnosti vypívající ze zákona č. /000 Sb., autorský zákon, zejména se skutečnosti, že niverzita Pardubice má právo na uzavření icenční smouvy o užití této práce jako škoního día pode 60 odst. autorského zákona, a s tím, že pokud dojde k užití této práce mnou nebo bude poskytnuta icence o užití jinému subjektu, je niverzita Pardubice oprávněna ode mne požadovat přiměřený příspěvek na úhradu nákadů, které na vytvoření día vynaožia, a to pode okoností až do jejich skutečné výše. Souhasím s prezenčním zpřístupněním své práce v niverzitní knihovně. V Pardubicích dne Jan DOTÁČ
5 AOTACE Cíem bakaářské práce je měření deformací na součásti pomocí tenzometrického snímače. Z naměřených výsedků výpočet napětí a ověření výsedků pomocí metody konečných prvků (pomocí software ASYS). edínou součástí bakaářské práce je zpracování teorie tenzometrického měření a metody KP. KLÍČOVÁ SLOVA tenzometrické snímače, KP, napětí, deformace, nejistoty měření, diskretizace TITLE easurement of deformation on the part through the strain gage and confirmation through the FE. AOTATIO The target of bacheor thesis is deformation measurements of the beam with the assistance of tensometer. Cacuation of tension from measured resuts and verification with a hep of FE (software ASYS). Part of bacheor thesis is theory of tensometric measurements and FE theory. KEYWODS tensometer sensing eement, FE, stress, deformation, measurement uncertainty, discretization
6 PODĚKOVÁÍ V prvé řadě bych rád poděkova své rodině, především rodičům že mě vždy vedy ke studiu. Veké dík patří mé přítekyni za podporu a trpěivost v době studia a především v době příprav na zkoušky, kdy se snažia vytvářet ty nejepší podmínky pro studium. Dáe bych chtě poděkovat svému zaměstnavatei za umožnění studia při zaměstnání. Děkuji vedoucímu práce panu Ing. ichau usiovi, Ph.D. za obětavost, čas, důežité rady, poskytnutí prostoru a vybavení pro provedení experimentu.
7 Obsah Úvod... 9 Tenzometrické snímače Apikace tenzometrických snímačů ěřící obvody....3 Lepení tenzometrů....4 ěřící ústředna....5 Odvození zákadních vzorců....6 Výpočet obvodu ejistoty měření ejistota typu A (označení u A ) ejistota typu B (označení u B )... 7 Zákadní principy pružnosti a pevnosti.... Předpokady řešení:.... Saint-Vénantův princip:....3 Jednoosá napjatost:....4 Přetvoření....5 Pracovní diagram Hookeův zákon Poissonovo číso Výpočet napětí při ohybu nosníku etoda konečných prvků Historie Charakteristika Diskretizace Experimentání nosník Popis nosníku a zatěžovacích stavů KP mode Výpočet napětí Porovnání výsedků Závěr Literatura Seznam obrázků Obrázek : Schéma zapojení měřícího obvodu... 4 Obrázek : Štítek z obau snímače... 7 Obrázek 3: Geometrické nepřesnosti... 8 Obrázek 4: Jednoosá napjatost... Obrázek 5: Přírůstek déky při přetvoření... Obrázek 6: Pracovní diagram... 3 Obrázek 7: Deformace nosníku... 5 Obrázek 8: Zatížení nosníku... 6 Obrázek 9: Průběh o... 6 Obrázek 0: Kvadratický moment průřezu... 7 Obrázek : Diskretizace kruhu Obrázek : ěřený nosník... 3 Obrázek 3: ozměrový nárt nosníku... 3 Obrázek 4: Okrajové podmínky Obrázek 5: Výsedné normáové napětí Obrázek 6: apětí v místě tenzometru Obrázek 7: apětí v místě tenzometru... 36
8 Obrázek 8: Výsedné normáové napětí Obrázek 9: apětí v místě tenzometru Obrázek 0: apětí v místě tenzometru Obrázek : Výsedné normáové napětí Obrázek : apětí v místě tenzometru Obrázek 3: apětí v místě tenzometru Obrázek 4: Výsedné normáové napětí Obrázek 5: apětí v místě tenzometru Obrázek 6: apětí v místě tenzometru Obrázek 7: Průběh o Obrázek 8: Grafické porovnání výsedků v místě tenzometru I. (8)... 4 Obrázek 9: Grafické porovnání výsedků v místě tenzometru II. (8)... 4 Obrázek 30:Grafické porovnání výsedků v místě tenzometru I. (6,5)... 4 Obrázek 3: Grafické porovnání v místě tenzometru II. (6,5)... 4
9 Úvod V současné době je jednou z nejdůežitějších činností konstruktéra navrhnout součást tak, aby snesa požadované zatížení po dobu své životnosti a přitom bya ekonomicky výhodná. K tomu je zapotřebí navrhnout součást tak, aby by pně využit materiá, z kterého je vyrobena a rozožení napětí nevykazovao obastí s příiš vysokým napětím a oproti tomu obasti téměř bez napětí, což samozřejmě není vždy možné. K uehčení práce nám v současné době souží především výpočetní programy a samozřejmě měření napětí na již vyrobené součásti pomocí tenzometrických snímačů. Cíem mé práce je porovnat výsedky těchto dvou odišných metod mezi s sebou na jednoduché součásti a výsedky ověřit i kasickým výpočtem, čímž ověřit důvěryhodnost těchto odišných metod. Práce se skádá ze čtyř havních části. První tři části popisují teorii tenzometrického měření, pružnosti a pevnosti a metody konečných prvků. Posední kapitoa srovnává výsedky z praktického měření a výpočtu. -9-
10 Tenzometrické snímače Jedná se o zařízení soužící k měření deformace na povrchu těesa, která je převedena na změnu eektrického odporu. Jde o eektrický odporový snímač, který je tvořen drátkem z vhodného materiáu a podožkou na které je drátek připevněn. Pomocí výpočtu a znaosti Hookova zákona je deformace převedena na povrchové napětí vyšetřované součásti. Tenzometrický snímač pracuje na principu změny ohmického odporu vodiče při produžování a současném zužování příčného profiu. Při zatížení vyšetřovaného těesa dochází k deformaci krajních váken. Tato deformace je přenesena na tenzometrický snímač čímž dochází k deformaci odporového drátku a tím i změně odporu snímače. Závisost mezi poměrnou deformací a poměrnou změnou odporu nazýváme konstantou snímače. Hodnota konkrétní konstanty je uvedena u každého snímače. Pro správnou funkci je potřeba, aby snímač spňova násedující podmínky: [] - Citivost snímačů vyjádřená poměrnou změnou odporu musí být co možná největší. - Cekový odpor snímače musí být co možná největší, aby se nežádoucí viv odporů v měřícím obvodě a jejich změny udržey na co možná nejmenší hodnotě. - Tepotní koeficient odporu musí být maý, aby se chyby způsobené koísáním tepoty, zmenšiy na minimum. - Drátek musí být dobře zpracován, aby neby křehký a da se pájet. - Drátek snímače musí vykazovat v co největším rozsahu ineární závisost mezi poměrnou deformací a změnou odporu drátku. V současné době se tenzometry vyrábějí ve dvou zákadních provedeních, a to kovovém a poovodičovém (křemíkovém). ěřicí mřížky kovových tenzometrů jsou nejčastěji vinuty z konstantanového drátku. kovových tenzometrů je změna ohmického odporu způsobena změnou průřezu drátku (fóie) měřicí mřížky a její déky, u poovodičových tenzometrů ve tvaru tyčinky je způsobena především změnou jejího měrného odporu což je primární projev piezorezistentního jevu. Předností poovodičových tenzometrů je vysoká citivost přibižně 60 větší než kovových tenzometrů.. Apikace tenzometrických snímačů V současné době se tenzometrické snímače upatňují havně v ověřování již vyrobených konstrukcí nebo jako měřící čen v různých sioměrech, snímačích krouticího momentu, snímačů taku, diagnostických zařízení atd. Jejich výhodou je že ze proměřovat sožité -0-
11 sestavy a to při provozním nebo testovacím zatížení kdy okrajové podmínky odpovídají reánému stavu což u metody KP není vždy možné. Samozřejmostí je měření jak při dynamickém tak statickém zatížení. Daší výhodou je, že při apikaci na konkrétní součást jsou do měření zahrnuty jak výrobní tak materiáové nepřesnosti.. ěřící obvody Aby se daa měřit deformace s naepenými tenzometry, musí být připojeny k eektronickému obvodu, jenž je schopen odpovídající změny odporu snímat. Převodníky pro tenzometry mají obvyke vstupy pro čtyři tenzometry eektricky spojeny do Wheatstoneova můstku. V současné době se také používá zapojení do tzv. poovičního Wheatstoneova můstku, který využívá dvou rezistorů umístěných uvnitř zesiovače a spoečně s měřícími tenzometry tvoří pný můstek. Wheatstoneův můstek je také vemi vhodný pro tepotní kompenzaci. V každém obvodu jsou zapojeny dva tenzometry, jeden aktivní a jeden jako kompenzační. Kompenzační souží k eiminaci vivu tepoty a je přiepen v bízkosti měřícího tenzometru na destičku z materiáu, jako je měřená součást. Destička je k součásti přiepena tak, aby nedocházeo k přenosu napětí na destičku. Před měřením je zapotřebí můstek vyvážit, tj. napětí na m = 0. Jakmie dojde ke změně odporu aktivního tenzometru v důsedku deformace rovnováha můstku se poruší a na svorkách m se objeví rozdí napětí. Výstupní napětí Wheatstoneova můstku se vyjadřuje v mv na Vot (mv/v) napájecího napětí..3 Lepení tenzometrů Kvaita naepení je jedním z nejdůežitějších činiteů ovivňujících přesnost měření. Před naepením snímače je důežité místo důkadně očistit a odmastit. ejprve vybrousíme ruční bruskou nebo hrubým smirkovým pátnem pošku pro umístění snímače. a povrchu nesmí zůstat viditené stopy po broušení proto se povrch vyrovná jemným smirkovým pátnem a zároveň dostatečně zdrsní pro správné přinutí epida. Po té se povrch dokonae očistí a odmastí vhodným přípravkem (na bázi acetonu). K nanášení epida používáme pochý štěteček. ejprve naneseme sabou vrstvičku epida, necháme po krátkou dobu zaschnout. Dáe se nanese epido na rub snímače a na pošku kam přijde snímač naepit. Snímač přiožíme na připravenou pošku, konečky prstů jemně přes papírek vymáčkneme přebytečné epido a vzduch. Snímač přidržujeme ceou jeho pochou po dobu nezbytně nutnou k dostatečnému vytvrzení epida. Při epení je nutné dodržovat násedující zásady: - Dodržovat důkadnou čistotu měřeného místa a veškerých chemikáií potřebných k naepení snímače. --
12 - Snímač správně nasměrovat ve směru měřené deformace a zároveň i umístit na správné místo. - Použít pouze tenkou vrstvu epida. - ezi měřenou konstrukcí a tenzometrem nesmí dojít k průrazu (odpor minimáně 00 Ω). Po naepení je vhodné snímač chránit vůči nepříznivým vivům (vhkost, agresivní átky, nečistoty) a to buď zažehením pod vrstvu vosku, vhodnou foii nebo ochranným geem..4 ěřící ústředna Pro naše měření bya použita měřící ústředna DC Pus - HB, jedná se o pně digitání měřicí systém spoupracující s PC prostřednictvím sběrnice GPIB, ceý proces měření i záznam naměřených dat je řízen a reaizován přísušným softwarem Catman3. ěřicí systém DC Pus umožňuje 8-kanáové měření ve statickém a dynamickém režimu, přičemž je možno využít vzorkovací frekvence až 9600 Hz na kaná. ěřicí systém umožňuje využít onine i offine digitání fitraci měřených signáů. Pro připojení tenzometrů jsou používány dvoukanáové měřicí moduy DV Odvození zákadních vzorců Jedním ze zákadních vzorců je výpočet ohmického odporu: 0 [Ω] (.) A kde ρ měrný eektrický odpor materiáu drátku [Ω/m]; 0 déka drátku [m]; A pocha průřezu drátku [m ]; Poměrnou změnu odporu vyjádříme jako d kde si d vyjádříme jako parciání derivaci přes všechny proměnné po dosazení (.) a (.3) do (.) dostaneme 0 da d d d A A A (.) (.3) --
13 dáe patí pomocí (.5) a (.6) vyjádříme d d d da A (.4) A r (.5) da dr da dr A r pomocí definice Poissonova čísa vyjádříme poměrné zúženi po té pomocí (.7) a (.8) dostaneme (.9) dosadíme do (.4) da A d r da rdr (.6) dr r d dr r d (.7) (.8) d (.9) d d d d d d (.0) d přičemž d nazýváme deformační konstantou tenzometru, značíme K d. d ( x ) (.) Kde ε značíme rativní deformaci (poměrné prodoužení). Po dosazení (.) do (.0) dostaneme: d d 0 K d K d Výsednou poměrnou změnu získáme pomocí integrace (.) (.) d K d d g K d g -3-
14 a po odogaritmování dostaneme K d n K d n( ) n( ) ( ) K d Kd závisost poměrné deformace na změně odporu je K d (.3) Pomocí Hookova zákona vypočteme z poměrné deformace veikost napětí K d (.4) E [Pa].6 Výpočet obvodu Obrázek : Schéma zapojení měřícího obvodu Zdroj: Autor -4-
15 -5- Použité veičiny: T odpor měřícího tenzometru [Ω]; K odpor kompenzačního tenzometru [Ω];, odpor uvnitř zesiovače kde = [Ω]; Δ změna odporu měřícího tenzometru [Ω]; napájecí eektrické napětí [V]; měřené eektrické napětí [V]; Pro zapojení de schématu patí: T T T (.5) K K (.6) T (.7) Při vyvážení můstku patí: T = K = = = což dosadíme do (.5), (.6) a po té do (.7): ) ( ) ( ) ( 4 (.8) Což dosadíme do vztahu pro stanovení poměrné deformace (.4): 4 d d K K Čen můžeme vzhedem k jeho veikosti zanedbat, pak dostaneme:
16 4 K d (.9) Po dosazení do Hookeová zákonu E dostaneme: Vztah (.0) použijeme pro kaibraci ústředny kde: K D =,03 = V = mv/v K 4 d E (.0), ,03 43,7Pa.7 ejistoty měření Při měření získáváme hodnotu, která je zatížená chybou išící naměřenou hodnotou od hodnoty skutečné. Tato chyba je definována jako rozdí naměřené hodnoty od hodnoty skutečné přičemž skutečná hodnota nám není známa. Chyby měření se vyskytují náhodně a dosahují jak kadných tak i záporných hodnot přičemž menší chyby jsou pravděpodobnější, větší chyba spíše vypovídá o hrubé chybě anebo nedodržení správného měřícího postupu. Vzhedem k těmto chybám hovoříme o nejistotě měření. Standardní nejistoty měření děíme pode způsobu vyhodnocování na: - Standardní nejistota typu A - Standardní nejistota typu B - Kombinovaná nejistota.7. ejistota typu A (označení u A ) Její hodnota s počtem měření kesá a vychází z Gaussovy teorie chyb z tzv. křivky normáního rozděení. ejistota typu A odpovídá směrodatné odchyce. Za předpokadu normáního rozděení, pak pravděpodobnost, že se hodnota náhodné veičiny bude od střední hodnoty išit nejvýše o jednu směrodatnou odchyku odpovídá 68% pravděpodobnosti správného výsedku. ejistotu typu A vypočteme ze vztahu: -6-
17 u A n( n n ) i ( x i x) kde x n n x i i Stanovit nejistotu typu A má význam v případě s minimáním počtem měření větší jak 0 což v našem měření nebyo provedeno a proto nebudeme nejistotu typu A uvádět..7. ejistota typu B (označení u B ) Její hodnota nezávisí na počtu opakování měření, ae na použitém měřícím řetězci. Patří sem tedy chyby měřících přístrojů, použitých metod měření, podmínek měření atd. V našem případě se bude jednat o nejistotu tenzometrického snímače, geometrické poohy umístění snímače, nejistota měřícího zesiovače a nejistota kabeu propojující měřící zesiovač s PC. ejistota hardwaru a softwaru se neuvažuje vzhedem k tomu že signá je v digitání podobě a byo použito pouze ověřený software. Výsedná nejistota typu B se stanoví součením díčích nejistot různého původu použitím zákona šíření nejistot. ejistota tenzometrického snímače ejistota odporu a deformačního faktoru tenzometrického snímače se stanoví na zákadě hodnot uvedených výrobcem na obau snímače. Obrázek : Štítek z obau snímače Zdroj: Autor -7-
18 važujeme- i normání rozděení pravděpodobnosti hodnot, redukuje se nejistota vztažená k odporu snímače součiniteem hodnoty 3 de []. u B0 0,35 3 0,% ejistota deformačního K-faktoru snímače předpokádá odchyku výsedku měření pode rozděení pravděpodobnosti rovnoměrného, pak se redukuje K-faktor součiniteem hodnoty,73 de []. u B,73 0,58% ejistota geometrie snímače Její veikost vypívá z míry přesnosti naepení snímače. Pro snadnější zapoohování je každý snímač opatřen osovým křížem a taktéž na měřené součásti je předem orýsován střed místa určeného pro naepení snímače. Přípustná míra nepřesnosti činí 0, mm v ose x a y a 3 natočení od podéné roviny. Obrázek 3: Geometrické nepřesnosti Zdroj: etodika AL--06 Vzhedem k naší konstrukci můžeme uvažovat výchyku v ose y nuovou, jeikož veikost napětí je po ceé šířce konstantní. snímače I. můžeme vzhedem k pooze v obasti s konstantním o uvažovat za nuovou i výchyku v ose x. aximání poměrná deformace tenzometru řady Y je 50 mm/m. Potom je koeficient změny dán vztahem: k 50 x Kde x je nejvzdáenější pocha hrany tenzometru vzhedem k neutrání ose. ejistotu měření při předpokadu rozděení pravděpodobnosti odchyky měření rovnoměrného stanovíme de []. u B k -8- x 3
19 kde Δx je definovaná přípustná míra nepřesnosti naepení. ejistota z hediska natočení snímače vůči podéné ose nosníku závisí na veikosti měřené poměrné deformace. Jestiže je osa snímače vychýená o úhe α, pak pro déku měřeného vákna nezatíženého nosníku 0 vůči déce snímače 0T patí vztah: 0 cos 0T a při zatížení dojde k prodoužení snímače vůči měřenému váknu o déku Δ 0T : T cos Výsednou nejistotu určíme z rozdíu poměrných deformací tenzometru a nosníku. Vzhedem k normánímu rozděení chyby musíme ceou hodnotu děit 3. ub3 3 T T T 0 cos 0T cos u B 3 T cos cos 3 ejvyšší hodnota napětí, kterou jsme naměřio byo 55 Pa, potom tedy: a T E T,6 4,6 0 cos 3 7 u B 3,39 0 m / m 0,39 m / m T T T ejistota epida Pro epení byo použito epido HB Z70, pro které je pastická deformace při třetím a daším cyku 0,5 μm/m, potom tedy: u B 0,5 m/ m 4 ejistota měřícího zesiovače Pro nejistotu měření zde použijeme Gaussův zákon šíření nejistot pro nepřímo měřené veičiny: u m f B5 ubj (.) j X j -9-
20 -0- kde X j f jsou parciání derivace poměrné deformace u Bj jsou nejistoty jednotivých zdrojů Parciání derivace pode a K d : K d K D 4 4 (.) 4 n 4 d K d K K D (.3) Po dosazení (.) a (.3) do (.) dostaneme výsedný tvar pro určení nejistoty měřícího zesiovače: 5 4 n B d K BD K d B u K u K u D D kde u BD je nejistota měřícího zesiovače stanovená na zákadě kaibračního istu. Výsedná nejistota typu B Výsedná nejistota typu B se stanoví součením díčích nejistot typu B B B B B B B B u u u u u u u Kombinovaná nejistota Stanovíme součením nejistot typu A a B. B A C u u u ozšířená nejistota měření ozšířenou nejistotu měření stanovíme z kombinované nejistoty vynásobené koeficientem rozšíření k =, což při normáním rozděení odpovídá 95% pravděpodobnosti správného výsedku. u C k u
21 Zákadní principy pružnosti a pevnosti Pružnost těesa: je schopnost těesa po odstranění vnějších si se vrátit do původního stavu Tuhost těesa:. Předpokady řešení: je vyjádřením jeho odonosti proti deformaci od vnějších si. patnost předpokadu maých poměrných deformací. ineární závisost mezi napětím a deformací (Hookeův zákon) 3. patnost St. Vénantova principu 4. materiá -homogenní: tj. stejné sožení a vastnosti v ceém objemu -isotropní:. Saint-Vénantův princip: tj. stejné mechanické vastnosti ve všech směrech Viv místního působení si a vetknutí součásti se projevuje jen v jeho bízkém okoí a zaniká přibižně ve vzdáenosti řádově rovné příčným rozměrům prutu. Proto viv vetknutí ve zjednodušených příkadech zanedbáváme..3 Jednoosá napjatost: Pro řešení nejjednodušších úoh pružnosti a pevnosti používáme metodu řezu. Prut, který je v siové rovnováze rozděíme myšeným řezem na části. Tuto rovnováhu zajišťují vnitřní síy: F 0 Obrázek 4: Jednoosá napjatost Zdroj: Pružnost a pevnost I. --
22 d ( x) ( x ) [Pa] da( x) V případě rovnoměrného rozožení taku/tahu: ( x) ( x ) [Pa] A( x) Jeikož napětí je funkcí jedné osy (x) nazýváme tuto napjatost jednoosou..4 Přetvoření Obrázek 5: Přírůstek déky při přetvoření Zdroj: Pružnost a pevnost I. Prut neproměnného průřezu o déce 0 po zatížené osovou siou změní svou déku na hodnotu. Přírůstek déky (absoutní deformace): 0 eativní deformace (poměrné prodoužení): Při uvažování pouze eementární části prutu: ( x ) ( x) 0 dx dx --
23 V případě že ε není po ceé déce prutu konstantní, je nutné změnu déky určit jako součet jednotivých eementárních změn: a po integraci: dx ( x) dx dx ( x) dx ( ) ( ).5 Pracovní diagram Při tahové zkoušce na trhacím stroji, obdržíme závisost síy a jí odpovídající deformaci. Závisost σ = σ (ε), kde napětí je vztahováno stáe k počátečnímu průřezu A 0, nazýváme smuvní pracovní diagram. Obrázek 6: Pracovní diagram Zdroj: Pružnost a pevnost I. -3-
24 Pro materiá pode obr.5 je závisost σ = σ (ε) až do hodnoty napětí σ u (mez úměrnosti) ineární. Při zatěžování do hodnoty σ E (mez pružnosti) nevznikají po odehčení trvaé deformace, materiá se deformuje pouze pružně. některých materiáů (poykrystaických) se jednoznačná mez pružnosti prakticky nevyskytuje, v tom případě zavádíme smuvní mez pružnosti σ 0,005, tj. napětí při níž je trvaá deformace po odehčení 0,005%. Při dosažení napětí meze kuzu σ k, začnou deformace ryche vzrůstat. Poměrná deformace je pak sožená z části vratné eastické a trvaé pastické. Řada materiáů nemá výraznou mez kuzu, u nich je zaváděná smuvní mez kuzu, což je napětí, které způsobí určitou trvaou deformaci, většinou se uvádí σ 0,. V průběhu zatěžování dochází ke zmenšování příčného průřezu a tím ke změně A 0, proto má pracovní diagram skutečné napětí σ s = F/A (kde A je okamžitá veikost průřezu). Průběh je znázorněn na grafu čárkovaně a napjetí dosahuje meze..6 Hookeův zákon Lineární část funkční závisosti σ = σ (ε) je matematicky vyjádřená Hookeovým zákonem v případě jednoosé napjatosti ve tvaru a vyjadřuje nám ineární závisost napětí na deformaci: E [Pa] Konstana E se nazývá modu pružnosti v tahu nebo také Yongův modu. Jednotkou moduu pružnosti je Pa. odu pružnosti je konstantní v obasti eastických deformací a je závisý na tepotě. a zákadě znaosti vnitřních si a Hookeova zákona ze určit deformaci (prodoužení) prutu. apětí v obecném řezu x je rovno: ( x ) ( x) A 0 F A 0 [Pa] Z Hookeova zákona: ( x ) ( x) E F E A 0 F E 0 A 0 Prodoužení Δ: -4-
25 F 0 E A0 V případě že ε není po ceé déce konstantní: F d ( x) E dx A Cekové prodoužení je rovno součtu jednotivých díčích prodoužení: 0 dx 0 F E dx A ( 0 ) Poissonovo číso Při natahování tyče nedochází jen ke změně jejího podéného rozměru, ae mění se i rozměry příčné. Připojíme-i k poměrným deformacím indexy os, v niž deformaci zjišťujeme, pak vypívá: b a x y x 0 b 0 a 0 Obrázek 7: Deformace nosníku Zdroj: Pružnost a pevnost I. hodnot ε x, ε y vycházejí záporné hodnoty, což značí, že jde o poměrné zkrácení (zúžení). I při jednoosé napjatosti tedy dochází k deformaci ve třech směrech. Součinite příčného zúžení μ, nazýváme Poissonovo číso a je pro daný materiá v obasti pružných -5-
26 deformací přibižně konstantní. Hodnoty μ definujeme při jednoosé napjatosti jako absoutní hodnota poměru příčné a podéné deformace: y x.8 Výpočet napětí při ohybu nosníku Vzhed k naší úoze budeme uvažovat pouze nosník zatížený ohybovým momentem, jeikož posouvající sía má pouze zanedbatený viv na výsedné napětí. Veikost výsedného napětí je závisé jak na zatížení, tak na způsobu jeho uožení. V našem případě uvažujeme pravou podpěru jako neposuvnou koubovou podpěru a evou podpěru jako posuvnou koubovou podpěru. Obrázek 8: Zatížení nosníku Zdroj: Autor Průběh ohybového mementu je zobrazen na obrázku níže. Obrázek 9: Průběh o Zdroj: Autor -6-
27 Stopa ohybového momentu je totožná s havní centrání osou průřezu proto se jedná o rovinný ohyb. Výpočet ohybového momentu: F F o x respektive o y Veikost výsedného napětí je přímo úměrná vzdáenosti krajního vákna od neutrání osy, která se vždy nachází v těžišti průřezu. Což v našem případě vzhedem k souměrnosti nosníku podé os bude znamenat, že veikost napětí v krajních váknech bude jak v taku, tak v tahu stejná. aximání napětí bude samozřejmě ve váknech nejvzdáenějších od neutrání osy. Pokud vzdáenost tohoto místa označíme jako e bude pak veikost napětí rovna: AX J kde J Z je kvadratický moment průřezu k neutrání ose. Z e o Obrázek 0: Kvadratický moment průřezu Zdroj: Pružnost a pevnost I. J Z h h y b dy b h h y dy b 3 y 3 3 y 3 h h b h 3 3 h 3 3 b h 3 Čen J Z e nazýváme průřezovým moduem v ohybu a značíme jako W o W o J Z e b h h 3 b h 6-7-
28 3 etoda konečných prvků 3. Historie etoda vznika v období koem roku 956 ve výzkumném ústavu aeronautické a kosmické mechaniky v Ohiu, SA (Wright Paterson Air Force Base). Výzkumný tým by veden prof..w. Coughem a spoupracovai zejména.l. eosh, H.C. artin, J.L. Tocher a daší. Výzkum a vývoj uvedené numerické metody vyvoa striktní požadavek "měsíčního" programu Apoo v obasti vývoje a konstrukce nosných raket. V daném čase a při známém objemu financí (3 miiardy ) se po rozboru zjistio, že se pomocí experimentu nedá úko spnit. Zbya jediná cesta a sice vývoj takové numerické metody, která by výpočty potřebné pro projekty nových typů raket a daších systémů projektu Apoo zváda. Výsedky výzkumu byy dáe intenzívně využívány na uvedené vojenské zákadně při projektech etade, ponorek, raket všech typů, atd. Tato skutečnost způsobia utajení detaiů metody tak, že programy a teoretické čánky ežey nejméně deset roků ve vojenských sejfech. První konference v Ohiu (965 a968) uváděy jen kusé informace. Daší vývoj by pak často poznamenán četnými dupicitami v odvození zákadních "nástrojů" metody (uvádí se, že deskový trojúheníkový prvek odvodio na sobě nezávise aspoň 7 autorů). Je zajímavé, že inženýři s metodou douhé roky úspěšně počítai, než matematikové dokázai konvergenci metody a vastně posvětii desetieté výpočtářské úspěchy. V civiním sektoru se nejbouřivěji metoda konečných prvků (KP) rozvíjea v etech Prvním propagátorem a neochvějným zastáncem metody by v ČSF prof. V. Koář, DrSc. z Brna, který také dosáh značného mezinárodního uznání. Pomocí KP se dnes řeší ceá řada úoh, jejichž reaizace nebya dosud možná a to nejen v obasti mechaniky spojitých těes či soustav. Svou obecnou matematickou formuací umožňuje KP řešit probém: mechaniky hornin, proudění kapain a pynů, šíření tepa a záření, stacionárních a nestacionárních eektromagnetických poí atd. Dokonce jsou známy pokusy o řešení socioogických úoh a modeování ekonomických probémů. O KP má smys hovořit pouze v souvisosti s nasazením na čísicových počítačích - směe se dá říci, že metoda je produktem doby moderních počítačů. V současné době jsou to pro zajímavost vědecko-technické výpočty meteoroogů, které mají největší požadavky na veikost a rychost počítačů tak, aby předpověď počasí pro ceou zeměkoui bya vypočítána do dvou hodin po shromáždění naměřených dat. -8-
29 3. Charakteristika Anaýza metodou konečných prvků (KP) je napodobení fyzikáního systému (geometrie a zatížení) matematickou aproximací reáného systému. žitím jednoduchých vzájemně spojených boků nazývaných eementy, je reáný systém s nekonečně mnoha neznámými aproximován systémem s konečným počtem neznámých, tzv. diskretizace. Jedná se o numerickou metodu pro získání přibižného řešení široké třídy inženýrských úoh. Těeso (příp. soustava těes) se nahrazuje odpovídající soustavou menších částí (prvků). amísto řešení probému ceého těesa je probém formuován pro jeho jednotivé části, v nichž jsou neznámé f-ce (např. deformace) přibižně popsány jen maým počtem parametrů ve zvoených bodech (uzech). Dáe se systematicky "zkompetuje" řešení pro ceé těeso [4]. Veká část inženýrských probémů není bez užití moderních metod anayticky řešitená. Před nástupem počítačů do praxe se postupovao tak, že se sožitá soustava značně zjednodušia a to tak aby se dai použít již známé vzorce. Používání KP se rozšířio v praxi spou se vzrůstajícím použití počítačů v konstrukční praxi a v dostupnosti těchto softwarů. Vekou výhodou použití KP je jeho použití již při vývoji součásti a umožnění optimaizace konstrukce bez zhotovení prototypu, což má za násedek veké finanční a časové úspory. V současnosti je KP široce a podrobně rozpracovávaný vědní obor obsahující tyto části [4]: a) teoretická- formuace variačních principů, odvozování vztahů pro různé typy prvků atd. b) matematická - probematika vhodných numerických metod, výběr agoritmů,důkazy existence a konvergence řešení, odhad chyby řešení atd. c) počítačová: ) preprocessing - generování vstupních dat, grafické zobrazení čenění, vstupní data, okrajové podmínky, zatížení, opravy a úpravy dat atd. ) processing - výpočet matic prvků, sestavení matic ceého systému, sestavení maticových rovnic a jejich řešení atd. 3) postprocessing - výpočty závisých parametrů, výstupní soubory, grafické znázornění výsedků, výstupy výsedků na periferie atd. d) inženýrsko probémová - využití možnosti KP pro konkrétní inž. úohy tj. děení těesa na prvky, výběr typu prvku, výběr vhodného prvku pro danou úohu, zadání potřebných vstupních údajů, voba forem výstupů atd. KP umožňuje řešit kvaitativně nové úohy (jak rozsahem, tak obsahem). Dnes jsou vyvinuty stovky typů konečných prvků a na světě existují desítky ceosvětově známých programových systémů (ADIA, ASYS, APPLE-SAP, ASAS, ASKA, BEASY, COSOS, -9-
30 CASTE, DIAL, AC, SC/ASTA, PAFEC, SAP7, SYSTS, SYSOISE, TITS,TPS0...) [4]. 3.3 Diskretizace Zákadním krokem metody je rozděit (diskretizovat) ibovoný mechanický systém na konečný počet prvků obvyke geometricky jednoduchých (úsečka, trojúheník, obdéník, hrano, ), tzv. eementu; resp. rozděení sožité obasti na jednoduché části. Děení na prvky není v žádném případě jednoznačné a je sině ovivněno technickými zkušenostmi a citem řešitee. Příkadem této jednoduché a ve všech odvětvích hojně používané myšenky je např. způsob výpočtu pochy kruhu dané součtem poch jednotivých trojúheníku. Obrázek : Diskretizace kruhu Zdroj: Autor S i cos sin Jeikož sin( x ) cos( x) sin( x) Voíme sin( x) cos( x) sin( x) x pak S i sin S i i S i sin -30-
31 4 Experimentání nosník 4. Popis nosníku a zatěžovacích stavů V našem případě by použit jednoduchý na dvou místech podepřený pochý nosník toušťky 3,5 mm z materiáu třídy., viz násedující obr. Tento jednoduchý tvar by vybrán z důvodu možné apikace vzorců pro výpočet napětí, jeikož se bude jednat pouze o rovinný průhyb a tím i možnosti ověření správnosti výsedků naměřených pomocí tenzometrického snímače a výpočtu pomocí KP. Pro měření napětí byy umístěny na nosník dva tenzometrické snímače. Snímač I eží uprostřed součásti a snímač II je vyosen o 95 mm. Zatížení byo apikováno pomocí předem zvážených závaží a to vždy dva zatěžovací stavy. Přenos zatížení na nosník by pomocí dvou podpěr umístěných 5 mm od středu součásti. Obrázek : ěřený nosník Zdroj: Autor -3-
32 Obrázek 3: ozměrový nárt nosníku Zdroj: Autor ěření byo provedeno ve dvou zákadních zatěžovacích stavech viz níže uvedená tabuka. - stav : tenzometry umístěné na horní poše nosníku a zatížené na tak - stav : tenzometry umístěné na spodní poše nosníku a zatížené na tah V každém stavu byo apikováno zatížení o dvou veikostech a každé měření byo provedeno 3x. Tabuka : Zátěžové stavy amáhání tenzometru Veikost zatížení F [] Zátěžový stav. Stav. tak 8 Stav. tak 6,5 Zátěžový stav. Stav. tah 8 Stav. tah 6,5-3-
33 Tabuka : aměřené hodnoty ěření [Pa] Střední Ztížení hodnota Zátěžový stav Tenzometr [] I II III [Pa]. 6,89 6,9 6,98 6,97 8 3,53 3,56 3,57 3, , 53,4 53,7 53,07 6,5 6,8 6,87 6,88 6,850. 7,74 6,96 7,8 7, ,85 3,88 3,9 3, ,56 54,67 54,7 54,650 6,5 7,7 7,77 7,79 7, KP mode Pro výpočet napětí by použit software ASYS 0.0. Vzhedem k jednoduchosti nosníku bya použitá síť tvořená z hexa prvků. Okrajové podmínky osník by podepřen v místě podpěr a to pouze ve směru komém k nosníku (směr osy Y) jako náhrada evé podpěry (posuvná koubová podpora) a ve směru komém a podéném k nosníku (směr osy Y a X) v místě pravé podpěry (pevná koubová podpora). Pro zamezení pohybu v ose Z by nosníku zakázán pohyb v tomto směru. Zatížení byo apikováno ve směru komém k nosníku na průsečnici mezi nosníkem a podpěrami přenášejícími zatížení na nosník o veikosti odpovídající hmotnosti závaží (viz. násedující obr). Veikost eementu K stanovení vhodné veikosti eementu byo použito někoik výpočtů o různé veikosti sítě, kdy každý násedující výpočet mě na příčném průřezu nosníku a jeden eement více přičemž se začínao na dvou eementech. Jako výsedek bya sedována veikost změny napětí dvou sousedních výpočtů a pro zajímavost by sedován výpočetní čas. aměřené výsedky jsou shrnuty v násedující tabuce a jako nejvhodnější počet eementu na příčný průřez byo 6-33-
34 eementů. Při každém daším zvyšování počtu eementů již docházeo pouze k zanedbatené změně vypočteného napětí a docházeo pouze k nárůstu výpočetního času. Tabuka 3: Tabuka porovnání přesnosti výpočtu v závisosti na veikosti eementů Počet eementů / průřez apětí [Pa] ozdí sousedních výpočtů [%] Výpočetní čas [s] 5,69 4,96 4 6,48 0, , ,49-43 Obrázek 4: Okrajové podmínky Zdroj: Autor -34-
35 Tabuka 4: Vypočtené hodnoty KP Zátěžový stav Tenzometr Ztížení Vypočtená hodnota [] [Pa]. 6,49 8 Obr. 4 až 6 3,36. 5,695 6,5 Obr. 7 až 9 6,64. 6,49 8 Obr. 0 až 3,36. 5,695 6,5 Obr. 3 až 5 6,64-35-
36 Zátěžový stav.: Obrázek 5: Výsedné normáové napětí Zdroj: Autor Obrázek 6: apětí v místě tenzometru Zdroj: Autor Obrázek 7: apětí v místě tenzometru Zdroj: Autor -36-
37 Zátěžový stav.: Obrázek 8: Výsedné normáové napětí Zdroj: Autor Obrázek 9: apětí v místě tenzometru Zdroj: Autor Obrázek 0: apětí v místě tenzometru Zdroj: Autor -37-
38 Zátěžový stav.: Obrázek : Výsedné normáové napětí Zdroj: Autor Obrázek : apětí v místě tenzometru Zdroj: Autor Obrázek 3: apětí v místě tenzometru Zdroj: Autor -38-
39 Zátěžový stav.: Obrázek 4: Výsedné normáové napětí Zdroj: Autor Obrázek 5: apětí v místě tenzometru Zdroj: Autor Obrázek 6: apětí v místě tenzometru -39-
40 4.3 Výpočet napětí Zákadní vzorec pro výpočet ohybového napětí v krajním vákně viz kapitoa. o [Pa] W kde o F F o x [m] resp. o y [m] Geometrické rozměry nosníku: 6 W O b h [m 3 ] Obrázek 7: Průběh o Zdroj: Autor šířka nosníku: výška nosníku: Tabuka 5: Vypočtené hodnoty b = 68,3 mm h = 3,5 mm x = 89 mm y = 45 mm Ztížení -40- Vypočtené hodnoty O W O σ Zátěžový stav Tenzometr [] [m] [m 3 ] [Pa] ,5 6,49 8 8,5 3, ,75 5,695 6,5 3633,75 6,643 36, ,5 6,49 8 8,5 3, ,75 5,695 6,5 3633,75 6,643
41 4.4 Porovnání výsedků Tabuka 6: Porovnání výsedků Vypočtené hodnoty Ztížení Tenzometr KP Výpočet Zátěžový stav Tenzometr [] [Pa]. 6,97 6,49 6,49 8 3,553 3,36 3, ,07 5,695 5,695 6,5 6,850 6,64 6,643. 7,507 6,49 6,49 8 3,877 3,36 3, ,650 5,695 5,695 6,5 7,757 6,64 6,643 Obrázek 8: Grafické porovnání výsedků v místě tenzometru I. (8) Zdroj: autor Obrázek 9: Grafické porovnání výsedků v místě tenzometru II. (8) Zdroj: autor -4-
42 Obrázek 30:Grafické porovnání výsedků v místě tenzometru I. (6,5) Zdroj: autor Obrázek 3: Grafické porovnání v místě tenzometru II. (6,5) Zdroj: autor -4-
43 5 Závěr Úkoem práce byo porovnat výsedky jednotivých metod určených k vyšetřování napětí na namáhané součásti. Pro tento experiment by jako vhodná součást vybrán jednoduchý nosník zatížený siou komou na nosník a to především z důvodu, že tato jednoduchá součást nám omezí možnosti vzniku chyb získaných především z geometrického a výpočetního hediska. Cíem této práce nebyo vyhodnotit napětí na sožité součásti, ae především co nejpřesněji stanovit napětí jednotivými metodami zatíženými co nejmenší chybou a navzájem tyto výsedky porovnat. Jeho vekou výhodou je také jednoduchost výpočtu napětí popsaného v nauce o pružnosti a pevnosti. Taktéž při výpočtu pomocí KP nemusíme vzhedem k jednoduchosti součásti provádět výpočet na zjednodušeném modeu, ae na modeu přesně odpovídajícímu zatěžovanému nosníku. Vzhedem k jednoduchosti součásti považuji výpočet pomocí zákadních vzorců jako nejpřesnější metodu a výsedek této metody považuji za směrodatný s kterým porovnávám zbývající metody. Z výše uvedených výsedků je patrné že v našem případě anaytickému řešení nejépe odpovídají výsedky vypočtené metodou KP. Ovšem této přesnosti byo dosaženo až po odadění úohy, které se týkao především způsobu vetknutí nosníku nejépe popisující reáný stav. této metody byo také experimentováno s veikosti eementu respektive počtu eementů na příčný průřez a jako nejepší v poměru přesnost a rychost řešení by počet 6 eementů na příčný průřez. Daší zvyšování počtu eementů vedo pouze k produžování výpočetního času bez dopadu na přesnost výsedků. Při tenzometrickém měření byo provedeno i někoik měření s účeně vyoseným zatížením, aby moh být sedován viv těchto nepřesností na výsedky měření a tím stanovení přesnosti rozměření jednotivých podpěr. Také zde vzhedem k štíhosti nosníku museo být uvažováno s vivem gravitace a při obrácení nosníku muse být výstup vynuován, aby došo k odstranění tohoto vivu. Úkoem této práce nebyo jednoznačně říci která metoda je epší anebo přesnější ve stanovení napětí jeikož každá metoda má své opodstatnění. Tenzometrické měření je vhodné pro již vyrobené a provozované zařízení jeikož se ve výsedcích projeví výrobní a materiáové nepřesnosti, jeho nevýhodou je však možnost zjistit pouze povrchové napětí a to pouze v přístupných místech a místech umožňující naepení tenzometrického snímače. Je zde také veký prostor k chybám způsobených převážně naepením tenzometru na součást. KP je moderní metodou a siným nástrojem konstruktéra, který umožní vyšetřovat napětí s poměrně vysokou přesností už v době návrhu součásti. Jeho nevýhodou je odborná -43-
44 náročnost na obsuhu, která musí mít zkušenosti a cit především pro stanovaní okrajových podmínek mající veký viv na přesnost výsedků. Kasická metoda výpočtu je již v dnešní době vytačovaná především díky rozvoji KP. Její obrovskou výhodou je její rychost a vhodnost především v době návrhu konstrukce, kdy nám pomůže získat aespoň předběžnou představu o zákadních rozměrech konstrukce. -44-
45 Literatura [] Tenzometrické měření oceových konstrukcí-metodika, Zkušební aboratoř AL DFJP, dokument AL--06 [] ĚEC, Jindřich. Odporové tenzometry v praxi. Vyd.. Praha : akadateství technické iteratury n. p., s. [3] ICHALEC, Jiří, et a. Pružnost a pevnost I. Vyd.. Praha 6 : Vydavateství ČVT, s. [4] HOYL, Petr. Inženýrské zákady KP. Technická univerzita Ostrava, s. Oborová práce. VŠB - Technická univerzita Ostrava. -45-
Normálové napětí a přetvoření prutu namáhaného tahem (prostým tlakem) - staticky určité úlohy
 Pružnost a pasticita, 2.ročník bakaářského studia ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) - staticky určité úohy Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného
Pružnost a pasticita, 2.ročník bakaářského studia ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) - staticky určité úohy Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného
Přednáška 12 Obecná deformační metoda, nelineární úlohy u prutových soustav
 Statika stavebních konstrukcí II., 3.ročník bakaářského studia Přednáška Obecná deformační metoda, neineární úohy u prutových soustav Fyzikáně neineární úoha Geometricky neineární úoha Konstrukčně neineární
Statika stavebních konstrukcí II., 3.ročník bakaářského studia Přednáška Obecná deformační metoda, neineární úohy u prutových soustav Fyzikáně neineární úoha Geometricky neineární úoha Konstrukčně neineární
Přednáška 10, modely podloží
 Statika stavebních konstrukcí II.,.ročník kaářského studia Přednáška, modey podoží Úvod Winkerův mode podoží Pasternakův mode podoží Nosník na pružném Winkerově podoží, řešení OD atedra stavební mechaniky
Statika stavebních konstrukcí II.,.ročník kaářského studia Přednáška, modey podoží Úvod Winkerův mode podoží Pasternakův mode podoží Nosník na pružném Winkerově podoží, řešení OD atedra stavební mechaniky
2.1 Stáčivost v závislosti na koncentraci opticky aktivní látky
 1 Pracovní úkoy 1. Změřte závisost stočení poarizační roviny na koncentraci vodního roztoku gukozy v rozmezí 0 500 g/. Pro jednu zvoenou koncentraci proveďte 5 měření úhu stočení poarizační roviny. Jednu
1 Pracovní úkoy 1. Změřte závisost stočení poarizační roviny na koncentraci vodního roztoku gukozy v rozmezí 0 500 g/. Pro jednu zvoenou koncentraci proveďte 5 měření úhu stočení poarizační roviny. Jednu
Téma 4 Normálové napětí a přetvoření prutu namáhaného tahem (prostým tlakem)
 Pružnost a pasticita, 2.ročník bakaářského studia Téma 4 ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného prutu
Pružnost a pasticita, 2.ročník bakaářského studia Téma 4 ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného prutu
1 ROZMĚRY STĚN. 1.1 Délka vnější stěny. 1.2 Výška vnější stěny
 1 ROZMĚRY STĚN Důežitými kritérii pro zhotovení cihených stěn o větších rozměrech (déce a výšce) je rozděení stěn na diatační ceky z hediska zatížení tepotou a statického posouzení stěny na zatížení větrem.
1 ROZMĚRY STĚN Důežitými kritérii pro zhotovení cihených stěn o větších rozměrech (déce a výšce) je rozděení stěn na diatační ceky z hediska zatížení tepotou a statického posouzení stěny na zatížení větrem.
Univerzita Tomáše Bati ve Zlíně, Fakulta technologická Ústav fyziky a materiálového inženýrství
 Univerzita Tomáše Bati ve Zíně, Fakuta technoogická Ústav fyziky a materiáového inženýrství Jméno a příjmení Josef Novák Ročník / Skupina x Předmět Laboratorní cvičení z předmětu Datum měření xx. xx. xxxx
Univerzita Tomáše Bati ve Zíně, Fakuta technoogická Ústav fyziky a materiáového inženýrství Jméno a příjmení Josef Novák Ročník / Skupina x Předmět Laboratorní cvičení z předmětu Datum měření xx. xx. xxxx
Řešení úloh 1. kola 60. ročníku fyzikální olympiády. Kategorie B Autoři úloh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6)
 Řešení úoh 1. koa 60. ročníku fyzikání oympiády. Kategorie B Autoři úoh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6) h 1.a) Protože vzdáenost bodů K a O je cos α, je doba etu kuičky z bodu K do bodu
Řešení úoh 1. koa 60. ročníku fyzikání oympiády. Kategorie B Autoři úoh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6) h 1.a) Protože vzdáenost bodů K a O je cos α, je doba etu kuičky z bodu K do bodu
Mechanické vlastnosti materiálů.
 Mechancké vastnost materáů. Obsah přednášky : tahová zkouška, zákadní mechancké vastnost materáu, prodoužení př tahu nebo taku, potencání energe, řešení statcky neurčtých úoh Doba studa : as hodna Cí přednášky
Mechancké vastnost materáů. Obsah přednášky : tahová zkouška, zákadní mechancké vastnost materáu, prodoužení př tahu nebo taku, potencání energe, řešení statcky neurčtých úoh Doba studa : as hodna Cí přednášky
1. Stanovení modulu pružnosti v tahu přímou metodou
 . Stanovení moduu pružnost v tahu přímou metodou.. Zadání úohy. Určte modu pružnost v tahu přímou metodou pro dva vzorky různých materáů a výsedky porovnejte s tabukovým hodnotam.. Z naměřených hodnot
. Stanovení moduu pružnost v tahu přímou metodou.. Zadání úohy. Určte modu pružnost v tahu přímou metodou pro dva vzorky různých materáů a výsedky porovnejte s tabukovým hodnotam.. Z naměřených hodnot
Inovace předmětů studijních programů strojního inženýrství v oblasti teplotního namáhání
 Grantový projekt FRVŠ MŠMT č.97/7/f/a Inovace předmětů studijních programů strojního inženýrství v obasti tepotního namáhání Některé apikace a ukázky konkrétních řešení tepeného namáhání těes. Autorky:
Grantový projekt FRVŠ MŠMT č.97/7/f/a Inovace předmětů studijních programů strojního inženýrství v obasti tepotního namáhání Některé apikace a ukázky konkrétních řešení tepeného namáhání těes. Autorky:
NOVÁ METODA NÁVRHU PRŮMYSLOVÝCH PODLAH Z VLÁKNOBETONU
 NOVÁ METODA NÁVRHU PRŮMYSLOVÝCH PODLAH Z VLÁKNOBETONU Jan Loško, Lukáš Vrábík, Jaromír Jaroš Úvod Nejrozšířenějším příkadem využití váknobetonu v současné době jsou zřejmě podahové a zákadové desky. Při
NOVÁ METODA NÁVRHU PRŮMYSLOVÝCH PODLAH Z VLÁKNOBETONU Jan Loško, Lukáš Vrábík, Jaromír Jaroš Úvod Nejrozšířenějším příkadem využití váknobetonu v současné době jsou zřejmě podahové a zákadové desky. Při
Linearní teplotní gradient
 Poznámky k semináři z předmětu Pružnost pevnost na K68 D ČVUT v Praze (pracovní verze). Tento materiá má pouze pracovní charakter a ude v průěhu semestru postupně dopňován. utor: Jan Vyčich E mai: vycich@fd.cvut.cz
Poznámky k semináři z předmětu Pružnost pevnost na K68 D ČVUT v Praze (pracovní verze). Tento materiá má pouze pracovní charakter a ude v průěhu semestru postupně dopňován. utor: Jan Vyčich E mai: vycich@fd.cvut.cz
I Stabil. Lepený kombinovaný nosník se stojnou z desky z orientovaných plochých třísek - OSB. Navrhování nosníků na účinky zatížení podle ČSN 73 1701
 I Stabi Lepený kombinovaný nosník se stojnou z desky z orientovaných pochých třísek - OSB Navrhování nosníků na účinky zatížení pode ČSN 73 1701 Část A Část B Část C Část D Výchozí předpokady, statické
I Stabi Lepený kombinovaný nosník se stojnou z desky z orientovaných pochých třísek - OSB Navrhování nosníků na účinky zatížení pode ČSN 73 1701 Část A Část B Část C Část D Výchozí předpokady, statické
Název: Studium kmitání matematického kyvadla
 Název: Studium kmitání matematického kyvada Autor: Doc. RNDr. Mian Rojko, CSc. Název škoy: Gymnázium Jana Nerudy, škoa h. města Prahy Předmět, mezipředmětové vztahy: fyzika, biooie Ročník: 3. (1. ročník
Název: Studium kmitání matematického kyvada Autor: Doc. RNDr. Mian Rojko, CSc. Název škoy: Gymnázium Jana Nerudy, škoa h. města Prahy Předmět, mezipředmětové vztahy: fyzika, biooie Ročník: 3. (1. ročník
Statika 2. Vetknuté nosníky. Miroslav Vokáč 2. listopadu ČVUT v Praze, Fakulta architektury. Statika 2. M.
 3. přednáška Průhybová čára Mirosav Vokáč mirosav.vokac@kok.cvut.cz ČVUT v Praze, Fakuta architektury 2. istopadu 2016 Průhybová čára ohýbaného nosníku Znaménková konvence veičin M z x +q +w +ϕ + q...
3. přednáška Průhybová čára Mirosav Vokáč mirosav.vokac@kok.cvut.cz ČVUT v Praze, Fakuta architektury 2. istopadu 2016 Průhybová čára ohýbaného nosníku Znaménková konvence veičin M z x +q +w +ϕ + q...
Kmitavý pohyb trochu jinak
 Kmitavý pohyb trochu jinak JIŘÍ ESAŘ, PER BAROŠ Katedra fyziky, Pedaoická fakuta, JU České Budějovice Kmitavý pohyb patří mezi zákadní fyzikání děje. Většinou se tato část fyziky redukuje na matematický
Kmitavý pohyb trochu jinak JIŘÍ ESAŘ, PER BAROŠ Katedra fyziky, Pedaoická fakuta, JU České Budějovice Kmitavý pohyb patří mezi zákadní fyzikání děje. Většinou se tato část fyziky redukuje na matematický
Senzory síly a kroutícího momentu
 Senzory síy a kroutícího momentu Zadání 1. Seznamte se s fyzikáními principy a funkčností tenzometrů, inkrementáního optoeektronického senzoru otočení a senzoru FSR. 2. Změřte závisost odporu FSR senzoru
Senzory síy a kroutícího momentu Zadání 1. Seznamte se s fyzikáními principy a funkčností tenzometrů, inkrementáního optoeektronického senzoru otočení a senzoru FSR. 2. Změřte závisost odporu FSR senzoru
Stav napjatosti materiálu.
 tav napjatosti materiáu. Zákad mechanik, 9. přednáška Obsah přednášk : jednoosý a dvojosý stav napjatosti, stav napjatosti ohýbaného nosníku, deformace ohýbaného nosníku, řešení statick neurčitých úoh
tav napjatosti materiáu. Zákad mechanik, 9. přednáška Obsah přednášk : jednoosý a dvojosý stav napjatosti, stav napjatosti ohýbaného nosníku, deformace ohýbaného nosníku, řešení statick neurčitých úoh
Elastické deformace těles
 Eastické eformace těes 15 Na oceový rát ék L 15 m a průměru 1 mm zavěsíme závaží o hmotnosti m 110 kg přičemž Youngův mou pružnosti ocei v tahu E 16 GPa a mez pružnosti ocei σ P 0 Pa Určete reativní prooužení
Eastické eformace těes 15 Na oceový rát ék L 15 m a průměru 1 mm zavěsíme závaží o hmotnosti m 110 kg přičemž Youngův mou pružnosti ocei v tahu E 16 GPa a mez pružnosti ocei σ P 0 Pa Určete reativní prooužení
Pružnost a plasticita II
 Pružnost a pasticita II 3. ročník bakaářského studia doc. Ing. artin Krejsa, Ph.D. Katedra stavební echaniky Neineární chování ateriáů, podínky pasticity, ezní pastická únosnost Úvod, zákadní pojy Teorie
Pružnost a pasticita II 3. ročník bakaářského studia doc. Ing. artin Krejsa, Ph.D. Katedra stavební echaniky Neineární chování ateriáů, podínky pasticity, ezní pastická únosnost Úvod, zákadní pojy Teorie
Jev elektromagnetické indukce
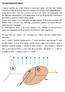 Jev eektromagnetické indukce V minuých kapitoách jsme si jistě uvědomii, že pojmy kid a pohyb, které byy vemi významné u mechanických dějů, při zkoumání eektrických a magnetických jevů nabyy přímo zásadní
Jev eektromagnetické indukce V minuých kapitoách jsme si jistě uvědomii, že pojmy kid a pohyb, které byy vemi významné u mechanických dějů, při zkoumání eektrických a magnetických jevů nabyy přímo zásadní
Z toho se η využije na zajištění funkcí automobilu a na překonání odporu vzduchu. l 100 km. 2 body b) Hledáme minimum funkce θ = 1.
 Řešení úoh. koa 59. ročníku fyzikání oympiády. Kategorie A Autor úoh: J. Thomas.a) Na dráze vt bude zapotřebí objem paiva V θ θv t. Při jeho spáení se získá tepo Q mh ρv H ρθvh t. Z toho se η využije na
Řešení úoh. koa 59. ročníku fyzikání oympiády. Kategorie A Autor úoh: J. Thomas.a) Na dráze vt bude zapotřebí objem paiva V θ θv t. Při jeho spáení se získá tepo Q mh ρv H ρθvh t. Z toho se η využije na
Podpora digitalizace a využití ICT na SPŠ CZ.1.07/1.5.00/34.0632 1
 Střední průmysová škoa a Vyšší odborná škoa technická Brno, Sokoská 1 Šabona: Inovace a zkvaitnění výuky prostřednictvím ICT Název: Téma: Autor: Číso: Anotace: echanika, pružnost pevnost Nosníky stejné
Střední průmysová škoa a Vyšší odborná škoa technická Brno, Sokoská 1 Šabona: Inovace a zkvaitnění výuky prostřednictvím ICT Název: Téma: Autor: Číso: Anotace: echanika, pružnost pevnost Nosníky stejné
PRAKTIKUM II. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. úlohač.19 Název: Měření s torzním magnetometrem
 Odděení fyzikáních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM II. úohač.19 Název: Měření s torzním magnetometrem Pracova: Lukáš Ledvina stud.skup.14 dne:16.10.2009 Odevzdadne: Možný počet
Odděení fyzikáních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM II. úohač.19 Název: Měření s torzním magnetometrem Pracova: Lukáš Ledvina stud.skup.14 dne:16.10.2009 Odevzdadne: Možný počet
EXPERIMENTÁLNÍ MECHANIKA 2. Jan Krystek
 EXPERIMENTÁLNÍ MECHANIKA 2 4. přednáška Jan Krystek 15. března 2018 ODPOROVÁ TENZOMETRIE Elektrická odporová tenzometrie je nepřímá metoda. Poměrné prodloužení je určováno na základě poměrné změny elektrického
EXPERIMENTÁLNÍ MECHANIKA 2 4. přednáška Jan Krystek 15. března 2018 ODPOROVÁ TENZOMETRIE Elektrická odporová tenzometrie je nepřímá metoda. Poměrné prodloužení je určováno na základě poměrné změny elektrického
Řešení úloh 1. kola 49. ročníku fyzikální olympiády. Kategorie D. Dosazením do rovnice(1) a úpravou dostaneme délku vlaku
 Řešení úoh koa 49 ročníku fyzikání oympiády Kategorie D Autořiúoh:JJírů(,3,4,5,6,),TDenkstein(), a) Všechny uvažované časy jsou měřené od začátku rovnoměrně zrychené pohybu vaku a spňují rovnice = at,
Řešení úoh koa 49 ročníku fyzikání oympiády Kategorie D Autořiúoh:JJírů(,3,4,5,6,),TDenkstein(), a) Všechny uvažované časy jsou měřené od začátku rovnoměrně zrychené pohybu vaku a spňují rovnice = at,
Téma 4 Výpočet přímého nosníku
 Stavební statika, 1.ročník bakaářského studia Téma 4 Výpočet přímého nosníku Výpočet nosníku v osové úoze Výpočet nosníku v příčné úoze ve svisé a vodorovné havní rovině Výpočet nosníku v krutové úoze
Stavební statika, 1.ročník bakaářského studia Téma 4 Výpočet přímého nosníku Výpočet nosníku v osové úoze Výpočet nosníku v příčné úoze ve svisé a vodorovné havní rovině Výpočet nosníku v krutové úoze
BETONOVÉ KONSTRUKCE B03C +B03K ŠTÍHLÉ BETONOVÉ KONSTRUKCE. Betonové konstrukce B03C + B03K. Betonové konstrukce B03C +6B03K
 BETONOVÉ KONSTRUKCE B03C +B03K ŠTÍHLÉ BETONOVÉ KONSTRUKCE Betonové konstrukce B03C +4B03K Betonové konstrukce B03C +5B03K Betonové konstrukce B03C +6B03K prvky namáhané kombinací [M+N] N M tak (tah) s
BETONOVÉ KONSTRUKCE B03C +B03K ŠTÍHLÉ BETONOVÉ KONSTRUKCE Betonové konstrukce B03C +4B03K Betonové konstrukce B03C +5B03K Betonové konstrukce B03C +6B03K prvky namáhané kombinací [M+N] N M tak (tah) s
Vlastnosti a zkoušení materiálů. Přednáška č.4 Úvod do pružnosti a pevnosti
 Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Mezní napětí v soudržnosti
 Mení napětí v soudržnosti Pro žebírkovou výtuž e stanovit návrhovou hodnotu meního napětí v soudržnosti vtahu: = η η ctd kde je η součinite ávisý na kvaitě podmínek v soudržnosti a pooe prutu během betonáže
Mení napětí v soudržnosti Pro žebírkovou výtuž e stanovit návrhovou hodnotu meního napětí v soudržnosti vtahu: = η η ctd kde je η součinite ávisý na kvaitě podmínek v soudržnosti a pooe prutu během betonáže
FYZIKA I. Kyvadlový pohyb. Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STRONÍ FYZIKA I Kyvadový pohyb Prof. RNDr. Viém Mádr, CSc. Prof. Ing. Libor Haváč, Ph.D. Doc. Ing. Irena Haváčová, Ph.D. Mgr. Art. Dagmar Mádrová
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STRONÍ FYZIKA I Kyvadový pohyb Prof. RNDr. Viém Mádr, CSc. Prof. Ing. Libor Haváč, Ph.D. Doc. Ing. Irena Haváčová, Ph.D. Mgr. Art. Dagmar Mádrová
7 Mezní stavy použitelnosti
 7 Mezní stavy použitenosti Cekové užitné vastnosti konstrukcí mají spňovat dva zákadní požadavky. Prvním požadavkem je bezpečnost, která je zpravida vyjádřena únosností. Druhým požadavkem je použitenost,
7 Mezní stavy použitenosti Cekové užitné vastnosti konstrukcí mají spňovat dva zákadní požadavky. Prvním požadavkem je bezpečnost, která je zpravida vyjádřena únosností. Druhým požadavkem je použitenost,
4.1 Shrnutí základních poznatků
 4.1 Shrnutí zákadních poznatků V případech příčných deformací přímých prutů- nosníků se zabýváme deformací jejich střednice, tj. spojnice těžiště příčných průřezů. Tuto deformovanou křivku nazýváme průhybová
4.1 Shrnutí zákadních poznatků V případech příčných deformací přímých prutů- nosníků se zabýváme deformací jejich střednice, tj. spojnice těžiště příčných průřezů. Tuto deformovanou křivku nazýváme průhybová
Stabilita přímých prutů
 Kapitoa 1 Stabiita přímých prutů 1.1 Úvod Předpokádejme, že tvar stačovaného přímého prizmatického prutu je ideání. To znamená, že předpokádáme jeho přímý tvar, výsedná sía působí v jeho podéné ose a materiá
Kapitoa 1 Stabiita přímých prutů 1.1 Úvod Předpokádejme, že tvar stačovaného přímého prizmatického prutu je ideání. To znamená, že předpokádáme jeho přímý tvar, výsedná sía působí v jeho podéné ose a materiá
PŘÍČNÉ LISOVANÉ ZTUŽIDLO VE STŘEŠNÍ ROVINĚ KONSTRUKCÍ Z DŘEVĚNÝCH
 PŘÍČNÉ LISOVANÉ ZTUŽIDLO VE STŘEŠNÍ ROVINĚ KONSTRUKCÍ Z DŘEVĚNÝCH VAZNÍKŮ S KOVOVÝMI DESKAMI S PROLISOVANÝMI TRNY Petr Kukík 1, Micha Grec 2, Aeš Tajbr 3 Abstrakt Timber trusses with punched meta pate
PŘÍČNÉ LISOVANÉ ZTUŽIDLO VE STŘEŠNÍ ROVINĚ KONSTRUKCÍ Z DŘEVĚNÝCH VAZNÍKŮ S KOVOVÝMI DESKAMI S PROLISOVANÝMI TRNY Petr Kukík 1, Micha Grec 2, Aeš Tajbr 3 Abstrakt Timber trusses with punched meta pate
1.5. DYNAMIKA OTÁČIVÉHO A SLOŽENÉHO POHYBU TĚLESA
 .5. OTÁČIVÉHO A SLOŽENÉHO POHYBU TĚLESA.5. ZÁKLADNÍ ROVNICE DYNAMIKY PRO ROTAČNÍ POHYB Fz F Z výsednce zrychujících s F m.a n m a t a n r z F Zrychující moment M F. r F. r z z z m.a t r6,5cm ρ r ω,ε r
.5. OTÁČIVÉHO A SLOŽENÉHO POHYBU TĚLESA.5. ZÁKLADNÍ ROVNICE DYNAMIKY PRO ROTAČNÍ POHYB Fz F Z výsednce zrychujících s F m.a n m a t a n r z F Zrychující moment M F. r F. r z z z m.a t r6,5cm ρ r ω,ε r
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Cvičení 7 (Matematická teorie pružnosti)
 VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Pružnost a pevnost v energetice (Návo do cvičení) Cvičení 7 (Matematická teorie pružnosti) Autor: Jaroslav Rojíček Verze:
VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Pružnost a pevnost v energetice (Návo do cvičení) Cvičení 7 (Matematická teorie pružnosti) Autor: Jaroslav Rojíček Verze:
Couloumbuv zákon stejne jako vetsina zakonu elektrostatiky jsou velmi podobna zakonum gravitacniho pole.
 1) Eektrostaticke poe, Cooumbuv zákon, Permitivita kazde dve teesa nabite eektrickym nabojem Q na sebe pusobi vzajemnou siou. Ta je vysise pomoci Couombovyho zákona: F = 1 4 Q Q 1 2 r r 2 0 kde první cast
1) Eektrostaticke poe, Cooumbuv zákon, Permitivita kazde dve teesa nabite eektrickym nabojem Q na sebe pusobi vzajemnou siou. Ta je vysise pomoci Couombovyho zákona: F = 1 4 Q Q 1 2 r r 2 0 kde první cast
Reakce. K618 FD ČVUT v Praze (pracovní verze). Tento materiál má pouze pracovní charakter a bude v průbehu semestru
 Poznámky ke cvičení z předmětu Pružnost pevnost na K618 D ČVU v Praze (pracovní verze). ento materiá má pouze pracovní charakter a bude v průbehu semestru postupně dopňován. Autor: Jan Vyčich E mai: vycich@fd.cvut.cz
Poznámky ke cvičení z předmětu Pružnost pevnost na K618 D ČVU v Praze (pracovní verze). ento materiá má pouze pracovní charakter a bude v průbehu semestru postupně dopňován. Autor: Jan Vyčich E mai: vycich@fd.cvut.cz
PRUŽNOST A PLASTICITA I
 Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
KONSTITUČNÍ VZTAHY. 1. Tahová zkouška
 1. Tahová zkouška Tahová zkouška se provádí dle ČSN EN ISO 6892-1 (aktualizována v roce 2010) Je nejčastější mechanickou zkouškou kovových materiálů. Zkoušky se realizují na trhacích strojích, kde se zkušební
1. Tahová zkouška Tahová zkouška se provádí dle ČSN EN ISO 6892-1 (aktualizována v roce 2010) Je nejčastější mechanickou zkouškou kovových materiálů. Zkoušky se realizují na trhacích strojích, kde se zkušební
Pružnost a pevnost I
 Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
UNIVERZITA PARDUBICE FAKULTA CHEMICKO-TECHNOLOGICKÁ. katedra fyziky ZÁKLADY FYZIKY II. Pro obory DMML, TŘD a AID prezenčního studia DFJP
 UNIVERZITA PARDUBICE FAKULTA CHEMICKO-TECHNOLOGICKÁ katedra fyziky ZÁKLADY FYZIKY II Pro obory DMML, TŘD a AID prezenčního studia DFJP RNDr Jan Z a j í c, CSc, 005 4 MAGNETICKÉ JEVY 4 NESTACIONÁRNÍ ELEKTROMAGNETICKÉ
UNIVERZITA PARDUBICE FAKULTA CHEMICKO-TECHNOLOGICKÁ katedra fyziky ZÁKLADY FYZIKY II Pro obory DMML, TŘD a AID prezenčního studia DFJP RNDr Jan Z a j í c, CSc, 005 4 MAGNETICKÉ JEVY 4 NESTACIONÁRNÍ ELEKTROMAGNETICKÉ
STRUKTURA A VLASTNOSTI KAPALIN
 I N V E S T I C E D O O Z V O J E V Z D Ě L Á V Á N Í STUKTUA A VLASTNOSTI KAPALIN. Povrchové napětí a) yzikání jev Povrch kapain se chová jako napjatá pružná membrána (důkaz vodoměrka, maé kapičky koue)
I N V E S T I C E D O O Z V O J E V Z D Ě L Á V Á N Í STUKTUA A VLASTNOSTI KAPALIN. Povrchové napětí a) yzikání jev Povrch kapain se chová jako napjatá pružná membrána (důkaz vodoměrka, maé kapičky koue)
Modelování kmitavých soustav s jedním stupněm volnosti
 Modeování kmitavých soustav s jedním stupněm vonosti Zpracova Doc. RNDr. Zdeněk Haváč, CSc 1. Zákadní mode Zákadním modeem kmitavé soustavy s jedním stupněm vonosti je tzv. diskrétní podéně kmitající mode,
Modeování kmitavých soustav s jedním stupněm vonosti Zpracova Doc. RNDr. Zdeněk Haváč, CSc 1. Zákadní mode Zákadním modeem kmitavé soustavy s jedním stupněm vonosti je tzv. diskrétní podéně kmitající mode,
1. Úvod do pružnosti a pevnosti
 1. Úvod do pružnosti a pevnosti Mechanika je nejstarší vědní obor a její nedílnou součástí je nauka o pružnosti a pevnosti. Pružností nazýváme schopnost pevných těles získat po odstranění vnějších účinků
1. Úvod do pružnosti a pevnosti Mechanika je nejstarší vědní obor a její nedílnou součástí je nauka o pružnosti a pevnosti. Pružností nazýváme schopnost pevných těles získat po odstranění vnějších účinků
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Úloha 2: Měření modulu pružnosti v tahu a ve smyku. Abstrakt
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Úoha : Měření moduu pružnosti v tahu a ve smyku Datum měření: 9. 10. 009 Jméno: Jiří Sabý Pracovní skupina: 1 Ročník a kroužek:. ročník, 1. kroužek, pátek 13:30 Spoupracovaa:
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Úoha : Měření moduu pružnosti v tahu a ve smyku Datum měření: 9. 10. 009 Jméno: Jiří Sabý Pracovní skupina: 1 Ročník a kroužek:. ročník, 1. kroužek, pátek 13:30 Spoupracovaa:
Obsah MECHANIKA PRUŽNÉHO TĚLESA. Tabulka III. Studijní text pro řešitele FO a ostatní zájemce o fyziku. Bohumil Vybíral.
 Tabuka III Mechanické vastnosti některých křehkých konstrukčních materiáů Pevnost v tahu Pevnost v taku Pevnost v ohybu Materiá σ pt/mpa σ pd /MPa σ po/mpa Šedá itina 4 4 1 10 500 80 Šedá itina 4 4 4 40
Tabuka III Mechanické vastnosti některých křehkých konstrukčních materiáů Pevnost v tahu Pevnost v taku Pevnost v ohybu Materiá σ pt/mpa σ pd /MPa σ po/mpa Šedá itina 4 4 1 10 500 80 Šedá itina 4 4 4 40
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6
 OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
Nelineární problémy a MKP
 Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Ztráta stability tenkých přímých prutů - vzpěr
 Ztráta stability tenkých přímých prutů - vzpěr Motivace štíhlé pruty namáhané tlakem mohou vybočit ze svého původně přímého tvaru a může dojít ke ztrátě stability a zhroucení konstrukce dříve, než je dosaženo
Ztráta stability tenkých přímých prutů - vzpěr Motivace štíhlé pruty namáhané tlakem mohou vybočit ze svého původně přímého tvaru a může dojít ke ztrátě stability a zhroucení konstrukce dříve, než je dosaženo
Hlavní body. Teplotní závislosti fyzikálních veličin. Teplota, měření
 e r i k a Havní body epota, ěření epotní závisosti fyzikáních veičin Kinetická teorie pynů Maxweova rozděovací funkce epo, ěrné tepo, kaorietrie epota Je zákadní veičinou, kterou neze odvodit? Čověk ji
e r i k a Havní body epota, ěření epotní závisosti fyzikáních veičin Kinetická teorie pynů Maxweova rozděovací funkce epo, ěrné tepo, kaorietrie epota Je zákadní veičinou, kterou neze odvodit? Čověk ji
3.2 Základy pevnosti materiálu. Ing. Pavel Bělov
 3.2 Základy pevnosti materiálu Ing. Pavel Bělov 23.5.2018 Normálové napětí představuje vazbu, která brání částicím tělesa k sobě přiblížit nebo se od sebe oddálit je kolmé na rovinu řezu v případě že je
3.2 Základy pevnosti materiálu Ing. Pavel Bělov 23.5.2018 Normálové napětí představuje vazbu, která brání částicím tělesa k sobě přiblížit nebo se od sebe oddálit je kolmé na rovinu řezu v případě že je
Nauka o materiálu. Přednáška č.4 Úvod do pružnosti a pevnosti
 Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění )
 1 Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění ) 1. Rozšířený Hookeův zákon pro jednoosou napjatost Základním materiálovým vztahem lineární teorie pružnosti
1 Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění ) 1. Rozšířený Hookeův zákon pro jednoosou napjatost Základním materiálovým vztahem lineární teorie pružnosti
Předmět: Ročník: Vytvořil: Datum: ŠČERBOVÁ M. PAVELKA V. NAMÁHÁNÍ NA OHYB A) NOSNÍKY NA DVOU PODPORÁCH ZATÍŽENÉ SOUSTAVOU ROVNOBĚŽNÝCH SIL
 Předmět: Ročník: Vytvoři: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 9. ČERVNA 2013 Název zpracovaného ceku: NAMÁHÁNÍ NA OHYB A) NOSNÍKY NA DVOU PODPORÁCH ZATÍŽENÉ SOUSTAVOU ROVNOBĚŽNÝCH SIL ÚLOHA 1
Předmět: Ročník: Vytvoři: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 9. ČERVNA 2013 Název zpracovaného ceku: NAMÁHÁNÍ NA OHYB A) NOSNÍKY NA DVOU PODPORÁCH ZATÍŽENÉ SOUSTAVOU ROVNOBĚŽNÝCH SIL ÚLOHA 1
Zapojení odporových tenzometrů
 Zapojení odporových tenzometrů Zadání 1) Seznamte se s konstrukcí a použitím lineárních fóliových tenzometrů. 2) Proveďte měření na fóliových tenzometrech zapojených do můstku. 3) Zjistěte rovnici regresní
Zapojení odporových tenzometrů Zadání 1) Seznamte se s konstrukcí a použitím lineárních fóliových tenzometrů. 2) Proveďte měření na fóliových tenzometrech zapojených do můstku. 3) Zjistěte rovnici regresní
Libor Kasl 1, Alois Materna 2
 SROVNÁNÍ VÝPOČETNÍCH MODELŮ DESKY VYZTUŽENÉ TRÁMEM Libor Kasl 1, Alois Materna 2 Abstrakt Příspěvek se zabývá modelováním desky vyztužené trámem. Jsou zde srovnány různé výpočetní modely model s prostorovými
SROVNÁNÍ VÝPOČETNÍCH MODELŮ DESKY VYZTUŽENÉ TRÁMEM Libor Kasl 1, Alois Materna 2 Abstrakt Příspěvek se zabývá modelováním desky vyztužené trámem. Jsou zde srovnány různé výpočetní modely model s prostorovými
MAGNETICKÉ POLE. 1. Stacionární magnetické pole I I I I I N S N N
 MAGETCKÉ POLE 1. Stacionární magnetické poe V E S T C E D O R O Z V O J E V Z D Ě L Á V Á Í je část prostoru, kde se veičiny popisující magnetické poe nemění s časem. Vzniká v bízkosti stacionárních vodičů
MAGETCKÉ POLE 1. Stacionární magnetické poe V E S T C E D O R O Z V O J E V Z D Ě L Á V Á Í je část prostoru, kde se veičiny popisující magnetické poe nemění s časem. Vzniká v bízkosti stacionárních vodičů
7 Kvantová částice v centrálně symetrickém potenciálu.
 7 Kvantová částice v centráně symetrickém potenciáu. Představte si, že hodíte kámen do vody a chcete popsat vny, které vzniknou. Protože hadina je D, můžete vny popsat funkcí f x, y. Ae pokud jste chytří,
7 Kvantová částice v centráně symetrickém potenciáu. Představte si, že hodíte kámen do vody a chcete popsat vny, které vzniknou. Protože hadina je D, můžete vny popsat funkcí f x, y. Ae pokud jste chytří,
ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady
 Teorie plasticity VŠB TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ KATEDRA PRUŽNOSTI A PEVNOSTI ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady 1. ŘEŠENÝ PŘÍKLAD NA TAH ŘEŠENÍ DLE DOVOLENÝCH NAMÁHÁNÍ
Teorie plasticity VŠB TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ KATEDRA PRUŽNOSTI A PEVNOSTI ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady 1. ŘEŠENÝ PŘÍKLAD NA TAH ŘEŠENÍ DLE DOVOLENÝCH NAMÁHÁNÍ
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí
 Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
Schöck Isokorb typ Q, Q-VV, QP, QP-VV
 Schöck Isokorb typ, -VV, P, P-VV Schöck Isokorb typ, -VV, P, P-VV P Schöck Isokorb typ Používá se u podepřených ů. Prvek přenáší kadné posouvající síy. Schöck Isokorb typ -VV Používá se u podepřených ů.
Schöck Isokorb typ, -VV, P, P-VV Schöck Isokorb typ, -VV, P, P-VV P Schöck Isokorb typ Používá se u podepřených ů. Prvek přenáší kadné posouvající síy. Schöck Isokorb typ -VV Používá se u podepřených ů.
Kombinace ohybu a tlaku
 1 Kapitoa 1 Kombinace ohybu a taku 1.1 Úvod ři současném působení příčných a osových si se nosník(obr. 1.1) nachází, v ceém procesu zatěžování, v prohnutém stavu. Vzniká kombinace ohybu a taku. Nejedná
1 Kapitoa 1 Kombinace ohybu a taku 1.1 Úvod ři současném působení příčných a osových si se nosník(obr. 1.1) nachází, v ceém procesu zatěžování, v prohnutém stavu. Vzniká kombinace ohybu a taku. Nejedná
Jednoduché výpočty ve fyzice živé přírody
 Jednoduché výpočty ve fyzice živé přírody ZDENĚK BOCHNÍČEK Přírodovědecká fakuta MU, Brno Abstrakt. V příspěvku je ukázáno někoik příkadů použití jednoduchých fyzikáních modeů na popis dějů v živé přírodě,
Jednoduché výpočty ve fyzice živé přírody ZDENĚK BOCHNÍČEK Přírodovědecká fakuta MU, Brno Abstrakt. V příspěvku je ukázáno někoik příkadů použití jednoduchých fyzikáních modeů na popis dějů v živé přírodě,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ. ING. JIŘÍ KYTÝR, CSc. ING. PETR FRANTÍK, Ph.D. STATIKA I MODUL BD03-MO1 ROZŠÍŘENÝ PRŮVODCE
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ ING. JIŘÍ KYTÝR, CSc. ING. PETR FRANTÍK, Ph.D. STATIKA I MODUL BD3-MO ROZŠÍŘENÝ PRŮVODCE STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ ING. JIŘÍ KYTÝR, CSc. ING. PETR FRANTÍK, Ph.D. STATIKA I MODUL BD3-MO ROZŠÍŘENÝ PRŮVODCE STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA
Učební text k přednášce UFY102
 Učební text k přeášce UFY0 Lom hranoem ámavé stěny ámavá hrana ámavý úhe ϕ deviace δ úhe, o který je po výstupu z hranou vychýen světený paprsek ežící v rovině komé k ámavé hraně (v tzv. havním řezu hranou),
Učební text k přeášce UFY0 Lom hranoem ámavé stěny ámavá hrana ámavý úhe ϕ deviace δ úhe, o který je po výstupu z hranou vychýen světený paprsek ežící v rovině komé k ámavé hraně (v tzv. havním řezu hranou),
Autor: Vladimír Švehla
 Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
1. Měření hodnoty Youngova modulu pružnosti ocelového drátu v tahu a kovové tyče v ohybu
 Měření modulu pružnosti Úkol : 1. Měření hodnoty Youngova modulu pružnosti ocelového drátu v tahu a kovové tyče v ohybu Pomůcky : - Měřící zařízení s indikátorovými hodinkami - Mikrometr - Svinovací metr
Měření modulu pružnosti Úkol : 1. Měření hodnoty Youngova modulu pružnosti ocelového drátu v tahu a kovové tyče v ohybu Pomůcky : - Měřící zařízení s indikátorovými hodinkami - Mikrometr - Svinovací metr
Definujte poměrné protažení (schematicky nakreslete a uved te jednotky) Napište hlavní kroky postupu při posouzení prutu na vzpěrný tlak.
 00001 Definujte mechanické napětí a uved te jednotky. 00002 Definujte normálové napětí a uved te jednotky. 00003 Definujte tečné (tangenciální, smykové) napětí a uved te jednotky. 00004 Definujte absolutní
00001 Definujte mechanické napětí a uved te jednotky. 00002 Definujte normálové napětí a uved te jednotky. 00003 Definujte tečné (tangenciální, smykové) napětí a uved te jednotky. 00004 Definujte absolutní
Dvě varianty rovinného problému: rovinná napjatost. rovinná deformace
 Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
9. MĚŘENÍ SÍLY TENZOMETRICKÝM MŮSTKEM
 9. MĚŘENÍ SÍLY TENZOMETICKÝM MŮSTKEM Úvod: Tenzometry se používají např. pro: Měření deformací objektů. Měření síly, tlaku, krouticího momentu, momentu síly, mechanického napětí spojů. Měření zatížení
9. MĚŘENÍ SÍLY TENZOMETICKÝM MŮSTKEM Úvod: Tenzometry se používají např. pro: Měření deformací objektů. Měření síly, tlaku, krouticího momentu, momentu síly, mechanického napětí spojů. Měření zatížení
Nosné desky. 1. Kirchhoffova teorie ohybu tenkých desek (h/l < 1/10) 3. Mindlinova teorie pro tlusté desky (h/l < 1/5)
 Nosné desky Deska je těleso, které má jeden rozměr mnohem menší než rozměry zbývající. Zatížení desky je orientováno výhradně kolmo k její střednicové rovině. 1. Kirchhoffova teorie ohybu tenkých desek
Nosné desky Deska je těleso, které má jeden rozměr mnohem menší než rozměry zbývající. Zatížení desky je orientováno výhradně kolmo k její střednicové rovině. 1. Kirchhoffova teorie ohybu tenkých desek
NOSNÍK NA PRUŽNÉM PODLOŽÍ (WINKLEROVSKÉM)
 NOSNÍK NA PRUŽNÉ PODLOŽÍ (WINKLEROVSKÉ) Uvažujeme spojitý nosník na pružných podporách. Pružná podpora - odpor je úměrný zatlačení. Pružné podpory velmi blízko sebe - jejich účinek lze nahradit spojitou
NOSNÍK NA PRUŽNÉ PODLOŽÍ (WINKLEROVSKÉ) Uvažujeme spojitý nosník na pružných podporách. Pružná podpora - odpor je úměrný zatlačení. Pružné podpory velmi blízko sebe - jejich účinek lze nahradit spojitou
F7 MOMENT SETRVAČNOSTI
 F7 MOMENT ETRVAČNOTI Evropský sociání fond Praha & EU: Investujeme do vaší budoucnosti F7 MOMENT ETRVAČNOTI V této části si spočteme některé jednoduché příkady na rotační pohyby a seznámíme se s někoika
F7 MOMENT ETRVAČNOTI Evropský sociání fond Praha & EU: Investujeme do vaší budoucnosti F7 MOMENT ETRVAČNOTI V této části si spočteme některé jednoduché příkady na rotační pohyby a seznámíme se s někoika
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil
 Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
MECHANIKA PRUŽNÉHO TĚLESA. Studijní text pro řešitele FO a ostatní zájemce o fyziku. Bohumil Vybíral. Předmluva 3
 MECHANIKA PRUŽNÉHO TĚLESA Studijní tet pro řešitee O a ostatní zájemce o fyziku Bohumi Vybíra Obsah Předmuva 3 1 ZÁKLADNÍ POZNATKY O PRUŽNOSTI TĚLES 4 1.1 Pevnépružnétěeso........................ 4 1.2
MECHANIKA PRUŽNÉHO TĚLESA Studijní tet pro řešitee O a ostatní zájemce o fyziku Bohumi Vybíra Obsah Předmuva 3 1 ZÁKLADNÍ POZNATKY O PRUŽNOSTI TĚLES 4 1.1 Pevnépružnétěeso........................ 4 1.2
OTÁZKY VSTUPNÍHO TESTU PP I LS 2010/2011
 OTÁZKY VSTUPNÍHO TESTU PP I LS 010/011 Pomocí Thumovy definice, s využitím vrubové citlivosti q je definován vztah mezi součiniteli vrubu a tvaru jako: Součinitel tvaru α je podle obrázku definován jako:
OTÁZKY VSTUPNÍHO TESTU PP I LS 010/011 Pomocí Thumovy definice, s využitím vrubové citlivosti q je definován vztah mezi součiniteli vrubu a tvaru jako: Součinitel tvaru α je podle obrázku definován jako:
ZKOUŠENÍ TEXTILIÍ PŘEDNÁŠKA 10 KONSTRUKČNÍ PARAMETRY PLOŠNÝCH TEXTILIÍ
 ZKOUŠENÍ TEXTILIÍ PŘEDNÁŠKA 10 KONSTRUKČNÍ PARAMETRY PLOŠNÝCH TEXTILIÍ KONSTRUKČNÍ PARAMETRY PLOŠNÝCH TEXTILIÍ U tkanin: Vazba Dostava Pošná hmotnost Objemová měrná hmotnost Pórovitost Toušťka Setkání
ZKOUŠENÍ TEXTILIÍ PŘEDNÁŠKA 10 KONSTRUKČNÍ PARAMETRY PLOŠNÝCH TEXTILIÍ KONSTRUKČNÍ PARAMETRY PLOŠNÝCH TEXTILIÍ U tkanin: Vazba Dostava Pošná hmotnost Objemová měrná hmotnost Pórovitost Toušťka Setkání
- AutoSympo a Kolokvium Božek až , Roztoky -
 automobiového průmysu - AutoSympo a Kookvium Božek 31. 10. až 2. 11. 2017, Roztoky - automobiového průmysu Popis obsahu baíčku WP12VaV Návrh a zkoušky přísušenství pro pnění a vstřikování paiva ve vznětových
automobiového průmysu - AutoSympo a Kookvium Božek 31. 10. až 2. 11. 2017, Roztoky - automobiového průmysu Popis obsahu baíčku WP12VaV Návrh a zkoušky přísušenství pro pnění a vstřikování paiva ve vznětových
SNÍMAČE PRO MĚŘENÍ DEFORMACE
 SNÍMAČE PRO MĚŘENÍ DEFORMACE 8.1. Odporové tenzometry 8.2. Optické tenzometry 8.3. Bezkontaktní optické metody 8.1. ODOPROVÉ TENZOMETRY 8.1.1. Princip měření deformace 8.1.2. Kovové tenzometry 8.1.3. Polovodičové
SNÍMAČE PRO MĚŘENÍ DEFORMACE 8.1. Odporové tenzometry 8.2. Optické tenzometry 8.3. Bezkontaktní optické metody 8.1. ODOPROVÉ TENZOMETRY 8.1.1. Princip měření deformace 8.1.2. Kovové tenzometry 8.1.3. Polovodičové
Pružnost a pevnost. zimní semestr 2013/14
 Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Statika soustavy těles.
 Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
6. Rozptyl Leoš Dvořák, MFF UK Praha, Rozptyl
 K přednášce NUFY8 Teoretická mechanika 6. Rozpty Leoš Dvořák, MFF UK Praha, 14 Rozpty Z předchozí kapitoy umíme spočítat pohyb částice v poi centrání síy. Nyní toho využijeme pro případ ehké částice (napříkad
K přednášce NUFY8 Teoretická mechanika 6. Rozpty Leoš Dvořák, MFF UK Praha, 14 Rozpty Z předchozí kapitoy umíme spočítat pohyb částice v poi centrání síy. Nyní toho využijeme pro případ ehké částice (napříkad
1.9.1 Vyjádření neznámé ze vzorce I
 .9. Vyjádření neznámé ze vzorce I Předpokady: 75, 85 Pedagogická poznámka: Ačkoiv v normání učebnici zabírá vyjadřování ze vzorce jenom tři stránky, věnova jsem ji ceou podkapitou, z někoika důvodů: Autor
.9. Vyjádření neznámé ze vzorce I Předpokady: 75, 85 Pedagogická poznámka: Ačkoiv v normání učebnici zabírá vyjadřování ze vzorce jenom tři stránky, věnova jsem ji ceou podkapitou, z někoika důvodů: Autor
1.1 Shrnutí základních poznatků
 1.1 Shrnutí základních poznatků Pojmem nádoba obvykle označujeme součásti strojů a zařízení, které jsou svým tvarem a charakterem namáhání shodné s dutými tělesy zatíženými vnitřním, popř. i vnějším tlakem.sohledemnatopovažujemezanádobyrůznápotrubíakotlovátělesa,alenapř.i
1.1 Shrnutí základních poznatků Pojmem nádoba obvykle označujeme součásti strojů a zařízení, které jsou svým tvarem a charakterem namáhání shodné s dutými tělesy zatíženými vnitřním, popř. i vnějším tlakem.sohledemnatopovažujemezanádobyrůznápotrubíakotlovátělesa,alenapř.i
Pružnost a plasticita II CD03
 Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Rovinná úloha v MKP. (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v. prostorové úlohy: u, v, w
 Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Cvičební texty 2003 programu celoživotního vzdělávání MŠMT ČR Požární odolnost stavebních konstrukcí podle evropských norem
 2.5 Příklady 2.5. Desky Příklad : Deska prostě uložená Zadání Posuďte prostě uloženou desku tl. 200 mm na rozpětí 5 m v suchém prostředí. Stálé zatížení je g 7 knm -2, nahodilé q 5 knm -2. Požaduje se
2.5 Příklady 2.5. Desky Příklad : Deska prostě uložená Zadání Posuďte prostě uloženou desku tl. 200 mm na rozpětí 5 m v suchém prostředí. Stálé zatížení je g 7 knm -2, nahodilé q 5 knm -2. Požaduje se
Obvody s rozprostřenými parametry
 Obvody s rozprostřenými parametry EO2 Přednáška 12 Pave Máša - Vedení s rozprostřenými parametry ÚVODEM Každá kroucená dvojinka UTP patch kabeu je samostaným vedením s rozprostřenými parametry Impedance
Obvody s rozprostřenými parametry EO2 Přednáška 12 Pave Máša - Vedení s rozprostřenými parametry ÚVODEM Každá kroucená dvojinka UTP patch kabeu je samostaným vedením s rozprostřenými parametry Impedance
Téma 2 Deformace staticky určitých prutových konstrukcí
 Statika stavebních konstrukcí I.,.ročník bakaářského studia Téma Deformace staticky určitých prutových konstrukcí Katedra stavební mechaniky Fakuta stavební, VŠB - Technická univerzita Ostrava Osnova přednášky
Statika stavebních konstrukcí I.,.ročník bakaářského studia Téma Deformace staticky určitých prutových konstrukcí Katedra stavební mechaniky Fakuta stavební, VŠB - Technická univerzita Ostrava Osnova přednášky
Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191
 Název školy Název projektu Registrační číslo projektu Autor Název šablony Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky
Název školy Název projektu Registrační číslo projektu Autor Název šablony Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky
KMITÁNÍ MECHANICKÉHO OSCILÁTORU
 KMITÁNÍ MECHANICKÉHO OSCILÁTORU V echanice jse se zabývai příočarý a křivočarý pohybe, nyní rozeberee třetí zákadní typ pohybu, pohyb kitavý, tedy echanické kitání. Kitající těeso (osciátor) se pohybuje
KMITÁNÍ MECHANICKÉHO OSCILÁTORU V echanice jse se zabývai příočarý a křivočarý pohybe, nyní rozeberee třetí zákadní typ pohybu, pohyb kitavý, tedy echanické kitání. Kitající těeso (osciátor) se pohybuje
VŠB- Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti. Úvod do MKP Napěťová analýza tenzometrického snímače ve tvaru háku
 VŠB- Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti Úvod do MKP Napěťová analýza tenzometrického snímače ve tvaru háku Autor: Michal Šofer Verze 0 Ostrava 20 Zadání: Proveďte
VŠB- Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti Úvod do MKP Napěťová analýza tenzometrického snímače ve tvaru háku Autor: Michal Šofer Verze 0 Ostrava 20 Zadání: Proveďte
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady. Část 1 - Test
 Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Vzpěr, mezní stav stability, pevnostní podmínky pro tlak, nepružný a pružný vzpěr Ing. Jaroslav Svoboda
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřednictvím ICT Název: Téma: Autor: Číslo: Anotace: Mechanika, pružnost pevnost Vzpěr,
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřednictvím ICT Název: Téma: Autor: Číslo: Anotace: Mechanika, pružnost pevnost Vzpěr,
R t = b + b l ŘÍDÍCÍ ÚSTROJÍ. Ackermanova podmínka
 ŘÍDÍCÍ ÚSTROJÍ Souží k udržování nebo ke změně směru jízdy automobiu v závisosti na přání řidiče. Řízení u automobiů je reaizováno natáčením předních ko koem rejdových čepů. Natáčení vnitřního a vnějšího
ŘÍDÍCÍ ÚSTROJÍ Souží k udržování nebo ke změně směru jízdy automobiu v závisosti na přání řidiče. Řízení u automobiů je reaizováno natáčením předních ko koem rejdových čepů. Natáčení vnitřního a vnějšího
