Stabilita přímých prutů

Transkript

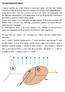
1 Kapitoa 1 Stabiita přímých prutů 1.1 Úvod Předpokádejme, že tvar stačovaného přímého prizmatického prutu je ideání. To znamená, že předpokádáme jeho přímý tvar, výsedná sía působí v jeho podéné ose a materiá je homogenní. Oba konce jsou uoženy koubově a třecí síy v uožení neuvažujeme. Chování prutu bude závisé na poměru jeho déky a geometrických charakteristik průřezu(obr. 1.1). U krátkého prutu budou vnitřní síy, reprezentované normáovým takovým napětím, s rostoucí siou narůstat. Osa prutu zůstane přímá v ceém procesu zatěžování, prut se nachází ve stabiní rovnováze mezi vnitřními a vnějšími siami. v() v() v v v v Obrázek 1.1: Štíhý prut je na počátku zatěžování rovněž ve stavu stabiní rovnováhy. Přesvědčímeseotomtak,žepřímýprutmírněvybočímepříčnousiou(obr.1.1vpravo) a uvoníme. Prut se vrátí do přímé poohy a obnoví se stabiní rovnováha vnitřních a vnějších si. Při daším zvyšování síy na určitou veikost prut tuto vastnost ztratí. 1

2 Po vybočeníosy prutuse prutpřitéto veikosti síy dostabiní poohy nevrátí a zůstane v prohnutém stavu, který mu by uděen. Tento stav rovnováhy označujeme jako indiferentní. Sía dosáha kritické hodnoty. Prut je nyní při vybočení namáhánkromětakutakéohybem.dašíminepatrnýmzvýšenímkritickésíy kr nebo narůstáním průhybu nastane zhroucení prutu. Rovnováha je abiní(nestabiní). Anaogii k uvedené definici stabiní, indiferentní a nestabiní rovnováhy uvedeme z mechaniky tuhých těes(obr. 1.2). Těeso kuička je ve stabiní rovnováze jestiže se povychýenívrátízpětdovýchozípoohy(obr.1.2vevo).naobr.1.2vpravojenaznačen abiní stav rovnováhy. Sebemenší impus způsobí samovoný pohyb těesa, který se zastaví až při zaujmutí zcea jiné rovnovážné poohy. Stav mezi stabiní a abiní rovnováhou je znázorněn na obr. 1.2 uprostřed. Přechod mezi oběma stavy je tvořen indiferentní rovnováhou. Kuička zůstává v ibovoné vychýené pooze. Rozhodující Obrázek 1.2: Stabiní rovnováha(vevo), indiferentní rovnováha(uprostřed) a abiní rovnováha(vpravo). proposouzenístabiityštíhýchprutůjestanoveníkritickésíy kr.vzpěrypoužívané v prai mají od ideáního geometrického tvaru odchyky vznikající pode použité technoogie v průběhu výroby a při apikaci výrobku. Mohou se vyskytovat i materiáové nehomogenity. Zde budeme kritickou síu určovat na prutech ideáního tvaru a viv různých odchyek a daších vivů zahrneme do součinitee bezpečnosti. Při sestavování rovnic rovnováhy jsme v předchozích kapitoách zanedbávai změny tvaru těes, které vznikay v důsedku působení vnějších si. Postupovai jsme pode teorie 1. řádu, pode které ze, vzhedem k zanedbatené veikosti deformací vůči rozměrům vyšetřovaných těes, sestavovat rovnice rovnováhy na nedeformovaném těese. Indiferentnímustavurovnováhystačovanéhoprutukritickousiou kr odpovídá prohnutý stav, vyvoaný příčnou siou. Po odstranění příčné síy zůstane prut v prohnutém stavu(obr. 1.1 vevo) jen za působení ohybového momentu M oz () = kr v() (1.1) Při vyšetřování stabiity přímých prutů musíme tudíž vycházet z přetvořené střednicepodeteorie2.řádu.veikostkritickésíy kr jezávisánatuhostistačovaného prutu. To znamená na rozměrech, materiáu, ae také na uožení jeho konců. Pode uožení konců prutu se rozišují čtyři zákadní případy stabiity vzpěru přímých prutů (obr.1.3). V technické prai ze obvyke sedované případy zařadit do jednoho ze čtyř zákadních případů a stanovit minimání veikost kritické síy. Na obrázku 1.3a je uveden prvnípřípadvzpěru.najednomkoncijevzpěravetknutaadruhýkonecjevoný.vdruhém případě vzpěru(obr. 1.3b) jsou oba konce uožené koubově s možností osového 2

3 posuvu. V třetím případě(obr. 1.3c) je jeden konec vzpěry vetknutý, druhý konec je uožený koubově s možností osového posuvu. Ve čtvrtém případě jsou oba konce prutu (obr. 1.3d) vetknuté s možností osového posuvu jednoho konce stačovaného prutu. Vetknutí předpokádáme nepoddajná. a b c d Obrázek 1.3: 1.2 Euerova kritická sía První případ vzpěru Přivýpočtukritickésíy kr vycházímezindiferentníhostavurovnováhy.připůsobení této síy může být prut vychýen(obr. 1.4). Veikost průhybu v() je v mezích Hookeova zákona ibovoná, tj. c je ibovoné vychýení konce prutu. Vobecnémřezu ξjeprůhyb v().ohybovýmomentvtémžeřezu M o () = kr (c v()) (1.2) Diferenciání rovnice průhybové čáry, za předpokadu maých výchyek má tvar Zavedeme v () = d2 v() d 2 Po úpravě má rovnice(1.3) tvar = M o() EJ z = + kr EJ z (c v()) (1.3) kr EJ z = α 2 (1.4) v () + α 2 v() = α 2 c (1.5) 3

4 c kr v() c-v() ξ v Obrázek 1.4: Rov.(1.5) je nehomogenní ineární diferenciání rovnice 2. řádu s konstantními činitei. Její partikuární integrá je zřejmě v p = c a obecný integrá nehomogenní rovnice má tvar kde AaBjsouintegračníkonstanty. v() = Asinα + Bcosα + c, (1.6) Vevetknutípro = je v() =.Pakintegračníkonstanta B = c Ve vetknutí je současně okrajová podmínka pomocí které stanovíme druhou integrační konstantu v () =, (1.7) A = Po dosazení konstant A a B do rov.(1.6) obdržíme rovnici průhybové čáry vzpěry s jedním vetknutým koncem ve tvaru v() = c(1 cosα) = cη(), (1.8) kde cjevastněibovonáampitudakřivky η() = (1 cosα).prokoncovýbod vzpěry je průhyb v() = c = c(1 cosα), odkud stanovíme ccosα = (1.9) 4

5 Pro spnění rovnice mohou nastat dva případy: a)buďje c = b)nebo cosα = prutjepřímýavzpěrnásía < kr,rovnováhajestabiní; cožznamená,žejemožnáibovonávýchyka cvmezíchhookeovazákona jednáseoindiferentnírovnováhuasía = kr aproargument αpyne α = k π 2, (1.1) kde k = 1,3,5... Pomocí rovnice(1.4) určíme kritickou síu kr = α 2 EJ z = k2 ( π ) 2EJz 2 (1.11) 2 Minimání veikost kritické síy pro první případ vzpěru určíme pro k = 1 ze vztahu I kr = π2 4 EJ zmin 2 (1.12) K případnému prohnutí prutu dochází koem osy, ke které je kvadratický moment průřezu Jminimání.Vpředchozíchvztazíchjsmepředpokádai,že J min = J z. Znovu je vhodné připomenout, že v rov.(1.3) jsme předpokádai patnost Hookeova zákona, tudíž vztah pro kritickou síu(1.12) ze použít pouze v případě, že kritické napětí nepřestoupí mez úměrnosti materiáu vzpěry σ kr = I kr A σ u (1.13) ProbémystabiitypřímýchprutůřešiLeonardEuer.Protosekritickásía kr často označujeanazývájakoeuerova ε. Tvary průhybové čáry vzpěry 1. případu, odpovídající indiferentní rovnováze pro k = 1,3,5...jsouuvedenynaobrázcích1.5Tytodašítvaryjsouabiníaprotovyžadují k dosažení vyšších hodnot kritické síy boční podporu Druhý případ vzpěru Dokonae přímý prizmatický prut, zatížený osovou siou působící v těžištti průřezu je uožen oběma konci koubově s možným osovým posuvem jednoho koubu(obr. 1.6). V indiferentním stavu rovnováhy prutu je možný průhyb s deformacemi v mezích Hookeova zákona. V obecném řezu ξ působí ohybový moment Diferenciání rovnice průhybové čáry má tvar M o () = kr v() (1.14) v () = M o() EJ z = kr EJ z v() (1.15) 5

6 kr1 = π2 4 E J z min 2 kr3 = 9 π2 4 E J z min 2 kr5 = 25 π2 4 E J z min 2 /3 /5 k=1 k=3 k=5 Obrázek 1.5: Poúpravěje kde opět v () + α 2 v() =, (1.16) α 2 = kr EJ z Rovnice(1.16) je homogenní ineární diferenciání rovnice druhého řádu s konstantními činitei. Její integrá je v() = Acosα + Bsinα (1.17) A, B jsou integrační konstanty, které stanovíme z násedujících okrajových podmínek: 1. pro = zrovnice(1.17)pyne Rovnice průhybové čáry je sinusoida o ampitudě B. 2. pro = zrov.(1.19)obdržíme v() = = A (1.18) v() = Bsinα (1.19) v() = = Bsinα (1.2) Podmínka(1.2)jespněnajestiže B = nebo sinα =.Vprvnímpřípaděpode rov.(1.19) nevzniká, pro ibovonou síu, průhyb, což znamená, že se jedná o statickou rovnováhuasía neníkritická.vdruhémpřípaděje sinα =,když α = kπ (1.21) 6

7 kr v() ξ v Obrázek 1.6: a k = 1,2,3... (1.22) Minimáníhodnotukritickésíydruhéhopřípaduvzpěruurčímepro k = 1aJ zmin II kr = π2ej zmin 2 (1.23) Vyšší hodnoty k poskytují větší kritické síy, ae tvar průhybové čáry v indiferentním stavu rovnováhy vyžaduje opět boční podporu(obr. 1.7). v() = Bsin kπ Vybočení vzpěry nastane v rovině nejmenší ohybové tuhosti. Z toho je patrné, že pruty s rozdínými kvadratickými momenty, např. I nebo U profi, jsou pro apikace jako vzpěryméněvhodné.optimáníjsouprutysprůřezy,kde J 1 = J 2 jakojekruhový průřez, čtvercový průřez nebo trubka. Navrhování vzpěry z více profiů je výhodné sestavittak,abyrozdímezi J ma a J min byconejmenší Třetí případ vzpěru Uožení konců vzpěry třetího případu je sožitější. Jeden konec je uožen pode prvního případu, druhý pode druhého případu vzpěru(obr. 1.8). Toznamená,žejedenkonecjevetknutýadruhýjeuoženkoubověsmožnostíposuvu koubu ve směru přímé osy prutu. Při prohnutí vzpěry, odpovídající indiferentnímu stavurovnováhy,vznikávkoubovémuoženípřipůsobeníosovésíy kr horizontání sía H.Ohybovýmomentodtěchtosivobecnémřezu ξjeroven M o () = kr v() H( ) (1.24) 7

8 kr1 = π 2 E J z min 2 kr2 = 4 π 2 E J z min 2 kr3 = 9 π 2 E J z min 2 /2 /3 /3 /2 /3 k=1 k=2 k=3 Obrázek 1.7: Vzpěra se nachází v indiferentním stavu rovnováhy mezi vnějšími a vnitřními siami a průhyb prutu je v mezích patnosti Hookeova zákona. Diferenciání rovnice průhybové čárymápaktvar Opět zavedeme v () = M o() EJ z = [ kr v() H ] ( ) EJ z kr α 2 = kr EJ z, tj. (1.25) Integrá diferenciání rovnice(1.26) má tvar v () + α 2 v() = α 2 H kr ( ) (1.26) v() = Acosα + Bsinα + v p (1.27) A, Bjsouintegračníkonstantyav p partikuárníintegrá,kterývzávisostinapravé straně rov.(1.26) odhadneme ve tvaru v p = K( ), (1.28) kde K je konstanta, kterou získáme pro dosazení odhadu partikuárního integráu(1.28) do rov.(1.26) + α 2 K( ) = α 2 H kr ( ), odkud K = H kr a v p = H kr ( ) (1.29) 8

9 kr H v() ξ v Obrázek 1.8: Obecné řešení nehomogenní rov.(1.26) je v() = Acosα + Bsinα + H ( ) (1.3) kr Nyní stanovíme integrační konstanty A, B z okrajové podmínky uožení konce vzpěry: 1. pro = je v() = a 2. pro = je v () = a A = H kr B = 1 α H kr Hodnoty integračních konstant dosadíme do řešení(1.3), takže pro průhyb obecného místa osy vzpěru v indiferentním stavu rovnováhy pyne: v() = H ( ) sinα cosα + (1.31) kr α Průhybvzpěryvmístěkoubu,tj.vmístě = jezavšechpodmíneknuový: v() = = H ( ) sinα cosα (1.32) kr α Ztvarutétorovnicejepatrné,žemohounastatdvaodišnépřípady.Buďje H kr = : (1.33) Toznamená,žejepříčnásía H =,vzpěraneníprohnutá-jednáseostabiní rovnováhuapůsobícíosovátakovásía < kr.pokudjesía H,pakpode rov.(1.32) je sinα cosα = (1.34) α 9

10 nebo po úpravě tgα = α (1.35) Názorný grafický způsob stanovení kořenů této transcendentní rovnice je uveden na y tg (α) y = α π/4 α = 4,493 α π/2 π/2 π/2 Obrázek 1.9: obr Rovnici(1.35) vyhovuje kořen α =, což je nezatížená vzpěra. Daší kořen je α = 4,493, (1.36) tudíž α 2 2 = 4, ,19 2π 2, odkud nejmenší kritická sía pro třetí případ vzpěru je nebo přesněji III kr III kr. = 2π 2EJ zmin 2 (1.37). = π 2EJ zmin (,7) 2 (1.38) Čtvrtý případ vzpěru U čtvrtého případu jsou oba konce vzpěry(obr. 1.1) vetknuté, s možností posuvu ve vetknutí jednoho konce ve směru podéné osy. Jako u předešých případů předpokádáme, že vzpěra je přímá, prizmatická, materiá je homogenní a vetknutí nepoddajné. Je-i vzpěra opět v indiferentním stavu rovnováhy, je možný ibovoný stabiní průhyb s výchykou v mezích patnosti Hookeova zákona. V důsedku průhybu vzpěry působí vkaždémvetknutídvojice M.Výsednýohybovýmomentvobecnémřezu ξjedán vztahem M o () = kr v() M (1.39) 1

11 kr M v() ξ M v kr Obrázek 1.1: Diferenciání rovnice průhybové čáry má tvar Zavedeme-i opět v () = M o() EJ z = 1 EJ z (M kr v()) α 2 = kr EJ z, má diferenciání rovnice po úpravě tvar v () + α 2 v() = α 2 M kr (1.4) Je to nehomogenní ineární rovnice 2. řádu s konstantními koeficienty. řešení je opět určeno součtem obecného integráu homogenní rovnice a integráu partikuárního v() = Acosα + Bsinα + v p, kde partikuární integrá je pode tvaru pravé strany diferenciání rovnice(1.4) roven konstantě.podosazení v p =konst.dodiferenciánírovnicestanovíme v p = M kr Konečný tvar obecného integráu nehomogenní rovnice(1.4) je v() = Acosα + Bsinα + M kr (1.41) Integrační konstanty A, B určíme z počátečních podmínek: 1. pro = je v() = = A + M kr A = M kr 11

12 2. pro = jerovněž v () = = αb.jeikož α = B = ( kr EJ z ) 1/2 je Obecná rovnice průhybu pro dané počáteční podmínky je v() = M kr (1 cosα) (1.42) Ve druhém vetknutí vzpěry pro = je v() = 1 cosα =, tojest cosα = 1 to patí pro všechna α = k2π, (1.43) kde k =,1,2,3,... Z rov.(1.43) po úpravě stanovíme kritickou síu α 2 2 = k 2 4π 2 ; kr EJ z 2 = k 2 4π 2 Pro nejmenší kritickou síu voíme k = 1 min IV kr = 4π 2EJ zmin 2 (1.44) Srovnáme-i výsedné vztahy kritické síy pro uvedené zákadní případy stabiity přímých prutů(1.12)(1.23)(1.37)(1.44) je patrné, že je ze vyjádřit vztahem kde n i projednotivépřípadyvzpěruje i kr = ε = n i π 2EJ min 2, (1.45) n I = 1 4 ; n II = 1; n III = 2; n IV = 4 Někdy se k zápisu jednotného vztahu pro kritické(euerovy) síy zákadních případů vzpěrupožívátakétzv.srovnávacídéka i.vycházísezrovnosti i kr = π2ej min 2 i = n i π 2EJ min 2, (1.46) odkud pro srovnávací déku pyne vztah i = (1.47) 1/2 (n i ) Závisostikoeficientů n i asrovnávacíchdéekprozákadnípřípadyvzpěrujsouuvedeny na obr

13 I kr II kr III kr IV kr H kr = I /2 = II = 1,41. III = 2. IV n I = 1/4 n II = 1 n III = 2 n VI = 4 Obrázek 1.11: 1.3 Podmínka stabiity ve vzpěru v neineární obasti Kritické síy pro jednotivé případy vzpěru, odvozené z diferenciání rovnice průhybové čáry(rovnice 1.3), patí pouze v oboru patnosti Hookeova zákona. Při působení kritické síy kr navzpěrujeprotomaimánínapětírovnomeziúměrnosti σ kr = kr A σ u, (1.48) kde σ kr jekritickénapětí,kterésetéžnazýváeuerovonapětíaoznačujese σ ε.spoužitím vztahu(1.45) je toto napětí Jeikož poměr σ kr = σ ε = ε A = n iπ 2EJ min 2 A (1.49) J min A = i2 min, (1.5) je kvadrát minimáního pooměru kvadratického momentu průřezu, ze vztah(1.49) pro kritické Euerovo napětí vyjádřit násedovně σ kr = σ ε = n i π 2 E ( ) 2 (1.51) Poměr i min = λ se nazývá štíhostní poměr nebo krátce štíhost prutu. Graf závisosti kritického napětínaštíhostnímpoměrujeznázorněnnaobr Bod M (σ u,λ M )jeurčen 13 i min

14 mezníhodnotoukritickéhonapětí maσ kr = σ u a λ M jemezníštíhostvzpěry,v obasti patnosti Hookeova zákona, stanovená z rov.(1.51) ( ) ni E 1/2 λ M = π (1.52) σ u σ kr M (σ u, λ M ) σ u Euerova obast λ M / i = λ Obrázek 1.12: Z grafu na obr je patrné, že podmínku omezující patnost Hookeova zákona, danou rovnicí(1.48), ze též vyjádřit pomocí mezní štíhosti i λ M (1.53) Poznamenejme,žemezníštíhost λ M jezávisápouzenamateriáovýchcharakteristikách a podmínkách uožení konců vzpěry(rov. 1.52). Taknapř.provzpěruskonciuoženýmipode2.případu(n = 1)vyrobenouzocei (E = 2, 1 5 MPa; σ u = MPa)jemezníštíhostnípoměrpoderov.(1.52) λ M = ( ) i M ( ) E 1/2 = π 1 σ u Má-ivzpěranapř.kruhovýprůřezoprůměru d,je i = d/4apak ( ) i M = ( ) 4 d M = 1 Z uvedeného vztahu ze určit mezní déku vzpěry, pro kterou ze ještě použít rovnici pro kritickou Euerovu síu(rov. 1.45) 25d 14

15 1.4 Výpočet kritické síy v obasti pastických deformací Pro dimenzování vzpěry v obasti, kde vznikají pastické deformace, kde kritické napětí je vyšší než mez úměrnosti, neze najít jednoznačně patné teoretické řešení, anaogické k Euerovu řešení ve zcea eastické obasti. Pro nízké hodnoty štíhosti(obr. 1.12) přechází vzpěr v prostý tak. Dimenzování je zde zaoženo na podkadech získaných četnými eperimenty, provedenými pro různé tvary průřezů, štíhostní poměry a materiáy. Stanovení kritického napětí v pastické obasti můžeme v podstatě určit třemi zákadními postupy Zavedení redukovaného moduu pružnosti Snahou tohoto přístupu je rozšíření Euerových vztahů i za mez úměrnosti zavedením proměnivého moduu pružnosti pro ceý obor štíhostních poměrů(obr. 1.13). Tzv. redukovanýmodupružnosti E red respektujeneineárnízávisostnapětí σnapoměrném prodoužení ε. Vztah σ, E σ P E B P dσ dε σ u U E t ε Obrázek 1.13: dσ dε = tgβ = E t respektujeokamžitoutuhostmateriáuvzpěry. E t jetzv.tečný modu pružnosti vbodě B(obr.1.13).Zavedenímtečnéhomoduu E t místoyoungovamoduu EdoEuerových vztahů pro kritické napětí se ukázao vhodné pouze u tenkostěnných průřezů, jinak vznikají příiš hmotné konstrukce. Engesser později odvodi pro vzpěru obdéníkového průřezu redukovaný modu pružnosti používaný za předpokadu, že pastické deformace vznikají pouze v části průřezu a na vypuké straně dochází v důsedku prohnutí k pokesu napětí 4EE t E red = ( E ) 2 (1.54) + Et Kritická sía se stanoví z upraveného Euerova vztahu i kr = n iπ 2E redj min 2 (1.55) Vztah je možné použít i pro jiné jednoduché pné průřezy zavedením korekčních faktorů. 15

16 1.4.2 Řešení pode Tetmajera Někteříautořinahrazujívpružnopastickémrozsahu(σ kr > σ u )mezníkřivkustabiity pode Euera(obr. 1.12) body získanými eperimentáně. Eperimentání křivka má obvykeseuerovoupoytropouspoečnýbod (λ M,σ u )nebospoečnoutečnuvtomto bodě. V naší prai se často požívá Tetmajerův vztah, který reprezentuje přímkovou závisost v obasti pastických deformací(obr. 1.14). σ kr Tetmajer σ M Euer σ TET σ u λ λ λ M Obrázek 1.14: KritickénapětíprooceovévzpěrypodeTetmajeraσ TET stanovímezrovnicemezní přímky(obr. 1.14) σ kr = σ TET = σ M (σ M σ u ) λ λ M (1.56) Pro houževnaté materiáy je mezní napětí rovno mezi kuzu v taku t.j. σ M = σ kd, σ TET = σ kd (σ kd σ u ) λ λ M Pro křehké materiáy je mezní napětí rovno mezi pevnosti v taku σ M = σ pd V odborné iteratuře najdeme rovnici(1.56) ve tvaru σ TET = a bλ, (1.57) kde a,b,jakjepatrnozrov.(1.56),jsoumateriáovékonstanty.proitinuadaší křehké materiáy má Tetmajerova rovnice paraboickou závisost(obr. 1.15a) σ TET = a bλ + cλ 2 (1.58) 16

17 Tak např. pro určitou konstrukční oce se kritické napětí stanoví pode vztahu(1.52): σ kr = σ TET = λ, a = 36; b =,61 82 Kritická sía určená z Euerova vztahu(1.46) je z hediska materiáových vastností závisápouzenamoduupružnostie,kterýseuoceiisrůznoumezípevnostiprakticky nemění. Na obrázku 1.15b jsou uvedeny tři podmínky určující kritická Tetmajerova napětí ve vzpěrách vyrobených ze tří materiáů o různých mechanických vastnostech. Z obrázku je patrný viv zvýšení mechanických vastností materiáu na stabiitu vzpěry v pastické obasti. σ kr Tetmajer Euer σ TET σ kr σ TET σ pd3 σ pd2 σ M σ ε σ pd1 σ ε σ u λ M a λ b λ Obrázek 1.15: Součinite vzpěrnosti Při výrobě vzpěr se často požívá omezený počet druhů materiáů. V takovém případě ze kritické napětí v eastické i pastické obasti tabeovat v závisosti na štíhostním poměru.vtabuce1.1jeuvedentzv. součinitevzpěrnosti c,stanovenýpoměrem c = σ mez σ kr, (1.59) kdezavztažnénapětí σ mez seobvykezavádímezkuzuvtaku σ kd.ztétorovnice určíme kritické napětí σ kr = σ kd c a kritickou síu kr = σ kr A = σ kd A (1.6) c Příkad hodnot součiniteů vzpěrnosti v závisosti na štíhostním poměru λ, pode normy ČSN511,jeuvedenvtabuce.1.1. Příkad 1.1: Postup při dimenzování prutů na vzpěr Máme za úko navrhnout pro oceovou vzpěru kruhového průřezu, koubově uoženou, 17

18 Součinite vzpěrnosti c štíhost λ Oce137 Oce152 Dřevo 1 1,3 1,3 1,2 2 1,5 1,5 1,1 3 1,8 1,9 1,19 4 1,12 1,14 1,3 5 1,17 1,21 1,43 6 1,24 1,32 1,59 7 1,33 1,47 1,78 8 1,44 1,68 2,3 9 1,59 1,95 2,37 1 1,77 2,26 2, ,99 2,63 3, ,23 3,3 4,9 13 2,51 3,48 4, ,82 3,97 5, ,15 4,49 6, ,51 5,5 7, ,89 5, ,3 6, ,73 6,94-2 5,18 7,65 - Tabuka 1.1: Součinitee vzpěrnosti de ČSN přípustný průměr d. Vzpěra je stačována siou = 25 kn. Mechanické vastnosti použitéoceijsou: E = 2,1 1 5 MPa; σ kd = 36MPa; σ u = 31MPa.Materiámá stejnémechanickévastnostivtahuitaku.minimánípožadovanábezpečnost k kr = 4 adékavzpěry = 1m. Postup výpočtu: Ze zadaných vstupních dat neze určit štíhostní poměr λ, není známý průměr vzpěry. Neze proto stanovit zda bude úoha řešena pode Euerova nebo Tetmajerova vztahu (obr. 1.14), tj. v obasti eastické nebo pastické. V takovém případě zahájíme výpočet kritické síy pode Euera odkud stanovíme a průměr vzpěry kr = ε = π 2EJ min 2 = k kr, (P-1.a) J = 2 π 2 E k kr = π 2 2, = mm 4 ( ) 64J 1/4 d 1 = π ( ) /4 = 56mm (P-1.b) π 18

19 Nyní můžeme určit štíhostní poměr vzpěry a porovnat ho s mezní štíhostí(1.52) λ = i = 4 = 4 13 d 1 56 = 71, 43 (P-1.c) ( ) E 1/2 ) 2, /2 λ M = π = π( = 81,77 (P-1.d) σ u 31 Ze srovnání numerických výsedků rovnic(p-1.c) a(p-1.d) vypývá, že výpočet průměru vzpěry d 1 podeeueranevyhovuje, λ < λ M.ÚohujenutnétudížřešitpodeTetmajera, kde patí σ kr = σ TET = σ kd (σ kd σ u ) λ 4 = σ kd (σ kd σ u ) λ M dλ M Zároveň patí (P-1.e) σ kr = kr A = 4k kr πd 2 (P-1.f) Dáme-i do rovnosti rovnice(p-1.e) a(p-1.f), tak po úpravě dostaneme kvadratickou rovnici σ kd d 2 (σ kd σ u ) 4 d 4k kr =, (P-1.g) λ M π odkud d 1,2 = 62,97mm a 56,17mm Průměr vzpěry voíme d = 63mm 1.5 Přibižné řešení kritické síy Sožitější případy řešení stabiity přímých prutů v pružné obasti, tj. stanovení kritické síy, se určuje pomocí přibižných metod. Jedná se o případy, kdy vnější osové síy působí mimo koncové řezy vzpěry nebo o pruty s proměnivými průřezy. Nejčastěji používanou přibižnou metodou je Rayeighova energetická metoda a také metoda postupných aproimací. Přibižnost metod spočívá ve vobě funkce průhybové křivky a spnění okrajových podmínek Rayeighova energetická metoda Kritickému zatížení vzpěry odpovídá indiferentní stav rovnováhy, který v rámci eastických deformací umožňuje ibovoné prohnutí prutu(obr. 1.16). Vychýením přímého prutu do prohnutého stavu se změní jeho deformační energie o přírůstek práce vnitřníchsi U avnějšísía vykonápráci W naposuvu u.vdůsedkuindiferentní rovnováhy je pro ibovoné prohnutí přírůstek práce vnitřních a vnějších si stejný U = W (1.61) 19

20 u d ξ ds v() dv() v Obrázek 1.16: Přírůstek deformační energie U od ohybu určíme pode vztahu U = 1 Mo 2() d (1.62) 2 EJ min a práci vnější síy Ohybovýmoment,vrovnici(1.62),vřezu ξ takže deformační energie () W = kr u (1.63) M o () = kr v(), U = 2 kr 2 [v()] 2 EJ min d (1.64) Pro stanovení posuvu koubu u(rov. 1.63) je nutné určit rektifikaci průhybové křivky v(). Z obrázku 1.16 pyne ds = [d 2 + [dv()] 2] 1/2 = d [ 1 + [ v () ] 2 ] 1/2 (1.65) S ohedem na maou křivost průhybové křivky ze tento vztah upravit pode pravide počítánísmaýmičísy(v () 1)natvar [ ds = d [ v () ] ] 2 (1.66) 2 a stanovit posuv působiště síy u = (ds d) = [ [ v () ] ] 2 1 d = [ v () ] 2 d (1.67)

21 Práce vnější síy(1.63) pak je W = kr 2 Z rovnosti prací(1.64) a(1.68) v rov.(1.61) určíme kritickou síu [ v () ] 2 d (1.68) [ v () ] 2 d kr = [v()] 2 EJ d (1.69) Voená funkce průhybové křivky v() je vyjádřena ve tvaru v() = v η(), kde η()jetvarováfunkceav konstanta ampitudakřivky v(),kterásevrovnici(1.69) vykrátí. Tak napříkad zvoíme-i pro koubové uožení prizmatické vzpěry přesnou funkci průhybové křivky ve tvaru, který jsme odvodii z diferenciání rovnice průhybové čáry(1.19) v() = v sin π, je tvarová funkce η() = sin π a kritickou síu určíme pode rovnice(1.69) kr = EJ min ( π ) 2 a η () = π cos 2 π d sin 2 π d cos π = π 2EJ min 2 K výsedku připomeňme, že stanovená kritická sía pode přibižné energetické Rayeighovy metody je za předpokadu voby eaktní průhybové křivky stejná, jako výsedek získaný z diferenciání rovnice průhybové čáry(1.15) vzpěry, nacházející se rovněž v indiferentním stavu rovnováhy. Stejný výsedek potvrzuje patnost podmínky minima deformační energie rovněž u Rayeighovy metody. Z toho vypývá, že každé zvoené funkci, která se iší od vastní funkce, přísuší v obasti eastického přetvoření větší deformační energie Metoda postupných aproimací Metoda postupných aproimací ke stanovení přibižné veikosti kritické síy rovněž apikuje diferenciání rovnici průhybové křivky od ohybových účinků vzpěry, nacházející se v indiferentním stavu rovnováhy vnitřních a vnějších si. K názornosti výkadu použijeme opět vzpěru koubově uoženou. Ohybový moment působící v obecném řezu vzpěry má tvar M o () = v (), (1.7) 21

22 kde v ()jezvoenávstupnífunkceprůhybovékřivky(1.14)a předpokádanákritická veikost vzpěrné síy. Diferenciání rovnice první aproimace průhybové křivky v 1 ()je v 1() = M () EJ = v () EJ (1.71) řešením této rovnice, s respektováním okrajových podmínek, získáme funkci průhybové křivky v 1 ().Kontrouprvníaproimace,zdajevyhovující,zjistímezpoměru v () v 1 () = ζ 1() (1.72) Není-i tento poměr roven konstantě v ceém rozsahu nezávise proměnné, použijeme vprvnímpřibíženízjištěnoufunkci v 1 (),kestanovenídruhéaproimace v 2() = v 1 () EJ (1.73) Stanovenoudruhouaproimacifunkceprůhybovékřivky v 2 ()opětkontroujemepoměrem dvou po sobě násedujících aproimací v 1 () v 2 () = ζ 2() Naznačený postup se opakuje do stavu, kdy poměr dvou po sobě násedujících aproimací v n 1 () = ζ n () = konst±ε, (1.74) v n () kde εjepředemstanovenáprocentníodchykaav n ()jehedanáfunkceprůhybové křivky, pode požadované přesnosti ε. Posedníaproimaci v n ()jsmestanoviizdiferenciánírovnice v n() v n 1 () = (1.75) EJ Současnězeprozjištěnoufunkci v n ()zapsatdiferenciánírovniciprůhybovéčáryve tvaru v n () = v n () kr EJ, (1.76) kde kr jeskutečná kritická sía. Zrovnosti obou diferenciáních rovnic stanovíme kritickou síu v n 1 () kr = (1.77) v n () Příkad 1.2: Jako příkad uvedeme postup při určování kritické síy koubově uožené vzpěry, abychom mohi posoudit výhodnost apikace metody postupných aproimací. Vstupní průhybovoufunkci v ()(1.71)navrhnemerovnukonstantě v.pakdiferenciánírovniceprůhybové křivky je v 1() v = EJ (P-2.a) 22

23 řešením diferenciání rovnice a upatněním okrajových podmínek koubově uožené vzpěry v 1 () = a v 1 () =, zjistíme tvar první aproimace průhybové křivky v 1 () = v 2 Poměr navržené a výpočtem stanovené průhybové křivky ( 2 ) (P-2.b) EJ v () v 1 () seišíažo33%.jenutnépokračovatvzískánídašíaproimacestím,žepoužijeme jakovstupnífunkciprůhybovoukřivku v 1 ()vrov.(p-2.b) ( ) v 2() v 1 () 2 = EJ = v ( 2 ) (P-2.c) EJ 2 řešením diferenciání rovnice je druhá aproimace funkce průhybové křivky Zpoměru v 2 () = v 24 v 1 () v 2 () = ( EJ ) 2 ( ) (P-2.d) v ( 2 ) 2 EJ ( ) v 2 ( ) (P-2.e) 24 EJ napříkadvmístě = 2,určímekritickousíu kr =,9737 π 2EJ 2, (P-2.f) kteráseišíodpřesnéhořešeníccao2,63%.propraktickéúčeyjetopřijatenýrozdí. Dašíaproimace v 2() v 3 () jejižzceavyhovující v 2 () v 3 () = v 72 ( v 24 ( EJ ) 2 ( ) EJ ) 3 ( ) (P-2.g) Uprostředvzpěrypro = 2 jeodchykaodpřesnéhořešeníkritickésíypouze,34%. kr =,9976 π 2EJ 2 Pro zjednodušení jsme určovai kritickou síu z poměru ) (P-2.h) ( v n 1 2 ( ) v n 2 23

24 Věrohodnější výsedek získáme ze stanovení střední hodnoty poměru pode rov.(1.77) ve více bodech. Rovnici můžeme upravit na sumační tvar n = krn = vn 1 ( i ) vn ( i ) (P-2.i) nebo integrání n = krn = v n 1 ()d v n ()d = A n 1 A n kde A n 1 a A n jsouobsahypochomezenékřivkami v n 1 a v n. (P-2.j) 1.6 Neprizmatické vzpěry Symetrická vzpěra Předpokádejme, že tyč je neprizmatická a průřez je symetrický ke střednímu řezu = /2 obr. 1.17a. Konce vzpěry jsou uoženy koubově. kr /2 v() ξ /2 a b kr v Obrázek 1.17: Diferenciánírovniceprůhybovékřivkynamáhanékritickousiou kr je v () = M o() EJ() (1.78) 24

25 Ohybovýmomentvřezu ξ(obr.1.17b) a kvadratický moment průřezu Po dosazení těchto vztahů do rov.(1.78) M o () = kr v() (1.79) J = J() (1.8) v () = kr v(), (1.81) EJ() je patrné, že se jedná o ineární diferenciání rovnici 2. řádu s proměnivým koeficientem J() při v(). Protože její řešení je obtížné i v jednoduchých případech, použijeme řešení přibižné(1.71) nebo opačný postup, kdy voíme v() a z rovnice(1.78) určíme J(). Zvoíme tvar průhybové křivky v() vyhovující okrajovým podmínkám s tím, že křivka musíbýtvintervau vypuká v () < (1.82) Přizatíženíkritickousíou kr sevzpěranacházívindiferentnímstavurovnováhyavypukost zvoené průhybové křivky je v mezích Hookeova zákona ibovoná. Za průhybovou křivku zvoíme např. parabou s okrajovými podmínkami v() = v() =. Její tvar popisuje rovnice v() = c( ), (1.83) kde c je konstanta určující ibovonou vypukost paraboy. Dáe z druhé derivace pyne v () = 2c < (1.84) c > Z rovnice(1.81) stanovíme funkci změny průřezu J() = kr E Pro = /2 je kvadratický moment průřezu maimání Odsud stanovíme podmínku pro kritickou síu v() v () = kr ( ) (1.85) 2E J ( ) kr 2 = 8E 2 = J ma (1.86) kr = 8 EJ ma 2 = k, (1.87) kde k je součinite bezpečnosti určující veikost síy, zajišťující stabiní rovnováhu vzpěry. Proměnivost kvadratického průřezu vzpěry stanovíme z poměru J() J ma = kr ( ) 2E ( ) = 4 kr 2, (1.88) 8E 2 25

26 odkud je např. pro kruhový průřez změna průměru d() vzpěry určena vztahem ( ) ( ) 1/4 d() = d ma 4 2 (1.89) Koncevzpěry,vzhedemkd() = d() = seupravujízpůsobemnaznačenýmna obr. 1.17a, pode podmínky otačení σ ot A = kr k, (1.9) odkudurčímeupravenouveikostkoncovéhoprůřezuvzpěry A = A()sohedemna předepsanénapětí σ ot A kr kσ ot (1.91) 26

27 Obsah 1 Stabiita přímých prutů Úvod Euerovakritickásía Prvnípřípadvzpěru Druhýpřípadvzpěru Třetípřípadvzpěru Čtvrtýpřípadvzpěru Podmínkastabiityvevzpěruvneineárníobasti Výpočetkritickésíyvobastipastickýchdeformací Zavedeníredukovanéhomoduupružnosti ŘešenípodeTetmajera Součinitevzpěrnosti Přibižnéřešeníkritickésíy Rayeighovaenergetickámetoda Metodapostupnýchaproimací Neprizmatickévzpěry Symetrickávzpěra