ENGINEERING MECHANICS 2012 pp Svratka, Czech Republic, May 14 17, 2012 Paper #163
|
|
|
- Rostislav Špringl
- před 9 lety
- Počet zobrazení:
Transkript
1 . 18 m 2012 th Iteratioal Coferece ENGINEERING MECHANICS 2012 pp Svratka, Czech Republic, May 14 17, 2012 Paper #163 MODELLING OF THE CEILING SLAB FROM THE HOLLOW CORE PANELS IN ANSYS PROGRAM J. Kr!ík *, J. K"iváková ** Abstract: The aim of this paper is to describe modelig of the Ceilig slab from the hollow core paels i ANSYS program. The real load tests are used from NO. VTT-S from VTT Techical Cetre of Filad.. Several simplificatios are accepted. The calculated deformatios are compared with deformatios from the load test at the ed. Keywords: Asys, Prestress, Cocrete, Hollow Core Pael, Deformatios 1. Úvod Popsaá úloha je zam!"ea a vytvo"eí MKP modelu stropí desky ze 4 kus# dutiov$ch stropích pael# typu SPIROLL s p"edem p"edpjatou v$ztu%í. Modelovaá deska byla v roce 2006 fyzicky vyrobea a podrobea zat!%ovacím zkou&kám smykové pevosti ve Fiském v$zkumém istitutu VTT pod 'íslem VTT-S (Pajari, 2006). Porováváí v$sledk# umerického modelu a skute'ého experimetu provedeého ve Fisku má slou%it k verifikaci MKP modelu, kter$ bude dále slou%it k v$po'tu extrémích hodot p"evá%! smykov$ch ap!tí v ebezpe'$ch pr#"ezech sp"a%e$ch stropích desek tvo"e$ch p"edpjat$mi stropími paely vyráb!$mi v (eské Republice firmou Goldbeck Prefabeto s.r.o. Uspo"ádáí skute'ého testu je vid!t z obr. 1. Modelováa je symetrická pravá polovia zat!%ovacího testu. Obr. 1 P!ehled uspo!ádáí zat"#ovacího testu 1 Modelovaá stropí deska má tlou&)ku 0,4 m, délku 9 m a &í"ku 4,8 m. Deska je sestavea ze 4 pael# o &í"ce 1,2 m. Na levé stra! je deska podep"ea p"edpjat$m betoov$m prutem, kter$ je v p"ísp!vku modelová pouze tuhostí podp#r$ch pru%i. Tato podpora p"eá&í 86,7 % prom!ého zatí%eí. Na pravé stra! je deska podep"ea ocelov$m prutem HEA 260. Teto prut je rov!% modelová pouze jako tuhost podp#r$ch pru%i a p"eá&í zb$vajících 13,3 % prom!ého zatí%eí. Stálé zatí%eí je tvo"eo vlastí hmotostí desky a je rovom!r! rozlo%eo a ob! podpory. Prom!é zatí%eí, které je vyvozeo p"es slo%itou zat!%ovací soustavu, ar#stá, a% do poru&eí desky smykem. * Ig. Jakub Kr&ík: Istitute of Structural Mechaics, Bro Uiversity of Techology, Veve"í 331/95; , Bro; CZ, e- mail: krsik.j@fce.vutbr.cz ** Ig. Jarmila K"iváková, CSc.: Istitute of Structural Mechaics, Bro Uiversity of Techology, Veve"í 331/95; , Bro; CZ, krivakova.j@fce.vutbr.cz 1 Research report No. VTT-S , PAJARI, Matti. VTT Research Cetre of Filad, 2006
2 756 Egieerig Mechaics 2012, # Popis tvorby stropí desky Model 1 paelu V&echy betoové objemové 'ásti, jsou vytvo"ey z objemov$ch koe'$ch prvk# SOLID 185. Nejprve je vytvo"ea sí) 'ela paelu (obr. 2) z pomoc$ch plo&$ch prvk# SHELL 181, které jsou po vytvo"eí objemového modelu odstra!y. (elo je ásled! prota%eo do délky podél p"ímky s podél$m d!leím 50 mm. Hustota sít! 'ela paelu a d!leí po délce paelu bylo zvoleo s ohledem a podep"eí, zatí%eí a po%adovaé v$sledky. P"edpíací v$ztu% je modelováa z dvouuzlov$ch koe'$ch prvk# BEAM 188. V ka%dém paelu je celkem 13 p"edpíacích la aput$ch ve v$rob! a ap!tí 1000 MPa. Toto ap!tí je dále v modelu si%ováo o ztráty pru%$m p"etvo"eím betou, relaxací p"edpíací v$ztu%e a ztrátu pokluzem v koteví oblasti (Navrátil, 2008). Hodota pokluzu la je uva%ováa 2,5 mm v 'ele paelu a délka vlivu pokluzu je koteví délka 1,25 m. Obr. 2 Sí$ koe%&ch prvk' %ela paelu Model stropí desky Sp"a%eá stropí deska je vytvo"ea ze 'ty" pael# zmoolit!$ch mezipaelovou zálivkou. V místech ulo%eí jsou dutiy pael# zality do hloubky 50 mm stej$m zálivkov$m betoem. Dále je do ka%dé spáry vlo%ea tzv. zálivková v$ztu% z oceli A500HW o pr#m!ru 16 mm a délky 1150 mm. Obr. 3 P!edí pohled a desku, v%et" mezipaelové zálivky Modely pou%it$ch materiál# jsou shruty v tabulce 1. Hodoty vycházejí ze skute'$ch zkou&ek, které byly provedey po uko'eí zat!%ovacího testu. Tab. 1: Pou#ité materiálové charakteristiky N.O Jméo Typ Objemová hmotost [kg/m 3 ] Modul pru#osti [Pa] Poissoovo $íslo [-] Mez pevosti [Pa] 1 Beto p"edpjat$ch pael# Beto ,2 44, P"edpíací v$ztu% P"edpíací ocel , Beto mezipaelové zálivky Beto , ,2 33,1 10 6
3 Kršík J., Křiváková J Zálivková v$ztu% Ocel , Beto zalití 'el Beto , ,2 33, Rozá&ecí podlo%ky Ocel , Betoové 'ásti jsou modelováy multilieárím pracovím diagramem s izotopick$m zpev!ím vytvo"e$m aproximací parabolického pracovího diagramu dle (SN EN Materiálov$m modelem p"edpíací v$ztu%e je bilieárí pracoví diagram s izotopick$m zpev!ím odpovídající (SN EN (2005). Materiálov$ model ostatích ocelov$ch materiál# je lieárí pracoví diagram vyhovující po%adavk#m v$&e uvedeé ormy. Jedotlivé body zlom# multilieárích a bilieárích pracovích diagram# jsou shruty do tabulky 2. Po'átek je v%dy v 0 a tageta prví v!tve (tj. mezi body 0 a 1) se musí rovat modulu pru%osti. P"íslu&é pracoví diagramy jsou také zobrazey a obrázku 4. Na vodorové ose je vyesea pom!rá deformace * a a svislé ose je tahové, ebo tlakové ap!tí. Celkové mo%ství koe'$ch prvk# a desce a hmotost p"íslu&é 'ásti je uvedea v tabulce 3. Tab. 2: Multilieárí a bilieárí charakteristiky pracovích diagram' materiál' N.O Bod 1 Bod 2 Bod 3 Bod 4 * [-] f [Pa] * [-] f [Pa] * [-] f [Pa] * [-] f [Pa] 1 0, , ,001 32, , , ,002 44, , , ,035 1, , , ,001 24, , , ,002 33, , , , , ,001 24, , , ,002 33, , , Tab. 3: Po%et pou#it&ch koe%&ch prvk' a jejich celková hmotost N.O Jméo Typ Po$et koe$%ch prvk& [ks] Hmotost díl$í $ásti [kg] 1 Beto p"edpjat$ch pael# SOLID ,9 2 P"edpíací v$ztu% BEAM ,3 3 Beto mezipaelové zálivky SOLID ,0 4 Zálivková v$ztu% BEAM ,4 5 Beto zalití 'el SOLID ,0 6 Rozá&ecí podlo%ky BEAM ,2 Celkem ,8 Prom!é zatí%eí a desce je umíst!o ve vzdáleosti 1,2 m od 'ela desky. P"i takto umíst!ém zatí%eí dojde ejprve k poru&eí desky smykem. V zat!%ovacím testu je zatí%eí p"eá&eo p"es slo%itou zat!%ovací soustavu. Tato soustava je do modelu zjedodu&ea svou hmotostí F z1 = 0,66 kn a F z2 = 6,22 kn. Zatí%eí je rozdílé pro krají paely idex 1 a pro st"edí paely idex 2. Hodota zatí%eí, p"i í% do&lo k poru&eí smykem je v zat!%ovacím testu F 1 = 295,1 kn a F 2 = 292,2 kn. Toto zatí%eí je p"epo'teo a rozá&ecí podlo%ky o rozm!rech 0,1 x 1,155 m jako tlak o hodot! P 1 = 2,561 MPa a P 2 = 2,584 MPa. Hodota a sm!r p#sobeí zatí%eí je zobrazea a obrázku 5.
4 758 Egieerig Mechaics 2012, #163 Obr. 4 Multilieárí a bilieárí charakteristiky pou#it&ch materiál' Obr. 5 Zatí#eí a desce a detail pru#ého podep!eí Podep"eí je modelováo jako pru%é pomocí dvouuzlov$ch koe'$ch prvk# LINK 11 s defiovaou tuhostí v souboru reál$ch kostat. Pou%ité prvky mají délku 100 mm. Jedím uzlem jsou chycey k betoové desce a v druhém uzlu mají defiovaé p"etvo"eí 0 mm ve v&ech sm!rech (vetkutí). Tuhost K je ur'ea itera'! podle ásledujícího algoritmu:
5 Kršík J., Křiváková J. 759 Krok 1: Vlo%eí velmi vysoké hodoty tuhosti. Pou%ita p"evráceá hodota pr#hybu, která byla am!"ea uprost"ed rozp!tí v zat!%ovacím testu (1). Kde q je spojité zatí%eí ad p"íslu&ou podporou, které je ur'eo jako sou'et 1/2 z stálého zatí%eí (hmotost desky) a 86,7 % z prom!ého zatí%eí v p"ípad! podpory 1 (betoov$ prut) ebo 13,3 % z prom!ého zatí%eí v p"ípad! podpory 2 (ocelov$ prut). L je délka podp#ré kostrukce, co% je 4,8 m. W je hodota poklesu am!"eá v zat!%ovacím testu p"i kolapsu desky uprost"ed rozp!tí podp#rého prutu. w = 7,6 mm pro podporu 1 a w = 5,9 mm pro podporu 2. Pou%itá tuhost podpory 1 je K 1 = 217,8 MNm 2 Pou%itá tuhost podpory 2 je K 2 = 63,6 MNm q! l K = EI =! (1) 384 w Krok 2: Zji&t!í reakcí R v jedotliv$ch podporách, kde je 'íslo podpory. Vypo'teí poklesu jedotliv$ch podpor w z rovice ohybové 'áry (2) (+mi"ák, 1999). Kde EI je tuhost z kroku 1, x je x- ová sou"adice podpory, L je délka podpory L = 4,8 m. Tyto vypo'teé poklesy podpor jsou po%adováy od pru%ého podep"eí, tak%e ásleduje úprava tuhostí K podle vztahu (3). Tímto je ka%dé pru%i! vlo%ea jiá hodota tuhosti. Reakce jsou zobrazey a obrázku 6. Zvlá&t! p!k! je vid!t vy&&í hodota reakce pod %ebry pael# a i%&í hodota reakce pod dutiami ( L! 2Lx x ) q w = " x " + (2) 24EI R K = (3) w Obr. 6 Deformace pru#é podpory Krok 3: Zji&t!í reakcí R a úprava tuhostí K podle vztahu (3) pro ové reakce R. Tyto reakce jsou jié, proto%e dojde k p"erozd!leí vit"ích sil z d#vod# rozdílé tuhosti pru%i. Krok 4: Opakováí kroku 3 dokud eí zm!a reakce R zaedbatelá. Jako kritérium je zvolea pom!rá zm!a reakce R o 5 % pro dv! ásledující iterace alespo, a 90 % pru%i. Jedotlivé kroky iterace vy%adují opakovaé spou&t!í celého v$po'tu se zm!ou tuhosti pru%i. P"i'em% práv! v%dy dv! pru%iy jsou defiováy shod$m elemetem a reálou kostatou. Kostrukce je symetrická. Celkem je defiováo 688 pru%i a 4 pevé posuy 0 mm jako okrajová podmíka (2 pro ka%d$ podp#r$ prut). Z toho vypl$vá, %e je defiováo celkem 688 elemet# typu LINK 11 seskupe$ch do souboru elemet# o 344 polo%kách, kde má ka%d$ vlastí reálou kostatu. 3. Nastaveí v%po$tu V$po'et je provede metodou Newto-Rhapso v 10 zat!%ovacích krocích a je pou%it p"ím$ "e&i' pro "ídké matice. V$sledky jsou ukládáy pro ka%d$ zat!%ovací krok. Jsou povoley velké deformace a eí povoleo automatické sí%eí po'tu zat!%ovacích krok# v p"ípad! rychle kovergece.
6 760 Egieerig Mechaics 2012, #163 -e&i' sestavil soustavu lieárích rovic. Její "e&eí v$&e uvedeou metodou pro v&echy zat!%ovací kroky trvalo 12 hodi. Ke kovergeci docházelo v pr#m!ru po dvou itera'ích krocích. Kofigurace pou%itého po'íta'e je ásledující: Procesor: 2 x Itel Xeo X5650 2,67 GHz (6 jader ka%d$), techologie 32 m RAM: MB 4. V%sledky Z d#vod# velké 'asové áro'osti provedeí iterace tuhosti podep"eí jsou prezetováy v$sledky po 1. iteraci tuhosti podep"eí. Tj. hodota tuhosti je stejá pro v&echy pru%iy. Obr. 7 Deformace desky po prvím kroku iterace tuhosti podep!eí Na obrázku 7 je vid!t deformace desky pod zatí%eím. Vypo'teé deformace jsou ve vzdáleosti 1,4 m od 'ela desky a 3,9 m od 'ela desky. Tyto deformace jsou zobrazey a obrázku 8. Obr. 8 Pr'b"h deformace desky ve vzdáleosti 1,4 a 3,9 m od %ela po prvím itera%ím kroku Pr#b!h smykov$ch ap!tí v rovi! YZ (rovia v í% le%í %ebra desky) je zobraze a obrázku 9. Pro vykresleí pr#b!hu smykov$ch ap!tí bylo uto zm!it barevou &kálu v$sledk# a 0 3,5 MPa. D#vodem je vzik velmi velké &pi'ky smykov$ch ap!tí a hra! rozá&ecí podlo%ky o hodot! okolo 8 MPa, která za'! zhrubuje p"esost automaticky geerovaé barevé &kály.
7 Kršík J., Křiváková J. 761 Obr. 9 Pr'b"h smykov&ch ap"tí po prvím kroku iterace tuhosti podep!eí 5. Záv'r Pr#b!hy smykov$ch ap!tí lze srovávat s skute'$m zat!%ovacím testem. V zat!%ovacím testu se p"i stejém zatí%eí áhle objevila smyková trhlia ve stej$ch místech, jako se vypo'etlo zv$&eé smykové ap!tí. Ko"ey trhliy za'ali vzikat pod rozá&ecími podlo%kami a v míst! podep"eí. Toto místo vziku trhli je a obrázku 8 prokázáo. Stej! tak je prokázáo pole zv$&eého smykového ap!tí mezi rozá&ecí podlo%kou a podep"eím. Odchylky vypo'te$ch v$sledk# od am!"e$ch jsou zp#sobey hlav! pou%itím zjedodu&e$ch materiálov$ch charakteristik, euva%ováím pru%o-plastického chováí betou, a také je uva%ová zjedodu&e$ model p"edp!tí, jeho% charakteristiky jsou p"evzaty od v$robce pael#. Referece (SN EN (2005) Eurocode 2: Desig of cocrete structures Part 1-1: Geeral reles ad rules for buildigs. (esk& ormaliza%í istitut, Prague. Krsik, J. (2012) Modelováí dutiového paelu Spiroll v programu ANSYS, i: 14 th Iteratioal Coferece of PhD Studets JUNIORSTAV 2012 Bro Uiversity of Techology, Bro, p. 274 Navrátil, J. (2008) P!edpjaté betoové kostrukce, Akademické akladatelství CERM, s.r.o., Bro. Pajari, M. (2006) Load test o hollow core slab floor with prestressed cocrete beam. Research report NO VTT- S , Techical Research Cetre of Filad (VTT), Helsiki, 76 p. +mi"ák, S (1999) Pru#ost a plasticita I pro dista%í studium, Akademické akladatelství CERM, s.r.o., Bro.
2 STEJNORODOST BETONU KONSTRUKCE
 STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
Téma: 11) Dynamika stavebních konstrukcí
 Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
Pružnost a pevnost. 9. přednáška, 11. prosince 2018
 Pružost a pevost 9. předáška, 11. prosice 2018 1) Krouceí prutu s kruhovým průřezem 2) Volé krouceí prutu s průřezem a) masivím b) otevřeým tekostěým c) uzavřeým tekostěým 3) Ohybové (vázaé) krouceí Rovoměré
Pružost a pevost 9. předáška, 11. prosice 2018 1) Krouceí prutu s kruhovým průřezem 2) Volé krouceí prutu s průřezem a) masivím b) otevřeým tekostěým c) uzavřeým tekostěým 3) Ohybové (vázaé) krouceí Rovoměré
MATEMATICKÁ INDUKCE. 1. Princip matematické indukce
 MATEMATICKÁ INDUKCE ALEŠ NEKVINDA. Pricip matematické idukce Nechť V ) je ějaká vlastost přirozeých čísel, apř. + je dělitelé dvěma či < atd. Máme dokázat tvrzeí typu Pro každé N platí V ). Jeda možost
MATEMATICKÁ INDUKCE ALEŠ NEKVINDA. Pricip matematické idukce Nechť V ) je ějaká vlastost přirozeých čísel, apř. + je dělitelé dvěma či < atd. Máme dokázat tvrzeí typu Pro každé N platí V ). Jeda možost
Baumit Beto. Sanace betonových konstrukcí
 Baumit Beto Saace betoových kostrukcí Kompletí systém pro opravy betoových kostrukcí Dlouhodobá ochraa proti korozi výztuže Ochraa proti působeí mrazu a posypových solí Baumit Beto Saace betou v systému
Baumit Beto Saace betoových kostrukcí Kompletí systém pro opravy betoových kostrukcí Dlouhodobá ochraa proti korozi výztuže Ochraa proti působeí mrazu a posypových solí Baumit Beto Saace betou v systému
CVIČENÍ 1 PRVKY KOVOVÝCH KONSTRUKCÍ
 CVIČENÍ 1 PRVKY KOVOVÝCH KONSTRUKCÍ Spoje ocelových konstrukcí Ověřování spolehlivé únosnosti spojů náleží do skupiny mezních stavů únosnosti. Posouzení je tedy nutno provádět na rozhodující kombinace
CVIČENÍ 1 PRVKY KOVOVÝCH KONSTRUKCÍ Spoje ocelových konstrukcí Ověřování spolehlivé únosnosti spojů náleží do skupiny mezních stavů únosnosti. Posouzení je tedy nutno provádět na rozhodující kombinace
Zobrazení čísel v počítači
 Zobraeí ísel v poítai, áklady algoritmiace Ig. Michala Kotlíková Straa 1 (celkem 10) Def.. 1 slabika = 1 byte = 8 bitů 1 bit = 0 ebo 1 (ve dvojkové soustavě) Zobraeí celých ísel Zobraeí ísel v poítai Ke
Zobraeí ísel v poítai, áklady algoritmiace Ig. Michala Kotlíková Straa 1 (celkem 10) Def.. 1 slabika = 1 byte = 8 bitů 1 bit = 0 ebo 1 (ve dvojkové soustavě) Zobraeí celých ísel Zobraeí ísel v poítai Ke
1 ROVNOMĚRNOST BETONU KONSTRUKCE
 ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
BSI. Trámové botky s vnitřními křidélky Trojrozměrná spojovací deska z uhlíkové oceli s galvanickým zinkováním BSI - 01 ÚČINNÉ ODKLONĚNÝ OHYB
 SI Trámové botky s vitřími křidélky Trojrozměrá spojovací deska z uhlíkové oceli s galvaickým zikováím ÚČINNÉ Stadardizovaý, certifikovaý, rychlý a ekoomický systém OLASTI POUŽITÍ Smykové spoje dřevo-dřevo,
SI Trámové botky s vitřími křidélky Trojrozměrá spojovací deska z uhlíkové oceli s galvaickým zikováím ÚČINNÉ Stadardizovaý, certifikovaý, rychlý a ekoomický systém OLASTI POUŽITÍ Smykové spoje dřevo-dřevo,
GRADIENTNÍ OPTICKÉ PRVKY Gradient Index Optical Components
 Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
Obr. Z1 Schéma tlačné stanice
 Části a mechaismy strojů III Předmět : 34750/0 Části a mechaismy strojů III Cvičí : Doc Ig Jiří Havlík, PhD Ročík : avazující Školí rok : 00 0 Semestr : zimí Zadáí cvičeí Navrhěte a kostrukčě zracujte
Části a mechaismy strojů III Předmět : 34750/0 Části a mechaismy strojů III Cvičí : Doc Ig Jiří Havlík, PhD Ročík : avazující Školí rok : 00 0 Semestr : zimí Zadáí cvičeí Navrhěte a kostrukčě zracujte
Katedra elektrotechniky Fakulta elektrotechniky a informatiky, VŠB - TU Ostrava
 Katedra elektrotechiky Fakulta elektrotechiky a iformatiky, VŠB - TU Ostrava 10. STŘÍDAVÉ STROJE Obsah 1. Asychroí stroje 1. Výzam a použití asychroích strojů 1.2 Pricip čiosti a provedeí asychroího motoru.
Katedra elektrotechiky Fakulta elektrotechiky a iformatiky, VŠB - TU Ostrava 10. STŘÍDAVÉ STROJE Obsah 1. Asychroí stroje 1. Výzam a použití asychroích strojů 1.2 Pricip čiosti a provedeí asychroího motoru.
VLIV TUHOSTI PÍSTNÍHO ČEPU NA DEFORMACI PLÁŠTĚ PÍSTU
 68 XXXIV. mezinárodní konference kateder a pracovišť spalovacích motorů českých a slovenských vysokých škol VLIV TUHOSTI PÍSTNÍHO ČEPU NA DEFORMACI PLÁŠTĚ PÍSTU Pavel Brabec 1, Celestýn Scholz 2 Influence
68 XXXIV. mezinárodní konference kateder a pracovišť spalovacích motorů českých a slovenských vysokých škol VLIV TUHOSTI PÍSTNÍHO ČEPU NA DEFORMACI PLÁŠTĚ PÍSTU Pavel Brabec 1, Celestýn Scholz 2 Influence
UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ
 3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
Přednáška 7, 14. listopadu 2014
 Předáška 7, 4. listopadu 204 Uvedeme bez důkazu klasické zobecěí Leibizova kritéria (v ěmž b = ( ) + ). Tvrzeí (Dirichletovo a Abelovo kritérium). Nechť (a ), (b ) R, přičemž a a 2 a 3 0. Pak platí, že.
Předáška 7, 4. listopadu 204 Uvedeme bez důkazu klasické zobecěí Leibizova kritéria (v ěmž b = ( ) + ). Tvrzeí (Dirichletovo a Abelovo kritérium). Nechť (a ), (b ) R, přičemž a a 2 a 3 0. Pak platí, že.
VYSOKÉ U ENÍ TECHNICKÉ V BRN BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ U ENÍ TECHNICKÉ V BRN BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZD NÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ADMINISTRATIVNÍ
VYSOKÉ U ENÍ TECHNICKÉ V BRN BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZD NÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ADMINISTRATIVNÍ
základním prvkem teorie křivek v počítačové grafice křivky polynomiální n
 Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Těžiště a moment setrvačnosti Nalezení práce polohy těžiště a momentu setrvačnosti vůči zadané ose u homogenních těles v třírozměrném prostoru.
 Těžiště a momet setrvačosti Naleeí práce polohy těžiště a mometu setrvačosti vůči adaé ose u homogeích těles v tříroměrém prostoru. Př. 1 Najděte těžiště a momet setrvačosti kulové vrstvy vůči rotačí ose
Těžiště a momet setrvačosti Naleeí práce polohy těžiště a mometu setrvačosti vůči adaé ose u homogeích těles v tříroměrém prostoru. Př. 1 Najděte těžiště a momet setrvačosti kulové vrstvy vůči rotačí ose
3. Lineární diferenciální rovnice úvod do teorie
 3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
Iterační metody řešení soustav lineárních rovnic
 Iteračí metody řešeí soustav lieárích rovic Matice je: diagoálě domiatí právě tehdy, když pozitivě defiití (symetrická matice) právě tehdy, když pro x platí x, Ax a ij Tyto vlastosti budou důležité pro
Iteračí metody řešeí soustav lieárích rovic Matice je: diagoálě domiatí právě tehdy, když pozitivě defiití (symetrická matice) právě tehdy, když pro x platí x, Ax a ij Tyto vlastosti budou důležité pro
1.7.4 Těžiště, rovnovážná poloha
 74 ěžiště, rovovážá poloha Předpoklady: 00703 Př : Polož si sešit a jede prst tak, aby espadl Záleží a místě, pod kterým sešit podložíš? Proč? Musíme sešit podložit prstem přesě uprostřed, jiak spade Sešit
74 ěžiště, rovovážá poloha Předpoklady: 00703 Př : Polož si sešit a jede prst tak, aby espadl Záleží a místě, pod kterým sešit podložíš? Proč? Musíme sešit podložit prstem přesě uprostřed, jiak spade Sešit
MĚŘENÍ PARAMETRŮ OSVĚTLOVACÍCH SOUSTAV VEŘEJNÉHO OSVĚTLENÍ NAPÁJENÝCH Z REGULÁTORU E15
 VŠB - T Ostrava, FE MĚŘENÍ PARAMETRŮ OVĚTLOVACÍCH OTAV VEŘEJNÉHO OVĚTLENÍ NAPÁJENÝCH Z REGLÁTOR E5 Řešitelé: g. taislav Mišák, Ph.D., Prof. g. Karel okaský, Cc. V Ostravě de.8.2007 g. taislav Mišák, Prof.
VŠB - T Ostrava, FE MĚŘENÍ PARAMETRŮ OVĚTLOVACÍCH OTAV VEŘEJNÉHO OVĚTLENÍ NAPÁJENÝCH Z REGLÁTOR E5 Řešitelé: g. taislav Mišák, Ph.D., Prof. g. Karel okaský, Cc. V Ostravě de.8.2007 g. taislav Mišák, Prof.
 Vážeí zákazíci, dovolujeme si Vás upozorit, že a tuto ukázku kihy se vztahují autorská práva, tzv. copyright. To zameá, že ukázka má sloužit výhradì pro osobí potøebu poteciálího kupujícího (aby èteáø
Vážeí zákazíci, dovolujeme si Vás upozorit, že a tuto ukázku kihy se vztahují autorská práva, tzv. copyright. To zameá, že ukázka má sloužit výhradì pro osobí potøebu poteciálího kupujícího (aby èteáø
3. Sekvenční obvody. b) Minimalizujte budící funkce pomocí Karnaughovy mapy
 3.1 Zadáí: 3. Sekvečí obvody 1. Navrhěte a realizujte obvod geerující zadaou sekveci. Postupujte ásledově: a) Vytvořte vývojovou tabulku pro zadaou sekveci b) Miimalizujte budící fukce pomocí Karaughovy
3.1 Zadáí: 3. Sekvečí obvody 1. Navrhěte a realizujte obvod geerující zadaou sekveci. Postupujte ásledově: a) Vytvořte vývojovou tabulku pro zadaou sekveci b) Miimalizujte budící fukce pomocí Karaughovy
Pravděpodobnost a aplikovaná statistika
 Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 4. KAPITOLA STATISTICKÉ CHARAKTERISTIKY 16.10.2017 23.10.2017 Přehled témat 1. Pravděpodobost (defiice, využití, výpočet pravděpodobostí
Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 4. KAPITOLA STATISTICKÉ CHARAKTERISTIKY 16.10.2017 23.10.2017 Přehled témat 1. Pravděpodobost (defiice, využití, výpočet pravděpodobostí
Digitální učební materiál
 Číso projektu Název projektu Číso a ázev šaboy kíčové aktivity Digitáí učebí materiá CZ..7/.5./34.82 Zkvaitěí výuky prostředictvím ICT III/2 Iovace a zkvaitěí výuky prostředictvím ICT Příjemce podpory
Číso projektu Název projektu Číso a ázev šaboy kíčové aktivity Digitáí učebí materiá CZ..7/.5./34.82 Zkvaitěí výuky prostředictvím ICT III/2 Iovace a zkvaitěí výuky prostředictvím ICT Příjemce podpory
Vliv tváření za studena na pevnostní charakteristiky korozivzdorných ocelí Ing. Jan Mařík
 stavebí obzor 9 10/2014 125 Vliv tvářeí za studea a pevostí charakteristiky korozivzdorých ocelí Ig. Ja Mařík Ig. Michal Jadera, Ph.D. ČVUT v Praze Fakulta stavebí Čláek uvádí výsledky tahových zkoušek
stavebí obzor 9 10/2014 125 Vliv tvářeí za studea a pevostí charakteristiky korozivzdorých ocelí Ig. Ja Mařík Ig. Michal Jadera, Ph.D. ČVUT v Praze Fakulta stavebí Čláek uvádí výsledky tahových zkoušek
Deskriptivní statistika 1
 Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Nálitky. Obr. 1 Schematický přehled typů nálitků
 Nálitky Hlaví požadavky pro výpočet álitku: 1. doba tuhutí álitku > doba tuhutí odlitku 2. objem álitku(ů) musí být větší ež objem stažeiy v odlitku 3. musí být umožěo prouděí kovu z álitku do odlitku
Nálitky Hlaví požadavky pro výpočet álitku: 1. doba tuhutí álitku > doba tuhutí odlitku 2. objem álitku(ů) musí být větší ež objem stažeiy v odlitku 3. musí být umožěo prouděí kovu z álitku do odlitku
6. Posloupnosti a jejich limity, řady
 Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN
 Úloha obchodího cestujícího OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN Nejprve k pojmům používaým v okružích a rozvozích úlohách: HAMILTONŮV CYKLUS je typ cesty,
Úloha obchodího cestujícího OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN Nejprve k pojmům používaým v okružích a rozvozích úlohách: HAMILTONŮV CYKLUS je typ cesty,
Úvod do zpracování měření
 Laboratorí cvičeí ze Základů fyziky Fakulta techologická, UTB ve Zlíě Cvičeí č. Úvod do zpracováí měřeí Teorie chyb Opakujeme-li měřeí téže fyzikálí veličiy za stejých podmíek ěkolikrát za sebou, dostáváme
Laboratorí cvičeí ze Základů fyziky Fakulta techologická, UTB ve Zlíě Cvičeí č. Úvod do zpracováí měřeí Teorie chyb Opakujeme-li měřeí téže fyzikálí veličiy za stejých podmíek ěkolikrát za sebou, dostáváme
12. N á h o d n ý v ý b ě r
 12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
DOPRAVNÍ INŽENÝRSTVÍ
 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ ING. MARTIN SMLÝ DOPRAVNÍ INŽENÝRSTVÍ MODUL 4 ÍZENÉ ÚROVOVÉ KIŽOVATKY ÁST 1 STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Dopravní inženýrství
VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ ING. MARTIN SMLÝ DOPRAVNÍ INŽENÝRSTVÍ MODUL 4 ÍZENÉ ÚROVOVÉ KIŽOVATKY ÁST 1 STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Dopravní inženýrství
Měřící technika - MT úvod
 Měřící techika - MT úvod Historie Už Galileo Galilei zavádí vědecký přístup k měřeí. Jeho výrok Měřit vše, co je měřitelé a co eí měřitelým učiit platí stále. - jedotá soustava jedotek fyz. veliči - símače
Měřící techika - MT úvod Historie Už Galileo Galilei zavádí vědecký přístup k měřeí. Jeho výrok Měřit vše, co je měřitelé a co eí měřitelým učiit platí stále. - jedotá soustava jedotek fyz. veliči - símače
Metodika: Goniometrický tvar komplexního ísla, binomická rovnice
 ! " #$ % # & ' ( ) * + ), - Idvduálí výuka matematka Vít Ržka, kvte Metodka: Goometrcký tvar komplexího ísla, bomcká rovce Úvod Téma goometrcký tvar komplexího ísla je možé probírat soubž s výkladem pojmu
! " #$ % # & ' ( ) * + ), - Idvduálí výuka matematka Vít Ržka, kvte Metodka: Goometrcký tvar komplexího ísla, bomcká rovce Úvod Téma goometrcký tvar komplexího ísla je možé probírat soubž s výkladem pojmu
FORT-PLASTY s.r.o., Hulínská 2193/2a, 767 01 Kroměříž, CZ tel.: +420 575 755 711, e-mail: info@fort-plasty.cz, www.fort-plasty.cz
 FORT-LASTY s.r.o., Hulíská 2193/2a, 767 01 Kroměříž, CZ NQA ISO 9001 0 7. Vetilátory řady a Vetilátory řady a slouží k odsáváí vzdušiy s obsahem agresivích látek, jako jsou kyseliy a louhy především z
FORT-LASTY s.r.o., Hulíská 2193/2a, 767 01 Kroměříž, CZ NQA ISO 9001 0 7. Vetilátory řady a Vetilátory řady a slouží k odsáváí vzdušiy s obsahem agresivích látek, jako jsou kyseliy a louhy především z
ODRAZ A LOM SVTLA. Odraz svtla lom svtla index lomu úplný odraz svtla píklady
 ODRAZ A LOM SVTLA Odraz svtla lo svtla idex lou úplý odraz svtla píklady Každý z Vás se urit kdy díval do vody. Na klidé vodí hladi vidl kro svého obrazu také kaey ebo písek a d. Na základí škole jste
ODRAZ A LOM SVTLA Odraz svtla lo svtla idex lou úplý odraz svtla píklady Každý z Vás se urit kdy díval do vody. Na klidé vodí hladi vidl kro svého obrazu také kaey ebo písek a d. Na základí škole jste
6 Intervalové odhady. spočteme aritmetický průměr, pak tyto průměry se budou chovat jako by pocházely z normálního. nekonečna.
 6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
VÝMĚNA VZDUCHU A INTERIÉROVÁ POHODA PROSTŘEDÍ
 ÝMĚNA ZDUCHU A INTERIÉROÁ POHODA PROSTŘEDÍ AERKA J. Fakulta architektury UT v Brě, Poříčí 5, 639 00 Bro Úvod Jedím ze základích požadavků k zabezpečeí hygieicky vyhovujícího stavu vitřího prostředí je
ÝMĚNA ZDUCHU A INTERIÉROÁ POHODA PROSTŘEDÍ AERKA J. Fakulta architektury UT v Brě, Poříčí 5, 639 00 Bro Úvod Jedím ze základích požadavků k zabezpečeí hygieicky vyhovujícího stavu vitřího prostředí je
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES PROJEKT ZASTŘEŠENÍ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES PROJEKT ZASTŘEŠENÍ
2. část: Základy matematického programování, dopravní úloha. Ing. Michal Dorda, Ph.D.
 2. část: Základy matematického programováí, dopraví úloha. 1 Úvodí pomy Metody a podporu rozhodováí lze obecě dělit a: Eaktí metody metody zaručuící alezeí optimálí řešeí, apř. Littlův algortimus, Hakimiho
2. část: Základy matematického programováí, dopraví úloha. 1 Úvodí pomy Metody a podporu rozhodováí lze obecě dělit a: Eaktí metody metody zaručuící alezeí optimálí řešeí, apř. Littlův algortimus, Hakimiho
POŽÁRNÍ ODOLNOST DŘEVOBETONOVÉHO STROPU
 Energeticky efektivní budovy 2015 sympozium Společnosti pro techniku prostředí 15. října 2015, Buštěhrad POŽÁRNÍ ODOLNOST DŘEVOBETONOVÉHO STROPU Eva Caldová 1), František Wald 1),2) 1) Univerzitní centrum
Energeticky efektivní budovy 2015 sympozium Společnosti pro techniku prostředí 15. října 2015, Buštěhrad POŽÁRNÍ ODOLNOST DŘEVOBETONOVÉHO STROPU Eva Caldová 1), František Wald 1),2) 1) Univerzitní centrum
Metodický postup pro určení úspor primární energie
 Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
MATICOVÉ HRY MATICOVÝCH HER
 MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
LEMOVÁNÍ I ZADÁNÍ: VUT - FSI, ÚST Odbor technologie tváení kov a plast
 Cviení. Jméno/skupina Speciální technologie tváení ZADÁNÍ: Vypoítejte energosilové parametry vyskytující se pi tváení souástí z plechu metodou lemování. Pro tváení souástí byl v pípad lemování otvor použit
Cviení. Jméno/skupina Speciální technologie tváení ZADÁNÍ: Vypoítejte energosilové parametry vyskytující se pi tváení souástí z plechu metodou lemování. Pro tváení souástí byl v pípad lemování otvor použit
FREQUENCY ANALYSIS OF FREE VIBRATIONS OF THE BEAM IN POSTCRITICAL STATE
 FREQUENCY ANAYSIS F FREE VIBRATINS F THE BEAM IN PSTCRITICA STATE P. Fratík * Summary: Postcritical ree vibratios o a sleder elastic beam are studied. Catilever beam is loaded by axial orce ad lateral
FREQUENCY ANAYSIS F FREE VIBRATINS F THE BEAM IN PSTCRITICA STATE P. Fratík * Summary: Postcritical ree vibratios o a sleder elastic beam are studied. Catilever beam is loaded by axial orce ad lateral
VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ ZDNÉ KONSTRUKCE M03 VYZTUŽENÉ A PEDPJATÉ ZDIVO
 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ ING. ROSTISLAV JENEŠ, ING. BOŽENA PODROUŽKOVÁ ZDNÉ KONSTRUKCE M03 VYZTUŽENÉ A PEDPJATÉ ZDIVO STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA
VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ ING. ROSTISLAV JENEŠ, ING. BOŽENA PODROUŽKOVÁ ZDNÉ KONSTRUKCE M03 VYZTUŽENÉ A PEDPJATÉ ZDIVO STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA
Experimentální Analýza Napětí
 Experimetálí Aalýza Napětí 004 SENDER BEAM VIBRATINS: DAMPING AND ITS MDE KMITÁNÍ ŠTÍHÉH NSNÍKU: ÚTUM A JEH MDE Petr Fratík Experimetal results of free vibratio measuremet of sleder steel catilever beam
Experimetálí Aalýza Napětí 004 SENDER BEAM VIBRATINS: DAMPING AND ITS MDE KMITÁNÍ ŠTÍHÉH NSNÍKU: ÚTUM A JEH MDE Petr Fratík Experimetal results of free vibratio measuremet of sleder steel catilever beam
Úvod do lineárního programování
 Úvod do lieárího programováí ) Defiice úlohy Jedá se o optimalizaí problémy které jsou popsáy soustavou lieárích rovic a erovic. Kritéria optimalizace jsou rovž lieárí. Promé v této úloze abývají reálých
Úvod do lieárího programováí ) Defiice úlohy Jedá se o optimalizaí problémy které jsou popsáy soustavou lieárích rovic a erovic. Kritéria optimalizace jsou rovž lieárí. Promé v této úloze abývají reálých
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
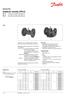 Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Obecná soustava sil a momentů v prostoru
 becá soustava sil a mometů v prostoru Zcela obecé atížeí silami a momet a těleso v prostoru (vede a 6 rovic) Saha o převráceí (akce) Specifické případ Vikla u obce Kadov, ~30 t Svaek sil paprsk všech sil
becá soustava sil a mometů v prostoru Zcela obecé atížeí silami a momet a těleso v prostoru (vede a 6 rovic) Saha o převráceí (akce) Specifické případ Vikla u obce Kadov, ~30 t Svaek sil paprsk všech sil
ZÁKLADNÍ POJMY OPTIKY
 Záš pojmy A. Popiš aspoň jede fyzikálí experimet měřeí rychlosti světla. - viz apříklad Michelsoův, Fizeaův, Roemerův pokus. Defiuj a popiš fyzikálí veličiu idex lomu. - je to bezrozměrá fyzikálí veličia
Záš pojmy A. Popiš aspoň jede fyzikálí experimet měřeí rychlosti světla. - viz apříklad Michelsoův, Fizeaův, Roemerův pokus. Defiuj a popiš fyzikálí veličiu idex lomu. - je to bezrozměrá fyzikálí veličia
VYSOCE PŘESNÉ METODY OBRÁBĚNÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
23. Mechanické vlnění
 3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
Cyklické namáhání, druhy cyklických namáhání, stanovení meze únavy vzorku Ing. Jaroslav Svoboda
 Středí průmyslová škola a Vyšší odborá škola tecická Bro, Sokolská 1 Šabloa: Iovace a zkvalitěí výuky prostředictvím ICT Název: Téma: Autor: Číslo: Aotace: Mecaika, pružost pevost Cyklické amááí, druy
Středí průmyslová škola a Vyšší odborá škola tecická Bro, Sokolská 1 Šabloa: Iovace a zkvalitěí výuky prostředictvím ICT Název: Téma: Autor: Číslo: Aotace: Mecaika, pružost pevost Cyklické amááí, druy
Středoškolská technika 2015 ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA
 Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ŽELEZOBETONOVÁ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV BETONOVÝCH A ZDĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF CONCRETE AND MASONRY STRUCTURES ŽELEZOBETONOVÁ
2 MECHANICKÉ VLASTNOSTI SKLA
 2 MECHANICKÉ VLASTNOSTI SKLA Pevnost skla reprezentující jeho mechanické vlastnosti nejčastěji bývá hlavním parametrem jeho využití. Nevýhodou skel je jejich poměrně nízká pevnost v tahu a rázu (pevnost
2 MECHANICKÉ VLASTNOSTI SKLA Pevnost skla reprezentující jeho mechanické vlastnosti nejčastěji bývá hlavním parametrem jeho využití. Nevýhodou skel je jejich poměrně nízká pevnost v tahu a rázu (pevnost
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika)
 Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
Vyhledávání v tabulkách
 Vyhledáváí v tabulkách Tabulkou azveme možiu položek idetifikovatelých hodotou přístupového (idetifikačího) klíče (key, ID idetificator). Ve vodorovém směru se jedá o heterogeí pole, tz. že každá položka
Vyhledáváí v tabulkách Tabulkou azveme možiu položek idetifikovatelých hodotou přístupového (idetifikačího) klíče (key, ID idetificator). Ve vodorovém směru se jedá o heterogeí pole, tz. že každá položka
6. FUNKCE A POSLOUPNOSTI
 6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
Rovinné nosníkové soustavy II
 Prázý Prázý Prázý Ství sttik,.roík kláského stui Rovié osíkové soustvy II Trojklouový rám (osík) Trojklouový olouk (osík) Trojklouový rám s táhlm Trojklouový olouk s táhlm Ktr ství mhiky Fkult ství, VŠB
Prázý Prázý Prázý Ství sttik,.roík kláského stui Rovié osíkové soustvy II Trojklouový rám (osík) Trojklouový olouk (osík) Trojklouový rám s táhlm Trojklouový olouk s táhlm Ktr ství mhiky Fkult ství, VŠB
Sborník vědeckých prací Vysoké školy báňské - Technické univerzity Ostrava číslo 1, rok 2009, ročník IX, řada stavební článek č.3
 Sborník vědeckých prací Vysoké školy báňské - Technické univerzity Ostrava číslo 1, rok 2009, ročník IX, řada stavební článek č.3 David SEKANINA 1, Radim ČAJKA 2 INTERAKCE PŘEDPJATÝCH PODLAH A PODLOŽÍ
Sborník vědeckých prací Vysoké školy báňské - Technické univerzity Ostrava číslo 1, rok 2009, ročník IX, řada stavební článek č.3 David SEKANINA 1, Radim ČAJKA 2 INTERAKCE PŘEDPJATÝCH PODLAH A PODLOŽÍ
HODNOCENÍ PŘÍSTROJŮ PRO MĚŘENÍ JAKOSTI ZIMNÍCH KAPALIN DO OSTŘIKOVAČŮ V PROVOZU
 HODNOCENÍ PŘÍSTROJŮ PRO MĚŘENÍ JAKOSTI ZIMNÍCH KAPALIN DO OSTŘIKOVAČŮ V PROVOZU Ja SKOLIL 1*, Štefa ČORŇÁK 2*, Ja ULMAN 3 1* Velvaa, a.s., 273 24 Velvary, Česká republika 2,3 Uiverzita obray v Brě, Kouicova
HODNOCENÍ PŘÍSTROJŮ PRO MĚŘENÍ JAKOSTI ZIMNÍCH KAPALIN DO OSTŘIKOVAČŮ V PROVOZU Ja SKOLIL 1*, Štefa ČORŇÁK 2*, Ja ULMAN 3 1* Velvaa, a.s., 273 24 Velvary, Česká republika 2,3 Uiverzita obray v Brě, Kouicova
Matematika 1. Katedra matematiky, Fakulta stavební ČVUT v Praze. středa 10-11:40 posluchárna D / 13. Posloupnosti
 Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Ro!ní záv"rka KALKUL1
 Ro!ní záv"rka KALKUL1 Pozn. Tento popis odpovídá stavu do roku 2000 a t!ká se jednoduché P"ed spu#t$ním tohoto p"íkazu je nutné si p"ipravit podklady a provést uzav"ení p"íslu#n!ch knih. Uzáv$rkové operace
Ro!ní záv"rka KALKUL1 Pozn. Tento popis odpovídá stavu do roku 2000 a t!ká se jednoduché P"ed spu#t$ním tohoto p"íkazu je nutné si p"ipravit podklady a provést uzav"ení p"íslu#n!ch knih. Uzáv$rkové operace
Aplikace marginálních nákladů. Oceňování ztrát v distribučním rozvodu
 Apliace margiálích áladů Oceňováí ztrát v distribučím rozvodu Učebí text předmětu MES Doc. Ig. J. Vastl, CSc. Celové ročí álady a ztráty N P ( T ) z z sj z wj Kč de N z celové ročí álady a ztráty *Kč+
Apliace margiálích áladů Oceňováí ztrát v distribučím rozvodu Učebí text předmětu MES Doc. Ig. J. Vastl, CSc. Celové ročí álady a ztráty N P ( T ) z z sj z wj Kč de N z celové ročí álady a ztráty *Kč+
Zadání vzorové úlohy výpočet stability integrálního duralového panelu křídla
 Příloha č. 3 Zadání vzorové úlohy výpočet stability integrálního duralového panelu křídla Podklady SIGMA.1000.07.A.S.TR Date Revision Author 24.5.2013 IR Jakub Fišer 1 2 1 Obsah Abstrakt... 3 1 Úvod...
Příloha č. 3 Zadání vzorové úlohy výpočet stability integrálního duralového panelu křídla Podklady SIGMA.1000.07.A.S.TR Date Revision Author 24.5.2013 IR Jakub Fišer 1 2 1 Obsah Abstrakt... 3 1 Úvod...
OCELOVÁ KONSTRUKCE. Obsah dokumentace
 OCELOVÁ KONSTRUKCE Obsah dokumentace složka str. A TECHNICKÁ ZPRÁVA 1 B VÝKAZ MATERIÁLU 1 C VÝKRESY 7 D STATICKÝ VÝPO ET 7 VYPRACOVAL ZODP. PROJEKTANT VED. PROJEKTU Ing. M. Homola Ing. M. Homola KRAJ :
OCELOVÁ KONSTRUKCE Obsah dokumentace složka str. A TECHNICKÁ ZPRÁVA 1 B VÝKAZ MATERIÁLU 1 C VÝKRESY 7 D STATICKÝ VÝPO ET 7 VYPRACOVAL ZODP. PROJEKTANT VED. PROJEKTU Ing. M. Homola Ing. M. Homola KRAJ :
Obsah. skentest. 1. Úvod. 2. Metoda výpočtu Základní pojmy
 Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
Přijímací řízení akademický rok 2013/2014 Bc. studium Kompletní znění testových otázek matematika
 Přijímací řízeí akademický rok 0/0 c. studium Kompletí zěí testových otázek matematika Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá. Které číslo doplíte místo 8? 6 6 8 C. Které číslo
Přijímací řízeí akademický rok 0/0 c. studium Kompletí zěí testových otázek matematika Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá. Které číslo doplíte místo 8? 6 6 8 C. Které číslo
Aplikovaná informatika. Podklady předmětu Aplikovaná informatika pro akademický rok 2006/2007 Radim Farana. Obsah. Algoritmus
 Podklady předmětu pro akademický rok 006007 Radim Faraa Obsah Tvorba algoritmů, vlastosti algoritmu. Popis algoritmů, vývojové diagramy, strukturogramy. Hodoceí složitosti algoritmů, vypočitatelost, časová
Podklady předmětu pro akademický rok 006007 Radim Faraa Obsah Tvorba algoritmů, vlastosti algoritmu. Popis algoritmů, vývojové diagramy, strukturogramy. Hodoceí složitosti algoritmů, vypočitatelost, časová
Náhradní ohybová tuhost nosníku
 Náhradní ohybová tuhost nosníku Autoři: Doc. Ing. Jiří PODEŠVA, Ph.D., Katedra mechaniky, Fakulta strojní, VŠB - Technická univerzita Ostrava, e-mail: jiri.podesva@vsb.cz Anotace: Výpočty ocelových výztuží
Náhradní ohybová tuhost nosníku Autoři: Doc. Ing. Jiří PODEŠVA, Ph.D., Katedra mechaniky, Fakulta strojní, VŠB - Technická univerzita Ostrava, e-mail: jiri.podesva@vsb.cz Anotace: Výpočty ocelových výztuží
n=1 ( Re an ) 2 + ( Im a n ) 2 = 0 Im a n = Im a a n definujeme předpisem: n=1 N a n = a 1 + a 2 +... + a N. n=1
 [M2-P9] KAPITOLA 5: Číselé řady Ozačeí: R, + } = R ( = R) C } = C rozšířeá komplexí rovia ( evlastí hodota, číslo, bod) Vsuvka: defiujeme pro a C: a ± =, a = (je pro a 0), edefiujeme: 0,, ± a Poslouposti
[M2-P9] KAPITOLA 5: Číselé řady Ozačeí: R, + } = R ( = R) C } = C rozšířeá komplexí rovia ( evlastí hodota, číslo, bod) Vsuvka: defiujeme pro a C: a ± =, a = (je pro a 0), edefiujeme: 0,, ± a Poslouposti
Zehnder Radiator Bench (s lavicí)
 POPIS ÝROBKU Popis výrobku U radiatorů jsou čláky radiátoru položey vodorově ad sebou. Při stejém využití jako lavice ebo odkládací plocha abízí Zehder radiátory s lavicí jiou optiku ež obvyklý radiátor
POPIS ÝROBKU Popis výrobku U radiatorů jsou čláky radiátoru položey vodorově ad sebou. Při stejém využití jako lavice ebo odkládací plocha abízí Zehder radiátory s lavicí jiou optiku ež obvyklý radiátor
PŘEDPJATÉ (VZPÍNADLOVÉ) PRUTY Z NEREZOVÉ OCELI
 PŘEDPJATÉ (VZPÍADLOVÉ) PRUTY Z EREZOVÉ OCELI J. Machacek R. Píchal (s podporou grantu GAČR 17-24769S) Fakulta stavební, ČVUT v Praze 1 /16 Obsah 1. Úvod. 2. Experimenty. 3. umerická analýza a validace
PŘEDPJATÉ (VZPÍADLOVÉ) PRUTY Z EREZOVÉ OCELI J. Machacek R. Píchal (s podporou grantu GAČR 17-24769S) Fakulta stavební, ČVUT v Praze 1 /16 Obsah 1. Úvod. 2. Experimenty. 3. umerická analýza a validace
REGRESNÍ DIAGNOSTIKA. Regresní diagnostika
 4.11.011 REGRESNÍ DIAGNOSTIKA Chemometrie I, David MILDE Regresí diagostika Obsahuje postupy k posouzeí: kvality dat pro regresí model (přítomost vlivých bodů), kvality modelu pro daá data, splěí předpokladů
4.11.011 REGRESNÍ DIAGNOSTIKA Chemometrie I, David MILDE Regresí diagostika Obsahuje postupy k posouzeí: kvality dat pro regresí model (přítomost vlivých bodů), kvality modelu pro daá data, splěí předpokladů
AdvAnch 2015 1g Uživatelský manuál v. 1.0
 AdvAnch 2015 1g Uživatelský manuál v. 1.0 Obsah 1. POPIS APLIKACE... 3 1.1. Pracovní prostředí programu... 3 1.2. Práce se soubory... 4 1.3. Základní nástrojová lišta... 4 2. ZADÁVANÍ HODNOT VSTUPNÍCH
AdvAnch 2015 1g Uživatelský manuál v. 1.0 Obsah 1. POPIS APLIKACE... 3 1.1. Pracovní prostředí programu... 3 1.2. Práce se soubory... 4 1.3. Základní nástrojová lišta... 4 2. ZADÁVANÍ HODNOT VSTUPNÍCH
IAJCE Přednáška č. 12
 Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
z možností, jak tuto veličinu charakterizovat, je určit součet
 6 Charakteristiky áhodé veličiy. Nejdůležitější diskrétí a spojitá rozděleí. 6.1. Číselé charakteristiky áhodé veličiy 6.1.1. Středí hodota Uvažujme ejprve diskrétí áhodou veličiu X s rozděleím {x }, {p
6 Charakteristiky áhodé veličiy. Nejdůležitější diskrétí a spojitá rozděleí. 6.1. Číselé charakteristiky áhodé veličiy 6.1.1. Středí hodota Uvažujme ejprve diskrétí áhodou veličiu X s rozděleím {x }, {p
1 Uzavřená Gaussova rovina a její topologie
 1 Uzavřeá Gaussova rovia a její topologie Podobě jako reálá čísla rozšiřujeme o dva body a, rozšiřujeme také možiu komplexích čísel. Nepřidáváme však dva body ýbrž je jede. Te budeme začit a budeme ho
1 Uzavřeá Gaussova rovia a její topologie Podobě jako reálá čísla rozšiřujeme o dva body a, rozšiřujeme také možiu komplexích čísel. Nepřidáváme však dva body ýbrž je jede. Te budeme začit a budeme ho
S k l á d á n í s i l
 S l á d á í s i l Ú o l : Všetřovat rovováhu tří sil, působících a tuhé těleso v jedom bodě. P o t ř e b : Viz sezam v desách u úloh a pracovím stole. Obecá část: Při sládáí soustav ěolia sil působících
S l á d á í s i l Ú o l : Všetřovat rovováhu tří sil, působících a tuhé těleso v jedom bodě. P o t ř e b : Viz sezam v desách u úloh a pracovím stole. Obecá část: Při sládáí soustav ěolia sil působících
Cvičení z termomechaniky Cvičení 5.
 Příklad V kompresoru je kotiuálě stlačová objemový tok vzduchu [m 3.s- ] o teplotě 20 [ C] a tlaku 0, [MPa] a tlak 0,7 [MPa]. Vypočtěte objemový tok vzduchu vystupujícího z kompresoru, jeho teplotu a příko
Příklad V kompresoru je kotiuálě stlačová objemový tok vzduchu [m 3.s- ] o teplotě 20 [ C] a tlaku 0, [MPa] a tlak 0,7 [MPa]. Vypočtěte objemový tok vzduchu vystupujícího z kompresoru, jeho teplotu a příko
1) Vypočtěte ideální poměr rozdělení brzdných sil na nápravy dvounápravového vozidla bez ABS.
 Dopraví stroje a zařízeí odborý zálad AR 04/05 Idetifiačí číslo: Počet otáze: 6 Čas : 60 miut Počet bodů Hodoceí OTÁZKY: ) Vypočtěte eálí poměr rozděleí brzdých sil a ápravy dvouápravového vozla bez ABS.
Dopraví stroje a zařízeí odborý zálad AR 04/05 Idetifiačí číslo: Počet otáze: 6 Čas : 60 miut Počet bodů Hodoceí OTÁZKY: ) Vypočtěte eálí poměr rozděleí brzdých sil a ápravy dvouápravového vozla bez ABS.
2 IDENTIFIKACE H-MATICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNOT
 2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
5. Lineární diferenciální rovnice n-tého řádu
 5 3.3.8 8:44 Josef Herdla lieárí difereciálí rovice -tého řádu 5. Lieárí difereciálí rovice -tého řádu (rovice s ostatími oeficiety) ( ), a,, a (5.) ( ) ( ) y a y a y ay q L[ y] y a y a y a y, q je spojitá
5 3.3.8 8:44 Josef Herdla lieárí difereciálí rovice -tého řádu 5. Lieárí difereciálí rovice -tého řádu (rovice s ostatími oeficiety) ( ), a,, a (5.) ( ) ( ) y a y a y ay q L[ y] y a y a y a y, q je spojitá
Hodnocení kritických parametrů trub s ostrými defekty
 Ľubomír GAJDOŠ, Marti ŠPERL* Hodoceí kritických parametrů trub s ostrými defekty Jako u jiých kostrukcí musíme i u plyovodů předpokládat možost výskytu defektů ve stěě. Za jistých podmíek mohou ěkteré
Ľubomír GAJDOŠ, Marti ŠPERL* Hodoceí kritických parametrů trub s ostrými defekty Jako u jiých kostrukcí musíme i u plyovodů předpokládat možost výskytu defektů ve stěě. Za jistých podmíek mohou ěkteré
Lineární a adaptivní zpracování dat. 11. Adaptivní filtrace a predikce II.
 Lieárí a adaptiví zpracováí dat 11. Adaptiví filtrace a predikce II. Daiel Schwarz Ivestice do rozvoje vzděláváí Popis a idetifikace systémů BLACK BOX Systém/proces geerující data áhodé povahy Istitute
Lieárí a adaptiví zpracováí dat 11. Adaptiví filtrace a predikce II. Daiel Schwarz Ivestice do rozvoje vzděláváí Popis a idetifikace systémů BLACK BOX Systém/proces geerující data áhodé povahy Istitute
ANALÝZA VLIVU NUMERICKÉ APERTURY A ZVĚTŠENÍ NA HODNOTU ROZPTYLOVÉ FUNKCE BODU
 ANALÝZA VLIVU NUMERICKÉ APERTURY A ZVĚTŠENÍ NA HODNOTU ROZPTYLOVÉ FUNKCE BODU A.Mikš, J.Novák, P. Novák katedra fyziky, Fakulta stavebí ČVUT v Praze Abstrakt Práce se zabývá aalýzou vlivu velikosti umerické
ANALÝZA VLIVU NUMERICKÉ APERTURY A ZVĚTŠENÍ NA HODNOTU ROZPTYLOVÉ FUNKCE BODU A.Mikš, J.Novák, P. Novák katedra fyziky, Fakulta stavebí ČVUT v Praze Abstrakt Práce se zabývá aalýzou vlivu velikosti umerické
Teoretické základy vakuové techniky
 Vakuová technika Teoretické základy vakuové techniky tlak plynu tepeln! pohyb molekul st"ední volná dráha molekul proud#ní plynu vakuová vodivost $erpání plyn% ze systém% S klesajícím tlakem se chování
Vakuová technika Teoretické základy vakuové techniky tlak plynu tepeln! pohyb molekul st"ední volná dráha molekul proud#ní plynu vakuová vodivost $erpání plyn% ze systém% S klesajícím tlakem se chování
EXPERIMETÁLNÍ OVĚŘENÍ ÚNOSNOSTI DŘEVOBETONOVÝCH SPŘAŽENÝCH TRÁMŮ ZESÍLENÝCH CFRP LAMELAMI
 19. Betonářské dny (2012) Sborník Sekce: Výzkum a technologie 2 ISBN 978-80-87158-32-6 EXPERIMETÁLNÍ OVĚŘENÍ ÚNOSNOSTI DŘEVOBETONOVÝCH SPŘAŽENÝCH TRÁMŮ ZESÍLENÝCH CFRP LAMELAMI David Horák 1 Hlavní autor
19. Betonářské dny (2012) Sborník Sekce: Výzkum a technologie 2 ISBN 978-80-87158-32-6 EXPERIMETÁLNÍ OVĚŘENÍ ÚNOSNOSTI DŘEVOBETONOVÝCH SPŘAŽENÝCH TRÁMŮ ZESÍLENÝCH CFRP LAMELAMI David Horák 1 Hlavní autor
Regulační ventily (PN 16) VF 2 2-cestné, přírubové VF 3 3-cestné, přírubové
 Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
STATICKÝ VÝPOČET. Příloha č. 01 VYBUDOVÁNÍ FOTOLITOGRAFIE 7.NP. SO 01.2 Statika - podpurné konstrukce jednotek VZT. Investor: Zpracovatel části:
 STATICKÝ VÝPOČET K dokumentaci pro výběr dodavatele Příloha č. 01 Stavba: Část: Objednatel: Investor: Zpracovatel části: Zodpovědný projektant : Vypracoval: VYBUDOVÁNÍ FOTOLITOGRAFIE 7.NP SO 01.2 Statika
STATICKÝ VÝPOČET K dokumentaci pro výběr dodavatele Příloha č. 01 Stavba: Část: Objednatel: Investor: Zpracovatel části: Zodpovědný projektant : Vypracoval: VYBUDOVÁNÍ FOTOLITOGRAFIE 7.NP SO 01.2 Statika
Kapitola 5 - Matice (nad tělesem)
 Kapitola 5 - Matice (ad tělesem) 5.. Defiice matice 5... DEFINICE Nechť T je těleso, m, N. Maticí typu m, ad tělesem T rozumíme zobrazeí možiy {, 2,, m} {, 2,, } do T. 5..2. OZNAČENÍ Možiu všech matic
Kapitola 5 - Matice (ad tělesem) 5.. Defiice matice 5... DEFINICE Nechť T je těleso, m, N. Maticí typu m, ad tělesem T rozumíme zobrazeí možiy {, 2,, m} {, 2,, } do T. 5..2. OZNAČENÍ Možiu všech matic
je vstupní kvantovaný signál. Průběh kvantizační chyby e { x ( t )}
 ČÍSLICOVÉ ZPRACOVÁNÍ ZVUKOVÝCH SIGNÁLŮ Z HLEDISKA PSYCHOAKUSTIKY Fratišek Kadlec ČVUT, fakulta elektrotechická, katedra radioelektroiky, Techická 2, 66 27 Praha 6 Úvod Při číslicovém zpracováí zvukových
ČÍSLICOVÉ ZPRACOVÁNÍ ZVUKOVÝCH SIGNÁLŮ Z HLEDISKA PSYCHOAKUSTIKY Fratišek Kadlec ČVUT, fakulta elektrotechická, katedra radioelektroiky, Techická 2, 66 27 Praha 6 Úvod Při číslicovém zpracováí zvukových
PARAMETRICKÁ STUDIE PRŮBĚHU RYCHLOSTI PROUDĚNÍ V PULTOVÉ DVOUPLÁŠŤOVÉ PROVĚTRÁVANÉ STŘEŠE NA VSTUPNÍ RYCHLOSTI
 PARAMETRICKÁ STUDIE PRŮBĚHU RYCHLOSTI PROUDĚNÍ V PULTOVÉ DVOUPLÁŠŤOVÉ PROVĚTRÁVANÉ STŘEŠE NA VSTUPNÍ RYCHLOSTI TOMÁŠ BARTOŠ, JAN PĚNČÍK Vysoké učení technické v Brně, Fakulta stavební, Veveří 331/95, 602
PARAMETRICKÁ STUDIE PRŮBĚHU RYCHLOSTI PROUDĚNÍ V PULTOVÉ DVOUPLÁŠŤOVÉ PROVĚTRÁVANÉ STŘEŠE NA VSTUPNÍ RYCHLOSTI TOMÁŠ BARTOŠ, JAN PĚNČÍK Vysoké učení technické v Brně, Fakulta stavební, Veveří 331/95, 602
stručná osnova jarní semestr podzimní semestr
 Brýlová optika stručá osova jarí semestr základy geometrické optiky pro brýlovou optiku Gullstradovo schématické oko, další modely, otoreceptory oka, vizus, optotypy myopie, hypermetropie, aakie a jejich
Brýlová optika stručá osova jarí semestr základy geometrické optiky pro brýlovou optiku Gullstradovo schématické oko, další modely, otoreceptory oka, vizus, optotypy myopie, hypermetropie, aakie a jejich
Přijímací řízení akademický rok 2012/2013 Kompletní znění testových otázek matematické myšlení
 Přijímací řízeí akademický rok 0/0 Kompletí zěí testových otázek matematické myšleí Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá odpověď. Které číslo doplíte místo otazíku? 6 8 8 6?.
Přijímací řízeí akademický rok 0/0 Kompletí zěí testových otázek matematické myšleí Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá odpověď. Které číslo doplíte místo otazíku? 6 8 8 6?.
