NUMERICKÉ MODELOVÁNÍ VLIVU MAGNETICKÉ SUSCEPTIBILITY NA MR OBRAZY
|
|
|
- Barbora Machová
- před 6 lety
- Počet zobrazení:
Transkript
1 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV TEORETICKÉ A EXPERIMENTÁLNÍ ELEKTROTECHNIKY FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF THEORETICAL AND EXPERIMENTAL ELECTRICAL ENGINEERING NUMERICKÉ MODELOVÁNÍ VLIVU MAGNETICKÉ SUSCEPTIBILITY NA MR OBRAZY NUMERICAL MODELING OF MAGNETIC SUSCEPTIBILITY INFLUENCE TO MR IMAGES DIPLOMOVÁ PRÁCE MASTER S THESIS AUTOR PRÁCE AUTHOR Bc. Mchal Julín VEDOUCÍ PRÁCE prof. In. Karl Bartuš DrSc. SUPERVISOR BRNO 00
2 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Faulta ltrotchny a ounačních tchnoloí Ústav radoltrony Dploová prác astrsý navazuící studní obor Eltrona a sdělovací tchna Studnt: Bc. Mchal Julín ID: 788 Roční: Aadcý ro: 009/00 NÁZEV TÉMATU: Nurcé odlování vlvu antcé suscptblty na MR obrazy POKYNY PRO VYPRACOVÁNÍ: Sznat s s prncpy ěřní suscptblty poocí MR toorafu. Prostudut tody odlování antcých polí. Provďt nurcé odlování a vyhodnocní rozložní antcého pol v vybraných odlových struturách porézních atrálů. Exprntálně ověřt rozložní antcého pol odlového uspořádání. Provďt návrh a ověřní nvrzní úlohy. Stanovt atrálové charatrsty zéna vlost antcé suscptblty z zěřnýho rozložní antcého pol vybraného uspořádání. DOPORUČENÁ LITERATURA: [] BLUMLICH B. NMR an of atrals. Oxford (Enland): Clarnton Prss 000. ISBN X. [] STEINBAUER M. Měřní antcé suscptblty tchna tooraf antcé rzonanc. Dsrtační prác Brno [] DĚDKOVÁ J. Modlování ltroantcých polí. Srptu. Brno: FEKT VUT v Brně 005. Trín zadání: Trín odvzdání:.5.00 Vdoucí prác: prof. In. Karl Bartuš DrSc. UPOZORNĚNÍ: prof. Dr. In. Zbyně Rada Přdsda oborové rady Autor dploové prác nsí př vytvářní dploové prác porušt autorsá práva třtích osob zéna nsí zasahovat ndovolný způsob do czích autorsých práv osobnostních a usí s být plně vědo násldů porušní ustanovní a náslduících autorsého záona č. /000 Sb. včtně ožných trstněprávních důsldů vyplývaících z ustanovní část druhé hlavy VI. díl 4 Trstního záoníu č.40/009 Sb.
3 LICENČNÍ SMLOUVA POSKYTOVANÁ K VÝKONU PRÁVA UŽÍT ŠKOLNÍ DÍLO uzavřná z sluvní strana:. Pan/paní Jéno a příní: Bc. Mchal Julín Byt: Jílova 7 Brno Narozn/a (datu a ísto): 8. února 986 v Brně (dál n autor ). Vysoé uční tchncé v Brně a Faulta ltrotchny a ounačních tchnoloí s sídl Údolní 5 Brno íž én dná na záladě písného pověřní děan faulty: prof. Dr. In. Zbyně Rada přdsda rady oboru Eltrona a sdělovací tchna (dál n nabyvatl ) Čl. Spcfac šolního díla. Přdět této slouvy vysoošolsá valfační prác (VŠKP): dsrtační prác dploová prác baalářsá prác ná prác íž druh spcfován ao... (dál n VŠKP nbo dílo) Názv VŠKP: Vdoucí/ šoltl VŠKP: Ústav: Datu obhaoby VŠKP: Nurcé odlování vlvu antcé suscptblty na MR obrazy prof. In. Karl Brtuš DrSc. Ústav radoltrony VŠKP odvzdal autor nabyvatl * : v tštěné forě počt xplářů: v ltroncé forě počt xplářů:. Autor prohlašu ž vytvořl saostatnou vlastní tvůrčí čnností dílo shora popsané a spcfované. Autor dál prohlašu ž př zpracovávání díla s sá ndostal do rozporu s autorsý záon a přdpsy souvsící a ž dílo díl původní.. Dílo chráněno ao dílo dl autorsého záona v platné znění. 4. Autor potvrzu ž lstnná a ltroncá vrz díla dntcá. * hodící s zašrtnět
4 Člán Udělní lcnčního oprávnění. Autor touto slouvou posytu nabyvatl oprávnění (lcnc) výonu práva uvdné dílo nvýdělčně užít archvovat a zpřístupnt studní výuový a výzuný účlů včtně pořzovaní výpsů opsů a roznožnn.. Lcnc posytována closvětově pro clou dobu trvání autorsých a atových práv dílu.. Autor souhlasí s zvřnění díla v databáz přístupné v znárodní sít hnd po uzavřní této slouvy ro po uzavřní této slouvy roy po uzavřní této slouvy 5 lt po uzavřní této slouvy 0 lt po uzavřní této slouvy (z důvodu utaní v ně obsažných nforací) 4. Nvýdělčné zvřňování díla nabyvatl v souladu s ustanovní 47b záona č. / 998 Sb. v platné znění nvyžadu lcnc a nabyvatl něu povnn a oprávněn z záona. Člán Závěrčná ustanovní. Slouva spsána v třch vyhotovních s platností ornálu přčž po dno vyhotovní obdrží autor a nabyvatl další vyhotovní vložno do VŠKP.. Vztahy z sluvní strana vznlé a nupravné touto slouvou s řídí autorsý záon občansý záoní vysoošolsý záon záon o archvnctví v platné znění a popř. další právní přdpsy.. Lcnční slouva byla uzavřna na záladě svobodné a pravé vůl sluvních stran s plný porozuění íu txtu důsldů nolv v tísn a za nápadně nvýhodných podín. 4. Lcnční slouva nabývá platnost a účnnost dn ího podpsu oběa sluvní strana. V Brně dn:. větna 00
5 ABSTRAKT Tato dploová prác s zabývá antcou suscptbltou onrétního vzoru (slněná rychl naplněná vodou a acton). V první část byla provdna sulac antcého pol v prorau ANSYS. Výpočt byl prováděn na D obtu todou ončných prvů. Sulací bylo zísáno rozložní antcého pol uvntř obtu. V druhé část prác byly popsány tody ěřní antcé suscptblty a bylo provdno ěřní úlohy s vyhodnocní rozložní antcého pol. V posldní část prác popsána nvrzní sulační úloha. J stanovna hodnota antcé suscptblty poocí zěny antcého pol v sulac. KLÍČOVÁ SLOVA MRI NMR ANSYS nurcé odlování nvrzní úlohy ABSTRACT Ths thss dals wth th antc suscptblty of th partcular sapl. In ths cas th sapl s a lass cub flld wth watr and acton. At frst a sulaton of th antc fld was ad n ANSYS. Ths calculaton was prford on D buldn by th fnt lnt thod. Th antc fld dstrbuton nsd th buldn was obtand by ans of sulatons. So thods of th asurnt of th antc suscptblty wr dfnd n th scond part. And also t was carrd out th assssn of th rol of th antc fld dstrbuton. Th last part dscrbs to th rol of th nvrs sulaton. Th valu of th antc suscptblty s dtrnd by th odfcaton of th antc fld n th sulaton n th nd. KEYORDS MRI NMR ANSYS nurc sulaton nvrson tas
6 JULÍNEK M. Nurcé odlování vlvu antcé suscptblty na MR obrazy. Brno: Vysoé uční tchncé v Brně Faulta ltrotchny a ounačních tchnoloí. Ústav Tortcé a xprntální ltrotchny s. s. příloh. Dploová prác. Vdoucí prác: prof. n. Karl Bartuš CSc.
7 PROHLÁŠENÍ Prohlašu ž svou dploovou prác na téa Nurcé odlování vlvu antcé suscptblty na MR obrazy s vypracoval saostatně pod vdní vdoucího dploové prác a s použtí odborné ltratury a dalších nforačních zdroů tré sou všchny ctovány v prác a uvdny v sznau ltratury na onc prác. Jao autor uvdné dploové prác dál prohlašu ž v souvslost s vytvořní této dploové prác s nporušl autorsá práva třtích osob zéna s nzasáhl ndovolný způsob do czích autorsých práv osobnostních a nbo atových a s s plně vědo násldů porušní ustanovní a náslduících záona č. /000 Sb. o právu autorsé o právch souvsících s práv autorsý a o zěně nětrých záonů (autorsý záon) v znění pozděších přdpsů včtně ožných trstněprávních důsldů vyplývaících z ustanovní část druhé hlavy VI. díl 4 Trstního záoníu č. 40/009 Sb. V Brně dn (podps autora) PODĚKOVÁNÍ Děu vdoucíu dploové prác prof. n. Karlu Bartušov DrCs. za účnnou todcou pdaocou a odbornou pooc a další cnné rady př zpracování é baalářsé prác. V Brně dn (podps autora)
8 OBSAH: Úvod... Záladní rovnc pol... Nurcé tody pro výpočt polí.... Přhld tod..... Mtoda ončných prvů... 4 Mantcé vlastnost lát Mantcá suscptblta Daantzus Paraantsus Froantsus Nurcý odl Gotr úlohy pro nurcé odlování Matatcý pops nurcého odlu č Matatcý pops nurcého odlu č Výsldy sulací Mantcá rzonanc Mtoda spnového cha Mtoda radntní cha Exprntální ěřní Pops ěřné úlohy Pops onfurac ěřné úlohy Použtá toda ěřní Výsldy ěřní Stanovní zěny antcého pol Stanovní nvrzní úlohy Závěr: Ltratura:... 47
9 SEZNAM OBRÁZKŮ Obr. Uzly na sít ončných prvů(přvzato z [])... Obr. Elntární rovnné a prostorové prvy (přvzato z [])... 4 Obr. Froantcá láta v nzantované stavu (přvzato z [7])... 6 Obr. 4 Froantcá láta v nasycné tvaru (přvzato z [7])... 7 Obr. 5 Gotr úlohy pro nurcé odlování rozěry v... 8 Obr. 6 Rozložní odulu antcé nduc v řzu 5 od lvého ora Obr. 7 Čtyřstěnný lnt (přvzato z [9])... 5 Obr. 8 Pětstěnný lnt (přvzato z [9])... 5 Obr. 9 Šststěnný lnt (přvzato z [9])... 6 Obr. 0 Troúhlníový lnt.... Obr. Zobrazní řzů rozložní odulu antcé nduc v vzoru rozěry v... 5 Obr. Rozložní odulu antcé nduc v vzdálnost 5 od lvého ora Obr. Rozložní odulu antcé nduc v vzdálnost 5 pro pozadí (voda) Obr. 4 Rozložní odulu antcé nduc v vzdálnost 5 od lvého po odčtní pozadí (voda)... 7 Obr. 5 Rozložní odulu antcé nduc v vzdálnost 0 od lvého ora Obr. 6 Rozložní odulu antcé nduc v vzdálnost 0 od lvého ora po odčtní pozadí (voda) Obr. 7 Rozložní odulu antcé nduc v vzdálnost 5 od lvého ora Obr. 8 Rozložní odulu antcé nduc v vzdálnost 5 od lvého ora po odčtní pozadí (voda) Obr. 9 Rozložní odulu antcé nduc v vzdálnost 0 od lvého ora... 9 Obr. 0 Rozložní odulu antcé nduc v vzdálnost 0 pro pozadí (voda)... 0 Obr. Rozložní odulu antcé nduc v vzdálnost 0 od lvého ora po odčtní pozadí (voda)... 0 Obr. K prncpu antcé rzonanc (přvzato z [0] )... Obr. 4 Pohyb vtoru antzac (přvzato z [0]).... Obr. 5 K prncpu tody spnového cha (přvzato z [0])... 4 Obr. 6 K prncpu tody radntního cha (přvzato z [0]) Obr. 7 MR tooraf... 6 Obr. 8 Pops MR toorafu (přvzato z [])... 7 Obr. 9 Vzor... 8 Obr. 0 Dforac pol způsobná vložní paraantcého vzoru (přvzato z [])... 9 Obr. Měřná apa račního pol B R pro onfurac voda slo acton Obr. Mapa račního pol B R pro lvou stranu (vlvo) a řz v ístě označní Obr. Sptrální čára ěřného vzoru voda + acton Obr. 4 Měřný fázový obraz přpočtný na B 0 [T] Obr. 5 Mapa pol B 0 [T] pro lvou stranu s řz v ístě označní pro ěřní č.... 4
10 Obr. 6 Řz račního antcého pol pro pravou stranu ěřného fázového obrazu pro T E = 0 s Obr. 7 Mapa pol ěřná pro onfurac voda-slo-voda Obr. 8 Měřný fázový obraz ěřný pro onfurac voda-slo-voda... 4 Obr. 9 Rozložní odulu antcé nduc v vzdálnost 0 od lvého ora po odčtní pozadí (voda) Obr. 40 Rozložní záporných hodnot odulu antcé nduc v vzdálnost 0 od lvého ora po odčtní pozadí (voda)
11 Úvod Cíl dploové prác bylo prostudovat problatu ěřní suscptblty atrálů ndávaící MR obraz. Byly prostudovány tody MR zobrazní a odlování antcých polí. Byl provdn nurcý odl s vyhodnocní rozložní antcého pol v vybraných odlových struturách atrálů. Data byla zpracována a byla vypočtna zěna antcého pol v prorau ANSYS poocí tody ončných prvů. J navržna nvrzní sulační úloha t. stanovní antcé suscptblty atrálu poocí zěny antcého pol v sulac. Záladní rovnc pol Záony ltroantcého pol tré byly obvny do polovny nulého stoltí shrnul Jas Clar Maxwll do soustavy rovnc. Můžou být uvdny v ntrální v dfrncální tvaru. V dfrncální tvaru popsuí ltroantcé pol v sté oblast al v dfrncální tvaru v určté bodu této oblast [] []. První Maxwllova rovnc Apérův záon clového proudu záon antoltrcé nduc. Intrální tvar první Maxwllovy rovnc l d H dl I. () dt Crulac vtoru H po orntované řvc l rovna clovéu vodvéu proudu I a d posuvnéu proudu trý prochází v ladné sěru plochy S ohrančné řvou l. d t Křva l a lbovolná plocha S ž řvu obpíná sou vzáně orntovány pravotočvě. Dfrncální tvar první Maxwllovy rovnc D rot H J. () t Rotac vtoru ntnzty antcého pol H rovna hustotě vodvého proudu a D hustotě posuvného (Maxwllova) proudu. t
12 Druhá Maxwllova rovnc l Faradayův nduční záon záon ltroantcé nduc dφ E d l. () d t Crulac vtoru E po lbovolně orntované uzavřné řvc c rovna záporně vzaté časové drvac antcého ndučního tou spřažného řvou c. Křva c a lbovolná plocha S íž řva obpíná sou vzáně orntovány pravotočvě. Dfrncální tvar druhé Maxwllovy rovnc rot E B. (4) t Rotac vtoru ntnzty ltrcého pol E rovna záporně vzaté drvac antcé nduc B. Třtí Maxwllova rovnc Gaussova věta ltrostaty. Intrální tvar třtí Maxwllova rovnc S D d S Q. (5) Eltrcý nduční to lbovolnou vně orntovanou plochou S rovn clovéu volnéu nábo v prostorové oblast V ohrančné plochou S. Dfrncální tvar třtí Maxwllovy rovnc dv D. (6) Výto vtoru nduc D rovn clovéu nábo Q v obu V trý uzavřný plochou S. Čtvrtá Maxwllova rovnc Záon spotost ndučního tou. Intrální tvar S B d S 0. (7) Výto vtoru antcé nduc lbovolnou uzavřnou orntovanou plochou S rovn nul.
13 Dfrncální tvar čtvrté Maxwllova rovnc dv B 0. (8) Dvrnc vtoru antcé nduc B rovna nul. Nurcé tody pro výpočt polí V posldních dvact ltch byly vyvnuty nurcé tody tré uožňuí odlovat D a D pol. U těchto tod řšní nalzno poocí arttcých procsů [].. Přhld tod ontová toda řšní dfrncální ntrální ntro-dfrncální rovnc toda hrančních prvů řšní ntrální rovnc toda nduovaných náboů řšní ntrální rovnc toda ončných obů řšní dfrncální rovnc toda ončných dfrncí (Fnt Dffrnc Mthod) řšní dfrncální rovnc toda ončných prvů (Fnt Elnt Mthod) řšní dfrncální rovnc... Mtoda ončných prvů Jž něol lt přdstavuí nurcé tody význaný výpočtní nástro. Mtoda ončných prvů (MKP) s dns stala dní z hlavních výpočtních prostřdů nn v stroírnství pro tré byla prvotně určna al taé v všch oblastch ltrotchncého průyslu. MPK účnná toda řšní všch oraových úloh nžnýrsé prax popsaných dfrncální rovnc. Byla vyvnuta s nástup dtálních počítačů onc Obr. Uzly na sít ončných prvů(přvzato z []) padsátých lt. Svou nzastuptlnou rol shrává a př vývo návrhu a onstruc nových ltrotchncých výrobů ta v případné rozěrové č atrálové optalzac stávaícího zařízní. Hlavní význa MKP spočívá v rafcé znázornění často vl abstratních fyzálních polí v trých lascá tchna řšní zavádí nohdy značná
14 zdnodušní na úor přsnost. U tody MKP sou zavdny oblast d s počítá pol uzly a uzlové potncály. Uzly vša ohou být rozložny v oblast nrovnoěrně a ohou ta sldovat tvar hrančních ploch. V ístch d s očává prudá zěna pol zavdna větší hustota sítě. Přílad sítě uzlů a prvů na obr.. Podobně ao v MKD s sstaví soustava rovnc pro nznáé uzlové potncály. Kofcnty atc soustavy a pravých stran s npočítaí z dfrncí nahrazuících drvac al ao ntrály přs lntární plošy nbo oby v chž vrcholch sou uzly. Tyto lntární útvary sou nazývány ončné prvy. Na obr. a naznačn ončný prv tvaru troúhlníu a čtyřúhlníu a další záladní rovnné prvy lnární a parabolcý troúhlní a čtyřúhlní. Parabolcý prv á zařvné hrany s další uzl na hraně. Prostorové lntární prvy sou na obr. b. Prostorové ončné prvy aí tvar čtyřstěnu pětstěnu a šststěnu. Mohou ít rovněž další uzly v střdu hran []. Postup př aplac MKP sstává z těchto roů: Obr. Elntární rovnné a prostorové prvy (přvzato z []) Gnrac sítě prvů s uzly. Aproxac potncálu na dnotlvých prvcích z uzlových hodnot. Sstavní soustavy rovnc pro nznáé uzlové hodnoty. Vyřšní soustavy. Zpracování dodatčných požadavů výpočt dalších vlčn a zobrazní výsldů. 4 Mantcé vlastnost lát J-l láta vložna [] do vněšího antcého pol stý způsob s zantzu a obví s v ní vntřní antcé pol B tré lz chápat ao hustotu antcých dpólových ontů B. (9) V Vlastní příčnou antcých vlastností lát sou antcé dpóly tré sou buď pranntní nbo s nduuí př působní vněšího antcého pol. Jstlž v 4
15 npřítonost vněšího antcého pol nobsahu láta antcé onty hovoří o tzv. daantách v opačné případě o paraantách. Zvláštní případ paraant sou tzv. froanta v trých sou prablta a suscptblta podstatně větší nž v ostatních paraantách. Clové antcé pol v látc lz poto napsat ao suprpozc pol vntřního a pol původního B B 0. (0) B Můž-l přdpoládat lnární chování platí B B 0. () B Paratr suscptblta trá ůž být větší nší nž nula. Dosadí-l do první rovnc B rb 0 0. () Clová (absolutní) prablta dfnována ao 0 r () d μ 0 prablta vaua a μ r = ( + χ ) rlatvní prablta daného atrálu. 4. Mantcá suscptblta Mantcá suscptblta χ (nědy taé κ nbo K) fyzální vlčna trá popsu chování atrálu v vněší antcé pol [4]. Záladní vztah pro výpočt suscptblty: χ M (4) H d M vtor antzac a H ntnzta antcého pol. Obě uvdné vlčny s ěří v apérch na tr Podl hodnoty antcé suscptblty lz rozdělt atrály na: daantcé pro ně < χ < 0 paraantcé poud 0 < χ << froantcé stlž χ >> 4. Daantzus Daantzus [4] v spolčný pro všchny láty trý v srovnání s ný vy vl slabý a proví s proto n u těch lát u trých nní přryt slněší provy paraantcý nbo froantcý. J způsobn antcý onty atoů ltrcy nabtých částc tré nduuí saotné vněší antcé pol. Mantcé pol 5
16 od nduovaných dpólů bud zslabovat původní pol tré ho způsoblo. Výsldné pol proto vždy nší nž původní (antuící ) pol. Daantcé láty s sládaí z daantcých atoů a ch prablta npatrně nší něž. Tyto láty írně zslabuí antcé pol (patří s nrtní plyny zlato ěď rtuť) [5]. Mantcá suscptblta daantcých lát χ vyádřná vztah μ O n rs (5) 6 d n oncntrac atoů a r S součt poloěrů ruhové dráhy tého ltronu 4. Paraantsus Paraantsus [4] lát způsobn tí ž atoy a oluly aí své stálé nnulové antcé onty tré sou vša v npřítonost vněšího antcého pol v důsldu chaotcého pohybu rozložny ta ž s navzá zcla opnzuí. Navn tdy láta nantcá. Až přítonost vněšího antcého pol vyvolává souhlasnou orntac antcých polí dnotlvých atoů a tí dod značnéu zsílní antcého pol v látc [5]. V sutčnost [6] tnto v nnastává brání u tplný pohyb. J to chaotcý pohyb trý vyonávaí všchny záladní částc ltrony protony nutrony atoy oluly. An slné vněší antcé pol ndoáž uspořádat do dnoho sěru ndoáží vněší antcé pol podstatně zsílt. Paraantcá láta s antu přtahu a bud saa přtahovat drobné ovové přděty pouz v případě ž bud v blízost antu. Paraantcou látu nní ožné trval zantovat Mantcá suscptblta paraantcých lát určna vztah: n μ0 C (6) T T d C tzv. Curho onstanta. 4.4 Froantsus Froantcé [6] láty sou složny z paraantcých atoů al v taové Obr. Froantcá láta v nzantované stavu (přvzato z [7]) 6
17 Obr. 4 Froantcá láta v nasycné tvaru (přvzato z [7]) uspořádání ž výrazně zsluí antcé pol. Tyto láty s vyznačuí tí ž ch rlatvní prablta µ r = + χ aí vlé hodnoty až 0 6. Mantcé pol podíněné uspořádání antcých dpólů tdy podstatně slněší nž vněší antcé pol. Jž slabý antcý pol lz u nch vyvolat taové uspořádání atoů. Mantcá suscptblta froant splňu nad určtou tplotou T c tzv. Curův- C (7) T T ssův záon d rtcá tplota T c s nazývá Curova tplota. Po přroční Currovy tploty láta ztrácí froantcé vlastnost a stává s látou paraantcou [4][5]. Na obr. sou zobrazny [7] doény tré s provuí ao anty s různou orntací. Př působní vněšího antcého pol s doéna s stnou orntací začn zvětšovat. Čí vněší antcé pol slněší tí s doéna s souhlasnou orntací zvětšu a ostatní doény znšuí. Láta tdy zslu vněší antcé pol čí dál výrazně. Př určté hodnotě vněšího antcého pol bud souhlasně zorntovaná clá láta doény s nou orntací zannou obr. 4 Láta tdy nasycná a í r s přstává zvětšovat. Hystrzní syča c Vloží-l [8] odantovanou froantcou látu do vněšího antcého pol a bud-l postupně zvyšovat ntnztu antcého pol H pa zísá řvu prvotní antzac. Př určté hodnotě ntnzty antcého pol s dosáhn nasycného stavu dy antcá nduc B rost n npatrně. Bud-l nyní ntnztu antcého pol snžovat bud řva závslost antcé nduc B na ntnztě vněšího antcého pol H vypadat na dostan tzv. hystrzní řvu (hystrz = zpožďování). Př nulové ntnztě antcého pol zůstan láta ště zantzovaná. Provd-l clý antzační cylus dostan uzavřnou hystrzní syču froanta. Hystrzní syčy dnotlvých froant s od sb lší tvar obsah plochy trou ohrančuí. Podl tvaru hystrzní syčy rozlšu froantcé láty na antcy ěé s vl úzou hystrzní syčou tré s snadno zantuí al po zánu vněšího antcého pol přstávaí být antcé. Jsou vhodné ta d chc ěnt vlost antcé nduc pol ltroantu. A antcy tvrdé s šroou hystrzní syčou 7
18 zůstanou antcé po zánu pol trý byly zantovány a chovaí s ao trvalé anty. Po zrušní antcého pol pozoru zbytový antsus (antcé rsduu) trý vl slabý u antcy ěých lát džto u antcy tvrdých lát značný ění látu na trvalý ant. 5 Nurcý odl 5. Gotr úlohy pro nurcé odlování Obr. 5 Gotr úlohy pro nurcé odlování rozěry v V systéu ANSYS byl vytvořn nurcý odl podl onfurac uvdné na obr. 5. Nurcý odl byl vytvořn s využtí MKP sítě prvů poocí typu prvu Sold5 a Sold v systéu ANSYS. V odlu sou cl čtyř oby s různou suscptbltou: atrál č. zvolná suscptblta = atrál č. voda = atrál č. slo = atrál č. 4 vzduch = 0 Matrály byly dfnovány prabltou poocí vztahu µ = + vzhld vyčíslní výsldů bylo nutné zvýšt prabltu o 0 8. Dál bylo nutné přřadt dnotlvý oblast atrály. Vlost lntu byla v horzontální rovně V vrtální rovně byla zvolna zhušťovací sít vždy sěr přchodu dvou atrálů. Mantcá nduc byla zadána poocí vtorového potncálu na horní a dolní ora odlu. Po sulac byl 8
19 provdn řz obr. 6 v vzdálnost 5 od lvého ora. Csta byla dfnována poocí uzlů. Vzhld špčá tré sou na přchodch atrálů nní vhodné pro tnto typ úlohy vhodné použt vtorový potncál B [T] l [] Obr. 6 Rozložní odulu antcé nduc v řzu 5 od lvého ora 5. Matatcý pops nurcého odlu č. Pops nstaconárního antcého pol otrcy třírozěrného odlu antcé úlohy podl [9] ozn na uzavřné oblast. Platí = = = = =. slo - voda slo acton slo - voda Z rduovaných Maxwllových rovnc D rot H = J J v oblast t (9) B rot E t a z vlastnost antcého pol dv B 0 (0) (8) 9
20 dv D = d obová hustota ltrcého nábo. Modl antcého pol s forulu př použtí atrálových vztahů D = E. () B H = B. () Vířvé proudy sou z Ohova záona J = E. () Po dosazní vztahů () až () do rovnc (9) í tvar E rot B = E J (4) t a zavdní vtorového antcého potncálu A poocí vztahu () B rot A (5) s zísá rovnc (4) v tvaru rot rot E A = EJ. (6) t Dosazní vztahu () za ntnztu ltrcého pol do rovnc (6) s í tvar zění na A rot t A =. (7) t t rot A rad rad J Aby bylo zaručno dnoznačné řšní rovnc (7) přdpsaná další podína dv A =0. (8) t Úpravou rovnc (7) a (8) s zísá výsldný vztah odlu antcého pol rotrot rad dv rad A t A t A A = J. (9) Pro zvolnou oblast sou oraové podíny n rot A = 0 na hranc 5 n A A 0 rot rot = =.. 4 na hranc n A dv dv A =0 =..4 na hranc n rad 0 n rad rad = 0 =.. n = na hranc 4 (0) () 4 na hranc () A = 0 na hranc t 4 () A A n = 0 =..4 na hranc (4) t t n =0=..5 na hranc. (5) t t Počátční podíny zapsané poocí salárních a vtorových potncálů sou 0
21 t t0 xyz 0xyz xyz t 0 t0 x y z xyz 0 t 0 xyz xyz t t A t xyz A xyz 0 0 A A 0 t0 xyz xyz t t A A0 t 0 x y z xyz. t t Zvolní bázové func totožné s bázovou funcí proudového pol N xyzt t xyz N A xyzt t xyz A a t 0 xyz t 0 xyz (6) (7) (8) J. (9) v vztazích (6) a(7) aplací Galrnovy tody na výraz (9) s zísá rovnc A A rot rot A rad dv A rad J d Nu t t 0.. (40) Výraz (8) s upraví aplací II. Grnovy forul a Gaussovy věty na tvar rot Arot d n rot A d dv Arad d dv A nd A A d t d t rad d Jd. Rsptování oraových podín úlohy podl výrazů (6) až (9)s vztah (4) zění na A rot Arot d dv Arad d d t A d t rad d Jd. Tnzor antcé rlutvty funcí tploty a antcé nduc B B T x y z t t 0 xyz. (4) J (4) (4) Lz vyádřt poocí náslduícího vztahu B x 0 0 x 0 0 B T xyzt 0 yb 0 0 y 0 T xyzt 0 0 B z 0 0 z x y 0 T xyzt. 0 0 z Dosazní func do vztahu (4) s zísá sdsrétní řšní (44)
22 rot N A = N A = a rad rot d d N = dt a d d dv N A = N A = N J = a d a rad dt d d. Rovnc (4) lz přpsat na tvar a x rot rot d a x dv rad d N A N A ay rot rot d ay dv rad d = = az rot rot d az dvrad d N A N A N d a d a d d rad d dt dt = = = N J = d Zdnodušný záps soustavy rovnc (46) N. d a da l dt dt A A A a A A A A A = = = = N J s.. N. = J Tvar ofcntů vyádřn v vztazích (46) až (5) A x = rot rot d N u A y = rot rot d A z = rot rot d A x= dv rad d A y= dv rad d A z = dv d rad N A = d (50) N d (45) (46) (47) (48) (49)
23 la = d (5) A = rad d (5) s J = d. (5) Alortus sstavní atc ofcntů (48) až (5) s zdnoduší dyž s soustava rovnc (47) přpíš do tvaru. a a l a s A A A A A J..N. (54) Kofcnty soustavy rovnc (5) sou vyádřny v vztazích A x = rot rot d =.. Nu =.. N A y = rot rotd A z = rot rotd A x= dvrad d A y= dv rad d A z= dvrad d l A A s = d = d A J = rad d = d (55) (56) (57) (58) (59). (60) Alortus sstavní atc ofcntů (56) až (60)s zdnoduší dyž s soustava rovnc (47) přpíš do tvaru a a l a s A A A A A J..N. (6) Kofcnty soustavy rovnc (59) sou vyádřny v vztazích
24 A x = rot rot d =.. Nu =.. N A y = rot rotd A z = rot rotd A x= dvrad d A y= dv rad d A z= dvrad d l A A s A J = d = d = rad d (6) (6) (64) (65) (66) = d. (67) Soustava rovnc (6) s zapíš v tvaru M 0 0 a L 0 a K K K a s = J 0. (68) A A A A A Postup vyčíslní ofcntů pro čtyřstěnný pětstěnný a šststěnný lnt. Aby bylo ožné určt vlost ofcntů nutné zvolt typ lntů dsrtzační sítě. Záladní tvary lntů sou čtyřstěn pětstěn a šststěn. Stručný pops lntů na obr. 7 obr. 8 obr. 9. Čtyřstěnný lnt v obr. 7 á bázovou func = a bx cy dz (xyz) =.. 4. (69) 6 Platí x y z 6 x y z = x y z x y z (70) d ndxy u souřadnc x y z sou loální čísla uzlů. Kofcnty func lz vyádřt x y z a = x y z l=.. 4 (7) x y z l l l 4
25 b c y y l z z = y z (7) x x l z l z = x z (7) l d = x y (74) x x l y y l d ndxy l s cylcy ění v dané ntrvalu. Indx přrozné číslo func lntu ndxy l sou ndxy souřadnc uzlů lntu. Dosazní vztahů (8) až () do výrazu pro vyádřní ofcntů atc soustavy rovnc (7) s zísá výraz pro ofcnty loální atc. z 4 Čísla uzlů lntu 4 Číslo lntu () () N = 4 u x o y Obr. 7 Čtyřstěnný lnt (přvzato z [9]) 4 () o Čísla uzlů lntu 456 Číslo lntu () Souřadnc N u= 6 Obr. 8 Pětstěnný lnt (přvzato z [9]) 5
26 8 o 7 5 () 6 Čísla uzlů lntu Číslo lntu () Souřadnc N u = 8 4 Obr. 9 Šststěnný lnt (přvzato z [9]) J-l zvoln prv pětstěnný podl obr. 8 a na ně func pa ch záps př zvolné loální artézsé souřadné soustavě o náslduící = 4 = = 5 = (75) = 6 = 0 0 a radnt func vyádřn v artézsé souřadné soustavě xyz rad = =.. Nu. (76) x y z Po transforac func do lobální artézsé souřadné soustavy xyz z loální souřadné soustavy o. d d v loální souřadné soustavě c d = J d d d. (77) V vztahu (77) drvac polohového vtoru R p vyádřna náslduící výraz Rp y z = x (78) souřadnc xyz a ch drvac podl loálních souřadnc s vyádří x = y = z = N u = N u N = u = x x = y y = z z = N u = N u N = u = x x = y y = z z = N u = u N N = u = x x = y y = z z = N u u N = N = u = x y z (79) 6
27 J-l zvoln šststěnný lnt podl obr. 9 sou ho bázové func zapsány = 8 = 8 = 8 4 = 8 6 = 8 8 =. 8 5 = 8 7 = 8 U šststěnného lntu s vlost ofcntů z soustavy rovnc (59). Intrac v vztazích (55)-(60) lz provést analytcy. Tnto způsob obtížný a zdlouhavý. Npoužtí analytcy vyádřných ntrálů v vlé většně případů npřns podstatné zhoršní přsnost řšní soustavy rovnc (44). Jné rychlší a snazší řšní ntrac spočívá v použtí Gaussovy vadratury. Jí tvar použtí a vlastnost sou znáy. Kofcnty soustavy rovnc (68) s pa vyčíslí pro nurcé řšní n l = = = AJ = HHH rad rad Jc. (8) Druhý ofcnt s poocí zvolné vadratury vyčíslí ao n l l AJ = HHH rad J c. (8) = = = Počt ntračních bodů loálních souřadnc pro čtyřstěnný lnt byl zvoln n = = l = 5. Tnto počt podl tstů pro přsnost a rychlost vyčíslní vadraturního vztahu vyhovu atatcéu odlu. Vyádřní poocné func L shodné s funcí (69). Poocí func L s určí souřadnc ntračních bodů podl níž uvdného vztahu (7). Nastavné hodnoty poocné func L a váhové func H pro 5 bodů zvolných uvntř oblast sou.bod: L =0.5L =L =L 4 =0.66 H =0.45.bod : L = 0.5 L = L = L 4 = 0.66 H = 0.45.bod : L = 0.5 L 4 = L = L = 0.66 H = bod : L 4 = 0.5 L = L = L = 0.66 H = bod : L = L = L = L = 0.5 H = Souřadnc bodu ntrac s určí pro čtyřstěnný prv N u = L s (84) s= (80) (8) 7
28 N u = L s (85) s= N u = L s. (86) s= U pětstěnného lntu bylo zvolno šst bodů ntrac n = = l = 6. Počt odpovídá požadované přsnost a rychlost výpočtu vadratury. Souřadnc bodů sou určny = H =.0 = = Podobně u šststěnného lntu d n = = l = 8. Souřadnc bodu pro výpočt vadratury podl (86) vyádřna poocnou funcí L.bod: L = H =.0.bod : L = bod : L =L 4.bod : L 4 = bod : L 5 =L 4 6.bod : L 6 =L 7.bod : L 7 =L 4 8.bod : L 8 = Pro čtyřstěnný lnt sou ofcnty A x = 6 A y A z = = 6 6 c d c d d b b c d d b c d d b b c b c c d d b b c d d (87) (88) (89) A x b b c d d = 6 c b c d d A y= 6 d b c d d A z= 6 A = d (9) (90) 8
29 9 l A d = (9) x y z d A = (9) s J u d N = - =... (94) J-l zvoln šststěnný lnt ofcnty s určí poocí vztahů (90) až (94) al func volna podl vztahů (80). Poud by byla použta Gaussova vadratura pro vyčíslní ofcntů (75) až (78) ch tvar = n l c x A J H H H (95) = n l c y A J H H H (96)
30 0 = n l c z A J H H H (97) c x A J n l = H H H (98) c y A J n l = H H H (99) c A J n l = H H H (00) l A c J = H H H l n (0) J A c = H H H l n (0)
31 u n l s J = -HHH =.. N J c. (0) Toto řšní pro nstaconární antcé pol D otrcého odlu s v dnodušší vazstaconární varantě odlu zdnoduší ta ž nětré z ofcntů (6)-(67) budou nulové. Tdy budou brány v úvahu pouz ofcnty A x = rot rot d (04) A y = rot rot d (05) A z = rot rot d (06) A x= dv rad d (07) A y= dv rad d (08) = dv rad d (09) A z s d J =. (0) Vyčíslní těchto ofcntů podl vztahů (8)-(88) by odpovídalo D otr ltů podl obr. 7 až obr. 9 čtyřstěnný pětstěnný a šststěnný. Poud bycho uvažoval D otrcý odl bz rotační sytr s lnární vlastnost atrálů fyzální odl dnodušší. Z aproxac A x y z t a t x y z t 0 xyz J. () lz po dosazní souřadnc uzlů troúhlnía dnoduchou úpravou zísat = xy yxy yxx xy S = x y y x y y xx x y S = x y y x y y xx x y S v nchž ()
32 S = xy xy xy xy xy xy () Protož soustava rovnc (68) lnární staconární í řšní poocí znáých tod s zísá sloupcová atc salárních ltrcých potncálů. Aplací výrazů rad rad rad = S = S = S y y x x y y x x y y x x. (4) z řšní lz zísat vtory ntnzty a nduc antcého pol v uzlch troúhlníového prvu. Obdobně ao pro D odl s provd pro D troúhlníový lnt vyčíslní ofcntů - nurcé hodnoty z vztahů D (04) až (0). uzl= y () uzl= uzl= o x V nstaconární ltroantcé pol antcého toorafu s záladní frvncí f 0 =00MHz s v výrazu (9) za nětrých oolností (vlastnost tstovaného atrálu) nprovuí posuvné proudy v dltru. Proto lz př sstavování odlu úlohu zdnodušt na antostatcou úlohu. Tato sutčnost s porovná z laboratorní xprnt a nurcý xprnt. Poud dod v sldovaných částch rozhraní atrálů shodě lz s uvdný postup v dalších xprntch řídt. 5. Matatcý pops nurcého odlu č. V další nurcého odlu byla ao hranční podína zadán salární antcý potncál podl [4]. Mantcý potncál řšní Laplacovy rovnc dv rad 0 (5) s Drchltovou hranční podínou Obr. 0 Troúhlníový lnt onst. na oblastch a (6)
33 a Nuannovou hranční podínou u rad 0 na oblastch a 4. (7) n Spotost tčných slož ntnzty antcého pol na rozhraní oblast vzoru vyádřna výraz u rad 0. (8) n Pops MKP quazstaconárního odlu vychází z rduovaných Maxwllových rovnc rot H J (9) dv B 0 (0) d H vtor ntnzty antcého pol B vtor nduc antcého pol J vtor proudové hustoty. Pro případ statcého antcého nvírového pol s rovnc (9) zdnoduší na výraz () rot H 0. () Matrálové vztahy sou rprzntovány rovncí B 0rH () d 0 prablta vaua r (B) rlatvní prablta froantcého atrálu. Uzavřná oblast na tré budou rovnc (0) a () řšny rozdělna na oblast vzoru a oblast oolí. Platí pro ně. Pro ntnztu antcého pol H v oblast platí vztah (). Vyádřní rozložní antcého pol z vnutí poocí Bot-Savartova záona forulovaného ao J R T d 4 () R d R vzdálnost z bod v něž hldaná ntnzta antcého pol T a bod v něž uvažována proudová hustota J. Intnztu antcého pol H v oblast lz vyádřt ao H T rad = 0 (4) d T přdchozí nbo odhadnutá ntnzta antcého pol antcý salární potncál. Oraové podíny sou zapsány ao rad 0 u n T na oblastch a 4 (5) d u n norálový vtor F-0 rozhraní z oblastí F a 0. Oblast 0 prostor vzduchu v odlu oblast prostor s vnutí. Spotost tčných slož ntnzty antcého pol na rozhraní oblast s froantcé atrál vyádřn u n T rad. (6) Aplací vztahu (4) v vztahu (6) s zísá výraz dv 0 T r - dv 0 r rad = 0. (7) Dsrtzac rovnc (7) lz provést poocí aproxac salárního antcého potncálu NN x y z pro xyz (8) d hodnota salárního antcého potncálu v -té uzlu aproxační
34 func NN počt uzlů dsrtzační sítě. Aplací aproxac (8) do vztahu (7) a nalzací rzduí podl Galrnovy tody s zísá sdsrétní řšní NN radrad d0 NN. (9) Soustavu rovnc (9) lz zrácně zapsat T 0 NN Soustavu (0) lz rozdělt na U 0 D I K U 0 d T. (0) () U I NI vtor nznáých vntřních uzlů oblast včtně bodů na plochách a 4. T U D ND vtor znáých potncálů na plochách a (Drchltovy hranční podíny). NI v ndxu značí počt vntřních uzlů dsrtzační sítě ND počt hrančních uzlů sítě. Soustavu pa ůž rozpsat na 4 subatc UI 0 UD 0 a dostává soustavu s zavdný hranční podína trá s v MKP řší I D 0 () U U. () Kofcnty subatc sou nnulové n poud lnt sítě obsahu oba uzly a. Příspěv prvu ofcntu rad rad d NE (4) d oblast lntu dsrtzační sítě prablta prostřdí zvolného lntu NE počt lntů dsrtzační sítě. Prvy atc sou pa součty příspěvů dnotlvých lntů NE (5). Soustavu rovnc (0) lz řšt poocí standardních alortů. Z hodnoty salárního antcého potncálu s pa stanoví ntnzta antcého pol podl (4). Oraové podíny / byly zadány na hrany odlu na vněší lvý a pravý ora vzduchového prostřdí. Vlost buzní / bylo opět zadáno vztah (6). Tn s odvodí pro přdpolad ž v clé oblast nxstuí budící proudy platí tdy rot H = 0 a pol nvírové. Proto pro salární antcý potncál platí H rad. (6) Potncál budícího statcého pol s ntnztou H 0 H u 0 z dz H 0 z (7) 4
35 d B H 0. Poto 0 r (8) B z T H (9) d z clová déla hrany odlu. Pro případ analo s ltrcý salární potncál s pouz zění oraová podína. B z 4 c 54 0 T s (40) 5.4 Výsldy sulací Obr. Zobrazní řzů rozložní odulu antcé nduc v vzoru rozěry v Vyhodnocní sulac nurcého odlu č. v systéu ANSYS bylo provdno v řzch v vzdálnostch od lvého ora podl obr.. V těchto řzch taé provdna sulac rozložní odulu antcé nduc pro pozadí (voda). 5
36 B [T] l [] Obr. Rozložní odulu antcé nduc v vzdálnost 5 od lvého ora B [T] l [] Obr. Rozložní odulu antcé nduc v vzdálnost 5 pro pozadí (voda) 6
37 B [T] l [] Obr. 4 Rozložní odulu antcé nduc v vzdálnost 5 od lvého po odčtní pozadí (voda) B [T] l [] Obr. 5 Rozložní odulu antcé nduc v vzdálnost 0 od lvého ora 7
38 B [T] l [] Obr. 6 Rozložní odulu antcé nduc v vzdálnost 0 od lvého ora po odčtní pozadí (voda) B [T] l [] Obr. 7 Rozložní odulu antcé nduc v vzdálnost 5 od lvého ora 8
39 B [T] l [] Obr. 8 Rozložní odulu antcé nduc v vzdálnost 5 od lvého ora po odčtní pozadí (voda) B [T] l [] Obr. 9 Rozložní odulu antcé nduc v vzdálnost 0 od lvého ora 9
40 B [T] l [] Obr. 0 Rozložní odulu antcé nduc v vzdálnost 0 pro pozadí (voda) B [T] l [] Obr. Rozložní odulu antcé nduc v vzdálnost 0 od lvého ora po odčtní pozadí (voda) 0
41 5.5 Vyhodnocní zěny antcého pol Na obr. obr. 5 obr. 7 obr. 9 sou zobrazny průběhy odulu antcé nduc v daných vzdálnostch v vzoru podl obr.. Jsou zd patrné zěny antcého pol na rozhraní atrálů. Nní zd zachycna zěna antcého pol z přchody slo - voda. J to dáno podobnou vlostí suscptblty vody a sla trá byla použta v sulac. Na obr. a obr. 0 zobrazn průběh odulu antcé nduc bz atrálu č. (zvolná suscptblta). Odčtní průběhů bylo provdno v prorau Mcrosoft Excl. J zísáno rozložní odulu antcé nduc po odčtní pozadí. Vzhld podobný průběhů rozložní odulu antcého pol pozadí (voda) sou zd uvdny průběhy pro 5 a 0. Výsldná zěna antcého pol v řzu způsobna odlšnou suscptbltou. 6 Pro suscptbltu 80 zěna B po odčtní pozadí: po řz 5 od lvého ora pro řz 0 od lvého ora pro řz 5 od lvého ora B 04μT B 00μT B 98 μt pro řz 0 od lvého ora B 96μT 6 Mantcá rzonanc Zobrazování [0][] antcou rzonancí (MR MRI) využívá fyzálního vu zvaného nulární antcá rzonanc (NMR) trý v ltratuř popsován od rou 940 (F.Bloch 940 E. Purcll 946). Z počátu s obvovaly aplac zéna v ch s využtí MR sptrosop (MRS). Zobrazování poocí NMR s obvu po roc 970 a byl přat názv MR (MRI). Obr. K prncpu antcé rzonanc (přvzato z [0] ) Mantcá rzonanc vychází z vzáného působní adr atoů aících antcý ont obr. s vněší antcý pol. Tato rotuící ádra rauí na přítonost
42 dalšího antcého pol v případě ž byly uístěny v onstantní antcé pol B 0. Osa ádra bud rotovat ol sěru působícího pol B 0. Tnto pohyb vzná př aždé zěně antcého pol. Jádro s vrací do své původní polohy poud vněší pol přstan působt. Tí s vytvoří rotuící rychl slábnoucí snál odzvy nulární antcé rzonanc trý nazýván FID. Přsný vztah z rzonační točt a vněší antcý pol závslý na typu rzonuícího ádra. V MRI ožné dtovat nzávsl různá atoová ádra. Pro MR zobrazování vhodné ádro vodíu H (t. dný proton). Této vlastnost využto v léařsé zobrazování protož vodí tvoří téěř dvě třtny všch atoů ldsého těla. Pro další pops budou použta vodíová ádra (protony). Za norálních oolností (bz působní vněšího antcého pol) orntac rotačních os dnotlvých protonů zcla náhodná. Navn nsou vyazovány žádné antcé vlastnost. Po xpozc slnéu vněšíu antcéu pol dod dvěa zásadní zěná. Obr. Prcsní pohyb s úhlový točt 0 (přvzato z [0]) Dod srovnání antcých ontů (os rotac) s vněší antcý pol. Proton s pa nachází v dno z dvou nrtcých (vantových) stavů. Vtor ho antcého ontu ůž být orntován "parallně". t. v shodě s sěr vněšího antcého pol (nrtcy éně náročný stav) nbo "antparallně" t. protchůdně touto sěru (nrtcy náročněší stav). Protony začnou vyonávat ště dn typ pohybu. Kroě "rotac" ol vlastní osy vyonávaí navíc tzv. prcsní pohyb obr. trý s lz přdstavt ao pohyb po plášt poyslného užl. Frvnc prcsního pohybu (nazvaná Larorovou frvncí) závsí na ntnztě vněšího antcého pol al taé na typu atoového ádra vyádřné yroantcý poěr. Pro vodí H yroatcý poěr = 458MHz/T(69T - ). V pol s nducí B 0 = T budou ít ádra frvnc prcsního pohybu f 0 = 458MHz.
43 B 0 f 0 (4) Vtor výsldné antzac M 0 á tdy sěr totožný s sěr vtoru vněšího antcého pol B 0. K tou abycho ohl zěřt s snaží dosáhnout ho vychýlní z sěru osy z do rovny x y (v této rovně uístěný dttor - příací cíva). Toho lz dosáhnout dodání nr vhodnou forou např. ltroantcý pulsy označovaný taé ao radofrvnční pulsy (RF pulsy). Protony nsou schopny absorbovat nr z clého sptra la. zářní. Aby došlo přdání nr ltroantcého pulsu prcduícíu protonu usí být Larorova frvnc (úhlová frvnc prcduícího protonu) a frvnc ltroantcého pulsu stná. Prcduící protony ta s ltroantcý puls na dané frvnc rzonuí (odtud názv "antcá rzonanc"). Pohyb vtoru antzac obr. 4 s pa ví ao pouhé "slápění" do rovny x y přčž úhl slopní závsí na ntrálu dodané nr (tdy na vlost RF pulsu a délc ho trvání). Obr. 4 Pohyb vtoru antzac (přvzato z [0]) Po dodání nr 90 RF puls (vtor M s slopí právě o 90 ) rotu vtor táňové antzac M v rovně x y s Larorovou frvncí 0. Uístí-l do rovny xy příací cívu bud s v ní nduovat napětí. Tato zísaný snál s označu zratou FID (fr nducton dcay) a á tvar haroncého průběhu s xponncálně lsaící apltudou. Jstlž přstan ltroantcý puls na táň působt dod tzv. rlaxac. Dochází navrácní z xctovaného do původního rovnovážného stavu [0][4][].
44 6. Mtoda spnového cha Spnové cho (SE) dna z záladních sníacích tod antcé rzonanc. Sládá s z 90 RF pulzu a dnoho nbo něola náslduících 80 pulzů. Tato toda využívá prncpu slopní vtoru antzac M 0 o 90 do transvrzální rovny x y. Sěr Obr. 5 K prncpu tody spnového cha (přvzato z [0]) shodný s vtor antcé nduc B 0 záladního pol. Začíná s provovat T rlaxac. t. nětré protony prcduí s npatrně vyšší a nětré s nší frvnc. Dochází rozfázování. Spny sou opět sfázovány násldu l xctační 80 RF puls trý přlopí dnotlvé spny v rovně x y o 80. V příací cívc dtován cho snál [0][]. 6. Mtoda radntní cha Gradntní cho (GE) taé vl používaná zobrazovací toda MR. Tato svnc začíná 90 RF puls trý slopí vtor antzac do rovny x y. K vyvolání cha zd al narozdíl od tody SE použto radntu antcého pol ísto dalšího pulzu. J-l antcéu pol B 0 přdáno radntní antcé pol budou sousdící protony prcdovat s írně odlšnou Larorovou frvncí. To způsobí rozfázování dnotlvých spnů. Násldu radnt s opačný znaén trý znovu sfázu dnotlvé spny a tí vyvolá cho. Narozdíl od SE tchny pols apltudy cho snálu prot vlost FID snálu závslý na rlaxační čas T *. Tato tchna pracu s nší časy T E nž SE a pro xctac s využívá nších slápěcích úhlů (tzv. flp anl < 90 ) což vd ožnost nších opaovacích časů T R => 4
45 dná s o vl rychlou zobrazovací tchnu trá slouží ao zálad pro zobrazovací tchny používané v současnost.[0][] Mantcá suscptblta ěřného vzoru ovlvňu antcé pol uvntř vzoru v ho oolí protož rzonanční točt adr závsí na vlost antcého pol v tré s nachází ůž vlv dforací antcého pol doít dforací v MR obraz. Obr. 6 K prncpu tody radntního cha (přvzato z [0]) V todě [] radntní cho ndochází opnzac nhoonty záladního antcého pol a v výsldné obraz s obvuí artfaty způsobné loální zěnou suscptblty xctovaného obu ěřného vzoru. Pro další účly zavd rační pol s nducí B R pro trou platí: B R (xyz) = B (xyz) - B 0. (4) V rační pol sou uvažovány roě nhoonty záladního antcého pol MR antu taé loální zěny antcého pol způsobné antcou suscptbltou ěřného vzoru. Výrazné sou zěny račního pol na ostrých hranách zěn suscptblty v ěřné vzoru. Nhoonta antcého pol způsobu rozfázování vtorů antzac adr vzoru a provu s rychlší pols snálu volné prcs. Tnto pols lz vyádřt ftvní rlaxační čas T * podl vztahu B. * (4) T T Vtor antzac v čas T E bud ít vlost M TE TE * * T E T BT T M T M T E E E (44) 5
46 d xponncální čln xp(t E /T * ) popsu pols antzac daný rozfázování antcých ontů adr vlv ftvního rlaxačního času T * čln xp(t E /T ) BTE popsu vlv přrozného rlaxačního času a čln zohldňu odchyly antcého pol od záladního pol. Rovnc pro dstrbuc transvrzální antzac v MR obraz př todě GE Čln π BT E x y x y x y M x y BT E x y TE T d x d. (45) v rovnc (45) vyadřu fázovou odulac MR obrazu způsobnou rozdílový pol s nducí B. Vyhodnocní snálu zísaného todou GE dostan MR obraz v hož fáz BT E (46) zaódováno prostorové rozložní račního antcého pol vzoru. Poud rační pol B R vyvoláno antcou suscptbltou vzoru lz př vhodné uspořádání xprntu vyhodnott vlost antcé suscptblty nznáého atrálu. 7 Exprntální ěřní 7. Pops ěřné úlohy Pro xprntální ěřní úlohy bylo použto MR toorafu obr. 7 ÚPT AV ČR. Pops MR antu toorafu uvdn na obr.8. Mantcé pol B 0 vytvářno supravodvý ant hož záladní pol B 0 = 47 T tré nrováno poocí čtyř radntních cív G x G y G z a G 0. Tyto radntní cívy uožňuí ěnt pol v sěrch x y a z. Poocí posldní cívy G 0 ožné nastavt nduc záladního pol B 0. Mant chlazn tutý y Obr. 7 MR tooraf 6
47 hél. Běh ěřní byl tooraf ovládán poocí počítač. Exprntální vzor uístěn na držá a poocí ovladač zasunut do toorafu. Bylo nutné nastavt hoontu záladního antcého pol a radntní cho. Pooc tody radntního cha byl zísán MR obraz. Naěřná data z toorafu byla zpracována v prorau Marvz ÚPT. Naěřná data byla podrobna rychlé Fourrově transforac (FFT). Poocí této transforac zísán fázový obraz trý byl dál zpracováván ax 70 toorafcá sonda pracovní prostor vf cívy radntní cívy orční cívy stěna ryostatu radační štít ostra antu vnutí antu Obr. 8 Pops MR toorafu (přvzato z []) 7
48 7. Pops onfurac ěřné úlohy Měřný vzor byla slněná rychlová nádoba (45 x 45 x 45 ) naplněná donzovanou vodou s síran nlnatý pro zrácní rlaxačních časů. Suscptblta vody s zění z 6 H na H Stěny nádoby sou uístěny Obr. 9 Vzor v souřadné soustavě x y z. V rovně y z sou uprostřd nádoby uístěny parallní slněné stěny tloušťy s vzdálností od sb. Vntřní prostor vyplněn acton. Byla provdna cl ěřní s různý cho - časy T E. Mtodou GE ěřn fázový obraz v transvrzální rovně o rozěrch 60x60 (56x56 bodů 044 /pxl). Paratry: v ěřní č. T E = 0 s v ěřní č. T E = 0 s opaovací čas T R = 500 s počt snů NS = šířa sptra S = 0 Hz (Tvz = 50 s) tloušťa xctované vrstvy d = 5. Byl použt systé ant MAGNEX 47T/00 proray MR Soluton radnty MAGNEX uístění ÚPT AV ČR. 7. Použtá toda ěřní Mantcou suscptbltu [] lz ěřt poocí něola tod ao sou např. Faradayova váha Guoynova váha nduční toda SQUID antotr a MR tchny ěřní. Pro o xprntální ěřní byla použta MR tchna ěřní. J založna na prncpu dforac hoonního antcého pol běh antzac ěřného vzoru. U této tody nutné dodržt něol pravdl. Induc nutno ěřt v prostoru nhoonního 8
49 antcého pol protož tato tchna nní ctlvá na né pol nž v záladní sěru. Běh ěřní nlz použít froantcé atrály protož vytváří antcé pol tré způsobu chyby běh ěřní. Mantcou nduc nutno ěřt poocí vlé hodnoty radntu. z x B S a B 0 - x B z (x) Obr. 0 Dforac pol způsobná vložní paraantcého vzoru (přvzato z []) Pooc této tody lz ěřt suscptbltu atrálů tré ndávaí MR snál. Měřný vzor vša usí být oblopn vodou. Lz stanovt zěnu antcého pol poocí zobrazovací MR tchny a tody radntního cha. Dforac antcého pol na způsobna vloží vzoru s nou suscptbltou nž suscptblta oolí. Na obr. 0 průběh antcé nduc v oolí a v vzoru. Do hoonního antcého pol B 0 byl vložn paraantcý vzor o šířc a a suscptbltou. Vlost antcé nduc v vzoru dána vztah S 0 B B (47) Zěny antcé nduc na rozhraní atrálů sou způsobny onstantní nduční to Φ plochou S Z s norálou v sěru osy z. S Z B d S onst. (48) Hodnota antcé nduc B S v nětrých stuacích nůž být přío zštěna v případě ž vzor ndává ěřtlný snál. Lz využít npříé tody. Na obr. 0 pro oblast trá šrafována platí B xdx 0 d bod v tré ž antcá nduc téěř nulová. (49) 9
50 7.4 Výsldy ěřní x B [T] l [] Obr. Měřná apa račního pol B R pro onfurac voda slo acton Na obr. zobrazno antcé pol v ěřné vzoru. Pravá a lvá strana s nlší. Zěna barvy způsobna posunutí fáz o π. Na obrázu taé vdět šu trý v oblastch bz snálu př rozvnutí fázových soů v fázové obrazu. Průběhy antcého pol vpravo vlvo sou stné. Na obr. apa pol lvé polovny ěřného vzoru s průběh antcého pol v dané řzu x B [T] x l [] l [] Obr. Mapa račního pol B R pro lvou stranu (vlvo) a řz v ístě označní 40
51 7.5 Stanovní zěny antcého pol Na obr. zobrazna sptrální čára ěřného vzoru. Větší vrchol sptrální čáry x Modul sptra [-] f [Hz] Obr. Sptrální čára ěřného vzoru voda + acton způsobn ádry vody nší vrchol sptrální čáry způsobn ádry actonu. Podl sptra na obr. á být posun 7Hz což odpovídá zěně antcého pol o 878μT. Po odčtní chcého posuvu actonu (vůč vodě) 40Hz posuv sptrální čáry actonu vlv antcé suscptblty Hz což odpovídá zěně antcého pol 54μ T x B [T] l [] Obr. 4 Měřný fázový obraz přpočtný na B 0 [T] Součt ntnzt antcého pol v vodě (pro 90 bodů) -μt. Součt ntnzt 4
52 antcého pol uvntř actonu (pro 6.4 bodů) á být rovna součtu ntnzt antcého pol v vodě. Z toho lz vypočítat ntnztu antcého pol v actonu trá 64μT. Tnto výsld vznl podělní hodnoty -μt hodnotou 64. Tato hodnota přdstavu počt pxlů polovny tloušťy vrstvy actonu. Intnzta račního antcého pol B R vyádřna v frvnc B f R 55 Hz. (50) x B [T] x l [] l [] Obr. 5 Mapa pol B 0 [T] pro lvou stranu s řz v ístě označní pro ěřní č. Na obr. 4 a obr. 5 sou zobrazny výsldy pro stné ěřní al pro T E = 0 s. Z toho plyn ž zaódování nhoonty něší. Po odčtu z fázových obrazů (obr. 6) hodnota račního pol v actonu T. Tuto hodnotu třba určt z ntrálu průběhu račního pol v vodě. Tato vypočtná x B [T] l [] Obr. 6 Řz račního antcého pol pro pravou stranu ěřného fázového obrazu pro T E = 0 s 4
53 x B [T] l [] Obr. 7 Mapa pol ěřná pro onfurac voda-slo-voda hodnota račního pol v actonu T. Mnu račního pol v vodě T vz. obr. 6. Průběhy antcého pol sou v lvé a pravé část vzoru stné. Na obr. 8 zobrazn fázový obraz v onfurac voda-slo-voda sloužící n pro ontrolu tody ěřní poocí MRI. Uprostřd obrazu patrná zěna račního pol trá způsobna sucptbltou sla a danou onfurací. Zěna pol pro oolí voda-slo-voda R Obr. 8 Měřný fázový obraz ěřný pro onfurac voda-slo-voda 8 B T. 4
54 8 Stanovní nvrzní úlohy Cíl nvrzní úlohy bylo zstt hodnotu suscptblty daného atrálu (acton) podl zěny antcého pol př ěřní. Hodnoty račního pol BR na obr. sou vdny blízo vzdálnost 0 od lvého ora. Proto byla vyhodnocní úlohy použta sulac zěny odulu antcé nduc v vzdálnost 0 od lvého ora po odčtní pozadí (voda) podl obr. 6. Stanovt hodnotu suscptblty lz poocí dvou tod: 8. Stanovní hodnoty suscptblty toda č B [T] l [] Obr. 9 Rozložní odulu antcé nduc v vzdálnost 0 od lvého ora po odčtní pozadí (voda) Poocí toho způsobu lz zstt vlost antcé suscptblty z ladných hodnot zěny odulu antcé nduc v atrálu č. po odčtní pozadí (voda). Podl obr. byla z sptrální čáry zštěna po odčtní chcého posunu actonu zěna frvnc f Hz což odpovídá zěně antcého pol 54μ T. Běh dalších sulací byla násldně snžována hodnota suscptblty atrálu č. (zvolná suscptblta) až na hodnotu Př této hodnotě vz. obr. 9 zěna odulu antcé nduc v atrálu č. 54μ T. Suscptblta actonu tdy
55 8. Stanovní hodnoty suscptblty toda č. Podl obr. byl zštěn průběh račního pol B R v dané řzu. Nnší hodnota račního pol v vodě byla 056T. Bylo provdno zvětšní ěříta v obr. 6 v ístě B [T] l [] Obr. 40 Rozložní záporných hodnot odulu antcé nduc v vzdálnost 0 od lvého ora po odčtní pozadí (voda). záporné zěny odulu antcé nduc vz. obr. 40. Nnší hodnota odulu antcé nduc podl obr. 40 byla 056 T. Suscptblta atrálu tdy
56 9 Závěr: V dploové prác bylo provdno řšní nurcého odlu. Konfurac nurcé úlohy shodná s xprnt. Byl použt systé ANSYS s todou ončných prvů. V nurcé odlu č. byl použt zadání oraových podín vtorový potncál. Byly provdny řzy antcého pol v vzdálnostch od ora nurcého odlu. Na přchodch z atrály s uázalo ž prczní přsnost výsldů na rozhraní dvou atrálů sou zatížny núěrnou nurcou chybou proto zcla nodpovídaí naěřných hodnotá. Z toho důvodu byl použt pro oraové podíny salární antcý potncál. Taové průběhy ž odpovídaí xprntální výsldů. V průběhu nurcého odlování byl pro ontrolu přsnost nurcého odlu č. použt analoový odl s ltrcý salární potncál a nurcého výsldy potvrdly přsnost obou ěřní. Dál bylo provdno xprntální ěřní suscptblty actonu poocí MR tody radntního cha. Byla provdna cl dvě ěřní pro různé časy T E z důvodu ontroly ěřní. J zapována zěna račního antcého pol B R v zvolné os v shodné onfurac v sulac. Vypočtná zěna odulu antcé nduc 54 μt. Byla taé zštěna nnší hodnota račního pol v ístě přchodu voda - acton B R = μt. S využtí nvrzní sulační úlohy byla stanovna hodnota antcé suscptblty actonu poocí dvou tod. V první todě byly porovnány zěny ladných hodnot zěřného račního pol BR v actonu s odul zěny antcé nduc zísaných poocí sulací. Zštěná hodnota suscptblty touto todou (č. ) V todě č. byly porovnány zěny záporných hodnot račního pol na rozhraní vodaacton a byla stanovna suscptblta actonu trá Mapování antcého pol v oolí rozhraní dvou atrálů nní zatížno systatcou chybou př rozvíní fázového obrazu. Protož slo nvytváří MR snál přchod voda - acton v MR obraz bz snálu a obsahu n šu. Tnto šu ůž být zdro šuu př rozbalování fázového obrazu vz. obr. 5. Systatcou chybu vytvoří taé zěna račního pol v actonu trá způsobí zěnu fáz MR snálu větší nž n. Tato systatcá chyby důvod považovat todu č. pro stanovní antcé suscptblty za přsněší. 46
Agregace vzájemné spojování destabilizovaných částic ve větší celky, případně jejich adheze na povrchu jiných materiálů
 Agregace - úvod 1 Agregace vzáemné spoování destablzovaných částc ve větší cely, případně ech adheze na povrchu ných materálů Částce mohou agregovat, poud vyazuí adhezní schopnost a poud e umožněno ech
Agregace - úvod 1 Agregace vzáemné spoování destablzovaných částc ve větší cely, případně ech adheze na povrchu ných materálů Částce mohou agregovat, poud vyazuí adhezní schopnost a poud e umožněno ech
Příloha 1. Náleţitosti a uspořádání textové části VŠKP
 Příloha 1 Náleţitosti a uspořádání textové části VŠKP Náležitosti a uspořádání textové části VŠKP je určeno v tomto pořadí: a) titulní list b) zadání VŠKP c) abstrakt v českém a anglickém jazyce, klíčová
Příloha 1 Náleţitosti a uspořádání textové části VŠKP Náležitosti a uspořádání textové části VŠKP je určeno v tomto pořadí: a) titulní list b) zadání VŠKP c) abstrakt v českém a anglickém jazyce, klíčová
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA ELEKTROTECHNICKÁ KATEDRA ŘÍDICÍ TECHNIKY
 ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRZE FKUL ELEKROECHNICKÁ KEDR ŘÍDICÍ ECHNIKY DIPLOMOVÁ PRÁCE LGORIMY PRO NELINEÁRNÍ SLDĚNÍ D OMÁŠ VÍEK 24 BSRK Měřná data, trá slouží řídcí procsů v průyslu, bývají často
ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRZE FKUL ELEKROECHNICKÁ KEDR ŘÍDICÍ ECHNIKY DIPLOMOVÁ PRÁCE LGORIMY PRO NELINEÁRNÍ SLDĚNÍ D OMÁŠ VÍEK 24 BSRK Měřná data, trá slouží řídcí procsů v průyslu, bývají často
Příklad 70 Vypočet konstanty šíření (fázová konstanta, měrný útlum)
 Přílad 7 Vypočt onstanty šířní (fáová onstanta, ěný útlu) adání : Rovinná haonicá ltoagnticá vlna o itočtu : a) f 5 b) f 7 M c) f 9 G s šíří v postřdí s těito paaty:.[ S ], ε 8, µ. Vaianta a) Vaianta b)
Přílad 7 Vypočt onstanty šířní (fáová onstanta, ěný útlu) adání : Rovinná haonicá ltoagnticá vlna o itočtu : a) f 5 b) f 7 M c) f 9 G s šíří v postřdí s těito paaty:.[ S ], ε 8, µ. Vaianta a) Vaianta b)
Difúze. 0 m n pu p m n pu kbt n. n u D n n m. Fickův zákon Po dosazení do rovnice kontinuity
 Dfúz Fckův zákon dfúz v plynu Přdpokládjm dální plyn s konstantní tplotou T a konstantním tlakm p v kldu, v ktrém j nízká nhomognní hmotnostní koncntrac příměs Pak v staconárním stavu musí být clková síla
Dfúz Fckův zákon dfúz v plynu Přdpokládjm dální plyn s konstantní tplotou T a konstantním tlakm p v kldu, v ktrém j nízká nhomognní hmotnostní koncntrac příměs Pak v staconárním stavu musí být clková síla
M ě ř e n í o d p o r u r e z i s t o r ů
 M ě ř n í o d p o r u r z s t o r ů Ú k o l : Proměřt sadu rzstorů s nznámým odporm různým mtodam a porovnat přsnost jdnotlvých měřní P o t ř b y : Vz sznam v dskách u úlohy na pracovním stol Obcná část:
M ě ř n í o d p o r u r z s t o r ů Ú k o l : Proměřt sadu rzstorů s nznámým odporm různým mtodam a porovnat přsnost jdnotlvých měřní P o t ř b y : Vz sznam v dskách u úlohy na pracovním stol Obcná část:
1. Okrajové podmínky pro tepeln technické výpo ty
 1. Okrajové podmínky pro tpln tchncké výpo ty Správné stanovní okrajových podmínk j jdnou z základních součástí jakéhokol tchnckého výpočtu. Výjmkou njsou an tplně tchncké analýzy. V násldující kaptol
1. Okrajové podmínky pro tpln tchncké výpo ty Správné stanovní okrajových podmínk j jdnou z základních součástí jakéhokol tchnckého výpočtu. Výjmkou njsou an tplně tchncké analýzy. V násldující kaptol
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY NÁVRH STRATEGIE ROZVOJE MALÉ RODINNÉ FIRMY THE DEVELOPMENT OF SMALL FAMILY OWNED COMPANY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA PODNIKATELSKÁ ÚSTAV FACULTY OF BUSINESS AND MANAGEMENT INSTITUT OF NÁVRH STRATEGIE ROZVOJE MALÉ RODINNÉ FIRMY THE DEVELOPMENT OF SMALL
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA PODNIKATELSKÁ ÚSTAV FACULTY OF BUSINESS AND MANAGEMENT INSTITUT OF NÁVRH STRATEGIE ROZVOJE MALÉ RODINNÉ FIRMY THE DEVELOPMENT OF SMALL
MOMENT SETRVAČNOSTI. Obecná část Pomocí Newtonova pohybového zákona síly můžeme odvodit pohybovou rovnici pro rotační pohyb:
 MOMENT SETRVAČNOST Obecná část Pomocí Newtonova pohybového záona síly můžeme odvodit pohybovou rovnici pro rotační pohyb: dω M = = ε, (1) d t de M je moment vnější síly působící na těleso, ω úhlová rychlost,
MOMENT SETRVAČNOST Obecná část Pomocí Newtonova pohybového záona síly můžeme odvodit pohybovou rovnici pro rotační pohyb: dω M = = ε, (1) d t de M je moment vnější síly působící na těleso, ω úhlová rychlost,
7. ZÁKLADNÍ TYPY DYNAMICKÝCH SYSTÉMŮ
 7. ZÁKADNÍ TYPY DYNAMICKÝCH SYSTÉMŮ 7.. SPOJITÉ SYSTÉMY Téměř všechny fyzálně realzovatelné spojté lneární systémy (romě systémů s dopravním zpožděním lze vytvořt z prvů tří typů: proporconálních členů
7. ZÁKADNÍ TYPY DYNAMICKÝCH SYSTÉMŮ 7.. SPOJITÉ SYSTÉMY Téměř všechny fyzálně realzovatelné spojté lneární systémy (romě systémů s dopravním zpožděním lze vytvořt z prvů tří typů: proporconálních členů
POTENCIÁL ELEKTRICKÉHO POLE ELEKTRICKÉ NAPĚTÍ
 POTENCIÁL ELEKTRICKÉHO POLE ELEKTRICKÉ NAPĚTÍ ELEKTRICKÝ POTENCIÁL Elektrcká potencální energe Newtonův zákon pro gravtační sílu mm F = G r 1 2 2 Coulombův zákon pro elektrostatckou sílu QQ F = k r 1 2
POTENCIÁL ELEKTRICKÉHO POLE ELEKTRICKÉ NAPĚTÍ ELEKTRICKÝ POTENCIÁL Elektrcká potencální energe Newtonův zákon pro gravtační sílu mm F = G r 1 2 2 Coulombův zákon pro elektrostatckou sílu QQ F = k r 1 2
MODERNÍ METODY MĚŘENÍ FÁZOVÉHO ROZDÍLU - OVĚŘENÍ VLASTNOSTÍ V PROSTĚDÍ MATLAB
 ODERÍ ETODY ĚŘEÍ FÁZOVÉHO ROZDÍLU - OVĚŘEÍ VLSTOSTÍ V PROSTĚDÍ TLB 1. Úvod chal Krupholc, loš Sdláčk Čské vysoké uční tchncké v Praz Fakulta lktrotchncká, katdra ěřní Článk porovnává dvě nové tody ěřní
ODERÍ ETODY ĚŘEÍ FÁZOVÉHO ROZDÍLU - OVĚŘEÍ VLSTOSTÍ V PROSTĚDÍ TLB 1. Úvod chal Krupholc, loš Sdláčk Čské vysoké uční tchncké v Praz Fakulta lktrotchncká, katdra ěřní Článk porovnává dvě nové tody ěřní
MĚŘENÍ MOMENTU SETRVAČNOSTI Z DOBY KYVU
 Úloha č 5 MĚŘENÍ MOMENTU SETRVAČNOSTI Z DOBY KYVU ÚKOL MĚŘENÍ: Určete moment setrvačnosti ruhové a obdélníové desy vzhledem jednotlivým osám z doby yvu Vypočtěte moment setrvačnosti ruhové a obdélníové
Úloha č 5 MĚŘENÍ MOMENTU SETRVAČNOSTI Z DOBY KYVU ÚKOL MĚŘENÍ: Určete moment setrvačnosti ruhové a obdélníové desy vzhledem jednotlivým osám z doby yvu Vypočtěte moment setrvačnosti ruhové a obdélníové
4. PRŮBĚH FUNKCE. = f(x) načrtnout.
 Etrém funkc 4. PRŮBĚH FUNKCE Průvodc studim V matmatic, al i v fzic a tchnických oborch s často vsktn požadavk na sstrojní grafu funkc K nakrslní grafu funkc lz dns většinou použít vhodný matmatický softwar.
Etrém funkc 4. PRŮBĚH FUNKCE Průvodc studim V matmatic, al i v fzic a tchnických oborch s často vsktn požadavk na sstrojní grafu funkc K nakrslní grafu funkc lz dns většinou použít vhodný matmatický softwar.
Měrná vnitřní práce tepelné turbíny při adiabatické expanzi v T-s diagramu
 - 1 - Tato Příloha 307 j součástí článku: ŠKORPÍK, Jří. Enrgtcké blanc lopatkových strojů, Transformační tchnolog, 2009-10. Brno: Jří Škorpík, [onln] pokračující zdroj, ISSN 1804-8293. Dostupné z http://www.transformacn-tchnolog.cz/nrgtckblanc-lopatkovych-stroju.html.
- 1 - Tato Příloha 307 j součástí článku: ŠKORPÍK, Jří. Enrgtcké blanc lopatkových strojů, Transformační tchnolog, 2009-10. Brno: Jří Škorpík, [onln] pokračující zdroj, ISSN 1804-8293. Dostupné z http://www.transformacn-tchnolog.cz/nrgtckblanc-lopatkovych-stroju.html.
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV MIKROELEKTRONIKY FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV MIKROELEKTRONIKY FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF
ZÁKLADNÍ METODY REFLEKTOMETRIE
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV RADIOELEKTRONIKY FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ ÚSTAV RADIOELEKTRONIKY FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION DEPARTMENT OF
4. Třídění statistických dat pořádek v datech
 4. Třídění statstcých dat pořáde v datech Záladní členění statstcých řad: řada časová, řada prostorová, řada věcná věcná slovní řada, věcná číselná řada. Záladem statstcého třídění je uspořádání hodnot
4. Třídění statstcých dat pořáde v datech Záladní členění statstcých řad: řada časová, řada prostorová, řada věcná věcná slovní řada, věcná číselná řada. Záladem statstcého třídění je uspořádání hodnot
ANOVA. Analýza rozptylu při jednoduchém třídění. Jana Vránová, 3.lékařská fakulta UK, Praha
 ANOVA Analýza rozptylu př jednoduchém třídění Jana Vránová, 3.léařsá faulta UK, Praha Teore Máme nezávslých výběrů, > Mají rozsahy n, teré obecně nemusí být stejné V aždém z nch známe průměr a rozptyl
ANOVA Analýza rozptylu př jednoduchém třídění Jana Vránová, 3.léařsá faulta UK, Praha Teore Máme nezávslých výběrů, > Mají rozsahy n, teré obecně nemusí být stejné V aždém z nch známe průměr a rozptyl
Měření indukčností cívek
 7..00 Ṫeorie eletromagneticého pole Měření indučností cíve.......... Petr Česá, studijní supina 05 Letní semestr 000/00 . Měření indučností cíve Měření vlastní a vzájemné indučnosti válcových cíve ZAÁNÍ
7..00 Ṫeorie eletromagneticého pole Měření indučností cíve.......... Petr Česá, studijní supina 05 Letní semestr 000/00 . Měření indučností cíve Měření vlastní a vzájemné indučnosti válcových cíve ZAÁNÍ
Funkce hustoty pravděpodobnosti této veličiny je. Pro obecný počet stupňů volnosti je náhodná veličina
 Přdnáša č 6 Náhodné vličiny pro analyticou statistiu Při výpočtch v analyticé statistic s používají vhodné torticé vličiny, tré popisují vlastnosti vytvořných tstovacích charatristi Mzi njpoužívanější
Přdnáša č 6 Náhodné vličiny pro analyticou statistiu Při výpočtch v analyticé statistic s používají vhodné torticé vličiny, tré popisují vlastnosti vytvořných tstovacích charatristi Mzi njpoužívanější
TEXTILNÍ UPÍNACÍ PROSTŘEDKY
 TEXTILNÍ UPÍNÍ PROSTŘEKY 1 2 * n x = vntřní šíř = ová é = šíř ruot RVS = nrzvěíí o Písno Č. proutu Šíř pásu Mx. npíní sí N/ 1 2 n x 980 975 911 811 8* 931 930 (=RVS) 914 914H 9 91 908 917 909 90 919Ero
TEXTILNÍ UPÍNÍ PROSTŘEKY 1 2 * n x = vntřní šíř = ová é = šíř ruot RVS = nrzvěíí o Písno Č. proutu Šíř pásu Mx. npíní sí N/ 1 2 n x 980 975 911 811 8* 931 930 (=RVS) 914 914H 9 91 908 917 909 90 919Ero
INOVACE PŘEDNÁŠEK KURZU Fyzikální chemie, KCH/P401
 Fakulta životního prostřdí v Ústí nad Labm INOVACE PŘEDNÁŠEK KURZU Fyzikální chmi, KCH/P401 - ZAVEDENÍ EXPERIMENTU DO PŘEDNÁŠEK Vypracovala Z. Kolská (prozatímní učbní txt, srpn 2012) K několika kapitolám
Fakulta životního prostřdí v Ústí nad Labm INOVACE PŘEDNÁŠEK KURZU Fyzikální chmi, KCH/P401 - ZAVEDENÍ EXPERIMENTU DO PŘEDNÁŠEK Vypracovala Z. Kolská (prozatímní učbní txt, srpn 2012) K několika kapitolám
Globální matice konstrukce
 Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Řešení Navierových-Stokesových rovnic metodou
 Řšní Navrovýc-Stoksovýc rovnc mtodou končnýc prvků Lbor Črmák prosnc 2009 Označní: Abstrakt Txt obsauj klasckou a varační formulac 2D-úloy nstlačtlnéo nstaconárnío proudění, pops prostorové dskrtzac mtodou
Řšní Navrovýc-Stoksovýc rovnc mtodou končnýc prvků Lbor Črmák prosnc 2009 Označní: Abstrakt Txt obsauj klasckou a varační formulac 2D-úloy nstlačtlnéo nstaconárnío proudění, pops prostorové dskrtzac mtodou
INSTITUT FYZIKY VŠB-TU OSTRAVA NÁZEV PRÁCE
 Studnt Skupina/Osob. číslo INSTITUT FYZIKY VŠB-TU OSTRAVA NÁZEV PRÁCE 5. Měřní ěrného náboj lktronu Číslo prác 5 Datu Spolupracoval Podpis studnta: Cíl ěřní: Pozorování stopy lktronů v baňc s zřděný plyn
Studnt Skupina/Osob. číslo INSTITUT FYZIKY VŠB-TU OSTRAVA NÁZEV PRÁCE 5. Měřní ěrného náboj lktronu Číslo prác 5 Datu Spolupracoval Podpis studnta: Cíl ěřní: Pozorování stopy lktronů v baňc s zřděný plyn
SIGNÁLY A LINEÁRNÍ SYSTÉMY
 SIGNÁLY A LINEÁRNÍ SYSTÉMY prof. Ing. Jří Holčí, CSc. holc@ba.un.cz, Kaence 3, 4. patro, dv.č.424 INVESTICE Insttut DO bostatsty ROZVOJE VZDĚLÁVÁNÍ a analýz XIII. ZÁKLADNÍ TYPY DYNAMICKÝCH SYSTÉMŮ SPOJITÉ
SIGNÁLY A LINEÁRNÍ SYSTÉMY prof. Ing. Jří Holčí, CSc. holc@ba.un.cz, Kaence 3, 4. patro, dv.č.424 INVESTICE Insttut DO bostatsty ROZVOJE VZDĚLÁVÁNÍ a analýz XIII. ZÁKLADNÍ TYPY DYNAMICKÝCH SYSTÉMŮ SPOJITÉ
Absolutní nebo relativní?
 Statstcká odynaka II dální plyn chcká rovnováha a kntka bsolutní nbo rlatvní? absolutní ají přrozné a unvrzální rrnční stavy ( K), ( a), ( ), n ( ol),, rlatvní číslnou hodnotu ůž přsoudt jn zěně U, H,,
Statstcká odynaka II dální plyn chcká rovnováha a kntka bsolutní nbo rlatvní? absolutní ají přrozné a unvrzální rrnční stavy ( K), ( a), ( ), n ( ol),, rlatvní číslnou hodnotu ůž přsoudt jn zěně U, H,,
I. MECHANIKA 8. Pružnost
 . MECHANKA 8. Pružnost Obsah Zobcněný Hookův zákon. ntrprtac invariantů. Rozklad tnzorů na izotropní část a dviátor. Křivka dformac. Základní úloha tori pružnosti. Elmntární Hookův zákon pro jdnoosý tah.
. MECHANKA 8. Pružnost Obsah Zobcněný Hookův zákon. ntrprtac invariantů. Rozklad tnzorů na izotropní část a dviátor. Křivka dformac. Základní úloha tori pružnosti. Elmntární Hookův zákon pro jdnoosý tah.
Určení geometrických a fyzikálních parametrů čočky
 C Určení geoetrickýc a yzikálníc paraetrů čočky Úkoly :. Určete poloěry křivosti ploc čočky poocí séroetru. Zěřte tloušťku čočky poocí digitálnío posuvnéo ěřítka 3. Zěřte oniskovou vzdálenost spojné čočky
C Určení geoetrickýc a yzikálníc paraetrů čočky Úkoly :. Určete poloěry křivosti ploc čočky poocí séroetru. Zěřte tloušťku čočky poocí digitálnío posuvnéo ěřítka 3. Zěřte oniskovou vzdálenost spojné čočky
Dřevěné dveře v dýze BASIS ART
 Dřvěné dvř v dz - modr Studio intriérovch dvří Indora.cz mail: wb: Wrichova 9/ raha Dřvěné dvř v dz SIS RT Vzor ovrchů dvří ál an ub i D us t R s r vo n u ař on ag l í l í an ah s La or ba ch ic ř r O
Dřvěné dvř v dz - modr Studio intriérovch dvří Indora.cz mail: wb: Wrichova 9/ raha Dřvěné dvř v dz SIS RT Vzor ovrchů dvří ál an ub i D us t R s r vo n u ař on ag l í l í an ah s La or ba ch ic ř r O
Kapitola 2. o a paprsek sil lze ztotožnit s osou x (obr.2.1). sil a velikost rovnou algebraickému součtu sil podle vztahu R = F i, (2.
 Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
MOMENT SETRVAČNOSTI. Obecná část Pomocí Newtonova pohybového zákona síly můžeme odvodit pohybovou rovnici pro rotační pohyb:
 MOMENT SETRVAČNOST Obecná část Pomocí Newtonova pohybového záona síly můžeme odvodit pohybovou rovnici pro rotační pohyb: dω M = = ε, (1) d t de M je moment vnější síly působící na těleso, ω úhlová rychlost,
MOMENT SETRVAČNOST Obecná část Pomocí Newtonova pohybového záona síly můžeme odvodit pohybovou rovnici pro rotační pohyb: dω M = = ε, (1) d t de M je moment vnější síly působící na těleso, ω úhlová rychlost,
Univerzita Tomáše Bati ve Zlíně
 Unvrzta Tomáš Bat v Zlíně LABORATORNÍ CVIČENÍ Z FYZIKY II Názv úlohy: Vntřní odpor zdroj a voltmtru Jméno: Ptr Luzar Skupna: IT II/ Datum měřní: 0.října 2007 Obor: Informační tchnolog Hodnocní: Přílohy:
Unvrzta Tomáš Bat v Zlíně LABORATORNÍ CVIČENÍ Z FYZIKY II Názv úlohy: Vntřní odpor zdroj a voltmtru Jméno: Ptr Luzar Skupna: IT II/ Datum měřní: 0.října 2007 Obor: Informační tchnolog Hodnocní: Přílohy:
4.KMITÁNÍ VOLNÉ. Rozlišujeme: 1. nepoddajné vazby - nedovolující pohyb 2. pružně poddajné vazby - dovolují pohyb
 4.MITÁNÍ VOLNÉ 4. Lárí ktáí (harocký osclátor v fyzc) Vl časý pohy hotého odu j ktavý pohy. táí ud lárí, jstlž síla, ktrá př výchylc x vrací hotý od do rovovážé polohy, j úěrá výchylc F x (4..) kostata
4.MITÁNÍ VOLNÉ 4. Lárí ktáí (harocký osclátor v fyzc) Vl časý pohy hotého odu j ktavý pohy. táí ud lárí, jstlž síla, ktrá př výchylc x vrací hotý od do rovovážé polohy, j úěrá výchylc F x (4..) kostata
KOMPLEXNÍ DVOJBRANY - PŘENOSOVÉ VLASTNOSTI
 Koplexní dvobrany http://www.sweb.cz/oryst/elt/stranky/elt7.ht Page o 8 8. 6. 8 KOMPEXNÍ DVOJBNY - PŘENOSOVÉ VSTNOSTI Intergrační a derivační článek patří ezi koplexní dvobrany. Integrační článek á vlastnost
Koplexní dvobrany http://www.sweb.cz/oryst/elt/stranky/elt7.ht Page o 8 8. 6. 8 KOMPEXNÍ DVOJBNY - PŘENOSOVÉ VSTNOSTI Intergrační a derivační článek patří ezi koplexní dvobrany. Integrační článek á vlastnost
Bakalářská práce bakalářský studijní obor Teleinformatika
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta elektrotechniky a komunikačních technologií Ústav telekomunikací Bakalářská práce bakalářský studijní obor Teleinformatika Student: Bílek Petr ID: 78462 Ročník: 3
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta elektrotechniky a komunikačních technologií Ústav telekomunikací Bakalářská práce bakalářský studijní obor Teleinformatika Student: Bílek Petr ID: 78462 Ročník: 3
Vliv prostupů tepla mezi byty na spravedlivost rozúčtování nákladů na vytápění
 Vlv prostupů tpla mz byty na spravdlvost rozúčtování nákladů na vytápění Anotac Fnanční částky úhrady za vytápění mz srovnatlným byty rozpočítané frmam používajícím poměrové ndkátory crtfkované podl norm
Vlv prostupů tpla mz byty na spravdlvost rozúčtování nákladů na vytápění Anotac Fnanční částky úhrady za vytápění mz srovnatlným byty rozpočítané frmam používajícím poměrové ndkátory crtfkované podl norm
Transformátory. Mění napětí, frekvence zůstává
 Transformátory Mění napětí, frevence zůstává Princip funce Maxwell-Faradayův záon o induovaném napětí e u i d dt N d dt Jednofázový transformátor Vstupní vinutí Magneticý obvod Φ h0 u u i0 N i 0 N u i0
Transformátory Mění napětí, frevence zůstává Princip funce Maxwell-Faradayův záon o induovaném napětí e u i d dt N d dt Jednofázový transformátor Vstupní vinutí Magneticý obvod Φ h0 u u i0 N i 0 N u i0
3.10. Magnetické vlastnosti látek
 3.10. Magntické vlastnosti látk 1. Sznáit s s klasifikací látk podl charaktru intrakc s agntický pol. 2. Nastudovat zdroj agntického pol atou, ktré souvisí s pohyb lktronu v lktronové obalu atou. 3. Vysvětlit
3.10. Magntické vlastnosti látk 1. Sznáit s s klasifikací látk podl charaktru intrakc s agntický pol. 2. Nastudovat zdroj agntického pol atou, ktré souvisí s pohyb lktronu v lktronové obalu atou. 3. Vysvětlit
1 Gaussova kvadratura
 Cvičení - zadání a řešení úloh Zálady numericé matematiy - NMNM0 Verze z 7. prosince 08 Gaussova vadratura Fat, že pro něterá rovnoměrná rozložení uzlů dostáváme přesnost o stupeň vyšší napovídá, že pro
Cvičení - zadání a řešení úloh Zálady numericé matematiy - NMNM0 Verze z 7. prosince 08 Gaussova vadratura Fat, že pro něterá rovnoměrná rozložení uzlů dostáváme přesnost o stupeň vyšší napovídá, že pro
Praktikum 1. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Úloha č...xvi... Název: Studium Brownova pohybu
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktiku 1 Úloha č...xvi... Název: Studiu Brownova pohybu Pracoval: Jan Kotek stud.sk.: 17 dne: 7.3.2012 Odevzdal dne:... ožný počet
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktiku 1 Úloha č...xvi... Název: Studiu Brownova pohybu Pracoval: Jan Kotek stud.sk.: 17 dne: 7.3.2012 Odevzdal dne:... ožný počet
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA INFORMAČNÍCH TECHNOLOGIÍ ÚSTAV INTELIGENTNÍCH SYSTÉMŮ FACULTY OF INFORMATION TECHNOLOGY DEPARTMENT OF INTELLIGENT SYSTEMS VLIV PŘESNOSTI
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA INFORMAČNÍCH TECHNOLOGIÍ ÚSTAV INTELIGENTNÍCH SYSTÉMŮ FACULTY OF INFORMATION TECHNOLOGY DEPARTMENT OF INTELLIGENT SYSTEMS VLIV PŘESNOSTI
ELEKTRICKÝ POHON S ASYNCHRONNÍM MOTOREM
 4 EEKTCKÝ POHON AYNCHONNÍ OTOE Asynchronní otory (A), zvláště pa s otvou naráto, jsou jž řadu let nejrozšířenější eletrootory na naší planetě. talo se ta díy jejch onstruční jednoduchost, nízé ceně, vysoé
4 EEKTCKÝ POHON AYNCHONNÍ OTOE Asynchronní otory (A), zvláště pa s otvou naráto, jsou jž řadu let nejrozšířenější eletrootory na naší planetě. talo se ta díy jejch onstruční jednoduchost, nízé ceně, vysoé
Příklady: - počet členů dané domácnosti - počet zákazníků ve frontě - počet pokusů do padnutí čísla šest - životnost televizoru - věk člověka
 Náhodná veličina Náhodnou veličinou nazýváme veličinu, terá s určitými p-stmi nabývá reálných hodnot jednoznačně přiřazených výsledům příslušných náhodných pousů Náhodné veličiny obvyle dělíme na dva záladní
Náhodná veličina Náhodnou veličinou nazýváme veličinu, terá s určitými p-stmi nabývá reálných hodnot jednoznačně přiřazených výsledům příslušných náhodných pousů Náhodné veličiny obvyle dělíme na dva záladní
Ivana Linkeová SPECIÁLNÍ PŘÍPADY NURBS REPREZENTACE. 2 NURBS reprezentace křivek
 25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Ivana Lnkeová SPECIÁLNÍ PŘÍPADY NURBS REPREZENTACE Abstrakt Příspěvek prezentuje B-splne křvku a Coonsovu, Bézerovu a Fergusonovu kubku jako specální případy
25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Ivana Lnkeová SPECIÁLNÍ PŘÍPADY NURBS REPREZENTACE Abstrakt Příspěvek prezentuje B-splne křvku a Coonsovu, Bézerovu a Fergusonovu kubku jako specální případy
Matematika I A ukázkový test 1 pro 2018/2019
 Matematka I A ukázkový test 1 pro 2018/2019 1. Je dána soustava rovnc s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napšte Frobenovu větu (předpoklady + tvrzení). b) Vyšetřete
Matematka I A ukázkový test 1 pro 2018/2019 1. Je dána soustava rovnc s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napšte Frobenovu větu (předpoklady + tvrzení). b) Vyšetřete
02 Systémy a jejich popis v časové a frekvenční oblasti
 Modul: Analýza a modlování dynamických biologických dat Přdmět: Linární a adaptivní zpracování dat Autor: Danil Schwarz Číslo a názv výukové dnotky: Systémy a ich popis v časové a frkvnční oblasti Výstupy
Modul: Analýza a modlování dynamických biologických dat Přdmět: Linární a adaptivní zpracování dat Autor: Danil Schwarz Číslo a názv výukové dnotky: Systémy a ich popis v časové a frkvnční oblasti Výstupy
QUADRO. ProfiScale QUADRO Přístroj na měření vzdálenosti. www.burg-waechter.de. cz Návod k obsluze. ft 2 /ft 3 QUADRO PS 7350
 QUADRO PS 7350 QUADRO 0,5 32 m 0,5 32 m m 2 /m 3 t 2 /t 3 prcson +1% ProScal QUADRO Přístro na měřní vzdálnost cz Návod obsluz BURG-WÄCHTER KG Altnor Wg 15 58300 Wttr Grmany www.burg-wactr.d Structur Extra
QUADRO PS 7350 QUADRO 0,5 32 m 0,5 32 m m 2 /m 3 t 2 /t 3 prcson +1% ProScal QUADRO Přístro na měřní vzdálnost cz Návod obsluz BURG-WÄCHTER KG Altnor Wg 15 58300 Wttr Grmany www.burg-wactr.d Structur Extra
1. Zpracování rastrových obrazů
 1 Zpracování rastrových obrazů Studní cíl V tomto bloku kurzu s budm zabývat něktrým unkcm zpracování rastrových obrazů ktré sou běžnou součástí rackých proramů V počítačové rac to znamná vylpšování něktrých
1 Zpracování rastrových obrazů Studní cíl V tomto bloku kurzu s budm zabývat něktrým unkcm zpracování rastrových obrazů ktré sou běžnou součástí rackých proramů V počítačové rac to znamná vylpšování něktrých
Mechatronické systémy s elektronicky komutovanými motory
 Mechatroncké systémy s elektroncky komutovaným motory 1. EC motor Uvedený motor je zvláštním typem synchronního motoru nazývaný též bezkartáčovým stejnosměrným motorem (anglcky Brushless Drect Current
Mechatroncké systémy s elektroncky komutovaným motory 1. EC motor Uvedený motor je zvláštním typem synchronního motoru nazývaný též bezkartáčovým stejnosměrným motorem (anglcky Brushless Drect Current
f (k) (x 0 ) (x x 0 ) k, x (x 0 r, x 0 + r). k! f(x) = k=1 Řada se nazývá Taylorovou řadou funkce f v bodě x 0. Přehled některých Taylorových řad.
 8. Taylorova řada. V urzu matematiy jsme uázali, že je možné funci f, terá má v oolí bodu x derivace aproximovat polynomem, jehož derivace se shodují s derivacemi aproximované funce v bodě x. Poud má funce
8. Taylorova řada. V urzu matematiy jsme uázali, že je možné funci f, terá má v oolí bodu x derivace aproximovat polynomem, jehož derivace se shodují s derivacemi aproximované funce v bodě x. Poud má funce
Geometrická zobrazení
 Pomocný text Geometricá zobrazení hodná zobrazení hodná zobrazení patří nejjednodušším zobrazením na rovině. Je jich vša hrozně málo a často se stává, že musíme sáhnout i po jiných, nědy výrazně složitějších
Pomocný text Geometricá zobrazení hodná zobrazení hodná zobrazení patří nejjednodušším zobrazením na rovině. Je jich vša hrozně málo a často se stává, že musíme sáhnout i po jiných, nědy výrazně složitějších
Ž ř ě Ž ů š ř š ě ř š ů ř ř ž ř ě ě ř ě É ř š ř ď Í ě ř ž ř ř ř ě š ž ř ě ě ě ž ž ř ž š ž ů ú ř ď ě É ě š ř ú ř ř ě ž ď š Í ď š ř ú ě ň ě ď ž ě ř ř ó
 ř Ž É Í ř ř ž ěž ú ď ěž ú É ú ú ě Ú š ž ú ď ž ě ď ě ř ž ě ú ř ě š ž ě ř š ž ě ů š ě ř ě ě ě ř ě ř ě ř š ž ň ě š ž Í š ť ž ř š Ž ř ě Ž ů š ř š ě ř š ů ř ř ž ř ě ě ř ě É ř š ř ď Í ě ř ž ř ř ř ě š ž ř ě ě
ř Ž É Í ř ř ž ěž ú ď ěž ú É ú ú ě Ú š ž ú ď ž ě ď ě ř ž ě ú ř ě š ž ě ř š ž ě ů š ě ř ě ě ě ř ě ř ě ř š ž ň ě š ž Í š ť ž ř š Ž ř ě Ž ů š ř š ě ř š ů ř ř ž ř ě ě ř ě É ř š ř ď Í ě ř ž ř ř ř ě š ž ř ě ě
Teoretický souhrn k 2. až 4. cvičení
 SYSTÉMOVÁ ANALÝZA A MODELOVÁNÍ Teoretcký souhrn k 2. ž 4. cvčení ZS 2009 / 200 . Vyezení zákldních poů.. Systé e Systé e účelově defnovná nožn prvků vze ez n, která spolu se svý vstupy výstupy vykzue ko
SYSTÉMOVÁ ANALÝZA A MODELOVÁNÍ Teoretcký souhrn k 2. ž 4. cvčení ZS 2009 / 200 . Vyezení zákldních poů.. Systé e Systé e účelově defnovná nožn prvků vze ez n, která spolu se svý vstupy výstupy vykzue ko
1. Úvod do základních pojmů teorie pravděpodobnosti
 1. Úvod do záladních pojmů teore pravděpodobnost 1.1 Úvodní pojmy Většna exatních věd zobrazuje své výsledy rgorózně tj. výsledy jsou zísávány na záladě přesných formulí a jsou jejch nterpretací. em je
1. Úvod do záladních pojmů teore pravděpodobnost 1.1 Úvodní pojmy Většna exatních věd zobrazuje své výsledy rgorózně tj. výsledy jsou zísávány na záladě přesných formulí a jsou jejch nterpretací. em je
FYZIKA 3. ROČNÍK. Vlastní kmitání oscilátoru. Kmitavý pohyb. Kinematika kmitavého pohybu. y m
 Vlastní itání oscilátoru Kitavý pohb Kitání periodicý děj zařízení oná opaovaně stejný pohb a periodic se vrací do určitého stavu. oscilátor zařízení, teré ůže volně itat (závaží na pružině, vadlo) it
Vlastní itání oscilátoru Kitavý pohb Kitání periodicý děj zařízení oná opaovaně stejný pohb a periodic se vrací do určitého stavu. oscilátor zařízení, teré ůže volně itat (závaží na pružině, vadlo) it
Měření příkonu míchadla při míchání suspenzí
 U8 Ústav procesní a zpracovatelské technky FS ČVUT v Praze Měření příkonu rotačních íchadel př íchání suspenzí I. Úkol ěření V průyslu téěř 60% všech operacích, kdy je íchání používáno, představuje íchání
U8 Ústav procesní a zpracovatelské technky FS ČVUT v Praze Měření příkonu rotačních íchadel př íchání suspenzí I. Úkol ěření V průyslu téěř 60% všech operacích, kdy je íchání používáno, představuje íchání
Aplikace VAR ocenění tržních rizik
 Aplkac VAR ocnění tržních rzk Obsah: Zdroj rzka :... 2 Řízní tržního rzka... 2 Měřní tržního rzka... 3 Modly... 4 Postup výpočtu... 7 Nastavní modlu a gnrování Mont-Carlo scénářů... 7 Vlčny vyjadřující
Aplkac VAR ocnění tržních rzk Obsah: Zdroj rzka :... 2 Řízní tržního rzka... 2 Měřní tržního rzka... 3 Modly... 4 Postup výpočtu... 7 Nastavní modlu a gnrování Mont-Carlo scénářů... 7 Vlčny vyjadřující
Lomová houževnatost. plastická deformace. R e = K C
 Loová houžvntost UM - 5 Loová houžvntost Jéno: St. suin: Dtu cviční: ) Stručně oišt, co vyjdřují ojy ) nětí - z luzu b) součinitl intnzity nětí - loová houžvntost. Disutujt oužití vzthu ro výočt součinitl
Loová houžvntost UM - 5 Loová houžvntost Jéno: St. suin: Dtu cviční: ) Stručně oišt, co vyjdřují ojy ) nětí - z luzu b) součinitl intnzity nětí - loová houžvntost. Disutujt oužití vzthu ro výočt součinitl
Pavol Bukviš 1, Pavel Fiala 2
 MODEL MIKROVLNNÉHO VYSOUŠEČE OLEJE Pavol Bukviš 1, Pavel Fiala 2 ANOTACE Příspěvek přináší výsledky numerického modelování při návrhu zařízení pro úpravy transformátorového oleje. Zařízení pracuje v oblasti
MODEL MIKROVLNNÉHO VYSOUŠEČE OLEJE Pavol Bukviš 1, Pavel Fiala 2 ANOTACE Příspěvek přináší výsledky numerického modelování při návrhu zařízení pro úpravy transformátorového oleje. Zařízení pracuje v oblasti
Úloha č. 11. H0 e. (4) tzv. Stefanův - Bo1tzmannův zákon a 2. H λ dλ (5)
 pyromtrm - vrz 01 Úloha č. 11 Měřní tplotní vyzařovací charaktristiky wolframového vlákna žárovky optickým pyromtrm 1) Pomůcky: Měřicí zařízní obsahující zdroj lktrické nrgi, optický pyromtr a žárovku
pyromtrm - vrz 01 Úloha č. 11 Měřní tplotní vyzařovací charaktristiky wolframového vlákna žárovky optickým pyromtrm 1) Pomůcky: Měřicí zařízní obsahující zdroj lktrické nrgi, optický pyromtr a žárovku
7.3.9 Směrnicový tvar rovnice přímky
 7.3.9 Směrnicový tvar rovnice přímy Předpolady: 7306 Pedagogicá poznáma: Stává se, že v hodině nestihneme poslední část s určováním vztahu mezi směrnicemi olmých příme. Vrátíme se obecné rovnici přímy:
7.3.9 Směrnicový tvar rovnice přímy Předpolady: 7306 Pedagogicá poznáma: Stává se, že v hodině nestihneme poslední část s určováním vztahu mezi směrnicemi olmých příme. Vrátíme se obecné rovnici přímy:
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta stavební. Laboratoře TZB. Ing. Daniel Adamovský, Ph.D. Katedra TZB, fakulta stavební, ČVUT v Praze
 ČESKÉ YSOKÉ UČENÍ TECHNICKÉ PRAZE Fakulta stavbní Laboratoř TZB Cvční č. 3 Stanovní účnnost výměníku ZZT Ing. Danl Adamovský, Ph.D. Katdra TZB, fakulta stavbní, ČUT v Praz Praha 2011 Evropský socální fond
ČESKÉ YSOKÉ UČENÍ TECHNICKÉ PRAZE Fakulta stavbní Laboratoř TZB Cvční č. 3 Stanovní účnnost výměníku ZZT Ing. Danl Adamovský, Ph.D. Katdra TZB, fakulta stavbní, ČUT v Praz Praha 2011 Evropský socální fond
č é č ř č
 Á č ř č Á Á Ň Á č é č ř č Á Ů Ě Í Ý Ř Í Ě É Á Č Ň Í Í Š Á Í Á Ů Ž ČÁ Č ÉÚ Á Í Á Ů É Á Í Ž É Ř ý š ž ř é š ř é ř č é ř é Č é ě ý é ý ú ě š é ý ř é Á ý č ů ú č ř ě ó Á ú č ě ě ů ý ú ů š č é Á ř č ě ř ý č
Á č ř č Á Á Ň Á č é č ř č Á Ů Ě Í Ý Ř Í Ě É Á Č Ň Í Í Š Á Í Á Ů Ž ČÁ Č ÉÚ Á Í Á Ů É Á Í Ž É Ř ý š ž ř é š ř é ř č é ř é Č é ě ý é ý ú ě š é ý ř é Á ý č ů ú č ř ě ó Á ú č ě ě ů ý ú ů š č é Á ř č ě ř ý č
MECHANICKÉ KMITÁNÍ NETLUMENÉ
 MECHANICKÉ KMITÁNÍ NETLUMENÉ Kitání je PERIODICKÝ pohyb hotného bodu (tělesa). Pohybuje se z jedné rajní polohy KP do druhé rajní polohy KP a zpět. Jaýoliv itající objet se nazývá OSCILÁTOR. A je aplituda
MECHANICKÉ KMITÁNÍ NETLUMENÉ Kitání je PERIODICKÝ pohyb hotného bodu (tělesa). Pohybuje se z jedné rajní polohy KP do druhé rajní polohy KP a zpět. Jaýoliv itající objet se nazývá OSCILÁTOR. A je aplituda
VZDUCH V MÍSTNOSTI POMŮCKY NASTAVENÍ MĚŘICÍHO ZAŘÍZENÍ. Vzdělávací předmět: Fyzika. Tematický celek dle RVP: Látky a tělesa
 VZDUCH V MÍSTNOSTI Vzdělávací předět: Fyzika Teatický celek dle RVP: Látky a tělesa Teatická oblast: Měření fyzikálních veličin Cílová skupina: Žák 6. ročníku základní školy Cíle pokusu je určení rozěrů
VZDUCH V MÍSTNOSTI Vzdělávací předět: Fyzika Teatický celek dle RVP: Látky a tělesa Teatická oblast: Měření fyzikálních veličin Cílová skupina: Žák 6. ročníku základní školy Cíle pokusu je určení rozěrů
 ý ý ž ž Č š ř ů ř ý ž ň ý ú ý ř ů ů ž š ý ý š ů ť ý ů ž ř ř ů ý ů ý ů ž ý ů ů ů ý ý ů ú ř Š ó ů ř ý ů š ž š Á Í Á ž š ř ž š Ě Á ň ž ó ň ž Á ř Ď Á ň š Ď ř Č É Ž Í ůž ž ž ř ř ř ř ž ý ó š ů ů š ř ž ř š ů
ý ý ž ž Č š ř ů ř ý ž ň ý ú ý ř ů ů ž š ý ý š ů ť ý ů ž ř ř ů ý ů ý ů ž ý ů ů ů ý ý ů ú ř Š ó ů ř ý ů š ž š Á Í Á ž š ř ž š Ě Á ň ž ó ň ž Á ř Ď Á ň š Ď ř Č É Ž Í ůž ž ž ř ř ř ř ž ý ó š ů ů š ř ž ř š ů
Vznik střídavého proudu Obvod střídavého proudu Výkon Střídavý proud v energetice
 Střídavý proud Vznik střídavého proudu Obvod střídavého proudu Výkon Střídavý proud v energetice Vznik střídavého proudu Výroba střídavého napětí:. indukční - při otáčivé pohybu cívky v agnetické poli
Střídavý proud Vznik střídavého proudu Obvod střídavého proudu Výkon Střídavý proud v energetice Vznik střídavého proudu Výroba střídavého napětí:. indukční - při otáčivé pohybu cívky v agnetické poli
INTERGRÁLNÍ POČET. PRIMITIVNÍ FUNKCE (neurčitý integrál)
 INTERGRÁLNÍ POČET Motivac: Užití intgrálního počtu spočívá mj. v výpočtu obsahu rovinného obrazc ohraničného různými funkcmi příp. čarami či v výpočtu objmu rotačního tělsa, vzniklého rotací daného obrazc
INTERGRÁLNÍ POČET Motivac: Užití intgrálního počtu spočívá mj. v výpočtu obsahu rovinného obrazc ohraničného různými funkcmi příp. čarami či v výpočtu objmu rotačního tělsa, vzniklého rotací daného obrazc
Příklady k přednášce 6 - Ustálený stav, sledování a zadržení poruchy
 Přílady přdnášc 6 - Utálný tav, ldování a zadržní poruchy Mchal Šb Automatcé řízní 05 9-3-5 Frvnční odzva - odvozní Automatcé řízní - Kybrnta a robota Na vtup tablního ytému přnom y () = Gu ()(), trý j
Přílady přdnášc 6 - Utálný tav, ldování a zadržní poruchy Mchal Šb Automatcé řízní 05 9-3-5 Frvnční odzva - odvozní Automatcé řízní - Kybrnta a robota Na vtup tablního ytému přnom y () = Gu ()(), trý j
Pružnost a plasticita II
 Pružnost a plastcta II 3 ročník bakalářského studa doc Ing Martn Kresa PhD Katedra stavební mechank Řešení pravoúhlých nosných stěn metodou sítí Statcké schéma nosné stěn q G υ (μ) h l d 3 wwwfastvsbcz
Pružnost a plastcta II 3 ročník bakalářského studa doc Ing Martn Kresa PhD Katedra stavební mechank Řešení pravoúhlých nosných stěn metodou sítí Statcké schéma nosné stěn q G υ (μ) h l d 3 wwwfastvsbcz
FYZIKA 3. ROČNÍK. Nestacionární magnetické pole. Magnetický indukční tok. Elektromagnetická indukce. π Φ = 0. - magnetické pole, které se s časem mění
 FYZKA 3. OČNÍK - magntické pol, ktré s s časm mění Vznik nstacionárního magntického pol: a) npohybující s vodič s časově proměnným proudm b) pohybující s vodič s proudm c) pohybující s prmanntní magnt
FYZKA 3. OČNÍK - magntické pol, ktré s s časm mění Vznik nstacionárního magntického pol: a) npohybující s vodič s časově proměnným proudm b) pohybující s vodič s proudm c) pohybující s prmanntní magnt
Příklady k přednášce 6 - Ustálený stav, sledování a zadržení poruchy
 Přílady přdnášc 6 - Utálný tav, ldování a zadržní poruchy Mchal Šb Automatcé řízní 08 3-3-8 Automatcé řízní - Kybrnta a robota Frvnční odzva, charatrta, přno Má-l tablní LTI ytém y () = Gu ()() na vtupu
Přílady přdnášc 6 - Utálný tav, ldování a zadržní poruchy Mchal Šb Automatcé řízní 08 3-3-8 Automatcé řízní - Kybrnta a robota Frvnční odzva, charatrta, přno Má-l tablní LTI ytém y () = Gu ()() na vtupu
7. TRANSFORMÁTORY. 7.1 Štítkové údaje. 7.2 Měření odporů vinutí. 7.3 Měření naprázdno
 7. TRANSFORMÁTORY Pro zjednodušení budeme měření provádět na jednofázovém transformátoru. Na trojfázovém transformátoru provedeme pouze ontrolu jeho zapojení měřením hodinových úhlů. 7.1 Štítové údaje
7. TRANSFORMÁTORY Pro zjednodušení budeme měření provádět na jednofázovém transformátoru. Na trojfázovém transformátoru provedeme pouze ontrolu jeho zapojení měřením hodinových úhlů. 7.1 Štítové údaje
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV FYZIKÁLNÍHO INŽENÝRSTVÍ FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF PHYSICAL ENGINEERING PŘÍPRAVA 2D HETEROSTRUKTUR
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV FYZIKÁLNÍHO INŽENÝRSTVÍ FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF PHYSICAL ENGINEERING PŘÍPRAVA 2D HETEROSTRUKTUR
š ý é á ě ý ěž é á áž íž š í á š íř á ší ř í ě ž é ž š ř í í ě ž á á íž č í ě í í ě á í á č ž á ý ě š ť ř ů ý ř í é á ž í éč é í č ý á ň á í ž ě á í ž
 Š Í Ř Ě É Í Ř Á Ř Á Í É á ý á ý í é á í ž č í é ř ý č í í í ý žš ě á í é í ě í í ě é á ž š č í í ů á č é á š ú ž í ř á í á é í úč ý ěšé í í é á ř é íú é í ů ří š í á í ří š á ě í í š ř í ž í ě á ž é ě
Š Í Ř Ě É Í Ř Á Ř Á Í É á ý á ý í é á í ž č í é ř ý č í í í ý žš ě á í é í ě í í ě é á ž š č í í ů á č é á š ú ž í ř á í á é í úč ý ěšé í í é á ř é íú é í ů ří š í á í ří š á ě í í š ř í ž í ě á ž é ě
7.3.9 Směrnicový tvar rovnice přímky
 739 Směrnicový tvar rovnice přímy Předpolady: 7306 Pedagogicá poznáma: Stává se, že v hodině nestihneme poslední část s určováním vztahu mezi směrnicemi olmých příme Vrátíme se obecné rovnici přímy: Obecná
739 Směrnicový tvar rovnice přímy Předpolady: 7306 Pedagogicá poznáma: Stává se, že v hodině nestihneme poslední část s určováním vztahu mezi směrnicemi olmých příme Vrátíme se obecné rovnici přímy: Obecná
 š ř Č šť ň ř ž Č Č ř ž š š ď Č Č ť ř ř ž ř ř ž š ř ř ř ř š ř ď š ř š ř ž š š ř š š š š š ď š ď š š ř š ř Ž Á š ř ž ř ů š ř ů ř Ú ř Ú ů ů ň ř ů š ř š Ú ř š ď š š š š ůž ř ň ř ň š š š Č Ú š ž ř ž ř ř š š
š ř Č šť ň ř ž Č Č ř ž š š ď Č Č ť ř ř ž ř ř ž š ř ř ř ř š ř ď š ř š ř ž š š ř š š š š š ď š ď š š ř š ř Ž Á š ř ž ř ů š ř ů ř Ú ř Ú ů ů ň ř ů š ř š Ú ř š ď š š š š ůž ř ň ř ň š š š Č Ú š ž ř ž ř ř š š
( ) Příklady na otočení. Předpoklady: Př. 1: Je dána kružnice k ( S ;5cm)
 3.5.9 Přílady na otočení Předpolady: 3508 Př. 1: Je dána ružnice ( ;5cm), na teré leží body, '. Vně ružnice leží bod L, uvnitř ružnice bod M. Naresli obrazy bodů L, M v zobrazení řeš bez úhloměru. R (
3.5.9 Přílady na otočení Předpolady: 3508 Př. 1: Je dána ružnice ( ;5cm), na teré leží body, '. Vně ružnice leží bod L, uvnitř ružnice bod M. Naresli obrazy bodů L, M v zobrazení řeš bez úhloměru. R (
u (x i ) U i 1 2U i +U i+1 h 2. Na hranicích oblasti jsou uzlové hodnoty dány okrajovými podmínkami bud přímo
 Metoda sítí základní schémata h... krok sítě ve směru x, tj. h = x x q... krok sítě ve směru y, tj. q = y j y j τ... krok ve směru t, tj. τ = j... hodnota přblžného řešení v uzlu (x,y j ) (Possonova rovnce)
Metoda sítí základní schémata h... krok sítě ve směru x, tj. h = x x q... krok sítě ve směru y, tj. q = y j y j τ... krok ve směru t, tj. τ = j... hodnota přblžného řešení v uzlu (x,y j ) (Possonova rovnce)
Vliv marketingového dotazování na identifikaci tržních segmentů
 Vliv aretingového dotazování na identifiaci tržních segentů Jední z líčových fatorů stanovení optiální aretingové strategie e správně provedená identifiace a následné vyezení tržních segentů cílového trhu.
Vliv aretingového dotazování na identifiaci tržních segentů Jední z líčových fatorů stanovení optiální aretingové strategie e správně provedená identifiace a následné vyezení tržních segentů cílového trhu.
- Pokud máme na množině V zvoleno pevné očíslování vrcholů, můžeme váhovou funkci jednoznačně popsat. Symbolem ( i)
 DSM2 C 8 Problém neratší cesty Ohodnocený orientoaný graf: - Definice: Ohodnoceným orientoaným grafem na množině rcholů V = { 1, 2,, n} nazýáme obet G = V, w, de zobrazení w : V V R { } se nazýá áhoá funce
DSM2 C 8 Problém neratší cesty Ohodnocený orientoaný graf: - Definice: Ohodnoceným orientoaným grafem na množině rcholů V = { 1, 2,, n} nazýáme obet G = V, w, de zobrazení w : V V R { } se nazýá áhoá funce
č á ž á ž ý ý Ú ď ě é ř ářž ž ý ř ůž ř š á ů ž é á é ř ť á ě á ž É ř á é ř ť éž ě é é ě ů ě č é ě á é éř ý ě ě š ý š ř é ě š š á ě šá á é á ň é á ž á
 ďť č á ž á ž ý ý Ú ď ě é ř ářž ž ý ř ůž ř š á ů ž é á é ř ť á ě á ž É ř á é ř ť éž ě é é ě ů ě č é ě á é éř ý ě ě š ý š ř é ě š š á ě šá á é á ň é á ž á é ž š ý ř ášý ě ý ů é é á é ěž ř ý á š ů ž ě š š
ďť č á ž á ž ý ý Ú ď ě é ř ářž ž ý ř ůž ř š á ů ž é á é ř ť á ě á ž É ř á é ř ť éž ě é é ě ů ě č é ě á é éř ý ě ě š ý š ř é ě š š á ě šá á é á ň é á ž á é ž š ý ř ášý ě ý ů é é á é ěž ř ý á š ů ž ě š š
Elektromagnetické pole
 Elektroagnetcké pole Časově proěnné elektrcké proudy v čase se ění velkost proudu a napětí v obvodu kvazstaconární proudy elektroagnetcký rozruch se šířívodče rychlostí světla c doba potřebná k přenosu
Elektroagnetcké pole Časově proěnné elektrcké proudy v čase se ění velkost proudu a napětí v obvodu kvazstaconární proudy elektroagnetcký rozruch se šířívodče rychlostí světla c doba potřebná k přenosu
3.1.3 Rychlost a zrychlení harmonického pohybu
 3.1.3 Rychlost a zrychlení haronického pohybu Předpoklady: 312 Kroě dráhy (výchylky) popisujee pohyb i poocí dalších dvou veličin: rychlosti a zrychlení. Jak budou vypadat jejich rovnice? Společný graf
3.1.3 Rychlost a zrychlení haronického pohybu Předpoklady: 312 Kroě dráhy (výchylky) popisujee pohyb i poocí dalších dvou veličin: rychlosti a zrychlení. Jak budou vypadat jejich rovnice? Společný graf
Mapování indukce magnetického pole v okolí malých cívkových aplikátorů metodou magnetické rezonance
 Mapování indukce magnetického pole v okolí malých cívkových aplikátorů metodou magnetické rezonance 1 Petr Bidman, 2 Karel Bartušek 1 Fakulta elektrotechniky a komunikačních technologií, Vysoké učení technické
Mapování indukce magnetického pole v okolí malých cívkových aplikátorů metodou magnetické rezonance 1 Petr Bidman, 2 Karel Bartušek 1 Fakulta elektrotechniky a komunikačních technologií, Vysoké učení technické
Měrná vnitřní práce tepelné turbíny při adiabatické expanzi v T-s diagramu
 1 ato Příloha 307 j oučátí článku 13. Enrgtcké blanc lopatkových trojů, http://www.tranformacntchnolog.cz/nrgtck-blanc-lopatkovychtroju.html. Měrná vntřní prác tplné turbíny př adabatcké xpanz v - dagramu
1 ato Příloha 307 j oučátí článku 13. Enrgtcké blanc lopatkových trojů, http://www.tranformacntchnolog.cz/nrgtck-blanc-lopatkovychtroju.html. Měrná vntřní prác tplné turbíny př adabatcké xpanz v - dagramu
Viz též stavová rovnice ideálního plynu, stavová rovnice reálného plynu a van der Waalsova stavová rovnice.
 5.1 Stavová rovnice 5.1.1 Stavová rovnice ideálního plynu Stavová rovnice pro sěs ideálních plynů 5.1.2 Stavová rovnice reálného plynu Stavové rovnice se dvěa onstantai Viriální rovnice Stavové rovnice
5.1 Stavová rovnice 5.1.1 Stavová rovnice ideálního plynu Stavová rovnice pro sěs ideálních plynů 5.1.2 Stavová rovnice reálného plynu Stavové rovnice se dvěa onstantai Viriální rovnice Stavové rovnice
Úvod do Kalmanova filtru
 Kalmanův filtr = odhadovač stavu systému Úvod do Kalmanova filtru KF dává dohromady model systému a měření. Model systému použije tomu, aby odhadl, ja bude stav vypadat a poté stav porovná se sutečným
Kalmanův filtr = odhadovač stavu systému Úvod do Kalmanova filtru KF dává dohromady model systému a měření. Model systému použije tomu, aby odhadl, ja bude stav vypadat a poté stav porovná se sutečným
2. Určete optimální pracovní bod a účinnost solárního článku při dané intenzitě osvětlení, stanovte R SH, R SO, FF, MPP
 FP 5 Měření paraetrů solárních článků Úkoly : 1. Naěřte a poocí počítače graficky znázorněte voltapérovou charakteristiku solárního článku. nalyzujte vliv různé intenzity osvětlení, vliv sklonu solárního
FP 5 Měření paraetrů solárních článků Úkoly : 1. Naěřte a poocí počítače graficky znázorněte voltapérovou charakteristiku solárního článku. nalyzujte vliv různé intenzity osvětlení, vliv sklonu solárního
DIDAKTICKÝ TEST MAGNETICKÉ POLE
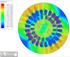 DIDAKTICKÝ TEST MAGNETICKÉ POLE Použité zdroje: Blahovec, A.: Elektrotechnika I, Inforatoriu, Praha 2005 Černý, V.: Repetitoriu, Základní vztahy v elektrotechnice, časopis ELEKTRO ročník 2003 http://www.odbornecasopisy.cz
DIDAKTICKÝ TEST MAGNETICKÉ POLE Použité zdroje: Blahovec, A.: Elektrotechnika I, Inforatoriu, Praha 2005 Černý, V.: Repetitoriu, Základní vztahy v elektrotechnice, časopis ELEKTRO ročník 2003 http://www.odbornecasopisy.cz
symetrická rovnice, model Redlich- Kister dvoukonstantové rovnice: Margules, van Laar model Hildebrandt - Scatchard mřížková teorie roztoků příklady
 symetrcá rovnce, model Redlch- Kster dvouonstantové rovnce: Margules, van Laar model Hldebrandt - Scatchard mřížová teore roztoů přílady na procvčení 0 lm Bnární systémy: 0 atvtní oefcenty N I E N I E
symetrcá rovnce, model Redlch- Kster dvouonstantové rovnce: Margules, van Laar model Hldebrandt - Scatchard mřížová teore roztoů přílady na procvčení 0 lm Bnární systémy: 0 atvtní oefcenty N I E N I E
15 Mletí. I Základní vztahy a definice. Oldřich Holeček (aktualizace v roce 2014 Michal Přibyl & Marek Schöngut)
 15 Mletí Oldřch Holeče (atualzace v roce 2014 Mchal Přbyl & Mare Schöngut) I Záladní vztahy a defnce I.1 Úvod Rychlost mnoha chemcých a fyzálních procesů závsí na velost mezfázového povrchu. Je-l v nch
15 Mletí Oldřch Holeče (atualzace v roce 2014 Mchal Přbyl & Mare Schöngut) I Záladní vztahy a defnce I.1 Úvod Rychlost mnoha chemcých a fyzálních procesů závsí na velost mezfázového povrchu. Je-l v nch
teorie elektronických obvodů Jiří Petržela analýza obvodů s regulárními prvky
 Jiří Petržela příklad pro příčkový filtr na obrázku napište aditanční atici etodou uzlových napětí zjistěte přenos filtru identifikujte tp a řád filtru Obr. : Příklad na příčkový filtr. aditanční atice
Jiří Petržela příklad pro příčkový filtr na obrázku napište aditanční atici etodou uzlových napětí zjistěte přenos filtru identifikujte tp a řád filtru Obr. : Příklad na příčkový filtr. aditanční atice
MODELOVÁNÍ A SIMULACE
 MODELOVÁNÍ A SIMULACE základní pojmy a postupy vytváření matematckých modelů na základě blancí prncp numerckého řešení dferencálních rovnc základy práce se smulačním jazykem PSI Základní pojmy matematcký
MODELOVÁNÍ A SIMULACE základní pojmy a postupy vytváření matematckých modelů na základě blancí prncp numerckého řešení dferencálních rovnc základy práce se smulačním jazykem PSI Základní pojmy matematcký
Základy elektrotechniky
 Základy elektrotechniky 3. přednáška Řešení obvodů napájených haronický napětí v ustálené stavu ZÁKADNÍ POJMY Časový průběh haronického napětí: kde: U u U. sin( t ϕ ) - axiální hodnota [V] - úhlový kitočet
Základy elektrotechniky 3. přednáška Řešení obvodů napájených haronický napětí v ustálené stavu ZÁKADNÍ POJMY Časový průběh haronického napětí: kde: U u U. sin( t ϕ ) - axiální hodnota [V] - úhlový kitočet
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY POSOUZENÍ KOTLE NA ODPADNÍ TEPLO ASSESSMENT OF TRANSFER LINE EXCHANGER
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV ENERGETICKÝ FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF ENERGETIC POSOUZENÍ KOTLE NA ODPADNÍ TEPLO ASSESSMENT
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV ENERGETICKÝ FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF ENERGETIC POSOUZENÍ KOTLE NA ODPADNÍ TEPLO ASSESSMENT
Osově namáhaný prut základní veličiny
 Pružnost a pevnost BD0 Osově namáhaný prut základní velčny ormálová síla půsoící v průřezu osově namáhaného prutu se získá ntegrací normálového napětí po ploše průřezu. da A Vzhledem k rovnoměrnému rozložení
Pružnost a pevnost BD0 Osově namáhaný prut základní velčny ormálová síla půsoící v průřezu osově namáhaného prutu se získá ntegrací normálového napětí po ploše průřezu. da A Vzhledem k rovnoměrnému rozložení
Statika soustavy těles v rovině
 Statka soustavy těles v rovně Zpracoval: Ing. Mroslav yrtus, Ph.. U mechancké soustavy s deálním knematckým dvojcem znázorněné na obrázku určete: počet stupňů volnost početně všechny reakce a moment M
Statka soustavy těles v rovně Zpracoval: Ing. Mroslav yrtus, Ph.. U mechancké soustavy s deálním knematckým dvojcem znázorněné na obrázku určete: počet stupňů volnost početně všechny reakce a moment M
