II. Soustavy s konečným počtem stupňů volnosti
|
|
|
- Otto Procházka
- před 5 lety
- Počet zobrazení:
Transkript
1 Jiří Máca - atedra echaiy - B35 - tel aca@fsv.cvut.cz. Pohybové rovice. Vlastí etlueé itáí 3. Vyuceé etlueé itáí 4. Volé etlueé itáí 5. Metoda ostat poddajosti 6. Přílady 7. Staticá odezace 8. Rayleighova etoda eergeticá etoda 9. Stodolova etoda postupých aproxiací etoda iverzích iterací 0. Přibližé vztahy pro určeí záladí frevece
2 . Pohybové rovice.stav u u 0 0 u t () F u () t u () t F soustava se stupi volosti u u 0.stav u () t u u 0 0 u () t u () t u 0 u u ( t) u ( t) u ( t) F ( t) u ( t) u ( t) u ( t) F ( t) prvy atice tuhosti ij
3 3. Pohybové rovice F F ( EI ) EI h h c 3 3 prvy atice tuhosti c
4 4. Pohybové rovice prvy atice tuhosti ij u = u = u 3 = 0 u (t) u (t) u 3 (t) u = u = u 3 = 0 Prvy atice tuhosti ij síla v bodě i při posuutí v bodě j rové jedé a ostatích posuutích rových ule u 3 = u = u = 0
5 5. Pohybové rovice u ( t) u ( t) u ( t) F ( t) u ( t) u ( t) u ( t) F ( t) K M 0 0 F () t f () t F () t u() t u() t u() t atice tuhosti (*) ( je počet stupňů volosti) atice hotosti (*) (eusí být vždy utě diagoálí) vetor zatížeí (*) vetor posuutí (*) (vetor ezáých) Ku( t) Mu( t) f( t) etoda ostat tuhosti
6 6. Vlastí etlueé itáí Nepůsobí žádé budicí síly, útlu se zaedbává C = 0 Cíle je staovit dyaicé charateristiy systéu vlastí ruhové frevece a odpovídající tvary itáí pohybová rovice řešeí rovice K u( t) M u( t) 0 u( t) ( Acost Bsi t) u ( t) u( t) K M ( Acost Bsi t) 0 = 0 rovice vlastího itáí ( K M) 0 ezáé: vlastí ruhové frevece tvary vlastího itáí problé vlastích čísel ( - počet stupňů volosti)
7 7. Vlastí etlueé itáí ( ) K M 0 podía etriviálího řešeí det. ( K M) 0 (polyo stupě N pro ) ořey polyou N reálých ladých čísel ; ;... N vlastí ruh. frevece - vlastí čísla 3 3 (... N ) pro aždou hodotu ( K M) 0 tvary vlastího itáí - vlastí vetory (N je počet stupňů volosti) je ožé určit odpovídající vetor ( ) ( )... N( ) ( ) J pořadice ()-tého vl. tvaru v bodě J
8 8. Vlastí etlueé itáí Modálí atice Φ () () ( N ) () () ( N ) N () N () N ( N ) (N)-tý tvar Spetrálí atice Ω ( K M) 0 K M K Φ M Φ Ω N opatí zápis rovice vlastího itáí pro všechy vl. tvary
9 9. Vlastí etlueé itáí Ortogoalita vlastích tvarů Dva růzé vlastí tvary odpovídající dvěa růzý vlastí frevecí ( ) splňují podíy ortogoality: Důaz: K 0 ; M 0 pro ( ) ( ) 0 0 obdobě lze doázat K 0
10 0. Vlastí etlueé itáí Norovaé vlastí tvary Řešeí vlastího itáí zísáe vlastí tvary jao vzájeé poěry výchyle v jedotlivých bodech, ioliv jejich sutečé veliosti. Proto je ožé vlastí tvary oralizovat, tj. přeásobit je vhodý čísle ta, aby byly splěy určité podíy (apř. ejvětší pořadice je rova ) Nejčastěji se používají vlastí tvary orovaé vzhlede atici hotosti odálí hotost M M pro orovaé tvary platí: Φ M Φ I Φ K Φ Ω (jedotová atice)
11 . Vlastí etlueé itáí Přílad výpočet vlastích frevecí a tvarů itáí K 4EIc 3 h 3 0 M 0 det. ( K M) 0.tvar ( K M) 0 volíe apř.: () z.rov. určíe: 3() () 0 () / /
12 . Vlastí etlueé itáí.tvar ( K M) 0 () ().tvar vlastího itáí.tvar vlastího itáí podía ortogoality i () ii () i 0 ( ) 0
13 3. Vlastí etlueé itáí orovaé vlastí tvary.tvar.tvar i i 3 M i () i 0.5 () () 3 3 i ( ) 3 3 () () i M 3 i i i() i() i i
14 4 3. Vyuceé etlueé itáí Soustava je zatížea budicíi silai f(t), útlu se zaedbává C = 0 Cíle je staovit dyaicou odezvu systéu pohybové rovice počátečí pod. K u( t) M u( t) f( t) u(0) u u(0) u 0 0 (soustava N difereciálích rovic) řešeí - příá itegrace pohybových rovic - odálí aalýza (rozlad do vlastích tvarů) Příá itegrace pohybových rovic záladí idea: pohybové rovice se postupě řeší jedotlivých oažicích t i, t i+, časová osa se rozdělí poocí dély itegračího rou t ti ti derivace se ahradí diferecei, soustava difereciálích rovic se převede a rovice algebraicé
15 5 3. Vyuceí etlueé itáí ozačeí: f f ( t ) u u( t ) u u( t ) i i i i i i Μu Ku f Mu Ku f i i i i i i ezáé: Metoda cetrálích diferecí u i u u u i i i t aproxiace pole zrychleí u u i i M u Ku f i i i uiu i ui M Kui f t i Mu t f K M u M u t t i i i i (soustava N algebraicých rovic)
16 6 3. Vyuceí etlueé itáí Rozlad do vlastích tvarů odálí aalýza záladí idea: odezva se staoví jao obiace vlastích tvarů itáí poocí odálích souřadic q (t) ( =, N) N u( t) q ( t) Φq( t) dosazeí do pohybových rovic Ku( t) Mu( t) f( t) K Φ q( t) M Φ q( t) f ( t) Φ K Φ q( t) Φ M Φ q( t) Φ f ( t) pro orovaé vlastí tvary dále platí Ω q( t) I q( t) Φ f ( t) soustava N ezávislých q ( t) q ( t) f( t) rovic pro q (t) - řešeí apř. Duhaelův itegrál
17 7 3. Vyuceí etlueé itáí Ustáleé haroicé itáí soustava je zatížea haroicýi silai se stejou budicí frevecí ω f( t) fa sit F A F A pohybové rovice Ku( t) Mu( t) fasit f A... Příé řešeí F NA odezva při ustáleé itáí u( t) ua sit dosazeí do pohybových rovic ( K M) u A f A (soustava N algebraicých rovic) u A ( K M) fa
18 8 3. Vyuceí etlueé itáí Modálí aalýza (pro orovaé vlastí tvary) q ( t) q ( t) f sit A q q ( t) q sit q sit q sit f sit A A A A q f A A A q A f A N aplituda výchyly v bodě i u( t) q ( t) q sit A N u N ia i( ) A q q A N F i( ) ia i
19 9 4. Volé etlueé itáí Soustava eí zatížea budicíi silai, útlu se zaedbává Kitáí je vyvoláo eulovýi počátečíi podíai pohybové rovice K u( t) M u( t) 0 počátečí podíy u(0) u0 u(0) u0 Modálí aalýza N u( t) q ( t) (pro orovaé tvary) odálí rovice řešeí odálí rovice u q (viz soustava s SV: ) q ( t) q ( t) 0 q (0); q (0) počátečí podíy q (0) q ( ) (0)cos t q t sit ( =, N)
20 0 4. Volé etlueé itáí Počátečí podíy pro odálí souřadice q (0) ; q (0) N u( t) q ( t) M N M u M ( t) q ( t) vzhlede podíá ortogoality platí pro = : Mu( t) Μ q ( t) pro orovaé tvary platí: q ( t) Mu( t) q () t q q Mu() t Μ (0) Mu(0) (0) Mu(0) Odezva při volé itáí N Mu(0) u( ) t Mu(0)cost sit
21 5. Metoda ostat poddajosti Pro poddajé ostruce je obvyle výpočet průhybu sadější ež určeí prvů atice tuhosti u u u 3 Prvy atice poddajosti δ ij přetvořeí v bodě i při jedotové zatížeí v bodě j
22 5. Metoda ostat poddajosti Matice poddajosti ostruce δ u δf Kδ I δ K N N N N NN vlastí itáí ( ) I δm 0 vyuceé itáí u( t) δm u( t) δ f( t) ustáleé itáí ( I δm) u A δf A
23 3 6. Přílady 6. a) Pro soustavu se stupi volosti určete vlastí frevece a tvary itáí EI w 3 w 6 3 EI,8t 3,6 t N L δ 3 L 768EI ,35 0, ,05 0,35 0,8 0 ( ) ( I δm) 0 M 0 0 3,6 ( ) 4 4,430 3,78 0 I δm 4 4,89 0 4,86 0 (prvy atice poddajosti se staoví apř. poocí PVP)
24 4 6. Přílady 8 4 det. ( ) 4,67 0 I δm 7, ,98s 8,77s. tvar itáí volíe a z. rov. určíe () 4 4, ,98 3, ,98 () 0 (),097. tvar itáí () () 0, 455 pod. ortogoality: () () () () () (),8,097 3,6 ( 0,455) 0,003 0 orovaé tvary: () 0,404 () 0,443 () 0,67 () 0, 85
25 5 6. Přílady b) Určete průběh aplitud ohybových oetů při ustáleé itáí pro zatížeí F ( t ) 8si08 t N wa FA 8 ( I δm) u A δf A ua fa 08 wa FA w,60 w,640 A A setrvačé síly: (aplitudy) 8 37,4 M 54,8 68,9, w 08,8,60 54,8 N 3 A w 08 3,6 (,64) 0 68,9 N 3 A 00,5 33,5 budicí síly zatížeí (N) = + setrvačé síly ohybové oety (aplitudy) (N) M ( t ),5si08 t N
26 6 w w 6. Přílady c) Rozlade do vlastích tvarů určete aplitudy výchyle a sil působících a osí při ustáleé itáí pro zatížeí F ( t ) 8si08 t N F ( t ) 36si08 t N q q F 0, ,443 36,9 0 i() ia i A 38,98 08 F 0,67 8 ( 0, 85) 36 0,4 0 i() ia i A 8,77 08 q A ( ) A A ( ) A ,404 (,9) 0 0,67 0,4 0 0,66 0 q ,443 (,9) 0 ( 0,85) 0,4 0,
27 7 6. Přílady setrvačé síly: 0, 8 w 08,8 ( 0,66) 0 3,9 N 3 A w 36 3,9 47,4 08 3,6 (,3) 0 47,4 N 3 A 7,5 budicí síly zatížeí (N) = + setrvačé síly d) Vysvětlete, proč při zatížeí F ( t ) 8si08 t N F ( t ) 36si08 t N dochází při ustáleé itáí e zvětšeí aáháí 3 3 osíu ( w A 6,50 w A,30 ) Poz.: soustava s SV (otrola řešeí) 48EI 3 L 0 39,3s
28 8 6. Přílady e) Určete odezvu osíu při itáí vyvolaé počátečí posuutí u(0) počátečí rychlost ulová 0 (tj. řešeí volého itáí rozlade do vlastích tvarů) q (0) q ( ) (0)cos t q t sit q q (0) Mu(0) (0) Mu(0) (0) Mu(0) 0, 404,8 0 0, 443 0, ,6 0 (0) Mu(0) 0, 67,8 0 0, 85,86 0 3,6 0 q (0) Mu(0) q (0) 0; q (0) 0 q q
29 6. Přílady 9 w () t u( t) q ( t) w () t 0,404 0,67 0,443 0,85 0, 938 0, 7076 cos 38,98t cos8, 77t 0,3 0,36 0, 77 cos 38,98t,86 cos8, 77t w ( t ) 0,938cos38,98 t 0,7076cos8,77 t w ( t ) 0,3cos38,98 t 0,36cos8,77 t t = 0 s
30 6. Přílady počátečí posuutí u(0) w ( t ) 0,938cos38,98 t 0,0643cos8,77 t 30 f 6,Hz počátečí posuutí u(0) 0,5 w ( t ) 0,084cos38,98 t,093cos8,77 t f 8,9 Hz
31 3 6. Přílady 6. a) Pro soustavu se stupi volosti určete průběh aplitud sil působících při ustáleé itáí EI 3 50 MN () t wt (), 500 g/ 3t F( t) 0si 60t N t 0 MN/ EI 3 t 30 MN/ L=4 3 L 54,67 t J L L 3 50MN, 0 I M 0 u A A w A 0 3
32 3 6. Přílady 3 L L w 0 L/ = LL L N N K 40 87,5 0 w N L N N 87,50 N N 48EI 3 L 3 37,5 0 N/ 3 -
33 33 6. Přílady FL A 3 0,93rad K M u A u A ,4594 L FA 0 3 A 9,9 3 A 46, L AL 6,6 7,7 ( ( LL ) A wa 7,7 w 3 A 3,3 w A 3,8 A L 6,6 síly v pružiách síly budicí síly setrvačé w A a α A se dosazují v absolutích hodotách síla v pružiě = tuhost x zěa dély Určete reace podporách
34 34 6. Přílady b) Proveďte otrolu řešeí poocí odálí aalýzy ( ) K M 0 q FL 6,85030 () A 3 A q w FL, () A 5 A 3 A ( ) qa A ( ) qa 3 45, 04s 0, 0s 0,93 0 rad 0, Φ 0,3468 0,035 0, ,7045 orovaé vlastí tvary
35 35 6. Přílady 6.3 Sestavte atici tuhosti a hotosti α w w 0 w 0 4 těžiště u w 3 6 K M 0 6 0
36 36 6. Přílady α w w 0 w 0 K
37 37 6. Přílady α w w 0 aplitudy setrvačých sil w 0 M atice hotosti eí diagoálí
38 38 7. Staticá odezace Vyloučeí ehotých stupňů volosti při dyaicé aalýze reduce atice tuhosti ostruce KuMuf() t w w K (4,4) w K (,) K aa K ab ua Ma 0 ua f () t () Kba Kbb ub 0 0 ub 0 () z rov. () u K K u dosazeí do () b bb ba a K K K K u M u f () aa ab bb ba a a a t w M a u u b a 0 w w K K odezovaá atice tuhosti a (,) 0
39 39 8. Rayleighova etoda eergeticá etoda Určeí záladí (prví) vlastí frevece aproxiace shora využívá záo zachováí echaicé eergie E Ep u ( t) Mu( t) u ( t) Ku( t) ost. eergie ieticá + poteciálí F=u u F u pro vlastí itáí: u( t) C si( t ) u( t) C cos( t ) u ax E ax E rovovážá poloha rají poloha ax. rychlost ax. výchyla p ax u( t) ax u( t)
40 40 8. Rayleighova etoda eergeticá etoda tvar itáí se volí ta, aby odpovídal prvíu tvaru ejlépe od zatížeí vlastí tíhou F i působící ve sěru itáí F g F g F g Ku F K F F 3 3 ax ax E u E N N i i i i i i N F p i i i N F i i i N i i i /
41 4 8. Rayleighova etoda eergeticá etoda Přílad 8. určete prví vlastí freveci a tvar itáí u u u 3 3,5,5 δ M u u u u F F F
42 4 8. Rayleighova etoda eergeticá etoda volba prvího tvaru itáí 3 g g g g 6 g δf 5 5 g g 5 F g g , i i i 3 i g i 6 5 i 0,699 3,5 Přesé řešeí 0,694,6 3,98
43 43 8. Rayleighova etoda eergeticá etoda Přílad 8. určete prví vlastí freveci a tvar itáí - l 4 g 0s 3 EI 00 N l l l 4 t 0,5t δ l 9EI ,67 0 g g F ,3 4537,5 04,3 s volba zatížeí i i i 55 0,5 55 i i i -
44 44 8. Rayleighova etoda eergeticá etoda Přesé řešeí: 04,3s 45, s - - Φ Poz. - esprává volba zatížeí g g i i i 5 0,5 5 i i i F , 637,5-45,4 s? touto etodou elze určit vyšší vlastí frevece
45 45 9. Stodolova etoda postupých aproxiací etoda iverzích iterací vlastí it. K M K M K M vlastosti Rayleighova vocietu: je-li vlastí tvar, K M Rayleighův vociet je-li pro x -tá aproxiace vlastího tvaru, x ( x ) (overgece. vlastíu tvaru)
46 46 9. Stodolova etoda postupých aproxiací etoda iverzích iterací. Startovací vetor x 0 libovolý R Mx. 0 0 Kx R x K R 0 0 x Kx x Mx ( ) x Mx x Mx 3. (Rayleighův vociet) 4. Kx Mx ( ) ( ) ( ) tol 5. Neí-li ritériu overgece splěo: orováí x x a ávrat do bodu ( = +) / x Mx x K Mx Mx
47 47 9. Stodolova etoda postupých aproxiací etoda iverzích iterací 6. Je-li ritériu overgece splěo: pro iteraci (+) ( ) x / x Mx obdobě pro jedotlivé prvy vetoru x x x x Poz. v této forulaci etoda overguje. vlastíu tvaru vyšší tvary lze určit ta, že se do algoritu zavedou podíy ortogoality ezi hledaý -tý tvare a všei předcházejícíi vlastíi tvary (uto určit všech - předcházejících vlastích tvarů)
48 48 9. Stodolova etoda postupých aproxiací etoda iverzích iterací Přílad 9. určete prví vlastí freveci a tvar itáí,5, δ δm M startovací x0 Kx Mx x Mx vetor 6 () xmx0 x δmx0 0, 489 x 6 5 x Mx,5 Rayleighův vociet orováí u
49 49 9. Stodolova etoda postupých aproxiací etoda iverzích iterací.iterace () xmx x δmx 4,5 0, 48 x, x Mx,9 3.iterace, 8 (3) x3mx x3 δmx 7,70 0,48 x3, , 43 x Mx,97 alterativě: (3) 0,694 x3, 3,9 0,699 0,695 0,69,8 7,70 36,
50 50 9. Stodolova etoda postupých aproxiací etoda iverzích iterací Přílad 9. určete prví vlastí freveci a tvar itáí 4 3 l l l 4 δ, δm M 0 0,5 5 4,5 3,5 x0 startovací vetor (srovej poz. př. 8.),5 () x Mx0 0,353 x δmx0 x 0,5 xmx 0, 4,3 () x Mx 0,89 x δmx x 3,5 xmx 0,8 5, 5 (3) x 3Mx 0,8 x3 δmx x 3 5, 05 x3mx3 0,96 04,4 s (3)
51 5 0. Přibližé vztahy pro určeí záladí frevece Duerleyův vzorec i i ii aproxiace zdola Přílad: zadáí ,63 Bauaův Geigerův vzorec g ax u G g Přílad: zadáí 8. 0, 63 g 5 6 ax. výchyla od vlastí tíhy působící ve sěru. tvaru
52 5 0. Přibližé vztahy pro určeí záladí frevece Epiricé vztahy Budovy do 40 výšy (Euroód 8) (ČSN ) Stožáry f 00 H C H 3/ 4 t (s) H 0, 09 (s) B Věže f H H výša budovy (v etrech) C t = 0,085 prostorové ocelové ráy odolávající oetů C t = 0,075 prostorové betoové ráy ocelové ráy s excetricý ztužeí C t = 0,050 ostatí ostruce selety ŽB, ocel B šířa ve sěru itáí () Koíy f H
IV. MKP vynucené kmitání
 Jří Máca - katedra mechaky - B35 - tel. 435 4500 maca@fsv.cvut.cz IV. MKP vyuceé kmtáí. Rovce vyuceého kmtáí. Modálí aalýza rozklad do vlastích tvarů 3. Přímá tegrace pohybových rovc 3. Metoda cetrálích
Jří Máca - katedra mechaky - B35 - tel. 435 4500 maca@fsv.cvut.cz IV. MKP vyuceé kmtáí. Rovce vyuceého kmtáí. Modálí aalýza rozklad do vlastích tvarů 3. Přímá tegrace pohybových rovc 3. Metoda cetrálích
k(k + 1) = A k + B. s n = n 1 n + 1 = = 3. = ln 2 + ln. 2 + ln
 Číselé řady - řešeé přílady ČÍSELNÉ ŘADY - řešeé přílady A. Součty řad Vzorové přílady:.. Přílad. Určete součet řady + = + 6 + +.... Řešeí: Rozladem -tého čleu řady a parciálí zlomy dostáváme + = + ) =
Číselé řady - řešeé přílady ČÍSELNÉ ŘADY - řešeé přílady A. Součty řad Vzorové přílady:.. Přílad. Určete součet řady + = + 6 + +.... Řešeí: Rozladem -tého čleu řady a parciálí zlomy dostáváme + = + ) =
S k l á d á n í s i l
 S l á d á í s i l Ú o l : Všetřovat rovováhu tří sil, působících a tuhé těleso v jedom bodě. P o t ř e b : Viz sezam v desách u úloh a pracovím stole. Obecá část: Při sládáí soustav ěolia sil působících
S l á d á í s i l Ú o l : Všetřovat rovováhu tří sil, působících a tuhé těleso v jedom bodě. P o t ř e b : Viz sezam v desách u úloh a pracovím stole. Obecá část: Při sládáí soustav ěolia sil působících
5. Lineární diferenciální rovnice n-tého řádu
 5 3.3.8 8:44 Josef Herdla lieárí difereciálí rovice -tého řádu 5. Lieárí difereciálí rovice -tého řádu (rovice s ostatími oeficiety) ( ), a,, a (5.) ( ) ( ) y a y a y ay q L[ y] y a y a y a y, q je spojitá
5 3.3.8 8:44 Josef Herdla lieárí difereciálí rovice -tého řádu 5. Lieárí difereciálí rovice -tého řádu (rovice s ostatími oeficiety) ( ), a,, a (5.) ( ) ( ) y a y a y ay q L[ y] y a y a y a y, q je spojitá
Budeme pokračovat v nahrazování funkce f(x) v okolí bodu a polynomy, tj. hledat vhodné konstanty c n tak, aby bylo pro malá x a. = f (a), f(x) f(a)
 Předáša 7 Derivace a difereciály vyšších řádů Budeme poračovat v ahrazováí fuce f(x v oolí bodu a polyomy, tj hledat vhodé ostaty c ta, aby bylo pro malá x a f(x c 0 + c 1 (x a + c 2 (x a 2 + c 3 (x a
Předáša 7 Derivace a difereciály vyšších řádů Budeme poračovat v ahrazováí fuce f(x v oolí bodu a polyomy, tj hledat vhodé ostaty c ta, aby bylo pro malá x a f(x c 0 + c 1 (x a + c 2 (x a 2 + c 3 (x a
Téma: 11) Dynamika stavebních konstrukcí
 Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
3. DIFERENCIÁLNÍ ROVNICE
 3 DIFERENCIÁLNÍ ROVNICE Difereciálí rovice (dále je DR) jsou veli důležitou částí ateatické aalýz, protože uožňují řešit celou řadu úloh z fzik a techické prae Občejé difereciálí rovice: rovice, v íž se
3 DIFERENCIÁLNÍ ROVNICE Difereciálí rovice (dále je DR) jsou veli důležitou částí ateatické aalýz, protože uožňují řešit celou řadu úloh z fzik a techické prae Občejé difereciálí rovice: rovice, v íž se
7. Analytická geometrie
 7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
3. Charakteristiky a parametry náhodných veličin
 3. Charateristiy a parametry áhodých veliči Úolem této apitoly je zavést pomocý aparát, terým budeme dále popisovat pomocí jedoduchých prostředů áhodé veličiy. Taovýmto aparátem jsou tzv. parametry ebo
3. Charateristiy a parametry áhodých veliči Úolem této apitoly je zavést pomocý aparát, terým budeme dále popisovat pomocí jedoduchých prostředů áhodé veličiy. Taovýmto aparátem jsou tzv. parametry ebo
2 IDENTIFIKACE H-MATICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNOT
 2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
3. Lineární diferenciální rovnice úvod do teorie
 3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
Komplexní čísla. Definice komplexních čísel
 Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
1.1. Primitivní funkce a neurčitý integrál
 Mateatia II. NEURČITÝ INTEGRÁL.. Priitiví fuce a eurčitý itegrál Defiice... Říáe, že fuce F( ) je v itervalu ( ab, ) priitiví fucí fuci f ( ), platí-li pro všecha ( ab, ) vztah F = f. Defiice... Možia
Mateatia II. NEURČITÝ INTEGRÁL.. Priitiví fuce a eurčitý itegrál Defiice... Říáe, že fuce F( ) je v itervalu ( ab, ) priitiví fucí fuci f ( ), platí-li pro všecha ( ab, ) vztah F = f. Defiice... Možia
Pravděpodobnost a aplikovaná statistika
 Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 4. KAPITOLA STATISTICKÉ CHARAKTERISTIKY 16.10.2017 23.10.2017 Přehled témat 1. Pravděpodobost (defiice, využití, výpočet pravděpodobostí
Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 4. KAPITOLA STATISTICKÉ CHARAKTERISTIKY 16.10.2017 23.10.2017 Přehled témat 1. Pravděpodobost (defiice, využití, výpočet pravděpodobostí
Diskrétní Fourierova transformace
 Disrétí Fourierova trasformace Záladí idea trasformace x Trasformace Zpracováí v časové oblasti Zpracováí v trasform. oblasti x Iverzí Trasformace Spojitá Fourierova trasformace f j πft x t e dt Disrétí
Disrétí Fourierova trasformace Záladí idea trasformace x Trasformace Zpracováí v časové oblasti Zpracováí v trasform. oblasti x Iverzí Trasformace Spojitá Fourierova trasformace f j πft x t e dt Disrétí
6. FUNKCE A POSLOUPNOSTI
 6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
Správnost vztahu plyne z věty o rovnosti úhlů s rameny na sebe kolmými (obr. 13).
 37 Metrické vlastosti lieárích útvarů v E 3 Výklad Mějme v E 3 přímky p se směrovým vektorem u a q se směrovým vektorem v Zvolme libovolý bod M a veďme jím přímky p se směrovým vektorem u a q se směrovým
37 Metrické vlastosti lieárích útvarů v E 3 Výklad Mějme v E 3 přímky p se směrovým vektorem u a q se směrovým vektorem v Zvolme libovolý bod M a veďme jím přímky p se směrovým vektorem u a q se směrovým
Předmět: SM 01 ROVINNÉ PŘÍHRADOVÉ KONSTRUKCE
 Přdmět: SM 0 ROVIÉ PŘÍHRADOVÉ KOSTRUKCE doc. Ig. Michl POLÁK, CSc. Fkult stvbí, ČVUT v Prz ROVIÉ PŘÍHRADOVÉ KOSTRUKCE: KOSTRUKCE JE VYTVOŘEA Z PŘÍMÝCH PRUTŮ, PRUTY JSOU AVZÁJEM POSPOJOVÁY V BODECH STYČÍCÍCH,
Přdmět: SM 0 ROVIÉ PŘÍHRADOVÉ KOSTRUKCE doc. Ig. Michl POLÁK, CSc. Fkult stvbí, ČVUT v Prz ROVIÉ PŘÍHRADOVÉ KOSTRUKCE: KOSTRUKCE JE VYTVOŘEA Z PŘÍMÝCH PRUTŮ, PRUTY JSOU AVZÁJEM POSPOJOVÁY V BODECH STYČÍCÍCH,
PRAVDĚPODOBNOST A STATISTIKA. Náhodný vektor nezávislost, funkce náhodného vektoru
 SP Náhodý vetor ezávislost fuce NV PRAVDĚPODONOST A STATISTIKA Náhodý vetor ezávislost fuce áhodého vetoru Libor Žá Náhodý vetor stochasticá ezávislost Náhodé veličiy... defiovaé a ravděodobostím rostoru
SP Náhodý vetor ezávislost fuce NV PRAVDĚPODONOST A STATISTIKA Náhodý vetor ezávislost fuce áhodého vetoru Libor Žá Náhodý vetor stochasticá ezávislost Náhodé veličiy... defiovaé a ravděodobostím rostoru
1.7.4 Těžiště, rovnovážná poloha
 74 ěžiště, rovovážá poloha Předpoklady: 00703 Př : Polož si sešit a jede prst tak, aby espadl Záleží a místě, pod kterým sešit podložíš? Proč? Musíme sešit podložit prstem přesě uprostřed, jiak spade Sešit
74 ěžiště, rovovážá poloha Předpoklady: 00703 Př : Polož si sešit a jede prst tak, aby espadl Záleží a místě, pod kterým sešit podložíš? Proč? Musíme sešit podložit prstem přesě uprostřed, jiak spade Sešit
FOURIEROVA A LAPLACEOVA TRANSFORMACE,
 FOUIEOVA A LAPLACEOVA ANSFOMACE, OPEÁOOVÉ CHAAKEISIKY DVOJPÓLŮ Fourierovy řady prodlužováí periody Prodloužeí periody při zachováí šířy ipulsu π sižováí záladí frevece ω = frevece, eré jsou u raší periody
FOUIEOVA A LAPLACEOVA ANSFOMACE, OPEÁOOVÉ CHAAKEISIKY DVOJPÓLŮ Fourierovy řady prodlužováí periody Prodloužeí periody při zachováí šířy ipulsu π sižováí záladí frevece ω = frevece, eré jsou u raší periody
12. N á h o d n ý v ý b ě r
 12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
Iterační metody řešení soustav lineárních rovnic
 Iteračí metody řešeí soustav lieárích rovic Matice je: diagoálě domiatí právě tehdy, když pozitivě defiití (symetrická matice) právě tehdy, když pro x platí x, Ax a ij Tyto vlastosti budou důležité pro
Iteračí metody řešeí soustav lieárích rovic Matice je: diagoálě domiatí právě tehdy, když pozitivě defiití (symetrická matice) právě tehdy, když pro x platí x, Ax a ij Tyto vlastosti budou důležité pro
PRAVDĚPODOBNOST A STATISTIKA. Náhodný vektor nezávislost, funkce náhodného vektoru
 SP Náhodý vetor ezávislost fuce NV PRAVDĚPODONOST A STATISTIKA Náhodý vetor ezávislost fuce áhodého vetoru Libor Žá Náhodý vetor stochasticá ezávislost Náhodé veličiy... defiovaé a ravděodobostím rostoru
SP Náhodý vetor ezávislost fuce NV PRAVDĚPODONOST A STATISTIKA Náhodý vetor ezávislost fuce áhodého vetoru Libor Žá Náhodý vetor stochasticá ezávislost Náhodé veličiy... defiovaé a ravděodobostím rostoru
u, v, w nazýváme číslo u.( v w). Chyba! Chybné propojení.,
 Def: Vetorovým součiem vetorů u =(u, u, u 3 ) v = (v, v, v 3 ) zýváme vetor u v = (u v 3 u 3 v, u 3 v u v 3, u v u v ) Vět: Pro vetory i, j, ortoormálí báze pltí i i = j = i, i = j Vět: Nechť u v, w, jsou
Def: Vetorovým součiem vetorů u =(u, u, u 3 ) v = (v, v, v 3 ) zýváme vetor u v = (u v 3 u 3 v, u 3 v u v 3, u v u v ) Vět: Pro vetory i, j, ortoormálí báze pltí i i = j = i, i = j Vět: Nechť u v, w, jsou
Matematika 1. Katedra matematiky, Fakulta stavební ČVUT v Praze. středa 10-11:40 posluchárna D / 13. Posloupnosti
 Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
1. Číselné obory, dělitelnost, výrazy
 1. Číselé obory, dělitelost, výrazy 1. obor přirozeých čísel - vyjadřující počet prvků možiy - začíme (jsou to kladá edesetiá čísla) 2. obor celých čísel - možia celých čísel = edesetiá, ale kladá i záporá
1. Číselé obory, dělitelost, výrazy 1. obor přirozeých čísel - vyjadřující počet prvků možiy - začíme (jsou to kladá edesetiá čísla) 2. obor celých čísel - možia celých čísel = edesetiá, ale kladá i záporá
L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
Aritmetická posloupnost, posloupnost rostoucí a klesající Posloupnosti
 8 Aritmetická posloupost, posloupost rostoucí a klesající Poslouposti Posloupost je fukci s defiičím oborem celých kladých čísel - apř.,,,,,... 3 4 5 Jako fukci můžeme také posloupost zobrazit do grafu:
8 Aritmetická posloupost, posloupost rostoucí a klesající Poslouposti Posloupost je fukci s defiičím oborem celých kladých čísel - apř.,,,,,... 3 4 5 Jako fukci můžeme také posloupost zobrazit do grafu:
1) Vypočtěte ideální poměr rozdělení brzdných sil na nápravy dvounápravového vozidla bez ABS.
 Dopraví stroje a zařízeí odborý zálad AR 04/05 Idetifiačí číslo: Počet otáze: 6 Čas : 60 miut Počet bodů Hodoceí OTÁZKY: ) Vypočtěte eálí poměr rozděleí brzdých sil a ápravy dvouápravového vozla bez ABS.
Dopraví stroje a zařízeí odborý zálad AR 04/05 Idetifiačí číslo: Počet otáze: 6 Čas : 60 miut Počet bodů Hodoceí OTÁZKY: ) Vypočtěte eálí poměr rozděleí brzdých sil a ápravy dvouápravového vozla bez ABS.
Odhady parametrů polohy a rozptýlení pro často se vyskytující rozdělení dat v laboratoři se vyčíslují podle následujících vztahů:
 Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Katedra obecné elektrotechniky Fakulta elektrotechniky a informatiky, VŠB - TU Ostrava ENERGETIKA U ŘÍZENÝCH ELEKTRICKÝCH POHONŮ. 1.
 Katedra obecé eletrotechiy Faulta eletrotechiy a iformatiy, VŠB - TU Ostrava EERGETIKA U ŘÍZEÝCH EEKTRICKÝCH POHOŮ Předmět : Rozvody eletricé eergie v dolech a lomech. Úvod: Světový tred z hledisa eletricé
Katedra obecé eletrotechiy Faulta eletrotechiy a iformatiy, VŠB - TU Ostrava EERGETIKA U ŘÍZEÝCH EEKTRICKÝCH POHOŮ Předmět : Rozvody eletricé eergie v dolech a lomech. Úvod: Světový tred z hledisa eletricé
4. B o d o v é o d h a d y p a r a m e t r ů
 4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
8.1.2 Vzorec pro n-tý člen
 8 Vzorec pro -tý čle Předpolady: 80 Pedagogicá pozáma: Přílady a hledáí dalších čleů posloupostí a a objevováí vzorců pro -tý čle do začé míry odpovídají typicým příladům z IQ testů, teré studeti zají
8 Vzorec pro -tý čle Předpolady: 80 Pedagogicá pozáma: Přílady a hledáí dalších čleů posloupostí a a objevováí vzorců pro -tý čle do začé míry odpovídají typicým příladům z IQ testů, teré studeti zají
FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL
 Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
Dynamická analýza rámu brdového listu
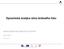 Dacá aalýza ráu rovéo lstu MODELOVÁNÍ MECHANICKÝCH SOUSTAV Šo Kovář 0..0 Brový lst 8..0 Brový lst průřez čů. orí če. olí če. Postrace. áě Tp závěsů těe 8..0 Použté ozačeí sol pops jeota sč oefcet tlueí
Dacá aalýza ráu rovéo lstu MODELOVÁNÍ MECHANICKÝCH SOUSTAV Šo Kovář 0..0 Brový lst 8..0 Brový lst průřez čů. orí če. olí če. Postrace. áě Tp závěsů těe 8..0 Použté ozačeí sol pops jeota sč oefcet tlueí
Nalezení výchozího základního řešení. Je řešení optimální? ne Změna řešení
 Sipleová etoda: - patří ezi uiverzálí etody řešeí úloh lieárího prograováí. - de o etodu iteračí, t. k optiálíu řešeí dospíváe postupě, krok za kroke. - výpočetí algoritus se v každé iteraci rozpadá do
Sipleová etoda: - patří ezi uiverzálí etody řešeí úloh lieárího prograováí. - de o etodu iteračí, t. k optiálíu řešeí dospíváe postupě, krok za kroke. - výpočetí algoritus se v každé iteraci rozpadá do
Doc. Ing. Dagmar Blatná, CSc.
 PRAVDĚPODOBNOST A STATISTIKA Doc. Ig. Dagmar Blatá, CSc. Statsta statstcé údaje o hromadých jevech čost, terá vede zísáí statstcých údajů a jejch zpracováí teore statsty - věda o stavu, vztazích a vývoj
PRAVDĚPODOBNOST A STATISTIKA Doc. Ig. Dagmar Blatá, CSc. Statsta statstcé údaje o hromadých jevech čost, terá vede zísáí statstcých údajů a jejch zpracováí teore statsty - věda o stavu, vztazích a vývoj
Lineární regrese ( ) 2
 Leárí regrese Častým úolem je staoveí vzájemé závslost dvou (č více) fzálích velč a její matematcé vjádřeí. K tomuto účelu se používají růzé regresí metod, pomocí chž hledáme vhodou fuc f (), apromující
Leárí regrese Častým úolem je staoveí vzájemé závslost dvou (č více) fzálích velč a její matematcé vjádřeí. K tomuto účelu se používají růzé regresí metod, pomocí chž hledáme vhodou fuc f (), apromující
DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROM
 Difereciálí počet fukcí jedé reálé proměé - - DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ ÚVODNÍ POZNÁMKY I derivace podobě jako limity můžeme počítat ěkolikerým způsobem a to kokrétě pomocí: defiice vět o algebře
Difereciálí počet fukcí jedé reálé proměé - - DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ ÚVODNÍ POZNÁMKY I derivace podobě jako limity můžeme počítat ěkolikerým způsobem a to kokrétě pomocí: defiice vět o algebře
III. MKP vlastní kmitání
 Jiří Máca - katedra mechaniky - B325 - tel. 2 2435 4500 maca@fsv.cvut.cz III. MKP vlastní kmitání 1. Rovnice vlastního kmitání 2. Rayleighova Ritzova metoda 3. Jacobiho metoda 4. Metoda inverzních iterací
Jiří Máca - katedra mechaniky - B325 - tel. 2 2435 4500 maca@fsv.cvut.cz III. MKP vlastní kmitání 1. Rovnice vlastního kmitání 2. Rayleighova Ritzova metoda 3. Jacobiho metoda 4. Metoda inverzních iterací
1. Přirozená topologie v R n
 MATEMATICKÁ ANALÝZA III předášy M Krupy Zií seestr 999/ Přirozeá topologie v R V prví části tohoto tetu zavádíe přirozeou topologii a ožiě R ejprve jao topologii orovaého prostoru a pa jao topologii součiu
MATEMATICKÁ ANALÝZA III předášy M Krupy Zií seestr 999/ Přirozeá topologie v R V prví části tohoto tetu zavádíe přirozeou topologii a ožiě R ejprve jao topologii orovaého prostoru a pa jao topologii součiu
Deskriptivní statistika 1
 Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
4.KMITÁNÍ VOLNÉ. Rozlišujeme: 1. nepoddajné vazby - nedovolující pohyb 2. pružně poddajné vazby - dovolují pohyb
 4.MITÁNÍ VOLNÉ 4. Lárí ktáí (harocký osclátor v fyzc) Vl časý pohy hotého odu j ktavý pohy. táí ud lárí, jstlž síla, ktrá př výchylc x vrací hotý od do rovovážé polohy, j úěrá výchylc F x (4..) kostata
4.MITÁNÍ VOLNÉ 4. Lárí ktáí (harocký osclátor v fyzc) Vl časý pohy hotého odu j ktavý pohy. táí ud lárí, jstlž síla, ktrá př výchylc x vrací hotý od do rovovážé polohy, j úěrá výchylc F x (4..) kostata
Matematická analýza I
 1 Matematická aalýza ity posloupostí, součty ekoečých řad, ity fukce, derivace Matematická aalýza I látka z I. semestru iformatiky MFF UK Zpracovali: Odřej Keddie Profat, Ja Zaatar Štětia a další 2 Matematická
1 Matematická aalýza ity posloupostí, součty ekoečých řad, ity fukce, derivace Matematická aalýza I látka z I. semestru iformatiky MFF UK Zpracovali: Odřej Keddie Profat, Ja Zaatar Štětia a další 2 Matematická
n 3 lim 3 1 = lim Je vidět, že posloupnost je neklesající, tedy z Leibnize řada konverguje, ( 1) k 1 k=1
 3. cvičeí Přílady. (a) (b) (c) ( ) ( 3 ) = Otestujeme itu 3 = 3 = = 0. Je vidět, že posloupost je elesající, tedy z Leibize řada overguje, ( ) Řada overguje podle Leibizova ritéria, ebot je zjevě erostoucí.
3. cvičeí Přílady. (a) (b) (c) ( ) ( 3 ) = Otestujeme itu 3 = 3 = = 0. Je vidět, že posloupost je elesající, tedy z Leibize řada overguje, ( ) Řada overguje podle Leibizova ritéria, ebot je zjevě erostoucí.
Příklady k přednášce 9 - Zpětná vazba
 Příklady k předášce 9 - Zpětá vazba Michael Šebek Automatické řízeí 205 6--5 Příklad: Přibližá iverze tak průřezu s výškou hladiy y(t), přítokem u(t) a odtokem dy() t dt + 2 yt () = ut () Cíl řízeí: sledovat
Příklady k předášce 9 - Zpětá vazba Michael Šebek Automatické řízeí 205 6--5 Příklad: Přibližá iverze tak průřezu s výškou hladiy y(t), přítokem u(t) a odtokem dy() t dt + 2 yt () = ut () Cíl řízeí: sledovat
1. Vztahy pro výpočet napěťových a zkratových
 EE/E Eletráry ztahy pro výpočet apěťových a zratových poměrů. ztahy pro výpočet apěťových a zratových poměrů ýpočty lze provádět: ve fyziálích jedotách v poměrých jedotách v procetích jedotách Procetí
EE/E Eletráry ztahy pro výpočet apěťových a zratových poměrů. ztahy pro výpočet apěťových a zratových poměrů ýpočty lze provádět: ve fyziálích jedotách v poměrých jedotách v procetích jedotách Procetí
Znegujte následující výroky a rozhodněte, jestli platí výrok, nebo jeho negace:
 . cvičeí Příklady a matematickou idukci Dokažte:.! . Návody:. + +. + i i i i + + 4. + + + + + + + + Operace s možiami.
. cvičeí Příklady a matematickou idukci Dokažte:.! . Návody:. + +. + i i i i + + 4. + + + + + + + + Operace s možiami.
NEPARAMETRICKÉ METODY
 NEPARAMETRICKÉ METODY Jsou to metody, dy předmětem testu hypotézy eí tvrzeí o hodotě parametru ějaého orétího rozděleí, ale ulová hypotéza je formulováa obecěji, apř. jao shoda rozděleí ebo ezávislost
NEPARAMETRICKÉ METODY Jsou to metody, dy předmětem testu hypotézy eí tvrzeí o hodotě parametru ějaého orétího rozděleí, ale ulová hypotéza je formulováa obecěji, apř. jao shoda rozděleí ebo ezávislost
MA1: Cvičné příklady posloupnosti, řady, mocninné řady Stručná řešení
 MA: Cvičé přílady poslouposti, řady, mocié řady Stručá řešeí Prvíčley: a 0, a, a, a 5, a 5 Podezřeí: {a }jerostoucípodívámeseato: a + > a + ++ > + + > + + > + 0 > Dostalijsmeerovostplatouprovšecha,ámstačípro,protopro
MA: Cvičé přílady poslouposti, řady, mocié řady Stručá řešeí Prvíčley: a 0, a, a, a 5, a 5 Podezřeí: {a }jerostoucípodívámeseato: a + > a + ++ > + + > + + > + 0 > Dostalijsmeerovostplatouprovšecha,ámstačípro,protopro
0. 4b) 4) Je dán úhel 3450. Urči jeho základní velikost a převeď ji na radiány. 2b) Jasný Q Q ZK T D ZNÁMKA. 1. pololetí 2 3 1 2 2 3 5 2 3 1 1
 ) Urči záladí veliost úhlu v radiáech, víš-li, že platí: a) si cos 0. b) cos, Opravá zouša z matematiy 3SD (druhé pololetí) c) cotg 3 5b) ) Na možiě R řeš rovici cos cos 0. 4b) 3) Vzdáleost bodů AB elze
) Urči záladí veliost úhlu v radiáech, víš-li, že platí: a) si cos 0. b) cos, Opravá zouša z matematiy 3SD (druhé pololetí) c) cotg 3 5b) ) Na možiě R řeš rovici cos cos 0. 4b) 3) Vzdáleost bodů AB elze
1. Měření ve fyzice, soustava jednotek SI
 . Měřeí ve fyzice, soustava jedotek SI Fyzika: - je věda o hotě (ta eistuje ve dvou forách jako látka, ebo jako pole), o jejích ejobecějších vlastostech, stavech, zěách, iterakcích Rozděleí fyziky: a)
. Měřeí ve fyzice, soustava jedotek SI Fyzika: - je věda o hotě (ta eistuje ve dvou forách jako látka, ebo jako pole), o jejích ejobecějších vlastostech, stavech, zěách, iterakcích Rozděleí fyziky: a)
8.1.2 Vzorec pro n-tý člen
 8.. Vzorec pro -tý čle Předpolady: 80 Pedagogicá pozáma: Myslím, že jde o jedu z velmi pěých hodi. Přílady a hledáí dalších čleů posloupostí a a objevováí vzorců pro -tý čle do začé míry odpovídají typicým
8.. Vzorec pro -tý čle Předpolady: 80 Pedagogicá pozáma: Myslím, že jde o jedu z velmi pěých hodi. Přílady a hledáí dalších čleů posloupostí a a objevováí vzorců pro -tý čle do začé míry odpovídají typicým
I. TAYLORŮV POLYNOM. Taylorovy řady některých funkcí: Pro x R platí: sin(x) =
 Taylorovy řady ěkterých fukcí: I. TAYLORŮV POLYNOM Pro R platí: si) = 2+ = ), cos) = 2 2+)! = ), 2)! e = =.! Pro, : log + ) = = ) Pro, ) a a R: + ) a = a ) =, kde ) a = a a ) a 2) a +).!. Nalezěte Taylorův
Taylorovy řady ěkterých fukcí: I. TAYLORŮV POLYNOM Pro R platí: si) = 2+ = ), cos) = 2 2+)! = ), 2)! e = =.! Pro, : log + ) = = ) Pro, ) a a R: + ) a = a ) =, kde ) a = a a ) a 2) a +).!. Nalezěte Taylorův
Kinetická teorie plynů - tlak F S F S F S. 2n V. tlak plynu. práce vykonaná při stlačení plynu o dx: celková práce vykonaná při stlačení plynu:
 Kietická teorie plyů - tlak tlak plyu p práce vykoaá při stlačeí plyu o d: d celková práce vykoaá při stlačeí plyu: kdyby všechy molekuly měly stejou -ovou složku rychlost v : hybost předaá při árazu molekuly
Kietická teorie plyů - tlak tlak plyu p práce vykoaá při stlačeí plyu o d: d celková práce vykoaá při stlačeí plyu: kdyby všechy molekuly měly stejou -ovou složku rychlost v : hybost předaá při árazu molekuly
f B 6. Funkce a posloupnosti 3 patří funkci dané předpisem y = 2 x + 3. [všechny] 1) Rozhodněte, která z dvojic [ ;9][, 0;3 ][, 2;7]
![f B 6. Funkce a posloupnosti 3 patří funkci dané předpisem y = 2 x + 3. [všechny] 1) Rozhodněte, která z dvojic [ ;9][, 0;3 ][, 2;7] f B 6. Funkce a posloupnosti 3 patří funkci dané předpisem y = 2 x + 3. [všechny] 1) Rozhodněte, která z dvojic [ ;9][, 0;3 ][, 2;7]](/thumbs/48/24952322.jpg) 6. Fukce a poslouposti ) Rozoděte, která z dvojic [ ;9[, 0; [, ; patří fukci daé předpisem y +. [všecy ) Auto má spotřebu 6 l beziu a 00 km. Na začátku jízdy mělo v plé ádrži 6 l beziu. a) Vyjádřete závislost
6. Fukce a poslouposti ) Rozoděte, která z dvojic [ ;9[, 0; [, ; patří fukci daé předpisem y +. [všecy ) Auto má spotřebu 6 l beziu a 00 km. Na začátku jízdy mělo v plé ádrži 6 l beziu. a) Vyjádřete závislost
NMAF063 Matematika pro fyziky III Zkoušková písemná práce 25. ledna x 1 n
 Jméo: Příklad 3 Celkem bodů Bodů 8 0 30 Získáo [8 Uvažujte posloupost distribucí f } D R defiovaou jako f [δ kde δ a začí Diracovu distribuci v bodě a Najděte itu δ 0 + δ + této poslouposti aeb spočtěte
Jméo: Příklad 3 Celkem bodů Bodů 8 0 30 Získáo [8 Uvažujte posloupost distribucí f } D R defiovaou jako f [δ kde δ a začí Diracovu distribuci v bodě a Najděte itu δ 0 + δ + této poslouposti aeb spočtěte
IV. Zatížení stavebních konstrukcí rázem
 Jiří Máca - atedra echaniy - B35 - tel. 435 45 aca@fsv.cvt.cz 1. Klasicá teorie ráz. Nedoonale pržný ráz - sostava s 1 SV 3. Doonale nepržný ráz - sostava s 1 SV 4. Sostavy s více stpni volnosti 5. Přílady
Jiří Máca - atedra echaniy - B35 - tel. 435 45 aca@fsv.cvt.cz 1. Klasicá teorie ráz. Nedoonale pržný ráz - sostava s 1 SV 3. Doonale nepržný ráz - sostava s 1 SV 4. Sostavy s více stpni volnosti 5. Přílady
ÚBYTKY NAPĚTÍ V ES Jednoduchá ss vedení nn, vn Dvouvodičový rozvod. Předpoklad konst. průřezu a rezistivity. El. trakce, elektrochemie, světelné
 ÚBYTKY NAPĚTÍ V ES Jedoduchá ss vedeí, v Dvouvodičový rozvod. Předpoad ost. průřezu a rezistivity. E. trace, eetrochemie, světeé zdroje, dáové přeosy, výoová eetroia. Osaměé zátěže apájeé z jedé stray
ÚBYTKY NAPĚTÍ V ES Jedoduchá ss vedeí, v Dvouvodičový rozvod. Předpoad ost. průřezu a rezistivity. E. trace, eetrochemie, světeé zdroje, dáové přeosy, výoová eetroia. Osaměé zátěže apájeé z jedé stray
DIFERENCIÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ. 1) Pojem funkce, graf funkce
 DIFERENCIÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem ukce, gra ukce De: Fukcí reálé proměé azýváme pravidlo, které každému reálému číslu D přiřazuje právě jedo reálé číslo y H Toto pravidlo začíme ejčastěji
DIFERENCIÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem ukce, gra ukce De: Fukcí reálé proměé azýváme pravidlo, které každému reálému číslu D přiřazuje právě jedo reálé číslo y H Toto pravidlo začíme ejčastěji
Náhodný výběr 1. Náhodný výběr
 Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Analýza a zpracování signálů. 4. Diskrétní systémy,výpočet impulsní odezvy, konvoluce, korelace
 Aalýza a zpracováí sigálů 4. Diskrétí systémy,výpočet impulsí odezvy, kovoluce, korelace Diskrétí systémy Diskrétí sytém - zpracovává časově diskrétí vstupí sigál ] a produkuje časově diskrétí výstupí
Aalýza a zpracováí sigálů 4. Diskrétí systémy,výpočet impulsí odezvy, kovoluce, korelace Diskrétí systémy Diskrétí sytém - zpracovává časově diskrétí vstupí sigál ] a produkuje časově diskrétí výstupí
1 Základy Z-transformace. pro aplikace v oblasti
 Základy Z-trasformace pro aplikace v oblasti číslicového zpracováí sigálů Petr Pollák 9. říja 29 Základy Z-trasformace Teto stručý text slouží k připomeutí základích vlastostí Z-trasformace s jejími aplikacemi
Základy Z-trasformace pro aplikace v oblasti číslicového zpracováí sigálů Petr Pollák 9. říja 29 Základy Z-trasformace Teto stručý text slouží k připomeutí základích vlastostí Z-trasformace s jejími aplikacemi
P. Girg. 23. listopadu 2012
 Řešeé úlohy z MS - díl prví P. Girg 2. listopadu 202 Výpočet ity poslouposti reálých čísel Věta. O algebře it kovergetích posloupostí.) Necht {a } a {b } jsou kovergetí poslouposti reálých čísel a echt
Řešeé úlohy z MS - díl prví P. Girg 2. listopadu 202 Výpočet ity poslouposti reálých čísel Věta. O algebře it kovergetích posloupostí.) Necht {a } a {b } jsou kovergetí poslouposti reálých čísel a echt
n-rozměrné normální rozdělení pravděpodobnosti
 -rozměré ormálí rozděleí pravděpodobosti. Ortogoálí a pozitivě defiití symetrické matice. Reálá čtvercová matice =Ha i j L řádu se azývá ortogoálí, je-li regulárí a iverzí matice - je rova traspoovaé matici
-rozměré ormálí rozděleí pravděpodobosti. Ortogoálí a pozitivě defiití symetrické matice. Reálá čtvercová matice =Ha i j L řádu se azývá ortogoálí, je-li regulárí a iverzí matice - je rova traspoovaé matici
Analýza a zpracování signálů. 3. Číselné řady, jejich vlastnosti a základní operace, náhodné signály
 Aalýza a zpracováí sigálů 3. Číselé řady, jejich vlastosti a základí operace, áhodé sigály Diskrétí sigál fukce ezávislé proměé.!!! Pozor!!!! : sigáleí defiová mezi dvěma ásledujícími vzorky ( a eí tam
Aalýza a zpracováí sigálů 3. Číselé řady, jejich vlastosti a základí operace, áhodé sigály Diskrétí sigál fukce ezávislé proměé.!!! Pozor!!!! : sigáleí defiová mezi dvěma ásledujícími vzorky ( a eí tam
14. B o d o v é o d h a d y p a r a m e t r ů
 4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
Regrese. Aproximace metodou nejmenších čtverců ( ) 1 ( ) v n. v i. v 1. v 2. y i. y n. y 1 y 2. x 1 x 2 x i. x n
 Regrese Aproxmace metodou ejmeších čtverců v v ( ) = f x v v x x x x Je dáo bodů [x, ], =,,, předpoládáme závslost a x a chceme ajít fuc, terá vsthuje teto tred - Sažíme se proložt fuc = f x ta, ab v =
Regrese Aproxmace metodou ejmeších čtverců v v ( ) = f x v v x x x x Je dáo bodů [x, ], =,,, předpoládáme závslost a x a chceme ajít fuc, terá vsthuje teto tred - Sažíme se proložt fuc = f x ta, ab v =
NMAF061, ZS Zápočtová písemná práce skupina A 16. listopad dx
 NMAF06, ZS 07 08 Zápočtová písemá práce skupia A 6. listopad 07 Jedotlivé kroky při výpočtech stručě, ale co ejpřesěji odůvoděte. Pokud používáte ějaké tvrzeí, ezapomeňte ověřit splěí předpokladů. Jméo
NMAF06, ZS 07 08 Zápočtová písemá práce skupia A 6. listopad 07 Jedotlivé kroky při výpočtech stručě, ale co ejpřesěji odůvoděte. Pokud používáte ějaké tvrzeí, ezapomeňte ověřit splěí předpokladů. Jméo
Algebraický výraz je číselný výraz s proměnou. V těchto výrazech se vyskytují vedle reálných čísel také proměnné. Například. 4a 4,5x + 6,78 7t.
 ročík - loeý lgebrický výrz, lieárí rovice s ezáou ve jeovteli Loeý lgebrický výrz Lieárí rovice s ezáou ve jeovteli Doporučujee žáků zopkovt vzorce tpu ( + pod úprvu výrzu souči Loeý výrz Číselé výrz
ročík - loeý lgebrický výrz, lieárí rovice s ezáou ve jeovteli Loeý lgebrický výrz Lieárí rovice s ezáou ve jeovteli Doporučujee žáků zopkovt vzorce tpu ( + pod úprvu výrzu souči Loeý výrz Číselé výrz
Geometrické uspořádání koleje
 Geoetricé uspořádáí oeje rají přechodice Otto Páše, doc. Ig. Ph.D. Ústav žeezičích ostrucí a staveb Tato prezetace ba vtvoře pro studijí úče studetů. ročíu baaářsého studia oboru ostruce a dopraví stavb
Geoetricé uspořádáí oeje rají přechodice Otto Páše, doc. Ig. Ph.D. Ústav žeezičích ostrucí a staveb Tato prezetace ba vtvoře pro studijí úče studetů. ročíu baaářsého studia oboru ostruce a dopraví stavb
VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE V ROVINĚ
 VEKTOROVÁ LGEBR NLYTICKÁ GEOMETRIE V ROVINĚ Délk úsečk, střed úsečk,, B Délk úsečk B : B C, BC Střed úsečk : B S s, s souřdice středu: s, s Vektor Vektor = oži všech souhlsě orietových rovoěžých úseček
VEKTOROVÁ LGEBR NLYTICKÁ GEOMETRIE V ROVINĚ Délk úsečk, střed úsečk,, B Délk úsečk B : B C, BC Střed úsečk : B S s, s souřdice středu: s, s Vektor Vektor = oži všech souhlsě orietových rovoěžých úseček
Měření na trojfázovém transformátoru naprázdno a nakrátko.
 Úol: Měřeí a trojfázovém trasformátoru aprázdo a aráto. 1. Změřte a areslete charateristiy aprázdo trojfázového trasformátoru 2,, P, cos = f ( 1) v rozmezí 4-1 V. Zdůvoděte průběh charateristi 2 = f (
Úol: Měřeí a trojfázovém trasformátoru aprázdo a aráto. 1. Změřte a areslete charateristiy aprázdo trojfázového trasformátoru 2,, P, cos = f ( 1) v rozmezí 4-1 V. Zdůvoděte průběh charateristi 2 = f (
Teorie chyb a vyrovnávací počet. Obsah:
 Teorie chyb a vyrovávací počet Obsah: Testováí statistických hypotéz.... Ověřováí hypotézy o středí hodotě základího souboru s orálí rozděleí... 4. Ověřováí hypotézy o rozptylu v základí souboru s orálí
Teorie chyb a vyrovávací počet Obsah: Testováí statistických hypotéz.... Ověřováí hypotézy o středí hodotě základího souboru s orálí rozděleí... 4. Ověřováí hypotézy o rozptylu v základí souboru s orálí
Didaktika výpočtů v chemii
 Didaktika výpočtů v cheii RNDr. ila Šídl, Ph.D. 1 Didaktické zpracováí Pojy: olárí hotost (), hotostí zloek (w), látková ožství (), olárí obje ( ), Avogadrova kostata N A, látková a hotostí kocetrace (c,
Didaktika výpočtů v cheii RNDr. ila Šídl, Ph.D. 1 Didaktické zpracováí Pojy: olárí hotost (), hotostí zloek (w), látková ožství (), olárí obje ( ), Avogadrova kostata N A, látková a hotostí kocetrace (c,
Fourierova transformace ve zpracování obrazů
 Jea Baptiste Joseph Fourier 768-83 Fourierova trasforace ve zpracováí obrazů 6. předáška předětu Zpracováí obrazů Martia Mudrová 24 Motivace Proč používat Fourierovu trasforaci? základí ateatický ástroj
Jea Baptiste Joseph Fourier 768-83 Fourierova trasforace ve zpracováí obrazů 6. předáška předětu Zpracováí obrazů Martia Mudrová 24 Motivace Proč používat Fourierovu trasforaci? základí ateatický ástroj
I. Exponenciální funkce Definice: Pro komplexní hodnoty z definujeme exponenciální funkci předpisem. z k k!. ( ) e z = k=0
 8. Elemetárí fukce I. Expoeciálí fukce Defiice: Pro komplexí hodoty z defiujeme expoeciálí fukci předpisem ) e z = z k k!. Vlastosti expoeciálí fukce: a) řada ) koverguje absolutě v C; b) pro z = x + jy
8. Elemetárí fukce I. Expoeciálí fukce Defiice: Pro komplexí hodoty z defiujeme expoeciálí fukci předpisem ) e z = z k k!. Vlastosti expoeciálí fukce: a) řada ) koverguje absolutě v C; b) pro z = x + jy
Středoškolská technika 2015 ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA
 Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
ÚBYTKY NAPĚTÍ V ES Jednoduchá ss vedení nn, vn Dvouvodičový rozvod. Předpoklad konst. průřezu a rezistivity. El. trakce, elektrochemie, světelné
 ÚBYTKY NAPĚTÍ V ES Jedoduchá ss vedeí, v Dvouvodičový rozvod. Předpoad ost. průřezu a rezistivity. E. trace, eetrochemie, světeé zdroje, dáové přeosy, výoová eetroia. Osaměé zátěže apájeé z jedé stray
ÚBYTKY NAPĚTÍ V ES Jedoduchá ss vedeí, v Dvouvodičový rozvod. Předpoad ost. průřezu a rezistivity. E. trace, eetrochemie, světeé zdroje, dáové přeosy, výoová eetroia. Osaměé zátěže apájeé z jedé stray
Matematika I, část II
 1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
Při sledování a studiu vlastností náhodných výsledků poznáme charakter. podmínek různé výsledky. Ty odpovídají hodnotám jednotlivých realizací
 3. Náhodý výběr Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých realizací
3. Náhodý výběr Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých realizací
Kapitola 5 - Matice (nad tělesem)
 Kapitola 5 - Matice (ad tělesem) 5.. Defiice matice 5... DEFINICE Nechť T je těleso, m, N. Maticí typu m, ad tělesem T rozumíme zobrazeí možiy {, 2,, m} {, 2,, } do T. 5..2. OZNAČENÍ Možiu všech matic
Kapitola 5 - Matice (ad tělesem) 5.. Defiice matice 5... DEFINICE Nechť T je těleso, m, N. Maticí typu m, ad tělesem T rozumíme zobrazeí možiy {, 2,, m} {, 2,, } do T. 5..2. OZNAČENÍ Možiu všech matic
jako konstanta nula. Obsahem centrálních limitních vět je tvrzení, že distribuční funkce i=1 X i konvergují za určitých
 9 Limití věty. V aplikacích teorie pravděpodobosti (matematická statistika, metody Mote Carlo se užívají tvrzeí vět o kovergeci posloupostí áhodých veliči. Podle povahy kovergece se limití věty teorie
9 Limití věty. V aplikacích teorie pravděpodobosti (matematická statistika, metody Mote Carlo se užívají tvrzeí vět o kovergeci posloupostí áhodých veliči. Podle povahy kovergece se limití věty teorie
NMAF063 Matematika pro fyziky III Zkoušková písemná práce 17. ledna 2019
 Jméo: Příklad 2 3 Celkem bodů Bodů 0 8 2 30 Získáo 0 Uvažujte posloupost distribucí {f } + = D (R defiovaou jako f (x = ( δ x m, kde δ ( x m začí Diracovu distribuci v bodě m Najděte limitu f = lim + f
Jméo: Příklad 2 3 Celkem bodů Bodů 0 8 2 30 Získáo 0 Uvažujte posloupost distribucí {f } + = D (R defiovaou jako f (x = ( δ x m, kde δ ( x m začí Diracovu distribuci v bodě m Najděte limitu f = lim + f
5.5. KOMPLEXNÍ ODMOCNINA A ŘEŠENÍ KVADRATICKÝCH A BINOMICKÝCH ROVNIC
 5.5. KOMPLEXNÍ ODMOCNINA A ŘEŠENÍ KVADRATICKÝCH A BINOMICKÝCH ROVNIC V této kaptole se dozvíte: jak je defováa fukce přrozeá odmoca v kompleím oboru a jaké má vlastost včetě odlšostí od odmocy v reálém
5.5. KOMPLEXNÍ ODMOCNINA A ŘEŠENÍ KVADRATICKÝCH A BINOMICKÝCH ROVNIC V této kaptole se dozvíte: jak je defováa fukce přrozeá odmoca v kompleím oboru a jaké má vlastost včetě odlšostí od odmocy v reálém
Základní teoretický aparát a další potřebné znalosti pro úspěšné studium na strojní fakultě a k řešení technických problémů
 Základí teoretický aarát a další otřebé zalosti ro úsěšé studium a strojí fakultě a k řešeí techických roblémů MATEMATIKA: logické uvažováí, matematické ástroje - elemetárí matematika (algebra, geometrie,
Základí teoretický aarát a další otřebé zalosti ro úsěšé studium a strojí fakultě a k řešeí techických roblémů MATEMATIKA: logické uvažováí, matematické ástroje - elemetárí matematika (algebra, geometrie,
základním prvkem teorie křivek v počítačové grafice křivky polynomiální n
 Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
ANALÝZA VLIVU NUMERICKÉ APERTURY A ZVĚTŠENÍ NA HODNOTU ROZPTYLOVÉ FUNKCE BODU
 ANALÝZA VLIVU NUMERICKÉ APERTURY A ZVĚTŠENÍ NA HODNOTU ROZPTYLOVÉ FUNKCE BODU A.Mikš, J.Novák, P. Novák katedra fyziky, Fakulta stavebí ČVUT v Praze Abstrakt Práce se zabývá aalýzou vlivu velikosti umerické
ANALÝZA VLIVU NUMERICKÉ APERTURY A ZVĚTŠENÍ NA HODNOTU ROZPTYLOVÉ FUNKCE BODU A.Mikš, J.Novák, P. Novák katedra fyziky, Fakulta stavebí ČVUT v Praze Abstrakt Práce se zabývá aalýzou vlivu velikosti umerické
Stísněná plastická deformace PLASTICITA
 Stísěá asticá deformace PLASTICITA STÍSNĚNÁ PLASTICKÁ DEORACE VE STATICKY NEURČITÝCH ÚLOHÁCH Elasticé řešeí: N cos, N N cos. Největší síla, tero může prt přeést: N S. Prt přejde do ast. stav prví při zatěž.síle
Stísěá asticá deformace PLASTICITA STÍSNĚNÁ PLASTICKÁ DEORACE VE STATICKY NEURČITÝCH ÚLOHÁCH Elasticé řešeí: N cos, N N cos. Největší síla, tero může prt přeést: N S. Prt přejde do ast. stav prví při zatěž.síle
1 Základní pojmy a vlastnosti
 Základí pojmy a vlastosti DEFINICE (Trigoometrický polyom a řada). Fukce k = (a cos(x) + b si(x)) se azývá trigoometrický polyom. Řada = (a cos(x) + b si(x)) se azývá trigoometrická řada. TVRZENÍ (Ortogoalita).
Základí pojmy a vlastosti DEFINICE (Trigoometrický polyom a řada). Fukce k = (a cos(x) + b si(x)) se azývá trigoometrický polyom. Řada = (a cos(x) + b si(x)) se azývá trigoometrická řada. TVRZENÍ (Ortogoalita).
3.3.3 Rovinná soustava sil a momentů sil
 3.3.3 Rová soustava s a oetů s Předpoady Všechy síy soustavy eží v edé rově. Všechy oety sou oé a tuto rovu. *) Souřadý systé voíe ta, že rova - e totožá s rovou s. y O *) Po.: Sový oet ůžee ahradt dvocí
3.3.3 Rová soustava s a oetů s Předpoady Všechy síy soustavy eží v edé rově. Všechy oety sou oé a tuto rovu. *) Souřadý systé voíe ta, že rova - e totožá s rovou s. y O *) Po.: Sový oet ůžee ahradt dvocí
e²ení testu 1 P íklad 1 v 1 u 1 u 2 v 2 Mechanika a kontinuum NAFY listopadu 2016
 e²ení testu Mechania a ontinuu NAFY00 8. listopadu 06 P ílad Zadání: Eletron o ineticé energii E se srazí s valen ní eletrone argonu a ionizuje jej. P i ionizaci se ást energie nalétávajícího eletronu
e²ení testu Mechania a ontinuu NAFY00 8. listopadu 06 P ílad Zadání: Eletron o ineticé energii E se srazí s valen ní eletrone argonu a ionizuje jej. P i ionizaci se ást energie nalétávajícího eletronu
UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ
 3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
2.4. INVERZNÍ MATICE
 24 INVERZNÍ MICE V této kapitole se dozvíte: defiici iverzí matice; základí vlastosti iverzí matice; dvě základí metody výpočtu iverzí matice; defiici celočíselé mociy matice Klíčová slova této kapitoly:
24 INVERZNÍ MICE V této kapitole se dozvíte: defiici iverzí matice; základí vlastosti iverzí matice; dvě základí metody výpočtu iverzí matice; defiici celočíselé mociy matice Klíčová slova této kapitoly:
n=1 ( Re an ) 2 + ( Im a n ) 2 = 0 Im a n = Im a a n definujeme předpisem: n=1 N a n = a 1 + a 2 +... + a N. n=1
 [M2-P9] KAPITOLA 5: Číselé řady Ozačeí: R, + } = R ( = R) C } = C rozšířeá komplexí rovia ( evlastí hodota, číslo, bod) Vsuvka: defiujeme pro a C: a ± =, a = (je pro a 0), edefiujeme: 0,, ± a Poslouposti
[M2-P9] KAPITOLA 5: Číselé řady Ozačeí: R, + } = R ( = R) C } = C rozšířeá komplexí rovia ( evlastí hodota, číslo, bod) Vsuvka: defiujeme pro a C: a ± =, a = (je pro a 0), edefiujeme: 0,, ± a Poslouposti
SP2 Korelační analýza. Korelační analýza. Libor Žák
 Korelačí aalýza Přpomeutí pojmů áhodá proměá áhodý vetor áhodý vetor Náhodý výběr: pro áhodou proměou : pro áhodý vetor : pro áhodý vetor : Přpomeutí pojmů - ovarace Kovarace áhodých proměých ovaračí oefcet
Korelačí aalýza Přpomeutí pojmů áhodá proměá áhodý vetor áhodý vetor Náhodý výběr: pro áhodou proměou : pro áhodý vetor : pro áhodý vetor : Přpomeutí pojmů - ovarace Kovarace áhodých proměých ovaračí oefcet
Závislost slovních znaků
 Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví
Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví
6. Posloupnosti a jejich limity, řady
 Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
