abuď ftaková T periodickáfunkce,žeplatí: Projekt1. Buď T= π 2 { cos(3t), je-li t 0, ... Projekt3. Buď T=4abuď ftaková T periodickáfunkce,žeplatí:
|
|
|
- Denis Radovan Toman
- před 10 lety
- Počet zobrazení:
Transkript
1 Projekt1. Buď T= 2 abuď ftaková T periodickáfunkce,žeplatí: { cos(3t je-li t 0, 6 2, je-li t 6, 2 ). Projekt2. Buď T=3abuď ftaková T periodickáfunkce,žeplatí: { 1+e t, je-li t 0,1 2, je-li t 1,3). Projekt3. Buď T=4abuď ftaková T periodickáfunkce,žeplatí: 0, je-li t 0,2 t 3, je-li t 2,3 2t 1, je-li t 3,4).
2 Projekt4. Buď T= abuď ftaková T periodickáfunkce,žeplatí: { cos(2t je-li t 0, 4 1, je-li t 4,). Projekt5. Buď T=2abuď ftaková T periodickáfunkce,žeplatí: { 1+e t, je-li t 0, 1 2 0, je-li t 1 2,2). Projekt6. Buď T=3abuď ftaková T periodickáfunkce,žeplatí: t+2, je-li t 0,1 2 t, je-li t 1,2 3, je-li t 2,3).
3 Projekt7. Buď T=3abuď ftaková T periodickáfunkce,žeplatí: { cos t, je-li t 0,, 2, je-li t (,3). Projekt8. Buď T=5abuď ftaková T periodickáfunkce,žeplatí: { 2e 3t, je-li t 0,3 0, je-li t 3,5). Projekt9. Buď T=2abuď ftaková T periodickáfunkce,žeplatí: 2, je-li t 0, 1 2 t 1, je-li t 1 2,1 3 t, je-li t 1,2).
4 Projekt10. Buď T= 2 abuď ftaková T periodickáfunkce,žeplatí: { sin(2t je-li t 0, 4 3, je-li t 4, 2 ). Projekt11. Buď T=2abuď ftaková T periodickáfunkce,žeplatí: { e 3t, je-li t 0,1 2, je-li t 1,2). Projekt12. Buď T=5abuď ftaková T periodickáfunkce,žeplatí: 3, je-li t 0,3 t 2, je-li t 3,4 1 t, je-li t 4,5).
5 Projekt13. Buď T= abuď ftaková T periodickáfunkce,žeplatí: { sin(2t je-li t 0, 2 3, je-li t 2,). Projekt14. Buď T=2abuď ftaková T periodickáfunkce,žeplatí: { 3e t, je-li t 0, 3 2 1, je-li t 3 2,2). Projekt15. Buď T=4abuď ftaková T periodickáfunkce,žeplatí: 0, je-li t 0,2 t+1, je-li t 2,3 2 t, je-li t 3,4).
6 Projekt16. Buď T= 3 2abuď ftaková T periodickáfunkce,žeplatí: { sin(2t je-li t 0, 4 1, je-li t 4,3 2 ). Projekt17. Buď T=2abuď ftaková T periodickáfunkce,žeplatí: { 1 e t, je-li t 0,1 2, je-li t 1,2). Projekt18. Buď T=3abuď ftaková T periodickáfunkce,žeplatí: 2, je-li t 0,1 t 2, je-li t 1,2 3 t, je-li t 2,3).
7 Projekt19. Buď T=2abuď ftaková T periodickáfunkce,žeplatí: { sin(2t je-li t 0, 2 1, je-li t 2,2). Projekt20. Buď T=3abuď ftaková T periodickáfunkce,žeplatí: { 3e 3t, je-li t 0,2 0, je-li t 2,3). Projekt21. Buď T=4abuď ftaková T periodickáfunkce,žeplatí: t+1, je-li t 0,1 0, je-li t 1,3 t+2, je-li t 3,4).
8 Projekt22. Buď T= abuď ftaková T periodickáfunkce,žeplatí: { cos(3t je-li t 0, 6 1, je-li t 6,). Projekt23. Buď T=3abuď ftaková T periodickáfunkce,žeplatí: { 2e t, je-li t 0,2 2, je-li t 2,3). Projekt24. Buď T=7abuď ftaková T periodickáfunkce,žeplatí: t 3, je-li t 0,3 2 t, je-li t 3,4 0, je-li t 4,7).
9 Projekt25. Buď T= 2 abuď ftaková T periodickáfunkce,žeplatí: { sint, je-li t 0, 4 2, je-li t 4, 2 ). Projekt26. Buď T=2abuď ftaková T periodickáfunkce,žeplatí: { 1 3e 3t, je-li t 0,1 1, je-li t 1,2). Projekt27. Buď T=6abuď ftaková T periodickáfunkce,žeplatí: 0, je-li t 0,4 t+1, je-li t 4,5 2t 1, je-li t 5,6).
10 Projekt28. Buď T=3abuď ftaková T periodickáfunkce,žeplatí: { cos t, je-li t 0, 2 1, je-li t 2,3). Projekt29. Buď T=4abuď ftaková T periodickáfunkce,žeplatí: { 1+2e t, je-li t 0,1, 2, je-li t (1,4). Projekt30. Buď T=8abuď ftaková T periodickáfunkce,žeplatí: 1 t, je-li t 0,1 t 2, je-li t 1,2 0, je-li t 2,8).
6. URČITÝ INTEGRÁL Výpočet určitého integrálu Úlohy k samostatnému řešení... 68
 Sbírka úloh z matematik 6. URČITÝ INTEGRÁL... 68 6.. Výpočet určitého integrálu... 68 Úloh k samostatnému řešení... 68 6.. Geometrické aplikace... 69 6... Obsah rovinného obrazce... 69 Úloh k samostatnému
Sbírka úloh z matematik 6. URČITÝ INTEGRÁL... 68 6.. Výpočet určitého integrálu... 68 Úloh k samostatnému řešení... 68 6.. Geometrické aplikace... 69 6... Obsah rovinného obrazce... 69 Úloh k samostatnému
x 2 +1 x 3 3x 2 4x = x 2 +3
 I. Určitý integrál I.. Eistence určitých integrálů Zjistěte, zda eistují určité integrály : Příklad. + + d Řešení : Ano eistuje, protože funkce f() + + je spojitá na intervalu,. Příklad. + 4 d Řešení :
I. Určitý integrál I.. Eistence určitých integrálů Zjistěte, zda eistují určité integrály : Příklad. + + d Řešení : Ano eistuje, protože funkce f() + + je spojitá na intervalu,. Příklad. + 4 d Řešení :
11. KŘIVKOVÝ INTEGRÁL Křivkový integrál I. druhu Úlohy k samostatnému řešení
 Sbíra úloh z matematia 11 Křivový integrál 11 KŘIVKOVÝ INTEGRÁL 115 111 Křivový integrál I druhu 115 Úloh samostatnému řešení 115 11 Křivový integrál II druhu 116 Úloh samostatnému řešení 116 11 Greenova
Sbíra úloh z matematia 11 Křivový integrál 11 KŘIVKOVÝ INTEGRÁL 115 111 Křivový integrál I druhu 115 Úloh samostatnému řešení 115 11 Křivový integrál II druhu 116 Úloh samostatnému řešení 116 11 Greenova
1c. Prohlášení provozovatele potravinářského podniku o lihovině uvedené na trh v České republice, která byla vyrobena mimo území České republiky
 Mount Gay rum L2311 0,7 40% 60 16,8 Barbados Connexion International B.V. Sint Jansstraat 2h, Groningen, Holandsko 27.9.2012 Mount Gay rum L2990 0,7 40% 60 16,8 Barbados Connexion International B.V. Sint
Mount Gay rum L2311 0,7 40% 60 16,8 Barbados Connexion International B.V. Sint Jansstraat 2h, Groningen, Holandsko 27.9.2012 Mount Gay rum L2990 0,7 40% 60 16,8 Barbados Connexion International B.V. Sint
VÝKON V HARMONICKÉM USTÁLENÉM STAVU
 VÝKON V HARMONICKÉM USTÁLENÉM STAVU Základní představa: Rezistor: proud, procházející rezistorem, ho zahřívá, energie, dodaná rezistoru, se tak nevratně mění na teplo Kapacitor: pokud ke kondenzátoru připojíme
VÝKON V HARMONICKÉM USTÁLENÉM STAVU Základní představa: Rezistor: proud, procházející rezistorem, ho zahřívá, energie, dodaná rezistoru, se tak nevratně mění na teplo Kapacitor: pokud ke kondenzátoru připojíme
Cvi ení 3. Cvi ení 3. Modelování systém a proces. Mgr. Lucie Kárná, PhD. March 28, 2017
 Modelování systém a proces Mgr. Lucie Kárná, PhD karna@fd.cvut.cz March 28, 2017 1 Jednoduché modely 2 Modelování diferenciálních rovnic 3 Model ovce a vlci Jednoduché modely Jednoduchý p íklad Namodelujte
Modelování systém a proces Mgr. Lucie Kárná, PhD karna@fd.cvut.cz March 28, 2017 1 Jednoduché modely 2 Modelování diferenciálních rovnic 3 Model ovce a vlci Jednoduché modely Jednoduchý p íklad Namodelujte
Cvi ení 5 Simulink. Cvi ení 5 Simulink. Modelování systém a proces. Lucie Kárná. March 26, 2018
 Cvi ení 5 Simulink Modelování systém a proces Lucie Kárná karna@fd.cvut.cz March 26, 2018 1 Jednoduché modely Archimédova spirála Logaritmická spirála Asteroida Cykloida 2 Modelování diferenciálních rovnic
Cvi ení 5 Simulink Modelování systém a proces Lucie Kárná karna@fd.cvut.cz March 26, 2018 1 Jednoduché modely Archimédova spirála Logaritmická spirála Asteroida Cykloida 2 Modelování diferenciálních rovnic
9. cvičení z Matematické analýzy 2
 9. cvičení z Matematické analýzy 7. listopadu -. prosince 7 9. Určete Fourierovu řadu periodického rozšíření funkce ft = t na, a její součet. Definice: Necht f je -periodická funkce, která je integrabilní
9. cvičení z Matematické analýzy 7. listopadu -. prosince 7 9. Určete Fourierovu řadu periodického rozšíření funkce ft = t na, a její součet. Definice: Necht f je -periodická funkce, která je integrabilní
sin(x) x lim. pomocí mocninné řady pro funkci sin(x) se středem x 0 = 0. Víme, že ( ) k=0 e x2 dx.
 Použití mocniných řad Nejprve si ukážeme dvě jednoduchá použití Taylorových řad. Příklad Spočtěte následující limitu: ( ) sin(x) lim. x x ( ) Najdeme lim sin(x) x x pomocí mocninné řady pro funkci sin(x)
Použití mocniných řad Nejprve si ukážeme dvě jednoduchá použití Taylorových řad. Příklad Spočtěte následující limitu: ( ) sin(x) lim. x x ( ) Najdeme lim sin(x) x x pomocí mocninné řady pro funkci sin(x)
Základní topologické pojmy:
 Křivky Marie Ennemond Camille Jordan (88 9): Křivka je množina bodů, která je surjektivním obrazem nějakého intervalu Giuseppe Peano (858 9): Zobrazení intervalu na čtverec Wacław Franciszek Sierpiński
Křivky Marie Ennemond Camille Jordan (88 9): Křivka je množina bodů, která je surjektivním obrazem nějakého intervalu Giuseppe Peano (858 9): Zobrazení intervalu na čtverec Wacław Franciszek Sierpiński
Obchodní název lihoviny: Kategorie lihoviny: Číslo šarže/datum výroby: Ballantines 12 YO Whisky LKAD2695
 Ballantines 12 YO Whisky LKAD2695 1 40% 48 19,2 14.11.2012 Ballantines 12 YO Whisky LPAD2141 1 40% 12 4,8 29.1.2013 Ballantines 12 YO Whisky LKAG1329 1 40% 12 4,8 8.7.2013 Ballantines 12 YO Whisky LKAG1696
Ballantines 12 YO Whisky LKAD2695 1 40% 48 19,2 14.11.2012 Ballantines 12 YO Whisky LPAD2141 1 40% 12 4,8 29.1.2013 Ballantines 12 YO Whisky LKAG1329 1 40% 12 4,8 8.7.2013 Ballantines 12 YO Whisky LKAG1696
Přechodné děje 2. řádu v časové oblasti
 Přechodné děje 2. řádu v časové oblasti EO2 Přednáška 8 Pavel Máša - Přechodné děje 2. řádu ÚVODEM Na předchozích přednáškách jsme se seznámili s obecným postupem řešení přechodných dějů, jmenovitě pak
Přechodné děje 2. řádu v časové oblasti EO2 Přednáška 8 Pavel Máša - Přechodné děje 2. řádu ÚVODEM Na předchozích přednáškách jsme se seznámili s obecným postupem řešení přechodných dějů, jmenovitě pak
V. Zatížení stavebních konstrukcí stroji
 Jiří Máca - katedra mechaniky - B325 - tel. 2 2435 4500 maca@fsv.cvut.cz V. Zatížení stavebních konstrukcí stroji 1. Typy základových konstrukcí 2. Budicí síly 3. Výpočet odezvy 4. Zmenšování dynamických
Jiří Máca - katedra mechaniky - B325 - tel. 2 2435 4500 maca@fsv.cvut.cz V. Zatížení stavebních konstrukcí stroji 1. Typy základových konstrukcí 2. Budicí síly 3. Výpočet odezvy 4. Zmenšování dynamických
1 Modelování systémů 2. řádu
 OBSAH Obsah 1 Modelování systémů 2. řádu 1 2 Řešení diferenciální rovnice 3 3 Ukázka řešení č. 1 9 4 Ukázka řešení č. 2 11 5 Ukázka řešení č. 3 12 6 Ukázka řešení č. 4 14 7 Ukázka řešení č. 5 16 8 Ukázka
OBSAH Obsah 1 Modelování systémů 2. řádu 1 2 Řešení diferenciální rovnice 3 3 Ukázka řešení č. 1 9 4 Ukázka řešení č. 2 11 5 Ukázka řešení č. 3 12 6 Ukázka řešení č. 4 14 7 Ukázka řešení č. 5 16 8 Ukázka
Tématické celky { kontrolní otázky.
 Tématické celky kontrolní otázky. Základy teorie pravdìpodobnosti..pravdìpodobnostní míra základní pojmy... Vysvìtlete pojem náhody, náhodného pokusu, náhodného jevu a jeho mno- ¾inovou interpretaci. Popi¹te
Tématické celky kontrolní otázky. Základy teorie pravdìpodobnosti..pravdìpodobnostní míra základní pojmy... Vysvìtlete pojem náhody, náhodného pokusu, náhodného jevu a jeho mno- ¾inovou interpretaci. Popi¹te
Seznámíte se s další aplikací určitého integrálu výpočtem obsahu pláště rotačního tělesa.
 .4. Obsh pláště otčního těles.4. Obsh pláště otčního těles Cíle Seznámíte se s dlší plikcí učitého integálu výpočtem obshu pláště otčního těles. Předpokládné znlosti Předpokládáme, že jste si postudovli
.4. Obsh pláště otčního těles.4. Obsh pláště otčního těles Cíle Seznámíte se s dlší plikcí učitého integálu výpočtem obshu pláště otčního těles. Předpokládné znlosti Předpokládáme, že jste si postudovli
MATEMATIKA PŘÍKLADY NA PROCVIČENÍ Parametrický popis křivek
 MATEMATIKA ŘÍKLADY NA RCVIČENÍ arametrický ois křivek 1 Jedánakřivka k(t)=[t t+ ; t 3 3t], t R. Nakresletečástkřivk kro t 3 ;3.Naišterovnicetečenkřivkvbodech k( 1), k(1) a k(). Dosazením několika hodnot
MATEMATIKA ŘÍKLADY NA RCVIČENÍ arametrický ois křivek 1 Jedánakřivka k(t)=[t t+ ; t 3 3t], t R. Nakresletečástkřivk kro t 3 ;3.Naišterovnicetečenkřivkvbodech k( 1), k(1) a k(). Dosazením několika hodnot
HARMONICKÝ USTÁLENÝ STAV - FÁZOR, IMPEDANCE
 HAMONICKÝ USTÁLENÝ STAV - FÁZO, IMPEDANCE Úvodem Fyzikální popis induktoru a kapacitoru vede na integrodiferenciální rovnice, jejichž řešení je značně obtížné, zvláště v případě soustav rovnic. Příklad
HAMONICKÝ USTÁLENÝ STAV - FÁZO, IMPEDANCE Úvodem Fyzikální popis induktoru a kapacitoru vede na integrodiferenciální rovnice, jejichž řešení je značně obtížné, zvláště v případě soustav rovnic. Příklad
[obrázek γ nepotřebujeme, interval t, zřejmý, integrací polynomu a per partes vyjde: (e2 + e) + 2 ln 2. (e ln t = t) ] + y2
![[obrázek γ nepotřebujeme, interval t, zřejmý, integrací polynomu a per partes vyjde: (e2 + e) + 2 ln 2. (e ln t = t) ] + y2 [obrázek γ nepotřebujeme, interval t, zřejmý, integrací polynomu a per partes vyjde: (e2 + e) + 2 ln 2. (e ln t = t) ] + y2](/thumbs/102/153207878.jpg) 4.1 Křivkový integrál ve vektrovém poli přímým výpočtem 4.1 Spočítejte práci síly F = y i + z j + x k při pohybu hmotného bodu po orientované křivce, která je dána jako oblouk ABC na průnikové křivce ploch
4.1 Křivkový integrál ve vektrovém poli přímým výpočtem 4.1 Spočítejte práci síly F = y i + z j + x k při pohybu hmotného bodu po orientované křivce, která je dána jako oblouk ABC na průnikové křivce ploch
3. AMPLITUDOVĚ MODULOVANÉ SIGNÁLY
 3. AMPLITUDOVĚ MODULOVANÉ SIGNÁLY Modulací nazýváme proces při kterém je jedním signálem přetvář en jiný signál za účelem př enosu informace. Př i amplitudové modulaci dochází k ovlivňování amplitudy nosného
3. AMPLITUDOVĚ MODULOVANÉ SIGNÁLY Modulací nazýváme proces při kterém je jedním signálem přetvář en jiný signál za účelem př enosu informace. Př i amplitudové modulaci dochází k ovlivňování amplitudy nosného
Smysl otáčení. Aplikace. Pravotočivá
 Šroubovice Definice Šroubovice je křivka generovaná bodem A, který se otáčí kolem dané přímky o a zároveň se posouvá podél této přímky, oboje rovnoměrnou rychlostí. Pohyb bodu A šroubový pohyb Přímka o
Šroubovice Definice Šroubovice je křivka generovaná bodem A, který se otáčí kolem dané přímky o a zároveň se posouvá podél této přímky, oboje rovnoměrnou rychlostí. Pohyb bodu A šroubový pohyb Přímka o
Zimní semestr akademického roku 2014/ prosince 2014
 Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 24/25 2. prosince 24 Předmluva iii
Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 24/25 2. prosince 24 Předmluva iii
Veronika Chrastinová, Oto Přibyl
 Integrální počet II. Příklady s nápovědou. Veronika Chrastinová, Oto Přibyl 16. září 2003 Ústav matematiky a deskriptivní geometrie FAST VUT Brno Obsah 1 Dvojný integrál 3 2 Trojný integrál 7 3 Křivkový
Integrální počet II. Příklady s nápovědou. Veronika Chrastinová, Oto Přibyl 16. září 2003 Ústav matematiky a deskriptivní geometrie FAST VUT Brno Obsah 1 Dvojný integrál 3 2 Trojný integrál 7 3 Křivkový
IV. Zatížení stavebních konstrukcí rázem
 Jiří Máca - atedra echaniy - B35 - tel. 435 45 aca@fsv.cvt.cz 1. Klasicá teorie ráz. Nedoonale pržný ráz - sostava s 1 SV 3. Doonale nepržný ráz - sostava s 1 SV 4. Sostavy s více stpni volnosti 5. Přílady
Jiří Máca - atedra echaniy - B35 - tel. 435 45 aca@fsv.cvt.cz 1. Klasicá teorie ráz. Nedoonale pržný ráz - sostava s 1 SV 3. Doonale nepržný ráz - sostava s 1 SV 4. Sostavy s více stpni volnosti 5. Přílady
Funkce komplexní proměnné a integrální transformace
 Funkce komplexní proměnné a integrální transformace Fourierovy řady I. Marek Lampart Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.07/2.2.00/07.0332), na
Funkce komplexní proměnné a integrální transformace Fourierovy řady I. Marek Lampart Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.07/2.2.00/07.0332), na
Úvod do programu MAXIMA
 Jedná se o rozpracovaný návod k programu wxmaxima pro naprosté začátečníky. Návod lze libovolně kopírovat a používat ke komerčním i osobním účelům. Momentálně chybí mnoho důležitých kapitol které budou
Jedná se o rozpracovaný návod k programu wxmaxima pro naprosté začátečníky. Návod lze libovolně kopírovat a používat ke komerčním i osobním účelům. Momentálně chybí mnoho důležitých kapitol které budou
Soustavy lineárních rovnic
 Soustavy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních diferenciálních rovnic y = a (x)y + a (x)y + + a n (x)y n + f (x) y = a (x)y + a (x)y + + a n (x)y n + f (x). y n = a
Soustavy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních diferenciálních rovnic y = a (x)y + a (x)y + + a n (x)y n + f (x) y = a (x)y + a (x)y + + a n (x)y n + f (x). y n = a
Parametrické rovnice křivek
 Parametrické rovnice křivek Kreslení křivek a tečný vektor Parametrizace křivek, tečna ke křivce. p.1/8 Kreslení křivek a tečný vektor Příklad 6.1.1 Máme křivku K zadanou parametrickými rovnicemi K : x
Parametrické rovnice křivek Kreslení křivek a tečný vektor Parametrizace křivek, tečna ke křivce. p.1/8 Kreslení křivek a tečný vektor Příklad 6.1.1 Máme křivku K zadanou parametrickými rovnicemi K : x
0 = 2e 1 (z 3 1)dz + 3z. z=0 z 3 4z 2 + 3z + rez. 4. Napište Fourierův rozvoj vzhledem k trigonometrickému systému periodickému
 2 1 1 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1 x 1 2 Jméno a příjmení: ID.č. 9.5.2016 1. Řešte diferenciální rovnici: y + 2xy x 2 + 3 = sin x x 2 + 3. y = C cos x x 2 + 1 2. Vypočtěte z 2 e z dz, kde je křivka
2 1 1 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1 x 1 2 Jméno a příjmení: ID.č. 9.5.2016 1. Řešte diferenciální rovnici: y + 2xy x 2 + 3 = sin x x 2 + 3. y = C cos x x 2 + 1 2. Vypočtěte z 2 e z dz, kde je křivka
Laboratorní měření 1. Seznam použitých přístrojů. Popis měřicího přípravku
 Laboratorní měření 1 Seznam použitých přístrojů 1. Generátor funkcí 2. Analogový osciloskop 3. Měřící přípravek na RL ČVUT FEL, katedra Teorie obvodů Popis měřicího přípravku Přípravek umožňuje jednoduchá
Laboratorní měření 1 Seznam použitých přístrojů 1. Generátor funkcí 2. Analogový osciloskop 3. Měřící přípravek na RL ČVUT FEL, katedra Teorie obvodů Popis měřicího přípravku Přípravek umožňuje jednoduchá
Management rekreace a sportu. 10. Derivace
 Derivace Derivace Před mnoha lety se matematici snažily o obecné vyřešení úlohy, jak sestrojit tečnu k dané křivce a také yzici zápolili s problémem určení rychlosti nerovnoměrného pohybu K zásadnímu obratu
Derivace Derivace Před mnoha lety se matematici snažily o obecné vyřešení úlohy, jak sestrojit tečnu k dané křivce a také yzici zápolili s problémem určení rychlosti nerovnoměrného pohybu K zásadnímu obratu
NÁHODNÁ VELIČINA. 3. cvičení
 NÁHODNÁ VELIČINA 3. cvičení Náhodná veličina Náhodná veličina funkce, která každému výsledku náhodného pokusu přiřadí reálné číslo. Je to matematický model popisující více či méně dobře realitu, který
NÁHODNÁ VELIČINA 3. cvičení Náhodná veličina Náhodná veličina funkce, která každému výsledku náhodného pokusu přiřadí reálné číslo. Je to matematický model popisující více či méně dobře realitu, který
x 2(A), x y (A) y x (A), 2 f
 II.10. Etrém funkcí Věta (nutná podmínka pro lokální etrém). Necht funkce f(, ) je diferencovatelná v bodě A. Má-li funkce f v bodě A lokální etrém, pak gradf(a) = 0. Onačme hlavní minor matice druhých
II.10. Etrém funkcí Věta (nutná podmínka pro lokální etrém). Necht funkce f(, ) je diferencovatelná v bodě A. Má-li funkce f v bodě A lokální etrém, pak gradf(a) = 0. Onačme hlavní minor matice druhých
KMS cvičení 6. Ondřej Marek
 KMS cvičení 6 Ondřej Marek NETLUMENÝ ODDAJNÝ SYSTÉM S DOF analytické řešení k k Systém se stupni volnosti popisují pohybové rovnice: x m m x m x + k + k x k x = m x k x + k x = k x m x k x x m k x x m
KMS cvičení 6 Ondřej Marek NETLUMENÝ ODDAJNÝ SYSTÉM S DOF analytické řešení k k Systém se stupni volnosti popisují pohybové rovnice: x m m x m x + k + k x k x = m x k x + k x = k x m x k x x m k x x m
ŠPANĚLSKO AKCE - LAST MINUTE. Costa Brava - AKCE FORTUNA **/*** AUTOKAREM - 7denní pobyt. Cena za osobu. neděle 9.8.15. pátek 31.7.
 pátek 31.7.15 neděle 9.8.15 VYPRODÁNO 10 990,- POLOPENZE šv. stůl 12 190,- pátek 7.8.15 neděle 16.8.15 POLOPENZE šv. stůl 10 990,- POLOPENZE šv. stůl 12 390,- pátek 14.8.15 POLOPENZE šv. stůl 10 990,-
pátek 31.7.15 neděle 9.8.15 VYPRODÁNO 10 990,- POLOPENZE šv. stůl 12 190,- pátek 7.8.15 neděle 16.8.15 POLOPENZE šv. stůl 10 990,- POLOPENZE šv. stůl 12 390,- pátek 14.8.15 POLOPENZE šv. stůl 10 990,-
Vlnová teorie. Ing. Bc. Michal Malík, Ing. Bc. Jiří Primas. TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií
 Ing. Bc. Michl Mlík, Ing. Bc. Jiří Prims ECHNICKÁ UNIVERZIA V LIBERCI Fkult mechtroniky, informtiky mezioborových studií ento mteriál vznikl v rámci projektu ESF CZ.1.7/../7.47, který je spolufinncován
Ing. Bc. Michl Mlík, Ing. Bc. Jiří Prims ECHNICKÁ UNIVERZIA V LIBERCI Fkult mechtroniky, informtiky mezioborových studií ento mteriál vznikl v rámci projektu ESF CZ.1.7/../7.47, který je spolufinncován
Moravské gymnázium Brno s.r.o. Mgr. Věra Jeřábková, Mgr. Marie Chadimová. Matematika, Goniometrické funkce v pravoúhlém trojúhelníku
 Číslo projektu CZ.1.07/1.5.00/34.0743 Název školy Moravské gymnázium Brno s.r.o. Autor Mgr. Věra Jeřábková, Mgr. Marie Chadimová Tematická oblast Matematika, Goniometrické funkce v pravoúhlém trojúhelníku
Číslo projektu CZ.1.07/1.5.00/34.0743 Název školy Moravské gymnázium Brno s.r.o. Autor Mgr. Věra Jeřábková, Mgr. Marie Chadimová Tematická oblast Matematika, Goniometrické funkce v pravoúhlém trojúhelníku
Lineární algebra s Matlabem cvičení 3
 Lineární algebra s Matlabem cvičení 3 Grafika v Matlabu Základní příkazy figure o vytvoří prázdné okno grafu hold on/hold off o zapne/vypne možnost kreslení více funkcí do jednoho grafu ezplot o slouží
Lineární algebra s Matlabem cvičení 3 Grafika v Matlabu Základní příkazy figure o vytvoří prázdné okno grafu hold on/hold off o zapne/vypne možnost kreslení více funkcí do jednoho grafu ezplot o slouží
Metodika zpracování bakalářských a diplomových prací. Zdeněk Plíva Jindra Drábková Jan Koprnický Leoš Petržílka
 Metodika zpracování bakalářských a diplomových prací Zdeněk Plíva Jindra Drábková Jan Koprnický Leoš Petržílka Liberec 2014 2 Times New Roman Century Cambria Garamond Myriad Pro Calibri Arial
Metodika zpracování bakalářských a diplomových prací Zdeněk Plíva Jindra Drábková Jan Koprnický Leoš Petržílka Liberec 2014 2 Times New Roman Century Cambria Garamond Myriad Pro Calibri Arial
Analytická geometrie přímky, roviny (opakování středoškolské látky) = 0. Napište obecnou rovnici. 8. Jsou dány body A [ 2,3,
 Analytická geometrie přímky roviny opakování středoškolské látk Jsou dány body A [ ] B [ 5] a C [ 6] a) přímky AB b) osy úsečky AB c) přímky na které leží výška vc trojúhelníka ABC d) přímky na které leží
Analytická geometrie přímky roviny opakování středoškolské látk Jsou dány body A [ ] B [ 5] a C [ 6] a) přímky AB b) osy úsečky AB c) přímky na které leží výška vc trojúhelníka ABC d) přímky na které leží
Podmínka samosvornosti:
 Šroubové spoje Šroubové spoje patří mezi rozebíratelné spojení strojních součástí. Šrouby se podle funkce dělí na šrouby spojovací a pohybové. Spojovací šrouby se používají pro pevné spojení dvou nebo
Šroubové spoje Šroubové spoje patří mezi rozebíratelné spojení strojních součástí. Šrouby se podle funkce dělí na šrouby spojovací a pohybové. Spojovací šrouby se používají pro pevné spojení dvou nebo
Fázory, impedance a admitance
 Fázory, impedance a admitance 1 Dva harmonické zdroje napětí s frekvencí jsou zapojeny sériově a S použitím fázorů vypočítejte časový průběh napětí mezi výstupními svorkami, jestliže = 30 sin(100¼t);u
Fázory, impedance a admitance 1 Dva harmonické zdroje napětí s frekvencí jsou zapojeny sériově a S použitím fázorů vypočítejte časový průběh napětí mezi výstupními svorkami, jestliže = 30 sin(100¼t);u
Příklad: Řešte soustavu lineárních algebraických rovnic 10x 1 + 5x 2 +70x 3 + 5x 4 + 5x 5 = 275 2x 1 + 7x 2 + 6x 3 + 9x 4 + 6x 5 = 100 8x 1 + 9x 2 +
 Příklad: Řešte soustavu lineárních algebraických rovnic 1x 1 + 5x 2 +7x 3 + 5x 4 + 5x 5 = 275 2x 1 + 7x 2 + 6x 3 + 9x 4 + 6x 5 = 1 A * x = b 8x 1 + 9x 2 + x 3 +45x 4 +22x 5 = 319 3x 1 +12x 2 + 6x 3 + 8x
Příklad: Řešte soustavu lineárních algebraických rovnic 1x 1 + 5x 2 +7x 3 + 5x 4 + 5x 5 = 275 2x 1 + 7x 2 + 6x 3 + 9x 4 + 6x 5 = 1 A * x = b 8x 1 + 9x 2 + x 3 +45x 4 +22x 5 = 319 3x 1 +12x 2 + 6x 3 + 8x
Cyklometrické funkce
 Cyklometrické funkce Definice. Cyklometrické funkce jsou funkce arcsin(x) (čteme arkussinus x), arccos(x) (čteme arkuskosinus x), arctg(x) (čteme arkustangens x) a arccotg(x) (čteme arkuskotangens x),
Cyklometrické funkce Definice. Cyklometrické funkce jsou funkce arcsin(x) (čteme arkussinus x), arccos(x) (čteme arkuskosinus x), arctg(x) (čteme arkustangens x) a arccotg(x) (čteme arkuskotangens x),
Derivace a monotónnost funkce
 Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je
Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je
Optika. v = f. c = f. světlo elektromagnetické vlnění spektrum: ve vakuu: viditelné záření (světlo): 400 nm (fialová) 700 nm (červená)
 Optika světlo elektromagnetickévlnění spektrum: v = f vevakuu: c = f viditelnézáření(světlo):400nm(fialová) 700nm(červená) Optika šířenísvětla(vlnění):huygensůvprincip Každýbodprostoru,kamvlněnídorazí,jebodovým
Optika světlo elektromagnetickévlnění spektrum: v = f vevakuu: c = f viditelnézáření(světlo):400nm(fialová) 700nm(červená) Optika šířenísvětla(vlnění):huygensůvprincip Každýbodprostoru,kamvlněnídorazí,jebodovým
SBÍRKA PŘÍKLADŮ Z MATEMATICKÉ ANALÝZY 3 Jiří Bouchala. Katedra aplikované matematiky, VŠB TU Ostrava jiri.bouchala@vsb.cz www.am.vsb.
 SBÍRKA PŘÍKLADŮ Z MATEMATICKÉ ANALÝZY 3 Jiří Bouchala Katedra aplikované matematiky, VŠB TU Ostrava jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala 2000 3 Předmluva Tato sbírka doplňuje přednášky z Matematické
SBÍRKA PŘÍKLADŮ Z MATEMATICKÉ ANALÝZY 3 Jiří Bouchala Katedra aplikované matematiky, VŠB TU Ostrava jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala 2000 3 Předmluva Tato sbírka doplňuje přednášky z Matematické
Kapitola 9: Aplikace integrálů funkcí jedné proměnné
 Sbírka příkladů Matematika II pro strukturované studium Kapitola 9: Aplikace integrálů funkcí jedné proměnné Chcete-li ukončit prohlížení stiskněte klávesu Esc. Chcete-li pokračovat stiskněte klávesu Enter..
Sbírka příkladů Matematika II pro strukturované studium Kapitola 9: Aplikace integrálů funkcí jedné proměnné Chcete-li ukončit prohlížení stiskněte klávesu Esc. Chcete-li pokračovat stiskněte klávesu Enter..
6.3. Lineární diferenciální rovnice druhého řádu s konstantními koeficienty
 H VRBENSKÁ J BĚLOHLÁVKOVÁ 63 Lineární diferenciální rovnice druhého řádu s onstantními oeficienty 631 Definice Definice Lineární diferenciální rovnicí druhého řádu s onstantními oeficienty nazýváme rovnici
H VRBENSKÁ J BĚLOHLÁVKOVÁ 63 Lineární diferenciální rovnice druhého řádu s onstantními oeficienty 631 Definice Definice Lineární diferenciální rovnicí druhého řádu s onstantními oeficienty nazýváme rovnici
Kristýna Kuncová. Matematika B3
 (7) Křivky a křivkový integrál Kristýna Kuncová Matematika B3 Kristýna Kuncová (7) Křivky a křivkový integrál 1 / 39 y Kristýna Kuncová (7) Křivky a křivkový integrál 2 / 39 y Kristýna Kuncová (7) Křivky
(7) Křivky a křivkový integrál Kristýna Kuncová Matematika B3 Kristýna Kuncová (7) Křivky a křivkový integrál 1 / 39 y Kristýna Kuncová (7) Křivky a křivkový integrál 2 / 39 y Kristýna Kuncová (7) Křivky
Obvodové rovnice v časové oblasti a v operátorovém (i frekvenčním) tvaru
 Obvodové rovnice v časové oblasti a v oerátorovém (i frekvenčním) tvaru EO Přednáška 5 Pavel Máša - 5. řednáška ÚVODEM V ředchozím semestru jsme se seznámili s obvodovými rovnicemi v SUS a HUS Jak se liší,
Obvodové rovnice v časové oblasti a v oerátorovém (i frekvenčním) tvaru EO Přednáška 5 Pavel Máša - 5. řednáška ÚVODEM V ředchozím semestru jsme se seznámili s obvodovými rovnicemi v SUS a HUS Jak se liší,
vysledek = ((1:1:50).*(100-(1:1:50))) *ones(50,1) vysledek = ((1:1:75)./2).*sqrt(1:1:75) *ones(75,1)
 ZKOUŠKA ČÍSLO 1 x=linspace(0,100,20); y=sqrt(x); A=[x;y]'; save('data.txt','a','-ascii'); polyn = polyfit(x,y,3); polyv = polyval(polyn,x); plot(x,y,'r*') plot(x,polyv,'b') p1=[1 0 0 0 0 0 0-1]; k=roots(p1);
ZKOUŠKA ČÍSLO 1 x=linspace(0,100,20); y=sqrt(x); A=[x;y]'; save('data.txt','a','-ascii'); polyn = polyfit(x,y,3); polyv = polyval(polyn,x); plot(x,y,'r*') plot(x,polyv,'b') p1=[1 0 0 0 0 0 0-1]; k=roots(p1);
Vzdálenosti a východ Slunce
 Vzdálenosti a východ Slunce Zdeněk Halas KDM MFF UK, 2011 Aplikace matem. pro učitele Zdeněk Halas (KDM MFF UK, 2011) Vzdálenosti a východ Slunce Aplikace matem. pro učitele 1 / 8 Osnova Zdeněk Halas (KDM
Vzdálenosti a východ Slunce Zdeněk Halas KDM MFF UK, 2011 Aplikace matem. pro učitele Zdeněk Halas (KDM MFF UK, 2011) Vzdálenosti a východ Slunce Aplikace matem. pro učitele 1 / 8 Osnova Zdeněk Halas (KDM
Neurčitý integrál. Robert Mařík. 4. března 2012
 Neurčitý integrál Robert Mařík 4. března 0 V tomto souboru jsou vysvětleny a na příkladech s postupným řešením demonstrovány základní integrační metody. Ikonka za integrálem načte integrál do online aplikace
Neurčitý integrál Robert Mařík 4. března 0 V tomto souboru jsou vysvětleny a na příkladech s postupným řešením demonstrovány základní integrační metody. Ikonka za integrálem načte integrál do online aplikace
ANALÝZA PNUS, EFEKTIVNÍ HODNOTA, ČINITEL ZKRESLENÍ, VÝKON NEHARMONICKÉHO PROUDU
 ANALÝZA PNUS, EFEKIVNÍ HODNOA, ČINIEL ZKRESLENÍ, VÝKON NEHARMONICKÉHO PROUDU EO Přednáška 4 Pavel Máša X3EO - Pavel Máša X3EO - Pavel Máša - PNUS ÚVODEM Při analýze stejnosměrných obvodů jsme vystačili
ANALÝZA PNUS, EFEKIVNÍ HODNOA, ČINIEL ZKRESLENÍ, VÝKON NEHARMONICKÉHO PROUDU EO Přednáška 4 Pavel Máša X3EO - Pavel Máša X3EO - Pavel Máša - PNUS ÚVODEM Při analýze stejnosměrných obvodů jsme vystačili
z možností, jak tuto veličinu charakterizovat, je určit součet
 6 Charakteristiky áhodé veličiy. Nejdůležitější diskrétí a spojitá rozděleí. 6.1. Číselé charakteristiky áhodé veličiy 6.1.1. Středí hodota Uvažujme ejprve diskrétí áhodou veličiu X s rozděleím {x }, {p
6 Charakteristiky áhodé veličiy. Nejdůležitější diskrétí a spojitá rozděleí. 6.1. Číselé charakteristiky áhodé veličiy 6.1.1. Středí hodota Uvažujme ejprve diskrétí áhodou veličiu X s rozděleím {x }, {p
4.5.9 Vznik střídavého proudu
 4.5.9 Vzik střídavého proudu Předpoklady: 4508 Miulá hodia: Pokud se v uzavřeém závitu měí magetický idukčí tok, idukuje se v ěm elektrické apětí =. Př. 1: Vodorově orietovaá smyčka se pohybuje rovoměrě
4.5.9 Vzik střídavého proudu Předpoklady: 4508 Miulá hodia: Pokud se v uzavřeém závitu měí magetický idukčí tok, idukuje se v ěm elektrické apětí =. Př. 1: Vodorově orietovaá smyčka se pohybuje rovoměrě
1/15. Kapitola 12: Soustavy diferenciálních rovnic 1. řádu
 1/15 Kapitola 12: Soustavy diferenciálních rovnic 1. řádu 2/15 Vsuvka: Vlastní čísla matic Definice: Bud A čtvercová matice a vektor h 0 splňující rovnici A h = λ h pro nějaké číslo λ R. Potom λ nazýváme
1/15 Kapitola 12: Soustavy diferenciálních rovnic 1. řádu 2/15 Vsuvka: Vlastní čísla matic Definice: Bud A čtvercová matice a vektor h 0 splňující rovnici A h = λ h pro nějaké číslo λ R. Potom λ nazýváme
Pomocné relé RP 701 RP 701 KCU RP 701 S9 KCU RP 701 S4 PC RP 701 V
 RP 701 KCU - průmyslové relé v modulovém neprůhledném krytu se šroubovými svorkami (S9 je speciální stejnosměrné provedení s malou spotřebou, určené pro přímé připojení v tranzistorových obvodech) RP 701
RP 701 KCU - průmyslové relé v modulovém neprůhledném krytu se šroubovými svorkami (S9 je speciální stejnosměrné provedení s malou spotřebou, určené pro přímé připojení v tranzistorových obvodech) RP 701
1. Tlumení stavebních konstrukcí 2. Volné tlumené kmitání 3. Vynucené netlumené kmitání 4. Soustavy s konečným počtem stupňů volnosti 5.
 Jiří Máca - katedra mechaniky - B35 - tel. 435 45 maca@fsv.cvt.cz 1. Tlmení stavebních konstrkcí. Volné tlmené kmitání 3. Vyncené netlmené kmitání 4. Sostavy s konečným počtem stpňů volnosti 5. Příklady
Jiří Máca - katedra mechaniky - B35 - tel. 435 45 maca@fsv.cvt.cz 1. Tlmení stavebních konstrkcí. Volné tlmené kmitání 3. Vyncené netlmené kmitání 4. Sostavy s konečným počtem stpňů volnosti 5. Příklady
Rhinoceros a matematika_ Ω
 1 x sinx μ z ν α_matematika a Rhinoceros π Rhinoceros a matematika_ Ω cosx arcsinx 2 cotgx φ tgx 3 arctgx 5 y 4 6 arccosx 7 8 9 zpracoval David Seidler vedoucí práce RNDr. Vladimíra Hájková, Ph.D. Fakulta
1 x sinx μ z ν α_matematika a Rhinoceros π Rhinoceros a matematika_ Ω cosx arcsinx 2 cotgx φ tgx 3 arctgx 5 y 4 6 arccosx 7 8 9 zpracoval David Seidler vedoucí práce RNDr. Vladimíra Hájková, Ph.D. Fakulta
Jak již bylo uvedeno v předcházející kapitole, můžeme při výpočtu určitých integrálů ze složitějších funkcí postupovat v zásadě dvěma způsoby:
 .. Substituční metod pro určité integrály.. Substituční metod pro určité integrály Cíle Seznámíte se s použitím substituční metody při výpočtu určitých integrálů. Zákldní typy integrálů, které lze touto
.. Substituční metod pro určité integrály.. Substituční metod pro určité integrály Cíle Seznámíte se s použitím substituční metody při výpočtu určitých integrálů. Zákldní typy integrálů, které lze touto
Guideline hliníková válečková vedení Technické informace
 Všeobecné informace 1. Charakteristika vodícího systému se skládají z dvojité kolejnice a kazety, resp. jednotlivé kolejnice a válečkové opěry. Vyznačují se nízkou hmotností, malými rozměry a vysokou pojezdovou
Všeobecné informace 1. Charakteristika vodícího systému se skládají z dvojité kolejnice a kazety, resp. jednotlivé kolejnice a válečkové opěry. Vyznačují se nízkou hmotností, malými rozměry a vysokou pojezdovou
Příklady pro předmět Aplikovaná matematika (AMA) část 1
 Příklady pro předmět plikovaná matematika (M) část 1 1. Lokální extrémy funkcí dvou a tří proměnných Nalezněte lokální extrémy funkcí: (a) f 1 : f 1 (x, y) = x 3 3x + y 2 + 2y (b) f 2 : f 2 (x, y) = 1
Příklady pro předmět plikovaná matematika (M) část 1 1. Lokální extrémy funkcí dvou a tří proměnných Nalezněte lokální extrémy funkcí: (a) f 1 : f 1 (x, y) = x 3 3x + y 2 + 2y (b) f 2 : f 2 (x, y) = 1
X31ZZS 3. PŘEDNÁŠKA 6. října Periodické průběhy Fourierovy řady Spektrum Barva zvuku Aplikace
 X31ZZS 3. PŘEDNÁŠKA 6. října 214 Periodické průběhy Fourierovy řady Spektrum Barva zvuku Aplikace Fourierovy řady Jean Baptiste Fourier (francouzský matematik 1768-183) Harmonická analýza Libovolný periodický
X31ZZS 3. PŘEDNÁŠKA 6. října 214 Periodické průběhy Fourierovy řady Spektrum Barva zvuku Aplikace Fourierovy řady Jean Baptiste Fourier (francouzský matematik 1768-183) Harmonická analýza Libovolný periodický
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Geometrie Různé metody řešení Téma: Kružnice, kruh, tečny, obsahy, goniometrické funkce, integrace
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Geometrie Různé metody řešení Téma: Kružnice, kruh, tečny, obsahy, goniometrické funkce, integrace
Seznámíte se s další aplikací určitého integrálu výpočtem objemu rotačního tělesa.
 .. Ojem rotčního těles Cíle Seznámíte se s dlší plikcí určitého integrálu výpočtem ojemu rotčního těles. Předpokládné znlosti Předpokládáme, že jste si prostudovli zvedení pojmu určitý integrál (kpitol.).
.. Ojem rotčního těles Cíle Seznámíte se s dlší plikcí určitého integrálu výpočtem ojemu rotčního těles. Předpokládné znlosti Předpokládáme, že jste si prostudovli zvedení pojmu určitý integrál (kpitol.).
NÁVRH NA POVOLENÍ ODDLUŽENÍ
 NÁVRH NA POVOLENÍ ODDLUŽENÍ Soud: Sp. zn.: i DLUŽNÍK 01 Typ: Fyzická osoba ii Osobní údaje Trvalé Dat. narození: iii Osobní stav: 02 Typ: Právnická osoba ii Právnická Název/obch.firma: osoba sídlo iv adresa
NÁVRH NA POVOLENÍ ODDLUŽENÍ Soud: Sp. zn.: i DLUŽNÍK 01 Typ: Fyzická osoba ii Osobní údaje Trvalé Dat. narození: iii Osobní stav: 02 Typ: Právnická osoba ii Právnická Název/obch.firma: osoba sídlo iv adresa
Téma 13, Úvod do dynamiky stavebních konstrukcí dynamiky
 Statika staveních konstrukcí II., 3.ročník akalářského studia Téma 3, Úvod do dynamiky staveních konstrukcí dynamiky Úvod Vlastní kmitání Vynucené kmitání Tlumené kmitání Podmínky dynamické rovnováhy konstrukcí
Statika staveních konstrukcí II., 3.ročník akalářského studia Téma 3, Úvod do dynamiky staveních konstrukcí dynamiky Úvod Vlastní kmitání Vynucené kmitání Tlumené kmitání Podmínky dynamické rovnováhy konstrukcí
Délka oblouku křivky
 Přechodnice podle Blosse Vypočtěte délku oblouku Blossovy přechodnice na intervalu 0, L Např pro vysokorychlostní tratě mezi ČR a Německem je R 6500m, L 198m 4 1 y ) ( R 4L 5 10L ( 2 3 - vzdálenost bodu
Přechodnice podle Blosse Vypočtěte délku oblouku Blossovy přechodnice na intervalu 0, L Např pro vysokorychlostní tratě mezi ČR a Německem je R 6500m, L 198m 4 1 y ) ( R 4L 5 10L ( 2 3 - vzdálenost bodu
GeoGebra známá i neznámá (pokročilí)
 GeoGebra známá i neznámá (pokročilí) MODAM 2017 Mgr. Zuzana Morávková, Ph.D. MODAM 2017 GeoGebra známá i neznámá (pokročilí) Příklad 1: Cykloida Zadání: Kotálením kružnice vytvoříme cykloidu. 3. 2. 1.
GeoGebra známá i neznámá (pokročilí) MODAM 2017 Mgr. Zuzana Morávková, Ph.D. MODAM 2017 GeoGebra známá i neznámá (pokročilí) Příklad 1: Cykloida Zadání: Kotálením kružnice vytvoříme cykloidu. 3. 2. 1.
Takže platí : x > 0 : x y 1 x = x+1 y x+1 x < 0 : x y 1 x = x+1 y x+1 D 1 = {[x,y] E 2 : x < 0, x+1 y 1 x}, D 2 = {[x,y] E 2 : x > 0, 1 x y x+1}.
![Takže platí : x > 0 : x y 1 x = x+1 y x+1 x < 0 : x y 1 x = x+1 y x+1 D 1 = {[x,y] E 2 : x < 0, x+1 y 1 x}, D 2 = {[x,y] E 2 : x > 0, 1 x y x+1}. Takže platí : x > 0 : x y 1 x = x+1 y x+1 x < 0 : x y 1 x = x+1 y x+1 D 1 = {[x,y] E 2 : x < 0, x+1 y 1 x}, D 2 = {[x,y] E 2 : x > 0, 1 x y x+1}.](/thumbs/55/35861219.jpg) E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II (206 II. Diferenciální počet funkcí více proměnných II.. Definiční obor funkce z = f(, Určete definiční obor funkcí a zakreslete jej
E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II (206 II. Diferenciální počet funkcí více proměnných II.. Definiční obor funkce z = f(, Určete definiční obor funkcí a zakreslete jej
plazmový plyn stlačený vzduch plazmový hořák s jednotlivým připojením vysokofrekvenční zapalování tepelná ochrana velmi robusní a spolehlivé zařízení
 plazmový hořák s jednotlivým připojením velmi robusní a spolehlivé zařízení Technická data Plasma 33 Plasma 60 Jištění 10 A 20 A Max. příkon 5,5 kva 18 kva Řezací proud 33 A 60 A Napětí naprázdno 230 V
plazmový hořák s jednotlivým připojením velmi robusní a spolehlivé zařízení Technická data Plasma 33 Plasma 60 Jištění 10 A 20 A Max. příkon 5,5 kva 18 kva Řezací proud 33 A 60 A Napětí naprázdno 230 V
Mateřská škola a Základní škola při dětské léčebně, Křetín 12
 Mateřská škola a Základní škola při dětské léčebně, Křetín 12 Autor: Mgr. Miroslav Páteček Vytvořeno: červen 2012 Klíčová slova: Matematika a její aplikace Podobnost, funkce, goniometrické funkce, lomený
Mateřská škola a Základní škola při dětské léčebně, Křetín 12 Autor: Mgr. Miroslav Páteček Vytvořeno: červen 2012 Klíčová slova: Matematika a její aplikace Podobnost, funkce, goniometrické funkce, lomený
Laplaceova transformace
 Lalaceova transformace EO2 Přednáška 3 Pavel Máša ÚVODEM Víme, že Fourierova transformace díky řísným odmínkám existence neexistuje ro řadu běžných signálů dokonce i funkce sin musela být zatlumena Jak
Lalaceova transformace EO2 Přednáška 3 Pavel Máša ÚVODEM Víme, že Fourierova transformace díky řísným odmínkám existence neexistuje ro řadu běžných signálů dokonce i funkce sin musela být zatlumena Jak
f(x)dx, kde a < b < c
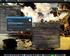 URČITÝ INTEGRÁL jeho plikce Newton-Leibnizov formule f(x)=f(b) F(), kde F (x)=f(x). Vlstnosti ) ) ) 4) Substituce f(x)+ c f(x)= f(x)= f(x)= b f(g(x))g (x)= f(x)= f(x) c f(x), kde < b < c pro fsudou, =
URČITÝ INTEGRÁL jeho plikce Newton-Leibnizov formule f(x)=f(b) F(), kde F (x)=f(x). Vlstnosti ) ) ) 4) Substituce f(x)+ c f(x)= f(x)= f(x)= b f(g(x))g (x)= f(x)= f(x) c f(x), kde < b < c pro fsudou, =
Několik poznámek na téma lineární algebry pro studenty fyzikální chemie
 Několik poznámek na téma lineární algebry pro studenty fyzikální chemie Jiří Kolafa Vektory. Vektorový prostor Vektor je často zaveden jako n-tice čísel, (v,..., v n ), v i R (pro reálný vektorový prostor);
Několik poznámek na téma lineární algebry pro studenty fyzikální chemie Jiří Kolafa Vektory. Vektorový prostor Vektor je často zaveden jako n-tice čísel, (v,..., v n ), v i R (pro reálný vektorový prostor);
MODEL KORSIKA 1 NÁHLED
 MODEL KORSIKA 1 NÁHLED Doba náběhu na provoz.teplotu (65 C) 84 kg 1400 W 1,82 kwh 22900,00 Kč MODEL BIBIONE 1 NÁHLED Doba náběhu na provoz.teplotu (65 C) 76 kg 1340 W 1,74 kwh 21900,00 Kč MODEL SPLIT N1
MODEL KORSIKA 1 NÁHLED Doba náběhu na provoz.teplotu (65 C) 84 kg 1400 W 1,82 kwh 22900,00 Kč MODEL BIBIONE 1 NÁHLED Doba náběhu na provoz.teplotu (65 C) 76 kg 1340 W 1,74 kwh 21900,00 Kč MODEL SPLIT N1
4.4 Exploratorní analýza struktury objektů (EDA)
 4.4 Exploratorní analýza struktury objektů (EDA) Průzkumová analýza vícerozměrných dat je stejně jako u jednorozměrných dat založena na vyšetření grafckých dagnostk. K tomuto účelu se využívá různých technk
4.4 Exploratorní analýza struktury objektů (EDA) Průzkumová analýza vícerozměrných dat je stejně jako u jednorozměrných dat založena na vyšetření grafckých dagnostk. K tomuto účelu se využívá různých technk
Diferenciálne rovnice druhého rádu
 Diferenciálne rovnice druhého rádu Lineárne DR n n 1 n n 3... = a y a y a y a y a y g n n1 n n3 Veta 1 (Cauchyho veta) : Lineárna diferenciálna rovnica s danými počiatočnými podmienkami má jednoznačné
Diferenciálne rovnice druhého rádu Lineárne DR n n 1 n n 3... = a y a y a y a y a y g n n1 n n3 Veta 1 (Cauchyho veta) : Lineárna diferenciálna rovnica s danými počiatočnými podmienkami má jednoznačné
2.8 Zobecnění vztahů mezi zatížením a vnitřními silami prutu (rovinný prut zatížený v rovině) df x =f x.ds df z =f z.ds. M+dM x. ds=r.dϕ.
 .8 Zobecnění vtahů mei atížením a vnitřními silami prutu (rovinný prut atížený v rovině) µ x N V M dm µ df df x =R. MdM x NdN VdV Náhradní břemena: df x = x. df =. dm µ =µ. Obecný rovinný prut: spojité
.8 Zobecnění vtahů mei atížením a vnitřními silami prutu (rovinný prut atížený v rovině) µ x N V M dm µ df df x =R. MdM x NdN VdV Náhradní břemena: df x = x. df =. dm µ =µ. Obecný rovinný prut: spojité
Matematická analýza 1b. 9. Primitivní funkce
 Matematická analýza 1b 9. Primitivní funkce 9.1 Základní vlastnosti Definice Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
Matematická analýza 1b 9. Primitivní funkce 9.1 Základní vlastnosti Definice Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
Seznámení s přístroji, používanými při měření. Nezatížený a zatížený odporový dělič napětí, měření a simulace PSpice
 Cvičení Seznámení s přístroji, používanými při měření Nezatížený a zatížený odporový dělič napětí, měření a simulace PSpice eaktance kapacitoru Integrační článek C - přenos - měření a simulace Derivační
Cvičení Seznámení s přístroji, používanými při měření Nezatížený a zatížený odporový dělič napětí, měření a simulace PSpice eaktance kapacitoru Integrační článek C - přenos - měření a simulace Derivační
III. Dvojný a trojný integrál
 E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II 6 III. vojný a trojný integrál III.. Eistence Necht je měřitelná v Jordanově smslu množina v E resp. E a funkce f je omezená na. Necht
E. Brožíková, M. Kittlerová, F. Mráz: Sbírka příkladů z Matematik II 6 III. vojný a trojný integrál III.. Eistence Necht je měřitelná v Jordanově smslu množina v E resp. E a funkce f je omezená na. Necht
Úvod do RMON. The. Leaders, reducing the cost and complexity of RMON
 Úvod do RMON R The Leaders, reducing the cost and complexity of RMON Co je RMON? Sonda RMON (Agent) Promiskuitně sleduje data na síti LAN, ke které je připojena Uživatelské PC Konsole pro řízení sítě (kontroluje
Úvod do RMON R The Leaders, reducing the cost and complexity of RMON Co je RMON? Sonda RMON (Agent) Promiskuitně sleduje data na síti LAN, ke které je připojena Uživatelské PC Konsole pro řízení sítě (kontroluje
5.8 Jak se změní velikost elektrické síly mezi dvěma bodovými náboji v případě, že jejich vzdálenost a) zdvojnásobíme, b) ztrojnásobíme?
 Elektrostatika 1 1) Co je elektrický náboj? 2) Jaké znáš jednotky elektrického náboje? 3) Co je elementární náboj? Jakou má hodnotu? 4) Jak na sebe silově působí nabité částice? 5) Jak můžeme graficky
Elektrostatika 1 1) Co je elektrický náboj? 2) Jaké znáš jednotky elektrického náboje? 3) Co je elementární náboj? Jakou má hodnotu? 4) Jak na sebe silově působí nabité částice? 5) Jak můžeme graficky
MODAM Mgr. Zuzana Morávková, Ph.D.
 GeoGebra známá i neznámá (pokročilí) MODAM 2016 Mgr. Zuzana Morávková, Ph.D. MODAM 2016 GeoGebra známá i neznámá (pokročilí) Příklad 1: Hod kostkou Zadání: Vytvoříme simulaci hodů hrací kostkou a budeme
GeoGebra známá i neznámá (pokročilí) MODAM 2016 Mgr. Zuzana Morávková, Ph.D. MODAM 2016 GeoGebra známá i neznámá (pokročilí) Příklad 1: Hod kostkou Zadání: Vytvoříme simulaci hodů hrací kostkou a budeme
Vlastnosti členů regulačních obvodů Osnova kurzu
 Osnova kurzu 1) Základní pojmy; algoritmizace úlohy 2) Teorie logického řízení 3) Fuzzy logika 4) Algebra blokových schémat 5) Statické vlastnosti členů regulačních obvodů 6) Dynamické vlastnosti členů
Osnova kurzu 1) Základní pojmy; algoritmizace úlohy 2) Teorie logického řízení 3) Fuzzy logika 4) Algebra blokových schémat 5) Statické vlastnosti členů regulačních obvodů 6) Dynamické vlastnosti členů
9.5. Soustavy diferenciálních rovnic
 Cíle Budeme se nyní zabývat úlohami, v nichž je cílem najít dvojici funkcí y(x), z(x), pro které jsou zadány dvě lineární rovnice prvního řádu, obsahující tyto funkce a jejich derivace. Výklad Omezíme-li
Cíle Budeme se nyní zabývat úlohami, v nichž je cílem najít dvojici funkcí y(x), z(x), pro které jsou zadány dvě lineární rovnice prvního řádu, obsahující tyto funkce a jejich derivace. Výklad Omezíme-li
při vykreslování křivky je důležitá velikost kroku, příp. počet prvků, ve vektoru t (na ose x). t = linspace(0,2*pi,500); y = sin(t); t =
 při vykreslování křivky je důležitá velikost kroku, příp. počet prvků, ve vektoru t (na ose x). t = linspace(0,2*pi,500); y = sin(t); t = linspace(0,2*pi,5); plot(t,y,'b') y = sin(t); plot(t,y,'c') při
při vykreslování křivky je důležitá velikost kroku, příp. počet prvků, ve vektoru t (na ose x). t = linspace(0,2*pi,500); y = sin(t); t = linspace(0,2*pi,5); plot(t,y,'b') y = sin(t); plot(t,y,'c') při
Galileova transformace
 Glileov trnsformce r V Neeistuje v čse t = působ 0: = jk určit bsolutní rchlost m F m F m F ' konst.. Newtonův ákon r ' ' ' m ' F m ' F m ' F poloh ' ' v Vt ' rchlost ' v v ' v v ' v rchlení ' ' ' V ovnoměrně
Glileov trnsformce r V Neeistuje v čse t = působ 0: = jk určit bsolutní rchlost m F m F m F ' konst.. Newtonův ákon r ' ' ' m ' F m ' F m ' F poloh ' ' v Vt ' rchlost ' v v ' v v ' v rchlení ' ' ' V ovnoměrně
ELEKTRICKÉ STROJE - POHONY
 ELEKTRICKÉ STROJE - POHONY Ing. Petr VAVŘIŇÁK 2013 2.7 VOLBA VELIKOSTI MOTORU Vlastní volba elektrického motoru pro daný pohon vychází z druhu zatížení a ze způsobu řízení otáček. Potřebný výkon motoru
ELEKTRICKÉ STROJE - POHONY Ing. Petr VAVŘIŇÁK 2013 2.7 VOLBA VELIKOSTI MOTORU Vlastní volba elektrického motoru pro daný pohon vychází z druhu zatížení a ze způsobu řízení otáček. Potřebný výkon motoru
β 180 α úhel ve stupních β úhel v radiánech β = GONIOMETRIE = = 7π 6 5π 6 3 3π 2 π 11π 6 Velikost úhlu v obloukové a stupňové míře: Stupňová míra:
 GONIOMETRIE Veliost úhlu v oblouové a stupňové míře: Stupňová míra: Jednota (stupeň) 60 600 jeden stupeň 60 minut 600 vteřin Př. 5,4 5 4 0,4 0,4 60 4 Oblouová míra: Jednota radián radián je veliost taového
GONIOMETRIE Veliost úhlu v oblouové a stupňové míře: Stupňová míra: Jednota (stupeň) 60 600 jeden stupeň 60 minut 600 vteřin Př. 5,4 5 4 0,4 0,4 60 4 Oblouová míra: Jednota radián radián je veliost taového
22. Mechanické a elektromagnetické kmity
 . Mechanicé a eletromagneticé mity. Mechanicé mity Mechanicé mitání je jev, při terém se periodicy mění fyziální veličiny popisující mitavý pohyb. Oscilátor těleso, teré je schopné mitat, (mitání způsobuje
. Mechanicé a eletromagneticé mity. Mechanicé mity Mechanicé mitání je jev, při terém se periodicy mění fyziální veličiny popisující mitavý pohyb. Oscilátor těleso, teré je schopné mitat, (mitání způsobuje
MATEMATIKA II V PŘÍKLADECH
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ MATEMATIKA II V PŘÍKLADECH CVIČENÍ Č. Ing. Petra Schreiberová, Ph.D. Ostrava 0 Ing. Petra Schreiberová, Ph.D. Vysoká škola báňská Technická
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ MATEMATIKA II V PŘÍKLADECH CVIČENÍ Č. Ing. Petra Schreiberová, Ph.D. Ostrava 0 Ing. Petra Schreiberová, Ph.D. Vysoká škola báňská Technická
11. Rotační a šroubové plochy
 Rotační a šroubové plochy ÚM FSI VU v Brně Studijní text. Rotační a šroubové plochy. Rotační plochy Rotační plochy jsou plochy, které lze získat rotačním šablonováním křivky. Jejich rovnice je tedy tvaru
Rotační a šroubové plochy ÚM FSI VU v Brně Studijní text. Rotační a šroubové plochy. Rotační plochy Rotační plochy jsou plochy, které lze získat rotačním šablonováním křivky. Jejich rovnice je tedy tvaru
Zavádění metodik full cost na vysokých školách v Evropě a pravidla Rámcových programů EU pro výzkum
 Zavádění metodik full cost na vysokých školách v Evropě a pravidla Rámcových programů EU pro výzkum Konference Full cost: výzva nebo hrozba? 11. října 2012, Masarykova univerzita, Brno Lenka Chvojková
Zavádění metodik full cost na vysokých školách v Evropě a pravidla Rámcových programů EU pro výzkum Konference Full cost: výzva nebo hrozba? 11. října 2012, Masarykova univerzita, Brno Lenka Chvojková
ES-prohlášení o shodě EG-Konformitätserklärung EC Declaration of Conformity
 Výrobní závod Wienerberger Div. Beerse Plant 1210 werk B-2340 Beerse, Absheide 28 0749-CPD BC2-201-676-500/08-07 ES-prohlášení o shodě / Lícovky / Belgie / 1210 Výrobní závod Wienerberger Div. Warneton
Výrobní závod Wienerberger Div. Beerse Plant 1210 werk B-2340 Beerse, Absheide 28 0749-CPD BC2-201-676-500/08-07 ES-prohlášení o shodě / Lícovky / Belgie / 1210 Výrobní závod Wienerberger Div. Warneton
NÁČRT VÝKRESU SOUČÁSTI, DIAGRAMY
 NÁČRT VÝKRESU SOUČÁSTI, DIAGRAMY Metodický postup kreslení náčrtu výkresu součásti Diagramy v kartézských souřadnicích Diagramy v polárních souřadnicích Prostorové diagramy Informativní a vysvětlující
NÁČRT VÝKRESU SOUČÁSTI, DIAGRAMY Metodický postup kreslení náčrtu výkresu součásti Diagramy v kartézských souřadnicích Diagramy v polárních souřadnicích Prostorové diagramy Informativní a vysvětlující
. Opakovací kurs středoškolské matematiky podzim 2015
 . Opakovací kurs středoškolské matematiky podzim 0 František Mráz Ústav technické matematiky, Frantisek.Mraz@fs.cvut.cz I. Mocniny, odmocniny, algeraické výrazy Upravte (zjednodušte), případně určete číselnou
. Opakovací kurs středoškolské matematiky podzim 0 František Mráz Ústav technické matematiky, Frantisek.Mraz@fs.cvut.cz I. Mocniny, odmocniny, algeraické výrazy Upravte (zjednodušte), případně určete číselnou
