Téma 10 Relační model dat a jazyk SQL. Relace je podmnožina kartézského součinu. K čemu relace?
|
|
|
- Matyáš Janda
- před 7 lety
- Počet zobrazení:
Transkript
1 Tém 0 Relční model dt jzyk SQL Osh. Relční lge. Opece elční lgey. Rozšíření elční lgey 4. Hodnoty null 5. Úpvy elcí 6. Stučný úvod do SQL 7. SQL elce 8. Zákldní příkzy SQL 9. Hodnoty null tříhodnotová logik v SQL 0. Příkzy SQL po modifikci oshu dtází K čemu elce? Viděli jsme tulky. Poč potřeujeme něco jiného? Je k tomu řd důvodů: Potře igoózního mtemtického modelu Model umožní fomlizci Tulk klient dtázových opecí Přesný model je potřený k tvoě dekltivně fomulovných dotzů k optimlizci jejich povádění Hlvní myšlenkou je popst dtázi jko souhn logických pedikátů nd konečnou množinou pedikátových poměnných definovt tk omezení n přípustné hodnoty komince hodnot Relční model dt jzyk SQL Relční model dt jzyk SQL Co to je elce? Mtemticky: Jsou dány množiny,,, n, pk elcí ozumíme podmnožinu ktézského součinu x x x n. Relce tedy je množin n-tic (,,, n ), kde i i Příkld: klient_jmeno = {Novák, Mtes, un, Novotný } /* množn jmen klientů */ klient_ulice = {Spálená, Hlvní, Honí, } /* množin jmen ulic*/ klient_mesto = {Ph, no, Nymuk, } /* množin jmen měst */ pk = { (Novák, Spálená, Ph), (Mtes, Honí, no), (un, Hlvní, no), (Novotný, Honí, Nymuk) } je elce, tj. podmnožin klient_jmeno x klient_ulice x klient_mesto Vzhledem k tomu, že jde vždy o konečné množiny, lze je vyjádřit výčtem, tedy tulkmi Relce je podmnožin ktézského součinu V množinách neexistuje duplicit Velmi důležité po dtázové plikce Pvky množiny mohou ýt v jkémkoliv pořdí neexistuje uspořádání Příjmení ush Cte Clinton Jeffeson Kenedy Lincoln Om Roosevelt Wshington hm c ill Fnklin Geoge Jimmy Jmén John Theodoe Vyní meičtí pezidenti Thoms Relční model dt jzyk SQL Relční model dt jzyk SQL 4
2 Typy tiutů Kždý tiut v elci má své jméno Množin přípustných hodnot tiutu je definiční doménou tiutu Hodnoty tiutu jsou (téměř vždy) tomické, tj. dále nedělitelné Npř. hodnotou tiutu číslo_účtu smí ýt číslo jednoho účtu, nikoliv množin čísel účtů Speciální hodnot null ptří do kždé domény pázdná (nezdná) hodnot null znčně komplikuje definici mnoh množinových opecí, poto zpočátku tuto hodnotu udeme ignoovt důsledky uvedeme později Relční schém instnce Relční schém,,, n jsou tiuty R = (,,, n ) je elční schém Příkld: Klient_schem = (klient_jmeno, klient_ulice, klient_mesto) (R) znčí elci nd elčním schémtem R Příkld: klient (Klient_schem) Instnce elce (elční instnce) Skutečné hodnoty (elční instnce) jsou definovány výčtem, tj. tulkou Pvek t elce je n-tice, epezentovná řádkem tulky klient_jmeno klient_ulice klient_mesto tiuty (tj. sloupce) Novák Novotný un Mtes Spálená Honí Hlvní Honí Ph Nymuk no no n-tice (řádky) Relční model dt jzyk SQL 5 klient Relční model dt jzyk SQL 6 Klíče (znovu) Nechť K R. K je supeklíč schémtu R, když hodnoty K stčí k jednoznčné identifikci (R) Npř. {klient_jmeno, klient_mesto} je supeklíčem po schém Klient_schem. Supeklíčem je všk i {klient_jmeno} K je kndidát n klíč jestliže K je minimální supeklíč Npř. {klient_jmeno} je kndidátem n klíč po schém Klient_schem, neoť je to supeklíč žádná podmnožin již supeklíčem není Pimání klíč je vyán mezi kndidátními klíči tk, y se ěhem život příslušné elce neměnil Npř. {klient_jmeno} může sloužit jko pimání klíč po nši instnci elce, všk když přijde dlší Novák, všechno ude šptně e-milová des může ýt pimáním klíčem, všk lidé svůj e-mil očs mění (což je jiný typ komplikce) Relční model dt jzyk SQL 7 Cizí klíče Relční schém může oshovt tiut, kteý koesponduje s pimáním klíčem v jiné elci. Tkový tiut se nzývá cizí klíč Npř. tiuty custome_nme ccount_nume elčního schémtu deposito jsou cizí klíče do custome ccount Hodnotmi cizího klíče v efeencující (odkzující) elci smí ýt jen ty hodnoty, kteé se vyskytují jko pimání klíč v elci efeencovné (odkzovné) Důležitý typ omezení efeenční integit nch nch_nme nch_city ssets ccount ccount_nume nch_nme lnce lon lon_nume nch_nme mount deposito custome_nme ccount_nume oowe custome_nme lon_nume custome custome_nme custome_steet custome_city Relční model dt jzyk SQL 8
3 Relční lge Relční lge je vlstně poceduální jzyk Šest zákldních opeátoů Selekce (estikce) σ Výě jen někteých pvků elce Pojekce: Výě jen učitých tiutů Sjednocení: Spojení několik elcí v jednu (spojovné elce musí mít stejné schém) Rozdíl (množin): Výě těch pvků pvní elce, kteé nejsou osženy v duhé elci Ktézský součin: x Klsická množinová opece Přejmenování: ρ Změn jmén jednoho či více tiutů Všechny tyto opeátoy pcují s jednou neo dvěm elcemi vytváří elci novou Selekce Zápis σ p () p je selekční pedikát Definice σp () = {t t p(t)} Selekční pedikát p je výoková fomule složená z temů popojených logickými opeátoy: (nd), (o), (not) Kždý tem má tv: tiut op tiut neo konstnt, kde op je jeden z =,, >,, <, Příkld selekce: σ klient_mesto= Ph (klient) C D σ = D > 5 () C D 7 0 Relční model dt jzyk SQL 9 Relční model dt jzyk SQL 0 Pojekce Zápis: ( ),, K, k kde, jsou jmén tiutů je jméno elce Výsledek je definován jko elce s k tiuty ( sloupci ) vytvořená z elce výěem pouze vyjmenovných tiutů Tedy vynecháním zývjících (neuvedených) tiutů Duplicitní pvky (řádky) jsou odstněny elce jsou množiny! Příkld: V elci klient nás nezjímá tiut klient_ulice klient_jmeno, klient_mesto (klient) Sjednocení Zápis: s Definice: s = {t t t s} Relce s musí ýt komptiilní, tj. s musí mít stejnou itu (počet tiutů). Domény tiutů musí ýt po řdě shodné Npř. duhý tiut elce duhý tiut elce s musí mít shodný dtový typ (definiční doménu) Příkld: njít všechny zákzníky nky, kteří mjí vkld neo půjčku custome_nme (deposito) custome_nme (oowe) C C,C () = C Relční model dt jzyk SQL Relce, s: s: s Relční model dt jzyk SQL
4 Rozdíl Zápis: s Definice: s = {t t t s} Relce vstupující do množinového ozdílu musí opět ýt vzájemně komptiilní Relce, s: s s: Relční model dt jzyk SQL Ktézský součin Zápis: x s Definice: x s = {t q t q s} Předpokládejme, že tiuty (R) s(s) jsou disjunktní tj., R S =. Lze použít i n více než dvě elce Nejsou-li tiuty disjunktní, tzn. někteé tiuty (R) mjí stejné jméno jko jmén tiutů v s(s), musí se použít opece přejmenování Relce, s: POZOR: Mohou vznikt tulky gigntické velikosti C D s x s: C D Relční model dt jzyk SQL 4 Opece přejmenování Pomocná opece Fkticky nejde o pvou opeci elční lgey, zvádí se z pgmtických důvodů Umožňuje nově pojmenovt ( tím i efeencovt) výsledek jiné elční opece Umožňuje též pojmenovt elci více jmény Příkld: ρ X vátí výsledek výzu pod jménem X Jestliže elční výz má itu n, pk ρ X ( ),,..., ) ( ) n ( vátí výsledek výzu pod jménem X s tiuty přejmenovnými n,,., n. Skládání opecí Skutečně užitečné elční opece vzniknou tepve skládáním opecí zákldních x s: σ =C ( x s): C D C D Relční model dt jzyk SQL 5 Relční model dt jzyk SQL 6
5 Příkld nkovní dtáze Relce nch(nch_nme, nch_city, ssets) custome(custome_nme, custome_steet, custome_city) ccount(ccount_nume, nch_nme, lnce) lon(lon_nume, nch_nme, mount) deposito(custome_nme, ccount_nume) oowe(custome_nme, lon_nume) Příkldy dotzů Njdi všechny půjčky (lon) přes 00 σ ( lon mount>00 ) Njdi čísl půjček vyšších než 00 Π ( σ ( 00 lon)) Njdi jmén zákzníků mjících vkldový účet v poočce Nymuk Π σ lon _ nume mount> _ nme( nch _ nme = "Nymuk" ( σ ( deposito ccount ))) custome deposito.ccount_nume = ccount.ccount_num e Relční model dt jzyk SQL 7 Příkld nkovní dtáze () Dlší příkldy dotzů Njdi jmén zákzníků mjících půjčku v poočce Nymuk přitom nemjí vkldový účet v žádné poočce Π σ Njdi jmén zákzníků, kteří mjí půjčku vedenou v poočce Nymuk. možnost Π σ. možnost Π custome_nme ( nch_nme= "Nymuk" ( σ Π ( σ oowe.lon_nume = lon.lon_nume custome_nme ( deposito) custome _ nme ( nch _ nme = "Nymuk " custome _ nme ( σ oowe.l on_nume = lon.lon _nume ( σ oowe.lon_nume = lon.lon_nume nch _ nme= "Nymuk" ( oowe lon))) ( oowe ( oowe)) lon)) ( lon ))) Relční model dt jzyk SQL 8 Příkld nkovní dtáze () Příkldy dotzu (použití opece přejmenování) Njdi největší zůsttek vkldového účtu Sttegie: Njdi zůsttky, kteé nejsou největší K tomu účelu přejmenuj elci ccount n temp, ychom mohli poovnávt jednotlivé zůsttky se všemi osttními Použij množinový ozdíl k nlezení těch zůsttků, kteé nejsou mezi těmi, kteé jsme učili v předchozím koku Dotz pk vypdá tkto: П lnce (ccount) П ccount.lnce (σ ccount.lnce < temp.lnce (ccount x ρ temp (ccount) ) ) Relční model dt jzyk SQL 9 Doplňkové opece, půnik Z pktických důvodů se definují dlší opeátoy, kteé umožňují zjednodušení čstých dotzů do dtáze Půnik Přiozené spojení (spojení přes ovnost) Dělení Přiřzení Půnik Zápis: s Definice: s = { t t t s } Předpokld: Relce s jsou vzájemně komptiilní Poznámk: s = ( s) Relce, s: s s: Relční model dt jzyk SQL 0
6 Přiozené spojení Zápis: s Nechť s jsou elce podle schémt R S. s je pk elce podle schémtu R S vytvořená jko: Uvžme všechny páy n-tic t z t s z s Jestliže t t s mjí stejné hodnoty všech tiutů z R S, pk n-tice t se ojeví ve výsledku, přičemž t má stejné hodnoty tiutů jko t n t má stejné hodnoty tiutů jko t s n s Výsledek přiozeného spojení je tedy množin všech komincí řádků z R S, kteé mjí shodné hodnoty stejnojmenných tiutů Příkld: R = (,, C, D) S = (,, D) Výsledné schém = (,, C, D, ) s pk je: ( ( s) ) Π.,.,. C,. D, s. σ. = s.. D= s. D Relční model dt jzyk SQL Relce, s: s: Pktický příkld Přiozené spojení příkld δ 4 C µ D Zmestnnec Jmeno ZmId Oddel Fnt 5 Finnce Pvl 4 Ochod Josef 40 Výo Pet 0 Výo Zmestnnec D s δ Oddeleni Odddel Mnge Finnce Jik Ochod Pet Vyo Kel Oddeleni Jmeno ZmId Oddel Mnge Fnt 5 Finnce Jik Pvl 4 Ochod Pet Josef 40 Výo Kel Pet 0 Výo Kel δ Relční model dt jzyk SQL C µ D δ Opece dělení Zápis: s Učeno po dotzy oshující fázi po všechny Nechť s jsou elce podle schémt R S, kde R = (,, m,,, n ) S = (,, n ) Výsledkem s je elce dle schémtu R S = (,, m ) s = { t t R-S () u s (tu ) }, kde tu znčí zřetězení řádků t u chápné jko jediná n-tice Vlstnost Nechť q = s, pk q je největší elce splňující q x s Definice pomocí zákldních opecí elční lgey Nechť (R) s(s) jsou elce nechť S R s = R-S () R-S (( R-S () x s) R-S,S ()) R-S,S () přeuspořádá tiuty R-S ( R-S () x s ) R-S,S ()) dá ty n-tice t z R-S (), po kteé pltí, že někteá n-tice u s je tková, že tu Relce, s: Pktický příkld Pcuje_po Jmeno Mnge Fnt Jik Pvl Pet Josef Kel Pet Kel Opece dělení příkld δ δ δ εε 4 6 s Šéf Mnge Jik Kel s: Pcuje_po Šéf Jmeno Fnt Josef Pet Relční model dt jzyk SQL Relční model dt jzyk SQL 4
7 Přiřzovcí opece Přiřzovcí opece ( ) umožňuje pohodlný zápis složitých výzů Dovoluje zpisovt dotzy ve fomě sekvence pogmových příkzů ve tvu séie přiřzení následovných snáze čitelnými výzy Přiřzuje se vždy vhodné pcovní poměnné typu elce Pcovní poměnné jsou pk dostupné v dlších výzech Příkld: Opeci dělení s lze zpst jko temp R-S () temp R-S ((temp x s) R-S,S ()) vysledek = temp temp Relční model dt jzyk SQL 5 Příkld nkovní dtáze dlší dotzy Njdi jmén všech zákzníků, kteří mjí součsně vkldový účet půjčku custome_nme (oowe) custome_nme (deposito) Njdi jmén zákzníků, kteří mjí půjčku, výši této půjčky custome_nme, lon_nume, mount (oowe lon) Njdi jmén všech zákzníků, kteří mjí vkldový účet v poočce Nymuk neo enešov Možnost custome_nme (σ nch_nme = Nymuk (deposito ccount)) custome_nme (σ nch_nme = enešov (deposito ccount)) Možnost custome_nme, nch_nme (deposito ccount) ρ temp(nch_nme) ({( Nymuk ), ( enešov )}) Všimněme si, že Možnost používá konstntní elci temp ve funkci dělitele při dělení ptáme se totiž po všechny uvedené poočky Relční model dt jzyk SQL 6 Pgmtická ozšíření elčních opeátoů Po čsto kldené dotzy se zvádějí ozšířené opece Zoecněná pojekce gegátní funkce Vnější spojení (Oute Join) Zoecněná pojekce zvádí itmetické funkce do seznmu možných výstupních tiutů ( ) je elční výz F, F,, F n jsou itmetické výzy zhnující tiuty ze schémtu výzu konstnty Tkto se získjí odvozené (počítné) tiuty Příkld: Relce cedit_info(custome_nme, limit, cedit_lnce), Uči, kolik může kždá oso ještě uttit: custome_nme, limit cedit_lnce (cedit_info) F, F, L, F n Relční model dt jzyk SQL 7 gegátní funkce opece gegátní funkce pcují s kolekcí hodnot vcí jedinou výslednou hodnotu vg: půměná hodnot min: minimum mx: mximum sum: součet hodnot count: počet hodnot gegátní opece elční lgey vytvářejí elci se syntetickými tiuty přípdným seskupováním pvků G je elční výz G, G,, G m je seznm tiutů, podle nich se má seskupovt (může ýt i pázdný) F i jsou gegátní funkce i jsou jmén tiutů ze schémtu, podle něhož je tvořen,,, ( ), ( ),, ( )( ) G K G ϑ m F F K Fn n Relční model dt jzyk SQL 8
8 Relce : Příkld gegátních opecí funkcí ϑ sum(c) (): Relce ccount seskupená podle nch_nme: nch_nme ϑ sum(lnce) (ccount): C sum(c) 7 nch_nme ccount_nume Nymuk Nymuk Ph Ph enešov nch_nme Nymuk Ph enešov lnce sum(lnce) Relční model dt jzyk SQL 9 Vnější spojení Vnější spojení je opece, kteá ozšiřuje přiozené spojení zmezuje ztátě infomce Učí se přiozené spojení pk se přidjí pvky z jedné ze spojovných elcí, kteé nesplňují poždvky n ovnost stejnojmenných tiutů Podle toho, ze kteé elce se přidávjí pvky, ozlišuje se levé vnější spojení pvé vnější spojení Lze též přidt pvky z oou spojovných elcí pk jde o plné vnější spojení Při doplňování mohou vznikt pvky s neznámými neo nedefinovnými hodnotmi, po jejichž epezentci se zvádí hodnot null Relční model dt jzyk SQL 0 Typy příkldy vnějšího spojení lon lon_nume nch_nme mount L-70 Ph 000 L-0 Nymuk 4000 L-60 enešov 700 přiozené spojení levé vnější spojení pvé vnější spojení plné vnější spojení oowe custome_nme lon_nume Jonáš L-70 Kovář L-0 Slám L-55 lon oowe lon_nume nch_nme mount custome_nme L-70 Ph 000 Jonáš L-0 Nymuk 4000 Kovář lon oowe lon_nume nch_nme mount custome_nme L-70 Ph 000 Jonáš L-0 Nymuk 4000 Kovář L-60 enešov 700 null lon oowe lon_nume nch_nme mount custome_nme L-70 Ph 000 Jonáš L-0 Nymuk 4000 Kovář L-55 null null Slám lon oowe lon_nume nch_nme mount custome_nme L-70 Ph 000 Jonáš L-0 Nymuk 4000 Kovář L-60 enešov 700 null L-55 null null Slám Relční model dt jzyk SQL Hodnoty Null null se užívá po neznámou hodnotu neo po oznčení situce, že hodnot neexistuje itmetický výz oshující null dává výsledek null gegátní funkce ignoují hodnoty null Po eliminci duplikátů seskupování se null uvžuje jko jkákoliv jiná hodnot; dvě null hodnoty se povžují z identické Pedikáty zhnující null vyždují tříúovňovou logiku s doplňkovou hodnotou unknown Logik s pvdivostní hodnotou unknown: OR: (unknown o tue) = tue, (unknown o flse) = unknown (unknown o unknown) = unknown ND: (tue nd unknown) = unknown, (flse nd unknown) = flse, (unknown nd unknown) = unknown NOT: (not unknown) = unknown Selekční pedikát vyhodnocený jko unknown se povžuje z flse Relční model dt jzyk SQL
9 Modifikce elcí v dtázi K modifikci oshu dtáze potřeujeme opece Deletion (výmz = odstnění pvku z elce) Insetion (vložení pvku do elce) Updting (ktulizce změn pvku v elci) Vše se elizuje opeátoem přiřzení Výmz (deletion) kde je elce je elční výz učující mzné pvky Příkldy Vymž všechny záznmy v poočce enešov ccount ccount σ nch_nme = enešov (ccount ) Vymž všechny záznmy o půjčkách se zůsttkem 0 ž 50 lon lon σ mount 0 nd mount 50 (lon) Vložení Vložení v elční lgeře je opět přiřzení kde je elce, do níž vkládáme je elční výz Vložení jediného pvku se elizuje tk, že ude konstntní výz popisující pvek Vložit lze njednou i více pvků, pokud ude elční výz komptiilní s Příkld Vlož do dtáze infomci, že zákzník Kovář má účet -97 se zůsttkem 00 v poočce enešov ccount ccount {( -97, enešov, 00)} deposito deposito {( Kovář, -97 )} Relční model dt jzyk SQL Relční model dt jzyk SQL 4 ktulizce Mechnismus po změnu hodnoty zvolených tiutů, niž y se měnily hodnoty všech tiutů Použije se zoecněná pojekce ( F ), F, K, Fl, F i je uď i-tý tiut, pokud i-tý tiut nemá ýt změněn, neo F i je výz sestvený z konstnt tiutů, kteý dává novou hodnotu tiutu Příkldy Připočti úok 5% ccount ccount_nume, nch_nme, lnce *.05 (ccount) Přičti úok 6% k účtům se zůsttkem přes % ke všem osttním ccount ccount_nume, nch_nme, lnce *.06 (σ lnce>0000 (ccount )) ccount_nume, nch_nme, lnce *.05 (σ lnce 0000 (ccount)) Stuktuovný dotzovcí jzyk SQL Stuctued Quey Lnguge (SQL) jzyk po kldení dotzů do dtáze oshuje jk příkzy DML (mnipulce s dty), tk i po definici dt (DDL) Svojí syntxí připomíná přiozenou ngličtinu SQL se opíá o výzy elční lgey xistuje mnoho dilektů SQL liší se ůznými ozšířeními či speciálními gegátními funkcemi skld vestvěných pedikátů se ovněž může lišit Poeeme jen zákldní konstukty jzyk konkétní vinty vždy závisí n příslušném dilektu použitého dtázového systému Poznámk k syntxi SQL identifikátoy jmén tiutů NROZLIŠUJÍ mlá velká písmen (tj. nch_nme RNCH_NM nch_nme Relční model dt jzyk SQL 5 Relční model dt jzyk SQL 6
10 Konstukce cete tle Relce v SQL je definován příkzem cete tle ( D, D,..., n D n, (integitní-omezení ),..., (integitní-omezení k )) je jméno vytvářené elce i jsou jmén tiutů schémtu elce D i jsou příslušné dtové typy hodnot domén tiutů i Integitní omezení jsou stnddně tvu not null pimy key(,..., L ) Příkld cete tle nch ( nch_nme ch(5) not null, nch_city ch(0), ssets intege, pimy key(nch_nme) ) Zákldní stuktu SQL dotzu Typický SQL dotz má tv: select,,..., n fom R, R,..., R m whee p i jsou tiuty, R i jsou elce p je pedikát Tento dotz je ekvivlentní elčnímu výzu σ K ( p ( R R R n,, K, m Výsledek dotzu je elce Důležité pozntky SQL je dekltivní (dotzovcí) jzyk, ztímco elční lge je poceduální Zození SQL dotzů n elční výzy převádí dekltivní dotzy n poceduy Povedení ( výpočet výsledku ) dotzu ude implementovt poceduy opecí elční lgey )) Relční model dt jzyk SQL 7 Relční model dt jzyk SQL 8 Kluzule select Kluzule select uvádí tiuty výsledné elce dotzu odpovídá elční opeci pojekce Příkldy: Získej jmén pooček z elce (tulky) lon: select nch_nme fom lon V elční lgeře nch_nme (lon) N ozdíl od elcí SQL připouští duplikáty v elcích i ve výsledcích dotzů To nušuje elční model, všk může význě zychlit zpcování liminci duplikátů lze vynutit použitím klíčového slov distinct z select. Získej jmén pooček z elce (tulky) lon odstň duplikáty select distinct nch_nme fom lon Nopk klíčové slovo ll explicitně říká, y se duplikáty ponechly select ll nch_nme fom lon Relční model dt jzyk SQL 9 Kluzule select (pok.) Hvězdičk v kluzuli select znčí všechny tiuty select fom lon Kluzule select může oshovt itmetické výzy oshující opece +,,, / konstnty neo tiuty Dotz select lon_nume, nch_nme, mount 00 fom lon vátí elci shodnou s lon ž n to, hodnot tiutu mount ude vynásoen 00 Jde vlstně o zoecněnou pojekci Π lon_nume, nch_nme, mount 00 (lon) Relční model dt jzyk SQL 40
11 Kluzule whee Kluzule whee učuje podmínky, kteé musí splňovt výsledek Odpovídá selekčnímu pedikátu elční lgey Příkld Njdi čísl půjček z poočky enešov vyšší než 00 select lon_nume fom lon whee nch_nme="enešov" nd mount>00 Poovnání Výsledky mohou ýt kominovány logickými spojkmi nd, o not Poovnání lze plikovt i n výsledky itmetických výzů SQL zhnuje i poovnávcí opeáto etween Npř.: Njdi čísl půjček se zůsttky mezi (tj ) select lon_nume fom lon whee mount etween nd což odpovídá elčnímu výzu Π lon_nume(σ(mount 90000) (mount 00000)(lon)) Relční model dt jzyk SQL 4 Kluzule fom Kluzule fom uvádí seznm elcí, kteých se dotz týká Odpovídá ktézskému součinu elcí Příkz select fom oowe, lon vátí ktézský součin elcí oowe x lon Njdi jmén, čísl půjček výši dluhů všech zákzníků mjících půjčku v poočce Nymuk select custome_nme, oowe.lon_nume, mount fom oowe, lon whee oowe.lon_nume = lon.lon_nume nd nch_nme = "Nymuk" odpovídá elčnímu výzu Π custome_nme, oowe.lon_nume, mount ( σ oowe.lon_nume = lon.lon_nume nch_nme="nymuk" (oowe x lon)) Relční model dt jzyk SQL 4 Opece přejmenování SQL umožňuje elce tiuty pomocí kluzule s old-nme s new-nme Njdi jmén, čísl půjček dlužné částky všech zákzníků pojmenuj sloupec lon_nume jko lon_id select custome_nme, oowe.lon_nume s lon_id, mount fom oowe, lon whee lon_id = lon.lon_nume Domácí úkol: Přepište tento dotz do fomy elčního výzu n-tice jko poměnné Poměnné ve tvu n-tic se definují jko poměnné v kluzuli fom s použitím kluzule s Příkld Njdi jmén zákzníků, čísl jejich půjček výši dluhů přes všechny poočky select custome_nme,.lon_nume, L.mount fom oowe s, lon s L whee.lon_nume = L.lon_nume Njdi jmén pooček, kteé mjí součet vkldů (ssets) větší někteá z pooček v Pze select distinct T.nch_nme fom nch s T, nch s S whee T.ssets > S.ssets nd S.nch_city = "Ph " Relční model dt jzyk SQL 4 Relční model dt jzyk SQL 44
12 SQL připouští duplikáty Po zjištění doé nlogie SQL množinového modelu potřeujeme tzv. multisety Multiset je množin s opkujícími se pvky Potřeujeme multisetové veze elčních opeátoů mezi elcemi σ θ ( ): Je-li c kopií n-tice t v, t splňuje selekční pedikát θ,, pk ude c kopií t v σ θ ( ). Π ( ): Po kždou kopii t v ude kopie Π (t ) i v Π ( ) x : Je-li c kopií t v c kopií t v, pk ude c c kopií n-tice t t v x Příkld: Multisetové elce (, ) (C) jsou = {(, ) (,)} = {(), (), ()} Pk Π ( ) ude {(), ()}, Π ( ) x dá {(,), (,), (,), (,), (,), (,)} SQL sémntik příkzu select,,,..., n fom,,..., m whee P je ekvivlentní multisetové vezi výzu ( )) ( σ K,, K, n P m Relční model dt jzyk SQL 45 Množinové opece v SQL Množinové opeátoy union, intesect except jsou SQL ekvivlentem elčních (množinových) opecí, Njdi zákzníky mjící vkldový účet neo půjčku (neo ooje) (select custome_nme fom deposito) union (select custome_nme fom oowe) Njdi zákzníky mjící jk vkldový účet tk půjčku (select custome_nme fom deposito) intesect (select custome_nme fom oowe) Njdi zákzníky mjící vkldový účet nemjící půjčku (select custome_nme fom deposito) except (select custome_nme fom oowe) SQL má dále opeáto in, kteý testuje příslušnost či členství v množině ekvivlent Relční model dt jzyk SQL 46 gegátní funkce v SQL Tyto funkce pcují s multisety hodnot vcí hodnotu jedinou jink jsou shodné s dříve uvedenými gegátními funkcemi vg, min, mx, sum count Njdi půměný vkld v poočce enešov select vg(lnce) fom ccount whee nch_nme = "enešov" Uči počet vkldtelů select count (distinct custome_nme) fom deposito Hodnoty null v SQL Pedikát is null slouží k testu null hodnot Npř.: V elci lon vyhledej čísl půjček s null hodnotou tiutu mount select lon_nume fom lon whee mount is null itmetické opece zhnující null dávjí null Npř.: 5 + null vcí null gegátní funkce null hodnoty ignoují Je zveden tříhodnotová logik s unknown Npř.: 5 < null, null <> null neo null = null se vždy vyhodnotí jko unknown Konstukt p is unknown se vyhodnotí jko pvdivý, pokud pedikát p má hodnotu unknown Relční model dt jzyk SQL 47 Relční model dt jzyk SQL 48
13 Vnořené dotzy SQL má mechnismus po vnořování dotzů (suquey) někdy zvné pod-dotzy Vnořený dotz má ovyklý tv select-fom-whee, je všk znořen do jiného dotzu Nejčstěji se používá k elizci testu členství v elci, poovnávání množin učování kdinlity elcí Příkld: Njdi zákzníky mjící jk vkldový účet tk i půjčku select distict custome_nme fom oowe whee custome_nme in (select custome_nme fom deposito) Vnořený dotz Pohledy Čsto je nevhodné poskytovt uživteli všechn dt tedy celý logický model dtáze všechny uložené elce nkovní úředník n jisté pozici potřeuje znát jméno zákzník poočku, kde má půjčku, ne všk výši půjčky. (select custome_nme, nch_nme fom oowe, lon whee oowe.lon_nume = lon.lon_nume ) Mechnismus pohledů (view) umožňuje skýt učitá dt Lze tk vytvořit jkoukoliv elci, kteá není součástí konceptuálního modelu zpřístupnit ji uživteli jko "vituální elci". Tková "vituální elce" se nzývá pohled. Zvede se příkzem cete view ve tvu cete view v s <fomulce dotzu> kde v je jméno pohledu Jkmile je pohled definován, jeho jméno lze používt jko zktku celého definičního dotzu Relční model dt jzyk SQL 49 Relční model dt jzyk SQL 50 SQL příkzy po modifikci dtáze Výmz (deletion) Příkz má stuktuu delete-fom-whee s gumenty nlogickými konstuktu select-fom-whee Vymž všechny vkldové účty v poočce Nymuk delete fom ccount whee nch_nme = Nymuk Vložení (insetion) inset into elce vlues <komptiilní_elce> Přidej záznm do tulky ccount inset into ccount (nch_nme, lnce, ccount_nume) vlues ('eoun', 00, '-97') ktulizce (updte) updte elce set tiut = výz whee podmínk Přidej 6% pémie ke vkldovým účtům přes 000 updte ccount set lnce = lnce.06 whee lnce > 000 Relční model dt jzyk SQL 5 Spojení elcí v SQL Zákldní syntxe je <Typ> join on <podmínk> using (,...) Úplná SQL syntxe je popsán v příslušných dilektech stnddizce je jen částečná Typicky se používá jko součást pod-dotzu v kluzuli fom. Typ spojení "přívlstek" klíčového slov join Jde o úplnou ekvivlenci se spojeními z elční lgey Typy: inne join, left oute join, ight oute join, full oute join Spojovcí podmínk učuje, n zákldě čeho má dojít ke spojení kteé tiuty udou ve výsledném spojení Příkld Njdi všechny zákzníky, kteří mjí uď půjčku neo vkldový účet, le ne ooje select custome_nme fom (deposito full oute join oowe ) whee ccount_nume is null o lon_nume is null Relční model dt jzyk SQL 5
14 Dotzy Relční model dt jzyk SQL 5
Téma 10 Relační model dat a jazyk SQL
 Téma 0 Relační model dat a jazyk SQL Obsah. Relační algebra 2. Operace relační algebry 3. Rozšíření relační algebry 4. Hodnoty null 5. Úpravy relací 6. Stručný úvod do SQL 7. SQL a relace 8. Základní příkazy
Téma 0 Relační model dat a jazyk SQL Obsah. Relační algebra 2. Operace relační algebry 3. Rozšíření relační algebry 4. Hodnoty null 5. Úpravy relací 6. Stručný úvod do SQL 7. SQL a relace 8. Základní příkazy
2.8.5 Lineární nerovnice s parametrem
 2.8.5 Lineární nerovnice s prmetrem Předpokldy: 2208, 2802 Pedgogická poznámk: Pokud v tom necháte studenty vykoupt (což je, zdá se, jediné rozumné řešení) zere tto látk tk jednu půl vyučovcí hodiny (první
2.8.5 Lineární nerovnice s prmetrem Předpokldy: 2208, 2802 Pedgogická poznámk: Pokud v tom necháte studenty vykoupt (což je, zdá se, jediné rozumné řešení) zere tto látk tk jednu půl vyučovcí hodiny (první
OBECNÝ URČITÝ INTEGRÁL
 OBECNÝ URČITÝ INTEGRÁL Zobecnění Newtonov nebo Riemnnov integrálu se definují různým způsobem dostnou se někdy různé, někdy stejné pojmy. V tomto textu bude postup volen jko zobecnění Newtonov integrálu,
OBECNÝ URČITÝ INTEGRÁL Zobecnění Newtonov nebo Riemnnov integrálu se definují různým způsobem dostnou se někdy různé, někdy stejné pojmy. V tomto textu bude postup volen jko zobecnění Newtonov integrálu,
4. přednáška 22. října Úplné metrické prostory. Metrický prostor (M, d) je úplný, když každá cauchyovská posloupnost bodů v M konverguje.
 4. přednášk 22. říjn 2007 Úplné metrické prostory. Metrický prostor (M, d) je úplný, když kždá cuchyovská posloupnost bodů v M konverguje. Příkldy. 1. Euklidovský prostor R je úplný, kždá cuchyovská posloupnost
4. přednášk 22. říjn 2007 Úplné metrické prostory. Metrický prostor (M, d) je úplný, když kždá cuchyovská posloupnost bodů v M konverguje. Příkldy. 1. Euklidovský prostor R je úplný, kždá cuchyovská posloupnost
Téma 9 Relační algebra a jazyk SQL
 Téma 9 Relační algebra a jazyk SQL Obsah. Relační algebra 2. Operace relační algebry 3. Rozšíření relační algebry 4. Hodnoty null 5. Úpravy relací 6. Stručný úvod do SQL 7. SQL a relace 8. Základní příkazy
Téma 9 Relační algebra a jazyk SQL Obsah. Relační algebra 2. Operace relační algebry 3. Rozšíření relační algebry 4. Hodnoty null 5. Úpravy relací 6. Stručný úvod do SQL 7. SQL a relace 8. Základní příkazy
Je regulární? Pokud ne, na regulární ji upravte. V původní a nové gramatice odvod te řetěz 1111.
 Grmtiky. Vytvořte grmtiku generující množinu řetězů { n m } pro n, m N {} tková, že n m. Pomocí této grmtiky derivujte řetezy,. 2. Grmtik je dán prvidly S ɛ S A A S B B A B. Je regulární? Pokud ne, n regulární
Grmtiky. Vytvořte grmtiku generující množinu řetězů { n m } pro n, m N {} tková, že n m. Pomocí této grmtiky derivujte řetezy,. 2. Grmtik je dán prvidly S ɛ S A A S B B A B. Je regulární? Pokud ne, n regulární
Zavedení a vlastnosti reálných čísel PŘIROZENÁ, CELÁ A RACIONÁLNÍ ČÍSLA
 Zvedení vlstnosti reálných čísel Reálná čísl jsou zákldním kmenem mtemtické nlýzy. Konstrukce reálných čísel sice není náplní mtemtické nlýzy, le množin reálných čísel R je pro mtemtickou nlýzu zákldním
Zvedení vlstnosti reálných čísel Reálná čísl jsou zákldním kmenem mtemtické nlýzy. Konstrukce reálných čísel sice není náplní mtemtické nlýzy, le množin reálných čísel R je pro mtemtickou nlýzu zákldním
Sémantický Web SPARQL
 4 TVEZEWXYHMN LSTVSKVEQY-JSVQEXMOENITSHTSVSZ ETVSNIOXIQEGSZE Q ^)ZVSTWO LSWSGM P LSJSHYEVS^TS XYLPEZ LSQ WXE4VEL] 4VELE)9-ZIWXYNIQIHSZE% FYHSYGSWXM Sémntický We SPAQL BI - TWA Peter Vojtáš Od XML ke DF,
4 TVEZEWXYHMN LSTVSKVEQY-JSVQEXMOENITSHTSVSZ ETVSNIOXIQEGSZE Q ^)ZVSTWO LSWSGM P LSJSHYEVS^TS XYLPEZ LSQ WXE4VEL] 4VELE)9-ZIWXYNIQIHSZE% FYHSYGSWXM Sémntický We SPAQL BI - TWA Peter Vojtáš Od XML ke DF,
56. ročník Matematické olympiády. b 1,2 = 27 ± c 2 25
 56. ročník Mtemtické olympiády Úlohy domácí části I. kol ktegorie 1. Njděte všechny dvojice (, ) celých čísel, jež vyhovují rovnici + 7 + 6 + 5 + 4 + = 0. Řešení. Rovnici řešíme jko kvdrtickou s neznámou
56. ročník Mtemtické olympiády Úlohy domácí části I. kol ktegorie 1. Njděte všechny dvojice (, ) celých čísel, jež vyhovují rovnici + 7 + 6 + 5 + 4 + = 0. Řešení. Rovnici řešíme jko kvdrtickou s neznámou
Databáze SQL SELECT. David Hoksza http://siret.cz/hoksza
 Databáze SQL SELECT David Hoksza http://siret.cz/hoksza Osnova Úvod do SQL Základní dotazování v SQL Cvičení základní dotazování v SQL Structured Query Language (SQL) SQL napodobuje jednoduché anglické
Databáze SQL SELECT David Hoksza http://siret.cz/hoksza Osnova Úvod do SQL Základní dotazování v SQL Cvičení základní dotazování v SQL Structured Query Language (SQL) SQL napodobuje jednoduché anglické
Lineární algebra. 1) Vektor, lineární závislost a nezávislost. Def.: Číselným vektorem n-rozměrného prostoru nazýváme uspořádanou množinu n čísel
 Lineání lge ) Vekto, lineání záislost nezáislost Def: Číselným ektoem n-ozměného postou nzýáme uspořádnou množinu n čísel,, ) ( n Čísl,, n nzýáme souřdnice ektou, číslo n dimenzí neo ozměem ektou Opece
Lineání lge ) Vekto, lineání záislost nezáislost Def: Číselným ektoem n-ozměného postou nzýáme uspořádnou množinu n čísel,, ) ( n Čísl,, n nzýáme souřdnice ektou, číslo n dimenzí neo ozměem ektou Opece
Půjdu do kina Bude pršet Zajímavý film. Jedině poslední řádek tabulky vyhovuje splnění podmínky úvodního tvrzení.
 4. Booleov lger Booleov lger yl nvržen v polovině 9. století mtemtikem Georgem Boolem, tehdy nikoliv k návrhu digitálníh ovodů, nýrž jko mtemtikou disiplínu k formuli logikého myšlení. Jko příkld použijeme
4. Booleov lger Booleov lger yl nvržen v polovině 9. století mtemtikem Georgem Boolem, tehdy nikoliv k návrhu digitálníh ovodů, nýrž jko mtemtikou disiplínu k formuli logikého myšlení. Jko příkld použijeme
4. Determinanty. Výpočet: a11. a22. a21. a12. = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 a 13 a 22 a 31. a 11 a 23 a 32 a 12 a 21 a 33
 . Determinnty Determinnt, znčíme deta, je číslo přiřzené čtvercové mtici A. Je zveden tk, by pro invertibilní mtici byl nenulový pro neinvertibilní mtici byl roven nule. Výpočet: = + = + + - - - + + +
. Determinnty Determinnt, znčíme deta, je číslo přiřzené čtvercové mtici A. Je zveden tk, by pro invertibilní mtici byl nenulový pro neinvertibilní mtici byl roven nule. Výpočet: = + = + + - - - + + +
Logaritmické rovnice I
 .9.9 Logritmické rovnice I Předpokldy: 95 Pedgogická poznámk: Stejně jko u eponenciálních rovnic rozkldů n součin bereme ritmické rovnice jko nácvik výběru metody. Sestvujeme si rzenál metod n konci máme
.9.9 Logritmické rovnice I Předpokldy: 95 Pedgogická poznámk: Stejně jko u eponenciálních rovnic rozkldů n součin bereme ritmické rovnice jko nácvik výběru metody. Sestvujeme si rzenál metod n konci máme
V předchozích kapitolách byla popsána inverzní operace k derivování. Zatím nebylo jasné, k čemu tento nástroj slouží.
 NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování Ztím nebylo jsné, k čemu tento nástroj slouží Uvžujme trmvj, která je poháněn elektřinou při brždění vyrábí dynmem elektřinu:
NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování Ztím nebylo jsné, k čemu tento nástroj slouží Uvžujme trmvj, která je poháněn elektřinou při brždění vyrábí dynmem elektřinu:
Formální jazyky. Z. Sawa (VŠB-TUO) Úvod do teoretické informatiky 7. března / 46
 Formální jzyky Z. Sw (VŠB-TUO) Úvod do teoretické informtiky 7. řezn 2012 1/ 46 Teorie formálních jzyků motivce Příkldy typů prolémů, při jejichž řešení se využívá pozntků z teorie formálních jzyků: Tvor
Formální jzyky Z. Sw (VŠB-TUO) Úvod do teoretické informtiky 7. řezn 2012 1/ 46 Teorie formálních jzyků motivce Příkldy typů prolémů, při jejichž řešení se využívá pozntků z teorie formálních jzyků: Tvor
( ) ( ) Sinová věta II. β je úhel z intervalu ( 0;π ). Jak je vidět z jednotkové kružnice, úhly, pro které platí. Předpoklady:
 4.4. Sinová vět II Předpokldy 44 Kde se stl hy? Námi nlezené řešení je správné, le nenšli jsme druhé hy ve hvíli, kdy jsme z hodnoty sin β určovli úhel β. β je úhel z intervlu ( ;π ). Jk je vidět z jednotkové
4.4. Sinová vět II Předpokldy 44 Kde se stl hy? Námi nlezené řešení je správné, le nenšli jsme druhé hy ve hvíli, kdy jsme z hodnoty sin β určovli úhel β. β je úhel z intervlu ( ;π ). Jk je vidět z jednotkové
Podobnosti trojúhelníků, goniometrické funkce
 1116 Podonosti trojúhelníků, goniometriké funke Předpokldy: 010104, úhel Pedgogiká poznámk: Zčátek zryhlit α γ β K α' l M γ' m k β' L Trojúhelníky KLM n nšem orázku mjí stejný tvr (vypdjí stejně), le liší
1116 Podonosti trojúhelníků, goniometriké funke Předpokldy: 010104, úhel Pedgogiká poznámk: Zčátek zryhlit α γ β K α' l M γ' m k β' L Trojúhelníky KLM n nšem orázku mjí stejný tvr (vypdjí stejně), le liší
Seznámíte se s další aplikací určitého integrálu výpočtem obsahu pláště rotačního tělesa.
 .4. Obsh pláště otčního těles.4. Obsh pláště otčního těles Cíle Seznámíte se s dlší plikcí učitého integálu výpočtem obshu pláště otčního těles. Předpokládné znlosti Předpokládáme, že jste si postudovli
.4. Obsh pláště otčního těles.4. Obsh pláště otčního těles Cíle Seznámíte se s dlší plikcí učitého integálu výpočtem obshu pláště otčního těles. Předpokládné znlosti Předpokládáme, že jste si postudovli
P2 Číselné soustavy, jejich převody a operace v čís. soustavách
 P Číselné soustvy, jejich převody operce v čís. soustvách. Zobrzení čísl v libovolné číselné soustvě Lidé využívjí ve svém životě pro zápis čísel desítkovou soustvu. V této soustvě máme pro zápis čísel
P Číselné soustvy, jejich převody operce v čís. soustvách. Zobrzení čísl v libovolné číselné soustvě Lidé využívjí ve svém životě pro zápis čísel desítkovou soustvu. V této soustvě máme pro zápis čísel
NEWTONŮV INTEGRÁL. V předchozích kapitolách byla popsána inverzní operace k derivování. Zatím nebylo jasné, k čemu tento nástroj slouží.
 NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování. Ztím nebylo jsné, k čemu tento nástroj slouží. Uvžujme trmvj, která je poháněn elektřinou při brždění vyrábí dynmem elektřinu:
NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování. Ztím nebylo jsné, k čemu tento nástroj slouží. Uvžujme trmvj, která je poháněn elektřinou při brždění vyrábí dynmem elektřinu:
Matice. a B =...,...,...,...,..., prvků z tělesa T (tímto. Definice: Soubor A = ( a. ...,..., ra
 Definice: Soubor A ( i j ) Mtice 11 12 1n 21 22 2n m 1 m2 prvků z těles T (tímto tělesem T bude v nší prxi nejčstěji těleso reálných čísel R resp těleso rcionálních čísel Q či těleso komplexních čísel
Definice: Soubor A ( i j ) Mtice 11 12 1n 21 22 2n m 1 m2 prvků z těles T (tímto tělesem T bude v nší prxi nejčstěji těleso reálných čísel R resp těleso rcionálních čísel Q či těleso komplexních čísel
( a) Okolí bodu
 0..5 Okolí bodu Předpokldy: 40 Pedgogická poznámk: Hodin zjevně překrčuje možnosti většiny studentů v 45 minutách. Myslím, že nemá cenu přethovt do dlší hodiny, příkldy s redukovnými okolími nejsou nutné,
0..5 Okolí bodu Předpokldy: 40 Pedgogická poznámk: Hodin zjevně překrčuje možnosti většiny studentů v 45 minutách. Myslím, že nemá cenu přethovt do dlší hodiny, příkldy s redukovnými okolími nejsou nutné,
Geometrické a fyzikální aplikace určitého integrálu. = b a. je v intervalu a, b záporná, je integrál rovněž záporný.
 4. přednášk Geometické zikální plikce učitého integálu Geometické plikce. Osh ovinného útvu A. Pokud se jedná o ovinný útv omezený osou přímkmi gem spojité nezáponé unkce pk je jeho osh dán učitým integálem
4. přednášk Geometické zikální plikce učitého integálu Geometické plikce. Osh ovinného útvu A. Pokud se jedná o ovinný útv omezený osou přímkmi gem spojité nezáponé unkce pk je jeho osh dán učitým integálem
Axiální ložiska. Průměr díry Strana. S rovinnou nebo kulovou dosedací plochou, nebo s podložkou AXIÁLNÍ VÁLEČKOVÁ LOŽISKA
 xiální ložisk JEDNOSMĚNÁ XIÁLNÍ KULIČKOVÁ LOŽISK Půmě díy Stn neo kulovou, neo s podložkou 0 00 mm... B242 0 60 mm... B246 OBOUSMĚNÁ XIÁLNÍ KULIČKOVÁ LOŽISK neo kulovou, neo s podložkou XIÁLNÍ VÁLEČKOVÁ
xiální ložisk JEDNOSMĚNÁ XIÁLNÍ KULIČKOVÁ LOŽISK Půmě díy Stn neo kulovou, neo s podložkou 0 00 mm... B242 0 60 mm... B246 OBOUSMĚNÁ XIÁLNÍ KULIČKOVÁ LOŽISK neo kulovou, neo s podložkou XIÁLNÍ VÁLEČKOVÁ
Obecně: K dané funkci f hledáme funkci ϕ z dané množiny funkcí M, pro kterou v daných bodech x 0 < x 1 <... < x n. (δ ij... Kroneckerovo delta) (4)
 KAPITOLA 13: Numerická integrce interpolce [MA1-18:P13.1] 13.1 Interpolce Obecně: K dné funkci f hledáme funkci ϕ z dné množiny funkcí M, pro kterou v dných bodech x 0 < x 1
KAPITOLA 13: Numerická integrce interpolce [MA1-18:P13.1] 13.1 Interpolce Obecně: K dné funkci f hledáme funkci ϕ z dné množiny funkcí M, pro kterou v dných bodech x 0 < x 1
Definice. Nechť k 0 celé, a < b R. Definujeme. x < 1. ϕ(x) 0 v R. Lemma [Slabá formulace diferenciální rovnice.] x 2 1
![Definice. Nechť k 0 celé, a < b R. Definujeme. x < 1. ϕ(x) 0 v R. Lemma [Slabá formulace diferenciální rovnice.] x 2 1 Definice. Nechť k 0 celé, a < b R. Definujeme. x < 1. ϕ(x) 0 v R. Lemma [Slabá formulace diferenciální rovnice.] x 2 1](/thumbs/103/161289080.jpg) 9. Vriční počet. Definice. Nechť k 0 celé, < b R. Definujeme C k ([, b]) = { ỹ [,b] : ỹ C k (R) } ; C 0 ([, b]) = { y C ([, b]) : y() = y(b) = 0 }. Důležitá konstrukce. Shlzovcí funkce (molifiér, bump
9. Vriční počet. Definice. Nechť k 0 celé, < b R. Definujeme C k ([, b]) = { ỹ [,b] : ỹ C k (R) } ; C 0 ([, b]) = { y C ([, b]) : y() = y(b) = 0 }. Důležitá konstrukce. Shlzovcí funkce (molifiér, bump
Minimalizace automatů. M. Kot, Z. Sawa (VŠB-TU Ostrava) Úvod do teoretické informatiky 28. března / 31
 Minimlizce utomtů M. Kot, Z. Sw (VŠB-TU Ostrv) Úvod do teoretické informtiky 28. řezn 2007 1/ 31 Ekvivlence utomtů 1 2 3 1 2 3 1 2 Všechny 3 utomty přijímjí jzyk všech slov se sudým počtem -ček Nejvýhodnějšíjepronásposledníznich-mánejméněstvů
Minimlizce utomtů M. Kot, Z. Sw (VŠB-TU Ostrv) Úvod do teoretické informtiky 28. řezn 2007 1/ 31 Ekvivlence utomtů 1 2 3 1 2 3 1 2 Všechny 3 utomty přijímjí jzyk všech slov se sudým počtem -ček Nejvýhodnějšíjepronásposledníznich-mánejméněstvů
5.1.5 Základní vztahy mezi body, přímkami a rovinami
 5.1.5 Zákldní vzthy mezi body, přímkmi rovinmi Předpokldy: 510 Prostor má tři rozměry, skládá se z bodů přímk - jednorozměrná podmnožin prostoru (množin bodů), rovin - dvojrozměrná podmnožin prostoru (množin
5.1.5 Zákldní vzthy mezi body, přímkmi rovinmi Předpokldy: 510 Prostor má tři rozměry, skládá se z bodů přímk - jednorozměrná podmnožin prostoru (množin bodů), rovin - dvojrozměrná podmnožin prostoru (množin
3 Algebraické výrazy. 3.1 Mnohočleny Mnohočleny jsou zvláštním případem výrazů. Mnohočlen (polynom) proměnné je výraz tvaru
 Algerické výrz V knize přírod může číst jen ten, kdo zná jzk, ve kterém je npsán. Jejím jzkem je mtemtik jejím písmem jsou mtemtické vzorce. (Glileo Glilei) Algerickým výrzem rozumíme zápis, ve kterém
Algerické výrz V knize přírod může číst jen ten, kdo zná jzk, ve kterém je npsán. Jejím jzkem je mtemtik jejím písmem jsou mtemtické vzorce. (Glileo Glilei) Algerickým výrzem rozumíme zápis, ve kterém
Definice. Necht M = (Q, T, δ, q 0, F ) je konečný automat. Dvojici (q, w) Q T nazveme konfigurací konečného automatu M.
 BI-AAG (20/202) J. Holu: 2. Deterministické nedeterministické konečné utomty p. 2/3 Konfigurce konečného utomtu BI-AAG (20/202) J. Holu: 2. Deterministické nedeterministické konečné utomty p. 4/3 Automty
BI-AAG (20/202) J. Holu: 2. Deterministické nedeterministické konečné utomty p. 2/3 Konfigurce konečného utomtu BI-AAG (20/202) J. Holu: 2. Deterministické nedeterministické konečné utomty p. 4/3 Automty
Funkce. Mgr. Jarmila Zelená. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
 Funkce Mg. Jmil Zelená Gymnázium, SOŠ VOŠ Ledeč nd Sázvou Eponenciální ovnice VY INOVACE_05 M Gymnázium, SOŠ VOŠ Ledeč nd Sázvou Eponenciální ovnice = ovnice, ve kteých se neznámá vyskytuje v eponentu
Funkce Mg. Jmil Zelená Gymnázium, SOŠ VOŠ Ledeč nd Sázvou Eponenciální ovnice VY INOVACE_05 M Gymnázium, SOŠ VOŠ Ledeč nd Sázvou Eponenciální ovnice = ovnice, ve kteých se neznámá vyskytuje v eponentu
Automaty a gramatiky(bi-aag)
 BI-AAG (2011/2012) J. Holu: 3. Operce s konečnými utomty p. 2/33 Převod NKA ndka BI-AAG (2011/2012) J. Holu: 3. Operce s konečnými utomty p. 4/33 Automty grmtiky(bi-aag) 3. Operce s konečnými utomty Jn
BI-AAG (2011/2012) J. Holu: 3. Operce s konečnými utomty p. 2/33 Převod NKA ndka BI-AAG (2011/2012) J. Holu: 3. Operce s konečnými utomty p. 4/33 Automty grmtiky(bi-aag) 3. Operce s konečnými utomty Jn
Úvod do databázových systémů
 Vysoká škola báňská Technická univerzita Ostrava Fakulta elektrotechniky a informatiky Úvod do databázových systémů Cvičení 3 Ing. Petr Lukáš petr.lukas@vsb.cz Ostrava, 2014 Opakování 4 fáze vytváření
Vysoká škola báňská Technická univerzita Ostrava Fakulta elektrotechniky a informatiky Úvod do databázových systémů Cvičení 3 Ing. Petr Lukáš petr.lukas@vsb.cz Ostrava, 2014 Opakování 4 fáze vytváření
8. Elementární funkce
 Historie přírodních věd potvrzuje, že většinu reálně eistujících dějů lze reprezentovt mtemtickými model, které jsou popsán tzv. elementárními funkcemi. Elementární funkce je kždá funkce, která vznikne
Historie přírodních věd potvrzuje, že většinu reálně eistujících dějů lze reprezentovt mtemtickými model, které jsou popsán tzv. elementárními funkcemi. Elementární funkce je kždá funkce, která vznikne
Přednáška 9: Limita a spojitost
 4 / XI /, 5: Přednášk 9: Limit spojitost V minulých přednáškách jsme podrobněji prozkoumli důležitý pojem funkce. Při řešení konkrétních problémů se nše znlosti (npř. nměřená dt) zpisují jko funkční hodnoty
4 / XI /, 5: Přednášk 9: Limit spojitost V minulých přednáškách jsme podrobněji prozkoumli důležitý pojem funkce. Při řešení konkrétních problémů se nše znlosti (npř. nměřená dt) zpisují jko funkční hodnoty
INTEGRACE KOMPLEXNÍ FUNKCE KŘIVKOVÝ INTEGRÁL
 INTEGRAE KOMPLEXNÍ FUNKE KŘIVKOVÝ INTEGRÁL N konci kpitoly o derivci je uveden souvislost existence derivce s potenciálním polem. Existuje dlší chrkterizce potenciálného pole, která nebyl v kpitole o derivci
INTEGRAE KOMPLEXNÍ FUNKE KŘIVKOVÝ INTEGRÁL N konci kpitoly o derivci je uveden souvislost existence derivce s potenciálním polem. Existuje dlší chrkterizce potenciálného pole, která nebyl v kpitole o derivci
Odraz na kulové ploše
 Odz n kulové ploše Duté zcdlo o.. os zcdl V.. vchol zcdl S.. střed zcdl (kul. ploch).. polomě zcdl (kul. ploch) Ppsek vchází z odu A n ose zcdl po odzu n zcdle dopdá do nějkého odu B n ose. tojúhelníků
Odz n kulové ploše Duté zcdlo o.. os zcdl V.. vchol zcdl S.. střed zcdl (kul. ploch).. polomě zcdl (kul. ploch) Ppsek vchází z odu A n ose zcdl po odzu n zcdle dopdá do nějkého odu B n ose. tojúhelníků
Odraz na kulové ploše Duté zrcadlo
 Odz n kulové ploše Duté zcdlo o.. os zcdl V.. vchol zcdl S.. střed zcdl (kul. ploch).. polomě zcdl (kul. ploch) Ppsek vchází z odu A n ose zcdl po odzu n zcdle dopdá do nějkého odu B n ose. Podle oázku
Odz n kulové ploše Duté zcdlo o.. os zcdl V.. vchol zcdl S.. střed zcdl (kul. ploch).. polomě zcdl (kul. ploch) Ppsek vchází z odu A n ose zcdl po odzu n zcdle dopdá do nějkého odu B n ose. Podle oázku
Převody Regulárních Výrazů. Minimalizace Konečných. Regulární jazyky 2 p.1/35
 Převody Regulárních Výrzů Minimlizce Konečných Automtů Regulární jzyky 2 p.1/35 Kleeneho lger Definice 2.1 Kleeneho lger sestává z neprázdné množiny se dvěm význčnými konstntmi 0 1, dvěm inárními opercemi
Převody Regulárních Výrzů Minimlizce Konečných Automtů Regulární jzyky 2 p.1/35 Kleeneho lger Definice 2.1 Kleeneho lger sestává z neprázdné množiny se dvěm význčnými konstntmi 0 1, dvěm inárními opercemi
Integrální počet - III. část (určitý vlastní integrál)
 Integrální počet - III. část (určitý vlstní integrál) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 8. přednášk z AMA1 Michl Fusek (fusekmi@feec.vutbr.cz) 1 / 18 Obsh 1 Určitý vlstní (Riemnnův)
Integrální počet - III. část (určitý vlstní integrál) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 8. přednášk z AMA1 Michl Fusek (fusekmi@feec.vutbr.cz) 1 / 18 Obsh 1 Určitý vlstní (Riemnnův)
Lineární nerovnice a jejich soustavy
 teorie řešené úlohy cvičení tipy k mturitě výsledky Lineární nerovnice jejich soustvy Víš, že pojem nerovnice není opkem pojmu rovnice? lineární rovnice má většinou jediné řešení, kdežto lineární nerovnice
teorie řešené úlohy cvičení tipy k mturitě výsledky Lineární nerovnice jejich soustvy Víš, že pojem nerovnice není opkem pojmu rovnice? lineární rovnice má většinou jediné řešení, kdežto lineární nerovnice
= b a. V případě, že funkce f(x) je v intervalu <a,b> záporná, je integrál rovněž záporný.
 5. přednášk APLIKAE URČITÉHO INTERÁLU Pomocí integálního počtu je možné vpočítt osh ovinných útvů ojem otčních těles délk ovinných křivek. Velké upltnění má učitý integál tké ve zice chemii. eometické
5. přednášk APLIKAE URČITÉHO INTERÁLU Pomocí integálního počtu je možné vpočítt osh ovinných útvů ojem otčních těles délk ovinných křivek. Velké upltnění má učitý integál tké ve zice chemii. eometické
3.2.1 Shodnost trojúhelníků I
 3.2.1 hodnost trojúhelníků I Předpokldy: 3108 v útvry jsou shodné, pokud je možné je přemístěním ztotožnit. v prxi těžko proveditelné hledáme jinou možnost ověření shodnosti v útvry jsou shodné, pokud
3.2.1 hodnost trojúhelníků I Předpokldy: 3108 v útvry jsou shodné, pokud je možné je přemístěním ztotožnit. v prxi těžko proveditelné hledáme jinou možnost ověření shodnosti v útvry jsou shodné, pokud
Databázové systémy Cvičení 5.3
 Databázové systémy Cvičení 5.3 SQL jako jazyk pro manipulaci s daty SQL jako jazyk pro manipulaci s daty Aktualizace dat v SQL úprava záznamů v relacích (tabulkách) vložení záznamu INSERT INTO oprava záznamu
Databázové systémy Cvičení 5.3 SQL jako jazyk pro manipulaci s daty SQL jako jazyk pro manipulaci s daty Aktualizace dat v SQL úprava záznamů v relacích (tabulkách) vložení záznamu INSERT INTO oprava záznamu
2. Funkční řady Studijní text. V předcházející kapitole jsme uvažovali řady, jejichž členy byla reálná čísla. Nyní se budeme zabývat studiem
 2. Funkční řd Studijní text 2. Funkční řd V předcházející kpitole jsme uvžovli řd, jejichž člen bl reálná čísl. Nní se budeme zbývt studiem obecnějšího přípdu, kd člen řd tvoří reálné funkce. Definice
2. Funkční řd Studijní text 2. Funkční řd V předcházející kpitole jsme uvžovli řd, jejichž člen bl reálná čísl. Nní se budeme zbývt studiem obecnějšího přípdu, kd člen řd tvoří reálné funkce. Definice
MATA Př 2. Složené výroky: Jsou dány výroky: a: Číslo 5 je prvočíslo. b: Číslo 5 je sudé. c: Číslo 5 je liché. d: Číslo 5 je záporné.
 MATA Př 2 Složené výroky: Jsou dány výroky: : Číslo 5 je prvočíslo. : Číslo 5 je sudé. c: Číslo 5 je liché. d: Číslo 5 je záporné. Konjunkce disjunkce Konjunkce liovolných výroků, je výrok, který vznikne
MATA Př 2 Složené výroky: Jsou dány výroky: : Číslo 5 je prvočíslo. : Číslo 5 je sudé. c: Číslo 5 je liché. d: Číslo 5 je záporné. Konjunkce disjunkce Konjunkce liovolných výroků, je výrok, který vznikne
KŘIVKOVÉ INTEGRÁLY. Křivka v prostoru je popsána spojitými funkcemi ϕ, ψ, τ : [a, b] R jako množina bodů {(ϕ(t), ψ(t), τ(t)); t
![KŘIVKOVÉ INTEGRÁLY. Křivka v prostoru je popsána spojitými funkcemi ϕ, ψ, τ : [a, b] R jako množina bodů {(ϕ(t), ψ(t), τ(t)); t KŘIVKOVÉ INTEGRÁLY. Křivka v prostoru je popsána spojitými funkcemi ϕ, ψ, τ : [a, b] R jako množina bodů {(ϕ(t), ψ(t), τ(t)); t](/thumbs/88/114636682.jpg) KŘIVKOVÉ INTEGRÁLY Má-li se spočítt npř. spotřeb betonu n rovný plot s měnící se výškou, stčí spočítt integrál z této výšky podle zákldny plotu. o když je le zákldnou plotu nikoli rovná úsečk, le křivá
KŘIVKOVÉ INTEGRÁLY Má-li se spočítt npř. spotřeb betonu n rovný plot s měnící se výškou, stčí spočítt integrál z této výšky podle zákldny plotu. o když je le zákldnou plotu nikoli rovná úsečk, le křivá
Vzdělávací materiál. vytvořený v projektu OP VK. Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20. Číslo projektu: CZ.1.07/1.5.00/34.
 Vzdělávcí mteriál vytvořený v projektu OP VK Název školy: Gymnázium, Zářeh, náměstí Osvoození 20 Číslo projektu: Název projektu: Číslo název klíčové ktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek pro
Vzdělávcí mteriál vytvořený v projektu OP VK Název školy: Gymnázium, Zářeh, náměstí Osvoození 20 Číslo projektu: Název projektu: Číslo název klíčové ktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek pro
Technická dokumentace Ing. Lukáš Procházka
 Tehniká dokumente ng Lukáš Proházk Tém: hlvní část dokumentu, orázky, tulky grfy 1) Osh hlvní části dokumentu ) Orázky, tulky grfy ) Vzore rovnie Hlvní část dokumentu Hlvní část dokumentu je řzen v následujíím
Tehniká dokumente ng Lukáš Proházk Tém: hlvní část dokumentu, orázky, tulky grfy 1) Osh hlvní části dokumentu ) Orázky, tulky grfy ) Vzore rovnie Hlvní část dokumentu Hlvní část dokumentu je řzen v následujíím
VIII. Primitivní funkce a Riemannův integrál
 VIII. Primitivní funkce Riemnnův integrál VIII.2. Riemnnův integrál opkování Vět. Nechť f je spojitá funkce n intervlu, b nechť c, b. Oznčíme-li F (x) = x (, b), pk F (x) = f(x) pro kždé x (, b). VIII.3.
VIII. Primitivní funkce Riemnnův integrál VIII.2. Riemnnův integrál opkování Vět. Nechť f je spojitá funkce n intervlu, b nechť c, b. Oznčíme-li F (x) = x (, b), pk F (x) = f(x) pro kždé x (, b). VIII.3.
Křivkový integrál funkce
 Kpitol 6 Křivkový integrál funkce efinice způsob výpočtu Hlvním motivem pro definici určitého integrálu funkce jedné proměnné byl úloh stnovit obsh oblsti omezené grfem dné funkce intervlem n ose x. Řd
Kpitol 6 Křivkový integrál funkce efinice způsob výpočtu Hlvním motivem pro definici určitého integrálu funkce jedné proměnné byl úloh stnovit obsh oblsti omezené grfem dné funkce intervlem n ose x. Řd
Úvod do Teoretické Informatiky (456-511 UTI)
 Úvod do Teoretické Informtiky (456-511 UTI) Doc. RNDr. Petr Hliněný, Ph.D. petr.hlineny@vs.cz 25. ledn 2006 Verze 1.02. Copyright c 2004 2006 Petr Hliněný. (S využitím části mteriálů c Petr Jnčr.) Osh
Úvod do Teoretické Informtiky (456-511 UTI) Doc. RNDr. Petr Hliněný, Ph.D. petr.hlineny@vs.cz 25. ledn 2006 Verze 1.02. Copyright c 2004 2006 Petr Hliněný. (S využitím části mteriálů c Petr Jnčr.) Osh
Úvod do databázových systémů
 Vysoká škola báňská Technická univerzita Ostrava Fakulta elektrotechniky a informatiky Katedra informatiky Database Research Group Úvod do databázových systémů Cvičení 3 Ing. Petr Lukáš petr.lukas@vsb.cz
Vysoká škola báňská Technická univerzita Ostrava Fakulta elektrotechniky a informatiky Katedra informatiky Database Research Group Úvod do databázových systémů Cvičení 3 Ing. Petr Lukáš petr.lukas@vsb.cz
s N, r > s platí: Základní požadavek na krásu matematického pravidla: Musí být co nejobecnější s minimem a a = a = a. Nemohli bychom ho upravit tak,
 .6. Mocniny celý ocnitele I Předpokldy: 6, 6 Př. : Kteé ze dvou pvidel je teticky hezčí? ) Po kždé R, N pltí: +. ) Po kždé R,, N, > pltí:. Zákldní poždvek n káu tetického pvidl: Muí ýt co nejoecnější inie
.6. Mocniny celý ocnitele I Předpokldy: 6, 6 Př. : Kteé ze dvou pvidel je teticky hezčí? ) Po kždé R, N pltí: +. ) Po kždé R,, N, > pltí:. Zákldní poždvek n káu tetického pvidl: Muí ýt co nejoecnější inie
2.9.14 Věty o logaritmech I
 .9.1 Věty o itmech I Předpokldy: 910 Pedgogická poznámk: Tto náledující hodin e djí tihnout njednou, pokud oželíte počítání v tbulce někteé příkldy n konci příští hodiny. Přijde mi to tochu škod, nžím
.9.1 Věty o itmech I Předpokldy: 910 Pedgogická poznámk: Tto náledující hodin e djí tihnout njednou, pokud oželíte počítání v tbulce někteé příkldy n konci příští hodiny. Přijde mi to tochu škod, nžím
+ c. n x ( ) ( ) f x dx ln f x c ) a. x x. dx = cotgx + c. A x. A x A arctgx + A x A c
 ) INTEGRÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem neurčitého integrálu Je dán funkce Pltí všk tké F tk, y pltilo F ( ) f ( ) Zřejmě F ( ), protože pltí, 5,, oecně c, kde c je liovolná kon- stnt f ( ) nším
) INTEGRÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem neurčitého integrálu Je dán funkce Pltí všk tké F tk, y pltilo F ( ) f ( ) Zřejmě F ( ), protože pltí, 5,, oecně c, kde c je liovolná kon- stnt f ( ) nším
Diferenciální počet. Spojitost funkce
 Dierenciální počet Spojitost unkce Co to znmená, že unkce je spojitá? Jký je mtemtický význm tvrzení, že gr unkce je spojitý? Jké jsou vlstnosti unkce v bodě? Jké jsou vlstnosti unkce v intervlu I? Vlstnosti
Dierenciální počet Spojitost unkce Co to znmená, že unkce je spojitá? Jký je mtemtický význm tvrzení, že gr unkce je spojitý? Jké jsou vlstnosti unkce v bodě? Jké jsou vlstnosti unkce v intervlu I? Vlstnosti
množina, na které je zavedena určitá struktura. Zejména, součet každých dvou prvků X = [x 1,..., x n ] R n,
![množina, na které je zavedena určitá struktura. Zejména, součet každých dvou prvků X = [x 1,..., x n ] R n, množina, na které je zavedena určitá struktura. Zejména, součet každých dvou prvků X = [x 1,..., x n ] R n,](/thumbs/99/140214707.jpg) Náplní předmětu bude klkulus R n R (přípdně R m ). Proč se zbývt funkcemi více proměnných? V prxi je čsto třeb uvžovt veličiny, které závisejí n více než jedné proměnné, npř. objem rotčního kužele závisí
Náplní předmětu bude klkulus R n R (přípdně R m ). Proč se zbývt funkcemi více proměnných? V prxi je čsto třeb uvžovt veličiny, které závisejí n více než jedné proměnné, npř. objem rotčního kužele závisí
Deterministický konečný automat
 Deterministický konečný utomt Formálně je deterministický konečný utomt definován jko pětice (Q,Σ,δ,q 0,F) kde: Q je konečná množin stvů Σ je konečná eced δ:q Σ Qjepřechodováfunkce q 0 Qjepočátečnístv
Deterministický konečný utomt Formálně je deterministický konečný utomt definován jko pětice (Q,Σ,δ,q 0,F) kde: Q je konečná množin stvů Σ je konečná eced δ:q Σ Qjepřechodováfunkce q 0 Qjepočátečnístv
13. Exponenciální a logaritmická funkce
 @11 1. Eponenciální logritmická funkce Mocninná funkce je pro r libovolné nenulové reálné číslo dán předpisem f: y = r, r R, >0 Eponent r je konstnt je nezávisle proměnná. Definičním oborem jsou pouze
@11 1. Eponenciální logritmická funkce Mocninná funkce je pro r libovolné nenulové reálné číslo dán předpisem f: y = r, r R, >0 Eponent r je konstnt je nezávisle proměnná. Definičním oborem jsou pouze
Integrální počet - II. část (určitý integrál a jeho aplikace)
 Integrální počet - II. část (určitý integrál jeho plikce) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 7. přednášk z ESMAT Michl Fusek (fusekmi@feec.vutbr.cz) 1 / 23 Obsh 1 Určitý vlstní (Riemnnův)
Integrální počet - II. část (určitý integrál jeho plikce) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 7. přednášk z ESMAT Michl Fusek (fusekmi@feec.vutbr.cz) 1 / 23 Obsh 1 Určitý vlstní (Riemnnův)
Až dosud jsme se zabývali většinou reálnými posloupnostmi, tedy zobrazeními s definičním
 Limit funkce. Zákldní pojmy Až dosud jsme se zbývli většinou reálnými posloupnostmi, tedy zobrzeními s definičním oborem N. Nyní obrátíme svou pozornost n širší třídu zobrzení. Definice.. Zobrzení f, jehož
Limit funkce. Zákldní pojmy Až dosud jsme se zbývli většinou reálnými posloupnostmi, tedy zobrzeními s definičním oborem N. Nyní obrátíme svou pozornost n širší třídu zobrzení. Definice.. Zobrzení f, jehož
Souhrn základních výpočetních postupů v Excelu probíraných v AVT 04-05 listopad 2004. r r. . b = A
 Souhrn zákldních výpočetních postupů v Ecelu probírných v AVT 04-05 listopd 2004. Řešení soustv lineárních rovnic Soustv lineárních rovnic ve tvru r r A. = b tj. npř. pro 3 rovnice o 3 neznámých 2 3 Hodnoty
Souhrn zákldních výpočetních postupů v Ecelu probírných v AVT 04-05 listopd 2004. Řešení soustv lineárních rovnic Soustv lineárních rovnic ve tvru r r A. = b tj. npř. pro 3 rovnice o 3 neznámých 2 3 Hodnoty
B0M33BDT Technologie pro velká data. Supercvičení SQL, Python, Linux
 B0M33BDT Technologie pro velká data Supercvičení SQL, Python, Linux Sergej Stamenov, Jan Hučín 18. 10. 2017 Osnova cvičení Linux SQL Python 2 SQL pro uživatele aneb co potřebuje znát a umět bigdatový uživatel:
B0M33BDT Technologie pro velká data Supercvičení SQL, Python, Linux Sergej Stamenov, Jan Hučín 18. 10. 2017 Osnova cvičení Linux SQL Python 2 SQL pro uživatele aneb co potřebuje znát a umět bigdatový uživatel:
1.3.8 Množiny - shrnutí
 1.3.8 Množiny - shrnutí Předpokldy: 010307 Pedgogická poznámk: Kpitol o množinách spolu s následujícími dvěm kpitolmi (výroky dělitelnost) slouží k nácviku učení. Součástí učení je tké příprv n písemky
1.3.8 Množiny - shrnutí Předpokldy: 010307 Pedgogická poznámk: Kpitol o množinách spolu s následujícími dvěm kpitolmi (výroky dělitelnost) slouží k nácviku učení. Součástí učení je tké příprv n písemky
2.1 - ( ) ( ) (020201) [ ] [ ]
![2.1 - ( ) ( ) (020201) [ ] [ ] 2.1 - ( ) ( ) (020201) [ ] [ ]](/thumbs/102/155984102.jpg) - FUNKCE A ROVNICE Následující zákldní znlosti je nezbytně nutné umět od okmžiku probrání ž do konce studi mtemtiky n gymnáziu. Vyždováno bude porozumění schopnost plikovt ne pouze mechnicky zopkovt. Některé
- FUNKCE A ROVNICE Následující zákldní znlosti je nezbytně nutné umět od okmžiku probrání ž do konce studi mtemtiky n gymnáziu. Vyždováno bude porozumění schopnost plikovt ne pouze mechnicky zopkovt. Některé
ZÁKLADNÍ POZNATKY. p, kde ČÍSELNÉ MNOŽINY (OBORY) N... množina všech přirozených čísel: 1, 2, 3,, n,
 ZÁKLADNÍ POZNATKY ČÍSELNÉ MNOŽINY (OBORY) N... množin všech přirozených čísel: 1, 2, 3,, n, N0... množin všech celých nezáporných čísel (přirozených čísel s nulou: 0,1, 2, 3,, n, Z... množin všech celých
ZÁKLADNÍ POZNATKY ČÍSELNÉ MNOŽINY (OBORY) N... množin všech přirozených čísel: 1, 2, 3,, n, N0... množin všech celých nezáporných čísel (přirozených čísel s nulou: 0,1, 2, 3,, n, Z... množin všech celých
VIII. Primitivní funkce a Riemannův integrál
 VIII. Primitivní funkce Riemnnův integrál VIII.2. Primitivní funkce Definice. Nechť funkce f je definován n neprázdném otevřeném intervlu I. Řekneme, že funkce F : I R je primitivní funkce k f n intervlu
VIII. Primitivní funkce Riemnnův integrál VIII.2. Primitivní funkce Definice. Nechť funkce f je definován n neprázdném otevřeném intervlu I. Řekneme, že funkce F : I R je primitivní funkce k f n intervlu
Formální jazyky. M. Kot, Z. Sawa (VŠB-TU Ostrava) Úvod do teoretické informatiky 6. března / 48
 Formální jzyky M. Kot, Z. Sw (VŠB-TU Ostrv) Úvod do teoretické informtiky 6. březn 2007 1/ 48 Motivce 1: Vyhledávání v textu Potřebujeme řešit následující problém: Máme řdu různých textů(npř. soubory n
Formální jzyky M. Kot, Z. Sw (VŠB-TU Ostrv) Úvod do teoretické informtiky 6. březn 2007 1/ 48 Motivce 1: Vyhledávání v textu Potřebujeme řešit následující problém: Máme řdu různých textů(npř. soubory n
DERIVACE A INTEGRÁLY VE FYZICE
 DOPLŇKOVÉ TEXTY BB0 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ DERIVACE A INTEGRÁLY VE FYZICE Obsh Derivce... Definice derivce... Prciální derivce... Derivce vektorů... Výpočt derivcí... 3 Algebrická
DOPLŇKOVÉ TEXTY BB0 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ DERIVACE A INTEGRÁLY VE FYZICE Obsh Derivce... Definice derivce... Prciální derivce... Derivce vektorů... Výpočt derivcí... 3 Algebrická
Definice limit I
 08 Definice limit I Předpokld: 006 Pedgogická poznámk: N úvod je třeb upozornit, že tto hodin je ze strn studentů snd nejvíce sbotovnou látkou z celé studium (podle rekcí 4B009) Jejich ochot brát n vědomí
08 Definice limit I Předpokld: 006 Pedgogická poznámk: N úvod je třeb upozornit, že tto hodin je ze strn studentů snd nejvíce sbotovnou látkou z celé studium (podle rekcí 4B009) Jejich ochot brát n vědomí
Spojitost funkce v bodě, spojitost funkce v intervalu
 10.1.6 Spojitost funkce v bodě, spojitost funkce v intervlu Předpokldy: 10104, 10105 Př. 1: Nkresli, jk funkce f ( x ) dná grfem zobrzí vyznčené okolí bodu n ose x n osu y. Poté nkresli n osu x vzor okolí
10.1.6 Spojitost funkce v bodě, spojitost funkce v intervlu Předpokldy: 10104, 10105 Př. 1: Nkresli, jk funkce f ( x ) dná grfem zobrzí vyznčené okolí bodu n ose x n osu y. Poté nkresli n osu x vzor okolí
8. cvičení z Matematiky 2
 8. cvičení z Mtemtiky 2 11.-1. dubn 2016 8.1 Njděte tři pozitivní čísl jejichž součin je mximální, jejichž součet je roven 100. Zdání příkldu lze interpretovt tké tk, že hledáme mximální objem kvádru,
8. cvičení z Mtemtiky 2 11.-1. dubn 2016 8.1 Njděte tři pozitivní čísl jejichž součin je mximální, jejichž součet je roven 100. Zdání příkldu lze interpretovt tké tk, že hledáme mximální objem kvádru,
Integrální počet - IV. část (aplikace na určitý vlastní integrál, nevlastní integrál)
 Integrální počet - IV. část (plikce n určitý vlstní integrál, nevlstní integrál) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 9. přednášk z AMA Michl Fusek (fusekmi@feec.vutbr.cz) / 4 Obsh
Integrální počet - IV. část (plikce n určitý vlstní integrál, nevlstní integrál) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 9. přednášk z AMA Michl Fusek (fusekmi@feec.vutbr.cz) / 4 Obsh
10. Suffixové stromy 1 2014-01-23
 10. Suffixové stromy V této kpitole popíšeme jednu pozoruhodnou dtovou strukturu, pomocí níž dokážeme prolémy týkjící se řetězců převádět n grfové prolémy řešit je tk v lineárním čse. Řetězce, trie suffixové
10. Suffixové stromy V této kpitole popíšeme jednu pozoruhodnou dtovou strukturu, pomocí níž dokážeme prolémy týkjící se řetězců převádět n grfové prolémy řešit je tk v lineárním čse. Řetězce, trie suffixové
5.2.4 Kolmost přímek a rovin II
 5..4 Kolmost přímek rovin II Předpokldy: 503 Př. 1: Zformuluj stereometrické věty nlogické k plnimetrické větě: ným bodem lze v rovině k dné přímce vést jedinou kolmici. Vět: ným bodem lze v prostoru k
5..4 Kolmost přímek rovin II Předpokldy: 503 Př. 1: Zformuluj stereometrické věty nlogické k plnimetrické větě: ným bodem lze v rovině k dné přímce vést jedinou kolmici. Vět: ným bodem lze v prostoru k
4.4.1 Sinová věta. Předpoklady: Trigonometrie: řešení úloh o trojúhelnících.
 4.4. Sinová vět Předpokldy Trigonometrie řešení úloh o trojúhelnííh. Prktiké využití změřování měření vzdáleností, tringulční síť Tringulční síť je prolém měřit vzdálenosti dvou odů v krjině změříme velmi
4.4. Sinová vět Předpokldy Trigonometrie řešení úloh o trojúhelnííh. Prktiké využití změřování měření vzdáleností, tringulční síť Tringulční síť je prolém měřit vzdálenosti dvou odů v krjině změříme velmi
Úlohy krajského kola kategorie A
 67. ročník mtemtické olympiády Úlohy krjského kol ktegorie A 1. Pvel střídvě vpisuje křížky kolečk do políček tbulky (zčíná křížkem). Když je tbulk celá vyplněná, výsledné skóre spočítá jko rozdíl X O,
67. ročník mtemtické olympiády Úlohy krjského kol ktegorie A 1. Pvel střídvě vpisuje křížky kolečk do políček tbulky (zčíná křížkem). Když je tbulk celá vyplněná, výsledné skóre spočítá jko rozdíl X O,
5.1.5 Základní vztahy mezi body přímkami a rovinami
 5.1.5 Zákldní vzthy mezi body přímkmi rovinmi Předpokldy: 510 Prostor má tři rozměry, skládá se z bodů. Přímk - jednorozměrná podmnožin prostoru (množin bodů) Rovin - dvojrozměrná podmnožin prostoru (množin
5.1.5 Zákldní vzthy mezi body přímkmi rovinmi Předpokldy: 510 Prostor má tři rozměry, skládá se z bodů. Přímk - jednorozměrná podmnožin prostoru (množin bodů) Rovin - dvojrozměrná podmnožin prostoru (množin
7.5.8 Středová rovnice elipsy
 758 Středová rovnice elips Předpokld: 7501, 7507 Př 1: Vrchol elips leží v odech A[ 1;1], [ 3;1], [ 1;5], [ 1; 3] elips souřdnice jejích ohnisek Urči prmetr Zdné souřdnice už n první pohled vpdjí podezřele,
758 Středová rovnice elips Předpokld: 7501, 7507 Př 1: Vrchol elips leží v odech A[ 1;1], [ 3;1], [ 1;5], [ 1; 3] elips souřdnice jejích ohnisek Urči prmetr Zdné souřdnice už n první pohled vpdjí podezřele,
Svazy. Def Svaz je algebra S ( M ;, ) = se dvěma binárními operacemi taková, že pro libovolné prvky c M platí následující podmínky axiomy svazu:
 vz je lgebr ( M ; ) vzy = se dvěm binárními opercemi tková že pro libovolné prvky b c M pltí následující podmínky xiomy svzu: ( b) c = ( b c) ( b) c = ( b c) b = b b = b ( ) ( ) b = b =. Operce se nzývá
vz je lgebr ( M ; ) vzy = se dvěm binárními opercemi tková že pro libovolné prvky b c M pltí následující podmínky xiomy svzu: ( b) c = ( b c) ( b) c = ( b c) b = b b = b ( ) ( ) b = b =. Operce se nzývá
Mocniny, odmocniny, úpravy. Repetitorium z matematiky
 Mociy, odmociy, úpvy lgeických výzů epetitoium z mtemtiky Podzim Iv culová . Mociy přiozeým celým mocitelem Po kždé eálé čílo kždé přiozeé čílo pltí:... čiitelů moci Zákld mociy (mocěec) mocitel (expoet)
Mociy, odmociy, úpvy lgeických výzů epetitoium z mtemtiky Podzim Iv culová . Mociy přiozeým celým mocitelem Po kždé eálé čílo kždé přiozeé čílo pltí:... čiitelů moci Zákld mociy (mocěec) mocitel (expoet)
Konstrukce na základě výpočtu I
 ..11 Konstrukce n zákldě výpočtu I Předpokldy: Pedgogická poznámk: Původně yl látk rozepsnou do dvou hodin, v první ylo kromě dělení úseček zřzen i čtvrtá geometrická úměrná. Právě její prorání se nestíhlo,
..11 Konstrukce n zákldě výpočtu I Předpokldy: Pedgogická poznámk: Původně yl látk rozepsnou do dvou hodin, v první ylo kromě dělení úseček zřzen i čtvrtá geometrická úměrná. Právě její prorání se nestíhlo,
m n. Matice typu m n má
 MATE ZS KONZ B Mtice, hodnost mtice, Gussův tvr Mtice uspořádné schém reálných čísel: m m n n mn Toto schém se nzývá mtice typu m řádků n sloupců. m n. Mtice typu m n má Oznčujeme ji A, B,někdy používáme
MATE ZS KONZ B Mtice, hodnost mtice, Gussův tvr Mtice uspořádné schém reálných čísel: m m n n mn Toto schém se nzývá mtice typu m řádků n sloupců. m n. Mtice typu m n má Oznčujeme ji A, B,někdy používáme
Jazyk SQL 1. Michal Valenta. Katedra softwarového inženýrství FIT České vysoké učení technické v Praze c Michal Valenta, 2012 BI-DBS, ZS 2011/12
 Jazyk SQL 1 Michal Valenta Katedra softwarového inženýrství FIT České vysoké učení technické v Praze c Michal Valenta, 2012 BI-DBS, ZS 2011/12 https://edux.fit.cvut.cz/courses/bi-dbs/ Michal Valenta (FIT
Jazyk SQL 1 Michal Valenta Katedra softwarového inženýrství FIT České vysoké učení technické v Praze c Michal Valenta, 2012 BI-DBS, ZS 2011/12 https://edux.fit.cvut.cz/courses/bi-dbs/ Michal Valenta (FIT
je jedna z orientací určena jeho parametrizací. Je to ta, pro kterou je počátečním bodem bod ϕ(a). Im k.b.(c ) ( C ) (C ) Obr Obr. 3.5.
 10. Komplexní funkce reálné proměnné. Křivky. Je-li f : (, b) C, pk lze funkci f povžovt z dvojici (u, v), kde u = Re f v = Im f. Rozdíl proti vektorovému poli je v tom, že jsou pro komplexní čísl definovány
10. Komplexní funkce reálné proměnné. Křivky. Je-li f : (, b) C, pk lze funkci f povžovt z dvojici (u, v), kde u = Re f v = Im f. Rozdíl proti vektorovému poli je v tom, že jsou pro komplexní čísl definovány
Petriho sítě PES 2007/2008. ceska@fit.vutbr.cz. Doc. Ing. Tomáš Vojnar, Ph.D. vojnar@fit.vutbr.cz
 PES Petriho sítě p. 1/34 Petriho sítě PES 2007/2008 Prof. RNDr. Miln Češk, CS. esk@fit.vutr.z Do. Ing. Tomáš Vojnr, Ph.D. vojnr@fit.vutr.z Sz: Ing. Petr Novosd, Do. Ing. Tomáš Vojnr, Ph.D. (verze 06.04.2010)
PES Petriho sítě p. 1/34 Petriho sítě PES 2007/2008 Prof. RNDr. Miln Češk, CS. esk@fit.vutr.z Do. Ing. Tomáš Vojnr, Ph.D. vojnr@fit.vutr.z Sz: Ing. Petr Novosd, Do. Ing. Tomáš Vojnr, Ph.D. (verze 06.04.2010)
Téma 5 Spojitý nosník
 Stvení mechnik.očník kářského studi AST Tém 5 Spojitý nosník Zákdní vstnosti spojitého nosníku Řešení spojitého nosníku siovou metodou yužití symetie spojitého nosníku Kted stvení mechniky Fkut stvení
Stvení mechnik.očník kářského studi AST Tém 5 Spojitý nosník Zákdní vstnosti spojitého nosníku Řešení spojitého nosníku siovou metodou yužití symetie spojitého nosníku Kted stvení mechniky Fkut stvení
8 Mongeovo promítání
 8 Mongeovo promítání Pomocí metod uvedených v kpitolách 3. 4., 3. 6. bychom mohli promítnout do roviny 3 libovolný útvr U E. V prxi všk většinou nestčí sestrojit jeden průmět. Z průmětu útvru U je většinou
8 Mongeovo promítání Pomocí metod uvedených v kpitolách 3. 4., 3. 6. bychom mohli promítnout do roviny 3 libovolný útvr U E. V prxi všk většinou nestčí sestrojit jeden průmět. Z průmětu útvru U je většinou
Databázové systémy. Datová integrita + základy relační algebry. 4.přednáška
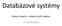 Databázové systémy Datová integrita + základy relační algebry 4.přednáška Datová integrita Datová integrita = popisuje pravidla, pomocí nichž hotový db. systém zajistí, že skutečná fyzická data v něm uložená
Databázové systémy Datová integrita + základy relační algebry 4.přednáška Datová integrita Datová integrita = popisuje pravidla, pomocí nichž hotový db. systém zajistí, že skutečná fyzická data v něm uložená
( a, { } Intervaly. Předpoklady: , , , Problém zapíšeme snadno i výčtem: { 2;3; 4;5}?
 1.3.8 Intervly Předpokldy: 010210, 010301, 010302, 010303 Problém Množinu A = { x Z;2 x 5} zpíšeme sndno i výčtem: { 2;3; 4;5} Jk zpst množinu B = { x R;2 x 5}? A =. Jde o nekonečně mnoho čísel (2, 5 všechno
1.3.8 Intervly Předpokldy: 010210, 010301, 010302, 010303 Problém Množinu A = { x Z;2 x 5} zpíšeme sndno i výčtem: { 2;3; 4;5} Jk zpst množinu B = { x R;2 x 5}? A =. Jde o nekonečně mnoho čísel (2, 5 všechno
Automaty a gramatiky. Trochu motivace. Roman Barták, KTIML. rní jazyky. Regulárn. Kleeneova věta. L = { w w=babau w=uabbv w=ubaa, u,v {a,b}* }
 ochu motivce L = { w w=u w=uv w=u, u,v {,}* } Automty gmtiky Romn Bták, KIML tk@ktiml.mff.cuni.cz htt://ktiml.mff.cuni.cz/~tk L = L L L, kde L = { w w=u, u {,}* }, L = { w w=uv, u,v {,}* } L = { w w=u,
ochu motivce L = { w w=u w=uv w=u, u,v {,}* } Automty gmtiky Romn Bták, KIML tk@ktiml.mff.cuni.cz htt://ktiml.mff.cuni.cz/~tk L = L L L, kde L = { w w=u, u {,}* }, L = { w w=uv, u,v {,}* } L = { w w=u,
Logické obvody - kombinační Booleova algebra, formy popisu Příklady návrhu
 MIKROPROCESORY PRO VÝKONOVÉ SYSTÉMY MIKROPROCESORY PRO VÝKONOVÉ SYSTÉMY Logické ovody - kominční Booleov lger, ormy popisu Příkldy návrhu České vysoké učení technické Fkult elektrotechnická ABMIS Mikroprocesory
MIKROPROCESORY PRO VÝKONOVÉ SYSTÉMY MIKROPROCESORY PRO VÝKONOVÉ SYSTÉMY Logické ovody - kominční Booleov lger, ormy popisu Příkldy návrhu České vysoké učení technické Fkult elektrotechnická ABMIS Mikroprocesory
ANALYTICKÁ GEOMETRIE V PROSTORU
 ANALYTICKÁ GEOMETRIE V PROSTORU 3. přednášk Vektorová lger Prvoúhlé souřdnice odu v prostoru Poloh odu v prostoru je vzhledem ke třem osám k soě kolmým určen třemi souřdnicemi, které tvoří uspořádnou trojici
ANALYTICKÁ GEOMETRIE V PROSTORU 3. přednášk Vektorová lger Prvoúhlé souřdnice odu v prostoru Poloh odu v prostoru je vzhledem ke třem osám k soě kolmým určen třemi souřdnicemi, které tvoří uspořádnou trojici
Digitální učební materiál
 Digitální učení mteriál Číslo projektu CZ.1.07/1.5.00/34.080 Název projektu Zkvlitnění výuky prostřednictvím ICT Číslo název šlony klíčové ktivity III/ Inovce zkvlitnění výuky prostřednictvím ICT Příjemce
Digitální učení mteriál Číslo projektu CZ.1.07/1.5.00/34.080 Název projektu Zkvlitnění výuky prostřednictvím ICT Číslo název šlony klíčové ktivity III/ Inovce zkvlitnění výuky prostřednictvím ICT Příjemce
ZÁKLADY. y 1 + y 2 dx a. kde y je hledanou funkcí proměnné x.
 VARIAČNÍ POČET ZÁKLADY V prxi se čsto hledjí křivky nebo plochy, které minimlizují nebo mximlizují jisté hodnoty. Npř. se hledá nejkrtší spojnice dvou bodů n dné ploše, nebo tvr zvěšeného ln (má minimální
VARIAČNÍ POČET ZÁKLADY V prxi se čsto hledjí křivky nebo plochy, které minimlizují nebo mximlizují jisté hodnoty. Npř. se hledá nejkrtší spojnice dvou bodů n dné ploše, nebo tvr zvěšeného ln (má minimální
a i,n+1 Maticový počet základní pojmy Matice je obdélníkové schéma tvaru a 11
 Mticový počet zákldní pojmy Mtice je obdélníkové schém tvru 2...... n 2 22. 2n A =, kde ij R ( i =,,m, j =,,n ) m m2. mn ij R se nzývjí prvky mtice o mtici o m řádcích n sloupcích říkáme, že je typu m/n
Mticový počet zákldní pojmy Mtice je obdélníkové schém tvru 2...... n 2 22. 2n A =, kde ij R ( i =,,m, j =,,n ) m m2. mn ij R se nzývjí prvky mtice o mtici o m řádcích n sloupcích říkáme, že je typu m/n
Větu o spojitosti a jejich užití
 0..7 Větu o spojitosti jejich užití Předpokldy: 706, 78, 006 Pedgogická poznámk: Při proírání této hodiny je tře mít n pměti, že všechny věty, které studentům sdělujete z jejich pohledu neuvěřitelně složitě
0..7 Větu o spojitosti jejich užití Předpokldy: 706, 78, 006 Pedgogická poznámk: Při proírání této hodiny je tře mít n pměti, že všechny věty, které studentům sdělujete z jejich pohledu neuvěřitelně složitě

 Riemnnův určitý integrál. Definice 1. Budiž
Riemnnův určitý integrál. Definice 1. Budiž