České vysoké učení technické v Praze, Fakulta strojní. Dynamická pevnost a životnost & Mezní stavy konstrukcí - Jur III.
|
|
|
- Eva Helena Kubíčková
- před 6 lety
- Počet zobrazení:
Transkript
1 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. Dynmická penost žiotnost Ju Miln Růžičk, Josef Juenk, Mtin Nesláek Poěkoání: Děkuji pof. ng. Jiřímu unzoi, CSc z lské solení s yužitím někteých obázků z jeho knihy Aplikoná lomoá mechnik, ČVUT, 5 této přenášce. josef.juenk@fs.cut.cz
2 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. Litetu J. unz: Aplikoná lomoá mechnik, ČVUT, 5 J. unz: Zákly lomoé mechniky, ČVUT, J. Němec: Polužoání žiotnosti konstukcí přecházení jejich háiím, Asocice stojních inženýů České epublice, 994 J. uče: Úo o mechniky lomu : uby thliny : nestbilní lom při sttickém ztížení,. y. Ost : Vysoká škol báňská - Technická uniezit Ost, J. uče: Úo o mechniky lomu : Ún mteiálu, Ost : Vysoká škol báňská - Technická uniezit Ost, 994 V. Moec, D. Pišťáček: Penost ynmicky nmáhných stojních součástí, Ost : Vysoká škol báňská - Technická uniezit Ost, 6 D Boek: lementy ngineeing Fctue Mechnics,. e. Mtinus Nijhoff Publ., Boston 98 D Boek: The Pcticl Use of Fctue Mechnics, luwe Acemic Publishes, Doecht, The Nethelns, 988 Růžičk, M., Finský, J. Penost žiotnost letel. ČVUT,. Růžičk, M., Hnke, M., Rost, M. Dynmická penost žiotnost. ČVUT, 987. Pook, L. Metl Ftigue Wht it is, why it mttes. Spinge, 7.
3 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 3 W Hncí síl thliny - efinice Pole iffitho kitei křehkého lomu může nstt nestbilní šíření thliny, poku enegie potřebná po ozšíření thliny o příůstek bue oán z příslušného systému těles s thlinou. negie po šíření thliny může být oáán pcí nějších sil A nebo částí elstické efomční enegie U, kteá je uolňoán při šíření thliny. negetickou bilnci těles s thlinou, kteé je ztíženého nějšími silmi je možné yjářit pomocí zthu: A U W S B pl W t k W A U W S B pl t k celkoá enegie těles páce nějších sil efomční enegie isipční enegie thliny enegie potřebná po znik thliny specifická enegie thliny elikost lomoé plochy tloušťk těles spec. pot. pochoá enegie spec. pot. enegie plstické efomce spec. teplo uolněné n čele thliny spec. kin. enegie nejbližsího okolí čel thliny
4 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 4 Hncí síl thliny enegetická bilnce Po esku jenotkoé tloušťky B lze npst pomínku stbility thliny: Veličin: U A W, nebo A U A U J/m N/m W se nzýá HNACÍ SÍLA TRHLNY (ychlost uolňoání efomční enegie) Veličin: R W J/m N/m přestuje opo mteiálu poti šíření thliny lomoou houžentost yjářenou pomocí enegie (i)
5 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 5 Potom lze pomínku stbility yjářit e tu: Ukázk ýpočtu : užujme těleso tloušťky B, s thlinou élky, ztížené silou P le ob. Působením sil oje k eltinímu posuu jejího působiště. V okmžiku, ky oje k poloužení thliny o zětší se posunutí o. Potom páce ykonná nějšími silmi je P. Z přepoklu elstické efomce je posunutí popltné pojnosti esky, kteou lze yjářit: Potom příůstek páce nějších sil lze zpst jko: A CP P B B P R C (ii)
6 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 6 Potom efomční enegie kumuloná tělese (s thlinou) je án zthem: Doszením (ii) (iii) o (i) ostneme: (iii) C P B U CP B P B U, C B P C P C P B P U B U B C B P Hncí síl není záislá n způsobu ztěžoání.
7 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 7 Z poslení onice plyne, že honot hncí síly thliny je žy on eici efomční enegie AŽ NA ZNAMÉNO. fické znázonění enegetické bilnce P = konst. P P A C OAB - efomční enegie U pře poloužením thliny OCD - efomční enegie U po poloužením thliny konstntní síl P B D ACBD páce nějších sil náůst efomční enegie těles = OCD - OAB = / ACBD = OAC konstntní síl P B U P
8 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 8 fické znázonění enegetické bilnce = konst. konstntní posu P P P B A C D OAB - efomční enegie U pře poloužením thliny OB - efomční enegie U po poloužením thliny pokles efomční enegie těles = OAB - OB OAC = / ACBD AC = /P, znebáme konstntní posu B U
9 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 9 iteium stbility le iffith iffithe kiteium ooil po nekonečné těleso s centální thlinou eliptického tu élky pomínkách nuloých posuů okjů těles mó nmáhání s užoáním okonle křehkého mteiálu isipční enegie thliny užol pouze jko funkci specifické potenciání pochoé enegie. Pomínku ztáty stbility lze yjářit e tu: S U W R B pl t k R
10 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. lstickou efomční enegii těles s thlinou lze yjářit jko: Výpočet U n záklě řešení pole npětí efomcí okolí thliny U U U U efomční enegie těles bez thliny U úbytek efomční enegie těles ůsleku existence thliny = uolněná efomční enegie, x y y y U,, y, y, RN 4, RD 4,
11 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. ntegcí ostneme: y U,, RD U RN U Hncí síl thliny: lim U U U U U RD RN Pomínk stbility po st RD:., esp U c c
12 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. Zobecnění kiteium stbility le iffith onečné ozměy těles yjáření hncí síly thliny pomocí fktou intenzity npětí, ke koekční funkce Y zohleňuje skutečné ozměy těles. Nekonečné těleso: RD, RN,, onečné těleso: Y
13 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 3 lstoplstický mteiál znik plstické efomce okolí čel thliny ýznmně oliní jk elikost hncí síly thliny, tk i opo mteiálu poti šíření thliny R. Změn honoty : Plstická efomce mlého ozshu honotu lze učit pomocí, kteé je koigoné pomocí winoy koekce n elikost plstické zóny. Změn honoty R: U táných mteiálů je třeb zít úhu lší složky specifické enegie thliny, kteé byly říe znebány. Nejýznmnější z nich je pl : p iteium stbility: j jc, j,, R Pltí pouze n zčátku šíření thliny.
14 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 4 c R-křiky s. hncí síl thliny Honot R opoíá kitické honotě c učení R pobíhá npř. expeimentálně, ky po změřenou honotu c eoucí k lomu ypočteme c, esp. R: c c RD c c oceli R J/m 6 RN Vli: mteiáloých lstností, pomínek ztěžoání okolního postřeí iteium stbility lze yjářit gficky jko záislost, esp. R n élce thliny jejím příůstku. N úo ýjeme z přepoklů: Ve stu oinné efomce lze užot R jko konstntní funkci tey jko mteiáloou chkteistiku. (lom. houž.) Bueme užot nekonečné těleso hncí síl thliny bue přímo úměná élce thliny. W RD. Stbilit thliny < R. itická élk thliny c jko funkce npětí.
15 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 5 Uniezálnější zobzení n oooné ose ynášen jk élk thliny, tk i její příůstek : RD. konst. j W Počátek ůstu thliny = R Šíření thliny > R Stbilit thliny < R RD. konst. konst. W Šíření thliny > R Po ktší thlinu npětí hncí síl neosáhl kitické honoty R thlin se nezčne šířit! = V pomínkách konstntního posuu klesá npjtost hncí síl thliny s élkou thliny oste pomleji.
16 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 6 P P i St oinné npjtosti opo mteiálu poti šíření R není konstntní, le funkcí élky thliny R(). Ztátě stbility přechází stbilní šíření thliny ke stbilnímu ůstu thliny ochází pouze poku oste ztížení, esp. npětí. Stbilní šíření nstne, poku honot osáhne phoé honoty i, nestbilní šíření nstne, poku honot osáhne kitické honoty c, esp. R. P c Stbilní šíření pomíněno ůstem ztížení. Nestbilní šíření, bez nutnosti zětšoání npětí < i thlin se nešíří t Počátek stbilního šíření R R c i i < < c thlin se šíří stbilně c < thlin se šíří nestbilně
17 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 7 St oinné npjtosti R-křiky 4 3 R R R R R (4,i+c) = R(RN,i+c) / = R/ nstne nestbilní šíření thliny (4,i+c+ ) > R(RN,i+c+ ) (3,i) > R(RD) > R(RN,i) stbilní šíření thliny o ž o okmžiku (3,i+) = R(RN,i+), potom bez zýšení npětí pltí: (3,i++ ) < R(RN,i++ ), (,i) = R(RD) < R(RN, i) nestbilní šíření thliny nstne pomínkách RD, pomínkách RN může nstt stbilní šíření, poku bue zýšeno npětí. Počáteční élk thliny i R (,i) < R(RD, RN, i) šíření thliny nenstne
18 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 8 St oinné npjtosti R-křiky po houženté mteiály f ukzuje záislost kitického npětí c, esp. zbytkoé penosti celkoé kitické élky thliny okmžiku ztáty stbility c n počáteční élce thliny. Velikost kitického npětí c, esp. zbytkoé penosti je přímo úměná sklonu tečny R-křiky. Opo mteiálu poti šíření thliny je án přeeším pcí potřebnou n ytoření plstické efomce, páce n spojoání mikopouch mnohem menší R-křik pochází počátkem.
19 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 9 St oinné efomce, esp. oinné npjtosti li konečných ozměů těles, způsobu ztěžoání okjoých pomínek. Vli těchto fktoů lze o ýpočtu zhnout pomocí koekčních funkcí Y půoně lineání záislost se mění n obecnou změn kitických honot yhonoconých eličin c c!
20 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. Fkto hustoty efomční enegie S Doposu ueená kitei lomoé mechniky (fkto intenzity npětí) (hncí síl thliny) byl zložen n přepoklu, že opřeu známe (přepoklááme) smě lšího šíření thliny, kteý byl přepokláán e směu stájící thliny. Součásti jsou čsto ztížené kombinoným móem nmáhání + (+) lší šíření thlin se těchto přípech neoeháá půoním směu. Obecně lze řící, že smě šíření thliny bue záiset n ozložení enegie tělese n lstnostech stuktuře mteiálu Sih sestil teoii peikce stbility směu šíření thlin, kteá ychází z hustoty efomční enegie.
21 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. Hustot efomční enegie Přepoklááme lineání elstický mteiál potom hustot efomční enegie bue: U V ij i, j ij ij i, j, i, j x, y, z. J/m 3 ij ij, MP Rozšířený Hookeů zákon U x x y z,, x y z x y y z z x V xy,,. xy xy yz zx ij Užujme smíšený mó nmáhání složky tenzou npětí blízkosti čel: ij ij ijk f ijk k f, i, j x, y, z; k,, ijk
22 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. Jenotlié složky tenzou npětí okolí thliny při smíšeném móu nmáhání buou:. sin, cos, 3 sin sin cos 3 cos cos sin porn, pord, sin cos, 3 cos cos sin 3 sin sin cos, 3 cos cos sin 3 sin sin cos yz yz xy z z y x zx yz xy x z z y y x z y x V U 33 V U
23 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 3 U V cos cos 3 cos cos, 6 sin cos, 8 sin cos, cos cos 3cos cos cos 3cos,,, po RD po RN po RD po RN po RD po RN
24 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 4 Fkto hustoty efomční enegie S - efinice Díky užoání smíšeného móu nmáhání je fkto hustoty efomční enegie směoě citliý: U S 33, N/m, J/m. V Siho teoie nestbilního šíření je zložen n ou záklních hypotézách: ) šíření thliny oje e směu, e kteém je fkto hustoty efomční enegie S minimální S S ) šíření oje, jestliže fkto hustoty efomční enegie S osáhne e směu kitické honoty c S S
25 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 5 Fkto hustoty efomční enegie S ptří mezi kitei lineání lomoé mechniky. Stejně jko přechozí ě kitéi ychází i S z přepoklu mlé plstické zóny n čele thliny. Bueme-li n pohlížet jko n sklání eličiny popisující st těles s thlinou zhleem ke křehkému lomu, potom n eličinu S musíme pohlížet jko n ekto toto kitéium nám ooluje učit jk okmžik nestbilního šíření thliny, tk i smě, e kteém k tomuto šíření oje.
26 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 6 Fkto hustoty efomční enegie S příkl : Nekonečné těleso s thlinou mó Nmáhání těles s thlinou: Doszením o S ostneme: S Pomínk minim: S sin 8 S 8,, cos cos cos, ccos cos cos
27 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 7 Fkto hustoty efomční enegie S příkl : Nekonečné těleso s thlinou mó Pomínk minim: 4 σ θ S σ θ S θ θ S S min 4 Minimální honot S: Ztát stbility thliny ( pomínkách RD): 4 4 c c c S S
28 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 8 Fkto hustoty efomční enegie S příkl : Nekonečné těleso s thlinou mó Nmáhání těles s thlinou: Doszením o S ostneme: S 4 6 Pomínk minim: S sin 8 S 8,, cos cos 3cos 3cos cos 3cos, ccos 3
29 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 9 Fkto hustoty efomční enegie S příkl : Nekonečné těleso s thlinou mó Pomínk minim: 6 4 S S S S min 3 ccos Minimální honot S: Ztát stbility thliny ( pomínkách RD) z přepoklu, že Sc je mteiáloá konstnt: S S c c c c c 4 4
30 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 3 Fkto hustoty efomční enegie S příkl 3: Nekonečné těleso s thlinou mó nmáhání Složky npětí jsou hlní npětí esce k je eálné číslo. Po ypočet S musíme znát honoty fktou intenzity npětí po jenotlié móy nmáhání, Výpočet potřebných npětí je možné poést plikcí Mohoy kužnice po oinnou npjtost: cos sin
31 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 3 Honoty esp. potom jsou: k cos sin sin cos sin cos cos k k k k k k k k k cos sin cos sin
32 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 3 Půběh nomlizoné honoty záislosti n úhlu oklonu thliny poměu hlních npětí k., Půběh nomlizoné honoty záislosti n úhlu oklonu thliny poměu hlních npětí k. S S S S S c
33 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 33 Fkto hustoty efomční enegie S příkl: thlin e stěně zkuconé álcoé náoby Ve stěně uzřené álcoé náoby, byl zjištěn efekt. Po jenouchost užujeme půchozí thlinu le ob. A X cck Y cck A Oblst efektu A - A
34 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 34 Ve stěně uzřené álcoé náoby tloušťky t, kteá je nmáhán nitřním přetlkem p, je po elké honoty poměu poloměu ku tloušťce stěny možné znebt iální složku npětí. V elementu stěny potom bue ojosá npjtost, ke npětí je npětí směu obooém npětí je npětí směu osoém. t p 5 p, 4 t 4 5 t k sin k sin k cos ksin cos cos k sin cos 6
35 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 35 Doszení o S k cos, ksin cos sin 64S 3 4 cos cos sin kcos 4 sin cos sin kcos ksin cos 4 cos cos 3cos ksin cos Výpočet směu šíření thliny: S,, f Ronici může splňot několik úhlů. S Vybeeme pouze ty kořeny,, po kteé pltí ná neonost.
36 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 36, f f,, onkétně po k =,5 lze opočíst: Z půběhu funkce f, je iět, že nejětší oklon inicioné thliny o jejího půoního směu si = 33,5 po úhel oklonu thliny - / = 57. Thlin se přitom snží zujmout tkoý smě, ke by nomál jejích lícních ploch síl se směem ětšího hlního npětí minimální úhel. Dosíme-li řešení, esp. úhel o onice po S ostneme honotu fktou hustoty efomční enegie. Půběh funkce, záislosti n - /. Stbilitu thliny lze potom posouit pole: c S S
37 České ysoké učení technické Pze, Fkult stojní Dynmická penost žiotnost & Mezní sty konstukcí - Ju. 37 "S" Dosíme-li několik boů řešení, esp. úhlů f(,) po ůzné o onice po S ostneme záislost honoty fktou hustoty efomční enegie n úhlu oklonu thliny - / Poissono poměu. Velikost S po oklon thliny - / = 9 je přibližně 4x menší než po - / = přípustná élk thliny n mezi stbility je potom e směu obooém si čtyřikát ětší, nežli e směu osoém. c S S Teoie hustoty efomční enegie je zložen n singuláním řešení stu npjtosti (přepokl elstické choání mteiálu) blízkém okolí čel thliny yhonocení směu šíření pltí pouze po toto blízké okolí po poloužení thliny nepltí.
České vysoké učení technické v Praze, Fakulta strojní. Dynamická pevnost a životnost & Mezní stavy konstrukcí - Jur II. Dynamická pevnost a životnost
České vysoké učení technické v Pze Fkult stojní Dynmická evnost životnost & Mezní stvy konstukcí - Ju II. Dynmická evnost životnost Ju II Miln ůžičk Jos Juenk Mtin Nesládek Poděkování: Děkuji of. Ing.
Kmity vynucené
1.7.3. Kmit nucené 1. Umět sětlit posttu nucených kmitů.. Pochopit ýznm buící síl. 3. Vsětlit přechooý st. 4. Věět, jk se mění mplitu nucených kmitů záislosti n fekenci buící síl. 5. Věět, co je ezonnční
České vysoké učení technické v Praze, Fakulta strojní. Dynamická pevnost a životnost Jur I. Dynamická pevnost a životnost. Jur I
České vysoké učení technické v Pze Fkult stojní Dynmická pevnost životnost Ju I. /75 Dynmická pevnost životnost Ju I Miln Růžičk Josef Juenk Mtin Nesládek Poděkování: Děkuji pof. Ing. Jiřímu unzovi CSc
Dynamická pevnost a životnost Jur I
České vysoké učení technické v Pze Fkult stojní Dynmická pevnost životnost Ju I. /75 Dynmická pevnost životnost Ju I Miln Růžičk Josef Juenk Mtin Nesládek Poděkování: Děkuji pof. Ing. Jiřímu unzovi CSc
Kinematika hmotného bodu. Petr Šidlof
et Šilof Úo Kinemtik popis pohybu (nezkoumá příčiny pohybu) Šiší souislosti: mechnik tuhých těles sttik kinemtik ynmik Mechnik mechnik poných těles sttik kinemtik ynmik mechnik tekutin hyosttik ynmik tekutin
29. OBJEMY A POVRCHY TĚLES
9. OBJEMY A POVRCHY TĚLES 9.. Vypočítejte poch kádu ABCDEFGH, jestliže ) AB =, BC = b, BH = u b) AB =, BH = u, odchylk AG EH je ϕ H G Poch kádu učíme podle zoce: S = b + c + bc ( ) c E F D b C ) A B u
Napětí horninového masivu
Npětí honinového msivu pimání npjtostí sekundání npjtostí účinky n stbilitu podzemního díl Dále můžeme uvžovt * bobtnání honiny * teplotní stv honiny J. Pušk MH 6. přednášk 1 Pimání npjtost gvitční (vyvolán
Lineární algebra. 1) Vektor, lineární závislost a nezávislost. Def.: Číselným vektorem n-rozměrného prostoru nazýváme uspořádanou množinu n čísel
Lineání lge ) Vekto, lineání záislost nezáislost Def: Číselným ektoem n-ozměného postou nzýáme uspořádnou množinu n čísel,, ) ( n Čísl,, n nzýáme souřdnice ektou, číslo n dimenzí neo ozměem ektou Opece
České vysoké učení technické v Praze, Fakulta strojní. Pevnost a životnost Jur I. Pevnost a životnost. Jur I
1/49 Pevnost životnost Jur I Miln Růžičk, Josef Jurenk, Zbyněk Hrubý Poděkování: Děkuji prof. Ing. Jiřímu Kunzovi, CSc z lskvé svolení s využitím některých obrázků z jeho knihy Aplikovná lomová mechnik,
Geometrie. RNDr. Yvetta Bartáková. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
Geometie RND. Yett Btákoá Gymnázium, OŠ VOŠ Ledeč nd ázou Objemy pochy těles komolá těles VY INOVACE_05 9_M Gymnázium, OŠ VOŠ Ledeč nd ázou Objemy pochy těles A) Komolý jehln - je těleso, kteé znikne půnikem
České vysoké učení technické v Praze, Fakulta strojní. Pevnost a životnost Jur II. Pevnost a životnost. Jur II
České vysoké učení technické v Praze, Fakulta strojní 1/13 Pevnost a životnost Jur II Milan Růžička, Josef Jurenka, Zbyněk Hrubý Poděkování: Děkuji prof. Ing. Jiřímu Kunzovi, CSc za laskavé svolení s využitím
Dynamika vozidla, přímá jízda, pohon a brzdění
Dynik ozil, příá jíz, pohon bzění Dynik ozil, příá jíz, pohon bzění Dynik ozil, příá jíz, pohon bzění lk ntišk : Dynik otooých ozil 0, y 0, z 0 - pný souřný systé, y, z - tělsoý souřný systé s počátk těžišti
OBJEMY A POVRCHY TĚLES
OBJEMY A POVRCHY TĚLES Metodický mteiál do semináře MA SDM Růžen Blžkoá, Ien Budínoá KOMOLÝ JEHLAN Ojem komolého jehlnu Po zjednodušení ododíme zthy po komolý jehln, jehož podstmi jsou čtece. Oznčení:
Přednášky část 6 Úvod do lineární lomové mechaniky
Přednášky část 6 Úvod do lineární lomové mechniky Miln Růžičk, Josef Jurenk miln.ruzick@fs.cvut.cz Litertur J. unz: Aplikovná lomová mechnik, ČVUT, 005 J. unz: Zákldy lomové mechniky, ČVUT, 000 J. Němec:
Příklad 1 (25 bodů) řešení Pro adiabatický děj platí vztah (3 body) pv konstanta, (1)
Přijímcí zkoušk n nvzující mgisteské stuium - 14 Stuijní pogm Fyzik - všechny oboy komě Učitelství fyziky mtemtiky po stření školy Vint A Příkl 1 (5 boů) Zjenoušený moel výstřelu ze vzuchovky si přestvme
Hlavní body. Keplerovy zákony Newtonův gravitační zákon. Konzervativní pole. Gravitační pole v blízkosti Země Planetární pohyby
Úvod do gavitace Hlavní body Kepleovy zákony Newtonův gavitační zákon Gavitační pole v blízkosti Země Planetání pohyby Konzevativní pole Potenciál a potenciální enegie Vztah intenzity a potenciálu Úvod
( ) ( ) ( ) Vzdálenost bodu od přímky II. Předpoklady: 7312
.. Vzálenost bou o přímk II Přepokl: Pegogiká poznámk: Průběh hoin honě závisí n tom, jk oolní jsou stuenti v oszování o vzorů, které je nejtěžší částí hoin. Dlším problémem pk mohou být rovnie s bsolutní
( ) Kinematika a dynamika bodu. s( t) ( )
Kineika a ynamika bou Kineika bou Bo se pohybuje posou po křice, keá se nazýá ajekoie nebo áha bou. Tajekoie je učena půoičem (polohoým ekoem), keý je funkcí času ( ) V záislosi na ypu ajekoie ozlišujeme:
cos cos φ ω Převod mechanismu Aplikovaná mechanika, 9. přednáška analytické řešení mechanismu s pravoúhlou kulisou ω, ε φ převod derivace převodu
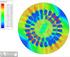Přeod mechnismu nlytické řešení mechnismu s oúhlou kulisou, ε, y y sin y& & cos && y && cos & & && ε cos y& && y ε cos mechnismus s oměnným řeodem ( ) likoná mechnik, 9. řednášk f řeod sin sin deice řeodu
A Pohyb silničních vozidel
A Pohyb silničních voziel Po popisování pohybu silničních voziel a sil na ně působící bueme vzcházet ze souřaného systému vozila, tak jak byl popsán v přechozím tématu. Tyto postupy je možno obecně aplikovat
je dána vzdáleností od pólu pohybu πb
7_kpta Tyč tvaru le obrázku se pohybuje v rohu svislé stěny tak, že bo A se o rohu (poloha A 0 ) vzaluje s konstantním zrychlením a A 1. m s. Počáteční rychlost bou A byla nulová. Bo B klesá svisle olů.
FYZIKA I. Rovnoměrný, rovnoměrně zrychlený a nerovnoměrně zrychlený translační pohyb
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Ronoměrný, ronoměrně zrychlený neronoměrně zrychlený trnslční pohyb Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hláč, Ph.D. Doc.
F9 SOUSTAVA HMOTNÝCH BODŮ
F9 SOUSTAVA HMOTNÝCH BODŮ Evopský sociální fon Ph & EU: Investujee o vší buoucnosti F9 SOUSTAVA HMOTNÝCH BODŮ Nyní se nučíe popisovt soustvu hotných boů Přepokláeje, že áe N hotných boů 1,,, N N násleující
POHYB BODU V CENTRÁLNÍM POLI SIL
POHYB BODU V CENTRÁLNÍM POLI SIL SPECIFIKCE PROBLÉMU Centální siloé pole je takoé pole sil, kdy liboolném bodě postou nositelka síly působící na pohybující se bod pochází peným bodem postou (tz centem
Vlnovody. Obr. 7.1 Běžné příčné průřezy kovových vlnovodů: obdélníkový, kruhový, vlnovod, vlnovod H.
7 Vlnovody Běžná vedení (koaxiální kabel, dvojlinka) jsou jen omezeně použitelná v mikovlnné části kmitočtového spekta. S ůstem kmitočtu přenášeného signálu totiž významně ostou ztáty v dielektiku těchto
Konstrukční a technologické koncentrátory napětí
Obsah: 6 lekce Konstukční a technologické koncentátoy napětí 61 Úvod 6 Účinek lokálních konstukčních koncentací napětí 63 Vliv kuhového otvou na ozložení napjatosti v dlouhém tenkém pásu zatíženém tahem
Nadměrné daňové břemeno
Nměrné ňové břemeno Nměrné ňové břemeno je efinováno jko ztrát přebytku spotřebitele přebytku výrobe, ke kterému ohází v ůsleku znění. Něky se tož nzývá jko ztrát mrtvé váhy. Připomenutí: Přebytek spotřebitele:
JEDNOOSÁ STLAČITELNOST A KONSOLIDACE (EDOMETRICKÁ ZKOUŠKA)
JEDNOOSÁ STLAČITELNOST A KONSOLIDACE (EDOMETRICKÁ ZKOUŠKA) 1 VYSVĚTLENÍ/UJASNĚNÍ DŮLEŽITÝCH POJMŮ Stlčení (komprese) zeminy je přípd ztížení zeminy, při kterém dochází k redukci objemu zeminy ytlčením
Stavební mechanika 1 (K132SM01)
Stní mnik 1 (K132SM01) Přnáší: o. ng. Mtěj Lpš, P.D. Ktr mniky K132 místnost D2034 konzult Čt 9:30-11:00 -mil: mtj.lps@fs.ut.z ttp://m.fs.ut.z/~lps/ting/inx.tml Řáný trmín zápočtoé písmky j ÚTERÝ 25. un
Příklad 33 : Energie elektrického pole deskového kondenzátoru. Ověření vztahu mezi energií, kapacitou a veličinami pole.
Přík 33 : Energie eektrického poe eskového konenzátoru. Ověření vzthu mezi energií, kpcitou veičinmi poe. Přepokáné znosti: Eektrické poe kpcit eskového konenzátoru Přík V eskovém konenzátoru je eektrické
POVRCH A OBJEM KOULE A JEJÍCH ČÁSTÍ
Pojekt ŠABLONY NA GVM Gymnázium Velké Meziříčí egistační číslo pojektu: CZ..07/.5.00/4.0948 IV- Inoace a zkalitnění ýuky směřující k ozoji matematické gamotnosti žáků středníc škol POVRCH A OBJEM KOULE
Dráhy planet. 28. července 2015
Dáhy plnet Pet Šlecht 28. čevence 205 Výpočet N střední škole se zpvidl učí, že dáhy plnet jsou elipsy se Sluncem v ohnisku. Tké se učí, že tento fkt je možné dokázt z Newtonov gvitčního zákon. Příslušný
Elektromagnetické pole
Elekomagneické pole Zákon elekomagneické inukce pohybujeme-li uzařeným oičem honým způsobem magneickém poli, zniká e oiči elekický pou nachází-li se uzařený oič časoě poměnném magneickém poli, zniká e
F5 JEDNODUCHÁ KONZERVATIVNÍ POLE
F5 JEDNODUCHÁ KONZERVATIVNÍ POLE Evopský sociální fond Paha & EU: Investujeme do vaší budoucnosti F5 JEDNODUCHÁ KONZERVATIVNÍ POLE Asi nejznámějším konzevativním polem je gavitační silové pole Ke gavitační
Elektrický náboj [q] - základní vlastnost částic z hlediska EM pole - kladný (nositel proton), záporný (nositel elektron) 19
![Elektrický náboj [q] - základní vlastnost částic z hlediska EM pole - kladný (nositel proton), záporný (nositel elektron) 19](/thumbs/31/14844695.jpg "Elektrický náboj [q] - základní vlastnost částic z hlediska EM pole - kladný (nositel proton), záporný (nositel elektron) 19")
34 Elektomagnetické pole statické, stacionání, nestacionání zásady řešení v jednoduchých geometických stuktuách, klasifikace postředí (lineaita, homogenita, dispeze, anizotopie). Vypacoval: Onda, otja@seznam.cz
Obecný rovinný pohyb. teorie současných pohybů, Coriolisovo zrychlení dynamika obecného rovinného pohybu,
Obecný oinný pohyb ynik, 7. přednášk Obsh přednášky : teoie součsných pohybů, Coiolisoo zychlení dynik obecného oinného pohybu, ob studi : si 1,5 hodiny Cíl přednášky : seznáit studenty se zákldy teoie
Geometrická optika. Aberace (vady) optických soustav
Geometická optika Abeace (vady) optických soustav abeace (vady) optických soustav jsou odchylky zobazení eálné optické soustavy od zobazení ideální optické soustavy v důsledku abeací není obazem bodu bod,
Kinematika hmotného bodu
K přenášce NUFY080 Fzik I (mechnik) proztímní učební tet, erze 0. Kinemtik hmotného bou Leoš Dořák, MFF UK Prh, 06. Hmotný bo Kinemtik hmotného bou V prní ruhé kpitole se bueme zbýt pohbem si nejjenouššího
Neurčité výrazy
.. Neurčité výrzy Předpokldy: Př. : Vypočti ity: ) d) ) d) neeistuje,, Zjímvé. Získli jsme čtyři nprosto rozdílné výsledky, přestože přímým doszením do všech výrzů získáme to smé: výrz může při výpočtu
A) Dvouvodičové vedení
A) Dvouvodičové vedení vedení symetické (shodné impednce vodičů vůči zemi) vede vění od MHz do mx. stovek MHz, dominntní vid TEM běžné hodnoty vové impednce: 3 Ω, 6 Ω impednce se zvětší, pokud se zmenší
S S obsahy podstav S obsah pláště
Předmět: Ročník: ytořil: Datum: MATEMATIKA DRUHÝ MGR. JÜTTNEROÁ 7.. 04 Náze zpacoaného celku: PORCHY A OBJEMY KOMOLÝCH TĚLE, KOULE A JEJÍCH ČÁTÍ PORCH A OBJEM KOMOLÉHO JEHLANU Komolý jehlan: má dě podstay,
C Charakteristiky silničních motorových vozidel
C Chaaktetky lnčních otoových vozel Toto téa e zabývá záklaní etoa tanovení někteých povozních chaaktetk lnčních otoových vozel, kteé pak náleně louží k pouzování užtných vlatnotí těchto vozel. Stanovení
Auto během zrychlování z počáteční rychlost 50 km/h se zrychlením dráhu 100 m. Jak dlouho auto zrychlovalo? Jaké rychlosti dosáhlo?
..7 Ronoměrně zrychlený pohyb příkldech III Předpokldy: 6 Pedgogická poznámk: Hodinu dělím n dě části: 5 minut n prní d příkldy zbytek n osttní. I když šichni nestihnout spočítt druhý příkld je potřeb,
Osové namáhání osová síla N v prutu
Osové nmáhání osová síl v prutu 3 typy úloh:. Pruty příhrdové konstrukce, táhl Dvě podmínky rovnováhy v kždém styčníku: F ix 0 F iz 0. Táhl podporující pevnou ztíženou desku R z M ib 0 P R R b P 6 6 P
Houževnatost. i. Základní pojmy (tranzitní lomové chování ocelí, teplotní závislost pevnostních vlastností, fraktografie)
Houževnatost i. Základní pojmy (tranzitní lomové chování ocelí, teplotní závislost pevnostních vlastností, fraktografie) ii. (Empirické) zkoušky houževnatosti (Charpy, TNDT) iii. Lineárně-elastická elastická
Diferenciální operátory vektorové analýzy verze 1.1
Úvod Difeenciální opeátoy vektoové analýzy veze. Následující text popisuje difeenciální opeátoy vektoové analýzy. Měl by sloužit především studentům předmětu MATEMAT na Univezitě Hadec Kálové k přípavě
Úloha č. 1 pomůcky Šíření tepla v ustáleném stavu základní vztahy
Úloha č. pomůcky Šíření tepla v ustáleném stavu záklaní vztahy Veení Fourriérův zákon veení tepla, D: Hustota tepelného toku je úměrná změně teploty ve směru šíření tepla, konstantou úměrnosti je součinitel
Seznámíte se s další aplikací určitého integrálu výpočtem obsahu pláště rotačního tělesa.
.4. Obsh pláště otčního těles.4. Obsh pláště otčního těles Cíle Seznámíte se s dlší plikcí učitého integálu výpočtem obshu pláště otčního těles. Předpokládné znlosti Předpokládáme, že jste si postudovli
I. Statické elektrické pole ve vakuu
I. Statické elektické pole ve vakuu Osnova:. Náboj a jeho vlastnosti 2. Coulombův zákon 3. Intenzita elektostatického pole 4. Gaussova věta elektostatiky 5. Potenciál elektického pole 6. Pole vodiče ve
třecí síla (tečná vazba podložky) F normálová reakce podložky výsledná reakce podložky Podmínky rovnováhy:
SPŠ VOŠ KLADO SAIKA - PASIVÍ ODPORY PASIVÍ ODPORY Při vzájemném pohybu těles vznikjí v reálných vzbách psivní odpory, jejichž práce se mění v teplo. Psivní odpory předstvují ztráty, které snižují účinnost
Odraz na kulové ploše Duté zrcadlo
Odz n kulové ploše Duté zcdlo o.. os zcdl V.. vchol zcdl S.. střed zcdl (kul. ploch).. polomě zcdl (kul. ploch) Ppsek vchází z odu A n ose zcdl po odzu n zcdle dopdá do nějkého odu B n ose. Podle oázku
Učební text k přednášce UFY102
Učební text k přenášce UFY vou ovinných světených vn V této kpitoe si ukážeme, jk vznikjí intefeenční použky, jestiže se vě ovinné světené vny setkávjí v nějkém postou. Mějme vě ovinné vny popsné náseujícími
Pružnost a plasticita II
Pružnost plsticit II. ročník klářského studi doc. In. Mrtin Krejs, Ph.D. Ktedr stvení mechnik Řešení nosných stěn pomocí Airho funkce npětí inverzní metod Stěnová rovnice ΔΔ(, ) Stěnová rovnice, nzývná
Analytická geometrie v rovině
nltická geometrie roině Zč je toho loket (ořnice) ) [ ], [ 7], [ ], [ 5] ; b) = 7 j, = j, = 4 j, = 8 j, = j R M P 9 8 7 6 5 4 ) L[ 7], M[ ] ; b) Q[ ], R[ 5] 9 8 7 6 5 4 4 5 6 7 [ 5], [, 5], [ ] Q 9 5 c),
2.1 Shrnutí základních poznatků
.1 Shnutí základních poznatků S plnostěnnými otujícími kotouči se setkáváme hlavně u paních a spalovacích tubín a tubokompesoů. Matematický model otujících kotoučů můžeme s úspěchem využít např. i při
Práce vykonaná v elektrickém poli, napětí, potenciál Vzájemná souvislost mezi intenzitou elektrického pole, napětím a potenciálem Práce vykonaná v
Páce vykonaná v eektickém poi, napětí, potenciá Vzájemná souvisost mezi intenzitou eektického poe, napětím a potenciáem Páce vykonaná v eektostatickém poi po uzavřené dáze Gadient skaání funkce Skaání
Rovinné nosníkové soustavy III Příhradový nosník. Zjednodušená styčníková metoda. Rovinný kloubový příhradový nosník
Stní sttik, 1.ročník klářského stui Roinné nosníkoé sousty III Příhroý nosník Zjnoušná styčníkoá mto Roinný klouoý příhroý nosník Skl roinného příhroého nosníku Pomínk sttiké určitosti příhroého nosníku
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Spojité rozložení náboje
EEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Spojité ozložení náboje Pete Doumashkin MIT 006, překlad: Jan Pacák (007) Obsah. SPOJITÉ OZOŽENÍ NÁBOJE.1 ÚKOY. AGOITMY PO ŘEŠENÍ POBÉMU ÚOHA 1: SPOJITÉ OZOŽENÍ
4. konference o matematice a fyzice na VŠT Brno, Fraktály ve fyzice. Oldřich Zmeškal
4. konfeence o matematice a fyzice na VŠT Bno, 15. 9. 25 Faktály ve fyzice Oldřich Zmeškal Ústav fyzikální a spotřební chemie, Fakulta chemická, Vysoké učení technické, Pukyňova 118, 612 Bno, Česká epublika
= = Řešení: Pro příspěvek k magnetické indukci v bodě A platí podle Biot-Savartova zákona. d 1
Mgntiké pol 8 Vypočtět mgntikou inuki B kuhové smyčky o poloměu 5 m n jjí os symti v válnosti 1 m o oviny smyčky, jstliž smyčkou potéká lktiký pou 1 A Řšní: Po příspěvk k mgntiké inuki v boě A pltí pol
Příklady elektrostatických jevů - náboj
lektostatika Hlavní body Příklady elektostatických jevů. lektický náboj, elementání a jednotkový náboj Silové působení náboje - Coulombův zákon lektické pole a elektická intenzita, Páce v elektostatickém
Mechanická silová pole
Mechanická siloá pole siloé pole mechanice je ekooé pole chaakeizoané z. inenziou siloého pole (inenziou síly): E m [ms ] inenzia je oožná se zychlením, keé siloé pole aném mísě uělí liboolnému ělesu Siloé
FYZIKA I. Mechanika a molekulová fyzika. Doc. RNDr. Karla BARČOVÁ, Ph.D. Institut fyziky.
FYZIKA I. Mechnik molekuloá fyzik Doc. RND. Kl BARČOVÁ, Ph.D. Iniu fyziky O Poub ř. 17. liopu 15 A 98, kl. 31 O Výškoice Lumío 1 LD 84, kl. 88 kl.bco@b.cz hp://if.b.cz - konky Kl Bčoá www.nnoechnologie.cz
Téma 5 Spojitý nosník
Stvení mechnik.očník kářského studi AST Tém 5 Spojitý nosník Zákdní vstnosti spojitého nosníku Řešení spojitého nosníku siovou metodou yužití symetie spojitého nosníku Kted stvení mechniky Fkut stvení
Povrchy a objemy těles
G Kolín JK 0 Pocy objemy těles Hnol jeln Řešené příkldy:. Ceopso pymid má t pidelnéo čtyřbokéo jelnu o zákldně 0 metů. Úel sklonu stěn ϕ (odcylk oiny boční stěny podsty) je oen 5 50.. Kolik kmennýc kádů
Rovinná napjatost tenzometrická růžice Obsah:
5. leke Rovinná npjtost tenzometriká růžie Osh: 5. Úvod 5. Rovinná npjtost 5. Tenzometriká růžie 4 5.4 Posouzení přípustnosti nměřenýh hodnot deforme resp. vyhodnoenýh npět 7 strn z 8 5. Úvod Při měření
8. Základy lomové mechaniky. Únava a lomová mechanika Pavel Hutař, Luboš Náhlík
Únava a lomová mechanika Koncentrace napětí nesingulární koncentrátor napětí singulární koncentrátor napětí 1 σ = σ + a r 2 σ max = σ 1 + 2( / ) r 0 ; σ max Nekonečný pás s eliptickým otvorem [Pook 2000]
Duktilní deformace, část 1
uktilní defomace, část uktilní (plastická) defomace je taková defomace, při níž se mateiál defomuje bez přeušení koheze (soudžnosti). Plasticita mateiálu záleží na tzv. mezi plasticity (yield stess) -
PRUŽNOST A PLASTICITA
PRUŽOST A PLASTICITA Ing. Lenk Lusová LPH 407/1 Povinná litertur tel. 59 732 1326 lenk.lusov@vs.cz http://fst10.vs.cz/lusov http://mi21.vs.cz/modul/pruznost-plsticit Doporučená litertur Zákldní typy nmáhání
Houževnatost. i. Základní pojmy (tranzitní lomové chování ocelí, teplotní závislost pevnostních vlastností, fraktografie)
Houževnatost i. Základní pojmy (tranzitní lomové chování ocelí, teplotní závislost pevnostních vlastností, fraktografie) ii. (Empirické) zkoušky houževnatosti (Charpy, TNDT) iii. Lineárně-elastická elastická
GEOMETRICKÉ APLIKACE INTEGRÁLNÍHO POČTU
Integální počet funkcí jedné eálné poměnné - 4. - GEOMETRICKÉ APLIKACE INTEGRÁLNÍHO POČTU PŘÍKLAD Učete plochu pod gfem funkce f ( x) = sinx n intevlu,. Ploch pod gfem nezáponé funkce f(x) se n intevlu,
České vysoké učení technické v Praze, Fakulta strojní. DPŽ + MSK Jurenka, příklad I. Dynamická pevnost a životnost. Jur, příklad I
1/10 Dynmická pevnst živtnst Jur, příkld I Miln Růžičk, Jsef Jurenk, Mrtin Nesládek jsef.jurenk@fs.cvut.cz /10 ktr intenzity npětí příkld 1 Jk velké mhu být síly půsbící n nsník n dvu pdprách s převislými
M A = M k1 + M k2 = 3M k1 = 2400 Nm. (2)
5.3 Řešené příkldy Příkld 1: U prutu kruhového průřezu o průměrech d d b, který je ztížen kroutícími momenty M k1 M k2 (M k2 = 2M k1 ), viz obr. 1, vypočítejte rekční účinek v uložení prutu, vyšetřete
Odraz na kulové ploše
Odz n kulové ploše Duté zcdlo o.. os zcdl V.. vchol zcdl S.. střed zcdl (kul. ploch).. polomě zcdl (kul. ploch) Ppsek vchází z odu A n ose zcdl po odzu n zcdle dopdá do nějkého odu B n ose. tojúhelníků
ž š ř ú ž ř ž š ř ř ř ř ů š ř ž ř ó ň ó ř š š ž š ř ú ž ú ž ň ř š ř ů ž ž ř ň ř ú ř ř ů ú ú ů ř ú ň ř ž ó ř š ž ž ř ň ř ř ž Ť ó ř ž ú š Á ž ž ř ž ž ž š ž ř š š Á ž ž ž ž ú š ú š ť š ú š ž Š ž ř ž ř š š
Cavendishův pokus: Určení gravitační konstanty,,vážení Země
Cavendishův pokus: Učení gavitační konstanty,,vážení Země Jiří Kist - Mendlovo gymnázium, Opava, SO@seznam.cz Teeza Steinhatová - gymnázium J. K. Tyla Hadec Kálové, SteinT@seznam.cz 1. Úvod Abstakt: Cílem
Kuličková ložiska s kosoúhlým stykem
Kuličková ložisk s kosoúhlým stykm JEDNOŘADÁ A PÁROVANÁ KULIČKOVÁ LOŽISKA S KOSOÚHLÝM STYKEM DVOUŘADÁ KULIČKOVÁ LOŽISKA S KOSOÚHLÝM STYKEM ČTYŘODOVÁ KULIČKOVÁ LOŽISKA KONSTRUKCE, TYPY A VLASTNOSTI Půmě
ZATĚŽOVACÍ ZKOUŠKY. Obr. 1. Statická zatěžovací zkouška; zatížení (N) zatlačení (cm)
ZATĚŽOVACÍ ZKOUŠKY ZATĚŽOVACÍ ZKOUŠKY Sttiká ztěžoví zkoušk položí poklníh vrstev Zřízení - ztěžoví (nákl. uto, ztěžoví most) - kruh. ztěžoví esk (mlá, velká) - kulový kloub - ynmometr - průhyboměr - tuhý
Matematické metody v kartografii
Mtemtické metody v krtogrfii. Přednášk Referenční elipsoid zákldní vzthy. Poloměry křivosti. Délky poledníkového rovnoběžkového oblouku. 1. Zákldní vzthy n rotčním elipoidu Rotční elipsoid dán následujícími
Rovinné nosníkové soustavy Gerberův nosník
Stvení sttik, 1.ročník klářského stui Rovinné nosníkové soustvy Gererův nosník Spojitý nosník s vloženými klouy - Gererův nosník Kter stvení mehniky Fkult stvení, VŠB - Tehniká univerzit Ostrv Sttiky neurčité
Dynamika vozidla Hnací a dynamická charakteristika vozidla
Dynamika ozidla Hnací a dynamická charakteristika ozidla Zpracoal: Pael BRABEC Pracoiště: VM Tento materiál znikl jako součást projektu In-TECH, který je spoluinancoán Eropským sociálním ondem a státním
Stabilita a vzpěrná pevnost tlačených prutů
Pružnost psticit,.ročník kářského studi Stiit vzpěrná pevnost tčených prutů Euerovo řešení stiity přímého pružného prutu Ztrát stiity prutů v pružno-pstickém ooru Posouzení oceových konstrukcí n vzpěr
LABORATORNÍ CVIČENÍ Z FYZIKY. Měření činitele zvukové pohltivosti materiálů v akustickém interferometru
ČESKÉ VYSOKÉ ČENÍ TECHNICKÉ V PRAZE KATEDRA FYZIKY LABORATORNÍ CVIČENÍ Z FYZIKY Jméno: Petr Česák Datum měření: 0..000 Stuijní rok: 000-00, Ročník: Datum oezání: 3..000 Stuijní skupina: 5 Laboratorní skupina:
5.4.2 Objemy a povrchy mnohostěnů I
5.. Objemy orchy mnohostěnů I Předokldy: 51 Význm slo objem i orch je intuitině jsný. Mtemtická definice musí být oněkud řesnější. Okoání z lnimetrie: Obsh obrzce je kldné číslo, řiřzené obrzci tk, že
PODÉLNÁ STABILITA PLOVOUCÍHO TĚLESA VÁLCOVÉHO TVARU PLOVÁKŮ - 1. FÁZE LONGITUDINAL STABILITY OF THE FLOATING BODY BY CYLINDRICAL FORM OF FLOATS - 1
Ročník 5., Číslo III., listopad 00 PODÉLNÁ STABILITA PLOVOUCÍHO TĚLESA VÁLCOVÉHO TVARU PLOVÁKŮ -. FÁZE LONGITUDINAL STABILITY OF THE FLOATING BODY BY CYLINDRICAL FORM OF FLOATS - Leopold Habovský Anotace:
Střídavá magnetická pole pro biomedicínské experimenty
Rok / Ye: Svzek / Volume: Číslo / Numbe: 11 1 Střívá mgnetická pole po biomeicínské expeimenty Oscilte mgnetic fiel fo biomeicl expeiments Mioslv Ptočk, Roslv Cipín, Jn Otýpk ptock@feecvutbcz, xcipin@stufeecvutbcz,
Vyzařovací(směrová) charakteristika F(θ,ϕ), výkonová směrová charakteristika F 2 (θ,ϕ), hustota vyzářeného výkonu S r
Vyzařovací(sěová chaakteistika F(θ,, výkonová sěová chaakteistika F (θ,, hustota vyzářeného výkonu konst hustota vyzářeného výkonu výkon co poje jenotkou pochy v ané ístě, je to stření honota oyntingova
Doplňkové kapitoly. dynamika relativního pohybu základy teorie rázu reaktivní pohyb. asi 1 hodina
Doplňkoé kpitoly Dynik I, 13. přednášk Obsh přednášky : dynik eltiního pohybu zákldy teoie ázu ektiní pohyb Dob studi : si 1 hodin Cíl přednášky : seznáit studenty se způsobe řešení dyniky eltiního pohybu,
Téma 5 Rovinný rám. Základní vlastnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzavřený rám
Stvební mechnik,.ročník bklářského studi AST Tém 5 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit
Rovinné nosníkové soustavy Gerberův nosník
Stvení sttik, 1.ročník klářského stui Rovinné nosníkové soustvy Gererův nosník Spojitý nosník s vloženými klouy - Gererův nosník Kter stvení mehniky Fkult stvení, VŠB - Tehniká univerzit Ostrv Opkování
ELEKTRICKÝ NÁBOJ COULOMBŮV ZÁKON INTENZITA ELEKTRICKÉHO POLE
ELEKTRICKÝ NÁBOJ COULOMBŮV ZÁKON INTENZITA ELEKTRICKÉHO POLE 1 ELEKTRICKÝ NÁBOJ Elektický náboj základní vlastnost někteých elementáních částic (pvní elektické jevy pozoovány již ve staověku janta (řecky
Zjednodušená styčníková metoda
Stvní sttik, 1.ročník klářského stui Rovinné nosníkové soustvy III Příhrový nosník Zjnoušná styčníková mto Rovinný klouový příhrový nosník Skl rovinného příhrového nosníku Pomínk sttiké určitosti příhrového
Kinematika hmotného bodu
DOPLŇKOVÉ TEXTY BB1 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ Kinemik hmoného bodu Obsh Klsická mechnik... Vzžný sysém... Polohoý ekor... Trjekorie... Prmerické ronice rjekorie... 3 Příkld 1... 3
Pevnost a životnost Jur III
1/48 Pevnost a životnost Jur III Milan Růžička, Josef Jurenka, Zbyněk Hrubý Poděkování: Děkuji prof. Ing. Jiřímu Kunzovi, CSc za laskavé svolení s využitím některých obrázků z jeho knihy Aplikovaná lomová
Smíšený součin
7..14 Smíšený součin Předpokldy: 713 Je dán ronoěžnostěn LMNOPR. R O P N M L Jeho ojem umíme spočítt stereometrikým zorem: V = S. p Ronoěžnostěn je tké určen třemi ektory, : R O P N M L jeho ojem musí
Válečková ložiska JEDNOŘADÁ VÁLEČKOVÁ LOŽISKA. Průměr díry Strana mm... B mm... B mm... B126
Válečková ložiska JEDNOŘADÁ VÁLEČKOVÁ LOŽISKA Příložné koužky po válečková ložiska DVOUŘADÁ VÁLEČKOVÁ LOŽISKA Čtyřřadá válečková ložiska jsou popsána na stanách 322 až 331. Půmě díy Stana 20 55 mm... 110
TERMOMECHANIKA 16. Přenos tepla vedením
FSI VU v Bně, Enegetický ústv Odbo temomechniky techniky postředí pof. Ing. Miln Pvelek, CSc. ERMOMECHANIKA 6. Přenos tepl vedením OSNOVA 6. KAPIOLY Difeenciální ovnice vedení tepl Počáteční okjové podmínky
k + q. Jestliže takový dipól kmitá s frekvencí ν (odpovídající
Vlastnosti kmitajíího dipólu Podle klasiké teoie je nejefektivnějším zdojem elektomagnetikého záření kmitajíí elektiký dipól. Intenzita jeho záření o několik řádů převyšuje intenzity ostatníh zdojů záření
MG - Stacionární a kvazistacionární magnetické pole
Stcionání kzistcionání g. poe MG- Mgnetická indukce, iot-stů zákon V MG - Stcionání kzistcionání gnetické poe Mgnetické poe síy gnetické poi jsou yoné půsoení poyujícíc se eektickýc náojů. Těito náoji
I. MECHANIKA 4. Soustava hmotných bodů II
I. CHIK 4. Soustaa hmotných bodů II 1 Obsah Spojté ozložení hmotnost. Počet stupňů olnost. Knematka tuhého tělesa. Zjednodušení popsu otace kolem osy a peného bodu. Chaslesoa ěta. Dynamka tuhého tělesa.