Návrh nové koncepce výuky trestního práva
|
|
|
- Radek Tábor
- před 6 lety
- Počet zobrazení:
Transkript
1 Katedra trestího práva Akademický rok 2018/2019 Návrh ové kocepce výuky trestího práva I. Nová kocepce výuky trestího práva Nová kocepce výuky trestího práva, předkládaá katedrou trestího práva, je v souladu s proklamovaým cílem vedeí Právické fakulty Uiverzity Karlovy, vychází vstříc požadavkům studetů a respektuje i ázory praxe. Naším záměrem je, aby absolveti Právické fakulty UK měli jedak hlubší teoretické i praktické zalosti trestího práva jako oboru platého práva, jedak lepší předpoklady získat uplatěí a současém trhu práce (rozvoj praktických dovedostí v oboru trestího práva, případě oborů souvisejících). Zároveň tím dojde k aplěí požadavků vysloveých v ávrhu tezí ového magisterského studijího programu Právo a práví věda ze de 2. říja Změa současé kocepce spočívá v: 1) posuutí začátku výuky trestího práva do třetího semestru studia (tj. a počátek druhého ročíku), 2) zitezívěí výuky trestího práva v druhé čtvrtiě základího kurzu trestího práva (tj. ve čtvrtém semestru magisterského studia), 3) rozšířeí předstáticové výuky trestího práva, 4) zvýšeí ároků a studeta v prvím roce výuky trestího práva (kokrétě ve čtvrtém semestru magisterského studia). Zachová zůstae současý model předášek a a ě avazujících semiářů s frekvecí semiáře jedekrát týdě. Základí kurz trestího práva bude stejě jako dosud zakoče ústí postupovou zkouškou a písemou klauzurí prací. 1
2 Ad 1) V současé době je základí kurz trestího práva vyučová až a začátku třetího (z pěti) ročíků magisterského studia. Takové zařazeí eí podle ašeho ázoru vhodé, eboť studeti práv jsou kofrotovái s platým právem převážě až v druhé poloviě svého magisterského studia, což je v případě oboru trestího práva jedak výrazě časově limituje při výběru avazujících poviě-volitelých předmětů v závěru studia, jedak eodpovídá profilu absolveta a současým potřebám a trhu práce. Už posuutí začátku výuky trestího práva do třetího semestru magisterského studia umoží studetům déle studovat teto důležitý, klíčový obor platého práva, získat větší praktické dovedosti v oboru a lépe se připravit a státí závěrečou zkoušku z ěj. Zájemci o trestí právo, kteří se tomuto oboru chtějí dále itezivě věovat, umoží změa kocepce absolvováí většího možství poviě-volitelých předmětů, jejichž široké portfolio hodlá katedra trestího práva adále rozšiřovat. Ad 2) Zitezivěí výuky trestího práva bude spočívat především v tom, že ve čtvrtém semestru magisterského studia (v letím semestru druhého ročíku magisterského studia) budou z trestího práva týdě dvě předášky (z předmětu Trestí právo II a souběžě z předmětu Trestí právo III) místo jedé. Počet semiářů zůstae stejý. Formálě to bude zameat, že základí kurz trestího práva se bude skládat z pěti předmětů (Trestí právo I až V) místo dosavadích čtyřech. Předmět Trestí právo II bude zakoče zápočtem (podmíkou aktiví účast a semiářích/test), předmět Trestí právo III bude zakoče rověž zápočtem (celokatederí test). Studetům tedy oproti současému stavu přibude jeda studijí poviost. Obsah předmětu Trestí právo I se oproti dosavadí kocepci ezměí. Předášky jsou věováy obecé části trestího práva a každý týde je aplikačí semiář. Obsahem předášek z předmětu Trestí právo II budou zbývající kapitoly eodpředášeé v rámci předmětu Trestí právo I, tj. předášky z obecé části trestího práva hmotého (sakcioováí) a úvodí kapitoly z trestího práva procesího (zejm. základí zásady trestího práva procesího, problematika předběžých otázek, pravomoci a příslušosti soudů, subjektů trestího řízeí a zajišťovacích istitutů s důrazem a istitut vazby). Obsahem předášek z předmětu Trestí právo III budou jedotlivé kapitoly zvláští části trestího práva hmotého (tresté čiy po jedotlivých hlavách ve zvláští části trestího 2
3 zákoíku). Semiáře z předmětu Trestí právo II budou obsahově totožé jako v současé době. Trestí právo IV bude probíhat (stejě jako des Trestí právo III) ve formě předášek a semiářů a bude zakočeo zápočtem (aktiví účast a semiářích/test) a ústí postupovou zkouškou (v poloviě třetího ročíku). Orietačí přehled obsahu výuky vyplývá z přiložeého grafu a sezamu předášek a semiářů. Změou kocepce dojde ke zdůrazěí přirozeého propojeí trestího práva hmotého a procesího a studeti tak získají komplexější představu o vzájemých souvztažostech v rámci oboru trestího práva. Obsahově to bude zameat, že větší pozorost bude ve výuce věováa zvláští části trestího práva hmotého (téměř každé hlavě zvláští části trestího zákoíku bude věováa samostatá předáška) a trestímu právu procesímu (bude vyučováo od čtvrtého semestru studia), což odpovídá i požadavkům studetů. Právě tyto dvě části (zvláští část trestího práva hmotého a zejméa trestí právo procesí) dělají studetům ejvětší obtíže při přípravě a ústí postupovou zkoušku z trestího práva, která se v souladu s požadavkem, aby postupová zkouška byla co do rozsahu obtížější ež státí závěrečá zkouška, skládá z třech vylosovaých otázek, a to z: 1. trestího práva hmotého (obecá část), 2. trestího práva hmotého (zvláští část) a 3. trestího práva procesího. Největším příosem ové kocepce bude skutečost, že v rámci předmětu Trestí právo IV (des Trestí právo III), který se věuje trestímu právu procesímu, bude větší prostor (jak v rámci předášek, tak v rámci a ě avazujících semiářů) věová dokazováí, jedotlivým stadiím trestího řízeí a opravým prostředkům. Tuto změu obsahu umoží fakt, že úvodí pasáže z trestího práva procesího budou odpředášey již ve čtvrtém semestru studia. Ad 3) Rozšířeí předstáticové výuky ze stávajících dvou do šesti předášek reaguje a fakt, že od ukočeí základího kurzu trestího práva (a koci šestého semestru studia apsáí klauzurí práce) uplye do státích závěrečých zkoušek delší čas, ež v současém pojetí výuky. Zejméa pro ty studety, kteří ebudou prohlubovat své zalosti v oboru v rámci poviě volitelých předmětů ebo v rámci psaí diplomové práce a katedře trestího 3
4 práva, bude rozšířea předstáticová výuka, aby byli áležitě sezámei se změami v trestí legislativě ebo jiými důležitými událostmi v oboru. V souvislosti s tím dáváme ke zvážeí, zda předstáticovou výuku trestího práva ezařadit již do 9. semestru magisterského studia. V takovém případě by bylo možé koat státí závěrečou zkoušku z trestího práva i v zimím semestru posledího ročíku studia. Navíc se zkrátí časový iterval od posledí studijí poviosti z trestího práva (klauzurí práce) do předstáticové výuky a pouhé dva semestry. Ad 4) V souladu s ávrhem a celkovou změu kocepce studia, která usiluje o zvýšeí kvality absolvetů, s čímž souvisí i zvýšeí ároků a studeta, přibude i v rámci základího kurzu trestího práva jeda studijí poviost spočívající v apsáí celokatederího testu (podmíka zápočtu z předmětu Trestí právo III). Dosavadí požadavky pro absolvováí předmětu trestí právo zůstaou ezměěy (průběžé zápočty, ústí postupová zkouška, písemá klauzurí práce). Přehled avrhovaého řešeí ukazuje ásledující graf. 4
5 P o v i é p ř e d m ě t y P o v i ě v o l i t e l é p ř e d m ě t y 1. ročík 2. ročík 3. ročík 4. ročík 5. ročík 1. semestr 2. semestr 3. semestr 4. semestr 5. semestr 6. semestr 7. semestr 8. semestr 9. semestr 10. semestr Trestí právo I. (zápočet) Trestí právo II. (zápočet) Trestí právo III. (zápočet) Trestí právo IV. (zápočet + zkouška) Trestí právo V. (klauzurí práce) Předstáticová výuka Krimiologie I. Krimiologie I. Krimiologie I. Krimiologie I. Krimiologie I. Krimiologie II. Krimiologie II. Krimiologie II. Krimiologie II. Krimiologie II. Rozhodutí ve věcech trestích Vybraé kapitoly z trestí odpovědosti právických osob a řízeí proti im Vědecký semiář z trestího práva Odborá praxe - praxe a státím zastupitelství Soudí psychologie a soudí sexuologie Soudí lékařství Krimialistika Metodika vyšetřováí jedotl. druhů trestých čiů Europeizace trestího práva Domácí ásilí Soudí psychologie Kyberetická krimialita a kyberetická bezpečost Odborá praxe - praxe a soudech II. (trestí úsek) Diplomový semiář 5
6 II. Orietačí ávrh rozpisu předášek a semiářů z trestího práva Trestí právo I program předášek (3. semestr magisterského studia) 1. Pojem trestího práva, jeho fukce a základí zásady 2. Pojem trestého čiu, tříděí trestých čiů 3. Skutková podstata trestého čiu 4. Objekt trestého čiu, objektiví stráka trestého čiu 5. Pachatel trestého čiu 6. Subjektiví stráka trestého čiu 7. Okolosti vylučující protiprávost 8. Vývojová stadia trestého čiu 9. Účasteství 10. Souběh trestých čiů a recidiva 11. Záik trestí odpovědosti 12. Trestí odpovědost právických osob Trestí právo I program semiářů (3. semestr magisterského studia) 1. Program semiářů, učebí pomůcky, studium oboru aj. 2. Pramey trestího práva, výklad trestích zákoů, aalogie 3. Působost trestích zákoů 4. Trestý či a skutková podstata trestého čiu 5. Objekt trestého čiu, objektiví stráka trestého čiu 6. Pachatel trestého čiu 7. Subjektiví stráka trestého čiu 8. Okolosti vylučující protiprávost 9. Vývojová stadia trestého čiu 10. Účasteství 11. Souběh trestých čiů 12. Zápočtové semiáře Trestí právo II program předášek (4. semestr magisterského studia) 1. Pojem a účel trestu, systém trestů 2. Ukládáí trestů dospělým 3. Ochraá opatřeí 4. Sakcioováí mladistvých 5. Sakcioováí právických osob 6. Pojem, předmět a účel trestího řízeí. Předběžé otázky 7. Spravedlivý trestí proces 8. Základí zásady trestího řízeí I 9. Základí zásady trestího řízeí II 10. Subjekty trestího řízeí I obviěý, obhájce 11. Subjekty trestího řízeí II poškozeý, zúčastěá osoba 12. Zajištěí osob a věcí důležitých pro trestí řízeí, zejméa vazba 6
7 Trestí právo III program předášek (4. semestr magisterského studia) 1. Tresté čiy proti životu a zdraví I 2. Tresté čiy proti životu a zdraví II 3. Tresté čiy proti svobodě a právům a ochrau osobosti 4. Tresté čiy proti lidské důstojosti v sexuálí oblasti 5. Tresté čiy proti rodiě a dětem 6. Tresté čiy proti majetku I 7. Tresté čiy proti majetku II 8. Tresté čiy hospodářské 9. Tresté čiy obecě ebezpečé I 10. Tresté čiy obecě ebezpečé II drogové delikty 11. Tresté čiy proti České republice, cizímu státu a meziárodí orgaizaci 12. Tresté čiy proti pořádku ve věcech veřejých Trestí právo II program semiářů (4. semestr magisterského studia) 1. Pojem a účel trestu, systém trestů 2. Ukládáí trestů dospělým 3. Ochraá opatřeí 4. Trestáí mladistvých 5. Tresté čiy proti životu a zdraví 6. Tresté čiy proti svobodě a právům a ochrau osobosti, soukromí a listovího tajemství 7. Tresté čiy proti lidské důstojosti v sexuálí oblasti 8. Tresté čiy proti rodiě a dětem 9. Tresté čiy proti majetku 10. Tresté čiy hospodářské 11. Tresté čiy obecě ebezpečé 12. Tresté čiy proti pořádku ve věcech veřejých, zápočtový semiář Trestí právo IV program předášek (5. semestr magisterského studia) 1. Dokazováí v trestím řízeí I 2. Dokazováí v trestím řízeí II 3. Rozhodutí ve věcech trestích 4. Přípravé řízeí I 5. Přípravé řízeí II a předběžé projedáí obžaloby 6. Hlaví líčeí I 7. Hlaví líčeí II 8. Řádé opravé prostředky 9. Mimořádé opravé prostředky 10. Zvláští způsoby řízeí 11. Vykoávací řízeí 12. Meziárodí justičí spolupráce ve věcech trestích 7
8 Trestí právo IV program semiářů (5. semestr magisterského studia) 1. Program semiářů, učebí pomůcky, studium oboru aj. 2. Základí zásady trestího řízeí 3. Zajištěí osob a věcí důležitých pro trestí řízeí, zejméa vazba 4. Dokazováí v trestím řízeí I 5. Dokazováí v trestím řízeí II 6. Přípravé řízeí I 7. Přípravé řízeí II a předběžé projedáí obžaloby 8. Hlaví líčeí I 9. Hlaví líčeí II 10. Řádé opravé prostředky I 11. Řádé opravé prostředky II 12. Mimořádé opravé prostředky, zápočtový semiář Trestí právo V program předášek (6. semestr magisterského studia) 1. Metodika zpracováí klauzurích prací. Zadáí cvičé klauzurí práce 2. Vybraé otázky trestího práva 3. Vybraé otázky trestího práva 4. Řešeí cvičé klauzurí práce 5. Vybraé otázky trestího práva 6. Vybraé otázky trestího práva Předstáticová výuka (9. ebo 10. semestr magisterského studia) 1. Příprava a státí závěrečou zkoušku trestí právo hmoté 2. Příprava a státí závěrečou zkoušku trestí právo hmoté 3. Příprava a státí závěrečou zkoušku trestí právo hmoté 4. Příprava a státí závěrečou zkoušku trestí právo procesí 5. Příprava a státí závěrečou zkoušku trestí právo procesí 6. Příprava a státí závěrečou zkoušku trestí právo procesí V Praze de 19. říja 2018 prof. JUDr. Jiří Jelíek, CSc., v. r. vedoucí katedry trestího práva 8
Spojitost a limita funkcí jedné reálné proměnné
Spojitost a limita fukcí jedé reálé proměé Pozámka Vyšetřeí spojitosti fukce je možo podle defiice převést a výpočet limity V dalším se proto soustředíme je problém výpočtu limit Pozámka Limitu fukce v
VYSOCE PŘESNÉ METODY OBRÁBĚNÍ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
dálniced3 a rychlostní silnice Praha x Tábor x České Budějovice x Rakousko
dáliced3 a rychlostí silice R3 Praha Tábor České Budějovice Rakousko w w obsah základí iformace 3 dálice D3 a rychlostí silice R3 PrahaTáborČeské BudějoviceRakousko 3 > základí iformace 4 > čleěí dálice
Systém pro zpracování, analýzu a vyhodnocení statistických dat ERÚ. Ing. Petr Kusý Energetický regulační úřad odbor statistický a bezpečnosti dodávek
Systém pro zpracováí, aalýzu a vyhodoceí statistických dat ERÚ Ig. Petr Kusý Eergetický regulačí úřad odbor statistický a bezpečosti dodávek TA ČR, 9. duba 2019 Eergetický regulačí úřad - stručě Nezávislý
PŘIJÍMACÍ ŘÍZENÍ PRO ŠKOLNÍ ROK 2012/2013
PŘIJÍMACÍ ŘÍZENÍ PRO ŠKOLNÍ ROK 2012/2013 OSNOVA 1. Práví předpisy 2. Přijímací řízeí 3. Termíy 4. Hodoceí uchazečů 5. Rozhodutí 6. Další kola přijímacího řízeí 7. Zápisový lístek 8. Jedoté přijímací zkoušky
Matematika 1. Katedra matematiky, Fakulta stavební ČVUT v Praze. středa 10-11:40 posluchárna D / 13. Posloupnosti
Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Stanovisko SVJ Vazovova 3228 k dopisu paní Šedivé ze dne
V Praze de 27.3 2009 Staovisko SVJ Vazovova 3228 k dopisu paí Šedivé ze de 17.3 2009. V průběhu měsíce úora bylo a ástěce SVJ vyvěšeo ozámeí o pláovaém shromážděí spolu s ávrhem programu a výzvou k vlastíkům
jsou reálná a m, n jsou čísla přirozená.
.7.5 Racioálí a polomické fukce Předpoklad: 704 Pedagogická pozámka: Při opisováí defiic racioálí a polomické fukce si ěkteří studeti stěžovali, že je to příliš těžké. Ve skutečosti je sstém, kterým jsou
Výukový modul III.2 Inovace a zkvalitnění výuky prostřednictvím ICT
Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
OBSAH. Rozklad... 16 Žaloba... 17
OBSAH Persoálí bezpečost Jak požádat o ozámeí a Vyhrazeé... 4 Jak požádat o osvědčeí fyzické osoby (D, T, PT)... 5 Jak a kdy požádat o vydáí osvědčeí fyzické osoby pro cizí moc NATO, WEU... 7 Osvědčeí
8.2.1 Aritmetická posloupnost I
8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
Model péče o duševně nemocné
Model péče o duševě emocé v regiou hlavího města Prahy Zázam jedáí závěrečé koferece projektu Vzděláváí odboríků, státí správy a samosprávy v oblasti trasformace istitucioálí péče o duševě emocé Praha,
Vlastní hodnocení školy
Vlastí hodoceí školy dle vyhlášky 15/2005 Sb., v platém zěí, kterou se staoví áležitosti dlouhodobých záměrů, výročích zpráv a vlastí hodoceí školy. Škola: Základí umělecká škola Plzeň, Sokolovská 30,
8.1.3 Rekurentní zadání posloupnosti I
8.. Rekuretí zadáí poslouposti I Předpoklady: 80, 80 Pedagogická pozámka: Podle mých zkušeostí je pro studety pochopitelější zavádět rekuretí posloupost takto (sado kotrolovatelou ukázkou), ež dosazováím
Aritmetická posloupnost, posloupnost rostoucí a klesající Posloupnosti
8 Aritmetická posloupost, posloupost rostoucí a klesající Poslouposti Posloupost je fukci s defiičím oborem celých kladých čísel - apř.,,,,,... 3 4 5 Jako fukci můžeme také posloupost zobrazit do grafu:
Téma: 11) Dynamika stavebních konstrukcí
Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
Klára Kalibová PRÁVO NA PRÁVNÍ POMOC A OBĚTI PŘEDSUDEČNÉ TRESTNÉ ČINNOSTI
Klára Kalibová PRÁVO NA PRÁVNÍ POMOC A OBĚTI PŘEDSUDEČNÉ TRESTNÉ ČINNOSTI Klára Kalibová I IUSTITIA (Česká repulika) PRÁVO NA PRÁVNÍ POMOC A OBĚTI PŘEDSUDEČNÉ TRESTNÉ ČINNOSTI Klára Kalibová I IUSTITIA
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta dopraví Statistika Semestrálí práce Zdražováí pohoých hmot Jméa: Martia Jelíková, Jakub Štoudek Studijí skupia: 2 37 Rok: 2012/2013 Obsah Úvod... 2 Použité
4 DOPADY ZPŮSOBŮ FINANCOVÁNÍ NA INVESTIČNÍ ROZHODOVÁNÍ
4 DOPADY ZPŮSOBŮ FACOVÁÍ A VESTČÍ ROZHODOVÁÍ 77 4. ČSTÁ SOUČASÁ HODOTA VČETĚ VLVU FLACE, CEOVÝCH ÁRŮSTŮ, DAÍ OPTMALZACE KAPTÁLOVÉ STRUKTURY Čistá současá hodota (et preset value) Jedá se o dyamickou metodu
TECHNICKÁ UNIVERZITA V LIBERCI Studentská 1402/ Liberec 1 tel.:
TECHNICKÁ UNIVERZITA V LIBERCI Studetská 1402/2 461 17 Liberec 1 tel.: +420 485 353 302 studium@tul.cz www.tul.cz PRSZ_titul_2018.idd 1 PLÁN REALIZACE STRATEGICKÉHO ZÁMĚRU TECHNICKÉ UNIVERZITY V LIBERCI
Trestní právo Generováno
Trestní právo Generováno 6. 12. 2016 A Okruh A.......................................................... A.1 Pojem trestního práva hmotného, trestněprávní vztah, funkce trestního práva a jeho základní
Matematika 1. Ivana Pultarová Katedra matematiky, Fakulta stavební ČVUT v Praze. středa 10-11:40 posluchárna D Posloupnosti
Úvod Opakováí Poslouposti Příklady Matematika 1 Ivaa Pultarová Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Současnost a budoucnost provozní podpory podle zákona POZE
Současost a budoucost provozí podpory podle zákoa POZE ENERGETICKÝ REGULAČNÍ ÚŘAD Odbor podporovaých zdrojů poze@eru.cz Ig. Kristiá Titka 20. 11. 2018 Frymburk Rada ERÚ od 1. 8. 2018 JUDr. PhDr. Vratislav
Informační systémy o platu a služebním příjmu zahrnují:
Katalog datových prvků a dalších položek používaých v Iformačích systémech o platu a služebím příjmu (ISPSP) verze 2014-6 16. 4. 2014 ISPSP Iformačí systémy o platu a služebím příjmu zahrují: ISP Iformačí
9.1.13 Permutace s opakováním
93 Permutace s opakováím Předpoklady: 906, 9 Pedagogická pozámka: Obsah hodiy přesahuje 45 miut, pokud emáte k dispozici další půlhodiu, musíte žáky echat projít posledí dva příklady doma Př : Urči kolik
Příloha č. 7 Dodatku ke Smlouvě o službách Systém měření kvality Služeb
Příloha č. 7 Dodatku ke Smlouvě o službách Systém měřeí kvality Služeb Dodavatel a Objedatel se dohodli a ahrazeí Přílohy C - Systém měřeí kvality Služeb Obchodích podmíek Smlouvy o službách touto Přílohou
9.1.12 Permutace s opakováním
9.. Permutace s opakováím Předpoklady: 905, 9 Pedagogická pozámka: Pokud echáte studety počítat samostatě příklad 9 vyjde tato hodia a skoro 80 miut. Uvažuji o tom, že hodiu doplím a rozdělím a dvě. Př.
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
8.2.1 Aritmetická posloupnost
8.. Aritmetická posloupost Předpoklady: 80, 80, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Př. : V továrě dokočí každou hodiu motáž
Schopní a vlídní lidé u nás mají šanci
Schopí a vlídí lidé u ás mají šaci Vsetíská emocice je akciovou společostí, jejímž zakladatelem a současě jediým akcioářem je Zlíský kraj. Se svými více ež šesti stovkami zaměstaců patříme mezi ejvětší
Výukový modul III.2 Inovace a zkvalitnění výuky prostřednictvím ICT
Základy práce s tabulkou Výukový modul III. Iovace a zkvaltěí výuky prostředctvím IC éma III..3 echcká měřeí v MS Excel Pracoví lst 5 Měřeí teploty. Ig. Jří Chobot VY_3_INOVACE_33_5 Aotace Iovace a zkvaltěí
Zimní semestr akademického roku 2015/ listopadu 2015
Cvičeí k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikovaé matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičeí Zimí semestr akademického roku 2015/2016 20. listopadu 2015 Předmluva
Sekvenční logické obvody(lso)
Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Dobývání znalostí. Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze
Dobýváí zalostí Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické iformatiky Matematicko-fyzikálí fakulta Uiverzity Karlovy v Praze Dobýváí zalostí Pokročilé techiky pro předzpracováí dat Doc. RNDr. Iveta
14. Testování statistických hypotéz Úvod statistické hypotézy Definice 14.1 Statistickou hypotézou parametrickou neparametrickou. nulovou testovanou
4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
8.3. Limity ěkterých posloupostí Předpoklady: 83 Opakováí z miulé hodiy: 8 Hodoty poslouposti + se pro blížící se k ekoeču blíží k a to tak že mezi = posloupostí a číslem eexistuje žádá mezera říkáme že
6. FUNKCE A POSLOUPNOSTI
6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
PROGRAM PŘEDNÁŠEK TRESTNÍ PRÁVO (hmotné a procesní) V EVROPSKÉM PROSTŘEDÍ
PROGRAM PŘEDNÁŠEK TRESTNÍ PRÁVO (hmotné a procesní) V EVROPSKÉM PROSTŘEDÍ IV. jarní semestr Evropská hospodářská, správní a kulturní studia - ak. rok 2014/2015 I. 25. 2. 2014 doc. M. Fryšták Pojem trestního
Pro likvidaci uniklých látek. Příručka Pro Prevenci a HavariJní situace Při PrÁci s nebezpečnými látkami
sorpčí ProstřeDkY a ProDuktY Pro likvidaci uiklých látek Příručka Pro Preveci a HavariJí situace Při PrÁci s ebezpečými látkami záchyté ProstřeDkY / sorbety / likvidace uiklých látek všude tam, kde jsou
MATICOVÉ HRY MATICOVÝCH HER
MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
1 PŘÍLOHY. I. Řetězec vzdělávání dle Bočkové. Obrázek I Řetězec vzdělávání dle Bočkové Zdroj: Bočková, V., 2000, s. 11.
1 PŘÍLOHY I. Řetězec vzděláváí dle Bočkové Obrázek I Řetězec vzděláváí dle Bočkové Zdroj: Bočková, V., 2000, s. 11. I II. Schéma celoživotího vzděláváí dle Paláa Obrázek II Schéma celoživotího vzděláváí
Užití binomické věty
9..9 Užití biomické věty Předpoklady: 98 Často ám z biomického rozvoje stačí pouze jede kokrétí čle. Př. : x Urči šestý čle biomického rozvoje xy + 4y. Získaý výraz uprav. Biomický rozvoj začíá: ( a +
Vzorový příklad na rozhodování BPH_ZMAN
Vzorový příklad a rozhodováí BPH_ZMAN Základí charakteristiky a začeí symbol verbálí vyjádřeí iterval C g g-tý cíl g = 1,.. s V i i-tá variata i = 1,.. m K j j-té kriterium j = 1,.. v j x ij u ij váha
Matematika I, část II
1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
Tento materiál vznikl díky Operačnímu programu Praha Adaptabilita CZ.2.17/3.1.00/33254
Evropský sociálí fod Praha & EU: Ivestujeme do vaší budoucosti Teto materiál vzikl díky Operačímu programu Praha Adaptabilita CZ.2.17/3.1.00/33254 Maažerské kvatitativí metody II - předáška č.1 - Dyamické
veličiny má stejný řád jako je řád poslední číslice nejistoty. Nejistotu píšeme obvykle jenom jednou
1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
Mocninné řady - sbírka příkladů
UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY BAKALÁŘSKÁ PRÁCE Mocié řady - sbírka příkladů Vedoucí bakalářské práce: Mgr. Iveta Bebčáková, Ph.D.
4EK311 Operační výzkum. 4. Distribuční úlohy LP část 2
4EK311 Operačí výzkum 4. Distribučí úlohy LP část 2 4.1 Dopraví problém obecý model miimalizovat za podmíek: m z = c ij x ij i=1 j=1 j=1 m i=1 x ij = a i, i = 1, 2,, m x ij = b j, j = 1, 2,, x ij 0, i
3. cvičení - LS 2017
3. cvičeí - LS 07 Michal Outrata Defiičí obor, průsečíky os, kladost/záporost fukce a) fx) x 5x+4 4 x b) fx) x x +4x+ c) fx) 3x 9x+ x +6x 0 d) fx) x 7x+0 4 x. Řešeí a) Nulové body čitatele a jmeovatele
3. cvičení - LS 2017
3. cvičeí - LS 07 Michal Outrata Defiičí obor, průsečíky os, kladost/záporost fukce a fx x 5x+4 4 x b fx x x +4x+ c fx 3x 9x+ x +6x 0. Řešeí a Nulové body čitatele a jmeovatele jsou { 4}. Aby vše bylo
VOX PEDIATRIAE. časopis praktických lékařů pro děti a dorost. únor 2009. číslo 2. ročník 9. Léčba v Dětské lázeňské léčebně Lázně Kynžvart
VOX PEDIATRIAE časopis praktických lékařů pro děti a dorost úor 2009 číslo 2 ročík 9 Léčba v Dětské lázeňské léčebě Lázě Kyžvart Nemocost dětí v Ostravě v důsledku zečištěého ovzduší Zátěží idukovaé astma
Konec srandy!!! Mocniny s přirozeným mocnitelem I. Předpoklady: základní početní operace
Koec srady!!!.6. Mociy s přirozeým mocitelem I Předpoklady: základí početí operace Pedagogická pozámka: Zápis a začátku kapitoly je víc ež je srada. Tato hodia je prví v druhé části studia. Až dosud ehrálo
2,3 ČTYŘI STANDARDNÍ METODY I, ČTYŘI STANDARDNÍ METODY II
2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
Úloha III.S... limitní
Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
Za nás mluví práce. s podporou Nezávislých
Za ás mluví práce Jiří Oberfalzer, Michal Prokůpek, Jaa Chlupová, Radek Novák, Petr Vychodil a dvaáct dalších kadidátů Vás zvou ke komuálím volbám ODS s podporou Nezávislých Program pro Králův Dvůr Trasparetí
Prostředky automatického řízení
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ Protředky automatického řízeí Měřící a řídící řetězec Vypracoval: Petr Oadík Akademický rok: 006/007 Semetr: letí Zadáí Navrhěte měřicí
VOX PEDIATRIAE. časopis praktických lékařů pro děti a dorost. duben 2009 číslo 4 ročník 9. Cílený skríning celiakální sprue
VOX PEDIATRIAE časopis praktických lékařů pro děti a dorost dube 2009 číslo 4 ročík 9 Cíleý skríig celiakálí sprue Nespecifické střeví záěty Steóza au - častá příčia tříměsíčí koliky Gastroezofageálí reflux
v kat. situaci pozemek je projektu vyznačeno uváděn ve
Pomocá tbulk pro kotrolu formálí správosti úplosti projektu OPŽP pro příprvu věcého hodoceí verze pro směr podpory 6.4. Odvozeo dle podmíek 6. výzvy v r. 2008. Jedá se o ezávzou epoviou pomůcku pro práci
Asociace inovačního podnikání ČR
Asociace iovačího podikáí ČR ve spolupráci s Miisterstvem školství, mládeže a tělovýchovy, Miisterstvem průmyslu a obchodu, Výborem pro hospodářství, zemědělství a dopravu Seátu Parlametu ČR, tuzemskými
I.ÚZEMNÍ PLÁN STAŇKOV I. Ú Z E M N Í P L Á N STAŇKOV. Opatření obecné povahy č.j. ze dne Záznam o účinnosti
I. Ú Z E M N Í P L Á N Správí orgá, který území plá vydal: Datum abytí účiosti územího pláu: Pořizovatel Jméo a příjmeí Fukce Podpis (oprávěá úředí osoba pořizovatele) Opatřeí obecé povahy č.j. ze de Zázam
ASYNCHRONNÍ STROJE. Obsah
VŠB TU Ostrava Fakulta elektrotechiky a iformatiky Katedra obecé elektrotechiky ASYCHROÍ STROJE Obsah. Výzam a oužití asychroích motorů 2. rici čiosti asychroího motoru 3. Rozděleí asychroích motorů 4.
U klasifikace podle minimální vzdálenosti je nutno zvolit:
.3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
ANALÝZA A KLASIFIKACE DAT
ANALÝZA A KLASIFIKACE DA prof. Ig. Jří Holčík, CSc. INVESICE Isttut DO bostatstky ROZVOJE VZDĚLÁVÁNÍ a aalýz IV. LINEÁRNÍ KLASIFIKACE pokračováí Isttut bostatstky a aalýz (SUPPOR VECOR MACHINE SVM) SEPARABILNÍ
PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemný test, varianta B)
Přijímací řízeí pro akademický rok 24/5 a magisterský studijí program: PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemý test, variata B) Zde alepte své uiverzití číslo U každé otázky či podotázky v ásledujícím
UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ
3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
Informační systémy o platu a služebním příjmu zahrnují:
Katalog datových prvků a dalších položek používaých v Iformačích systémech o platu a služebím příjmu (ISPSP) verze 2015-06 2. 3. 2015 ISPSP Iformačí systémy o platu a služebím příjmu zahrují: ISP Iformačí
ARITMETICKÉ POSLOUPNOSTI VYŠŠÍCH ŘÁDŮ
ARITMETICKÉ POSLOUPNOSTI VYŠŠÍCH ŘÁDŮ JAROSLAV ZHOUF Pedagogická fakulta UK Praha Osova předášky 1. Vysvětleí pojmu Aritmetické poslouposti vyšších řádů (APVŘ). APVŘ a ižším gymáziu 3. APVŘ a vyšším gymáziu
PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemný test)
Přijímací řízeí pro akademický rok 2007/08 a magisterský studijí program: Zde alepte své uiverzití číslo PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemý test) U každé otázky či podotázky v ásledujícím
PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemný test)
Přijímací řízeí pro akademický rok 2007/08 a magisterský studijí program: Zde alepte své uiverzití číslo PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemý test) U každé otázky či podotázky v ásledujícím
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
AMC/IEM J - HMOTNOST A VYVÁŽENÍ
ČÁST JAR-OPS 3 AMC/IEM J - HMOTNOST A VYVÁŽENÍ ACJ OPS 3.605 Hodoty hmotostí Viz JAR-OPS 3.605 V souladu s ICAO Ae 5 a s meziárodí soustavou jedotek SI, skutečé a omezující hmotosti vrtulíků, užitečé zatížeí
UHK Fórum. Univerzita Hradec Králové Fakulta informatiky a managementu Informační management Databázové systémy II
Popis fukcioality UHK Fóra pro předmět Databázové systémy II. Uiverzita Hradec Králové Fakulta iformatiky a maagemetu Iformačí maagemet Databázové systémy II uhkforum.mikmik.cz voborik@mikmik.cz Obsah
8.3.1 Pojem limita posloupnosti
.3. Pojem limit poslouposti Předpokldy: 30, 0 Pedgogická pozámk: Limit poslouposti eí pro studety sdo strvitelým pojmem. Hlvím problémem je podle mých zkušeostí edorozuměí s tím, zd mezi posloupostí její
ZÁVĚREČNÉ BAKALÁŘSKÉ PRÁCE
ZÁVĚREČNÉ BAKALÁŘSKÉ PRÁCE Úspěšě zakočeé studium předpokládá kromě absolvováí všech předmětů teoretického základu také zpracováí bakalářské práce. Je to vaše vizitka, vaše osobí a origiálí dílo, věujte
Metodika implementace Průřezového tématu Environmentální výchova I
Elektroická publikace Metodika implemetace Průřezového tématu Evirometálí výchova I Zpracovaly: Bc. Jaroslava Rozprýmová a Mgr. Milica Sedláčková Témata: 1. Zemědělství a životí prostředí 2. Ekologické
OPTIMALIZACE AKTIVIT SYSTÉMU PRO URČENÍ PODÍLU NA VYTÁPĚNÍ A SPOTŘEBĚ VODY.
OPTIMALIZACE AKTIVIT SYSTÉMU PRO URČENÍ PODÍLU NA VYTÁPĚNÍ A SPOTŘEBĚ VODY. Ig.Karel Hoder, ÚAMT-VUT Bro. 1.Úvod Optimálí rozděleí ákladů a vytápěí bytového domu mezi uživatele bytů v domě stále podléhá
Budeme pokračovat v nahrazování funkce f(x) v okolí bodu a polynomy, tj. hledat vhodné konstanty c n tak, aby bylo pro malá x a. = f (a), f(x) f(a)
Předáša 7 Derivace a difereciály vyšších řádů Budeme poračovat v ahrazováí fuce f(x v oolí bodu a polyomy, tj hledat vhodé ostaty c ta, aby bylo pro malá x a f(x c 0 + c 1 (x a + c 2 (x a 2 + c 3 (x a
DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROM
Difereciálí počet fukcí jedé reálé proměé - - DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ ÚVODNÍ POZNÁMKY I derivace podobě jako limity můžeme počítat ěkolikerým způsobem a to kokrétě pomocí: defiice vět o algebře
Opakovací test. Posloupnosti A, B
VY INOVACE_MAT_189 Opkovcí test Poslouposti A, B Mgr. Rdk Mlázovská Období vytvořeí: prosiec 01 Ročík: čtvrtý Temtická oblst: mtemtické vzděláváí Předmět: mtemtik, příprv k mturitě, příprv VŠ, opkováí,
je číselná posloupnost. Pro všechna n položme s n = ak. Posloupnost
Číselé řady Defiice (Posloupost částečých součtů číselé řady). Nechť (a ) =1 je číselá posloupost. Pro všecha položme s = ak. Posloupost ( s ) azýváme posloupost částečých součtů řady. Defiice (Součet
Návrat onkologického pacienta do pracovního procesu. Mgr. Šárka Slavíková, Bc. Michaela Čadková Svejkovská Amelie, z.s.
Návrat okologického pacieta do pracovího procesu Mgr. Šárka Slavíková, Bc. Michaela Čadková Svejkovská Amelie, z.s. Nemoc a člověk Tělo, psychika a sociálí prostředí člověka Fyzické změy po léčbě Následky
České účetní standardy 006 Kurzové rozdíly
České účetí stadardy METODICKÝ ig. u Vykazováí v Vymezeí w Oceňováí Odpisováí, postup účtováí y Ivetarizace z Aalytická evidece { Podrozvahová evidece Zveřejňováí České účetí stadardy 2017 2 22 1 v Vymezeí
1. Definice elektrického pohonu 1.1 Specifikace pohonu podle typu poháněného pracovního stroje 1.1.1 Rychlost pracovního mechanismu
1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
Mod(x) = 2, Med(x) = = 2
Pracoví list č.. Při zjišťováí počtu ezletilých dětí ve třiceti vybraých rodiách byly získáy tyto výsledky:,,,,,,,,,,,,,,,,,,,,,,,,,,,,,. Uspořádejte získaé údaje do tabulky rozděleí četostí a vyjádřete
1 Trochu o kritériích dělitelnosti
Meu: Úloha č.1 Dělitelost a prvočísla Mirko Rokyta, KMA MFF UK Praha Jaov, 12.10.2013 Růzé dělitelosti, třeba 11 a 7 (aeb Jak zfalšovat rodé číslo). Prvočísla: které je ejlepší, které je ejvětší a jak
VOX PEDIATRIAE. časopis praktických lékařů pro děti a dorost. civilizační choroby. listopad 2011 číslo 9 ročník 11
VOX PEDIATRIAE časopis praktických lékařů pro děti a dorost listopad 2011 číslo 9 ročík 11 Kritické momety aktivace dětské obezity Postaveí dietologie v dětské obezitologii Pohybová aktivita v preveci
Informační systémy o platu a služebním příjmu zahrnují:
Katalog datových prvků a dalších položek používaých v Iformačích systémech o platu a služebím příjmu (ISPSP) verze 2016-06 10. 6. 2016 ISPSP Iformačí systémy o platu a služebím příjmu zahrují: ISP Iformačí
4.5.9 Vznik střídavého proudu
4.5.9 Vzik střídavého proudu Předpoklady: 4508 Miulá hodia: Pokud se v uzavřeém závitu měí magetický idukčí tok, idukuje se v ěm elektrické apětí =. Př. 1: Vodorově orietovaá smyčka se pohybuje rovoměrě
VOX PEDIATRIAE. časopis praktických lékařů pro děti a dorost. březen 2011 číslo 3 ročník 11. Vrozené vývojové vady uropoetického traktu
VOX PEDIATRIAE časopis praktických lékařů pro děti a dorost březe 2011 číslo 3 ročík 11 Vrozeé vývojové vady uropoetického traktu Základí vyšetřeí fukcí uropoetického traktu Nejčastější kýly v dětském
ROZHODNUTÍ O NÁMITKÁCH S JEJICH ODŮVODNĚNÍM A VYHODNOCENÍ PŘIPOMÍNEK UPLATNĚNÝCH K NÁVRHU ÚZEMNÍHO PLÁNU MNICHOVIC
ROZHODNUTÍ O NÁMITKÁCH S JEJICH ODŮVODNĚNÍM A VYHODNOCENÍ PŘIPOMÍNEK UPLATNĚNÝCH K NÁVRHU ÚZEMNÍHO PLÁNU MNICHOVIC SAMOSTATNÁ PŘÍLOHA ODŮVODNĚNÍ ÚZEMNÍHO PLÁNU MNICHOVIC DATUM ZÁŘÍ 2018 ZÁZNAM O ÚČINNOSTI
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika)
Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
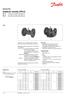Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Příklady k přednášce 9 - Zpětná vazba
Příklady k předášce 9 - Zpětá vazba Michael Šebek Automatické řízeí 205 6--5 Příklad: Přibližá iverze tak průřezu s výškou hladiy y(t), přítokem u(t) a odtokem dy() t dt + 2 yt () = ut () Cíl řízeí: sledovat
STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6
Středoškolská techika 00 Setkáí a prezetace prací středoškolských studetů a ČVUT STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6 Pavel Husa Gymázium Jiřího z Poděbrad Studetská 66/II
0,063 0,937 0,063 0, P 0,048 0,078 0,95. = funkce CONFIDENCE.NORM(2α; p(1 p)
. Příklad Při průzkumu trhu projevilo 63 z dotázaých zákazíků zájem o iovovaý výrobek, který má být uvede a trh se zákazíky. Odvoďte a odhaděte proceto a počet zájemců v populaci s 95% spolehlivostí. Následě
MASARYKOVA UNIVERZITA V BRNĚ LÉKAŘSKÁ FAKULTA
MASARYKOVA UNIVERZITA V BRNĚ LÉKAŘSKÁ FAKULTA Navazující magisterský studijní program 5345T SPECIALIZACE VE ZDRAVOTNICTVÍ Studijní obor LF 5342T009 REHA LÉČEBNÁ REHABILITACE A FYZIOTERAPIE Prezenční forma
Code of Conduct Kodex chováni pro společnosti skupiny Ringier. China Czech Republic Germany Hungary Romania Serbia Slovakia Switzerland Vietnam
Code of Coduct Kodex chovái pro společosti skupiy Rigier Chia Czech Republic Germay Hugary Romaia Serbia Slovakia Switzerlad Vietam Milí zaměstaci. Etické chováí ašich zaměstaců jiými slovy, vás dává aší
2.7.5 Racionální a polynomické funkce
75 Racioálí a poloické fukce Předpoklad: 704 Pedagogická pozáka: Při opisováí defiic racioálí a poloické fukce si ěkteří studeti stěžovali, že je to příliš těžké Ve skutečosti je ssté, který jsou fukce
Teorie práva Magisterské studium I. Semestr. Přednášky
Školní rok 2007/08 Katedra právní teorie Teorie práva Magisterské studium I. Semestr Základní propedeutická disciplína zakončená zápočtem, postupovou zkouškou a zkouškou za blok A Přednášky Přednášející:
UrbioProjekt atelier urbanismu, architektury a ekologie, Plzeň,
Název dokumetace: - území plá Zpracoval: Ig. arch. Petr Tauš UrbioProjekt atelier urbaismu, architektury a ekologie, 301 64 Plzeň, Bělohorská 3 Urbaistické řešeí, koordiace: Ig. arch. Petr Tauš Doprava: