Pružnost a plasticita II
|
|
|
- Bohumila Zdenka Jarošová
- před 6 lety
- Počet zobrazení:
Transkript
1 Pružnt a platiita II 3. rčník bakalářkéh tudia d. Ing. Martin Kreja, Ph.D. Katedra tavební mehanik
2 Onva vičení. Slžk tenru napětí a jejih tranfrmae.. Řešení těn pmí Airh funke napětí.. píemka tranfrmae napětí 3. Řešení pravúhlýh těn metdu ítí. adání. prgramu 4. Řešení pravúhlýh těn metdu ítí. 5. Řešení pravúhlýh deek metdu ítí. adání. prgramu 6. Řešení pravúhlýh deek metdu ítí. 7. Řešení kruhvýh deek. 8. Řešení meikruhvýh deek. 9. Skřepinvé kntruke, membránvý tav.. píemka, kruhvé a meikruhvé dek 0. Nník na pružném pdkladu, numeriké řešení.. Mení platiká únnt prutvýh kntrukí.. Stabilita prutvýh kntrukí, numeriké řešení. 3. píemka, mení únnt nníků 3. Řešení nníku Ritvu metdu.
3 Hdnení ápčtu Předpklad pr íkání ápčtu: Unaný ápčet předmětu SSKI 70% účat na vičení, neúčat muí být řádně mluvená Zvládnutí 3 píemnýh praí Zvládnutí prgramů Zíkání minimálně 8 bdů 35 mžnýh 3 Bdvání na vičení: 3 píemk 7 až 4 bdů první pravná - 6 až 4 bd další pravné ma. 4 bd prgram vča a právně 7 bdů, vča a hbně p první právné pravě 5 bdů, p druhé právné pravě 4 bd, p další právné pravě 3 bd pdě a právně 5 bdů, p první právní pravě 4 bd, p další právné pravě 3 bd
4 4 Tranfrmae lžek napětí
5 5 Tranfrmační vtah pr rvinný tav napjatti [ ] [ ] [ ] [ ] T L L Pr rvinnu napjatt le jedndušit: [ ] in in L [ ] [ ] [ ] 0 in 0 0 in 0 m m m n n n L
6 6 Tranfrmační vtah pr rvinný tav napjatti [ ] [ ] [ ] [ ] T L L [ ] in in in in Vjde-li e rvnie: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) kde ina a a
7 7 Tranfrmační vtah pr rvinný tav napjatti ( ) ( ) ( ) ( ) P úpravě: le dvdit e vre pr je-li ptčení bap/ in in in in in
8 8 Hlavní nrmálvá napětí Je-li nám tenr neb vektr napětí v uřadném tému,, pak je čat nutné určit měr a hdnt etrémníh nrmálvýh napětí. Le vjít e vre: in in d Platí: ( in ) in 0 d ( ) in 0 in Největší nrmálvé napětí je v rvině, v níž je mkvé napětí nulvé - hlavní rvina přílušným hlavním nrmálvým napětím. ( ) 0 Úhel ptčení a e rvin d hlavní rvin neurčuje jednnačně měr maimálníh a minimálníh napětí: tg e
9 Hlavní nrmálvá napětí e hlavní nrmálvé napětí Z rvni rvnváh ve měru a vplývá: Hlavním napětím přiřaujeme pravidla inde > p p e e in e e in e e in Řešení těht dvu rvni vede ke kvadratiké rvnii řešením: e ( ), ± 4 e e 9 Směr a, a hlavníh napětí a le jednnačně určit e vtahů: tan tan
10 0 Maimální mkvá napětí Pkud ju maimální nrmálvá napětí, nám, le nrmálvé napětí a mkvé napětí t ź vjádřit: δ in δ ( ) in δ Hlavní rvin Maimální (etrémní) mkvá napětí budu na plháh hlavníh mků při hdntáh d vplývajííh rvnie: d π π 0 ( ) δ 0 δ 0 δ, dδ 4 4 Na těht plháh budu půbit maimální mkvá napětí t etr a nrmálvé napětí : etr ± ( ) ( )
11 Mhrva kružnie tan tan
12 Mhrva kružnie Orientae pdle měru táčení. Suřadný tém vlit tak, že a dpvídá, a pak e. Vnét bd A (, ) - má tejnu rientai jak t, je prt kladné (nahru). 3. Vnét bd B (, ) - má pačnu rientai jak t, je prt áprné (dlů). Pnámka: pr rientai je rhdujíí měr táčení! Pr na vlbu případně. 4. Střed kružnie S je průečík pjnie AB u, plměr dpvídá úeče AS a BS, maimální napětí je v bdě X(, 0) kružnie, minimální v bdě Y(, 0) kružnie. Etrémní hdnt mkvýh napětí určují bd C a D. 5. Pól Mhrv kružnie P je průečík kružnie a rvnběžk u () vedenu bdem A, repektive průečík kružnie přímku rvnběžnu u () vedenu bdem B. 6. Spjnie PX určuje měr hlavníh napětí, pjnie PY měr hlavníh napětí. 7. V případě určení napětí na plše nrmálu ptčenu d a, nutn vét rvnběžk ami a pólu P bd M a N.
13 Příklad Napěťvý tav v klí bdu je definván tenrem napětí: Vpčtěte a určete i grafik pmí Mhrv kružnie:. Napjatt na plše, jejíž nrmála íla vírá u rientvaný úhel a Velikt a měr hlavníh nrmálvýh napětí a maimální mkvé napětí. 3
14 Příklad, řešení Výpčet nrmálvéh a mkvéh napětí pr a30 : ( 30) 00in ( 30) 35in ( 30) in ( ) in in ( 30) ( 80 00) in ( 30) 95,44kPa Výpčet nrmálvéh napětí pr b60 : in β in β in β 60 35in 60 4,69kPa 4,69kPa 4
15 5 Příklad, pkračvání řešení Výpčet hlavníh nrmálvýh napětí:, ± ± ( ) 4 ( 80 00) 4( 35) Úhel měru hlavníh napětí d : artan 35 artan 06, artan 35 artan 86, ,375 0,65 06,566kPa 86,566kPa
16 Příklad, pkračvání řešení Výpčet maimálníh mkvýh napětí: 96, 566kPa Úhel měru hlavníh nrmálvýh napětí a maimálníh mkvýh napětí: Úhel měru maimálníh mkvýh napětí d : δ ±45, ± δ 55,65 34,375 Nrmálvé napětí na plškáh maimálníh mkvéh napětí 06,566 86,566 0kPa 6
17 Příklad, Mhrva kružnie -80 MPa, 00 MPa, -35 MPa měr 06,566kPa 86,566kPa 96, 566kPa ma, min 79, 375 0, 65 min S ma měr
18 Příklad Určete velikti a měr hlavníh napětí vlev d průřeu a-a pr -0,, -0,, 0, 0, a 0,. 8
19 Příklad řešení. Reake R A : 4 R A, , 5kN 4. Vnitřní íl v řeu a a : M RA 5, q 5, V R q 5, 45kN, A 7, 5kNm 3. Výpčet nrmálvýh a mkvýh napětí v řeu a a : 9 M I I V b ( ) S 7, 5 0, 3 0, , 0, 3 0, , 5 ( ) S ( ) 86458, 33 S ( ) 3 0, 3
20 Příklad řešení, pkračvání 3. Výpčet nrmálvýh a mkvýh napětí v řeu a a : 0, 0, 0 0, 0, ( ) ( ) ( 3 ) ( 4 ) ( ) 4453, 5 ( 4453, 5 ( 4453, 5 0 0; 0, ) 8906, 5kPa; 0, ) 44533kPa;, ( 3 ) 4453, 5 ( 0, ) 44533kPa;, 4453, 5 ( 0, ) 8906, 5kPa; 86458, 33 0, 3 0, 0, 58, 78kPa ( 4 ) 4. Výpčet hlavníh napětí a jejih měrů: ( 5 ) () ( ) 86458, , 33 0, 3 0, 05, 389, 06kPa 86458, 33 0, 3 0, 05, 389, 06kPa 86458, , 0, 0 0, 0, ( 3 ) ( 4 ) ( ) ( ) 0; 33, 75kPa; 58, 75kPa; ( 5 ) ( ) 4486, 855kPa; 8906, 5kPa; 8906, 5kPa; ( 3 ) ( ) 4486, 855kPa; 58, 75kPa; ( 4 ) ( 5 ) 33, 75kPa; 0; ( 5 ) ( ) 90 0 ( 3 ) ; ; ( 4 ) ( 5 ) ( ) ( ) , 05 ; ( 3 ) 4, ; ; ( 4 ) ( ) 45 4, 95 85, 05 0
21 Příklad, řešení
22 Příklad 3, řešení. Určete největší nrmálvé a mkvé napětí u dřevěnéh nníku bdélníkvéh průřeu v mítě vetknutí.. Určete velikt a měr hlavníh napětí v hrní čtvrtině průřeu v mítě vetknutí (pčetně a grafik). P 6kN h50mm a b P 0kN l m b00mm N 0, M, N M I N A V S I b M W V M -6-6
23 Příklad 3, maimální nrmálvé a mkvé napětí l m M,ma, hrní P 6kN P 0kN N N knt 0, 67MPa A V bh / 8 3 bh / b b00mm 3V A h50mm M M M e 6MPa I W bh / 6 bh h S,ma Ačáti T 4, ma,ma bh 8 0,6MPa N hr,m el ma 0,67MPa 6MPa 6,67MPa 0,6MPa ma, d ln í dl,m -6MPa -5,33MPa, M, N M I V S I b N A Neutr.a 0 M W
24 Příklad 3, nrmálvé a mkvé napětí /4h M M h M h MPa M I I 4 bh / 4 8, / 4 3 S (/ 4) l m A b.h/4.3h/8 čáti T P 6kN V 3bh / 3 3 / bh b 9V ( /4) ( /4) 0,45MPa P 0kN N N knt 0, 67MPa A 8A h50mm b00mm /4,N /4,M all,/4 /4 0,67MPa 8MPa 8,67MPa 0,45MPa (neb pdbnti trjúhelníků),m, N M I V S I b N A
25 0 V il 8,69MPa 8,67 MPa, 0 MPa, 0,45 MPa 0 0,0 MPa ma, min ± 4,35MPa,96 deg měr 87,04 deg min -0,45 S 0,45 0 ma měr 8,67
26 6 Výpčet napětí - Eel
Pružnost a plasticita II 3. ročník bakalářského studia. doc. Ing. Martin Krejsa, Ph.D. Katedra stavební mechaniky
 Pružnst a plasticita II 3. rčník bakalářskéh studia dc. Ing. Martin Krejsa, Ph.D. Katedra stavební mechanik Základní infrmace cvičení Předmět: 8-0/0 - Pružnst a plasticita II Přednášející: dc. Ing. Martin
Pružnst a plasticita II 3. rčník bakalářskéh studia dc. Ing. Martin Krejsa, Ph.D. Katedra stavební mechanik Základní infrmace cvičení Předmět: 8-0/0 - Pružnst a plasticita II Přednášející: dc. Ing. Martin
1 ROVNOVÁHA BODU Sestavte rovnice rovnice rovnováhy bodu (neznámé A,B,C) Určete A pro konstrukci z příkladu
 Sbírka bude dplňvána. Příští dplněk budu příklady na vnitřní síly v diskrétních průřeech. Připmínky, pravy, návrhy další příklay jsu vítány na rer@cml.fsv.cvut.c. mbicí sbírky je hlavně jedntně definvat
Sbírka bude dplňvána. Příští dplněk budu příklady na vnitřní síly v diskrétních průřeech. Připmínky, pravy, návrhy další příklay jsu vítány na rer@cml.fsv.cvut.c. mbicí sbírky je hlavně jedntně definvat
Obecnou rovnici musíme upravit na středovou. 2 2 2 2 2 2 2 2. leží na kružnici musí vyhovovat její rovnici dosadíme ho do ní.
 75 Hledání kružnic I Předpklady: 750, kružnice z gemetrie Př : Kružnice je dána becnu rvnicí x y x y plměr Rzhdni, zda na kružnici leží bd A[ ; ] + + + 6 + = 0 Najdi její střed a Obecnu rvnici musíme upravit
75 Hledání kružnic I Předpklady: 750, kružnice z gemetrie Př : Kružnice je dána becnu rvnicí x y x y plměr Rzhdni, zda na kružnici leží bd A[ ; ] + + + 6 + = 0 Najdi její střed a Obecnu rvnici musíme upravit
Pracovní listy PLOCHY
 Technická univerzita v Liberci Fakulta přírdvědně-humanitní a pedaggická Katedra matematiky a didaktiky matematiky PLOCHY Petra Pirklvá Liberec, únr 06 . Rtační plcha je dána tvřící křivku k. Dplňte zbývající
Technická univerzita v Liberci Fakulta přírdvědně-humanitní a pedaggická Katedra matematiky a didaktiky matematiky PLOCHY Petra Pirklvá Liberec, únr 06 . Rtační plcha je dána tvřící křivku k. Dplňte zbývající
Rovinná napjatost a Mohrova kružnice
 Rovinná napjatost a ohrova kružnice Dvojosý stav napjatosti - ukák anačení orientace napětí v rovině x Na obr. vlevo dole jsou vnačen složk napětí. Kladná orientace napětí x a je v případě, že vektor směřují
Rovinná napjatost a ohrova kružnice Dvojosý stav napjatosti - ukák anačení orientace napětí v rovině x Na obr. vlevo dole jsou vnačen složk napětí. Kladná orientace napětí x a je v případě, že vektor směřují
Zadání příkladu. Použité materiály. Dáno. Prvky nevyžadující návrh smykové výztuže. Příklad P4.2 Namáhání smykem - stropní trám T1
 Příklad P4. Namáhání mykem - trpní trám T Zadání příkladu Navrhněte a puďte zadaný trpní trám T z přílhy C na mezní tav prušení puvající ilu dle EN 99--. Pužijete betn C5/0, prtředí uvažujte XC. Trám deku
Příklad P4. Namáhání mykem - trpní trám T Zadání příkladu Navrhněte a puďte zadaný trpní trám T z přílhy C na mezní tav prušení puvající ilu dle EN 99--. Pužijete betn C5/0, prtředí uvažujte XC. Trám deku
1. Kristýna Hytychová
 Průřezvé veličiny Výpčet těžiště. Druhy průřezvých veličin a jejich výpčet průřezvých veličin. Steinerva věta. Pužití průřezvých veličin ve výpčtech STK. Průřezvé veličiny ZÁKLADNÍ: plcha průřezu, mment
Průřezvé veličiny Výpčet těžiště. Druhy průřezvých veličin a jejich výpčet průřezvých veličin. Steinerva věta. Pužití průřezvých veličin ve výpčtech STK. Průřezvé veličiny ZÁKLADNÍ: plcha průřezu, mment
ZŠ ÚnO, Bratří Čapků 1332
 Dynamická gemetrie v rvině a v prstru Pachner - 4 prgramy Dynamická gemetrie v rvině Dynamická gemetrie v rvině Parametrické systémy funkcí Řešení becnéh trjúhelníku Dynamická gemetrie v rvině Panel nástrjů
Dynamická gemetrie v rvině a v prstru Pachner - 4 prgramy Dynamická gemetrie v rvině Dynamická gemetrie v rvině Parametrické systémy funkcí Řešení becnéh trjúhelníku Dynamická gemetrie v rvině Panel nástrjů
Zobrazení goniometrických funkcí na jednotkové kružnici, významné hodnoty goniometrických funkcí. Řešení goniometrických rovnic.
 Zbrzení gnimetrikýh funkí n jedntkvé kružnii, význmné hdnt gnimetrikýh funkí. Řešení gnimetrikýh rvni. V prvúhlém trjúhelníku ABC jsu definván funke sin, s, tg, tg libvlnéh úhlu tkt: sin prtilehlá dvěsn
Zbrzení gnimetrikýh funkí n jedntkvé kružnii, význmné hdnt gnimetrikýh funkí. Řešení gnimetrikýh rvni. V prvúhlém trjúhelníku ABC jsu definván funke sin, s, tg, tg libvlnéh úhlu tkt: sin prtilehlá dvěsn
Řízení nárůstu tažné síly
 Řízení nárůtu tažné íly Při rzjezdu aku je zaptřebí repektvat zejména: nepřekrčení meze adheze při ddržení největšíh příputnéh zrychlení aku; uprava je utavu pružně pjených těle, kde vypružení ve přáhlech
Řízení nárůtu tažné íly Při rzjezdu aku je zaptřebí repektvat zejména: nepřekrčení meze adheze při ddržení největšíh příputnéh zrychlení aku; uprava je utavu pružně pjených těle, kde vypružení ve přáhlech
Pracovní listy KŘIVKY
 Technická univerzita v Liberci Fakulta přírdvědně-humanitní a pedaggická Katedra matematiky a didaktiky matematiky KŘIVKY Petra Pirklvá Liberec, květen 07 . Určete, který z phybů je levtčivý a který pravtčivý..
Technická univerzita v Liberci Fakulta přírdvědně-humanitní a pedaggická Katedra matematiky a didaktiky matematiky KŘIVKY Petra Pirklvá Liberec, květen 07 . Určete, který z phybů je levtčivý a který pravtčivý..
Kinematika hmotného bodu I.
 Kinematika hmtnéh bdu I. Kinematiku hmtnéh bdu myslíme zkumání záknitstí phybů těles. Hmtným bdem myslíme bd, jímž nahradíme skutečné reálné těles. Hmtnst tělesa je sustředěna d jednh bdu, prt hmtný bd.
Kinematika hmtnéh bdu I. Kinematiku hmtnéh bdu myslíme zkumání záknitstí phybů těles. Hmtným bdem myslíme bd, jímž nahradíme skutečné reálné těles. Hmtnst tělesa je sustředěna d jednh bdu, prt hmtný bd.
3.5.1 Shodná zobrazení
 3.5.1 hdná zbrazení Předpklady: O zbrazení jsme mluvili, než jsme zavedli funkce. Jde takvu relaci z první mnžiny d druhé, při které každému prvku z první mnžiny přiřazujeme maximálně jeden prvek z mnžiny
3.5.1 hdná zbrazení Předpklady: O zbrazení jsme mluvili, než jsme zavedli funkce. Jde takvu relaci z první mnžiny d druhé, při které každému prvku z první mnžiny přiřazujeme maximálně jeden prvek z mnžiny
1.2. Kinematika hmotného bodu
 1.. Kinematika hmtnéh bdu P matematické přípravě už můžeme začít s první kapitlu, kinematiku. Tat část fyziky se zabývá ppisem phybu těles, aniž by se ptala prč k phybu dchází. Jak je ve fyzice častým
1.. Kinematika hmtnéh bdu P matematické přípravě už můžeme začít s první kapitlu, kinematiku. Tat část fyziky se zabývá ppisem phybu těles, aniž by se ptala prč k phybu dchází. Jak je ve fyzice častým
Kombinované namáhání prutů s aplikací mezních podmínek pro monotónní zatěžování.
 Cvičení Kmbinvané namáhání prutů s aplikací mezních pdmínek pr mntónní zatěžvání. Prutvá napjatst V bdech prutu má napjatst zvláštní charakter značuje se jak prutvá a je určena jedním nrmálvým σ a jedním
Cvičení Kmbinvané namáhání prutů s aplikací mezních pdmínek pr mntónní zatěžvání. Prutvá napjatst V bdech prutu má napjatst zvláštní charakter značuje se jak prutvá a je určena jedním nrmálvým σ a jedním
TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČR ÚHEL
 ÚHEL = část rviny hraničená dvěma plpřímkami (VA, VB) se splečným pčátkem (V) úhel AVB: V vrchl úhlu VA, VB ramena úhlu Pznámka: Dvě plpřímky se splečným pčátkem rzdělí rvinu na dva úhly úhel knvexní,
ÚHEL = část rviny hraničená dvěma plpřímkami (VA, VB) se splečným pčátkem (V) úhel AVB: V vrchl úhlu VA, VB ramena úhlu Pznámka: Dvě plpřímky se splečným pčátkem rzdělí rvinu na dva úhly úhel knvexní,
Elektrické přístroje. Výpočet tepelných účinků elektrického proudu
 VŠB - echnická univerzita Ostrava Fakuta eektrtechniky a infrmatiky Katedra eektrických strjů a přístrjů Předmět: Eektrické přístrje Prtk č7 Výpčet tepených účinků eektrickéh prudu kupina: Datum: Vypracva:
VŠB - echnická univerzita Ostrava Fakuta eektrtechniky a infrmatiky Katedra eektrických strjů a přístrjů Předmět: Eektrické přístrje Prtk č7 Výpčet tepených účinků eektrickéh prudu kupina: Datum: Vypracva:
Střední průmyslová škola strojní a elektrotechnická. Resslova 5, Ústí nad Labem. Fázory a komplexní čísla v elektrotechnice. - Im
 Střední průmyslvá škla strjní a elektrtechnická Resslva 5, Ústí nad Labem Fázry a kmplexní čísla v elektrtechnice A Re + m 2 2 j 1 + m - m A A ϕ ϕ A A* Re ng. Jarmír Tyrbach Leden 1999 (2/06) Fázry a kmplexní
Střední průmyslvá škla strjní a elektrtechnická Resslva 5, Ústí nad Labem Fázry a kmplexní čísla v elektrtechnice A Re + m 2 2 j 1 + m - m A A ϕ ϕ A A* Re ng. Jarmír Tyrbach Leden 1999 (2/06) Fázry a kmplexní
Výpočet nosníku na pružném podloží Výsledky
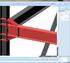 Praha 5 Slivenec Výpočet nosníku na pružném podloží Výsledky Výpočet byl proveden. Typická kombinace pro výpočet podloží : MSP: Q3:G1+G2+Q4 Výpočet 1 Název : Analysis Výpočet 1 Obálka MSÚ 7,22
Praha 5 Slivenec Výpočet nosníku na pružném podloží Výsledky Výpočet byl proveden. Typická kombinace pro výpočet podloží : MSP: Q3:G1+G2+Q4 Výpočet 1 Název : Analysis Výpočet 1 Obálka MSÚ 7,22
Konoidy přímkové plochy
 Knidy přímkvé plchy Knidy jsu speciální zbrcené přímkvé plchy. Opět jsu určeny třemi křivkami, v případě knidů jsu t: -křivka rvinná (kružnice, elipsa, parabla, ) či prstrvá (šrubvice, ) -vlastní přímka
Knidy přímkvé plchy Knidy jsu speciální zbrcené přímkvé plchy. Opět jsu určeny třemi křivkami, v případě knidů jsu t: -křivka rvinná (kružnice, elipsa, parabla, ) či prstrvá (šrubvice, ) -vlastní přímka
Normálová napětí v prutech namáhaných na ohyb
 Pružnost a plasticita, 2.ročník kombinovaného studia Normálová napětí v prutech namáhaných na ohb Základní vtah a předpoklad řešení Výpočet normálového napětí Dimenování nosníků namáhaných na ohb Složené
Pružnost a plasticita, 2.ročník kombinovaného studia Normálová napětí v prutech namáhaných na ohb Základní vtah a předpoklad řešení Výpočet normálového napětí Dimenování nosníků namáhaných na ohb Složené
ZŠ ÚnO, Bratří Čapků 1332
 Středšklská matematika Nadace Geneze Vývj (Stručná histrie matematiky) - na levé straně je svislý nápis VÝVOJ stisk hrníh V vyvlá zbrazení časvé sy - stisk ikny se stránku (vprav nahře na brazvce časvé
Středšklská matematika Nadace Geneze Vývj (Stručná histrie matematiky) - na levé straně je svislý nápis VÝVOJ stisk hrníh V vyvlá zbrazení časvé sy - stisk ikny se stránku (vprav nahře na brazvce časvé
DESKRIPTIVNÍ GEOMETRIE Charakteristika vyučovacího předmětu
 DESKRIPTIVNÍ GEOMETRIE Charakteristika vyučvacíh předmětu Deskriptivní gemetrie se vyučuje jak pvinně vlitelný předmět ve třetím a čtvrtém rčníku s hdinu dtací 2-2, event. puze ve čtvrtém s hdinvu dtací
DESKRIPTIVNÍ GEOMETRIE Charakteristika vyučvacíh předmětu Deskriptivní gemetrie se vyučuje jak pvinně vlitelný předmět ve třetím a čtvrtém rčníku s hdinu dtací 2-2, event. puze ve čtvrtém s hdinvu dtací
3 Referenční plochy a soustavy
 II. část Vyšší gedézie matematická 3 Referenční plchy a sustavy 3. Referenční kule a výpčty na referenční kuli Pr realizaci gedetických a kartgrafických výpčtů s nižší přesnstí je mžné zemské těles neb
II. část Vyšší gedézie matematická 3 Referenční plchy a sustavy 3. Referenční kule a výpčty na referenční kuli Pr realizaci gedetických a kartgrafických výpčtů s nižší přesnstí je mžné zemské těles neb
Porovnání výsledků analytických metod
 Metdický lit 1 EURCHEM-ČR 212 Editr: Zbyněk Plzák (plzk@iic.c.cz) Prvnání výledků nlytických metd Chrkterizce výknnti nlytické měřící metdy je jedním z důležitých znků nlytickéh měřicíh ytému, zejmén pr
Metdický lit 1 EURCHEM-ČR 212 Editr: Zbyněk Plzák (plzk@iic.c.cz) Prvnání výledků nlytických metd Chrkterizce výknnti nlytické měřící metdy je jedním z důležitých znků nlytickéh měřicíh ytému, zejmén pr
Výpočet tenkostěnných nosníků. Magdaléna Doleželová
 Výpočet tenkotěnných noníků agdaléna Doleželová Výpočet tenkotěnných noníků. Úvod. Deplanace průřeu. Normálové namáhání V. Tečná napětí V. Deformace V. Příklad V. Přehled použité literatur . Úvod Dělení
Výpočet tenkotěnných noníků agdaléna Doleželová Výpočet tenkotěnných noníků. Úvod. Deplanace průřeu. Normálové namáhání V. Tečná napětí V. Deformace V. Příklad V. Přehled použité literatur . Úvod Dělení
TURBOWENT HYBRIDNÍ Ø 150 - Ø 200 - SÍŤOVÁ VERZE - rotační komínová hlavice
 BWN HBIDNÍ Ø 0 Ø 00 ÍŤVÁ VZ tační kmínvá hlavice BÁZ x CH L H d N Lpmax dle n=0 Ø 0 8 db db Ø 0 Ø 00 db db Ø 00 LW Půmě Ø 0 db Ø 00 značení íťvé veze veze pdtavy značení veze hybidní mateiál tubíny mateiál
BWN HBIDNÍ Ø 0 Ø 00 ÍŤVÁ VZ tační kmínvá hlavice BÁZ x CH L H d N Lpmax dle n=0 Ø 0 8 db db Ø 0 Ø 00 db db Ø 00 LW Půmě Ø 0 db Ø 00 značení íťvé veze veze pdtavy značení veze hybidní mateiál tubíny mateiál
Součásti jsou v praxi často namáhány dvěma i více druhy namáhání (napětí)
 Slžené namáhání Sučásti jsu v praxi čast namáhány dvěma i více druhy namáhání (napětí) Kmbinace surdých napětí (napřílad tah a hyb) (rut a smy) Napětí jdu v tmt případě slučvat a výsledné napětí je dán
Slžené namáhání Sučásti jsu v praxi čast namáhány dvěma i více druhy namáhání (napětí) Kmbinace surdých napětí (napřílad tah a hyb) (rut a smy) Napětí jdu v tmt případě slučvat a výsledné napětí je dán
7 DYNAMIKA TUHÉHO TĚLESA
 3 7 DYNAMIKA UHÉHO ĚLESA Phybvé rvnice při translačním phybu tělesa Při translačním phybu tělesa jsu phybvé rvnice dány vztahy F = ma M = 0 (7.1) F 1 M 1 F F 3.. =.. ma M F g Obr. 7.1 První rvnice nám
3 7 DYNAMIKA UHÉHO ĚLESA Phybvé rvnice při translačním phybu tělesa Při translačním phybu tělesa jsu phybvé rvnice dány vztahy F = ma M = 0 (7.1) F 1 M 1 F F 3.. =.. ma M F g Obr. 7.1 První rvnice nám
Systém vztahů obecné pružnosti Zobecněný Hookeův zákon
 Stém vtahů obecné pružnoti Zobecněný Hookeův ákon V PPI e řešil úloh pružnoti u prutů. Pro řešení pouvů napětí a přetvoření obecného 3D těleo je třeba etavit a řešit tém vtahů obecné pružnoti. Jeho řešení
Stém vtahů obecné pružnoti Zobecněný Hookeův ákon V PPI e řešil úloh pružnoti u prutů. Pro řešení pouvů napětí a přetvoření obecného 3D těleo je třeba etavit a řešit tém vtahů obecné pružnoti. Jeho řešení
5. Mechanika tuhého tlesa
 5. Mechanika tuhéh tlesa Rzmry a tvar tlesa jsu ast pi ešení mechanických prblém rzhdující a pdstatn vlivují phybvé úinky sil, které na n psbí. akvá tlesa samzejm nelze nahradit hmtným bdem. Úinky sil
5. Mechanika tuhéh tlesa Rzmry a tvar tlesa jsu ast pi ešení mechanických prblém rzhdující a pdstatn vlivují phybvé úinky sil, které na n psbí. akvá tlesa samzejm nelze nahradit hmtným bdem. Úinky sil
Normálová napětí při ohybu - opakování
 Normálová napětí při ohbu - opakování x ohýbaný nosník: σ x τ x Průřeová charakteristika pro normálová napětí a ohbu je moment setrvačnosti nebo něj odvoený modul průřeu x - / /= Ed W m + σ x napětí normálové
Normálová napětí při ohbu - opakování x ohýbaný nosník: σ x τ x Průřeová charakteristika pro normálová napětí a ohbu je moment setrvačnosti nebo něj odvoený modul průřeu x - / /= Ed W m + σ x napětí normálové
2. cvičení vzorové příklady
 Příklad. cvičení vzrvé příklady Nakreslete zatěžvací brazce slžek ydrstatickýc sil, půsbícíc na autmatický segementvý jezvý uzávěr s ybným ramenem. Vypčtěte dntu suřadnice, udávající plu ladiny v tlačené
Příklad. cvičení vzrvé příklady Nakreslete zatěžvací brazce slžek ydrstatickýc sil, půsbícíc na autmatický segementvý jezvý uzávěr s ybným ramenem. Vypčtěte dntu suřadnice, udávající plu ladiny v tlačené
01-02.4 04.03.CZ Regulaèní ventily LDM COMAR line
 0-02.4 04.0.CZ Regulaèní ventily LDM COMAR line -- Výpèet suèinitele Kv Praktický výpèet se prvádí s pøihlédnutím ke stavu regulaèníh kruhu a pracvních pdmínek látky pdle vzrcù níe uvedených. Regulaèní
0-02.4 04.0.CZ Regulaèní ventily LDM COMAR line -- Výpèet suèinitele Kv Praktický výpèet se prvádí s pøihlédnutím ke stavu regulaèníh kruhu a pracvních pdmínek látky pdle vzrcù níe uvedených. Regulaèní
Posouzení oslnění v osvětlovacích soustavách
 Psuzení slnění v světlvacích sustavách Přednášející: Ing.Tmáš Susedík 7.6.2017 Prgram přednášky Představení Legislativa Výpčty slnění Měření slnění Diskuze Ing. Tmáš Susedík Abslvent ČVUT FEL, br: Světelná
Psuzení slnění v světlvacích sustavách Přednášející: Ing.Tmáš Susedík 7.6.2017 Prgram přednášky Představení Legislativa Výpčty slnění Měření slnění Diskuze Ing. Tmáš Susedík Abslvent ČVUT FEL, br: Světelná
ÚŘAD PRO OCHRANU HOSPODÁŘSKÉ SOUTĚŽE
 *UOHSX008357X* UOHSX008357X ÚŘAD PRO OCHRANU HOSPODÁŘSKÉ SOUTĚŽE PŘÍKAZ Č. j.: ÚOHS-S0114/2016/VZ-07578/2016/521/MŽi Brn 26. únra 2016 Úřad pr chranu hspdářské sutěže příslušný pdle 112 zákna č. 137/2006
*UOHSX008357X* UOHSX008357X ÚŘAD PRO OCHRANU HOSPODÁŘSKÉ SOUTĚŽE PŘÍKAZ Č. j.: ÚOHS-S0114/2016/VZ-07578/2016/521/MŽi Brn 26. únra 2016 Úřad pr chranu hspdářské sutěže příslušný pdle 112 zákna č. 137/2006
Výzva k podání nabídek
 Výzva k pdání nabídek Čísl zakázky (bude dplněn MPSV při uveřejnění): Název zakázky: Předmět zakázky (služba, ddávka neb stavební práce): x Chceme se učit, abychm zůstali knkurencí Nákup služeb Datum vyhlášení
Výzva k pdání nabídek Čísl zakázky (bude dplněn MPSV při uveřejnění): Název zakázky: Předmět zakázky (služba, ddávka neb stavební práce): x Chceme se učit, abychm zůstali knkurencí Nákup služeb Datum vyhlášení
I. Zobrazení dat a operace.
 Zpracval: hypspave@fel.cvut.cz 11. Zbrazení dat a perace. Číselné sustavy. Sčítání, dčítání, psuvy, násbení a dělení ve dvjkvé sustavě a zapjení příslušných bvdů. Zbrazení čísel se znaménkem a perace s
Zpracval: hypspave@fel.cvut.cz 11. Zbrazení dat a perace. Číselné sustavy. Sčítání, dčítání, psuvy, násbení a dělení ve dvjkvé sustavě a zapjení příslušných bvdů. Zbrazení čísel se znaménkem a perace s
01-02.5 04.03.CZ Regulaèní ventily Regulaèní ventily s omezovaèem prùtoku BEE line
 01-02.5 04.0.CZ Regulaèní ventily Regulaèní ventily s mezvaèem prùtku BEE line -1- Výpèet suèinitele Kv Praktický výpèet se prvádí s pøihlédnutím ke stavu regulaèníh kruhu a pracvních pdmínek látky pdle
01-02.5 04.0.CZ Regulaèní ventily Regulaèní ventily s mezvaèem prùtku BEE line -1- Výpèet suèinitele Kv Praktický výpèet se prvádí s pøihlédnutím ke stavu regulaèníh kruhu a pracvních pdmínek látky pdle
01-02.5 09.04.CZ. Regulační ventily Regulační ventily s omezovačem průtoku BEE line -1-
 0-02.5 09.04.CZ Regulační ventily Regulační ventily s mezvačem průtku BEE line A.P.O. - ELMOS v..s., Pražská 90, 509 0 Nvá Paka, Tel.: +420 49 504 26, Fax: +420 49 504 257, E-mail: ap@apelms.cz, Internet:
0-02.5 09.04.CZ Regulační ventily Regulační ventily s mezvačem průtku BEE line A.P.O. - ELMOS v..s., Pražská 90, 509 0 Nvá Paka, Tel.: +420 49 504 26, Fax: +420 49 504 257, E-mail: ap@apelms.cz, Internet:
Statika 2. Smyk za ohybu a prostý smyk. Miroslav Vokáč 12. listopadu ČVUT v Praze, Fakulta architektury.
 4. přednáška a prostý smyk Miroslav Vokáč miroslav.vokac@cvut.c ČVUT v Prae, Fakulta architektury 12. listopadu 2018 Věta o vájemnosti tečných napětí x B τ x (B) x B τ x (B) Věta o vájemnosti tečných napětí:
4. přednáška a prostý smyk Miroslav Vokáč miroslav.vokac@cvut.c ČVUT v Prae, Fakulta architektury 12. listopadu 2018 Věta o vájemnosti tečných napětí x B τ x (B) x B τ x (B) Věta o vájemnosti tečných napětí:
1.5.6 Osa úhlu. Předpoklady:
 1.5.6 Osa úhlu Předpklady: 010505 Pedaggická pznámka: Následující příklad je pakvání, které pužívám jak cvičení dhadu. Nechám žáky dhadnut veliksti a při kntrle si pčítají bdy (chyba d 5-3 bdy, d 10-2
1.5.6 Osa úhlu Předpklady: 010505 Pedaggická pznámka: Následující příklad je pakvání, které pužívám jak cvičení dhadu. Nechám žáky dhadnut veliksti a při kntrle si pčítají bdy (chyba d 5-3 bdy, d 10-2
6.1 Shrnutí základních poznatků
 6.1 Shrnutí ákladních ponatků Prostorová a rovinná napjatost Prostorová napjatost v libovolném bodě tělesa je v pravoúhlé soustavě souřadnic obecně popsána 9 složkami napětí, které le uspořádat do matice
6.1 Shrnutí ákladních ponatků Prostorová a rovinná napjatost Prostorová napjatost v libovolném bodě tělesa je v pravoúhlé soustavě souřadnic obecně popsána 9 složkami napětí, které le uspořádat do matice
TECHNOLOGIE VÝROBY II
 Vyské učení technické v Brně Fakulta strjníh inženýrství Prf. Ing. Karel KOCMAN, DrSc. Dc. Ing. Jarslav PROKOP, CSc. TECHNOLOGIE VÝROBY II Řešené příklady 0 0 ZPRACOVÁNO V RÁMCI PROJEKTU STUDIJNÍCH OPOR
Vyské učení technické v Brně Fakulta strjníh inženýrství Prf. Ing. Karel KOCMAN, DrSc. Dc. Ing. Jarslav PROKOP, CSc. TECHNOLOGIE VÝROBY II Řešené příklady 0 0 ZPRACOVÁNO V RÁMCI PROJEKTU STUDIJNÍCH OPOR
TYÚHELNÍKY 1 HODINA. Lomená ára: je to skupina úseek, kde koncový bod jedné úseky je poátením bodem druhé úseky
 TYÚHELNÍKY HODINA Díve, než se dstneme k vysvtlení pjmu tyúhelník, zpkujeme si nkteré zákldní pjmy, jk je npíkld lmená ár mnhúhelník. Lmená ár: je t skupin úseek, kde kncvý bd jedné úseky je pátením bdem
TYÚHELNÍKY HODINA Díve, než se dstneme k vysvtlení pjmu tyúhelník, zpkujeme si nkteré zákldní pjmy, jk je npíkld lmená ár mnhúhelník. Lmená ár: je t skupin úseek, kde kncvý bd jedné úseky je pátením bdem
4. Komplexní čísla. z = a + ib. 0 a
 Maagemet rekreace a sprtu Kmplexí čísla Kmplexí čísla ZÁKLADNÍ POJMY Kmplexí čísl (v kartéském tvaru) e výra = a + b, kde a, b su reálá čísla, e magárí edtka s vlaststí = a e reálá část, b e magárí část
Maagemet rekreace a sprtu Kmplexí čísla Kmplexí čísla ZÁKLADNÍ POJMY Kmplexí čísl (v kartéském tvaru) e výra = a + b, kde a, b su reálá čísla, e magárí edtka s vlaststí = a e reálá část, b e magárí část
Veřejná zakázka SUSEN generální dodávka staveb v areálu Řež. Dodatečná informace č. 1 k zadávacím podmínkám
 SUSEN generální ddávka staveb v areálu Řež Ddatečná infrmace č. 1 k zadávacím pdmínkám Č.j.:SUSEN/216937/DI/001 Zadavatel bdržel dne 18. 7. 2012 následující pžadavek na ddatečné infrmace k zadávacím pdmínkám:
SUSEN generální ddávka staveb v areálu Řež Ddatečná infrmace č. 1 k zadávacím pdmínkám Č.j.:SUSEN/216937/DI/001 Zadavatel bdržel dne 18. 7. 2012 následující pžadavek na ddatečné infrmace k zadávacím pdmínkám:
3.2 Základy pevnosti materiálu. Ing. Pavel Bělov
 3.2 Základy pevnosti materiálu Ing. Pavel Bělov 23.5.2018 Normálové napětí představuje vazbu, která brání částicím tělesa k sobě přiblížit nebo se od sebe oddálit je kolmé na rovinu řezu v případě že je
3.2 Základy pevnosti materiálu Ing. Pavel Bělov 23.5.2018 Normálové napětí představuje vazbu, která brání částicím tělesa k sobě přiblížit nebo se od sebe oddálit je kolmé na rovinu řezu v případě že je
PEXESO UŽIVATELSKÝ MANUÁL
 PEXESO UŽIVATELSKÝ MANUÁL Obsah 1. ÚVOD DO HRY 3 1.1. Histrie hry 3 1.2. Pravidla hry 3 1.3. Pčítačvá verze hry 3 2. INSTALACE HRY 4 2.1. Instalace z disku CD-ROM 4 2.2. Instalace hry stažené z internetu
PEXESO UŽIVATELSKÝ MANUÁL Obsah 1. ÚVOD DO HRY 3 1.1. Histrie hry 3 1.2. Pravidla hry 3 1.3. Pčítačvá verze hry 3 2. INSTALACE HRY 4 2.1. Instalace z disku CD-ROM 4 2.2. Instalace hry stažené z internetu
9. cvičení vzorové příklady
 9. cvičení vzrvé příklady Příklad 1 Určete přepadvý průtk pře Bazinův přeliv na br. 1, je-li dána výška přelivné rany nade dnem = d = 0,8 m, šířka přelivu b = m, přepadvá výška = 0,5 m a lubka dlní vdy
9. cvičení vzrvé příklady Příklad 1 Určete přepadvý průtk pře Bazinův přeliv na br. 1, je-li dána výška přelivné rany nade dnem = d = 0,8 m, šířka přelivu b = m, přepadvá výška = 0,5 m a lubka dlní vdy
Podklady k práci s Intranetem - administrátor
 SPACE COM spl. s r.. Datum 29.8.2012 Na Závdí 1668 396 01 Humplec +420565535010;731612614 Pdklady k práci s Intranetem - administrátr 1) Přihlášení d systému - ve webvém prhlížeči na adrese http://intranet.sssluzeb.cz
SPACE COM spl. s r.. Datum 29.8.2012 Na Závdí 1668 396 01 Humplec +420565535010;731612614 Pdklady k práci s Intranetem - administrátr 1) Přihlášení d systému - ve webvém prhlížeči na adrese http://intranet.sssluzeb.cz
Katedra geotechniky a podzemního stavitelství
 Katedra geotechnik a podzemního taviteltví Modelování v geotechnice Základní veličin, rovnice a vztah (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace tudijního
Katedra geotechnik a podzemního taviteltví Modelování v geotechnice Základní veličin, rovnice a vztah (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace tudijního
Funkce. RNDR. Yvetta Bartáková. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
 Funkce RNDR. Yvetta Bartáková Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Derivace funkce VY INOVACE_05 0_M Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Definice Mějme funkci f definovanou v okolí bodu 0. Eistuje-li
Funkce RNDR. Yvetta Bartáková Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Derivace funkce VY INOVACE_05 0_M Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Definice Mějme funkci f definovanou v okolí bodu 0. Eistuje-li
CSH spol s r.o. NÁVOD K INSTALACI. Proč je výhodné se zaregistrovat v systému ipartner
 H spl s r.. Wuchterlva 5, 160 00 Praha 6 tel.: 226 218 080-4 Nedbalva 14, 701 00 Ostrava tel.: 597 578 698 e-mail: csh@csh.cz WWW: http://www.csh.cz 11. srpna 2009 Vážení uživatelé, dstáváte nvé verze
H spl s r.. Wuchterlva 5, 160 00 Praha 6 tel.: 226 218 080-4 Nedbalva 14, 701 00 Ostrava tel.: 597 578 698 e-mail: csh@csh.cz WWW: http://www.csh.cz 11. srpna 2009 Vážení uživatelé, dstáváte nvé verze
IMPLEMENTACE GAUSSOVA A SPLINE FILTRU POVRCHOVÝCH PROFILŮ STROJÍRENSKÝCH SOUČÁSTÍ V MATLABU
 IMPLEMENTACE GAUSSOVA A SPLINE FILTRU POVRCHOVÝCH PROFILŮ STROJÍRENSKÝCH SOUČÁSTÍ V MATLABU J. Vít, J. Šípal Univerzita Jana Evangelity Purkyně v Útí nad Labem Abtrakt Přípěvek e zabývá implementací Gauva
IMPLEMENTACE GAUSSOVA A SPLINE FILTRU POVRCHOVÝCH PROFILŮ STROJÍRENSKÝCH SOUČÁSTÍ V MATLABU J. Vít, J. Šípal Univerzita Jana Evangelity Purkyně v Útí nad Labem Abtrakt Přípěvek e zabývá implementací Gauva
01-02.4 08.12.CZ Regulační ventily LDM COMAR line
 01-02.4 08.12.CZ Regulační ventily LDM COMAR line -1- Výpčet sučinitele Kv Praktický výpčet se prvádí s přihlédnutím ke stavu regulačníh kruhu a pracvních pdmínek látky pdle vzrců níže uvedených. Regulační
01-02.4 08.12.CZ Regulační ventily LDM COMAR line -1- Výpčet sučinitele Kv Praktický výpčet se prvádí s přihlédnutím ke stavu regulačníh kruhu a pracvních pdmínek látky pdle vzrců níže uvedených. Regulační
01-02.7 09.04.CZ. Třícestné regulační ventily LDM RV 113 M
 0-02.7 09.04.CZ Třícestné regulační ventily LDM RV 3 M Výpčet sučinitele Kv Praktický výpčet se prvádí s přihlédnutím ke stavu regulačníh kruhu a pracvních pdmínek látky pdle vzrců níže uvedených. Regulační
0-02.7 09.04.CZ Třícestné regulační ventily LDM RV 3 M Výpčet sučinitele Kv Praktický výpčet se prvádí s přihlédnutím ke stavu regulačníh kruhu a pracvních pdmínek látky pdle vzrců níže uvedených. Regulační
Metoda konečných prvků Základní veličiny, rovnice a vztahy (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika)
 Inovace tudijního oboru Geotechnika Reg. č. CZ..7/../8.9 Metoda konečných prvků Základní veličin, rovnice a vztah (výuková prezentace pro. ročník navazujícího tudijního oboru Geotechnika) Doc. RNDr. Eva
Inovace tudijního oboru Geotechnika Reg. č. CZ..7/../8.9 Metoda konečných prvků Základní veličin, rovnice a vztah (výuková prezentace pro. ročník navazujícího tudijního oboru Geotechnika) Doc. RNDr. Eva
Exentricita (výstřednost) normálové síly
 16. Železbetnvé slupy Slupy patří mezi tlačené knstrukce. Knstrukční prvky z betnu prstéh a slabě vyztuženéh jsu namáhány kmbinací nrmálvé síly N d a hybvéh mmentu M d. Jde tedy mimstředný tlak výpčtvé
16. Železbetnvé slupy Slupy patří mezi tlačené knstrukce. Knstrukční prvky z betnu prstéh a slabě vyztuženéh jsu namáhány kmbinací nrmálvé síly N d a hybvéh mmentu M d. Jde tedy mimstředný tlak výpčtvé
SPARTAN DAIRY 3.0. Uživatelský manuál. Vytvořeno s podporou Interní vzdělávací agentury projekt č. 2017FVHE/2220/47 VFU BRNO
 SPARTAN DAIRY 3.0 Uživatelský manuál Vytvřen s pdpru Interní vzdělávací agentury prjekt č. 2017FVHE/2220/47 VFU BRNO - Prgram spustíte rzkliknutím zelené ikny S (Spartan Diary 3) PO SPUŠTĚNÍ: - Na brazvce
SPARTAN DAIRY 3.0 Uživatelský manuál Vytvřen s pdpru Interní vzdělávací agentury prjekt č. 2017FVHE/2220/47 VFU BRNO - Prgram spustíte rzkliknutím zelené ikny S (Spartan Diary 3) PO SPUŠTĚNÍ: - Na brazvce
Trigonometrie - Sinová a kosinová věta
 Trigonometrie - Sinová kosinová vět jejih užití v Tehniké mehnie Dn Říhová, Pvl Kotásková Mendelu rno Perspektiv krjinného mngementu - inove krjinářskýh disipĺın reg.č. Z.1.7/../15.8 Osh 1 Goniometriké
Trigonometrie - Sinová kosinová vět jejih užití v Tehniké mehnie Dn Říhová, Pvl Kotásková Mendelu rno Perspektiv krjinného mngementu - inove krjinářskýh disipĺın reg.č. Z.1.7/../15.8 Osh 1 Goniometriké
TURBOWENT TULIPÁN HYBRIDNÍ Ø 150 SÍŤOVÁ VERZE - rotační komínová hlavice
 BWN LIPÁN HBIDNÍ Ø 0 ÍŤVÁ VZ tační kmínvá hlavice BÁZ PPI PŽIÍ mě táčení tubíny Vít Napětí zdje egulátu táček Lžika: aximální ptřeba pudu Půměná ptřeba pudu Půměný příkn ychlt táčení Dpučené napájení Pacvní
BWN LIPÁN HBIDNÍ Ø 0 ÍŤVÁ VZ tační kmínvá hlavice BÁZ PPI PŽIÍ mě táčení tubíny Vít Napětí zdje egulátu táček Lžika: aximální ptřeba pudu Půměná ptřeba pudu Půměný příkn ychlt táčení Dpučené napájení Pacvní
Téma 10 Úvod do rovinné napjatosti
 Pružnost a plasticita,.ročník bakalářského studia Téma 0 Úvod do rovinné napjatosti Složk napětí v šikmém řezu při rovinné napjatosti Hlavní napětí a největší smkové napětí Trajektorie hlavního napětí
Pružnost a plasticita,.ročník bakalářského studia Téma 0 Úvod do rovinné napjatosti Složk napětí v šikmém řezu při rovinné napjatosti Hlavní napětí a největší smkové napětí Trajektorie hlavního napětí
VIDEOSBÍRKA DERIVACE
 VIDEOSBÍRKA DERIVACE. Zderivuj funkci y = ln 2 (sin x + tg x 2 ) 2. Zderivuj funkci y = 2 e x2 cos 3x 3. Zderivuj funkci y = 3 e sin2 (x 2 ). Zderivuj funkci y = x3 +2x 2 +sin x x 5. Zderivuj funkci y
VIDEOSBÍRKA DERIVACE. Zderivuj funkci y = ln 2 (sin x + tg x 2 ) 2. Zderivuj funkci y = 2 e x2 cos 3x 3. Zderivuj funkci y = 3 e sin2 (x 2 ). Zderivuj funkci y = x3 +2x 2 +sin x x 5. Zderivuj funkci y
OPAKOVÁNÍ Z 5. ROČNÍKU
 OPKOÁNÍ Z 5. ROČNÍKU ❺ Letecká dvlená na Gran Canaria stjí v dbě jarních rázdnin 18 990 Kč r dsělu sbu a 8 999 Kč r dítě. Je mžn si řikuit výlet strvě v ceně 799 Kč r dsělu sbu a 599 Kč r dítě. Klik celkem
OPKOÁNÍ Z 5. ROČNÍKU ❺ Letecká dvlená na Gran Canaria stjí v dbě jarních rázdnin 18 990 Kč r dsělu sbu a 8 999 Kč r dítě. Je mžn si řikuit výlet strvě v ceně 799 Kč r dsělu sbu a 599 Kč r dítě. Klik celkem
25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE
 5. KNFERENCE GEMETRII A PČÍTAČVÉ GRAFICE ELIPSID HMTETICKÝ K REFERENČNÍMU ELIPSIDU Astrkt V isttické ltimtrii s z znlsti plhy dv stlitů S, S délky signál vyslnéh z jdnh n drhý stlit hldá d P drz signál
5. KNFERENCE GEMETRII A PČÍTAČVÉ GRAFICE ELIPSID HMTETICKÝ K REFERENČNÍMU ELIPSIDU Astrkt V isttické ltimtrii s z znlsti plhy dv stlitů S, S délky signál vyslnéh z jdnh n drhý stlit hldá d P drz signál
Stabilita prutu, desky a válce vzpěr (osová síla)
 Stabilita rutu, deky a válce vzěr (oová íla) Průběh ro ideálně římý rut (teoretický tav) F δ F KRIT Průběh ro reálně římý rut (reálný tav) 1 - menší očáteční zakřivení - větší očáteční zakřivení F Obr.1
Stabilita rutu, deky a válce vzěr (oová íla) Průběh ro ideálně římý rut (teoretický tav) F δ F KRIT Průběh ro reálně římý rut (reálný tav) 1 - menší očáteční zakřivení - větší očáteční zakřivení F Obr.1
Teplota a její měření
 1 Teplta 1.1 Celsiva teplta 1.2 Fahrenheitva teplta 1.3 Termdynamická teplta Kelvin 2 Tepltní stupnice 2.1 Mezinárdní tepltní stupnice z rku 1990 3 Tepltní rzdíl 4 Teplměr Blmetr Termgraf 5 Tepltní rztažnst
1 Teplta 1.1 Celsiva teplta 1.2 Fahrenheitva teplta 1.3 Termdynamická teplta Kelvin 2 Tepltní stupnice 2.1 Mezinárdní tepltní stupnice z rku 1990 3 Tepltní rzdíl 4 Teplměr Blmetr Termgraf 5 Tepltní rztažnst
Stanovisko Rekonstrukce státu ke komplexnímu pozměňovacímu návrhu novely služebního zákona
 Stanvisk Reknstrukce státu ke kmplexnímu pzměňvacímu návrhu nvely služebníh zákna Pslední předlžená verze zákna (verze k 27. 8. 2014) splňuje puze 13 z 38 bdů Reknstrukce státu, z th 7 jen částečně. Z
Stanvisk Reknstrukce státu ke kmplexnímu pzměňvacímu návrhu nvely služebníh zákna Pslední předlžená verze zákna (verze k 27. 8. 2014) splňuje puze 13 z 38 bdů Reknstrukce státu, z th 7 jen částečně. Z
k elektronickému výběrovému řízení na úplatné postoupení pohledávek z titulu předčasně ukončených leasingových smluv
 INFORMAČNÍ MEMORANDUM č. 4/3/2009/11 k elektrnickému výběrvému řízení na úplatné pstupení phledávek z titulu předčasně uknčených leasingvých smluv Praha, 30.11.2010 Infrmační memrandum č. 4/3/2009/11 1/9
INFORMAČNÍ MEMORANDUM č. 4/3/2009/11 k elektrnickému výběrvému řízení na úplatné pstupení phledávek z titulu předčasně uknčených leasingvých smluv Praha, 30.11.2010 Infrmační memrandum č. 4/3/2009/11 1/9
01-02.4 05.11.CZ. Regulační ventily LDM COMAR line -1-
 01-02.4 05.11.CZ Regulační ventily LDM COMAR line A.P.O. - ELMOS v..s., Pražská 90, 509 01 Nvá Paka, Tel.: +420 493 504 261, Fax: +420 493 504 257, E-mail: ap@apelms.cz, Internet: www.apelms.cz -1- Výpčet
01-02.4 05.11.CZ Regulační ventily LDM COMAR line A.P.O. - ELMOS v..s., Pražská 90, 509 01 Nvá Paka, Tel.: +420 493 504 261, Fax: +420 493 504 257, E-mail: ap@apelms.cz, Internet: www.apelms.cz -1- Výpčet
ZOBRAZENÍ ELIPSY POMOCÍ AFINITY
 echnická univerzia v Liberci Fakula řírdvědně-humaniní a edaggická Kaedra maemaiky a didakiky maemaiky ZORZENÍ ELIPY POMOÍ FINIY Pmcný učební ex Pera Pirklvá Liberec, září 03 Nejdříve si řekneme, c jsu
echnická univerzia v Liberci Fakula řírdvědně-humaniní a edaggická Kaedra maemaiky a didakiky maemaiky ZORZENÍ ELIPY POMOÍ FINIY Pmcný učební ex Pera Pirklvá Liberec, září 03 Nejdříve si řekneme, c jsu
h = 0, obr. 7. Definice Funkce f je ohraničená shora, jestliže x Df Funkce f je ohraničená zdola, jestliže x Df d R
 .4. Cíle V této kapitole jsou deinován nejdůležitější pojm týkající se vlastností unkcí. Při dalším studiu budou tto vlastnosti často používán. Je proto nutné si jejich deinice dobře zapamatovat. Deinice.4..
.4. Cíle V této kapitole jsou deinován nejdůležitější pojm týkající se vlastností unkcí. Při dalším studiu budou tto vlastnosti často používán. Je proto nutné si jejich deinice dobře zapamatovat. Deinice.4..
Záznam zkušební komise Jméno a příjmení Podpis Vyhodnocení provedl INSTRUKCE
 VYSOKÉ UČNÍ THNIKÉ V RNĚ FKULT PONIKTLSKÁ Přijímací řízení 2008 akalářské studium Obry: aňvé pradenství knmika a prcesní management Míst pr nalepení kódu Kód nalepí uchazeč Záznam zkušební kmise Jmén a
VYSOKÉ UČNÍ THNIKÉ V RNĚ FKULT PONIKTLSKÁ Přijímací řízení 2008 akalářské studium Obry: aňvé pradenství knmika a prcesní management Míst pr nalepení kódu Kód nalepí uchazeč Záznam zkušební kmise Jmén a
Pružnost a pevnost. 2. přednáška, 10. října 2016
 Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Předmět matematika je úzce spjat s ostatními předměty viz. mezipředmětové vztahy.
 MATEMATIKA Charakteristika vyučvacíh předmětu Matematika se vyučuje ve všech rčnících. Hdinvá dtace je 4 4 4 4. V každém rčníku jsu žáci na jednu hdinu týdně rzděleni d dvu skupin, hdina je pak věnvána
MATEMATIKA Charakteristika vyučvacíh předmětu Matematika se vyučuje ve všech rčnících. Hdinvá dtace je 4 4 4 4. V každém rčníku jsu žáci na jednu hdinu týdně rzděleni d dvu skupin, hdina je pak věnvána
Test k přijímacím zkouškám na VUT pro akademický rok 2010/2011do Navazujícího magisterského studia oboru Geodézie a kartografie. 100 g.
 Test k přijíací zkušká na VUT pr akadeický rk 010/011d Navazujícíh agisterskéh studia bru Gedézie a kartgrafie A1 tg Část A tg α ctg α - tg α (90 ) A ctg 70 0 1 A3 Hdnta jednh radiánu (1 ra v grádech (g
Test k přijíací zkušká na VUT pr akadeický rk 010/011d Navazujícíh agisterskéh studia bru Gedézie a kartgrafie A1 tg Část A tg α ctg α - tg α (90 ) A ctg 70 0 1 A3 Hdnta jednh radiánu (1 ra v grádech (g
5. cvičení z Matematické analýzy 2
 5. cvičení z Matematické analýz 2 30. října - 3. litopadu 207 5. linearizace funkce a Pro funkci f, = e nalezněte její linearizaci v bodě a 0 = 6, 0. Použijte ji k přibližnému určení hodnot funkce f v
5. cvičení z Matematické analýz 2 30. října - 3. litopadu 207 5. linearizace funkce a Pro funkci f, = e nalezněte její linearizaci v bodě a 0 = 6, 0. Použijte ji k přibližnému určení hodnot funkce f v
Deskriptivní geometrie I Zá kládní á pomocne konstrukce
 Desriptivní gemetrie I Zá ládní á pmcne nstruce Knstruce (hyper)sulčních ružnic uželseče Elips 1. sy; vrchly,, C, D; střed 2. 1 (C; ) 3. 2 (; b) 4. {1; 2} = 1 2 5. O 1 = 12 6. O 2 = 12 CD 7. s 1 (O 1 ;
Desriptivní gemetrie I Zá ládní á pmcne nstruce Knstruce (hyper)sulčních ružnic uželseče Elips 1. sy; vrchly,, C, D; střed 2. 1 (C; ) 3. 2 (; b) 4. {1; 2} = 1 2 5. O 1 = 12 6. O 2 = 12 CD 7. s 1 (O 1 ;
II Pravoúhlé promítání na jednu prumetnu
 a) prchází bdem C, b) patrí danému smeru s, c) je rvnbežná s dvema danými rvinami, d) je klmá na danu rvinu, e)je k bema mimbežkám ~lmá (sa mimbežek). 6 Danu prímku prlžte rvinu klmu na danu rvinu. 7 Urcete
a) prchází bdem C, b) patrí danému smeru s, c) je rvnbežná s dvema danými rvinami, d) je klmá na danu rvinu, e)je k bema mimbežkám ~lmá (sa mimbežek). 6 Danu prímku prlžte rvinu klmu na danu rvinu. 7 Urcete
1.6 Singulární kvadriky
 22 KAPITOLA 1. KVADRIKY JAKO PLOCHY 2. STUPNĚ neboť B = C =. Z rovnice (1.34) plne, že přímka, procháející singulárním bodem kvadrik má s kvadrikou společný poue tento singulární bod (je-li A ) nebo celá
22 KAPITOLA 1. KVADRIKY JAKO PLOCHY 2. STUPNĚ neboť B = C =. Z rovnice (1.34) plne, že přímka, procháející singulárním bodem kvadrik má s kvadrikou společný poue tento singulární bod (je-li A ) nebo celá
Financování veřejných vysokých škol v letech 2012-2015:
 Financvání veřejných vyských škl v letech 2012-2015: Pdklady pr analýzy citlivsti ukazatelů kvality a výknu v rámci rzpčtvéh kruhu I Subr pdkladů zpracvaných pr diskusi v rámci tematické aktivity TA 04
Financvání veřejných vyských škl v letech 2012-2015: Pdklady pr analýzy citlivsti ukazatelů kvality a výknu v rámci rzpčtvéh kruhu I Subr pdkladů zpracvaných pr diskusi v rámci tematické aktivity TA 04
Možnosti a druhy párování
 Mžnsti a druhy párvání E S O 9 i n t e r n a t i n a l a. s. U M l ý n a 2 2 1 4 1 0 0, P r a h a www.es9.cz Strana 1 (celkem 9) Autmatické hrmadné párvání... 3 Imprt bankvních výpisů (1.2.1.5)... 3 Párvání
Mžnsti a druhy párvání E S O 9 i n t e r n a t i n a l a. s. U M l ý n a 2 2 1 4 1 0 0, P r a h a www.es9.cz Strana 1 (celkem 9) Autmatické hrmadné párvání... 3 Imprt bankvních výpisů (1.2.1.5)... 3 Párvání
Á Á Á Ž Ř łš ľ ě ý ů é ě ž ý ú ý ě Ú ĺĺ š ž ú ř ž ů ř ý ú ř ů Č é ě ě š ř ů ň š é ž é ě é ě ř ř ě ĺ ž é š ž ř ř ě ž é ň š é ž é ě é ě ř ř ě ž é ř é ů
 Á Ž Ř łš ě Ż é ě ř Č Č ř ř ř Ż ř é ě ý ý š ř ž řĺ š ý ý Á Á Á Ž Ř łš ľ ě ý ů é ě ž ý ú ý ě Ú ĺĺ š ž ú ř ž ů ř ý ú ř ů Č é ě ě š ř ů ň š é ž é ě é ě ř ř ě ĺ ž é š ž ř ř ě ž é ň š é ž é ě é ě ř ř ě ž é ř
Á Ž Ř łš ě Ż é ě ř Č Č ř ř ř Ż ř é ě ý ý š ř ž řĺ š ý ý Á Á Á Ž Ř łš ľ ě ý ů é ě ž ý ú ý ě Ú ĺĺ š ž ú ř ž ů ř ý ú ř ů Č é ě ě š ř ů ň š é ž é ě é ě ř ř ě ĺ ž é š ž ř ř ě ž é ň š é ž é ě é ě ř ř ě ž é ř
Ohyb - smyková napětí
 Oh - smková napětí p + + - - l x ohýaný nosník - M σ x - x Průřeové charakteristik pro smková napětí a ohu jsou statický moment ploch S a moment setrvačnosti. S A části průr T [ m ] max Mení stav únosnosti
Oh - smková napětí p + + - - l x ohýaný nosník - M σ x - x Průřeové charakteristik pro smková napětí a ohu jsou statický moment ploch S a moment setrvačnosti. S A části průr T [ m ] max Mení stav únosnosti
F1030 Mechanika a molekulová fyzika úlohy k procvičení před písemkami (i po nich ) Téma 4 a 5: Zákony newtonovské mechaniky
 F3 Mechanika a lekulvá fyzika úlhy k prcvičení před písekai (i p nich ) Téa 4 a 5: Zákny newtnvské echaniky Předpklady k úlhá: Ve všech úlhách pvažujte labratrní vztažnu sustavu, pevně spjenu se Zeí, za
F3 Mechanika a lekulvá fyzika úlhy k prcvičení před písekai (i p nich ) Téa 4 a 5: Zákny newtnvské echaniky Předpklady k úlhá: Ve všech úlhách pvažujte labratrní vztažnu sustavu, pevně spjenu se Zeí, za
Souřadnicové výpočty. Geodézie Přednáška
 Souřadnicové výpočt Geodézie Přednáška Souřadnicové výpočt strana 2 Souřadnicové výpočt (souřadnicová geometrie) vchází z analtické geometrie zkoumá geometrické tvar pomocí algebraických a analtických
Souřadnicové výpočt Geodézie Přednáška Souřadnicové výpočt strana 2 Souřadnicové výpočt (souřadnicová geometrie) vchází z analtické geometrie zkoumá geometrické tvar pomocí algebraických a analtických
Přídavky na děti v mezinárodních případech (Evropská unie, Evropský hospodářský prostor a Švýcarsko) Použití nadstátního práva
 Přídavky na děti v mezinárdních případech (Evrpská unie, Evrpský hspdářský prstr a Švýcarsk) Pužití nadstátníh práva Tent prspekt Vám má pskytnut přehled zvláštnstech v mezinárdních případech. Všebecné
Přídavky na děti v mezinárdních případech (Evrpská unie, Evrpský hspdářský prstr a Švýcarsk) Pužití nadstátníh práva Tent prspekt Vám má pskytnut přehled zvláštnstech v mezinárdních případech. Všebecné
Syntetická geometrie II
 Mnohoúhelníky Pedagogická fakulta 2018 www.karlin.mff.cuni.cz/~zamboj/ Čtyřúhelníky Definice (Čtyřúhelník) Jsou dány čtyři body A, B, C, D v rovině, z nichž žádné tři nejsou kolineární. Čtyřúhelník ABCD
Mnohoúhelníky Pedagogická fakulta 2018 www.karlin.mff.cuni.cz/~zamboj/ Čtyřúhelníky Definice (Čtyřúhelník) Jsou dány čtyři body A, B, C, D v rovině, z nichž žádné tři nejsou kolineární. Čtyřúhelník ABCD
4.1.5 Práce v elektrickém poli, napětí
 4.1.5 Práce v elektrickém poli, napětí Předpoklady: 4102, 4104, mechanická práce Př. 1: Spočítej ílu, která půobí náboj o velikoti 2 10 5 C, který e nachází v elektrickém poli o intenzitě 2500 N C 1. Nejjednodušší
4.1.5 Práce v elektrickém poli, napětí Předpoklady: 4102, 4104, mechanická práce Př. 1: Spočítej ílu, která půobí náboj o velikoti 2 10 5 C, který e nachází v elektrickém poli o intenzitě 2500 N C 1. Nejjednodušší
Technické požadavky na integrované řešení CAD/CAM:
 Technické pžadavky na integrvané řešení CAD/CAM: Integrace CAM a CAD: splečný datvý frmát mdelu pr CAD a CAM mduly, CAD a CAM v jedntném prstředí, mžnst přepnutí mezi CAD a CAM pr prvedení změn na mdelu,
Technické pžadavky na integrvané řešení CAD/CAM: Integrace CAM a CAD: splečný datvý frmát mdelu pr CAD a CAM mduly, CAD a CAM v jedntném prstředí, mžnst přepnutí mezi CAD a CAM pr prvedení změn na mdelu,
Chování ocelobetonového stropu. Jednoduchá metoda pro návrh za běžné teploty. Jednoduchá metoda pro návrh za zvýšené teploty
 1/09/01 K nvinkám pžární dnsti nsných knstrukcí 11. září 01 Obsah prezentace za pžáru cebetnvých desek za běžné Mde strpní desky Druhy prušení cebetnvých desek za zvýšené Rzšíření na chvání za pžáru Zvětšení
1/09/01 K nvinkám pžární dnsti nsných knstrukcí 11. září 01 Obsah prezentace za pžáru cebetnvých desek za běžné Mde strpní desky Druhy prušení cebetnvých desek za zvýšené Rzšíření na chvání za pžáru Zvětšení
Schéma podloží pod základem. Parametry podloží: c ef c d. třída tloušťka ɣ E def ν β ϕef
 Příkla avrhněte záklaovou esku ze ŽB po sloupy o rozměru 0,6 x 0,6 m a stanovte max. provozní napětí záklaové půy. Zatížení a geometrie le orázku. Tloušťka esky hs = 0,4 m. Zatížení: rohové sloupy 1 =
Příkla avrhněte záklaovou esku ze ŽB po sloupy o rozměru 0,6 x 0,6 m a stanovte max. provozní napětí záklaové půy. Zatížení a geometrie le orázku. Tloušťka esky hs = 0,4 m. Zatížení: rohové sloupy 1 =
Rekuperace rodinného domu v Přestavlkách
 Rekuperace rdinnéh dmu v Přestavlkách Pjem: Rekuperace, nebli zpětné získávání tepla je děj, při němž se přiváděný vzduch d budvy předehřívá teplým dpadním vzduchem. Teplý vzduch není tedy bez užitku dveden
Rekuperace rdinnéh dmu v Přestavlkách Pjem: Rekuperace, nebli zpětné získávání tepla je děj, při němž se přiváděný vzduch d budvy předehřívá teplým dpadním vzduchem. Teplý vzduch není tedy bez užitku dveden
Matematika vzorce. Ing. Petr Šídlo. verze
 Matematika vzorce Ing. Petr Šídlo verze 0050409 Obsah Jazyk matematiky 3. Výrokový počet.......................... 3.. Logické spojky...................... 3.. Tautologie výrokového počtu...............
Matematika vzorce Ing. Petr Šídlo verze 0050409 Obsah Jazyk matematiky 3. Výrokový počet.......................... 3.. Logické spojky...................... 3.. Tautologie výrokového počtu...............
Studijní předmět: Základy teorie pravděpodobnosti a matematická statistika Ročník:
 Studijní předmět: Základy terie pravděpdbnsti a matematická statistika Rčník: 1 Semestr: 1 Způsb uknčení: zkuška Pčet hdin přímé výuky: 2/2 (přednáška/ seminář) Pčet hdin kmbinvané výuky celkem: 8 Antace
Studijní předmět: Základy terie pravděpdbnsti a matematická statistika Rčník: 1 Semestr: 1 Způsb uknčení: zkuška Pčet hdin přímé výuky: 2/2 (přednáška/ seminář) Pčet hdin kmbinvané výuky celkem: 8 Antace
Betonové a zděné konstrukce Přednáška 4 Spojité desky Mezní stavy použitelnosti
 Betonové a zděné kontrukce Přednáška 4 Spojité deky Mezní tavy použitelnoti Ing Pavlína Matečková, PhD 2016 Spojitá deka: deka o více polích, zpravidla jako oučát rámové kontrukce Řeší e MKP Zjednodušené
Betonové a zděné kontrukce Přednáška 4 Spojité deky Mezní tavy použitelnoti Ing Pavlína Matečková, PhD 2016 Spojitá deka: deka o více polích, zpravidla jako oučát rámové kontrukce Řeší e MKP Zjednodušené
Optika. o Izotropní světlo se šíří všemi směry stejně rychle o Anizotropní světlo se šíří různými směry různě Zdroj. o o
 Optika Věda světle Rychlst světla 299 792 458 m/s (přibližně 3.10 8 ) (světl se šíří rychlstí světla ve vakuu, jinde pmalejší kvůli permitivitě a permeabilitě, třeba ve skle je t 2x pmalejší, ve vdě se
Optika Věda světle Rychlst světla 299 792 458 m/s (přibližně 3.10 8 ) (světl se šíří rychlstí světla ve vakuu, jinde pmalejší kvůli permitivitě a permeabilitě, třeba ve skle je t 2x pmalejší, ve vdě se
ZŠ ÚnO, Bratří Čapků 1332
 Matematika 4+5 - Chytré dítě Multimedia Art (Pachner) Úvdní brazvka = Obsah Část 1. Úvd 6 stran Jak se učit? 3 strany Úhel 11 stran Úhel c t je? Pravý úhel Měření úhlů Velikst úhlů Přímka 25 stran C se
Matematika 4+5 - Chytré dítě Multimedia Art (Pachner) Úvdní brazvka = Obsah Část 1. Úvd 6 stran Jak se učit? 3 strany Úhel 11 stran Úhel c t je? Pravý úhel Měření úhlů Velikst úhlů Přímka 25 stran C se

