Metoda analýzy datových obalů (DEA)
|
|
|
- Františka Jandová
- před 8 lety
- Počet zobrazení:
Transkript
1
2
3 Kapitola 1 Metoda analýzy datových obalů (DEA) Modely datových obalů slouží pro hodnocení technické efektivity produkčních jednotek na základě velikosti vstupů a výstupů. Hodnocenými jednotkami mohou být pobočky bank, supermarkety, nemocnice, školy, úřady apod. Protože vstupů a výstupů, podle kterých příslušné jednotky hodnotíme, může být více druhů, řadí se DEA mezi metody vícekriteriálního rozhodování. Analýza datových obalů je vhodná ke zjišťování technické efektivity jednotek, které jsou vzájemně srovnatelné. To znamená, že používají stejné vstupy k produkování stejných výstupů, avšak v jejich výkonech jsou jisté rozdíly. Jednotky jsou porovnávány mezi sebou a zjišťuje se, které z nich jsou efektivní a které nefektivní. V případě neefektivních jednotek lze metodou datových obalů zjistit, jak má taková jednotka redukovat své vstupy, popřípadě navýšit své výstupy, aby se stala efektivní. Příklad 1. Obchodní řetězec má patnáct poboček, přičemž každá z těchto poboček je charakterizována počtem zaměstnanců, režijními náklady, celkovými náklady, prodejní plochou, počtem obsloužených zákazníků a denními tržbami. Které z patnácti poboček jsou a které nejsou efektivní? Které vstupy a do jaké míry je nutné u neefektivních jednotek redukovat, popřípadě které výstupy navyšovat? Počet porovnávaných jednotek musí být dostatečně velký, protože při malém počtu srovnávaných jednotek a velkém počtu kritérií by byly považovány všechny jednotky za efektivní. Velkou pozornost je nutné věnovat výběru vhodných kritérií, podle kterých jsou jednotky hodnoceny. Důležité je vybrat kritéria, která jsou pro výkon jednotky zásadní, jsou známy jejich hodnoty u všech jednotek a zároveň to jsou kritéria, která spolu příliš nekorelují. 1.1 Podstata metody DEA Cílem této metody je rozdělení zkoumaných objektů na efektivní a neefektivní podle velikosti spotřebovávaných zdrojů a množství vyráběné produkce nebo jiného typu výstupů. DEA porovnává jednotky vzhledem k nejlepším jednotkám. Modely DEA vycházejí z Farrelova modelu pro měření efektivity jednotek s jedním vstupem a jedním výstupem, který rozšířili Charnes, Cooper a Rhodes (CCR) a Banker, Charnes a Cooper (BCC). DEA modely jsou založeny na tom, že pro daný problém existuje množina produkčních možností, tvořená všemi přípustnými kombinacemi vstupů a výstupů. Množina produkčních možností je určena efektivní hranicí. Pokud kombinace vstupů a výstupů u příslušné jednotky leží na této hranici, jedná se o efektivní jednotku. Jednotka je efektivní, pokud spotřebovává malé množství vstupů na velké množství výstupů. V případě, že jednotka efektivní není (neleží 1
4 2 KAPITOLA 1. METODA ANALÝZY DATOVÝCH OBALŮ (DEA) na hranici produkčních možností), je nutné upravit velikost jejích vstupů, popřípadě výstupů. Jak snížit vstupy nebo jak zvýšit výstupy lze zjistit opět pomocí řešení modelů DEA. 1.2 Hodnocení jednotek s jedním vstupem a jedním výstupem V případě, že uvažujeme pouze jeden vstup a jeden výstup, efektivita jednotek je dána vztahem: efektivita = výstup vstup (1.1) Příklad 2. Obchodní řetězec má osm poboček, přičemž každá z těchto poboček je charakterizována počtem zaměstnanců a denními tržbami v 10 tisících Kč. Potřebné údaje naleznete v následující tabulce: A B C D E F G H Zaměstnanci (x) Tržby (y) y/x 0,5 1 0,67 0,75 0,8 0,4 0,5 0,63 Čím je podíl y/x větší, tím je pobočka efektivnější (větší objem tržeb na zaměstnance) Výnosy z rozsahu Efektivní hranice může mít různý tvar podle toho, zda v úloze uvažujeme konstantní či variabilní výnosy z rozsahu. Konstantní výnosy z rozsahu (Constant returns to scale - CRS) Je-li kombinace vstupů a výstupů (x,y) prvkem množiny produkčních možností, pak je prvkem této množiny i kombinace této množiny (αx, αy), kde α > 0. Neboli pokud je jednotka s určitou kombinací vstupů a výstupů efektivní, pak bude efektivní i jednotka, jejíž vstupy a výstupy jsou α násobky vstupů a výstupů původní efektivní jednotky. Množina produkčních možností a efektivní hranice pro příklad 2 jsou znázorněny na obrázku 1.1 Efektivní hranici tvoří přímka a jedinou efektivní jednotkou, která na této hranici leží, je jednotka B. Neefektivní jednotky by měly snížit množství vstupů nebo zvýšit množství výstupů. Například aby se neefektivní jednotka A stala efektivní, musela by udělat jedno z následujících opatření: Zvýšit hodnotu výstupu na hodnotu y (y = 2) při zachování současné výše vstupu x. Získáme tak virtuální jednotku U s virtuálním vstupem a výstupem (x, y ) = (2, 2). Tato virtuální jednotka je pak vzorová pro neefektivní jednotku A. Pokud by tedy jednotka A měla být efektivní a zaměstnávala dva zaměstnance, musela by zvýšit tržby z 10 tisíc Kč na 20 tisíc Kč. Toto je tzv. výstupově orientovaný model. Snížit hodnotu vstupu na hodnotu x (x = 1) při zachování současné výše výstupu y. Získáme tak virtuální jednotku U s virtuálním vstupem a výstupem (x, y) = (1, 1). I tato virtuální jednotka je pak vzorová pro skutečnou jednotku A. Pokud by tedy jednotka A měla být efektivní a měla tržby 10 tisíc Kč, musela by zaměstnávat pouze jednoho zaměstnance. Tento model je vstupově orientovaný. Kombinovat oba předchozí způsoby, například zaměstnat jednoho zaměstnance na plný úvazek, druhého na poloviční a tržby navýšit na 15 tisíc Kč.
5 1.2. HODNOCENÍ JEDNOTEK S JEDNÍM VSTUPEM A JEDNÍM VÝSTUPEM 3 Obrázek 1.1: Hranice efektivity - CRS Relativní míru efektivity neefektivních jednotek lze vypočítat porovnáním tržeb na jednoho zaměstnance s tržbami na jednoho zaměstnance u efektivní jednotky. Výpočet pro jednotku A by pak byl: 0, 5/1 = 0, 5. Tato míra efektivity je relativní, neboť závisí na souboru hodnocených jednotek. Míru efektivity jednotky A můžeme počítat i z velikosti vstupů a výstupů této jednotky a virtuálních jednotek U, U : Pokud vezmeme v úvahu výstupově orientovaný model, virtuální jednotku U, míru efektivnosti vypočteme jako y/y = 1/2 = 0,5. Je to tedy podíl tržeb neefektivní jednotky A a tržeb virtuální jednotky U. Vzhledem k tomu, že se jedná o výstup a my chceme zjistit, jak se má výstup upravit - navýšit, je vhodné pracovat s převrácenou hodnotou y /y = 2/1 = 2. Pokud vezmeme v úvahu vstupově orientovaný model, virtuální jednotku U, míru efektivnosti vypočteme jako x /x = 1/2 = 0,5. Je to tedy podíl počtu zaměstnanců virtuální jednotky U a skutečné neefektivní jednotky A. Zjistili jsme, jak se má vstup jednotky A upravit - snížit, a to na 1/2 původní hodnoty. Variabilní výnosy z rozsahu (Variable returns to scale - VRS) Zde neplatí požadavek, že α násobek vstupů musí být vyvážen nárůstem výstupů o stejný násobek. Jednotka tedy může být efektivní, i když poměrný nárůst výnosů bude nižší nebo vyšší než nárůst vstupů. Pro příklad 2 je množina produkčních možností a efektivní hranice znázorněna na obrázku 1.2. Efektivní hranici zde tvoří konvexní obal množiny produkčních možností (obal dat). Všimněme si, že nyní jsou efektivní jednotky tři, a to B, E a H. Obecně platí, že míra efektivity hodnocených jednotek za předpokladu VRS je stejná nebo vyšší, než za předpokladu CRS. Vezměme neefektivní jednotku D. Za předpokladu CRS je míra efektivity 0,75/1 = 0,75 a nezáleží na tom, zda uvažujeme vstupově či výstupově orientovaný model. V případě variabilních výnosů z rozsahu lze opět dosáhnout efektivní hranice třemi způsoby:
6 4 KAPITOLA 1. METODA ANALÝZY DATOVÝCH OBALŮ (DEA) Tržby 5 Hranice efektivity H 4 U` E 3 U``= B D G 2 C F 1 A Množina produkčních možností Zaměstnanci Obrázek 1.2: Hranice efektivity - VRS Zvýšit hodnotu výstupu na hodnotu y (y = 3,5) při zachování současné výše vstupu x. Získáme tak virtuální jednotku U s virtuálním vstupem a výstupem (x, y ) = (4; 3,5). Tato virtuální jednotka je pak vzorová pro neefektivní jednotku D. Pokud by tedy jednotka D měla být efektivní a zaměstnávala čtyři zaměstnance, musela by zvýšit tržby z 30 tisíc Kč na 35 tisíc Kč. Toto je tzv. výstupově orientovaný model. Snížit hodnotu vstupu na hodnotu x (x = 3) při zachování současné výše výstupu y. Získáme tak virtuální jednotku U s virtuálním vstupem a výstupem (x, y) = (3, 3). I tato virtuální jednotka je pak vzorová pro skutečnou jednotku D. Všimněte si, že velikost vstupů a výstupů u virtuální jednotky U je shodná s velikostí vstupů a výstupů u jednotky B. V tomto případě můžeme vynechat pojem virtuální jednotka. Vzorovou jednotkou pro neefektivní jednotku D je skutečná jednotka B. Pokud by tedy jednotka D měla být efektivní a měla tržby 30 tisíc Kč, musela by zaměstnávat pouze tři zaměstnance. Tento model je vstupově orientovaný. Kombinovat oba předchozí způsoby.
7 1.3. HODNOCENÍ JEDNOTEK SE DVĚMA VSTUPY A JEDNÍM VÝSTUPEM 5 Míru efektivity jednotky D můžeme počítat i u tohoto modelu z velikosti vstupů a výstupů této jednotky a virtuálních jednotek U, U : Pokud vezmeme v úvahu výstupově orientovaný model, virtuální jednotku U, míru efektivnosti vypočteme jako y/y = 3/3,5 = 0, Je to tedy podíl tržeb neefektivní jednotky D a tržeb virtuální jednotky U. Vzhledem k tomu, že se jedná o výstup a my chceme zjistit, jak se má výstup upravit - navýšit, je vhodné pracovat s převrácenou hodnotou y /y = 3,5/3 = 1, Pokud vezmeme v úvahu vstupově orientovaný model, virtuální jednotku U, míru efektivnosti vypočteme jako x /x = 3/4 = 0,75. Je to tedy podíl počtu zaměstnanců virtuální jednotky U a skutečné neefektivní jednotky D. Zjistili jsme, jak se má vstup jednotky D upravit - snížit, a to na 3/4 původní hodnoty. Z výsledků je patrné, že za předpokladu VRS se míra efektivity mění v závislosti na zvoleném modelu (vstupově či výstupově orientovaný). 1.3 Hodnocení jednotek se dvěma vstupy a jedním výstupem Efektivitu jednotek, které spotřebovávají dva vstupy k produkci jednoho výstupu lze zjistit graficky i metodou, která bude popsána v kapitole 1.5. Řešený příklad 1.1. Obchodní řetězec má devět poboček, přičemž každá z těchto poboček je charakterizována počtem zaměstnanců, režijními náklady v tisících Kč a denními tržbami v 10 tisících Kč. Potřebné údaje naleznete v následující tabulce. A B C D E F G H I Zaměstnanci Režijní náklady Prodej Řešení. Proto, aby se úloha nechala graficky znázornit, je nutné znormovat vstupy na jednotku výstupu. Vydělíme počet zaměstnanců a režijní náklady velikostí prodeje pro každou jednotku. Například pro jednotku A budeme počítat 12/3 a 9/3. Graficky pak znázorňujeme velikost dvou vstupů potřebných pro dosažení jednotky výstupu. A B C D E F G H I Zaměstnanci Režijní náklady Prodej Grafické řešení je znázorněno na obrázku 1.3. Z grafu je patrné, že efektivní jsou jednotky C, D a E. Jsou to jednotky, ke kterým v hodnoceném souboru jednotek neexistuje žádná jednotka s lepšími hodnotami obou vstupů na jednotku výstupu. Uvedené efektivní jednotky tvoří efektivní hranici. Jednotky A, B, F, G, H, I jsou neefektivní. Modely DEA se liší tím, jak měří vzdálenost neefektivní jednotky od efektivní hranice. Jeden z možných způsobů je měření radiální, které budeme používat v našem textu. Radiální způsob měření určuje redukci obou (všech) vstupů nutnou pro dosažení efektivní hranice a realizuje se tak, že je spojena neefektivní jednotka s počátečním bodem. Tam, kde se protne tato spojnice s hranicí efektivity, zjistíme velikost vstupů, která je potřebná pro dosažení efektivity. Mohou nastat dva základní případy: Skutečná jednotka je vzorovou (peer) jednotkou, jako je tomu například v případě neefektivní jednotky H, pro kterou je vzorovou jednotkou jednotka D. Zde můžeme vynechat termín hypotetická jednotka, protože vzorová jednotka je jednotkou skutečnou, spojnice
8 6 KAPITOLA 1. METODA ANALÝZY DATOVÝCH OBALŮ (DEA) Režijní náklady 5 4 Hranice efektivity E Množina produkčních možností G 3 2 U`` D A H F I B 1 C Zaměstnanci Obrázek 1.3: Hranice efektivity pro dva vstupy a jeden výstup prochází bodem D. Efektivitu jednotky H pak vypočítáme jako podíl vzdálenosti jednotky D od počátku a jednotky H od počátku, tedy 0D / 0H = 0,7996. Můžeme říci, že pro dosažení efektivity by jednotka H měla snížit své vstupy na 79,96% původní velikosti vstupů. Vzorovou jednotkou je hypotetická jednotka, která je tvořena kombinací skutečných vzorových jednotek. Například spojnice neefektivní jednotky A s počátkem protíná efektivní hranici mezi dvěma efektivními jednotkami D a E. V tomto průsečíku leží hypotetická jednotka U, která udává velikost vstupů pro jednotku A, aby dosahovala efektivity. Efektivitu jednotky A počítáme jako podíl vzdálenosti jednotky U od počátku a vzdálenosti bodu A od počátku, tedy 0U / 0A. Vstupy této hypotetické jednotky mohou být počítány jako kombinace velikosti vstupů dvou sousedních efektivních jednotek D a E. Tento postup si ukážeme později.
9 1.4. HODNOCENÍ JEDNOTEK S JEDNÍM VSTUPEM A DVĚMA VÝSTUPY Hodnocení jednotek s jedním vstupem a dvěma výstupy Efektivitu jednotek, které spotřebovávají jeden vstup k produkci dvou výstupů, lze zjistit graficky i metodou, která je popsána v kapitole 1.5. Řešený příklad 1.2. Obchodní řetězec má sedm poboček, přičemž každá z těchto poboček je charakterizována počtem zaměstnanců, počtem obsloužených zákazníků za hodinu a denními tržbami v 10 tisících Kč. Potřebné údaje naleznete v následující tabulce. A B C D E F G Zaměstnanci Zákazníci Prodej Řešení. Nejprve si znormujeme velikosti výstupů na jednotku vstupu. Provede se to tak, že vydělíme oba výstupy vstupem. Například pro jednotku A dělíme počet zákazníků a velikost tržeb počtem zaměstnanců, tedy 2/2 a 10/2. A B C D E F G Zaměstnanci Zákazníci Prodej Grafické řešení tohoto příkladu naleznete na obrázku 1.4. Z grafu je patrné, že efektivní jsou jednotky B, E, F, G. Jsou to jednotky, ke kterým v hodnoceném souboru jednotek neexistuje žádná jednotka s lepšími hodnotami obou výstupů na jednotku vstupu. Uvedené efektivní jednotky tvoří efektivní hranici. Jednotky A, C, D, H jsou neefektivní. I v tomto případě budeme používat radiální způsob dosažení efektivní hranice. Radiální způsob měření určuje navýšení obou (všech) výstupů, nutné pro dosažení efektivní hranice, a realizuje se tak, že je spojena neefektivní jednotka s počátečním bodem. Tam, kde se protne tato spojnice s hranicí efektivity, zjistíme velikost výstupů, která je potřebná pro dosažení efektivity. Mohou nastat dva základní případy: Skutečná jednotka je vzorovou (peer) jednotkou, jako je tomu například v případě neefektivní jednotky C, pro kterou je vzorovou jednotkou jednotka E. Zde můžeme vynechat termín hypotetická jednotka, protože vzorová jednotka je jednotkou skutečnou, spojnice prochází bodem E. Efektivitu jednotky C vypočítáme pak jako podíl vzdálenosti jednotky E od počátku a jednotky C od počátku, tedy 0E / 0C = 2. Můžeme říci, že pro dosažení efektivity by jednotka C měla zvýšit své výstupy na dvojnásobek původní velikosti výstupů. Vzorovou jednotkou je hypotetická jednotka, která je tvořena kombinací skutečných vzorových jednotek. Například spojnice neefektivní jednotky D s počátkem protíná efektivní hranici mezi dvěma efektivními jednotkami F a G. V tomto průsečíku leží hypotetická jednotka U, která udává velikost výstupů pro jednotku D, aby dosahovala efektivity. Efektivitu jednotky D počítáme jako podíl 0U / 0D, což je vzdálenost jednotky U od počátku a vzdálenosti bodu D od počátku. Výstupy této hypotetické jednotky mohou být počítány jako kombinace velikosti vstupů dvou sousedních efektivních jednotek F a G. Tento postup si ukážeme později. Poznámka. Všimněte si zvláštního případu vzorové jednotky Q (pro neefektivní jednotku A).
10 8 KAPITOLA 1. METODA ANALÝZY DATOVÝCH OBALŮ (DEA) Tržby 7 Q B Hranice efektivity 6 E 5 A F 4 U` 3 2 C D H G 0 1 Množina produkčních možností Zákazníci Obrázek 1.4: Hranice efektivity pro jeden vstup a dva výstupy 1.5 Hodnocení jednotek s více vstupy a výstupy V případě více spotřebovávaných vstupů na produkci více výstupů se používá míra efektivity: efektivita = vážená suma výstupu vážená suma vstupu, (1.2) což lze vyjádřit vztahem: e k = u j y jk, k = 1, 2,..., p, (1.3) v i x ik kde u j, v i jsou jednotné váhy vstupů a výstupů pro všechny hodnocené jednotky, x ik je velikost i-tého vstupu pro k-tou jednotkou a y jk je velikost j -tého výstupu pro k-tou jednotkou (celkem je hodnoceno p jednotek).
11 1.5. HODNOCENÍ JEDNOTEK S VÍCE VSTUPY A VÝSTUPY 9 Vstupní údaje můžeme zapsat do tabulky, která má charakter kriteriální matice (sloupce vstupů odpovídají hodnocení podle minimalizačního kritéria a sloupce výstupů podle maximalizačního kritéria). Je akceptována kompenzace (vyšší výstupy potřebují více vstupů při zachování efektivity spotřeby). Předpokládejme, že zkoumaný objekt zahrnuje p jednotek, jsou označeny S 1, S 2,..., S p. Každá z nich spotřebovává m vstupů na produkci n výstupů. Potom x ik je množství spotřebovávaného i-tého vstupu k-tou jednotkou a y jk je množství j-tého výstupu produkovaného k-tou jednotkou. Vstupy a výstupy lze zapsat do přehledné tabulky, viz tabulka 1.1. Tabulka 1.1: Obecné zadání vstupní matice pro metodu DEA Vstupy Výstupy X 1 X 2 X m Y 1 Y 2 Y n S 1 x 11 x x m1 y 11 y y n1 S 2 x 12 x x m2 y 12 y y n S p x 1p x 2p... x mp y 1p y 2p... y np Vzhledem k tomu, že každé středisko je jinak zaměřené, lze uvažovat váhy odděleně pro každé středisko. Tyto váhy nejsou odvozené od ceny, ale spíše od používané technologie v jednotlivých střediskách. Z tohoto důvodu se používá termín technická efektivita, kterou vyjadřuje vztah 1.4: e k = u jk y jk, k = 1, 2,..., p, (1.4) v ik x ik u jk a v ik jsou individuální váhy vstupů a výstupů pro hodnocené jednotky, x ik je velikost i-tého vstupu pro k-tou jednotkou a y jk je velikost j -tého výstupu pro k-tou jednotkou (celkem je hodnoceno p jednotek). Modely DEA tedy hledají individuální váhy pro jednotlivé hodnocené jednotky. Tyto váhy jsou hledány tak, aby byla maximalizována efektivita jednotek. V souboru hodnocených jednotek jsou některé jednotky efektivní a jiné neefektivní. Pro neefektivní jednotky lze určit tzv. hypotetickou (virtuální) jednotku, která je charakterizována jako vážený průměr určitých skutečných efektivních jednotek (peer jednotek). Tato jednotka (velikost jejích vstupů a výstupů) slouží jako vzor pro skutečnou neefektivní jednotku, která produkuje méně výstupů nebo spotřebovává více vstupů než její virtuální jednotka. V některých případech může být vzorovou jednotkou některá z efektivních skutečných jednotek. Pro hodnocení efektivity jednotek s více vstupy a výstupy bylo vyvinuto mnoho metod, které byly již dále modifikovány. V rámci našeho kurzu se budeme zabývat pouze metodami CCR a BCC (viz dále) CCR vstupově orientovaný model U modelů CCR předpokládejme konstantní výnos z rozsahu. Koeficient technické efektivity je definován jako poměr vážené sumy výstupů a vážené sumy vstupů. Jsou hledány takové váhy (koeficienty), aby koeficient technické efektivity byl z intervalu 0, 1. Jednotka s koeficientem technické efektivity rovným 1 je efektivní, koeficient menší než 1 ukazuje na neefektivní jednotku a určuje míru potřebného snížení vstupů k zajištění efektivity jednotky.
12 10 KAPITOLA 1. METODA ANALÝZY DATOVÝCH OBALŮ (DEA) Model CCR hodnotí efektivitu jednotek pro libovolný počet vstupů a výstupů. Neznámými jsou v tomto modelu váhy přidělené vstupu i a váhy přidělené výstupu j jednotkou k. Váhy jsou hledány individuálně, proto je nutno vyřešit p modelů. Tento počet modelů se řeší proto, že celkem v hodnoceném souboru je p jednotek a pro každou jednotku se sestavuje zvláštní model. Matematický model pro jednotku H (jedna z p jednotek) se skládá: z účelové funkce e H = u jh y jh max, (1.5) v ih x ih která maximalizuje poměr vážených výstupů a vážených vstupů, z omezujících podmínek u jh y jk 1, k = 1, 2,..., p, (1.6) v ih x ik které zajištují, aby poměr výstupů a vstupů s váhami pro k-tou jednotku byl u ostatních jednotek v hodnoceném souboru menší nebo roven jedné, z podmínek nezápornosti u jh 0, j = 1, 2,..., n, v ih 0, i = 1, 2,..., m, (1.7) které požadují nezápornost hledaných neznámých (vah). Model lze upravit na lineární tak, že čitatele účelové funkce budeme maximalizovat za předpokladu, že jmenovatel se bude rovnat hodnotě 1. e H = v ih x ik + u jh y jh max v ih x ih = 1 u jh y jk 0, k = 1, 2,..., p, (1.8) u jh 0, j = 1, 2,..., n, v ih 0, i = 1, 2,..., m. Poznámka. První index představuje vždy číslo vstupu a výstupu, druhý index číslo jednotky, pro kterou je model sestaven. Předpokládejme, že jednotka H není efektivní. Když sestavíme k primárnímu modelu model duální, zjistíme, které jednotky tvoří množinu peer jednotek neefektivní jednotky H a zároveň získáme koeficienty λ kh kombinace peer jednotek, které tvoří virtuální efektivní jednotku k jednotce H.
13 1.5. HODNOCENÍ JEDNOTEK S VÍCE VSTUPY A VÝSTUPY 11 Duální model se skládá z účelové funkce a omezujících podmínek x ih z H z H min (1.9) p λ kh x ik 0; i = 1, 2,..., m, (1.10) k=1 p λ kh y jk y jh, j = 1, 2,..., n, k=1 Proměnná z H může nabývat libovolných hodnot. λ kh 0, k = 1, 2,..., p. Poznámka. První index je číslo jednotky, ke které se vztahuje příslušná λ - koeficient kombinace, druhý index je číslo jednotky, pro kterou je model sestaven. Velikost vstupů a výstupů virtuální jednotky lze vypočítat jako kombinaci vstupů a výstupů peer jednotek. Pro vstupy: p x ih = λ kh x ik ; i = 1, 2,..., m, (1.11) a pro výstupy y jh = k=1 p λ kh y jk ; j = 1, 2,..., n. (1.12) k=1 Řešený příklad 1.3. Obchodní řetězec má sedm poboček, přičemž každá z těchto poboček je charakterizována počtem zaměstnanců, režijními náklady v tisících Kč, počtem obsloužených zákazníků za hodinu a denními tržbami v 10 tisících Kč. Potřebné údaje naleznete v následující tabulce. Pobočka A B C D E F G Zaměstnanci Režijní náklady Zákazníci Tržby Řešení. Vzhledem k tomu, že budeme hodnotit sedm poboček, je nutné sestavit sedm modelů. Primární model pro první pobočku - pobočku A: Výsledky: e 1 = u u 21 max 4v v 21 = 1 4v 11 3v 21 + u u v 11 3v u u v 11 v u u v 11 2v u u v 11 4v u u v 11 2v u u v 11 4v u u 21 0 u j1 0, j = 1, 2, v i1 0, i = 1, 2.
14 12 KAPITOLA 1. METODA ANALÝZY DATOVÝCH OBALŮ (DEA) Proměnná Hodnota e 1 0, v 11 0, v 21 0, u 11 0 u 21 0, Z výsledků je patrné, že jednotka A (první) není efektivní, neboť hodnota e 1 je menší než 1. Proto přistoupíme k sestavení duálně sdruženého modelu, jehož vyřešením získáme vhodnou kombinaci vzorových jednotek pro dosažení efektivity neefektivní jednotky A. Duální model pro první jednotku - jednotku A: z 1 min 4z 1 4λ 11 7λ 21 8λ 31 4λ 41 2λ 51 5λ 61 6λ z 1 3λ 11 3λ 21 λ 31 2λ 41 4λ 51 2λ 61 4λ 71 0 λ λ λ λ λ λ λ λ λ λ λ λ λ λ 71 5 Proměnná Hodnota z 1 0, z 1 0, λ 11 0 λ 21 0 λ 31 0 λ 41 0 λ 51 0, λ 61 0, λ 71 0 λ k1 0, k = 1, 2,..., 7 Z výsledků vyplývá, že vzorovými (peer) jednotkami pro jednotku A jsou jednotky pátá (E) a šestá (F), neboť hodnoty proměnných λ 51 a λ 61 jsou nenulové. Proměnná λ 51 se vztahuje k páté jednotce (E) - první index je 5, proměnná λ 61 se vztahuje k páté jednotce (F) - první index je 6. Známe tedy koeficienty kombinace. Nyní musíme vstupy efektivních jednotek E a F pronásobit koeficienty a pro každý vstup zvlášť tyto výsledky sečíst, abychom získali optimální velikost vstupů pro jednotku A. Konkrétně pro první vstup: Pro druhý vstup: x 11 = λ 51x 15 + λ 61 x 16 = 0, , = 3, x 21 = λ 52x 25 + λ 62 x 26 = 0, , = 2, Jednotka A by měla snížit svůj první vstup - počet zaměstnanců z původních 4 na 3,5 (jednomu pracovníkovi snížit úvazek zhruba na polovinu). Druhý vstup - režijní náklady by měla snížit z původních 3 tisíc Kč na zhruba 2,6 tisíc Kč. Potom bude jednotka A efektivní. Stejně jako pro jednotku A je nutné sestavit modely pro všechny ostatní jednotky a vyřešit stejným způsobem. V tabulce 1.2 jsou uvedeny výsledky pro všechny jednotky. Neuvádíme hodnotu účelové funkce duálního modelu, neboť je shodná s hodnotou účelové funkce primárního modelu.
15 1.5. HODNOCENÍ JEDNOTEK S VÍCE VSTUPY A VÝSTUPY 13 Tabulka 1.2: Výsledky primárních a duálních modelů Primární model Duální model e k v 1i v 2i u 1j u 2j λ 1k λ 2k λ 3k λ 4k λ 5k λ 6k λ 7k A 0,870 0,087 0, , ,380 0,544 0 B 0,966 0,069 0, , ,060 1,328 0 C 1 0,068 0, , D 0,941 0,177 0,147 0, ,118 0,706 0 E 1 0,083 0, , F 1 0,15 0,125 0, G 0,857 0,107 0,089 0, ,429 0, CCR výstupově orientovaný model Vychází ze stejných předpokladů, jako vstupově orientovaný model. Zde je koeficient technické efektivity určen jako poměr vážené sumy vstupů a vážené sumy výstupů. Jsou hledány takové váhy, aby hodnota tohoto koeficientu byla větší nebo rovna 1. Neznámými jsou v tomto modelu váhy přidělené vstupu i a váhy přidělené výstupu j jednotkou k. I v tomto modelu jsou váhy určovány individuálně, proto je nutno vyřešit p modelů (hodnotíme soubor p jednotek). Matematický model pro jednotku H (jedna z p jednotek) se skládá: z účelové funkce e H = v ih x ih min, u jh y jh (1.13) která minimalizuje poměr vážených vstupů a vážených výstupů, z omezujících podmínek v ih x ik 1, k = 1, 2,..., p, u jh y jk (1.14) které zajištují, aby poměr vstupů a výstupů s váhami pro k-tou jednotku byl u ostatních jednotek v hodnoceném souboru větší nebo roven jedné z podmínek nezápornosti u jh 0, j = 1, 2,..., n, v ih 0, i = 1, 2,..., m, které požadují nezápornost hledaných neznámých (vah).
16 14 KAPITOLA 1. METODA ANALÝZY DATOVÝCH OBALŮ (DEA) Model lze upravit na lineární tak, že váženou sumu výstupů položíme rovnou jedné a minimalizuje váženou sumu vstupů: e H = v ih x ik v ih x ih min u jh y jh = 1 u jh y jk 0, k = 1, 2,..., p (1.15) u jh 0, j = 1, 2,..., n v ih 0, i = 1, 2,..., m Poznámka. První index představuje vždy číslo vstupu a výstupu, druhý index číslo jednotky, pro kterou je model sestaven. Duální model má tvar y jh z H z H max p λ kh y jk 0, j = 1, 2,..., n, (1.16) k=1 p λ kh x ik x ih, i = 1, 2,..., m, k=1 Proměnná z H může nabývat libovolných hodnot. λ kh 0, k = 1, 2,..., p. Poznámka. První index je číslo jednotky, ke které se vztahuje příslušná λ - koeficient kombinace, druhý index je číslo jednotky, pro kterou je model sestaven. Velikost vstupů a výstupů virtuální jednotky lze vypočítat jako kombinaci vstupů a výstupů peer jednotek. Řešený příklad 1.4. Vyhodnoťte efektivitu jednotek z příkladu 1.3, použijte výstupově orientovaný CCR model. Řešení. Primární model pro první pobočku - pobočku A: Výsledky: e 1 = 4v v 21 min u u 21 = 1 4v v 21 u 11 5u v v 21 2u 11 7u v 11 + v 21 3u 11 4u v v 21 4u 11 3u v v 21 4u 11 6u v v 21 5u 11 5u v v 21 6u 11 2u 21 0 u j1 0, j = 1, 2, v i1 0, i = 1, 2.
17 1.5. HODNOCENÍ JEDNOTEK S VÍCE VSTUPY A VÝSTUPY 15 Proměnná Hodnota e 1 1,15 v 11 0,1 v 21 0,25 u 11 0 u 21 0,2 Z výsledků je patrné, že jednotka A (první) není efektivní, neboť hodnota e 1 je větší než 1. Proto přistoupíme k sestavení duálně sdruženého modelu, jehož vyřešením získáme vhodnou kombinaci vzorových jednotek pro dosažení efektivity neefektivní jednotky A. Duální model pro první jednotku - jednotku A: z 1 max 4λ λ λ λ λ λ λ λ λ 21 + λ λ λ λ λ 71 3 λ 11 λ 11 2λ 21 3λ 31 4λ 41 4λ 51 5λ 61 6λ λ 11 5λ 11 7λ 21 4λ 31 3λ 41 6λ 51 5λ 61 2λ 71 0 Proměnná Hodnota z 1 1,15 z 1 1,15 λ 11 0 λ 21 0 λ 31 0 λ 41 0 λ 51 0,4375 λ 61 0,625 λ 71 0 λ k1 0, k = 1, 2,..., 7. Z výsledků vyplývá, že vzorovými (peer) jednotkami pro jednotku A jsou jednotky pátá (E) a šestá (F), neboť hodnoty proměnných λ 51 a λ 61 jsou nenulové. Proměnná λ 51 se vztahuje k páté jednotce (E) - první index je 5, proměnná λ 61 se vztahuje k páté jednotce (F) - první index je 6. Známe tedy koeficienty kombinace. Nyní musíme výstupy efektivních jednotek E a F pronásobit koeficienty a pro každý vstup zvlášť tyto výsledky sečíst, abychom získali optimální velikost výstupů pro jednotku A. Konkrétně pro první vstup: Pro druhý vstup: y 11 = λ 51y 15 + λ 61 y 16 = 0, ,625 5 = 4,875 y 21 = λ 52y 25 + λ 62 y 26 = 0, ,625 2 = 5,75 Jednotka A by měla zvýšit svůj první výstup - počet obsloužených zákazníků z původního 1 na zhruba 5. Druhý výstup - tržby by měla zvýšit z původních 50 tisíc Kč na zhruba 57,5 tisíce Kč. Potom bude jednotka A efektivní. Stejně jako pro jednotku A je nutné sestavit modely pro všechny ostatní jednotky a vyřešit stejným způsobem. V tabulce 1.3 jsou uvedeny výsledky pro všechny jednotky. Neuvádíme hodnotu účelové funkce duálního modelu, neboť je shodná s hodnotou účelové funkce primárního modelu.
18 16 KAPITOLA 1. METODA ANALÝZY DATOVÝCH OBALŮ (DEA) Tabulka 1.3: Výsledky primárních a duálních modelů Primární model Duální model e k v 1i v 2i u 1j u 2j λ 1k λ 2k λ 3k λ 4k λ 5k λ 6k λ 7k A 1,15 0,1 0,25 0 0, ,438 0,625 0 B 1,036 0,072 0, , ,063 1,375 0 C 1 0,068 0, , D 1,063 0,188 0,156 0, ,125 0,75 0 E 1 0,083 0, , F 1 0,15 0,125 0, G 1,167 0,125 0,104 0, , BCC modely BCC model, navržený Bankerem, Charnesem a Cooperem, je vlastně modifikace předchozího CCR modelu. Tento model uvažuje variabilní výnosy z rozsahu. Jak již bylo uvedeno výše, efektivních jednotek je při použití tohoto typu modelu více. V modelech BCC je požadováno, aby virtuální jednotka pro jednotku H byla konvexní kombinací svých vzorových jednotek. Toto se projeví v duálním modelu přidanou podmínkou, aby součet λ kh pro k = 1, 2,..., p byl roven 1. V primárním modelu se tato podmínka projeví přidáním jedné proměnné, která představuje velikost odchylky od konstantního výnosu z rozsahu. Pro ilustraci zde budou uvedeny primární a duální vstupově orientované modely pro jednotku H. Primární model: e H = u jh y jh + q H max Duální model: v ih x ik + x ih z H v ih x ih = 1 u jh y jk + q H 0, k = 1, 2,..., p (1.17) u jh 0, j = 1, 2,..., n v ih 0, i = 1, 2,..., m q H R z H min p λ kh x ik 0, i = 1, 2,..., m, k=1 p λ kh y jk y jh, j = 1, 2,..., n, (1.18) k=1 p λ kh = 1 k=1 λ kh 0, k = 1, 2,..., p, z H R
19 1.5. HODNOCENÍ JEDNOTEK S VÍCE VSTUPY A VÝSTUPY 17 Řešený příklad 1.5. Předpokládejte, že výnosy z rozsahu u příkladu 1.3 jsou variabilní. Vyhodnoťte efektivitu jednotky A. Řešení. Nyní si pro první jednotku - jednotku A sestavíme primární model: e 1 = u u 21 + q 1 max 4v v 21 = 1 4v 11 3v 21 + u u 21 + q 1 0 7v 11 3v u u 21 + q 1 0 8v 11 v u u 21 + q 1 0 4v 11 2v u u 21 + q 1 0 2v 11 4v u u 21 + q 1 0 5v 11 2v u u 21 + q 1 0 6v 11 4v u u 21 + q 1 0 Výsledky primárního modelu pro jednotku A: u j1 0, j = 1, 2 v i1 0, i = 1, 2 q 1 R Proměnná Hodnota e 1 0,9189 v 11 0,1081 v 21 0,1892 u 11 0 u 21 0,0541 q 1 0,6486 Jednotka A je neefektivní (e 1 = 0,9189), proto je nutné sestavit duálně sdružený model. Duální model pro jednotku A: z 1 min 4z 1 4λ 11 7λ 21 8λ 31 4λ 41 2λ 51 5λ 61 6λ z 1 3λ 11 3λ 21 λ 31 2λ 41 4λ 51 2λ 61 4λ 71 0 λ λ λ λ λ λ λ λ λ λ λ λ λ λ 71 5 λ 11 + λ 21 + λ 31 + λ 41 + λ 51 + λ 61 + λ 71 = 1 Výsledky duálního modelu pro jednotku A: Proměnná Hodnota z 1 0,9189 z 1 0,9189 λ 11 0 λ 21 0 λ 31 0 λ 41 0,1892 λ 51 0,3784 λ 61 0,4324 λ 71 0 λ k1 0, k = 1, 2,..., 7
20 18 KAPITOLA 1. METODA ANALÝZY DATOVÝCH OBALŮ (DEA) Vzorové jednotky pro jednotku A jsou čtvrtá (D), pátá (E) a šestá (F) jednotka, protože λ 41 = 0,1892, λ 51 = 0,3784, λ 61 = 0,4324, ostatní jsou nulové. Aby jednotka A byla efektivní, měla by své vstupy upravit. Konkrétně pro první vstup: x 11 = λ 41x 14 +λ 51 x 15 +λ 61 x 16 = 0, , , = 3, Pro druhý vstup: x 21 = λ 42x 24 +λ 52 x 25 +λ 62 x 26 = 0, , , = 2, Firma by měla zaměstnávat pouze tři zaměstnance na plný úvazek a jednoho k tomu zhruba na 70%, režijní náklady by měla snížit zhruba na 2757 Kč. Ostatní pobočky se jeví při použití BCC modelu jako efektivní, proto podrobné výsledky nebudeme uvádět. Počet efektivních jednotek při použití BCC modelu je tedy skutečně vyšší než při užití CCR modelu. Obdobně bychom mohli upravit i CCR výstupově orientovaný model a vytvořit z něj BCC výstupově orientovaný model. Podrobnější výklad tohoto typu modelů přesahuje rámec těchto skript. V případě potřeby toto naleznete v [7].
21 1.5. HODNOCENÍ JEDNOTEK S VÍCE VSTUPY A VÝSTUPY 19 Cvičení Cvičení 1.1. Autoopravny provádějí přípravu aut na měření emisí. Určete graficky, které servisy jsou efektivní, když předpokládáte a) konstantní výnosy z rozsahu b) variabilní výnosy z rozsahu. Potřebné údaje naleznete v následující tabulce: A B C D E F G Počet techniků Počet aut , Cvičení 1.2. Pro jednotku C ze cvičení 1.1 za předpokladu konstantních výnosů z rozsahu určete a) její míru efektivity b) potřebné snížení vstupu při zachování výstupu c) potřebné zvýšení výstupu při zachování velikosti vstupu. Cvičení 1.3. Pro jednotku C ze cvičení 1.1 za předpokladu variabilních výnosů z rozsahu určete a) její míru efektivity b) potřebné snížení vstupu při zachování výstupu c) potřebné zvýšení výstupu při zachování velikosti vstupu. Cvičení 1.4. Předpokládejme, že autoopravny uvažují dva vstupy a jeden výstup. Určete graficky, které servisy jsou efektivní. Potřebné údaje naleznete v následující tabulce: A B C D E F G Počet techniků Počet PC Počet aut Určete, které jednotky jsou a které nejsou efektivní. Pro všechny neefektivní jednotky určete jejich peer jednotky. Cvičení 1.5. Autoopravny uvažují jeden vstup a dva výstupy, jejich hodnoty jsou uvedeny v následující tabulce. Graficky znázorněte, které jednotky jsou efektivní. A B C D E F Počet techniků Počet aut Tržby (v 10 tisících Kč) ,7 Určete, které jednotky jsou a které nejsou efektivní. Určete peer jednotky pro neefektivní jednotky. Dále spočítejte, jak by některá neefektivní jednotka musela navýšit své výstupy, aby byla efektivní. Cvičení 1.6. Banka chce zhodnotit výkon svých poboček v menších městech. Jako podstatné vstupy si vybrala mzdové a provozní náklady v tisících Kč na pobočce za měsíc. Jako výstupy pro hodnocení si vybrala počet běžných účtů osobních, počet běžných účtů firemních a výnosy v tisících Kč za měsíc. Hodnoty vstupů a výstupů jsou uvedeny v tabulce.
22 20 KAPITOLA 1. METODA ANALÝZY DATOVÝCH OBALŮ (DEA) Mzdové náklady Provoz. náklady BÚ osobní BÚ firemní Výnosy A B C D E a) Sestavte primární vstupově orientované CCR modely pro všechny jednotky. b) Vyřešte v Solveru. c) Pro neefektivní jednotky sestavte duálně sdružené modely a tyto vyřešte. d) Interpretujte výsledky. e) Totéž proveďte u výstupově orientovaného modelu. f) Vyřešte v programu Frontier Analyst. g) Totéž proveďte pro výstupově orientované modely. Otázky Vysvětlete podstatu metody DEA. Vysvětlete pojmy množina produkčních možností, efektivní hranice, efektivní a neefektivní jednotka. Jak je v modelech DEA vyjádřena efektivita? Jaký je rozdíl mezi konstantními a variabilními výnosy z rozsahu? Jaký je rozdíl mezi vstupově a výstupově orientovaným modelem? Co je to virtuální jednotka? Co jsou peer jednotky?
23 Literatura [1] Brožová, H., Houška, M., Šubrt, T. (2003): Modely pro vícekriteriální rozhodování. ČZU, Praha. [2] Fiala, P., Jablonský, J., Maňas, M. (1997): Vícekriteriální rozhodování. VŠE, Praha. [3] Fotr J., Dědina, J. (1997): Manažerské rozhodování. Ekopress, Praha. [4] Gros, I. (2003): Kvantitativní metody v manažerském rozhodování. Grada Publishing, Praha. [5] Holman, R. (2003): Ekonomie. C. H. Beck, Praha. [6] Jablonský, J. (2002): Operační výzkum. Professional Publishing, Praha. [7] Jablonský, J., Dlouhý, M. (2004): Modely hodnocení efektivnosti produkčních jednotek. Professional Publishing, Praha. [8] Saaty, T., L. (2005): Theory and Applications of the Analytic Network Process. RWS Publications, Pittsburg. [9] Soukupová, J. (2002): Mikroekonomie. Management Press, Praha. [10] Vaněčková, E. (1996): Ekonomicko-matematické metody. ZF JU, skripta, České Budějovice. [11] Vaněčková, E. (1998): Rozhodovací modely. ZF JU, skripta, České Budějovice. 21
Metoda analýzy datových obalů (DEA)
 Kapitola 1 Metoda analýzy datových obalů (DEA) Modely datových obalů slouží pro hodnocení technické efektivity produkčních jednotek na základě velikosti vstupů a výstupů. Hodnocenými jednotkami mohou být
Kapitola 1 Metoda analýzy datových obalů (DEA) Modely datových obalů slouží pro hodnocení technické efektivity produkčních jednotek na základě velikosti vstupů a výstupů. Hodnocenými jednotkami mohou být
Západočeská univerzita v Plzni. Fakulta aplikovaných věd. Ivana Kozlová. Modely analýzy obalu dat
 Západočeská univerzita v Plzni Fakulta aplikovaných věd SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU MATEMATICKÉ MODELOVÁNÍ Ivana Kozlová Modely analýzy obalu dat Plzeň 2010 Obsah 1 Efektivnost a její hodnocení 2 2 Základní
Západočeská univerzita v Plzni Fakulta aplikovaných věd SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU MATEMATICKÉ MODELOVÁNÍ Ivana Kozlová Modely analýzy obalu dat Plzeň 2010 Obsah 1 Efektivnost a její hodnocení 2 2 Základní
Analýza obalu dat úvod
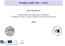 Analýza obalu dat úvod Jana Klicnarová Katedra aplikované matematiky a informatiky Jihočeská Univerzita v Českých Budějovicích, Ekonomická fakulta 2010 Analýza obalu dat (DEA) Analýza obalu dat (Data envelopement
Analýza obalu dat úvod Jana Klicnarová Katedra aplikované matematiky a informatiky Jihočeská Univerzita v Českých Budějovicích, Ekonomická fakulta 2010 Analýza obalu dat (DEA) Analýza obalu dat (Data envelopement
Hodnocení efektivnosti podniků pomocí analýzy obalu dat
 Hodnocení efektivnosti podniků pomocí analýzy obalu dat Markéta Matulová workshop Finanční matematika v praxi III, září 2013 Úvod Modely datových obalů (DEA) slouží k hodnocení technické efektivity produkčních
Hodnocení efektivnosti podniků pomocí analýzy obalu dat Markéta Matulová workshop Finanční matematika v praxi III, září 2013 Úvod Modely datových obalů (DEA) slouží k hodnocení technické efektivity produkčních
Modely hodnocení efektivnosti a jejich aplikace
 JIHOČESKÁ UNIVERZITA V ČESKÝCH BUDĚJOVICÍCH Ekonomická fakulta Katedra aplikované matematiky a informatiky Studijní program: N6208 Ekonomika a management Studijní obor: Účetnictví a finanční řízení podniku
JIHOČESKÁ UNIVERZITA V ČESKÝCH BUDĚJOVICÍCH Ekonomická fakulta Katedra aplikované matematiky a informatiky Studijní program: N6208 Ekonomika a management Studijní obor: Účetnictví a finanční řízení podniku
Operační výzkum. Vícekriteriální hodnocení variant. Grafická metoda. Metoda váženého součtu.
 Operační výzkum Vícekriteriální hodnocení variant. Grafická metoda. Metoda váženého součtu. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu
Operační výzkum Vícekriteriální hodnocení variant. Grafická metoda. Metoda váženého součtu. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu
4EK213 LINEÁRNÍ MODELY
 4EK213 LINEÁRNÍ MODELY Úterý 11:00 12:30 hod. učebna SB 324 Mgr. Sekničková Jana, Ph.D. 2. PŘEDNÁŠKA MATEMATICKÝ MODEL ÚLOHY LP Mgr. Sekničková Jana, Ph.D. 2 OSNOVA PŘEDNÁŠKY Obecná formulace MM Množina
4EK213 LINEÁRNÍ MODELY Úterý 11:00 12:30 hod. učebna SB 324 Mgr. Sekničková Jana, Ph.D. 2. PŘEDNÁŠKA MATEMATICKÝ MODEL ÚLOHY LP Mgr. Sekničková Jana, Ph.D. 2 OSNOVA PŘEDNÁŠKY Obecná formulace MM Množina
Data Envelopment Analysis (Analýza obalu dat)
 Data Envelopment Analysis (Analýza obalu dat) Martin Branda Univerzita Karlova v Praze Matematicko-fyzikální fakulta Katedra pravděpodobnosti a matematické statistiky Optimalizace s aplikací ve financích
Data Envelopment Analysis (Analýza obalu dat) Martin Branda Univerzita Karlova v Praze Matematicko-fyzikální fakulta Katedra pravděpodobnosti a matematické statistiky Optimalizace s aplikací ve financích
Operační výzkum. Vícekriteriální programování. Lexikografická metoda. Metoda agregace účelových funkcí. Cílové programování.
 Operační výzkum Lexikografická metoda. Metoda agregace účelových funkcí. Cílové programování. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu
Operační výzkum Lexikografická metoda. Metoda agregace účelových funkcí. Cílové programování. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu
Vícekriteriální programování příklad
 Vícekriteriální programování příklad Pražírny kávy vyrábějí dva druhy kávy (Super a Standard) ze dvou druhů kávových bobů KB1 a KB2, které mají smluvně zajištěny v množství 4 t a 6 t. Složení kávy (v procentech)
Vícekriteriální programování příklad Pražírny kávy vyrábějí dva druhy kávy (Super a Standard) ze dvou druhů kávových bobů KB1 a KB2, které mají smluvně zajištěny v množství 4 t a 6 t. Složení kávy (v procentech)
4 Kriteriální matice a hodnocení variant
 4 Kriteriální matice a hodnocení variant V teorii vícekriteriálního rozhodování pracujeme s kritérii, kterých je obecně k, a s variantami, kterých je obecně p. Hodnotu, které dosahuje varianta i pro j-té
4 Kriteriální matice a hodnocení variant V teorii vícekriteriálního rozhodování pracujeme s kritérii, kterých je obecně k, a s variantami, kterých je obecně p. Hodnotu, které dosahuje varianta i pro j-té
Modely analýzy obalu dat a jejich aplikace při hodnocení efektivnosti bankovních poboček
 Modely analýzy obalu dat a jejich aplikace při hodnocení efektivnosti bankovních poboček Josef Jablonský VŠE Praha, fakulta informatiky a statistiky nám. W. Churchilla 4, 13067 Praha 3 jablon@vse.cz, http://nb.vse.cz/~jablon
Modely analýzy obalu dat a jejich aplikace při hodnocení efektivnosti bankovních poboček Josef Jablonský VŠE Praha, fakulta informatiky a statistiky nám. W. Churchilla 4, 13067 Praha 3 jablon@vse.cz, http://nb.vse.cz/~jablon
7 Kardinální informace o kritériích (část 1)
 7 Kardinální informace o kritériích (část 1) Předpokládejme stejná značení jako v předchozích cvičeních. Kardinální informací o kritériích se rozumí ohodnocení jejich důležitosti k pomocí váhového vektoru
7 Kardinální informace o kritériích (část 1) Předpokládejme stejná značení jako v předchozích cvičeních. Kardinální informací o kritériích se rozumí ohodnocení jejich důležitosti k pomocí váhového vektoru
ANALYTICKÁ GEOMETRIE V ROVINĚ
 ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
e-mail: RadkaZahradnikova@seznam.cz 1. července 2010
 Optimální výrobní program Radka Zahradníková e-mail: RadkaZahradnikova@seznam.cz 1. července 2010 Obsah 1 Lineární programování 2 Simplexová metoda 3 Grafická metoda 4 Optimální výrobní program Řešení
Optimální výrobní program Radka Zahradníková e-mail: RadkaZahradnikova@seznam.cz 1. července 2010 Obsah 1 Lineární programování 2 Simplexová metoda 3 Grafická metoda 4 Optimální výrobní program Řešení
Postupy při hodnocení variant a výběru nejvhodnějšího řešení. Šimon Kovář Katedra textilních a jednoúčelových strojů
 Postupy při hodnocení variant a výběru nejvhodnějšího řešení Šimon Kovář Katedra textilních a jednoúčelových strojů Znáte nějaké postupy hodnocení variant řešení? Vícekriteriální rozhodování Při výběru
Postupy při hodnocení variant a výběru nejvhodnějšího řešení Šimon Kovář Katedra textilních a jednoúčelových strojů Znáte nějaké postupy hodnocení variant řešení? Vícekriteriální rozhodování Při výběru
4EK201 Matematické modelování. 2. Lineární programování
 4EK201 Matematické modelování 2. Lineární programování 2.1 Podstata operačního výzkumu Operační výzkum (výzkum operací) Operational research, operations research, management science Soubor disciplín zaměřených
4EK201 Matematické modelování 2. Lineární programování 2.1 Podstata operačního výzkumu Operační výzkum (výzkum operací) Operational research, operations research, management science Soubor disciplín zaměřených
Ekonomická formulace. Matematický model
 Ekonomická formulace Firma balící bonboniéry má k dispozici 60 čokoládových, 60 oříškových a 85 karamelových bonbónů. Může vyrábět dva druhy bonboniér. Do první bonboniéry se dávají dva čokoládové, šest
Ekonomická formulace Firma balící bonboniéry má k dispozici 60 čokoládových, 60 oříškových a 85 karamelových bonbónů. Může vyrábět dva druhy bonboniér. Do první bonboniéry se dávají dva čokoládové, šest
6 Ordinální informace o kritériích
 6 Ordinální informace o kritériích Ordinální informací o kritériích se rozumí jejich uspořádání podle důležitosti. Předpokládejme dále standardní značení jako v předchozích cvičeních. Existují tři základní
6 Ordinální informace o kritériích Ordinální informací o kritériích se rozumí jejich uspořádání podle důležitosti. Předpokládejme dále standardní značení jako v předchozích cvičeních. Existují tři základní
fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu http://akademie.ldf.mendelu.cz/cz (reg. č. CZ.1.07/2.2.00/28.
 Základy lineárního programování Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem
Základy lineárního programování Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem
Diskrétní náhodná veličina
 Lekce Diskrétní náhodná veličina Výsledek náhodného pokusu může být vyjádřen slovně to vede k zavedení pojmu náhodného jevu Výsledek náhodného pokusu můžeme někdy vyjádřit i číselně, což vede k pojmu náhodné
Lekce Diskrétní náhodná veličina Výsledek náhodného pokusu může být vyjádřen slovně to vede k zavedení pojmu náhodného jevu Výsledek náhodného pokusu můžeme někdy vyjádřit i číselně, což vede k pojmu náhodné
LDF MENDELU. Simona Fišnarová (MENDELU) Základy lineárního programování VMAT, IMT 1 / 25
 Základy lineárního programování Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem
Základy lineárního programování Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem
Vícekriteriální hodnocení variant úvod
 Vícekriteriální hodnocení variant úvod Jana Klicnarová Katedra aplikované matematiky a informatiky Jihočeská Univerzita v Českých Budějovicích, Ekonomická fakulta 2010 Vícekriteriální hodnocení variant
Vícekriteriální hodnocení variant úvod Jana Klicnarová Katedra aplikované matematiky a informatiky Jihočeská Univerzita v Českých Budějovicích, Ekonomická fakulta 2010 Vícekriteriální hodnocení variant
Operační výzkum. Přiřazovací problém.
 Operační výzkum Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo projektu: CZ..7/2.2./28.326
Operační výzkum Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu Registrační číslo projektu: CZ..7/2.2./28.326
12. Lineární programování
 . Lineární programování. Lineární programování Úloha lineárního programování (lineární optimalizace) je jedním ze základních problémů teorie optimalizace. Našim cílem je nalézt maximum (resp. minimum)
. Lineární programování. Lineární programování Úloha lineárního programování (lineární optimalizace) je jedním ze základních problémů teorie optimalizace. Našim cílem je nalézt maximum (resp. minimum)
Matematika I, část I. Rovnici (1) nazýváme vektorovou rovnicí roviny ABC. Rovina ABC prochází bodem A a říkáme, že má zaměření u, v. X=A+r.u+s.
 3.4. Výklad Předpokládejme, že v prostoru E 3 jsou dány body A, B, C neležící na jedné přímce. Těmito body prochází jediná rovina, kterou označíme ABC. Určíme vektory u = B - A, v = C - A, které jsou zřejmě
3.4. Výklad Předpokládejme, že v prostoru E 3 jsou dány body A, B, C neležící na jedné přímce. Těmito body prochází jediná rovina, kterou označíme ABC. Určíme vektory u = B - A, v = C - A, které jsou zřejmě
VÍCEKRITERIÁLNÍ ROZHODOVANÍ
 VÍCEKRITERIÁLNÍ ROZHODOVANÍ 1 Obsah Typy modelů vícekriteriálního rozhodování Základní pojmy Typy informací Cíl modelů Užitek, funkce užitku Grafické zobrazení Metody vícekriteriální analýzy variant 2
VÍCEKRITERIÁLNÍ ROZHODOVANÍ 1 Obsah Typy modelů vícekriteriálního rozhodování Základní pojmy Typy informací Cíl modelů Užitek, funkce užitku Grafické zobrazení Metody vícekriteriální analýzy variant 2
GEODETICKÉ VÝPOČTY I.
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. TABELACE FUNKCE LINEÁRNÍ INTERPOLACE TABELACE FUNKCE Tabelace funkce se v minulosti často využívala z důvodu usnadnění
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. TABELACE FUNKCE LINEÁRNÍ INTERPOLACE TABELACE FUNKCE Tabelace funkce se v minulosti často využívala z důvodu usnadnění
5 Informace o aspiračních úrovních kritérií
 5 Informace o aspiračních úrovních kritérií Aspirační úroveň kritérií je minimální (maximální) hodnota, které musí varianta pro dané maximalizační (minimalizační) kritérium dosáhnout, aby byla akceptovatelná.
5 Informace o aspiračních úrovních kritérií Aspirační úroveň kritérií je minimální (maximální) hodnota, které musí varianta pro dané maximalizační (minimalizační) kritérium dosáhnout, aby byla akceptovatelná.
Funkce jedné reálné proměnné. lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou
 Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
4EK212 Kvantitativní management. 2. Lineární programování
 4EK212 Kvantitativní management 2. Lineární programování 1.7 Přídatné proměnné Přídatné proměnné jsou nezáporné Mají svoji ekonomickou interpretaci, která je odvozena od ekonomické interpretace omezení
4EK212 Kvantitativní management 2. Lineární programování 1.7 Přídatné proměnné Přídatné proměnné jsou nezáporné Mají svoji ekonomickou interpretaci, která je odvozena od ekonomické interpretace omezení
14. přednáška. Přímka
 14 přednáška Přímka Začneme vyjádřením přímky v prostoru Přímku v prostoru můžeme vyjádřit jen parametricky protože obecná rovnice přímky v prostoru neexistuje Přímka v prostoru je určena bodem A= [ a1
14 přednáška Přímka Začneme vyjádřením přímky v prostoru Přímku v prostoru můžeme vyjádřit jen parametricky protože obecná rovnice přímky v prostoru neexistuje Přímka v prostoru je určena bodem A= [ a1
KOMPLEXNÍ ČÍSLA INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ
 KOMPLEXNÍ ČÍSLA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu INVESTICE
KOMPLEXNÍ ČÍSLA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu INVESTICE
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
Kvízové otázky Obecná ekonomie I. Teorie firmy
 1. Firmy působí: a) na trhu výrobních faktorů b) na trhu statků a služeb c) na žádném z těchto trhů d) na obou těchto trzích Kvízové otázky Obecná ekonomie I. Teorie firmy 2. Firma na trhu statků a služeb
1. Firmy působí: a) na trhu výrobních faktorů b) na trhu statků a služeb c) na žádném z těchto trhů d) na obou těchto trzích Kvízové otázky Obecná ekonomie I. Teorie firmy 2. Firma na trhu statků a služeb
Obecná úloha lineárního programování. Úloha LP a konvexní množiny Grafická metoda. Jiří Neubauer. Katedra ekonometrie FEM UO Brno
 Přednáška č. 3 Katedra ekonometrie FEM UO Brno Optimalizace portfolia Investor se s pomocí makléře rozhoduje mezi následujícími investicemi: akcie A, akcie B, státní pokladniční poukázky, dluhopis A, dluhopis
Přednáška č. 3 Katedra ekonometrie FEM UO Brno Optimalizace portfolia Investor se s pomocí makléře rozhoduje mezi následujícími investicemi: akcie A, akcie B, státní pokladniční poukázky, dluhopis A, dluhopis
1 Diference a diferenční rovnice
 1 Diference a diferenční rovnice Nechť je dána ekvidistantní síť uzlů x 0, x 1,..., x n tj. h R, h > 0 takové, že x i = x 0 + ih, i = 0, 1,..., n. Číslo h se nazývá krok. Někdy můžeme uvažovat i nekonečnou
1 Diference a diferenční rovnice Nechť je dána ekvidistantní síť uzlů x 0, x 1,..., x n tj. h R, h > 0 takové, že x i = x 0 + ih, i = 0, 1,..., n. Číslo h se nazývá krok. Někdy můžeme uvažovat i nekonečnou
Slovní úlohy I
 ..1 Slovní úlohy I Předpoklady: 0008 Pedagogická poznámka: Slovní úlohy jsou problém, hlavně pro to, že neexistuje jednoznačný algoritmus na jejich řešení. Této první hodiny se však problémy netýkají,
..1 Slovní úlohy I Předpoklady: 0008 Pedagogická poznámka: Slovní úlohy jsou problém, hlavně pro to, že neexistuje jednoznačný algoritmus na jejich řešení. Této první hodiny se však problémy netýkají,
4EK201 Matematické modelování. 10. Teorie rozhodování
 4EK201 Matematické modelování 10. Teorie rozhodování 10. Rozhodování Rozhodování = proces výběru nějaké možnosti (varianty) podle stanoveného kritéria za účelem dosažení stanovených cílů Rozhodovatel =
4EK201 Matematické modelování 10. Teorie rozhodování 10. Rozhodování Rozhodování = proces výběru nějaké možnosti (varianty) podle stanoveného kritéria za účelem dosažení stanovených cílů Rozhodovatel =
Parametrické programování
 Parametrické programování Příklad 1 Parametrické pravé strany Firma vyrábí tři výrobky. K jejich výrobě potřebuje jednak surovinu a jednak stroje, na kterých dochází ke zpracování. Na první výrobek jsou
Parametrické programování Příklad 1 Parametrické pravé strany Firma vyrábí tři výrobky. K jejich výrobě potřebuje jednak surovinu a jednak stroje, na kterých dochází ke zpracování. Na první výrobek jsou
Statistika pro geografy
 Statistika pro geografy 2. Popisná statistika Mgr. David Fiedor 23. února 2015 Osnova 1 2 3 Pojmy - Bodové rozdělení četností Absolutní četnost Absolutní četností hodnoty x j znaku x rozumíme počet statistických
Statistika pro geografy 2. Popisná statistika Mgr. David Fiedor 23. února 2015 Osnova 1 2 3 Pojmy - Bodové rozdělení četností Absolutní četnost Absolutní četností hodnoty x j znaku x rozumíme počet statistických
Firma. Spotřebitel. Téma cvičení. Mikroekonomie. Příjmy, zisk Produkční analýza. Opakování. Příklad. Příklad. Příklad
 Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Téma cvičení Firma Příjmy, zisk Produkční analýza Opakování Spotřebitel Máte danou funkci celkového užitku TU ve tvaru: 300X - 10X 2 (X značí
Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Téma cvičení Firma Příjmy, zisk Produkční analýza Opakování Spotřebitel Máte danou funkci celkového užitku TU ve tvaru: 300X - 10X 2 (X značí
Firma. Příklad zadání. Příklad řešení. Téma cvičení. náklady firmy. Příklady k opakování. Mikroekonomie. Příjmy, zisk Produkční analýza
 Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Téma cvičení Firma Příjmy, zisk Produkční analýza zadání y k opakování náklady firmy Q FC VC TC AC AVC AFC MC 0 X X X X X X X 1 5 5 X X X
Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Téma cvičení Firma Příjmy, zisk Produkční analýza zadání y k opakování náklady firmy Q FC VC TC AC AVC AFC MC 0 X X X X X X X 1 5 5 X X X
1.1 Příklad z ekonomického prostředí 1
 1.1 Příklad z ekonomického prostředí 1 Smysl solidního zvládnutí matematiky v bakalářských oborech na Fakultě podnikatelské VUT v Brně je především v aplikační síle matematiky v odborných předmětech a
1.1 Příklad z ekonomického prostředí 1 Smysl solidního zvládnutí matematiky v bakalářských oborech na Fakultě podnikatelské VUT v Brně je především v aplikační síle matematiky v odborných předmětech a
Příklady ke cvičením. Modelování produkčních a logistických systémů
 Modelování produkčních a logistických systémů Katedra logistiky, kvality a automobilové techniky Garant, přednášející, cvičící: Jan Fábry 10.12.2018 Příklady ke cvičením Opakování lineárního programování
Modelování produkčních a logistických systémů Katedra logistiky, kvality a automobilové techniky Garant, přednášející, cvičící: Jan Fábry 10.12.2018 Příklady ke cvičením Opakování lineárního programování
Náhodný vektor a jeho charakteristiky
 Náhodný vektor a jeho číselné charakteristiky 1 Náhodný vektor a jeho charakteristiky V následující kapitole budeme věnovat pozornost pouze dvourozměřnému náhodnému vektoru, i když uvedené pojmy a jejich
Náhodný vektor a jeho číselné charakteristiky 1 Náhodný vektor a jeho charakteristiky V následující kapitole budeme věnovat pozornost pouze dvourozměřnému náhodnému vektoru, i když uvedené pojmy a jejich
Řešení domácího úkolu
 Úkol 1 Řešení domácího úkolu Podrobný popis řešení - analogie na seminář IV. a) Napište produkční funkce Na 1 botu potřebujeme 4 jednotky práce Na 1 tkaničku potřebujeme 2 jednotky práce b) Odvoďte v algebraické
Úkol 1 Řešení domácího úkolu Podrobný popis řešení - analogie na seminář IV. a) Napište produkční funkce Na 1 botu potřebujeme 4 jednotky práce Na 1 tkaničku potřebujeme 2 jednotky práce b) Odvoďte v algebraické
Mikroekonomie. Minulá přednáška - podstatné. Náklady firmy v krátkém a dlouhém období. Důležité vzorce. Náklady v krátkém období - graficky
 Minulá přednáška - podstatné Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Typologie nákladů firmy Náklady v krátkém období Náklady v dlouhém období Důležité vzorce TC = FC + VC AC =
Minulá přednáška - podstatné Mikroekonomie Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Typologie nákladů firmy Náklady v krátkém období Náklady v dlouhém období Důležité vzorce TC = FC + VC AC =
Popisná statistika kvantitativní veličiny
 StatSoft Popisná statistika kvantitativní veličiny Protože nám surová data obvykle žádnou smysluplnou informaci neposkytnou, je žádoucí vyjádřit tyto ve zhuštěnější formě. V předchozím dílu jsme začali
StatSoft Popisná statistika kvantitativní veličiny Protože nám surová data obvykle žádnou smysluplnou informaci neposkytnou, je žádoucí vyjádřit tyto ve zhuštěnější formě. V předchozím dílu jsme začali
Operační výzkum. Teorie her cv. Hra v normálním tvaru. Optimální strategie. Maticové hry.
 Operační výzkum Teorie her cv. Hra v normálním tvaru. Optimální strategie. Maticové hry. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty
Operační výzkum Teorie her cv. Hra v normálním tvaru. Optimální strategie. Maticové hry. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty
Simplexové tabulky z minule. (KMI ZF JU) Lineární programování EMM a OA O6 1 / 25
 Simplexové tabulky z minule (KMI ZF JU) Lineární programování EMM a OA O6 1 / 25 Simplexová metoda symbolicky Výchozí tabulka prom. v bázi zákl. proměné přídatné prom. omez. A E b c T 0 0 Tabulka po přepočtu
Simplexové tabulky z minule (KMI ZF JU) Lineární programování EMM a OA O6 1 / 25 Simplexová metoda symbolicky Výchozí tabulka prom. v bázi zákl. proměné přídatné prom. omez. A E b c T 0 0 Tabulka po přepočtu
Aplikovaná numerická matematika
 Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Matematika I, část I Vzájemná poloha lineárních útvarů v E 3
 3.6. Vzájemná poloha lineárních útvarů v E 3 Výklad A. Vzájemná poloha dvou přímek Uvažujme v E 3 přímky p, q: p: X = A + ru q: X = B + sv a hledejme jejich společné body, tj. hledejme takové hodnoty parametrů
3.6. Vzájemná poloha lineárních útvarů v E 3 Výklad A. Vzájemná poloha dvou přímek Uvažujme v E 3 přímky p, q: p: X = A + ru q: X = B + sv a hledejme jejich společné body, tj. hledejme takové hodnoty parametrů
Operační výzkum. Teorie her. Řešení maticových her převodem na úlohu LP.
 Operační výzkum Řešení maticových her převodem na úlohu LP. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu
Operační výzkum Řešení maticových her převodem na úlohu LP. Operační program Vzdělávání pro konkurenceschopnost Název projektu: Inovace magisterského studijního programu Fakulty ekonomiky a managementu
10. cvičení z PST. 5. prosince T = (n 1) S2 X. (n 1) s2 x σ 2 q χ 2 (n 1) (1 α 2 ). q χ 2 (n 1) 2. 2 x. (n 1) s. x = 1 6. x i = 457.
 0 cvičení z PST 5 prosince 208 0 (intervalový odhad pro rozptyl) Soubor (70, 84, 89, 70, 74, 70) je náhodným výběrem z normálního rozdělení N(µ, σ 2 ) Určete oboustranný symetrický 95% interval spolehlivosti
0 cvičení z PST 5 prosince 208 0 (intervalový odhad pro rozptyl) Soubor (70, 84, 89, 70, 74, 70) je náhodným výběrem z normálního rozdělení N(µ, σ 2 ) Určete oboustranný symetrický 95% interval spolehlivosti
Jiří Neubauer. Katedra ekonometrie FEM UO Brno
 Přednáška č. 11 Katedra ekonometrie FEM UO Brno Jedná se o speciální případ dopravních úloh, řeší např. problematiku optimálního přiřazení strojů na pracoviště. Příklad Podnik má k dispozici 3 jeřáby,
Přednáška č. 11 Katedra ekonometrie FEM UO Brno Jedná se o speciální případ dopravních úloh, řeší např. problematiku optimálního přiřazení strojů na pracoviště. Příklad Podnik má k dispozici 3 jeřáby,
4EK311 Operační výzkum. 3. Optimalizační software a stabilita řešení úloh LP
 4EK311 Operační výzkum 3. Optimalizační software a stabilita řešení úloh LP 3.1 Příklad matematický model Lis: 1 x 1 + 2 x 2 120 [min] Balení: 1 x 1 + 4 x 2 180 [min] Poptávka: 1 x 1 1 x 2 90 [krabiček]
4EK311 Operační výzkum 3. Optimalizační software a stabilita řešení úloh LP 3.1 Příklad matematický model Lis: 1 x 1 + 2 x 2 120 [min] Balení: 1 x 1 + 4 x 2 180 [min] Poptávka: 1 x 1 1 x 2 90 [krabiček]
Ing. Alena Šafrová Drášilová, Ph.D.
 Rozhodování Ing. Alena Šafrová Drášilová, Ph.D. Rozhodování??? video Obsah typy rozhodování principy rozhodování rozhodovací fáze základní pojmy hodnotícího procesu rozhodovací podmínky rozhodování v podmínkách
Rozhodování Ing. Alena Šafrová Drášilová, Ph.D. Rozhodování??? video Obsah typy rozhodování principy rozhodování rozhodovací fáze základní pojmy hodnotícího procesu rozhodovací podmínky rozhodování v podmínkách
4EK311 Operační výzkum. 1. Úvod do operačního výzkumu
 4EK311 Operační výzkum 1. Úvod do operačního výzkumu Mgr. Jana SEKNIČKOVÁ, Ph.D. Nová budova, místnost 433 Konzultační hodiny InSIS E-mail: jana.seknickova@vse.cz Web: jana.seknicka.eu/vyuka Garant kurzu:
4EK311 Operační výzkum 1. Úvod do operačního výzkumu Mgr. Jana SEKNIČKOVÁ, Ph.D. Nová budova, místnost 433 Konzultační hodiny InSIS E-mail: jana.seknickova@vse.cz Web: jana.seknicka.eu/vyuka Garant kurzu:
Vzdělávací oblast: Matematika a její aplikace Vzdělávací obor: Matematický kroužek pro nadané žáky ročník 9.
 Vzdělávací oblast: Matematika a její aplikace Vzdělávací obor: Matematický kroužek pro nadané žáky ročník 9. Školní rok 2013/2014 Mgr. Lenka Mateová Kapitola Téma (Učivo) Znalosti a dovednosti (výstup)
Vzdělávací oblast: Matematika a její aplikace Vzdělávací obor: Matematický kroužek pro nadané žáky ročník 9. Školní rok 2013/2014 Mgr. Lenka Mateová Kapitola Téma (Učivo) Znalosti a dovednosti (výstup)
Řešení domácího úkolu
 Úkol 1 Řešení domácího úkolu Podrobný popis řešení - analogie na seminář IV. a) Napište produkční funkce Na 1 hektolitr Spritu potřebujeme 48 jednotek práce Na 1 hektolitr Coly potřebujeme 24 jednotek
Úkol 1 Řešení domácího úkolu Podrobný popis řešení - analogie na seminář IV. a) Napište produkční funkce Na 1 hektolitr Spritu potřebujeme 48 jednotek práce Na 1 hektolitr Coly potřebujeme 24 jednotek
4EK213 Lineární modely. 4. Simplexová metoda - závěr
 4EK213 Lineární modely 4. Simplexová metoda - závěr 4. Simplexová metoda - závěr Konečnost simplexové metody Degenerace Modifikace pravidla pro volbu vstupující proměnné Blandovo pravidlo Kontrola výpočtu
4EK213 Lineární modely 4. Simplexová metoda - závěr 4. Simplexová metoda - závěr Konečnost simplexové metody Degenerace Modifikace pravidla pro volbu vstupující proměnné Blandovo pravidlo Kontrola výpočtu
Numerická matematika. Zadání 25. Řešení diferenciální rovnice Rungovou Kuttovou metodou
 Numerická matematika Zadání 25. Řešení diferenciální rovnice Rungovou Kuttovou metodou Václav Bubník, xbubni01, sk. 60 FIT VUT v Brně, 2004 Obsah Numerická matematika...1 1. Teorie... 3 1.1 Diferenciální
Numerická matematika Zadání 25. Řešení diferenciální rovnice Rungovou Kuttovou metodou Václav Bubník, xbubni01, sk. 60 FIT VUT v Brně, 2004 Obsah Numerická matematika...1 1. Teorie... 3 1.1 Diferenciální
8.3). S ohledem na jednoduchost a názornost je výhodné seznámit se s touto Základní pojmy a vztahy. Definice
 9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA EKONOMICKÁ FAKULTA KATEDRA FINANCÍ
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA EKONOMICKÁ FAKULTA KATEDRA FINANCÍ Hodnocení eficience finanční výkonnosti podniků potravinářského průmyslu pomocí metody DEA Evaluation of Financial Performance
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA EKONOMICKÁ FAKULTA KATEDRA FINANCÍ Hodnocení eficience finanční výkonnosti podniků potravinářského průmyslu pomocí metody DEA Evaluation of Financial Performance
Řešení domácího úkolu
 Úkol 1 Řešení domácího úkolu Podrobný popis řešení - analogie na seminář IV. a) Napište produkční funkce Na 1 hektolitr Smoothie potřebujeme 72 jednotek práce Na 1 hektolitr Kofoly potřebujeme 36 jednotek
Úkol 1 Řešení domácího úkolu Podrobný popis řešení - analogie na seminář IV. a) Napište produkční funkce Na 1 hektolitr Smoothie potřebujeme 72 jednotek práce Na 1 hektolitr Kofoly potřebujeme 36 jednotek
4. Aplikace matematiky v ekonomii
 4. Aplikace matematiky v ekonomii 1 Lineární algebra Soustavy 1) Na základě statistických údajů se zjistilo, že závislost množství statku z poptávaného v průběhu jednoho týdne lze popsat vztahem q d =
4. Aplikace matematiky v ekonomii 1 Lineární algebra Soustavy 1) Na základě statistických údajů se zjistilo, že závislost množství statku z poptávaného v průběhu jednoho týdne lze popsat vztahem q d =
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
a počtem sloupců druhé matice. Spočítejme součin A.B. Označme matici A.B = M, pro její prvky platí:
 Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují
 Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují 1. u + v = v + u, u, v V 2. (u + v) + w = u + (v + w),
Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují 1. u + v = v + u, u, v V 2. (u + v) + w = u + (v + w),
Obr. P1.1 Zadání úlohy v MS Excel
 Přílohy Příloha 1 Řešení úlohy lineárního programování v MS Excel V této příloze si ukážeme, jak lze řešit úlohy lineárního programování pomocí tabulkového procesoru MS Excel. Výpočet budeme demonstrovat
Přílohy Příloha 1 Řešení úlohy lineárního programování v MS Excel V této příloze si ukážeme, jak lze řešit úlohy lineárního programování pomocí tabulkového procesoru MS Excel. Výpočet budeme demonstrovat
Přehled matematického aparátu
 Přehled matematického aparátu Ekonomie je směsí historie, filozofie, etiky, psychologie, sociologie a dalších oborů je tak příslovečným tavicím kotlem ostatních společenských věd. Ekonomie však často staví
Přehled matematického aparátu Ekonomie je směsí historie, filozofie, etiky, psychologie, sociologie a dalších oborů je tak příslovečným tavicím kotlem ostatních společenských věd. Ekonomie však často staví
5 NÁKLADY PODNIKU A JEJICH KALKULACE
 5 NÁKLADY PODNIKU A JEJICH KALKULACE Náklady podniku můžeme charakterizovat jako peněžně vyjádřenou spotřebu výrobních faktorů účelně vynaložených na tvorbu podnikových výnosů včetně dalších nutných nákladů
5 NÁKLADY PODNIKU A JEJICH KALKULACE Náklady podniku můžeme charakterizovat jako peněžně vyjádřenou spotřebu výrobních faktorů účelně vynaložených na tvorbu podnikových výnosů včetně dalších nutných nákladů
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
4EK311 Operační výzkum. 2. Lineární programování
 4EK311 Operační výzkum 2. Lineární programování 2.2 Matematický model úlohy LP Nalézt extrém účelové funkce z = c 1 x 1 + c 2 x 2 + + c n x n na soustavě vlastních omezení a 11 x 1 + a 12 x 2 + a 13 x
4EK311 Operační výzkum 2. Lineární programování 2.2 Matematický model úlohy LP Nalézt extrém účelové funkce z = c 1 x 1 + c 2 x 2 + + c n x n na soustavě vlastních omezení a 11 x 1 + a 12 x 2 + a 13 x
4EK213 LINEÁRNÍ MODELY
 4EK213 LINEÁRNÍ MODELY Úterý 11:00 12:30 hod. učebna SB 324 3. přednáška SIMPLEXOVÁ METODA I. OSNOVA PŘEDNÁŠKY Standardní tvar MM Základní věta LP Princip simplexové metody Výchozí řešení SM Zlepšení řešení
4EK213 LINEÁRNÍ MODELY Úterý 11:00 12:30 hod. učebna SB 324 3. přednáška SIMPLEXOVÁ METODA I. OSNOVA PŘEDNÁŠKY Standardní tvar MM Základní věta LP Princip simplexové metody Výchozí řešení SM Zlepšení řešení
5. Lokální, vázané a globální extrémy
 5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
CVIČNÝ TEST 51. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 51 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 V obchodě s kouzelnickými potřebami v Kocourkově
CVIČNÝ TEST 51 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 V obchodě s kouzelnickými potřebami v Kocourkově
Soustavy se spínanými kapacitory - SC. 1. Základní princip:
 Obvody S - popis 1 Soustavy se spínanými kapacitory - S 1. Základní princip: Simulace rezistoru přepínaným kapacitorem viz známý obrázek! (a rovnice) Modifikace základního spínaného obvodu: Obr. 2.1: Zapojení
Obvody S - popis 1 Soustavy se spínanými kapacitory - S 1. Základní princip: Simulace rezistoru přepínaným kapacitorem viz známý obrázek! (a rovnice) Modifikace základního spínaného obvodu: Obr. 2.1: Zapojení
Číselné charakteristiky a jejich výpočet
 Katedra ekonometrie, FVL, UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz charakteristiky polohy charakteristiky variability charakteristiky koncetrace charakteristiky polohy charakteristiky
Katedra ekonometrie, FVL, UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz charakteristiky polohy charakteristiky variability charakteristiky koncetrace charakteristiky polohy charakteristiky
Matematická analýza III.
 2. Parciální derivace Miroslav Hušek, Lucie Loukotová UJEP 2010 Parciální derivace jsou zobecněním derivace funkce jedné proměnné. V této kapitole poznáme jejich základní vlastnosti a využití. Co bychom
2. Parciální derivace Miroslav Hušek, Lucie Loukotová UJEP 2010 Parciální derivace jsou zobecněním derivace funkce jedné proměnné. V této kapitole poznáme jejich základní vlastnosti a využití. Co bychom
Příklady k T 2 (platí pro seminární skupiny 1,4,10,11)!!!
 Příklady k T 2 (platí pro seminární skupiny 1,4,10,11)!!! Příklad 1.: Obchodník prodává pouze jeden druh zboží a ten také výhradně nakupuje. Činí tak v malém rozsahu, a proto koupil 500 výrobků po 10 Kč
Příklady k T 2 (platí pro seminární skupiny 1,4,10,11)!!! Příklad 1.: Obchodník prodává pouze jeden druh zboží a ten také výhradně nakupuje. Činí tak v malém rozsahu, a proto koupil 500 výrobků po 10 Kč
1 Mnohočleny a algebraické rovnice
 1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
Poznámka. V některých literaturách se pro označení vektoru také používá symbolu u.
 Vektory, operace s vektory Ž3 Orientovaná úsečka Mějme dvojici bodů, (na přímce, v rovině nebo prostoru), které spojíme a vznikne tak úsečka. Pokud budeme rozlišovat, zda je spojíme od k nebo od k, říkáme,
Vektory, operace s vektory Ž3 Orientovaná úsečka Mějme dvojici bodů, (na přímce, v rovině nebo prostoru), které spojíme a vznikne tak úsečka. Pokud budeme rozlišovat, zda je spojíme od k nebo od k, říkáme,
V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti
 Kapitola 5 Vektorové prostory V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti operací sčítání a násobení
Kapitola 5 Vektorové prostory V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti operací sčítání a násobení
Metodický list č. 1 FUNKCE, ZISK A VZTAHY MEZI ZÁKLADNÍMI EKONOMICKÝMI VELIČINAMI PODNIKU
 Metodické listy pro kombinované studium předmětu MANAŽERSKÁ EKONOMIKA Přednášející: Ing. Jana Kotěšovcová Metodický list č. 1 Název tematického celku: ZALOŽENÍ PODNIKU, VÝNOSY, NÁKLADY, NÁKLADOVÉ FUNKCE,
Metodické listy pro kombinované studium předmětu MANAŽERSKÁ EKONOMIKA Přednášející: Ing. Jana Kotěšovcová Metodický list č. 1 Název tematického celku: ZALOŽENÍ PODNIKU, VÝNOSY, NÁKLADY, NÁKLADOVÉ FUNKCE,
1 Projekce a projektory
 Cvičení 3 - zadání a řešení úloh Základy numerické matematiky - NMNM20 Verze z 5. října 208 Projekce a projektory Opakování ortogonální projekce Definice (Ortogonální projekce). Uvažujme V vektorový prostor
Cvičení 3 - zadání a řešení úloh Základy numerické matematiky - NMNM20 Verze z 5. října 208 Projekce a projektory Opakování ortogonální projekce Definice (Ortogonální projekce). Uvažujme V vektorový prostor
CVIČNÝ TEST 15. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
4EK213 Lineární modely. 5. Dualita v úlohách LP
 4EK213 Lineární modely 5. Dualita v úlohách LP 5. Dualita v úlohách LP Obecné vyjádření simplexové tabulky Formulace duálního problému Formulace symetrického duálního problému Formulace nesymetrického
4EK213 Lineární modely 5. Dualita v úlohách LP 5. Dualita v úlohách LP Obecné vyjádření simplexové tabulky Formulace duálního problému Formulace symetrického duálního problému Formulace nesymetrického
M - Příprava na 3. čtvrtletní písemnou práci
 M - Příprava na 3. čtvrtletní písemnou práci Určeno pro třídu ODK VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
M - Příprava na 3. čtvrtletní písemnou práci Určeno pro třídu ODK VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
příkladů do cvičení. V textu se objeví i pár detailů, které jsem nestihl (na které jsem zapomněl) a(b u) = (ab) u, u + ( u) = 0 = ( u) + u.
 Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
Regresní a korelační analýza
 Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
Regresní a korelační analýza Mějme dvojici proměnných, které spolu nějak souvisí. x je nezávisle (vysvětlující) proměnná y je závisle (vysvětlovaná) proměnná Chceme zjistit funkční závislost y = f(x).
i=1 Přímka a úsečka. Body, které leží na přímce procházející body a a b můžeme zapsat pomocí parametrické rovnice
 I. Funkce dvou a více reálných proměnných 1. Úvod Značení: V textu budeme používat označení: N pro množinu všech přirozených čísel; R pro množinu všech reálných čísel; R n pro množinu všech uspořádaných
I. Funkce dvou a více reálných proměnných 1. Úvod Značení: V textu budeme používat označení: N pro množinu všech přirozených čísel; R pro množinu všech reálných čísel; R n pro množinu všech uspořádaných
Funkce pro studijní obory
 Variace 1 Funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce Funkce je přiřazení,
Variace 1 Funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce Funkce je přiřazení,
4EK212 Kvantitativní management. 1. Úvod do kvantitativního managementu a LP
 4EK212 Kvantitativní management 1. Úvod do kvantitativního managementu a LP Mgr. Jana SEKNIČKOVÁ, Ph.D. Nová budova, místnost 433 Konzultační hodiny InSIS E-mail: jana.seknickova@vse.cz Web: jana.seknicka.eu/vyuka
4EK212 Kvantitativní management 1. Úvod do kvantitativního managementu a LP Mgr. Jana SEKNIČKOVÁ, Ph.D. Nová budova, místnost 433 Konzultační hodiny InSIS E-mail: jana.seknickova@vse.cz Web: jana.seknicka.eu/vyuka
IB112 Základy matematiky
 IB112 Základy matematiky Řešení soustavy lineárních rovnic, matice, vektory Jan Strejček IB112 Základy matematiky: Řešení soustavy lineárních rovnic, matice, vektory 2/53 Obsah Soustava lineárních rovnic
IB112 Základy matematiky Řešení soustavy lineárních rovnic, matice, vektory Jan Strejček IB112 Základy matematiky: Řešení soustavy lineárních rovnic, matice, vektory 2/53 Obsah Soustava lineárních rovnic
T T. Think Together 2013. Jan Rydval THINK TOGETHER
 Česká zemědělská univerzita v Praze Provozně ekonomická fakulta Doktorská vědecká konference 4. února 2013 T T THINK TOGETHER Think Together 2013 Měření efektivnosti jazykových kurzů pomocí DEA modelů
Česká zemědělská univerzita v Praze Provozně ekonomická fakulta Doktorská vědecká konference 4. února 2013 T T THINK TOGETHER Think Together 2013 Měření efektivnosti jazykových kurzů pomocí DEA modelů
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice
 Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: graf funkce, derivace funkce a její
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: graf funkce, derivace funkce a její
