Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra mechaniky. Optimalizace akustického pole
|
|
|
- Petra Beranová
- před 9 lety
- Počet zobrazení:
Transkript
1 Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra mechaniky BAKALÁŘSKÁ PRÁCE Optimalizace akustického pole Plzeň 2013 Zdeněk Novotný
2 Prohlášení Prohlašuji, že jsem bakalářskou práci vypracoval samostatně a výhradně s použitím citovaných pramenů. V Plzni dne 28. května 2013 Zdeněk Novotný
3 Poděkování Při této příležitosti bych rád poděkoval vedoucímu bakalářské práce Prof. Dr. Ing. Eduardu Rohanovi, DrSc. za motivaci ke studiu a vedení práce a Ing. Vladimíru Lukešovi, Ph.D. za všechny cenné rady a věnovaný čas. 2
4 Abstrakt Hlavním cílem této práce je provedení tvarové optimalizace akustického pole popsaného omezenou 2D oblastí Ω. Nejdříve se odvodily rovnice akustiky potřebné k získání vlnové rovnice pro tekutiny. Z těchto rovnic se určila vlnová rovnice. Hledáním jednofrekvenčního řešení se z ní odvodila Helmholtzova rovnice. Pak se zde ukázaly možné přístupy k řešení vlnové a Helmholtzovy rovnice pro 1D kontinuum, kde se využilo Fourierovy metody. Z úvah o šíření akustických vln se odvodily okrajové podmínky na hranici Ω. Naformulovala se úloha tvarové optimalizace. Jako stavovou rovnici se využila slabá formulace Helmholtzovy rovnice. Provedla se citlivostní analýza. Zparametrizoval se design oblasti Ω parametry α pomocí spline-boxu. Optimalizační úloze se přiřadila Lagrangeova funkce a posléze se přešlo k úloze adjungované. Touto cestou se získá celková derivace neboli citlivost účelové funkce Φ na změnu parametrů α. Dále jsou porovnány pro kontrolu výsledky citlivostní analýzy a konečných diferencí. Pomocí softwaru SfePy a Matlabu jsme provedli několik optimalizačních výpočtů ve 2D. Výsledky se zobrazily programem ParaView a následně vyhodnotily. Abstract The main objective of this study is to implement shape optimization of an acoustic field described by 2D domain Ω. The very first step was the familiarization with derivation of acoustic equations necessary to obtain wave equation for fluids. From these equations, the wave equation was derived. By searching for a single-frequency solution, the Helmhotz equation was found. Possible approach in solving wave and Helmholtz equation for 1D continuum, where Fourier method was used, was shown. From our knowledge about acoustic propagation boundary conditions at boundary Ω were derived. A problem of shape optimization was defined. As a state equation weak formulation of Helmhotz equation was applied. Then the sensitive analysis was performed. Design of Ω domain was parameterized by parameters α using spline-box. Lagrange equation was assigned to the optimization problem. Consecutively, there was a proceeding to solve an adjugate problem. This way allowed to obtain a total derivation of objective function that is a sensitivity of objective function to the change of parameters α. Furthermore, there were compared results from sensitive analysis and finite differences. Using software SfePy and Matlab we performed a few optimization calculations in 2D. At the end the results were displayed with software ParaView and also appraised.
5 Obsah 1 Úvod 1 2 Odvození rovnic akustiky Úvodem Eulerova rovnice Rovnice kontinuity Stavová rovnice Vlnová rovnice v kartézských souřadnicích Helmholtzova rovnice Řešení úloh pro 1D kontinuum Vlnová rovnice Helmholtzova rovnice Form. úloh akust. pro danou frekv. ve 3D Okrajová úloha Slabé řešení Numerické řešení MKP Formulace úloh tvarové optimalizace Úvod Citlivostní analýza Metoda adjungované proměnné Výpočet citlivosti pomocí materiálové derivace Implementace Adjungovaná úloha Příprava oblasti Ω Spline-box Porovnání konečných diferencí a citlivostní analýzy Optimalizace Optimalizační výpočty Úvodem Vlastní výpočty
6 OBSAH OBSAH 6 Závěr 40 5
7 1 Úvod Řešení problémů akustiky, například tvarovou optimalizací, má potencionální aplikace v mnoha oblastech mechaniky. Například při optimalizaci částí strojů a mechanických zařízení, která svým chodem způsobují přílišnou hlučnost. Pak je nutné tyto hlukové emise snížit. Nicméně tato práce není vázána na konkrétní úlohu nebo aplikaci, ale zabývá se optimalizací spíše teoreticky. V druhé kapitole se seznámíme s odvozením rovnic potřebných k získání vlnové rovnice pro tekutiny. Tyto rovnice odvodíme s předpokladem, že prostředí je stlačitelné, spojité, homogenní, izotropní a neviskózní. Akustické pole budeme předpokládat za nevírové. Odvodíme si Eulerovu pohybovou rovnici pro proudění, která zanedbává tření a vazkost. Rovnice kontinuity vyjadřuje zákon zachování hmoty. Poslední stavová rovnice vychází z popsání termodynamického chování plynu při šíření zvukové vlny. Za dalších předpokladů těchto rovnic určíme tvar vlnové rovnice v kartézských souřadnicích pro neznámou rychlostní potenciál φ a akustický tlak P. Při hledání jednofrekvenčního řešení vlnové rovnice pro frekvenci ω z ní odvodíme Helmholtzovu rovnici, která popisuje stojaté vlnění. Zde čerpáme zejména z [Škvor(2001)]. V třetí kapitole si ukážeme některé přístupy k analytickému řešení vlnové a Helmholtzovy rovnice v jednorozměrných případech, kde použijeme Fourierovu metodu řešení parciálních diferenciálních rovnic, viz [Míka(1983)] a [Škvor(2001)]. Budeme uvažovat šíření zvukových vln mezi dvěma rovnoběžnými dokonale odrazivými deskami. Z toho vyplynou okrajové a počáteční podmínky. Pomocí Matlabu si zobrazíme některá řešení. Ve čtvrté kapitole formulujeme úlohu akustiky pro danou frekvenci ω. Budeme tedy řešit slabou formulaci, viz [Míka(2007)], Helmholtzovy rovnice. Zavedeme si oblast Ω. V softwaru MSC.Marc Mentat si vygenerujeme její MKP sít. Z úvah o šíření akustických vln si odvodíme okrajové podmínky na hranici Ω = Γ in Γ out Γ 0, viz, viz [E. Bängtsson(2002)]. Pomocí MKP provedeme řešení v systému SfePy. Na dané oblasti vyzkoušíme různé frekvence ω incidenční vlny. Výslednou mapu řešení na oblasti si zobrazíme v programu ParaView. Ve páté kapitole formulujeme úlohu tvarové optimalizace pro akustické pole. Uvažujeme oblast Ω a rozdělíme ji na dvě podoblasti, designovou Ω D a zbylou Ω C. MKP sít oblasti vygenerujeme v MSC.Marc Mentat. Podél oblasti Ω D zavedeme hranici Γ D Γ 0. Úvaha byla taková, že změnou tvaru hranice Γ D, zprostředkovanou změnou parametrů α, se nám bude měnit řešení p v celé oblasti. Změna se nám projeví i na účelové funkci Φ. Definujeme optimalizační úlohu, kde jako stavovou rovnici využijeme Helmholtzovu rovnici a její slabou formulaci. Provedeme citlivostní analýzu, viz [Rohan(2012)]. Tím se rozumí výpočet citlivosti změny účelové funkce v závislosti na změně optimalizačních parametrů, když na nich závisí nepřímo prostřednictvím stavové proměnné. Zparametrizu- 1
8 Úvod jeme design pomocí spline-boxu, viz [Rohan(2007)]. Zavedeme pole designových rychlostí. Optimalizační úloze přiřadíme Lagrangeovu funkci a posléze přejdeme k řešení adjungované úlohy. Touto cestou, počítanou v systému SfePy, získáme celkovou derivaci neboli citlivost účelové funkce Φ na změnu parametrů α. Následně porovnáme pro kontrolu výsledky citlivostní analýzy a konečných diferencí. Další zdroje v této kapitole byly [E. Bängtsson(2002)],[B. Engquist(1977)],[Rohan(2007)],[D. Cioranescu(2008)], [J. Haslinger(1996)],[E. Rohan(2011b)],[E. Rohan(2006)],[E. Rohan(2011a)]. Na závěr provedeme několik optimalizačních výpočtů pro 2D oblast Ω. Optimalizováním tvaru hranice Γ D budeme hledat minimum dvou účelových funkcí Φ I,II. Výpočet provedeme pomocí Matlabu a SfePy. Výsledky zobrazíme v ParaView a zhodnotíme. 2
9 2 Odvození rovnic akustiky 2.1 Úvodem V tekutém prostředí je zvuk vyvolán změnami, které v čase a prostoru způsobí změny tlaku, hustoty a kmitání jednotlivých částic prostředí s lokálními výchylkami ξ = (x, y, z) a rychlostmi v = (v x, v y, v z ). O prostředí předpokládáme, že je stlačitelné, spojité, homogenní, izotropní a neviskózní. Výchylky částic podle našeho předpokladu jsou malé a všechny sledované jevy budeme považovat za lineární. (Při zpracování této kapitoly se vychází vesměs z knihy [Škvor(2001)] a z [Linhart(2009)].) V nepohybujícím se prostředí je akustické pole popsáno vektory akustických rychlostí jednotlivých částic prostředí. V prostředí s uvažováním pohybu částic je vyjádření složitější o složku proudění a pohyb popisujeme Lagrangeovými nebo Eulerovými proměnnými. Zde nebudeme dále proudění částic uvažovat. Akustické pole pokládáme na nevírové, a tak se tedy předpokládá, že rot v = 0. (2.1) Výjímku tvoří případy velkých rychlostí u reálných plynů a kapalin, kdy se uplatňuje vliv viskozity. Vektorové pole lze rozdělit na dvě složky, na složku nevírovou v n a vírovou (rotační) v r. v = v n + v r (2.2) Pro nevírovou složku platí rot v n = 0 a div v n 0. Na základě toho zavedeme skalární fci φ [m 2 s 1 ]. Nazveme ji rychlostním potenciálem, jehož gradient je roven rychlosti v n [ms 1 ] Podle předpokladu je pole rychlostí nevírové, a bude tedy platit grad φ = v n. (2.3) v = v n = grad φ div v = div v n 0. (2.4) Při odvození vlnové rovnice vyjdeme z pohybové (Eulerovy) rovnice, rovnice kontinuity (spojitosti) a stavové rovnice. 2.2 Eulerova rovnice Eulerova rovnice je pohybová rovnice pro proudění, která zanedbává tření a vazkost. Odvození je provedeno pro elementární krychli dxdydz. Vyjdeme ze známého D Alembertova 3
10 Odvození rovnic akustiky Eulerova rovnice principu, který řiká, že v každém okamžiku je soustava vnitřních a vnějších sil v rovnováze dm a = i df i, kde levá strana reprezentuje vnitřní (setrvačné) síly a pravá vnější síly působící na element. Pro zrychlení a [ms 2 ] platí a = i a x + j a y + k a z = (a x, a y, a z ) = d v ( dt = dvx dt, dv y dt, dv ) z, (2.5) dt kde i, j a k jsou jednotkové vektory orientovány v kladném smyslu ve směrech os x, y a z. Elementární krychle má hmotnost dm a tekutina v ní hustotu ρ [kg m 3 ] dm = ρdv = dxdydz. Setrvačná síla působící na elementární krychli ve směrech os x, y a z je Obrázek 2.1: Síly působící na elementární krychli df x1 = i dm dv x dt, df y1 = j dm dv y dt, df z1 = k dm dv z dt. (2.6) Výsledná setrvačná síla bude tedy rovna součtu jednotlivých setrvačných sil (2.6) df s = df x1 + df y1 + df ( z1 = dm i dv x dt + j dv y dt + k dv ) z = dm d v dt dt. (2.7) 4
11 Odvození rovnic akustiky Eulerova rovnice V kartézských souřadnicích je akustický tlak p [P a] funkcí času a prostorových proměnných x, y a z. Takže p = p(t, x, y, z). Přepokládejme podle obr.(2.2), že na protilehlých ploškách elementární krychle kolmých na osu y působí akustické tlaky p a proti p + p dy. Tlakové y Obrázek 2.2: Tlak na elementární krychli síly působící na elemetární plošku dxdz představují účinek okolní tekutiny nacházející se vně elementární krychle. Výsledná složka síly j df y1 ve směru osy y bude rovna výslednici povrchových sil působících na protilehlých stěnách j df y2 [ ( = j p p + p )] y dy dxdy df y2 = j p dydxdz. (2.8) y Podobně se odvodí Výsledná síla df x2 = i p x dxdydz, df v se rovná df z2 = k p dzdydx. (2.9) z df v = i p x dxdydz j p y dydxdz k p dzdydx. (2.10) z Z D Alembertova principu musí platit dfv = df s. Dosadíme tedy z (2.10) a (2.7) ( i p x + j p y + k p ) = ρ v z t, grad p = ρ v t. (2.11) Rovnice (2.11) je Eulerova rovnice dynamiky ideální tekutiny bez přihlížení k jejímu proudění a působení vnějších sil z jejího okolí. 5
12 Odvození rovnic akustiky Rovnice kontinuity 2.3 Rovnice kontinuity Další z rovnic je rovnice kontinuity vyjadřující zákon zachování hmoty. Budeme uvažovat podle obr.(4.4) elementární objem. Předpokládejme, že podél osy y v kladném smyslu vtéká a vytéká tekutina ploškami dx, dz. Hmotnost přitékající tekutiny za dt je ρ v y dx dz dt = ρ dw y dt. (2.12) kde w y [m 3 s 1 ] je průtoková rychlost ve směru osy y. Hmotnost vytékající tekutiny za dt je ρ dw y dt + (ρ dw y dt) dy. (2.13) y Je vidět, že vyteče z elementární krychle o hmotnost (ρ dwy dt) dy více než vteklo. Obdobně y Obrázek 2.3: Průtok elementární krychlí tento rozdíl určíme pro proudění podél zbylých os x a z. Celkem tedy (ρ dw x dt) dx, x (ρ dw y dt) dy, y (ρ dw z dt) dz. (2.14) z Fakt, že víc hmotnosti odteče než vteče, se musí projevit poklesem hustoty v elementárním objemu. Čas dt a elementární objemy dxdydz se zkrátí (ρ dw x dt) x dx + (ρ dw y dt) y (ρ dv x ) x dy + (ρ dw z dt) z + (ρ dv y) + (ρ dv z) y z 6 dz = ρ dt dx dy dz t = ρ t div (ρ v) = ρ t (2.15)
13 Odvození rovnic akustiky Stavová rovnice V lineární akustice uvažujeme v celém objemu tekutiny ve stejném čase přibližně stejnou hustotu ρ = ρ 0 + ρ. Odchylky ρ od počáteční hustoty ρ 0 jsou velmi malé. Proto mohu celou rovnici vydělit ρ 0 a získám tím rovnici kontinuity ve zjednodušeném tvaru div v = 1 ρ 0 ρ t. (2.16) 2.4 Stavová rovnice Termodynamické chování plynu je popsáno vzájemnou souvislostí tlaku p [P a], hustoty ρ [kg m 3 ] a teploty T [K]. Stavová rovnice ideálního plynu má tvar p = ρ r T, (2.17) kde r [Jkg 1 K 1 ] je měrná plynová konstanta. Jevy probíhající v akustice jsou zpravidla tak rychlé, že nedochází ke sdílení tepla, neboli dq = 0, a děje se stávají adiabatickými. Při nízkých kmitočtech jsou změny pomalé a termodynamické chování plynu se blíží izotermickému ději, tedy ději, který probíhá při T = konst. V těchto případech je hustota plynu pouze funkcí tlaku ρ = ρ(p) a hovoříme o baratropním ději. Pro izotermickou stavovu změnu platí podle Boyleova-Mariottova zákona p ρ = konst. (2.18) Pro adiabatickou stavovou změnu platí Poissonova rovnice pro tlak a objem p V κ = konst. (2.19) Objem je tedy přibližně nepřímo úměrný hustotě V ρ 1. Pak můžeme zapsat p ρ κ = konst, (2.20) kde konstanta κ je poměr měrné tepelné kapacity plynu při stálém tlaku c p a stálém objemu c v κ = c p c v,. (2.21) Podle adiabatického děje popsaného v (2.20) jsou hustota ρ a tlak p v určitém místě závislé na čase, a tak lze stanovit závislost časové změny tlaku na změně hustoty p t ρ κ κ 1 ρ κ p ρ t p t = 0 = κ p ρ ρ t. (2.22) 7
14 Odvození rovnic akustiky Vlnová rovnice v kartézských souřadnicích Když budeme uvažovat tlak p a hustotu ρ jako superpozici klidových hodnot p 0, ρ 0 a změn p, ρ ρ = ρ 0 + ρ, p = p 0 + p. (2.23) A předpokládáme p p 0, ρ ρ 0. Potom bude mít rovnice (2.22) tvar p t = κ p 0 ρ ρ 0 t. (2.24) 2.5 Vlnová rovnice v kartézských souřadnicích V předchozích odstavcích jsme odvodili tři rovnice, které využijeme ke stanovení vlnové rovnice. Jde o Eulerovo pohybovou rovnici (2.11), rovnici kontinuity(2.16) a stavovou rovnici (2.24) grad p = ρ v t, div v = 1 ρ 0 ρ t, p t = κ p 0 ρ ρ 0 t. Podle dřívějšího předpokladu je rot v = 0 a místo rychlosti v zavedeme rychlostní potenciál φ. Do rovnice (2.11) dosadíme rychlostní potenciál a dostaneme ( ) φ grad p = ρ 0 t (grad φ) = ρ 0grad (2.25) t a dále po úpravě p = ρ 0 φ t + konst. (2.26) V rovnici (2.16) také přejdeme k rychlostnímu potenciálu a dostaneme Zavedeme Laplaceoův operátor pak rovnice dostane tvar Rovnici (2.26) zderivujeme podle času div grad φ = 1 ρ 0 ρ t. (2.27) div grad φ = φ, φ = 1 ρ 0 ρ t. (2.28) p t = ρ 2 φ 0 (2.29) t 2 8
15 Odvození rovnic akustiky Vlnová rovnice v kartézských souřadnicích a pak dáme v rovnost pravou stranu (2.29) s pravou stranou z (2.24) κ p 0 ρ 0 ρ t 1 ρ 0 ρ t = ρ 0 2 φ t 2 = ρ 0 κ p 0 2 φ t 2 (2.30) Do (2.30) dosadíme z (2.28) a konečně získáme vlnovou rovnici pro rychlostní potenciál φ φ = ρ 0 κ p 0 2 φ t 2 (2.31) Dále využijeme toho, že známe vzorec pro výpočet rychlosti zvuku κ p0 c 0 =. ρ 0 Rovnice (2.31) po dosazení za rychlost zvuku bude vypadat takto φ = 1 c φ t 2, (2.32) nebo po rozepsání Laplaceova operátoru do kartézských souřadnic na jednotlivé složky 2 φ x + 2 φ 2 y + 2 φ 2 z = 1 2 φ 2 c 2 0 t. (2.33) 2 Uvedeným způsobem můžeme ze tří základních rovnic stanovit též vlnovou rovnici pro akustický tlak. Vztah (2.11) zdivergujeme a dosadíme z (2.16) Z rovnice (2.24) určíme div grad p = ρ 0 div v t div grad p = 2 ρ t 2, p = 2 ρ t 2. 2 p = κ p 0 2 ρ t 2 ρ 0 t 2 2 p ρ 0 = 2 ρ t 2 κ p 0 t. 2 Po dosazení z předchozí rovnice dostaneme vlnovou rovnici pro akustický tlak, kde ještě použijeme opět vztahu pro rychlost zvuku p = 1 c p t 2. (2.34)
16 Odvození rovnic akustiky Helmholtzova rovnice 2.6 Helmholtzova rovnice Při odvození Helmholtzovy rovnice (HR) uvažujeme jednofrekvenční časově harmonické řešení pro jednu frekvenci ω. Celkové řešení vlnové rovnice 2.32 pro tři prostorové proměnné x, y, z a proměnnou čas t budeme předpokládat ve tvaru To dosadíme do (2.20). Po zkrácení e iωt dostaneme φ(x, y, z, t) = p(x, y, z) e iωt, (2.35) ω 2 p + c 2 2 p = 0 2 p + κ 2 p = 0, (2.36) kde κ = ω. Tím jsme získali Helmholtzovu rovnici, která popisuje šíření vlnění ve třech c dimenzích. Zápis pro HR s jednou prostorovou proměnnou x bude vypadat p (x) + κ 2 p(x) = 0. (2.37) 10
17 3 Řešení úloh pro 1D kontinuum 3.1 Vlnová rovnice Vlnová rovnice (2.32) je parciální diferenciální rovnice hyperbolického typu, jejíž řešení popisuje šíření akustického potenciálu. Pro jednoduchost ji budeme řešit v 1D pro jednu proměnnou x viz (3.1), viz [Míka(1983)] a [Škvor(2001)]. c 2 2 φ x 2 2 φ t 2 = 0 (3.1) Při řešení rovnice (3.1) využijeme Fourierovy metody neboli metody oddělení (separace) proměnných. Tato metoda nahradí parciální derivace obyčejnými. U úloh s pevně stanovenými okrajovými podmínkami, se hledá řešení ve tvaru součinu více funkcí, kde každá z nich je funkcí jedné nezávisle proměnné. Tato metoda se používá hlavně k řešení počátečněokrajových úloh pro hyperbolické i parabolické rovnice. Zde budeme rychlostní potenciál φ(x, t) předpokládat jako součin dvou funkcí, funkce X(x), která je funkcí jedné nezávisle proměnné x, a funkce T (t), která je funkcí jedné nezávisle proměnné t. Řešení lze tedy zapsat ve tvaru φ(x, t) = T (t) X(x). (3.2) Po dosazení do rovnice (3.1) získáme c 2 X X = T T. (3.3) Má-li platit rovnice (3.3), tak musí být obě její strany rovny jedné konstantě λ = κ 2, kde κ je vlnové číslo a uvažujeme λ 0. Zavedli jsme zápornou konstantu, protože kladná by vedla na hyperbolické funkce. Předpokládáme, že ani jedna z funkcí, nebo její druhá derivace, není v uvažovaném oboru rovna nule. Z (3.3) získáme soustavu dvou obyčejných homogenních diferenciálních rovnic s konstantními koeficienty c 2 X + λx = 0, (3.4) T + λt = 0. (3.5) Vyřešením soustavy bychom měli získat systém (φ 1 (x, t), φ 2 (x, t),..., φ k (x, t)) řešení původní vlnové rovnice. Jako celkové řešení musíme volit vhodnou kombinaci funkcí φ(x, t) = D k φ k (x, t) = D k X k (x) T k (t), 11
18 Řešení úloh pro 1D kontinuum Vlnová rovnice kde konstatní koeficienty D k se volí tak, aby řešení φ(x, t) vyhovovalo okrajovým i počátečním podmínkám. Dále budeme řešit soustavu diferenciálních rovnic jako vyšetřování kmitů mezi dvěma dokonale odrazivými plochami. Jedna bude umístěna v počátku x = 0 a druhá ve vzdálenosti x = l. Vyjdeme z předpokladu, že akustická rychlost je na obou plochách nulová. Pro akustickou rychlost v platí vztah (2.3). V 1D pro jedinou prostorovou proměnnou x postačuje v = φ. Použijeme tyto okrajové podmínky x Jako počáteční podmínky uvažujeme x φ(0, t) = X (0) T (t) = 0, x φ(l, t) = X (l) T (t) = 0. (3.6) φ(x, 0) = 0, t φ(x, 0) = g(x), (3.7) kde g(x) popisuje rozložení akustické rychlosti mezi dvěma deskami v čase t = 0. Nyní budeme řešit (3.4) s okrajovými podmínkami. Řešení povede k úloze na vlastní čísla a vlastní funkce. c 2 X + λx = 0, X (0) = 0, X (l) = 0. (3.8) Hledáme netriviální řešení ve tvaru X(x) = A e αx. (3.9) Po dosazení (3.9) do (3.8) získáme c 2 α 2 e αx = λe αx α 2 = λ c 2 α = ± 1 c λ (3.10) Po dosazení α do (3.9) α = ±i 1 c λ. X(x) = A e ±i 1 ( c λx 1 ) ( 1 ) = B cos λx + C sin λx. (3.11) c c 12
19 Řešení úloh pro 1D kontinuum Vlnová rovnice Nyní s použitím okrajových podmínek určíme konstanty B a C. Najdeme první derivaci X (x) ( 1 ) X (x) = B sin λx 1 ( 1 ) λ + C cos λx 1 λ. (3.12) c c c c Ted dosadíme první okrajovou podmínku z (3.6) 0 = C cos(0) 1 λ. (3.13) c Konstanta C musí tedy být rovna nule. Dále využijeme druhou okrajovou podmínku z (3.6) ( 1 ) 0 = B sin λ l 1 λ. (3.14) c c Z (3.14) vyplývají dvě možnosti řešení. Řešení pro B 0 vyhovuje (3.14), jestliže sin( 1 c λ l) = 0. Odtud plyne 1 λk l = kπ c ( kπc ) 2 λ k = k N. l (3.15) Nyní již známe systém vlastních fcí X k (x) a vlastních čísel λ k ( X k (x) = cos k πx ) ( kπc ) 2, λ k = ; k N. (3.16) l l Vypočteme si normu vlastních funkcí pro k > 0 a k = 0 l ( kπ ) 2 cos 0 l x dx = l 2 ( kπ ) l cos l x =, k > 0 2 l Normovaná vlastní funkce nabude tvaru 2 X k (x) = l 1 X 0 (x) = l Obecné řešení rovnice (3.4) má tvar 0 cos(0) 2 dx = l X(x) = cos(0) = l, k = 0 ( kπ ) cos l x k = 0. k > 0, (3.17) (3.18) B k X k (x), (3.19) 13
20 Řešení úloh pro 1D kontinuum Vlnová rovnice kde B k jsou neznámé koeficienty. Pro známé koeficienty λ k lze nyní řešit rovnici (3.5) s počátečními podmínkami (3.7) T + λ k T = 0, φ(x, 0) = 0, φ(x, 0) = g(x). (3.20) Uvažujeme její řešení ve tvaru Dosadíme (3.21) do (3.20), odkud získáme T k (t) = C e iω kt. (3.21) ω 2 k = λ k ω k = ± λ k = ± kπc l. (3.22) Nyní můžeme vyjádřit řešení pro k tou funkci T k T k (t) = D k cos(ω k t) + E k sin(ω k t), kde D k a E k jsou neznáme konstanty. Potom celkové řešení φ(x, t) = φ(x, t) = B k X k (x) T k (t) B k [D k cos(ω k t) + E k sin(ω k t)] X k (x). Dále přeznačíme konstanty a budeme uvažovat D k = B k D k a E k = B k E k. Vyjádříme první derivaci φ(x, t) = [ D k ω k sin(ω k t) + E k ω k cos(ω k t)] X k (x). Řešení musí splňovat počáteční podmínky z (3.20). Použijeme první z nich φ(x, 0) = (0 + E k ω k ) X k (x) = 0. Z toho vyplývá, že E k = 0, k N, a tedy platí φ(x, t) = D k T k (t) X k (x) = 0, (3.23) 14
21 Řešení úloh pro 1D kontinuum Vlnová rovnice kde zbývá určit koeficienty D k. U druhé podmínky z (3.20) zvolíme fci g(x) jako nekonečnou řadu vlastních fcí, kde g k jsou konstantní koeficienty vlastních funkcí X k (x) g(x) = g k X k (x). Celou rovnost vynásobíme j-tou vlastni funkcí a zintegrujeme v intervalu [0, l]. l 0 g(x) X j (x) dx = = l 0 g k l g k X k (x) X j (x) dx 0 X k (x) X j (x) dx. (3.24) Víme, že systém vlastních funkcí je ortonormální. Pro skalární součin j-té a k-té vlastní funkce potom platí, když j k, že a když j = k l 0 X k (x) X j (x) dx = 0 l 0 X k (x) X k (x) dx = 1. Na pravé straně (3.24) zbude jediný člen řady, kdy k = j, a dostaneme předpis pro koeficinty g j řady zastupující funkci g(x) Nyní můžeme g(x) zapsat g j = l 0 g(x) X j (x) dx. g(x) = l 0 g(x) X k (x)dx X k (x). (3.25) Aplikujeme druhou počáteční podmínku z (3.20) na (3.23) g k X k (x) = D k cos(0) X k (x) g k X k (x) = D k X k (x) l l 2 D k = g k = g(x) X k (x)dx = g(x) cos (κx) dx, (3.26) 0 0 l l l 1 D 0 = g(x) X 0 (x)dx = g(x) l dx,
22 Řešení úloh pro 1D kontinuum Vlnová rovnice kde l 2 je norma vlastní fce. Celkové řešení rovnice (3.1) bude tedy mít tento tvar φ(x, t) = φ(x, t) = [ ] 2 D k cos(ω k t) cos (κx) l [ ( ) ( )] 2 kπc kπ g k cos t cos l l l x. (3.27) Pokud chceme nyní volit funkci g(x), tak musí splňovat okrajové podmínky (3.6). Když si zvolíme třeba g(x) = cos( 3π x), kde víme, že jde vlastní funkci pro k = 3. Z kolmosti l vlastních funkcí X k (x) a z (3.26) vyplývá, že jen pro k = 3 bude D k nenulové l ( ) 2 2 3π D 3 = cos 0 l l x dx (3.28) 2 l 2 D 3 = l 2 = l. Celkové řešení tedy nabude tvaru ( ) kπc φ(x, t) = D 3 cos t l ( ) kπ cos l x. (3.29) Řešení si zobrazíme pomocí Matlabu viz obr.(3.1) pro následující hodnoty parametrů l = 10 [m], c = 100 [m/s]. (3.30) Obrázek 3.1: Řešení vlnové rovnice pro 1D případ 16
23 Řešení úloh pro 1D kontinuum Helmholtzova rovnice Z obr.(3.1) je vidět, jak zvolená funkce g(x) splňuje z okrajových podmínek (3.6) nulové derivace. 3.2 Helmholtzova rovnice Uvažujeme jednofrekvenční časově harmonické řešení pro úhlovou frekvenci ω. Již dříve odvozenou HR (2.36) budeme řešit pro jednu prostorovou neznámou x. HR nabude tvaru ω 2 p(x) + c 2 p (x) = 0 p (x) + κ 2 p(x) = 0. (3.31) Řešíme opět 1D úlohu, kterou si lze představit jako vlnění mezi dvěma deskami. První deska v x = 0 bude kmitat frekvencí ω s amplitudou p A. Půjde tedy o případ vibroakustiky. Druhá deska bude nehybnou dokonale odrazivou překážkou, takže akustická rychlost zde musí být nulová. p (l) = 0, Dále si p(x) zvolíme jako součet dvou funkcí p (0) = iωp A. Pro funkce q(x) a q(x) volíme okrajové podmínky ve tvaru (3.32) p(x) = q(x) + q(x). (3.33) q (0) = iωp A, q (l) = 0, q (0) = 0, q (l) = 0. (3.34) Funkci q(x) zvolíme tak, aby splňovala výše uvedené okrajové podmínky ( π ) q(x) = iωp A sin 2l x. (3.35) A funkci q(x) budume uvažovat jako lineární kombinaci k vlastních funkcí určených Fourierovou metodou (3.18) s konstatními koeficienty H k q(x) = H k X k (x). (3.36) Když dosadíme za p(x) fuknkce q(x) a q(x), tak rovnice (3.31) dostane tvar ω 2 q(x) + ω 2 q(x) + c 2 q (x) + c 2 q (x) = 0 ω 2 q(x) + c 2 q(x) = (ω 2 q(x) + c 2 q (x)). (3.37) 17
24 Řešení úloh pro 1D kontinuum Helmholtzova rovnice Pravou stranu (3.31) označíme f(x) a zvolíme zase jako nekonečnou řadu vlastních funkcí s konstantami f k f(x) = (ω 2 q(x) + c 2 q (x)) = f k X k (x). (3.38) Koeficienty f k budeme uvažovat ve tvaru f k = l 0 f(x) X k (x) dx. (3.39) Po dosazení za pravou stranu můžeme celou rovnici vynásobit j-tou vlastní fcí a integrovat přes interval [0, l] l l ω 2 q(x) X j (x) dx + c 2 q (x) X j (x) dx = 0 0 ω 2 q(x) + c 2 q (x) = l 0 f k X k (x) (3.40) f k X k (x) X j (x) dx. (3.41) Víme, že vlastní fce jsou ortonormální, takže integrál ze součinu dvou vlastních fcí, k-té a j-té, je roven nule, pokud j k. Pokud platí j = k, skalární součin je roven jedné. Na pravé straně zbude tedy f j. Na levé dosadíme za q(x) a q (x). Víme, že ω 2 l 0 l H k X k (x) X j (x) dx + c 2 takže po dosazení (3.42) do (3.43) 0 H k X k (x) X j (x) dx = f j (3.42) c 2 X k (x) = ( λ k ) X k (x), (3.43) l ω 2 H k X k (x) X j (x) dx + l 0 0 H k ( λ k ) X k (x) X j (x) dx = f j H j (ω 2 λ j ) = f j. (3.44) Vyjádříme konstanty H j (dále už H k ) H k = f k ω 2 λ k = l 0 f(x) X k dx ω 2 λ k = l 0 ( ω2 q(x) c 2 q (x)) X k dx ω 2 λ k. (3.45) Níže určíme druhou derivaci funkce q(x) q(x) = iωp A 2l π sin ( π 2l x ) q (x) = iωp A π ( π ) 2l sin 2l x. (3.46) 18
25 Řešení úloh pro 1D kontinuum Helmholtzova rovnice Dopočteme koeficienty f k l ( 2ω 2 l f k = ( iωp A ) 0 π c2 π 2l 2 l ( π ) ( kπ ) f k = µ l sin 0 2l x cos l x dx = µ 2 2l f k = µ k > 0 l π (1 4k 2 ) 1 2l f 0 = µ k = 0, l π ) ( π ) ( kπ ) sin 2l x cos l x 2 l I 2 l dx (3.47) kde µ je konstanta ( ) 2ω 2 l iωp A π c2 π. (3.48) 2l Výpočet integrálu I jsme provedli metodou Per partes l ( π ) ( kπ ) I = sin 2l x cos l x dx I ( 1 1 4k 2 ) = 0 [ l ( π ) πk sin 2l x + 1 4k 2 l = l 2πk 2 2l I = π(1 4k 2 ) 0 ( kπ ) sin l x + l ( π ) sin 2l x cos Konstatní koeficienty H k mají tedy tvar ( π ) 2πk cos 2 2l x ( kπ ) l x dx ( kπ )] l cos l x + 0 k N. (3.49) H k = f k ω 2 ( kπc l ) 2 k > 0 H 0 = f 0 k = 0. ω 2 Nyní již známe vše a můžeme vyjádřit hledané řešení HR (3.31) p(x) = q(x) + q(x) ( π ) p(x) = H k X k (x) + iωp A sin 2l x. Na obr.(3.2) je zobrazeno řešení. Použili jsme tyto hodnoty parametrů l = 10 [m], ω = 750 [rad/s], c = 342 [m/s], p A = 20 [m/rad]. (3.50) (3.51) 19
26 Řešení úloh pro 1D kontinuum Helmholtzova rovnice Obrázek 3.2: Řešení Hemholtzovy rovnice pro 1D případ Je vidět, že všechny reálné části vychází nulové. Je to způsobeno tím, že jsme okrajovou podmínku z (3.32) 2, neboli buzení, zvolili imaginární. 20
27 4 Formulace úloh akustiky pro danou frekvenci ve 3D Pokud chceme řešit vlnovou rovnici pro akustický tlak (2.34) pro jednu danou frekvenci ω (jednofrekvenční řešení), musíme vlastně řešit Helmholtzovu rovnici (2.36) s vhodnými okrajovými podmínkami jako okrajovou úlohu. 4.1 Okrajová úloha K odvození okrajových podmínek využijeme oblast Ω (obr.(4.1)). Hranici označíme Ω. Platí Ω = Γ in Γ out Γ 0, kde Γ in je hranice vstupu incidenční vlny. Výstup z Ω představuje Γ out. Zbývající hranici označíme Γ 0. Půjde o pevnou dokonale odrazivou překážkou. n je vnější jednotkový normálový vektor hranice Ω. (Zde vyjdeme hlavně z [E. Bängtsson(2002)].) Obrázek 4.1: Obecná oblast Ω se vstupní hranicí Γ in, výstupní Γ out a dokonale odrazivou Γ 0 V praktických výpočtech je často dobré použít umělé okrajové podmínky, které omezí oblast výpočtu. Na Γ in, kde vniká incidenční vlna do oblasti Ω, by měla být určena její amplituda, zatímco odchozí, odražená vlna, by měla zůstat nepoznamenána. Necht x popisuje prostorové souřadnice. Předpokládáme, že jednofrekvenční rovinné vlny, procházející Γ in, můžeme zapsat ve tvaru P (x, t) = A e i(κ x n+ωt) + B e i( κ x n+ωt), A, B C, (4.1) kde první člen odpovídá incidenční vlně a druhý vlně odražené. Skalární součin vektorů 21
28 Form. úloh akust. pro danou frekv. ve 3D Slabé řešení x n = n je vlastně průmět x do n. Derivováním rovnice (4.1) dostaneme P t = Aiω e i(κ x n+ωt) + Biω e i( κ x n+ωt), (4.2) P n = Aiκ ei(κ x n+ωt) Biκ e i( κ x n+ωt), (4.3) kde P = n gradp popisuje derivaci ve směru vnější normály. Sečtením (4.2) a (4.3) n vynásobenou c a využitím ω = κ c získáme okrajovou podmínku na Γ in P t + c P n = 2iωA ei(κ x n+ωt). (4.4) Podmínka (4.4) je splněna pro každou vlnu typu (4.1) a může tedy být použita k nastavení amplitudy A incidenční vlny bez vlivu na amplitudu B vlny odražené. Vhodná absorbční okrajová podmínka na Γ out je radiační podmínka prvního stupně [B. Engquist(1977)]. Nebo můžeme uvažovat, že na výstupu není žádná incidenční vlna a tedy A = 0 P t + c P n = 0. (4.5) Tato podmínka nezpůsobí odraz vln na hranici Γ out jdoucích přímo přesně ve směru normály. Na zbylých hranicích Γ 0 předpokládáme akustický tvrdý materiál, takže budeme uvažovat podmínku P n = 0. (4.6) Pokud chceme řešit úlohu pro jednu frekvenci, uvažujeme řešení (2.35) jako v kapitole, kde jsme Helmhotzovu rovnici odvodili. Dosadíme do okrajových podmínek za P. Po zkrácení e iωt a za předpokladu, že na Γ in je v x = 0 získáme okrajové podmínky c p n + iωp = 0 na Γ out, c p n + iωp = 2iωA na Γ in, p n = 0 na Γ 0. (4.7) 4.2 Slabé řešení Při odvození slabého řešení, viz [Míka(2007)], vyjdeme z HR (2.36) pro akustický tlak p = p(x). Kde κ je vlnové číslo, ω je úhlová frekvence a c je rychlost šíření vlny prostředím (v tomhle případě jde o rychlost ve vzduchu), pro které platí κ = ω. HR celou vynásobíme c 22
29 Form. úloh akust. pro danou frekv. ve 3D Numerické řešení MKP testovacím tlakem q, kde q Q a Qje množina všech přípustných tlaků, které vyhovují okrajovým podmínkám (4.7) 2 p q + κ 2 p q = 0 q Q. (4.8) Celou rovnici integrujeme přes oblast Ω 2 p q dω + κ 2 p q dω = 0 q Q. (4.9) Využijeme následující Greenovy věty 2 p q dω = Ω Dosadíme (4.10) do (4.9) a dostaneme κ 2 p q dω + q p n d Ω Ω Ω Ω Ω Ω q p n d Ω q p dω. (4.10) Ω Ω q p dω = 0 q Q. (4.11) Po dosazení okrajových podmínek (4.7) do (4.11) dostaneme tento tvar slabého řešení q p dω κ 2 pq dω (2iκũ iκp)q dγ in + iκpq dγ out = 0 q Q (4.12). Γ in Γ out Ω Ω 4.3 Numerické řešení MKP s různými okrajovými podmínkami Výpočet budeme provádět v oblasti Ω (obr.(4.2)), kde Ω bude její hranice. Platí Ω = Γ in Γ out Γ 0, kde Γ in je hranice vstupu (červená linie), kde vzniká incidenční vlna. Γ out představuje výstup z Ω (modrá linie) a Γ 0 je dokonalé odrazivá stěna. 23
30 Form. úloh akust. pro danou frekv. ve 3D Numerické řešení MKP Obrázek 4.2: Popsaná použitá oblast Ω Obrázek 4.3: Detail MKP sítě oblasti Ω Na obr.(4.3) vidíme použitou sít MKP. Jako elementy jsme použili trojuhelníky. Celkem sít obsahuje uzlů a elemetů, a tudíž má stupňů volnosti. Budící funkci označím jako ũ. Použijeme následující okrajovou podmínku na Γ in. Budeme uvažovat buzení konstantou ũ = u A. (4.13) Buzení funkcí (4.13) interpretujeme jako kmitání desky vě směru osy x s amplitudou u A a úhlovou frekvencí ω. Parametry úlohy jsme si navolili c = 342 [m/s], ω = 500, 1000 [rad/s], κ = ω c [rad/m], u A = [ ], l = 10 [m], a = 4 [m], b = 2 [m], (4.14) kde l je délka hrany oblasti Ω, b šířka zvukovodů, a délka zvukovodů, c rychlost šíření zvuku ve vzduchu, ω úhlová frekvence a κ vlnové číslo. Pro úhlovou frekvenci ω jsme volili dvě hodnoty. Výpočet jsme prováděli v systému SfePy a výsledky zobrazili v programu ParaView. Sít MKP (obr.(4.3)) jsme vygenerovali v MSC.Marc/Mentat. Pro buzení jsme provedli výpočty pro dvě různé hodnoty ω viz (4.14). 24
31 Form. úloh akust. pro danou frekv. ve 3D Numerické řešení MKP Obrázek 4.4: Imaginární část p; Obrázek 4.5: Reálná část p; ω = 500 [rad/s], ũ = u A ω = 500 [rad/s], ũ = u A Obrázek 4.6: Graf znázorňující hodnoty podél přímky z A do B. ω = 500 [rad/s], ũ = u A Vyjdeme-li pro kontrolu ze vzorců T = λ/c a T = 2π/ω, kde λ je vlnová délka a T perioda, získáme vzorec pro λ: λ = 2πc/ω. Po dosazení ω = 500 [rad/s] a c = 342 [m/s] zjistíme, že λ = 4, 298 [m], což odpovídá obr.(4.4). 25
32 Form. úloh akust. pro danou frekv. ve 3D Numerické řešení MKP Obrázek 4.7: Imaginární část p; Obrázek 4.8: Reálná část p; ω = 1000 [rad/s], ũ = u A ω = 1000 [rad/s], ũ = u A Obrázek 4.9: Graf znázorňující hodnoty podél přímky z bodu A do bodu B. ω = 1000 [rad/s], ũ = u A Na obr.(4.9) je už lépe vidět, jak se vlivem kratší vlnové délky mění hladkost zobrazení gradientů. Nedokonalost je způsobena nedostatečnou hustotou sítě oblasti. 26
33 5 Formulace úloh tvarové optimalizace 5.1 Úvod V této kapitole formulujeme úlohu tvarové optimalizace pro akustické pole. Oblast Ω (obr.(5.1)) je rozdělena na dvě disjunktní podoblasti: platí Ω = Ω D Ω C, kde Ω D představuje takzvanou designovou oblast, a pro Ω C platí: Ω C = Ω \ Ω D. Hranice Ω je rozdělena na dílčí hranice Ω = Γ 0 Γ in Γ out. Na pravé hranici je designová hranice Γ D Γ 0 Ω. Tato designová hranice bude optimalizací měnit tvar a to následně ovlivní sít MKP v Ω D, ale už ne v Ω C. Změnou tvaru hranice Γ D, zprostředkovanou změnou parametrů α, se bude měnit řešení p v celé oblasti. Změna se projeví také na účelové funkci Φ, která se vyhodnocuje v Ω C. Obrázek 5.1: Popsaná oblast Ω Jako stavovou rovnici budeme uvažovat Hemholtzovu rovnici (2.36) pro akustický tlak p. Úlohu budeme řešit na Ω a použijeme na její hranici Ω již odvozené okrajové podmínky (4.7). Dále zavedeme slabou formulaci úlohy (viz (4.12)) Pomocí bilineární formy zapíšeme naši stavovou úlohu jako ( p, q) Ω κ 2 (p, q) Ω + iκp, q Γin Γ } {{ out 2iκũ, q } Γin = 0, (5.1) } {{ } Ψ(p,q) f(q) kterou můžeme zapsat v obstraktní formě Ψ(p, q) = f(q) p, q Q. (5.2) 27
34 Formulace úloh tvarové optimalizace Citlivostní analýza Uvažujeme následující optimalizační úlohu min α Φ(p), p Q : Ψ(p, q) = f(q) q Q, α U, γ : α Γ D, (5.3) kde p splňuje stavovou úlohu (5.2), Φ je účelová funkce a U je množina přípustných parametrů α. Zvolíme účelovou funkci Φ I (p) = p 2 = p 2 Ω c [P a 2 m 2 ], Ω c ( ) (5.4) p ΩA Φ II (p) = 20 log [db]. p ΩB 5.2 Citlivostní analýza Provedením citlivostní analýzy rozumíme výpočet citlivosti změny účelové funkce Φ v závislosti na změně optimalizačních parametrů α, když na nich závisí účelová funkce nepřímo prostřednictvím stavové proměnné p. Potřebujeme tedy vypočítat gradient funkce Φ(α, p(α)) podle jednotlivých optimalizačních parametrů α. Máme zde tedy implicitní funkci p = p(α). V oblasti Ω definujeme vektorové pole V, s pomocí Spline-boxu [Rohan(2007)] Metoda adjungované proměnné Zabývejme se nyní úlohou, kdy tvar hranice závisí na jediném parametru τ R Γ(τ) = Γ D + τ {V(x)} x ΓD, (5.5) kde x je prostorová souřadnice. Musí platit, že V(x) = 0 pro x Ω C a pro body na linii zvýrazněné černou přerušovanou čárou (viz obr.(5.1)). K problému (5.3) 2, v němž je α nahrazeno parametrem τ, můžeme přiřadit Lagrangeovu funkci L L τ (p, q) = Φ(p) + Ψ τ (p, q) f(q) + Ψ τ(p, q ) f (q ), (5.6) kde q je Lagrangeovův multiplikátor vazby splnění stavové úlohy. Poznamenejme, že pokud platí (5.3) 2 pro Ψ(p, q) = f(q), tak i pro Ψ (p, q) = f (q), kde * značí komplexně 28
35 Formulace úloh tvarové optimalizace Citlivostní analýza sdruženou hodnotu. Nyní formulujeme úlohu (5.3) jako úlohu sedlového bodu max q Q min L(α, p, q). (5.7) α U,p Q Rovnici (5.6) zderivujeme podle řešení p. Gâteauxovu derivaci, viz[drábek(1994)], podle p označíme δ p (derivace ve směru q) δ p L τ (p, q; δp) = δφ(p; δp) + Ψ τ (δp, q) + Ψ τ(δp, q ) } {{ } 2Re{Ψ τ (δp,q)}. (5.8) Pro splnění podmínky optimality se musí (5.8) rovnat nule. Dostaneme se k řešení adjungované úlohy pro adjungovanou proměnnou q Q 2Re {Ψ τ (δp, q)} δp Q = δφ(p; δp). (5.9) Adjungovanou úlohu můžeme řešit za předpokladu, že Φ R, pro p H 1 (Ω; C). Řešení adjungované úlohy je efektivní řešení nalezení gradientu účelové funkce. Účelovou funkci budeme vyhodnocovat na Ω C, tedy oblastí, která není ovlivněna změnou Γ D. Účelovou funkci zderivujeme podle řešení p { } δφ(p; δp) = [p(δp) + p δp] = 2Re (p δp). Ω C Ω C Proto můžeme (5.9) přepsat ve tvaru ( p, q) Ω κ 2 (p, q) Ω + iκp, q Γin Γ out + + p, q ) Ω κ 2 (p, q ) Ω iκp, q Γin Γ out = 2Re {Ψ(p, q)}. Zapíšeme adjungovanou úlohu takto pro účelovou funkci Φ definovanou dle Φ I, viz (5.4), { } Re {Ψ(ˆp, q)} = Re p q = 1 (pq + p q) q Q, (5.10) Ω C 2 Ω C kde ˆp označuje odjungovanou proměnnou. Vypočteme-li adjungovanou proměnnou, využijeme ji dále v (5.6) jako Lagrangeův multiplikátor a provedeme totální drivaci rovnice (5.6) podle τ δ τ L(p, ˆp) + δ p L(p, ˆp; δp) = δ } {{ } τ Φ(p) + δ τ (Ψ τ (p, ˆp) f(ˆp)) + δ τ (Ψ τ(p, ˆp ) f (ˆp )).(5.11) =0 Je-li splněna adjungovaná rovnice (5.9), tak druhý člen na levé straně (5.11) je roven nule a platí δφ = δψ. 29
36 Formulace úloh tvarové optimalizace Citlivostní analýza Výpočet citlivosti pomocí materiálové derivace V tomto odstavci vyjádříme členy v citlivostním vztahu (5.11) s využitím materiálové derivace známé z mechaniky kontinua, viz [Rohan(2012)],[E. Rohan(2012)],[E. Rohan(2010a)], [E. Rohan(2010b)]. Zavedeme zobrazení F parametrizované pomocí τ kde F(τ, ) : Ω Ω(τ), z(τ) = F(τ, x), (5.12) z = x + τv(x), x Ω, z Ω(τ), Ω(τ) = Ω + τ {V(x)} x Ω, J = det( x F), kde x F je Jacobiova matice zobrazení F. Platí, viz [Rohan(2012)] ( z p, z q) Ω(τ) = i z x k k x p j z x l l x qδ ij J(F), Ω (p, q) Ω(τ) = pqj((f )) a odtud plyne d ( z p, z q) Ω(τ) = dτ τ=0 d (p, q) Ω(τ) = dτ τ=0 Nyní označíme a(p, q) = m(p, q) = Ω Ω Ω Ω Ω (div( V)δ ij k V j δ ki δ ej e V i ) j p i q, pq div( V). (div( V)δ ij k V j δ ki δ ej e V i ) j p i q, pq div( V). Využili jsme těchto skutečností ( ) zi ( j F i ) = = ( j V i ) = ( V) x ij j x k = (z k τv k ) = δ ki τ V k, z i z i z i (5.13) (5.14) (5.15) (5.16) (5.17) F ij = F i x j, F F 1 = I F F 1 + F (F 1 ) = 0 (F 1 ) = F 1 F F 1 (F 1 ) τ=0 = F τ=0 = V, (5.18) 30
37 Formulace úloh tvarové optimalizace Implementace k V j = V j x k. (5.19) S využitím vztahů (5.16) již můžeme dosadit do (5.11). Dostaneme totální derivaci δφ vyjadřující derivaci účelové funkce ve směru vektorového pole V kde δφ = a(p, ˆp ) κ 2 m(p, ˆp ) + a(p, ˆp) κ 2 m(p, ˆp), (5.20) a(p, ˆp ) = m(p, ˆp ) = a(p, ˆp) = m(p, ˆp) = Ω Ω Ω Ω (div( V)δ ij k V j δ ki δ ej e V i ) j p iˆp, p ˆp div( V), (div( V)δ ij k V j δ ki δ ej e V i ) j p iˆp, pˆp div( V). (5.21) Touto cestou získáme úplnou derivaci účelové funkce Φ vůči α, tj. její citlivost. V (5.20) derivace δφ ve skutečnosti znamená d Φ dτ τ=0, kde Φ je implicitní funkce hranice Γ(τ) parametrizované vztahem (5.5) a závisí tedy na vektorovém poli V. 5.3 Implementace Adjungovaná úloha Výpočet citlivosti změny účelové funkce Φ jsme provedli ve SfePy. Řešení p a zkušební tlak q jsou komplexní hodnoty. Hvězdička znamená komplexně sdruženou hodnotu Později využijeme těchto rovností q = q r + i q i, q = q r i q i, p = p r + i p i, p = p r i p i. (5.22) p q = (pq) = ((p r q r q i p i ) + i(p r q i + p i q r )), ( p, q ) = ( p, q). (5.23) Reálné části v adjungované úloze (5.10) bude vhodné pro implementaci zapsat takto Re {( (p r + i p i ), (q r i q i )) Ω } = ( p r, q r ) Ω + ( p i, q i ) Ω, Re { κ 2 (p, q) Ω } = κ 2 [(p r, q r ) Ω + (p i, q i ) Ω ], Re { (i κp, q Γin Γ out ) } = κ [ p r, q i Γin Γ out + p i, q r Γin Γ out ]. (5.24) 31
38 Formulace úloh tvarové optimalizace Implementace Z účelové funkce Φ I také vybereme reálnou část { } 2Re p q = 2 (p r q r + p i q i ). (5.25) Ω C Ω C Využijeme (5.24), (5.25) a rozdělíme adjungovanou úlohu (5.10) na řešení zvlášt reálné a imaginární části. Zapíšeme maticově ( ) ( ) (, ) qr q Ω κ 2 T ) (, ) Ω κ, Γin Γ (ˆpr out i κ, Γin Γ out (, ) Ω κ 2 = ( ) ( ) (, p q (, ) Ω ˆp r q r ) Ωc i, i (, p i ) Ωc (5.26) což platí pro (q i, q r ) Q Příprava oblasti Ω V MSC.Marc/Mentat jsme vygenerovali MKP sít oblasti Ω se čtvercovými elementy Obrázek 5.2: Sít MKP oblasti Ω; Obrázek 5.3: Oblast Ω s podoblastmi Ω C, uzlů; elementů; stupňů volnosti Ω D, Ω A a Ω B V oblasti Ω budeme uvažovat, jak již bylo zmíněno dříve, podoblasti Ω C a Ω D. V Ω C zavedeme ještě Ω A Ω C a Ω B Ω C obě o šířce jen dva elementy. Účelové funkce Φ I a Φ II, viz (5.4), budeme vyhodnocovat přes Ω A a Ω B Spline-box Spline-box pomáhá vytvářet geometrickou parametrizaci 2D i 3D oblastí. Použili jsme spline-box implementovaný v systému SfePy. Využijeme ho k vytvoření parametrizace tvaru hranice Γ D při hledání jejího optimálního designu. Platí Ω D Ω, viz obr.(5.1), která je 32
39 Formulace úloh tvarové optimalizace Implementace tvořena 2D MKP sítí, viz obr.(5.2). Jako zdroj k tomuto tématu jsem využil [Rohan(2007)]. Uvažujeme oblast Ω D, viz obr.(5.1), a parametrizaci její hranice Γ D, viz (5.5). Spline 2D reprezentaci pro nezměněnou Ω 0 D zapíšeme x 0 (τ, s) = 4 i 4 N i (τ)n j (s) b 0 ij, (5.27) j kde N(τ) je B-spline báze svislých splinů a N(s) vodorovných. Počáteční polohu řídících bodů určuje b 0 ij. Polohu uzlů nezdeformované sítě popisuje x. Vytvořili jsem tedy nad Ω 0 D 2D Spline-box s 16 řídícími body, viz obr.(5.4) Obrázek 5.4: Umístění řídících bodů po vytvoření spline-boxu nad Ω D Změnu polohy řídících bodů popíšeme bij = b 0 ij + d ij α ij. (5.28) Směr změny umístění (pohybu) řídících bodů určují jednotkové vektory d ij a velikost této změny parametry α ij. Pro nenulové α ij platí x(τ, s) = 4 i 4 N i (τ)n j (s) b ij. (5.29) j Když zderivujeme (5.29) podle α ij, dostaneme Získáme tedy v Ω D vektorové pole V(τ, s) ij od parametru α ij x α ij = N i (τ)n j (s) d ij. (5.30) V(τ, s) ij = N i (τ)n j (s) d ij. (5.31) 33
40 Formulace úloh tvarové optimalizace Implementace V našem případě budeme měnit tvar jen hranice Ω D. Půjde tedy o 1D úlohu a budeme uvžovat jen 4 parametry α i, i = 1, 2, 3, 4. Ztotožníme parametry α i s τ. Z toho vyplývá, že úplná derivace účelové funkce Φ je vlastně derivací ve směru vektorového pole V. δ αi Φ = δ τ Φ = δφ V i. (5.32) S ohledem na obr.(5.4) budeme uvažovat posun řídících bodů ve vodorovném směru. Parametr α i proporcionálně řekne, o kolik se posune i-tá řada řídících bodů. Řídící body označím B i,j. Když bod B 4,4 posuneme o α 4 ve směru d 44 = ( 1, 0), tak B 3,4 se posune o 2/3α 4, B 2,4 o 1/3α 4 a B 1,4 o 0, viz obr.(5.5). Obrázek 5.5: Posun řady řídících bodů pro α Porovnání konečných diferencí a citlivostní analýzy Získání citlivosti účelové funkce Φ na parametrech α znamená získání totální derivace δ τ Φ. To jde nejen pomocí citlivostní analýzy (CA), ale také numericky pomocí konečných diferencí (KD). Druhá možnost výpočtu je však v optimalizaci výpočetně náročnější a méně přesná. Porovnáme KD s CA a ověříme si tím správnost výpočtu citlivosti účelové funkce pomocí CA. Při použití konečných diferencí budeme uvažovat velmi malou změnu dτ na hranici Γ D. Posuneme řídící body, viz obr.(5.4), na Γ D o dτ nejdříve ve směru d + = (1, 0) a poté d ( 1, 0). Ω + D = Ω D + dτ {V(x)} x ΩD, Ω D = Ω D dτ {V(x)} x ΩD. (5.33) Postupně vyhodnotíme účelovou funkci (5.4) 1 v nových oblastech Ω + a Ω. Získáme Φ + a Φ. Provedeme centrální poměrnou diferenci, jejíž výsledkem bude hledaná citlivost δ τ Φ = Φ+ Φ. (5.34) 2dτ Přesnost závisí samožřejmě na volbě velikosti dτ. Porovnali jsme výsledky cilivostní analýzy a konečných diferencí pro několik frekvencí ω na oblasti obr.(5.3). Výsledné citlivosti a jejich rozdíly jsou v následující tabulce. 34
41 Formulace úloh tvarové optimalizace Optimalizační výpočty dτ ω[rad s 1] Citlivostní analýza Konečné diference Rozdíl(CA-KD) 1e i i i e-11i i e-11i e-11i i e-11i e-11i i e-11i e-11i i e-11i Optimalizace Výpočet provedeme v softwaru SfePy a Matlab. SfePy bude vypočítávat citlivost účelové funkce na změnu parametrů α. Citlivost se předá Matlabu, kde se využije knihovní optimalizační funkce fmincon, viz [MathWorks(2013)], která použije citlivost k optimalizaci. Matlab bude vracet nové hodnoty optimalizovaných parametrů α do SfePy, kde začne další iterace. 5.4 Optimalizační výpočty Úvodem Výpočty budeme provádět na oblasti Ω (obr.(5.1)), rozdělené na podoblasti (obr.(5.3)). Na hranici Γ = Γ in Γ out Γ 0 použijeme okrajové podmínky (4.7). Zavedeme spline-box nad Ω D, viz obr.(5.4). Optimální tvar hranice Γ D budeme hledat pro minimum účelových funkcí Φ I a Φ II, viz (5.4). Platí Φ I (p) = p 2 = p 2 Ω A Ω B [P a 2 m 2 ], Ω A Ω B ( ) (5.35) p ΩA Φ II (p) = T AB (p) = 20 log [db], p ΩB kde Φ II se rovná funkci transmisních ztrát T AB, která řiká, o kolik decibelů [db] se utlumí (T AB > 0) nebo zesílí (T AB < 0) zvuková vlna jdoucí z Ω A do Ω B. Účelovou funkci Φ I budeme počítat přes Ω A Ω B a Φ II dle (5.35) 2. Výpočet provedeme pro tři úhlové frekvence ω = 200, 600, 1000 [rads 1 ]. 35
42 Formulace úloh tvarové optimalizace Optimalizační výpočty Parametry oblasti Ω navolíme následovně c = 342 [m/s], κ = ω c [rad/m], u A = 50 [ ], l = 15 [m], v = 10 [m], a = 5 [m], b = 2 [m]. (5.36) Vlastní výpočty Nejprve vypočteme řešení p v neoptimalizované oblasti Ω a získáme optimalizací neovlivněné hodnoty účelových funkcí Φ N I a Φ N II. Pak provedene optimalizace pro Φ I a Φ II. Z optimalizované oblasti Ω získáme optimalizované hodnoty účelových funkcí Φ O I a Φ O II. Zobrazíme závislost velikosti Φ na iteračním kroku. Toto provedeme pro všechny tři ω. Obrázek 5.6: Zobrazeno p v neoptimalizované oblasti Ω; ω = 200 [rads 1 ] Obrázek 5.7: Zobrazeno p v optimalizované oblasti Ω pro Φ I ; ω = 200 [rads 1 ] Obrázek 5.8: Zobrazeno p v optimalizované oblasti Ω pro Φ II ; ω = 200 [rads 1 ] 36
43 Formulace úloh tvarové optimalizace Optimalizační výpočty Obrázek 5.9: Graf závislosti hodnoty Φ I na iteračním kroku optimalizace Obrázek 5.10: Graf závislosti hodnoty Φ II na iteračním kroku optimalizace Obrázek 5.11: Zobrazeno p v neoptimalizované oblasti Ω; ω = 600 [rads 1 ] Obrázek 5.12: Zobrazeno p v optimalizované oblasti Ω pro Φ I ; ω = 600 [rads 1 ] Obrázek 5.13: Zobrazeno p v optimalizované oblasti Ω pro Φ II ; ω = 600 [rads 1 ] 37
44 Formulace úloh tvarové optimalizace Optimalizační výpočty Obrázek 5.14: Graf závislosti hodnoty Φ I na iteračním kroku optimalizace Obrázek 5.15: Graf závislosti hodnoty Φ II na iteračním kroku optimalizace Obrázek 5.16: Zobrazeno p v neoptimalizované oblasti Ω; ω = 1000 [rads 1 ] Obrázek 5.17: Zobrazeno p v optimalizované oblasti Ω pro Φ I ; ω = 1000 [rads 1 ] Obrázek 5.18: Zobrazeno p v optimalizované oblasti Ω pro Φ II ; ω = 1000 [rads 1 ] 38
45 Formulace úloh tvarové optimalizace Optimalizační výpočty Obrázek 5.19: Graf závislosti hodnoty Φ I na iteračním kroku optimalizace Obrázek 5.20: Graf závislosti hodnoty Φ II na iteračním kroku optimalizace Níže vidíme tabulku, která ukazuje hodnoty účelových funkcí (5.35) před (Φ N ) a po (Φ O ) optimalizaci a jejich procentuální srovnání, které řiká, o kolik procent se zvětšila či zmenšila hodnota Φ. ω [rad s 1] Φ N I [ Pa 2 m 2] Φ O I [ Pa 2 m 2] ±% Φ N II [db] ΦO II [db] ±% e e e e e e Podle tabulky vidíme, že optimalizace, podle očekávání, snížila hodnoty obou účelových funkcí pro všechny úhlové frekvence ω. Postup minimalizování Φ I,II je vidět z grafů, viz obrázky (5.9), (5.10), (5.14), (5.15), (5.19) a (5.20). Na obrázcích (5.7), (5.8), (5.12), (5.13), (5.17) a (5.18) je viditelná změna geometrie designové hranice Γ D, což zapříčinilo zřejmou změnu barevné mapy řešení. Některé výsledné optimalizované hodnoty Φ II jsou záporné, protože optimalizací se dosáhlo toho, že akustický tlak v Ω A je menší než v Ω B neboli p ΩA < p ΩB. Čímž nabývá logaritmus (5.35) 2 záporné hodnoty. 39
46 6 Závěr V druhé kapitole jsme se seznámili s odvozením rovnic potřebných k získání vlnové rovnice pro tekutiny: Eulerovo pohybovou rovnicí, rovnicí kontinuity, stavovou rovnicí. Z nich jsme odvodili vlnovou rovnici a následně i Helmholtzovu rovnici pro stojaté vlnění. V třetí kapitole jsme analyticky vyřešili vlnovou a Helmholtzovu rovnici v 1D pomocí Fourierovu metody a zobrazili některá řešení v Matlabu. Ve čtvrté kapitole jsme řešili slabé formulace Helmholtzovy rovnice na oblasti Ω. Z úvah o šíření akustických vln jsme si odvodili okrajové podmínky na hranici Ω, pomocí MKP provedli řešení v systému SfePy. Na dané oblasti jsme vyzkoušeli různé frekvence ω incidenční vlny. Řešení jsme si zobrazili v programu ParaView. V páté kapitole jsme naformulovali úlohu tvarové optimalizace pro akustické pole, zparametrizovali design pomocí spline-boxu. Zavedli pole designových rychlostí. Optimalizační úloze jsme přiřadili Lagrangeovu funkci a přešli k řešení adjungované úlohy. Porovnali jsme pro kontrolu výsledky citlivostní analýzy a konečných diferencí. Oba přístupy jsme implementovali ve SfePy. Ujistili jsme se, že výsledky citlivostní analýzy a konečných diferencí si celkem odpovídají. V závěru kapitoly jsme provedli několik optimalizačních výpočtů ve 2D oblasti Ω v Matlabu a SfePy pro několik frekvencí ω. Využili jsme dvě účelové funkce Φ I,II. Našli jsme několik optimálních tvarů designové hranice Ω D. Výsledky jsme zobrazili programem ParaView. Vykreslili jsme závislosti hodnot Φ I,II na iteraci optimalizace. Z grafů je vidět, že hodnoty správně klesly u všech výpočtů. Vypočetli jsme, o kolik procent klesly optimalizací hodnoty Φ I,II. Zprovoznili jsme tedy úspěšně tvarovou optimalizaci akustického pole. Práce nemá zatím určitou konkrétní aplikaci. Jde v ní spíše jen o zprovoznění a vyzkoušení samotné optimalizace. Má určitě mnoho prostoru pro vylepšení a rozšíření. Třeba převedení na vícerozměrnou úlohu se složitější geometrií, kde se objeví více optimalizačních parametrů. Poté by se našla určitě nějaká potenciální aplikace pro tuto práci. Jednou z možností je optimalizace tvaru skříně nějakého stroje. Ve skříni bude zdroj vibrací (nějaká nevyvážená rotující hmotnost), které se budou konstrukcí přenášet na skříň, tím by vznikala emise hluku, kterou bychom chtěli regulovat. V tomto směru by mohla pokračovat má další práce. 40
9. Úvod do teorie PDR
 9. Úvod do teorie PDR A. Základní poznatky o soustavách ODR1 Diferenciální rovnici nazveme parciální, jestliže neznámá funkce závisí na dvou či více proměnných (příslušná rovnice tedy obsahuje parciální
9. Úvod do teorie PDR A. Základní poznatky o soustavách ODR1 Diferenciální rovnici nazveme parciální, jestliže neznámá funkce závisí na dvou či více proměnných (příslušná rovnice tedy obsahuje parciální
Vedení tepla v MKP. Konstantní tepelné toky. Analogické úlohám statiky v mechanice kontinua
 Vedení tepla v MKP Stacionární úlohy (viz dále) Konstantní tepelné toky Analogické úlohám statiky v mechanice kontinua Nestacionární úlohy (analogické dynamice stavebních konstrukcí) 1 Základní rovnice
Vedení tepla v MKP Stacionární úlohy (viz dále) Konstantní tepelné toky Analogické úlohám statiky v mechanice kontinua Nestacionární úlohy (analogické dynamice stavebních konstrukcí) 1 Základní rovnice
BAKALÁŘSKÁ PRÁCE. Numerické metody jednorozměrné minimalizace
 UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY BAKALÁŘSKÁ PRÁCE Numerické metody jednorozměrné minimalizace Vedoucí bakalářské práce: RNDr. Horymír
UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY BAKALÁŘSKÁ PRÁCE Numerické metody jednorozměrné minimalizace Vedoucí bakalářské práce: RNDr. Horymír
K přednášce NUFY028 Teoretická mechanika prozatímní učební text, verze 01 10. Spojitá prostředí: rovnice struny Leoš Dvořák, MFF UK Praha, 2014
 K přednášce NUFY8 Teoretická mechanika prozatímní učební text, verze 1 1 Spojitá prostředí: rovnice strun Leoš Dvořák, MFF UK Praha, 14 Spojitá prostředí: rovnice strun Dosud jsme se zabývali pohbem soustav
K přednášce NUFY8 Teoretická mechanika prozatímní učební text, verze 1 1 Spojitá prostředí: rovnice strun Leoš Dvořák, MFF UK Praha, 14 Spojitá prostředí: rovnice strun Dosud jsme se zabývali pohbem soustav
Řešené úlohy ze statistické fyziky a termodynamiky
 Řešené úlohy ze statistické fyziky a termodynamiky Statistická fyzika. Uvažujme dvouhladinový systém, např. atom s celkovým momentem hybnosti h v magnetickém ) ) poli. Bázové stavy označme = a =, první
Řešené úlohy ze statistické fyziky a termodynamiky Statistická fyzika. Uvažujme dvouhladinový systém, např. atom s celkovým momentem hybnosti h v magnetickém ) ) poli. Bázové stavy označme = a =, první
1. Alternativní rozdělení A(p) (Bernoulli) je diskrétní rozdělení, kdy. p(0) = P (X = 0) = 1 p, p(1) = P (X = 1) = p, 0 < p < 1.
 2. Některá důležitá rozdělení Diskrétní rozdělení. Alternativní rozdělení Ap) Bernoulli) je diskrétní rozdělení, kdy náhodná veličina X nabývá pouze dvou hodnot a a pro její pravděpodobnostní funkci platí:
2. Některá důležitá rozdělení Diskrétní rozdělení. Alternativní rozdělení Ap) Bernoulli) je diskrétní rozdělení, kdy náhodná veličina X nabývá pouze dvou hodnot a a pro její pravděpodobnostní funkci platí:
Funkce zadané implicitně
 Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
+ ω y = 0 pohybová rovnice tlumených kmitů. r dr dt. B m. k m. Tlumené kmity
 Tlumené kmit V praxi téměř vžd brání pohbu nějaká brzdicí síla, jejíž původ je v třecích silách mezi reálnými těles. Matematický popis těchto sil bývá dosti komplikovaný. Velmi často se vsktuje tzv. viskózní
Tlumené kmit V praxi téměř vžd brání pohbu nějaká brzdicí síla, jejíž původ je v třecích silách mezi reálnými těles. Matematický popis těchto sil bývá dosti komplikovaný. Velmi často se vsktuje tzv. viskózní
CVIČENÍ č. 3 STATIKA TEKUTIN
 Rovnováha, Síly na rovinné stěny CVIČENÍ č. 3 STATIKA TEKUTIN Příklad č. 1: Nákladní automobil s cisternou ve tvaru kvádru o rozměrech H x L x B se pohybuje přímočarým pohybem po nakloněné rovině se zrychlením
Rovnováha, Síly na rovinné stěny CVIČENÍ č. 3 STATIKA TEKUTIN Příklad č. 1: Nákladní automobil s cisternou ve tvaru kvádru o rozměrech H x L x B se pohybuje přímočarým pohybem po nakloněné rovině se zrychlením
MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z. Obsah. 1. Parciální diferenciální rovnice obecně. 2. Kvaazilineární rovnice prvního řádu
 MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Parciální diferenciální rovnice obecně 1. Kvaazilineární rovnice prvního řádu 1 3. Lineární rovnice druhého řádu
MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Parciální diferenciální rovnice obecně 1. Kvaazilineární rovnice prvního řádu 1 3. Lineární rovnice druhého řádu
Elektronický učební text pro podporu výuky klasické mechaniky pro posluchače učitelství I. Mechanika hmotného bodu
 Elektronický učební text pro podporu výuky klasické mechaniky pro posluchače učitelství I Mechanika hmotného bodu Autor: Kateřina Kárová Text vznikl v rámci bakalářské práce roku 2006. Návod na práci s
Elektronický učební text pro podporu výuky klasické mechaniky pro posluchače učitelství I Mechanika hmotného bodu Autor: Kateřina Kárová Text vznikl v rámci bakalářské práce roku 2006. Návod na práci s
Projekty do předmětu MF
 Univerzita Palackého v Olomouci Přírodovědecká fakulta Katedra optiky ZÁVĚREČNÁ PRÁCE Projekty do předmětu MF Vypracoval: Miroslav Mlynář E-mail: mlynarm@centrum.cz Studijní program: B1701 Fyzika Studijní
Univerzita Palackého v Olomouci Přírodovědecká fakulta Katedra optiky ZÁVĚREČNÁ PRÁCE Projekty do předmětu MF Vypracoval: Miroslav Mlynář E-mail: mlynarm@centrum.cz Studijní program: B1701 Fyzika Studijní
3.2 Rovnice postupné vlny v bodové řadě a v prostoru
 3 Vlny 3.1 Úvod Vlnění můžeme pozorovat například na vodní hladině, hodíme-li do vody kámen. Mechanické vlnění je děj, při kterém se kmitání šíří látkovým prostředím. To znamená, že například zvuk, který
3 Vlny 3.1 Úvod Vlnění můžeme pozorovat například na vodní hladině, hodíme-li do vody kámen. Mechanické vlnění je děj, při kterém se kmitání šíří látkovým prostředím. To znamená, že například zvuk, který
Fyzikální praktikum 1
 Fyzikální praktikum 1 FJFI ČVUT v Praze Úloha: #9 Základní experimenty akustiky Jméno: Ondřej Finke Datum měření: 3.11.014 Kruh: FE Skupina: 4 Klasifikace: 1. Pracovní úkoly (a) V domácí přípravě spočítejte,
Fyzikální praktikum 1 FJFI ČVUT v Praze Úloha: #9 Základní experimenty akustiky Jméno: Ondřej Finke Datum měření: 3.11.014 Kruh: FE Skupina: 4 Klasifikace: 1. Pracovní úkoly (a) V domácí přípravě spočítejte,
AKUSTICK E JEVY V KONTINU ICH Petr Hora 30. kvˇ etna 2001
 AKUSTICKÉ JEVY V KONTINUÍCH Petr Hora 30. května 2001 Tento text obsahuje sylabus přednášek z předmětu Akustické jevy v kontinuích (AJK), který se přednáší na Fakultě aplikovaných věd Západočeské univerzity
AKUSTICKÉ JEVY V KONTINUÍCH Petr Hora 30. května 2001 Tento text obsahuje sylabus přednášek z předmětu Akustické jevy v kontinuích (AJK), který se přednáší na Fakultě aplikovaných věd Západočeské univerzity
Měřicí a řídicí technika Bakalářské studium 2007/2008. odezva. odhad chování procesu. formální matematický vztah s neznámými parametry
 MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
6. T e s t o v á n í h y p o t é z
 6. T e s t o v á n í h y p o t é z Na základě hodnot z realizace náhodného výběru činíme rozhodnutí o platnosti hypotézy o hodnotách parametrů rozdělení nebo o jeho vlastnostech. Používáme k tomu vhodně
6. T e s t o v á n í h y p o t é z Na základě hodnot z realizace náhodného výběru činíme rozhodnutí o platnosti hypotézy o hodnotách parametrů rozdělení nebo o jeho vlastnostech. Používáme k tomu vhodně
Základní radiometrické veličiny
 Základní radiometrické veličiny Radiometrické veličiny se v textech, se kterými jsem se setkal, zavádějí velmi formálně, např. iradiance E= dφ da.pokusiljsemsepřesnějipopsat,cojednotlivéfunkceznamenají.formálnízápisyjsouzde
Základní radiometrické veličiny Radiometrické veličiny se v textech, se kterými jsem se setkal, zavádějí velmi formálně, např. iradiance E= dφ da.pokusiljsemsepřesnějipopsat,cojednotlivéfunkceznamenají.formálnízápisyjsouzde
1. Pravděpodobnost a statistika (MP leden 2010)
 1. Pravděpodobnost a statistika (MP leden 2010) Pravděpodobnost pojmy 1. Diskrétní pravděpodobnostní prostor(definice, vlastnosti, příklad). Diskrétní pravděpodobnostní prostor je trojice(ω, A, P), kde
1. Pravděpodobnost a statistika (MP leden 2010) Pravděpodobnost pojmy 1. Diskrétní pravděpodobnostní prostor(definice, vlastnosti, příklad). Diskrétní pravděpodobnostní prostor je trojice(ω, A, P), kde
FAKULTA STAVEBNÍ MATEMATIKA II MODUL 2 STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ MATEMATIKA II MODUL KŘIVKOVÉ INTEGRÁLY STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Typeset by L A TEX ε c Josef Daněček, Oldřich Dlouhý,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ MATEMATIKA II MODUL KŘIVKOVÉ INTEGRÁLY STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Typeset by L A TEX ε c Josef Daněček, Oldřich Dlouhý,
Jazyk matematiky. 2.1. Matematická logika. 2.2. Množinové operace. 2.3. Zobrazení. 2.4. Rozšířená číslená osa
 2. Jazyk matematiky 2.1. Matematická logika 2.2. Množinové operace 2.3. Zobrazení 2.4. Rozšířená číslená osa 1 2.1 Matematická logika 2.1.1 Výrokový počet logická operace zapisujeme čteme česky negace
2. Jazyk matematiky 2.1. Matematická logika 2.2. Množinové operace 2.3. Zobrazení 2.4. Rozšířená číslená osa 1 2.1 Matematická logika 2.1.1 Výrokový počet logická operace zapisujeme čteme česky negace
Euklidovský prostor Stručnější verze
 [1] Euklidovský prostor Stručnější verze definice Eulidovského prostoru kartézský souřadnicový systém vektorový součin v E 3 vlastnosti přímek a rovin v E 3 a) eprostor-v2, 16, b) P. Olšák, FEL ČVUT, c)
[1] Euklidovský prostor Stručnější verze definice Eulidovského prostoru kartézský souřadnicový systém vektorový součin v E 3 vlastnosti přímek a rovin v E 3 a) eprostor-v2, 16, b) P. Olšák, FEL ČVUT, c)
ELEKTRICKÉ SVĚTLO 1 Řešené příklady
 ČESKÉ VYSOKÉ UČENÍ TECHNCKÉ V PRAE FAKULTA ELEKTROTECHNCKÁ magisterský studijní program nteligentní budovy ELEKTRCKÉ SVĚTLO Řešené příklady Prof. ng. Jiří Habel DrSc. a kolektiv Praha Předmluva Předkládaná
ČESKÉ VYSOKÉ UČENÍ TECHNCKÉ V PRAE FAKULTA ELEKTROTECHNCKÁ magisterský studijní program nteligentní budovy ELEKTRCKÉ SVĚTLO Řešené příklady Prof. ng. Jiří Habel DrSc. a kolektiv Praha Předmluva Předkládaná
ELEKTŘINA A MAGNETIZMUS
 EEKTŘINA A MAGNETIZMUS XII Střídavé obvody Obsah STŘÍDAÉ OBODY ZDOJE STŘÍDAÉHO NAPĚTÍ JEDNODUHÉ STŘÍDAÉ OBODY EZISTO JAKO ZÁTĚŽ 3 ÍKA JAKO ZÁTĚŽ 5 3 KONDENZÁTO JAKO ZÁTĚŽ 6 3 SÉIOÝ OBOD 7 3 IMPEDANE 3
EEKTŘINA A MAGNETIZMUS XII Střídavé obvody Obsah STŘÍDAÉ OBODY ZDOJE STŘÍDAÉHO NAPĚTÍ JEDNODUHÉ STŘÍDAÉ OBODY EZISTO JAKO ZÁTĚŽ 3 ÍKA JAKO ZÁTĚŽ 5 3 KONDENZÁTO JAKO ZÁTĚŽ 6 3 SÉIOÝ OBOD 7 3 IMPEDANE 3
Část 3. Literatura : Otakar Maštovský; HYDROMECHANIKA Jaromír Noskijevič, MECHANIKA TEKUTIN František Šob; HYDROMECHANIKA
 HYDROMECHANIKA HYDROSTATIKA základní zákon hdrostatik Část 3 Literatura : Otakar Maštovský; HYDROMECHANIKA Jaromír Noskijevič, MECHANIKA TEKUTIN František Šob; HYDROMECHANIKA Hdrostatika - obsah Základn
HYDROMECHANIKA HYDROSTATIKA základní zákon hdrostatik Část 3 Literatura : Otakar Maštovský; HYDROMECHANIKA Jaromír Noskijevič, MECHANIKA TEKUTIN František Šob; HYDROMECHANIKA Hdrostatika - obsah Základn
(Auto)korelační funkce. 2. 11. 2015 Statistické vyhodnocování exp. dat M. Čada www.fzu.cz/ ~ cada
 (Auto)korelační funkce 1 Náhodné procesy Korelace mezi náhodnými proměnnými má široké uplatnění v elektrotechnické praxi, kde se snažíme o porovnávání dvou signálů, které by měly být stejné. Příkladem
(Auto)korelační funkce 1 Náhodné procesy Korelace mezi náhodnými proměnnými má široké uplatnění v elektrotechnické praxi, kde se snažíme o porovnávání dvou signálů, které by měly být stejné. Příkladem
DYNAMICKÁ ANALÝZA A OPTIMALIZACE
 Závěrečná výzkumná zpráva z řešení projektu FRVŠ 2282/2003/G1 DYNAMICKÁ ANALÝZA A OPTIMALIZACE PŘEVODOVÝCH ÚSTROJÍ Michal HAJŽMAN Miroslav BYRTUS Vladimír ZEMAN Katedra mechaniky, Univerzitní 22, 30614,
Závěrečná výzkumná zpráva z řešení projektu FRVŠ 2282/2003/G1 DYNAMICKÁ ANALÝZA A OPTIMALIZACE PŘEVODOVÝCH ÚSTROJÍ Michal HAJŽMAN Miroslav BYRTUS Vladimír ZEMAN Katedra mechaniky, Univerzitní 22, 30614,
Vybrané problémy lineární algebry v programu Maple
 UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA Katedra matematické analýzy a aplikací matematiky BAKALÁŘSKÁ PRÁCE Vybrané problémy lineární algebry v programu Maple Vedoucí bakalářské práce: RNDr.
UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA Katedra matematické analýzy a aplikací matematiky BAKALÁŘSKÁ PRÁCE Vybrané problémy lineární algebry v programu Maple Vedoucí bakalářské práce: RNDr.
Akustika. Rychlost zvukové vlny v v prostředí s hustotou ρ a modulem objemové pružnosti K
 zvuk každé mechanické vlnění v látkovém prostředí, které je schopno vyvolat v lidském uchu sluchový vjem akustika zabývá se fyzikálními ději spojenými se vznikem zvukového vlnění, jeho šířením a vnímáním
zvuk každé mechanické vlnění v látkovém prostředí, které je schopno vyvolat v lidském uchu sluchový vjem akustika zabývá se fyzikálními ději spojenými se vznikem zvukového vlnění, jeho šířením a vnímáním
ČÁST VI - K M I T Y A V L N Y
 ČÁST VI - K M I T Y A V L N Y 23. Harmonický oscilátor 24. Vlnění 25. Elektromagnetické vlnění 26. Geometrická optika 27. Fyzikální optika 28. Nelineární optika 261 Periodické pohyby částic a těles (jako
ČÁST VI - K M I T Y A V L N Y 23. Harmonický oscilátor 24. Vlnění 25. Elektromagnetické vlnění 26. Geometrická optika 27. Fyzikální optika 28. Nelineární optika 261 Periodické pohyby částic a těles (jako
Světlo v multimódových optických vláknech
 Světlo v multimódových optických vláknech Tomáš Tyc Ústav teoretické fyziky a astrofyziky, Masarykova univerzita, Kotlářská 2, 61137 Brno Úvod Optické vlákno je pozoruhodný fyzikální systém: téměř dokonalý
Světlo v multimódových optických vláknech Tomáš Tyc Ústav teoretické fyziky a astrofyziky, Masarykova univerzita, Kotlářská 2, 61137 Brno Úvod Optické vlákno je pozoruhodný fyzikální systém: téměř dokonalý
ELEKTRICKÉ SVĚTLO 1 Řešené příklady
 ČESKÉ VYSOKÉ UČENÍ TECHNCKÉ V PRAE FAKULTA ELEKTROTECHNCKÁ magisterský studijní program nteligentní budovy ELEKTRCKÉ SVĚTLO Řešené příklady Prof. ng. Jiří Habel DrSc. a kolektiv Praha Předmluva Předkládaná
ČESKÉ VYSOKÉ UČENÍ TECHNCKÉ V PRAE FAKULTA ELEKTROTECHNCKÁ magisterský studijní program nteligentní budovy ELEKTRCKÉ SVĚTLO Řešené příklady Prof. ng. Jiří Habel DrSc. a kolektiv Praha Předmluva Předkládaná
Západočeská univerzita v Plzni. Fakulta aplikovaných věd Katedra matematiky. Geometrie pro FST 1. Pomocný učební text
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky Geometrie pro FST 1 Pomocný učební text František Ježek, Marta Míková, Světlana Tomiczková Plzeň 29. srpna 2005 verze 1.0 Předmluva
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky Geometrie pro FST 1 Pomocný učební text František Ježek, Marta Míková, Světlana Tomiczková Plzeň 29. srpna 2005 verze 1.0 Předmluva
6. Střídavý proud. 6. 1. Sinusových průběh
 6. Střídavý proud - je takový proud, který mění v čase svoji velikost a smysl. Nejsnáze řešitelný střídavý proud matematicky i graficky je sinusový střídavý proud, který vyplývá z konstrukce sinusovky.
6. Střídavý proud - je takový proud, který mění v čase svoji velikost a smysl. Nejsnáze řešitelný střídavý proud matematicky i graficky je sinusový střídavý proud, který vyplývá z konstrukce sinusovky.
Některé zákony rozdělení pravděpodobnosti. 1. Binomické rozdělení
 Přednáška 5/1 Některé zákony rozdělení pravděpodobnosti 1. Binomické rozdělení Předpoklady: (a) pst výskytu jevu A v jediném pokuse P (A) = π, (b) je uskutečněno n pokusů, (c) pokusy jsou nezávislé, tj.
Přednáška 5/1 Některé zákony rozdělení pravděpodobnosti 1. Binomické rozdělení Předpoklady: (a) pst výskytu jevu A v jediném pokuse P (A) = π, (b) je uskutečněno n pokusů, (c) pokusy jsou nezávislé, tj.
MASARYKOVA UNIVERZITA. Michal Burián
 MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA Modelování vyzařovací charakteristiky ultrazvukových měničů BAKALÁŘSKÁ PRÁCE Michal Burián Brno, jaro 2009 Prohlášení Prohlašuji, že tato bakalářská práce je
MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA Modelování vyzařovací charakteristiky ultrazvukových měničů BAKALÁŘSKÁ PRÁCE Michal Burián Brno, jaro 2009 Prohlášení Prohlašuji, že tato bakalářská práce je
Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech.
 Kapitola 9 Skalární součin Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech. Definice 9.1 Je-li x = (x 1,..., x n ) T R n 1 reálný
Kapitola 9 Skalární součin Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech. Definice 9.1 Je-li x = (x 1,..., x n ) T R n 1 reálný
Několik poznámek na téma lineární algebry pro studenty fyzikální chemie
 Několik poznámek na téma lineární algebry pro studenty fyzikální chemie Jiří Kolafa Vektory. Vektorový prostor Vektor je často zaveden jako n-tice čísel, (v,..., v n ), v i R (pro reálný vektorový prostor);
Několik poznámek na téma lineární algebry pro studenty fyzikální chemie Jiří Kolafa Vektory. Vektorový prostor Vektor je často zaveden jako n-tice čísel, (v,..., v n ), v i R (pro reálný vektorový prostor);
Západočeská univerzita v Plzni Fakulta aplikovaných věd KKY/LS2. Plzeň, 2008 Pavel Jedlička
 Západočeská univerzita v Plzni Fakulta aplikovaných věd KKY/LS2 Semestrální práce Plzeň, 2008 Jan Krčmář Pavel Jedlička 1 Měřený model Je zadán systém (1), který budeme diskretizovat použitím funkce c2d
Západočeská univerzita v Plzni Fakulta aplikovaných věd KKY/LS2 Semestrální práce Plzeň, 2008 Jan Krčmář Pavel Jedlička 1 Měřený model Je zadán systém (1), který budeme diskretizovat použitím funkce c2d
Západočeská univerzita. Lineární systémy 2
 Západočeská univerzita FAKULTA APLIKOVANÝCH VĚD Lineární systémy Semestrální práce vypracoval: Jan Popelka, Jiří Pročka 1. květen 008 skupina: pondělí 7-8 hodina 1) a) Jelikož byly měřící přípravky nefunkční,
Západočeská univerzita FAKULTA APLIKOVANÝCH VĚD Lineární systémy Semestrální práce vypracoval: Jan Popelka, Jiří Pročka 1. květen 008 skupina: pondělí 7-8 hodina 1) a) Jelikož byly měřící přípravky nefunkční,
Řízení a regulace II. Analýza a řízení nelineárních systémů Verze 1.34 8. listopadu 2004
 Řízení a regulace II Analýza a řízení nelineárních systémů Verze 1.34 8. listopadu 2004 Prof. Ing. František Šolc, CSc. Ing. Pavel Václavek, Ph.D. Prof. Ing. Petr Vavřín, DrSc. ÚSTAV AUTOMATIZACE A MĚŘICÍ
Řízení a regulace II Analýza a řízení nelineárních systémů Verze 1.34 8. listopadu 2004 Prof. Ing. František Šolc, CSc. Ing. Pavel Václavek, Ph.D. Prof. Ing. Petr Vavřín, DrSc. ÚSTAV AUTOMATIZACE A MĚŘICÍ
Ideální krystalová mřížka periodický potenciál v krystalu. pásová struktura polovodiče
 Cvičení 3 Ideální krystalová mřížka periodický potenciál v krystalu Aplikace kvantové mechaniky pásová struktura polovodiče Nosiče náboje v polovodiči hustota stavů obsazovací funkce, Fermiho hladina koncentrace
Cvičení 3 Ideální krystalová mřížka periodický potenciál v krystalu Aplikace kvantové mechaniky pásová struktura polovodiče Nosiče náboje v polovodiči hustota stavů obsazovací funkce, Fermiho hladina koncentrace
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Měření Poissonovy konstanty vzduchu. Abstrakt
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Úloha 4: Měření dutých objemů vážením a kompresí plynu Datum měření: 23. 10. 2009 Měření Poissonovy konstanty vzduchu Jméno: Jiří Slabý Pracovní skupina: 1 Ročník
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Úloha 4: Měření dutých objemů vážením a kompresí plynu Datum měření: 23. 10. 2009 Měření Poissonovy konstanty vzduchu Jméno: Jiří Slabý Pracovní skupina: 1 Ročník
plynu, Měření Poissonovy konstanty vzduchu
 Úloha 4: Měření dutých objemů vážením a kompresí plynu, Měření Poissonovy konstanty vzduchu FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 2.11.2009 Jméno: František Batysta Pracovní skupina: 11 Ročník
Úloha 4: Měření dutých objemů vážením a kompresí plynu, Měření Poissonovy konstanty vzduchu FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 2.11.2009 Jméno: František Batysta Pracovní skupina: 11 Ročník
Experimentální metody EVF II.: Mikrovlnná
 Experimentální metody EVF II.: Mikrovlnná měření parametrů plazmatu Vypracovali: Štěpán Roučka, Jan Klusoň Zadání: Měření admitance kolíku impedančního transformátoru v závislosti na hloubce zapuštění.
Experimentální metody EVF II.: Mikrovlnná měření parametrů plazmatu Vypracovali: Štěpán Roučka, Jan Klusoň Zadání: Měření admitance kolíku impedančního transformátoru v závislosti na hloubce zapuštění.
http://user.mendelu.cz/marik, kde je dostupný ve formě vhodné pro tisk i ve formě vhodné pro prohlížení na obrazovce a z adresy http://is.mendelu.
 Inženýrská matematika Robert Mařík Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného základu (reg.
Inženýrská matematika Robert Mařík Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného základu (reg.
A NUMERICKÉ METODY. Matice derivací: ( ) ( ) Volím x 0 = 0, y 0 = -2.
 A NUMERICKÉ METODY Fourierova podmínka: f (x) > 0 => rostoucí, f (x) < 0 => klesající, f (x) > 0 => konvexní ᴗ, f (x) < 0 => konkávní ᴖ, f (x) = 0 ᴧ f (x)!= 0 => inflexní bod 1. Řešení nelineárních rovnic:
A NUMERICKÉ METODY Fourierova podmínka: f (x) > 0 => rostoucí, f (x) < 0 => klesající, f (x) > 0 => konvexní ᴗ, f (x) < 0 => konkávní ᴖ, f (x) = 0 ᴧ f (x)!= 0 => inflexní bod 1. Řešení nelineárních rovnic:
Poznámky z matematiky
 Poznámky z matematiky Verze: 14. dubna 2015 Petr Hasil hasil@mendelu.cz http://user.mendelu.cz/hasil/ Ústav matematiky Lesnická a dřevařská fakulta Mendelova univerzita v Brně Vytvořeno s podporou projektu
Poznámky z matematiky Verze: 14. dubna 2015 Petr Hasil hasil@mendelu.cz http://user.mendelu.cz/hasil/ Ústav matematiky Lesnická a dřevařská fakulta Mendelova univerzita v Brně Vytvořeno s podporou projektu
Geometrie pro FST 2. Plzeň, 28. srpna 2013, verze 6.0
 Geometrie pro FST 2 Pomocný učební text František Ježek, Světlana Tomiczková Plzeň, 28. srpna 2013, verze 6.0 Předmluva Tento pomocný text vznikl pro potřeby předmětu Geometrie pro FST 2, který vyučujeme
Geometrie pro FST 2 Pomocný učební text František Ježek, Světlana Tomiczková Plzeň, 28. srpna 2013, verze 6.0 Předmluva Tento pomocný text vznikl pro potřeby předmětu Geometrie pro FST 2, který vyučujeme
Derivace funkcí více proměnných
 Derivace funkcí více proměnných Pro studenty FP TUL Martina Šimůnková 16. května 019 1. Derivace podle vektoru jako funkce vektoru. Pro pevně zvolenou funkci f : R d R n a bod a R d budeme zkoumat zobrazení,
Derivace funkcí více proměnných Pro studenty FP TUL Martina Šimůnková 16. května 019 1. Derivace podle vektoru jako funkce vektoru. Pro pevně zvolenou funkci f : R d R n a bod a R d budeme zkoumat zobrazení,
Clemův motor vs. zákon zachování energie
 Clemův motor vs. zákon zachování energie (c) Ing. Ladislav Kopecký, 2009 V učebnicích fyziky se traduje, že energii nelze ani získat z ničeho, ani ji zničit, pouze ji lze přeměnit na jiný druh. Z této
Clemův motor vs. zákon zachování energie (c) Ing. Ladislav Kopecký, 2009 V učebnicích fyziky se traduje, že energii nelze ani získat z ničeho, ani ji zničit, pouze ji lze přeměnit na jiný druh. Z této
TEORIE MATIC. Tomáš Vondra
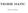 TEORIE MATIC Tomáš Vondra 2 Obsah 1 Opakování 5 1.1 Základní operace s maticemi..................... 5 1.2 Determinant matice......................... 7 1.2.1 Cauchyův-Binedův vzorec..................
TEORIE MATIC Tomáš Vondra 2 Obsah 1 Opakování 5 1.1 Základní operace s maticemi..................... 5 1.2 Determinant matice......................... 7 1.2.1 Cauchyův-Binedův vzorec..................
2 Spojité modely rozhodování
 2 Spojité modely rozhodování Jak již víme z přednášky, diskrétní model rozhodování lze zapsat ve tvaru úlohy hodnocení variant: f(a i ) max, a i A = {a 1, a 2,... a p }, kde f je kriteriální funkce a A
2 Spojité modely rozhodování Jak již víme z přednášky, diskrétní model rozhodování lze zapsat ve tvaru úlohy hodnocení variant: f(a i ) max, a i A = {a 1, a 2,... a p }, kde f je kriteriální funkce a A
Studium kladného sloupce doutnavého výboje pomocí elektrostatických sond: jednoduchá sonda
 1 Úvod Studium kladného sloupce doutnavého výboje pomocí elektrostatických sond: jednoduchá sonda V této úloze se zaměříme na měření parametrů kladného sloupce doutnavého výboje, proto je vhodné se na
1 Úvod Studium kladného sloupce doutnavého výboje pomocí elektrostatických sond: jednoduchá sonda V této úloze se zaměříme na měření parametrů kladného sloupce doutnavého výboje, proto je vhodné se na
Matematika I: Aplikované úlohy
 Matematika I: Aplikované úlohy Zuzana Morávková Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava 260. Řy 283 - Pálkař Zadání Pálkař odpálí míč pod úhlem α = 30 a rychlostí
Matematika I: Aplikované úlohy Zuzana Morávková Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava 260. Řy 283 - Pálkař Zadání Pálkař odpálí míč pod úhlem α = 30 a rychlostí
FAKULTA STAVEBNÍ VUT V BRNĚ PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK 2003 2004
 PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK 003 004 TEST Z MATEMATIKY PRO PŘIJÍMACÍ ZKOUŠKY ČÍSLO M 0030 Vyjádřete jedním desetinným číslem (4 ½ 4 ¼ ) (4 ½ + 4 ¼ ) Správné řešení: 0,5 Zjednodušte výraz : ( 4)
PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK 003 004 TEST Z MATEMATIKY PRO PŘIJÍMACÍ ZKOUŠKY ČÍSLO M 0030 Vyjádřete jedním desetinným číslem (4 ½ 4 ¼ ) (4 ½ + 4 ¼ ) Správné řešení: 0,5 Zjednodušte výraz : ( 4)
Netlumené kmitání tělesa zavěšeného na pružině
 Netlumené kmitání tělesa zavěšeného na pružině Kmitavý pohyb patří k relativně jednoduchým pohybům, které lze analyzovat s použitím jednoduchých fyzikálních zákonů a matematických vztahů. Zároveň je tento
Netlumené kmitání tělesa zavěšeného na pružině Kmitavý pohyb patří k relativně jednoduchým pohybům, které lze analyzovat s použitím jednoduchých fyzikálních zákonů a matematických vztahů. Zároveň je tento
Teoretická rozdělení
 Teoretická rozdělení Diskrétní rozdělení Obsah kapitoly Studijní cíle Doba potřebná ke studiu Pojmy k zapamatování Úvod Některá teoretická rozdělení diskrétních veličin: Alternativní rozdělení Binomické
Teoretická rozdělení Diskrétní rozdělení Obsah kapitoly Studijní cíle Doba potřebná ke studiu Pojmy k zapamatování Úvod Některá teoretická rozdělení diskrétních veličin: Alternativní rozdělení Binomické
ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ
 ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ Ročník LII 6 Číslo 3, 2004 Gasser-Müllerův odhad J. Poměnková Došlo: 8.
ACTA UNIVERSITATIS AGRICULTURAE ET SILVICULTURAE MENDELIANAE BRUNENSIS SBORNÍK MENDELOVY ZEMĚDĚLSKÉ A LESNICKÉ UNIVERZITY V BRNĚ Ročník LII 6 Číslo 3, 2004 Gasser-Müllerův odhad J. Poměnková Došlo: 8.
5.2.4 Rayleighova Taylorova nestabilita
 74 Nestability v plazmatu 5..4 Rayleighova Taylorova nestabilita Rayleighova Taylorova nestabilita (RT nestabilita) vzniká na rozhraní dvou tekutin různých hustot (například je-li v gravitačním poli hustší
74 Nestability v plazmatu 5..4 Rayleighova Taylorova nestabilita Rayleighova Taylorova nestabilita (RT nestabilita) vzniká na rozhraní dvou tekutin různých hustot (například je-li v gravitačním poli hustší
Elektrotechnická fakulta
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Elektrotechnická fakulta OPTIMÁLNÍ ROZHODOVÁNÍ A ŘÍZENÍ Jan Štecha Katedra řídicí techniky 1999 Předmluva Toto skriptum je určeno posluchačům 4. ročníku oboru technická
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Elektrotechnická fakulta OPTIMÁLNÍ ROZHODOVÁNÍ A ŘÍZENÍ Jan Štecha Katedra řídicí techniky 1999 Předmluva Toto skriptum je určeno posluchačům 4. ročníku oboru technická
Regresní a korelační analýza
 Přednáška STATISTIKA II - EKONOMETRIE Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Regresní analýza Cíl regresní analýzy: stanovení formy (trendu, tvaru, průběhu)
Přednáška STATISTIKA II - EKONOMETRIE Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Regresní analýza Cíl regresní analýzy: stanovení formy (trendu, tvaru, průběhu)
Určování výměr Srážka mapového listu Výpočet objemů Dělení pozemků
 Geodézie přednáška 9 Určování výměr Srážka mapového listu Výpočet objemů Dělení pozemků Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.: 545134015 Určování výměr určování
Geodézie přednáška 9 Určování výměr Srážka mapového listu Výpočet objemů Dělení pozemků Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.: 545134015 Určování výměr určování
( ) Úloha č. 9. Měření rychlosti zvuku a Poissonovy konstanty
 Fyzikální praktikum IV. Měření ryhlosti zvuku a Poissonovy konstanty - verze Úloha č. 9 Měření ryhlosti zvuku a Poissonovy konstanty 1) Pomůky: Kundtova trubie, mikrofon se sondou, milivoltmetr, měřítko,
Fyzikální praktikum IV. Měření ryhlosti zvuku a Poissonovy konstanty - verze Úloha č. 9 Měření ryhlosti zvuku a Poissonovy konstanty 1) Pomůky: Kundtova trubie, mikrofon se sondou, milivoltmetr, měřítko,
4.1 Shrnutí základních poznatků
 4.1 Shrnutí základních poznatků V celé řadě konstrukcí se setkáváme s případy, kdy o nosnosti nerozhoduje pevnost materiálu, ale stabilitní stav rovnováhy. Tuto problematiku souhrnně nazýváme stabilita
4.1 Shrnutí základních poznatků V celé řadě konstrukcí se setkáváme s případy, kdy o nosnosti nerozhoduje pevnost materiálu, ale stabilitní stav rovnováhy. Tuto problematiku souhrnně nazýváme stabilita
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE. Optimalizace trasy při revizích elektrospotřebičů
 VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Hlavní specializace: Ekonometrie a operační výzkum Název diplomové práce Optimalizace trasy při revizích elektrospotřebičů Diplomant: Vedoucí
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Hlavní specializace: Ekonometrie a operační výzkum Název diplomové práce Optimalizace trasy při revizích elektrospotřebičů Diplomant: Vedoucí
Výtok kapaliny otvorem ve dně nádrže (výtok kapaliny z danaidy)
 Výtok kapaliny otvorem ve dně nádrže (výtok kapaliny z danaidy) Úvod: Problematika výtoku kapaliny z nádrže se uplatňuje při vyprazdňování nádrží a při nejjednodušším nastavování konstantních průtoků.
Výtok kapaliny otvorem ve dně nádrže (výtok kapaliny z danaidy) Úvod: Problematika výtoku kapaliny z nádrže se uplatňuje při vyprazdňování nádrží a při nejjednodušším nastavování konstantních průtoků.
Experimentální analýza hluku
 Experimentální analýza hluku Mezi nejčastěji měřené akustické veličiny patří akustický tlak, akustický výkon a intenzita zvuku (resp. jejich hladiny). Vedle členění dle měřené veličiny lze měření v akustice
Experimentální analýza hluku Mezi nejčastěji měřené akustické veličiny patří akustický tlak, akustický výkon a intenzita zvuku (resp. jejich hladiny). Vedle členění dle měřené veličiny lze měření v akustice
Jak pracovat s absolutními hodnotami
 Jak pracovat s absolutními hodnotami Petr Matyáš 1 Co to je absolutní hodnota Absolutní hodnota čísla a, dále ji budeme označovat výrazem a, je jeho vzdálenost od nuly na ose x, tedy je to vždy číslo kladné.
Jak pracovat s absolutními hodnotami Petr Matyáš 1 Co to je absolutní hodnota Absolutní hodnota čísla a, dále ji budeme označovat výrazem a, je jeho vzdálenost od nuly na ose x, tedy je to vždy číslo kladné.
MATLAB V ANALÝZE NAMĚŘENÝCH DAT PRŮMYSLOVÉHO PODNIKU.
 MATLAB V ANALÝZE NAMĚŘENÝCH DAT PRŮMYSLOVÉHO PODNIKU. J. Šípal Fakulta výrobních technologií a managementu; Univerzita Jana Evangelisty Purkyně Abstrakt Příspěvek představuje model popisující dodávku tepelené
MATLAB V ANALÝZE NAMĚŘENÝCH DAT PRŮMYSLOVÉHO PODNIKU. J. Šípal Fakulta výrobních technologií a managementu; Univerzita Jana Evangelisty Purkyně Abstrakt Příspěvek představuje model popisující dodávku tepelené
Reference 10. Předpokládejme stavový popis spojitého, respektive diskrétního systému
 Módy systému Teorie dynamických systémů Obsah Úvod 2 Příklady 2 3 Domácí úlohy 8 Reference Úvod Řešení stavových rovnic Předpokládejme stavový popis spojitého, respektive diskrétního systému ẋ(t)=ax(t)+bu(t)
Módy systému Teorie dynamických systémů Obsah Úvod 2 Příklady 2 3 Domácí úlohy 8 Reference Úvod Řešení stavových rovnic Předpokládejme stavový popis spojitého, respektive diskrétního systému ẋ(t)=ax(t)+bu(t)
UNIVERSITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA. KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY školní rok 2009/2010 BAKALÁŘSKÁ PRÁCE
 UNIVERSITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY školní rok 2009/2010 BAKALÁŘSKÁ PRÁCE Testy dobré shody Vedoucí diplomové práce: RNDr. PhDr. Ivo
UNIVERSITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY školní rok 2009/2010 BAKALÁŘSKÁ PRÁCE Testy dobré shody Vedoucí diplomové práce: RNDr. PhDr. Ivo
Vzpěr jednoduchého rámu, diferenciální operátory. Lenka Dohnalová
 1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
1. Náhodný vektor (X, Y ) má diskrétní rozdělení s pravděpodobnostní funkcí p, kde. p(x, y) = a(x + y + 1), x, y {0, 1, 2}.
 VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
Obsah. 1. Komplexní čísla
 KOMPLEXNÍ ANALÝZA - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Komplexní čísla 1 2. Holomorfní funkce 3 3. Elementární funkce komplexní proměnné 4 4. Křivkový integrál 7 5. Index bodu vzhledem ke křivce 9 6.
KOMPLEXNÍ ANALÝZA - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Komplexní čísla 1 2. Holomorfní funkce 3 3. Elementární funkce komplexní proměnné 4 4. Křivkový integrál 7 5. Index bodu vzhledem ke křivce 9 6.
Dnešní látka: Literatura: Kapitoly 3 a 4 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Lineární programování
 Lineární programování Úlohy LP patří mezi takové úlohy matematického programování, ve kterých jsou jak kriteriální funkce, tak i všechny rovnice a nerovnice podmínek výhradně tvořeny lineárními výrazy.
Lineární programování Úlohy LP patří mezi takové úlohy matematického programování, ve kterých jsou jak kriteriální funkce, tak i všechny rovnice a nerovnice podmínek výhradně tvořeny lineárními výrazy.
CHEMICKÁ ENERGETIKA. Celá termodynamika je logicky odvozena ze tří základních principů, které mají axiomatický charakter.
 CHEMICKÁ ENERGETIKA Energetickou stránkou soustav a změnami v těchto soustavách se zabývá fyzikální disciplína termodynamika. Z široké oblasti obecné termodynamiky se chemická termodynamika zajímá o chemické
CHEMICKÁ ENERGETIKA Energetickou stránkou soustav a změnami v těchto soustavách se zabývá fyzikální disciplína termodynamika. Z široké oblasti obecné termodynamiky se chemická termodynamika zajímá o chemické
skladbu obou směsí ( v tunách komponenty na 1 tunu směsi):
 Klíčová slova: simplexová metoda 1 Simplexová metoda Postup výpočtu: 1. Nalezení výchozího řešení. 2. Test optima: pokud je řešení optimální výpočet končí, jinak krok 3. 3. Iterační krok, poté opět test
Klíčová slova: simplexová metoda 1 Simplexová metoda Postup výpočtu: 1. Nalezení výchozího řešení. 2. Test optima: pokud je řešení optimální výpočet končí, jinak krok 3. 3. Iterační krok, poté opět test
Petr Chvosta. vlevo, bude pravděpodobnost toho, že se tyč na počátku intervalu τ B nachází nad vpravo
 MOLEKULÁRNÍ MOTORY Petr Chvosta. Automobil v krupobití aneb brzděním k pohybu Uvažme automobil stojící na mírném svahu a bombardovaný rovnoměrně ze všech stran obrovskými kroupami. Svah stoupá směrem doprava
MOLEKULÁRNÍ MOTORY Petr Chvosta. Automobil v krupobití aneb brzděním k pohybu Uvažme automobil stojící na mírném svahu a bombardovaný rovnoměrně ze všech stran obrovskými kroupami. Svah stoupá směrem doprava
Modelování kmitavých soustav s jedním stupněm volnosti
 Modeování kmitavých soustav s jedním stupněm vonosti Zpracova Doc. RNDr. Zdeněk Haváč, CSc 1. Zákadní mode Zákadním modeem kmitavé soustavy s jedním stupněm vonosti je tzv. diskrétní podéně kmitající mode,
Modeování kmitavých soustav s jedním stupněm vonosti Zpracova Doc. RNDr. Zdeněk Haváč, CSc 1. Zákadní mode Zákadním modeem kmitavé soustavy s jedním stupněm vonosti je tzv. diskrétní podéně kmitající mode,
Obr.94. Tečná reakce T r musí být menší nebo rovna třecí síle F t
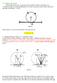 7.3 Odpory při valení Valení je definováno tak, že dotykové body valícího se tělesa a podložky jsou v relativním klidu. Je zaručeno příkladně tak, že těleso omotáme dvěma vlákny, která jsou upevněna na
7.3 Odpory při valení Valení je definováno tak, že dotykové body valícího se tělesa a podložky jsou v relativním klidu. Je zaručeno příkladně tak, že těleso omotáme dvěma vlákny, která jsou upevněna na
Úvod. Integrování je inverzní proces k derivování Máme zderivovanou funkci a integrací získáme původní funkci kterou jsme derivovali
 NEURČITÝ INTEGRÁL Úvod Integrování je inverzní proces k derivování Máme zderivovanou funkci a integrací získáme původní funkci kterou jsme derivovali Umět pracovat s integrálním počtem Je důležité pro
NEURČITÝ INTEGRÁL Úvod Integrování je inverzní proces k derivování Máme zderivovanou funkci a integrací získáme původní funkci kterou jsme derivovali Umět pracovat s integrálním počtem Je důležité pro
0. Lineární rekurence Martin Mareš, 2010-07-04
 0 Lineární rekurence Martin Mareš, 2010-07-04 V tomto krátkém textu se budeme zabývat lineárními rekurencemi, tj posloupnostmi definovanými rekurentní rovnicí typu A n+k = c 0 A n + c 1 A n+1 + + c k 1
0 Lineární rekurence Martin Mareš, 2010-07-04 V tomto krátkém textu se budeme zabývat lineárními rekurencemi, tj posloupnostmi definovanými rekurentní rovnicí typu A n+k = c 0 A n + c 1 A n+1 + + c k 1
1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu
![1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu 1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu](/thumbs/102/155926571.jpg) [M2-P1] KAPITOLA 1: Diferenciální rovnice 1. řádu diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu G(x, y, y, y,..., y (n) ) = 0 y (n) = F (x, y, y,..., y (n 1) ) Příklad 1.1:
[M2-P1] KAPITOLA 1: Diferenciální rovnice 1. řádu diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu G(x, y, y, y,..., y (n) ) = 0 y (n) = F (x, y, y,..., y (n 1) ) Příklad 1.1:
III. Diferenciál funkce a tečná rovina 8. Diferenciál funkce. Přírůstek funkce. a = (x 0, y 0 ), h = (h 1, h 2 ).
 III. Diferenciál funkce a tečná rovina 8. Diferenciál funkce. Přírůstek funkce = f(x 0 + h 1, y 0 + h 2 ) f(x 0, y 0 ) f u (x 0, y 0 ), kde u = (h 1, h 2 ). ( ) = f(x 0 + h 1, y 0 ) f(x 0, y 0 ) x (x 0,
III. Diferenciál funkce a tečná rovina 8. Diferenciál funkce. Přírůstek funkce = f(x 0 + h 1, y 0 + h 2 ) f(x 0, y 0 ) f u (x 0, y 0 ), kde u = (h 1, h 2 ). ( ) = f(x 0 + h 1, y 0 ) f(x 0, y 0 ) x (x 0,
Lineární algebra II. Adam Liška. 9. února 2015. Zápisky z přednášek Jiřího Fialy na MFF UK, letní semestr, ak. rok 2007/2008
 Lineární algebra II Zápisky z přednášek Jiřího Fialy na MFF UK, letní semestr, ak rok 2007/2008 Adam Liška 9 února 2015 http://kammffcunicz/~fiala http://wwwadliskacom 1 Obsah 10 Permutace 3 11 Determinant
Lineární algebra II Zápisky z přednášek Jiřího Fialy na MFF UK, letní semestr, ak rok 2007/2008 Adam Liška 9 února 2015 http://kammffcunicz/~fiala http://wwwadliskacom 1 Obsah 10 Permutace 3 11 Determinant
VLASTNOSTI KOMPONENTŮ MĚŘICÍHO ŘETĚZCE - ANALOGOVÁČÁST
 VLASTNOSTI KOMPONENTŮ MĚŘICÍHO ŘETĚZCE - ANALOGOVÁČÁST 5.1. Snímač 5.2. Obvody úpravy signálu 5.1. SNÍMAČ Napájecí zdroj snímač převod na el. napětí - úprava velikosti - filtr analogově číslicový převodník
VLASTNOSTI KOMPONENTŮ MĚŘICÍHO ŘETĚZCE - ANALOGOVÁČÁST 5.1. Snímač 5.2. Obvody úpravy signálu 5.1. SNÍMAČ Napájecí zdroj snímač převod na el. napětí - úprava velikosti - filtr analogově číslicový převodník
Matematika I (KX001) Užití derivace v geometrii, ve fyzice 3. října f (x 0 ) (x x 0) Je-li f (x 0 ) = 0, tečna: x = 3, normála: y = 0
 Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Gymnázium, Brno. Matice. Závěrečná maturitní práce. Jakub Juránek 4.A Školní rok 2010/11
 Gymnázium, Brno Matice Závěrečná maturitní práce Jakub Juránek 4.A Školní rok 2010/11 Konzultant: Mgr. Aleš Kobza Ph.D. Brno, 2011 Prohlášení Prohlašuji, že jsem předloženou práci zpracoval samostatně
Gymnázium, Brno Matice Závěrečná maturitní práce Jakub Juránek 4.A Školní rok 2010/11 Konzultant: Mgr. Aleš Kobza Ph.D. Brno, 2011 Prohlášení Prohlašuji, že jsem předloženou práci zpracoval samostatně
Rozptyl. Pozn.: rozptyl je nezávislý na posunu hustoty pravděpodobnosti na ose x, protože Var(X) mi určuje jen šířku rozdělení.
 Rozptyl Základní vlastnosti disperze Var(konst) = 0 Var(X+Y) = Var(X) + Var(Y) (nezávislé proměnné) Lineární změna jednotek Y = rx + s, například z C na F. Jak vypočítám střední hodnotu a rozptyl? Pozn.:
Rozptyl Základní vlastnosti disperze Var(konst) = 0 Var(X+Y) = Var(X) + Var(Y) (nezávislé proměnné) Lineární změna jednotek Y = rx + s, například z C na F. Jak vypočítám střední hodnotu a rozptyl? Pozn.:
2D transformací. červen Odvození transformačního klíče vybraných 2D transformací Metody vyrovnání... 2
 Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
Skalár- veličina určená jedním číselným údajem čas, hmotnost (porovnej životní úroveň, hospodaření firmy, naše poloha podle GPS )
 LINEÁRNÍ ALGEBRA Úvod vektor Skalár- veličina určená jedním číselným údajem čas, hmotnost (porovnej životní úroveň, hospodaření firmy, naše poloha podle GPS ) Kartézský souřadnicový systém -je taková soustava
LINEÁRNÍ ALGEBRA Úvod vektor Skalár- veličina určená jedním číselným údajem čas, hmotnost (porovnej životní úroveň, hospodaření firmy, naše poloha podle GPS ) Kartézský souřadnicový systém -je taková soustava
z možností, jak tuto veličinu charakterizovat, je určit součet
 6 Charakteristiky áhodé veličiy. Nejdůležitější diskrétí a spojitá rozděleí. 6.1. Číselé charakteristiky áhodé veličiy 6.1.1. Středí hodota Uvažujme ejprve diskrétí áhodou veličiu X s rozděleím {x }, {p
6 Charakteristiky áhodé veličiy. Nejdůležitější diskrétí a spojitá rozděleí. 6.1. Číselé charakteristiky áhodé veličiy 6.1.1. Středí hodota Uvažujme ejprve diskrétí áhodou veličiu X s rozděleím {x }, {p
Diplomová práce. Sbírka úloh z mechaniky kontinua PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO KATEDRA TEORETICKÉ FYZIKY. Vypracoval: Michal Kolář
 PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO KATEDRA TEORETICKÉ FYZIKY Diplomová práce Sbírka úloh z mechaniky kontinua Vypracoval: Michal Kolář studující V. ročníku obor M F studijní rok 00/003 Vedoucí
PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO KATEDRA TEORETICKÉ FYZIKY Diplomová práce Sbírka úloh z mechaniky kontinua Vypracoval: Michal Kolář studující V. ročníku obor M F studijní rok 00/003 Vedoucí
Kapitola 7: Neurčitý integrál. 1/14
 Kapitola 7: Neurčitý integrál. 1/14 Neurčitý integrál 2/14 Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní
Kapitola 7: Neurčitý integrál. 1/14 Neurčitý integrál 2/14 Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní
24 VLNĚNÍ. 24.1 Základní druhy vlnění a vlnová rovnice
 278 24 VLNĚNÍ Základní druhy vlnění a vlnová rovnice Skládání vln, interference a polarizace Fázová a grupová rychlost, disperze Dopplerův jev, Čerenkovův jev Vlny v omezeném prostředí Energie a hybnost
278 24 VLNĚNÍ Základní druhy vlnění a vlnová rovnice Skládání vln, interference a polarizace Fázová a grupová rychlost, disperze Dopplerův jev, Čerenkovův jev Vlny v omezeném prostředí Energie a hybnost
Matematické symboly a značky
 Matematické symboly a značky Z Wikipedie, otevřené encyklopedie Matematický symbol je libovolný znak, používaný v. Může to být znaménko pro označení operace s množinami, jejich prvky, čísly či jinými objekty,
Matematické symboly a značky Z Wikipedie, otevřené encyklopedie Matematický symbol je libovolný znak, používaný v. Může to být znaménko pro označení operace s množinami, jejich prvky, čísly či jinými objekty,
Obsah Obyčejné diferenciální rovnice
 Obsah 1 Obyčejné diferenciální rovnice 3 1.1 Základní pojmy............................................ 3 1.2 Obyčejné diferenciální rovnice 1. řádu................................ 5 1.3 Exaktní rovnice............................................
Obsah 1 Obyčejné diferenciální rovnice 3 1.1 Základní pojmy............................................ 3 1.2 Obyčejné diferenciální rovnice 1. řádu................................ 5 1.3 Exaktní rovnice............................................
Interpolace, ortogonální polynomy, Gaussova kvadratura
 Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
