VLASTNOSTI VLÁKEN. 1. Molekulová a nadmolekulová struktur\a polymerů, strukturní modely

Transkript

1 VLASTNOSTI VLÁKEN 1. Molekulová a nadmolekulová struktur\a polymerů, strukturní modely 1.1. Molekulová struktura Vazby v polymerech Celou řadu vlastností polymerních vláken ovlvňují vazby mez atomy v hlavním řetězc a mez řetězc. Rozdíly v síle těchto vazeb umožňují deformační zpevnění př dloužení, tvarování, př fxac a stablzac, barvení atd. V hlavním řetězc jsou jednotlvé atomy poutány slným kovalentním vazbam, jejchž porušení vyžaduje poměrně vysokou energ. Mez polymerním řetězc působí kohezní vazby vyvolané vodíkovým můstky resp. van der Waalsovým slam. V tab.1.1. jsou pro lustrac uvedeny typcké energe vazeb vyskytujících se ve vláknotvorných polymerech. Tabulka 1.1: Energe typů vazeb v polymerech [ev=1, J] typ vazby energe [ev] kovalentní vazby 4 8 vodíkové můstky 0, 0,5 van der Waalsovy síly 0,01 0,1 tepelná energe př 30 C 0,03 Energe vazeb typckých skupn v hlavním řetězc jsou uvedeny v tab. 1. Tabulka 1..: Energe typckých vazeb v polymerech [kj/mol] vazba energe [kj/mol] C-C 368 C-O-C 360 C-N-C 305 S-O-S 14 Mezřetězcové síly vyvolávají soudržnost (kohez) polymeru. Jsou sce řádově slabší než prmární vazby v řetězcích, ale je jch poměrně mnoho. Zodpovídají za množství tepla potřebné k tání polymeru a nterakce s kapalnam resp. plyny. Celková energe mezmolekulového působení zahrnuje jak přtažlvou energ tak energ vzájemného odpuzování. Energe nterakce mez dvěma elektrcky nabtým částcem je úměrná E 1/r. Je patrné, že jde o přtažlvost poměrně dalekého dosahu. Pro nterakc mez ontem a dpólem je přtažlvá energe úměrná E 1/r 4. Pro dvě dspergované částce o poloměrech R je přtažlvá energe úměrná E R/(1*r). Je patrné, že přtažlvé resp. odpudvé síly jsou výrazně ovlvněny především vzdáleností r mez molekulam resp. skupnam a částcem. Energe E V [J] potřebná k oddělení makromolekul amorfního polymeru objemu V [cm 3 ], se nazývá výparná (polymer však nelze odpařt). Pro charakterzac kohezních sl se používá hustota kohezní energe CED CED = E V /V [Jcm -3 ] Velkost CED pro typcké vláknotvorné polymery jsou v tab. 1.3 Tabulka 1.3 : Hodnoty CED (př 98oK) polymer CED [J cm -3 ] polyakrylontrl 993 polyamd polyester 479 polyvnylchlord 380 1

2 Kohezní síly ovlvňují také rozpustnost polymerů v rozpouštědlech. Schopnost rozpustnost polymerů se charakterzuje parametrem rozpustnost δ[(jm -3 ) 1/ ] pro který platí δ = CED. Rozpouští-l se polymer s parametrem rozpustnost δ pol v rozpouštědle s parametrem rozpustnost δ rozp, je δ pol =δ rozp.. Pro semkrystalcké polymery platí, že př δ pol =δ rozp dochází v těchto rozpouštědlech k nejvyššímu bobtnání. Př znalost δ lze pak snadno určt CED. Pro chování všech vláken jsou důležté mezřetězcové elektrostatcké vazby. Nejslnější jsou vodíkové můstky. Praktcky u všech vláken působí van der Waalsovy síly tj. dpólové elektrostatcké nterakce. Dpól dpólové nterakce vznkající př nerovnoměrném rozdělení vazebných elektronů mají energ kolem 1, 1 kj/mol. Interakce dpól ndukovaný dpól vznkající polarzací neutrální molekuly permanentním dpólem mají energ kolem 0,8 kj/mol. Ve vláknech se také vyskytují nterakce ndukovaný dpól ndukovaný dpól s energí kolem 0,1 kj/mol. I tyto velm slabé nterakce mohou př dostatečném počtu daném prostorovým uspořádáním a délkou řetězců vést až k velm pevným vláknům (vysoce pevný polyetylén). Typckým příkladem permanentních dpólů jsou sekundární vazby v PAN vláknech. Také mez aromatckým jádry sousedních řetězců mohou vznkat slné sekundární van der Waalsovy nterakce díky pohyblvost (sdílení) elektronů jader. Slné sekundární vazby vedou ke zvýšení teploty tání nebo tání zabraňují (vz. přírodní vlákna). Na druhé straně je pevnost vláken spíše otázkou počtu sekundárních vazeb a dá se zvýšt např. dodloužením resp. do jsté míry protažením vláken (deformační zpevnění). Síla mez dvěma atomy závsí také na mezatomové vzdálenost. Pohyblvost a prostorové uspořádání molekul Důležtou charakterstkou je také pohyblvost polymerních řetězců, která souvsí s potencální energí různých konformací. Nejpravděpodobnější tvar je takový, který má nejmenší potencální energ. Tomu odpovídá tzv. zákrytová (trans) konformace kdy jsou dva sousední uhlíky pootočeny o 180 o. Stablní je také vykloněná (gauche) konformace, kdy je pootočení pouze 60 o. V polymerních řetězcích se obyčejně tvoří rovnná ck cak (trans nebo trans s defekty gauche), skládaná (gauche nebo TGT) a prostorová sprála (gauche GGG) komformace resp. jejch kombnace. Rovnná ck cak Skládaná Prostorová sprála U makromolekulárních látek nemají ontové a kovové vazby an ontové dpólové síly podstatný význam. Velký vlv mají nterakce, způsobené sférckým zábranam, propletením řetězců makromolekul a zaklesnutí bočních řetězců. Prmární a sekundární vazebné síly se svou velkostí řádově lší. Pomocí nasycených prmárních vazeb vznkají molekuly, kdežto sekundární vazebné síly způsobují soudržnost molekul v tuhých látkách. Jsou rozhodující pro krystalzac, pro pevnost a pro všechny děje spojené se vzájemným působením molekul (např. adsorpce, lepení, rozpustnost, bobtnání apod.). Molekulová hmotnost Základní charakterstkou polymerních řetězců jsou průměrná molekulová hmotnost řetězců M P resp. průměrný polymerační stupeň PPS. Platí přblžně, že M P = PPS* M M kde M M je molekulová hmotnost monomeru. Tyto velčny ovlvňují řadu vlastností polymerů. Např. pro docílení mnmální pevnost vláken nesmí PPS klesnout pod jstou hodnotu závslou na typu polymeru.

3 V reálných polymerech exstuje vždy dstrbuce délek řetězců charakterzovaných číselnou střední délkou M n M = n ( M * n ) / n resp. hmotnostní střední délkou M W M w = ( M * w ) / w = M * w = ( M * n ) / M * n ) = M n / M n Zde M je hmotnost řetězce relatvní délky l, n je počet řetězců délky l a w = (M n ) / (Σ M n ) je relatvní hmotnostní podíl řetězců délky l (opakující se jednotce odpovídá stejná relatvní délka). Symbol M označuje střední číselnou hodnotu čtverce délky na rozdíl od M ), což n je čtverec číselné délky. Platí, že pro nestejné délky řetězců je M w /M n > 1. Pro nestejné délky řetězců je možno defnovat faktor polydsperzty Q = M w /M n - 1. Dstrbuce molekulových hmotností se charakterzuje střední hodnotou E(M)=M n a rozptylem D(M) = E(M ) E (M). Po úpravách vyjde M w = M n + D(M) / Mn. Faktor polydsperzty je tedy Q = D(M)/(M n ) Pro normální rozdělení je pak M w = M n. Čím je větší polydsperzta (rozptyl), tím větší je rozdíl mez středním délkam řetězců. Lze odvodt, že teoretcky : a) př polykondenzac je M w = M n b) př radkálové polymerac M w = 1,5 M n Pro pops dstrbuce délek řetězců postačuje znát Q a M w. Řada mechanckých a reologckých vlastností polymerních vláken je pak funkcí těchto dvou parametrů. Pro vlákna vznklá polykondenzací je Q a pro vlákna vznklá polymerací je Q 10. Pro mechancké a termodynamcké vlastnost polymerů obyčejně platí obecná rovnce X X A / = M n kde X je zkoumaná vlastnost, X je její lmtní hodnota pro nekonečné řetězce a A je konstanta úměrnost. Ostatní vlastnost vláknotvorných polymerů lze rozdělt do dvou skupn: 1) souvsející přímo s chemckým složením polymeru a polydsperztou (kohezní síly, hustota uspořádání, molekulová moblta, fázové chování) ) souvsející nepřímo s chemckým složením polymeru a polydsperztou (morfologe a relaxační jevy) 1.. Nadmolekulová struktura Typy makromolekulárních látek Exstují tř velké skupny makromolekulárních látek: 1. Lneární polymery. Jejch monomer obsahuje dvě funkční skupny. Vznkající řetězce jsou vzájemně spojeny vedlejším vazebným slam. Lneární molekuly vytvářejí klubka, někdy jsou paralelně orentovány a velm často vytvářejí částečně krystalcké struktury.. Rozvětvené polymery. Makromolekuly obsahují buď v pravdelných nebo statstcky rozdělených vzdálenostech kratší č delší boční řetězce. Zaklesnutí těchto řetězců ovlvňuje vznk tuhé látky. 3. Zesíťované pryskyřce. Vznkly z monomerů, z nchž alespoň část obsahuje tř nebo více funkčních skupn. Jsou to prostorově zesíťované struktury, tvořené nerozpustným a netavtelným obřím molekulam. Někdy vznkají tyto struktury tím, že se lneární molekuly spojí v kratších a delších vzdálenostech můstky, přtom pohyblvost segmentů mez můstky zůstává zachována. V techncké prax se kromě toho užívá materálů, které vznkají smíšením polymeru s plnvy a pgmenty, které ovlvňují tvorbu pevné fáze. 3 ( n

4 Struktura makromolekulárních látek v tuhém stavu. Vntřní síly, tvar molekul a tepelný pohyb určují strukturu makromolekulární látky, přčemž rychlost vznku této struktury závsí na tepelném pohybu. Působení těchto čntelů můžeme modelově znázornt pomocí určtého počtu tyčnek. Jestlže těmto tyčnkam třeseme, vznkne neuspořádaný soubor. Nahradíme-l tyčnky stejným počtem tyčových magnetů, budou se magnety př třepání pozvolna antparalelně uspořádávat a budou se vytvářet struktura odpovídající krystalcké látce. Totéž chování lze očekávat u polymerů. Budou se tedy vedle sebe vyskytovat neuspořádané, tj. amorfní (beztvaré) oblast a oblast krystalcké vznklé paralelním uspořádáním molekul, jakož oblast, v nchž je určtý směr os molekul preferován, které označujeme jako orentované. Krystalcký stav. Látku označujeme jako krystalckou, jestlže se její elementární strukturní jednotky opakují v pravdelných vzdálenostech ve třech prostorových směrech, jež neleží v jedné rovně. Složtost vazebných sl a exstence vazeb působících v určtém směru jsou příčnou toho, že u polymerů vznkají oprot anorganckým krystalům struktury podstatně složtější. Amorfní stav. Jsou-l molekuly statstcky neuspořádané nebo orentované, anž jsou jejch vzájemné vzdálenost nějak pravdelně rozděleny, pak nelze proložt strukturním body žádné mřížkové rovny. Příčny exstence amorfního stavu jsou tyto: Jsou-l boční skupny složté nebo obsahují atomy o velkém poloměru, stércké zábrany omezují sklon ke krystalzac. Nesmíme zapomenou an na neuspořádaný růst řetězců, které od začátku obsahují zauzlení. Důležtý je rovněž entropcký člen (TS) ve vztahu pro volnou energ G = H TS Tímto vztahem je určován stav látky. U polymerů se vntřní energe U amorfní látky přílš nelší od krystalckého stavu. Některé práce však ukazují, že u amorfního polymeru může vedle orentace exstovat určtý stupeň uspořádání. Hovoříme o tzv. nodulání (chomáčkovté) struktuře amorfního polymeru. Amorfní polymer také vznká př prudkém ochlazení tavenny polymeru na teplotu nžší než je teplota skelného přechodu. Semkrystalcká stav. Ve většně případů se vyskytují vedle sebe oba stavy: krystalcký amorfní. Makromolekuly mohou čstě krystalcký stav vytvořt jen teoretcky a jž z postaty vznku krystalcké fáze musí vedle maxmálně krystalcké oblast vznknout nutně též oblast amorfní. Statstcké rozdělení krystalckých a amorfních oblastí a jejch velkost nezávsí na délce lneárních molekul. Jednotlvá molekula může náležet současně k různým oblastem a může být podstatně větší než krystalt. Orentovaný stav. Polymerní látky, tvořené lneárním molekulam, lze v oblast měknutí a někdy př nžších teplotách (tzv. dloužení za studena) převést do orentovaného stavu. Př tom je určtý směr os molekul preferován, anž však uhlíkové atomy tvoří mřížkové rovny. Paralelní uspořádání není dokonalé. Orentace se může projevt u zesťovaných lneárních molekul, pokud stupeň zesítění není přílš vysoký. Protažená vysokomolekulární látka má poněkud nžší měrné teplot než neprotažená. Vznklá entropcko-elastcká deformace bude způsobovat, že molekuly mají v orentované látce tendenc obnovt své původní smotání. Skládání řetězců. Př vznku krystalcké fáze sce tvoří lneární makromolekuly paralelní řetězce, ale delší řetězce se uspořádávají skládáním řetězců. Délka skladu je závslá na teplotě krystalzace. Nadmolekulární struktura. Vysokomolekulární látka tvoří statstcky se střídající amorfní a krystalcké oblast. Velkost těchto oblastí značně kolísá. Za určtých podmínek mohou vytvářet pravdelné struktury. Popsu této struktury říkáme nadmolekulární struktura. 4

5 1.3. Strukturní modely Syntetcká vlákna mají řadu vlastností, které přírodní vlákna postrádají, jako je vysoká pevnost, trvanlvost, nemačkavost, tvarová stálost atd. Na druhé straně však mají také řadu nedostatků: nízkou hydroflnost, nabíjejí se statckou elektřnou, mají vyšší špnvost, horší barvtelnost, méně příjemný omak a podobně. Vývoj syntetckých vláken však dosud neřekl své poslední slovo. Vyvíjí se stále nové typy vláken, které se získávají chemckou nebo fyzkální modfkací základních typů vláken, ale objevují se stále nové polymery, které lze využít pro výrobu vláken. Je však nutno přznat, že nejlepších výsledků př konstrukc tkann se dosahuje kombnací obou typů vláken. V případě technckých textlí však syntetcká vlákna svým vlastnostm většnou předčí vlákna přírodní. Objev syntetckých vláken neznamenal pouze revoluc v celé technolog textlního průmyslu, ale současně otevřel nové pole působnost pro výzkum vlastností specelních polymerních útvarů. Překvapující je skutečnost, že př vývoj syntetckých vláken nebyla napodobena an chemcká, an fyzkální struktura přírodních vláken, ale syntetcká vlákna se podařlo přpravt na zcela jném základě, a to jak z hledska chemckého složení, tak z hledska nadmolekulárního uspořádání makromolekul ve vlákně. Na rozdíl od přírodních vláken je možno u syntetckých vláken studovat nejen konečnou strukturu a vlastnost vláken, ale vlv fyzkálních podmínek přípravy na tyto vlastnost. Současný stupeň poznání umožňuje tyto procesy řídt a dokonce předvídat chování a konečné vlastnost vlákna. Vlákna mají zcela charakterstckou vntřní strukturu, která se od ostatních polymerních materálů výrazně lší. Objev syntetckých vláken nebyl přínosem jen pro prax, ale rozšířl naše obecné poznatky o chování hmoty. Základní vlastností vláken je především vysoká orentace polymerních řetězců. Dlouhé lneární řetězce makromolekul nejsou uspořádány náhodně, ale převládající směr jejch orentace souhlasí s osou vláken. Další charakterstkou je menší nebo větší stupeň krystalckého uspořádání. Znamená to, že se zde střídají krystalcké a amorfní (nekrystalcké) oblast. Střídání těchto oblastí podél osy vlákna dává vláknu jeho charakterstcké vlastnost. Od třcátých let mnulého století, kdy bylo přpraveno první syntetcké vlákno, zaznamenaly názory na fyzkální strukturu syntetckých vláken značný rozvoj. Dříve používaný model struktury krystalckých polymerů, tak zvaný model roztřepených mcel (frnged mcelle structure), se stal základem nterpretace vntřní struktury celulózových a pozděj syntetckých vláken. Předpokládalo se, že rozdíl ve struktuře zotropního polymerního výrobku a vlákna je jen kvanttatvní a že ve vlákně jsou krystalcké mcely orentovány převážně ve směru osy vlákna. Model umožňoval poměrně jednoduchou nterpretac rentgenových dfrakcí a pomocí této představy bylo možno vysvětlt některé další vlastnost vláken. Mcelární struktura orentovaného polymeru Aplkace nových metod na studum vntřní struktury syntetckých vláken, jako je nfračervená spektroskope, nukleární magnetcká rezonance, elektronová mkroskope a další přnesla nové poznatky. Proto byla postupně navržena celá řada modelů, které více č méně posthují zjštěná fakta. 5

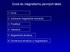
6 Př studu vlákntých krystalů vznklých krystalzací ze zředěných roztoků za současného míchání se ukázalo, že tyto útvary jsou tvořeny centrální částí, kde převažují natažené řetězce makromolekul a z nch pak do stran nepravdelně vyrůstají krystalcké lamely tvořené skládaným polymerním řetězc. Struktura shsh kebab ( ražnč ) u polyetylénu Př výčtu strukturních modelů nelze opomnout Hosemanův model, který vychází z pojmu parakrystalcké fáze, tedy z představy polymerního krystalu s řadou nehomogent a defektů. Tato představa umožňuje především dokonalejší nterpretac rentgenových dfrakcí. Strukturní model podle Hosemanna Základní přínos pro objasnění struktury syntetckých vláken byly Peterlnovy práce z polovny šedesátých let, př kterých sledoval strukturní změny př tzv. dloužení za studena. Tento proces není jen technologckou operací, která umožňuje získat vlákno požadovaných mechanckých vlastností. V tomto případě jde také o zajímavý fyzkální jev pozorovaný př jednosměrné deformac termoplastů v tahu. Jestlže natahujeme neorentované vlákno nebo fol v jednom směru, dojde po několka procentech deformace k zaškrcení vzorku v jednom místě a vytvoření krčku. Př postupné deformac v tahu neprobíhá další zúžení, ale krček postupuje po vlákně za současného protahování vlákna na dvoj až desetnásobek délky. Peterln studoval strukturní změny, které probíhají př dloužení za studena vysoce krystalckých polyolefnových vláken (polyetylén, polypropylén). Tyto stude sce nevedly k objasnění příčn vznku krčku a dloužení za studena, zato však přnesly zcela nový pohled na strukturu orentovaných vláken. Před deformací vlákna tvoří krystaly sférolty. 6

7 A B Dendrtcký sférolt (A), sférolt (B) Př průchodu sfércky uspořádaných krystalckých lamel dloužícím krčkem dochází k jejch deformac, natáčení kolmo na směr protahování a posléze k lámání lamel. Po průchodu krčkem se úlomky uspořádají rovnoběžně a vytvářejí mkrofbrly. V mkrofbrlách se střídají krystalcké lamely s nekrystalckým oblastm. Jednotlvé fbrly jsou zolované, ale jsou propojeny vazebným molekulam, tzv. te molekulam, které tvoří procentně nízkou, zato však strukturně významnou složku ve vlákně. Podle současných představ především množství a orentace této nterfbrlární amorfní fáze ovlvňuje většnu vlastností vláken, jako je pevnost, tažnost,počáteční modul př deformac (a tím tuhost, mačkavost atd.), barvtelnost, rozměrovou stálost (smrštění za vyšších teplot), tvarovou stálost atd. Strukturní model polyamdu 6 (Prevorsekův nebo Peterlnův model strutury vláken) Př studu polyolefnových vláken bylo možno zanedbat přítomnost nekrystalcké fáze uvntř mkrofbrl. U polyamdů a polyesterů, které krystalzují do nžšího stupně, má význam tato ntrafbrlární fáze (uvntř mkrofbrl). Avšak v tomto modelu se předpokládá, že mkrofbrly tvoří poměrně tuhou složku struktury vlákna a že vlastnost vlákna jsou př deformac ovlvněny vzájemným posunem mkrofbrl omezovaným přítomností spojovacích te molekul. Kvanttatvním měřením vztahu mez vlastnostm amorfní fáze a mez fyzkálně-mechanckým vlastnostm vláken podpořl správnost daného modelu Samuels Z obecného hledska fyzky pevných látek lze chápat vlákno jako novu kvaltu ze zcela specfckou strukturou. Ta vznká na určtém stupn orentace makromolekulárních řetězců, nejčastěj dloužením za studena, které má charakter fázového strukturního přechodu. Vznku nové kvalty u vlákna nasvědčují některé další vlastnost syntetckých vláken, především to, že mechancké vlastnost vláken nelze odvodt z vlastností zotropního polymeru. U 7

8 amorfních polymerů dochází ke vznku mkrofbrlární struktury buď jž v průběhu dloužení za studena, nebo spontánně př zahřátí vlákna. Obdobnou mkrofbrlární strukturu můžeme pozorovat u orentovaných folí, případně u jných polymerních útvarů. Tedy její vznk není bezprostředně vázán na syntetcké vlákno, avšak syntetcké vlákno je nejčastěj nostelem této kvanttatvně odlšné struktury. Další zkoumání fyzkální struktury syntetckých vláken má svůj praktcký význam. Po první generac syntetckých vláken přšla druhá generace modfkovaných typů vláken až na vlákna štá na míru. 8