Základní principy fyziky semestrální projekt. Studium dynamiky kladky, závaží a vozíku

Transkript

1 Zákldní principy fyziky seestrální projekt Studiu dyniky kldky, závží vozíku Petr Luzr I/4 008/009

2 Zákldní principy fyziky Seestrální projekt Projekt zdl: Projekt vyprcovl: prof. In. rntišek Schuer, DrSc. Petr Luzr, obor Inforční technoloie. ročník bklářského studi Akdeický rok: 008/009 Místo zprcování: Kroěříž, 8.listopdu

3 Zákldní principy fyziky Seestrální projekt Obsh. Úvod popis siulčního plletu...4. eorie dyniky tuhého těles Druhý Newtonův zákon Důsledky zákon síly D'Alebertův princip Enerie tuhého těles Kinetická enerie Výpočet Závěr práce Použitá litertur

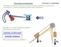
4 Zákldní principy fyziky Seestrální projekt. Úvod popis siulčního plletu Pro vyprcování seestrálního projektu do předětu Zákldní principy fyziky jse si zvolil té Studiu dyniky kldky, závží vozíku, které jse si vybrl z nepřeberného nožství nbízených náětů. Mý úkole je zjistit prostudovt čtyři fktory ze siulčního pletu: zrychlení systéu síl npínjící lno thová síl hotnost kldky oent setrvčnosti kldky Siulční plet se nchází n internetové drese: Zčátek Konec N siulci vidíe vozík odré závží zvěšené přes kldku, které vozík táhne po podložce s nízký třecí koeficiente

5 Zákldní principy fyziky Seestrální projekt. eorie dyniky tuhého těles uhé těleso ůžee chápt jko speciální přípd soustvy hotných bodů, pro kterou pltí, že bez ohledu n pohyb působící síly se vzdálenosti ezi jednotlivýi body neění. uhé těleso lze chápt i jko odel reálného těles z důvodu, že reálná těles jsou deforovtelná. Zákldníi typy pohybů u těchto těles jsou trnslční pohyby pohyby rotční kole stálé osy otáčení. U složitějších pohybů ůžee tyto pohyby rozdělit do jednotlivých složek pohybů. Pohybové rovnice tuhého těles lze získt buď podle druhého Newtonov zákon nebo podle d Alebertov principu... Druhý Newtonův zákon Druhý Newtonův zákon je též nzýván zákone síly. Říká, že velikost zrychlení hotného bodu je přío úěrná velikosti výslednice sil působících n hotný bod nepřío úěrná hotnosti hotného bodu [ ]. ento Newtonův pozntek vyplývá ze zákon setrvčnosti, který je forulován: Jkile n těleso zčne působit síl, zění se jeho pohybový stv. Jednotkou síly je tedy Newton, znčí se N. r r [ ] Pohybovou rovnici lze sestvit i z yšlenky, že zrychlení je derivce rychlosti, nebo-li druhá derivce polohy [ ]. r r d [ ] dt Rovnice ovše pltí z předpokldu, že hotnost těles se v čse neění. o le neusí být vždy splněno (strtující rketě ubývá plivo nebo se hotnost ění při reltivistických rychlostech). V to přípdě je třeb užít obecnější tvr pohybové rovnice [ 3 ], kde p je hybnost těles. r r dp [ 3 ] dt - 5 -

6 Zákldní principy fyziky Seestrální projekt... Důsledky zákon síly Koná-li těleso rovnoěrný příočrý pohyb, je jeho zrychlení nulové tké výslednice sil je rovn nule [ 4 ]. Popsná situce nstává, právě tehdy jestliže n těleso nepůsobí žádná síl nebo v přípdě, že se působící síly nvzáje ruší. 0N [ 4 ] Koná-li těleso rovnoěrně zrychlený nebo zpolený pohyb, je jeho zrychlení konstntní tké výslednice sil je konstntní [ 5 ]. konst. [ 5 ].. D'Alebertův princip D Alebertovů princip je zložen n rovnováze působících vnějších sil sil setrvčných. Při této etodě používáe soustvu spojenou s pohybující se tělese setrvčné síly jednotlivých eleentů těles, resp. jejich setrvčné oenty, sloučíe do výsledné setrvčné síly (setrvčného oentu). D'Alebertův princip se vzthuje k zákonů pohybu v klsické echnice. Prezentuje ekvivlentní vyjádření druhého Newtonov zákon. ento význný frncouzský fyzik tetik, celý jéne Jen le Rond d'alebert, díky svéu principu položil zákldy tzv. lrneovské echniky. ento princip říká, že součet rozdílů ezi sili působícíi n systé čsovýi zěni hybnosti systéu při virtuální posunutí systéu je nulový. D'Alebertův princip bývá tké vyjdřován tk, že při pohybu echnické soustvy jsou setrvčné síly v rovnováze s explicitníi sili. předstvuje jiné pojetí k popisu echniky než jké využívjí Newtonovy pohybové rovnice. K popisu echniky je ožné zvolit jiný vzth tohoto pohybu, který je v noh přípdech výhodnější

7 Zákldní principy fyziky Seestrální projekt.3. Enerie tuhého těles Enerii lze chápt jko schopnost vykonávt práci. Abycho ohli vykont práci, potřebujee k ní enerii. Celková echnická enerie je součet enerie kinetické potencionální. Jednotkou je Joule, znčný velký J. J k s.3.. Kinetická enerie Kinetická enerie je enerie pohybová. Vyjdřuje skutečnost, že pohybující se těleso je schopné kont práci jko důsledek svého pohybu. Kinetickou enerii ůžee rozdělit n enerii pro těles při posuvné pohybu [ 6 ] pro těles při otáčivé pohybu [ 7 ]. V é přípdě ovše budu tyto dvě rovnice enerie kobinovt [ 8 ], resp. sčítt, kde předstvuje hotnost, v rychlost posuvného pohybu w je rychlost otáčivého pohybu. E [ 6 ] k v E k J ω [ 7 ] Ek v J ω [ 8 ] - 7 -

8 Zákldní principy fyziky Seestrální projekt 3. Výpočet Systé I Hotnost,0 k Hotnost 0,5 k řecí koeficient f 0, Poloěr kldky r 0,05 y x Systé II Jko první jse se rozhodl řešit zrychlení soustvy. K výpočtu jse dospěl tk, že jse si překreslenou situci z plletu rozdělil do dvou systéů znázorňující působící síly. Systé I n Systé II Do dirů jse si vynesl jednotlivé složky působící v systéech I II, kde předstvuje třecí sílu působící proti thové síle. N tíhovou sílu resp. působí v opčné sěru síl n, znázorňující sílu od podložky. Z jednotlivých dirů působících sil si ohu nyní sestvit soustvu rovnic pro výpočet. SystéI: x y n. Systé II: x y 0-8 -

9 Zákldní principy fyziky Seestrální projekt Po vytvoření rovnic pro kždý systé si vypočítá celkové zrychlení. oho docílí tk, že si vyjádří npř. z x-ové složky prvního systéu thovou sílu, kterou pk následně dosdí do rovnice druhého systéu y-ové složky. řecí koeficient jse si zvolil 0,. Poto ně vznikne následující:,96,5,943 0,5 0, 9,8 9,8,5 0 s f f n Nyní po výpočtu zrychlení lze i vypočítt thovou sílu. N f 94 3,,96 0, 9,8 Zrychlení thovou silu tké rovnou vypočítt z následujících vzorců:,96 9,8 0,5 0, 0,5 s f N f 3,94 9,8 0,5 0,5 0,) ( ) ( Nyní přejdu k výpočtu oentu setrvčnosti úhlové rychlosti kldky. Poté zjistí i její hotnost. Moent setrvčnosti zjistí z rovnice [ 9 ], do které dosdí jednotlivé kinetické enerie červeného těles, zeleného těles kldky. kkldky k k E E E v J v ω [ 9 ]

10 Zákldní principy fyziky Seestrální projekt Úhlovou rychlost kldky vypočítá poocí vzorce [ ]. Poloěr kldky jse zjistil ze siulčního plletu. Z rychlost v jse dosdil hodnotu,5 s -, kterou jse tké zjistil ze siulčního plletu. Ovše jestliže vypočítá rychlost z ého zrychlení, kde jse zohlednil i třecí koeficient, který jse si zvolil 0, vyšl by rychlost,5696 s -. Rychlost se vypočítá rovnicí [ 0 ], čs jse opět zjistil ze siulčního plletu. v t [ 0 ] v ω [ ] r v ω 50rd s r 0,05,5 v J ω v v J ω 0,5,5,5 J 50 J 0,00375k 4 0 v 3 k Jko poslední krok vypočítá hotnost kldky to poocí vzorce pro oent setrvčnosti válce nebo disku [ ], v é přípdě kldky. J r [ ] J r J 0,004 r 0,05 3,k - 0 -

11 Zákldní principy fyziky Seestrální projekt 4. Závěr práce Úkole v toto projektu bylo zjistil několik fktorů vyskytujících se v ukázkové plletu. Poocí Newtonových zákonů jse zjistil celkové zrychlení soustvy,96 s -. o le z předpokldu, když jse si zvolil třecí koeficient 0,. V přípdě, kdy jse tento koeficient znedbl, tudíž byl nulový, vyšlo zrychlení jiné ělo vliv i n okžitou rychlost v čse 0,8 sekundy. Rychlost v toto čse s ohlede n třecí koeficient vyšl v,5696 s -. Z plletu jde tedy vidět, že rychlost je odlišná o s -. Dále jse tedy počítl už s hodnoti ze siulce, tzn. s rychlostí,5 s -. Po výpočtu úhlové rychlosti kldky, která vyšl ω 50 rds - jse zjistil z rovnic pro kinetickou enerii i její oent setrvčnosti. en vyšel J 40-3 k. Jko poslední jse zjišťovl hotnost kldky, která vyšl 3, k. K projektu jse se snžil přistupovt s co největší pečlivostí to i z předpokldu, že ve výpočtech ohlo dojít k chybá způsobené lidský fktore nebo tké ze šptné úvhy fyzikálních zákonů. Ovše i tk povžuji tento úkol z velice poučný zjívý. - -

12 Zákldní principy fyziky Seestrální projekt 5. Použitá litertur DOSÁL J., JANÁČEK Z.: yzik, 5. vydání, Vysoké učení technické v Brně nkldtelství VUIUM, 997, ISBN: HALLIDAY D., RESNICK R., WALKER J.: yzik,. vydání, Vysoké učení technické v Brně nkldtelství VUIUM, 00, ISBN: