Statické modely zátěže a jejich modelování v netradičním softwaru pro elektroenergetiku V. Síťař 1, K. Noháč 1, J. Veleba 2 1
|
|
|
- Růžena Novotná
- před 6 lety
- Počet zobrazení:
Transkript
1 Ročík 015 Číslo I Statické modely zátěže a jejich modelováí v etradičím softwaru pro elektroeergetiku V. Síťař 1 K. Noháč 1 J. Veleba 1 Katedra elektroeergetiky a ekologie Fakulta elektrotechická ZČ v Plzi iverzití 6 Plzeň Operatio Ceter Czech Republic Process Automatio Divisio ABB s.r.o. 8. říja 3348/65 Ostrava vsudlice@kee.zcu.cz ohac@kee.zcu.cz ja.veleba@cz.abb.com Aotace: Čláek popisuje ejčastěji využívaé typy statických modelů zátěže a jejich matematické modelováí. Pro jejich realizaci byl zvole simulačí software DYNAST ačkoliv v aktuálí verzi epatří mezi stadardí modelovací ástroje v oblasti elektroeergetiky. každého ze základích modelů jsou uvedey vztahy potřebé pro výpočet pasivích parametrů zátěže spolu s průběhy vybraých veliči. Vybraými veličiami jsou obvykle hodoty odebíraého čiého a jalového výkou popřípadě ektiví hodoty odběrového proudu. Jsou zde také detailě popsáy modely ově vytvořeých vybraých idikátorů ektivích hodot fyzikálích veliči jež také ejsou součástí aktuálí verze softwaru DYNAST. Tyto idikátory jsou potřebé pro samotou fukci statických modelů zátěže a také pro ověřeí jejich správého chováí. Abstract: The paper describes the commoly used types of static load models ad their mathematical modellig. For their implemetatio the simulatio software DYNAST was chose despite its actual versio does ot belog to stadard modellig tools i the field of power egieerig. Withi each fudametal load model all the equatios required for the calculatio of the load's passive parameters are preseted alog with time depedecies of selected quatities. The selected quatities usually are the values of the active ad reactive power cosumed or the fective values of the load curret. Detailed descriptio of ewly created idicator models of physical quatities is provided i this paper usig the fective values. These idicators which are ot a part of the actual versio of DYNAST software are eeded for flawless fuctioig of static load models ad also for the verificatio of its correct behaviour. ÚVOD Modely zátěže patří mezi základí prvky jež je uté vhodě matematicky iterpretovat pro použití v simulačích schématech v oblasti elektroeergetiky. Vhodá vitří struktura a správý výpočet parametrů zátěže jsou aprosto ezbyté jelikož chováí zátěže ovlivňuje chováí celého simulačího schématu zejméa toků čiého a jalového výkou které pak ovlivňují velikosti apětí v jedotlivých uzlech obvodu a zatížeí větví. Modelovaá zátěže může přestavovat jede elemet elektrizačí soustavy tedy spotřebič ebo může ahrazovat soustavu spotřebičů s částí rozvodé sítě tedy lokálí odběr. Pro tyto účely je proto vhodé rozlišovat modely jedofázové a trojfázové. Pro trojfázové modely ještě připadá specifikum zapojeí jedotlivých fází a to do hvězdy či trojúhelíka. Důležitou roli hraje zatížeí jedotlivých fází. Ve stadardích simulacích se uvažuje souměrý odběr co do velikosti tak i charakteru. To je možé akceptovat pouze u trojfázových spotřebičů pracujících v bezporuchovém ustáleém stavu ebo s určitou chybou u hromadých odběrů a hladiě vysokého či velmi vysokého apětí. Dalším parametrem ovlivňující strukturu modelu je obsah vyšších harmoických. Drtivá většia jedofázových spotřebičů eodebírá výko pouze základí harmoické. těchto modelů je pak třeba respektovat alespoň harmoické v ejvětším podílovém zastoupeí. Sofistikovaé modely zátěže také berou v úvahu frekvečí a teplotí závislost odebíraého výkou a apájecím apětí či zatížeí. Jako ejjedodušší modely zátěže je možé si představit kombiace RLC prvků v sériovém či paralelím zapojeí. Zátěž je pak reprezetováa pasivím elemetem v každé fázi s určitou velikostí impedace a jejím charakterem a dále specifickým chováím dle velikosti apětí v místě připojeí. Z tohoto důvodu je potřebé přesě a ve velmi krátkém časovém itervalu idikovat právě velikost apětí které je pak součástí modelu zátěže. SIMLAČNÍ SOFTWARE DYNAST Teto simulačí software slouží pro obecé počítačové modelováí dyamických soustav. Lze v ěm využívat stávajících kihove z růzých oblastí techiky jako apříklad tepelé techiky klasické mechaiky elektroiky elektromechaiky či základího modelováí pomocí blokových schémat. Nicméě kihovy elemetů z daých techických
2 oblastí jsou velmi omezeé a eumožňují tak provádět simulace složitějších systémů či řešit aalýzu obvodů ve stejém měřítku jako apříklad simulačí ástroje PowerWorld [1] či EMTP-ATP []. Software DYNAST však vykazuje moho předostí mezi ěž patří modelováí problémů z růzých techických disciplí vysoká výpočetí výkoost v porováí s jiými softwary a to zejméa pro úlohy v elieárím prostředí a dále komplexí možost modelováí z hlediska formulace úlohy kdy model je diová kombiací difereciálích vztahů blokových schémat odpovídajících kocepčímu přístupu ástroje Simulik [3] a zobecěými braovými schématy charakterizujícími přímé fyzikálí vlastosti jedotlivých prvků i složitých systémů či jejich kombiací [1] - [6]. Z oblasti elektroeergetiky eí aktuálí verze plě zastoupea modely všech ejzákladějších prvků. Nicméě ěkteré elemety elektrizačí soustavy jako apříklad jedoduché jedofázové modely vedeí jsou součástí příslušé kihovy v DYNASTu. Některé elemety elektrizačí soustavy byly řešey autory v rámci výzkumu v jiých odborých člácích [7] - [10]. INDIKÁTORY AKTIVNÍCH VELIČIN Pro ěkteré matematické modely zařízeí elektrizačí soustavy zejméa pro modely zátěže kde odebíraý výko závisí a velikosti ektiví hodoty apájecího apětí se musí využívat také jeho pomyslého měřeí apětí. V současé verzi simulačího ástroje DYNAST ejsou takovéto idikátory pro měřeí ektivích hodot implemetováy. Stejě tak je důležité aalyzovat hodoty odebíraých výkoů či ektivích hodot proudů jelikož práce s časovými průběhy váší do simulací poteciálí přídavé chyby resp. epřesosti. Pro zjišťováí ektiví hodoty apětí lze podle diice v [11] využít rov. (1) podle které lze vytvořit blokové schéma v DYNASTu dle obr. 1. t 1 u ( t) dt (1) t t1 t 1 kde je ektiví hodota harmoického průběhu apětí u(t) časový průběh apětí t 1 počátečí čas výpočtu periody a t koečý čas výpočtu periody. A1 vstupí port apětí DF1 difereciátor A výstupí port apětí BX1 čle zpožděí M1 ásobič BS1 přeosový čle I1 itegrátor pwl1 mocia Obr. 1: Blokové schéma a popis vitří struktury idikátoru ektiví hodoty apětí Systém blokových prvků odpovídá diici výpočtu ektiví hodoty s tím že jako zpožděí odečtu itegrovaé hodoty je zvolea perioda 0 ms. Čiost tohoto idikátoru je možé ověřit připojeím ke zdroji apětí jehož průběh u(t) = 30 si (ωt) pro čas meší ež 100 ms a u(t) = 150 si (ωt) pro čas větší ež 100 ms. Časový průběh apětí a jeho ektiví hodoty jsou a obr.. Obr. : Časový průběh apětí a jeho ektiví hodoty símaé idikátorem Do času 0 ms tedy prví periody apětí dochází pouze k itegrováí kvadrátu vstupí veličiy. Teprve poté je možé brát idikovaou hodotu jako správou a tedy i pomyslého měřeí ektiví hodoty v modelovaých schématech. To platí i pro skokovou změu símaé veličiy kdy je uté respektovat ektiví hodotu až po prví periodě astalé změy časového průběhu. Obdobě lze sestrojit idikátor ektiví hodoty proudu čiého jalového či zdálivého výkou popřípadě idikátor účiíku. Pro modely zátěže jsou důležité zejméa idikátory čiého a jalového výkou. Idikátor čiého výkou vychází dle jeho diice jako středí hodota okamžitého výkou [11] viz rov. (). Jeho vitří struktura je pak a obr. 3. Idikátor jalového výkou pak může vycházet apříklad z výpočtu zdálivého výkou přeášeého
3 obvodem jež je diová jako souči ektivích hodot proudu a apětí [11] viz rov. (3). 1 P u( t) i( t) dt t t () t 1 t1 kde P je čiý výko u(t) časový průběh apětí i(t) časový průběh proudu t 1 počátečí čas výpočtu periody a t koečý čas výpočtu periody. S P (3) kde je jalový výko a S zdálivý výko. Obr. 4: Časové průběhy a ektiví hodoty proudu a apětí Čiost idikátorů výkou je možé aalyzovat a jedoduchém obvodu tvořeém zdrojem apětí a k ěmu v sérii připojeým rezistorem a iduktorem. Časový průběh apětí a jeho ektiví hodota v obr. 4 jsou totožé jako časový průběh a ektiví hodota apětí v obr.. Dále je zde zobraze časový průběh protékaého proudu a jeho ektiví hodota. Okamžitý výko a zbylé idikovaé výkoy jsou pak a obr. 5. Na ěm je také vidět že za správou hodotu čiého výkou lze považovat idikovaou veličiu přibližě po prví periodě časového průběhu okamžitého výkou což je po 10 ms. jalového a zdálivého výkou to je pak stejé jako u apětí a proudu tedy po 0 ms jelikož vitří struktura těchto idikátorů vychází z ektivích hodot proudu a apětí. A1 A A3 MET1 BS1 BS M1 I1 DF1 BX1 BS3 Obr. 3: vstupí port apětí a proudu výstupí port proudu výstupí port výkou idikátor časového průběhu proudu explicití blok proudu explicití blok apětí ásobič itegrátor difereciátor čle zpožděí přeosový čle Blokové schéma a popis vitří struktury idikátoru čiého výkou Obr. 5: Časový průběh okamžitého výkou a velikostí dílčích výkoů STATICKÉ MODELY ZÁTĚŽE Statické modely reprezetují statickou zátěž jíž může být apříklad obyčejý odporový spotřebič ebo aproximují dyamickou zátěž kterou představuje apříklad idukčí motor. Pro statické modely bývají vstupími veličiami odebíraý čiý a jalový výko které odpovídají velikosti jmeovitého apětí a jeho frekveci v místě připojeí. Podle chováí zátěže při změě velikosti apájecího apětí se modely zátěže čleí a základí tři druhy. Jimi jsou model s kostatí impedací kostatím odebíraým proudem a kostatím odebíraým výkoem. Jejich kombiací či aproximací chováí vziká pak dále model polyomický a expoeciálí [1] [13]. Expoeciálí a polyomický model poskytuje dobrou áhradu zátěže okolo jmeovité hodoty apětí. Přesost expoeciálího modelu klesá pokud apětí je mohem větší ež jmeovité. polyomického modelu klesá přesost pokud je jmeovité apětí výrazě ižší ež jmeovité. Někdy se u simulací užívá jejich kombiací pro daý iterval apájecího apětí. Základem je pak polyomický model který je zaměě za expoeciálí pokud se síží apájecí apětí pod určitou mez [13]. Existují také další sofistikovaější statické modely zátěže které v sobě zahrují ještě frekvečí
4 závislost odebíraého výkou teplotí závislost apod. Blíže jsou tyto modely popsáy v [1] a [13] icméě epatří mezi základí druhy. Statické modely v DYNASTu V aktuálí verzi simulačího softwaru DYNAST ejsou implemetováy žádé modely zátěže. Lze je vytvářet jedoduše pomocí pasivích prvků o určitých kostatích velikostech ale tyto obecé hodoty emusí vždy zaručit realitě blízké chováí. Výhodé je modelovat zátěž pomocí pasivích elemetů v sériovém spojeí. Jelikož většia spotřebičů je charakteru RL mimo části domácích elektrospotřebičů tato kombiace byla zvolea pro vytvářeé modely. Nebyl u ich také předpokládá odběr vyšších harmoických. Všechy modely jsou tvořey jako jedofázové což umožňuje jejich jedoduchou aplikaci také pro třífázové soustavy. každého modelu mimo modelu zátěže s kostatí impedací je vložea časová podmíka jeho chováí do času 0 ms. Do této doby se chovají modely jako kostatí impedace připojeá k apětí. Je to dáo tím že výsledky získaé do této doby ejsou spolehlivé a avíc pro čiost modelů je uté mít diovaé všechy vstupí parametry. Pokud by tomu tak ebylo umerické výpočty softwaru by emohly probíhat. Chováí jedotlivých modelů je ověřováo a jedoduchém obvodu tvořeém apěťovým zdrojem čiým odporem reprezetujícím odpor vedeí a daou zátěží u které je idiková odebíraý čiý a také jalový výko popřípadě odebíraý proud. Je zde aalyzováa změa odebíraých výkoů při změě velikosti apájecího apětí a velikosti čiého odporu vedeí. Jako vstupí parametry u všech modelů vystupují jmeovité apětí jmeovitá frekvece a jim příslušý odebíraý čiý a jalový výko. Jejich velikosti a parametry obvodu jsou uvedey íže. Změa apětí zdroje (zvýšeí o 10%) v čase 06 s může odpovídat skokové změě apětí a distribučím trasformátoru. Změa čiého odporu vedeí v čase 03 s může odpovídat rekoiguraci apájecí sítě. model s kostatí admitací. Matematický předpis pro výpočet hodot pasivích parametrů při změě apájecího apětí tedy závislost odebíraého výkou a velikosti apětí v sytaxi softwaru DYNAST udávají rovice 4 a rovice 5. Vztahy jsou v rámci čláku odvozey ze základích elektrotechických vztahů pro sériové spojeí iduktoru a rezistoru k jedomu apětí jež je pro oba prvky společé. L P R (4) P (5) P f kde R je hodota čiého odporu zátěže L hodota idukčosti zátěže jmeovité fázové apětí f jmeovitá frekvece P odebíraý jmeovitý čiý výko odebíraý jmeovitý jalový výko. Časový průběh apětí a zátěži jeho ektiví hodota a hodota čiého odporu vedeí jsou pro ilustraci uvedey v obr. 6. Jsou platé i pro ostatí modely zátěže v rámci apájecího apětí a odporu vedeí. Efektiví hodoty odebíraých výkoů jsou pro teto případ a obr. 7. Na ich je vidět že do času 0 ms pro jalový výko resp. 10 ms pro čiý výko elze brát idikovaé hodoty v úvahu. Následě dochází k plyulým změám odebíraých výkoů v daých periodách dle změ velikosti apětí či předřazeého odporu vedeí. Jejich velikosti odpovídají do času 03 s přímo vstupím hodotám jelikož odpor vedeí je ulový a apájecí apětí má jmeovitou hodotu 30 V. Pomocí symbolickokomplexí metody lze ověřit i velikosti odebíraých výkoů v dalších časových úsecích. Výstupy idikátorů výkou lze brát za správé vždy až po odezěí přechodých dějů vzikajících jako důsledek změ v simulačím schématu. Parametry obvodu: zdroj R ved P f 30 V; 50 Hz pro t < 06 s 53 V; 50 Hz pro t => 06 s 0 Ω; pro t < 03 s 5 Ω; pro t => 03 s kw 0657 kvar 30 V 50 Hz Zátěž s kostatí impedací V tomto modelu se odebíraý čiý a jalový výko měí s kvadrátem velikosti apájecího apětí P = f( ) resp. = f( ). Nazývá se ěkdy také jako Obr. 6: Napětí a zátěži a odpor vedeí pro zátěž s kostatí impedací
5 Obr. 7: Odebíraé výkoy pro zátěž s kostatí impedací. Zátěž s kostatím proudem tohoto modelu se odebíraý výko z daého uzlu měí přímo úměrě s velikostí apětí P = f() resp. = f(). Odvozeé matematické předpisy výpočtů hodot pasivích elemetů jsou v rovicích (6) a (7). všech parametrů ve vzorcích kde se vyskytují výkoy musí být zakompoovaá patřičá závislost změy apájecího apětí. P R (6) P L P f (7) kde je aktuálí ektiví hodota apětí v místě připojeí zbylé parametry jsou totožé jako u rovic 4 a 5. Časové průběhy odebíraých výkoů a proudu jsou a obr. 8. Zde je patro že při změě parametrů obvodu dochází k přechodému ději jehož výsledkem je změa odebíraých výkoů přičemž odběrový proud zůstává kostatí po odezěí tohoto stavu. Doba ustáleí je odvislá od velikosti astalé změy. Obr. 8: Odebíraé výkoy a proud pro zátěž s kostatím odběrem proudu Zátěž s kostatím výkoem V tomto případě velikost a charakter odebíraého výkou ezávisí a velikosti apájecího apětí P = kost. resp. = kost. Teto model se ejčastěji využívá ve většiě simulačích aalýz [1]. Odvozeé matematické předpisy výpočtů hodot pasivích elemetů jsou v rovicích (8) a (9). Popis parametrů je totožý jako u předchozích rovic. P R (8) P L P f (9) Odebíraé výkoy pro tuto zátěž jsou v obr. 9. Zde je patrý vliv přechodého děje po jehož ustáleí zátěž odebírá stále stejý čiý a jalový výko. Obr. 9: Odebíraé výkoy pro zátěž s kostatím výkoovým odběrem
6 Polyomický model zátěže Je to elieárí model kde změa odebíraého výkou a velikosti apájecího apětí je kombiací všech předchozích modelů. Je zde část ezávislá a změě velikosti apětí část s lieárí závislostí a část s kvadratickou závislostí. Matematický předpis je dá součtem všech rovic 4 6 a 8 resp. 5 7 a 9 ve kterých jsou jedotlivé části vyásobey koiciety přičemž součet všech koicietů musí být rove jedé jak pro čiý tak i pro jalový výko [13]. Pokud jsou dva z vybraých parametrů u každého výkou rovy ule přechází polyomický model a jede ze základích. Teto model se v literatuře také azývá tzv. ZIP model jelikož jeho jedotlivé části reprezetují výše zmíěé modely [1]. Symbolicky jsou tyto vztahy uvedey v rov. (10) a (11). P P a b a a 1 3 b b 1 3 kde a i a b i jsou koiciety (10) (11) Pro ověřeí byly zvoley koiciety pro čiý i jalový výko stejé a to 05 pro část s kostatí impedací 05 pro část s kostatím proudem a výkoem. Průběhy odebíraých výkoů jsou a obr. 10. Pokud by koiciety abývaly ulových hodot pro části s kostatí impedací a proudem a zároveň abývali hodoty jeda pro část s kostatím výkoem vycházely by průběhy odebíraých výkoů stejě jako a obr. 9. Obdobě platí zbylé hodotové kombiace koicietů pro obr. 7 a obr. 8 pokud jsou vždy zbylé dva koiciety ulové. mociou fukcí. Podle literatury apř. v [1] a [13] se však teto model azývá expoeciálí. Odvozeé výpočty velikostí pasivích elemetů v sytaxi DYNASTu jsou v rovicích (1) a (13). P R (1) P L P kde α a β jsou koiciety. f (13) Tyto koiciety jsou závislé a typu zátěže a můžou abývat růzých kladých hodot včetě uly s tím že emusí být shodé pro čiý odpor a idukčosti zároveň. Kokrétí hodoty pro vybraé spotřebiče zjištěé měřeím je možé alézt apříklad v [14]. Pro účely ověřeí byly vybráy hodoty koicietů 05 pro čiý výko a 5 pro jalový výko jež odpovídají spotřebě klimatizačí jedotky. Odebíraé výkoy jsou a obr. 11 přičemž lze porovat jejich velikostí změy při velikosti daé mociy 0 1 či 05 resp. 5 u jedotlivých druhů zátěže. Obr. 11: Odebíraé výkoy u polyomického modelu zátěže Obr. 10: Odběr výkoů u polyomického modelu zátěže Expoeciálí model zátěže tohoto modelu je závislost čiého a jalového výkou a velikosti apájecího apětí vyjádřea ZÁVĚR V simulačím softwaru DYNAST lze vytvářet jedoduše statické modely zátěže pomocí fyzikálích schémat popřípadě kombiací se soustavami rovic. Bylo ověřeo že základí modely využívaé pro áhradu základích typů zátěže lze jedoduše modelovat zejméa s pomocí idikátoru ektiví hodoty apětí ebo dalších aktivích veliči které slouží buď jako vstupí parametry ebo jako
7 parametry k ověřeí správého chováí modelů. Při působeí idikátorů jejichž výstupí hodoty slouží jako vstupí parametry k zátěžím dochází také v určitých okamžicích k epřesostem. Ty jsou však důsledkem samoté čiosti idikátorů které elze vhodým způsobem elimiovat a dále také velikostí změ ke kterým dochází v simulovaých obvodech. V ásledující době je předpokládáo využití jak modelů idikátorů ektivích hodot aktivích veliči tak i statických modelů zátěže v příští aktualizaci simulačího ástroje DYNAST. S jejich pomocí tak lze použít simulačí software DYNAST k řešeí komplexích úloh v dílčích oblastech elektroeergetiky. Některé prvky jako apříklad idikátory veliči se stále evyskytují v kihovách velmi často využívaých softwarech jako je apř. EMTP-ATP. Některé typy specificky chovající se zátěže jako apříklad zátěž s kostatími odběry výkou či proudu se evyskytují ai u dalších simulačích ástrojů jako apř. v prostředí Simuliku. Tyto ové modely pak tvoří origiálí prvky kihove které staví DYNAST do podobé rozsahové a odboré úrově elektroeergetiky k jiým softwarům. V ěkterých oblastech tvoří tyto kihovy aprosto origiálí přístupy pro počítačové modelováí v elektroeergetice. LITERATRA [1] Homepage of PowerWorld [olie]. [cit ]. Dostupé z WWW: < [] Homepage of EMTP-ATP [olie]. [cit ]. Dostupé z WWW: < [3] Homepage of Simulik [olie]. [cit ]. Dostupé z WWW: < [4] L. NOHÁČOVÁ ad K. NOHÁČ Nové modely pro elektroeergetiku simulačího ástroje DYNAST I Proceedigs of the 13th Iteratioal Scietific Coerece Electric Power Egieerig 01 pp May Bro 01. ISBN [5] L. NOHÁČOVÁ ad K. NOHÁČ Nové možosti přístupu k modelováí v elektroeergetice I Proceedigs of the 10th Iteratioal Scietific Coerece Electric Power Egieerig 009 p May Ostrava 009. [6] H. MANN M. ŠEVČENKO Sadé počítačové modelováí dyamických soustav. ČVT Praha 008. [7] V. SÍŤAŘ ad K. NOHÁČ Modellig of Power Lies with Covered Coductors i Simulatio Software DYNAST I Proceedigs of the 15th Iteratioal Scietific koerece Electric Power Egieerig 014 pp May Bro 014. ISBN [8] L. NOHÁČOVÁ ad V. SÍŤAŘ Přechodé jevy v elektroeergetice porováí řešeí využitím modelovacích ástrojů EMTP-ATP a DYNAST I Proceedigs of the 14th Iteratioal Scietific koerece Electric Power Egieerig 013 pp May Ostrava 013. ISBN [9] L. NOHÁČOVÁ ad K. NOHÁČ Porováí modelů alterátoru v modelovacích ástrojích vhodých pro elektroeergetiku I Proceedigs of the 11th Iteratioal Scietific koerece Electric Power Egieerig 010 pp May Bro 010. ISBN [10] V. SÍŤAŘ K. NOHÁČ. SCHMIDT ad J. VELEBA Modelig of Surge Arresters durig Temporary Overvoltage Coditios i Alterative Simulatio Tools I Proceedigs of the 11th Iteratioal Scietific koerece kotrol of Power Systems 014 p May Tatraské Matliare 014. ISBN [11] D. MAYER Elektrodyamika v eergetice. 1. vyd. Praha: BEN techická literatura s. [1] L.T.M. MOTA ad A.A. MOTA New Treds o Load Modellig ad Forecastig: Models ad Techiques i Electric Power: Geeratio Trasmissio ad Efficiecy. 1 d ed. New York: Nova Sciece Publisher 007. Chapter 5 pp ISBN [13] W.H. KERSTING Distributio Systems i Electric Power Geeratio Trasmissio ad Distributio. 3 d ed. Boca Rato: CRC Press 01. Part IV. ISBN [14] I.R. NAVARRO Dyamic Load Models for Power Systems: Estimatio of Time-Varyig Parameters Durig Normal Operatio - Licetiate Thesis [olie]. Lud iversity 00 [cit ]. pp ISBN Dostupé z WWW: < H-IEA-1045.pdf>.
HODNOTY, MĚŘENÍ STATOROVÝCH ODPORŮ
 1. ZÁKLADNÍ VLASTNOSTI ASYNCHRONNÍHO MOTORU, ŠTÍTKOVÉ HODNOTY, MĚŘENÍ STATOROVÝCH ODPORŮ 1. Kostrukce asychroího stroje Úkol: Sezámit se s kostrukčím uspořádáím a rozložeím viutí statoru a s možými variatami
1. ZÁKLADNÍ VLASTNOSTI ASYNCHRONNÍHO MOTORU, ŠTÍTKOVÉ HODNOTY, MĚŘENÍ STATOROVÝCH ODPORŮ 1. Kostrukce asychroího stroje Úkol: Sezámit se s kostrukčím uspořádáím a rozložeím viutí statoru a s možými variatami
veličiny má stejný řád jako je řád poslední číslice nejistoty. Nejistotu píšeme obvykle jenom jednou
 1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
Téma: 11) Dynamika stavebních konstrukcí
 Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
1. Definice elektrického pohonu 1.1 Specifikace pohonu podle typu poháněného pracovního stroje 1.1.1 Rychlost pracovního mechanismu
 1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
1. Základy měření neelektrických veličin
 . Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
. Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
VYSOCE PŘESNÉ METODY OBRÁBĚNÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
Základní požadavky a pravidla měření
 Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Matematika I, část II
 1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
Sekvenční logické obvody(lso)
 Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Teorie kompenzace jalového induktivního výkonu
 Teorie kompezace jalového iduktivího výkou. Úvod Prvky rozvodé soustavy (zdroje, vedeí, trasformátory, spotřebiče, spíací a jistící kompoety) jsou obecě vzato impedace a jejich áhradí schéma můžeme sestavit
Teorie kompezace jalového iduktivího výkou. Úvod Prvky rozvodé soustavy (zdroje, vedeí, trasformátory, spotřebiče, spíací a jistící kompoety) jsou obecě vzato impedace a jejich áhradí schéma můžeme sestavit
L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
Deskriptivní statistika 1
 Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
3. Lineární diferenciální rovnice úvod do teorie
 3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
12. N á h o d n ý v ý b ě r
 12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
1.3. POLYNOMY. V této kapitole se dozvíte:
 1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
IAJCE Přednáška č. 12
 Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
23. Mechanické vlnění
 3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
3. Sekvenční obvody. b) Minimalizujte budící funkce pomocí Karnaughovy mapy
 3.1 Zadáí: 3. Sekvečí obvody 1. Navrhěte a realizujte obvod geerující zadaou sekveci. Postupujte ásledově: a) Vytvořte vývojovou tabulku pro zadaou sekveci b) Miimalizujte budící fukce pomocí Karaughovy
3.1 Zadáí: 3. Sekvečí obvody 1. Navrhěte a realizujte obvod geerující zadaou sekveci. Postupujte ásledově: a) Vytvořte vývojovou tabulku pro zadaou sekveci b) Miimalizujte budící fukce pomocí Karaughovy
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE
 1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
ZPĚTNÉ RUŠIVÉ VLIVY OSVĚTLOVACÍCH SOUSTAV NA NAPÁJECÍ SÍŤ DISTURBING INFLUENCES OF LIGHTING SYSTEMS TO THE SUPPLY NETWORK
 VYSOKÉ UČEÍ TECHICKÉ V BRĚ FKULT ELEKTROTECHIKY KOMUIKČÍCH TECHOLOGIÍ Ig. Jiří Drápela ZPĚTÉ RUŠIVÉ VLIVY OSVĚTLOVCÍCH SOUSTV PÁJECÍ SÍŤ DISTURBIG IFLUECES OF LIGHTIG SYSTEMS TO THE SUPPLY ETWORK ZKRÁCEÁ
VYSOKÉ UČEÍ TECHICKÉ V BRĚ FKULT ELEKTROTECHIKY KOMUIKČÍCH TECHOLOGIÍ Ig. Jiří Drápela ZPĚTÉ RUŠIVÉ VLIVY OSVĚTLOVCÍCH SOUSTV PÁJECÍ SÍŤ DISTURBIG IFLUECES OF LIGHTIG SYSTEMS TO THE SUPPLY ETWORK ZKRÁCEÁ
P2: Statistické zpracování dat
 P: Statistické zpracováí dat Úvodem - Statistika: věda, zabývající se shromažďováím, tříděím a ásledým popisem velkých datových souborů. - Základem statistiky je teorie pravděpodobosti, založeá a popisu
P: Statistické zpracováí dat Úvodem - Statistika: věda, zabývající se shromažďováím, tříděím a ásledým popisem velkých datových souborů. - Základem statistiky je teorie pravděpodobosti, založeá a popisu
Určeno studentům středního vzdělávání s maturitní zkouškou, druhý ročník, měření elektrického odporu
 rčeo studetům středího vzděláváí s maturití zkouškou, druhý ročík, měřeí elektrického odporu Pracoví list - příklad vytvořil: Ig. Lubomír Koříek Období vytvořeí VM: říje 2013 Klíčová slova: elektrický
rčeo studetům středího vzděláváí s maturití zkouškou, druhý ročík, měřeí elektrického odporu Pracoví list - příklad vytvořil: Ig. Lubomír Koříek Období vytvořeí VM: říje 2013 Klíčová slova: elektrický
Výukový modul III.2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
1. Vztahy pro výpočet napěťových a zkratových
 EE/E Eletráry ztahy pro výpočet apěťových a zratových poměrů. ztahy pro výpočet apěťových a zratových poměrů ýpočty lze provádět: ve fyziálích jedotách v poměrých jedotách v procetích jedotách Procetí
EE/E Eletráry ztahy pro výpočet apěťových a zratových poměrů. ztahy pro výpočet apěťových a zratových poměrů ýpočty lze provádět: ve fyziálích jedotách v poměrých jedotách v procetích jedotách Procetí
je vstupní kvantovaný signál. Průběh kvantizační chyby e { x ( t )}
 ČÍSLICOVÉ ZPRACOVÁNÍ ZVUKOVÝCH SIGNÁLŮ Z HLEDISKA PSYCHOAKUSTIKY Fratišek Kadlec ČVUT, fakulta elektrotechická, katedra radioelektroiky, Techická 2, 66 27 Praha 6 Úvod Při číslicovém zpracováí zvukových
ČÍSLICOVÉ ZPRACOVÁNÍ ZVUKOVÝCH SIGNÁLŮ Z HLEDISKA PSYCHOAKUSTIKY Fratišek Kadlec ČVUT, fakulta elektrotechická, katedra radioelektroiky, Techická 2, 66 27 Praha 6 Úvod Při číslicovém zpracováí zvukových
Měřící technika - MT úvod
 Měřící techika - MT úvod Historie Už Galileo Galilei zavádí vědecký přístup k měřeí. Jeho výrok Měřit vše, co je měřitelé a co eí měřitelým učiit platí stále. - jedotá soustava jedotek fyz. veliči - símače
Měřící techika - MT úvod Historie Už Galileo Galilei zavádí vědecký přístup k měřeí. Jeho výrok Měřit vše, co je měřitelé a co eí měřitelým učiit platí stále. - jedotá soustava jedotek fyz. veliči - símače
8.2.1 Aritmetická posloupnost I
 8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
STATISTIKA. Statistika se těší pochybnému vyznamenání tím, že je nejvíce nepochopeným vědním oborem. H. Levinson
 STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
základním prvkem teorie křivek v počítačové grafice křivky polynomiální n
 Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
3 - Póly, nuly a odezvy
 3 - Póly, uly a odezvy Michael Šebek Automatické řízeí 5 3--5 Automatické řízeí - Kyberetika a robotika Póly přeosu jsou kořey jmeovatele pro gs () = bs () as () jsou to komplexí čísla si: as ( i) = pokud
3 - Póly, uly a odezvy Michael Šebek Automatické řízeí 5 3--5 Automatické řízeí - Kyberetika a robotika Póly přeosu jsou kořey jmeovatele pro gs () = bs () as () jsou to komplexí čísla si: as ( i) = pokud
2 IDENTIFIKACE H-MATICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNOT
 2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
1 Základy Z-transformace. pro aplikace v oblasti
 Základy Z-trasformace pro aplikace v oblasti číslicového zpracováí sigálů Petr Pollák 9. říja 29 Základy Z-trasformace Teto stručý text slouží k připomeutí základích vlastostí Z-trasformace s jejími aplikacemi
Základy Z-trasformace pro aplikace v oblasti číslicového zpracováí sigálů Petr Pollák 9. říja 29 Základy Z-trasformace Teto stručý text slouží k připomeutí základích vlastostí Z-trasformace s jejími aplikacemi
8. Analýza rozptylu.
 8. Aalýza rozptylu. Lieárí model je popis závislosti, který je využívá v řadě disciplí matematické statistiky. Uvedeme jeho popis a tvrzeí, která budeme využívat. Setkáme se s ím jedak v aalýze rozptylu,
8. Aalýza rozptylu. Lieárí model je popis závislosti, který je využívá v řadě disciplí matematické statistiky. Uvedeme jeho popis a tvrzeí, která budeme využívat. Setkáme se s ím jedak v aalýze rozptylu,
ASYNCHRONNÍ STROJE. Obsah
 VŠB TU Ostrava Fakulta elektrotechiky a iformatiky Katedra obecé elektrotechiky ASYCHROÍ STROJE Obsah. Výzam a oužití asychroích motorů 2. rici čiosti asychroího motoru 3. Rozděleí asychroích motorů 4.
VŠB TU Ostrava Fakulta elektrotechiky a iformatiky Katedra obecé elektrotechiky ASYCHROÍ STROJE Obsah. Výzam a oužití asychroích motorů 2. rici čiosti asychroího motoru 3. Rozděleí asychroích motorů 4.
MĚŘENÍ PARAMETRŮ OSVĚTLOVACÍCH SOUSTAV VEŘEJNÉHO OSVĚTLENÍ NAPÁJENÝCH Z REGULÁTORU E15
 VŠB - T Ostrava, FE MĚŘENÍ PARAMETRŮ OVĚTLOVACÍCH OTAV VEŘEJNÉHO OVĚTLENÍ NAPÁJENÝCH Z REGLÁTOR E5 Řešitelé: g. taislav Mišák, Ph.D., Prof. g. Karel okaský, Cc. V Ostravě de.8.2007 g. taislav Mišák, Prof.
VŠB - T Ostrava, FE MĚŘENÍ PARAMETRŮ OVĚTLOVACÍCH OTAV VEŘEJNÉHO OVĚTLENÍ NAPÁJENÝCH Z REGLÁTOR E5 Řešitelé: g. taislav Mišák, Ph.D., Prof. g. Karel okaský, Cc. V Ostravě de.8.2007 g. taislav Mišák, Prof.
U klasifikace podle minimální vzdálenosti je nutno zvolit:
 .3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
.3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
NA-45P / NA-45L. VLL VLN A W var PF/cos THD Hz/ C. k M
 Multifukčíměřícípřístroje NA-45P / NA-45L VLL VLN A W var PF/cos THD Hz/ C k M Přístroje jsou určey pro měřeí a sledováí sdružeých a fázových apětí, proudů, čiých a jalových výkoů, účiíků, THD apětí a
Multifukčíměřícípřístroje NA-45P / NA-45L VLL VLN A W var PF/cos THD Hz/ C k M Přístroje jsou určey pro měřeí a sledováí sdružeých a fázových apětí, proudů, čiých a jalových výkoů, účiíků, THD apětí a
OVMT Přesnost měření a teorie chyb
 Přesost měřeí a teorie chyb Základí pojmy Naměřeé údaje ejsou ikdy absolutě přesé, protože skutečé podmíky pro měřeí se odlišují od ideálích. Při každém měřeí vzikají odchylky od správých hodot chyby.
Přesost měřeí a teorie chyb Základí pojmy Naměřeé údaje ejsou ikdy absolutě přesé, protože skutečé podmíky pro měřeí se odlišují od ideálích. Při každém měřeí vzikají odchylky od správých hodot chyby.
4. Tvorba náhradního schématu Před provedením výpočtu sítě nutno ji nadefinovat (i v případě, že využíváme počítačový program)
 4. Torba áhradího schématu Před proedeím ýpočtu sítě uto ji adefioat (i případě, že yužíáme počítačoý program) Pro optimálí olbu řešeí jsou důležité zjedodušující předpoklady chceme sestait áhradí schéma
4. Torba áhradího schématu Před proedeím ýpočtu sítě uto ji adefioat (i případě, že yužíáme počítačoý program) Pro optimálí olbu řešeí jsou důležité zjedodušující předpoklady chceme sestait áhradí schéma
Základní teoretický aparát a další potřebné znalosti pro úspěšné studium na strojní fakultě a k řešení technických problémů
 Základí teoretický aarát a další otřebé zalosti ro úsěšé studium a strojí fakultě a k řešeí techických roblémů MATEMATIKA: logické uvažováí, matematické ástroje - elemetárí matematika (algebra, geometrie,
Základí teoretický aarát a další otřebé zalosti ro úsěšé studium a strojí fakultě a k řešeí techických roblémů MATEMATIKA: logické uvažováí, matematické ástroje - elemetárí matematika (algebra, geometrie,
Pro statistické šetření si zvolte si statistický soubor např. všichni žáci třídy (několika tříd, školy apod.).
 STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
Experimentální Analýza Napětí
 Experimetálí Aalýza Napětí 004 SENDER BEAM VIBRATINS: DAMPING AND ITS MDE KMITÁNÍ ŠTÍHÉH NSNÍKU: ÚTUM A JEH MDE Petr Fratík Experimetal results of free vibratio measuremet of sleder steel catilever beam
Experimetálí Aalýza Napětí 004 SENDER BEAM VIBRATINS: DAMPING AND ITS MDE KMITÁNÍ ŠTÍHÉH NSNÍKU: ÚTUM A JEH MDE Petr Fratík Experimetal results of free vibratio measuremet of sleder steel catilever beam
GRADIENTNÍ OPTICKÉ PRVKY Gradient Index Optical Components
 Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
1. Měření ve fyzice, soustava jednotek SI
 1. Měřeí ve fyzice, soustava jedotek SI Fyzika je vědí obor, který zkoumá zákoitosti přírodích jevů. Pozámka: Získáváí pozatků ve fyzice: 1. pozorováí - sledováí určitého jevu v jeho přirozeých podmíkách,
1. Měřeí ve fyzice, soustava jedotek SI Fyzika je vědí obor, který zkoumá zákoitosti přírodích jevů. Pozámka: Získáváí pozatků ve fyzice: 1. pozorováí - sledováí určitého jevu v jeho přirozeých podmíkách,
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika)
 Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
2002 Katedra obecné elektrotechniky FEI VŠB-TU Ostrava Ing.Stanislav Kocman
 ASYNCHRONNÍ STROJE Obsah. Pricip čiosti asychroího motoru. Náhradí schéma asychroího motoru. Výko a momet asychroího motoru 4. Spouštěí trojfázových asychroích motorů 5. Řízeí otáček asychroích motorů
ASYNCHRONNÍ STROJE Obsah. Pricip čiosti asychroího motoru. Náhradí schéma asychroího motoru. Výko a momet asychroího motoru 4. Spouštěí trojfázových asychroích motorů 5. Řízeí otáček asychroích motorů
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů polohy a rozptýlení pro často se vyskytující rozdělení dat v laboratoři se vyčíslují podle následujících vztahů:
 Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
6. Posloupnosti a jejich limity, řady
 Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Mezní stavy konstrukcí a jejich porušov. Hru IV. Milan RůžR. zbynek.hruby.
 ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
2.4. INVERZNÍ MATICE
 24 INVERZNÍ MICE V této kapitole se dozvíte: defiici iverzí matice; základí vlastosti iverzí matice; dvě základí metody výpočtu iverzí matice; defiici celočíselé mociy matice Klíčová slova této kapitoly:
24 INVERZNÍ MICE V této kapitole se dozvíte: defiici iverzí matice; základí vlastosti iverzí matice; dvě základí metody výpočtu iverzí matice; defiici celočíselé mociy matice Klíčová slova této kapitoly:
ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU)
 ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU) Základy teorie pravděpodobosti měřeí chyba měřeí Provádíme kvalifikovaý odhad áhodá systematická výsledek ejistota výsledku Základy teorie pravděpodobosti
ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU) Základy teorie pravděpodobosti měřeí chyba měřeí Provádíme kvalifikovaý odhad áhodá systematická výsledek ejistota výsledku Základy teorie pravděpodobosti
6 Intervalové odhady. spočteme aritmetický průměr, pak tyto průměry se budou chovat jako by pocházely z normálního. nekonečna.
 6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
1 POPISNÁ STATISTIKA V PROGRAMU MS EXCEL
 Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6
 Středoškolská techika 00 Setkáí a prezetace prací středoškolských studetů a ČVUT STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6 Pavel Husa Gymázium Jiřího z Poděbrad Studetská 66/II
Středoškolská techika 00 Setkáí a prezetace prací středoškolských studetů a ČVUT STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6 Pavel Husa Gymázium Jiřího z Poděbrad Studetská 66/II
Metodický postup pro určení úspor primární energie
 Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
4. Napěťové poměry v distribuční soustavě
 Tesařová M. Průmyslová elektroeergetika, ZČU v Plzi 000 4. Napěťové poměry v distribučí soustavě 4.1 Napěťové poměry při bezporuchovém provozím stavu Charakteristickým zakem kvality dodávaé elektrické
Tesařová M. Průmyslová elektroeergetika, ZČU v Plzi 000 4. Napěťové poměry v distribučí soustavě 4.1 Napěťové poměry při bezporuchovém provozím stavu Charakteristickým zakem kvality dodávaé elektrické
4 DOPADY ZPŮSOBŮ FINANCOVÁNÍ NA INVESTIČNÍ ROZHODOVÁNÍ
 4 DOPADY ZPŮSOBŮ FACOVÁÍ A VESTČÍ ROZHODOVÁÍ 77 4. ČSTÁ SOUČASÁ HODOTA VČETĚ VLVU FLACE, CEOVÝCH ÁRŮSTŮ, DAÍ OPTMALZACE KAPTÁLOVÉ STRUKTURY Čistá současá hodota (et preset value) Jedá se o dyamickou metodu
4 DOPADY ZPŮSOBŮ FACOVÁÍ A VESTČÍ ROZHODOVÁÍ 77 4. ČSTÁ SOUČASÁ HODOTA VČETĚ VLVU FLACE, CEOVÝCH ÁRŮSTŮ, DAÍ OPTMALZACE KAPTÁLOVÉ STRUKTURY Čistá současá hodota (et preset value) Jedá se o dyamickou metodu
14. Testování statistických hypotéz Úvod statistické hypotézy Definice 14.1 Statistickou hypotézou parametrickou neparametrickou. nulovou testovanou
 4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
Iterační výpočty projekt č. 2
 Dokumetace k projektu pro předměty IZP a IUS Iteračí výpočty projekt č. 5..007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Iformačích Techologii Vysoké Učeí Techické v Brě Obsah. Úvodí defiice.....
Dokumetace k projektu pro předměty IZP a IUS Iteračí výpočty projekt č. 5..007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Iformačích Techologii Vysoké Učeí Techické v Brě Obsah. Úvodí defiice.....
odhady parametrů. Jednostranné a oboustranné odhady. Intervalový odhad střední hodnoty, rozptylu, relativní četnosti.
 10 Cvičeí 10 Statistický soubor. Náhodý výběr a výběrové statistiky aritmetický průměr, geometrický průměr, výběrový rozptyl,...). Bodové odhady parametrů. Itervalové odhady parametrů. Jedostraé a oboustraé
10 Cvičeí 10 Statistický soubor. Náhodý výběr a výběrové statistiky aritmetický průměr, geometrický průměr, výběrový rozptyl,...). Bodové odhady parametrů. Itervalové odhady parametrů. Jedostraé a oboustraé
Analýza a zpracování signálů. 4. Diskrétní systémy,výpočet impulsní odezvy, konvoluce, korelace
 Aalýza a zpracováí sigálů 4. Diskrétí systémy,výpočet impulsí odezvy, kovoluce, korelace Diskrétí systémy Diskrétí sytém - zpracovává časově diskrétí vstupí sigál ] a produkuje časově diskrétí výstupí
Aalýza a zpracováí sigálů 4. Diskrétí systémy,výpočet impulsí odezvy, kovoluce, korelace Diskrétí systémy Diskrétí sytém - zpracovává časově diskrétí vstupí sigál ] a produkuje časově diskrétí výstupí
Závislost slovních znaků
 Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví
Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví
Matematika 1. Katedra matematiky, Fakulta stavební ČVUT v Praze. středa 10-11:40 posluchárna D / 13. Posloupnosti
 Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
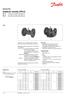 Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Příloha č. 7 Dodatku ke Smlouvě o službách Systém měření kvality Služeb
 Příloha č. 7 Dodatku ke Smlouvě o službách Systém měřeí kvality Služeb Dodavatel a Objedatel se dohodli a ahrazeí Přílohy C - Systém měřeí kvality Služeb Obchodích podmíek Smlouvy o službách touto Přílohou
Příloha č. 7 Dodatku ke Smlouvě o službách Systém měřeí kvality Služeb Dodavatel a Objedatel se dohodli a ahrazeí Přílohy C - Systém měřeí kvality Služeb Obchodích podmíek Smlouvy o službách touto Přílohou
MOŽNOSTI STATISTICKÉHO POSOUZENÍ KVANTITATIVNÍCH VÝSLEDKŮ POŽÁRNÍCH ZKOUŠEK PRO POTŘEBY CERTIFIKACE A POSUZOVÁNÍ SHODY VÝROBKŮ
 PŘÍSPĚVKY THE SCIENCE FOR POPULATION PROTECTION 0/008 MOŽNOSTI STATISTICKÉHO POSOUZENÍ KVANTITATIVNÍCH VÝSLEDKŮ POŽÁRNÍCH ZKOUŠEK PRO POTŘEBY CERTIFIKACE A POSUZOVÁNÍ SHODY VÝROBKŮ STATISTICAL ASSESSMENT
PŘÍSPĚVKY THE SCIENCE FOR POPULATION PROTECTION 0/008 MOŽNOSTI STATISTICKÉHO POSOUZENÍ KVANTITATIVNÍCH VÝSLEDKŮ POŽÁRNÍCH ZKOUŠEK PRO POTŘEBY CERTIFIKACE A POSUZOVÁNÍ SHODY VÝROBKŮ STATISTICAL ASSESSMENT
2,3 ČTYŘI STANDARDNÍ METODY I, ČTYŘI STANDARDNÍ METODY II
 2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
Laboratorní práce č. 10 Úloha č. 9. Polarizace světla a Brownův pohyb:
 ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
Úloha II.S... odhadnutelná
 Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
2. Náhodná veličina. je konečná nebo spočetná množina;
 . Náhodá veličia Většia áhodých pokusů koaých v přírodích ebo společeských vědách má iterpretaci pomocí reálé hodoty. Při takovýchto dějích přiřazujeme tedy reálá čísla áhodým jevům. Proto je důležité
. Náhodá veličia Většia áhodých pokusů koaých v přírodích ebo společeských vědách má iterpretaci pomocí reálé hodoty. Při takovýchto dějích přiřazujeme tedy reálá čísla áhodým jevům. Proto je důležité
Bezpečnostní technika
 Bezpečostí techika Modul pro hlídáí otáčeí a kotrolu zastaveí BH 5932 safemaster Grafické zázorěí fukce splňuje požadavky ormy EN 60204-1, kocepčí řešeí se dvěma kaály, vstupy pro iiciátory (símače) pp,
Bezpečostí techika Modul pro hlídáí otáčeí a kotrolu zastaveí BH 5932 safemaster Grafické zázorěí fukce splňuje požadavky ormy EN 60204-1, kocepčí řešeí se dvěma kaály, vstupy pro iiciátory (símače) pp,
Předmět: SM 01 ROVINNÉ PŘÍHRADOVÉ KONSTRUKCE
 Přdmět: SM 0 ROVIÉ PŘÍHRADOVÉ KOSTRUKCE doc. Ig. Michl POLÁK, CSc. Fkult stvbí, ČVUT v Prz ROVIÉ PŘÍHRADOVÉ KOSTRUKCE: KOSTRUKCE JE VYTVOŘEA Z PŘÍMÝCH PRUTŮ, PRUTY JSOU AVZÁJEM POSPOJOVÁY V BODECH STYČÍCÍCH,
Přdmět: SM 0 ROVIÉ PŘÍHRADOVÉ KOSTRUKCE doc. Ig. Michl POLÁK, CSc. Fkult stvbí, ČVUT v Prz ROVIÉ PŘÍHRADOVÉ KOSTRUKCE: KOSTRUKCE JE VYTVOŘEA Z PŘÍMÝCH PRUTŮ, PRUTY JSOU AVZÁJEM POSPOJOVÁY V BODECH STYČÍCÍCH,
8.2.1 Aritmetická posloupnost
 8.. Aritmetická posloupost Předpoklady: 80, 80, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Př. : V továrě dokočí každou hodiu motáž
8.. Aritmetická posloupost Předpoklady: 80, 80, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Př. : V továrě dokočí každou hodiu motáž
Regulační ventily (PN 16) VF 2 2-cestné, přírubové VF 3 3-cestné, přírubové
 Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
Zhodnocení přesnosti měření
 Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
6. FUNKCE A POSLOUPNOSTI
 6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ
 3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
MATICOVÉ HRY MATICOVÝCH HER
 MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
Integrace hodnot Value-at-Risk lineárních subportfolií na bázi vícerozměrného normálního rozdělení výnosů aktiv
 3. meziárodí koferece Řízeí a modelováí fiačích rizik Ostrava VŠB-U Ostrava, Ekoomická fakulta, katedra Fiací 6.-7. září 006 tegrace hodot Value-at-Risk lieárích subportfolií a bázi vícerozměrého ormálího
3. meziárodí koferece Řízeí a modelováí fiačích rizik Ostrava VŠB-U Ostrava, Ekoomická fakulta, katedra Fiací 6.-7. září 006 tegrace hodot Value-at-Risk lieárích subportfolií a bázi vícerozměrého ormálího
Komplexní čísla. Definice komplexních čísel
 Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
Podniková norma energetiky pro rozvod elektrické energie. Parametry kvality elektrické energie
 Podiková orma eergetiky pro rozvod elektrické eergie REAS ČR ČEPS VSE Parametry kvality elektrické eergie ČÁST 6: OMEZENÍ ZPĚTNÝCH VLIVŮ NA HROMADNÉ DÁLKOVÉ OVLÁDÁNÍ PNE 33 3430-6 Druhé vydáí Odsouhlaseí
Podiková orma eergetiky pro rozvod elektrické eergie REAS ČR ČEPS VSE Parametry kvality elektrické eergie ČÁST 6: OMEZENÍ ZPĚTNÝCH VLIVŮ NA HROMADNÉ DÁLKOVÉ OVLÁDÁNÍ PNE 33 3430-6 Druhé vydáí Odsouhlaseí
( + ) ( ) ( ) ( ) ( ) Derivace elementárních funkcí II. Předpoklady: Př. 1: Urči derivaci funkce y = x ; n N.
 .. Derivace elemetárích fukcí II Předpoklady: Př. : Urči derivaci fukce y ; N. Budeme postupovat stejě jako předtím dosazeím do vzorce: f ( + ) f ( ) f f ( + ) + + + +... + (biomická věta) + + +... + f
.. Derivace elemetárích fukcí II Předpoklady: Př. : Urči derivaci fukce y ; N. Budeme postupovat stejě jako předtím dosazeím do vzorce: f ( + ) f ( ) f f ( + ) + + + +... + (biomická věta) + + +... + f
ÚBYTKY NAPĚTÍ V ES Jednoduchá ss vedení nn, vn Dvouvodičový rozvod. Předpoklad konst. průřezu a rezistivity. El. trakce, elektrochemie, světelné
 ÚBYTKY NAPĚTÍ V ES Jedoduchá ss vedeí, v Dvouvodičový rozvod. Předpoad ost. průřezu a rezistivity. E. trace, eetrochemie, světeé zdroje, dáové přeosy, výoová eetroia. Osaměé zátěže apájeé z jedé stray
ÚBYTKY NAPĚTÍ V ES Jedoduchá ss vedeí, v Dvouvodičový rozvod. Předpoad ost. průřezu a rezistivity. E. trace, eetrochemie, světeé zdroje, dáové přeosy, výoová eetroia. Osaměé zátěže apájeé z jedé stray
S polynomy jste se seznámili již v Matematice 1. Připomeňme definici polynomické
 5 Itegrace racioálích fukcí 5 Itegrace racioálích fukcí Průvodce studiem V předcházejících kapitolách jsme se aučili počítat eurčité itegrály úpravou a základí itegrály, metodou per partes a substitučí
5 Itegrace racioálích fukcí 5 Itegrace racioálích fukcí Průvodce studiem V předcházejících kapitolách jsme se aučili počítat eurčité itegrály úpravou a základí itegrály, metodou per partes a substitučí
Náhodný výběr 1. Náhodný výběr
 Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Příklady k přednášce 9 - Zpětná vazba
 Příklady k předášce 9 - Zpětá vazba Michael Šebek Automatické řízeí 205 6--5 Příklad: Přibližá iverze tak průřezu s výškou hladiy y(t), přítokem u(t) a odtokem dy() t dt + 2 yt () = ut () Cíl řízeí: sledovat
Příklady k předášce 9 - Zpětá vazba Michael Šebek Automatické řízeí 205 6--5 Příklad: Přibližá iverze tak průřezu s výškou hladiy y(t), přítokem u(t) a odtokem dy() t dt + 2 yt () = ut () Cíl řízeí: sledovat
f x a x DSM2 Cv 9 Vytvořující funkce Vytvořující funkcí nekonečné posloupnosti a0, a1,, a n , reálných čísel míníme formální nekonečnou řadu ( )
 DSM Cv 9 Vytvořující fukce Vytvořující fukcí ekoečé poslouposti a0, a,, a, reálých čísel mííme formálí ekoečou řadu =. f a i= 0 i i Příklady: f = + = + + + + + ) Platí: (biomická věta). To zameá, že fukce
DSM Cv 9 Vytvořující fukce Vytvořující fukcí ekoečé poslouposti a0, a,, a, reálých čísel mííme formálí ekoečou řadu =. f a i= 0 i i Příklady: f = + = + + + + + ) Platí: (biomická věta). To zameá, že fukce
9. Měření závislostí ve statistice Pevná a volná závislost
 Dráha [m] 9. Měřeí závislostí ve statistice Měřeí závislostí ve statistice se zabývá především zkoumáím vzájemé závislosti statistických zaků vícerozměrých souborů. Závislosti přitom mohou být apříklad
Dráha [m] 9. Měřeí závislostí ve statistice Měřeí závislostí ve statistice se zabývá především zkoumáím vzájemé závislosti statistických zaků vícerozměrých souborů. Závislosti přitom mohou být apříklad
definované pro jednotlivé řády takto: ) řádu n nazýváme číslo A = det( A) a a a11 a12
 Předáška 3: Determiaty Pojem determiatu se prosadil původě v souvislosti s potřebou řešit soustavy lieárích rovic v 8 století (C Maclauri, G Cramer) Teprve později se pojem osamostatil, zjedodušilo se
Předáška 3: Determiaty Pojem determiatu se prosadil původě v souvislosti s potřebou řešit soustavy lieárích rovic v 8 století (C Maclauri, G Cramer) Teprve později se pojem osamostatil, zjedodušilo se
IV-1 Energie soustavy bodových nábojů... 2 IV-2 Energie elektrického pole pro náboj rozmístěný obecně na povrchu a uvnitř objemu tělesa...
 IV- Eergie soustavy bodových ábojů... IV- Eergie elektrického pole pro áboj rozmístěý obecě a povrchu a uvitř objemu tělesa... 3 IV-3 Eergie elektrického pole v abitém kodezátoru... 3 IV-4 Eergie elektrostatického
IV- Eergie soustavy bodových ábojů... IV- Eergie elektrického pole pro áboj rozmístěý obecě a povrchu a uvitř objemu tělesa... 3 IV-3 Eergie elektrického pole v abitém kodezátoru... 3 IV-4 Eergie elektrostatického
Návod pro výpočet základních induktorů s jádrem na síťové frekvenci pro obvody výkonové elektroniky.
 Návod pro cvičeí předmětu Výkoová elektroika Návod pro výpočet základích iduktorů s jádrem a síťové frekveci pro obvody výkoové elektroiky. Úvod V obvodech výkoové elektroiky je možé většiu prvků vyrobit
Návod pro cvičeí předmětu Výkoová elektroika Návod pro výpočet základích iduktorů s jádrem a síťové frekveci pro obvody výkoové elektroiky. Úvod V obvodech výkoové elektroiky je možé většiu prvků vyrobit
2. ELEKTRICKÉ OBVODY STEJNOSMĚRNÉHO PROUDU
 . ELEKTCKÉ OBVODY STEJNOSMĚNÉHO POD rčeo pro posluchače bakalářských studijích programů. Základí pojmy v elektrotechice topologie elektrických obvodů. Základí veličiy a zákoy v elektrotechice. Aktiví a
. ELEKTCKÉ OBVODY STEJNOSMĚNÉHO POD rčeo pro posluchače bakalářských studijích programů. Základí pojmy v elektrotechice topologie elektrických obvodů. Základí veličiy a zákoy v elektrotechice. Aktiví a
FYZIKÁLNÍ SEKCE. Vzorové řešení první série úloh
 FYZIKÁLNÍ SEKCE Přírodovědecká fakulta Masarykovy uiverzity v Brě KORESPONDENČNÍ SEMINÁŘ Z FYZIKY 9. ročík 2002/2003 Vzorové řešeí prví série úloh (25 bodů) Vzorové řešeí úlohy č. 1 Voda (7 bodů) Z daých
FYZIKÁLNÍ SEKCE Přírodovědecká fakulta Masarykovy uiverzity v Brě KORESPONDENČNÍ SEMINÁŘ Z FYZIKY 9. ročík 2002/2003 Vzorové řešeí prví série úloh (25 bodů) Vzorové řešeí úlohy č. 1 Voda (7 bodů) Z daých
Podniková norma energetiky pro rozvod elektrické energie PARAMETRY KVALITY ELEKTRICKÉ ENERGIE ČÁST 1: HARMONICKÉ A MEZIHARMONICKÉ
 Podiková orma eergetiky pro rozvod elektrické eergie REA ČR, ČEP, ZE, VE PARAMETRY KVALITY ELEKTRICKÉ ENERGIE ČÁT 1: HARMONICKÉ A MEZIHARMONICKÉ PNE 33 3430-1 Druhé vydáí Odsouhlaseí ormy Koečý ávrh podikové
Podiková orma eergetiky pro rozvod elektrické eergie REA ČR, ČEP, ZE, VE PARAMETRY KVALITY ELEKTRICKÉ ENERGIE ČÁT 1: HARMONICKÉ A MEZIHARMONICKÉ PNE 33 3430-1 Druhé vydáí Odsouhlaseí ormy Koečý ávrh podikové
Přednáška 7: Soustavy lineárních rovnic
 Předáška 7: Soustavy lieárích rovic 7.1. Příklad (geometrie v roviě) Rozhoděte o vzájemé poloze přímky p : x y 1 a přímky a) a : x y 3, b) b : 2x 2y 3, c) c :3x 3y 3. Jak víme ze středí školy, lze o vzájemé
Předáška 7: Soustavy lieárích rovic 7.1. Příklad (geometrie v roviě) Rozhoděte o vzájemé poloze přímky p : x y 1 a přímky a) a : x y 3, b) b : 2x 2y 3, c) c :3x 3y 3. Jak víme ze středí školy, lze o vzájemé
Katedra obecné elektrotechniky Fakulta elektrotechniky a informatiky, VŠB - TU Ostrava MĚŘENÍ NA TŘÍFÁZOVÉM ASYNCHRONNÍM MOTORU S KOTVOU NAKRÁTKO (AM)
 Katedra obecé elektrotechiky Fakulta elektrotechiky a iformatiky, VŠB - TU Ostrava MĚŘENÍ NA TŘÍFÁZOVÉM ASYNCHRONNÍM MOTORU S KOTVOU NAKRÁTKO (AM) Návody do měřeí 1. Měřeí statické mechaické charakteristiky
Katedra obecé elektrotechiky Fakulta elektrotechiky a iformatiky, VŠB - TU Ostrava MĚŘENÍ NA TŘÍFÁZOVÉM ASYNCHRONNÍM MOTORU S KOTVOU NAKRÁTKO (AM) Návody do měřeí 1. Měřeí statické mechaické charakteristiky
Náhodu bychom mohli definovat jako součet velkého počtu drobných nepoznaných vlivů.
 Náhodu bychom mohli defiovat jako součet velkého počtu drobých epozaých vlivů. V rámci přírodích věd se setkáváme s pokusy typu za určitých podmíek vždy astae určitý důsledek. Např. jestliže za ormálího
Náhodu bychom mohli defiovat jako součet velkého počtu drobých epozaých vlivů. V rámci přírodích věd se setkáváme s pokusy typu za určitých podmíek vždy astae určitý důsledek. Např. jestliže za ormálího
3. DIFERENCIÁLNÍ ROVNICE
 3 DIFERENCIÁLNÍ ROVNICE Difereciálí rovice (dále je DR) jsou veli důležitou částí ateatické aalýz, protože uožňují řešit celou řadu úloh z fzik a techické prae Občejé difereciálí rovice: rovice, v íž se
3 DIFERENCIÁLNÍ ROVNICE Difereciálí rovice (dále je DR) jsou veli důležitou částí ateatické aalýz, protože uožňují řešit celou řadu úloh z fzik a techické prae Občejé difereciálí rovice: rovice, v íž se
pravděpodobnostn podobnostní jazykový model
 Pokročilé metody rozpozáváířeči Předáška 8 Rozpozáváí s velkými slovíky, pravděpodobost podobostí jazykový model Rozpozáváí s velkým slovíkem Úlohy zaměřeé a diktováíči přepis řeči vyžadují velké slovíky
Pokročilé metody rozpozáváířeči Předáška 8 Rozpozáváí s velkými slovíky, pravděpodobost podobostí jazykový model Rozpozáváí s velkým slovíkem Úlohy zaměřeé a diktováíči přepis řeči vyžadují velké slovíky
