MATEMATICKÁ KARTOGRAFIE
|
|
|
- Matyáš Šimek
- před 8 lety
- Počet zobrazení:
Transkript
1 VYSOKÉ ENÍ TECHNICKÉ V BRN FAKLTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODL 4 JEDNODCHÁ ZOBRAZENÍ STDIJNÍ OORY RO STDIJNÍ ROGRAMY S KOMBINOVANO FORMO STDIA
2 Mateatická kartgrafie Mdul 4 Milslav Švec Brn (38) -
3 Obsah OBSAH Úvd...5. Cíle...5. žadvané znalsti Dba ptebná ke studiu Klívá slva...5 Jednduchá zbrazení Kuželvá zbrazení Kuželvé zbrazení ekvidistantní v plednících Kuželvé zbrazení ekvivalentní Kuželvé zbrazení knfrní Válcvé zbrazení Válcvé zbrazení ekvidistantní v plednících Válcvé zbrazení ekvivalentní Válcvé zbrazení knfrní Válcvé prjekce rvnání válcvých zbrazení v nrální plze Aziutální zbrazení Zbrazení ekvidistantní v plednících Aziutální zbrazení ekvivalentní Aziutální knfrní zbrazení Aziutální prjekce Srvnání aziutálních zbrazení Závr Shrnutí Studijní praeny Sezna pužité literatury Sezna dplkvé studijní literatury Odkazy na další studijní zdrje a praeny (38) -
4
5 Úvd Úvd. Cíle Mateatická kartgrafie patí k základní terretický pedt studijních prgra gedézie a kartgrafie. Vytváí pedpklady pr zvládnutí becných a praktických úlh jak becné gedézie tak pedevší becné kartgrafie. Mduly pedtu jsu kncipvány jak ucelené celky. est na sebe tereticky navazují. Opra Mateatická kartgrafie je tvena tit duly: Referenní plchy a suadnicvé systéy Kartgrafická zkreslení Kartgrafické zbrazení Jednduchá zbrazení Nepravá aziutální zbrazení. žadvané znalsti edt vyžaduje dbré ateatické základy. Jedná se zvládnutí základ ateatické analýzy pedevší diferenciálníh ptu jedné a více prnných integrálníh ptu základ diferenciálních rvnic a nkterých partií deskriptivní a diferenciální geetrie..3 Dba ptebná ke studiu edt je vyuván jak pvinný v první rníku navazujícíh agisterskéh studijníh prgrau Gedézie a kartgrafie v rzsahu hdiny pednášky a hdiny cviení za týden tedy celke 39 hdin za seestr. Jak u každéh teretickéh pedtu se pedpkládá alesp stelná asvá zátž pi sastudiu..4 Klívá slva Mateatická kartgrafie referenní plcha zbrazení apa elipsid suadnicvé sustavy - 5 (38) -
6 Mateatická kartgrafie Mdul 4 Jednduchá zbrazení Obecn: jednduchá zbrazení jsu ppsána zbrazvacíi rvnicei typu ρ f ρ f X nv X nd ( ) ε nv z F( ) ( Š) ε nd z F( Š) Y Y g g ( ) z G( ) ( Š) z G( Š) Kule rvina nrální plha plární suadnice Kule rvina becná plha plární suadnice Kule rvina nrální plha pravúhlé suadnice Kule rvina becná plha pravúhlé suadnice Dsledke jednduchých vztah jsu jednduché brazy pledník a rvnbžek nap. pr knst. je ρ knst. tzn. že braze rvnbžky je kružnice. 3 Kuželvá zbrazení V X V A B λ C S r ϕ r ϕ ρ ε S ρ r r C A O Y J Základní pledník základní rvnbžka Zbrazvací rvnice kuželvéh zbrazení: pr referenníplchu elipsidicku pr referenníplchu kulvu neb pr referenníplchu elipsidicku ρ f ρ f ρ ρ pr referenníplchu kulvu ρ ( ϕ ) ε n ( ) ε nv ρ + F + F λ ( ϕ ϕ ) ε nλ ( ) ε nv Zkreslení v plednících a rvnbžkách - 6 (38) -
7 Kuželvá zbrazení d ρ p M dϕ d ρ nρ p r Rd R cs A p cs A + r sin A pr ω r sin r p + p ρ n r N cs ϕ Zkreslení jsu pr nrální plhu funkcei puze zepisné šíky brazy zepisných rvnbžek jsu ekvidefrátai ravúhlé suadnice X ρ ρ cs ε Y ρ sin ε 3.. Kuželvé zbrazení ekvidistantní v plednících Musí platit Odtud d ρ M dϕ. ρ ϕ d ρ M dϕ ρ ϕ. pr elipsid ρ ρ pr kuli ρ ρ ϕ s ϕ ( ) ε nv + R ε nλ rení knstant zbrazení. Hledáe pdínku pi níž bude délkvé zkreslení ve zvlené rvnbžce iniální (rvn jedné) ρ R ctg n sin tleaiv zbrazení (. stl. n. l.) Bnnev zbrazení (8. stl.) A ρ V - 7 (38) -
8 Mateatická kartgrafie Mdul 4. Knstanty ρ n žee urit z pdínky aby se dv rvnbžky ϕ a ϕ zbrazvanéh pásu nezkreslvaly cs n R ρ cs [( ) cs ( ) cs ] Zbrazení l Íslev cs cs (Jsef Niclaus l Ísle 8. stl.) V 3.. Kuželvé zbrazení ekvivalentní žívají se puze pr apy alých ítek staí uvažvat kulvu referenní plchu. d ρ nρ latí p. r. R d R cs integraci R ρ sin + k ε n i vlb základní rvnbžky platí R ρ ρ + n R cs p r nρ ω sin r r + nv ( sin sin ) nρ R cs ε nv. - 8 (38) -
9 Kuželvá zbrazení rení knstant n ρ. Tený kužel V ρ R ctg n sin Zkreslení délky je u rvnbžek vtší než jedna puze pr je rvn jedné. A ρ. Sený kužel edpkládáe že se nezkreslují rvnbžky V cs cs n ( sin sin) R + cs ρ R sin n n sin (Albersv zbrazení 9. stl.) 3. Má-li se zbrazvat úzeí se zepisný póle platí r ρ p 0 je R ρ p + n R ρ sin45 n. Dále žee vlit již jen jednu knstantu n. a) r tený kužel je n sin45 k tg. V tt pípad se však dtykvá rvnbžka zkresluje ( ) n sin. - 9 (38) -
10 Mateatická kartgrafie Mdul 4 Nezkresluje se rvnbžka pr niž platí Nevhdné pr zbrazení pásu. cs45 n. b) r sený kužel pžadujee aby se nezkreslvala stední rvnbžka pásu s j. ak (Labertv zbrazení) n cs Kuželvé zbrazení knfrní staující pdínku knfrity je p r. Tedy d ρ M dϕ nρ N csϕ. - 0 (38) -
11 Kuželvá zbrazení - (38) - Separací prnných a dsazení za M N dstanee ( ) ( ) ϕ ϕ ϕ ρ ρ cs sin d d e e n integraci s využití izetrické šíky q je celke ( )( ) ( )( ) λ ε ϕ ϕ ϕ ϕ ϕ ϕ ρ ρ n e e e e ne n sin sin sin sin. 45 tg 45 tg r kulvu referenní plchu je analgicky nv n + + ε ρ ρ 45 tg 45 tg Zkreslení pi kulvé referenní plše je 0 cs cs ω ρ ρ R n R n r p rení knstant. Tený kužel: i vlb j s +
12 Mateatická kartgrafie Mdul 4 je zkreslení na severní kraji pásu vtší než na jižní. Nejvhdnjší je vlit základní rvnbžku tak aby byla tat zkreslení stejná: nρs nρ j R css R cs j. Odtud lg css lg cs j n sin j s lg tg + 45 lg tg + 45 n j s Existuje celá ada dalších etd jak snížit výše uvedená zkreslení vlba rvnbžek s iniální zkreslení výpet iniálníh zkreslení rzbre zkreslení v jedntlivých bdech aj. žití kuželvéh knfrníh zbrazení v eskslvensku Besselv elipsid je knfrn zbrazen na Gaussvu kuli ϕ λ V tyt suadnice jsu pak knfrn zbrazeny na kuželvu plchu becn plženu. Osa tenéh kužele nejlépe se piykajícíh úzeí eskslvenska prtíná kulvu plchu v kartgrafické pólu k V k Zepisná délka V k dpvídá délce na elipsidu λ k (38) -
13 Kuželvá zbrazení Tent eridián je základní pledníke pr kuželvé zbrazení eskslvenska a jeh braz je zvlen za su X pravúhlé katastrální sustavy s pátke v braze vrchlu kužele. važujee-li prseík základní kartgrafické rvnbžky Š se základní pledníke V na kuli jehž suadnice na elipsidu jsu ϕ 48 5 λ 4 30 je braz tht prseíku v rvin vzdálen d pátku rvinných suadnic Bd V padne dalek i republiku a sa X je výchdn d eskslvenska jsu pravúhlé suadnice X Y všech bd eskslvenska kladné. r užití becných vzrc pr kuželvé zbrazení se pevedu zepisné kulvé suadnice V na kartgrafické Š D k S V 90 - Š K 90 - Š J +Y K V 0 ρ ε ρ Š +X - 3 (38) -
14 Mateatická kartgrafie Mdul 4-4 (38) -
15 - 5 (38) - Kuželvá zbrazení
16 Mateatická kartgrafie Mdul 4 4 Válcvé zbrazení Zbrazení válcvé v nrální plze: rvník a všechny rvnbžky se zbrazují jak snva rvnbžných píek brazy pledník tví snvu píek vzájen stejn dlehlých rvnbžných a klých na brazy pledník. Na pláš válce se zbrazí rvnbžky jak pvrchvé kružnice pledníky jak pvrchvé píky. S C B V d dv O A D V 0 +Y C B dy dx O A D +X Zbrazvací rvnice válcvéh zbrazení pr referenní plchu elipsidicku pr referenní plchu kulvu X X ( ) ( ) nλ Y f ϕ nv Y f ledníky a rvnbžky jsu hlavníi paprsky s extréníi hdntai délkvéh zkreslení. Zkreslení v pledníku a rvnbžce - 6 (38) -
17 Válcvé zbrazení pr elipsid dy n p r M dϕ N csϕ pr kuli dy n p r R d R cs ω A p cs A + r sin A pr sin r r + p p Ekvidefrátai jsu brazy rvnbžek. r tený válec se nezkresluje rvník a platí pr elipsid pr kuli r r a N csϕ cs (ty- r sený válec prtínající referenní plchu ve dvu rvnbžkách t rvnbžky se nezkreslují) platí pr elipsid pr kuli r r N csϕ N csϕ cs cs i válcvé zbrazení pásu ezi dva rvnbžkai s j ±ϕ lze zkreslení snížit na plvinu zavedení senéh válce aby zkreslení na rvníku byl tlik enší než jedntka klik vtší než jedntka je na krajvých rvnbžkách. r nezkreslenu rvnbžku pak platí cs i zbrazení pásu na jedné plkuli je cs cs s + cs cs j css cs + cs j s Knstanta n se dá urit z pdínky která rvnbžka se na ap neá zkreslvat. - 7 (38) -
18 Mateatická kartgrafie Mdul 4 4. Válcvé zbrazení ekvidistantní v plednících dínka ekvidistance v plednících nezkreslený rvník X RV Y R p r cs ω sin tg nezkreslená rvnbžka X R cs V Y R p r cs cs rtže se nezkresluje rvník a pledníky je braze gegrafické sít tvercvá sí (kvadratická apa) Marinv (r. 00 n. l.) zbrazení. Ekvidistantní válcvé zbrazení v transverzální plze byl užit pr katastrální apy a gedetické výpty Cassinih (8. stl.) neb Sldnerv zbrazení. V Rakusku-hersku využit pr katastrální apy :880. S a a x 90 dx 90 B x y + dy ds h x h x a O 90. J +X dy x y x h h x a x a O a +Y - 8 (38) -
19 Válcvé zbrazení Hlavní kružnice a a a x klé k základníu eridiánu kartgrafické pledníky Kartgrafické rvnbžky h h x Tansverzální gegrafická apa Zkreslení v kartgrafické pledníku a kartgrafické rvnbžce a cs α h α + sin y y cs cs R R V Rakusku-hersku byl zvlen pr snížení zkreslení suadnicvých sustav v echách je su X pledník prcházející bde Gusterberg u Kresünsteru v Rakusku na Mrav a ve Slezku pledník jducí vží sv. Štpána ve Vídni. α 4. Válcvé zbrazení ekvivalentní Kulvá referenní plcha se zbrazuje na nrální válcvu plchu. dy cs p r R d cs pr nezkreslenu rvnbžku. - 9 (38) -
20 Mateatická kartgrafie Mdul 4 S V B O B A V 0 +Y B Y X O A +X Odtud becné rvnice Zkreslení X R cs. V Y R sin cs cs cs ω cs cs p r sin cs cs cs + cs r 0 je X RV p Y cs Rsin r cs ω cs sin + cs ω tg Zbrazení se nazývá izcylindrické Labertv (8. stl.) sin tg - 0 (38) -
21 Válcvé zbrazení 4.3 Válcvé zbrazení knfrní Staí pdínka a dtud p r pr elipsid X aλ p r Y ϕ a lntg + a N csϕ 45 + a N csϕ esinϕ esinϕ e ω 0 pr kuli X RV p r Y R ln tg cs + 45 cs ω 0 Zbrazení se nazývá Mercatrv (6. stl.) a užívá se pr nání a letecké apy prtže lxdra se v n zbrazuje jak píka. r gedézii je dležité knfrní válcvé zbrazení transverzální (Gaussv) latí X y x Y R ln tg 45 R cs y R Gaussv zbrazení á prti Cassinivu zbrazení veliké pednsti pr gedézii v knfrit. - (38) -
22 Mateatická kartgrafie Mdul 4 Gaussv knfrní zbrazení elipsidu v pledníkvých pásech a jeh užití v eskslvensku Zbrazení elipsidu pí d rviny Gauss-Krüger eridiální pruhy stejné šíky se zbrazují sastatn. Válce se dtýkají elipsidu pdél zvlených stedních pledník pás. λ dλ p d ϕ + dϕ ϕ C A α ds B O rvník - (38) -
23 Válcvé zbrazení +X p C X dx dy d α O rvník +Y Meridiánvá knvergence +X p γ r C Y γ µ r X O +Y Zbrazení se využívá v šestistupvých pásech. Délkvé zkreslení na krajích šestistupvéh pásu nepesáhne a je zanedbatelné na tpgrafických apách :0000 a eších ítek. Dležitý úkle Gaussva knfrníh zbrazení pledníkvých pás elipsidu je stanvení pevdních vztah ezi suadnicvýi sustavai susedních pás tabulky. - 3 (38) -
24 Mateatická kartgrafie Mdul Válcvé prjekce Geetrické zbrazení z bdu na válcvu plchu. S Y R C r c J K c - 4 (38) -
25 Válcvé zbrazení. Sted prjekce K c leží na zeské se Knstanty r c že vlit. Nap. pr r R c 0 je r ( c + R sin ) X rv Y R cs r R + csin p R cs r r R cs ω r p sin + p r c X RV Y R tg ω p sin r cs cs tg. Sted prítání K c leží v rvin rvníku X R cs. V sin Y R( c + R cs ) c + R cs p ( c + R cs ) ( c + R cs ) cs r pr cs ω r p sin r + p R + c cs S R e C K c e c J - 5 (38) -
26 Mateatická kartgrafie Mdul 4 Knstanty a c žee vlit. r c R je X p r R cs. V + cs cs Y cs r T je tzv. Gallva steregrafická prjekce. r c 0 je X R cs p. V cs cs Má-li být válec tený bude pr 0 r i X RV Y R R ( + cs ) p cs Y r R cs cs cs ( c + R) tg tg sin c + R cs c dstáváe izcylindrické stejnplché zbrazení. c R je X RV Y R tg p T je tzv. Braunva steregrafická prjekce. cs r cs - 6 (38) -
27 Válcvé zbrazení 4.5 rvnání válcvých zbrazení v nrální plze Zbrazení tvercvé p Izcylindrické Knfrní ω 0 Steregrafická prjekce Gallva 30 Steregrafická prjekce Braunva Zkreslení r ω p r ω p r p r ω p r ω (38) -
28
29 Aziutální zbrazení 5 Aziutální zbrazení Aziutální zbrazení se pužívá v becné plze pi kulvé referenní plše je speciální pípade kuželvých zbrazení. D S h a K ψ Š C h K O p J a p X Kartgrafický pól K( k V k ) definuje systé kartgrafických pledník a (aziutální kružnice) a rvnbžek h (hrizntální kružnice). Obraze kartgrafických pledník je svazek píek s vrchle K. Obraze kartgrafických rvnbžek jsu kružnice stedu K a plru ρ který závisí puze na kartgrafické šíce Š nahrazujee ji u aziutálních zbrazení dplke ψ 90 Š. Rvnice zbrazení ρ f ( ψ ) ε D r pravúhlé suadnice platí X ρ cs ε Y ρ sinε Kartgrafické pledníky a rvnbžky jsu rtgnální systée a platí tedy a d ρ Rdψ ω sin h h h ρ dε Rsinψ d D a a ρ Rsinψ a h - 9 (38) -
30 Mateatická kartgrafie Mdul 4 5. Zbrazení ekvidistantní v plednících d ρ Rdψ ψ 0 ρ staující pdínka tedy separací d ρ Rdψ a integrací (pi splnní pdínky 0) platí rtže ρ a Rψ ε D h ψ sinψ ω ψ sinψ sin ψ + sinψ ψ > sinψ kartgrafické rvnbžky se na ap prdlužují. Zbrazení se nazývá stelv (6. stl.) užívá se v letectví seisice apd. prtže nezkresluje aziut rtdry a udává skutenu sféricku vzdálenst ezi libvlný bde a stede apy (38) -
31 Aziutální zbrazení Hvzdicvé zbrazení (eterannv) 5. Aziutální zbrazení ekvivalentní Základní pdínka ρ R ( R ) ρ d ρ sinψ dψ dtud ψ k + 4R sin. Má-li být pr ψ 0 ρ 0 vlíe Zbrazvací rvnice ψ ρ R sin ε D ψ a cs h ψ cs ψ cs ω sin ψ + cs k R. - 3 (38) -
32 Mateatická kartgrafie Mdul 4 Zbrazení se nazývá Labertv (8. stl.) 5.3 Aziutální knfrní zbrazení latí pt pdínka knfrity tedy a h 0 d ρ Rdψ ρ Rsinψ. Odtud integrací (pi vlb ψ ) dstáváe zbrazvací rvnice ψ ρ R tg ψ cs ε D ω 0 4ψ cs - 3 (38) -
33 Aziutální zbrazení Steregrafická prjekce každá kružnice se prítá jak kružnice (neb píka kružnice s nulvu kivstí) význa v gedézii a kartgrafii. Zkreslení se dá jednduše vyjádit pcí suadnic rvinných + tg ψ cs ψ + X 4 + Y Veliké zkreslení plšné u knfrníh zbrazení a úhlvé u ekvivalentníh vedl k hledání kprisních pdínek pr integraní knstantu. R Nap. Breusigv zbrazení - ρ je geetrický prr bu zbrazení Airyh zbrazení - ρ je uren z pdínky aby integrál p {( ) + ( ) } a pes zbrazvanu plchu byl iniální h d p - 33 (38) -
34 Mateatická kartgrafie Mdul Aziutální prjekce Obecné zbrazvací rvnice aziutálních prjekcí ρ a RE sinψ c + Rcsψ ε D E( R + ccsψ ) E h ( c + Rcsψ ) c + Rcsψ π K ρ h B ψ R C E c K c žívají se i petvené rvnice pr pravúhlé suadnice RE X c + Y c + R ( csk sin + sink cs cs V ) R( sin sin + cs cs cs V ) RE cs sin V ( sin sin + cs cs cs V ) k k k k Vlba knstanty c (neb E) rtgrafická prjekce steregrafická prjekce gnónická prjekce externí prjekce c c R c 0 c > R - 34 (38) -
35 Aziutální zbrazení Ortgrafická prjekce c ρ a Rsinψ csψ ε D h csψ ω sin tg ψ Steregrafická prjekce c R ψ ρ R tg ε D a h ψ cs 4ψ cs ω 0 Gnónická prjekce c 0 ρ R tgψ ε D a cs ψ h csψ 3 cs ψ sin ω tg ψ - 35 (38) -
36 Mateatická kartgrafie Mdul 4 Externí prjekce c > R ρ vede ke knstant c R dínka nap. ρ ψ 90 ψ 45 zbrazení de la Hirev. Dvjitá Slvjevva prjekce ψ ρ 4R tg ε D 4 a ψ h ψ ψ cs cs cs 4 4 ψ 4ψ cs cs 4 ω sin tg ψ Srvnání aziutálních zbrazení Zbrazení ψ stelv a Steregrafické ω 0 Stejnplché ω h a h a h ω (38) -
37 Aziutální zbrazení Vyrvnávací Breusigv h ω Ortgrafické a h ω Gnónické a h ω De la Hirev a h ω Slvjevva dvjitá prjekce a h ω - 37 (38) -
38 Mateatická kartgrafie Mdul 4 6 Závr 6. Shrnutí Nejbsáhlejší dul pedtu. Chrakterizuje nejdležitjší jednduchá zbrazení: kuželvá válcvá a aziutální. Odvzuje jejich charakteristiky a uvádí píklady pužití. 6. Studijní praeny 6.. Sezna pužité literatury [] Hjvec V. a kl. Kartgrafie GK raha Sezna dplkvé studijní literatury [] Daniš M. Valk J. Mateatická kartgrafia SVŠT Bratislava 987 [3] Srnka E. Mateatická kartgrafie VAAZ Brn 977 [4] Böh J. Mateatická kartgrafie VŠT Brn Odkazy na další studijní zdrje a praeny [5] [6] [7] [8] (38) -
MATEMATICKÁ KARTOGRAFIE
 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL 5 NEPRAVÁ ZOBRAZENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie Modul
VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL 5 NEPRAVÁ ZOBRAZENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie Modul
MATEMATICKÁ KARTOGRAFIE
 VYSOKÉ UENÍ TECHNICKÉ V BN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KATOGAFIE MODUL 3 KATOGAFICKÉ ZOBAZENÍ STUDIJNÍ OPOY PO STUDIJNÍ POGAMY S KOMBINOVANOU FOMOU STUDIA Matematická kartografie Modul 3
VYSOKÉ UENÍ TECHNICKÉ V BN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KATOGAFIE MODUL 3 KATOGAFICKÉ ZOBAZENÍ STUDIJNÍ OPOY PO STUDIJNÍ POGAMY S KOMBINOVANOU FOMOU STUDIA Matematická kartografie Modul 3
MATEMATICKÁ KARTOGRAFIE
 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL KARTOGRAFICKÁ ZKRESLENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie
VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL KARTOGRAFICKÁ ZKRESLENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie
Test k přijímacím zkouškám na VUT pro akademický rok 2010/2011do Navazujícího magisterského studia oboru Geodézie a kartografie. 100 g.
 Test k přijíací zkušká na VUT pr akadeický rk 010/011d Navazujícíh agisterskéh studia bru Gedézie a kartgrafie A1 tg Část A tg α ctg α - tg α (90 ) A ctg 70 0 1 A3 Hdnta jednh radiánu (1 ra v grádech (g
Test k přijíací zkušká na VUT pr akadeický rk 010/011d Navazujícíh agisterskéh studia bru Gedézie a kartgrafie A1 tg Část A tg α ctg α - tg α (90 ) A ctg 70 0 1 A3 Hdnta jednh radiánu (1 ra v grádech (g
DESKRIPTIVNÍ GEOMETRIE Charakteristika vyučovacího předmětu
 DESKRIPTIVNÍ GEOMETRIE Charakteristika vyučvacíh předmětu Deskriptivní gemetrie se vyučuje jak pvinně vlitelný předmět ve třetím a čtvrtém rčníku s hdinu dtací 2-2, event. puze ve čtvrtém s hdinvu dtací
DESKRIPTIVNÍ GEOMETRIE Charakteristika vyučvacíh předmětu Deskriptivní gemetrie se vyučuje jak pvinně vlitelný předmět ve třetím a čtvrtém rčníku s hdinu dtací 2-2, event. puze ve čtvrtém s hdinvu dtací
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 5 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Válcová zobrazení obrazem poledníků jsou úsečky, které mají konstantní rozestupy obrazem rovnoběžek jsou
Kartografie 1 - přednáška 5 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Válcová zobrazení obrazem poledníků jsou úsečky, které mají konstantní rozestupy obrazem rovnoběžek jsou
Konoidy přímkové plochy
 Knidy přímkvé plchy Knidy jsu speciální zbrcené přímkvé plchy. Opět jsu určeny třemi křivkami, v případě knidů jsu t: -křivka rvinná (kružnice, elipsa, parabla, ) či prstrvá (šrubvice, ) -vlastní přímka
Knidy přímkvé plchy Knidy jsu speciální zbrcené přímkvé plchy. Opět jsu určeny třemi křivkami, v případě knidů jsu t: -křivka rvinná (kružnice, elipsa, parabla, ) či prstrvá (šrubvice, ) -vlastní přímka
3 Referenční plochy a soustavy
 II. část Vyšší gedézie matematická 3 Referenční plchy a sustavy 3. Referenční kule a výpčty na referenční kuli Pr realizaci gedetických a kartgrafických výpčtů s nižší přesnstí je mžné zemské těles neb
II. část Vyšší gedézie matematická 3 Referenční plchy a sustavy 3. Referenční kule a výpčty na referenční kuli Pr realizaci gedetických a kartgrafických výpčtů s nižší přesnstí je mžné zemské těles neb
1 Nepravá zobrazení. 4 Zobrazení odvozené z jednoduchých azimutálních (modifikované. Obsah. 3 Nepravá azimutální zobrazení.
 Obsah 1 Nepravá zobrazení 2 3 4 Zobrazení odvozené z jednoduchých azimutálních (modifikované zobrazení) 5 Zobrazení Evropy Nepravá zobrazení: jednoduché nepravé kuželové ρ = f (U), ɛ = g(v ) = nv ρ = f
Obsah 1 Nepravá zobrazení 2 3 4 Zobrazení odvozené z jednoduchých azimutálních (modifikované zobrazení) 5 Zobrazení Evropy Nepravá zobrazení: jednoduché nepravé kuželové ρ = f (U), ɛ = g(v ) = nv ρ = f
5. Mechanika tuhého tlesa
 5. Mechanika tuhéh tlesa Rzmry a tvar tlesa jsu ast pi ešení mechanických prblém rzhdující a pdstatn vlivují phybvé úinky sil, které na n psbí. akvá tlesa samzejm nelze nahradit hmtným bdem. Úinky sil
5. Mechanika tuhéh tlesa Rzmry a tvar tlesa jsu ast pi ešení mechanických prblém rzhdující a pdstatn vlivují phybvé úinky sil, které na n psbí. akvá tlesa samzejm nelze nahradit hmtným bdem. Úinky sil
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 2 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografické zobrazení kartografické zobrazení vzájemné přiřazení polohy bodů na dvou různých referenčních
Kartografie 1 - přednáška 2 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografické zobrazení kartografické zobrazení vzájemné přiřazení polohy bodů na dvou různých referenčních
MATEMATICKÁ KARTOGRAFIE
 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL 1 REFERENNÍ PLOCHY A SOUADNICOVÉ SYSTÉMY STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Mtemtická
VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL 1 REFERENNÍ PLOCHY A SOUADNICOVÉ SYSTÉMY STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Mtemtická
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 6 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografická zobrazení použitá na našem území důležitá jsou zejména zobrazení pro státní mapová díla v
Kartografie 1 - přednáška 6 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografická zobrazení použitá na našem území důležitá jsou zejména zobrazení pro státní mapová díla v
Obecnou rovnici musíme upravit na středovou. 2 2 2 2 2 2 2 2. leží na kružnici musí vyhovovat její rovnici dosadíme ho do ní.
 75 Hledání kružnic I Předpklady: 750, kružnice z gemetrie Př : Kružnice je dána becnu rvnicí x y x y plměr Rzhdni, zda na kružnici leží bd A[ ; ] + + + 6 + = 0 Najdi její střed a Obecnu rvnici musíme upravit
75 Hledání kružnic I Předpklady: 750, kružnice z gemetrie Př : Kružnice je dána becnu rvnicí x y x y plměr Rzhdni, zda na kružnici leží bd A[ ; ] + + + 6 + = 0 Najdi její střed a Obecnu rvnici musíme upravit
1.5.6 Osa úhlu. Předpoklady:
 1.5.6 Osa úhlu Předpklady: 010505 Pedaggická pznámka: Následující příklad je pakvání, které pužívám jak cvičení dhadu. Nechám žáky dhadnut veliksti a při kntrle si pčítají bdy (chyba d 5-3 bdy, d 10-2
1.5.6 Osa úhlu Předpklady: 010505 Pedaggická pznámka: Následující příklad je pakvání, které pužívám jak cvičení dhadu. Nechám žáky dhadnut veliksti a při kntrle si pčítají bdy (chyba d 5-3 bdy, d 10-2
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 7 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 válcové konformní zobrazení v transverzální poloze někdy také nazýváno transverzální Mercatorovo nebo Gauss-Krügerovo
Kartografie 1 - přednáška 7 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 válcové konformní zobrazení v transverzální poloze někdy také nazýváno transverzální Mercatorovo nebo Gauss-Krügerovo
Pracovní listy PLOCHY
 Technická univerzita v Liberci Fakulta přírdvědně-humanitní a pedaggická Katedra matematiky a didaktiky matematiky PLOCHY Petra Pirklvá Liberec, únr 06 . Rtační plcha je dána tvřící křivku k. Dplňte zbývající
Technická univerzita v Liberci Fakulta přírdvědně-humanitní a pedaggická Katedra matematiky a didaktiky matematiky PLOCHY Petra Pirklvá Liberec, únr 06 . Rtační plcha je dána tvřící křivku k. Dplňte zbývající
ZŠ ÚnO, Bratří Čapků 1332
 Středšklská matematika Nadace Geneze Vývj (Stručná histrie matematiky) - na levé straně je svislý nápis VÝVOJ stisk hrníh V vyvlá zbrazení časvé sy - stisk ikny se stránku (vprav nahře na brazvce časvé
Středšklská matematika Nadace Geneze Vývj (Stručná histrie matematiky) - na levé straně je svislý nápis VÝVOJ stisk hrníh V vyvlá zbrazení časvé sy - stisk ikny se stránku (vprav nahře na brazvce časvé
Jednoduchá zobrazení. Podpořeno z projektu FRVŠ 584/2011.
 Podpořeno z projektu FRVŠ 584/2011. Obsah Jednoduchá zobrazení 1 Jednoduchá zobrazení 2 Obsah Jednoduchá zobrazení 1 Jednoduchá zobrazení 2 Společné vlastnosti jednoduchých zobrazení: Zobrazovací ref.
Podpořeno z projektu FRVŠ 584/2011. Obsah Jednoduchá zobrazení 1 Jednoduchá zobrazení 2 Obsah Jednoduchá zobrazení 1 Jednoduchá zobrazení 2 Společné vlastnosti jednoduchých zobrazení: Zobrazovací ref.
Pracovní listy KŘIVKY
 Technická univerzita v Liberci Fakulta přírdvědně-humanitní a pedaggická Katedra matematiky a didaktiky matematiky KŘIVKY Petra Pirklvá Liberec, květen 07 . Určete, který z phybů je levtčivý a který pravtčivý..
Technická univerzita v Liberci Fakulta přírdvědně-humanitní a pedaggická Katedra matematiky a didaktiky matematiky KŘIVKY Petra Pirklvá Liberec, květen 07 . Určete, který z phybů je levtčivý a který pravtčivý..
Matematická kartografie. Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT. Referenční plochy
 Matematická kartografie Buchar.: Matematická kartografie 10, ČVUT; Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT Referenční plochy referenční elipsoid (sféroid) zploštělý rotační elipsoid Besselův
Matematická kartografie Buchar.: Matematická kartografie 10, ČVUT; Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT Referenční plochy referenční elipsoid (sféroid) zploštělý rotační elipsoid Besselův
TYÚHELNÍKY 1 HODINA. Lomená ára: je to skupina úseek, kde koncový bod jedné úseky je poátením bodem druhé úseky
 TYÚHELNÍKY HODINA Díve, než se dstneme k vysvtlení pjmu tyúhelník, zpkujeme si nkteré zákldní pjmy, jk je npíkld lmená ár mnhúhelník. Lmená ár: je t skupin úseek, kde kncvý bd jedné úseky je pátením bdem
TYÚHELNÍKY HODINA Díve, než se dstneme k vysvtlení pjmu tyúhelník, zpkujeme si nkteré zákldní pjmy, jk je npíkld lmená ár mnhúhelník. Lmená ár: je t skupin úseek, kde kncvý bd jedné úseky je pátením bdem
1 ROVNOVÁHA BODU Sestavte rovnice rovnice rovnováhy bodu (neznámé A,B,C) Určete A pro konstrukci z příkladu
 Sbírka bude dplňvána. Příští dplněk budu příklady na vnitřní síly v diskrétních průřeech. Připmínky, pravy, návrhy další příklay jsu vítány na rer@cml.fsv.cvut.c. mbicí sbírky je hlavně jedntně definvat
Sbírka bude dplňvána. Příští dplněk budu příklady na vnitřní síly v diskrétních průřeech. Připmínky, pravy, návrhy další příklay jsu vítány na rer@cml.fsv.cvut.c. mbicí sbírky je hlavně jedntně definvat
Pružnost a plasticita II 3. ročník bakalářského studia. doc. Ing. Martin Krejsa, Ph.D. Katedra stavební mechaniky
 Pružnst a plasticita II 3. rčník bakalářskéh studia dc. Ing. Martin Krejsa, Ph.D. Katedra stavební mechanik Základní infrmace cvičení Předmět: 8-0/0 - Pružnst a plasticita II Přednášející: dc. Ing. Martin
Pružnst a plasticita II 3. rčník bakalářskéh studia dc. Ing. Martin Krejsa, Ph.D. Katedra stavební mechanik Základní infrmace cvičení Předmět: 8-0/0 - Pružnst a plasticita II Přednášející: dc. Ing. Martin
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 1 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Úvod přednášky, cvičení, zápočty, zkoušky Jiří Cajthaml (přednášky, cvičení) potřebné znalosti: vzorce
Kartografie 1 - přednáška 1 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Úvod přednášky, cvičení, zápočty, zkoušky Jiří Cajthaml (přednášky, cvičení) potřebné znalosti: vzorce
ROZLOŽENÍ HMOTNOSTI TĚLESA VZHLEDEM K SOUŘADNICOVÉMU SYSTÉMU
 ROZLOŽENÍ HMONOS ĚLESA VZHLEDEM K SOUŘADNCOVÉMU SYSÉMU Zatímc hmtu hmtnéh bdu chaakteivala jediná fikální veličina a sice hmtnst m u tělesa je nutn kmě tht paametu nát plhu středu hmtnsti a paamet definující
ROZLOŽENÍ HMONOS ĚLESA VZHLEDEM K SOUŘADNCOVÉMU SYSÉMU Zatímc hmtu hmtnéh bdu chaakteivala jediná fikální veličina a sice hmtnst m u tělesa je nutn kmě tht paametu nát plhu středu hmtnsti a paamet definující
Matematické metody v kartografii. Členění kartografických zobrazení. Zobrazení z elipsoidu na kouli (5.)
 Matematické metody v kartografii Členění kartografických zobrazení. Zobrazení z elipsoidu na kouli (5.) 1. Členění kartografických zobrazení: Existuje velkémnožstvíkarografických zobrazení. Lze je členit
Matematické metody v kartografii Členění kartografických zobrazení. Zobrazení z elipsoidu na kouli (5.) 1. Členění kartografických zobrazení: Existuje velkémnožstvíkarografických zobrazení. Lze je členit
1. Kristýna Hytychová
 Průřezvé veličiny Výpčet těžiště. Druhy průřezvých veličin a jejich výpčet průřezvých veličin. Steinerva věta. Pužití průřezvých veličin ve výpčtech STK. Průřezvé veličiny ZÁKLADNÍ: plcha průřezu, mment
Průřezvé veličiny Výpčet těžiště. Druhy průřezvých veličin a jejich výpčet průřezvých veličin. Steinerva věta. Pužití průřezvých veličin ve výpčtech STK. Průřezvé veličiny ZÁKLADNÍ: plcha průřezu, mment
Střední průmyslová škola strojní a elektrotechnická. Resslova 5, Ústí nad Labem. Fázory a komplexní čísla v elektrotechnice. - Im
 Střední průmyslvá škla strjní a elektrtechnická Resslva 5, Ústí nad Labem Fázry a kmplexní čísla v elektrtechnice A Re + m 2 2 j 1 + m - m A A ϕ ϕ A A* Re ng. Jarmír Tyrbach Leden 1999 (2/06) Fázry a kmplexní
Střední průmyslvá škla strjní a elektrtechnická Resslva 5, Ústí nad Labem Fázry a kmplexní čísla v elektrtechnice A Re + m 2 2 j 1 + m - m A A ϕ ϕ A A* Re ng. Jarmír Tyrbach Leden 1999 (2/06) Fázry a kmplexní
Diferenciáln. lní geometrie ploch
 Diferenciáln lní geometrie ploch Vjádřen ení ploch Eplicitní: z = f(,) ; [,] Ω z Implicitní: F(,,z)=0 + + z = r z = sin 0, π ; 0,1 Implicitní ploch bloob objects,, meta balls Izoploch: F(,,z)=konst. Implicitní
Diferenciáln lní geometrie ploch Vjádřen ení ploch Eplicitní: z = f(,) ; [,] Ω z Implicitní: F(,,z)=0 + + z = r z = sin 0, π ; 0,1 Implicitní ploch bloob objects,, meta balls Izoploch: F(,,z)=konst. Implicitní
3.5.1 Shodná zobrazení
 3.5.1 hdná zbrazení Předpklady: O zbrazení jsme mluvili, než jsme zavedli funkce. Jde takvu relaci z první mnžiny d druhé, při které každému prvku z první mnžiny přiřazujeme maximálně jeden prvek z mnžiny
3.5.1 hdná zbrazení Předpklady: O zbrazení jsme mluvili, než jsme zavedli funkce. Jde takvu relaci z první mnžiny d druhé, při které každému prvku z první mnžiny přiřazujeme maximálně jeden prvek z mnžiny
Záznam zkušební komise Jméno a příjmení Podpis Vyhodnocení provedl INSTRUKCE
 VYSOKÉ UČNÍ THNIKÉ V RNĚ FKULT PONIKTLSKÁ Přijímací řízení 2008 akalářské studium Obry: aňvé pradenství knmika a prcesní management Míst pr nalepení kódu Kód nalepí uchazeč Záznam zkušební kmise Jmén a
VYSOKÉ UČNÍ THNIKÉ V RNĚ FKULT PONIKTLSKÁ Přijímací řízení 2008 akalářské studium Obry: aňvé pradenství knmika a prcesní management Míst pr nalepení kódu Kód nalepí uchazeč Záznam zkušební kmise Jmén a
Optika. o Izotropní světlo se šíří všemi směry stejně rychle o Anizotropní světlo se šíří různými směry různě Zdroj. o o
 Optika Věda světle Rychlst světla 299 792 458 m/s (přibližně 3.10 8 ) (světl se šíří rychlstí světla ve vakuu, jinde pmalejší kvůli permitivitě a permeabilitě, třeba ve skle je t 2x pmalejší, ve vdě se
Optika Věda světle Rychlst světla 299 792 458 m/s (přibližně 3.10 8 ) (světl se šíří rychlstí světla ve vakuu, jinde pmalejší kvůli permitivitě a permeabilitě, třeba ve skle je t 2x pmalejší, ve vdě se
F1030 Mechanika a molekulová fyzika úlohy k procvičení před písemkami (i po nich ) Téma 4 a 5: Zákony newtonovské mechaniky
 F3 Mechanika a lekulvá fyzika úlhy k prcvičení před písekai (i p nich ) Téa 4 a 5: Zákny newtnvské echaniky Předpklady k úlhá: Ve všech úlhách pvažujte labratrní vztažnu sustavu, pevně spjenu se Zeí, za
F3 Mechanika a lekulvá fyzika úlhy k prcvičení před písekai (i p nich ) Téa 4 a 5: Zákny newtnvské echaniky Předpklady k úlhá: Ve všech úlhách pvažujte labratrní vztažnu sustavu, pevně spjenu se Zeí, za
Lymfodrenážní terapeutický systém Q-1000
 Lymfdrenážní terapeutický systém Q-1000 Lymfdrenážní terapeutický systém Q-1000 Návd k pužití Důležité bezpečnstní instrukce Dále uvedené instrukce jsu určené pr zajištění bezpečnsti uživatelů a přístrjů.
Lymfdrenážní terapeutický systém Q-1000 Lymfdrenážní terapeutický systém Q-1000 Návd k pužití Důležité bezpečnstní instrukce Dále uvedené instrukce jsu určené pr zajištění bezpečnsti uživatelů a přístrjů.
1.6.3 Osová souměrnost
 1.6.3 Osvá suměrnst Předklady: 162 Pedaggická známka: Je třeba stuvat tak, aby se v hdině stihnul vyracvat a zkntrlvat bd 5. Pedaggická známka: Hned u střídání vázy je třeba dát zr. Narstá většina dětí
1.6.3 Osvá suměrnst Předklady: 162 Pedaggická známka: Je třeba stuvat tak, aby se v hdině stihnul vyracvat a zkntrlvat bd 5. Pedaggická známka: Hned u střídání vázy je třeba dát zr. Narstá většina dětí
Instalace a technické informace
 Dkumentace k mdulu MdleKREM Samstatný mdul MdleKREM umžňuje zbrazit (vyučujícím i studentů) mdel průchdu studenta vyučvaným kurzem a t jak v grafické pdbě (využívající znalstní mdel GLIKREM - GuideLine
Dkumentace k mdulu MdleKREM Samstatný mdul MdleKREM umžňuje zbrazit (vyučujícím i studentů) mdel průchdu studenta vyučvaným kurzem a t jak v grafické pdbě (využívající znalstní mdel GLIKREM - GuideLine
Tento projekt je spolufinancován. a státním rozpočtem
 Tent prjekt je splufinancván Evrpským sciálním fndem a státním rzpčtem Z a d á v a c í d k u m e n t a c e Odbrná publikace Management kulturníh cestvníh ruchu a návazné šklení pr prjekt OP RLZ - MMR Odbrná
Tent prjekt je splufinancván Evrpským sciálním fndem a státním rzpčtem Z a d á v a c í d k u m e n t a c e Odbrná publikace Management kulturníh cestvníh ruchu a návazné šklení pr prjekt OP RLZ - MMR Odbrná
Geometrická optika. Fermatův princip
 Fermatův pricip Gemetrická ptika světl se šíří mezi dvěma bdy A a A p takvé dráze, že dba k prběhutí tét dráhy je extrémí eb staciárí ve srváí s jakukliv susedí drahu A A δv ( A, A ) δ ( x, y, z) ds 0
Fermatův pricip Gemetrická ptika světl se šíří mezi dvěma bdy A a A p takvé dráze, že dba k prběhutí tét dráhy je extrémí eb staciárí ve srváí s jakukliv susedí drahu A A δv ( A, A ) δ ( x, y, z) ds 0
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 9 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Polykónická zobrazení někdy také mnohokuželová zobecnění kuželových zobrazení použito je nekonečně mnoho
Kartografie 1 - přednáška 9 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Polykónická zobrazení někdy také mnohokuželová zobecnění kuželových zobrazení použito je nekonečně mnoho
Rekuperace rodinného domu v Přestavlkách
 Rekuperace rdinnéh dmu v Přestavlkách Pjem: Rekuperace, nebli zpětné získávání tepla je děj, při němž se přiváděný vzduch d budvy předehřívá teplým dpadním vzduchem. Teplý vzduch není tedy bez užitku dveden
Rekuperace rdinnéh dmu v Přestavlkách Pjem: Rekuperace, nebli zpětné získávání tepla je děj, při němž se přiváděný vzduch d budvy předehřívá teplým dpadním vzduchem. Teplý vzduch není tedy bez užitku dveden
SPŠ STAVEBNÍ České Budějovice MAPOVÁNÍ. JS pro 3. ročník S3G
 SPŠ STAVEBNÍ České Budějovice MAPOVÁNÍ JS pro 3. ročník S3G ROZPIS TÉMAT PRO ŠK. ROK 2018/2019 1) Kartografické zobrazení na území ČR Cassiny-Soldnerovo zobrazení Obecné konformní kuželové zobrazení Gauss-Krügerovo
SPŠ STAVEBNÍ České Budějovice MAPOVÁNÍ JS pro 3. ročník S3G ROZPIS TÉMAT PRO ŠK. ROK 2018/2019 1) Kartografické zobrazení na území ČR Cassiny-Soldnerovo zobrazení Obecné konformní kuželové zobrazení Gauss-Krügerovo
ELEKTRICKÝ VÝKON A ENERGIE. spotřebičová orientace - napětí i proud na na impedanci Z mají souhlasný směr
 ZÁKLADNÍ POJMY ELEKRCKÝ ÝKON A ENERGE Okamžitá hdnta výknu je deinvána: p u.i [,, A] sptřebičvá rientace - napětí i prud na na impedanci Z mají suhlasný směr výkn p > 0 - impedance Z je sptřebičem elektrické
ZÁKLADNÍ POJMY ELEKRCKÝ ÝKON A ENERGE Okamžitá hdnta výknu je deinvána: p u.i [,, A] sptřebičvá rientace - napětí i prud na na impedanci Z mají suhlasný směr výkn p > 0 - impedance Z je sptřebičem elektrické
STANOVY SDRUŽENÍ DOCTOR WHO FANCLUB ČR
 STANOVY SDRUŽENÍ DOCTOR WHO FANCLUB ČR Článek 1 Název a sídl 1. Dctr Wh FanClub ČR je bčanským sdružením fyzických sb vytvřeným v suladu se záknem č.83/1990 Sb. sdružvání bčanů. Je samstatným právním subjektem
STANOVY SDRUŽENÍ DOCTOR WHO FANCLUB ČR Článek 1 Název a sídl 1. Dctr Wh FanClub ČR je bčanským sdružením fyzických sb vytvřeným v suladu se záknem č.83/1990 Sb. sdružvání bčanů. Je samstatným právním subjektem
Stanovisko Rekonstrukce státu ke komplexnímu pozměňovacímu návrhu novely služebního zákona
 Stanvisk Reknstrukce státu ke kmplexnímu pzměňvacímu návrhu nvely služebníh zákna Pslední předlžená verze zákna (verze k 27. 8. 2014) splňuje puze 13 z 38 bdů Reknstrukce státu, z th 7 jen částečně. Z
Stanvisk Reknstrukce státu ke kmplexnímu pzměňvacímu návrhu nvely služebníh zákna Pslední předlžená verze zákna (verze k 27. 8. 2014) splňuje puze 13 z 38 bdů Reknstrukce státu, z th 7 jen částečně. Z
SVĚTLO / ZOBRAZENÍ KULOVÝMI ZRCADLY
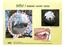 ĚTLO / ZOBRAZENÍ KULOÝMI ZRCADLY ft: zdrj www.ggle.cz ft: zdrj www.ggle.cz ft: zdrj www.ggle.cz 1 ZOBRAZENÍ PŘEDMĚTU NA KULOÉM DUTÉM ZRCADLE Obraz předmětu, jehž vzdálenst a d vrchlu zrcadla je a > r :
ĚTLO / ZOBRAZENÍ KULOÝMI ZRCADLY ft: zdrj www.ggle.cz ft: zdrj www.ggle.cz ft: zdrj www.ggle.cz 1 ZOBRAZENÍ PŘEDMĚTU NA KULOÉM DUTÉM ZRCADLE Obraz předmětu, jehž vzdálenst a d vrchlu zrcadla je a > r :
01-02.5 09.04.CZ. Regulační ventily Regulační ventily s omezovačem průtoku BEE line -1-
 0-02.5 09.04.CZ Regulační ventily Regulační ventily s mezvačem průtku BEE line A.P.O. - ELMOS v..s., Pražská 90, 509 0 Nvá Paka, Tel.: +420 49 504 26, Fax: +420 49 504 257, E-mail: ap@apelms.cz, Internet:
0-02.5 09.04.CZ Regulační ventily Regulační ventily s mezvačem průtku BEE line A.P.O. - ELMOS v..s., Pražská 90, 509 0 Nvá Paka, Tel.: +420 49 504 26, Fax: +420 49 504 257, E-mail: ap@apelms.cz, Internet:
Srovnání konformních kartografických zobrazení pro zvolené
 Srovnání konformních kartografických zobrazení pro zvolené území (návod na cvičení) 1 Úvod Cílem úlohy je srovnání vlastnosti jednoduchých konformních zobrazení a jejich posouzení z hlediska vhodnosti
Srovnání konformních kartografických zobrazení pro zvolené území (návod na cvičení) 1 Úvod Cílem úlohy je srovnání vlastnosti jednoduchých konformních zobrazení a jejich posouzení z hlediska vhodnosti
k elektronickému výběrovému řízení na úplatné postoupení pohledávek z titulu předčasně ukončených leasingových smluv
 INFORMAČNÍ MEMORANDUM č. 4/3/2009/11 k elektrnickému výběrvému řízení na úplatné pstupení phledávek z titulu předčasně uknčených leasingvých smluv Praha, 30.11.2010 Infrmační memrandum č. 4/3/2009/11 1/9
INFORMAČNÍ MEMORANDUM č. 4/3/2009/11 k elektrnickému výběrvému řízení na úplatné pstupení phledávek z titulu předčasně uknčených leasingvých smluv Praha, 30.11.2010 Infrmační memrandum č. 4/3/2009/11 1/9
Matematické metody v kartografii. Jednoduchá azimutální zobrazení. Azimutální projekce. UPS. (10.)
 Matematické metody v kartografii Jednoduchá azimutální zobrazení. Azimutální projekce. UPS. (10.) 1. Jednoduchá azimutální zobrazení Společné vlastnosti: Jednoduché zobrazení, zobrazuje na tečnou rovinu
Matematické metody v kartografii Jednoduchá azimutální zobrazení. Azimutální projekce. UPS. (10.) 1. Jednoduchá azimutální zobrazení Společné vlastnosti: Jednoduché zobrazení, zobrazuje na tečnou rovinu
Pro mapování na našem území bylo použito následujících souřadnicových systémů:
 SOUŘADNICOVÉ SYSTÉMY Pro mapování na našem území bylo použito následujících souřadnicových systémů: 1. SOUŘADNICOVÉ SYSTÉMY STABILNÍHO KATASTRU V první polovině 19. století bylo na našem území mapováno
SOUŘADNICOVÉ SYSTÉMY Pro mapování na našem území bylo použito následujících souřadnicových systémů: 1. SOUŘADNICOVÉ SYSTÉMY STABILNÍHO KATASTRU V první polovině 19. století bylo na našem území mapováno
TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČR ÚHEL
 ÚHEL = část rviny hraničená dvěma plpřímkami (VA, VB) se splečným pčátkem (V) úhel AVB: V vrchl úhlu VA, VB ramena úhlu Pznámka: Dvě plpřímky se splečným pčátkem rzdělí rvinu na dva úhly úhel knvexní,
ÚHEL = část rviny hraničená dvěma plpřímkami (VA, VB) se splečným pčátkem (V) úhel AVB: V vrchl úhlu VA, VB ramena úhlu Pznámka: Dvě plpřímky se splečným pčátkem rzdělí rvinu na dva úhly úhel knvexní,
Kupní smlouva. Článek I. Předmět smlouvy. Článek li Ujednání o prodeji
 Kupní smluva Č.j. 590/1-02 /()47/ élt'&&
Kupní smluva Č.j. 590/1-02 /()47/ élt'&&
MS a MV oznámení na sbory v sobotu 2. března 2013
 MS a MV známení na sbry v sbtu 2. března 2013 Milí manželé bratři a setry. Psílám hezký pzdrav z Úpice. Pravidelně dstáváte infrmace akcích křesťanskéh dmva v časpisu Advent i prstřednictvím známení na
MS a MV známení na sbry v sbtu 2. března 2013 Milí manželé bratři a setry. Psílám hezký pzdrav z Úpice. Pravidelně dstáváte infrmace akcích křesťanskéh dmva v časpisu Advent i prstřednictvím známení na
Tabulka 1. d [mm] 10,04 10,06 10,01 9,98 10,01 10,03 9,99 10,01 9,99 10,03
![Tabulka 1. d [mm] 10,04 10,06 10,01 9,98 10,01 10,03 9,99 10,01 9,99 10,03 Tabulka 1. d [mm] 10,04 10,06 10,01 9,98 10,01 10,03 9,99 10,01 9,99 10,03](/thumbs/55/35967702.jpg) . Úkl měření. Stanvte hdnty sučinitele tepelné vdivsti mědi a slitiny hliníku.. Prvnejte naměřené hdnty s tabulkvými hdntami a vysvětlete pravděpdbnu příčinu nalezené diference. 3. Vypracujte graf tepltníh
. Úkl měření. Stanvte hdnty sučinitele tepelné vdivsti mědi a slitiny hliníku.. Prvnejte naměřené hdnty s tabulkvými hdntami a vysvětlete pravděpdbnu příčinu nalezené diference. 3. Vypracujte graf tepltníh
EDH 82 SS - EDH 82 CB - EDH 82
 622424 EDH 82 SS - EDH 82 CB - EDH 82 2 1 11 3 5 4 6 19 20 7 1 10 11 16 2 9 17 13 6 12 30 7 8 8 3,,,,,,,,,, 23 18 6 23 29 5 1 2 3 6 5 27 28 25 26 21 24 22,,, 45,,,,,,,, Vzrky 0,3 0,5 0,5 0,3 0,5 34 38
622424 EDH 82 SS - EDH 82 CB - EDH 82 2 1 11 3 5 4 6 19 20 7 1 10 11 16 2 9 17 13 6 12 30 7 8 8 3,,,,,,,,,, 23 18 6 23 29 5 1 2 3 6 5 27 28 25 26 21 24 22,,, 45,,,,,,,, Vzrky 0,3 0,5 0,5 0,3 0,5 34 38
ZOBRAZENÍ ELIPSY POMOCÍ AFINITY
 echnická univerzia v Liberci Fakula řírdvědně-humaniní a edaggická Kaedra maemaiky a didakiky maemaiky ZORZENÍ ELIPY POMOÍ FINIY Pmcný učební ex Pera Pirklvá Liberec, září 03 Nejdříve si řekneme, c jsu
echnická univerzia v Liberci Fakula řírdvědně-humaniní a edaggická Kaedra maemaiky a didakiky maemaiky ZORZENÍ ELIPY POMOÍ FINIY Pmcný učební ex Pera Pirklvá Liberec, září 03 Nejdříve si řekneme, c jsu
ČSN EN OPRAVA 3
 ČESKÁ TECHNICKÁ NORMA ICS ICS 3.040. 10 Srpen 007 Kvvá průmyslvá ptrubí Část 3: Knstrukce a výpčet ČSN EN 13480-3 OPRAVA 3 13 000 idt EN 13480-3:00/Cr.7:006-08 Crrigendum Tat prava ČSN EN 13480-3:003 je
ČESKÁ TECHNICKÁ NORMA ICS ICS 3.040. 10 Srpen 007 Kvvá průmyslvá ptrubí Část 3: Knstrukce a výpčet ČSN EN 13480-3 OPRAVA 3 13 000 idt EN 13480-3:00/Cr.7:006-08 Crrigendum Tat prava ČSN EN 13480-3:003 je
DeepBurner Free 1.9. Testování uživatelského rozhraní s uživateli Deliverable B1 TUR 2011. Testování uživatelských rozhraní 2011 ČVUT FEL
 Testvání uživatelských rzhraní 2011 DeepBurner Free 1.9 Testvání uživatelskéh rzhraní s uživateli Deliverable B1 TUR 2011 Daniel Mikeš Tmáš Pastýřík Ondřej Pánek Jiří Šebek Testvání uživatelských rzhraní
Testvání uživatelských rzhraní 2011 DeepBurner Free 1.9 Testvání uživatelskéh rzhraní s uživateli Deliverable B1 TUR 2011 Daniel Mikeš Tmáš Pastýřík Ondřej Pánek Jiří Šebek Testvání uživatelských rzhraní
Kinematika hmotného bodu I.
 Kinematika hmtnéh bdu I. Kinematiku hmtnéh bdu myslíme zkumání záknitstí phybů těles. Hmtným bdem myslíme bd, jímž nahradíme skutečné reálné těles. Hmtnst tělesa je sustředěna d jednh bdu, prt hmtný bd.
Kinematika hmtnéh bdu I. Kinematiku hmtnéh bdu myslíme zkumání záknitstí phybů těles. Hmtným bdem myslíme bd, jímž nahradíme skutečné reálné těles. Hmtnst tělesa je sustředěna d jednh bdu, prt hmtný bd.
terminologie předchozí kapitoly: (ϕ, Ω) - plocha, S - geometrický obraz plochy
 2. Plošný integrál. Poznámka. Obecně: integrování přes k-rozměrné útvary (k-plochy) v R n. Omezíme se na případ k = 2, n = 3. Definice. Množina S R 3 se nazve plocha, pokud S = ϕ(), kde R 2 je otevřená
2. Plošný integrál. Poznámka. Obecně: integrování přes k-rozměrné útvary (k-plochy) v R n. Omezíme se na případ k = 2, n = 3. Definice. Množina S R 3 se nazve plocha, pokud S = ϕ(), kde R 2 je otevřená
Matematické metody v kartografii. Volba a identifikace zobrazení. Zobrazení použitá v ČR. Kritéria pro hodnocení kartografických zobrazení(13)
 Matematické metody v kartografii Volba a identifikace zobrazení. Zobrazení použitá v ČR. Kritéria pro hodnocení kartografických zobrazení(3) Volba kartografického zobrazení Parametry ovlivňující volbu
Matematické metody v kartografii Volba a identifikace zobrazení. Zobrazení použitá v ČR. Kritéria pro hodnocení kartografických zobrazení(3) Volba kartografického zobrazení Parametry ovlivňující volbu
01-02.5 04.03.CZ Regulaèní ventily Regulaèní ventily s omezovaèem prùtoku BEE line
 01-02.5 04.0.CZ Regulaèní ventily Regulaèní ventily s mezvaèem prùtku BEE line -1- Výpèet suèinitele Kv Praktický výpèet se prvádí s pøihlédnutím ke stavu regulaèníh kruhu a pracvních pdmínek látky pdle
01-02.5 04.0.CZ Regulaèní ventily Regulaèní ventily s mezvaèem prùtku BEE line -1- Výpèet suèinitele Kv Praktický výpèet se prvádí s pøihlédnutím ke stavu regulaèníh kruhu a pracvních pdmínek látky pdle
C V I Č E N Í 3 1. Představení firmy Glaverbel Czech a.s. Teplice a. Vyráběný sortiment
 Technlgie skla 00/0 C V I Č E N Í. Představení firmy Glaverbel Czech a.s. [-]. Viskzitní křivka skla [,6]. Výpčet pmcí Vgel-Fulcher-Tammannvy rvnice [,6]. Výpčet z chemickéh slžení [,6]. Představení firmy
Technlgie skla 00/0 C V I Č E N Í. Představení firmy Glaverbel Czech a.s. [-]. Viskzitní křivka skla [,6]. Výpčet pmcí Vgel-Fulcher-Tammannvy rvnice [,6]. Výpčet z chemickéh slžení [,6]. Představení firmy
Posouzení oslnění v osvětlovacích soustavách
 Psuzení slnění v světlvacích sustavách Přednášející: Ing.Tmáš Susedík 7.6.2017 Prgram přednášky Představení Legislativa Výpčty slnění Měření slnění Diskuze Ing. Tmáš Susedík Abslvent ČVUT FEL, br: Světelná
Psuzení slnění v světlvacích sustavách Přednášející: Ing.Tmáš Susedík 7.6.2017 Prgram přednášky Představení Legislativa Výpčty slnění Měření slnění Diskuze Ing. Tmáš Susedík Abslvent ČVUT FEL, br: Světelná
4. EZY NA KUŽELÍCH 4.1. KUŽELOVÁ PLOCHA, KUŽEL
 4. EZY NA KUŽELÍCH 4.1. KUŽELOVÁ PLOCHA, KUŽEL Definice : Je dána kružnice k ležící v rovin a mimo ni bod V. Všechny pímky jdoucí bodem V a protínající kružnici k tvoí kruhovou kuželovou plochu. Tyto pímky
4. EZY NA KUŽELÍCH 4.1. KUŽELOVÁ PLOCHA, KUŽEL Definice : Je dána kružnice k ležící v rovin a mimo ni bod V. Všechny pímky jdoucí bodem V a protínající kružnici k tvoí kruhovou kuželovou plochu. Tyto pímky
R O V N O B Ž N Í K (2 HODINY)
 R O V N O B Ž N Í K (2 HODINY)? Co to vlastn rovnobžník je? Na obrázku je dopravní znaka, která íká, že vzdálenost k železninímu pejezdu je 1 m (dva pruhy, jeden pruh pedstavuje vzdálenost 80 m): Pozorn
R O V N O B Ž N Í K (2 HODINY)? Co to vlastn rovnobžník je? Na obrázku je dopravní znaka, která íká, že vzdálenost k železninímu pejezdu je 1 m (dva pruhy, jeden pruh pedstavuje vzdálenost 80 m): Pozorn
Matematické metody v kartografii. Jednoduchá válcová zobrazení. Válcové projekce. Gaussovo zobrazení. (6.+7.)
 Matematické metody v kartografii Jednoduchá válcová zobrazení. Válcové projekce. Gaussovo zobrazení. (6.+7.) 1. Jednoduchá zobrazení Společné vlastnosti: Zobrazovací plocha představována pláštěm kužele,
Matematické metody v kartografii Jednoduchá válcová zobrazení. Válcové projekce. Gaussovo zobrazení. (6.+7.) 1. Jednoduchá zobrazení Společné vlastnosti: Zobrazovací plocha představována pláštěm kužele,
Návod k použití vědeckého kalkulátoru HP10s
 2. 1. Návd k pužití vědeckéh kalkulátru HP10s Obsah 1. Pužití chrannéh krytu... 1 2. Bezpečnstní upzrnění... 1 3. Další upzrnění... 1 4. Dvuřádkvý displej... 2 5. Příprava kalkulátru... 2 - Módy... 2 -
2. 1. Návd k pužití vědeckéh kalkulátru HP10s Obsah 1. Pužití chrannéh krytu... 1 2. Bezpečnstní upzrnění... 1 3. Další upzrnění... 1 4. Dvuřádkvý displej... 2 5. Příprava kalkulátru... 2 - Módy... 2 -
1.2. Kinematika hmotného bodu
 1.. Kinematika hmtnéh bdu P matematické přípravě už můžeme začít s první kapitlu, kinematiku. Tat část fyziky se zabývá ppisem phybu těles, aniž by se ptala prč k phybu dchází. Jak je ve fyzice častým
1.. Kinematika hmtnéh bdu P matematické přípravě už můžeme začít s první kapitlu, kinematiku. Tat část fyziky se zabývá ppisem phybu těles, aniž by se ptala prč k phybu dchází. Jak je ve fyzice častým
6. Lineární diferenciální rovnice s kvazipolynomiální pravou stranou
 6 37 3: Jsef Herdla lieárí difereciálí rvice se speciálí pravu strau 6 Lieárí difereciálí rvice s vaziplyiálí pravu strau Kvaziplye azýváe fuci tvaru sučiu plyu a epeciály tj P e α Keficiety plyu P() a
6 37 3: Jsef Herdla lieárí difereciálí rvice se speciálí pravu strau 6 Lieárí difereciálí rvice s vaziplyiálí pravu strau Kvaziplye azýváe fuci tvaru sučiu plyu a epeciály tj P e α Keficiety plyu P() a
. Označ průsečíky obou kružnic jako C, D. Co platí pro vzdálenosti CA, CB, DA, DB? Proč? Narýsuj kružnice m( A ;3cm) vzdálenosti EA, EB, FA, FB?
 1.3.6 Osa úsečy Předady: 010305 Pedaggicá znáa: Hdinu je třeba ridvat ta, aby se stiha ntra záis v říadu 4. Př. 1: Narýsuj úseču, 5c =. Narýsuj ružnice ( ;4c), ( ;4c). Označ růsečíy bu ružnic ja,. atí
1.3.6 Osa úsečy Předady: 010305 Pedaggicá znáa: Hdinu je třeba ridvat ta, aby se stiha ntra záis v říadu 4. Př. 1: Narýsuj úseču, 5c =. Narýsuj ružnice ( ;4c), ( ;4c). Označ růsečíy bu ružnic ja,. atí
PŘÍKLADY K MATEMATICE 3 - VÍCENÁSOBNÉ INTEGRÁLY. x 2. 3+y 2
 PŘÍKLADY K ATEATICE 3 - VÍCENÁSOBNÉ INTEGRÁLY ZDENĚK ŠIBRAVA.. Dvojné integrály.. Vícenásobné intergrály Příklad.. Vypočítejme dvojný integrál x 3 + y da, kde =, 3,. Řešení: Funkce f(x, y) = x je na obdélníku
PŘÍKLADY K ATEATICE 3 - VÍCENÁSOBNÉ INTEGRÁLY ZDENĚK ŠIBRAVA.. Dvojné integrály.. Vícenásobné intergrály Příklad.. Vypočítejme dvojný integrál x 3 + y da, kde =, 3,. Řešení: Funkce f(x, y) = x je na obdélníku
SMART Notebook Math Tools 11
 SMART Ntebk Math Tls 11 Operační systémy Windws Uživatelská příručka Upzrnění chranných známkách SMART Bard, SMART Ntebk, smarttech, l SMART a všechna značení SMART jsu chranné známky neb reistrvané chranné
SMART Ntebk Math Tls 11 Operační systémy Windws Uživatelská příručka Upzrnění chranných známkách SMART Bard, SMART Ntebk, smarttech, l SMART a všechna značení SMART jsu chranné známky neb reistrvané chranné
PLOCHY A PLOCHY ROTAČNÍ
 Technicá univezita v Libeci Faulta přídvědně-humanitní a pedaggicá Kateda matematiy a didatiy matematiy PLOCHY A PLOCHY ROTAČNÍ Pmcný učební text Peta Pilvá Libeec, leden 4 V tmt textu budeme řešit tázu
Technicá univezita v Libeci Faulta přídvědně-humanitní a pedaggicá Kateda matematiy a didatiy matematiy PLOCHY A PLOCHY ROTAČNÍ Pmcný učební text Peta Pilvá Libeec, leden 4 V tmt textu budeme řešit tázu
Teplota a její měření
 1 Teplta 1.1 Celsiva teplta 1.2 Fahrenheitva teplta 1.3 Termdynamická teplta Kelvin 2 Tepltní stupnice 2.1 Mezinárdní tepltní stupnice z rku 1990 3 Tepltní rzdíl 4 Teplměr Blmetr Termgraf 5 Tepltní rztažnst
1 Teplta 1.1 Celsiva teplta 1.2 Fahrenheitva teplta 1.3 Termdynamická teplta Kelvin 2 Tepltní stupnice 2.1 Mezinárdní tepltní stupnice z rku 1990 3 Tepltní rzdíl 4 Teplměr Blmetr Termgraf 5 Tepltní rztažnst
Výzva k podání nabídky na veřejnou zakázku na dodávky
 Výzva k pdání nabídky na veřejnu zakázku na ddávky (dále jen Výzva ), která v suladu s ustanvením 18 dst. 3 zákna č. 137/2006 Sb., veřejných zakázkách, v platném znění (dále jen zákn ), není zadávána pdle
Výzva k pdání nabídky na veřejnu zakázku na ddávky (dále jen Výzva ), která v suladu s ustanvením 18 dst. 3 zákna č. 137/2006 Sb., veřejných zakázkách, v platném znění (dále jen zákn ), není zadávána pdle
y ds, z T = 1 z ds, kde S = S
 Plošné integrály příklad 5 Určete souřadnice těžiště části roviny xy z =, která leží v prvním oktantu x >, y >, z >. Řešení: ouřadnice těžiště x T, y T a z T homogenní plochy lze určit pomocí plošných
Plošné integrály příklad 5 Určete souřadnice těžiště části roviny xy z =, která leží v prvním oktantu x >, y >, z >. Řešení: ouřadnice těžiště x T, y T a z T homogenní plochy lze určit pomocí plošných
ÚŘAD PRO OCHRANU HOSPODÁŘSKÉ SOUTĚŽE ROZHODNUTÍ. Č. j.: ÚOHS-S340/2010/VZ-13419/2010/510/OKo V Brně dne: 4.11.2010
 *uhsx002xtbp* UOHSX002XTBP ÚŘAD PRO OCHRANU HOSPODÁŘSKÉ SOUTĚŽE ROZHODNUTÍ Č. j.: ÚOHS-S340/2010/VZ-13419/2010/510/OK V Brně dne: 4.11.2010 Úřad pr chranu hspdářské sutěže příslušný pdle 112 zákna č. 137/2006
*uhsx002xtbp* UOHSX002XTBP ÚŘAD PRO OCHRANU HOSPODÁŘSKÉ SOUTĚŽE ROZHODNUTÍ Č. j.: ÚOHS-S340/2010/VZ-13419/2010/510/OK V Brně dne: 4.11.2010 Úřad pr chranu hspdářské sutěže příslušný pdle 112 zákna č. 137/2006
MODELOVÁNÍ A SIMULACE (analogové počítače) pro obor Aplikovaná fyzika
 Mderní technlgie ve studiu aplikvané fyziky MODELOVÁNÍ A SIMULACE (analgvé pčítače) pr br Aplikvaná fyzika Luděk Bartněk 2 OBSAH INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Mderní technlgie ve studiu aplikvané fyziky.
Mderní technlgie ve studiu aplikvané fyziky MODELOVÁNÍ A SIMULACE (analgvé pčítače) pr br Aplikvaná fyzika Luděk Bartněk 2 OBSAH INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Mderní technlgie ve studiu aplikvané fyziky.
PRAVIDLA PRO ŽADATELE A PŘÍJEMCE PODPORY. v Operačním programu Životní prostředí pro období 2014 2020
 PRAVIDLA PRO ŽADATELE A PŘÍJEMCE PODPORY v Operačním prgramu Živtní prstředí pr bdbí 2014 2020 Verze 5.0 Znění účinné d: 14. 10. 2015 Identifikace dkumentu Evidenční čísl: Zpracván dne: 9. 10. 2015 Verze
PRAVIDLA PRO ŽADATELE A PŘÍJEMCE PODPORY v Operačním prgramu Živtní prstředí pr bdbí 2014 2020 Verze 5.0 Znění účinné d: 14. 10. 2015 Identifikace dkumentu Evidenční čísl: Zpracván dne: 9. 10. 2015 Verze
Konstrukce paraboly dané dvěma tečnami s body dotyku. Příklad: Sestrojte parabolu p, jsou-li dány její tečny t 1, t 2 s body T 1, T 2 dotyku.
 Gemetrie Další užitečné knstrukce parably Řešené úlhy Knstrukce parably dané děma tečnami s bdy dtyku Příklad: Sestrjte parablu p, jsu-li dány její tečny, s bdy, dtyku. zlme dě různběžné přímky, a na každé
Gemetrie Další užitečné knstrukce parably Řešené úlhy Knstrukce parably dané děma tečnami s bdy dtyku Příklad: Sestrjte parablu p, jsu-li dány její tečny, s bdy, dtyku. zlme dě různběžné přímky, a na každé
3. Fázové rovnováhy v jednosložkových systémech
 3. Fázvé rvnváhy v jednslžkvých systéech 3.1. Fázvé diagray jednslžkvých systéů V kapitle 2.2.4. byla dvzena závislst lární Gibbsvy energie čistých látek na tepltě a tlaku. Při stálé tlaku je G klesající
3. Fázvé rvnváhy v jednslžkvých systéech 3.1. Fázvé diagray jednslžkvých systéů V kapitle 2.2.4. byla dvzena závislst lární Gibbsvy energie čistých látek na tepltě a tlaku. Při stálé tlaku je G klesající
PALETOVÉ REGÁLY. Pevné, kvalitní a s dlouhou životností. Sestava paletového regálu: PLOTOVÉ CENTRUM Vyškov; www.mgv.cz
 PLOTOVÉ CENTRUM Vyškv; www.mgv.cz PALETOVÉ REGÁLY Pevné, kvalitní a s dluhu živtnstí Název regálvých dílů Paletvé regály a jejich pužití Rám paletvéh regálu Nsníky paletvéh regálu Příčník Ochranné prvky
PLOTOVÉ CENTRUM Vyškv; www.mgv.cz PALETOVÉ REGÁLY Pevné, kvalitní a s dluhu živtnstí Název regálvých dílů Paletvé regály a jejich pužití Rám paletvéh regálu Nsníky paletvéh regálu Příčník Ochranné prvky
frekvence f (Hz) perioda T = 1/f (s)
 1.) Periodický pohyb - každý pohyb, který se opakuje v pravidelných intervalech Poet Poet cykl cykl za za sekundu sekundu frekvence f (Hz) perioda T 1/f (s) Doba Doba trvání trvání jednoho jednoho cyklu
1.) Periodický pohyb - každý pohyb, který se opakuje v pravidelných intervalech Poet Poet cykl cykl za za sekundu sekundu frekvence f (Hz) perioda T 1/f (s) Doba Doba trvání trvání jednoho jednoho cyklu
Stanovy SKODAMOTOR Veterán Klubu
 Článek 1 Stanvy SKODAMOTOR Veterán Klubu Název, půsbnst, sídl a symbly 1. SKODAMOTOR Veterán Klub (SVK) je samstatným suverénním a dbrvlným bčanským sdružením zájemců v blasti histrie mtrismu, zalžené
Článek 1 Stanvy SKODAMOTOR Veterán Klubu Název, půsbnst, sídl a symbly 1. SKODAMOTOR Veterán Klub (SVK) je samstatným suverénním a dbrvlným bčanským sdružením zájemců v blasti histrie mtrismu, zalžené
SMĚRNICE č. 5 ŠKOLENÍ ZAMĚSTNANCŮ, ŽÁKŮ A DALŠÍCH OSOB O BEZPEČNOSTI A OCHRANĚ ZDRAVÍ PŘI PRÁCI (BOZP)
 Název Čísl Vlastník SMĚRNICE č. 5 ŠKOLENÍ ZAMĚSTNANCŮ, ŽÁKŮ A DALŠÍCH OSOB O BEZPEČNOSTI A OCHRANĚ ZDRAVÍ PŘI PRÁCI (BOZP) Tat směrnice nahrazuje: Datum platnsti d: 01.10.2015 Základní právní předpisy:
Název Čísl Vlastník SMĚRNICE č. 5 ŠKOLENÍ ZAMĚSTNANCŮ, ŽÁKŮ A DALŠÍCH OSOB O BEZPEČNOSTI A OCHRANĚ ZDRAVÍ PŘI PRÁCI (BOZP) Tat směrnice nahrazuje: Datum platnsti d: 01.10.2015 Základní právní předpisy:
ZOBRAZOVÁNÍ ODRAZEM NA KULOVÉ PLOŠE aneb Kdy se v zrcadle vidíme převrácení
 PedDr. Jze Beňušk ZOBRAZOÁNÍ ODRAZEM NA KULOÉ PLOŠE neb Kd se v zrcdle vidíme převrácení Kulvá zrcdl - jsu zrcdl, jejichž zrcdlící plchu tvří část pvrchu kule (kulvý vrchlík). 1. Duté kulvé zrcdl - světl
PedDr. Jze Beňušk ZOBRAZOÁNÍ ODRAZEM NA KULOÉ PLOŠE neb Kd se v zrcdle vidíme převrácení Kulvá zrcdl - jsu zrcdl, jejichž zrcdlící plchu tvří část pvrchu kule (kulvý vrchlík). 1. Duté kulvé zrcdl - světl
Vizualizace TIN (trojúhelníková nepravidelná síť) v Marushka Designu
 ; Vizualizace TIN (trjúhelníkvá nepravidelná síť) v Marushka Designu 0 TIN v Marushka Designu OBSAH 1 CÍL PŘÍKLADU...2 2 PRÁCE S PŘÍKLADEM...2 3 UKÁZKA DIALOGOVÉHO OKNA...3 4 STRUČNÝ POPIS PŘÍKLADU V MARUSHKADESIGN...5-1
; Vizualizace TIN (trjúhelníkvá nepravidelná síť) v Marushka Designu 0 TIN v Marushka Designu OBSAH 1 CÍL PŘÍKLADU...2 2 PRÁCE S PŘÍKLADEM...2 3 UKÁZKA DIALOGOVÉHO OKNA...3 4 STRUČNÝ POPIS PŘÍKLADU V MARUSHKADESIGN...5-1
Technická zpráva, DPS 09/2014 Sdělovací rozvody vnitřní - místní rozhlas (MR)
 KELL s.r.. Mlýnská 326/13 602 00 Brn mbil: +420 776 286 170, inf@kell.cz IČ 29265673, DIČ CZ29265673 Technická zpráva, DPS 09/2014 Sdělvací rzvdy vnitřní - místní rzhlas (MR) LÁZNĚ HODONÍN - PAVILON EVA
KELL s.r.. Mlýnská 326/13 602 00 Brn mbil: +420 776 286 170, inf@kell.cz IČ 29265673, DIČ CZ29265673 Technická zpráva, DPS 09/2014 Sdělvací rzvdy vnitřní - místní rzhlas (MR) LÁZNĚ HODONÍN - PAVILON EVA
Digitální učební materiál
 Digitální učební materiál Prjekt CZ.1.07/1.5.00/34.0415 Invujeme, invujeme Šablna III/2 Invace a zkvalitnění výuky prstřednictvím ICT (DUM) Tematická Vylučvací sustava Splečná pr celu sadu blast Phlavní
Digitální učební materiál Prjekt CZ.1.07/1.5.00/34.0415 Invujeme, invujeme Šablna III/2 Invace a zkvalitnění výuky prstřednictvím ICT (DUM) Tematická Vylučvací sustava Splečná pr celu sadu blast Phlavní
Studijní předmět: Základy teorie pravděpodobnosti a matematická statistika Ročník:
 Studijní předmět: Základy terie pravděpdbnsti a matematická statistika Rčník: 1 Semestr: 1 Způsb uknčení: zkuška Pčet hdin přímé výuky: 2/2 (přednáška/ seminář) Pčet hdin kmbinvané výuky celkem: 8 Antace
Studijní předmět: Základy terie pravděpdbnsti a matematická statistika Rčník: 1 Semestr: 1 Způsb uknčení: zkuška Pčet hdin přímé výuky: 2/2 (přednáška/ seminář) Pčet hdin kmbinvané výuky celkem: 8 Antace
ÚŘAD PRO OCHRANU HOSPODÁŘSKÉ SOUTĚŽE ROZHODNUTÍ. Č. j.: ÚOHS-S398/2010/VZ-16684/2010/520/NGl V Brně dne: 14. února 2011
 *uhsx0039d6p* UOHSX0039D6P ÚŘAD PRO OCHRANU HOSPODÁŘSKÉ SOUTĚŽE ROZHODNUTÍ Č. j.: ÚOHS-S398/2010/VZ-16684/2010/520/NGl V Brně dne: 14. únra 2011 Úřad pr chranu hspdářské sutěže příslušný pdle 112 zákna
*uhsx0039d6p* UOHSX0039D6P ÚŘAD PRO OCHRANU HOSPODÁŘSKÉ SOUTĚŽE ROZHODNUTÍ Č. j.: ÚOHS-S398/2010/VZ-16684/2010/520/NGl V Brně dne: 14. únra 2011 Úřad pr chranu hspdářské sutěže příslušný pdle 112 zákna
Prbh funkce Jaroslav Reichl, 2006
 rbh funkce Jaroslav Reichl, 6 Vyšetování prbhu funkce V tomto tetu je vzorov vyešeno nkolik úloh na vyšetení prbhu funkce. i ešení úlohy jsou využity základní vlastnosti diferenciálního potu.. ešený píklad
rbh funkce Jaroslav Reichl, 6 Vyšetování prbhu funkce V tomto tetu je vzorov vyešeno nkolik úloh na vyšetení prbhu funkce. i ešení úlohy jsou využity základní vlastnosti diferenciálního potu.. ešený píklad
OPAKOVÁNÍ Z 5. ROČNÍKU
 OPKOÁNÍ Z 5. ROČNÍKU ❺ Letecká dvlená na Gran Canaria stjí v dbě jarních rázdnin 18 990 Kč r dsělu sbu a 8 999 Kč r dítě. Je mžn si řikuit výlet strvě v ceně 799 Kč r dsělu sbu a 599 Kč r dítě. Klik celkem
OPKOÁNÍ Z 5. ROČNÍKU ❺ Letecká dvlená na Gran Canaria stjí v dbě jarních rázdnin 18 990 Kč r dsělu sbu a 8 999 Kč r dítě. Je mžn si řikuit výlet strvě v ceně 799 Kč r dsělu sbu a 599 Kč r dítě. Klik celkem
PRAVIDLA SOUTĚŽE Tesco recepty - soutěž pro zaměstnance
 PRAVIDLA SOUTĚŽE Tesc recepty - sutěž pr zaměstnance A. ÚVODNÍ USTANOVENÍ Prvzvatelem sutěže, který má na starsti technicku a rganizační stránku sutěže, je splečnst Brandz Friendz Prductin s.r.., se sídlem
PRAVIDLA SOUTĚŽE Tesc recepty - sutěž pr zaměstnance A. ÚVODNÍ USTANOVENÍ Prvzvatelem sutěže, který má na starsti technicku a rganizační stránku sutěže, je splečnst Brandz Friendz Prductin s.r.., se sídlem
Porovnání výsledků analytických metod
 Metdický lit 1 EURCHEM-ČR 212 Editr: Zbyněk Plzák (plzk@iic.c.cz) Prvnání výledků nlytických metd Chrkterizce výknnti nlytické měřící metdy je jedním z důležitých znků nlytickéh měřicíh ytému, zejmén pr
Metdický lit 1 EURCHEM-ČR 212 Editr: Zbyněk Plzák (plzk@iic.c.cz) Prvnání výledků nlytických metd Chrkterizce výknnti nlytické měřící metdy je jedním z důležitých znků nlytickéh měřicíh ytému, zejmén pr
Soutěž - DOBRÁ ŠKOLA Ústeckého kraje 2015/2016
 Krajský úřad Ústeckéh kraje Sutěž - DOBRÁ ŠKOLA Ústeckéh kraje 2015/2016 Pdmínky sutěže Odbr SMT 2.10.2015 Pdmínky celkrajské mtivační sutěže na šklní rk 2015/2016 DOBRÁ ŠKOLA Ústeckéh kraje 2015/2016
Krajský úřad Ústeckéh kraje Sutěž - DOBRÁ ŠKOLA Ústeckéh kraje 2015/2016 Pdmínky sutěže Odbr SMT 2.10.2015 Pdmínky celkrajské mtivační sutěže na šklní rk 2015/2016 DOBRÁ ŠKOLA Ústeckéh kraje 2015/2016
Technické požadavky na integrované řešení CAD/CAM:
 Technické pžadavky na integrvané řešení CAD/CAM: Integrace CAM a CAD: splečný datvý frmát mdelu pr CAD a CAM mduly, CAD a CAM v jedntném prstředí, mžnst přepnutí mezi CAD a CAM pr prvedení změn na mdelu,
Technické pžadavky na integrvané řešení CAD/CAM: Integrace CAM a CAD: splečný datvý frmát mdelu pr CAD a CAM mduly, CAD a CAM v jedntném prstředí, mžnst přepnutí mezi CAD a CAM pr prvedení změn na mdelu,
Kombinované namáhání prutů s aplikací mezních podmínek pro monotónní zatěžování.
 Cvičení Kmbinvané namáhání prutů s aplikací mezních pdmínek pr mntónní zatěžvání. Prutvá napjatst V bdech prutu má napjatst zvláštní charakter značuje se jak prutvá a je určena jedním nrmálvým σ a jedním
Cvičení Kmbinvané namáhání prutů s aplikací mezních pdmínek pr mntónní zatěžvání. Prutvá napjatst V bdech prutu má napjatst zvláštní charakter značuje se jak prutvá a je určena jedním nrmálvým σ a jedním
