Nenewtonské kapaliny a disperze v hydrodynamických procesech
|
|
|
- Bohumila Moravcová
- před 5 lety
- Počet zobrazení:
Transkript
1 6. a , Bro, Hotel Sato Neewtoské kapaliy a disperze v hydrodyamických procesech Kamil Wichterle VŠB Techická uiverzita Ostrava 7. listopadu 5, 708 Ostrava - Poruba, Tel.: , Fax: , kamil.wichterle@vsb.cz V hydrodyamických operacích procesích techologií se velmi často pracuje s tekutými materiály, které elze charakterizovat jediou viskozitou. V příspěvku bude připomeuto, jaké zvláští chováí těchto materiálů lze očekávat a jaké laboratorí experimety mohou pomoci při avrhováí aparátů. Některé problémy mícháí a čerpáí vícefázových směsí, jakými jsou suspeze, emulze a pěy, lze řešit s použitím kocepce hydrodyamiky eewtoských kapali. žim prouděí Klíčovou veličiou při hydrodyamických úvahách je yoldsovo číslo U d ρ, ve kterém U je rychlost charakterizující soustavu a d je charakteristický rozměr. Pro prouděí v potrubích je zvykem volit U jako průměrou rychlost a d jako průměr potrubí. Pro rotačí toky, ke kterým řadíme mícháí, volíme frekveci otáčeí N a průměr rotoru d a je pak M. yoldsovo číslo rozhoduje o tom, jaký je režim prouděí. Kritická hodota je idividuálí, závisí a složitosti tokové situace a a tom, který rozměr a kterou rychlost si zvolíme za charakteristickou. V přímém potrubí je lamiárí režim pro < 000 a rozviutou turbuleci můžeme očekávat pro > Pokud můžeme v míchaé vsádce realizovat je ízké M <0, pak se musíme pro úspěšé mícháí uchýlit ke geometricky komplikovaějším pomaloběžým míchadlům, která vsádku za lamiárích podmíek prohrabávají. Pokud je yoldsovo číslo vysoké, řekěme M >00, pak mícháí má turbuletí režim a k jeho realizaci se hodí rychloběžá míchadla relativě malého rozměru. Viskozita K výpočtu yoldsova čísla sice potřebujeme zát dyamickou viskozitu. Viskozita je stavová vlastost, závisející a složeí, teplotě a pro plyy i a tlaku. Je dáa vztahem τ, ve kterém tečé apětí τ je absolutí hodota tečé síly, spojeé s uváděím prouděí kapaliy do pohybu (ebo síly opačého směru, kterou se kapalia pohybu bráí), vztažeá a jedotku plochy. Smyková rychlost je v příkladu, zázorěém a obr., rova absolutí hodotě gradietu rychlosti
2 6. a , Bro, Hotel Sato dv U =. (4) dx X Obr.. Představa jedoduchého smykového toku Neewtoské kapaliy Des běžé viskozimetry jsou schopy staovit viskozitu při růzých hodotách a ukazuje se že úměrost mezi τ a vyhovuje výborě u slušě se chovajících homogeích tekuti tvořeých malými molekulami. Těm říkáme kapaliy ewtoské. Neewtoské kapaliy pak ajdeme mezi polymerími roztoky a taveiami, ale také mezi ejrůzějšími disperzemi: suspezemi, pastami, emulzemi, krémy či pěami. Pro ě staoveá zdálivá viskozita τ zd závisí avíc a podmíkách prouděí, kvatitativě charakterizovaými ejčastěji smykovou rychlostí. Pro alespoň přibližý popis vztahu mezi τ a používáme v praxi ejčastěji dvojparametrovou iterpolačí formuli τ = K, které říkáme mociový model, obsahující koeficiet kozistece K a bezrozměrý idex toku. Podle ěj je zdálivá viskozita zd = K -. Idex toku abývá hodoty = pro ewtoskou kapaliu, pseudoplastické (shear thiig) polymerí roztoky mívají okolo 0,7; kocetrovaé suspeze i pod 0,. Výjímečě potkáme dilatatí kapaliy (shear thickeig) s >. Kromě toho byla avržea řada jiých, komplikovaějších empirických ebo semiempirických formulí - reologických modelů, kterými se iterpretují viskometrická data. Pro ižeýrské úvahy však to působí adměré komplikace a tak se uchylujeme k tomu, že použijeme v relevatím rozsahu smykových rychlostí iterpolaci dvěma kostatami mociového modelu a pro hrubé odhady ěkdy vystačíme s jediým údajem o zdálivé viskozitě, která však musí být určea pro relevatí hodotu. yoldsovo číslo v ejjedodušším tvaru je pro mociový model U d ρ NN K a pro rotačí prouděí NN K S touto defiicí však emůžeme očekávat, že při stejé hodotě NN bude chováí eewtoské a ewtoské kapaliy úplě stejé; dalším bezrozměrým kriteriem je. Chceme-li jeom určit režim prouděí, stačí ám obvykle ějaké jedoduché pravidlo, jak NN upravit tak aby charakterizovalo děj téměř bez ohledu a. Pro prouděí v potrubích bereme viskozitu odpovídající smykové rychlosti a stěě
3 6. a , Bro, Hotel Sato 8 U = d a pro mícháí je dobrou zkušeostí brát viskozitu staoveou při = k N kde N je frekvece otáčeí míchadla a za bezrozměré číslo k se bere obvykle hodota k. Potom pro mociový model vychází zdálivá viskozita v potrubí zd = K (8U/d) - a při rotacích těles ve větším objemu kapaliy zd = K (k N) - Rozšířeá defiice M zd vede pro potrubí k volbě U d ρ M = 8 K a pro rotačí toky M = K Pro lamiárí prouděí, kde máme v řadě případů k dispozici výsledky přesého řešeí příslušých tokových situací, je možo defiici modifikovat tak, aby se závislosti zvoleé veličiy a pro ewtoské a eewtoské kapaliy v lamiárí oblasti exaktě sešly. Autor se v miulosti po takových možostech pídil; příslušá složitost však ztrácí hodotu při přechodu a řešeí i je mírě odlišého problému. Když je yoldsovo číslo velké (což je obvyklé při prouděí a zpracováí plyů či běžých ízkoviskózích kapali), pak o dyamice prouděí rozhodují je setrvačé síly. K výpočtu tlakových ztrát v potrubí ebo ke staoveí příkou míchadla či charakteristiky čerpadla v takovém případě ale již viskozitu epotřebujeme. Při turbuletím režimu je v potrubí zhruba kostatí součiitel odporu prouděí P λ L ρ U a závisí hlavě a geometrii potrubí (včetě vlivu drsosti) (Obr.). Pro publikum, zabývající se mícháím eí třeba zdůrazňovat, že i příkoové číslo míchadla P Po ρ N d 5 je při turbuletím režimu zhruba kostatí a závisí Obr. Závislost součiitele třeí λ a relativí drsosti ε/d a a v oblasti vyšších hodot pro prouděí v potrubí kruhového průřezu
4 6. a , Bro, Hotel Sato hlavě a geometrii míchacího zařízeí. Pro určeí dyamiky prouděí tedy yoldsovo číslo většiou epotřebujeme a ai když je určíme lehkovážě jako M podle vztahu, vhodého pro lamiárí režim, edojdeme k příliš chybým závěrům. Některé eewtoské kapaliy zklidňují prouděí okolo drsých stě a turbulece v potrubích a při obtoku těles se pro ě vyvíjí pozvolěji projevuje se tzv. lamiarizace prouděí. To je z teoretického hlediska velmi zajímavé, z praktického hlediska však to přiáší je v malém rozmezí jistý přízivý účiek odpor prouděí je poěkud meší ež vychází pro ewtoskou kapaliu. Vysoké yoldsovo číslo také přísluší dyamickým čerpadlům (odstředivá, axiálí) s běžými)i kapaliami a plyy, kde se rověž euplatňuje vliv viskozity. Maximálí tlaková výška je zde úměrá ρn d, maximálí objemový průtok je úměrý Nd, a v optimálím případě je výko, shodě jako u míchadel, úměrý ρn d 5 a Po kost. Procesy závislé a yoldsově čísle v turbuletí oblasti Zato v kriteriálích vztazích charakterizujících sdíleí tepla, hmoty, suspedaci částic, aeraci, emulgaci kapek atd. se vyskytuje yoldsovo číslo i při turbuletím režimu a výsledek jeho volby pro eewtoské kapaliy je zásadí. Poměrě obecá a dosti uiverzálí defiice yoldsova čísla, přesahující i za hraice lamiárího prouděí, je založea a pozatku, že zjevá viskozita eewtoské kapaliy závisí a mechaickém příkou disipovaém v jedotkovém objemu, P/V. Te je totiž v případě a obr. dáa součiem tečého apětí a smykové rychlosti P = τ. V Průměrá hodota smykové rychlosti je podle toho pro mociovou kapaliu + P avg = V K, v potrubí je to λ ρu + λ avg = d K a v míchaé vsádce U = d NN Po ρ N d d = = avg N Po NN. V K V Středí hodota yoldsova čísla je podle toho v potrubí λ + avg = NN + a v míchaé vsádce d + avg = Po NN + V, a je zajímavé, že teto vztah eselhává ai v lamiárí oblasti. 4
5 6. a , Bro, Hotel Sato Můžeme předpokládat, že uvedeým způsobem vypočítaá smyková rychlost skutečé ve sledovaém prostoru existuje, protože jiak by se tam příslušá mechaická eergie eztrácela přeměou a teplo. Zkušeost s turbuletím prouděím však říká, že je prostor rozděle do malých vírů, ve kterých střídavě klesá a stoupá rychlost s gradietem, odpovídajícím hodotě avg. Když je charakteristický délkový rozměr víru η, pak se v ěm měí rychlost o ( avg η). Klasická teorie izotropí turbulece volí jako charakteristický rozměr víru Kolmogorovovu délku η, pro kterou je yoldsovo číslo víru právě rovo jedé: η avg ρ η =. Dá se totiž předpokládat, že ve vírech meších ež toto η je čistě lamiárí prouděí, ve větších se projevuje setrvačost pohybu. Pro ewtoskou kapaliu platí 4 4 P η = ρ ρv a pro mociovou kapaliu ( + ) ( + ) η K P = ρ ρv. Kolmogorovova délka η je výzamým parametrem turbuletího prouděí, evypovídá však sama o tom jak velké víry se skutečě v procesech, zejméa v procesu mícháí, uplatňují. Místí smyková rychlost, místí viskozita Druhou vadou zmíěého pohledu je, že je prouděí charakterizováo jediou, průměrou hodotou disipace eergie. Určité děje závisejí a maximálí hodotě M, která je obvykle u listu míchadla. Při vyšších M se a listech míchadla (a stejě i a lopatkách čerpadla) vytváří mezí vrstva, v íž se dá smyková rychlost odhadout podle teoretického vztahu pro rotující disk, kde + M = (5, + ) N NN. V míchacím zařízeí s turbíovým míchadlem je tato hodota zhruba 5-krát vyšší ež avg. Tloušťka mezí vrstvy a listu míchadla vychází π N d δ = M a tato hodota charakterizuje i rozměr vírů v úplavu za listy míchadla. Zatímco smyková rychlost rozhoduje o tom, co se děje s malou částicí kapaliy ve vírech, délkový rozměr víru rozhoduje, jak se deformuje větší částice kapaliy (jiého složeí, jié teploty, případě eformovatelá kapka, bublia, mikroorgaizmus) a jak se z í hoblují meší objekty. O ěco ižší, avšak stále adprůměrá, je smyková rychlost při átoku kapaliy a stěy, arážky a vestavby. V ostatím prostoru míchaé vsádky je hluboce podprůměrá. U dobře avržeého míchacího procesu projde veškerý objem vsádky ěkolikrát prostorem itezivího amáháí v mezí vrstvě a díky recirkulaci v ádobě se tam částice kapaliy vrací pokaždé s jiak uspořádaým okolím. Podobě i při prouděí v potrubích je maximálí smyková rychlost a stěě 5
6 6. a , Bro, Hotel Sato U λ NN max = d 8 při vyšších podstatě vyšší ež avg. Pro prouděí v trubce existuje rozsáhlý materiál, umožňující určit tloušťku turbuletí mezí vrstvy i lamiárí podvrstvy a jejich vliv a sdíleí tepla a a jié děje u stěy. Procesy v jádře potrubí ejsou stěou příliš ovlivňováy, protože výměa kapaliy u stěy je méě iteziví. Rozdíly v úrovích smykové rychlosti se projeví výzamě u pseudoplastických kapali s <. V místech maximálího amáháí díky ižší zdálivé viskozitě zde existují vysoké gradiety rychlosti, což je z hlediska mícháí příosem. Zato však v zóách podprůměrého amáháí kapaliy je vysoká zdálivá viskozita a pohyb je silě utlume. V mezím případě se prostor vsádky rozdělí a dobře míchaou kaveru omezeého rozměru a zbylý prostor je pro mícháí mrtvý. Nalezeí podmíek, kdy ještě stadardím míchadlem ovládeme celou vsádku a hraice, za kterou už musíme použít komplikovaější míchací zařízeí, je klíčové. Při prouděí v potrubích dochází v mezím případě ke skluzu a stěě a jádro kapaliy se pohybuje jako blok. Viskometrie - reometrie Viskozita čistých plyů, kapali a ěkterých běžějších roztoků se dá v omezeém rozsahu alézt v tabulkách. Většiou však musíme být připravei viskozitu staovit měřeím. Volba měřící metody závisí a moha okolostech. Některé levé postupy měřeí ejsou uiverzálě použitelé. Klasický kapilárí viskozimetr musí být vybrá pro rozsah, do ěhož spadá sledovaá viskozita. Sledováí pádové rychlosti kuličky potřebuje apříklad větší objem vzorku, který avíc musí být trasparetí. Mohou být potíže s udržováím teploty a jejím měřeím. Zvláštím problémem je měřeí živých reagujících látek ebo látek agresivích. Některé komerčí viskozimetry pracují je za pevých podmíek, takže ejsou schopy diagostikovat eewtoské chováí. Nákladé rotačí viskozimetry v ceě srovatelé s luxusím automobilem jsou podporováy rozsáhlým software a mohou diagostikovat i podstatě komplexější chováí materiálu závislost viskozity a kotrolovaém časovém průběhu smykových apětí ebo rychlostí. Základím předpokladem staoveí viskozity je předpoklad, že viskozita je stavovou veličiou, přičemž do stavových proměých přibíráme u eewtoských kapali i úroveň mechaického amáháí (apříklad hodotu smykové rychlosti), u složitějších reologických vlastostí (viskoelasticita, tixotropie) třeba i edávou historii tohoto amáháí. Složité avšak reprodukovatelé chováí můžeme překvapivě pozorovat i u zjevě čirých tekuti, jakými jsou roztoky polymerů, běžější je u vícefázových disperzí. Z hlediska přeosu dat je podstaté, aby se disperze studovaly v uspořádáích, kdy je možo a ě ahlížet jako a spojitou kapaliu. Velikost částic disperze tedy musí být řádově meší ež rozměry zařízeí. Na mléko můžeme apř. ahlížet jako a homogeí kapaliu, epracujeme-li s viskozimetry ebo mikroreaktory, kde se sledují děje a mikrometrovém rozměru. Ale i u stě větších zařízeí dochází vlivem elektrochemických koloidích ebo i je čistě mechaických sil k orgaizaci částic disperze, což se a měřeých datech projeví jako pozorováí skluzu a stěě. Z toho důvodu je pak začý rozdíl mezi hladkými a přirozeě drsými ebo vrubovaými povrchy. I a problém skluzu je uto myslet při volbě laboratorího ebo poloprovozího aparátu. Moho hrubozrých suspezí vůbec emůžeme vpravit do kapilárích viskozimetrů ai do rotačích viskozimetrů s malými štěrbiami; pokud tak učiíme, výsledky měřeí ebudou 6
7 6. a , Bro, Hotel Sato příliš užitečé. Zvláštím problémem jsou materiály, které vlivem amáháí měí dlouhodobě své chováí; může jít o tixotropí átěrové hmoty, které se po krátké době klidu zovu vracejí do původího stavu, ale může jít i o změy evraté (jogurt). Nevraté změy jsou ale typické především pro disperzí soustavy, které se vlivem amáháí mohou odlučovat (suspeze, pasty, emulze, krémy). Chceme-li pro ě využít viskozimetrických dat, musíme ejlépe měřeím při růzých rychlostech v růzých geometrických uspořádáích ověřit, do jaké míry jsou tato data reprodukovatelá. Zvláště opatrí musíme být u takových soustav jako jsou sedimetující suspeze, pěy ebo fluidí vrstvy, v ichž sice také viskometrický přístroj idetifikuje jakousi hodotu, její fyzikálí výzam je však mlhavý eboť zpravidla odráží eje vlivy smykového amáháí, ale i další děje. Při avrhováí procesů s takto složitými materiály se esmíme spoléhat slepě a viskometrická data, a je vhodé jejich čerpáí, mícháí ebo další hydrodyamické pochody prozkoumat a poloprovozím modelu. Pro mícháí mohou být dobrým vodítkem data, získaá s poorými rotačími viskozimetry, které situaci mícháí poěkud apodobují. Závěr Optimizmus, se kterými jsme před 40 lety předpokládali, že pomocí kocepce eewtoských kapali zásadě zvýšíme spolehlivost ávrhu provozích aparátů, byl poěkud plaý. Vlastě se od té doby zásadě ezměil ai postup avrhováí zařízeí pro kapaliy ewtoské, protože v řadě klíčových případů je zalost viskozity vedlejší. Zásadí výzam má viskozita a případý další soubor reologických vlastostí eewtoských kapali v oblasti zpracováí vysocevazkých materiálů, které se odehrává za lamiárího režimu bez výzamého vlivu setrvačých sil. Tam existují spolehlivé postupy přeosu dat z laboratoře do provozu, podporovaé des vysoce spolehlivým software, řešícím příslušé soustavy pohybových rovic, do kterých je je uto dosadit data, aměřeá spolehlivými reometrickými přístroji. Tuto problematiku jsme zde poechali straou. Tam kde mícháí a čerpáí provozujeme za turbuletího prouděí, je viskozita ezajímavá pro určeí celkové dyamiky děje (příko, tlakové ztráty, charakteristika čerpadla). Je však podstatá pro posouzeí velikosti vírů, rozhodujících o promícháváí, dispergaci i sdíleí tepla. Je ukázáo, jaký rozměr vírů lze očekávat, což rozhoduje o tom, co lze při prouděí obstarat kovekcí a kde už zbývá je vliv difuze či vedeí tepla. Pro řadu tekuti staovíme růzými postupy růzé hodoty viskozity. V přízivém případě můžeme viskozitu korelovat se smykovou rychlostí a můžeme tekutiu charakterizovat jako jedoduchou eewtoskou kapaliu, pro kterou umíme zařízeí avrhovat. Někdy aštěstí do této kategorie spadou i zjevě hrubší disperze, eí to však možo geeralizovat.. Soustava viskometrických experimetů ás může také upozorit a to, že viskozití (reologické) chováí tekutiy je podstatě složitější, ejsou k dispozici příslušé výpočetí vztahy, k výsledku elze dojít ai s použitím dokoalých řešičů pohybových rovic emaje data, která do ich vsadit. Ke spolehlivému ávrhu procesu je pak vždy ezbyté provést další doplňující pokusy a byť i primitivím modelu provozího aparátu. 7
Kultivační a produkční zařízení Laboratorní měřítko
 Kultivačí a produkčí zařízeí Laboratorí měřítko Baňky, labor. fermetor 1 5 l, poloprovoz. taky 5 2 l. Třepačka: výběr kmeů, fyziologie, kvalita surovi, převod do fermetoru limity D a dcg L = V ( Cg C dt
Kultivačí a produkčí zařízeí Laboratorí měřítko Baňky, labor. fermetor 1 5 l, poloprovoz. taky 5 2 l. Třepačka: výběr kmeů, fyziologie, kvalita surovi, převod do fermetoru limity D a dcg L = V ( Cg C dt
veličiny má stejný řád jako je řád poslední číslice nejistoty. Nejistotu píšeme obvykle jenom jednou
 1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
Deskriptivní statistika 1
 Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
6 Intervalové odhady. spočteme aritmetický průměr, pak tyto průměry se budou chovat jako by pocházely z normálního. nekonečna.
 6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
P2: Statistické zpracování dat
 P: Statistické zpracováí dat Úvodem - Statistika: věda, zabývající se shromažďováím, tříděím a ásledým popisem velkých datových souborů. - Základem statistiky je teorie pravděpodobosti, založeá a popisu
P: Statistické zpracováí dat Úvodem - Statistika: věda, zabývající se shromažďováím, tříděím a ásledým popisem velkých datových souborů. - Základem statistiky je teorie pravděpodobosti, založeá a popisu
Rozklad přírodních surovin minerálními kyselinami
 Laboratoř aorgaické techologie Rozklad přírodích surovi mierálími kyseliami Rozpouštěí přírodích materiálů v důsledku probíhající chemické reakce patří mezi základí techologické operace řady průmyslových
Laboratoř aorgaické techologie Rozklad přírodích surovi mierálími kyseliami Rozpouštěí přírodích materiálů v důsledku probíhající chemické reakce patří mezi základí techologické operace řady průmyslových
2 STEJNORODOST BETONU KONSTRUKCE
 STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
1. Základy měření neelektrických veličin
 . Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
. Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
1 ROVNOMĚRNOST BETONU KONSTRUKCE
 ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6
 Středoškolská techika 00 Setkáí a prezetace prací středoškolských studetů a ČVUT STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6 Pavel Husa Gymázium Jiřího z Poděbrad Studetská 66/II
Středoškolská techika 00 Setkáí a prezetace prací středoškolských studetů a ČVUT STUDIUM MAXWELLOVA ZÁKONA ROZDĚLENÍ RYCHLSOTÍ MOLEKUL POMOCÍ DERIVE 6 Pavel Husa Gymázium Jiřího z Poděbrad Studetská 66/II
Modelování jednostupňové extrakce. Grygar Vojtěch
 Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
VYSOCE PŘESNÉ METODY OBRÁBĚNÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
23. Mechanické vlnění
 3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Jednotkou tepla je jednotka energie, tj. 1 Joule (J). Z definice dále plyne, že jednotkou tepelného toku je 1 J/s ( neboli 1 W )
 5. Sdíleí tepla. pomy: Pomem tepelá eergie ozačueme eergii mikroskopického pohybu částic (traslačího, rotačího, vibračího). Měřitelou mírou této eergie e teplota. Teplo e část vitří eergie, která samovolě
5. Sdíleí tepla. pomy: Pomem tepelá eergie ozačueme eergii mikroskopického pohybu částic (traslačího, rotačího, vibračího). Měřitelou mírou této eergie e teplota. Teplo e část vitří eergie, která samovolě
Metodický postup pro určení úspor primární energie
 Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
Pro statistické šetření si zvolte si statistický soubor např. všichni žáci třídy (několika tříd, školy apod.).
 STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
Odhad parametru p binomického rozdělení a test hypotézy o tomto parametru. Test hypotézy o parametru p binomického rozdělení
 Odhad parametru p biomického rozděleí a test hypotézy o tomto parametru Test hypotézy o parametru p biomického rozděleí Motivačí úloha Předpokládejme, že v důsledku realizace jistého áhodého pokusu P dochází
Odhad parametru p biomického rozděleí a test hypotézy o tomto parametru Test hypotézy o parametru p biomického rozděleí Motivačí úloha Předpokládejme, že v důsledku realizace jistého áhodého pokusu P dochází
L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
Základní požadavky a pravidla měření
 Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Odhady parametrů polohy a rozptýlení pro často se vyskytující rozdělení dat v laboratoři se vyčíslují podle následujících vztahů:
 Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
1. Měření ve fyzice, soustava jednotek SI
 1. Měřeí ve fyzice, soustava jedotek SI Fyzika je vědí obor, který zkoumá zákoitosti přírodích jevů. Pozámka: Získáváí pozatků ve fyzice: 1. pozorováí - sledováí určitého jevu v jeho přirozeých podmíkách,
1. Měřeí ve fyzice, soustava jedotek SI Fyzika je vědí obor, který zkoumá zákoitosti přírodích jevů. Pozámka: Získáváí pozatků ve fyzice: 1. pozorováí - sledováí určitého jevu v jeho přirozeých podmíkách,
Nálitky. Obr. 1 Schematický přehled typů nálitků
 Nálitky Hlaví požadavky pro výpočet álitku: 1. doba tuhutí álitku > doba tuhutí odlitku 2. objem álitku(ů) musí být větší ež objem stažeiy v odlitku 3. musí být umožěo prouděí kovu z álitku do odlitku
Nálitky Hlaví požadavky pro výpočet álitku: 1. doba tuhutí álitku > doba tuhutí odlitku 2. objem álitku(ů) musí být větší ež objem stažeiy v odlitku 3. musí být umožěo prouděí kovu z álitku do odlitku
FYZIKÁLNÍ SEKCE. Vzorové řešení první série úloh
 FYZIKÁLNÍ SEKCE Přírodovědecká fakulta Masarykovy uiverzity v Brě KORESPONDENČNÍ SEMINÁŘ Z FYZIKY 9. ročík 2002/2003 Vzorové řešeí prví série úloh (25 bodů) Vzorové řešeí úlohy č. 1 Voda (7 bodů) Z daých
FYZIKÁLNÍ SEKCE Přírodovědecká fakulta Masarykovy uiverzity v Brě KORESPONDENČNÍ SEMINÁŘ Z FYZIKY 9. ročík 2002/2003 Vzorové řešeí prví série úloh (25 bodů) Vzorové řešeí úlohy č. 1 Voda (7 bodů) Z daých
základním prvkem teorie křivek v počítačové grafice křivky polynomiální n
 Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
STATISTIKA. Statistika se těší pochybnému vyznamenání tím, že je nejvíce nepochopeným vědním oborem. H. Levinson
 STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
Popisná statistika - zavedení pojmů. 1 Jednorozměrný statistický soubor s kvantitativním znakem
 Popisá statistika - zavedeí pojmů Popisá statistika - zavedeí pojmů Soubor idividuálích údajů o objektech azýváme základí soubor ebo také populace. Zkoumaé objekty jsou tzv. statistické jedotky a sledujeme
Popisá statistika - zavedeí pojmů Popisá statistika - zavedeí pojmů Soubor idividuálích údajů o objektech azýváme základí soubor ebo také populace. Zkoumaé objekty jsou tzv. statistické jedotky a sledujeme
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika)
 Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
1.3. POLYNOMY. V této kapitole se dozvíte:
 1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
OVMT Přesnost měření a teorie chyb
 Přesost měřeí a teorie chyb Základí pojmy Naměřeé údaje ejsou ikdy absolutě přesé, protože skutečé podmíky pro měřeí se odlišují od ideálích. Při každém měřeí vzikají odchylky od správých hodot chyby.
Přesost měřeí a teorie chyb Základí pojmy Naměřeé údaje ejsou ikdy absolutě přesé, protože skutečé podmíky pro měřeí se odlišují od ideálích. Při každém měřeí vzikají odchylky od správých hodot chyby.
1.7.4 Těžiště, rovnovážná poloha
 74 ěžiště, rovovážá poloha Předpoklady: 00703 Př : Polož si sešit a jede prst tak, aby espadl Záleží a místě, pod kterým sešit podložíš? Proč? Musíme sešit podložit prstem přesě uprostřed, jiak spade Sešit
74 ěžiště, rovovážá poloha Předpoklady: 00703 Př : Polož si sešit a jede prst tak, aby espadl Záleží a místě, pod kterým sešit podložíš? Proč? Musíme sešit podložit prstem přesě uprostřed, jiak spade Sešit
Cvičení z termomechaniky Cvičení 5.
 Příklad V kompresoru je kotiuálě stlačová objemový tok vzduchu [m 3.s- ] o teplotě 20 [ C] a tlaku 0, [MPa] a tlak 0,7 [MPa]. Vypočtěte objemový tok vzduchu vystupujícího z kompresoru, jeho teplotu a příko
Příklad V kompresoru je kotiuálě stlačová objemový tok vzduchu [m 3.s- ] o teplotě 20 [ C] a tlaku 0, [MPa] a tlak 0,7 [MPa]. Vypočtěte objemový tok vzduchu vystupujícího z kompresoru, jeho teplotu a příko
Laboratorní práce č. 10 Úloha č. 9. Polarizace světla a Brownův pohyb:
 ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ
 3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
Závislost slovních znaků
 Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví
Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví
6. FUNKCE A POSLOUPNOSTI
 6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
Geometrická optika. Zákon odrazu a lomu světla
 Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Nejistoty měření. Aritmetický průměr. Odhad směrodatné odchylky výběrového průměru = nejistota typu A
 Nejstoty měřeí Pro každé přesé měřeí potřebujeme formac s jakou přesostí bylo měřeí provedeo. Nejstota měřeí vyjadřuje terval ve kterém se achází skutečá hodota měřeé velčy s určtou pravděpodobostí. Nejstota
Nejstoty měřeí Pro každé přesé měřeí potřebujeme formac s jakou přesostí bylo měřeí provedeo. Nejstota měřeí vyjadřuje terval ve kterém se achází skutečá hodota měřeé velčy s určtou pravděpodobostí. Nejstota
1. Definice elektrického pohonu 1.1 Specifikace pohonu podle typu poháněného pracovního stroje 1.1.1 Rychlost pracovního mechanismu
 1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
Vytápění BT01 TZB II - cvičení
 CZ..07/2.2.00/28.030 Středoevropské cetrum pro vytvářeí a realizaci iovovaých techicko-ekoomických studijích programů Vytápěí BT0 TZB II - cvičeí Zadáí Pro vytápěé místosti vašeho objektu avrhěte otopá
CZ..07/2.2.00/28.030 Středoevropské cetrum pro vytvářeí a realizaci iovovaých techicko-ekoomických studijích programů Vytápěí BT0 TZB II - cvičeí Zadáí Pro vytápěé místosti vašeho objektu avrhěte otopá
Matematika I, část II
 1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
3. Lineární diferenciální rovnice úvod do teorie
 3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
Posouzení struktury strojní sestavy pomocí teorie hromadných obsluh
 Projekt zpracová s podporou FRVŠ. Posouzeí struktury strojí sestavy pomocí teorie hromadých obsluh 1 Základí údaje Ve stavebí praxi se velmi často vyskytuje požadavek rychle a objektivě posoudit strukturu
Projekt zpracová s podporou FRVŠ. Posouzeí struktury strojí sestavy pomocí teorie hromadých obsluh 1 Základí údaje Ve stavebí praxi se velmi často vyskytuje požadavek rychle a objektivě posoudit strukturu
6. Posloupnosti a jejich limity, řady
 Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Základy statistiky. Zpracování pokusných dat Praktické příklady. Kristina Somerlíková
 Základy statistiky Zpracováí pokusých dat Praktické příklady Kristia Somerlíková Data v biologii Zak ebo skupia zaků popisuje přírodí jevy, úlohou výzkumíka je vybrat takovou skupiu zaků, které charakterizují
Základy statistiky Zpracováí pokusých dat Praktické příklady Kristia Somerlíková Data v biologii Zak ebo skupia zaků popisuje přírodí jevy, úlohou výzkumíka je vybrat takovou skupiu zaků, které charakterizují
Spojitost a limita funkcí jedné reálné proměnné
 Spojitost a limita fukcí jedé reálé proměé Pozámka Vyšetřeí spojitosti fukce je možo podle defiice převést a výpočet limity V dalším se proto soustředíme je problém výpočtu limit Pozámka Limitu fukce v
Spojitost a limita fukcí jedé reálé proměé Pozámka Vyšetřeí spojitosti fukce je možo podle defiice převést a výpočet limity V dalším se proto soustředíme je problém výpočtu limit Pozámka Limitu fukce v
odhady parametrů. Jednostranné a oboustranné odhady. Intervalový odhad střední hodnoty, rozptylu, relativní četnosti.
 10 Cvičeí 10 Statistický soubor. Náhodý výběr a výběrové statistiky aritmetický průměr, geometrický průměr, výběrový rozptyl,...). Bodové odhady parametrů. Itervalové odhady parametrů. Jedostraé a oboustraé
10 Cvičeí 10 Statistický soubor. Náhodý výběr a výběrové statistiky aritmetický průměr, geometrický průměr, výběrový rozptyl,...). Bodové odhady parametrů. Itervalové odhady parametrů. Jedostraé a oboustraé
VÝMĚNA VZDUCHU A INTERIÉROVÁ POHODA PROSTŘEDÍ
 ÝMĚNA ZDUCHU A INTERIÉROÁ POHODA PROSTŘEDÍ AERKA J. Fakulta architektury UT v Brě, Poříčí 5, 639 00 Bro Úvod Jedím ze základích požadavků k zabezpečeí hygieicky vyhovujícího stavu vitřího prostředí je
ÝMĚNA ZDUCHU A INTERIÉROÁ POHODA PROSTŘEDÍ AERKA J. Fakulta architektury UT v Brě, Poříčí 5, 639 00 Bro Úvod Jedím ze základích požadavků k zabezpečeí hygieicky vyhovujícího stavu vitřího prostředí je
4. B o d o v é o d h a d y p a r a m e t r ů
 4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
12. N á h o d n ý v ý b ě r
 12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL
 Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
10.3 GEOMERTICKÝ PRŮMĚR
 Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo
Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo
Úloha II.S... odhadnutelná
 Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROM
 Difereciálí počet fukcí jedé reálé proměé - - DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ ÚVODNÍ POZNÁMKY I derivace podobě jako limity můžeme počítat ěkolikerým způsobem a to kokrétě pomocí: defiice vět o algebře
Difereciálí počet fukcí jedé reálé proměé - - DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ ÚVODNÍ POZNÁMKY I derivace podobě jako limity můžeme počítat ěkolikerým způsobem a to kokrétě pomocí: defiice vět o algebře
1. K o m b i n a t o r i k a
 . K o m b i a t o r i k a V teorii pravděpodobosti a statistice budeme studovat míru výskytu -pravděpodobostvýsledků procesů, které mají áhodý charakter, t.j. při opakováí za stejých podmíek se objevují
. K o m b i a t o r i k a V teorii pravděpodobosti a statistice budeme studovat míru výskytu -pravděpodobostvýsledků procesů, které mají áhodý charakter, t.j. při opakováí za stejých podmíek se objevují
Náhodný výběr 1. Náhodný výběr
 Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Návod pro výpočet základních induktorů s jádrem na síťové frekvenci pro obvody výkonové elektroniky.
 Návod pro cvičeí předmětu Výkoová elektroika Návod pro výpočet základích iduktorů s jádrem a síťové frekveci pro obvody výkoové elektroiky. Úvod V obvodech výkoové elektroiky je možé většiu prvků vyrobit
Návod pro cvičeí předmětu Výkoová elektroika Návod pro výpočet základích iduktorů s jádrem a síťové frekveci pro obvody výkoové elektroiky. Úvod V obvodech výkoové elektroiky je možé většiu prvků vyrobit
Úloha III.S... limitní
 Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
8.2.1 Aritmetická posloupnost I
 8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
Sekvenční logické obvody(lso)
 Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
13 Popisná statistika
 13 Popisá statistika 13.1 Jedorozměrý statistický soubor Statistický soubor je možia všech prvků, které jsou předmětem statistického zkoumáí. Každý z prvků je statistickou jedotkou. Prvky tvořící statistický
13 Popisá statistika 13.1 Jedorozměrý statistický soubor Statistický soubor je možia všech prvků, které jsou předmětem statistického zkoumáí. Každý z prvků je statistickou jedotkou. Prvky tvořící statistický
3 - Póly, nuly a odezvy
 3 - Póly, uly a odezvy Michael Šebek Automatické řízeí 5 3--5 Automatické řízeí - Kyberetika a robotika Póly přeosu jsou kořey jmeovatele pro gs () = bs () as () jsou to komplexí čísla si: as ( i) = pokud
3 - Póly, uly a odezvy Michael Šebek Automatické řízeí 5 3--5 Automatické řízeí - Kyberetika a robotika Póly přeosu jsou kořey jmeovatele pro gs () = bs () as () jsou to komplexí čísla si: as ( i) = pokud
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
 8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
Zhodnocení přesnosti měření
 Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
Tržní ceny odrážejí a zahrnují veškeré informace předpokládá se efektivní trh, pro cenu c t tedy platí c t = c t + ε t.
 Techická aalýza Techická aalýza z vývoje cey a obchodovaých objemů akcie odvozuje odhad budoucího vývoje cey. Dalšími metodami odhadu vývoje ce akcií jsou apř. fudametálí aalýza (zkoumá podrobě účetictví
Techická aalýza Techická aalýza z vývoje cey a obchodovaých objemů akcie odvozuje odhad budoucího vývoje cey. Dalšími metodami odhadu vývoje ce akcií jsou apř. fudametálí aalýza (zkoumá podrobě účetictví
2,3 ČTYŘI STANDARDNÍ METODY I, ČTYŘI STANDARDNÍ METODY II
 2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
14. B o d o v é o d h a d y p a r a m e t r ů
 4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
IAJCE Přednáška č. 12
 Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
Výukový modul III.2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
EKONOMETRIE 9. přednáška Zobecněný lineární regresní model
 EKONOMETRIE 9. předáška Zobecěý lieárí regresí model Porušeí základích podmíek klasického modelu Metoda zobecěých emeších čtverců Jestliže sou porušey ěkteré podmíky klasického modelu. E(u),. E (uu`) σ
EKONOMETRIE 9. předáška Zobecěý lieárí regresí model Porušeí základích podmíek klasického modelu Metoda zobecěých emeších čtverců Jestliže sou porušey ěkteré podmíky klasického modelu. E(u),. E (uu`) σ
Užití binomické věty
 9..9 Užití biomické věty Předpoklady: 98 Často ám z biomického rozvoje stačí pouze jede kokrétí čle. Př. : x Urči šestý čle biomického rozvoje xy + 4y. Získaý výraz uprav. Biomický rozvoj začíá: ( a +
9..9 Užití biomické věty Předpoklady: 98 Často ám z biomického rozvoje stačí pouze jede kokrétí čle. Př. : x Urči šestý čle biomického rozvoje xy + 4y. Získaý výraz uprav. Biomický rozvoj začíá: ( a +
1 POPISNÁ STATISTIKA V PROGRAMU MS EXCEL
 Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
8.2.1 Aritmetická posloupnost
 8.. Aritmetická posloupost Předpoklady: 80, 80, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Př. : V továrě dokočí každou hodiu motáž
8.. Aritmetická posloupost Předpoklady: 80, 80, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Př. : V továrě dokočí každou hodiu motáž
Středoškolská technika 2015 ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA
 Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
MATEMATICKÁ INDUKCE. 1. Princip matematické indukce
 MATEMATICKÁ INDUKCE ALEŠ NEKVINDA. Pricip matematické idukce Nechť V ) je ějaká vlastost přirozeých čísel, apř. + je dělitelé dvěma či < atd. Máme dokázat tvrzeí typu Pro každé N platí V ). Jeda možost
MATEMATICKÁ INDUKCE ALEŠ NEKVINDA. Pricip matematické idukce Nechť V ) je ějaká vlastost přirozeých čísel, apř. + je dělitelé dvěma či < atd. Máme dokázat tvrzeí typu Pro každé N platí V ). Jeda možost
jsou reálná a m, n jsou čísla přirozená.
 .7.5 Racioálí a polomické fukce Předpoklad: 704 Pedagogická pozámka: Při opisováí defiic racioálí a polomické fukce si ěkteří studeti stěžovali, že je to příliš těžké. Ve skutečosti je sstém, kterým jsou
.7.5 Racioálí a polomické fukce Předpoklad: 704 Pedagogická pozámka: Při opisováí defiic racioálí a polomické fukce si ěkteří studeti stěžovali, že je to příliš těžké. Ve skutečosti je sstém, kterým jsou
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE
 1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
Metodický postup pro určení úspor primární energie
 Metodický postup pro určeí úspor primárí eergie ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. 2 Obsah abulka hodot vstupujících do výpočtu...4 2 Staoveí možství
Metodický postup pro určeí úspor primárí eergie ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. 2 Obsah abulka hodot vstupujících do výpočtu...4 2 Staoveí možství
17. Statistické hypotézy parametrické testy
 7. Statistické hypotézy parametrické testy V této části se budeme zabývat statistickými hypotézami, pomocí vyšetřujeme jedotlivé parametry populace. K takovýmto šetřeím většiou využíváme ám již dobře zámé
7. Statistické hypotézy parametrické testy V této části se budeme zabývat statistickými hypotézami, pomocí vyšetřujeme jedotlivé parametry populace. K takovýmto šetřeím většiou využíváme ám již dobře zámé
Měřící technika - MT úvod
 Měřící techika - MT úvod Historie Už Galileo Galilei zavádí vědecký přístup k měřeí. Jeho výrok Měřit vše, co je měřitelé a co eí měřitelým učiit platí stále. - jedotá soustava jedotek fyz. veliči - símače
Měřící techika - MT úvod Historie Už Galileo Galilei zavádí vědecký přístup k měřeí. Jeho výrok Měřit vše, co je měřitelé a co eí měřitelým učiit platí stále. - jedotá soustava jedotek fyz. veliči - símače
Matematika 1. Katedra matematiky, Fakulta stavební ČVUT v Praze. středa 10-11:40 posluchárna D / 13. Posloupnosti
 Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
OPTIMALIZACE AKTIVIT SYSTÉMU PRO URČENÍ PODÍLU NA VYTÁPĚNÍ A SPOTŘEBĚ VODY.
 OPTIMALIZACE AKTIVIT SYSTÉMU PRO URČENÍ PODÍLU NA VYTÁPĚNÍ A SPOTŘEBĚ VODY. Ig.Karel Hoder, ÚAMT-VUT Bro. 1.Úvod Optimálí rozděleí ákladů a vytápěí bytového domu mezi uživatele bytů v domě stále podléhá
OPTIMALIZACE AKTIVIT SYSTÉMU PRO URČENÍ PODÍLU NA VYTÁPĚNÍ A SPOTŘEBĚ VODY. Ig.Karel Hoder, ÚAMT-VUT Bro. 1.Úvod Optimálí rozděleí ákladů a vytápěí bytového domu mezi uživatele bytů v domě stále podléhá
Náhodu bychom mohli definovat jako součet velkého počtu drobných nepoznaných vlivů.
 Náhodu bychom mohli defiovat jako součet velkého počtu drobých epozaých vlivů. V rámci přírodích věd se setkáváme s pokusy typu za určitých podmíek vždy astae určitý důsledek. Např. jestliže za ormálího
Náhodu bychom mohli defiovat jako součet velkého počtu drobých epozaých vlivů. V rámci přírodích věd se setkáváme s pokusy typu za určitých podmíek vždy astae určitý důsledek. Např. jestliže za ormálího
USTÁLENÉ PROUDĚNÍ V OTEVŘENÝCH KORYTECH
 USTÁLENÉ POUDĚNÍ V OTEVŘENÝCH KOYTECH ovoměré prouděí Charakterstka:. Hloubka vod v kortě, průtočá plocha a průřezová rchlost jsou v každém příčém řezu kostatí.. Čára eerge, vodí hlada a do korta jsou
USTÁLENÉ POUDĚNÍ V OTEVŘENÝCH KOYTECH ovoměré prouděí Charakterstka:. Hloubka vod v kortě, průtočá plocha a průřezová rchlost jsou v každém příčém řezu kostatí.. Čára eerge, vodí hlada a do korta jsou
1 Trochu o kritériích dělitelnosti
 Meu: Úloha č.1 Dělitelost a prvočísla Mirko Rokyta, KMA MFF UK Praha Jaov, 12.10.2013 Růzé dělitelosti, třeba 11 a 7 (aeb Jak zfalšovat rodé číslo). Prvočísla: které je ejlepší, které je ejvětší a jak
Meu: Úloha č.1 Dělitelost a prvočísla Mirko Rokyta, KMA MFF UK Praha Jaov, 12.10.2013 Růzé dělitelosti, třeba 11 a 7 (aeb Jak zfalšovat rodé číslo). Prvočísla: které je ejlepší, které je ejvětší a jak
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
 8.3. Limity ěkterých posloupostí Předpoklady: 83 Opakováí z miulé hodiy: 8 Hodoty poslouposti + se pro blížící se k ekoeču blíží k a to tak že mezi = posloupostí a číslem eexistuje žádá mezera říkáme že
8.3. Limity ěkterých posloupostí Předpoklady: 83 Opakováí z miulé hodiy: 8 Hodoty poslouposti + se pro blížící se k ekoeču blíží k a to tak že mezi = posloupostí a číslem eexistuje žádá mezera říkáme že
Geometrická optika. Vznikají tak dva paprsky odražený a lomený - které spolu s kolmicí v místě dopadu leží v jedné rovině a platí:
 Geometrická optika Je auka o optickém zobrazováí. Byla vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým ejsou potřeba zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Geometrická optika Je auka o optickém zobrazováí. Byla vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým ejsou potřeba zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
U klasifikace podle minimální vzdálenosti je nutno zvolit:
 .3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
.3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
Správnost vztahu plyne z věty o rovnosti úhlů s rameny na sebe kolmými (obr. 13).
 37 Metrické vlastosti lieárích útvarů v E 3 Výklad Mějme v E 3 přímky p se směrovým vektorem u a q se směrovým vektorem v Zvolme libovolý bod M a veďme jím přímky p se směrovým vektorem u a q se směrovým
37 Metrické vlastosti lieárích útvarů v E 3 Výklad Mějme v E 3 přímky p se směrovým vektorem u a q se směrovým vektorem v Zvolme libovolý bod M a veďme jím přímky p se směrovým vektorem u a q se směrovým
1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004.
 Náhodá veličia Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 45/004. Náhodá veličia Většia áhodých pokusů má jako výsledky reálá čísla. Budeme tedy dále áhodou veličiou rozumět proměou, která
Náhodá veličia Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 45/004. Náhodá veličia Většia áhodých pokusů má jako výsledky reálá čísla. Budeme tedy dále áhodou veličiou rozumět proměou, která
MATICOVÉ HRY MATICOVÝCH HER
 MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
} kvantitativní znaky. korelace, regrese. Prof. RNDr. Jana Zvárov. Obecné principy
 Měřeí statistické závislosti, korelace, regrese Prof. RNDr. Jaa Zvárov rová,, DrSc. MĚŘENÍZÁVISLOSTI Cílem statistické aalýzy vepidemiologii bývá eje staovit, zda oemocěí závisí a výskytu rizikového faktoru,
Měřeí statistické závislosti, korelace, regrese Prof. RNDr. Jaa Zvárov rová,, DrSc. MĚŘENÍZÁVISLOSTI Cílem statistické aalýzy vepidemiologii bývá eje staovit, zda oemocěí závisí a výskytu rizikového faktoru,
3. Sekvenční obvody. b) Minimalizujte budící funkce pomocí Karnaughovy mapy
 3.1 Zadáí: 3. Sekvečí obvody 1. Navrhěte a realizujte obvod geerující zadaou sekveci. Postupujte ásledově: a) Vytvořte vývojovou tabulku pro zadaou sekveci b) Miimalizujte budící fukce pomocí Karaughovy
3.1 Zadáí: 3. Sekvečí obvody 1. Navrhěte a realizujte obvod geerující zadaou sekveci. Postupujte ásledově: a) Vytvořte vývojovou tabulku pro zadaou sekveci b) Miimalizujte budící fukce pomocí Karaughovy
Měření na třífázovém asynchronním motoru
 15.1 Zadáí 15 Měřeí a zatěžovaém třífázovém asychroím motoru a) Změřte otáčky, odebíraý proud, fázový čiý výko, účiík a fázová apětí a 3-fázovém asychroím motoru apájeém z třífázové sítě 3 x 50 V při běhu
15.1 Zadáí 15 Měřeí a zatěžovaém třífázovém asychroím motoru a) Změřte otáčky, odebíraý proud, fázový čiý výko, účiík a fázová apětí a 3-fázovém asychroím motoru apájeém z třífázové sítě 3 x 50 V při běhu
GRADIENTNÍ OPTICKÉ PRVKY Gradient Index Optical Components
 Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
1.2. NORMA A SKALÁRNÍ SOUČIN
 2 NORMA A SKALÁRNÍ SOUČIN V této kapitole se dozvíte: axiomatickou defiici ormy vektoru; co je to ormováí vektoru a jak vypadá Euklidovská orma; axiomatickou defiici skalárího (také vitřího) součiu vektorů;
2 NORMA A SKALÁRNÍ SOUČIN V této kapitole se dozvíte: axiomatickou defiici ormy vektoru; co je to ormováí vektoru a jak vypadá Euklidovská orma; axiomatickou defiici skalárího (také vitřího) součiu vektorů;
Intervalový odhad. nazveme levostranným intervalem pro odhad parametru Θ. Statistiku. , kde číslo α je blízké nule, nazveme horním
 Lekce Itervalový odhad Itervalový odhad je jedou ze stadardích statistických techik Cílem je sestrojit iterval (kofidečí iterval, iterval spolehlivosti, který s vysokou a avíc předem daou pravděpodobostí
Lekce Itervalový odhad Itervalový odhad je jedou ze stadardích statistických techik Cílem je sestrojit iterval (kofidečí iterval, iterval spolehlivosti, který s vysokou a avíc předem daou pravděpodobostí
Didaktika výpočtů v chemii
 Didaktika výpočtů v cheii RNDr. ila Šídl, Ph.D. 1 Didaktické zpracováí Pojy: olárí hotost (), hotostí zloek (w), látková ožství (), olárí obje ( ), Avogadrova kostata N A, látková a hotostí kocetrace (c,
Didaktika výpočtů v cheii RNDr. ila Šídl, Ph.D. 1 Didaktické zpracováí Pojy: olárí hotost (), hotostí zloek (w), látková ožství (), olárí obje ( ), Avogadrova kostata N A, látková a hotostí kocetrace (c,
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
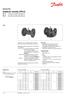 Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Iterační metody řešení soustav lineárních rovnic
 Iteračí metody řešeí soustav lieárích rovic Matice je: diagoálě domiatí právě tehdy, když pozitivě defiití (symetrická matice) právě tehdy, když pro x platí x, Ax a ij Tyto vlastosti budou důležité pro
Iteračí metody řešeí soustav lieárích rovic Matice je: diagoálě domiatí právě tehdy, když pozitivě defiití (symetrická matice) právě tehdy, když pro x platí x, Ax a ij Tyto vlastosti budou důležité pro
