Stanovení přetvoření ohýbaných nosníků. Mohrova metoda (Mohrova analogie)
|
|
|
- Marie Tesařová
- před 6 lety
- Počet zobrazení:
Transkript
1 Stnovení přetvoření ohýnýh nosníků ohrov metod (ohrov nlogie)
2 Přetvoření ohýnýh nosníků Posouzení z hledisk meze použitelnosti Ztížení, deforme w, φ Okrové podmínky (deforme) Šmiřák, S.: Pružnost plstiit I, Nkldtelství UT v Brně, Brno, 999, ISBN
3 ohrov metod využívá derivčně-integrční závislosti mezi ztížením, vnitřními silmi deformemi w I
4 Zdro: přednášky dr. Kresy ohrov metod postup. Sttiké řešení konstruke určení průěhu ohyového momentu. Definie fiktivního nosníku eho ztížení příčným ztížením Fiktivní nosník e podepřený tkovým způsoem, že splňue vůči ohyovému momentu posouvíí síle tytéž okrové podmínky (příp. podmínky spoitosti) ké plní skutečný nosník vůči průhyu w pootočení. Sttiké řešení fiktivního nosníku určení průěhu, čili w n skutečném nosníku (t. užití ohrovýh vět)
5 Příkld - číselně 0 w=0 w=0 R ohrovou metodou určete: - průhy w ve středu nosníku; - pootočení v podporáh. [knm [knm Q 6 6 ) Stnovení rekí vyřešení průěhu 0 0 [ knm R w ohyová čár Fiktivní nosník: w ohyového momentu R R 5kN l R 5 6 0kNm ) Sestvení fiktivního nosníku eho ztížení momentovým orzem R R [knm R 6 Q [knm w 60 =0 =0 R Q R ) Určete číselně velikost průhyu, e-li nosník z IPN0 mteriál E=0 GP: w 0,056m 5, 0,06 0
6 Příkld oené řešení w=0 w=0 R R ohyová čár [knm Fiktivní nosník: [knm F l/ l/ Q l/6 w 4 4 R =0 =0 Q l 4 6 R ohrovou metodou určete: - průhy w ve středu nosníku; - pootočení v podporáh. w U oeného řešení dete pozor n záměnu ztížení fiktivního skutečného, u fiktivního ztížení dodržute oznčení vlnovkou ) Reke ohyový moment F R R l F l R 4 ) Sestvení fiktivního nosníku eho ztížení momentovým orzem l R R [knm 4 6 l l l R Q Q [knm w 48
7 Příkld - číselně = knm = 0 = 0 ohrovou metodou určete: - průhy w n volném koni; - pootočení volného kone. w m m ) Stnovení rekí vyřešení průěhu ohyového momentu + knm ) Sestvení fiktivního nosníku eho ztížení momentovým orzem výpočet fiktivníh sil: 6 [knm Fiktivní nosník: [ knm m m w = 0 w = 0 8 [knm ) ýsledné hodnoty pootočení průhyu volného kone konzoly w 6 8 (znménko minus oznčue směr průhyu nhoru)
8 Příkld oené řešení Určete w
9 Příkld - číselně 4 m = knm = 0 = 0 ohrovou metodou určete: - průhy w n volném koni; - pootočení volného kone. w ) Stnovení rekí vyřešení průěhu ohyového momentu + knm ) Sestvení fiktivního nosníku eho ztížení momentovým orzem výpočet fiktivníh sil: 4 [knm Fiktivní nosník: [ knm 4 m w = 0 w = [knm ) ýsledné hodnoty pootočení průhyu volného kone konzoly w 4 (znménko minus oznčue směr průhyu nhoru)
10 Příkld oené řešení určete w
11 Příkld 4 - číselně = knm = knm ohrovou metodou určete: - průhy w n volném koni; - pootočení volného kone. w m m ) Stnovení rekí vyřešení průěhu ohyového momentu Fiktivní nosník: + [ knm m m w = 0 w = 0 ) Sestvení fiktivního nosníku eho ztížení momentovým orzem výpočet fiktivníh sil: 6 [knm 6 [knm ) ýsledné hodnoty pootočení průhyu volného kone konzoly w 6 6 (znménko minus oznčue směr průhyu nhoru)
12 Příkld 4 oené řešení Určete w
13 Příkld 5 - číselně w=0 w=0 d e R ohyová čár Fiktivní nosník: ohrovou metodou určete: - průhy w ve středu nosníku; - pootočení v podporáh. 6 ) Stnovení rekí vyřešení průěhu [knm Q Q [ knm =0 =0 d w d + 6 R ohyového momentu ) Sestvení fiktivního nosníku, eho ztížení momentovým orzem fiktivní vnitřní síly R R 6 [knm R 6 Q, ,5 7 [knm d wd w ) ýsledné hodnoty pootočení průhyu
14 Příkld 5 oené řešení určete w
15 Příkld 6 - složitěší F F R l l [knm ohrovou metodou určete průhy w pootočení volného kone konzoly. Stnovení rekí vyřešení průěhu ohyového momentu R F 0 F l R [knm Q l Q =0 =0 Sestvení fiktivního nosníku eho ztížení momentovým orzem ( ) l l [knm Q l 8 [knm Q 4
16 [knm Q Q Sttiké řešení fiktivního nosníku užití ohrovýh vět R l 5 R Q Q [knm Q l Q l l 4 l 8 l l [knm 5 8 w 7 6
17 Příkld 7- vnitřní podpor w=0 w=0 w =0 =0
18
Stanovení přetvoření ohýbaných nosníků. Clebschova a Mohrova metoda
 Stnovení přetvoření ohýnýh nosníků Ceshov Mohrov metod (pokrčování) (Mohrov nogie) Příkd Určete rovnii ohyové čáry pootočení nosníku stáého průřezu Ceshovou metodou. Stnovte veikost průhyu w pootočení
Stnovení přetvoření ohýnýh nosníků Ceshov Mohrov metod (pokrčování) (Mohrov nogie) Příkd Určete rovnii ohyové čáry pootočení nosníku stáého průřezu Ceshovou metodou. Stnovte veikost průhyu w pootočení
Téma Přetvoření nosníků namáhaných ohybem
 Pružnost plsticit,.ročník bklářského studi Tém Přetvoření nosníků nmáhných ohbem Zákldní vth předpokld řešení Přetvoření nosníků od nerovnoměrného oteplení etod přímé integrce diferenciální rovnice ohbové
Pružnost plsticit,.ročník bklářského studi Tém Přetvoření nosníků nmáhných ohbem Zákldní vth předpokld řešení Přetvoření nosníků od nerovnoměrného oteplení etod přímé integrce diferenciální rovnice ohbové
SMR 2. Pavel Padevět
 SR 2 Pvel Pevět PRINCIP VIRTUÁLNÍCH PRACÍ Silová meto Rámová konstruke, symetriké konstruke Prinipy pro symetriké konstruke ztížené oeným ztížením. Symetriká konstruke ntimetriké ztížení. Os symetrie
SR 2 Pvel Pevět PRINCIP VIRTUÁLNÍCH PRACÍ Silová meto Rámová konstruke, symetriké konstruke Prinipy pro symetriké konstruke ztížené oeným ztížením. Symetriká konstruke ntimetriké ztížení. Os symetrie
5 kn/m. E = 10GPa. 50 kn/m. a b c 0,1 0,1. 30 kn. b c. Statika stavebních konstrukcí I. Příklad č. 1 Posun na nosníku
 Sttik stveníh konstrukí I Příkl č. 1 Posun n nosníku Metoou jenotkovýh ztížení určete voorovný posun ou nosníku pole orázku. Nosník je vyroen z měkkého řev o moulu pružnosti 10 GP. 50 kn/m E = 10GP 0,1
Sttik stveníh konstrukí I Příkl č. 1 Posun n nosníku Metoou jenotkovýh ztížení určete voorovný posun ou nosníku pole orázku. Nosník je vyroen z měkkého řev o moulu pružnosti 10 GP. 50 kn/m E = 10GP 0,1
Podepření - 3 vazby, odebrány 3 volnosti, staticky určitá úloha
 nitřní síly Prut v rovině 3 volnosti Podepření - 3 vzy, oderány 3 volnosti, sttiky určitá úloh nější ztížení reke musí ýt v rovnováze, 3 podmínky rovnováhy, z nih 3 neznámé reke nější ztížení reke se nzývjí
nitřní síly Prut v rovině 3 volnosti Podepření - 3 vzy, oderány 3 volnosti, sttiky určitá úloh nější ztížení reke musí ýt v rovnováze, 3 podmínky rovnováhy, z nih 3 neznámé reke nější ztížení reke se nzývjí
Výpočet vnitřních sil I
 Stvení sttik, 1.ročník klářského studi ýpočet vnitřních sil I přímý nosník, ztížení odové nitřní síly - zákldní pojmy ýpočet vnitřních sil přímého vodorovného nosníku Ktedr stvení mechniky Fkult stvení,
Stvení sttik, 1.ročník klářského studi ýpočet vnitřních sil I přímý nosník, ztížení odové nitřní síly - zákldní pojmy ýpočet vnitřních sil přímého vodorovného nosníku Ktedr stvení mechniky Fkult stvení,
Téma 9 Přetvoření nosníků namáhaných ohybem II.
 Pružnost psticit,.ročník kářského studi Tém 9 Přetvoření nosníků nmáhných ohem. ohrov metod Přetvoření nosníků proměnného průřeu Sttick neurčité přípd ohu Viv smku n přetvoření ohýného nosníku Ktedr stvení
Pružnost psticit,.ročník kářského studi Tém 9 Přetvoření nosníků nmáhných ohem. ohrov metod Přetvoření nosníků proměnného průřeu Sttick neurčité přípd ohu Viv smku n přetvoření ohýného nosníku Ktedr stvení
Výpočet vnitřních sil přímého nosníku
 Stvení sttik, 1.ročník klářského studi ýpočet vnitřních sil přímého nosníku nitřní síly přímého vodorovného nosníku prostý nosník konzol nosník s převislým koncem Ktedr stvení mechniky Fkult stvení, ŠB
Stvení sttik, 1.ročník klářského studi ýpočet vnitřních sil přímého nosníku nitřní síly přímého vodorovného nosníku prostý nosník konzol nosník s převislým koncem Ktedr stvení mechniky Fkult stvení, ŠB
Rovinné nosníkové soustavy
 Stvení sttik,.ročník kominovného studi Rovinné nosníkové soustvy Složené rovinné nosníkové soustvy Sttiká určitost neurčitost rovinnýh soustv Trojklouový rám Trojklouový rám s táhlem Ktedr stvení mehniky
Stvení sttik,.ročník kominovného studi Rovinné nosníkové soustvy Složené rovinné nosníkové soustvy Sttiká určitost neurčitost rovinnýh soustv Trojklouový rám Trojklouový rám s táhlem Ktedr stvení mehniky
Výpočet vnitřních sil přímého nosníku I
 Stvení sttik, 1.ročník kominovného studi ýpočet vnitřních sil přímého nosníku I ýpočet vnitřních sil přímého vodorovného nosníku Ktedr stvení mechniky Fkult stvení, ŠB - Technická univerzit Ostrv nitřní
Stvení sttik, 1.ročník kominovného studi ýpočet vnitřních sil přímého nosníku I ýpočet vnitřních sil přímého vodorovného nosníku Ktedr stvení mechniky Fkult stvení, ŠB - Technická univerzit Ostrv nitřní
Příklad 1 Osově namáhaný prut průběhy veličin
 Příkld 1 Osově nmáhný prut průběhy veličin Zdání Oelový sloup složený ze dvou částí je neposuvně ukotven n obou koníh v tuhém rámu. Dolní část je vysoká, m je z průřezu 1 - HEB 16 (průřezová ploh A b =
Příkld 1 Osově nmáhný prut průběhy veličin Zdání Oelový sloup složený ze dvou částí je neposuvně ukotven n obou koníh v tuhém rámu. Dolní část je vysoká, m je z průřezu 1 - HEB 16 (průřezová ploh A b =
Trojkloubový nosník. Rovinné nosníkové soustavy
 Stvení sttik, 1.ročník klářského studi Rovinné nosníkové soustvy Trojklouový nosník Složené rovinné nosníkové soustvy Sttiká určitost neurčitost rovinnýh soustv Trojklouový nosník Trojklouový nosník Ktedr
Stvení sttik, 1.ročník klářského studi Rovinné nosníkové soustvy Trojklouový nosník Složené rovinné nosníkové soustvy Sttiká určitost neurčitost rovinnýh soustv Trojklouový nosník Trojklouový nosník Ktedr
Redukční věta princip
 SA Přednáška 4 Redukční věta Staticky neurčité příhradové konstrukce Spojité nosníky Uzavřené rámy Oecné vlastnosti staticky neurčitých konstrukcí Copyright (c) Vít Šmilauer Czech Technical University
SA Přednáška 4 Redukční věta Staticky neurčité příhradové konstrukce Spojité nosníky Uzavřené rámy Oecné vlastnosti staticky neurčitých konstrukcí Copyright (c) Vít Šmilauer Czech Technical University
Posouvající síla V. R a. R b. osa nosníku. Kladné směry kolmé složky vnitřních sil. Výpočet nosníku v příčné úloze (ve svislé hlavní rovině xz)
 Posouvjící sí Posouvjící síu v zdném průřezu c ze vypočítt jko gerický součet všech svisých si po jedné strně průřezu. Postupujei se z evé strny, do součtu se zhrnou kdně síy půsoící zdo nhoru, záporně
Posouvjící sí Posouvjící síu v zdném průřezu c ze vypočítt jko gerický součet všech svisých si po jedné strně průřezu. Postupujei se z evé strny, do součtu se zhrnou kdně síy půsoící zdo nhoru, záporně
Pohybové možnosti volných hmotných objektů v rovině
 REAKCE Pohyové možnosti volných hmotných ojektů v rovině Stupeň volnosti n v : možnost vykont jednu složku posunu v ose souřdného systému neo pootočení. +x volný hmotný od v rovině: n v =2 (posun v oecném
REAKCE Pohyové možnosti volných hmotných ojektů v rovině Stupeň volnosti n v : možnost vykont jednu složku posunu v ose souřdného systému neo pootočení. +x volný hmotný od v rovině: n v =2 (posun v oecném
Pohybové možnosti volných hmotných objektů v rovině
 REAKCE ohyové možnosti volných hmotných ojektů v rovině Stupeň volnosti n v : možnost vykont jednu složku posunu v ose souřdného systému neo pootočení. m [00] +x volný hmotný od v rovině: n v =2 (posun
REAKCE ohyové možnosti volných hmotných ojektů v rovině Stupeň volnosti n v : možnost vykont jednu složku posunu v ose souřdného systému neo pootočení. m [00] +x volný hmotný od v rovině: n v =2 (posun
Rovinné nosníkové soustavy Gerberův nosník
 Stvení sttik, 1.ročník klářského stui Rovinné nosníkové soustvy Gererův nosník Spojitý nosník s vloženými klouy - Gererův nosník Kter stvení mehniky Fkult stvení, VŠB - Tehniká univerzit Ostrv Sttiky neurčité
Stvení sttik, 1.ročník klářského stui Rovinné nosníkové soustvy Gererův nosník Spojitý nosník s vloženými klouy - Gererův nosník Kter stvení mehniky Fkult stvení, VŠB - Tehniká univerzit Ostrv Sttiky neurčité
Řešte daný nosník: a = 2m, b = 2m, c = 1m, F 1 = 10kN, F 2 = 20kN
 Řešte dný nosník: m, m, m, F kn, F kn yhom nl kompletně slové účnky půsoíí n nosník, nejprve vyšetříme reke v uloženíh. ek určíme npříkld momentové podmínky rovnováhy k odu. F F F ( ) ( ) F( ) 8 ( ) 5
Řešte dný nosník: m, m, m, F kn, F kn yhom nl kompletně slové účnky půsoíí n nosník, nejprve vyšetříme reke v uloženíh. ek určíme npříkld momentové podmínky rovnováhy k odu. F F F ( ) ( ) F( ) 8 ( ) 5
Téma 1 Obecná deformační metoda, podstata DM
 Sttik stveních konstrukcí II., 3.ročník klářského studi Tém 1 Oecná deformční metod, podstt D Zákldní informce o výuce hodnocení předmětu SSK II etody řešení stticky neurčitých konstrukcí Vznik vývoj deformční
Sttik stveních konstrukcí II., 3.ročník klářského studi Tém 1 Oecná deformční metod, podstt D Zákldní informce o výuce hodnocení předmětu SSK II etody řešení stticky neurčitých konstrukcí Vznik vývoj deformční
 Í ř Á Á Č Č ř Š ó ř Č ř š ř ů ř ň ň ň ř Ž Ž Ž ň ř ť ň Ť ř ř ů ř ř Ž ř š ň É ó Ť š š ř ř ř š ř ř ř ř š ř š ř ř š ř š š ř ť ř ň š ř ř ť ř ř š Ť ř ř ř š ř Ť š ř ř ř š ř š ř ř ř š ů ř š ř ř š ř ř š ř ř ť š
Í ř Á Á Č Č ř Š ó ř Č ř š ř ů ř ň ň ň ř Ž Ž Ž ň ř ť ň Ť ř ř ů ř ř Ž ř š ň É ó Ť š š ř ř ř š ř ř ř ř š ř š ř ř š ř š š ř ť ř ň š ř ř ť ř ř š Ť ř ř ř š ř Ť š ř ř ř š ř š ř ř ř š ů ř š ř ř š ř ř š ř ř ť š
Předpoklad: pružné chování materiálu. počet neznámých > počet podmínek rovnováhy. Řešení:
 Sttiky neurčité přípdy thu prostého tlku u pružnýh prutů Sttiky neurčité úlohy Předpokld: pružné hování mteriálu Sttiky neurčité úlohy: počet nenámýh > počet podmínek rovnováhy Řešení: počet nenámýh podmínky
Sttiky neurčité přípdy thu prostého tlku u pružnýh prutů Sttiky neurčité úlohy Předpokld: pružné hování mteriálu Sttiky neurčité úlohy: počet nenámýh > počet podmínek rovnováhy Řešení: počet nenámýh podmínky
Téma 8 Přetvoření nosníků namáhaných ohybem I.
 Pružnost psticit, ročník kářského studi Tém 8 Přetvoření nosníků nmáhných ohem Zákdní vzth předpokd řešení Přetvoření nosníků od nerovnoměrného otepení etod přímé integrce diferenciání rovnice ohové čár
Pružnost psticit, ročník kářského studi Tém 8 Přetvoření nosníků nmáhných ohem Zákdní vzth předpokd řešení Přetvoření nosníků od nerovnoměrného otepení etod přímé integrce diferenciání rovnice ohové čár
Téma Přetvoření nosníků namáhaných ohybem
 Pružnost psticit,.ročník bkářského studi Tém Přetvoření nosníků nmáhných ohbem Přetvoření nosníků - tížení nerovnoměrnou tepotou Přetvoření nosníků tížení siové Zákdní vth předpokd řešení Vth mei sttickými
Pružnost psticit,.ročník bkářského studi Tém Přetvoření nosníků nmáhných ohbem Přetvoření nosníků - tížení nerovnoměrnou tepotou Přetvoření nosníků tížení siové Zákdní vth předpokd řešení Vth mei sttickými
- Ohybový moment zleva:
 příkl 1 q = 10k/m =0 1) Ohněte směry rekí z pomínek rovnováhy určete jejih velikost, proveďte kontrolu ) ykreslete průěhy vnitřníh sil jejih honoty určete ve všeh vyznčenýh oeh,,. R z R Reke z pomínek
příkl 1 q = 10k/m =0 1) Ohněte směry rekí z pomínek rovnováhy určete jejih velikost, proveďte kontrolu ) ykreslete průěhy vnitřníh sil jejih honoty určete ve všeh vyznčenýh oeh,,. R z R Reke z pomínek
Obecná a zjednodušená deformační metoda
 SMA Přednášk 06 Oená zjednodušená deformční metod Pruty typu VV, KV, VK Sttiká kondenze Konové síly n prutu od ztížení Konové síly n prutu od teploty Příkldy Copyright ) 01 Vít Šmiluer Czeh Tehnil University
SMA Přednášk 06 Oená zjednodušená deformční metod Pruty typu VV, KV, VK Sttiká kondenze Konové síly n prutu od ztížení Konové síly n prutu od teploty Příkldy Copyright ) 01 Vít Šmiluer Czeh Tehnil University
Trojkloubový nosník. Rovinné nosníkové soustavy
 Stvení sttik, 1.ročník klářského stui Rovinné nosníkové soustvy Trojklouový nosník Složené rovinné nosníkové soustvy Sttiká určitost neurčitost rovinnýh soustv Trojklouový nosník Kter stvení mehniky Fkult
Stvení sttik, 1.ročník klářského stui Rovinné nosníkové soustvy Trojklouový nosník Složené rovinné nosníkové soustvy Sttiká určitost neurčitost rovinnýh soustv Trojklouový nosník Kter stvení mehniky Fkult
PŘETVOŘENÍ PŘÍHRADOVÝCH KONSTRUKCÍ
 Zdání PŘETVOŘENÍ PŘÍHRADOVÝCH KONSTRUKCÍ Příkd č. Uvžujte příhrdovou konstruki z Or., vypočítejte svisý posun v odě (znčený ). odře vyznčené pruty (pruty 3, 4, 5, 6 7) jsou ztíženy rovnoměrným otepením
Zdání PŘETVOŘENÍ PŘÍHRADOVÝCH KONSTRUKCÍ Příkd č. Uvžujte příhrdovou konstruki z Or., vypočítejte svisý posun v odě (znčený ). odře vyznčené pruty (pruty 3, 4, 5, 6 7) jsou ztíženy rovnoměrným otepením
Přednáška 1 Obecná deformační metoda, podstata DM
 Statika stavebních konstrukcí II., 3.ročník bakalářského studia Přednáška 1 Obecná deformační metoda, podstata DM Základní informace o výuce předmětu SSK II Metody řešení staticky neurčitých konstrukcí
Statika stavebních konstrukcí II., 3.ročník bakalářského studia Přednáška 1 Obecná deformační metoda, podstata DM Základní informace o výuce předmětu SSK II Metody řešení staticky neurčitých konstrukcí
SMR 2. Pavel Padevět
 SR Pve Pevět PRINCIP VIRTUÁLNÍCH PRACÍ Deformční meto jenošená eformční meto, Přetvárně nerčité konstrke POROVNÁNÍ OBECNÉ A JEDNODUŠENÉ DEF. ETODY V zjenošené eformční metoě (D) se zneává viv normáovýh
SR Pve Pevět PRINCIP VIRTUÁLNÍCH PRACÍ Deformční meto jenošená eformční meto, Přetvárně nerčité konstrke POROVNÁNÍ OBECNÉ A JEDNODUŠENÉ DEF. ETODY V zjenošené eformční metoě (D) se zneává viv normáovýh
Rovinné nosníkové soustavy. Pohyblivé zatížení. Trojkloubový nosník s táhlem Rovinně zakřivený nosník (oblouk) Příčinkové čáry
 Stvení sttik,.ročník kářského studi Rovinné nosníkové soustvy Pohyivé ztížení Trojkouový nosník s táhem Rovinně zkřivený nosník (oouk) Příčinkové čáry Ktedr stvení mehniky Fkut stvení, VŠB - Tehniká univerzit
Stvení sttik,.ročník kářského studi Rovinné nosníkové soustvy Pohyivé ztížení Trojkouový nosník s táhem Rovinně zkřivený nosník (oouk) Příčinkové čáry Ktedr stvení mehniky Fkut stvení, VŠB - Tehniká univerzit
Přetvořené ose nosníku říkáme ohybová čára. Je to rovinná křivka.
 OHYBOVÁ ČÁRA ZA PROSTÉHO OHYBU - rovinné průřez zůstávají po deformaci rovinnými, avšak natáčejí se. - při prostém ohbu hlavní centrální osa setrvačnosti všech průřezů leží v rovině vnějších sil, která
OHYBOVÁ ČÁRA ZA PROSTÉHO OHYBU - rovinné průřez zůstávají po deformaci rovinnými, avšak natáčejí se. - při prostém ohbu hlavní centrální osa setrvačnosti všech průřezů leží v rovině vnějších sil, která
Nosné stavební konstrukce Výpočet reakcí
 Stvení sttik 1.ročník klářského studi Nosné stvení konstrukce Výpočet rekcí Reálné ztížení nosných stveních konstrukcí Prut geometrický popis vnější vzy nehynost silové ztížení složky rekcí Ktedr stvení
Stvení sttik 1.ročník klářského studi Nosné stvení konstrukce Výpočet rekcí Reálné ztížení nosných stveních konstrukcí Prut geometrický popis vnější vzy nehynost silové ztížení složky rekcí Ktedr stvení
Spojitý nosník. Příklady
 Spojitý nosník Příklady Příklad, zadání A = konst. =, m I = konst. =,6 m 4 E = konst. = GPa q =kn / m F kn 3 = M = 5kNm F = 5kN 8 F3 = 8kN 4,5 . způsob řešení n p = (nepočítáme pootočení ve styčníku č.3)
Spojitý nosník Příklady Příklad, zadání A = konst. =, m I = konst. =,6 m 4 E = konst. = GPa q =kn / m F kn 3 = M = 5kNm F = 5kN 8 F3 = 8kN 4,5 . způsob řešení n p = (nepočítáme pootočení ve styčníku č.3)
Pruty namáhané. prostým tahem a tlakem. staticky neurčité úlohy
 Pruty nmáhné prostým them tlkem stticky neurčité úlohy Stticky neurčité úlohy Předpokld: pružné chování mteriálu Stticky neurčité úlohy: počet neznámých > počet podmínek rovnováhy Řešení: počet neznámých
Pruty nmáhné prostým them tlkem stticky neurčité úlohy Stticky neurčité úlohy Předpokld: pružné chování mteriálu Stticky neurčité úlohy: počet neznámých > počet podmínek rovnováhy Řešení: počet neznámých
Rovinné nosníkové soustavy Gerberův nosník
 Stvení sttik, 1.ročník klářského stui Rovinné nosníkové soustvy Gererův nosník Spojitý nosník s vloženými klouy - Gererův nosník Kter stvení mehniky Fkult stvení, VŠB - Tehniká univerzit Ostrv Opkování
Stvení sttik, 1.ročník klářského stui Rovinné nosníkové soustvy Gererův nosník Spojitý nosník s vloženými klouy - Gererův nosník Kter stvení mehniky Fkult stvení, VŠB - Tehniká univerzit Ostrv Opkování
Podmínky k získání zápočtu
 Podmínky k získání zápočtu 18 až 35 bodů 7 % aktivní účast, omluvená neúčast Odevzdání programů Testy: 8 nepovinných testů (-2 body nebo -3 body) 3 povinné testy s ohodnocením 5 bodů (povoleny 2 opravné
Podmínky k získání zápočtu 18 až 35 bodů 7 % aktivní účast, omluvená neúčast Odevzdání programů Testy: 8 nepovinných testů (-2 body nebo -3 body) 3 povinné testy s ohodnocením 5 bodů (povoleny 2 opravné
Přednáška 4 ODM, řešení rovinných rámů
 Sttik tveníh kontrkí II.,.ročník kářkého tdi Přednášk 4 OD, řešení rovinnýh rámů rnforme prmetrů deforme konovýh i z okáního do goáního ořdniového ytém zpět Goání mtie thoti goání vektor konovýh i prt
Sttik tveníh kontrkí II.,.ročník kářkého tdi Přednášk 4 OD, řešení rovinnýh rámů rnforme prmetrů deforme konovýh i z okáního do goáního ořdniového ytém zpět Goání mtie thoti goání vektor konovýh i prt
Výpočet vnitřních sil přímého nosníku III: šikmý nosník
 Stvení sttik,.ročník klářského studi Výpočet vnitřníh sil přímého nosníku III: šikmý nosník Výpočet vnitřníh sil šikmého nosníku - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku
Stvení sttik,.ročník klářského studi Výpočet vnitřníh sil přímého nosníku III: šikmý nosník Výpočet vnitřníh sil šikmého nosníku - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku
VÝPOČET PŘETVOŘENÍ NA STATICKY URIČTÝCH PŘÍMÝCH NOSNÍCÍCH
 Mioš Hüttner SMR přetvoření přímýh nosníků vičení VÝPOČET PŘETVOŘENÍ NA STATICKY URIČTÝCH PŘÍMÝCH NOSNÍCÍCH Zaání Příka č. 1 Vpočítejte maimání průh nosníku o rozpětí zatíženého uprostře siou, viz Or.
Mioš Hüttner SMR přetvoření přímýh nosníků vičení VÝPOČET PŘETVOŘENÍ NA STATICKY URIČTÝCH PŘÍMÝCH NOSNÍCÍCH Zaání Příka č. 1 Vpočítejte maimání průh nosníku o rozpětí zatíženého uprostře siou, viz Or.
Stavební statika. Úvod do studia předmětu na Stavební fakultě VŠB-TU Ostrava. Stavební statika, 1.ročník kombinovaného studia
 Stvební sttik, 1.ročník kombinovného studi Stvební sttik Úvod do studi předmětu n Stvební fkultě VŠB-TU Ostrv Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit Ostrv Stvební sttik přednášející
Stvební sttik, 1.ročník kombinovného studi Stvební sttik Úvod do studi předmětu n Stvební fkultě VŠB-TU Ostrv Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit Ostrv Stvební sttik přednášející
Pohyblivé zatížení. Pohyblivé zatížení. Příčinkové čáry na prostém nosníku, konzole a spojitém nosníku s vloženými klouby
 Stvní sttik,.ročník kářského stui Pohyivé ztížní zniká pojížěním vozi (vky, utomoiy, jřáy po stvní konstruki (mosty, jřáové ráhy, nájzové rmpy, pohy gráží. Pohyivé ztížní n prostém nosníku, konzo spojitém
Stvní sttik,.ročník kářského stui Pohyivé ztížní zniká pojížěním vozi (vky, utomoiy, jřáy po stvní konstruki (mosty, jřáové ráhy, nájzové rmpy, pohy gráží. Pohyivé ztížní n prostém nosníku, konzo spojitém
SMR 2. Pavel Padevět
 SR Pve Pevět Přenášk č. Přenášk č. PRINCIP VIRTUÁLNÍCH PRCÍ Výpočet přetvoření n sttk určtý konstrukí Přenášk č. Dopňková vrtuání práe momentů Vv n výpočet eformí: oment Posouvjíí sí Normáové sí (přírové
SR Pve Pevět Přenášk č. Přenášk č. PRINCIP VIRTUÁLNÍCH PRCÍ Výpočet přetvoření n sttk určtý konstrukí Přenášk č. Dopňková vrtuání práe momentů Vv n výpočet eformí: oment Posouvjíí sí Normáové sí (přírové
Stavební mechanika, 2.ročník bakalářského studia AST. Téma 4 Rovinný rám
 Stvební mechnik,.ročník bklářského studi AST Tém 4 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit
Stvební mechnik,.ročník bklářského studi AST Tém 4 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit
Téma 4 Rovinný rám Základní vlastnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzavřený rám
 Sttik stvebních konstrukcí I.,.ročník bklářského studi Tém 4 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická
Sttik stvebních konstrukcí I.,.ročník bklářského studi Tém 4 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická
Stavební mechanika 2 (K132SM02)
 Stvení mecnik 2 (K132SM02) Přednáší: Jn Sýkor Ktedr mecniky K132 místnost D2016 e-mil: jn.sykor.1@fsv.cvut.cz konzultční odiny: Po 12-14 Kldné směry vnitřníc sil: Kldný průřez vnitřní síly jsou kldné ve
Stvení mecnik 2 (K132SM02) Přednáší: Jn Sýkor Ktedr mecniky K132 místnost D2016 e-mil: jn.sykor.1@fsv.cvut.cz konzultční odiny: Po 12-14 Kldné směry vnitřníc sil: Kldný průřez vnitřní síly jsou kldné ve
Šikmý nosník rovnoměrné spojité zatížení. L průmětu. zatížení kolmé ke střednici prutu (vítr)
 Šikmý nosník Šikmý nosník rovnoměrné spojité ztížení ztížení kolmé ke střednii prutu (vítr) q h - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku prutu (vlstní tíh) - ztížení svislé
Šikmý nosník Šikmý nosník rovnoměrné spojité ztížení ztížení kolmé ke střednii prutu (vítr) q h - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku prutu (vlstní tíh) - ztížení svislé
Zesilování dřevěného prvku uhlíkovou lamelou při dolním líci. Zde budou normové hodnoty vypsány do tabulky!!!
 Zesilování dřevěného prvku uhlíkovou lamelou při dolním líci jméno: stud. skupina: příjmení: pořadové číslo: datum: Materiály: Lepené lamelové dřevo třídy GL 36h : norma ČSN EN 1194 (najít si hodnotu modulu
Zesilování dřevěného prvku uhlíkovou lamelou při dolním líci jméno: stud. skupina: příjmení: pořadové číslo: datum: Materiály: Lepené lamelové dřevo třídy GL 36h : norma ČSN EN 1194 (najít si hodnotu modulu
Osově namáhaný prut základní veličiny
 Pružnost a pevnost BD0 Osově namáhaný prut základní velčny ormálová síla půsoící v průřezu osově namáhaného prutu se získá ntegrací normálového napětí po ploše průřezu. da A Vzhledem k rovnoměrnému rozložení
Pružnost a pevnost BD0 Osově namáhaný prut základní velčny ormálová síla půsoící v průřezu osově namáhaného prutu se získá ntegrací normálového napětí po ploše průřezu. da A Vzhledem k rovnoměrnému rozložení
KVADRATICKÁ FUNKCE (vlastnosti, grafy)
 KVADRATICKÁ FUNKCE (vlstnosti, gr) Teorie Kvdrtikou unkí se nzývá kždá unke dná předpisem ; R,, R; D( ) je proměnná z příslušného deiničního ooru unke (nejčstěji množin R),, jsou koeiient kvdrtiké unke,
KVADRATICKÁ FUNKCE (vlstnosti, gr) Teorie Kvdrtikou unkí se nzývá kždá unke dná předpisem ; R,, R; D( ) je proměnná z příslušného deiničního ooru unke (nejčstěji množin R),, jsou koeiient kvdrtiké unke,
ZDM PŘÍMÉ NOSNÍKY. Příklad č. 1. Miloš Hüttner SMR2 ZDM přímé nosníky cvičení 09. Zadání
 iloš Hüttner SR D přímé nosníky cvičení 09 adání D PŘÍÉ NOSNÍKY Příklad č. 1 Vykreslete průběhy vnitřních sil na konstrukci zobrazené na Obr. 1. Příklad převzat z katedrové wikipedie (originál ke stažení
iloš Hüttner SR D přímé nosníky cvičení 09 adání D PŘÍÉ NOSNÍKY Příklad č. 1 Vykreslete průběhy vnitřních sil na konstrukci zobrazené na Obr. 1. Příklad převzat z katedrové wikipedie (originál ke stažení
Rekapitulace princip virtuálních sil pro tah/tlak
 SMA Přednáška Doplňková virtuální práce momentů Metody integrace dvou spojitých funkcí Doplňková virtuální práce posouvajících sil Vliv rovnoměrné a nerovnoměrné teploty Formulace principu virtuálních
SMA Přednáška Doplňková virtuální práce momentů Metody integrace dvou spojitých funkcí Doplňková virtuální práce posouvajících sil Vliv rovnoměrné a nerovnoměrné teploty Formulace principu virtuálních
Výpočet vnitřních sil přímého nosníku III: šikmý nosník
 Stvení sttik,.ročník klářského studi Výpočet vnitřníh sil přímého nosníku III: šikmý nosník Výpočet vnitřníh sil šikmého nosníku - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku
Stvení sttik,.ročník klářského studi Výpočet vnitřníh sil přímého nosníku III: šikmý nosník Výpočet vnitřníh sil šikmého nosníku - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku
 Á Í Č Ě Č ň ť Š Č Ť ň ň ď Ť Ú ť Č ň ď ť Č Š Ž Ú Ť Ť Ť Ť ň Ť Ť ť Ť Ť Á Ť Ť Ť ď Ť Ť Ť Ť Ť Ť Ť Ť Ť ň ďť Ť Ť Ť Š Š Š ď ň Č Š ň Š ť Š ň Š Š Ť Ť Ť Ť Ť Ť Ť Ť Ť Ť Ť Ť Ť Ť Ť Ú Š ň ť ť Š ň Š Ž ť ť ť ň Š Č Š Š Í
Á Í Č Ě Č ň ť Š Č Ť ň ň ď Ť Ú ť Č ň ď ť Č Š Ž Ú Ť Ť Ť Ť ň Ť Ť ť Ť Ť Á Ť Ť Ť ď Ť Ť Ť Ť Ť Ť Ť Ť Ť ň ďť Ť Ť Ť Š Š Š ď ň Č Š ň Š ť Š ň Š Š Ť Ť Ť Ť Ť Ť Ť Ť Ť Ť Ť Ť Ť Ť Ť Ú Š ň ť ť Š ň Š Ž ť ť ť ň Š Č Š Š Í
Pružnost a plasticita Program č.2. Fotografie reálné konstrukce
 Jméno: Suijní skupin : úerý 14.15 soupu = 2.50 m D = 0.25 m = 100 kn Při výpoču vsupních hono pí priori násoení, rozměry uveené konsrukce jsou v [m] zížení v [kn] [kn/m]. Součinie nhoiého zížení je γ Q
Jméno: Suijní skupin : úerý 14.15 soupu = 2.50 m D = 0.25 m = 100 kn Při výpoču vsupních hono pí priori násoení, rozměry uveené konsrukce jsou v [m] zížení v [kn] [kn/m]. Součinie nhoiého zížení je γ Q
Ohýbaný nosník - napětí
 Pružnost pevnost BD0 Ohýbný nosník - npětí Teorie Prostý ohb, rovinný ohb Při prostém ohbu je průřez nmáhán ohbovým momentem otáčejícím kolem jedné z hlvních os setrvčnosti průřezu, obvkle os. oment se
Pružnost pevnost BD0 Ohýbný nosník - npětí Teorie Prostý ohb, rovinný ohb Při prostém ohbu je průřez nmáhán ohbovým momentem otáčejícím kolem jedné z hlvních os setrvčnosti průřezu, obvkle os. oment se
PRUŽNOST A PLASTICITA
 PRUŽOST A PLASTICITA Ing. Lenk Lusová LPH 407/1 Povinná litertur tel. 59 732 1326 lenk.lusov@vs.cz http://fst10.vs.cz/lusov http://mi21.vs.cz/modul/pruznost-plsticit Doporučená litertur Zákldní typy nmáhání
PRUŽOST A PLASTICITA Ing. Lenk Lusová LPH 407/1 Povinná litertur tel. 59 732 1326 lenk.lusov@vs.cz http://fst10.vs.cz/lusov http://mi21.vs.cz/modul/pruznost-plsticit Doporučená litertur Zákldní typy nmáhání
* Modelování (zjednodušení a popis) tvaru konstrukce. pruty
 2. VNITŘNÍ SÍLY PRUTU 2.1 Úvod * Jak konstrukce přenáší atížení do vaeb/podpor? Jak jsou prvky konstrukce namáhány? * Modelování (jednodušení a popis) tvaru konstrukce. pruty 1 Prut: konstrukční prvek,
2. VNITŘNÍ SÍLY PRUTU 2.1 Úvod * Jak konstrukce přenáší atížení do vaeb/podpor? Jak jsou prvky konstrukce namáhány? * Modelování (jednodušení a popis) tvaru konstrukce. pruty 1 Prut: konstrukční prvek,
Složené soustavy. Úloha: Sestavení statického schématu, tj. modelu pro statický výpočet (např.výpočet reakcí)
 Složené soustavy Vznikají spojením jednotlivých konstrukčních prvků Úloha: Sestavení statického schématu, tj. modelu pro statický výpočet (např.výpočet reakcí) Metoda: Konstrukci idealizujeme jako soustavu
Složené soustavy Vznikají spojením jednotlivých konstrukčních prvků Úloha: Sestavení statického schématu, tj. modelu pro statický výpočet (např.výpočet reakcí) Metoda: Konstrukci idealizujeme jako soustavu
Téma 8 Příčně zatížený rám a rošt
 Statika stavebních konstrukcí I.,.ročník bakalářského studia Téma 8 Příčně zatížený rám a rošt Základní vlastnosti příčně zatíženého rámu Jednoduchý příčně zatížený otevřený rám Základní vlastnosti roštu
Statika stavebních konstrukcí I.,.ročník bakalářského studia Téma 8 Příčně zatížený rám a rošt Základní vlastnosti příčně zatíženého rámu Jednoduchý příčně zatížený otevřený rám Základní vlastnosti roštu
Betonové konstrukce (S) Přednáška 3
 Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Platnost Bernoulli Navierovy hypotézy
 Přednáška 0 Platnost Bernoulli Navierovy hypotézy Diferenciální rovnice ohybu prutu Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Vliv teploty na průhyb a křivost prutu Příklady
Přednáška 0 Platnost Bernoulli Navierovy hypotézy Diferenciální rovnice ohybu prutu Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Vliv teploty na průhyb a křivost prutu Příklady
FAKULTA STAVEBNÍ. Stavební statika. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Přednáška 2 pro kombinované studium Jiří Brožovský Kancelář: LP C 303/1 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Přednáška 2 pro kombinované studium Jiří Brožovský Kancelář: LP C 303/1 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí
 Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr.
 . cvičení Klopení nosníků Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr. Ilustrace klopení Obr. Ohýbaný prut a tvar jeho ztráty
. cvičení Klopení nosníků Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr. Ilustrace klopení Obr. Ohýbaný prut a tvar jeho ztráty
Statika 1. Reakce na rovinných staticky určitých konstrukcích. Miroslav Vokáč ČVUT v Praze, Fakulta architektury.
 reálných 3. přednáška Reakce na rovinných staticky určitých konstrukcích Miroslav Vokáč miroslav.vokac@cvut.cz ČVUT v Praze, Fakulta architektury 21. března 2016 Dřevěný trámový strop - Anežský klášter
reálných 3. přednáška Reakce na rovinných staticky určitých konstrukcích Miroslav Vokáč miroslav.vokac@cvut.cz ČVUT v Praze, Fakulta architektury 21. března 2016 Dřevěný trámový strop - Anežský klášter
Statický výpočet komínové výměny a stropního prostupu (vzorový příklad)
 KERAMICKÉ STROPY HELUZ MIAKO Tabulky statických únosností stropy HELUZ MIAKO Obsah tabulka č. 1 tabulka č. 2 tabulka č. 3 tabulka č. 4 tabulka č. 5 tabulka č. 6 tabulka č. 7 tabulka č. 8 tabulka č. 9 tabulka
KERAMICKÉ STROPY HELUZ MIAKO Tabulky statických únosností stropy HELUZ MIAKO Obsah tabulka č. 1 tabulka č. 2 tabulka č. 3 tabulka č. 4 tabulka č. 5 tabulka č. 6 tabulka č. 7 tabulka č. 8 tabulka č. 9 tabulka
Stavební statika. Úvod do studia předmětu na Stavební fakultě VŠB-TU Ostrava. Letní semestr. Stavební statika, 1.ročník bakalářského studia
 Stvení sttik, 1.ročník klářského studi Stvení sttik Úvod do studi předmětu n Stvení fkultě VŠB-TU Ostrv Letní semestr Ktedr stvení mechniky Fkult stvení, VŠB - Technická univerzit Ostrv Stvení sttik -
Stvení sttik, 1.ročník klářského studi Stvení sttik Úvod do studi předmětu n Stvení fkultě VŠB-TU Ostrv Letní semestr Ktedr stvení mechniky Fkult stvení, VŠB - Technická univerzit Ostrv Stvení sttik -
Rovinné nosníkové soustavy
 Stvení sttik, 1.ročník kominovného stui Rovinné nosníkové soustvy Složené rovinné nosníkové soustvy Sttiká určitost neurčitost rovinnýh soustv Gererův nosník Trojklouový rám Trojklouový rám s táhlem Kter
Stvení sttik, 1.ročník kominovného stui Rovinné nosníkové soustvy Složené rovinné nosníkové soustvy Sttiká určitost neurčitost rovinnýh soustv Gererův nosník Trojklouový rám Trojklouový rám s táhlem Kter
Návrh a posudek osově namáhaného nosníku podle obou MS
 Návrh a posudek osově namáhaného nosníku podle obou MS 1) Statický rozbor 2) Dobře pochopit zadání definovat, v jakých hodnotách počítat (charakteristické x návrh.) 2) MSÚ nutný průřez dle MSÚ a) pevnost
Návrh a posudek osově namáhaného nosníku podle obou MS 1) Statický rozbor 2) Dobře pochopit zadání definovat, v jakých hodnotách počítat (charakteristické x návrh.) 2) MSÚ nutný průřez dle MSÚ a) pevnost
Příklad 7 Průhyb nosníku - složitější případ
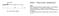 Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Téma 12, modely podloží
 Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Stavební mechanika 2 (K132SM02)
 Stavební mechanika 2 (K132SM02) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 místnost D2034 e-mail: matej.leps@fsv.cvut.cz konzultační hodiny budou upřesněny později https://mech.fsv.cvut.cz/student/
Stavební mechanika 2 (K132SM02) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 místnost D2034 e-mail: matej.leps@fsv.cvut.cz konzultační hodiny budou upřesněny později https://mech.fsv.cvut.cz/student/
Posouzení trapézového plechu - VUT FAST KDK Ondřej Pešek Draft 2017
 Posouzení trapézového plechu - UT FAST KDK Ondřej Pešek Draft 017 POSOUENÍ TAPÉOÉHO PLECHU SLOUŽÍCÍHO JAKO TACENÉ BEDNĚNÍ Úkolem je posoudit trapézový plech typu SŽ 11 001 v mezním stavu únosnosti a mezním
Posouzení trapézového plechu - UT FAST KDK Ondřej Pešek Draft 017 POSOUENÍ TAPÉOÉHO PLECHU SLOUŽÍCÍHO JAKO TACENÉ BEDNĚNÍ Úkolem je posoudit trapézový plech typu SŽ 11 001 v mezním stavu únosnosti a mezním
Vnitřní síly v prutových konstrukcích
 Vnitřní síly v prutových konstrukcích Síla je vektorová fyikální veličina, která vyjadřuje míru působení těles nebo polí. Zavedení síly v klasické Newtonově mechanice (popis pohybu těles) dp dv F = = m
Vnitřní síly v prutových konstrukcích Síla je vektorová fyikální veličina, která vyjadřuje míru působení těles nebo polí. Zavedení síly v klasické Newtonově mechanice (popis pohybu těles) dp dv F = = m
Téma 5 Spojitý nosník
 Sttik stveních konstukcí..očník kářského studi Tém 5 Sojitý nosník Zákdní vstnosti sojitého nosníku Řešení sojitého nosníku siovou metodou yužití symetie sojitého nosníku Příčinkové čáy nhodié ztížení
Sttik stveních konstukcí..očník kářského studi Tém 5 Sojitý nosník Zákdní vstnosti sojitého nosníku Řešení sojitého nosníku siovou metodou yužití symetie sojitého nosníku Příčinkové čáy nhodié ztížení
Téma 5 Rovinný rám. Základní vlastnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzavřený rám
 Stvební mechnik,.ročník bklářského studi AST Tém 5 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit
Stvební mechnik,.ročník bklářského studi AST Tém 5 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit
Výpočet nosníku na pružném podloží Výsledky
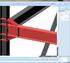 Praha 5 Slivenec Výpočet nosníku na pružném podloží Výsledky Výpočet byl proveden. Typická kombinace pro výpočet podloží : MSP: Q3:G1+G2+Q4 Výpočet 1 Název : Analysis Výpočet 1 Obálka MSÚ 7,22
Praha 5 Slivenec Výpočet nosníku na pružném podloží Výsledky Výpočet byl proveden. Typická kombinace pro výpočet podloží : MSP: Q3:G1+G2+Q4 Výpočet 1 Název : Analysis Výpočet 1 Obálka MSÚ 7,22
-R x,a. Příklad 2. na nejbližší vyšší celý mm) 4) Výpočet skutečné plochy A skut 5) Výpočet maximálního napětíσ max 6) Porovnání napětí. Výsl.
 Zákdy dimenzování prutu nmáhného prostým tkem them Th prostý tk-zákdy dimenzování Už známe:, 3 -, i i 3 3 ormáové npětí [P] konst. po výšce průřezu Deformce [m] ii E ově zákdní vzthy: Průřezová chrkteristik
Zákdy dimenzování prutu nmáhného prostým tkem them Th prostý tk-zákdy dimenzování Už známe:, 3 -, i i 3 3 ormáové npětí [P] konst. po výšce průřezu Deformce [m] ii E ově zákdní vzthy: Průřezová chrkteristik
JEDNODUCHÝ INTEGRÁL příklady. pro vysoké školy
 JEDNODUCHÝ INTEGRÁL příkldy pro vysoké školy Bohemicus mthemticus doctor Pvel Novotný 0 Vzor citce: NOVOTNÝ, P. Jednoduchý integrál příkldy : pro vysoké školy. Bučovice : Nkldtelství Mrtin Stříž, 0. 6
JEDNODUCHÝ INTEGRÁL příkldy pro vysoké školy Bohemicus mthemticus doctor Pvel Novotný 0 Vzor citce: NOVOTNÝ, P. Jednoduchý integrál příkldy : pro vysoké školy. Bučovice : Nkldtelství Mrtin Stříž, 0. 6
SMR 2. Pavel Padevět
 SR Pve Pevět PRICIP VIRTUÁLÍCH PRACÍ jenošená eformční meto, esiové vivy, Sčítání účinků ztížení ezi nesiové vivy vžjeme v D: viv posntí popor, viv tepoty. ESILOVÉ VLIVY Popštění popory vyvoává v sttiky
SR Pve Pevět PRICIP VIRTUÁLÍCH PRACÍ jenošená eformční meto, esiové vivy, Sčítání účinků ztížení ezi nesiové vivy vžjeme v D: viv posntí popor, viv tepoty. ESILOVÉ VLIVY Popštění popory vyvoává v sttiky
Úloha 5 - Návrh sedlového vazníku
 Úloha 5 - Návredlového vazníku V 6 6:57:7-5_Sedlovy vaznik.sm Zatížení a součinitele: Třída_provozu Třída_trvání_zatížení Nejnepříznivější kominace návrhového zatížení, % stálého a 6% sněhu (ze zadání):...
Úloha 5 - Návredlového vazníku V 6 6:57:7-5_Sedlovy vaznik.sm Zatížení a součinitele: Třída_provozu Třída_trvání_zatížení Nejnepříznivější kominace návrhového zatížení, % stálého a 6% sněhu (ze zadání):...
( ) ( ) Sinová věta II. β je úhel z intervalu ( 0;π ). Jak je vidět z jednotkové kružnice, úhly, pro které platí. Předpoklady:
 4.4. Sinová vět II Předpokldy 44 Kde se stl hy? Námi nlezené řešení je správné, le nenšli jsme druhé hy ve hvíli, kdy jsme z hodnoty sin β určovli úhel β. β je úhel z intervlu ( ;π ). Jk je vidět z jednotkové
4.4. Sinová vět II Předpokldy 44 Kde se stl hy? Námi nlezené řešení je správné, le nenšli jsme druhé hy ve hvíli, kdy jsme z hodnoty sin β určovli úhel β. β je úhel z intervlu ( ;π ). Jk je vidět z jednotkové
Smyková napětí v ohýbaných nosnících
 Pružnost a plasticita, 2.ročník kominovaného studia Smková napětí v ohýaných nosnících Základní vtah a předpoklad řešení ýpočet smkového napětí odélníkového průřeu Dimenování nosníků namáhaných na smk
Pružnost a plasticita, 2.ročník kominovaného studia Smková napětí v ohýaných nosnících Základní vtah a předpoklad řešení ýpočet smkového napětí odélníkového průřeu Dimenování nosníků namáhaných na smk
Kapitola 4. Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena. Každý prut v rovině má 3 volnosti (kap.1).
 Kapitola 4 Vnitřní síly přímého vodorovného nosníku 4.1 Analýza vnitřních sil na rovinných nosnících Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena rekapitulace
Kapitola 4 Vnitřní síly přímého vodorovného nosníku 4.1 Analýza vnitřních sil na rovinných nosnících Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena rekapitulace
Téma 6 Staticky neurčitý rovinný oblouk. kloubový příhradový nosník
 Stvení mechnik,.ročník klářského studi AST Tém 6 Stticky neurčitý rovinný olouk Stticky neurčitý rovinný klouový příhrdový nosník Zákldní vlstnosti stticky neurčitého rovinného olouku Dvoklouový olouk,
Stvení mechnik,.ročník klářského studi AST Tém 6 Stticky neurčitý rovinný olouk Stticky neurčitý rovinný klouový příhrdový nosník Zákldní vlstnosti stticky neurčitého rovinného olouku Dvoklouový olouk,
Výpočet přetvoření a dimenzování pilotové skupiny
 Inženýrský manuál č. 18 Aktualizace: 08/2018 Výpočet přetvoření a dimenzování pilotové skupiny Program: Soubor: Skupina pilot Demo_manual_18.gsp Cílem tohoto inženýrského manuálu je vysvětlit použití programu
Inženýrský manuál č. 18 Aktualizace: 08/2018 Výpočet přetvoření a dimenzování pilotové skupiny Program: Soubor: Skupina pilot Demo_manual_18.gsp Cílem tohoto inženýrského manuálu je vysvětlit použití programu
Platnost Bernoulli Navierovy hypotézy
 Přednáška 03 Diferenciální rovnice ohybu prutu Platnost Bernoulli Navierovy hypotézy Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Příklady Copyright (c) 011 Vít Šmilauer
Přednáška 03 Diferenciální rovnice ohybu prutu Platnost Bernoulli Navierovy hypotézy Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Příklady Copyright (c) 011 Vít Šmilauer
SLOUP NAMÁHANÝ TLAKEM A OHYBEM
 SOUP NAMÁHANÝ TAKEM A OHYBEM Posuďte únosnost centrick tlačeného sloupu délk 50 m profil HEA 4 ocel S 55 00 00. Schéma podepření a atížení je vidět na následujícím obráku: M 0 M N N N 5m 5m schéma pro
SOUP NAMÁHANÝ TAKEM A OHYBEM Posuďte únosnost centrick tlačeného sloupu délk 50 m profil HEA 4 ocel S 55 00 00. Schéma podepření a atížení je vidět na následujícím obráku: M 0 M N N N 5m 5m schéma pro
Zjednodušená deformační metoda (2):
 Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
ZATĚŽOVACÍ ZKOUŠKY. Obr. 1. Statická zatěžovací zkouška; zatížení (N) zatlačení (cm)
 ZATĚŽOVACÍ ZKOUŠKY ZATĚŽOVACÍ ZKOUŠKY Sttiká ztěžoví zkoušk položí poklníh vrstev Zřízení - ztěžoví (nákl. uto, ztěžoví most) - kruh. ztěžoví esk (mlá, velká) - kulový kloub - ynmometr - průhyboměr - tuhý
ZATĚŽOVACÍ ZKOUŠKY ZATĚŽOVACÍ ZKOUŠKY Sttiká ztěžoví zkoušk položí poklníh vrstev Zřízení - ztěžoví (nákl. uto, ztěžoví most) - kruh. ztěžoví esk (mlá, velká) - kulový kloub - ynmometr - průhyboměr - tuhý
1. výpočet reakcí R x, R az a R bz - dle kapitoly 3, q = q cosα (5.1) kolmých (P ). iz = P iz sinα (5.2) iz = P iz cosα (5.3) ix = P ix cosα (5.
 Kapitola 5 Vnitřní síly přímého šikmého nosníku Pojem šikmý nosník je používán dle publikace [1] pro nosník ležící v souřadnicové rovině xz, který je vůči vodorovné ose x pootočen o úhel α. Pro šikmou
Kapitola 5 Vnitřní síly přímého šikmého nosníku Pojem šikmý nosník je používán dle publikace [1] pro nosník ležící v souřadnicové rovině xz, který je vůči vodorovné ose x pootočen o úhel α. Pro šikmou
Střední škola obchodu, řemesel, služeb a Základní škola, Ústí nad Labem, příspěvková organizace Vzdělávací středisko Trmice
 Střední škol ohodu, řemesel, služe Zákldní škol, Ústí nd Lem, příspěvková orgnize Vzděláví středisko Trmie MATURITNÍ TÉMATA Předmět: Mtemtik Oor vzdělání: Ekonomik podnikání Školní rok: 0/06 Tříd: EKP
Střední škol ohodu, řemesel, služe Zákldní škol, Ústí nd Lem, příspěvková orgnize Vzděláví středisko Trmie MATURITNÍ TÉMATA Předmět: Mtemtik Oor vzdělání: Ekonomik podnikání Školní rok: 0/06 Tříd: EKP
Výpočet vnitřních sil lomeného nosníku
 Stvní sttik, 1.ročník klářského stui ýpočt vnitřníh sil lomného nosníku omný nosník v rovinné úloz Kontrol rovnováhy uvolněného styčníku nitřní síly n uvolněném prutu rostorově lomný nosník Ktr stvní mhniky
Stvní sttik, 1.ročník klářského stui ýpočt vnitřníh sil lomného nosníku omný nosník v rovinné úloz Kontrol rovnováhy uvolněného styčníku nitřní síly n uvolněném prutu rostorově lomný nosník Ktr stvní mhniky
Rovinné nosníkové soustavy III Příhradový nosník
 Stvení sttik,.ročník klářského stui Rovinné nosníkové soustvy III Příhrový nosník Rovinný klouový příhrový nosník Skl rovinného příhrového nosníku Pomínk sttiké určitosti příhrového nosníku Zjenoušená
Stvení sttik,.ročník klářského stui Rovinné nosníkové soustvy III Příhrový nosník Rovinný klouový příhrový nosník Skl rovinného příhrového nosníku Pomínk sttiké určitosti příhrového nosníku Zjenoušená
Schöck Isokorb typ K. Schöck Isokorb typ K
 Schöck Isokorb typ Schöck Isokorb typ (konzola) Používá se u volně vyložených ů. Přenáší záporné ohybové momenty a kladné posouvající síly. Prvek Schöck Isokorb typ třídy únosnosti ve smyku VV přenáší
Schöck Isokorb typ Schöck Isokorb typ (konzola) Používá se u volně vyložených ů. Přenáší záporné ohybové momenty a kladné posouvající síly. Prvek Schöck Isokorb typ třídy únosnosti ve smyku VV přenáší
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady. Část 1 - Test
 Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Téma 5 Spojitý nosník
 Stvení mechnik.očník kářského studi AST Tém 5 Spojitý nosník Zákdní vstnosti spojitého nosníku Řešení spojitého nosníku siovou metodou yužití symetie spojitého nosníku Kted stvení mechniky Fkut stvení
Stvení mechnik.očník kářského studi AST Tém 5 Spojitý nosník Zákdní vstnosti spojitého nosníku Řešení spojitého nosníku siovou metodou yužití symetie spojitého nosníku Kted stvení mechniky Fkut stvení
Zjednodušená styčníková metoda
 Stvní sttik, 1.ročník klářského stui Rovinné nosníkové soustvy III Příhrový nosník Zjnoušná styčníková mto Rovinný klouový příhrový nosník Skl rovinného příhrového nosníku Pomínk sttiké určitosti příhrového
Stvní sttik, 1.ročník klářského stui Rovinné nosníkové soustvy III Příhrový nosník Zjnoušná styčníková mto Rovinný klouový příhrový nosník Skl rovinného příhrového nosníku Pomínk sttiké určitosti příhrového


