Téma Přetvoření nosníků namáhaných ohybem
|
|
|
- Adam Čech
- před 6 lety
- Počet zobrazení:
Transkript
1 Pružnost psticit,.ročník bkářského studi Tém Přetvoření nosníků nmáhných ohbem Přetvoření nosníků - tížení nerovnoměrnou tepotou Přetvoření nosníků tížení siové Zákdní vth předpokd řešení Vth mei sttickými přetvárnými veičinmi etod přímé integrce diferenciání rovnice ohbové čár SU úoh Ktedr stvební mechnik Fkut stvební, VŠB - Technická univerit Ostrv
2 Přetvoření nosníků nmáhných ohbem tížení siové Tto obrák (přetvoření prostého nosníku kono) včetně nčení jsou tbuek více vi přednášk
3 Přetvoření nosníků nmáhných ohbem ohbová čár Je-i nosník dosttečně štíhý, určuje deformční stv křivk, do níž přejde původně přímá os nosníku vivem tížení. pooměr křivosti r w q b j U ohýbných nosníků definujeme druh přetvoření: w... j... průhb (kdný směr doů) pootočení, w Teorie mých deformcí: tg j j w 3
4 4 d r dw r r 1 E r. 1 w d d j w u d d u w u r j E w Vth mei sttickými přetvárnými veičinmi
5 Vth mei sttickými přetvárnými veičinmi E. Nm ohbová tuhost prutu tíženého v rovině Při E.... konst. Vcháí diferenciání podmínk rovnováh přímého nosníku (Schwederov vth) Ohb ve svisé rovině : (derivčně integrční schém) dv d q d d V q w b j 5
6 Přímá integrce diferenciání rovnice ohbové čár Vužití: sttick určité přípd ohýbných nosníků v ideáním přípdě momentová funkce spojitá E. E.. w. w E.. w.d C Nm 1.d.d C E.. w 1. C Diferenciání rovnice ohbové čár (.řádu) C 1,C... integrční konstnt ntegrční konstnt C 1, C se určí deformčních okrjových podmínek, v tomto přípdě deformčních okrjových podmínek: b b w 0 w 0 w 0, w 0 éně čsto používná DP: os smetrie w 0 6
7 Příkd Zdání: určete rovnici ohbové čár Rekce: R b R b R R b Vnitřní sí: V - L L V R R.. konst. R V + E.. w. Řešení: etod přímé integrce diferenciání rovnice ohbové čár 7
8 ntegrce E.. w E.. w Příkd určení integrčních konstnt C 1 C. b R R b E.. w nenámé integrční konstnt e určit deformčních okrjových podmínek: Okrjové deformční podmínk C 1, C w 0 0 w 0 etod přímé integrce diferenciání rovnice ohbové čár 8
9 Příkd výsedné rovnice ohbové čár pootočení Výsedné rovnice (po dosení): Ptí pro: 0, w 1 E E Rovnice ohbové čár w 1 E E.. 3 Funkce pro výpočet pootočení skon tečn ohbové čár Závěr: Vrůstjící řád ponomů jednotivých veičin Největší průhb v místě kde je nuová první derivce, tj. pootočení (podobně jko největší tm, kde V=0) Ponom stupně n n+1 n+ n+3 n+4 ntegrce q V j w 1º q=konst. q=0 º 3º 1º º 0º 1º 4º 3º º 5º 4º 3º Derivce etod přímé integrce diferenciání rovnice ohbové čár 9
10 Příkd k dopnění řešené probemtik e skript možnost superpoice tížení 10
11 Příkd k dopnění řešené probemtik tbuek 11
12 Návrh posudek ohýbného nosníku de obou S Postup příkdu přednášk ptí obecně vžd 1) Sttický robor ) SÚ nutný průře de SÚ ) Ed b) W,nut c) npř. PN nut, nebo d nut, nut 3) SP nutný průře de SP ) momentová funkce obecně b) integrce momentové funkce c) okrjové podmínk integrční konstnt d) dosení integrčních konstnt do rovnic w (průhbu), w (pootočení) e) obecné vjádření přetvoření (w nebo φ) pro poždovné místo f),nut g) npř. PN nut, nebo d nut, nut 4) Návrh průřeu ) určit rohodující průře b) stnovit skutečné průřeové chrkteristik 5) Posudek dného průřeu ) výpočet Rd posoudit, d Rd > Ed b) výpočet w skut posoudit, d w im >w skut 1
13 Příkd 1 návrh posouení ohýbného nosníku pode obou meních stvů Nvrhněte posuďte dný nosník pode obou meních stvů. Dáno: =6m, q k = 10kN/m, w im = /00, E=, P, S75, γ G = 1,35, γ = 1,00. 1) -profi q m = Ed = 1/8q d = 7,9 knm 1) = 6 m m W, nut Ed e W ení stv únosnosti Ed W, nut f Ed.. pro 1 -profi Počítt s q d! Návrh: -PN.: =.10-5 = m 4 13
14 Příkd návrh posouení ohýbného nosníku pode obou meních stvů ení stv použitenosti: q = 6 m Počítt s q k! 6 wim 0, 03m qk wm wim 384 E qk E 4 0, 03 nut qk E w 4 im 1), nut.. Pro 1 -profi,skut tbuek Návrh: -PN.: =.10-5 = m 4 14
15 Příkd návrh posouení ohýbného nosníku pode obou meních stvů Konečný návrh pode obou meních stvů: 1) Návrh: PN-180: W =.1, = 3,.10-4 m 4 Posouení: 1) SÚ: SP: Rd =f d W = ,.10-4 =88,55kNm> Ed = 60,8kNm 4 5 qk wm 0, 08m wim 0, 030m 384 E 15
16 Přetvoření nosníků nmáhných ohbem - tížení nerovnoměrnou tepotou 1. w r h T T h výšk prutu 16
17 Npětí nerovnoměrně otepeného prutu 17
18 Okruh probémů k ústní části koušk 1. Nerovnoměrné otepení nosníků. Zákdní tp prutů nmáhných ohbem tížení siové 3. Přetvoření ohýbných nosníků, ohbová čár 4. Vth mei sttickými přetvárnými veičinmi 5. Ohbová tuhost, diferenciání rovnice ohbové čár 6. etod přímé integrce diferenciání rovnice ohbové čár sttick určitých nosníků 7. Návrh posudek ohýbného nosníku pode meního stvu použitenosti 8. Návrh posudek ohýbného nosníku pode obou S 18
Téma Přetvoření nosníků namáhaných ohybem
 Pružnost plsticit,.ročník bklářského studi Tém Přetvoření nosníků nmáhných ohbem Zákldní vth předpokld řešení Přetvoření nosníků od nerovnoměrného oteplení etod přímé integrce diferenciální rovnice ohbové
Pružnost plsticit,.ročník bklářského studi Tém Přetvoření nosníků nmáhných ohbem Zákldní vth předpokld řešení Přetvoření nosníků od nerovnoměrného oteplení etod přímé integrce diferenciální rovnice ohbové
Téma 8 Přetvoření nosníků namáhaných ohybem I.
 Pružnost psticit, ročník kářského studi Tém 8 Přetvoření nosníků nmáhných ohem Zákdní vzth předpokd řešení Přetvoření nosníků od nerovnoměrného otepení etod přímé integrce diferenciání rovnice ohové čár
Pružnost psticit, ročník kářského studi Tém 8 Přetvoření nosníků nmáhných ohem Zákdní vzth předpokd řešení Přetvoření nosníků od nerovnoměrného otepení etod přímé integrce diferenciání rovnice ohové čár
Téma 9 Přetvoření nosníků namáhaných ohybem II.
 Pružnost psticit,.ročník kářského studi Tém 9 Přetvoření nosníků nmáhných ohem. ohrov metod Přetvoření nosníků proměnného průřeu Sttick neurčité přípd ohu Viv smku n přetvoření ohýného nosníku Ktedr stvení
Pružnost psticit,.ročník kářského studi Tém 9 Přetvoření nosníků nmáhných ohem. ohrov metod Přetvoření nosníků proměnného průřeu Sttick neurčité přípd ohu Viv smku n přetvoření ohýného nosníku Ktedr stvení
Posouvající síla V. R a. R b. osa nosníku. Kladné směry kolmé složky vnitřních sil. Výpočet nosníku v příčné úloze (ve svislé hlavní rovině xz)
 Posouvjící sí Posouvjící síu v zdném průřezu c ze vypočítt jko gerický součet všech svisých si po jedné strně průřezu. Postupujei se z evé strny, do součtu se zhrnou kdně síy půsoící zdo nhoru, záporně
Posouvjící sí Posouvjící síu v zdném průřezu c ze vypočítt jko gerický součet všech svisých si po jedné strně průřezu. Postupujei se z evé strny, do součtu se zhrnou kdně síy půsoící zdo nhoru, záporně
-R x,a. Příklad 2. na nejbližší vyšší celý mm) 4) Výpočet skutečné plochy A skut 5) Výpočet maximálního napětíσ max 6) Porovnání napětí. Výsl.
 Zákdy dimenzování prutu nmáhného prostým tkem them Th prostý tk-zákdy dimenzování Už známe:, 3 -, i i 3 3 ormáové npětí [P] konst. po výšce průřezu Deformce [m] ii E ově zákdní vzthy: Průřezová chrkteristik
Zákdy dimenzování prutu nmáhného prostým tkem them Th prostý tk-zákdy dimenzování Už známe:, 3 -, i i 3 3 ormáové npětí [P] konst. po výšce průřezu Deformce [m] ii E ově zákdní vzthy: Průřezová chrkteristik
Stabilita a vzpěrná pevnost tlačených prutů
 Pružnost psticit,.ročník kářského studi Stiit vzpěrná pevnost tčených prutů Euerovo řešení stiity přímého pružného prutu Ztrát stiity prutů v pružno-pstickém ooru Posouzení oceových konstrukcí n vzpěr
Pružnost psticit,.ročník kářského studi Stiit vzpěrná pevnost tčených prutů Euerovo řešení stiity přímého pružného prutu Ztrát stiity prutů v pružno-pstickém ooru Posouzení oceových konstrukcí n vzpěr
Téma 2 Úvod ke staticky neurčitým prutovým konstrukcím
 Stvební mechnik,.ročník bkářského studi AST Tém Úvod ke stticky neurčitým prutovým konstrukcím Ktedr stvební mechniky Fkut stvební, VŠB - Technická univerzit Ostrv Osnov přednášky Stticky neurčité konstrukce,
Stvební mechnik,.ročník bkářského studi AST Tém Úvod ke stticky neurčitým prutovým konstrukcím Ktedr stvební mechniky Fkut stvební, VŠB - Technická univerzit Ostrv Osnov přednášky Stticky neurčité konstrukce,
Téma 3 Úvod ke staticky neurčitým prutovým konstrukcím
 Sttik stvebních konstrukcí I.,.ročník bkářského studi Tém 3 Úvod ke stticky neurčitým prutovým konstrukcím Ktedr stvební mechniky Fkut stvební, VŠB - Technická univerzit Ostrv Osnov přednášky Stticky neurčité
Sttik stvebních konstrukcí I.,.ročník bkářského studi Tém 3 Úvod ke stticky neurčitým prutovým konstrukcím Ktedr stvební mechniky Fkut stvební, VŠB - Technická univerzit Ostrv Osnov přednášky Stticky neurčité
Téma 6 Staticky neurčitý rovinný oblouk
 ttik stveních konstrukcí I.,.ročník kářského studi Tém 6 tticky neurčitý rovinný oouk Zákdní vstnosti stticky neurčitého rovinného oouku Dvojkouový oouk Dvojkouový oouk s táhem Vetknuté oouky Přiižný výpočet
ttik stveních konstrukcí I.,.ročník kářského studi Tém 6 tticky neurčitý rovinný oouk Zákdní vstnosti stticky neurčitého rovinného oouku Dvojkouový oouk Dvojkouový oouk s táhem Vetknuté oouky Přiižný výpočet
Ohýbaný nosník - napětí
 Pružnost pevnost BD0 Ohýbný nosník - npětí Teorie Prostý ohb, rovinný ohb Při prostém ohbu je průřez nmáhán ohbovým momentem otáčejícím kolem jedné z hlvních os setrvčnosti průřezu, obvkle os. oment se
Pružnost pevnost BD0 Ohýbný nosník - npětí Teorie Prostý ohb, rovinný ohb Při prostém ohbu je průřez nmáhán ohbovým momentem otáčejícím kolem jedné z hlvních os setrvčnosti průřezu, obvkle os. oment se
Stanovení přetvoření ohýbaných nosníků. Clebschova a Mohrova metoda
 Stnovení přetvoření ohýnýh nosníků Ceshov Mohrov metod (pokrčování) (Mohrov nogie) Příkd Určete rovnii ohyové čáry pootočení nosníku stáého průřezu Ceshovou metodou. Stnovte veikost průhyu w pootočení
Stnovení přetvoření ohýnýh nosníků Ceshov Mohrov metod (pokrčování) (Mohrov nogie) Příkd Určete rovnii ohyové čáry pootočení nosníku stáého průřezu Ceshovou metodou. Stnovte veikost průhyu w pootočení
Normálová napětí v prutech namáhaných na ohyb
 Pružnost a plasticita, 2.ročník kombinovaného studia Normálová napětí v prutech namáhaných na ohb Základní vtah a předpoklad řešení Výpočet normálového napětí Dimenování nosníků namáhaných na ohb Složené
Pružnost a plasticita, 2.ročník kombinovaného studia Normálová napětí v prutech namáhaných na ohb Základní vtah a předpoklad řešení Výpočet normálového napětí Dimenování nosníků namáhaných na ohb Složené
Nosné stavební konstrukce, výpočet reakcí
 Stvení sttik.ročník kářského studi Nosná stvení konstrukce Nosné stvení konstrukce výpočet rekcí Nosná stvení konstrukce souží k přenosu ztížení ojektu do horninového msívu n němž je ojekt zožen. Musí
Stvení sttik.ročník kářského studi Nosná stvení konstrukce Nosné stvení konstrukce výpočet rekcí Nosná stvení konstrukce souží k přenosu ztížení ojektu do horninového msívu n němž je ojekt zožen. Musí
Stavební mechanika, 2.ročník bakalářského studia AST. Téma 4 Rovinný rám
 Stvební mechnik,.ročník bklářského studi AST Tém 4 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit
Stvební mechnik,.ročník bklářského studi AST Tém 4 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit
Téma 5 Rovinný rám. Základní vlastnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzavřený rám
 Stvební mechnik,.ročník bklářského studi AST Tém 5 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit
Stvební mechnik,.ročník bklářského studi AST Tém 5 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit
Stavební statika. Úvod do studia předmětu na Stavební fakultě VŠB-TU Ostrava. Stavební statika, 1.ročník kombinovaného studia
 Stvební sttik, 1.ročník kombinovného studi Stvební sttik Úvod do studi předmětu n Stvební fkultě VŠB-TU Ostrv Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit Ostrv Stvební sttik přednášející
Stvební sttik, 1.ročník kombinovného studi Stvební sttik Úvod do studi předmětu n Stvební fkultě VŠB-TU Ostrv Ktedr stvební mechniky Fkult stvební, VŠB - Technická univerzit Ostrv Stvební sttik přednášející
Normálová napětí při ohybu - opakování
 Normálová napětí při ohbu - opakování x ohýbaný nosník: σ x τ x Průřeová charakteristika pro normálová napětí a ohbu je moment setrvačnosti nebo něj odvoený modul průřeu x - / /= Ed W m + σ x napětí normálové
Normálová napětí při ohbu - opakování x ohýbaný nosník: σ x τ x Průřeová charakteristika pro normálová napětí a ohbu je moment setrvačnosti nebo něj odvoený modul průřeu x - / /= Ed W m + σ x napětí normálové
Téma 4 Rovinný rám Základní vlastnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzavřený rám
 Sttik stvebních konstrukcí I.,.ročník bklářského studi Tém 4 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická
Sttik stvebních konstrukcí I.,.ročník bklářského studi Tém 4 Rovinný rám Zákldní vlstnosti rovinného rámu Jednoduchý otevřený rám Jednoduchý uzvřený rám Ktedr stvební mechniky Fkult stvební, VŠB - Technická
Reakce. K618 FD ČVUT v Praze (pracovní verze). Tento materiál má pouze pracovní charakter a bude v průbehu semestru
 Poznámky ke cičení z předmětu Pružnost penost n K8 D ČVUT Prze (prconí erze). Tento mteriá má pouze prconí chrkter bude průbehu semestru postupně dopňoán. utor: Jn Vyčich E mi: ycich@fd.cut.cz Příkd reize:.
Poznámky ke cičení z předmětu Pružnost penost n K8 D ČVUT Prze (prconí erze). Tento mteriá má pouze prconí chrkter bude průbehu semestru postupně dopňoán. utor: Jn Vyčich E mi: ycich@fd.cut.cz Příkd reize:.
Výpočet vnitřních sil přímého nosníku
 Stvení sttik, 1.ročník klářského studi ýpočet vnitřních sil přímého nosníku nitřní síly přímého vodorovného nosníku prostý nosník konzol nosník s převislým koncem Ktedr stvení mechniky Fkult stvení, ŠB
Stvení sttik, 1.ročník klářského studi ýpočet vnitřních sil přímého nosníku nitřní síly přímého vodorovného nosníku prostý nosník konzol nosník s převislým koncem Ktedr stvení mechniky Fkult stvení, ŠB
Přetvořené ose nosníku říkáme ohybová čára. Je to rovinná křivka.
 OHYBOVÁ ČÁRA ZA PROSTÉHO OHYBU - rovinné průřez zůstávají po deformaci rovinnými, avšak natáčejí se. - při prostém ohbu hlavní centrální osa setrvačnosti všech průřezů leží v rovině vnějších sil, která
OHYBOVÁ ČÁRA ZA PROSTÉHO OHYBU - rovinné průřez zůstávají po deformaci rovinnými, avšak natáčejí se. - při prostém ohbu hlavní centrální osa setrvačnosti všech průřezů leží v rovině vnějších sil, která
Téma 5 Spojitý nosník
 Stvení mechnik.očník kářského studi AST Tém 5 Spojitý nosník Zákdní vstnosti spojitého nosníku Řešení spojitého nosníku siovou metodou yužití symetie spojitého nosníku Kted stvení mechniky Fkut stvení
Stvení mechnik.očník kářského studi AST Tém 5 Spojitý nosník Zákdní vstnosti spojitého nosníku Řešení spojitého nosníku siovou metodou yužití symetie spojitého nosníku Kted stvení mechniky Fkut stvení
Pružnost a plasticita II
 Pružnost plsticit II. ročník klářského studi doc. In. Mrtin Krejs, Ph.D. Ktedr stvení mechnik Řešení nosných stěn pomocí Airho funkce npětí inverzní metod Stěnová rovnice ΔΔ(, ) Stěnová rovnice, nzývná
Pružnost plsticit II. ročník klářského studi doc. In. Mrtin Krejs, Ph.D. Ktedr stvení mechnik Řešení nosných stěn pomocí Airho funkce npětí inverzní metod Stěnová rovnice ΔΔ(, ) Stěnová rovnice, nzývná
Předpoklad: pružné chování materiálu. počet neznámých > počet podmínek rovnováhy. Řešení:
 Sttiky neurčité přípdy thu prostého tlku u pružnýh prutů Sttiky neurčité úlohy Předpokld: pružné hování mteriálu Sttiky neurčité úlohy: počet nenámýh > počet podmínek rovnováhy Řešení: počet nenámýh podmínky
Sttiky neurčité přípdy thu prostého tlku u pružnýh prutů Sttiky neurčité úlohy Předpokld: pružné hování mteriálu Sttiky neurčité úlohy: počet nenámýh > počet podmínek rovnováhy Řešení: počet nenámýh podmínky
Rovnoměrně ohýbaný prut
 Přednáška 02 Prostý ohb Hpotéa o achování rovinnosti průřeu Křivost prutu, vtah mei momentem a křivostí Roložení napětí při ohbu Pružný průřeový modul Vliv teplot na křivost Copright (c) 2011 Vít Šmilauer
Přednáška 02 Prostý ohb Hpotéa o achování rovinnosti průřeu Křivost prutu, vtah mei momentem a křivostí Roložení napětí při ohbu Pružný průřeový modul Vliv teplot na křivost Copright (c) 2011 Vít Šmilauer
Pružnost a pevnost. 2. přednáška, 10. října 2016
 Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Smyková napětí v ohýbaných nosnících
 Pružnost a plasticita, 2.ročník kominovaného studia Smková napětí v ohýaných nosnících Základní vtah a předpoklad řešení ýpočet smkového napětí odélníkového průřeu Dimenování nosníků namáhaných na smk
Pružnost a plasticita, 2.ročník kominovaného studia Smková napětí v ohýaných nosnících Základní vtah a předpoklad řešení ýpočet smkového napětí odélníkového průřeu Dimenování nosníků namáhaných na smk
Téma 6 Spojitý nosník
 Stvení mechnik.očník kářského studi AST Tém Sojitý nosník Zákdní vstnosti sojitého nosníku Řešení sojitého nosníku siovou metodou yužití symetie sojitého nosníku Kted stvení mechniky Fkut stvení ŠB - Technická
Stvení mechnik.očník kářského studi AST Tém Sojitý nosník Zákdní vstnosti sojitého nosníku Řešení sojitého nosníku siovou metodou yužití symetie sojitého nosníku Kted stvení mechniky Fkut stvení ŠB - Technická
Téma 6 Staticky neurčitý rovinný oblouk. kloubový příhradový nosník
 Stvení mechnik,.ročník klářského studi AST Tém 6 Stticky neurčitý rovinný olouk Stticky neurčitý rovinný klouový příhrdový nosník Zákldní vlstnosti stticky neurčitého rovinného olouku Dvoklouový olouk,
Stvení mechnik,.ročník klářského studi AST Tém 6 Stticky neurčitý rovinný olouk Stticky neurčitý rovinný klouový příhrdový nosník Zákldní vlstnosti stticky neurčitého rovinného olouku Dvoklouový olouk,
MECHANIKA KONSTRUKCÍ ŘEŠENÍ STATICKY NEURČITÝCH KONSTRUKCÍ. Určení deformací metodou jednotkových sil. Silová metoda Deformační metoda
 ECHANIKA KONSTRUKCÍ ŘEŠENÍ STATICKY NEURČITÝCH KONSTRUKCÍ Určení deformcí metodou jednotkových si Siová metod Deformční metod Deformce (přetvoření) Deformce (přetvoření): ) Ceková podo deformovné konstrukce
ECHANIKA KONSTRUKCÍ ŘEŠENÍ STATICKY NEURČITÝCH KONSTRUKCÍ Určení deformcí metodou jednotkových si Siová metod Deformční metod Deformce (přetvoření) Deformce (přetvoření): ) Ceková podo deformovné konstrukce
Rovinné nosníkové soustavy. Pohyblivé zatížení. Trojkloubový nosník s táhlem Rovinně zakřivený nosník (oblouk) Příčinkové čáry
 Stvení sttik,.ročník kářského studi Rovinné nosníkové soustvy Pohyivé ztížení Trojkouový nosník s táhem Rovinně zkřivený nosník (oouk) Příčinkové čáry Ktedr stvení mehniky Fkut stvení, VŠB - Tehniká univerzit
Stvení sttik,.ročník kářského studi Rovinné nosníkové soustvy Pohyivé ztížení Trojkouový nosník s táhem Rovinně zkřivený nosník (oouk) Příčinkové čáry Ktedr stvení mehniky Fkut stvení, VŠB - Tehniká univerzit
Pružnost a plasticita Program č.1
 Ktedr stvební mecniky Fkut stvební VŠB-TU Ostrv Jméno : Studijní skupin : úterý 14.15 Průřez spodnío pásu Fotogrfie reáné konstrukce Nvrněte posuďte u výše zobrzené rovinné koubové přírdové konstrukce
Ktedr stvební mecniky Fkut stvební VŠB-TU Ostrv Jméno : Studijní skupin : úterý 14.15 Průřez spodnío pásu Fotogrfie reáné konstrukce Nvrněte posuďte u výše zobrzené rovinné koubové přírdové konstrukce
PRUŽNOST A PLASTICITA
 Doporučená itertur PRUŽOST A PLASTICITA Ing. Vdimír Michcová LPH 407/ te. 59 73 348 vdimir.michcov@vs.cz http://fst0.vs.cz/michcov Bend: Stvení sttik I., VŠBTU Ostrv 005 Podmínky zápočtu: Šmířák: Pružnost
Doporučená itertur PRUŽOST A PLASTICITA Ing. Vdimír Michcová LPH 407/ te. 59 73 348 vdimir.michcov@vs.cz http://fst0.vs.cz/michcov Bend: Stvení sttik I., VŠBTU Ostrv 005 Podmínky zápočtu: Šmířák: Pružnost
Ohyb - smyková napětí
 Oh - smková napětí p + + - - l x ohýaný nosník - M σ x - x Průřeové charakteristik pro smková napětí a ohu jsou statický moment ploch S a moment setrvačnosti. S A části průr T [ m ] max Mení stav únosnosti
Oh - smková napětí p + + - - l x ohýaný nosník - M σ x - x Průřeové charakteristik pro smková napětí a ohu jsou statický moment ploch S a moment setrvačnosti. S A části průr T [ m ] max Mení stav únosnosti
Výpočet vnitřních sil I
 Stvení sttik, 1.ročník klářského studi ýpočet vnitřních sil I přímý nosník, ztížení odové nitřní síly - zákldní pojmy ýpočet vnitřních sil přímého vodorovného nosníku Ktedr stvení mechniky Fkult stvení,
Stvení sttik, 1.ročník klářského studi ýpočet vnitřních sil I přímý nosník, ztížení odové nitřní síly - zákldní pojmy ýpočet vnitřních sil přímého vodorovného nosníku Ktedr stvení mechniky Fkult stvení,
SMR 2. Pavel Padevět
 SR Pve Pevět Přenášk č. Přenášk č. PRINCIP VIRTUÁLNÍCH PRCÍ Výpočet přetvoření n sttk určtý konstrukí Přenášk č. Dopňková vrtuání práe momentů Vv n výpočet eformí: oment Posouvjíí sí Normáové sí (přírové
SR Pve Pevět Přenášk č. Přenášk č. PRINCIP VIRTUÁLNÍCH PRCÍ Výpočet přetvoření n sttk určtý konstrukí Přenášk č. Dopňková vrtuání práe momentů Vv n výpočet eformí: oment Posouvjíí sí Normáové sí (přírové
SLOUP NAMÁHANÝ TLAKEM A OHYBEM
 SOUP NAMÁHANÝ TAKEM A OHYBEM Posuďte únosnost centrick tlačeného sloupu délk 50 m profil HEA 4 ocel S 55 00 00. Schéma podepření a atížení je vidět na následujícím obráku: M 0 M N N N 5m 5m schéma pro
SOUP NAMÁHANÝ TAKEM A OHYBEM Posuďte únosnost centrick tlačeného sloupu délk 50 m profil HEA 4 ocel S 55 00 00. Schéma podepření a atížení je vidět na následujícím obráku: M 0 M N N N 5m 5m schéma pro
Elastické deformace těles
 Eastické eformace těes 15 Na oceový rát ék L 15 m a průměru 1 mm zavěsíme závaží o hmotnosti m 110 kg přičemž Youngův mou pružnosti ocei v tahu E 16 GPa a mez pružnosti ocei σ P 0 Pa Určete reativní prooužení
Eastické eformace těes 15 Na oceový rát ék L 15 m a průměru 1 mm zavěsíme závaží o hmotnosti m 110 kg přičemž Youngův mou pružnosti ocei v tahu E 16 GPa a mez pružnosti ocei σ P 0 Pa Určete reativní prooužení
Osové namáhání osová síla N v prutu
 Osové nmáhání osová síl v prutu 3 typy úloh:. Pruty příhrdové konstrukce, táhl Dvě podmínky rovnováhy v kždém styčníku: F ix 0 F iz 0. Táhl podporující pevnou ztíženou desku R z M ib 0 P R R b P 6 6 P
Osové nmáhání osová síl v prutu 3 typy úloh:. Pruty příhrdové konstrukce, táhl Dvě podmínky rovnováhy v kždém styčníku: F ix 0 F iz 0. Táhl podporující pevnou ztíženou desku R z M ib 0 P R R b P 6 6 P
Napětí a únosnost. ohýbaných prutů
 Napětí a únosnost ohýbaných prutů Normálová napětí při ohbu ohýbaný nosník: x V τ x vlákna / max / Ed - - tažná tlačná + tažná tlačná tlačná tažná x Průřová charaktristika pro normálová napětí a ohbu j
Napětí a únosnost ohýbaných prutů Normálová napětí při ohbu ohýbaný nosník: x V τ x vlákna / max / Ed - - tažná tlačná + tažná tlačná tlačná tažná x Průřová charaktristika pro normálová napětí a ohbu j
Výpočet vnitřních sil přímého nosníku II
 Stveí sttik, 1.ročík komiového studi Shwederovy vzthy Difereiáí podmík rovováhy eemetu v osové úoze ýpočet vitříh si přímého osíku II 1 d z d ýpočet vitříh si osíků ztížeýh spojitým ztížeím ýpočet osíku
Stveí sttik, 1.ročík komiového studi Shwederovy vzthy Difereiáí podmík rovováhy eemetu v osové úoze ýpočet vitříh si přímého osíku II 1 d z d ýpočet vitříh si osíků ztížeýh spojitým ztížeím ýpočet osíku
PŘÍKLAD VÝPOČTU RÁMU PODLE ČSN EN
 PŘÍKLAD VÝPOČTU RÁU PODLE ČS E 99-- Jaub Dolejš*), Zdeně Sool**).Zadání avrhněte sloup plnostěnného dvouloubového rámu, jehož roměr jsou patrné obráu. Horní pásnice příčle je po celé délce ajištěna proti
PŘÍKLAD VÝPOČTU RÁU PODLE ČS E 99-- Jaub Dolejš*), Zdeně Sool**).Zadání avrhněte sloup plnostěnného dvouloubového rámu, jehož roměr jsou patrné obráu. Horní pásnice příčle je po celé délce ajištěna proti
PŘETVOŘENÍ PŘÍHRADOVÝCH KONSTRUKCÍ
 Zdání PŘETVOŘENÍ PŘÍHRADOVÝCH KONSTRUKCÍ Příkd č. Uvžujte příhrdovou konstruki z Or., vypočítejte svisý posun v odě (znčený ). odře vyznčené pruty (pruty 3, 4, 5, 6 7) jsou ztíženy rovnoměrným otepením
Zdání PŘETVOŘENÍ PŘÍHRADOVÝCH KONSTRUKCÍ Příkd č. Uvžujte příhrdovou konstruki z Or., vypočítejte svisý posun v odě (znčený ). odře vyznčené pruty (pruty 3, 4, 5, 6 7) jsou ztíženy rovnoměrným otepením
Nosné stavební konstrukce Výpočet reakcí
 Stvení sttik 1.ročník klářského studi Nosné stvení konstrukce Výpočet rekcí Reálné ztížení nosných stveních konstrukcí Prut geometrický popis vnější vzy nehynost silové ztížení složky rekcí Ktedr stvení
Stvení sttik 1.ročník klářského studi Nosné stvení konstrukce Výpočet rekcí Reálné ztížení nosných stveních konstrukcí Prut geometrický popis vnější vzy nehynost silové ztížení složky rekcí Ktedr stvení
Pruty namáhané. prostým tahem a tlakem. staticky neurčité úlohy
 Pruty nmáhné prostým them tlkem stticky neurčité úlohy Stticky neurčité úlohy Předpokld: pružné chování mteriálu Stticky neurčité úlohy: počet neznámých > počet podmínek rovnováhy Řešení: počet neznámých
Pruty nmáhné prostým them tlkem stticky neurčité úlohy Stticky neurčité úlohy Předpokld: pružné chování mteriálu Stticky neurčité úlohy: počet neznámých > počet podmínek rovnováhy Řešení: počet neznámých
Normálové napětí a přetvoření prutu namáhaného tahem (prostým tlakem) - staticky určité úlohy
 Pružnost a pasticita, 2.ročník bakaářského studia ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) - staticky určité úohy Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného
Pružnost a pasticita, 2.ročník bakaářského studia ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) - staticky určité úohy Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného
Cvičení 2 (Složená namáhání)
 VŠB Technická univerit Ostrv kult strojní Ktedr pružnosti pevnosti (339) Pružnost pevnost v energetice (Návod do cvičení) Cvičení (ložená nmáhání) Autor: Jroslv Rojíček Vere: Ostrv 009 ložená nmáhání princip
VŠB Technická univerit Ostrv kult strojní Ktedr pružnosti pevnosti (339) Pružnost pevnost v energetice (Návod do cvičení) Cvičení (ložená nmáhání) Autor: Jroslv Rojíček Vere: Ostrv 009 ložená nmáhání princip
Téma 1 Obecná deformační metoda, podstata DM
 Sttik stveních konstrukcí II., 3.ročník klářského studi Tém 1 Oecná deformční metod, podstt D Zákldní informce o výuce hodnocení předmětu SSK II etody řešení stticky neurčitých konstrukcí Vznik vývoj deformční
Sttik stveních konstrukcí II., 3.ročník klářského studi Tém 1 Oecná deformční metod, podstt D Zákldní informce o výuce hodnocení předmětu SSK II etody řešení stticky neurčitých konstrukcí Vznik vývoj deformční
Výpočet vnitřních sil přímého nosníku I
 Stvení sttik, 1.ročník kominovného studi ýpočet vnitřních sil přímého nosníku I ýpočet vnitřních sil přímého vodorovného nosníku Ktedr stvení mechniky Fkult stvení, ŠB - Technická univerzit Ostrv nitřní
Stvení sttik, 1.ročník kominovného studi ýpočet vnitřních sil přímého nosníku I ýpočet vnitřních sil přímého vodorovného nosníku Ktedr stvení mechniky Fkult stvení, ŠB - Technická univerzit Ostrv nitřní
Vnitřní síly v prutových konstrukcích
 Vnitřní síly v prutových konstrukcích Síla je vektorová fyikální veličina, která vyjadřuje míru působení těles nebo polí. Zavedení síly v klasické Newtonově mechanice (popis pohybu těles) dp dv F = = m
Vnitřní síly v prutových konstrukcích Síla je vektorová fyikální veličina, která vyjadřuje míru působení těles nebo polí. Zavedení síly v klasické Newtonově mechanice (popis pohybu těles) dp dv F = = m
Téma 7 Smyková napětí v ohýbaných nosnících
 Pružnost a plasticita,.ročník bakalářského studia Téma 7 Smková napětí v ohýbaných nosnících Základní vtah a předpoklad řešení Výpočet smkového napětí vbraných průřeů Dimenování nosníků namáhaných na smk
Pružnost a plasticita,.ročník bakalářského studia Téma 7 Smková napětí v ohýbaných nosnících Základní vtah a předpoklad řešení Výpočet smkového napětí vbraných průřeů Dimenování nosníků namáhaných na smk
SMR 2. Pavel Padevět
 SR Pve Pdevět PRICIP VIRTUÁLÍCH PRACÍ Deformční metod tice thosti prt, princip virtáních posnů PRICIP VIRTUÁLÍCH POSUUTÍ (oecný princip rovnováhy) Stečný stv E; A [] Virtání práce vnějších posntí W e
SR Pve Pdevět PRICIP VIRTUÁLÍCH PRACÍ Deformční metod tice thosti prt, princip virtáních posnů PRICIP VIRTUÁLÍCH POSUUTÍ (oecný princip rovnováhy) Stečný stv E; A [] Virtání práce vnějších posntí W e
Příklad 1 Osově namáhaný prut průběhy veličin
 Příkld 1 Osově nmáhný prut průběhy veličin Zdání Oelový sloup složený ze dvou částí je neposuvně ukotven n obou koníh v tuhém rámu. Dolní část je vysoká, m je z průřezu 1 - HEB 16 (průřezová ploh A b =
Příkld 1 Osově nmáhný prut průběhy veličin Zdání Oelový sloup složený ze dvou částí je neposuvně ukotven n obou koníh v tuhém rámu. Dolní část je vysoká, m je z průřezu 1 - HEB 16 (průřezová ploh A b =
Pružnost, pevnost, plasticita
 Pružnost, pevnost, plasticita Pracovní vere výukového skripta 22. února 2018 c Milan Jirásek, Vít Šmilauer, Jan Zeman České vsoké učení technické v Prae Fakulta stavební Katedra mechanik hákurova 7 166
Pružnost, pevnost, plasticita Pracovní vere výukového skripta 22. února 2018 c Milan Jirásek, Vít Šmilauer, Jan Zeman České vsoké učení technické v Prae Fakulta stavební Katedra mechanik hákurova 7 166
Výpočet vnitřních sil přímého nosníku II
 Stveí sttik, 1.ročík kářského studi ýpočet vitřích si přímého osíku II ýpočet vitřích si osíků ztížeých spojitým ztížeím: příčé kosttí trojúheíkové spojité ztížeí, spojité ztížeí v osové úoze, mometové
Stveí sttik, 1.ročík kářského studi ýpočet vitřích si přímého osíku II ýpočet vitřích si osíků ztížeých spojitým ztížeím: příčé kosttí trojúheíkové spojité ztížeí, spojité ztížeí v osové úoze, mometové
Řešení úloh celostátního kola 49. ročníku fyzikální olympiády. Autořiúloh:P.Šedivý(1),L.Richterek(2),I.Volf(3)aB.Vybíral(4)
 Řešení úoh ceostátního ko 49. ročníku fyzikání oympiády. Autořiúoh:.Šedivý(1),L.Richterek(),I.Vof(3)B.Vybír(4) 1.) Oznčme t 1, t, t 3čsyzábesků, v 1, v, v 3přísušnérychostistředukoue, veikost zrychení
Řešení úoh ceostátního ko 49. ročníku fyzikání oympiády. Autořiúoh:.Šedivý(1),L.Richterek(),I.Vof(3)B.Vybír(4) 1.) Oznčme t 1, t, t 3čsyzábesků, v 1, v, v 3přísušnérychostistředukoue, veikost zrychení
Normálová napětí při ohybu
 Normálová napětí při ohbu vlákna - tažná tlačná / max / Ed + tlačná - tažná tlačná x ohýbaný nosník: x V τ x Průřová charaktristika pro normálová napětí a ohbu j momnt strvačnosti nbo něj odvoný modul
Normálová napětí při ohbu vlákna - tažná tlačná / max / Ed + tlačná - tažná tlačná x ohýbaný nosník: x V τ x Průřová charaktristika pro normálová napětí a ohbu j momnt strvačnosti nbo něj odvoný modul
Stanovení přetvoření ohýbaných nosníků. Mohrova metoda (Mohrova analogie)
 Stnovení přetvoření ohýnýh nosníků ohrov metod (ohrov nlogie) Přetvoření ohýnýh nosníků Posouzení z hledisk meze použitelnosti Ztížení, deforme w, φ Okrové podmínky (deforme) Šmiřák, S.: Pružnost plstiit
Stnovení přetvoření ohýnýh nosníků ohrov metod (ohrov nlogie) Přetvoření ohýnýh nosníků Posouzení z hledisk meze použitelnosti Ztížení, deforme w, φ Okrové podmínky (deforme) Šmiřák, S.: Pružnost plstiit
Statika 2. Vetknuté nosníky. Miroslav Vokáč 2. listopadu ČVUT v Praze, Fakulta architektury. Statika 2. M.
 3. přednáška Průhybová čára Mirosav Vokáč mirosav.vokac@kok.cvut.cz ČVUT v Praze, Fakuta architektury 2. istopadu 2016 Průhybová čára ohýbaného nosníku Znaménková konvence veičin M z x +q +w +ϕ + q...
3. přednáška Průhybová čára Mirosav Vokáč mirosav.vokac@kok.cvut.cz ČVUT v Praze, Fakuta architektury 2. istopadu 2016 Průhybová čára ohýbaného nosníku Znaménková konvence veičin M z x +q +w +ϕ + q...
Pružnost a plasticita II CD03
 Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Téma 9 Těžiště Těžiště rovinných čar Těžiště jednoduchých rovinných obrazců Těžiště složených rovinných obrazců
 Stvení sttik, 1.ročník klářského studi Tém 9 Těžiště Těžiště rovinných čr Těžiště jednoduchých rovinných orců Těžiště složených rovinných orců Ktedr stvení mechniky Fkult stvení, VŠB - Technická univerit
Stvení sttik, 1.ročník klářského studi Tém 9 Těžiště Těžiště rovinných čr Těžiště jednoduchých rovinných orců Těžiště složených rovinných orců Ktedr stvení mechniky Fkult stvení, VŠB - Technická univerit
Téma 5 Spojitý nosník
 Sttik stveních konstukcí..očník kářského studi Tém 5 Sojitý nosník Zákdní vstnosti sojitého nosníku Řešení sojitého nosníku siovou metodou yužití symetie sojitého nosníku Příčinkové čáy nhodié ztížení
Sttik stveních konstukcí..očník kářského studi Tém 5 Sojitý nosník Zákdní vstnosti sojitého nosníku Řešení sojitého nosníku siovou metodou yužití symetie sojitého nosníku Příčinkové čáy nhodié ztížení
ÚVOD DO TEORIE MATEMATICKÉ PRUŽNOSTI
 ÚVOD DO TEORIE MATEMATICKÉ PRUŽNOSTI ZÁKLADNÍ PŘEDPOKLADY A POJMY 1. Látka, která vtváří příslušné těleso je dokonale lineárně pružné, mezi napětím a přetvořením je lineární závislost.. Látka hmotného
ÚVOD DO TEORIE MATEMATICKÉ PRUŽNOSTI ZÁKLADNÍ PŘEDPOKLADY A POJMY 1. Látka, která vtváří příslušné těleso je dokonale lineárně pružné, mezi napětím a přetvořením je lineární závislost.. Látka hmotného
Integrální definice vnitřních sil na prutu
 Přednáška 04 Integrální definice vnitřních sil Ohb prutu v rovinách x, x Šikmý ohb Kombinace normálové síl s ohbem Poloha neutrální os Jádro průřeu Příklad Copright (c) 011 Vít Šmilauer Cech Technical
Přednáška 04 Integrální definice vnitřních sil Ohb prutu v rovinách x, x Šikmý ohb Kombinace normálové síl s ohbem Poloha neutrální os Jádro průřeu Příklad Copright (c) 011 Vít Šmilauer Cech Technical
Posuďte oboustranně kloubově uložený sloup délky L = 5 m, který je centricky zatížen silou
 Příkld 1: SPŘAŽEÝ SLOUP (TRUBKA VYPLĚÁ BETOE) ZATÍŽEÝ OSOVOU SILOU Posuďte oboustrnně kloubově uložený sloup délk L 5 m, který je entrik ztížen silou 1400 kn. Sloup tvoří trubk Ø 45x7 z oeli S35 vplněná
Příkld 1: SPŘAŽEÝ SLOUP (TRUBKA VYPLĚÁ BETOE) ZATÍŽEÝ OSOVOU SILOU Posuďte oboustrnně kloubově uložený sloup délk L 5 m, který je entrik ztížen silou 1400 kn. Sloup tvoří trubk Ø 45x7 z oeli S35 vplněná
Návrh a posudek osově namáhaného nosníku podle obou MS
 Návrh a posudek osově namáhaného nosníku podle obou MS 1) Statický rozbor 2) Dobře pochopit zadání definovat, v jakých hodnotách počítat (charakteristické x návrh.) 2) MSÚ nutný průřez dle MSÚ a) pevnost
Návrh a posudek osově namáhaného nosníku podle obou MS 1) Statický rozbor 2) Dobře pochopit zadání definovat, v jakých hodnotách počítat (charakteristické x návrh.) 2) MSÚ nutný průřez dle MSÚ a) pevnost
SMR 2. Pavel Padevět
 SR Pve Pevět PRICIP VIRTUÁLÍCH PRACÍ jenošená eformční meto, esiové vivy, Sčítání účinků ztížení ezi nesiové vivy vžjeme v D: viv posntí popor, viv tepoty. ESILOVÉ VLIVY Popštění popory vyvoává v sttiky
SR Pve Pevět PRICIP VIRTUÁLÍCH PRACÍ jenošená eformční meto, esiové vivy, Sčítání účinků ztížení ezi nesiové vivy vžjeme v D: viv posntí popor, viv tepoty. ESILOVÉ VLIVY Popštění popory vyvoává v sttiky
SMR 2. Pavel Padevět
 SR Pve Pevět PRINCIP VIRTUÁLNÍCH PRACÍ Deformční meto jenošená eformční meto, Přetvárně nerčité konstrke POROVNÁNÍ OBECNÉ A JEDNODUŠENÉ DEF. ETODY V zjenošené eformční metoě (D) se zneává viv normáovýh
SR Pve Pevět PRINCIP VIRTUÁLNÍCH PRACÍ Deformční meto jenošená eformční meto, Přetvárně nerčité konstrke POROVNÁNÍ OBECNÉ A JEDNODUŠENÉ DEF. ETODY V zjenošené eformční metoě (D) se zneává viv normáovýh
Výpočet vnitřních sil přímého nosníku III: šikmý nosník
 Stvení sttik,.ročník klářského studi Výpočet vnitřníh sil přímého nosníku III: šikmý nosník Výpočet vnitřníh sil šikmého nosníku - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku
Stvení sttik,.ročník klářského studi Výpočet vnitřníh sil přímého nosníku III: šikmý nosník Výpočet vnitřníh sil šikmého nosníku - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku
Pohybové možnosti volných hmotných objektů v rovině
 REAKCE ohyové možnosti volných hmotných ojektů v rovině Stupeň volnosti n v : možnost vykont jednu složku posunu v ose souřdného systému neo pootočení. m [00] +x volný hmotný od v rovině: n v =2 (posun
REAKCE ohyové možnosti volných hmotných ojektů v rovině Stupeň volnosti n v : možnost vykont jednu složku posunu v ose souřdného systému neo pootočení. m [00] +x volný hmotný od v rovině: n v =2 (posun
Téma 6 Normálová napětí v prutech namáhaných na ohyb
 Pružnost a plasticita,.ročník bakalářského studia Téma 6 Normálová napětí v prutech namáhaných na ohb Základní vtah a předpoklad řešení Výpočet normálového napětí Dimenování nosníků namáhaných na ohb Složené
Pružnost a plasticita,.ročník bakalářského studia Téma 6 Normálová napětí v prutech namáhaných na ohb Základní vtah a předpoklad řešení Výpočet normálového napětí Dimenování nosníků namáhaných na ohb Složené
PRUŽNOST A PLASTICITA
 PRUŽOST A PLASTICITA Ing. Lenk Lusová LPH 407/1 Povinná litertur tel. 59 732 1326 lenk.lusov@vs.cz http://fst10.vs.cz/lusov http://mi21.vs.cz/modul/pruznost-plsticit Doporučená litertur Zákldní typy nmáhání
PRUŽOST A PLASTICITA Ing. Lenk Lusová LPH 407/1 Povinná litertur tel. 59 732 1326 lenk.lusov@vs.cz http://fst10.vs.cz/lusov http://mi21.vs.cz/modul/pruznost-plsticit Doporučená litertur Zákldní typy nmáhání
2002 Katedra obecné elektrotechniky FEI VŠB-TU Ostrava Ing.Stanislav Kocman
 STEJNOSĚRNÉ STROJE 1. Princip činnosti stejnosměrného stroje 2. Rekce kotvy komutce stejnosměrných strojů 3. Rozdělení stejnosměrných strojů 4. Stejnosměrné generátory 5. Stejnosměrné motory 2002 Ktedr
STEJNOSĚRNÉ STROJE 1. Princip činnosti stejnosměrného stroje 2. Rekce kotvy komutce stejnosměrných strojů 3. Rozdělení stejnosměrných strojů 4. Stejnosměrné generátory 5. Stejnosměrné motory 2002 Ktedr
Přednáška 12 Obecná deformační metoda, nelineární úlohy u prutových soustav
 Statika stavebních konstrukcí II., 3.ročník bakaářského studia Přednáška Obecná deformační metoda, neineární úohy u prutových soustav Fyzikáně neineární úoha Geometricky neineární úoha Konstrukčně neineární
Statika stavebních konstrukcí II., 3.ročník bakaářského studia Přednáška Obecná deformační metoda, neineární úohy u prutových soustav Fyzikáně neineární úoha Geometricky neineární úoha Konstrukčně neineární
Pohybové možnosti volných hmotných objektů v rovině
 REAKCE Pohyové možnosti volných hmotných ojektů v rovině Stupeň volnosti n v : možnost vykont jednu složku posunu v ose souřdného systému neo pootočení. +x volný hmotný od v rovině: n v =2 (posun v oecném
REAKCE Pohyové možnosti volných hmotných ojektů v rovině Stupeň volnosti n v : možnost vykont jednu složku posunu v ose souřdného systému neo pootočení. +x volný hmotný od v rovině: n v =2 (posun v oecném
* Modelování (zjednodušení a popis) tvaru konstrukce. pruty
 2. VNITŘNÍ SÍLY PRUTU 2.1 Úvod * Jak konstrukce přenáší atížení do vaeb/podpor? Jak jsou prvky konstrukce namáhány? * Modelování (jednodušení a popis) tvaru konstrukce. pruty 1 Prut: konstrukční prvek,
2. VNITŘNÍ SÍLY PRUTU 2.1 Úvod * Jak konstrukce přenáší atížení do vaeb/podpor? Jak jsou prvky konstrukce namáhány? * Modelování (jednodušení a popis) tvaru konstrukce. pruty 1 Prut: konstrukční prvek,
příklad 16 - Draft verze pajcu VUT FAST KDK Pešek 2016
 příklad - Drat vere pajcu VUT FAST KDK Pešek 0 VZPĚR SOŽEÉHO PRUTU A KŘÍŽOVÉHO PRUTU ZE DVOU ÚHEÍKŮ Vpočítejte návrhovou vpěrnou únosnost prutu délk 84 milimetrů kloubově uloženého na obou koncí pro všen
příklad - Drat vere pajcu VUT FAST KDK Pešek 0 VZPĚR SOŽEÉHO PRUTU A KŘÍŽOVÉHO PRUTU ZE DVOU ÚHEÍKŮ Vpočítejte návrhovou vpěrnou únosnost prutu délk 84 milimetrů kloubově uloženého na obou koncí pro všen
Desky. Petr Kabele. Pružnost a pevnost 132PRPE Přednášky. Deska/stěna/skořepina, desky základní předpoklady, proměnné a rovnice
 Pružnost a pevnost 13PRPE Přednášk Desk Deska/stěna/skořepina, desk ákladní předpoklad, proměnné a rovnice Petr Kabele České vsoké učení technické v Prae Fakulta stavební Úvod Přemístění, deformaci a napjatost
Pružnost a pevnost 13PRPE Přednášk Desk Deska/stěna/skořepina, desk ákladní předpoklad, proměnné a rovnice Petr Kabele České vsoké učení technické v Prae Fakulta stavební Úvod Přemístění, deformaci a napjatost
je parciální derivace funkce f v bodě a podle druhé proměnné (obvykle říkáme proměnné
 1. Prciální derivce funkce více proměnných. Prciální derivce funkce dvou proměnných. Je-li funkce f f(, ) definován v množině D f R 2 bod ( 1, 2 ) je vnitřním bodem množin D f, pk funkce g 1 (t) f(t, 2
1. Prciální derivce funkce více proměnných. Prciální derivce funkce dvou proměnných. Je-li funkce f f(, ) definován v množině D f R 2 bod ( 1, 2 ) je vnitřním bodem množin D f, pk funkce g 1 (t) f(t, 2
Přednáška 10, modely podloží
 Statika stavebních konstrukcí II.,.ročník kaářského studia Přednáška, modey podoží Úvod Winkerův mode podoží Pasternakův mode podoží Nosník na pružném Winkerově podoží, řešení OD atedra stavební mechaniky
Statika stavebních konstrukcí II.,.ročník kaářského studia Přednáška, modey podoží Úvod Winkerův mode podoží Pasternakův mode podoží Nosník na pružném Winkerově podoží, řešení OD atedra stavební mechaniky
Příklad 7 Průhyb nosníku - složitější případ
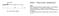 Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Výpočet vnitřních sil přímého nosníku III: šikmý nosník
 Stvení sttik,.ročník klářského studi Výpočet vnitřníh sil přímého nosníku III: šikmý nosník Výpočet vnitřníh sil šikmého nosníku - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku
Stvení sttik,.ročník klářského studi Výpočet vnitřníh sil přímého nosníku III: šikmý nosník Výpočet vnitřníh sil šikmého nosníku - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku
Název Řešený příklad: Pružná analýza jednolodní rámové konstrukce
 Dokument: SX09a-Z-EU Strana 8 Řešený příklad: Pružná analýa jednolodní rámové Je navržena jednolodní rámová vrobená válcovaných profilů podle E 993--. Příklad ahrnuje pružnou analýu podle teorie prvního
Dokument: SX09a-Z-EU Strana 8 Řešený příklad: Pružná analýa jednolodní rámové Je navržena jednolodní rámová vrobená válcovaných profilů podle E 993--. Příklad ahrnuje pružnou analýu podle teorie prvního
ŔᶑPř. 10 Ohyb nosníku se ztrátou stability. studentská kopie
 Navrhněe sropní průvla průřeu IPE oceli S35, aížený podle obráu reacemi e sropnic. Nosní je ajišěn proi ráě příčné a orní sabili (lopení) v podporách a v působiších osamělých břemen. haraerisicá hodnoa
Navrhněe sropní průvla průřeu IPE oceli S35, aížený podle obráu reacemi e sropnic. Nosní je ajišěn proi ráě příčné a orní sabili (lopení) v podporách a v působiších osamělých břemen. haraerisicá hodnoa
Řešený příklad: Návrh ocelového za studena tvarovaného sloupku stěny v tlaku a ohybu
 VÝPOČEÍ LS Dokuent: SX07a-Z-EU Strana 9 áev Řešený příklad: ávrh ocelového a studena tvarovaného sloupku stěn v tlaku a ohbu Eurokód E 99--, E 99-- Vpracovali V. Ungureanu,. Ru Datu leden 00 Kontroloval
VÝPOČEÍ LS Dokuent: SX07a-Z-EU Strana 9 áev Řešený příklad: ávrh ocelového a studena tvarovaného sloupku stěn v tlaku a ohbu Eurokód E 99--, E 99-- Vpracovali V. Ungureanu,. Ru Datu leden 00 Kontroloval
2 i i. = m r, (1) J = r m = r V. m V
 Měření momentu setrvčnosti 1 Měření momentu setrvčnosti Úko č. 1: Změřte moment setrvčnosti obdéníkové desky přímou metodou. Pomůcky Fyzické kyvdo (kovová obdéníková desk s třemi otvory), kovové těísko
Měření momentu setrvčnosti 1 Měření momentu setrvčnosti Úko č. 1: Změřte moment setrvčnosti obdéníkové desky přímou metodou. Pomůcky Fyzické kyvdo (kovová obdéníková desk s třemi otvory), kovové těísko
Řešený příklad: Požární odolnost částečně obetonovaného spřaženého nosníku
 Dokument: SX038-CZ-EU Strn 1 8 Vyprcovli P Schumnn & T Trutmnn Dtum Leden 006 Kontrolovl J Chic, Lbein Dtum Leden 006 Řešený příkld: Požární odolnost částečně obetonovného Řešený příkld ukuje výpočet momentové
Dokument: SX038-CZ-EU Strn 1 8 Vyprcovli P Schumnn & T Trutmnn Dtum Leden 006 Kontrolovl J Chic, Lbein Dtum Leden 006 Řešený příkld: Požární odolnost částečně obetonovného Řešený příkld ukuje výpočet momentové
Spojitý nosník. Příklady
 Spojitý nosník Příklady Příklad, zadání A = konst. =, m I = konst. =,6 m 4 E = konst. = GPa q =kn / m F kn 3 = M = 5kNm F = 5kN 8 F3 = 8kN 4,5 . způsob řešení n p = (nepočítáme pootočení ve styčníku č.3)
Spojitý nosník Příklady Příklad, zadání A = konst. =, m I = konst. =,6 m 4 E = konst. = GPa q =kn / m F kn 3 = M = 5kNm F = 5kN 8 F3 = 8kN 4,5 . způsob řešení n p = (nepočítáme pootočení ve styčníku č.3)
Téma 4 Normálové napětí a přetvoření prutu namáhaného tahem (prostým tlakem)
 Pružnost a pasticita, 2.ročník bakaářského studia Téma 4 ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného prutu
Pružnost a pasticita, 2.ročník bakaářského studia Téma 4 ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného prutu
5. Ohýbané nosníky Únosnost ve smyku, momentová únosnost, klopení, MSP, hospodárný nosník.
 5. Ohýbané nosník Únosnost ve smku, momentová únosnost, klopení, P, hospodárný nosník. Únosnost ve smku stojina pásnice poue pro válcované V d h t w Posouení na smk: V pružně: τ = ( τ pl, Rd) I V V t w
5. Ohýbané nosník Únosnost ve smku, momentová únosnost, klopení, P, hospodárný nosník. Únosnost ve smku stojina pásnice poue pro válcované V d h t w Posouení na smk: V pružně: τ = ( τ pl, Rd) I V V t w
IVC Nošovice sportoviště II etapa Cvičná ocelová věž pro hasičský záchranný zbor STAVEBNĚ KONSTRUKČNÍ ŘEŠENÍ TECHNICKÁ ZPRÁVA A STATICKÉ POSOUZENÍ
 IVC Nošovice sportoviště II etapa Cvičná ocelová věž pro hasičský áchranný bor 36-8/13 STAVEBNĚ KONSTRUKČNÍ ŘEŠENÍ TECHNICKÁ ZPRÁVA A STATICKÉ POSOUZENÍ vpracoval: ing. Robin Kulhánek kontroloval: ing.
IVC Nošovice sportoviště II etapa Cvičná ocelová věž pro hasičský áchranný bor 36-8/13 STAVEBNĚ KONSTRUKČNÍ ŘEŠENÍ TECHNICKÁ ZPRÁVA A STATICKÉ POSOUZENÍ vpracoval: ing. Robin Kulhánek kontroloval: ing.
studentská kopie Př. 9 Složený členěný prut ze dvou úhelníků 15ε = 15 = 15...bezpečně třída 3 (nemusíme redukovat plochu)
 Př. 9 Složený členěný prut e dou úhelníků Stnote únosnost prutu tořeného dojcí ronormenný úhelníků 9x8. Prut toří dgonálu příhrdoého tuždl sstémoá délk prutu je 4 m. Spojk P-8x8 jsou umístěn třetná prutu.
Př. 9 Složený členěný prut e dou úhelníků Stnote únosnost prutu tořeného dojcí ronormenný úhelníků 9x8. Prut toří dgonálu příhrdoého tuždl sstémoá délk prutu je 4 m. Spojk P-8x8 jsou umístěn třetná prutu.
Platnost Bernoulli Navierovy hypotézy
 Přednáška 03 Diferenciální rovnice ohybu prutu Platnost Bernoulli Navierovy hypotézy Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Příklady Copyright (c) 011 Vít Šmilauer
Přednáška 03 Diferenciální rovnice ohybu prutu Platnost Bernoulli Navierovy hypotézy Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Příklady Copyright (c) 011 Vít Šmilauer
Výpočet vnitřních sil přímého nosníku II
 Stveí sttik, 1.ročík kářského studi ýpočet vitřích si přímého osíku II ýpočet vitřích si osíků ztížeých spojitým ztížeím: příčé kosttí trojúheíkové spojité ztížeí, spojité ztížeí v osové úoze, mometové
Stveí sttik, 1.ročík kářského studi ýpočet vitřích si přímého osíku II ýpočet vitřích si osíků ztížeých spojitým ztížeím: příčé kosttí trojúheíkové spojité ztížeí, spojité ztížeí v osové úoze, mometové
ZÁKLADNÍ POJMY A VZTAHY V TECHNICKÉ PRUŽNOSTI
 ZÁKLDNÍ POJY VZTHY V TECHNICKÉ PRUŽNOSTI Napětí velikost vnitřní síl na jednotku ploch konečné podíl elementů vnitřních sil a ploch Podle směru vnitřních sil avádíme: ds napětí celkové σ r = v obecném
ZÁKLDNÍ POJY VZTHY V TECHNICKÉ PRUŽNOSTI Napětí velikost vnitřní síl na jednotku ploch konečné podíl elementů vnitřních sil a ploch Podle směru vnitřních sil avádíme: ds napětí celkové σ r = v obecném
R n výběr reprezentantů. Řekneme, že funkce f je Riemannovsky integrovatelná na
 Mtemtik II. Určitý integrál.1. Pojem Riemnnov určitého integrálu Definice.1.1. Říkáme, že funkce f( x ) je n intervlu integrovtelná (schopná integrce), je-li n něm ohrničená spoň po částech spojitá.
Mtemtik II. Určitý integrál.1. Pojem Riemnnov určitého integrálu Definice.1.1. Říkáme, že funkce f( x ) je n intervlu integrovtelná (schopná integrce), je-li n něm ohrničená spoň po částech spojitá.
VŠB Technická univerzita Ostrava Fakulta stavební Katedra stavební mechaniky. Pružnost a plasticita - příklady. Oldřich Sucharda
 VŠB Technická univerzita strava Fakuta stavební Katedra stavební mechanik Pružnost a pasticita - příkad dřich Sucharda strava, září 0 bsah. Průřezové charakteristik..... Těžiště omené čár..... Těžiště
VŠB Technická univerzita strava Fakuta stavební Katedra stavební mechanik Pružnost a pasticita - příkad dřich Sucharda strava, září 0 bsah. Průřezové charakteristik..... Těžiště omené čár..... Těžiště
Stavební statika. Úvod do studia předmětu na Stavební fakultě VŠB-TU Ostrava. Letní semestr. Stavební statika, 1.ročník bakalářského studia
 Stvení sttik, 1.ročník klářského studi Stvení sttik Úvod do studi předmětu n Stvení fkultě VŠB-TU Ostrv Letní semestr Ktedr stvení mechniky Fkult stvení, VŠB - Technická univerzit Ostrv Stvení sttik -
Stvení sttik, 1.ročník klářského studi Stvení sttik Úvod do studi předmětu n Stvení fkultě VŠB-TU Ostrv Letní semestr Ktedr stvení mechniky Fkult stvení, VŠB - Technická univerzit Ostrv Stvení sttik -
Stavební mechanika 2 (K132SM02)
 Stvení mecnik 2 (K132SM02) Přednáší: Jn Sýkor Ktedr mecniky K132 místnost D2016 e-mil: jn.sykor.1@fsv.cvut.cz konzultční odiny: Po 12-14 Kldné směry vnitřníc sil: Kldný průřez vnitřní síly jsou kldné ve
Stvení mecnik 2 (K132SM02) Přednáší: Jn Sýkor Ktedr mecniky K132 místnost D2016 e-mil: jn.sykor.1@fsv.cvut.cz konzultční odiny: Po 12-14 Kldné směry vnitřníc sil: Kldný průřez vnitřní síly jsou kldné ve
Přednáška 1 Obecná deformační metoda, podstata DM
 Statika stavebních konstrukcí II., 3.ročník bakalářského studia Přednáška 1 Obecná deformační metoda, podstata DM Základní informace o výuce předmětu SSK II Metody řešení staticky neurčitých konstrukcí
Statika stavebních konstrukcí II., 3.ročník bakalářského studia Přednáška 1 Obecná deformační metoda, podstata DM Základní informace o výuce předmětu SSK II Metody řešení staticky neurčitých konstrukcí
