2.1 Popis stavového chování
|
|
|
- Karel Černý
- před 6 lety
- Počet zobrazení:
Transkript
1 . SAOÉ CHOÁNÍ PLYNŮ A APALIN.1 Poi tvového chování Podle tvu uořádnoti, v jké e ohou vykytovt toy, olekuly, oř. ionty ři vytváření hotných celků, e rozlišují tři hlvní kuenké (gregátní) tvy hoty: lynné tvu jou olekuly oěrně řídce roztýleny v rotoru, který rovnoěrně vylňují. Pohybují e v ně zcel neuořádně, ři čež n ebe neutále nrážejí. ento ohyb brání olekulá hlukovt e v těnější vzky. Odtud vylývá dokonlá tvrová roěnlivot lynu velká roěnlivot jeho objeu ři zěnách tlku teloty. U klin jou již olekuly ve tálé tyku, který je udržován jejich řitžlivýi ili. Mjí ještě určitou volnot ohybu, tkže nezujíjí vzájeně tálé olohy, le ři to e neění jejich eziolekulární vzdálenoti. Proto kliny ndno ění vůj tvr, le objeové zěny záviející n vnějších odínkách jou znčně oezené. evné tvu jou toy, olekuly či ionty rovněž v těné tyku, le n rozdíl od klin jeví v celé objeu, který zujíjí, vnitřní uořádnot. ytvářejí evnou trukturu, ve které jou jejich vzájené olohy fixovány čátice ohou kitt jen ve vyezených olohách. Látky v tuhé tvu jou roto odolné jk roti tvrový tk roti objeový zěná. ždá látk e ůže obecně vykytovt v kterékoli z těchto kuenkých tvů. Snižování teloty odoruje ultnění řitžlivých il ezi čáticei, které e tk ohou těně hlukovt, ž vytvoří rvidelně uořádné ekuení. Zvyšování teloty tuto uořádnot nok ruší řevádí látku do klného lynného tvu. tou noáhá oučné nižování tlku. elot tlk, ři kterých dochází k řechodu látky z jednoho kuentví do druhého, závií n ovze látky é. zth ezi telotou, tlke, látkový nožtví ložek v ytéu jeho objee, tj. tvové chování ytéu, ůže být vyjádřeno grficky, oocí tvového digru nebo ve forě tetického vzthu tvové rovnice. N zákldě znloti tvového chování ytéu lze k zíkt řdu dlších důležitých terodynických veličin (viz 3. Cheická terodynik)..1.1 Stvový digr U jednoložkové outvy (tj. čité látky) je tvové chování vyjádřeno závilotí ezi třei roěnnýi, tlke, telotou olární objee. Pro grfické znázornění je tedy zotřebí rotorového digru. Ukázk tvového digru ro jednoložkovou outvu je uveden n obr. -1. Obr. -1 Fázový digr jednoložkové outvy + A B + + C A A + B + B + g C C g + kritický bod kritická telot kritický tlk telot trojného bodu tlk nycené áry v trojné bodě + + g oblt exitence tuhé fáze oblt exitence klné fáze oblt exitence lynné fáze. Stvové chování -1
2 digru jou vyznčeny oblti exitence lynné, klné tuhé fáze dále oblti dvoufázové l+g, +g +l, ve kterých jou v rovnováze vždy dvě uvedené fáze. Při odínkách dných říkou ABC koexitují tři fáze. Protorový digr všk není ro běžné oužívání říliš říhodný, roto e oužívá dvourozěrných digrů, které znázorňují závilot dvou roěnných ro kontntní hodnoty třetí roěnné (n obr. 1- znázorněny rojekce -, -, -)..1. Stvová rovnice Stvový digr je ice názorný, le ro výočty by bylo ideální ít k diozici vzth, který by oiovl závilot ezi tvovýi roěnnýi ro uvžovný yté to ro odínky, ři nichž exituje jk v lynné, tk v klné i tuhé tvu - tvovou rovnici: f (,,, n 1, n,...) = 0 (.1) Obecně všk tto relce není zná; je ožno k ní ouze v některých řídech jitý řiblížení dorcovt. Nejlée je tento roblé vyřešen ro lyny.. Ideální lyn..1 Stvová rovnice ideálního lynu První okuy o ytetické zkouání vzthů ezi telotou, tlke, objee nožtví lynu, rovedl Robert Boyle kole roku 1660 z zhrub kontntní teloty (Boyle ěření teloty ještě neznl); ke konci 18. toletí zčl být zkouán i vliv teloty (J. L. Gy-Luc, J. Dlton). N zákldě těchto zákonitotí Avogdrov zákon forulovl Cleyron r tvovou rovnici = nr, oř. = R (.) dne oznčovnou jko tvová rovnice ideálního lynu. ontnt R je tzv. univerzální lynová kontnt, která á v SI outvě hodnotu: R = 101,35 10, P 8, ,31447 J ol 73,15 ol neboť odle Avogdrov zákon je ve tejných objeech lynů různé cheické ovhy z tejné teloty tlku tejný očet olekul roto obje 0, který zujíá jeden ol lynu (tj. 6, olekul) z tlku 0 = 101,35 kp teloty 0 = 73,15 je tejný u všech lynů: 0 =,41361 d 3 ol 1 Plyny, které e řídí touto tvovou rovnicí, e nzývjí lyny ideální. Podle ředtv kinetické teorie (kinetická teorie lynů je ouhrn ředtv o ovze eleentárních čátic) lyn e kládá z velikého očtu veli lých čátic, které jou v neutálé neuořádné ohybu, olekuly ideálního lynu jou tk lé, že jejich obje je znedbtelný vedle objeu nádoby, ezi olekuli ideálního lynu neůobí řitžlivé ni odudivé íly, vzájené rážky olekul i rážky olekul ideálního lynu e těni nádoby jou dokonle ružné dochází ři nich ouze k ředávání hybnoti kinetické energie. e kutečnoti neexituje žádný lyn, který by zcel řeně lňovl tvovou rovnici ideálního lynu v libovolné rozhu telot tlků tvová rovnice ideálního lynu ředtvuje ouze liitní vzth. Mnoho lynů e všk z vyšších telot z nižších tlků řídí títo jednoduchý vzthe veli dobře. Grficky lze znázornit závilot všech tří roěnných,, rotorovou lochou (obr. -1). olbou kontntní hodnoty kterékoli roěnné zíkáe závilot ottních dvou ve forě křivky, oř. říky, která je růečnicí rotorové lochy rovinou, jež odovídá zvolené kontntní roěnné. Sěrnicei tečen k těto růečnicí jou definovány koeficienty, oocí kterých jou čto tbelován dt o tvové chování (tohoto zůobu tbelce je oužíváno nejen u lynů, le i u klin evných látek).. Stvové chování -
3 .. Izobry, izotery izochory Izobry ( = kont.) / = kont. (.3) 1 Izobrický koeficient objeové roztžnoti (.4) rotoucí Obr. - Izobry ideálního lynu 0 () Izotery ( = kont.) = kont., oř. = (1/ ) kont., (.5) (někdy je vhodnější íto olárního objeu oužívt hutotu látkového nožtví, 1/ ; zobrzení izotere je k jednodušší, rotože íto hyerbol dotnee vzek oloříek) 1 oeficient izoterické tlčitelnoti (.6) 4 rotoucí 4 3 rotoucí Obr. -3 Izotery ideálního lynu Izochory ( = kont.) / = kont. (.7) oeficient rozínvoti 1/ 1 (.8) rotoucí () Obr. -4 Izochory ideálního lynu. Stvové chování -3
4 .3 Reálné lyny Poi tvového chování lynů rovnicí ideálního lynu je ožný jen z nízkých tlků. vntittivně lze oblt oužitelnoti tohoto oiu vyezit jen obtížně, rotože záleží n vltní lynu, telotě n oždovné řenoti..3.1 Odchylky od ideálního chování, koreibilitní fktor Podle tvové rovnice ideálního lynu by z kontntní teloty ělo ltit = kont. 1 n R R Jk ukzují grfy obr. -5, kutečný růběh záviloti n e liší: (.9) H CH4 3 = R B 1 Obr. -5 Závilot oučinu n tlku. levo ro ideální lyn ro reálné lyny, vrvo ro reálné lyny ři různých telotách; B Boyleov telot Pro vyjádření odchylek od tvové rovnice ideálního lynu byl zveden koreibilitní fktor, z. (.10) n R R Pro ideální lyn je z = 1, ro reálný lyn z určité teloty li z 1, [] (.11) 0 Průběh izotere závilotí n (obr. -5 vrvo) je u všech lynů rkticky tejný, i když v různých oborech telot. elot, ři níž leží iniu této záviloti řío v oe ořdnic, odovídá řídu, kdy je ožno v oěrně široké rozezí tlků ot chování reálného lynu ideální tvovou rovnicí, e oznčuje jko Boyleov telot B. Je zřejé, že ro ni ltí ( ) li 0 (.1) 0 Chrkter závilotí n lze vyvětlit oěrně jednoduše n zákldě ředtvy o eziolekulárních řitžlivých odudivých ilách. Při telotách od B ři nižších tlcích řevládjí řitžlivé íly ezi olekuli, e toující tlke e tále více zčínjí ultňovt íly odudivé. Miniu n řílušné izoterě zjevně odovídá řídu, kdy e řitžlivé íly rávě rovnjí ilá odudivý. Při telotách vyšších než B e zřejě již od nejnižších tlků ultňují ouze odudivé íly. Zákony oiující tvové chování lynů vylynuly z ěření krokoických vltnotí. yto zákony e tedy hodí ice k oiu, ne všk k vyvětlení říčin, jež tyto zákony odiňují. Mkrokoické vltnoti ideálního lynu říčiny odchylek v chování reálných lynů od lynu ideálního lze nejlée vyvětlit n zákldě ředtv o ovze eleentárních čátic, které lyn tvoří. Zkouání krokoických jevů z tohoto hledik e zbývá kinetická teorie látek.. Stvové chování -4
5 .3. Stvové rovnice reálných lynů Stvové chování látek je ožno vyjádřit různý zůobe: tbulkou, digre, nlytický vzthe (tvovou rovnicí); ři dnešních ožnotech využití očítčů jeden z nejrcionálnějších zůobů ředtvuje tvová rovnice. Byl nvržen celá řd tvových rovnic, které buď zvádějí korekce n neideální chování, nebo vyjdřují odchylky ve tvru ocninového vzthu n der Wlov tvová rovnice (1873) byl rvní úěšnou tvovou rovnicí, která dokázl kvlittivně do znčné íry i kvntittivně, rávně ot tvové chování lynů z vyšších tlků včetně ožnoti kondenzce lynů. Při odvození tvové rovnice vycházel vn der Wl ze tvové rovnice ideálního lynu, do níž zvedl korekci n vltní obje olekul (íto něřeného objeu je nutno očítt výrze - b, kde b je ro dný lyn kontntou, která je rovn zhrub čtyřnáobku vltního objeu olekul obžených v jedno olu (á rozěr olárního objeu)), n exitenci řitžlivých odudivých eziolekulových il; zde vyšel z ředtvy kinetické teorie o vzniku tlku ředávání hybnoti jeho olekul těně nádoby, v níž je lyn obžen. řídě ideálního lynu není olekul blížící e ke těně nádoby ničí brzděn; v řídě reálného lynu jou všk olekuly v důledku řitžlivých il vthovány z blízkoti těny dovnitř do objeu lynu, tí e nižuje ložk rychloti ve ěru ke těně nádoby tí i očet nárzů n tuto těnu z jednotku ču velikot hybnoti ředné olekulou těně. lk reálného lynu je vždy nižší než tlk, který by z jink tejných odínek vykzovl ideální lyn. e kutečnéu, tj. něřenéu tlku lynu je třeb řičít korekci n vzájenou řitžlivot olekul, / (íl, kterou je olekul vthován zět je úěrná hutotě lynu očet olekul, které z jednotku ču nrážejí n těnu je rovněž úěrný hutotě lynu). n der Wlov rovnice á tvr ( + ) ( n b) = R, oř. ( + ) ( nb) = nr (.13) n der Wlovy kontnty b jou ro dný lyn chrkteritické lze je určit buď z říých dt o tvové chování, nebo neřío z kritických kontnt lynu (viz dále). Rovnice dovoluje jednoduše vyočítt telotu i tlk. Pro obje je všk rovnice třetího tuně 3 R b ( b ) 0 (.14) Její řešení je rcné obvykle e otuuje zkuo (jko rvní roxice e bere hodnot ze tvové rovnice ideálního lynu. Pro velké hodnoty (ři nižších tlcích) je ožno rovnici zjednodušit (/ /R znedbá e b/ ) n tvr R ( b ). (.15) R Odtud ro Boyleovu telotu dotnee B (.16) R b kto vyočtená B bývá v dobré hodě hodnotou exerientální. n der Wlov rovnice vytihuje chování reálných lynů oěrně dobře ouze v oblti neříliš vyokých tlků. rxi je dne álo oužívná; á všk vé íto v učebnicích fyzikální cheie, neboť vyvětluje názorný zůobe říčinu odchylek od ideálního chování, ředtvuje výchozí vzth ro nvrhování ložitějších řenějších tvových rovnic, dovoluje uokojivě vytihnout chování lynů ři zklňování ve vhodné forě ředtvuje dobrou ilutrci tzv. teoréu koreondujících tvů (viz dále).. Stvové chování -5
6 .3.. Dlší tvové rovnice Aby bylo doženo leší hody e kutečnotí, byl nvržen celá řd tvových rovnic (několik et). Příkldy nejoužívnějších jou uvedeny v náledující tbulce: Ideální lyn R R n der Wl b Berthelot Redlich-wong Dieterici Bettie-Bridgen iriální rozvoj R b R b ( b ) Re 1/ / R b (1 ) R ( ) (1 ) o (1 b b ) ; ; o R B C 1 z 1 B C D R R (erlingh-one) co ondenzce lynů kritický bod Při nižších telotách dochází u reálných lynů z vyšších tlků ke kondenzci lynů, což je jev, který tvová rovnice ideálního lynu nedokáže ot. Obr. -6 ukzuje výledky exerientálního tnovení záviloti tlku n objeu ři různých telotách. Při dottečně C B vyokých telotách leduje exerientálně zjiš- těná izoter téěř dokonle Boyleovu izoteru ro ideální lyn. S klející telotou ntávjí otuně větší odchylky od tvové rovnice ideálního lynu od určitou D telotou e n izoterě objevuje horizontální rodlev, jejíž délk e klející telotou zvětšuje. Stlčujee-li nř. lyn ři telotě 1, kleá jeho obje nejrve odle křivky AG. Po dožení bodu G e objeví rvní odíly zklněného lynu ři dlší korei e nezvyšuje tlk, kleá L G k 1 A nožtví lynu, vzrůtá nožtví kliny. nycená klin nycená ár g ( ) ( ) Obr. -6 Závilot tlku n objeu reálného lynu ři různých telotách 1 bodě L je všechen lyn již zklněn. lk 1e nzývá tlk nycené áry ři telotě 1 (jko nycená e oznčuje ár, která je ři dné telotě v rovnováze klinou, tzv. nenycená ár á tlk nižší než je tlk nycené áry, řeycená ár á nok tlk vyšší). Při dlší zvyšování tlku e obje kliny ění odél křivky LC, která je veli trá, neboť tlčitelnot kliny je o několik řádů enší než je tou u lynů. Potuujee-li od nižších telot, zjišťujee, že horizontální rodlev n izoterách e e toující telotou zkrcuje, ž e ři určité telotě zredukuje n jediný bod kritický bod, chrkterizovný ouřdnicei k (kritická telot), k (kritický tlk) k (kritický obje), oř. k (kritická hutot) dné látky. ritická izoter tvoří ředěl ezi obltí, kde lyn nelze zklnit obltí, ve které zvyšování tlku vede ke kondenzci. ritická telot je nejvyšší telotou, ři níž je ožno dný lyn zvyšování tlku zklnit. Nd ní nelze zklnění doáhnout ni ebevětší tlke Proto byly dříve některé lyny oznčovány jko ernentní nhy o zklnění e odehrávly nd kritickou telotou.. Stvové chování -6
7 .3.4 ontinuit lynného klného tvu Látk ři odkritické telotě tlku větší než tlk nycené áry (oblt nlevo od kritické izotery křivky L) je oznčován jko klin. Body ležící n křivce L znázorňují nycenou klinu (je v rovnováze e vou rou). Látk v lynné tvu, jejíž telot je vyšší než kritická, je oznčován jko lyn; je-li její telot nižší než kritická, je oznčován jko ár (nejde-li o nycenou áru, oužívá e terínu lyn čto i v odkritické oblti). Body ležící n křivce G znázorňují nycenou áru (tj. áru v rovnováze nycenou klinou). Z bodu A, který znázorňuje áru ři telotě 1 e do klného tvu ři telotě 1 (bod D) ůžee dott noh zůoby; nř. izoterní nižování objeu - ře dvoufázovou oblt GL. Jde o děj, dorovázený vznike otrého rozhrní ezi znikjící fází lynnou vznikjící fází klnou. Převod látky z klného do lynného tvu lze všk ukutečnit i tk, že e vyhnee dvoufázové oblti, nř. cetou ABCD (obr. -6). Páru, jejíž tv je vytižen bode A, nřed z kontntního objeu ohřejee n ndkritickou telotu (bod B). ento lyn (již ne ár!) izobricky ochldíe do bodu C nkonec z kontntního objeu ochldíe z B do D. bodě D ( D < ) látk exituje již jko klin. žádné bodě cety ABCD všk nebyly vedle ebe řítony obě fáze, klin i ár. Syté je tále hoogenní to i ři řechodu ře kritickou izoteru. Znená to tedy, že klinu lze řeěnit v áru nok áru v klinu bez řechodu ře dvoufázovou oblt. Lze tedy konttovt, že ezi lynný klný tve exituje kontinuit lynný i klný tv jou jen zvláštní fory jednoho fluidního tvu..3.5 Stvová rovnice kritický tv n der Wlov rovnice je vzhlede k objeu třetího tuně á tedy obecně tři řešení. Nd kritickou telotou je jedno řešení reálné, dvě jou iginární. Závilot - je vyjádřen ojitou onotonní křivkou. kritické bodě lývjí všechn tři řešení v jedno n kritické izoterě je inflexní bod. odkritické oblti je křivk -, jk je viděli v ředchozí odtvci, neojitá. uto kutečnot nedokáží tvové rovnice ot. Obr. -7 ukzuje dvě odkritické izotery, vyočtené z vn der Wlovy rovnice. Je vidět, že kutečný říkový růběh GL (obr. -6, obr. -7) je nhrzen eovitou křivkou GHML. odkritické oblti tedy odovídjí určitéu zvolenéu tlku vždy tři hodnoty objeu (nř. ři 1 hodnoty dné body G, N L). Pod kritický bode tedy exitují tři reálné kořeny ovše reálné jen z tetického hledik; z hledik fyzikálního jou reálné ouze dv kořeny, to obje áry ři dné tlku (bod G) obje kliny ři totéž tlku (bod L). Čáti GH LM jí rovněž fyzikální význ: neodovídjí ice tvu tbilní rovnováhy, le jou do jité íry exerientálně dotuné. řivk GH odovídá tzv. řeycené áře, úek LM tzv. řehřáté klině, tj. klině, která nevře, i když tlk nd ní byl nížen od hodnotu tlku nycené áry. Nroti tou růběh křivky ezi body M H nejen že neodovídá žádné exerientálně zjištěné kutečnoti, le dokonce odoruje fyzikální relitě. Neexituje totiž žádná látk, jejíž obje by e rotoucí tlke zvětšovl. kritické bodě lývjí všechn tři řešení v jedno n kritické izoterě je inflexní bod. Protože v inflexní bodě je rvní i druhá derivce tlku odle objeu je nulová, je ožno njít tyto vzthy ezi kontnti vn der Wlovy rovnice kritickýi veličini: 1 L M N H řehřátá klin nereálná čát G řeycená ár Obr. -7 Ndkritické, kritická odkritické izotery u lynu, který e řídí vdw rovnicí k 1. Stvové chování -7
8 7 64 R k 1 k, b k 8 k R 8, k k R (.17 ž.19) 3 Dození do vdw rovnice k k (.0) k k zvedení nových, tzv. redukovných roěnných, r, r, r (.1) k k k vede k zjívéu výledku - redukovné tvové rovnici: 3 r 3r 1 8 r (.) r to rovnice neobhuje žádné individuální kontnty jednotlivých látek (kontnty, b), tkže ji lze oužít ro libovolný lyn, znáe-li jeho kritické veličiny..3.6 Generlizovné koreibilitní fktory Redukovná vdw rovnice je rerezenttivní ilutrcí tzv. teoréu koreondujících tvů, odle kterého e různé látky chovjí totožně, nebo leoň odobně, je-li jejich tv tejně vzdálen od kritického bodu, tj. je-li oěr tvových veličin ke kritický veličiná u těchto látek totožný. N zákldě teoréu koreondujících tvů byl etrojen řd tzv. generlizovných koreibilitních digrů grfických vyjádření závilotí koreibilitního fktoru n redukovných, z nichž lze řío odečítt koreibilitní fktory ro široké rozezí redukovných roěnných. Generlizovné digry dovolují odhd koreibilitního fktoru u lynů chybou ž 5 %. k Obr. -8 Digr generlizovných koreibilitních digrů. Stvové chování -8
9 .4 Stvové chování ěí lynů.4.1 Ideální ě Podle Dltonov zákon je celkový tlk k-ložkové ěi dán oučte = k (.3) v něž veličin i e nzývá rciální tlk ložky i. Prciální tlk je definován jko tlk čité ložky i ři tejné látkové hutotě n i / = 1/ ři tejné telotě jko ve ěi. Pro říd ltnoti tvové rovnice ideálního lynu je i = x i (.4) kde x i je olární zloek ložky i Podle Agtov zákon je obje ěi určen oučte objeů čitých ložek ěi,, ři dné telotě tlku ytéu = 1 (.5) nebo n n1 n nk (.6) i 1 k 1 1 k k k x x x (.7) je olární obje čité ložky i z teloty tlku ěi ( ve tejné fázi jko ě)..4. Ideální ě reálných lynů Pokud znáe koreibilitní fktory všech čitých látek ři telotě tlku ěi ( i z i R/), dotli bycho odle Agtov zákon z 1 R z R z R R R x1 x x x z z k k i i i i (.8) eličin z, rovná oučtu oučinů x i z i, je oznčován jko koreibilitní fktor ěi odhdnutý odle Agtov zákon. Agtův zákon á ve fyzikální cheii zvláštní význ. Sě, která e jí řídí v široké telotní, tlkové intervlu v celé koncentrční rozhu, je definován jko ideální ě reálných lynů. ento oje je důležitý, neboť je dobrou roxicí reálné ěi ro tkovou ě je ožno určovt i dlší veličiny ouze n zákldě vltnotí čitých látek z dné teloty tlku. Obr. -9 ukzuje rozdíl ezi ideální chování ve ylu tvové rovnice ideálního lynu (řík ), kde z všech odínek ltí = R/ ideální chování ve ylu ideální ěi (řík c). Zde jí čité látky kždá olární obje jiný než odovídá ideálníu lynu, všk závilot n ložení, dná vzthe (.7), je lineární. Agtův zákon dovoluje oěrně řeně odhdovt tké olární obje klných ěí. Obr. -9 Závilot olárního objeu binární ěi n ložení () - ideální ě ideálních lynů, (rov. (.7)), (b) - reálná ě ideálních lynů, (c) - ideální ě reálných lynů, (rov. (.8)), (d) - reálná ě reálných lynů R z = (b) reálná ě ideálních lynů () ideální ě ideálních lynů (c) ideální ě reálných lynů R * = R 1 = z 1 0 x 1 1. Stvové chování -9
10 .4.3 Stvové rovnice ro lynné ěi Při likci tvových rovnic e n ě díváe jko n čitou látku kontnty vyočtee z kontnt ro čité ložky odle různých kobinčních rvidel, nř. b x i b i, ( x i i (.9) i i 1 / ).5 Stvové chování klin liny ředtvují řechodový tv hoty ezi tve lynný klný. řídě lynů evných látek exitují vhodné idelizovné odely, ideální lyn ideální krytl. Ideální lyn je chrkterizován dokonlou neuořádnotí n olekulární úrovni, ideální krytl ředtvuje nejdokonlejší uořádání eleentárních čátic, jké lze v řírodě nlézt. liny ředtvují z olekulárního hledik jkýi koroi ezi uořádnotí choe. Meziolekulární íly zde ůobí jen n veli krátké vzdálenoti roto e v klinách, n rozdíl od lynů, ultní ntolik, že jou to udržet kliny v určité objeu. toto objeu jí všk olekuly určitou volnot ohybu, roto jou kliny ohyblivé. Obje, který kliny zujíjí, není závilý n velikoti nádoby, v níž e ncházejí, je jně ohrničen volný ovrche. Podobně jko lyny, řizůobují e kliny vý tvre tvru nádoby. Jejich hutot je větší než hutot lynů koeficienty teelné roztžnoti tlčitelnoti jou odttně enší než u látek v lynné tvu. Stv klného ytéu určují hodnoty tvových, veličin jko jou telot, tlk hutot, re. olární obje. Hutot klin, zvláště ři telotách od norální telotou vru, je veli čto ěřenou veličinou. Protože hutotu lze určit veli řeně (běžně n 0,01 %), je čto důležitý kritérie čitoty látek..3. liv teloty tlku n hutotu klin Hutot kliny rotoucí telotou kleá v celé oboru její exitence; výjikou je vod, jejíž hutot á xiu ři 3,98C. vntittivně bývá telotní závilot hutoty vyjdřován oocí izobrického koeficientu telotní roztžnoti, = (1/)(/) (rov. (.4)), nebo eirickýi rovnicei tvru nř. = o (1 + t + bt + ct 3 + ), [] (.30) kde t je telot ve o C, o hutot ři t = 0 o C, b, c jou eirické kontnty. lk á n hutotu klin odttně enší vliv než telot. Hutot klin tlke oněkud touá (i o 0,005 % ři zvýšení tlku o 100 kp). tbulkách bývá tto závilot zchycen oocí izoterického koeficientu tlčitelnoti, = (1/)(/) (rov. (.6)) Pro terodynické výočty je výhodné vyjádřit vzth ezi tvovýi roěnnýi lgebrickou rovnicí. zhlede ke kontinuitě lynného klného tvu je ožno k touto účelu oužít vícekontntových tvových rovnic odvozených ro reálné lyny (vdw rovnice vytihuje chování klin ouze kvlittivně).. Stvové chování -10
101, , Pa m. 273,15 K mol
 2. STAVOVÉ CHOVÁNÍ PLYNŮ A KAPALIN Ideální lyn První okusy o systetické zkouání vzthů ezi telotou, tlke, objee nožství lynu, rovedl Robert Boyle kole roku 1660 z zhrub konstntní teloty (Boyle ěření teloty
2. STAVOVÉ CHOVÁNÍ PLYNŮ A KAPALIN Ideální lyn První okusy o systetické zkouání vzthů ezi telotou, tlke, objee nožství lynu, rovedl Robert Boyle kole roku 1660 z zhrub konstntní teloty (Boyle ěření teloty
Výpočty za použití zákonů pro ideální plyn
 ýočty za oužití zákonů ro ideální lyn Látka v lynné stavu je tvořena volnýi atoy(onoatoickýi olekulai), ionty nebo olekulai. Ideální lyn- olekuly na sebe neůsobí žádnýi silai, jejich obje je ve srovnání
ýočty za oužití zákonů ro ideální lyn Látka v lynné stavu je tvořena volnýi atoy(onoatoickýi olekulai), ionty nebo olekulai. Ideální lyn- olekuly na sebe neůsobí žádnýi silai, jejich obje je ve srovnání
Molekulová fyzika. Reálný plyn. Prof. RNDr. Emanuel Svoboda, CSc.
 Molekulová fyzik Reálný lyn Prof. RNDr. Enuel Svood, CSc. Reálný lyn Existence vzájeného silového ůsoení ezi částicei (tzv. vn der Wlsovské síly) Odudivá síl ezi částicei (interkce řekryvová) ři dosttečně
Molekulová fyzik Reálný lyn Prof. RNDr. Enuel Svood, CSc. Reálný lyn Existence vzájeného silového ůsoení ezi částicei (tzv. vn der Wlsovské síly) Odudivá síl ezi částicei (interkce řekryvová) ři dosttečně
11. Tepelné děje v plynech
 11. eelné děje v lynech 11.1 elotní roztažnost a rozínavost lynů elotní roztažnost obje lynů závisí na telotě ři stálé tlaku. S rostoucí telotou se roztažnost lynů ři stálé tlaku zvětšuje. Součinitel objeové
11. eelné děje v lynech 11.1 elotní roztažnost a rozínavost lynů elotní roztažnost obje lynů závisí na telotě ři stálé tlaku. S rostoucí telotou se roztažnost lynů ři stálé tlaku zvětšuje. Součinitel objeové
FYZIKA 2. ROČNÍK. Změny skupenství látek. Tání a tuhnutí. Pevná látka. soustava velkého počtu částic. Plyn
 Zěny skuenství látek Pevná látka Kaalina Plyn soustava velkého očtu částic Má-li soustava v rovnovážné stavu ve všech částech stejné fyzikální a cheické vlastnosti (stejnou hustotu, stejnou strukturu a
Zěny skuenství látek Pevná látka Kaalina Plyn soustava velkého očtu částic Má-li soustava v rovnovážné stavu ve všech částech stejné fyzikální a cheické vlastnosti (stejnou hustotu, stejnou strukturu a
Tento text doplňuje návod k úloze Měření momentu setrvačnosti uvedený ve skriptech Úvod do fyzikálních měření. V žádném případě si neklade za cíl být
 ento text dolňuje návod k úloze Měření oentu etvčnoti uvedený ve kitech Úvod do fyzikálních ěření. V žádné řídě i neklde z cíl být koletní návode o zěření úlohy. Cíle bylo dolnit teoetické infoce o obletice
ento text dolňuje návod k úloze Měření oentu etvčnoti uvedený ve kitech Úvod do fyzikálních ěření. V žádné řídě i neklde z cíl být koletní návode o zěření úlohy. Cíle bylo dolnit teoetické infoce o obletice
TECHNICKÁ UNIVERZITA V LIBERCI Katedra fyziky, Hálkova 6, Liberec
 TECHNICKÁ UNIVERITA V LIBERCI Ktedr fyziky, Hálkov 6, 46 7 Liberec htt://www.f.tul.cz/kfy/bs_uf_r.html POŽADAVKY PRO PŘIJÍMACÍ KOUŠKY FYIKY Akdemický rok: 008/009 fkult edgogická Témtické okruhy. Kinemtik
TECHNICKÁ UNIVERITA V LIBERCI Ktedr fyziky, Hálkov 6, 46 7 Liberec htt://www.f.tul.cz/kfy/bs_uf_r.html POŽADAVKY PRO PŘIJÍMACÍ KOUŠKY FYIKY Akdemický rok: 008/009 fkult edgogická Témtické okruhy. Kinemtik
VÝPOČET HLAVNÍCH ROZMĚRŮ ČTYŘTAKTNÍHO SPALOVACÍHO MOTORU
 Pítový alovací troj je teelný otor, kde e čát energie vzniklá álení aliva řeění v tlakovou energii. Tato energie oocí vhodného echaniu e ění v echanickou energii. Jako nejoužívanější echaniu k řeěně tlakové
Pítový alovací troj je teelný otor, kde e čát energie vzniklá álení aliva řeění v tlakovou energii. Tato energie oocí vhodného echaniu e ění v echanickou energii. Jako nejoužívanější echaniu k řeěně tlakové
MĚŘENÍ VLHKOSTI. Vlhkoměr CHM 10 s kapacitní sondou
 MĚŘENÍ VLHKOSTI 1. Úkol ěření a) Zěřte relativní vlhkost vzduchu v laboratoři sychroetre a oocí řístrojů s kaacitní olyerní sondou. b) S oocí tabulek a vzorců v teoretické úvodu vyočítejte rosný bod, absolutní
MĚŘENÍ VLHKOSTI 1. Úkol ěření a) Zěřte relativní vlhkost vzduchu v laboratoři sychroetre a oocí řístrojů s kaacitní olyerní sondou. b) S oocí tabulek a vzorců v teoretické úvodu vyočítejte rosný bod, absolutní
2.3. Fázové rovnováhy
 .3. Fázové rovováhy Buee e zabývat heterogeíi outavai obahujícíi jeu či více ložek, které olu cheicky ereagují. takové říaě očet ložek oovíá očtu cheických iiviuí (látek), kterýi je outava tvořea. Fázová
.3. Fázové rovováhy Buee e zabývat heterogeíi outavai obahujícíi jeu či více ložek, které olu cheicky ereagují. takové říaě očet ložek oovíá očtu cheických iiviuí (látek), kterýi je outava tvořea. Fázová
2.6.6 Sytá pára. Předpoklady: 2604
 .6.6 Sytá ára Předolady: 604 Oaování: aaliny se vyařují za aždé teloty. Nejrychlejší částice uniají z aaliny a stává se z nich ára. Do isy nalijee vodu voda se ostuně vyařuje naonec zůstane isa rázdná,
.6.6 Sytá ára Předolady: 604 Oaování: aaliny se vyařují za aždé teloty. Nejrychlejší částice uniají z aaliny a stává se z nich ára. Do isy nalijee vodu voda se ostuně vyařuje naonec zůstane isa rázdná,
Orientační odhad zatížitelnosti mostů pozemních komunikací v návaznosti na ČSN a TP200
 Orientční odhd ztížitelnoti motů pozemních komunikcí v návznoti n ČSN 73 6222 TP200 Úvod Ztížitelnot motů PK e muí tnovit jedním z náledujících potupů podle ČSN 73 6222, kpitol 6 : - podrobný ttický výpočet
Orientční odhd ztížitelnoti motů pozemních komunikcí v návznoti n ČSN 73 6222 TP200 Úvod Ztížitelnot motů PK e muí tnovit jedním z náledujících potupů podle ČSN 73 6222, kpitol 6 : - podrobný ttický výpočet
3. Kvadratické rovnice
 CZ..07/..08/0.0009. Kvdrtické rovnice se v tetice oznčuje lgebrická rovnice druhého stupně, tzn. rovnice o jedné neznáé, ve které neznáá vystupuje ve druhé ocnině (²). V zákldní tvru vypdá následovně:
CZ..07/..08/0.0009. Kvdrtické rovnice se v tetice oznčuje lgebrická rovnice druhého stupně, tzn. rovnice o jedné neznáé, ve které neznáá vystupuje ve druhé ocnině (²). V zákldní tvru vypdá následovně:
Stabilita prutu, desky a válce vzpěr (osová síla)
 Stabilita rutu, deky a válce vzěr (oová íla) Průběh ro ideálně římý rut (teoretický tav) F δ F KRIT Průběh ro reálně římý rut (reálný tav) 1 - menší očáteční zakřivení - větší očáteční zakřivení F Obr.1
Stabilita rutu, deky a válce vzěr (oová íla) Průběh ro ideálně římý rut (teoretický tav) F δ F KRIT Průběh ro reálně římý rut (reálný tav) 1 - menší očáteční zakřivení - větší očáteční zakřivení F Obr.1
( ) ( ) ( ) Exponenciální rovnice. 17.3. Řeš v R rovnici: 3 + 9 + 27 = ŘEŠENÍ: Postup z předešlého výpočtu doplníme využitím dalšího vztahu: ( ) t s t
 7. EXPONENCIÁLNÍ ROVNICE 7.. Řeš v R rovnice: ) 5 b) + c) 7 0 d) ( ) 0,5 ) 5 7 5 7 K { } c) 7 0 K d) ( ) b) + 0 + 0 K ( ) 5 0 5, 7 K { 5;7} Strtegie: potřebujeme zíkt tkový tvr rovnice, kd je n obou trnách
7. EXPONENCIÁLNÍ ROVNICE 7.. Řeš v R rovnice: ) 5 b) + c) 7 0 d) ( ) 0,5 ) 5 7 5 7 K { } c) 7 0 K d) ( ) b) + 0 + 0 K ( ) 5 0 5, 7 K { 5;7} Strtegie: potřebujeme zíkt tkový tvr rovnice, kd je n obou trnách
4.1 Kritéria rovnováhy
 4. F Á Z O V É R O V N O V Á H Y Fázové rovnováhy ředtavuji takové tavy ytéů, kdy jou ve vzájené terodynaické rovnováze dvě nebo více fázi. Fází oto rozuíe takovou čát outavy, jejíž vlatnoti jou v celé
4. F Á Z O V É R O V N O V Á H Y Fázové rovnováhy ředtavuji takové tavy ytéů, kdy jou ve vzájené terodynaické rovnováze dvě nebo více fázi. Fází oto rozuíe takovou čát outavy, jejíž vlatnoti jou v celé
IDEÁLNÍ PLYN II. Prof. RNDr. Emanuel Svoboda, CSc.
 IDEÁLNÍ PLYN II Prof. RNDr. Eanuel Svoboa, Sc. ZÁKLADNÍ RONIE PRO LAK IP F ýchoisko efinice tlaku vztahe S Náoba tvaru krychle, stejná rychlost olekul všei sěry (olekulární chaos, všechny sěry stejně ravěoobné)
IDEÁLNÍ PLYN II Prof. RNDr. Eanuel Svoboa, Sc. ZÁKLADNÍ RONIE PRO LAK IP F ýchoisko efinice tlaku vztahe S Náoba tvaru krychle, stejná rychlost olekul všei sěry (olekulární chaos, všechny sěry stejně ravěoobné)
2.3.6 Práce plynu. Předpoklady: 2305
 .3.6 Práce lynu Předoklady: 305 Děje v lynech nejčastěji zobrazujeme omocí diagramů grafů závislosti tlaku na objemu. Na x-ovou osu vynášíme objem a na y-ovou osu tlak. Př. : Na obrázku je nakreslen diagram
.3.6 Práce lynu Předoklady: 305 Děje v lynech nejčastěji zobrazujeme omocí diagramů grafů závislosti tlaku na objemu. Na x-ovou osu vynášíme objem a na y-ovou osu tlak. Př. : Na obrázku je nakreslen diagram
Výpo ty Výpo et hmotnostní koncentrace zne ující látky ,
 "Zracováno odle Skácel F. - Tekáč.: Podklady ro Ministerstvo životního rostředí k rovádění Protokolu o PRTR - řehled etod ěření a identifikace látek sledovaných odle Protokolu o registrech úniků a řenosů
"Zracováno odle Skácel F. - Tekáč.: Podklady ro Ministerstvo životního rostředí k rovádění Protokolu o PRTR - řehled etod ěření a identifikace látek sledovaných odle Protokolu o registrech úniků a řenosů
2.6.7 Fázový diagram. Předpoklady: Popiš děje zakreslené v diagramu křivky syté páry. Za jakých podmínek mohou proběhnout?
 2.6.7 Fázový diagram Předoklady: 2606 Př. 1: Poiš děje zakreslené v diagramu křivky syté áry. Za jakých odmínek mohou roběhnout? 4 2 1 3 1) Sytá ára je za stálého tlaku zahřívána. Zvětšuje svůj objem a
2.6.7 Fázový diagram Předoklady: 2606 Př. 1: Poiš děje zakreslené v diagramu křivky syté áry. Za jakých odmínek mohou roběhnout? 4 2 1 3 1) Sytá ára je za stálého tlaku zahřívána. Zvětšuje svůj objem a
( ) 1.2.19 Zákon zachování hybnosti II. Předpoklady: 010218
 ..9 Záon zchoání hybnoti II Předoldy: 8 Pedgogicá ozná: Cíl hodiny je jednoduchý. Studenti by e ěli nučit ottně rozhodot, j bude ydt dození onrétní ituce do záon zchoání hybnoti. Jde o jednu z nejleších
..9 Záon zchoání hybnoti II Předoldy: 8 Pedgogicá ozná: Cíl hodiny je jednoduchý. Studenti by e ěli nučit ottně rozhodot, j bude ydt dození onrétní ituce do záon zchoání hybnoti. Jde o jednu z nejleších
HYDROPNEUMATICKÝ VAKOVÝ AKUMULÁTOR
 HYDROPNEUMATICKÝ AKOÝ AKUMULÁTOR OSP 050 ŠEOBECNÉ INFORMACE ýočet hydroneumatického akumulátoru ZÁKLADNÍ INFORMACE Při výočtu hydroneumatického akumulátoru se vychází ze stavové změny lynu v akumulátoru.
HYDROPNEUMATICKÝ AKOÝ AKUMULÁTOR OSP 050 ŠEOBECNÉ INFORMACE ýočet hydroneumatického akumulátoru ZÁKLADNÍ INFORMACE Při výočtu hydroneumatického akumulátoru se vychází ze stavové změny lynu v akumulátoru.
2.2.9 Grafické řešení rovnic a nerovnic
 ..9 Grfické řešení rovnic nerovnic Předpokldy: 0, 06 Př. : Řeš početně i grficky rovnici x + = x. Početně: Už umíme. x + = x x = x = K = { } Grficky: Kždá ze strn rovnice je výrzem pro lineární funkci
..9 Grfické řešení rovnic nerovnic Předpokldy: 0, 06 Př. : Řeš početně i grficky rovnici x + = x. Početně: Už umíme. x + = x x = x = K = { } Grficky: Kždá ze strn rovnice je výrzem pro lineární funkci
i=1..k p x 2 p 2 s = y 2 p x 1 p 1 s = y 1 p 2
 i I i II... i F i..k Binární mě, ideální kaalina, ideální lyn x y y 2 Křivka bodů varu: Křivka roných bodů: Pákové ravidlo: x y y 2 n I n x I z II II z x Henryho zákon: 28-2 U měi hexan() + hetan(2) ři
i I i II... i F i..k Binární mě, ideální kaalina, ideální lyn x y y 2 Křivka bodů varu: Křivka roných bodů: Pákové ravidlo: x y y 2 n I n x I z II II z x Henryho zákon: 28-2 U měi hexan() + hetan(2) ři
Termodynamika ideálního plynu
 Přednáška 5 Termodynamika ideálního lynu 5.1 Základní vztahy ro ideální lyn 5.1.1 nitřní energie ideálního lynu Alikujme nyní oznatky získané v ředchozím textu na nejjednodužší termodynamickou soustavu
Přednáška 5 Termodynamika ideálního lynu 5.1 Základní vztahy ro ideální lyn 5.1.1 nitřní energie ideálního lynu Alikujme nyní oznatky získané v ředchozím textu na nejjednodužší termodynamickou soustavu
Základní principy fyziky semestrální projekt. Studium dynamiky kladky, závaží a vozíku
 Zákldní principy fyziky seestrální projekt Studiu dyniky kldky, závží vozíku Petr Luzr I/4 008/009 Zákldní principy fyziky Seestrální projekt Projekt zdl: Projekt vyprcovl: prof. In. rntišek Schuer, DrSc.
Zákldní principy fyziky seestrální projekt Studiu dyniky kldky, závží vozíku Petr Luzr I/4 008/009 Zákldní principy fyziky Seestrální projekt Projekt zdl: Projekt vyprcovl: prof. In. rntišek Schuer, DrSc.
1.2.4 Racionální čísla II
 .2.4 Racionální číla II Předoklady: 20 Pedagogická oznámka: S říkladem 0 je třeba začít nejozději 0 minut řed koncem hodiny. Př. : Sečti. Znázorni vůj otu graficky. 2 2 = = 2 Sčítáme netejné čáti muíme
.2.4 Racionální číla II Předoklady: 20 Pedagogická oznámka: S říkladem 0 je třeba začít nejozději 0 minut řed koncem hodiny. Př. : Sečti. Znázorni vůj otu graficky. 2 2 = = 2 Sčítáme netejné čáti muíme
s N, r > s platí: Základní požadavek na krásu matematického pravidla: Musí být co nejobecnější s minimem a a = a = a. Nemohli bychom ho upravit tak,
 .6. Mocniny celý ocnitele I Předpokldy: 6, 6 Př. : Kteé ze dvou pvidel je teticky hezčí? ) Po kždé R, N pltí: +. ) Po kždé R,, N, > pltí:. Zákldní poždvek n káu tetického pvidl: Muí ýt co nejoecnější inie
.6. Mocniny celý ocnitele I Předpokldy: 6, 6 Př. : Kteé ze dvou pvidel je teticky hezčí? ) Po kždé R, N pltí: +. ) Po kždé R,, N, > pltí:. Zákldní poždvek n káu tetického pvidl: Muí ýt co nejoecnější inie
13. Skupenské změny látek
 13. Skuenské změny látek Skuenství je konkrétní forma látky, charakterizovaná ředevším usořádáním částic v látce a rojevující se tyickými fyzikálními a chemickými vlastnostmi. Pro označení skuenství se
13. Skuenské změny látek Skuenství je konkrétní forma látky, charakterizovaná ředevším usořádáním částic v látce a rojevující se tyickými fyzikálními a chemickými vlastnostmi. Pro označení skuenství se
3.1.8 Přeměny energie v mechanickém oscilátoru
 3..8 Přeěny energie v echanické oscilátoru Předoklady: 0050, 03007 Pedagogická oznáka: Odvození zákona zachování energie rovádí na vodorovné ružině, rotože je říočařejší. Pro zájece je uvedeno na konci
3..8 Přeěny energie v echanické oscilátoru Předoklady: 0050, 03007 Pedagogická oznáka: Odvození zákona zachování energie rovádí na vodorovné ružině, rotože je říočařejší. Pro zájece je uvedeno na konci
Zavedení a vlastnosti reálných čísel PŘIROZENÁ, CELÁ A RACIONÁLNÍ ČÍSLA
 Zvedení vlstnosti reálných čísel Reálná čísl jsou zákldním kmenem mtemtické nlýzy. Konstrukce reálných čísel sice není náplní mtemtické nlýzy, le množin reálných čísel R je pro mtemtickou nlýzu zákldním
Zvedení vlstnosti reálných čísel Reálná čísl jsou zákldním kmenem mtemtické nlýzy. Konstrukce reálných čísel sice není náplní mtemtické nlýzy, le množin reálných čísel R je pro mtemtickou nlýzu zákldním
E = 1,1872 V ( = E Cu. (γ ± = 0, ,001 < I < 0,1 rozšířený D-H vztah)
 GALVANICKÉ ČLÁNKY E = E red,rvý E red,levý E D = E red,rvý E ox,levý E D G = z E E E S = z = z T E T T Q= T S [] G = z E rg E E rs = = z, r rg T rs z = = T E T T T E E T T ν i E = E ln i z i mimo rovnováhu
GALVANICKÉ ČLÁNKY E = E red,rvý E red,levý E D = E red,rvý E ox,levý E D G = z E E E S = z = z T E T T Q= T S [] G = z E rg E E rs = = z, r rg T rs z = = T E T T T E E T T ν i E = E ln i z i mimo rovnováhu
Hustota plynů - jak ji změřit?
 eletrh náadů učitelů fyziky 9 Hustota lynů - jak ji zěřit? ER SÁDEK, UKÁŠ AWERA edagogická fakulta U, Brno Abstrakt ěření hustoty evných látek a kaalin je běžná laboratorní úloha na řadě škol, nicéně ěření
eletrh náadů učitelů fyziky 9 Hustota lynů - jak ji zěřit? ER SÁDEK, UKÁŠ AWERA edagogická fakulta U, Brno Abstrakt ěření hustoty evných látek a kaalin je běžná laboratorní úloha na řadě škol, nicéně ěření
ROVNOBĚŽNÉ PROMÍTÁNÍ, VOLNÉ ROVNOBĚŽNÉ PROMÍTÁNÍ
 Technická univerzit v Liberci Fkult přírodovědně-humnitní pedgogická Ktedr mtemtiky didktiky mtemtiky ROVNOĚŽNÉ PROMÍTÁNÍ, VOLNÉ ROVNOĚŽNÉ PROMÍTÁNÍ Pomocný učební text Petr Pirklová Liberec, září 2013
Technická univerzit v Liberci Fkult přírodovědně-humnitní pedgogická Ktedr mtemtiky didktiky mtemtiky ROVNOĚŽNÉ PROMÍTÁNÍ, VOLNÉ ROVNOĚŽNÉ PROMÍTÁNÍ Pomocný učební text Petr Pirklová Liberec, září 2013
Oxidačně-redukční reakce (Redoxní reakce)
 Seminář z nlytické chemie idčně-redukční rekce (Redoxní rekce) RNDr. R. Čbl, Dr. Univerzit Krlov v Prze Přírodovědecká fkult Ktedr nlytické chemie Definice pojmů idce částice (tom, molekul, ion) ztrácí
Seminář z nlytické chemie idčně-redukční rekce (Redoxní rekce) RNDr. R. Čbl, Dr. Univerzit Krlov v Prze Přírodovědecká fkult Ktedr nlytické chemie Definice pojmů idce částice (tom, molekul, ion) ztrácí
1 Poznámka k termodynamice: Jednoatomový či dvouatomový plyn?
 Kvantová a statistická fyzika (erodynaika a statistická fyzika) 1 Poznáka k terodynaice: Jednoatoový či dvouatoový plyn? Jeden ol jednoatoového plynu o teplotě zaujíá obje V. Plyn však ůže projít cheickou
Kvantová a statistická fyzika (erodynaika a statistická fyzika) 1 Poznáka k terodynaice: Jednoatoový či dvouatoový plyn? Jeden ol jednoatoového plynu o teplotě zaujíá obje V. Plyn však ůže projít cheickou
Název školy. Moravské gymnázium Brno s.r.o. Mgr. Marie Chadimová Mgr. Věra Jeřábková. Autor. Matematika 02a Racionální čísla. Text a příklady.
 Čílo ojektu CZ..07/..00/4.074 Název školy Movké gymnázium Bno..o. Auto Temtiká olt Mg. Mie Chdimová Mg. Vě Jeřáková Mtemtik 0 Rionální číl. Text říkldy. Ročník. Dtum tvoy.. 0 Anote ) o žáky jko text látky,
Čílo ojektu CZ..07/..00/4.074 Název školy Movké gymnázium Bno..o. Auto Temtiká olt Mg. Mie Chdimová Mg. Vě Jeřáková Mtemtik 0 Rionální číl. Text říkldy. Ročník. Dtum tvoy.. 0 Anote ) o žáky jko text látky,
Lomová houževnatost. plastická deformace. R e = K C
 Loová houžvntost UM - 5 Loová houžvntost Jéno: St. suin: Dtu cviční: ) Stručně oišt, co vyjdřují ojy ) nětí - z luzu b) součinitl intnzity nětí - loová houžvntost. Disutujt oužití vzthu ro výočt součinitl
Loová houžvntost UM - 5 Loová houžvntost Jéno: St. suin: Dtu cviční: ) Stručně oišt, co vyjdřují ojy ) nětí - z luzu b) součinitl intnzity nětí - loová houžvntost. Disutujt oužití vzthu ro výočt součinitl
1.4.3 Zrychlující vztažné soustavy II
 143 Zrychlující vztažné outavy II Předoklady: 1402 Př 1: Vaón SVARME rovnoměrně zrychluje dorava Rozeber ilové ůobení a tav čidel na nátuišti z ohledu MOBILů Čidla na nátuišti (ohled MOBILŮ ze zrychlujícího
143 Zrychlující vztažné outavy II Předoklady: 1402 Př 1: Vaón SVARME rovnoměrně zrychluje dorava Rozeber ilové ůobení a tav čidel na nátuišti z ohledu MOBILů Čidla na nátuišti (ohled MOBILŮ ze zrychlujícího
25 Měrný náboj elektronu
 5 Měrný náboj elektronu ÚKOL Stnovte ěrný náboj elektronu e výsledek porovnejte s tbulkovou hodnotou. TEORIE Poěr náboje elektronu e hotnosti elektronu nzýváe ěrný náboj elektronu. Jednou z ožných etod
5 Měrný náboj elektronu ÚKOL Stnovte ěrný náboj elektronu e výsledek porovnejte s tbulkovou hodnotou. TEORIE Poěr náboje elektronu e hotnosti elektronu nzýváe ěrný náboj elektronu. Jednou z ožných etod
Fázové přechody. navzájem nezávislé chemicky čisté látky obsažené v termod.soustavě
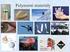 Fázoé řechody Složky soustay s: nazáje nezáislé cheicky čisté látky obsažené terod.soustaě Fáze látky f: hoogenní soubor olekul, který je akroskoické ěřítku ostře ohraničen od jiných souborů olekul, které
Fázoé řechody Složky soustay s: nazáje nezáislé cheicky čisté látky obsažené terod.soustaě Fáze látky f: hoogenní soubor olekul, který je akroskoické ěřítku ostře ohraničen od jiných souborů olekul, které
teorie elektronických obvodů Jiří Petržela syntéza elektronických obvodů
 Jiří Petržela příklad nalezněte dvě různé realizace admitanční funkce zadané formou racionální lomené funkce Y () () ( ) ( ) : první krok rozkladu do řetězového zlomku () 9 7 9 výledný rozklad ( ) 9 9
Jiří Petržela příklad nalezněte dvě různé realizace admitanční funkce zadané formou racionální lomené funkce Y () () ( ) ( ) : první krok rozkladu do řetězového zlomku () 9 7 9 výledný rozklad ( ) 9 9
ANALYTICKÁ GEOMETRIE V PROSTORU
 ANALYTICKÁ GEOMETRIE V PROSTORU 3. přednášk Vektorová lger Prvoúhlé souřdnice odu v prostoru Poloh odu v prostoru je vzhledem ke třem osám k soě kolmým určen třemi souřdnicemi, které tvoří uspořádnou trojici
ANALYTICKÁ GEOMETRIE V PROSTORU 3. přednášk Vektorová lger Prvoúhlé souřdnice odu v prostoru Poloh odu v prostoru je vzhledem ke třem osám k soě kolmým určen třemi souřdnicemi, které tvoří uspořádnou trojici
Obecně: K dané funkci f hledáme funkci ϕ z dané množiny funkcí M, pro kterou v daných bodech x 0 < x 1 <... < x n. (δ ij... Kroneckerovo delta) (4)
 KAPITOLA 13: Numerická integrce interpolce [MA1-18:P13.1] 13.1 Interpolce Obecně: K dné funkci f hledáme funkci ϕ z dné množiny funkcí M, pro kterou v dných bodech x 0 < x 1
KAPITOLA 13: Numerická integrce interpolce [MA1-18:P13.1] 13.1 Interpolce Obecně: K dné funkci f hledáme funkci ϕ z dné množiny funkcí M, pro kterou v dných bodech x 0 < x 1
1.2.2 Síly II. Předpoklady: 1201
 1.. Síly II Předoklady: 101 Oakování z minulé hodiny: Pohyb a jeho změny zůobují íly. Pro každou ravou ílu můžeme najít: ůvodce (těleo, které ji zůobuje), cíl (těleo, na které íla ůobí), artnerkou ílu
1.. Síly II Předoklady: 101 Oakování z minulé hodiny: Pohyb a jeho změny zůobují íly. Pro každou ravou ílu můžeme najít: ůvodce (těleo, které ji zůobuje), cíl (těleo, na které íla ůobí), artnerkou ílu
V p-v diagramu je tento proces znázorněn hyperbolou spojující body obou stavů plynu, je to tzv. izoterma :
 Jednoduché vratné děje ideálního lynu ) Děj izoter mický ( = ) Za ředokladu konstantní teloty se stavová rovnice ro zadané množství lynu změní na známý zákon Boylův-Mariottův, která říká, že součin tlaku
Jednoduché vratné děje ideálního lynu ) Děj izoter mický ( = ) Za ředokladu konstantní teloty se stavová rovnice ro zadané množství lynu změní na známý zákon Boylův-Mariottův, která říká, že součin tlaku
6. Zobrazení δ: (a) δ(q 0, x) obsahuje x i, x i Z. (b) δ(x i, y) obsahuje y j, x i y j P 7. Množina F je množinou koncových stavů.
 Vzth mezi reg. výrzy kon. utomty Automty grmtiky(bi-aag) 7. Převody mezi reg. grm., reg. výrzy kon. utomty Jn Holu Algoritmus (okrčování): 6. Zorzení δ: () δ(, x) oshuje x i, x i Z. () δ(x i, y) oshuje
Vzth mezi reg. výrzy kon. utomty Automty grmtiky(bi-aag) 7. Převody mezi reg. grm., reg. výrzy kon. utomty Jn Holu Algoritmus (okrčování): 6. Zorzení δ: () δ(, x) oshuje x i, x i Z. () δ(x i, y) oshuje
nebo její linearizovaný tvar a T
 lk syté áry záislost n telotě Úod: Měření záislosti tlku syté áry n telotě má ýznm ro zjišťoání telot ru klin jejich směsí ři různých tlcích nok k ýočtu složení r jejich směsí ři různých telotách ru, okud
lk syté áry záislost n telotě Úod: Měření záislosti tlku syté áry n telotě má ýznm ro zjišťoání telot ru klin jejich směsí ři různých tlcích nok k ýočtu složení r jejich směsí ři různých telotách ru, okud
ZÁKLADY. y 1 + y 2 dx a. kde y je hledanou funkcí proměnné x.
 VARIAČNÍ POČET ZÁKLADY V prxi se čsto hledjí křivky nebo plochy, které minimlizují nebo mximlizují jisté hodnoty. Npř. se hledá nejkrtší spojnice dvou bodů n dné ploše, nebo tvr zvěšeného ln (má minimální
VARIAČNÍ POČET ZÁKLADY V prxi se čsto hledjí křivky nebo plochy, které minimlizují nebo mximlizují jisté hodnoty. Npř. se hledá nejkrtší spojnice dvou bodů n dné ploše, nebo tvr zvěšeného ln (má minimální
Lineární nerovnice a jejich soustavy
 teorie řešené úlohy cvičení tipy k mturitě výsledky Lineární nerovnice jejich soustvy Víš, že pojem nerovnice není opkem pojmu rovnice? lineární rovnice má většinou jediné řešení, kdežto lineární nerovnice
teorie řešené úlohy cvičení tipy k mturitě výsledky Lineární nerovnice jejich soustvy Víš, že pojem nerovnice není opkem pojmu rovnice? lineární rovnice má většinou jediné řešení, kdežto lineární nerovnice
DOPLŇKOVÉ TEXTY BB01 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ TUHÉ TĚLESO
 DOPLŇKOÉ TXTY BB0 PAL SCHAUR INTRNÍ MATRIÁL FAST UT BRNĚ TUHÉ TĚLSO Tuhé těleso je těleso, o teé latí, že libovolná síla ůsobící na těleso nezůsobí jeho defoaci, ale ůže ít ouze ohybový účine. Libovolná
DOPLŇKOÉ TXTY BB0 PAL SCHAUR INTRNÍ MATRIÁL FAST UT BRNĚ TUHÉ TĚLSO Tuhé těleso je těleso, o teé latí, že libovolná síla ůsobící na těleso nezůsobí jeho defoaci, ale ůže ít ouze ohybový účine. Libovolná
Posloupnosti ( 1) ( ) 1. Různým způsobem (rekurentně i jinak) zadané posloupnosti. 2. Aritmetická posloupnost
 Poloupoti Růzým způobem (rekuretě i jik zdé poloupoti Urči prvích pět čleů poloupoti, ve které, + Urči prvích pět čleů poloupoti, je-li dáo:, + + Urči prvích pět čleů poloupoti, je-li dáo: 0,, Urči prvích
Poloupoti Růzým způobem (rekuretě i jik zdé poloupoti Urči prvích pět čleů poloupoti, ve které, + Urči prvích pět čleů poloupoti, je-li dáo:, + + Urči prvích pět čleů poloupoti, je-li dáo: 0,, Urči prvích
DERIVACE A INTEGRÁLY VE FYZICE
 DOPLŇKOVÉ TEXTY BB0 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ DERIVACE A INTEGRÁLY VE FYZICE Obsh Derivce... Definice derivce... Prciální derivce... Derivce vektorů... Výpočt derivcí... 3 Algebrická
DOPLŇKOVÉ TEXTY BB0 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ DERIVACE A INTEGRÁLY VE FYZICE Obsh Derivce... Definice derivce... Prciální derivce... Derivce vektorů... Výpočt derivcí... 3 Algebrická
I. termodynamický zákon
 řednášk 4 I. termodynmický zákon I. termodynmický zákon jkožto nejobecnější zákon zchování energie je jedním ze zákldních stvebních kmenů termodynmiky. této přednášce zopkujeme znění tohoto zákon n jeho
řednášk 4 I. termodynmický zákon I. termodynmický zákon jkožto nejobecnější zákon zchování energie je jedním ze zákldních stvebních kmenů termodynmiky. této přednášce zopkujeme znění tohoto zákon n jeho
3. V případě dvou na sebe kolmých posunutí o velikostech 3 cm a 4 cm obdržíme výsledné posunutí o velikosti a) 8 cm b) 7 cm c) 6 cm d) 5 cm *
 Fyzika 1 2009 Otázky za 2 body 1. Mezi tavové veličiny patří a) teplo b) teplota * c) práce d) univerzální plynová kontanta 2. Krychle má hranu o délce 2 mm. Jaký je její objem v krychlových metrech? a)
Fyzika 1 2009 Otázky za 2 body 1. Mezi tavové veličiny patří a) teplo b) teplota * c) práce d) univerzální plynová kontanta 2. Krychle má hranu o délce 2 mm. Jaký je její objem v krychlových metrech? a)
( t) ( t) ( ( )) ( ) ( ) ( ) Vzdálenost bodu od přímky I. Předpoklady: 7308
 731 Vzdálenost odu od římky I Předokldy: 7308 Pedgogiká oznámk: Pokud máte málo čsu, můžete odvodit vzore ez smosttné ráe studentů oužít některý z říkldů z dlší hodiny Tím jednu ze dvou hodin ro vzdálenost
731 Vzdálenost odu od římky I Předokldy: 7308 Pedgogiká oznámk: Pokud máte málo čsu, můžete odvodit vzore ez smosttné ráe studentů oužít některý z říkldů z dlší hodiny Tím jednu ze dvou hodin ro vzdálenost
Algebraický výraz je číselný výraz s proměnou. V těchto výrazech se vyskytují vedle reálných čísel také proměnné. Například. 4a 4,5x + 6,78 7t.
 9 očník - lomený lgeický vý, lineání ovnice nenámo ve jmenovteli Lomený lgeický vý Lineání ovnice nenámo ve jmenovteli Doočjeme žákům okovt voce t ( ) od úv vý n očin Lomený vý Číelné vý jo vý v nichž
9 očník - lomený lgeický vý, lineání ovnice nenámo ve jmenovteli Lomený lgeický vý Lineání ovnice nenámo ve jmenovteli Doočjeme žákům okovt voce t ( ) od úv vý n očin Lomený vý Číelné vý jo vý v nichž
VÝZNAM EVAPOTRANSPIRACE V HYDROLOGICKÉ BILANCI MALÉHO POVODÍ
 UNIVERZITA KARLOVA V PRAZE Přírodovědecká fkult Ktedr fyzické geogrfie geoekologie Studijní progrm: Geogrfie Studijní obor: Geogrfie krtogrfie Jitk KOFROŇOVÁ VÝZNAM EVAPOTRANSPIRACE V HYDROLOGICKÉ BILANCI
UNIVERZITA KARLOVA V PRAZE Přírodovědecká fkult Ktedr fyzické geogrfie geoekologie Studijní progrm: Geogrfie Studijní obor: Geogrfie krtogrfie Jitk KOFROŇOVÁ VÝZNAM EVAPOTRANSPIRACE V HYDROLOGICKÉ BILANCI
ZKRATOVÉ PROUDY VÝPOČET ÚČINKŮ ČÁST 2: PŘÍKLADY VÝPOČTŮ
 Podniková norm energetiky pro rozvod elektrické energie Konečný návrh ČEPS,.., ČEZ Ditribuce, E.ON CZ, E.ON Ditribuce, PREditribuce, ZKRATOVÉ PROUDY VÝPOČET ÚČINKŮ ČÁST : PŘÍKLADY VÝPOČTŮ PNE 041 Třetí
Podniková norm energetiky pro rozvod elektrické energie Konečný návrh ČEPS,.., ČEZ Ditribuce, E.ON CZ, E.ON Ditribuce, PREditribuce, ZKRATOVÉ PROUDY VÝPOČET ÚČINKŮ ČÁST : PŘÍKLADY VÝPOČTŮ PNE 041 Třetí
Popis fyzikálního chování látek
 Popis fyzikálního chování látek pro vysvětlení noha fyzikálních jevů již nevystačíe s pouhý echanický popise Terodynaika oblast fyziky, která kroě echaniky zkouá vlastnosti akroskopických systéů, zejéna
Popis fyzikálního chování látek pro vysvětlení noha fyzikálních jevů již nevystačíe s pouhý echanický popise Terodynaika oblast fyziky, která kroě echaniky zkouá vlastnosti akroskopických systéů, zejéna
8. Termodynamika a molekulová fyzika
 8. erodynaika a olekulová fyzika Princi energie je záležitost zkušenosti. Pokud by tedy jednoho dne ěla být jeho všeobecná latnost zochybněna, což v atoové fyzice není vyloučeno, stal by se náhle aktuální
8. erodynaika a olekulová fyzika Princi energie je záležitost zkušenosti. Pokud by tedy jednoho dne ěla být jeho všeobecná latnost zochybněna, což v atoové fyzice není vyloučeno, stal by se náhle aktuální
Úlohy školní klauzurní části I. kola kategorie C
 52. ročník mtemtické olympiády Úlohy školní kluzurní části I. kol ktegorie 1. Odtrhneme-li od libovolného lespoň dvojmístného přirozeného čísl číslici n místě jednotek, dostneme číslo o jednu číslici krtší.
52. ročník mtemtické olympiády Úlohy školní kluzurní části I. kol ktegorie 1. Odtrhneme-li od libovolného lespoň dvojmístného přirozeného čísl číslici n místě jednotek, dostneme číslo o jednu číslici krtší.
3. ROVNICE A NEROVNICE 85. 3.1. Lineární rovnice 85. 3.2. Kvadratické rovnice 86. 3.3. Rovnice s absolutní hodnotou 88. 3.4. Iracionální rovnice 90
 ROVNICE A NEROVNICE 8 Lineární rovnice 8 Kvdrtické rovnice 8 Rovnice s bsolutní hodnotou 88 Ircionální rovnice 90 Eponenciální rovnice 9 Logritmické rovnice 9 7 Goniometrické rovnice 98 8 Nerovnice 0 Úlohy
ROVNICE A NEROVNICE 8 Lineární rovnice 8 Kvdrtické rovnice 8 Rovnice s bsolutní hodnotou 88 Ircionální rovnice 90 Eponenciální rovnice 9 Logritmické rovnice 9 7 Goniometrické rovnice 98 8 Nerovnice 0 Úlohy
8. Elementární funkce
 Historie přírodních věd potvrzuje, že většinu reálně eistujících dějů lze reprezentovt mtemtickými model, které jsou popsán tzv. elementárními funkcemi. Elementární funkce je kždá funkce, která vznikne
Historie přírodních věd potvrzuje, že většinu reálně eistujících dějů lze reprezentovt mtemtickými model, které jsou popsán tzv. elementárními funkcemi. Elementární funkce je kždá funkce, která vznikne
Ohýbaný nosník - napětí
 Pružnost pevnost BD0 Ohýbný nosník - npětí Teorie Prostý ohb, rovinný ohb Při prostém ohbu je průřez nmáhán ohbovým momentem otáčejícím kolem jedné z hlvních os setrvčnosti průřezu, obvkle os. oment se
Pružnost pevnost BD0 Ohýbný nosník - npětí Teorie Prostý ohb, rovinný ohb Při prostém ohbu je průřez nmáhán ohbovým momentem otáčejícím kolem jedné z hlvních os setrvčnosti průřezu, obvkle os. oment se
2.1 - ( ) ( ) (020201) [ ] [ ]
![2.1 - ( ) ( ) (020201) [ ] [ ] 2.1 - ( ) ( ) (020201) [ ] [ ]](/thumbs/102/155984102.jpg) - FUNKCE A ROVNICE Následující zákldní znlosti je nezbytně nutné umět od okmžiku probrání ž do konce studi mtemtiky n gymnáziu. Vyždováno bude porozumění schopnost plikovt ne pouze mechnicky zopkovt. Některé
- FUNKCE A ROVNICE Následující zákldní znlosti je nezbytně nutné umět od okmžiku probrání ž do konce studi mtemtiky n gymnáziu. Vyždováno bude porozumění schopnost plikovt ne pouze mechnicky zopkovt. Některé
Souhrn základních výpočetních postupů v Excelu probíraných v AVT 04-05 listopad 2004. r r. . b = A
 Souhrn zákldních výpočetních postupů v Ecelu probírných v AVT 04-05 listopd 2004. Řešení soustv lineárních rovnic Soustv lineárních rovnic ve tvru r r A. = b tj. npř. pro 3 rovnice o 3 neznámých 2 3 Hodnoty
Souhrn zákldních výpočetních postupů v Ecelu probírných v AVT 04-05 listopd 2004. Řešení soustv lineárních rovnic Soustv lineárních rovnic ve tvru r r A. = b tj. npř. pro 3 rovnice o 3 neznámých 2 3 Hodnoty
V následující tabulce jsou uvedeny jednotky pro objemový a hmotnostní průtok.
 8. Měření růtoků V následující tabulce jsou uvedeny jednotky ro objemový a hmotnostní růtok. Základní vztahy ro stacionární růtok Q M V t S w M V QV ρ ρ S w ρ t t kde V [ m 3 ] - objem t ( s ] - čas, S
8. Měření růtoků V následující tabulce jsou uvedeny jednotky ro objemový a hmotnostní růtok. Základní vztahy ro stacionární růtok Q M V t S w M V QV ρ ρ S w ρ t t kde V [ m 3 ] - objem t ( s ] - čas, S
Přednášky část 2 Únavové křivky a únavová bezpečnost
 DPŽ 1 Přednášky čát 2 Únvové křivky únvová bezpečnot Miln Růžičk mechnik.f.cvut.cz miln.ruzick@f.cvut.cz DPŽ 2 Únvové křivky npětí (tre-life curve S-N curve) DPŽ 3 Hitorie únvy mteriálu 19. toletí rozvoj
DPŽ 1 Přednášky čát 2 Únvové křivky únvová bezpečnot Miln Růžičk mechnik.f.cvut.cz miln.ruzick@f.cvut.cz DPŽ 2 Únvové křivky npětí (tre-life curve S-N curve) DPŽ 3 Hitorie únvy mteriálu 19. toletí rozvoj
7. Fázové přeměny Separace
 7. Fázové řeměny Searace Fáze Fázové rovnováhy Searace látek Evroský sociální fond Praha & EU: Investujeme do vaší budoucnosti 7. Fázové řeměny Searace fáze - odlišitelný stav látky v systému; v určité
7. Fázové řeměny Searace Fáze Fázové rovnováhy Searace látek Evroský sociální fond Praha & EU: Investujeme do vaší budoucnosti 7. Fázové řeměny Searace fáze - odlišitelný stav látky v systému; v určité
Využití aproximačních funkcí pro kaskádní syntézu filtrů
 Pučochář, J.: Využití roximčích fukcí ro kkádí ytézu filtrů Využití roximčích fukcí ro kkádí ytézu filtrů Mteriál louží ouze jko růvodce k mteriálu odrobějšímu, který je dotuý trákách htt:mi.vb.cz Tm jou
Pučochář, J.: Využití roximčích fukcí ro kkádí ytézu filtrů Využití roximčích fukcí ro kkádí ytézu filtrů Mteriál louží ouze jko růvodce k mteriálu odrobějšímu, který je dotuý trákách htt:mi.vb.cz Tm jou
Zákon zachování hybnosti I
 8 Zákon zachování hybnoti I Předoklady: 007 Dneka e budeme zabývat třelbou z alných zbraní Při výtřelu zíká třela obrovkou rychlot a zbraň odkočí na druhou tranu Proč? Př : Na obrázku je nakrelena třela
8 Zákon zachování hybnoti I Předoklady: 007 Dneka e budeme zabývat třelbou z alných zbraní Při výtřelu zíká třela obrovkou rychlot a zbraň odkočí na druhou tranu Proč? Př : Na obrázku je nakrelena třela
Termodynamické základy ocelářských pochodů
 29 3. Termodynamické základy ocelářských ochodů Termodynamika ůvodně vznikla jako vědní discilína zabývající se účinností teelných (arních) strojů. Později byly termodynamické zákony oužity ři studiu chemických
29 3. Termodynamické základy ocelářských ochodů Termodynamika ůvodně vznikla jako vědní discilína zabývající se účinností teelných (arních) strojů. Později byly termodynamické zákony oužity ři studiu chemických
Komplexní čísla tedy násobíme jako dvojčleny s tím, že použijeme vztah i 2 = 1. = (a 1 + ia 2 )(b 1 ib 2 ) b 2 1 + b2 2.
 7 Komplexní čísl 71 Komplexní číslo je uspořádná dvojice reálných čísel Komplexní číslo = 1, ) zprvidl zpisujeme v tzv lgebrickém tvru = 1 + i, kde i je imginární jednotk, pro kterou pltí i = 1 Číslo 1
7 Komplexní čísl 71 Komplexní číslo je uspořádná dvojice reálných čísel Komplexní číslo = 1, ) zprvidl zpisujeme v tzv lgebrickém tvru = 1 + i, kde i je imginární jednotk, pro kterou pltí i = 1 Číslo 1
Termodynamický popis chemicky reagujícího systému
 5. CHEMICKÉ ROVNOVÁHY Všechny chemcké rekce směřují k dynmcké rovnováze, v níž jsou řítomny jk výchozí látky tk rodukty, které všk nemjí jž tendenc se měnt. V řdě řídů je všk oloh rovnováhy tk osunut ve
5. CHEMICKÉ ROVNOVÁHY Všechny chemcké rekce směřují k dynmcké rovnováze, v níž jsou řítomny jk výchozí látky tk rodukty, které všk nemjí jž tendenc se měnt. V řdě řídů je všk oloh rovnováhy tk osunut ve
WASH-OUT ALGORITMUS PRO ŘIDIČSKÉ A LETECKÉ SIMULÁTORY
 WASH-OUT ALGORITMUS PRO ŘIDIČSKÉ A LETECKÉ SIMULÁTORY E. Thöndel Ktedr elektrických pohonů trkce, FEL ČVUT v Prze Abtrkt Přípěvek popiuje vývoj imulčního modelu lgoritmu imulce pohybových vjemů (wh-out
WASH-OUT ALGORITMUS PRO ŘIDIČSKÉ A LETECKÉ SIMULÁTORY E. Thöndel Ktedr elektrických pohonů trkce, FEL ČVUT v Prze Abtrkt Přípěvek popiuje vývoj imulčního modelu lgoritmu imulce pohybových vjemů (wh-out
Zadání. Přílohy. Požadavky. Úloha č. 3. Výpočet denního osvětlení D = D S = 10 0 % E H D S. D e D i
 Ing. Martina Zapletalová, Ph.., K 124, A 728 F 1 Úloha č. 3 Výpočet denního ovětlení Zadání Pouďte zadanou ítnot - z hledika denního ovětlení (TANOVTE CELKOVÝ ČINITEL ENNÍ OVĚTLENOTI) na rovnávací rovině,
Ing. Martina Zapletalová, Ph.., K 124, A 728 F 1 Úloha č. 3 Výpočet denního ovětlení Zadání Pouďte zadanou ítnot - z hledika denního ovětlení (TANOVTE CELKOVÝ ČINITEL ENNÍ OVĚTLENOTI) na rovnávací rovině,
Větrání hromadných garáží
 ětrání hromadných garáží Domácí ředis: ČSN 73 6058 Hromadné garáže, základní ustanovení, latná od r. 1987 Zahraniční ředisy: ÖNORM H 6003 Lüftungstechnische Anlagen für Garagen. Grundlagen, Planung, Dimensionierung,
ětrání hromadných garáží Domácí ředis: ČSN 73 6058 Hromadné garáže, základní ustanovení, latná od r. 1987 Zahraniční ředisy: ÖNORM H 6003 Lüftungstechnische Anlagen für Garagen. Grundlagen, Planung, Dimensionierung,
Metoda konečných prvků Základní veličiny, rovnice a vztahy (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika)
 Inovace tudijního oboru Geotechnika Reg. č. CZ..7/../8.9 Metoda konečných prvků Základní veličin, rovnice a vztah (výuková prezentace pro. ročník navazujícího tudijního oboru Geotechnika) Doc. RNDr. Eva
Inovace tudijního oboru Geotechnika Reg. č. CZ..7/../8.9 Metoda konečných prvků Základní veličin, rovnice a vztah (výuková prezentace pro. ročník navazujícího tudijního oboru Geotechnika) Doc. RNDr. Eva
2.9.14 Věty o logaritmech I
 .9.1 Věty o itmech I Předpokldy: 910 Pedgogická poznámk: Tto náledující hodin e djí tihnout njednou, pokud oželíte počítání v tbulce někteé příkldy n konci příští hodiny. Přijde mi to tochu škod, nžím
.9.1 Věty o itmech I Předpokldy: 910 Pedgogická poznámk: Tto náledující hodin e djí tihnout njednou, pokud oželíte počítání v tbulce někteé příkldy n konci příští hodiny. Přijde mi to tochu škod, nžím
Head space. - technika výhradně spojená s plynovou chromatografií
 Izolační a eparační etody J. Poutka, VŠCHT Praha, ÚPV 204, http://web.vcht.cz/poutkaj Head pace (nebo Headpace nebo Head-pace) - technika výhradně pojená plynovou chroatografií - vzorkuje e tzv. hlavový
Izolační a eparační etody J. Poutka, VŠCHT Praha, ÚPV 204, http://web.vcht.cz/poutkaj Head pace (nebo Headpace nebo Head-pace) - technika výhradně pojená plynovou chroatografií - vzorkuje e tzv. hlavový
5. Výpočty s využitím vztahů mezi stavovými veličinami ideálního plynu
 . ýpočty s využití vztahů ezi stavovýi veličinai ideálního plynu Ze zkušenosti víe, že obje plynu - na rozdíl od objeu pevné látky nebo kapaliny - je vyezen prostore, v něž je plyn uzavřen. Přítonost plynu
. ýpočty s využití vztahů ezi stavovýi veličinai ideálního plynu Ze zkušenosti víe, že obje plynu - na rozdíl od objeu pevné látky nebo kapaliny - je vyezen prostore, v něž je plyn uzavřen. Přítonost plynu
Cvičení z termomechaniky Cvičení 5.
 Příklad V komresoru je kontinuálně stlačován objemový tok vzduchu *m 3.s- + o telotě 0 * C+ a tlaku 0, *MPa+ na tlak 0,7 *MPa+. Vyočtěte objemový tok vzduchu vystuujícího z komresoru, jeho telotu a říkon
Příklad V komresoru je kontinuálně stlačován objemový tok vzduchu *m 3.s- + o telotě 0 * C+ a tlaku 0, *MPa+ na tlak 0,7 *MPa+. Vyočtěte objemový tok vzduchu vystuujícího z komresoru, jeho telotu a říkon
4. TROJFÁZOVÉ OBVODY
 Katedra obecné elektrotechniky Fakulta elektrotechniky a inforatiky, VŠB - T Otrava 4. TROJFÁZOVÉ OBVODY rčeno pro poluchače všech bakalářkých tudijních prograů FS 4. Úvod 4. Trojfázová outava 4. Spojení
Katedra obecné elektrotechniky Fakulta elektrotechniky a inforatiky, VŠB - T Otrava 4. TROJFÁZOVÉ OBVODY rčeno pro poluchače všech bakalářkých tudijních prograů FS 4. Úvod 4. Trojfázová outava 4. Spojení
MIČKAL, Karel. Technická mechanika II: pro střední odborná učiliště. Vyd. 3., nezm. Praha: Informatorium, 1998c1990, 118 s. ISBN
 Identifikátor teriálu: ICT 0 Reitrční čílo rojektu Náze rojektu Náze říjee odory náze teriálu DUM Anote Autor Jzyk Očekáný ýtu Klíčoá lo Dru učenío teriálu Dru interktiity Cíloá kuin tueň ty zděláání Tyiká
Identifikátor teriálu: ICT 0 Reitrční čílo rojektu Náze rojektu Náze říjee odory náze teriálu DUM Anote Autor Jzyk Očekáný ýtu Klíčoá lo Dru učenío teriálu Dru interktiity Cíloá kuin tueň ty zděláání Tyiká
P2 Číselné soustavy, jejich převody a operace v čís. soustavách
 P Číselné soustvy, jejich převody operce v čís. soustvách. Zobrzení čísl v libovolné číselné soustvě Lidé využívjí ve svém životě pro zápis čísel desítkovou soustvu. V této soustvě máme pro zápis čísel
P Číselné soustvy, jejich převody operce v čís. soustvách. Zobrzení čísl v libovolné číselné soustvě Lidé využívjí ve svém životě pro zápis čísel desítkovou soustvu. V této soustvě máme pro zápis čísel
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE. 123TVVM homogenizace (směšovací pravidla)
 KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 23TVVM hoogenizce (sěšovcí prvidl) Hoogenizce Stvební teriály sou z hledisk zstoupení doinntních složek několikfázové systéy: Dvoufázové trice, vzduch (póry)
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 23TVVM hoogenizce (sěšovcí prvidl) Hoogenizce Stvební teriály sou z hledisk zstoupení doinntních složek několikfázové systéy: Dvoufázové trice, vzduch (póry)
Katedra geotechniky a podzemního stavitelství
 Katedra geotechnik a podzemního taviteltví Modelování v geotechnice Základní veličin, rovnice a vztah (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace tudijního
Katedra geotechnik a podzemního taviteltví Modelování v geotechnice Základní veličin, rovnice a vztah (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace tudijního
5.1.5 Základní vztahy mezi body přímkami a rovinami
 5.1.5 Zákldní vzthy mezi body přímkmi rovinmi Předpokldy: 510 Prostor má tři rozměry, skládá se z bodů. Přímk - jednorozměrná podmnožin prostoru (množin bodů) Rovin - dvojrozměrná podmnožin prostoru (množin
5.1.5 Zákldní vzthy mezi body přímkmi rovinmi Předpokldy: 510 Prostor má tři rozměry, skládá se z bodů. Přímk - jednorozměrná podmnožin prostoru (množin bodů) Rovin - dvojrozměrná podmnožin prostoru (množin
Pístový efekt výtahů ve stavebních objektech
 Pístový efekt výthů ve stvebních objektech Ing. Jiří Pokorný, Ph.D. Hsičský záchrnný sbor Morvskoslezského krje úzení odbor Opv Těšínská 39, 746 01 Opv e-il: jiripokorny@ujil.cz Klíčová slov Pístový efekt,
Pístový efekt výthů ve stvebních objektech Ing. Jiří Pokorný, Ph.D. Hsičský záchrnný sbor Morvskoslezského krje úzení odbor Opv Těšínská 39, 746 01 Opv e-il: jiripokorny@ujil.cz Klíčová slov Pístový efekt,
Obsah rovinného obrazce
 Osh rovinného orzce Nejjednodušší plikcí určitého integrálu je výpočet oshu rovinného orzce. Zčneme větou. Vět : Je-li funkce f spojitá nezáporná n n orázku níže roven f ( ) d. ;, je osh rovinného orzce
Osh rovinného orzce Nejjednodušší plikcí určitého integrálu je výpočet oshu rovinného orzce. Zčneme větou. Vět : Je-li funkce f spojitá nezáporná n n orázku níže roven f ( ) d. ;, je osh rovinného orzce
Posouzení stability svahu
 Verifikční nuál č. 3 Aktulizce 04/016 Posouzení stbility svhu Progr: Soubor: Stbilit svhu Deo_v_03.gst V toto verifikční nuálu je uveden ruční výpočet posouzení stbility svhu posouzení stbility svhu zbezpečeného
Verifikční nuál č. 3 Aktulizce 04/016 Posouzení stbility svhu Progr: Soubor: Stbilit svhu Deo_v_03.gst V toto verifikční nuálu je uveden ruční výpočet posouzení stbility svhu posouzení stbility svhu zbezpečeného
13. Exponenciální a logaritmická funkce
 @11 1. Eponenciální logritmická funkce Mocninná funkce je pro r libovolné nenulové reálné číslo dán předpisem f: y = r, r R, >0 Eponent r je konstnt je nezávisle proměnná. Definičním oborem jsou pouze
@11 1. Eponenciální logritmická funkce Mocninná funkce je pro r libovolné nenulové reálné číslo dán předpisem f: y = r, r R, >0 Eponent r je konstnt je nezávisle proměnná. Definičním oborem jsou pouze
Správné řešení písemné zkoušky z matematiky- varianta A Přijímací řízení do NMgr. studia učitelských oborů 2010
 právné řešení písemné koušky mtemtiky- vrint A Přijímcí říení do NMgr. studi učitelských oborů Příkld. Vyšetřete průběh funkce v jejím mimálním definičním oboru nčrtněte její grf y Určete pritu (sudá/lichá),
právné řešení písemné koušky mtemtiky- vrint A Přijímcí říení do NMgr. studi učitelských oborů Příkld. Vyšetřete průběh funkce v jejím mimálním definičním oboru nčrtněte její grf y Určete pritu (sudá/lichá),
LINEÁRNÍ DIFERENCIÁLNÍ ROVNICE 2.ŘÁDU
 LINEÁRNÍ DIFERENCIÁLNÍ ROVNICE 2.ŘÁDU ZDENĚK ŠIBRAVA 1. Obecné řešení lin. dif. rovnice 2.řádu s konstntními koeficienty 1.1. Vrice konstnt. Příkld 1.1. Njděme obecné řešení diferenciální rovnice (1) y
LINEÁRNÍ DIFERENCIÁLNÍ ROVNICE 2.ŘÁDU ZDENĚK ŠIBRAVA 1. Obecné řešení lin. dif. rovnice 2.řádu s konstntními koeficienty 1.1. Vrice konstnt. Příkld 1.1. Njděme obecné řešení diferenciální rovnice (1) y
x + F F x F (x, f(x)).
 I. Funkce dvou více reálných proměnných 8. Implicitně dné funkce. Budeme se zbývt úlohou, kdy funkce není zdná přímo předpisem, který vyjdřuje závislost její hodnoty n hodnotách proměnných. Jeden z možných
I. Funkce dvou více reálných proměnných 8. Implicitně dné funkce. Budeme se zbývt úlohou, kdy funkce není zdná přímo předpisem, který vyjdřuje závislost její hodnoty n hodnotách proměnných. Jeden z možných
1.1 Numerické integrování
 1.1 Numerické integrování 1.1.1 Úvodní úvhy Nším cílem bude přibližný numerický výpočet určitého integrálu I = f(x)dx. (1.1) Je-li znám k integrovné funkci f primitivní funkce F (F (x) = f(x)), můžeme
1.1 Numerické integrování 1.1.1 Úvodní úvhy Nším cílem bude přibližný numerický výpočet určitého integrálu I = f(x)dx. (1.1) Je-li znám k integrovné funkci f primitivní funkce F (F (x) = f(x)), můžeme
Viz též stavová rovnice ideálního plynu, stavová rovnice reálného plynu a van der Waalsova stavová rovnice.
 5.1 Stavová rovnice 5.1.1 Stavová rovnice ideálního plynu Stavová rovnice pro sěs ideálních plynů 5.1.2 Stavová rovnice reálného plynu Stavové rovnice se dvěa onstantai Viriální rovnice Stavové rovnice
5.1 Stavová rovnice 5.1.1 Stavová rovnice ideálního plynu Stavová rovnice pro sěs ideálních plynů 5.1.2 Stavová rovnice reálného plynu Stavové rovnice se dvěa onstantai Viriální rovnice Stavové rovnice
+ c. n x ( ) ( ) f x dx ln f x c ) a. x x. dx = cotgx + c. A x. A x A arctgx + A x A c
 ) INTEGRÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem neurčitého integrálu Je dán funkce Pltí všk tké F tk, y pltilo F ( ) f ( ) Zřejmě F ( ), protože pltí, 5,, oecně c, kde c je liovolná kon- stnt f ( ) nším
) INTEGRÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem neurčitého integrálu Je dán funkce Pltí všk tké F tk, y pltilo F ( ) f ( ) Zřejmě F ( ), protože pltí, 5,, oecně c, kde c je liovolná kon- stnt f ( ) nším
MIČKAL, Karel. Technická mechanika II: pro střední odborná učiliště. Vyd. 3., nezm. Praha: Informatorium, 1998c1990, 118 s. ISBN
 Identifikátor teriálu: ICT 0 Reitrční čílo rojektu CZ..07/.5.00/.0796 Náze rojektu zdělááe ro žiot Náze říjee odory OU lynárenké Prduie náze teriálu DUM Menik - Hydroenik - Hydrodyniké ýočty Anote Autor
Identifikátor teriálu: ICT 0 Reitrční čílo rojektu CZ..07/.5.00/.0796 Náze rojektu zdělááe ro žiot Náze říjee odory OU lynárenké Prduie náze teriálu DUM Menik - Hydroenik - Hydrodyniké ýočty Anote Autor
