Kombinace ohybu a tlaku
|
|
|
- Ludmila Vlčková
- před 6 lety
- Počet zobrazení:
Transkript
1 1
2 Kapitoa 1 Kombinace ohybu a taku 1.1 Úvod ři současném působení příčných a osových si se nosník(obr. 1.1) nachází, v ceém procesu zatěžování, v prohnutém stavu. Vzniká kombinace ohybu a taku. Nejedná se o stabiitní probém, tj. o stanovení podmínky ztráty přímosti prutu, ae o probém pevnostní. Aby nedošo k příčnému vybočení prutu od působení samotné osové síy, musíbýtsía F < F kr,kde F kr jekritickáeuerovasíazávisánazpůsobuuožení konců prutu. ξ q(x) F v q v(x) F x v F v x M o (x) M o (x) + N.v(x) + M o (x) N.v(x) Obrázek 1.1: říčnésíyjsouzachycenyvpodporáchapředpokádáse,žepůsobívjednézhavních rovin průřezu nosníku. Od příčných si vzniká v řezu ξ(obr. 1.1) ohybový moment M o (x)aprůhyb v q (x).růhybodosovésíyje v F (x)aohybovýmomentodtétosíy
3 F v(x),kde vjevýsednýprůhybodsoučasnéhopůsobenípříčnýchaosovýchsi v(x) = v q (x)+v F (x) (1.1) Výsedný ohybový moment v řezu ξ je určen součtem sožek momentu M o (x) = M o (x)+f v(x) (1.) Ze způsobu zatížení nosníku je patrné, že v případě zanedbání vivu posouvající síy se jedná o jednoosý stav napjatosti. evnostní podmínku zapíšeme pro řez, ve kterém je výsednénapětíodohybuatakumaximání.jetořez,vekterémjeohybovýmoment M o (x)maximání.výsednétakovénapětíjedánovztahem kde σ omax jetakovásožkanapětíodohybu a σ F jetakovásožkanapětíodosovésíy F, evnostní podmínka má pak tvar σ max = σ omax +σ F, (1.3) σ o max = M omax W o (1.4) σ F = F A (1.5) σ max = M omax W o + F A σ D (1.6) Unosníků,kterémajíhavníkvadratickémomentyprůřezurozdíné, J 1 J,ajsou příčnězatíženévrovině J max,sekontrouje,zdanevzniknevroviněmaximánítuhosti průřezu ztráta stabiity od působení samotné síy F. ři apikaci pevnostní podmínky (1.6), v konkrétním případě, je nutné vyšetřit funkci průhybové křivky v(x), pro kterou je ovšem nutné znát kvadratický moment průřezu. roto se postupuje tak, že přípustné rozměry průřezu se určují odhadem na zákadě rozměrů, které získáme z pevnostní podmínkypouzeodohybuodpříčnýchsi,t.j.jenzm o max apodmínkystabiitypro zvoenou hodnotu součinitee bezpečnosti k F = F kr F, kdeuvažujemekvadratickýmomentprůřezukoseohybuodpříčnýchsinatakodsíy F.Stanovenérozměryseponěkudzvětší,nežvyšyvdíčíchpodmínkáchapoužijísepři sestavení pevnostní podmínky(1.6), která respektuje kombinované namáhání v ohybu ataku. 1. Výpočet ohybového momentu Funkceprůhybovékřivkyv(1.)jezávisánavýsednémohybovémmomentu M o (x). Tuto závisost vyšetříme násedujícím postupem. Rovnici (1.) dvakrát derivujeme pode nezávisé proměnné x M o (x) = M o (x)+n v (x) (1.7) 3
4 aza v (x)dosadímediferenciánírovniciprůhybovékřivkyproprizmatickýnosník v (x) = M o(x) EJ (1.8) o úpravě získáme diferenciání rovnici. řádu s konstantními činitei pro ohybový moment M o (x). M o (x)+α M o (x) = M o (x), (1.9) kde α = F EJ Obecný integrá rovnice(1.9) je M o (x) = A sinαx+b cosαx+m op (1.1) A, Bjsouintegračníkonstanty,kteréurčímezokrajovýchpodmínek, M op jepartikuárníintegrárovnice(1.1).známe-inyní M o (x),můžemezrovnice(1.)určitprůhyb v(x). ostupovat ze i tak, že stanovíme funkci průhybu v(x), pomocí které vypočteme M o (x)rovněžpoderovnice(1.). 1.3 Výpočet průhybu ři sestavování diferenciání rovnice funkce v(x) vycházíme z diferenciání rovnice průhybové křivky(1.8) v (x) = M o(x) EJ Ohybovýmoment M o (x)dosadímepoderov.(1.)apoúpravědostanemediferenciání rovnici. řádu s konstantními činitei pro hedanou funkci v(x), popisující výsedný průhyb nosníku v (x)+α v(x) = α F M o(x), (1.11) kde Řešením je obecný integrá α = F EJ v(x) = Acosαx+Bsinαx+v p (1.1) A, B jsou integrační konstanty, které opět určíme z okrajových podmínekav p je partikuární integrá úpné rovnice(1.11). Dosazením funkce průhybové křivky v(x) zrov.(1.1)dorov.(1.),dostanemeohybovýmoment M o (x)aurčímejehomaximum M omax prodimenzovánípodepevnostnípodmínky(1.6). Obě rovnice(1.9) a(1.11) jsou formáně totožné diferenciání rovnice druhého řádu skonstantnímičiniteiaspravoustranou.kestanovenífunkce M o (x)resp. v(x)použijeme rovnici(1.9) resp.(1.11) a ke stanovení zbývající neznámé použijeme rov.(1.). římývýpočetmomentu M o (x)zrov.(1.7)jejednoduššípřiurčovánípartikuárníhointegráu M op vpřípadech,kdy M o (x)jevyjádřenpoynomem.druháderivacepoynomu M o (x)jenižšíhořáduanapř.přizatíženínosníkuosaměýmisiamije M o(x) = apartikuárníintegrájerovennue.kompikacemohounastatpřiurčováníokrajovýchpodmínekpro M o (x)am o (x),zatímcookrajovépodmínkyprořešení rov.(1.11) pynou z podmínek uožení nosníku. 4
5 1.4 říkady kombinací ohybu a taku Apikujme uvedené postupy řešení pevnosti nosníků namáhaných ohybem a takem na některé případy zatížení příčnými a osovými siovými účinky. říkad 1.1: Uvažujme případ uvedený na obr Nosník uožený na koubových podporách je zatíženpříčnousiou F aosovousiou. Vřezu ξvpoi a ( x a)jeohybový ξ F ξ F b x a b x F a M o (x) M o max + + M o (x) N. v(x) Obrázek -1.1: momentodpříčnésíy F M o (x) = F b x a M o(x) = Vřezu ξ,vpoi b ( x b)jeohybovýmomentodpříčnésíy F M o ( x) = F a x a M o ( x) = ro každé poe vyjádříme samostatnou homogenní diferenciání rovnici(1.9) Řešení obou rovnic je M o (x)+α M o (x) = a M o ( x)+α Mo ( x) = M o (x) = A cosαx+b sinαx Mo ( x) = C cosα x+d sinα x A, B, C, D jsou integrační konstanty, které určíme z násedujících okrajových podmínek 1. pro x = je M o () = aa = 5
6 . pro x = je M o () = ac= 3. pro x = aa x = bjeohybovýmomentprooběpoestejný M o (a) = M o (b) 4. pro x = aa x = bseposouvajícísía Tvpůsobištisíy Fměnískokemohodnotu F,cožvypývázrovnováhyeementunaobr.-1.. roto F F T dx T jeden z obrázků, u druhého obrázku je teba změnit popisek v textu T a b T Obrázek -1.: T(a) F T(b) =, resp. T(a) T(b) = F ApikacíSchwederovyvětyvetvaru M = Ta M = Tzedáepsát T(a) T(b) = M o (a)+ M o (b) = F o dosazení do okrajových podmínek 3 a 4 získáme soustavu B sinαa D sinαb =, αbcosαa+αdcosαb = F pro neznámé integrační konstanty B a D. Jejím řešením jsou konstanty B = F α sinαb sinα růběhy ohybových momentů v každém poi jsou M o (x) = F α sinαb sinα sinαx a D = F α sinαa sinα a Mo ( x) = F α sinαa sinα sinα x Maximáníohybovýmomentsenacházívdešímpoivmístě,kdenapř.pro a > b,je M o(x) =.ronosníkzatíženýsiou Fuprostředdéky, a = b = /,stanovíme M omax = F α sin α sin α cos α = F α tg α 6
7 Rovnici ze ještě dáe upravit kde M omax = F 4 tg α α M omax = F 4, = M omax µ F, jemaximáníohybovýmomentodpříčnésíy F a µ jefaktorvyjadřujícívivosové síy na maximání ohybový moment. růhyb stanovíme pomocí rovnice(1.) ro maximání průhyb pyne Rovnici ze opět upravit ( ) v v max = F 3 48 E J v(x) = 1 M o(x) M o (x)] = v max = F 4 tg α α tg α α ε π = v F max γ, kde v F max = F 3 48 E J jemaximáníprůhybodpříčnésíy Fa γ jefaktorvyjadřující vivosovésíy. ε jekritickáeuerovasíapronosníknamáhanýpouzeosovousiou. oznámka: ZrovnicproM o(x)av(x)jepatrné,žeoběfunkcejsouineárnězávisénapříčnémzatížení aneineárnězávisénaosovésíe.ůsobí-inapř.naprutvícepříčnýchsi F n,výsednýprůhybze získattak,ženanosníkpůsobísoučasněvšechnypříčnésíyasíaosová.akjenutnésestavit (n+1) diferenciáních rovnic(1.9) nebo(1.11) a pro každé řešení předepsat (n + 1) okrajových podmínek. Tento postup je zajisté obtížný, zejména při řešení úohy pode(1.9), kde pro okrajové podmínky je nutnéstanovit M o(x)resp. M o(x).výsednýprůhybpřipůsobenívětšíhopočtupříčnýchsizevšak získat také součtem díčích průhybů za současného působení jedné příčné síy a osové síy. ostup výpočtu je naznačen na obr růhyb stanovíme součtem v(x) = v 1(x)+v (x) a výsedný ohybový moment pomocí rovnice(1.). M o(x) = M o1(x)+m o(x) 7
8 F 1 v(x) F a b c F 1 v 1 (x) F v (x) Obrázek -1.3: říkad 1.: Daším příkadem, jehož řešení uvedeme je nosník zatížený spojitým břemenem a osovou siou F(obr.-.1). Stanovíme M omax a v max.oužijemeřešenípoderov.(1.9).ro x jeohybovýmomentodpříčnýchsi a M o (x) = q x q x M o(x) = q Diferenciání rovnice ohybového momentu bude mít tvar M o(x)+α M o (x) = q Obecný integrá je M o (x) = A cosαx+b sinαx q α Okrajové podmínky pro řešení integračních konstant jsou 1. pro x = je M o () =. pro x = je M o () = o dosazení do předchozí rovnice určíme integrační konstanty A, B: A = q α a B = q 1 cosα α sinα 8 = q α tan α
9 ξ q F v(x) F x M o (x) + + M o (x) N.v(x) N. v(x) Obrázek -.1: Výsedný ohybový moment v obecném řezu je M o (x) = q ( α cosαx+tg α ) sinαx 1 Maximáníohybovýmomentjepro x = /roven M omax = q 1 cos α 8 ( ) α cos α = M omax µ F, kde M omax jemaximáníohybovýmomentodpříčnéhozatížení q o a µ F jefaktor určujícívivosovésíy F. omocí rov.(1.) ze vyšetřit průhyb v obecném místě nosníku. Maximání průhyb uprostřed nosníku je v max = M ] omax Momax 1 F M omax Z předchozího vztahu určíme poměr M omax M omax = 1 cos α ) cos α ( α, dosadímedorovnicepro v max 9
10 α 1 cos v max = q 8 F ( ) α cos α aupravíme α v max = q 4 1 cos E J ( ) α cos α π F ε F = v qγ F, kde v q = 384 q 5 4 E J jemaximáníprůhybuprostřednosníkuvznikýpouzeodpříčného spojitéhozatížení q o a γ F jefaktornavyšujícíprůhybvdůsedkupůsobeníosovésíyf. 1.5 Energetická metoda přibižné řešení kombinace ohybu ataku V případech, kdy se jedná o sožitý způsob zatížení nosníku, jak jsme se již zmínii, jako je např. působení většího počtu příčných siových účinků a takové síy osové, je exaktnípostupvýpočtuohybovéhomomentum o (x)(1.)propevnostnípodmínku(1.6) sožitý a zdouhavý. ro praktické použití je přibižná energetická metoda výhodnější. Uvažujmekoubověuoženýnosníkzatíženýpříčnýmisiami F i,obr.1.aosovousiou, namáhající prut takem. x i x ds dx F i v i u u δv i Obrázek 1.: růhybovou čáru, respektující okrajové podmínky, zvoíme ve tvaru v(x) = K η(x), (1.13) kde η(x),jakbyojižzmíněno,jefunkceudávajícítvarprůhybovéčáryakjejívypukost měřítko, které pro daný případ zatížení neznáme. řipomeňme si, že se při 1
11 této kombinaci ohybu a taku nejedná o stabiitní případ, kdy vyšetřujeme indiferentní stav rovnováhy, kterému přísuší ibovoný průhyb v mezích Hookova zákona. Zde tudíž přísuší určitému zatížení určitý stabiní průhyb a odpovídá mu rovnováha vnějších avnitřníchsi.odsiou F i jeprůhyb v i = K η(x i ) (1.14) a v důsedkuprohnutínosníku se pravýkoub prutuposuneou. Veikost posuvu u(obr.1.)určímezevztahu u = (ds dx) = 1 v (x) ] dx, (1.15) jak pyne pode pravide počítání s maými čísy(rov.??)neme by byt odkaz na???. Vztah upravíme pomocí rov.(1.13) u = K kde Bjekonstantazávisánatvarufunkce η(x). η (x) ] K dx = B, (1.16) Nyní vnějším zásahem změníme rovnovážný stav vnějších a vnitřních si tak, že vyvoámevirtuáníposuv δupůsobištěosovésíy avirtuáníposuvy δv i působišťpříčných si F i.současněsezměníenergievnitřníchsiovirtuánípřírůstek.kdyžtytovirtuání změny posuvu opět uvoníme, prut zaujme svoji původní průhybovou křivku a vnější síy a F i přitomvykonajípráci.řírůstekprácevnějšíchsijerovenakumuované deformační energii, tj. δw = δu (1.17) Eementární práce vnějších si při vratném posuvu je kde δw = δu+ F i δv i, (1.18) δu = B K δk a δv i = δk η(x i ), (1.19) jakjepatrnézrov.(1.16)a(1.14).dosadímezpětdorov.(1.18) δw = B KδK +δk F i η(x i ) (1.) otenciání energie napjatosti v nosníku U, uvažujeme i pouze ohyb, je dána vztahem U = 1 Mo (x) dx (1.1) E J Za M o (x)dosadímezdiferenciánírovniceprůhybovékřivky M o (x) = E J v (x) U = 1 E J v (x) ] dx (1.) azrovnice(1.13)je v (x) = K η (x),takžepropotenciáníenergiidostanemevztah U = K E J η (x) ] dx = K C, (1.3) 11
12 kde C je konstanta závisá na zvoeném tvaru průhybové čáry η(x), stejně jako konstanta B, zavedená v rovnici(1.16) je to opět funkcioná s argumentem η(x). řírůstek potenciání energie(1.3) při virtuání změně průhybu nosníku je δu = Kδ K C (1.4) Rovnost eementárních přírůstku energie pode rov.(1.17) má tvar po úpravě K C δk = K C ( B K + ) F i η(x i ) δk, (1.5) ( 1 B ) = F i η(x i ), C odkud určíme vypukost K prohnutého nosníku K = Fi η(x i ) ( C 1 B ) = C Fi η(x i ) E J η (x) ] dx 1 1 η (x) ] dx E J η (x) ] dx (1.6) roprizmatickýnosník E J = konst.setvarvztahuzjednoduší K = Fi η(x i ) E J η (x) ] dx 1 E J 1 η (x) ] dx η (x) ] dx (1.7) Vrovnici v(x) = K η(x)voímetvarovoufunkci η(x)sohedemnaokrajovépodmínky. Ve vobě η(x) spočívá přibižnost řešení. ři uváživé vobě tvaru průhybové čáry η(x) je chyba zanedbatená. Z rovnice(1.6) je patrné, že metodu ze použít i pro neprizmatické pruty. ro souměrné zatížení a koubové uožení voíme nejčastěji funkci η(x) ve tvaru půvny sinusovky v(x) = K sin πx = K η(x) ro rovnici(1.6) určíme η (x) = π cos πx, η (x) ] = ( π ) cos πx, aintegráy ( π ) η πx (x) = sin, η (x) ] = ( π ) 4 sin πx η (x) ] dx = ( π ) cos πx π dx =, η (x) ] dx = ( π ) 4 sin πx π4 dx = 3 1
13 o dosazení do rov.(1.7) a úpravě stanovíme měřítko vypukosti K = Fi sin πx i π 4 E J E J ( ) = π Fi sin πx i π 4 E J ε Zavedeme-i do rovnice poměr ε = k ε, kde ε jekritickáeuerovasíapronosníkkoubověuoženýanamáhanýpouzeosovou siou, dostaneme konečný tvar rovnice pro vypukost průhybové čáry K = 3 F i sin πx i 48,7 E J k ε k ε 1 13
14 Literatura 1] DUCHÁČEK,J.:NaukaopružnostiapevnostiI.SNTL,raha1957 ] DUCHÁČEK, J.: Nauka o pružnosti a pevnosti II. SNTL, raha ] HÁJEK,E.akoektiv:ružnostapevnostII.VČVUT,raha,1979 4] HÁJEK, E., REIF,., VALENTA, F.: ružnost a pevnost I. SNTL/ALFA, raha ] HÖSCHL, C.: ružnost a pevnost ve strojírenství. SNTL/ALFA, raha ] JANATKA, J.: ružnost a pevnost I. SNTL-ČVUT, raha ] JANATKA, J.: ružnost a pevnost II. SNTL-ČVUT, raha ] JANÍČEK,.,ETRUŠKA,J.:ÚohyzpružnostiapevnostiII.ESVUT,Brno 199 9] LENERT, J.: ružnost a pevnost II. VŠB-TU, Ostrava ] MICHALEC, J.: ružnost a pevnost I. v.čvut, raha 1 11] MICHALEC, J.: ružnost a pevnost II. v. ČVUT, raha 1 1] NĚMEC, J.: Tuhost a pevnost oceových částí. ČSAV, raha ] ONDRÁČEK, E., FARLÍK, A.: Mezní stavy v pevnostních výpočtech. SNTL, raha ] ISARENKO, G.S.: Soprotivenije materiaov. VŠ Kyjev, ] EŠINA, E., REIF,., VALENTA, F.: Sbírka příkadů z pružnosti a pevnosti. SNTL, raha ] OOV, E..: Introduction to mechanics of soids. rentice-ha, London ] UCHMAJER,.: ružnost a pevnost. ČVUT raha ] RŮŽIČKA, M., HANKE, M., ROST,M.: Dynamická pevnost a životnost. FS- ČVUT, raha, ] SERVÍT, R., DOLEŽALOVÁ, E., CRHA, M.: Teorie pružnosti a pasticity I. SNTL/ALFA, raha
15 ] SERVÍT, R., DRAHOŇOVSKÝ, Z., ŠEJNOHA, J.: Teorie pružnosti a pasticity II. ČVUT, raha ] ŠEJNOHA, J., BITTNAROVÁ, J.: ružnost a pevnost. V-ČVUT, raha, 1998 ] TIMOSCHENKO, S.., GERE, J. M.: Mechanics of Materias. D. Van Nostrand, New York, 197 3] TREBUŇA, F., ŠIMČÁK, F., JURICA, V.: ružnosť a pevnosť I, II. Vienaa, Košice 4] WASCHIZU, K.: Variationa methods in easticity nad pasticity. ergamon, New York,
16 Obsah 1 Kombinace ohybu a taku 1.1 Úvod Výpočetohybovéhomomentu Výpočetprůhybu říkadykombinacíohybuataku Energetickámetoda přibižnéřešeníkombinaceohybuataku
Ztráta stability tenkých přímých prutů - vzpěr
 Ztráta stability tenkých přímých prutů - vzpěr Motivace štíhlé pruty namáhané tlakem mohou vybočit ze svého původně přímého tvaru a může dojít ke ztrátě stability a zhroucení konstrukce dříve, než je dosaženo
Ztráta stability tenkých přímých prutů - vzpěr Motivace štíhlé pruty namáhané tlakem mohou vybočit ze svého původně přímého tvaru a může dojít ke ztrátě stability a zhroucení konstrukce dříve, než je dosaženo
Stabilita přímých prutů
 Kapitoa 1 Stabiita přímých prutů 1.1 Úvod Předpokádejme, že tvar stačovaného přímého prizmatického prutu je ideání. To znamená, že předpokádáme jeho přímý tvar, výsedná sía působí v jeho podéné ose a materiá
Kapitoa 1 Stabiita přímých prutů 1.1 Úvod Předpokádejme, že tvar stačovaného přímého prizmatického prutu je ideání. To znamená, že předpokádáme jeho přímý tvar, výsedná sía působí v jeho podéné ose a materiá
Linearní teplotní gradient
 Poznámky k semináři z předmětu Pružnost pevnost na K68 D ČVUT v Praze (pracovní verze). Tento materiá má pouze pracovní charakter a ude v průěhu semestru postupně dopňován. utor: Jan Vyčich E mai: vycich@fd.cvut.cz
Poznámky k semináři z předmětu Pružnost pevnost na K68 D ČVUT v Praze (pracovní verze). Tento materiá má pouze pracovní charakter a ude v průěhu semestru postupně dopňován. utor: Jan Vyčich E mai: vycich@fd.cvut.cz
Autor: Vladimír Švehla
 Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Přednáška 12 Obecná deformační metoda, nelineární úlohy u prutových soustav
 Statika stavebních konstrukcí II., 3.ročník bakaářského studia Přednáška Obecná deformační metoda, neineární úohy u prutových soustav Fyzikáně neineární úoha Geometricky neineární úoha Konstrukčně neineární
Statika stavebních konstrukcí II., 3.ročník bakaářského studia Přednáška Obecná deformační metoda, neineární úohy u prutových soustav Fyzikáně neineární úoha Geometricky neineární úoha Konstrukčně neineární
Předmět: Ročník: Vytvořil: Datum: ŠČERBOVÁ M. PAVELKA V. NAMÁHÁNÍ NA OHYB A) NOSNÍKY NA DVOU PODPORÁCH ZATÍŽENÉ SOUSTAVOU ROVNOBĚŽNÝCH SIL
 Předmět: Ročník: Vytvoři: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 9. ČERVNA 2013 Název zpracovaného ceku: NAMÁHÁNÍ NA OHYB A) NOSNÍKY NA DVOU PODPORÁCH ZATÍŽENÉ SOUSTAVOU ROVNOBĚŽNÝCH SIL ÚLOHA 1
Předmět: Ročník: Vytvoři: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 9. ČERVNA 2013 Název zpracovaného ceku: NAMÁHÁNÍ NA OHYB A) NOSNÍKY NA DVOU PODPORÁCH ZATÍŽENÉ SOUSTAVOU ROVNOBĚŽNÝCH SIL ÚLOHA 1
Lineární stabilita a teorie II. řádu
 Lineární stabilita a teorie II. řádu Sestavení podmínek rovnováhy na deformované konstrukci Konstrukce s a bez počáteční imperfekce Výpočet s malými vs. s velkými deformacemi ANKC-C 1 Zatěžovacídráhy [Šejnoha,
Lineární stabilita a teorie II. řádu Sestavení podmínek rovnováhy na deformované konstrukci Konstrukce s a bez počáteční imperfekce Výpočet s malými vs. s velkými deformacemi ANKC-C 1 Zatěžovacídráhy [Šejnoha,
Křivé pruty. Kapitola Úvod
 Kapitola Křivé pruty. Úvod Zakřivené elementy konstrukcí, u kterých, stejně jako u přímých prutů, převládá jeden rozměr,senazývajíkřivýmipruty.mohoubýtstatickyurčité(obr..a,b,c,d), nebostatickyneurčité(obr..a,b,c,d).
Kapitola Křivé pruty. Úvod Zakřivené elementy konstrukcí, u kterých, stejně jako u přímých prutů, převládá jeden rozměr,senazývajíkřivýmipruty.mohoubýtstatickyurčité(obr..a,b,c,d), nebostatickyneurčité(obr..a,b,c,d).
Normálové napětí a přetvoření prutu namáhaného tahem (prostým tlakem) - staticky určité úlohy
 Pružnost a pasticita, 2.ročník bakaářského studia ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) - staticky určité úohy Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného
Pružnost a pasticita, 2.ročník bakaářského studia ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) - staticky určité úohy Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného
Statika 2. Vetknuté nosníky. Miroslav Vokáč 2. listopadu ČVUT v Praze, Fakulta architektury. Statika 2. M.
 3. přednáška Průhybová čára Mirosav Vokáč mirosav.vokac@kok.cvut.cz ČVUT v Praze, Fakuta architektury 2. istopadu 2016 Průhybová čára ohýbaného nosníku Znaménková konvence veičin M z x +q +w +ϕ + q...
3. přednáška Průhybová čára Mirosav Vokáč mirosav.vokac@kok.cvut.cz ČVUT v Praze, Fakuta architektury 2. istopadu 2016 Průhybová čára ohýbaného nosníku Znaménková konvence veičin M z x +q +w +ϕ + q...
Řešení úloh 1. kola 60. ročníku fyzikální olympiády. Kategorie B Autoři úloh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6)
 Řešení úoh 1. koa 60. ročníku fyzikání oympiády. Kategorie B Autoři úoh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6) h 1.a) Protože vzdáenost bodů K a O je cos α, je doba etu kuičky z bodu K do bodu
Řešení úoh 1. koa 60. ročníku fyzikání oympiády. Kategorie B Autoři úoh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6) h 1.a) Protože vzdáenost bodů K a O je cos α, je doba etu kuičky z bodu K do bodu
Inovace předmětů studijních programů strojního inženýrství v oblasti teplotního namáhání
 Grantový projekt FRVŠ MŠMT č.97/7/f/a Inovace předmětů studijních programů strojního inženýrství v obasti tepotního namáhání Některé apikace a ukázky konkrétních řešení tepeného namáhání těes. Autorky:
Grantový projekt FRVŠ MŠMT č.97/7/f/a Inovace předmětů studijních programů strojního inženýrství v obasti tepotního namáhání Některé apikace a ukázky konkrétních řešení tepeného namáhání těes. Autorky:
Mechanické vlastnosti materiálů.
 Mechancké vastnost materáů. Obsah přednášky : tahová zkouška, zákadní mechancké vastnost materáu, prodoužení př tahu nebo taku, potencání energe, řešení statcky neurčtých úoh Doba studa : as hodna Cí přednášky
Mechancké vastnost materáů. Obsah přednášky : tahová zkouška, zákadní mechancké vastnost materáu, prodoužení př tahu nebo taku, potencání energe, řešení statcky neurčtých úoh Doba studa : as hodna Cí přednášky
3.2 Základy pevnosti materiálu. Ing. Pavel Bělov
 3.2 Základy pevnosti materiálu Ing. Pavel Bělov 23.5.2018 Normálové napětí představuje vazbu, která brání částicím tělesa k sobě přiblížit nebo se od sebe oddálit je kolmé na rovinu řezu v případě že je
3.2 Základy pevnosti materiálu Ing. Pavel Bělov 23.5.2018 Normálové napětí představuje vazbu, která brání částicím tělesa k sobě přiblížit nebo se od sebe oddálit je kolmé na rovinu řezu v případě že je
Přednáška 10, modely podloží
 Statika stavebních konstrukcí II.,.ročník kaářského studia Přednáška, modey podoží Úvod Winkerův mode podoží Pasternakův mode podoží Nosník na pružném Winkerově podoží, řešení OD atedra stavební mechaniky
Statika stavebních konstrukcí II.,.ročník kaářského studia Přednáška, modey podoží Úvod Winkerův mode podoží Pasternakův mode podoží Nosník na pružném Winkerově podoží, řešení OD atedra stavební mechaniky
Napětí v ohybu: Výpočet rozměrů nosníků zatížených spojitým zatížením.
 Číslo projektu CZ.1.07/ 1.1.36/ 02.0066 Autor Pavel Florík Předmět Mechanika Téma Namáhání součástí na ohyb Metodický pokyn výkladový text s ukázkami Napětí v ohybu: Výpočet rozměrů nosníků zatížených
Číslo projektu CZ.1.07/ 1.1.36/ 02.0066 Autor Pavel Florík Předmět Mechanika Téma Namáhání součástí na ohyb Metodický pokyn výkladový text s ukázkami Napětí v ohybu: Výpočet rozměrů nosníků zatížených
PRUŽNOST A PEVNOST II
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ PRUŽNOST A PEVNOST II Navazující magisterské studium, 1. ročník Alois Materna (přednášky) Jiří Brožovský (cvičení) Kancelář: LP C 303/1
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ PRUŽNOST A PEVNOST II Navazující magisterské studium, 1. ročník Alois Materna (přednášky) Jiří Brožovský (cvičení) Kancelář: LP C 303/1
4.1 Shrnutí základních poznatků
 4.1 Shrnutí zákadních poznatků V případech příčných deformací přímých prutů- nosníků se zabýváme deformací jejich střednice, tj. spojnice těžiště příčných průřezů. Tuto deformovanou křivku nazýváme průhybová
4.1 Shrnutí zákadních poznatků V případech příčných deformací přímých prutů- nosníků se zabýváme deformací jejich střednice, tj. spojnice těžiště příčných průřezů. Tuto deformovanou křivku nazýváme průhybová
Únosnost kompozitních konstrukcí
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta strojní Ústav letadlové techniky Únosnost kompozitních konstrukcí Optimalizační výpočet kompozitních táhel konstantního průřezu Technická zpráva Pořadové číslo:
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta strojní Ústav letadlové techniky Únosnost kompozitních konstrukcí Optimalizační výpočet kompozitních táhel konstantního průřezu Technická zpráva Pořadové číslo:
1. Řešená konstrukce Statické řešení Výpočet průhybové čáry Dynamika Vlastní netlumené kmitání...
 . Řešená konstrukce.... Statické řešení.... Výpočet průhybové čáry... 5. Dynamika.... Vlastní netlumené kmitání..... Jacobiho metoda rovinné rotace... 4.. Popis algoritmu... 4. Vynucené kmitání... 5 4.
. Řešená konstrukce.... Statické řešení.... Výpočet průhybové čáry... 5. Dynamika.... Vlastní netlumené kmitání..... Jacobiho metoda rovinné rotace... 4.. Popis algoritmu... 4. Vynucené kmitání... 5 4.
Téma 4 Normálové napětí a přetvoření prutu namáhaného tahem (prostým tlakem)
 Pružnost a pasticita, 2.ročník bakaářského studia Téma 4 ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného prutu
Pružnost a pasticita, 2.ročník bakaářského studia Téma 4 ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného prutu
Martin NESLÁDEK. 14. listopadu 2017
 Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Vzpěr jednoduchého rámu, diferenciální operátory. Lenka Dohnalová
 1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
Vlastnosti a zkoušení materiálů. Přednáška č.4 Úvod do pružnosti a pevnosti
 Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
OTÁZKY VSTUPNÍHO TESTU PP I LS 2010/2011
 OTÁZKY VSTUPNÍHO TESTU PP I LS 010/011 Pomocí Thumovy definice, s využitím vrubové citlivosti q je definován vztah mezi součiniteli vrubu a tvaru jako: Součinitel tvaru α je podle obrázku definován jako:
OTÁZKY VSTUPNÍHO TESTU PP I LS 010/011 Pomocí Thumovy definice, s využitím vrubové citlivosti q je definován vztah mezi součiniteli vrubu a tvaru jako: Součinitel tvaru α je podle obrázku definován jako:
Reakce. K618 FD ČVUT v Praze (pracovní verze). Tento materiál má pouze pracovní charakter a bude v průbehu semestru
 Poznámky ke cvičení z předmětu Pružnost pevnost na K618 D ČVU v Praze (pracovní verze). ento materiá má pouze pracovní charakter a bude v průbehu semestru postupně dopňován. Autor: Jan Vyčich E mai: vycich@fd.cvut.cz
Poznámky ke cvičení z předmětu Pružnost pevnost na K618 D ČVU v Praze (pracovní verze). ento materiá má pouze pracovní charakter a bude v průbehu semestru postupně dopňován. Autor: Jan Vyčich E mai: vycich@fd.cvut.cz
ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady
 Teorie plasticity VŠB TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ KATEDRA PRUŽNOSTI A PEVNOSTI ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady 1. ŘEŠENÝ PŘÍKLAD NA TAH ŘEŠENÍ DLE DOVOLENÝCH NAMÁHÁNÍ
Teorie plasticity VŠB TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ KATEDRA PRUŽNOSTI A PEVNOSTI ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady 1. ŘEŠENÝ PŘÍKLAD NA TAH ŘEŠENÍ DLE DOVOLENÝCH NAMÁHÁNÍ
Návrh žebrové desky vystavené účinku požáru (řešený příklad)
 Návrh žebrové desky vystavené účinku požáru (řešený příklad) Posuďte spřaženou desku v bednění z trapézového plechu s tloušťkou 1 mm podle obr.1. Deska je spojitá přes více polí, rozpětí každého pole je
Návrh žebrové desky vystavené účinku požáru (řešený příklad) Posuďte spřaženou desku v bednění z trapézového plechu s tloušťkou 1 mm podle obr.1. Deska je spojitá přes více polí, rozpětí každého pole je
NOSNÍK NA PRUŽNÉM PODLOŽÍ (WINKLEROVSKÉM)
 NOSNÍK NA PRUŽNÉ PODLOŽÍ (WINKLEROVSKÉ) Uvažujeme spojitý nosník na pružných podporách. Pružná podpora - odpor je úměrný zatlačení. Pružné podpory velmi blízko sebe - jejich účinek lze nahradit spojitou
NOSNÍK NA PRUŽNÉ PODLOŽÍ (WINKLEROVSKÉ) Uvažujeme spojitý nosník na pružných podporách. Pružná podpora - odpor je úměrný zatlačení. Pružné podpory velmi blízko sebe - jejich účinek lze nahradit spojitou
A x A y. α = 30. B y. A x =... kn A y =... kn B y =... kn. Vykreslení N, V, M. q = 2kN/m M = 5kNm. F = 10 kn A c a b d ,5 2,5 L = 10
 Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
TENSOR NAPĚTÍ A DEFORMACE. Obrázek 1: Volba souřadnicového systému
 TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
Cvičení 7 (Matematická teorie pružnosti)
 VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Pružnost a pevnost v energetice (Návo do cvičení) Cvičení 7 (Matematická teorie pružnosti) Autor: Jaroslav Rojíček Verze:
VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Pružnost a pevnost v energetice (Návo do cvičení) Cvičení 7 (Matematická teorie pružnosti) Autor: Jaroslav Rojíček Verze:
α = 210 A x =... kn A y =... kn A M =... knm
 Vzorový příklad k 1. kontrolnímu testu Konzola Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A M A y y q = kn/m M = - 5kNm A α B c a b d F = 10 kn 1 1 3,5,5 L = 10 x α = 10 A
Vzorový příklad k 1. kontrolnímu testu Konzola Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A M A y y q = kn/m M = - 5kNm A α B c a b d F = 10 kn 1 1 3,5,5 L = 10 x α = 10 A
Statika soustavy těles.
 Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
Pružnost a plasticita II
 Pružnost a pasticita II 3. ročník bakaářského studia doc. Ing. artin Krejsa, Ph.D. Katedra stavební echaniky Neineární chování ateriáů, podínky pasticity, ezní pastická únosnost Úvod, zákadní pojy Teorie
Pružnost a pasticita II 3. ročník bakaářského studia doc. Ing. artin Krejsa, Ph.D. Katedra stavební echaniky Neineární chování ateriáů, podínky pasticity, ezní pastická únosnost Úvod, zákadní pojy Teorie
PRUŽNOST A PLASTICITA I
 Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Nosné desky. 1. Kirchhoffova teorie ohybu tenkých desek (h/l < 1/10) 3. Mindlinova teorie pro tlusté desky (h/l < 1/5)
 Nosné desky Deska je těleso, které má jeden rozměr mnohem menší než rozměry zbývající. Zatížení desky je orientováno výhradně kolmo k její střednicové rovině. 1. Kirchhoffova teorie ohybu tenkých desek
Nosné desky Deska je těleso, které má jeden rozměr mnohem menší než rozměry zbývající. Zatížení desky je orientováno výhradně kolmo k její střednicové rovině. 1. Kirchhoffova teorie ohybu tenkých desek
Příklad 7 Průhyb nosníku - složitější případ
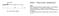 Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Podpora digitalizace a využití ICT na SPŠ CZ.1.07/1.5.00/34.0632 1
 Střední průmysová škoa a Vyšší odborná škoa technická Brno, Sokoská 1 Šabona: Inovace a zkvaitnění výuky prostřednictvím ICT Název: Téma: Autor: Číso: Anotace: echanika, pružnost pevnost Nosníky stejné
Střední průmysová škoa a Vyšší odborná škoa technická Brno, Sokoská 1 Šabona: Inovace a zkvaitnění výuky prostřednictvím ICT Název: Téma: Autor: Číso: Anotace: echanika, pružnost pevnost Nosníky stejné
OHYB (Napjatost) M A M + qc a + b + c ) M A = 2M qc a + b + c )
 3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
ÚVOD DO MODELOVÁNÍ V MECHANICE
 ÚVOD DO MODELOVÁNÍ V MECHANICE PRUŽNOST A PEVNOST Přednáška č. 5 Prof. Ing. Vladislav Laš. CSc. MECHANIKA PODDAJNÝCH TĚLES Úkolem PP z inženýrského hlediska je navrhnout součásti nebo konstrukce, které
ÚVOD DO MODELOVÁNÍ V MECHANICE PRUŽNOST A PEVNOST Přednáška č. 5 Prof. Ing. Vladislav Laš. CSc. MECHANIKA PODDAJNÝCH TĚLES Úkolem PP z inženýrského hlediska je navrhnout součásti nebo konstrukce, které
Betonové konstrukce (S) Přednáška 3
 Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
1 Ohyb desek - mindlinovské řešení
 1 OHYB DESEK - MINDLINOVSKÉ ŘEŠENÍ 1 1 Ohyb desek - mindlinovské řešení Kinematika přemístění Posun w se po tloušťce desky mění málo (vzhledem k hodnotě průhybu) w(x, y, z) = w(x, y) Normály ke střednicové
1 OHYB DESEK - MINDLINOVSKÉ ŘEŠENÍ 1 1 Ohyb desek - mindlinovské řešení Kinematika přemístění Posun w se po tloušťce desky mění málo (vzhledem k hodnotě průhybu) w(x, y, z) = w(x, y) Normály ke střednicové
Kˇriv e pruty Martin Fiˇser Martin Fiˇ ser Kˇ riv e pruty
 Obsah Dimenzování křivého tenkého prutu zde Deformace v daném místě prutu zde Castiglianova věta zde Dimenzování křivého tenkého prutu Mějme obecný křivý prut z homogeního izotropního materiálu. Obrázek:
Obsah Dimenzování křivého tenkého prutu zde Deformace v daném místě prutu zde Castiglianova věta zde Dimenzování křivého tenkého prutu Mějme obecný křivý prut z homogeního izotropního materiálu. Obrázek:
Dvě varianty rovinného problému: rovinná napjatost. rovinná deformace
 Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
3. kapitola. Průběhy vnitřních sil na lomeném nosníku. Janek Faltýnek SI J (43) Teoretická část: Příkladová část: Stavební mechanika 2
 3. kapitola Stavební mechanika Janek Faltýnek SI J (43) Průběhy vnitřních sil na lomeném nosníku Teoretická část: Naším úkolem je v tomto příkladu vyšetřit průběh vnitřních sil na lomeném rovinném nosníku
3. kapitola Stavební mechanika Janek Faltýnek SI J (43) Průběhy vnitřních sil na lomeném nosníku Teoretická část: Naším úkolem je v tomto příkladu vyšetřit průběh vnitřních sil na lomeném rovinném nosníku
ZÁPADOČESKÁ UNIVERZITA V PLZNI
 ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA STROJNÍ Semestrální práce z předmětu MM Stanovení deformace soustav ocelových prutů Václav Plánčka 6..006 OBSAH ZADÁNÍ... 3 TEORETICKÁ ČÁST... 4 PRAKTICKÁ ČÁST...
ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA STROJNÍ Semestrální práce z předmětu MM Stanovení deformace soustav ocelových prutů Václav Plánčka 6..006 OBSAH ZADÁNÍ... 3 TEORETICKÁ ČÁST... 4 PRAKTICKÁ ČÁST...
Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění )
 1 Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění ) 1. Rozšířený Hookeův zákon pro jednoosou napjatost Základním materiálovým vztahem lineární teorie pružnosti
1 Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění ) 1. Rozšířený Hookeův zákon pro jednoosou napjatost Základním materiálovým vztahem lineární teorie pružnosti
Elastické deformace těles
 Eastické eformace těes 15 Na oceový rát ék L 15 m a průměru 1 mm zavěsíme závaží o hmotnosti m 110 kg přičemž Youngův mou pružnosti ocei v tahu E 16 GPa a mez pružnosti ocei σ P 0 Pa Určete reativní prooužení
Eastické eformace těes 15 Na oceový rát ék L 15 m a průměru 1 mm zavěsíme závaží o hmotnosti m 110 kg přičemž Youngův mou pružnosti ocei v tahu E 16 GPa a mez pružnosti ocei σ P 0 Pa Určete reativní prooužení
7 Lineární elasticita
 7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
1. výpočet reakcí R x, R az a R bz - dle kapitoly 3, q = q cosα (5.1) kolmých (P ). iz = P iz sinα (5.2) iz = P iz cosα (5.3) ix = P ix cosα (5.
 Kapitola 5 Vnitřní síly přímého šikmého nosníku Pojem šikmý nosník je používán dle publikace [1] pro nosník ležící v souřadnicové rovině xz, který je vůči vodorovné ose x pootočen o úhel α. Pro šikmou
Kapitola 5 Vnitřní síly přímého šikmého nosníku Pojem šikmý nosník je používán dle publikace [1] pro nosník ležící v souřadnicové rovině xz, který je vůči vodorovné ose x pootočen o úhel α. Pro šikmou
1 ÚVOD 1. Odolání vlivům se prokazuje statickým resp. dynamickým výpočtem.
 1 ÚVOD 1 1 Úvod Stavební konstrukce musí být navržena (a provedena) tak, aby vyhovovala požadovanému účelu a odolala vlivům, které se mohou vyskytnout během její životnosti. Odolání vlivům se prokazuje
1 ÚVOD 1 1 Úvod Stavební konstrukce musí být navržena (a provedena) tak, aby vyhovovala požadovanému účelu a odolala vlivům, které se mohou vyskytnout během její životnosti. Odolání vlivům se prokazuje
Zjednodušená deformační metoda (2):
 Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
* Modelování (zjednodušení a popis) tvaru konstrukce. pruty
 2. VNITŘNÍ SÍLY PRUTU 2.1 Úvod * Jak konstrukce přenáší atížení do vaeb/podpor? Jak jsou prvky konstrukce namáhány? * Modelování (jednodušení a popis) tvaru konstrukce. pruty 1 Prut: konstrukční prvek,
2. VNITŘNÍ SÍLY PRUTU 2.1 Úvod * Jak konstrukce přenáší atížení do vaeb/podpor? Jak jsou prvky konstrukce namáhány? * Modelování (jednodušení a popis) tvaru konstrukce. pruty 1 Prut: konstrukční prvek,
Vzpěr, mezní stav stability, pevnostní podmínky pro tlak, nepružný a pružný vzpěr Ing. Jaroslav Svoboda
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřednictvím ICT Název: Téma: Autor: Číslo: Anotace: Mechanika, pružnost pevnost Vzpěr,
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřednictvím ICT Název: Téma: Autor: Číslo: Anotace: Mechanika, pružnost pevnost Vzpěr,
Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191
 Název školy Název projektu Registrační číslo projektu Autor Název šablony Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky
Název školy Název projektu Registrační číslo projektu Autor Název šablony Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky
Deformace nosníků při ohybu.
 Číslo projektu CZ.1.07/ 1.1.36/ 02.0066 Autor Pavel Florík Předmět Mechanika Téma Deformace nosníků při ohybu Metodický pokyn výkladový text s ukázkami Deformace nosníků při ohybu. Příklad č.2 Zalomený
Číslo projektu CZ.1.07/ 1.1.36/ 02.0066 Autor Pavel Florík Předmět Mechanika Téma Deformace nosníků při ohybu Metodický pokyn výkladový text s ukázkami Deformace nosníků při ohybu. Příklad č.2 Zalomený
Definujte poměrné protažení (schematicky nakreslete a uved te jednotky) Napište hlavní kroky postupu při posouzení prutu na vzpěrný tlak.
 00001 Definujte mechanické napětí a uved te jednotky. 00002 Definujte normálové napětí a uved te jednotky. 00003 Definujte tečné (tangenciální, smykové) napětí a uved te jednotky. 00004 Definujte absolutní
00001 Definujte mechanické napětí a uved te jednotky. 00002 Definujte normálové napětí a uved te jednotky. 00003 Definujte tečné (tangenciální, smykové) napětí a uved te jednotky. 00004 Definujte absolutní
Ing. Jan BRANDA PRUŽNOST A PEVNOST
 Ing. Jan BRANDA PRUŽNOST A PEVNOST Výukový text pro učební obor Technik plynových zařízení Vzdělávací oblast RVP Plynová zařízení a Tepelná technika (mechanika) Pardubice 013 Použitá literatura: Technická
Ing. Jan BRANDA PRUŽNOST A PEVNOST Výukový text pro učební obor Technik plynových zařízení Vzdělávací oblast RVP Plynová zařízení a Tepelná technika (mechanika) Pardubice 013 Použitá literatura: Technická
NOVÁ METODA NÁVRHU PRŮMYSLOVÝCH PODLAH Z VLÁKNOBETONU
 NOVÁ METODA NÁVRHU PRŮMYSLOVÝCH PODLAH Z VLÁKNOBETONU Jan Loško, Lukáš Vrábík, Jaromír Jaroš Úvod Nejrozšířenějším příkadem využití váknobetonu v současné době jsou zřejmě podahové a zákadové desky. Při
NOVÁ METODA NÁVRHU PRŮMYSLOVÝCH PODLAH Z VLÁKNOBETONU Jan Loško, Lukáš Vrábík, Jaromír Jaroš Úvod Nejrozšířenějším příkadem využití váknobetonu v současné době jsou zřejmě podahové a zákadové desky. Při
Stav napjatosti materiálu.
 tav napjatosti materiáu. Zákad mechanik, 9. přednáška Obsah přednášk : jednoosý a dvojosý stav napjatosti, stav napjatosti ohýbaného nosníku, deformace ohýbaného nosníku, řešení statick neurčitých úoh
tav napjatosti materiáu. Zákad mechanik, 9. přednáška Obsah přednášk : jednoosý a dvojosý stav napjatosti, stav napjatosti ohýbaného nosníku, deformace ohýbaného nosníku, řešení statick neurčitých úoh
Nauka o materiálu. Přednáška č.4 Úvod do pružnosti a pevnosti
 Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
4. Statika základní pojmy a základy rovnováhy sil
 4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
Ohyb nastává, jestliže v řezu jakožto vnitřní účinek působí ohybový moment, tj. dvojice sil ležící v rovině kolmé k rovině řezu.
 Ohyb přímých prutů nosníků Ohyb nastává, jestliže v řeu jakožto vnitřní účinek působí ohybový moment, tj dvojice sil ležící v rovině kolmé k rovině řeu Ohybový moment určíme jako součet momentů od všech
Ohyb přímých prutů nosníků Ohyb nastává, jestliže v řeu jakožto vnitřní účinek působí ohybový moment, tj dvojice sil ležící v rovině kolmé k rovině řeu Ohybový moment určíme jako součet momentů od všech
FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA Bakalářské studium, 4. ročník Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA Bakalářské studium, 4. ročník Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
4.1 Shrnutí základních poznatků
 4.1 Shrnutí základních poznatků V celé řadě konstrukcí se setkáváme s případy, kdy o nosnosti nerozhoduje pevnost materiálu, ale stabilitní stav rovnováhy. Tuto problematiku souhrnně nazýváme stabilita
4.1 Shrnutí základních poznatků V celé řadě konstrukcí se setkáváme s případy, kdy o nosnosti nerozhoduje pevnost materiálu, ale stabilitní stav rovnováhy. Tuto problematiku souhrnně nazýváme stabilita
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STROJNÍ
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STROJNÍ Ústav mechaniky, biomechaniky a mechatroniky Odbor pružnosti a pevnosti Program pro analýzu napjatosti a deformaci hřídelů Studentská práce Jan Pecháček
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STROJNÍ Ústav mechaniky, biomechaniky a mechatroniky Odbor pružnosti a pevnosti Program pro analýzu napjatosti a deformaci hřídelů Studentská práce Jan Pecháček
FAKULTA STAVEBNÍ. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
TENKOSTĚNNÉ A SPŘAŽENÉ KONSTRUKCE
 1 TENKOSTĚNNÉ A SPŘAŽENÉ KONSTRUKCE Michal Jandera, K134 Obsah přednášek 2 1. Stabilita stěn, nosníky třídy 4. 2. Tenkostěnné za studena tvarované profily: Výroba, chování průřezů, chování prutů. 3. Tenkostěnné
1 TENKOSTĚNNÉ A SPŘAŽENÉ KONSTRUKCE Michal Jandera, K134 Obsah přednášek 2 1. Stabilita stěn, nosníky třídy 4. 2. Tenkostěnné za studena tvarované profily: Výroba, chování průřezů, chování prutů. 3. Tenkostěnné
Geometricky válcová momentová skořepina
 Geometricky válcová momentová skořepina Dalším typem tenkostěnnéo rotačně souměrnéo tělesa je geometricky válcová momentová skořepina. Typický souřadnicový systém je opět systém s osami z, r, a t. Geometricky
Geometricky válcová momentová skořepina Dalším typem tenkostěnnéo rotačně souměrnéo tělesa je geometricky válcová momentová skořepina. Typický souřadnicový systém je opět systém s osami z, r, a t. Geometricky
Mezní napětí v soudržnosti
 Mení napětí v soudržnosti Pro žebírkovou výtuž e stanovit návrhovou hodnotu meního napětí v soudržnosti vtahu: = η η ctd kde je η součinite ávisý na kvaitě podmínek v soudržnosti a pooe prutu během betonáže
Mení napětí v soudržnosti Pro žebírkovou výtuž e stanovit návrhovou hodnotu meního napětí v soudržnosti vtahu: = η η ctd kde je η součinite ávisý na kvaitě podmínek v soudržnosti a pooe prutu během betonáže
Z toho se η využije na zajištění funkcí automobilu a na překonání odporu vzduchu. l 100 km. 2 body b) Hledáme minimum funkce θ = 1.
 Řešení úoh. koa 59. ročníku fyzikání oympiády. Kategorie A Autor úoh: J. Thomas.a) Na dráze vt bude zapotřebí objem paiva V θ θv t. Při jeho spáení se získá tepo Q mh ρv H ρθvh t. Z toho se η využije na
Řešení úoh. koa 59. ročníku fyzikání oympiády. Kategorie A Autor úoh: J. Thomas.a) Na dráze vt bude zapotřebí objem paiva V θ θv t. Při jeho spáení se získá tepo Q mh ρv H ρθvh t. Z toho se η využije na
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STROJNÍ ÚSTAV MECHANIKY, BIOMECHANIKY A MECHATRONIKY ZTRÁTA STABILITY PRUTŮ PROMĚNNÉHO PRŮŘEZU
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE AKULTA STROJNÍ ÚSTAV MECHANIKY, BIOMECHANIKY A MECHATRONIKY ZTRÁTA STABILITY PRUTŮ PROMĚNNÉHO PRŮŘEZU BAKALÁŘSKÁ PRÁCE Autor Matěj Mazur Vedoucí bakalářské práce Doc.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE AKULTA STROJNÍ ÚSTAV MECHANIKY, BIOMECHANIKY A MECHATRONIKY ZTRÁTA STABILITY PRUTŮ PROMĚNNÉHO PRŮŘEZU BAKALÁŘSKÁ PRÁCE Autor Matěj Mazur Vedoucí bakalářské práce Doc.
12. Prostý krut Definice
 p12 1 12. Prostý krut 12.1. Definice Prostý krut je označení pro namáhání přímého prizmatického prutu, jestliže jsou splněny prutové předpoklady, příčné průřezy se nedeformují, pouze se vzájemně natáčejí
p12 1 12. Prostý krut 12.1. Definice Prostý krut je označení pro namáhání přímého prizmatického prutu, jestliže jsou splněny prutové předpoklady, příčné průřezy se nedeformují, pouze se vzájemně natáčejí
Téma 4 Výpočet přímého nosníku
 Stavební statika, 1.ročník bakaářského studia Téma 4 Výpočet přímého nosníku Výpočet nosníku v osové úoze Výpočet nosníku v příčné úoze ve svisé a vodorovné havní rovině Výpočet nosníku v krutové úoze
Stavební statika, 1.ročník bakaářského studia Téma 4 Výpočet přímého nosníku Výpočet nosníku v osové úoze Výpočet nosníku v příčné úoze ve svisé a vodorovné havní rovině Výpočet nosníku v krutové úoze
I Stabil. Lepený kombinovaný nosník se stojnou z desky z orientovaných plochých třísek - OSB. Navrhování nosníků na účinky zatížení podle ČSN 73 1701
 I Stabi Lepený kombinovaný nosník se stojnou z desky z orientovaných pochých třísek - OSB Navrhování nosníků na účinky zatížení pode ČSN 73 1701 Část A Část B Část C Část D Výchozí předpokady, statické
I Stabi Lepený kombinovaný nosník se stojnou z desky z orientovaných pochých třísek - OSB Navrhování nosníků na účinky zatížení pode ČSN 73 1701 Část A Část B Část C Část D Výchozí předpokady, statické
Ing. Jan BRANDA PRUŽNOST A PEVNOST
 Ing. Jan BRANDA PRUŽNOST A PEVNOST Výukový text pro učební obor Technik plynových zařízení Vzdělávací oblast RVP Plynová zařízení a Tepelná technika (mechanika) Pardubice 2013 Aktualizováno: 2015 Použitá
Ing. Jan BRANDA PRUŽNOST A PEVNOST Výukový text pro učební obor Technik plynových zařízení Vzdělávací oblast RVP Plynová zařízení a Tepelná technika (mechanika) Pardubice 2013 Aktualizováno: 2015 Použitá
8. Základy lomové mechaniky. Únava a lomová mechanika Pavel Hutař, Luboš Náhlík
 Únava a lomová mechanika Koncentrace napětí nesingulární koncentrátor napětí singulární koncentrátor napětí 1 σ = σ + a r 2 σ max = σ 1 + 2( / ) r 0 ; σ max Nekonečný pás s eliptickým otvorem [Pook 2000]
Únava a lomová mechanika Koncentrace napětí nesingulární koncentrátor napětí singulární koncentrátor napětí 1 σ = σ + a r 2 σ max = σ 1 + 2( / ) r 0 ; σ max Nekonečný pás s eliptickým otvorem [Pook 2000]
1 Stabilita prutových konstrukcí
 1 STABLTA PRUTOVÝCH KONSTRUKCÍ 1 1 Stabilita prutových konstrukcí Pod účinky tlakových sil dochází u štíhlých prutů k vybočení stabilitní problém Posuny ve směru střednice u a rotace ϕ y zůstávají malé,
1 STABLTA PRUTOVÝCH KONSTRUKCÍ 1 1 Stabilita prutových konstrukcí Pod účinky tlakových sil dochází u štíhlých prutů k vybočení stabilitní problém Posuny ve směru střednice u a rotace ϕ y zůstávají malé,
Relaxační metoda. 1. krok řešení. , kdy stáří betonu v jednotlivých částech konstrukce je t 0
 PŘEDNÁŠKY Relaxační metoda 1. krok řešení V okamžiku t 0, kdy stáří betonu v jednotlivých částech konstrukce je t 0 a kdy je konstrukce namáhána vnitřními silami { }, nechť je konstrukce v celém svém rozsahu
PŘEDNÁŠKY Relaxační metoda 1. krok řešení V okamžiku t 0, kdy stáří betonu v jednotlivých částech konstrukce je t 0 a kdy je konstrukce namáhána vnitřními silami { }, nechť je konstrukce v celém svém rozsahu
Sedmé cvičení bude vysvětlovat tuto problematiku:
 Sedmé cvičení bude vysvětlovat tuto problematiku: Velmi stručně o parciálních derivacích Castiglianova věta k čemu slouží Castiglianova věta jak ji použít Castiglianova věta staticky určité přímé nosníky
Sedmé cvičení bude vysvětlovat tuto problematiku: Velmi stručně o parciálních derivacích Castiglianova věta k čemu slouží Castiglianova věta jak ji použít Castiglianova věta staticky určité přímé nosníky
Řešení úloh 1. kola 49. ročníku fyzikální olympiády. Kategorie D. Dosazením do rovnice(1) a úpravou dostaneme délku vlaku
 Řešení úoh koa 49 ročníku fyzikání oympiády Kategorie D Autořiúoh:JJírů(,3,4,5,6,),TDenkstein(), a) Všechny uvažované časy jsou měřené od začátku rovnoměrně zrychené pohybu vaku a spňují rovnice = at,
Řešení úoh koa 49 ročníku fyzikání oympiády Kategorie D Autořiúoh:JJírů(,3,4,5,6,),TDenkstein(), a) Všechny uvažované časy jsou měřené od začátku rovnoměrně zrychené pohybu vaku a spňují rovnice = at,
Pruty nam ahan e na vzpˇ er Martin Fiˇser Martin Fiˇ ser Pruty nam ahan e na vzpˇ er
 Obsah Úvod Eulerova teorie namáhání prutů na vzpěr První případ vzpěru zde Druhý případ vzpěru zde Třetí případ vzpěru zde Čtvrtý případ vzpěru zde Shrnutí vzorců potřebných pro výpočet Eulerovy teorie
Obsah Úvod Eulerova teorie namáhání prutů na vzpěr První případ vzpěru zde Druhý případ vzpěru zde Třetí případ vzpěru zde Čtvrtý případ vzpěru zde Shrnutí vzorců potřebných pro výpočet Eulerovy teorie
Téma 12, modely podloží
 Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
1.7 Magnetické pole stacionárního proudu
 1.7 Magnetické poe stacionárního proudu Pohybující se e. náboje (e. proud) vytvářejí magnetické poe. Naopak poe působí siou na pohybující se e. náboje. 1.7.1 E. proud, Ohmův zákon v diferenciáním tvaru
1.7 Magnetické poe stacionárního proudu Pohybující se e. náboje (e. proud) vytvářejí magnetické poe. Naopak poe působí siou na pohybující se e. náboje. 1.7.1 E. proud, Ohmův zákon v diferenciáním tvaru
BETONOVÉ KONSTRUKCE B03C +B03K ŠTÍHLÉ BETONOVÉ KONSTRUKCE. Betonové konstrukce B03C + B03K. Betonové konstrukce B03C +6B03K
 BETONOVÉ KONSTRUKCE B03C +B03K ŠTÍHLÉ BETONOVÉ KONSTRUKCE Betonové konstrukce B03C +4B03K Betonové konstrukce B03C +5B03K Betonové konstrukce B03C +6B03K prvky namáhané kombinací [M+N] N M tak (tah) s
BETONOVÉ KONSTRUKCE B03C +B03K ŠTÍHLÉ BETONOVÉ KONSTRUKCE Betonové konstrukce B03C +4B03K Betonové konstrukce B03C +5B03K Betonové konstrukce B03C +6B03K prvky namáhané kombinací [M+N] N M tak (tah) s
Nelineární problémy a MKP
 Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Předmět: Ročník: Vytvořil: Datum: ŠČERBOVÁ M. PAVELKA V. NAMÁHÁNÍ NA OHYB
 Předmět: Ročník: Vytvořil: Datum: MECHNIK DRUHÝ ŠČERBOVÁ M. PVELK V. 14. ČERVENCE 2013 Název zpracovaného celku: NMÁHÁNÍ N OHYB D) VETKNUTÉ NOSNÍKY ZTÍŽENÉ SOUSTVOU ROVNOBĚŽNÝCH SIL ÚLOH 1 Určete maximální
Předmět: Ročník: Vytvořil: Datum: MECHNIK DRUHÝ ŠČERBOVÁ M. PVELK V. 14. ČERVENCE 2013 Název zpracovaného celku: NMÁHÁNÍ N OHYB D) VETKNUTÉ NOSNÍKY ZTÍŽENÉ SOUSTVOU ROVNOBĚŽNÝCH SIL ÚLOH 1 Určete maximální
2. kapitola. Co jsou to vnitřní síly, jakými způsoby se dají určit, to vše jsme se naučili v první kapitole.
 2. kapitola Stavební mechanika 2 Janek Faltýnek SI J (43) Průběhy vnitřních sil Teoretická část: V tomto příkladu máme za úkol vyšetřit průběhy vnitřních sil na rovinné konstrukci zatížené libovolným spojitým
2. kapitola Stavební mechanika 2 Janek Faltýnek SI J (43) Průběhy vnitřních sil Teoretická část: V tomto příkladu máme za úkol vyšetřit průběhy vnitřních sil na rovinné konstrukci zatížené libovolným spojitým
Mechanika zemin II 3 Metody pro výpočet únosnosti. 1. Plastické teorémy 2. Metody mezní rovnováhy 3. Příklady jednoduchých použití
 Mechanika zemin II 3 Metody pro výpočet únosnosti 1. Plastické teorémy 2. Metody mezní rovnováhy 3. Příklady jednoduchých použití 1 ÚNOSNOST Mezní stav porušení (1. MS) napjatost splňuje podmínky porušení
Mechanika zemin II 3 Metody pro výpočet únosnosti 1. Plastické teorémy 2. Metody mezní rovnováhy 3. Příklady jednoduchých použití 1 ÚNOSNOST Mezní stav porušení (1. MS) napjatost splňuje podmínky porušení
písemky (3 příklady) Výsledná známka je stanovena zkoušejícím na základě celkového počtu bodů ze semestru, ze vstupního testu a z písemky.
 POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
Cvičební texty 2003 programu celoživotního vzdělávání MŠMT ČR Požární odolnost stavebních konstrukcí podle evropských norem
 2.5 Příklady 2.5. Desky Příklad : Deska prostě uložená Zadání Posuďte prostě uloženou desku tl. 200 mm na rozpětí 5 m v suchém prostředí. Stálé zatížení je g 7 knm -2, nahodilé q 5 knm -2. Požaduje se
2.5 Příklady 2.5. Desky Příklad : Deska prostě uložená Zadání Posuďte prostě uloženou desku tl. 200 mm na rozpětí 5 m v suchém prostředí. Stálé zatížení je g 7 knm -2, nahodilé q 5 knm -2. Požaduje se
Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr.
 . cvičení Klopení nosníků Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr. Ilustrace klopení Obr. Ohýbaný prut a tvar jeho ztráty
. cvičení Klopení nosníků Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr. Ilustrace klopení Obr. Ohýbaný prut a tvar jeho ztráty
Rovinná úloha v MKP. (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v. prostorové úlohy: u, v, w
 Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Základy teorie plasticity
 Kapitola 1 Základy teorie plasticity 1.1 Úvod V předešlých kapitolách jsme se zabývali případy, kdy se zatížené těleso po odlehčení vrátí do své původní(nezatížené) polohy nezmění své původní rozměry ani
Kapitola 1 Základy teorie plasticity 1.1 Úvod V předešlých kapitolách jsme se zabývali případy, kdy se zatížené těleso po odlehčení vrátí do své původní(nezatížené) polohy nezmění své původní rozměry ani
Přetvořené ose nosníku říkáme ohybová čára. Je to rovinná křivka.
 OHYBOVÁ ČÁRA ZA PROSTÉHO OHYBU - rovinné průřez zůstávají po deformaci rovinnými, avšak natáčejí se. - při prostém ohbu hlavní centrální osa setrvačnosti všech průřezů leží v rovině vnějších sil, která
OHYBOVÁ ČÁRA ZA PROSTÉHO OHYBU - rovinné průřez zůstávají po deformaci rovinnými, avšak natáčejí se. - při prostém ohbu hlavní centrální osa setrvačnosti všech průřezů leží v rovině vnějších sil, která
Obr. 0.1: Nosník se spojitým zatížením.
 Každý test obsahuje jeden příklad podobný níže uvedeným tpovým příkladům a několik otázek vbraných z níže uvedených testových otázek. Za příklad je možno získat maimálně bodů, celkový počet bodů z testu
Každý test obsahuje jeden příklad podobný níže uvedeným tpovým příkladům a několik otázek vbraných z níže uvedených testových otázek. Za příklad je možno získat maimálně bodů, celkový počet bodů z testu
7. Základní formulace lineární PP
 p07 1 7. Základní formulace lineární PP Podle tvaru závislosti mezi vnějšími silami a deformačně napěťovými parametry tělesa dělíme pružnost a pevnost na lineární a nelineární. Lineární pružnost vyšetřuje
p07 1 7. Základní formulace lineární PP Podle tvaru závislosti mezi vnějšími silami a deformačně napěťovými parametry tělesa dělíme pružnost a pevnost na lineární a nelineární. Lineární pružnost vyšetřuje
VI. Derivace složené funkce.
 VI. Derivace složené funkce. 17. Parciální derivace složené funkce Budeme uvažovat složenou funkci F = f(g, kde některá z jejich součástí může být funkcí více proměnných. Předpokládáme, že uvažujeme funkce,
VI. Derivace složené funkce. 17. Parciální derivace složené funkce Budeme uvažovat složenou funkci F = f(g, kde některá z jejich součástí může být funkcí více proměnných. Předpokládáme, že uvažujeme funkce,
