Matematický model šíření zvuku ve vnitřním uchu
|
|
|
- Petra Pešková
- před 8 lety
- Počet zobrazení:
Transkript
1 CENTER FOR MACHINE PERCEPTION Matematický model šíření zvuku ve vnitřním uchu CZECH TECHNICAL UNIVERSITY Martin Kukačka, Michal Navara ORL oddělení Ústřední vojenská nemocnice Praha U vojenské nemocnice Praha 6 tel.: , fax: navara@uvn.cz N - CTU CMP listopadu 2000 VÝZKUMNÁ ZPRÁVA Lze získat na ftp://cmp.felk.cvut.cz/pub/cmp/articles/navara/tr-ucho00.pdf Školitel: Mirko Navara Práce vznikla za podpory grantu Ministerstva školství ČR J04:98: Centrum strojového vnímání, Katedra kybernetiky Fakulta elektrotechnická ČVUT Karlovo náměstí 13, Praha 2 fax: (02) , tel: (02) , www:
2 Použité značení oblast hranice oblasti divergence gradient curl rotace skalární funkce: curl ψ = 2 ψ y ψ x Laplaceův operátor L 2 () vektorový prostor komplexních kvadraticky integrabilních funkcí na oblasti W vektorový prostor testovacích funkcí (, ) W skalární součin na prostoru W W norma na prostoru W indukovaná skalárním součinem δ(x) δ-distribuce H 1 () vektorový prostor funkcí, jejichž derivace patří do L 2 () 1
3 Kapitola 1 Úvod 1.1 Kochleární mechanika Úkolem kochleární mechaniky je vysvětlit mechanické procesy ve vnitřním uchu. Ačkoliv bylo tomuto tématu věnováno v minulosti značné úsilí, stále se objevují pochybnosti, neboť mechanismus nebyl dosud dostatečně objasněn. Tato práce si klade za cíl vytvoření přijatelného matematického modelu vnitřního ucha, který by mohl vysvětlit pozorované jevy, zejména vzdušné a kostní vedení a úlohu basilární membrány při vnímání jednotlivých tónů. První pozorování vnitřního ucha prováděl G.Békésy 1 ve 30-tých letech. Na základě svých měření mrtvé kochley navrhl dnes všeobecně přijímanou hypotézu postupné vlny. Békésyho vysvětlení postupné vlny je však nefyzikální. Hypotéza postupné vlny je postavena na předpokladu, že pohyb třmínku produkuje tlakové vlny šířící se ve scala vestibuli od báze k apexu a následně ve scala tympani od apexu k bázi. Působením těchto dvou vln na basilární membránu pak vzniká pohyb membrány v místě, které odpovídá kochleární frekvenční závislosti (tonotopie). Toto vysvětlení však předpokládá, že basilární membrána akustické vlny odráží. Protože však hustota i rychlost akustických vln v perilymfě i basilární membráně jsou téměř shodné, na rozhraní membrána-kapalina k odrazu akustických vln nedochází. V posledních dvaceti letech byly publikovány práce přinášející nové pohledy na tento problém. Ani v těchto pracích však nebyl pohyb membrány zcela objasněn. Uplatňují se zejména dva různé modely vnitřního ucha. První z nich předpokládá, že perilymfu lze pokládat za ideální (tj. neviskózní) nestlačitelnou kapalinu a postupná vlna vzniká díky tlumení basilární membrány. Druhý přístup perilymfu pokládá za viskózní nestlačitelnou kapalinu a neuvažuje tlumení basilární membrány. Oba tyto modely shodně dospívají k závěru, že basilární membrána koná složitý pohyb, který lze popsat 1 Georg von Békésy ( ), maďarský fyzik, jemuž byla v roce 1961 udělena Nobelova cena za lékařství za jeho výzkum vnitřního ucha 2
4 jako postupnou vlnu, jejíž amplituda se v určitém místě velmi zvětšuje. Toto místo závisí na frekvenci zvuku podle kochleární frekvenční závislosti. Ale ani tyto modely, ačkoliv velmi dobře splňují tonotopii, nepřinášejí uspokojivé vysvětlení pohybu basilární membrány. Námitky lze mít především proti tlumení basilární membrány, neboť tato veličina nebyla nikdy změřena a hodnoty používané v kochleárních modelech nemají tudíž žádné opodstatnění. Rovněž použití numerických metod (WKB metoda, čili fakticky vysokofrekční přiblížení) není dostatečně odůvodněno. Právě tyto slabiny předchozích modelů vnitřního ucha by navrhovaný matematický model měl odstranit. 1.2 Stručný přehled anatomie Ucho savců lze podle funkcí rozdělit na tři části: vnější, střední a vnitřní. Vnější ucho je tvořeno ušním boltcem a vnějším zvukovodem. Střední ucho se skládá z bubínku a dutiny středního ucha, v níž jsou tři sluchové kůstky: kladívko, kovadlinka a třmínek. Vnitřní ucho je pak tvořeno dutinou ve spánkové kosti, jenž je vyplněna kapalinou a rozděluje se dále na kochleu 2 a rovnovážné centrum. To sestává ze soustavy tří polokruhovitých kanálků a dvou váčků, které reagují na změny polohy hlavy a její pohyb. Obrázek 1.1: Anatomie lidského ucha. Funkci ucha lze stručně popsat takto: vnější ucho zachycuje a usměr- 2 řecké kochlos=hlemýžď 3
5 ňuje zvuk, který se dále šíří zvukovodem a rozkmitává bubínek. Vibrace této membrány jsou pak dále přenášeny pomocí sluchových kůstek. Poslední z nich, třmínek, je spojena se vstupem do kochley, jenž je pokryt membránou oválného okénka. Takto se akustické vlny přenášejí do kapaliny vyplňující kochleu. Kapalina pak přenáší vibrace na basilární membránu, jejíž pohyb se transformuje do nervových impulsů pomocí Cortiho orgánu. Kochlea, dutina ve spánkové kosti ve tvaru hlemýždí ulity, je basilární membránou rozdělena na dvě přibližně stejně velké části: scala vestibuli a scala tympani. Od středního ucha je kochlea oddělena dvěma membránami; membrána kruhového okénka (round window) pokrývá otvor ve scala tympani a membrána oválného okénka, na niž je připojen třmínek (stapes), pokrývá otvor ve scala vestibuli. Ačkoliv kochlea se v podélném směru (báze apex) zužuje, basilární membrána se v témže směru rozšiřuje a ztenčuje (jak je naznačeno na obr. 1.2). Obrázek 1.2: Rozvinutá kochlea. Toto geometrické uspořádání má zásadní vliv na tuhost basilární membrány, jež je pokryta Cortiho orgánem tvořeným nervovými vlákny. Pokud ucho vnímá jednotlivý tón, pouze jedno nervové vlákno spojené se zcela určitým místem je stimulováno. Díky tomuto vztahu lze zrekonstruovat tzv. 4
6 kochleární frekvenční závislost označovanou jako Greenwoodova funkce, která vyjadřuje vztah mezi charakteristickou frekvencí F vnímanou na místě ve vzdálenosti x od apexu: kde F = A(10 ax/l K), A = konstanta ovlivňující vysokofrekvenční část závislosti, a = konstatna ovlivňující tvar funkce, L = délka kochley, K = konstanta ovlivňující nízkofrekvenční část závislosti. Protože kochleární frekvenční závislost je výsledkem mnoha velmi přesných měření, je základním prvkem, který musí splňovat každý kochleární model. Tabulka 1.1: Greenwoodovy konstanty pro různé savce. Druh A a K L Člověk Kočka domácí Činčila Morče Myš domácí Krysa Kráva Slon Tonotopické hledisko však není jediným kritériem úspěšnosti matematického modelu vnitřního ucha. Je třeba vysvětlit především dva fenomény: kostní vedení a superpozici dvou tónů. Z experimentů je známo, že pokud je kost (např. lebka) rozkmitána, vnímá ucho zvuk o téže frekvenci. Díky kostnímu vedení může slyšet i ucho s nepohyblivým třmínkem (otoskleróza) nebo přerušeným zvukovodem (atrézie zvukovodu). Pokles intensity při kostním vedení je však značný (přibližně db). Experimentálně bylo rovněž zjištěno, že při superpozici dvou tónů o frekvencích f 1 a f 2 ucho vnímá navíc frekvenci 2f 1 f 2, kde f 1 značí vyšší frekvenci. Zatím žádné matematické modely vnitřního ucha tyto jevy nevysvětlily. 5
7 1.3 Model vnitřního ucha Při tvorbě matematického modelu se přirozeně musíme dopustit mnoha zjednodušení, avšak podstatné prvky vystihující skutečnost musí být zachovány. V práci se zabýváme dvoudimenzionálním modelem znázorněným na obr Obrázek 1.3: Zjednodušený 2-D kochleární model. Kochlea je modelována jako obdélník v polovině rozdělený basilární membránou. Tuhost basilární membrány je podle experimentálních výsledků dána vztahem K = C exp( λx), kde x značí vzdálenost od báze. Ačkoliv různá měření se velmi liší v absolutní hodnotě tuhosti (dané konstantou C), shodují se v tom, že podél basilární membrány dochází k poklesu tuhosti na 1/100 až 1/ Tím je tedy přibližně určena hodnota konstanty λ. Při modelování tonotopie se zajímáme o ustálený stav, tj. takový stav, ve kterém lze budící sílu považovat za harmonickou. Přitom vzdušné vedení, kdy budící silou je pohyb třmínku, modelujeme vtokem kapaliny do kochley v oblasti třmínku (viz obr. 1.3) a okrouhlé okénko modelujeme výtokem z kochley v oblasti okrouhlého okénka. Třmínek a okrouhlé okénko jsou přesně v protifázi, neboť předpokládáme stálý objem kochleární dutiny. U kostního vedení je otázka budící síly méně jasná. Předpokládejme však, že vibrace se kostmi šíří tak, že budící síla působí podél celé kochley (to by fakticky znamenalo dopad rovinné vlny). V takovém případě modelujeme budící sílu jako vtok kapaliny do kochleární dutiny skrze její jednu stěnu (viz obr. 1.4). Poloha okrouhlého okénka je zachována a velikost vtoku a výtoku je volena tak, aby objem kochleární dutiny zůstal zachován. V předložené práci se dále budeme zabývat kochleárním modelem činčily. Podle anatomických měření je basilární membrána činčily dlouhá 18 mm 6
8 Obrázek 1.4: Kostní vedení pro zjednodušený 2-D model. a výška kochley klesá podél basilární membrány od 0.75 mm k hodnotě 0.47 mm u apexu (viz. [Watts, 1993]). Obdélník, jímž kochleu modelujeme, bude mít rozměry 18 mm 0.4 mm. Podobným problémem se v nedávné době zabývaly např. následující práce: 1. L.Watts: Cochlear Mechanics: Analysis and Analog VLSI, 1993, Kochlea je modelována jako obdélník vyplněný ideální (neviskozní) nestlačitelnou kapalinou v polovině rozdělený basilární membránou (viz obr. 1.3) a předpokládá se, že proudění kapaliny je nevírové. Navíc se předpokládá, že basilární membrána je velmi silně tlumena, díky čemuž vzniká postupná vlna. Pro vhodné parametry je její maximální amplituda v souladu s tonotopií. Není zřejmé, že při disipaci energie zůstává proudění kapaliny nevírové. Podstatné však je, že nalezené řešení rychlostního potenciálu nesplňuje okrajové podmínky na něj kladené. 2. L. Kian-Meng: Physical and Mathematical Cochlear Models, 2000, Zabývá se 3-dimenzionálním modelem. Kochlea je modelována jako kvádr vyplněný nestlačitelnou viskozní kapalinou. Pro výpočet Navierovy-Stokesovy rovnice používá WKB metodu (vysokofrekvenční přiblížení). Díky disipaci energie opět dostává řešení postupnou vlnu, jejíž maximální amplituda je pro vhodné parametry ve shodě s reálnou tonotopií. 7
9 Není zcela jasné, zda použitá vysokofrekvenční aproximace je přípustná. Závažnější však je, že Navierova-Stokesova rovnice je řešena nikoliv s okrajovými podmínkami příslušnými viskozní kapalině (nulová jak normálová, tak i tečná složka rychlosti), ale kapalině ideální (nulová pouze tečná složka rychlosti). Toto zjednodušení ale může mít na výsledek podstatný vliv. 3. Leveque R. J., Peskin C. S., Lax P. D.: Solution of a Two-Dimensional Cochlea Model with Fluid Viscosity, 1998 Modeluje kochleu jako polorovinu, okrajové podmínky jsou zadány v nekonečnu a není přítomen zdroj buzení. Jde o velmi teoretický model, který rovněž vede k existenci postupné vlny. Z poznámek k uvedeným pracím je patrné, že pro řešení je velmi podstatná volba okrajových podmínek. V této práci požadujeme, aby řešení splňovalo na hranici obdélníka podmínku pro viskozní kapalinu, tj. aby tečná i normálová složka byly nulové. Pouze v místě vtoku a výtoku (třmínek a kruhové okénko) je předepsána nenulová tečná složka rychlosti. Podrobněji budou okrajové podmínky rozebrány v následující kapitole. 8
10 Kapitola 2 Matematický popis modelu vnitřního ucha 2.1 Formulace rovnic Pohyb nestlačitelné viskozní kapaliny je zcela obecně popsán Navierovou- Stokesovou rovnicí a rovnicí kontinuity ρ v t ν 2 v + ρv v + p = f (2.1) v = 0, (2.2) na oblasti a příslušnými okrajovými podmínkami na hranici. V těchto rovnicích značí ν viskozitu, ρ hustotu, p tlak, v rychlost kapaliny a f působící vnější síly. V rovnicích přistupujeme k následujícím linearizacím: 1. Nelineární konvektivní člen v v je zanedbán. Místo Navierovy Stokesovy rovnice řešíme tzv. časově závislou Stokesovu rovnici. 2. Působiště síly basilární membrány není v její skutečné poloze h = h(x, t), ale v klidové poloze y = 0. Toto zjednodušení je možné, předpokládáme-li, že výchylky membrány jsou malé. 3. Velikost síly basilární membrány je přímo úměrná její výchylce, konstantou úměrnosti je tuhost závisející na vzdálenosti od báze k = k(x). Díky uvedeným zjednodušením dostáváme soustavu tří rovnic: ρ v x t + p ( 2 ) x ν v x x v x y 2 = 0 (2.3) ρ v y t + p ( 2 ) y ν v y x v y y 2 = f y (2.4) 9
11 v x x + v y y = 0, (2.5) kde y-ová složka vnější síly je dána výrazem f y = k(x)h(x, t)δ(y) a znamená elastickou sílu membrány, která ji vrací do klidové polohy. Vztah výchylky membrány h a rychlosti je samozřejmě v y (x, y) y=0 = dh(x) dt. Setrvačná síla basilární membrány (člen úměrný 2 v t ) ve výrazu pro vnější sílu 2 nevystupuje, neboť hustotu basilární membrány a okolní kapaliny považujeme za stejnou a tudíž je tato síla již zahrnuta v pravé straně rovnice (2.4). Rovněž tlumení membrány (člen úměrný v) není ve výrazu pro vnější sílu zahrnuto, protože o velikosti tlumení basilární membrány nejsou k dispozici žádné experimentální údaje. Vzhledem k tomu, že uvažujeme ustálený stav, můžeme časové rovnice převést do frekvenční oblasti volbou v = R(Ve iωt ) p = R(P e iωt ) h = R(He iωt ), (2.6) Časové derivace v rovnicích (2.3) a (2.4) se tak změní na násobení výrazem iω: iωρv x + P ( 2 ) x ν V x x V x y 2 = 0 (2.7) ( i ωρ kδ(y) ) V y + P ( 2 ) ω y ν V y x V y y 2 = 0, (2.8) Rovnice kontinuity zůstává formálně stejná. V x x + V y y = 0, (2.9) Rovnicemi (2.7) (2.9) je pak popsán ustálený stav proudění kapaliny ve vnitřním uchu. K těmto rovnicím přistupují ještě okrajové podmínky na hranici oblasti. Kruhové a oválné okénko se modelují jako vtok, resp. výtok kapaliny, na zbytku hranice je rychlost nulová, což lze vyjádřit V Γ = V 0 Γ V \Γ = 0, (2.10) kde Γ značí tu část hranice, kde kapalina vtéká nebo vytéká a V 0 je zadaná rychlost. 2.2 Řešení pomocí metody konečných prvků Metoda konečných prvků je založena na tzv. slabé formulaci rovnic. Proto zde tuto formulaci odvodíme. Označme vektorové prostory komplexních kvadraticky integrabilních skalárních, vektorových a tenzorových funkcí po řadě 10
12 L 2 (), [L 2 ()] 2 a [L 2 ()] 4. Na těchto prostorech je definován obvyklý skalární součin, takže pro U, V [L 2 ()] 2 platí (U, V) [L2 ()] 2 = ( U, V) [L2 ()] 4 = Dále zvolme vektorový prostor W U V d U : V d W = {U : div U = 0, U = 0, U [L 2 ()] 2, U [L 2 ()] 4 } (2.11) se skalárním součinem (U, V) W () = (U, V) [L2 ()] 2 + ( U, V) [L 2 ()] 4 (2.12) a normou U W () = (U, U) W (), (2.13) Vektorový tvar rovnic (2.7) a (2.8) je kde K je matice K V + grad P ν 2 V = 0, (2.14) K = ( iωρ 0 0 i(ωρ k(x)δ(y) ω ) a skalární součin K V je pouze formální označení K ij V j. Násobíme-li skalárně (ve smyslu skalárního součinu na [L 2 ()] 2 ) rovnici (2.14) libovolnou testovací funkcí U z prostoru W, dostáváme U K V d + U grad P d ν U 2 V d = 0, (2.15) Jednotlivé členy rovnice (2.15) upravíme podle Greenovy věty, přičemž využijeme vlastností testovacích funkcí, díky kterým platí U 2 V d = n V U ds V : U d = V : U d U P d = Rovnice (2.15) má tedy tvar U K V d + ν P U n ds ) P U d = 0, V : U d = 0, (2.16) 11
13 Splňuje-li funkce V okrajovou podmínku V = V 0, můžeme řešení rovnic (2.7) (2.9) hledat ve tvaru V = V + V 0, kde V W. Rovnice (2.16) má po dosazení tohoto řešení tvar U K V d+ν V : U d = U K V 0 d ν V 0 : U d, který lze formálně zapsat (2.17) a(u, V) = f(u), U W, (2.18) Řešení rovnice (2.18) je jednoznačné, pokud kvadrilineární forma a(u, V) je V-eliptická, tj. pokud existuje konstanta α > 0 taková, že platí a(u, U) > α U W, K důkazu lze užít Friedrichsovu nerovnost (platnou pro U H 1 ()) ) 1 U H 1 () C ( U [L2()] 4 + U 2 U ds, (2.19) 0 ve které 0 a C je kladná konstanta. Pokud navíc U W, lze psát a spojením s rovnicí U W C U [L2 ()] 4 (2.20) a(u, U) R(a(U, U)) = ν U [L2 ()] 4 (2.21) dostáváme požadovanou V-elipticitu a(u, U) > α U W, (2.22) Princip metody konečných prvků spočívá v aproximaci prostoru testovacích funkcí W konečnědimenzionálním prostorem W h. Rovněž aproximaci řešení V W hledáme na prostoru W h. Hledáme tedy takové V h W h, které splňuje a(u h, V h ) = f(u h ), U h W h, (2.23) Vzhledem k tomu, že prostor W h je konečnědimenzionální, postačí, když rovnice (2.23) bude splněna pro všechny bázové funkce U i prostoru W h. Diskrétní řešení V h lze psát jako lineární kombinaci bázových funkcí V h = j c ju j, čímž rovnice (2.23) přejde na tvar c j a(u i, U j ) = f(u i ) i, (2.24) j Rovnice (2.24) je soustavou rovnic pro neznámé koeficienty c j a lze ji psát ve tvaru c j a ji = f i, (2.25) kde a ij se (z historických důvodů) nazývá maticí tuhosti a f i vektorem zatížení. Výhodnost této formulace spočívá v tom, že bázové funkce je možno volit tak, aby matice tuhosti byla pásová nebo alespoň řídká. To pak umožní využít efektivní algoritmy při řešení soustavy (2.25). 12
14 2.3 Formulace pomocí proudové funkce Pro dvoudimenzionální proudění nestlačitelné kapaliny lze rovnici kontinuity (2.9) splnit zavedením tzv. proudové funkce: V x = Ψ y V y = Ψ x (2.26) Ačkoliv funkce Ψ je komplexní, v diskrétním případě stačí uvažovat reálnou proudovou funkci ψ = R(Ψ) a testovací funkce volíme Ψ k = (1 + 0i)ψ k. Proto definujeme prostor W ψ = {ψ : 2 ψ x i x j L 2 (), i, j; div curl ψ = 0; curl ψ = 0}, (2.27) Prostor W ψh je pak opět konečnědimenzionální aproximací prostoru W ψ. Bázové funkce volme tak, aby jejich nosiče byly malé. Pro obdélníkovou oblast = a/2, a/2 b/2, b/2 toho můžeme dosáhnout volbou dělících bodů x 0 = a/2, x 1 = x 0 + h 1 x,..., x n 1 = a/2 h n x, x n = a/2, (2.28) y 0 = b/2, y 1 = y 0 + h 1 y,..., y m 1 = b/2 h m y, y m = b/2, (2.29) čímž oblast rozdělíme na nm obdélníků h i x h j y. Bázové funkce ψ k volíme na oblasti ve tvaru součinu ψ k (x, y) = φ i (x)φ j (y), k = 1 4nm, i = 1 2n, j = 1 2m, (2.30) kde elementární bázové funkce splňují podmínky φ 2i 1 (x j ) = δ ij, (φ 2i 1 ) (x j ) = 0, (2.31) φ 2i (x j ) = 0, (φ 2i ) (x j ) = δ ij, (2.32) Z podmínky d2 φ i dx L 2 2 () snadno dostáváme vyjádření elementárních bázových funkcí φ 2i 1 (x) = 2(x x i 1 ) 2 (x x i h i /2)/(h i ) 3, x K i φ 2i 1 (x) = 2(x x i+1 ) 2 (x x i + h i+1 /2)/(h i+1 ) 3, x K i+1 φ 2i (x) = (x x i 1 ) 2 (x x i )/(h i ) 2, x K i φ 2i (x) = (x x i+1 ) 2 (x x i )/(h i+1 ) 2, x K i+1, (2.33) kde K i = (x i 1, x i ). Prvky matice tuhosti lze zapsat pomocí těchto bázových funkcí ( 2 ψ i a ij = ν x 2 2 ψ i ) ( 2 ψ j y 2 x 2 2 ψ j ) 2 ψ i 2 ψ j y 2 d + 4ν x y x y d + ( ψ i ψ j + iωρ x x + ψi ψ j ) k(x)δ(y) ψ i ψ j d i y y ω x x d,(2.34) Prvky matice tuhosti jsou tvořeny integrály z kombinací derivací elementárních bázových funkcí; tyto integrály jsou v následujících tabulkách: 13
15 j = 2k 3 2k 2 2k 1 2k K i φ i φ j dx K i+1 φ i φ j dx i = 2k 1 2k 2k 1 2k 9h i 70 13h2 i 13h 2 i 420 h3 i 13h i 35 11h2 i h i h 3 i k h i h 2 i h i h 2 i h 3 i h 2 i k h2 i h3 i K i (φ i ) (φ j ) dx K i+1 (φ i ) (φ j ) dx i = 2k 1 2k 2k 1 2k j = 2k h i k h i k 1 5h i h i k 1 2h i 1 2h i k h i k h i+1 30 K i (φ i ) (φ j ) dx K i+1 (φ i ) (φ j ) dx i = 2k 1 2k 2k 1 2k j = 2k h 3 i h 2 i 2k h 2 h i i k h 3 i h 2 i h 3 i+1 h 2 i+1 2k h 2 h i i h 2 h i+1 i+1 2k h 3 i+1 h 2 i+1 2k h 2 i+1 2 h i+1 K i φ i (φ j ) dx K i+1 φ i (φ j ) dx i = 2k 1 2k 2k 1 2k 6 j = 2k 3 5h i h 2k 2 i k h i h i k 10 2h i h i k h i k h i
16 K i (φ i ) φ j dx K i+1 (φ i ) φ j dx i = 2k 1 2k 2k 1 2k 6 j = 2k 3 5h i h 2k 2 i k h i h i k 10 2h i h i k h i k h i Tyto integrály lze využít pro vyjádření viskozní části formy a(u, V), neboť ( ) ( ) 2 ψ i x 2 ψ i 2 ψ j 2 y 2 x 2 ψ j 2 y d ψ i 2 ψ j 2 ( x y x y d = (φ i1 ) φ i2 φ i1 (φ i2 ) ) ( (φ j1 ) φ j2 φ j1 (φ j2 ) ) d+ 4 (φi1 ) (φ i2 ) (φ j1 ) (φ j2 ) d, kde ψ i (x, y) = φ i1 (x)φ i2 (y) resp, ψ j (x, y) = φ j1 (x)φ j2 (y), Navíc, díky tomu, že bázové funkce mají omezený nosič, není třeba integrovat přes celou oblast, ale stačí jen přes (K i + K i+1 ) (K j + K j+1 ). 2.4 Okrajové podmínky Okrajové podmínky na hranici jsou dány funkcí V 0 z rovnice (2.17). Tuto funkci rovněž vyjádříme pomocí proudové funkce ψ 0. Zvolme: ψ 0 = 2(y + a 2 )2 (y + 3a 8 ) ( a 4 )3 φ 1 (x) y < 0 (2.35) ψ 0 = 2(y a 2 )2 (y + 5a 8 ) ( a 4 )3 φ 1 (x) y > 0 (2.36) Isolinie funkce ψ 0 (proudnice) jsou na obr Podobně volíme proudovou Obrázek 2.1: Isolinie okrajové podmínky ψ 0 pro vzdušné vedení. funkci ψ 0 pro kostní vedení (viz obr. 2.2). 15
17 Obrázek 2.2: Isolinie okrajové podmínky ψ 0 pro kostní vedení. 2.5 Tuhost basilární membrány Proudění kapaliny v hlemýždi rozhodujícím způsobem ovlivňuje zejména tuhost basilární membrány, která je určena především tuhostí příčných vláken v membráně. Youngův modul pružnosti ve směru těchto vláken je asi 100 větší, než modul pružnosti ve směru podélném (báze apex). To do jisté míry umožňuje modelovat basilární membránu jako řadu navzájem nezávislých nosníků. Zde však používáme exponenciální závislost tuhosti na vzdálenosti od báze: k(x) = Ce λx, (2.37) která byla zjištěna experimentálně, ale hodnoty konstant C a λ se velmi liší. Například [Watts, 1993] uvádí hodnoty a [Leveque at all., 1988] uvádí C = kg m 2 s 2 λ = 200 m 1 C = kg m 2 s 2 λ = 140 m 1, V této práci proto považujeme hodnoty C a λ za neznámé parametry, jejichž vhodnou volbou dosáhneme shodu s experimentálně známou tonotopií. 16
18 Kapitola 3 Výsledky V této části jsou popsány numerické výsledky. Program byl napsán v jazyce fortran 90 s využitím knihovny matematických funkcí IMSL (pro řešení soustavy rovnic). 3.1 Numerická konvergence Přesnost výpočtu při použití metody konečných prvků závisí na použitých bázových funkcích a zvolené diskretizaci oblasti. Ukázalo se, že v našem případě numerické řešení extrémně závisí na počtu uzlových bodů podél basilární membrány. To demonstrují následující obrázky (počítáno kostní vedení pro parametry C = kg m 2 s 2, λ = 555 m 1 a f = 1000 Hz). Přesný důvod těchto numerických oscilací není znám, jde však pravděpodobně o podobný efekt, jaký je popsán v [Křížek, Neittaanmäki, 1990] na str. 134 a dále 1. Je ale zřejmé, že se zlepšující se diskretizací oblasti se numerické řešení vyhlazuje. Velmi výrazně se však zvyšuje paměťová a časová náročnost výpočtu a proto přistupujeme k následujícímu kompromisu: počítáme s menší diskretizací, než by bylo třeba pro získání hladkého řešení, ale výsledné (oscilující) řešení vyhladíme proložením polynomu. Jelikož oscilace jsou rozloženy rovnoměrně na obě strany od skutečného řešení, není jimi prokládaný polynom (při vhodně zvoleném stupni n) příliš ovlivněn. Tím podstatně snížíme náročnost výpočtu při zachování požadované přesnosti. 1 Při řešení stacionární konvekčně-difusní rovnice s převládající konvekcí, např. ε d2 u dx 2 + du du = f, vznikají v numerickém řešení u h pro zmenšující se ε oscilace kolem skutečného řešení, což zpomaluje konvergenci numerického řešení. Zlepšení lze dosáhnout volbou speciálních bázových funkcí. 17
19 Reálná část proudové funkce podél basilární membrány při použití různého počtu uzlových bodů. 150 uzlových bodů 200 uzlových bodů 18
20 300 uzlových bodů 400 uzlových bodů 19
21 800 uzlových bodů Srovnání proudové funkce pro 300 uzlových bodů podél basilární membrány s proloženým polynomem (11. stupně) a řešením pro 800 uzlových bodů Uvedené výsledky nám umožňují považovat proložený polynom za zlepšenou aproximaci skutečného řešení. 20
22 3.2 Vzdušné vedení Při modelování vzdušného vedení (buzení třmínkem) docházíme k následujícím zjištěním: Pro každou frekvenci f má (příčná) rychlost basilární membrány v y maximum v jisté vzdálenosti x od báze. Domníváme se, že v tomto místě maximální rychlosti dochází vnímání tónu (stimulaci příslušného nervového vlákna). Maximální frekvence, kterou je možno vnímat (tj. frekvence, pro niž je maximum rychlosti na začátku basilární membrány x = 0), závisí na maximální hodnotě tuhosti basilární membrány (konstanta C ve vztahu (2.37)). S rostoucí hodnotou tuhosti se zvyšuje i hodnota maximální frekvence (a dochází k větším numerickým oscilacím). Frekvenční rozsah je ovlivněn rychlostí poklesu tuhosti podél basilární membrány (konstanta λ ve vztahu (2.37)). Se zvětšujícím se poklesem tuhosti se zvětšuje i frekvenční rozsah. Uvedené závěry vyplývají z kochleárního numerického modelu činčily, jejíž skutečná tonotopie je na následujícím obrázku: 21
23 C = kg m 2 s 2, λ = 833 m 1 proudová funkce frekvence 20 khz, 10 khz, 5 khz, 3 khz, 2 khz, 1 khz, 500 Hz a 100 Hz příčná rychlost frekvence 20 khz, 10 khz, 5 khz, 3 khz, 2 khz, 1 khz, 500 Hz a 100 Hz Na předchozím obrázku je znázorněna frekvenční závislost proudové funkce 22
24 a rychlosti podél basilární membrány pro dané hodnoty C a λ. Tonotopické křivky pro hodnoty C = kg m 2 s 2, C = kg m 2 s 2 a λ = 833m 1, λ = 555 m 1 jsou zobrazeny na následujícím souhrnném obrázku: 3.3 Kostní vedení Kostní vedení vykazuje shodnou závislost na hodnotách parametrů C a λ (viz. rovnice (2.37)) jako vzdušné vedení. Tonotopie kostního vedení se sice od tonotopie vzdušného vedení liší, ale pro dostatečně velkou maximální tuhost membrány jsou odchylky minimální. Následují ukázky řešení kostního vedení pro různé parametry tuhosti. 23
25 C = kg m 2 s 2, λ = 833 m 1 proudová funkce frekvence 20 khz, 10 khz, 5 khz, 3 khz, 2 khz, 1 khz, 500 Hz,100 Hz a 20 Hz příčná rychlost frekvence 20 khz, 10 khz, 5 khz, 3 khz, 2 khz, 1 khz, 500 Hz,100 Hz a 20 Hz 24
26 C = kg m 2 s 2, λ = 555 m 1 proudová funkce frekvence 20 khz, 10 khz, 5 khz, 1 khz a 500 Hz příčná rychlost frekvence 20 khz, 10 khz, 5 khz, 1 khz a 500 Hz 25
27 C = kg m 2 s 2, λ = 389 m 1 proudová funkce frekvence 20 khz, 10 khz, 5 khz, 2 khz a 1.5 khz příčná rychlost frekvence 20 khz, 10 khz, 5 khz, 2 khz a 1.5 khz 26
28 3.4 Diskuse výsledků Z uvedených vlastností řešení vyplývá, že vhodnou volbou parametrů C a λ v rovnici (2.37) lze dosáhnout shody změřené tonotopie a tonotopie spočtené pro vzdušné vedení. Podobně lze volbou vhodných parametrů dosáhnout shody mezi tonotopií měřenou a počítanou pro kostní vedení. Překvapující je však, že hodnoty parametrů C a λ jsou pro oba případy (téměř) shodné. Řešení pro vzdušné i kostní vedení a parametry C = kg m 2 s 2, λ = 725 m 1 je na následujícím obrázku: Tato práce podává velmi zjednodušený matematický model vnitřního ucha. Zjednodušení spočívají především v tom, že model je dvoudimenzionální a nerespektuje zakřivení kochley, změnu jejího průřezu ve směru báze apex ani polohu basilární membrány, která nerozděluje cochleu na dvě stejně velké části (např. pro lidské ucho je poměr objemů scala vestibuli a scala tympani přibližně 4:5). Dále je např. zanedbán vliv Reissnerovy membrány. Kromě těchto geometrických zjednodušení navíc kapalinu považujeme (podobně jako mnohé citované práce) za nestlačitelnou, a proto je možné uvedený model popsat Navierovou Stokesovou rovnicí. Vzhledem k drastickým zjednodušením je překvapivé, jak dobrou shodu reálné a spočítané tonotopie dostáváme, a to i pro velmi jednoduchý model kostního vedení. Této shody však dosahují i všechny citované práce; na rozdíl od jejich výsledků však nedostáváme jako řešení postupnou vlnu na basilární membráně, ale v našem modelu dospíváme ke stojatému vlnění basilární membrány. Domníváme se, že tento podstatný rozdíl je způsoben odlišnou volbou okrajových podmínek. Zde volíme podmínku nulové rychlosti na rozhraní kapalina-kost, avšak na rozhraní kapalina-membrána žádnou podmínku nepředepisujeme. 27
29 V modelu vzdušného vedení je ale nulová tečná složka rychlosti na basilární membráně zajištěna symetrií úlohy. Experimentálně bylo zjišťěno, že jediný tón vybudí pouze jednu aferentní nervovou dráhu v ušním nervu. To znamená, že maximum amplitudy či jiné kritérium pro stanovení výšky tónu se určuje již v Cortiho orgánu. Částečné vysvětlení podává struktura trámových buněk, které jsou uspořádány tak, že mohou čistě mechanickým způsobem derivovat. Výchylka buněk vychází přibližně úměrná h x. (Přesněji, jedná se o rozdíl výchylek basilární membrány v místech n. a (n + 2). buňky.) Při stojatém vlnění (jako v našem modelu) by v místě maximální výchylky basilární membrány byla tato derivace nulová. (To nastane i v místech, kde výchylka je nulová, což lze ale poměrně snadno rozlišit podle sousedních buňek.) V případě postupné vlny by takovéto jednoduché vyhodnocení nebylo možné. I v případě stojatého vlnění by však bylo obtížné zamezit zkreslenému vnímání více podobných tónů současně. Tomu by byla nejblíže Helmholtzova hypotéza oddělených rezonátorů, pokud by tyto rezonátory byly velmi málo tlumené, takže by reagovaly jen na velmi úzké pásmo kmitočtů. Tudíž žádný z nám známých dosavadních pokusů o vysvětlení převodu fyzikálních dějů ve vnitřním uchu na nervový signál nelze považovat za postačující. Námi uvažovný model nezahrnuje aktivní prvky, které by mohly přispět k odtlumení, případně i spontánnímu rozkmitání systému. Pozorování ukazují, že k takovým jevům zřejmě dochází, i když jejich mechanismus není znám. Proto ani nevíme, jak bychom aktivní roli basilární membrány nebo Cortiho orgánu zahrnuli do našeho popisu. Nutno poznamenat, že zpětná vazba, realizující aktivní pohyb basilární membrány, nemůže být realizována eferentními nervovými drahami, může jimi být pouze řízena, neboť se jedná o akustické frekvence řádově vyšší než ty, které lze přenášet neurony. Výjimku lze připustit pouze u nejnižších frekvencí. (Poznamenejme, že i technická řešení akustických zařízení někdy používají zpětnovazební mechanismus pro nezkreslené zpracování velmi nízkých frekvencí.) Navržený matematický model je možno ještě vylepšit. Kromě komplikovanější geometrie by bylo vhodné započítat hlavně vliv oválného a okrouhlého okénka (tj. např. do vnějších sil v rovnici (2.1) zahrnout elastické síly těchto membrán). Model by bylo možno zpřesnit tím, že by se uvažoval reálný tvar oválného a okrouhlého okénka, zatímco v jejich okolí tvoří hranici kost. Kromě toho se liší jejich dynamické vlastnosti: zatímco za okrouhlým okénkem je vzduch, za oválným okénkem je středoušní převodní aparát, tvořený kůstkami s nezanedbatelnou hmotností. Tato nesymetrie však nedovoluje zjednodušení úlohy redukcí na řešení ve scala vestibuli předpokladem, že pohyb kapaliny ve scala tympani je stejný, jen opačně orientovaný. Tento zjednodušující předpoklad byl použit nejen zde, ale i v řadě předchozích prací. Vodítkem pro posouzení vlivu středoušního převodního aparátu na jevy ve vnitřním uchu by mohlo být porovnání audiogramů pro kostní vedení u zdravých osob a u osob s poruchou (příp. absencí) středoušního aparátu. 28
30 Ještě komplikovanější by bylo vytvořit model tak, aby umožňoval excitaci dvěma tóny o různých frekvencích současně, což předložený model neumožňuje, neboť je počítán ve frekvenční oblasti. Toho by bylo možné dosáhnout výpočtem v časové oblasti, otázkou ovšem zůstává numerická konvergence takové úlohy. Zcela jinou možností studia se jeví pokus s fyzikálním modelem, tedy se zvětšenou napodobeninou kochley. Takový pokus se jeví velmi žádoucí, i když i jeho vypovídací schopnost je omezená. Jako každý model, i tento by mohl být zkreslen zanedbáním některé důležité vlastnosti. Jak vyplývá z přehledu literatury k tomuto tématu, není ani zdaleka jednotný názor na důležitost jednotlivých veličin (např. stlačitelnost kapaliny, viskozita, ztráty na rozhraních, přenos zvuku z kapaliny do kosti atd.). Nelze proto vyloučit zásadní opomenutí při snaze o fyzikální model. Určitým vodítkem pro srovnání modelů může být mj. pozorovaná stálost vnímané výšky tónu. Některé veličiny (např. rychlost zvuku, viskozita) jsou tak závislé na teplotě, že by to mohlo být pozorovatelné. Přesto nic takového nebylo, pokud víme, pozorováno. Též vnímání fáze zvuku, tolik důležité pro určení směru, odkud přichází, lze těžko vysvětlit v kterémkoli z uvažovaných modelů. Potíž je v tom, že časový posun řádově 10 4 s se zdá být příliš malý na přímé zpracování v nervových drahách. 3.5 Závěr V posledních letech došlo v matematickém modelování vnitřního ucha k podstatné změně, neboť kapalina se považuje za nestlačitelnou a tedy v ní nemohou existovat akustické vlny. Přesto však koncept postupné vlny navržený von Békésym nebyl dosud opuštěn. V této práci se ale ukazuje, že pro daný model, který i přes mnohá zjednodušení nepostrádá fyzikální smysl, se na basilární membráně vytváří stojatá vlna, jejíž amplituda závisí na vzdálenosti daného místa od báze ve shodě s reálnou tonotopií. Důležité však je, že byl navržen jednoduchý model kostního vedení a i tento model je ve shodě s reálnou tonotopií. Protože přímé měření pohybu basilární membrány je kvůli nepřístupnosti kochley možné jen na počátku a konci basilární membrány, nelze zatím o správnosti ani jedné z hypotéz definitivně rozhodnout. 29
31 Slovníček česky anglicky ekvivalentní označení basilární membrána basilar membrane bubínek eardrum tympanic membrane hlemýžď cochlea kladívko hammer malleus kovadlinka anvil incus kruhové okénko round window oválné okénko oval vindow polokruhovité kanálky semicircular canals sluchové kůstky ossicles spánková kost temporal bone střední ucho middle ear třmínek stapes stirrup ušní boltec pinna auricle vnější ucho outer ear vnější zvukovod ear canal external auditory canal vnitřní ucho inner ear 30
32 Literatura [Brdička, 1959] Brdička M.: Mechanika kontinua, Academia Praha 1959 [Bönke, Arnold, 1999] Böhnke F., Arnold W.: 3-D finite element model of the human cochlea including fluid-structure couplings, ORL, vol. 61, 1999, p [Feistauer, 1993] Feistauer M.: Mathematical methods in fluid dynamics, Longman New York 1993 [Kian-Meng, 2000] Kian-Meng L.: Physical and mathematical cochlear models, disertační práce, Stanford University, 2000 [Křížek, Neittaanmäki, 1990] Křížek M., Neittaanmäki P. : Finite element approximation of variational problems and applications, Longman New York, 1990 [Leveque at all., 1988] Leveque R. J., Peskin C. S., Lax P. D.: Solution of a two dimensional cochlea model with fluid viscosity, SIAM J. Appl. Math., vol. 48, No. 1, 1998, p [Navara at all., 1997] Navara M., Stejskal V., Valášek M., Stingl J., Rejmontová J.: Modelování přenosu akustické energie ve středním uchu, závěrečná zpráva grantového úkolu GA ČR 106/95/1134, Praha 1997 [Watts, 1993] Watts, L.: Cochlear Mechanics: Analysis and analog VLSI, disertační práce, CIT Pasadena, 1993 Velmi podrobnou bibliografii obsahují disertační práce Lloyda Wattse a Lim Kian-Menga. 31
Mechanika kontinua. Mechanika elastických těles Mechanika kapalin
 Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Dnešní látka: Literatura: Kapitoly 3 a 4 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Akustika. Teorie - slyšení. 5. Přednáška
 Akustika Teorie - slyšení 5. Přednáška Sluchové ústrojí Vnitřní a vnější slyšení Zpěv, vlastní hlas Dechové nástroje Vibrace a chvění Ucho Ucho je složeno z ucha vnějšího, středního a vnitřního. K vnějšímu
Akustika Teorie - slyšení 5. Přednáška Sluchové ústrojí Vnitřní a vnější slyšení Zpěv, vlastní hlas Dechové nástroje Vibrace a chvění Ucho Ucho je složeno z ucha vnějšího, středního a vnitřního. K vnějšímu
Co jsme udělali: Au = f, u D(A)
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Akustika. Teorie - slyšení. 5. Přednáška
 Akustika Teorie - slyšení 5. Přednáška http://data.audified.com/downlpublic/edu/zha_pdf.zip http://data.audified.com/downlpublic/edu/akustikaotazky03.pdf http://data.audified.com/downlpublic/edu/jamusimulatorspro103mac.dmg.zip
Akustika Teorie - slyšení 5. Přednáška http://data.audified.com/downlpublic/edu/zha_pdf.zip http://data.audified.com/downlpublic/edu/akustikaotazky03.pdf http://data.audified.com/downlpublic/edu/jamusimulatorspro103mac.dmg.zip
Vibrace atomů v mřížce, tepelná kapacita pevných látek
 Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
terminologie předchozí kapitoly: (ϕ, Ω) - plocha, S - geometrický obraz plochy
 2. Plošný integrál. Poznámka. Obecně: integrování přes k-rozměrné útvary (k-plochy) v R n. Omezíme se na případ k = 2, n = 3. Definice. Množina S R 3 se nazve plocha, pokud S = ϕ(), kde R 2 je otevřená
2. Plošný integrál. Poznámka. Obecně: integrování přes k-rozměrné útvary (k-plochy) v R n. Omezíme se na případ k = 2, n = 3. Definice. Množina S R 3 se nazve plocha, pokud S = ϕ(), kde R 2 je otevřená
Mechanické kmitání a vlnění
 Mechanické kmitání a vlnění Pohyb tělesa, který se v určitém časovém intervalu pravidelně opakuje periodický pohyb S kmitavým pohybem se setkáváme např.: Zařízení, které volně kmitá, nazýváme mechanický
Mechanické kmitání a vlnění Pohyb tělesa, který se v určitém časovém intervalu pravidelně opakuje periodický pohyb S kmitavým pohybem se setkáváme např.: Zařízení, které volně kmitá, nazýváme mechanický
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/ Vlnění
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Vlnění Vhodíme-li na klidnou vodní hladinu kámen, hladina se jeho dopadem rozkmitá a z místa rozruchu se začnou
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Vlnění Vhodíme-li na klidnou vodní hladinu kámen, hladina se jeho dopadem rozkmitá a z místa rozruchu se začnou
Dnešní látka Variačně formulované okrajové úlohy zúplnění prostoru funkcí. Lineární zobrazení.
 Předmět: MA4 Dnešní látka Variačně formulované okrajové úlohy zúplnění prostoru funkcí. Lineární zobrazení. Literatura: Kapitola 2 a)-c) a kapitola 4 a)-c) ze skript Karel Rektorys: Matematika 43, ČVUT,
Předmět: MA4 Dnešní látka Variačně formulované okrajové úlohy zúplnění prostoru funkcí. Lineární zobrazení. Literatura: Kapitola 2 a)-c) a kapitola 4 a)-c) ze skript Karel Rektorys: Matematika 43, ČVUT,
Aplikovaná numerická matematika
 Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Interpolace, ortogonální polynomy, Gaussova kvadratura
 Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
MODIFIKOVANÝ KLIKOVÝ MECHANISMUS
 MODIFIKOVANÝ KLIKOVÝ MECHANISMUS Michal HAJŽMAN Tento materiál je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Vyšetřování pohybu vybraných mechanismů v systému ADAMS
MODIFIKOVANÝ KLIKOVÝ MECHANISMUS Michal HAJŽMAN Tento materiál je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Vyšetřování pohybu vybraných mechanismů v systému ADAMS
Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe.
 4 Afinita Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe. Poznámka. Vzájemně jednoznačným zobrazením rozumíme zobrazení,
4 Afinita Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe. Poznámka. Vzájemně jednoznačným zobrazením rozumíme zobrazení,
Parametrické rovnice křivky
 Křivkový integrál Robert Mařík jaro 2014 Tento text je tištěnou verzí prezentací dostupných z http://user.mendelu.cz/marik/am. Křivkový integrál Jedná se o rozšíření Riemannova integrálu, kdy množinou
Křivkový integrál Robert Mařík jaro 2014 Tento text je tištěnou verzí prezentací dostupných z http://user.mendelu.cz/marik/am. Křivkový integrál Jedná se o rozšíření Riemannova integrálu, kdy množinou
Počítačová dynamika tekutin (CFD) Základní rovnice. - laminární tok -
 Počítačová dynamika tekutin (CFD) Základní rovnice - laminární tok - Základní pojmy 2 Tekutina nemá vlastní tvar působením nepatrných tečných sil se částice tekutiny snadno uvedou do pohybu (výjimka některé
Počítačová dynamika tekutin (CFD) Základní rovnice - laminární tok - Základní pojmy 2 Tekutina nemá vlastní tvar působením nepatrných tečných sil se částice tekutiny snadno uvedou do pohybu (výjimka některé
Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika)
 Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr.
Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr.
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6
 OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
TERMIKA II. Stacionární vedení s dokonalou i nedokonalou izolací; Obecná rovnice vedení tepla; Přestup a prostup tepla;
 TERMIKA II Šíření tepla vedením, prouděním a zářením; Stacionární vedení s dokonalou i nedokonalou izolací; Nestacionární vedení tepla; Obecná rovnice vedení tepla; Přestup a prostup tepla; 1 Šíření tepla
TERMIKA II Šíření tepla vedením, prouděním a zářením; Stacionární vedení s dokonalou i nedokonalou izolací; Nestacionární vedení tepla; Obecná rovnice vedení tepla; Přestup a prostup tepla; 1 Šíření tepla
Hydromechanické procesy Obtékání těles
 Hydromechanické procesy Obtékání těles M. Jahoda Klasifikace těles 2 Typy externích toků dvourozměrné osově symetrické třírozměrné (s/bez osy symetrie) nebo: aerodynamické vs. neaerodynamické Odpor a vztlak
Hydromechanické procesy Obtékání těles M. Jahoda Klasifikace těles 2 Typy externích toků dvourozměrné osově symetrické třírozměrné (s/bez osy symetrie) nebo: aerodynamické vs. neaerodynamické Odpor a vztlak
Potenciální proudění
 Hydromechanické procesy Potenciální proudění + plíživé obtékání koule M. Jahoda Proudění tekutiny Pohyby elementu tekutiny 2 čas t čas t + dt obecný pohyb posunutí lineární deformace rotace úhlová deformace
Hydromechanické procesy Potenciální proudění + plíživé obtékání koule M. Jahoda Proudění tekutiny Pohyby elementu tekutiny 2 čas t čas t + dt obecný pohyb posunutí lineární deformace rotace úhlová deformace
Reologické modely technických materiálů při prostém tahu a tlaku
 . lekce Reologické modely technických materiálů při prostém tahu a tlaku Obsah. Základní pojmy Vnitřní síly napětí. Základní reologické modely technických materiálů 3.3 Elementární reologické modely creepu
. lekce Reologické modely technických materiálů při prostém tahu a tlaku Obsah. Základní pojmy Vnitřní síly napětí. Základní reologické modely technických materiálů 3.3 Elementární reologické modely creepu
Mechanika s Inventorem
 Mechanika s Inventorem 2. Základní pojmy CAD data FEM výpočty Petr SCHILLING, autor přednášky Ing. Kateřina VLČKOVÁ, obsahová korekce Optimalizace Tomáš MATOVIČ, publikace 1 Obsah přednášky: Lagrangeův
Mechanika s Inventorem 2. Základní pojmy CAD data FEM výpočty Petr SCHILLING, autor přednášky Ing. Kateřina VLČKOVÁ, obsahová korekce Optimalizace Tomáš MATOVIČ, publikace 1 Obsah přednášky: Lagrangeův
10 Funkce více proměnných
 M. Rokyta, MFF UK: Aplikovaná matematika II kap. 10: Funkce více proměnných 16 10 Funkce více proměnných 10.1 Základní pojmy Definice. Eukleidovskou vzdáleností bodů x = (x 1,...,x n ), y = (y 1,...,y
M. Rokyta, MFF UK: Aplikovaná matematika II kap. 10: Funkce více proměnných 16 10 Funkce více proměnných 10.1 Základní pojmy Definice. Eukleidovskou vzdáleností bodů x = (x 1,...,x n ), y = (y 1,...,y
VEKTOROVÁ POLE Otázky
 VEKTOROVÁ POLE VEKTOROVÁ POLE Je-li A podmnožina roviny a f je zobrazení A do R 2, které je dáno souřadnicemi f 1, f 2, tj., f(x, y) = (f 1 (x, y), f 2 (x, y)) pro (x, y) A, lze chápat dvojici (f 1 (x,
VEKTOROVÁ POLE VEKTOROVÁ POLE Je-li A podmnožina roviny a f je zobrazení A do R 2, které je dáno souřadnicemi f 1, f 2, tj., f(x, y) = (f 1 (x, y), f 2 (x, y)) pro (x, y) A, lze chápat dvojici (f 1 (x,
Teorie tkaní. Modely vazného bodu. M. Bílek
 Teorie tkaní Modely vazného bodu M. Bílek 2016 Základní strukturální jednotkou tkaniny je vazný bod, tj. oblast v okolí jednoho zakřížení osnovní a útkové nitě. Proces tkaní tedy spočívá v tvorbě vazných
Teorie tkaní Modely vazného bodu M. Bílek 2016 Základní strukturální jednotkou tkaniny je vazný bod, tj. oblast v okolí jednoho zakřížení osnovní a útkové nitě. Proces tkaní tedy spočívá v tvorbě vazných
Pružnost a pevnost I
 Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
Výpočtové nadstavby pro CAD
 Výpočtové nadstavby pro CAD 4. přednáška eplotní úlohy v MKP Michal Vaverka, Martin Vrbka Přenos tepla Př: Uvažujme pro jednoduchost spalovací motor chlazený vzduchem. Spalováním vzniká teplo, které se
Výpočtové nadstavby pro CAD 4. přednáška eplotní úlohy v MKP Michal Vaverka, Martin Vrbka Přenos tepla Př: Uvažujme pro jednoduchost spalovací motor chlazený vzduchem. Spalováním vzniká teplo, které se
ELT1 - Přednáška č. 6
 ELT1 - Přednáška č. 6 Elektrotechnická terminologie a odborné výrazy, měřicí jednotky a činitelé, které je ovlivňují. Rozdíl potenciálů, elektromotorická síla, napětí, el. napětí, proud, odpor, vodivost,
ELT1 - Přednáška č. 6 Elektrotechnická terminologie a odborné výrazy, měřicí jednotky a činitelé, které je ovlivňují. Rozdíl potenciálů, elektromotorická síla, napětí, el. napětí, proud, odpor, vodivost,
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
stránkách přednášejícího.
 Předmět: MA 4 Dnešní látka Iterační metoda Jacobiova iterační metoda Gaussova-Seidelova iterační metoda Superrelaxační metoda (metoda SOR) Metoda sdružených gradientů Četba: Text o lineární algebře v Příručce
Předmět: MA 4 Dnešní látka Iterační metoda Jacobiova iterační metoda Gaussova-Seidelova iterační metoda Superrelaxační metoda (metoda SOR) Metoda sdružených gradientů Četba: Text o lineární algebře v Příručce
Globální matice konstrukce
 Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
SOUSTAVA SMYSLOVÁ UCHO (sluchový orgán)
 a) Stavba ucha Smyslové buňky vnímají zvukové podněty Zvuk = mechanické vlnění Ucho se skládá ze tří částí: 1. Vnější ucho (boltec a zevní zvukovod) 2. Střední ucho (středoušní dutina se středoušními kůstkami
a) Stavba ucha Smyslové buňky vnímají zvukové podněty Zvuk = mechanické vlnění Ucho se skládá ze tří částí: 1. Vnější ucho (boltec a zevní zvukovod) 2. Střední ucho (středoušní dutina se středoušními kůstkami
KMS cvičení 6. Ondřej Marek
 KMS cvičení 6 Ondřej Marek NETLUMENÝ ODDAJNÝ SYSTÉM S DOF analytické řešení k k Systém se stupni volnosti popisují pohybové rovnice: x m m x m x + k + k x k x = m x k x + k x = k x m x k x x m k x x m
KMS cvičení 6 Ondřej Marek NETLUMENÝ ODDAJNÝ SYSTÉM S DOF analytické řešení k k Systém se stupni volnosti popisují pohybové rovnice: x m m x m x + k + k x k x = m x k x + k x = k x m x k x x m k x x m
Rozdíly mezi MKP a MHP, oblasti jejich využití.
 Rozdíly mezi, oblasti jejich využití. Obě metody jsou vhodné pro určitou oblast problémů. základě MKP vyžaduje rozdělení těles na vhodný počet prvků, jejichž analýza je poměrně snadná a pro většinu částí
Rozdíly mezi, oblasti jejich využití. Obě metody jsou vhodné pro určitou oblast problémů. základě MKP vyžaduje rozdělení těles na vhodný počet prvků, jejichž analýza je poměrně snadná a pro většinu částí
Numerické řešení 2D stlačitelného proudění s kondenzací. Michal Seifert
 Numerické řešení 2D stlačitelného proudění s kondenzací Michal Seifert Úkoly diplomové práce Popsat matematické modely proudící tekutiny Popis numerických metod založených na metodě konečných objemů Porovnání
Numerické řešení 2D stlačitelného proudění s kondenzací Michal Seifert Úkoly diplomové práce Popsat matematické modely proudící tekutiny Popis numerických metod založených na metodě konečných objemů Porovnání
5. Lokální, vázané a globální extrémy
 5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
Fyziologická akustika. fyziologická akustika: jak to funguje psychologická akustika: jak to na nás působí
 Fyziologická akustika anatomie: jak to vypadá fyziologická akustika: jak to funguje psychologická akustika: jak to na nás působí hudební akustika: jak dosáhnout libých počitků Anatomie lidského ucha Vnější
Fyziologická akustika anatomie: jak to vypadá fyziologická akustika: jak to funguje psychologická akustika: jak to na nás působí hudební akustika: jak dosáhnout libých počitků Anatomie lidského ucha Vnější
2. Vlnění. π T. t T. x λ. Machův vlnostroj
 2. Vlnění 2.1 Vlnění zvláštní případ pohybu prostředí Vlnění je pohyb v soustavě velkého počtu částic navzájem vázaných, kdy částice kmitají kolem svých rovnovážných poloh. Druhy vlnění: vlnění příčné
2. Vlnění 2.1 Vlnění zvláštní případ pohybu prostředí Vlnění je pohyb v soustavě velkého počtu částic navzájem vázaných, kdy částice kmitají kolem svých rovnovážných poloh. Druhy vlnění: vlnění příčné
Vzpěr jednoduchého rámu, diferenciální operátory. Lenka Dohnalová
 1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
Sluch, rovnová ž né u strojí, chémorécéptory
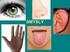 Sluch, rovnová ž né u strojí, chémorécéptory Pracovní list Olga Gardašová VY_32_INOVACE_Bi3r0116 Sluchové ústrojí Umožňuje rozlišování zvuků. Ucho se skládá ze tří částí. Najdi v obrázku níže uvedené části
Sluch, rovnová ž né u strojí, chémorécéptory Pracovní list Olga Gardašová VY_32_INOVACE_Bi3r0116 Sluchové ústrojí Umožňuje rozlišování zvuků. Ucho se skládá ze tří částí. Najdi v obrázku níže uvedené části
3.1. Newtonovy zákony jsou základní zákony klasické (Newtonovy) mechaniky
 3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Martin NESLÁDEK. 14. listopadu 2017
 Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Numerické modelování interakce proudění a pružného tělesa v lidském vokálním traktu
 Numerické modelování interakce proudění a pružného tělesa v lidském vokálním traktu Vedoucí práce: doc. Ing. Petr Šidlof, Ph.D. Bc. Petra Tisovská 22. května 2018 Studentská 2 461 17 Liberec 2 petra.tisovska@tul.cz
Numerické modelování interakce proudění a pružného tělesa v lidském vokálním traktu Vedoucí práce: doc. Ing. Petr Šidlof, Ph.D. Bc. Petra Tisovská 22. května 2018 Studentská 2 461 17 Liberec 2 petra.tisovska@tul.cz
Elektromagnetické pole je generováno elektrickými náboji a jejich pohybem. Je-li zdroj charakterizován nábojovou hustotou ( r r
 Záření Hertzova dipólu, kulové vlny, Rovnice elektromagnetického pole jsou vektorové diferenciální rovnice a podle symetrie bývá vhodné je řešit v křivočarých souřadnicích. Základní diferenciální operátory
Záření Hertzova dipólu, kulové vlny, Rovnice elektromagnetického pole jsou vektorové diferenciální rovnice a podle symetrie bývá vhodné je řešit v křivočarých souřadnicích. Základní diferenciální operátory
Skalární a vektorový popis silového pole
 Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Stabilizace Galerkin Least Squares pro
 Fakulta strojní ČVUT Ústav technické matematiky Stabilizace Galerkin Least Squares pro MKP na řešení proudění o vyšších Reynoldsových číslech Ing. Jakub Šístek Doc. RNDr. Pavel Burda, CSc. RNDr. Jaroslav
Fakulta strojní ČVUT Ústav technické matematiky Stabilizace Galerkin Least Squares pro MKP na řešení proudění o vyšších Reynoldsových číslech Ing. Jakub Šístek Doc. RNDr. Pavel Burda, CSc. RNDr. Jaroslav
12. Křivkové integrály
 12 Křivkové integrály Definice 121 Jednoduchou po částech hladkou křivkou v prostoru R n rozumíme množinu bodů [x 1,, x n ], které jsou dány parametrickými rovnicemi x 1 = ϕ 1 t), x 2 = ϕ 2 t), x n = ϕ
12 Křivkové integrály Definice 121 Jednoduchou po částech hladkou křivkou v prostoru R n rozumíme množinu bodů [x 1,, x n ], které jsou dány parametrickými rovnicemi x 1 = ϕ 1 t), x 2 = ϕ 2 t), x n = ϕ
GE - Vyšší kvalita výuky CZ.1.07/1.5.00/
 Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma : Diferenciální a integrální
Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma : Diferenciální a integrální
6. Viskoelasticita materiálů
 6. Viskoelasticita materiálů Viskoelasticita materiálů souvisí se schopností materiálů tlumit mechanické vibrace. Uvažujme harmonické dynamické namáhání (tzn. střídavě v tahu a tlaku) materiálu v oblasti
6. Viskoelasticita materiálů Viskoelasticita materiálů souvisí se schopností materiálů tlumit mechanické vibrace. Uvažujme harmonické dynamické namáhání (tzn. střídavě v tahu a tlaku) materiálu v oblasti
Propojení matematiky, fyziky a počítačů
 Propojení matematiky, fyziky a počítačů Název projektu: Věda pro život, život pro vědu Registrační číslo: CZ..7/.3./45.9 V Ústí n. L., únor 5 Ing. Radek Honzátko, Ph.D. Propojení matematiky, fyziky a počítačů
Propojení matematiky, fyziky a počítačů Název projektu: Věda pro život, život pro vědu Registrační číslo: CZ..7/.3./45.9 V Ústí n. L., únor 5 Ing. Radek Honzátko, Ph.D. Propojení matematiky, fyziky a počítačů
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY Komentovaný metodický list č. 1/4 Vytvořil: Ing. Oldřich Ševeček & Ing. Tomáš Profant, Ph.D.
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY Komentovaný metodický list č. 1/4 Vytvořil: Ing. Oldřich Ševeček & Ing. Tomáš Profant, Ph.D.
MODELOVÁNÍ PŘENOSU ZVUKU
 Abstrakt MODELOVÁNÍ PŘENOSU ZVUKU DO VNITŘNÍHO UCHA Modeling of Sound Transfer into Inner Ear František Rund Pochopení způsobu jakým funguje lidské slyšení je základním předpokladem pro návrh nových metod
Abstrakt MODELOVÁNÍ PŘENOSU ZVUKU DO VNITŘNÍHO UCHA Modeling of Sound Transfer into Inner Ear František Rund Pochopení způsobu jakým funguje lidské slyšení je základním předpokladem pro návrh nových metod
Nelineární obvody. V nelineárních obvodech však platí Kirchhoffovy zákony.
 Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
1.8. Mechanické vlnění
 1.8. Mechanické vlnění 1. Umět vysvětlit princip vlnivého pohybu.. Umět srovnat a zároveň vysvětlit rozdíl mezi periodickým kmitavým pohybem jednoho bodu s periodickým vlnivým pohybem bodové řady. 3. Znát
1.8. Mechanické vlnění 1. Umět vysvětlit princip vlnivého pohybu.. Umět srovnat a zároveň vysvětlit rozdíl mezi periodickým kmitavým pohybem jednoho bodu s periodickým vlnivým pohybem bodové řady. 3. Znát
Zvuk a akustika. Helena Uhrová
 Zvuk a akustika Helena Uhrová Zvuk Mechanické vlnění částic hmotného prostředí - zdroj rozruchu - prostředí ve kterém se rozruch šíří - vazba nebo mechanismus, kterým se přenos uskutečňuje Přenos energie
Zvuk a akustika Helena Uhrová Zvuk Mechanické vlnění částic hmotného prostředí - zdroj rozruchu - prostředí ve kterém se rozruch šíří - vazba nebo mechanismus, kterým se přenos uskutečňuje Přenos energie
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
VEKTOROVÁ POLE VEKTOROVÁ POLE
 Je-li A podmnožina roviny a f je zobrazení A do R 2, které je dáno souřadnicemi f 1, f 2, tj., f(x, y) = (f 1 (x, y), f 2 (x, y)) pro (x, y) A, lze chápat dvojici (f 1 (x, y), f 2 (x, y)) jako vektor s
Je-li A podmnožina roviny a f je zobrazení A do R 2, které je dáno souřadnicemi f 1, f 2, tj., f(x, y) = (f 1 (x, y), f 2 (x, y)) pro (x, y) A, lze chápat dvojici (f 1 (x, y), f 2 (x, y)) jako vektor s
Katedra geotechniky a podzemního stavitelství
 Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
PRAKTIKUM I. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne:
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. Úloha č. VII Název: Studium kmitů vázaných oscilátorů Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne: 27. 2. 2012 Odevzdal
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. Úloha č. VII Název: Studium kmitů vázaných oscilátorů Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne: 27. 2. 2012 Odevzdal
OHYB (Napjatost) M A M + qc a + b + c ) M A = 2M qc a + b + c )
 3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování. vypracovanou úlohu podle níže uvedených zadání. To mimo jiné znamená, že
 Kapitola Zadání Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování alespoň jedné úlohy je nutnou podmínkou pro úspěšné složení zkoušky resp. získaní (klasifikovaného) zápočtu (viz.
Kapitola Zadání Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování alespoň jedné úlohy je nutnou podmínkou pro úspěšné složení zkoušky resp. získaní (klasifikovaného) zápočtu (viz.
19 Eukleidovský bodový prostor
 19 Eukleidovský bodový prostor Eukleidovským bodovým prostorem rozumíme afinní bodový prostor, na jehož zaměření je definován skalární součin. Víme, že pomocí skalárního součinu jsou definovány pojmy norma
19 Eukleidovský bodový prostor Eukleidovským bodovým prostorem rozumíme afinní bodový prostor, na jehož zaměření je definován skalární součin. Víme, že pomocí skalárního součinu jsou definovány pojmy norma
a počtem sloupců druhé matice. Spočítejme součin A.B. Označme matici A.B = M, pro její prvky platí:
 Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
Fakt. Každou soustavu n lineárních ODR řádů n i lze eliminací převést ekvivalentně na jednu lineární ODR
 DEN: ODR teoreticky: soustavy rovnic Soustava lineárních ODR 1 řádu s konstantními koeficienty je soustava ve tvaru y 1 = a 11 y 1 + a 12 y 2 + + a 1n y n + b 1 (x) y 2 = a 21 y 1 + a 22 y 2 + + a 2n y
DEN: ODR teoreticky: soustavy rovnic Soustava lineárních ODR 1 řádu s konstantními koeficienty je soustava ve tvaru y 1 = a 11 y 1 + a 12 y 2 + + a 1n y n + b 1 (x) y 2 = a 21 y 1 + a 22 y 2 + + a 2n y
Úlohy nejmenších čtverců
 Úlohy nejmenších čtverců Petr Tichý 7. listopadu 2012 1 Problémy nejmenších čtverců Ax b Řešení Ax = b nemusí existovat, a pokud existuje, nemusí být jednoznačné. Často má smysl hledat x tak, že Ax b.
Úlohy nejmenších čtverců Petr Tichý 7. listopadu 2012 1 Problémy nejmenších čtverců Ax b Řešení Ax = b nemusí existovat, a pokud existuje, nemusí být jednoznačné. Často má smysl hledat x tak, že Ax b.
ČVUT v Praze Fakulta stavební Katedra Technických zařízení budov. Modelování termohydraulických jevů 3.hodina. Hydraulika. Ing. Michal Kabrhel, Ph.D.
 ČVUT v Praze Fakulta stavební Katedra Technických zařízení budov Modelování termohydraulických jevů 3.hodina Hydraulika Ing. Michal Kabrhel, Ph.D. Letní semestr 008/009 Pracovní materiály pro výuku předmětu.
ČVUT v Praze Fakulta stavební Katedra Technických zařízení budov Modelování termohydraulických jevů 3.hodina Hydraulika Ing. Michal Kabrhel, Ph.D. Letní semestr 008/009 Pracovní materiály pro výuku předmětu.
Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy
![Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy](/thumbs/97/130835283.jpg) Aproimace posuvů Pro každý prvek se musí nalézt vztahy kde jsou prozatím neznámé transformační matice. Neznámé funkce posuvů se obvykle aproimují ve formě mnohočlenů kartézských souřadnic. Například 1.
Aproimace posuvů Pro každý prvek se musí nalézt vztahy kde jsou prozatím neznámé transformační matice. Neznámé funkce posuvů se obvykle aproimují ve formě mnohočlenů kartézských souřadnic. Například 1.
PŘENOS ZVUKOVÝCH SIGNÁLŮ DO VNITŘNÍHO UCHA
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY FACULTY OF MECHANICAL ENGINEERING DEPARTMENT OF SOLID MECHANICS,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY FACULTY OF MECHANICAL ENGINEERING DEPARTMENT OF SOLID MECHANICS,
III. MKP vlastní kmitání
 Jiří Máca - katedra mechaniky - B325 - tel. 2 2435 4500 maca@fsv.cvut.cz III. MKP vlastní kmitání 1. Rovnice vlastního kmitání 2. Rayleighova Ritzova metoda 3. Jacobiho metoda 4. Metoda inverzních iterací
Jiří Máca - katedra mechaniky - B325 - tel. 2 2435 4500 maca@fsv.cvut.cz III. MKP vlastní kmitání 1. Rovnice vlastního kmitání 2. Rayleighova Ritzova metoda 3. Jacobiho metoda 4. Metoda inverzních iterací
SIMULACE ZVUKOVÉHO POLE VÍCE ZDROJŮ
 SIMULACE ZVUKOVÉHO POLE VÍCE ZDROJŮ F. Rund Katedra radioelektroniky, Fakulta elektrotechnická, České vysoké učení technické v Praze Abstrakt Studium zvukového pole vytvářeného soustavou jednotlivých zvukových
SIMULACE ZVUKOVÉHO POLE VÍCE ZDROJŮ F. Rund Katedra radioelektroniky, Fakulta elektrotechnická, České vysoké učení technické v Praze Abstrakt Studium zvukového pole vytvářeného soustavou jednotlivých zvukových
Dynamika tekutin popisuje kinematiku (pohyb částice v času a prostoru) a silové působení v tekutině.
 Dynamika tekutin popisuje kinematiku (pohyb částice v času a prostoru) a silové působení v tekutině. Přehled proudění Vazkost - nevazké - vazké (newtonské, nenewtonské) Stlačitelnost - nestlačitelné (kapaliny
Dynamika tekutin popisuje kinematiku (pohyb částice v času a prostoru) a silové působení v tekutině. Přehled proudění Vazkost - nevazké - vazké (newtonské, nenewtonské) Stlačitelnost - nestlačitelné (kapaliny
Vlastnosti a zkoušení materiálů. Přednáška č.4 Úvod do pružnosti a pevnosti
 Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Vybrané kapitoly z matematiky
 Vybrané kapitoly z matematiky VŠB-TU Ostrava 2018-2019 Vybrané kapitoly z matematiky 2018-2019 1 / 18 Vektorová analýza a teorie pole Vybrané kapitoly z matematiky 2018-2019 2 / 18 Vektorová funkce jedné
Vybrané kapitoly z matematiky VŠB-TU Ostrava 2018-2019 Vybrané kapitoly z matematiky 2018-2019 1 / 18 Vektorová analýza a teorie pole Vybrané kapitoly z matematiky 2018-2019 2 / 18 Vektorová funkce jedné
Nelineární úlohy při výpočtu konstrukcí s využitím MKP
 Nelineární úlohy při výpočtu konstrukcí s využitím MKP Obsah přednášky Lineární a nelineární úlohy Typy nelinearit (geometrická, materiálová, kontakt,..) Příklady nelineárních problémů Teorie kontaktu,
Nelineární úlohy při výpočtu konstrukcí s využitím MKP Obsah přednášky Lineární a nelineární úlohy Typy nelinearit (geometrická, materiálová, kontakt,..) Příklady nelineárních problémů Teorie kontaktu,
Základní otázky pro teoretickou část zkoušky.
 Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
FP - SEMINÁŘ Z NUMERICKÉ MATEMATIKY. Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci
 FP - SEMINÁŘ Z NUMERICKÉ MATEMATIKY Dana Černá http://www.fp.tul.cz/kmd/ Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci OBSAH A CÍLE SEMINÁŘE: Opakování a procvičení vybraných
FP - SEMINÁŘ Z NUMERICKÉ MATEMATIKY Dana Černá http://www.fp.tul.cz/kmd/ Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci OBSAH A CÍLE SEMINÁŘE: Opakování a procvičení vybraných
Stavební fakulta Katedra mechaniky. Jaroslav Kruis, Petr Štemberk
 České vysoké učení technické v Praze Stavební fakulta Katedra mechaniky Fuzzy množiny, fuzzy čísla a jejich aplikace v inženýrství Jaroslav Kruis, Petr Štemberk Obsah Nejistoty Teorie pravděpodobnosti
České vysoké učení technické v Praze Stavební fakulta Katedra mechaniky Fuzzy množiny, fuzzy čísla a jejich aplikace v inženýrství Jaroslav Kruis, Petr Štemberk Obsah Nejistoty Teorie pravděpodobnosti
Průhyb ocelového nosníku. Nezatížený a rovnoměrně zatížený nosník
 EVROPSKÝ SOCIÁLNÍ FOND Průhyb ocelového nosníku. Nezatížený a rovnoměrně zatížený nosník PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI České vysoké učení technické v Praze, Fakulta stavební, Katedra matematiky
EVROPSKÝ SOCIÁLNÍ FOND Průhyb ocelového nosníku. Nezatížený a rovnoměrně zatížený nosník PRAHA & EU INVESTUJEME DO VAŠÍ BUDOUCNOSTI České vysoké učení technické v Praze, Fakulta stavební, Katedra matematiky
Úvod do lineární algebry
 Úvod do lineární algebry 1 Aritmetické vektory Definice 11 Mějme n N a utvořme kartézský součin R n R R R Každou uspořádanou n tici x 1 x 2 x, x n budeme nazývat n rozměrným aritmetickým vektorem Prvky
Úvod do lineární algebry 1 Aritmetické vektory Definice 11 Mějme n N a utvořme kartézský součin R n R R R Každou uspořádanou n tici x 1 x 2 x, x n budeme nazývat n rozměrným aritmetickým vektorem Prvky
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Extrémy funkce dvou proměnných
 Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Výpočet stlačitelného proudění metodou konečných objemů
 Výpočet stlačitelného proudění metodou konečných objemů Petra Punčochářová Ústav technické matematiky, Fakulta strojní, Vysoké učení technické v Praze Vedoucí práce: Prof. RNDr. K. Kozel DrSc. Úvod V 80.
Výpočet stlačitelného proudění metodou konečných objemů Petra Punčochářová Ústav technické matematiky, Fakulta strojní, Vysoké učení technické v Praze Vedoucí práce: Prof. RNDr. K. Kozel DrSc. Úvod V 80.
Matice. Je dána matice A R m,n, pak máme zobrazení A : R n R m.
 Matice lineárních zobrazení [1] Připomenutí Zobrazení A : L 1 L 2 je lineární, když A( x + y ) = A( x ) + A( y ), A(α x ) = α A( x ). Což je ekvivalentní s principem superpozice: A(α 1 x 1 + + α n x n
Matice lineárních zobrazení [1] Připomenutí Zobrazení A : L 1 L 2 je lineární, když A( x + y ) = A( x ) + A( y ), A(α x ) = α A( x ). Což je ekvivalentní s principem superpozice: A(α 1 x 1 + + α n x n
Termomechanika 10. přednáška Doc. Dr. RNDr. Miroslav Holeček
 Termomechanika 10. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Termomechanika 10. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
1 Rozdělení mechaniky a její náplň
 1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
Pružnost a pevnost. zimní semestr 2013/14
 Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Elektromechanický oscilátor
 - 1 - Elektromechanický oscilátor Ing. Ladislav Kopecký, 2002 V tomto článku si ukážeme jeden ze způsobů, jak využít silové účinky cívky s feromagnetickým jádrem v rezonanci. I člověk, který neoplývá technickou
- 1 - Elektromechanický oscilátor Ing. Ladislav Kopecký, 2002 V tomto článku si ukážeme jeden ze způsobů, jak využít silové účinky cívky s feromagnetickým jádrem v rezonanci. I člověk, který neoplývá technickou
Pružnost a plasticita II CD03
 Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Zvuk a sluch. Stručný popis toho, jak vnímáme zvuk a jak funguje náš sluchový systém
 Zvuk a sluch 1 Stručný popis toho, jak vnímáme zvuk a jak funguje náš sluchový systém 1 Toto je první ze série brožurek firmy Widex o sluchu a o problémech se sluchem. 2 Od zvukové vlny ke slyšení Sluch
Zvuk a sluch 1 Stručný popis toho, jak vnímáme zvuk a jak funguje náš sluchový systém 1 Toto je první ze série brožurek firmy Widex o sluchu a o problémech se sluchem. 2 Od zvukové vlny ke slyšení Sluch
DIPLOMOVÁ PRÁCE OPTIMALIZACE MECHANICKÝCH
 DIPLOMOVÁ PRÁCE OPTIMALIZACE MECHANICKÝCH VLASTNOSTÍ MECHANISMU TETRASPHERE Vypracoval: Jaroslav Štorkán Vedoucí práce: prof. Ing. Michael Valášek, DrSc. CÍLE PRÁCE Sestavit programy pro kinematické, dynamické
DIPLOMOVÁ PRÁCE OPTIMALIZACE MECHANICKÝCH VLASTNOSTÍ MECHANISMU TETRASPHERE Vypracoval: Jaroslav Štorkán Vedoucí práce: prof. Ing. Michael Valášek, DrSc. CÍLE PRÁCE Sestavit programy pro kinematické, dynamické
INOVACE ODBORNÉHO VZDĚLÁVÁNÍ NA STŘEDNÍCH ŠKOLÁCH ZAMĚŘENÉ NA VYUŽÍVÁNÍ ENERGETICKÝCH ZDROJŮ PRO 21. STOLETÍ A NA JEJICH DOPAD NA ŽIVOTNÍ PROSTŘEDÍ
 INOVACE ODBORNÉHO VZDĚLÁVÁNÍ NA STŘEDNÍCH ŠKOLÁCH ZAMĚŘENÉ NA VYUŽÍVÁNÍ ENERGETICKÝCH ZDROJŮ PRO 21. STOLETÍ A NA JEJICH DOPAD NA ŽIVOTNÍ PROSTŘEDÍ CZ.1.07/1.1.00/08.0010 NUMERICKÉ SIMULACE ING. KATEŘINA
INOVACE ODBORNÉHO VZDĚLÁVÁNÍ NA STŘEDNÍCH ŠKOLÁCH ZAMĚŘENÉ NA VYUŽÍVÁNÍ ENERGETICKÝCH ZDROJŮ PRO 21. STOLETÍ A NA JEJICH DOPAD NA ŽIVOTNÍ PROSTŘEDÍ CZ.1.07/1.1.00/08.0010 NUMERICKÉ SIMULACE ING. KATEŘINA
Práce, energie a další mechanické veličiny
 Práce, energie a další mechanické veličiny Úvod V předchozích přednáškách jsme zavedli základní mechanické veličiny (rychlost, zrychlení, síla, ) Popis fyzikálních dějů usnadňuje zavedení dalších fyzikálních
Práce, energie a další mechanické veličiny Úvod V předchozích přednáškách jsme zavedli základní mechanické veličiny (rychlost, zrychlení, síla, ) Popis fyzikálních dějů usnadňuje zavedení dalších fyzikálních
Statika soustavy těles.
 Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
Literatura: Kapitoly 3, 4 a 2 d) ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Nehomogenní okrajové podmínky. Pokračování OÚ pro PDR (jen pro fajnšmekry). Jednoznačnost zobecněného řešení. Metoda sítí v 1D. Přibližné řešení okrajových úloh. Aproximace vlastních
Předmět: MA4 Dnešní látka: Nehomogenní okrajové podmínky. Pokračování OÚ pro PDR (jen pro fajnšmekry). Jednoznačnost zobecněného řešení. Metoda sítí v 1D. Přibližné řešení okrajových úloh. Aproximace vlastních
b) Maximální velikost zrychlení automobilu, nemají-li kola prokluzovat, je a = f g. Automobil se bude rozjíždět po dobu t = v 0 fg = mfgv 0
 Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami
 Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami (Numerical Modelling of Flow of Two Immiscible Fluids Past a NACA 0012 profile) Ing. Tomáš
Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami (Numerical Modelling of Flow of Two Immiscible Fluids Past a NACA 0012 profile) Ing. Tomáš
Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru. Kvadratická forma v n proměnných je tak polynom n proměnných s
 Kapitola 13 Kvadratické formy Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru f(x 1,..., x n ) = a ij x i x j, kde koeficienty a ij T. j=i Kvadratická forma v n proměnných
Kapitola 13 Kvadratické formy Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru f(x 1,..., x n ) = a ij x i x j, kde koeficienty a ij T. j=i Kvadratická forma v n proměnných
