Derivace a monotónnost funkce
|
|
|
- Pavla Kolářová
- před 6 lety
- Počet zobrazení:
Transkript
1 Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je na intervalu I klesající. je-li f (x) 0 x I, funkce f je na intervalu I neklesající. je-li f (x) 0 x I, funkce f je na intervalu I nerostoucí. Příklad : Určete intervaly monotónnosti funkce f (x) = x 3 3x + 1 Řešení: Budeme vycházet z funkce f (x) = 3x 3. Nulové body funkce f (x) jsou 1, 1, ty rozdělí reálnou osu na tři intervaly. Znamení funkce f (x) je následující : (-, 1) (-1,1) (1, ) Tedy podle předchozí věty je funkce f (x) rostoucí na intervalu (, 1), klesající na ( 1, 1) a opět rostoucí na (1, ).
2 Intervaly monotónnosti funkce - příklad Znázorněme si graf funkce f (x) = x 3 3x + 1 a graf její derivace f (x) = 3x 3.
3 Lokální extrémy Řekneme, že funkce f (x) má v bodě x 0 lokální minimum (resp. maximum), jestliže je definována v nějakém okolí bodu x 0 a jestliže pro všechna x z tohoto okolí platí f (x) f (x 0 ), resp. f (x) f (x 0 ). Lokální minima a maxima souhrnně nazýváme lokální extrémy. Věta : Pokud má funkce f (x) v bodě x 0 lokální extrém a existuje-li zde derivace, pak pro tuto derivaci platí f (x 0 ) = 0. Body s nulovou derivací nazýváme stacionární. Poznámka : Podmínka f (x 0 ) = 0 však není ani nutnou ani postačující podmínkou pro existenci extrému, viz funkce f 1 (x), která má v bodě x 0 = 0 lokální minimum, ale nemá zde derivaci nebo funkce f 3 (x), pro kterou platí f (0) = 0, ale nemá žádný lokální extrém Obrázek: f 1 (x) = x Obrázek: f (x) = x / Obrázek: f 3 (x) = x 3 /
4 Existence lokálního extrému Věta : Necht má funkce f (x) v bodě x 0 derivaci a platí f (x 0 ) = 0. Existuje-li δ > 0 takové, že: x (x 0 δ, x 0 ) : f (x 0 ) > 0 a x (x 0, x 0 + δ) : f (x 0 ) < 0, pak má funkce f v bodě x 0 lokální maximum x (x 0 δ, x 0 ) : f (x 0 ) < 0 a x (x 0, x 0 + δ) : f (x 0 ) > 0, pak má funkce f v bodě x 0 lokální minimum Příklad : Najděte lokální extrémy funkce f (x) = x 3 3x + 1 Řešení: Již dříve jsme spočetli f (x) = 3x 3 a našli stacionární body 1, 1. Víme, že derivace f (x) je kladná 5nalevo od bodu x 1 = 1 a napravo od bodu x = 1 a záporná mezi nimi. Takže v bodě x 1 = 1 nastává lokální maximum, 4 f ( 1) = 3 a v bodě x = 1 lokální minimum, f (1) =
5 Absolutní extrémy Řekneme, že funkce f (x) má na množině M absolutní minimum (resp. maximum) v bodě x 0, jestliže je funkce definována na M a platí x M : f (x) f (x 0 ), resp. x M : f (x) f (x 0 ). Poznámka : Absolutní minima a maxima nazýváme absolutní extrémy nebo též globální extrémy. Pokud v definici zaměníme neostré nerovnosti za ostré, dostaneme tzv. ostré (či vlastní) extrémy. Věta : (Weierstrassova) Necht funkce f (x) je spojitá na uzavřeném intervalu a, b. Pak funkce f (x) nabývá na tomto intervalu svého absolutního minima, a to bud v bodě lokálního extrému nebo v některém z krajních bodů a, b. Totéž platí pro absolutní maximum.
6 Absolutní extrémy - příklad Příklad : Celkové příjmy (TR) i celkové náklady (TC) jsou funkcí vyrobeného množství, bylo zjištěno, že: TR(Q) = Q 3 Q Q, TC(Q) = Q 3 Q 10Q Optimalizujte zisk P(Q) = TR(Q) TC(Q), jestliže výrobní kapacita je 10 jednotek produktu. Řešení: Hledáme tedy extrémy funkce P(Q) = Q + 8Q na intervalu 0, 10. Spočteme P (Q) = Q + 8, stacionární bod je Q = 4. Globální extrémy mohou nastat v bodech 0, 4, 10. Porovnáme hodnoty P(0) = 0, P(4) = 16, P(10) = 0. Maximálního zisku je tedy dosaženo pro množství Q = 4, naopak největší ztrátu způsobí úplné využití výrobních kapacit, Q = 10.
7 Konvexita a konkávnost funkce Řekneme, že funkce f (x) je na intervalu I ryze konvexní, jestliže pro libovolné tři body x 1, x, x 3 I platí: x 1 < x < x 3 bod T = [x, f (x )] leží pod úsečkou spojující body T 1 = [x 1, f (x 1 )] a T 3 = [x 3, f (x 3 )]. Obdobně o funkci f řekneme, že je na I ryze konkávní, jestliže pro libovolné tři body x 1, x, x 3 I platí: x 1 < x < x 3 bod T = [x, f (x )] leží nad úsečkou spojující body T 1 = [x 1, f (x 1 )] a T 3 = [x 3, f (x 3 )] Obrázek: Konvexní funkce Obrázek: Konkávní funkce
8 Konvexita a konkávnost funkce Poznámka : Připustíme-li v definici, aby bod T ležel i na úsečce T 1 T 3, pak vynecháme slůvko "ryze". Věta : Necht funkce f (x) má na intervalu I druhou derivaci. Pak platí x I : f (x) 0, pak je funkce konvexní na I x I : f (x) 0, pak je funkce konkávní na I Poznámka : Body, ve kterých "se mění konvexita a konkávnost funkce"nazýváme inflexní body. (Přesná definice je ve skriptech). Funkce může mít inflexní bod pouze v bodech, kde existuje první derivace a druhá derivace bud neexistuje nebo je nulová. Věta : Jestliže pro funkci f v bodě x 0 platí: f (x 0 ) = f (x 0 ) =... = f (n) (x 0 ) = 0 a f (n+1) (x 0 ) 0, pak je -li n sudé, má funkce f v bodě x 0 inflexní bod je -li n liché, má funkce f v bodě x 0 lokální extrém,a to maximum pro f (n+1) (x 0 ) < 0 a minimum f (n+1) (x 0 ) > 0.
9 Konvexita a konkávnost funkce - příklad Příklad : Je dána funkce f (x) = ln(x + ). Určete inflexní body této funkce a zjistěte, kde je konvexní a kde konkávní. Řešení: Určíme druhou derivaci, f (x) = x x +, f (x) = (x +) x.x = 4 x. (x +) (x +) Nulové body druhé derivace jsou ±. Určeme znamení funkce f (x): (-, ) (-, ) (, ) Tedy funkce je konkávní na intervalu (, ), konvexní na (, ) a opět konkávní na (, ). inflexní body jsou ±.
10 Asymptoty funkce Asymptoty jsou přímky, ke kterým "se blíží"graf funkce. Asymptotou bez směrnice nazveme přímku x = a, pokud lim a f (x) = ±, kde symbol lim a označuje některou z limit lim x a, lim x a, lim x a+ 1 Příklad : Funkce f (x) = x +5x+6 = 1 (x+)(x+3) x =, x = 3, nebot lim x 3 f (x) = lim x 3+ f (x) = lim x f (x) = lim x + f (x) = má asymptoty bez směrnice Přímku y = Ax + B nazveme asymptotou funkce f (x) ve nevlastním bodě, resp., jestliže lim x [f (x) (Ax + B)] = 0, resp. lim x [f (x) (Ax + B)] = 0. 1 Příklad : Funkce f (x) = má v nevlastních bodech asymptotu y = 0, x +5x+6 1 protože lim x ± ( 0) = 0. x +5x+6
11 Asymptoty funkce Poznámka : Funkce f (x) nemusí mít žádné asymptoty, např. funkce f (x) = sin x. Věta : Přímka y = Ax + B je asymptotou funkce f (x) v bodě +, resp. A = lim x f (x) x, B = lim x (f (x) Ax), resp. f (x) A = lim x x, B = lim x (f (x) Ax). Příklad : Určete asymptoty funkce f (x) = x +x+1 x v nevlastních bodech. Řešení: Nejprve určíme asymptotu v + : ( ) x A = lim +x+1 x x = 1, B = lim +x+1 x+1 x x x x = lim x x = Tedy hledaná asypmtota je: y = x +. Obdobně ( postupujeme ) v : x A = lim +x+1 x x = 1, B = lim +x+1 x+1 x x x x = lim x x = Tedy hledaná asypmtota je: y = x +.
12 Průběh funkce Při vyšetřování průběhu funkce zjišt ujeme: 1 Df, nulové body a znamení funkce, periodicitu, paritu funkce Intervaly monotónnosti a lokální extrémy funkce 3 Kde je funkce konvexní, konkávní a jaké jsou inflexní body funkce 4 Asymptoty a graf funkce Příklad : Vyšetřete průběh funkce f (x) = x + x +. Řešení: 1 Funkce je definovaná na R, je všude kladná, není sudá ani lichá ani periodická f x+1 (x) =, stacionární bod je 1, funkce je klesající na (, 1) x +x+ a rostoucí na ( 1, ), tedy v bodě 1 nabývá funkce lokálního minima f ( 1) = 1. 3 f 1 (x) = (x, druhá derivace je všude kladná, tedy funkce je +x+) 3 konvexní na R. 4 Funkce nemá svislé asymptoty. Určeme ještě asymptoty funkce f (x) = x + x + v nevlastních bodech.
13 Průběh funkce - příklad A = lim x x +x+ x B = lim x ( x + x + x lim x ( x + x + x x = lim +x+ x = 1, ) x = ) x +x++x x = lim x +x++x x+ x +x++x = 1 Tedy hledaná asypmtota je: y = x + 1. Obdobně postupujeme v : x A = lim +x+ x x x = lim x +x+ = 1, ( x x ) B = lim x + x + + x = ( x ) lim x x + x + + x +x+ x x = lim x+ x +x+ x x = 1 +x+ x Tedy hledaná asypmtota je: y = x 1. Nyní již můžeme nakreslit graf funkce.
14 Průběh funkce - příklad Zjistili jsme, že: funkce má lokální minimum v bodě 1, f ( 1) = 1 funkce je konvexní funkce má v + asymptotu y = x + 1 funkce má v asymptotu y = x 1 nyní již můžeme načrtnout graf Obrázek: Graf funkce f (x) = x + x +
15 Diferenciál Uvažujme funkci f (x), která má v bodě a derivaci f (a). Sestrojíme - li v bodě a tečnu ke grafu funkce f, t : y = f (a) + f (a).(x a), můžeme pro x blízká bodu a odhadnout hodnotu f (x) jako f (x) f (a) + f (a).(x a). Výraz df (a) = f (a).(x a) nazýváme diferenciálem funkce f v bodě a, píšeme df (a) = f (a).dx. Obrázek: Diferenciál funkce f (x) v bodě a pro dx = (x a)
16 Diferenciál - příklad Příklad : Je dána funkce f (x) = x a bod a = 4. 1 Určete diferenciál funkce f v bodě a Pomocí tohoto diferenciálu odhadněte 5. Řešení: 1 f (x) = 1, f (4) = 1 x 4. Tedy df (4) = dx 4. 5 = f (5) f (a) + f (a).(5 a) = =, 5 Pozn.: Skutečná hodnota zaokrouhlená na 3 desetinná místa je 5 =, 36.
17 Taylorův polynom Ještě přesnější odhady můžeme získat pomocí Taylorova polynomu. Má-li funkce f (x) derivace v bodě a derivace až do n-tého řádu, pak v tomto bodě definujeme Taylorův polynom stupně n: T n (x) = f (a) + f (a).(x a) + f (a)!.(x a) f (n) (a) n!.(x a) n Pro "x blízká bodu a"platí f (x) T n (x), chybu R n (x) = f (x) T n (x) lze vyjádřit v různých tvarech. Příklad : Pro funkci f (x) = x a bod a = 4 1 Určete Taylorův polynom T 3 (x) Pomocí tohoto polynomu odhadněte 5. Řešení: 1 f (x) = 1, f (x) = 1 x 4, f (x) = 3 x 3 8. x 5 Dosadíme: f (4) = 1 4, f (4) = 1 3, f (4) = 3 56 Tedy T 3 (x) = (x 4) (x 4) (x 4)3 5 = f (5) =, Pozn.: Skutečná hodnota zaokrouhlená na 3 desetinná místa je 5 =, 36.
18 Integrální počet - primitivní funkce Jestliže F(x) a f (x) jsou takové funkce, že pro všechna x z intervalu I platí f (x) = F (x), pak řekneme, že F (x) je primitivní k f (x) na intervalu I. Příklad : Funkce F(x) = x 3 + x + 3x + 5 je primitivní k f (x) = 3x + x + 3 na R, protože f (x) = F (x). Poznámka : Je-li F (x) primitivní k f (x) na intervalu I, pak funkce F(x) je zde spojitá (dokonce má derivaci). Jaké podmínky musí splňovat f (x)? Postačující podmínkou k tomu, aby k f (x) existovala primitivní funkce je spojitost f (x) na I. Je primitivní funkce určena jednoznačně? Příklad : Funkce G(x) = x 3 + x + 3x + 7 je též primitivní k funkci f (x) = 3x + x + 3 z předchozího příkladu. Věta : Jsou-li funkce F(x) a G(x) primitivní k funkci f (x) na intervalu I, pak existuje konstanta c R, taková, že pro x I : F (x) = G(x) + c
19 Neurčitý integrál Množinu všech funkcí primitivních k f (x) na I nazýváme neurčitý integrál f (x) na I a značíme f (x)dx. Píšeme f (x)dx = F(x) + c, kde F (x) je libovolná primitivní funkce k f (x) na I, dx je diferenciál x a c tzv. integrační konstanta. Příklad : Najděte neurčité integrály 1 sin xdx 3 x 3 dx e x dx Řešení: 1 sin xdx = cos x + c 3 x 3 dx = x c e x dx = ex + c
20 Základní neurčité integrály 0dx = c, x (, ) e x dx = e x + c, x (, ) sin xdx = cos x + c, x (, ) cos xdx = sin x + c, x (, ) dx 1+x = arctg(x) + c, x (, ) dx 1 x x n dx = x n+1 = arcsin(x) + c, x ( 1, 1) n+1 + c, n 1, x (, ) pro n 0 celé, x (, 0) nebo (0, ) pro n < 0 celé, x (0, ) pro n necelé dx x dx cos (x) dx sin (x) = ln x + c, x (0, ) nebo x (, 0) = tg(x) + c, pro interval, kde cos x 0 = cotg(x) + c, pro interval, kde sin x 0
21 Pravidla pro integrování Integrace lineární kombinace funkcí: Věta : Jestliže funkce f 1 (x), f (x),... f n (x) mají na I neurčité integrály, pak pro libovolné konstanty c 1, c,... c n existuje neurčitý integrál funkce f (x) = c 1 f 1 (x) + c f (x) c n f n (x) a platí: f (x)dx = c1 f1 (x)dx + c f (x)dx c n fn (x)dx Příklad : Najděte neurčitý integrál (e x + x x )dx Řešení: (e x + x x )dx = e x dx + 1 x +1 dx x dx = e x + arctgx + 3ln x + c. Metoda per partes: Věta : Jestliže funkce u(x), v(x) mají na otevřeném intervalu I spojité derivace, pak platí: u (x)v(x)dx = u(x)v(x) u(x)v (x)dx
22 Metoda per partes - příklady Příklad : Najděte neurčitý integrál x. sin xdx Řešení: Použijeme metodu per partes pro: u (x) = sin x, v(x) = x. Dopočítáme u(x) = cos x, v (x) = 1 a dosadíme: x. sin xdx = x cos x cos xdx = x cos x + sin x + c. Někdy je nutné použít pravidlo opakovaně. Příklad : Najděte neurčitý integrál x.e x dx Řešení: Použijeme metodu per partes pro: u (x) = e x, v(x) = x. Dopočítáme u(x) = e x, v (x) = x a dosadíme: x.e x dx = x.e x x.e x dx Per partes zopakujeme pro u (x) = e x, v(x) = x, tedy u(x) = e x, v (x) = : x.e x dx = x.e x [x.e x e x dx] = x.e x x.e x + e x + c.
23 I. výpočet integrálu substitucí: hledáme f (ϕ(t))ϕ (t)dt. Zvolíme substituci x = ϕ(t). Vypočítáme dx = ϕ (t)dt. Do daného integrálu dosadíme za ϕ(t) a ϕ (t)dt a dostaneme f (x)dx. Vypočítáme F (x) = f (x)dx. Určíme interval I, na kterém platí F (ϕ(t)) = f (ϕ(t))ϕ (t). Hledaný integrál je f (ϕ(t))ϕ (t)dt = F(ϕ(t)) + c, t I.
24 Příklad: Vypočítejte sin(x)dx. Řešení: sin(x)dx = 1 sin(x).dx = = 1 = substituce u = x du = dx = sin(u)du = 1 ( cos(u)) + c = 1 ( cos(x)) + c, x R.
25 Příklad: Vypočítejte e 3x+1 dx. Řešení: e 3x+1 dx = 1 3 e 3x+1.3dx = = 1 3 = substituce u = 3x + 1 du = 3dx = e u.du = 1 3 eu + c = 1 3 e3x+1 + c, x R.
26 Příklad: Vypočítejte x x +1 dx. Řešení: = 1 x x + 1 dx = 1 x x + 1 dx = = substituce u = x + 1 du = xdx = 1 u du = 1 ln u + c = 1 ln x c, x R.
27 Poznámka : Pro funkci ϕ(t), která je nenulová na intervalu I a má zde derivaci ϕ (t) platí: ϕ (t) ϕ(t) dt = ln ϕ(t) + c, t I : ϕ(t) 0. Důkaz: Ověřte sami.
28 II. výpočet integrálu substitucí: hledáme f (x)dx na intervalu J. Zvolíme substituci x = ϕ(t) tak, aby na J existovala ϕ 1 (x). Vypočítáme dx = ϕ (t)dt a do daného integrálu dosadíme místo x výraz ϕ(t) a místo dx výraz ϕ (t)dt. Určíme G(t) = f (ϕ(t))ϕ (t)dt. Dosadíme do G(t) místo t výraz ϕ 1 (x) a dostaneme F(x) = G(ϕ 1 (x)). Zkontrolujeme, zda na intervalu J platí F (x) = f (x).
29 Příklad: Vypočítejte 1 x dx, x ( 1, 1). Řešení: 1 x dx = = substituce x = sin(t) t ( π/, π/) dx = cos(t)dt = 1 sin (t)cos(t)dt = cos (t)dt = = = cos(t) + 1 dt = sin(t) 4 + t + c, x ( 1, 1). Nyní je nutné vrátit se k původní proměnné x. Pro t ( π/, π/) vyjádříme t = arcsin(x) a protože sin(t) = sin(t)cos(t) = sin(t) 1 sin (t), dostaneme výsledek x 1 x + arcsin(x) + c.
IX. Vyšetřování průběhu funkce
 IX. Vyšetřování průběhu funkce Úvodní poznámky: Cíl: vyšetřit průběh dané funkce f. Zahrnuje: základní vlastnosti: D(f), spojitost, limity v krajních bodech, průsečíky s osami souřadnic, intervaly, kde
IX. Vyšetřování průběhu funkce Úvodní poznámky: Cíl: vyšetřit průběh dané funkce f. Zahrnuje: základní vlastnosti: D(f), spojitost, limity v krajních bodech, průsečíky s osami souřadnic, intervaly, kde
Diferenciální počet funkcí jedné proměnné
 Diferenciální počet funkcí jedné proměnné 1 4. Derivace funkce 4.3. Průběh funkce 2 Pro přesné určení průběhu grafu funkce je třeba určit bližší vlastnosti funkce. Monotónnost funkce Funkce monotónní =
Diferenciální počet funkcí jedné proměnné 1 4. Derivace funkce 4.3. Průběh funkce 2 Pro přesné určení průběhu grafu funkce je třeba určit bližší vlastnosti funkce. Monotónnost funkce Funkce monotónní =
7.1 Extrémy a monotonie
 KAPITOLA 7: Průběh funkce [ZMA13-P38] 7.1 Extrémy a monotonie Řekneme, že funkce f nabývá na množině M Df svého globálního maxima globálního minima A v bodě x 0, jestliže x 0 M, fx 0 = A a pro každé x
KAPITOLA 7: Průběh funkce [ZMA13-P38] 7.1 Extrémy a monotonie Řekneme, že funkce f nabývá na množině M Df svého globálního maxima globálního minima A v bodě x 0, jestliže x 0 M, fx 0 = A a pro každé x
Diferenciální počet - II. část (Taylorův polynom, L Hospitalovo pravidlo, extrémy
 Diferenciální počet - II. část (Taylorův polynom, L Hospitalovo pravidlo, extrémy funkcí, průběh funkce) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 5. přednáška z AMA1 Michal Fusek (fusekmi@feec.vutbr.cz)
Diferenciální počet - II. část (Taylorův polynom, L Hospitalovo pravidlo, extrémy funkcí, průběh funkce) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 5. přednáška z AMA1 Michal Fusek (fusekmi@feec.vutbr.cz)
Kapitola 4: Průběh funkce 1/11
 Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Příklady na konvexnost a inflexní body. Funkce f (x) = x 3 9x. Derivace jsou f (x) = 3x 2 9 a f (x) = 6x. Funkce f je konvexní na intervalu (0, )
 Příklady na konvexnost a inflexní body. Funkce = x 3 9x. Derivace jsou f (x) = 3x 9 a f (x) = 6x. Funkce f je konvexní na intervalu (, ) a konkávní na intervalu (, ). Inflexní bod c =. 3 1 1 y = x 3 9x
Příklady na konvexnost a inflexní body. Funkce = x 3 9x. Derivace jsou f (x) = 3x 9 a f (x) = 6x. Funkce f je konvexní na intervalu (, ) a konkávní na intervalu (, ). Inflexní bod c =. 3 1 1 y = x 3 9x
Kapitola 4: Průběh funkce 1/11
 Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
LDF MENDELU. Simona Fišnarová (MENDELU) Průběh funkce ZVMT lesnictví 1 / 21
 Průběh funkce Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Průběh funkce Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Funkce jedn e re aln e promˇ enn e Derivace Pˇredn aˇska ˇr ıjna 2015
 Funkce jedné reálné proměnné Derivace Přednáška 2 15. října 2015 Obsah 1 Funkce 2 Limita a spojitost funkce 3 Derivace 4 Průběh funkce Informace Literatura v elektronické verzi (odkazy ze STAGu): 1 Lineární
Funkce jedné reálné proměnné Derivace Přednáška 2 15. října 2015 Obsah 1 Funkce 2 Limita a spojitost funkce 3 Derivace 4 Průběh funkce Informace Literatura v elektronické verzi (odkazy ze STAGu): 1 Lineární
Pavlína Matysová. 5. listopadu 2018
 Soubor řešených úloh Vyšetřování průběhu funkce Pavlína Matysová 5. listopadu 018 1 Soubor řešených úloh Tento text obsahuje 7 úloh na téma vyšetřování průběhu funkce. Každé úloha je řešena dvěma způsoby
Soubor řešených úloh Vyšetřování průběhu funkce Pavlína Matysová 5. listopadu 018 1 Soubor řešených úloh Tento text obsahuje 7 úloh na téma vyšetřování průběhu funkce. Každé úloha je řešena dvěma způsoby
Matematika B 2. Úvodní informace
 Matematika B 2 MIROSLAV KUČERA Úvodní informace Kontakt miroslav.kucera@vsfs.czvsfs.cz Studijní středisko Kladno IT oddělení 306B (kanceláře studijního oddělení) Konzultační hodiny Po Pá 8:30 15:00 možno
Matematika B 2 MIROSLAV KUČERA Úvodní informace Kontakt miroslav.kucera@vsfs.czvsfs.cz Studijní středisko Kladno IT oddělení 306B (kanceláře studijního oddělení) Konzultační hodiny Po Pá 8:30 15:00 možno
Aplikace derivace a průběh funkce
 Aplikace derivace a průběh funkce Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného
Aplikace derivace a průběh funkce Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného
Matematika I A ukázkový test 1 pro 2014/2015
 Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2011/2012. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a
 Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Zlín, 23. října 2011
 (. -. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 3. října 0 Postup při vyšetřování průběhu funkce. Definiční obor funkce,
(. -. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 3. října 0 Postup při vyšetřování průběhu funkce. Definiční obor funkce,
Přijímací zkouška na navazující magisterské studium 2018
 Přijímací zkouška na navazující magisterské studium 208 Studijní program: Studijní obory: Matematika MA, MMIT, MMFT, MSTR, MNVM, MPMSE Varianta A Řešení příkladů pečlivě odůvodněte. Věnujte pozornost ověření
Přijímací zkouška na navazující magisterské studium 208 Studijní program: Studijní obory: Matematika MA, MMIT, MMFT, MSTR, MNVM, MPMSE Varianta A Řešení příkladů pečlivě odůvodněte. Věnujte pozornost ověření
Výsledky Př.1. Určete intervaly monotónnosti a lokální extrémy funkce a) ( ) ( ) ( ) Stacionární body:
 Výsledky Př.. Určete intervaly monotónnosti a lokální extrémy funkce a) y < y > y < y > -2 0 3 Funkce je rostoucí v intervalech. Funkce je klesající v intervalech b) y < y > y < - Funkce je rostoucí v
Výsledky Př.. Určete intervaly monotónnosti a lokální extrémy funkce a) y < y > y < y > -2 0 3 Funkce je rostoucí v intervalech. Funkce je klesající v intervalech b) y < y > y < - Funkce je rostoucí v
Příklad 1 ŘEŠENÉ PŘÍKLADY Z M1A ČÁST 6
 Příklad 1 Vyšetřete průběh funkce: a) = b) = c) = d) =ln1+ e) =ln f) = Poznámka K vyšetřování průběhu funkce použijeme postup uvedený v zadání. Některé kroky nejsou již tak detailní, všechny by ale měly
Příklad 1 Vyšetřete průběh funkce: a) = b) = c) = d) =ln1+ e) =ln f) = Poznámka K vyšetřování průběhu funkce použijeme postup uvedený v zadání. Některé kroky nejsou již tak detailní, všechny by ale měly
Označení derivace čárkami, resp. římskými číslicemi, volíme při nižším řádu derivace, jinak užíváme horní index v závorce f (5), f (6),... x c g (x).
 9 Využití derivace 9.1 Derivace vyšších řádů Definice 1. Nechť funkce má derivaci v nějakém okolí bodu c D(f). Nechť funkce ϕ() =f () máderivacivboděc. Pak hodnotu ϕ (c) nazýváme derivací 2. řádu (2. derivací)
9 Využití derivace 9.1 Derivace vyšších řádů Definice 1. Nechť funkce má derivaci v nějakém okolí bodu c D(f). Nechť funkce ϕ() =f () máderivacivboděc. Pak hodnotu ϕ (c) nazýváme derivací 2. řádu (2. derivací)
Význam a výpočet derivace funkce a její užití
 OPAKOVÁNÍ ZÁKLADŮ MATEMATIKY Metodický list č. 1 Význam a výpočet derivace funkce a její užití 1. dílčí téma: Výpočet derivace přímo z definice a pomocí základních vzorců. K tomuto tématu je třeba zopakovat
OPAKOVÁNÍ ZÁKLADŮ MATEMATIKY Metodický list č. 1 Význam a výpočet derivace funkce a její užití 1. dílčí téma: Výpočet derivace přímo z definice a pomocí základních vzorců. K tomuto tématu je třeba zopakovat
Přijímací zkouška na navazující magisterské studium 2014
 Přijímací zkouška na navazující magisterské studium 4 Studijní program: Studijní obory: Příklad (5 bodů) Spočtěte Matematika MA, MMIB, MMFT, MSTR, NVM, PMSE, MDU Varianta A M xy dxdy, kde M = {(x, y) R
Přijímací zkouška na navazující magisterské studium 4 Studijní program: Studijní obory: Příklad (5 bodů) Spočtěte Matematika MA, MMIB, MMFT, MSTR, NVM, PMSE, MDU Varianta A M xy dxdy, kde M = {(x, y) R
Matematika 2 Průběh funkce
 Matematika 2 Průběh funkce Jiří Fišer KMA, PřF UP Olomouc ZS09 Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 1 / 1 Základní věty diferenciálního počtu Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09
Matematika 2 Průběh funkce Jiří Fišer KMA, PřF UP Olomouc ZS09 Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 1 / 1 Základní věty diferenciálního počtu Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09
Definice derivace v bodě
 Definice derivace v bodě tgϕ = f ( ) f () f () : = tgϕ = lim f f () tgϕ = f f () Obecně: f f f ( ) ( ) : = lim f ( + h) f f : = lim h h Derivace zleva (zprava): f ( ) : = lim f f ( ) f ( ) : = lim + +
Definice derivace v bodě tgϕ = f ( ) f () f () : = tgϕ = lim f f () tgϕ = f f () Obecně: f f f ( ) ( ) : = lim f ( + h) f f : = lim h h Derivace zleva (zprava): f ( ) : = lim f f ( ) f ( ) : = lim + +
Základy matematiky pro FEK
 Základy matematiky pro FEK 10. přednáška Blanka Šedivá KMA zimní semestr 016/017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 016/017 1 / 1 Použití derivace pro vyšetřování průběhu funkce
Základy matematiky pro FEK 10. přednáška Blanka Šedivá KMA zimní semestr 016/017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 016/017 1 / 1 Použití derivace pro vyšetřování průběhu funkce
Použití derivací L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT. Monotónie. Konvexita. V této části budou uvedena některá použití derivací.
 V této části budou uvedena některá použití derivací. Použití derivací L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT Tvrzení je uvedeno pro jednostrannou itu zprava. Samozřejmě obdobné tvrzení platí pro itu zleva
V této části budou uvedena některá použití derivací. Použití derivací L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT Tvrzení je uvedeno pro jednostrannou itu zprava. Samozřejmě obdobné tvrzení platí pro itu zleva
Matematická analýza 1, příklady na procvičení (Josef Tkadlec, )
 Matematická analýza, příklady na procvičení (Josef Tkadlec, 6.. 7) Reálná čísla. Určete maximum, minimum, supremum a infimum následujících množin: Z; b) M = (, ), 5 ; c) M =, Q; d) M = { + n : n N}; e)
Matematická analýza, příklady na procvičení (Josef Tkadlec, 6.. 7) Reálná čísla. Určete maximum, minimum, supremum a infimum následujících množin: Z; b) M = (, ), 5 ; c) M =, Q; d) M = { + n : n N}; e)
Použití derivací. V této části budou uvedena některá použití derivací. LEKCE08-PRU. Použití derivací. l Hospital
 V této části budou uvedena některá použití derivací. a derivace a derivace -zbytek L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT Tvrzení je uvedeno pro jednostrannou limitu zprava. Samozřejmě obdobné tvrzení platí
V této části budou uvedena některá použití derivací. a derivace a derivace -zbytek L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT Tvrzení je uvedeno pro jednostrannou limitu zprava. Samozřejmě obdobné tvrzení platí
Derivace a průběh funkce příklady z písemných prací
 Derivace a průběh funkce příklady z písemných prací Vyšetřete průběh následuících funkcí. Příklad. = x +arctg( x ). D(f) =R.. Funkce e spoitá na R. 3. Funkce není lichá, sudá, ani periodická.. lim x ±
Derivace a průběh funkce příklady z písemných prací Vyšetřete průběh následuících funkcí. Příklad. = x +arctg( x ). D(f) =R.. Funkce e spoitá na R. 3. Funkce není lichá, sudá, ani periodická.. lim x ±
Posloupnosti a řady. 28. listopadu 2015
 Posloupnosti a řady Přednáška 5 28. listopadu 205 Obsah Posloupnosti 2 Věty o limitách 3 Řady 4 Kritéria konvergence 5 Absolutní a relativní konvergence 6 Operace s řadami 7 Mocninné a Taylorovy řady Zdroj
Posloupnosti a řady Přednáška 5 28. listopadu 205 Obsah Posloupnosti 2 Věty o limitách 3 Řady 4 Kritéria konvergence 5 Absolutní a relativní konvergence 6 Operace s řadami 7 Mocninné a Taylorovy řady Zdroj
Matematika I (KX001) Užití derivace v geometrii, ve fyzice 3. října f (x 0 ) (x x 0) Je-li f (x 0 ) = 0, tečna: x = 3, normála: y = 0
 Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Derivace funkce. existuje limita lim 0 ) xx xx0. Jestliže tato limita neexistuje nebo pokud funkce ff
 Derivace funkce Derivace je základním pojmem v diferenciálním počtu. Má uplatnění tam, kde se zkoumá povaha funkčních závislostí určitých proměnných (veličin). V matematice, ekonomii, fyzice ale i v jiných
Derivace funkce Derivace je základním pojmem v diferenciálním počtu. Má uplatnění tam, kde se zkoumá povaha funkčních závislostí určitých proměnných (veličin). V matematice, ekonomii, fyzice ale i v jiných
Monotonie a lokální extrémy. Konvexnost, konkávnost a inflexní body. 266 I. Diferenciální počet funkcí jedné proměnné
 66 I. Diferenciální počet funkcí jedné proměnné I. 5. Vyšetřování průběhu funkce Monotonie a lokální etrémy Důsledek. Nechť má funkce f) konečnou derivaci na intervalu I. Je-li f ) > 0 pro každé I, pak
66 I. Diferenciální počet funkcí jedné proměnné I. 5. Vyšetřování průběhu funkce Monotonie a lokální etrémy Důsledek. Nechť má funkce f) konečnou derivaci na intervalu I. Je-li f ) > 0 pro každé I, pak
1 Množiny, výroky a číselné obory
 1 Množiny, výroky a číselné obory 1.1 Množiny a množinové operace Množinou rozumíme každé shrnutí určitých a navzájem různých objektů (které nazýváme prvky) do jediného celku. Definice. Dvě množiny jsou
1 Množiny, výroky a číselné obory 1.1 Množiny a množinové operace Množinou rozumíme každé shrnutí určitých a navzájem různých objektů (které nazýváme prvky) do jediného celku. Definice. Dvě množiny jsou
Funkce v ıce promˇ enn ych Extr emy Pˇredn aˇska p at a 12.bˇrezna 2018
 Funkce více proměnných Extrémy Přednáška pátá 12.března 2018 Zdroje informací Diferenciální počet http://homen.vsb.cz/~kre40/esfmat2/fceviceprom.html http://www.studopory.vsb.cz/studijnimaterialy/sbirka_uloh/pdf/7.pdf
Funkce více proměnných Extrémy Přednáška pátá 12.března 2018 Zdroje informací Diferenciální počet http://homen.vsb.cz/~kre40/esfmat2/fceviceprom.html http://www.studopory.vsb.cz/studijnimaterialy/sbirka_uloh/pdf/7.pdf
14. Monotonnost, lokální extrémy, globální extrémy a asymptoty funkce
 . Monotonnost, lokální extrém, globální extrém a asmptot funkce Studijní text. Monotonnost, lokální extrém, globální extrém a asmptot funkce A. Rostoucí a klesající funkce Pojm rostoucí, klesající a konstantní
. Monotonnost, lokální extrém, globální extrém a asmptot funkce Studijní text. Monotonnost, lokální extrém, globální extrém a asmptot funkce A. Rostoucí a klesající funkce Pojm rostoucí, klesající a konstantní
Derivace funkce. Přednáška MATEMATIKA č Jiří Neubauer
 Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
DERIVACE FUNKCE, L HOSPITALOVO PRAVIDLO
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA DERIVACE FUNKCE, L HOSPITALOVO PRAVIDLO Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA DERIVACE FUNKCE, L HOSPITALOVO PRAVIDLO Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem
NMAF 051, ZS Zkoušková písemná práce 26. ledna x. x 1 + x dx. q 1. u = x = 1 u2. = 1 u. u 2 (1 + u 2 ) (1 u 2 du = 2.
 Jednotlivé kroky při výpočtech stručně, ale co nejpřesněji odůvodněte Pokud používáte nějaké tvrzení, nezapomeňte ověřit splnění předpokladů Jméno a příjmení: Skupina: Příklad 4 Celkem bodů Bodů 5 6 8
Jednotlivé kroky při výpočtech stručně, ale co nejpřesněji odůvodněte Pokud používáte nějaké tvrzení, nezapomeňte ověřit splnění předpokladů Jméno a příjmení: Skupina: Příklad 4 Celkem bodů Bodů 5 6 8
Matematická analýza pro informatiky I. Derivace funkce
 Matematická analýza pro informatiky I. 7. přednáška Derivace funkce Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 31. března 2011 Jan Tomeček, tomecek@inf.upol.cz
Matematická analýza pro informatiky I. 7. přednáška Derivace funkce Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 31. března 2011 Jan Tomeček, tomecek@inf.upol.cz
MATEMATIKA. Příklady pro 1. ročník bakalářského studia. II. část Diferenciální počet. II.1. Posloupnosti reálných čísel
 MATEMATIKA Příklady pro 1. ročník bakalářského studia II. část II.1. Posloupnosti reálných čísel Rozhodněte, zda posloupnost a n (n = 1, 2, 3,...) je omezená (omezená shora, omezená zdola) resp. monotónní
MATEMATIKA Příklady pro 1. ročník bakalářského studia II. část II.1. Posloupnosti reálných čísel Rozhodněte, zda posloupnost a n (n = 1, 2, 3,...) je omezená (omezená shora, omezená zdola) resp. monotónní
Vypracoval: Mgr. Lukáš Bičík TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY
 Vlastnosti funkcí Vypracoval: Mgr. Lukáš Bičík TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY Definiční obor Definiční obor funkce je množina všech čísel,
Vlastnosti funkcí Vypracoval: Mgr. Lukáš Bičík TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY Definiční obor Definiční obor funkce je množina všech čísel,
Teorie. Hinty. kunck6am
 kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
D(f) =( 1, 1) [ ( 1, 1) [ (1, 1). 2( x)3 ( x) 2 1 = 2(x) 3. (x) 2 1 = f(x) Funkce je lichá, není periodická
 Vyšetříme funkci f(x): f(x) = 2x3.. Stanovme definiční obor funkce D(f) a zjistíme,ve kterých bodech je funkce sojitá D(f) =(, ) [ (, ) [ (, ). 2. Počítáme f( x) = 2( x)3 ( x) 2 = 2(x) 3 (x) 2 = f(x) Funkce
Vyšetříme funkci f(x): f(x) = 2x3.. Stanovme definiční obor funkce D(f) a zjistíme,ve kterých bodech je funkce sojitá D(f) =(, ) [ (, ) [ (, ). 2. Počítáme f( x) = 2( x)3 ( x) 2 = 2(x) 3 (x) 2 = f(x) Funkce
2. spojitost (7. cvičení) 3. sudost/lichost, periodicita (3. cvičení) 4. první derivace, stacionární body, intervaly monotonie (10.
 MA. cvičení průběh funkce Lukáš Pospíšil,202 Průběh funkce Pod úkolem vyšetřete průběh funkce budeme rozumět nalezení všech kvalitativních vlastností zadané funkce - tedy bude potřeba zjistit o funkci
MA. cvičení průběh funkce Lukáš Pospíšil,202 Průběh funkce Pod úkolem vyšetřete průběh funkce budeme rozumět nalezení všech kvalitativních vlastností zadané funkce - tedy bude potřeba zjistit o funkci
5. Lokální, vázané a globální extrémy
 5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
Funkce jedné proměnné
 Funkce jedné proměnné Příklad - V následujících příkladech v případě a) pro funkce dané rovnicí zjistěte zda jsou rostoucí klesající nebo konstantní vypočítejte průsečíky grafu s osami souřadnic a graf
Funkce jedné proměnné Příklad - V následujících příkladech v případě a) pro funkce dané rovnicí zjistěte zda jsou rostoucí klesající nebo konstantní vypočítejte průsečíky grafu s osami souřadnic a graf
MATEMATIKA II - vybrané úlohy ze zkoušek (2015)
 MATEMATIKA II - vybrané úlohy ze zkoušek (2015) doplněné o další úlohy 24. 2. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi (e-mail: Frantisek.Mraz@fs.cvut.cz
MATEMATIKA II - vybrané úlohy ze zkoušek (2015) doplněné o další úlohy 24. 2. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi (e-mail: Frantisek.Mraz@fs.cvut.cz
Omezenost funkce. Definice. (shora, zdola) omezená na množině M D(f ) tuto vlastnost. nazývá se (shora, zdola) omezená tuto vlastnost má množina
 Přednáška č. 5 Vlastnosti funkcí Jiří Fišer 22. října 2007 Jiří Fišer (KMA, PřF UP Olomouc) KMA MMAN1 Přednáška č. 4 22. října 2007 1 / 1 Omezenost funkce Definice Funkce f se nazývá (shora, zdola) omezená
Přednáška č. 5 Vlastnosti funkcí Jiří Fišer 22. října 2007 Jiří Fišer (KMA, PřF UP Olomouc) KMA MMAN1 Přednáška č. 4 22. října 2007 1 / 1 Omezenost funkce Definice Funkce f se nazývá (shora, zdola) omezená
Definice globální minimum (absolutní minimum) v bodě A D f, jestliže X D f
 Výklad Globální extrémy mají stejný význam jako u funkcí jedné proměnné. Hledáme je bud na celém definičním oboru dané funkce, nebo na předem zadané podmnožině definičního oboru. Definice 6..1. Řekneme,
Výklad Globální extrémy mají stejný význam jako u funkcí jedné proměnné. Hledáme je bud na celém definičním oboru dané funkce, nebo na předem zadané podmnožině definičního oboru. Definice 6..1. Řekneme,
soubor FUNKCÍ příručka pro studenty
 soubor FUNKCÍ příručka pro studenty 1 Obsah Poznámky 6 lineární funkce mocninné funkce s přirozeným exponentem o sudým o lichým s celým záporným exponentem o sudým o lichým s racionálním exponentem o druhá
soubor FUNKCÍ příručka pro studenty 1 Obsah Poznámky 6 lineární funkce mocninné funkce s přirozeným exponentem o sudým o lichým s celým záporným exponentem o sudým o lichým s racionálním exponentem o druhá
Průvodce studiem. do bodu B se snažíme najít nejkratší cestu. Ve firmách je snaha minimalizovat
 6. Extrémy funkcí více proměnných Průvodce studiem Hledání extrémů je v praxi často řešená úloha. Např. při cestě z bodu A do bodu B se snažíme najít nejkratší cestu. Ve firmách je snaha minimalizovat
6. Extrémy funkcí více proměnných Průvodce studiem Hledání extrémů je v praxi často řešená úloha. Např. při cestě z bodu A do bodu B se snažíme najít nejkratší cestu. Ve firmách je snaha minimalizovat
Diferenciální počet 1 1. f(x) = ln arcsin 1 + x 1 x. 1 x 1 a x 1 0. f(x) = (cos x) cosh x + 3x. x 0 je derivace funkce f(x) v bodě x0.
 Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Aplikační úlohy z diferenciálního počtu jedné proměnné
 Jihočeská univerzita v Českých Budějovicích Fakulta Katedra Bakalářská práce Aplikační úlohy z diferenciálního počtu jedné proměnné Vypracoval: Michaela Jelínková Vedoucí práce: RNDr. Vladimíra Petrášková,
Jihočeská univerzita v Českých Budějovicích Fakulta Katedra Bakalářská práce Aplikační úlohy z diferenciálního počtu jedné proměnné Vypracoval: Michaela Jelínková Vedoucí práce: RNDr. Vladimíra Petrášková,
Bakalářská matematika I
 1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
Petr Hasil. Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
 Neurčitý integrál Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Neurčitý integrál Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
2.7. Průběh funkce. Vyšetřit průběh funkce znamená určit (ne nutně v tomto pořadí): 1) Definiční obor; sudost, lichost; periodičnost
 .7. Průběh unkce Všetřit průběh unkce znamená určit ne nutně v tomto pořadí: deiniční obor; sudost, lichost; periodičnost, interval spojitosti a bod nespojitosti, průsečík grau unkce s osami, interval,
.7. Průběh unkce Všetřit průběh unkce znamená určit ne nutně v tomto pořadí: deiniční obor; sudost, lichost; periodičnost, interval spojitosti a bod nespojitosti, průsečík grau unkce s osami, interval,
{ } Ox ( 0) 4.2. Konvexnost, konkávnost, inflexe. Definice Obr. 52. Poznámka. nad tečnou
 Konvenost, konkávnost, inflee 4.. Konvenost, konkávnost, inflee Definice 4... Nechť eistuje f ( ), D f. Řekneme, že funkce f ( ) je v bodě konkávní, jestliže eistuje { } O ( ) tak, že platí D : O( )\ f(
Konvenost, konkávnost, inflee 4.. Konvenost, konkávnost, inflee Definice 4... Nechť eistuje f ( ), D f. Řekneme, že funkce f ( ) je v bodě konkávní, jestliže eistuje { } O ( ) tak, že platí D : O( )\ f(
Funkce - pro třídu 1EB
 Variace 1 Funkce - pro třídu 1EB Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv využití výukového materiálu je povoleno pouze s odkazem na www.jarjurek.cz. 1. Funkce Funkce je přiřazení, které každému
Variace 1 Funkce - pro třídu 1EB Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv využití výukového materiálu je povoleno pouze s odkazem na www.jarjurek.cz. 1. Funkce Funkce je přiřazení, které každému
5.3. Implicitní funkce a její derivace
 Výklad Podívejme se na následující problém. Uvažujme množinu M bodů [x,y] R 2, které splňují rovnici F(x, y) = 0, M = {[x,y] D F F(x,y) = 0}, kde z = F(x,y) je nějaká funkce dvou proměnných. Je-li F(x,y)
Výklad Podívejme se na následující problém. Uvažujme množinu M bodů [x,y] R 2, které splňují rovnici F(x, y) = 0, M = {[x,y] D F F(x,y) = 0}, kde z = F(x,y) je nějaká funkce dvou proměnných. Je-li F(x,y)
Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
INTEGRÁLY S PARAMETREM
 INTEGRÁLY S PARAMETREM b a V kapitole o integraci funkcí více proměnných byla potřeba funkce g(x) = f(x, y) dy proměnné x. Spojitost funkce g(x) = b a f(x, y) dy proměnné x znamená vlastně prohození limity
INTEGRÁLY S PARAMETREM b a V kapitole o integraci funkcí více proměnných byla potřeba funkce g(x) = f(x, y) dy proměnné x. Spojitost funkce g(x) = b a f(x, y) dy proměnné x znamená vlastně prohození limity
Přednáška z MA. Michal Tuláček 16. prosince 2004. 1 IV.7 Průběhy funkce 3. 2 Vyšetřování průběhu funkce- KUCHAŘKA 4
 Přednáška z MA Michal Tuláček 6. prosince 004 Obsah IV.7 Průběhy funkce 3 Vyšetřování průběhu funkce- KUCHAŘKA 4 3 Vzorový příklad na průběh funkce ze cvičení 4 4 Příkladynadobumezikapremahusou 7 Definice:
Přednáška z MA Michal Tuláček 6. prosince 004 Obsah IV.7 Průběhy funkce 3 Vyšetřování průběhu funkce- KUCHAŘKA 4 3 Vzorový příklad na průběh funkce ze cvičení 4 4 Příkladynadobumezikapremahusou 7 Definice:
Kapitola 1: Reálné funkce 1/13
 Kapitola 1: Reálné funkce 1/13 Číselné množiny N, N 0, Z, Q, I, R, C Definice: Kartézský součin M N množin M a N je množina všech uspořádaných dvojic, ve kterých je první složka prvkem množiny M a druhá
Kapitola 1: Reálné funkce 1/13 Číselné množiny N, N 0, Z, Q, I, R, C Definice: Kartézský součin M N množin M a N je množina všech uspořádaných dvojic, ve kterých je první složka prvkem množiny M a druhá
Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si zopakovat a orientovat se v pojmech: funkce, D(f), g 2 : y =
 0.1 Diferenciální počet Je částí infinitezimálního počtu, což je souhrnný název pro diferenciální a integrální počet. Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si
0.1 Diferenciální počet Je částí infinitezimálního počtu, což je souhrnný název pro diferenciální a integrální počet. Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si
Přednáška 11, 12. prosince Část 5: derivace funkce
 Přednáška 11, 12. prosince 2014 Závěrem pasáže o spojitých funkcích zmíníme jejich podtřídu, lipschitzovské funkce, nazvané podle německého matematika Rudolfa Lipschitze (1832 1903). Fukce f : M R je lipschitzovská,
Přednáška 11, 12. prosince 2014 Závěrem pasáže o spojitých funkcích zmíníme jejich podtřídu, lipschitzovské funkce, nazvané podle německého matematika Rudolfa Lipschitze (1832 1903). Fukce f : M R je lipschitzovská,
Neurčitý integrál. Robert Mařík. 4. března 2012
 Neurčitý integrál Robert Mařík 4. března 0 V tomto souboru jsou vysvětleny a na příkladech s postupným řešením demonstrovány základní integrační metody. Ikonka za integrálem načte integrál do online aplikace
Neurčitý integrál Robert Mařík 4. března 0 V tomto souboru jsou vysvětleny a na příkladech s postupným řešením demonstrovány základní integrační metody. Ikonka za integrálem načte integrál do online aplikace
Definice Řekneme, že funkce z = f(x,y) je v bodě A = [x 0,y 0 ] diferencovatelná, nebo. z f(x 0 + h,y 0 + k) f(x 0,y 0 ) = Ah + Bk + ρτ(h,k),
![Definice Řekneme, že funkce z = f(x,y) je v bodě A = [x 0,y 0 ] diferencovatelná, nebo. z f(x 0 + h,y 0 + k) f(x 0,y 0 ) = Ah + Bk + ρτ(h,k), Definice Řekneme, že funkce z = f(x,y) je v bodě A = [x 0,y 0 ] diferencovatelná, nebo. z f(x 0 + h,y 0 + k) f(x 0,y 0 ) = Ah + Bk + ρτ(h,k),](/thumbs/62/47835194.jpg) Definice 5.2.1. Řekneme, že funkce z = f(x,y) je v bodě A = [x 0,y 0 ] diferencovatelná, nebo má v tomto bodě totální diferenciál, jestliže je možné její přírůstek z na nějakém okolí bodu A vyjádřit jako
Definice 5.2.1. Řekneme, že funkce z = f(x,y) je v bodě A = [x 0,y 0 ] diferencovatelná, nebo má v tomto bodě totální diferenciál, jestliže je možné její přírůstek z na nějakém okolí bodu A vyjádřit jako
1. POJMY 1.1. FORMULE VÝROKOVÉHO POČTU
 Obsah 1. Pojmy... 2 1.1. Formule výrokového počtu... 2 1.2. Množina... 3 1.2.1. Operace s množinami... 3 1.2.2. Relace... 3 2. Číselné obory... 5 2.1. Uzavřenost množiny na operaci... 5 2.2. Rozšíření
Obsah 1. Pojmy... 2 1.1. Formule výrokového počtu... 2 1.2. Množina... 3 1.2.1. Operace s množinami... 3 1.2.2. Relace... 3 2. Číselné obory... 5 2.1. Uzavřenost množiny na operaci... 5 2.2. Rozšíření
Kapitola 1: Reálné funkce 1/13
 Kapitola 1: Reálné funkce 1/13 Číselné množiny 2/13 N = {1, 2, 3, 4,... }... přirozená čísla N 0 = N {0} = {0, 1, 2, 3, 4,... } Z = {..., 2, 1, 0, 1, 2, 3, 4,... }... celá čísla Q = { p q p, q Z}... racionální
Kapitola 1: Reálné funkce 1/13 Číselné množiny 2/13 N = {1, 2, 3, 4,... }... přirozená čísla N 0 = N {0} = {0, 1, 2, 3, 4,... } Z = {..., 2, 1, 0, 1, 2, 3, 4,... }... celá čísla Q = { p q p, q Z}... racionální
(5) Primitivní funkce
 (5) Primitivní funkce Kristýna Kuncová Matematika B2 18/19 Kristýna Kuncová (5) Primitivní funkce 1 / 20 Def: Primitivní funkce Definice Necht funkce f je definována na neprázdném otevřeném intervalu (a,
(5) Primitivní funkce Kristýna Kuncová Matematika B2 18/19 Kristýna Kuncová (5) Primitivní funkce 1 / 20 Def: Primitivní funkce Definice Necht funkce f je definována na neprázdném otevřeném intervalu (a,
MATEMATIKA I. Požadavky ke zkoušce pro skupinu C 1. ročník 2014/15. I. Základy, lineární algebra a analytická geometrie
 MATEMATIKA I Požadavky ke zkoušce pro skupinu C 1. ročník 2014/15 I. Základy, lineární algebra a analytická geometrie 1. Základní pojmy (a) Základy teorie množin: množina a její prvky, podmnožina, průnik,
MATEMATIKA I Požadavky ke zkoušce pro skupinu C 1. ročník 2014/15 I. Základy, lineární algebra a analytická geometrie 1. Základní pojmy (a) Základy teorie množin: množina a její prvky, podmnožina, průnik,
Funkce a limita. Petr Hasil. Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
 Funkce a limita Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Funkce a limita Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
y H = c 1 e 2x + c 2 xe 2x, Partikularni reseni hledam metodou variace konstant ve tvaru c 1(x)e 2x + c 2(x)xe 2x = 0
 1 Urcete vsechna maximalni reseni: y + 4y + 4y = e 2x x + 1 Definicni obor: x 1, tj. resim na intervalech (, 1) a ( 1, ) Charakteristicky polynom λ 2 + 4λ + 4 ma dvojnasobny koren -2, tedy tvar homogenniho
1 Urcete vsechna maximalni reseni: y + 4y + 4y = e 2x x + 1 Definicni obor: x 1, tj. resim na intervalech (, 1) a ( 1, ) Charakteristicky polynom λ 2 + 4λ + 4 ma dvojnasobny koren -2, tedy tvar homogenniho
Petr Hasil. Prvákoviny c Petr Hasil (MUNI) Úvod do infinitezimálního počtu Prvákoviny / 57
 Úvod do infinitezimálního počtu Petr Hasil Prvákoviny 2015 c Petr Hasil (MUNI) Úvod do infinitezimálního počtu Prvákoviny 2015 1 / 57 Obsah 1 Úvod Funkce Reálná čísla a posloupnosti Limita a spojitost
Úvod do infinitezimálního počtu Petr Hasil Prvákoviny 2015 c Petr Hasil (MUNI) Úvod do infinitezimálního počtu Prvákoviny 2015 1 / 57 Obsah 1 Úvod Funkce Reálná čísla a posloupnosti Limita a spojitost
Mocninná funkce: Příklad 1
 Mocninná funkce: Příklad 1 Zadání: Vyšetřete průběh mocninné funkce. Řešení: 1. Jako první si určíme definiční obor: D(f)=R. 2. Nyní si spočítáme zda je daná funkce sudá nebo lichá: Daná funkce je lichá.
Mocninná funkce: Příklad 1 Zadání: Vyšetřete průběh mocninné funkce. Řešení: 1. Jako první si určíme definiční obor: D(f)=R. 2. Nyní si spočítáme zda je daná funkce sudá nebo lichá: Daná funkce je lichá.
Matematika I. Funkce jedné proměnné. Funkce jedné proměnné Matematika I 1 / 212
 Matematika I Funkce jedné proměnné Funkce jedné proměnné Matematika I 1 / 212 1. Množiny a zobrazení Funkce jedné proměnné Matematika I 2 / 212 Množiny Definice 1.1.1: Množinou rozumíme soubor prvků se
Matematika I Funkce jedné proměnné Funkce jedné proměnné Matematika I 1 / 212 1. Množiny a zobrazení Funkce jedné proměnné Matematika I 2 / 212 Množiny Definice 1.1.1: Množinou rozumíme soubor prvků se
NMAF 051, ZS Zkoušková písemná práce 17. února ( sin (π 2 arctann) lim + 3. n 2. π 2arctan n. = lim + 3.
 Jednotlivé kroky při výpočtech stručně ale co nejpřesněji odůvodněte. Pokud používáte nějaké tvrzení nezapomeňte ověřit splnění předpokladů. Jméno a příjmení: Skupina: Příklad 3 Celkem bodů Bodů 5 7 0
Jednotlivé kroky při výpočtech stručně ale co nejpřesněji odůvodněte. Pokud používáte nějaké tvrzení nezapomeňte ověřit splnění předpokladů. Jméno a příjmení: Skupina: Příklad 3 Celkem bodů Bodů 5 7 0
, f g jsou elementární funkce.
 Průběh funkce použité definice a věty Definice. Řekneme, že funkce je spojitá na otevřeném intervalu (a, b), jestliže je spojitá v každém vnitřním bodě tohoto intervalu. Řekneme, že funkce je spojitá na
Průběh funkce použité definice a věty Definice. Řekneme, že funkce je spojitá na otevřeném intervalu (a, b), jestliže je spojitá v každém vnitřním bodě tohoto intervalu. Řekneme, že funkce je spojitá na
MATEMATIKA I - vybrané úlohy ze zkoušek v letech
 MATEMATIKA I - vybrané úlohy ze zkoušek v letech 008 0 doplněné o další úlohy. část DIFERENCIÁLNÍ POČET funkcí jedné proměnné Další část ( integrální počet) bude vydána na konci listopadu 9. 9. 0 Případné
MATEMATIKA I - vybrané úlohy ze zkoušek v letech 008 0 doplněné o další úlohy. část DIFERENCIÁLNÍ POČET funkcí jedné proměnné Další část ( integrální počet) bude vydána na konci listopadu 9. 9. 0 Případné
Matematika 5 FSV UK, ZS Miroslav Zelený
 Matematika 5 FSV UK, ZS 2018-19 Miroslav Zelený 1. Stabilita řešení soustav diferenciálních rovnic 2. Úvod do variačního počtu 3. Globální extrémy 4. Teorie optimálního řízení 5. Různé 1. Stabilita řešení
Matematika 5 FSV UK, ZS 2018-19 Miroslav Zelený 1. Stabilita řešení soustav diferenciálních rovnic 2. Úvod do variačního počtu 3. Globální extrémy 4. Teorie optimálního řízení 5. Různé 1. Stabilita řešení
10 Funkce více proměnných
 M. Rokyta, MFF UK: Aplikovaná matematika II kap. 10: Funkce více proměnných 16 10 Funkce více proměnných 10.1 Základní pojmy Definice. Eukleidovskou vzdáleností bodů x = (x 1,...,x n ), y = (y 1,...,y
M. Rokyta, MFF UK: Aplikovaná matematika II kap. 10: Funkce více proměnných 16 10 Funkce více proměnných 10.1 Základní pojmy Definice. Eukleidovskou vzdáleností bodů x = (x 1,...,x n ), y = (y 1,...,y
Univerzita Karlova v Praze Pedagogická fakulta
 Univerzita Karlova v Praze Pedagogická akulta DRUHÁ SEMINÁRNÍ PRÁCE Z DIFERENCIÁLNÍHO POČTU PRŮBĚH FUNKCE 000/001 Cirik, M-ZT Zadání: Vyšetřete průběh unkce ( ) : y Vypracování: ( ) : y Předně určíme deiniční
Univerzita Karlova v Praze Pedagogická akulta DRUHÁ SEMINÁRNÍ PRÁCE Z DIFERENCIÁLNÍHO POČTU PRŮBĚH FUNKCE 000/001 Cirik, M-ZT Zadání: Vyšetřete průběh unkce ( ) : y Vypracování: ( ) : y Předně určíme deiniční
Průběh funkce 1. Průběh funkce. Při vyšetření grafu funkce budeme postupovat podle následujícího algoritmu:
 Průběh funkce Průběh funkce Při vyšetření grafu funkce budeme postupovat podle následujícího algoritmu:. Určení definičního oboru. 2. Rozhodnutí, jestli je funkce sudá, lichá, periodická nebo nemá ani
Průběh funkce Průběh funkce Při vyšetření grafu funkce budeme postupovat podle následujícího algoritmu:. Určení definičního oboru. 2. Rozhodnutí, jestli je funkce sudá, lichá, periodická nebo nemá ani
Kapitola 7: Integrál.
 Kapitola 7: Integrál. Neurčitý integrál. Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f(x) x I nazýváme primitivní funkcí k funkci
Kapitola 7: Integrál. Neurčitý integrál. Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f(x) x I nazýváme primitivní funkcí k funkci
Zimní semestr akademického roku 2015/ ledna 2016
 Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Zimní semestr akademického roku 015/016 5. ledna 016 Obsah Cvičení Předmluva iii
Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Zimní semestr akademického roku 015/016 5. ledna 016 Obsah Cvičení Předmluva iii
IV. Základní pojmy matematické analýzy IV.1. Rozšíření množiny reálných čísel
 Matematická analýza IV. Základní pojmy matematické analýzy IV.1. Rozšíření množiny reálných čísel na množině R je definováno: velikost (absolutní hodnota), uspořádání, aritmetické operace; znázornění:
Matematická analýza IV. Základní pojmy matematické analýzy IV.1. Rozšíření množiny reálných čísel na množině R je definováno: velikost (absolutní hodnota), uspořádání, aritmetické operace; znázornění:
Teorie. Hinty. kunck6am
 kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
Univerzita Karlova v Praze Pedagogická fakulta
 Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z ÚVODU DO MATEMATICKÉ ANLÝZY FUNKCE 999/000 CIFRIK Funkce F a) Zadání: Vyšetřete bez užití limit a derivací funkci : y = { x } f Definice:
Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z ÚVODU DO MATEMATICKÉ ANLÝZY FUNKCE 999/000 CIFRIK Funkce F a) Zadání: Vyšetřete bez užití limit a derivací funkci : y = { x } f Definice:
10. cvičení - LS 2017
 10. cvičení - LS 2017 Michal Outrata Příklad 1 Spočtěte následující itu daných posloupností: (a) (b) (c) n 3 +5n 2 n 3 6n 2 +3 n ; n 4 3n 2 6 n 4 + 3n 2 + 6; n 2 15n+2(1 n). 2(n 2) 3 2n 3 Příklad 2 Pro
10. cvičení - LS 2017 Michal Outrata Příklad 1 Spočtěte následující itu daných posloupností: (a) (b) (c) n 3 +5n 2 n 3 6n 2 +3 n ; n 4 3n 2 6 n 4 + 3n 2 + 6; n 2 15n+2(1 n). 2(n 2) 3 2n 3 Příklad 2 Pro
MATEMATIKA I Požadavky ke zkoušce pro 1. ročník, skupina A 2017/18
 MATEMATIKA I Požadavky ke zkoušce pro 1. ročník, skupina A 2017/18 I. Základy, lineární algebra a analytická geometrie 1. Základní pojmy (a) Základy teorie množin: množina a její prvky, podmnožina, průnik,
MATEMATIKA I Požadavky ke zkoušce pro 1. ročník, skupina A 2017/18 I. Základy, lineární algebra a analytická geometrie 1. Základní pojmy (a) Základy teorie množin: množina a její prvky, podmnožina, průnik,
MATEMATIKA I. prof. RNDr. Gejza Dohnal, CSc. II. Základy matematické analýzy
 MATEMATIKA I. prof. RNDr. Gejza Dohnal, CSc. II. Základy matematické analýzy 1 Matematika I. I. Lineární algebra II. Základy matematické analýzy III. Diferenciální počet IV. Integrální počet 2 Matematika
MATEMATIKA I. prof. RNDr. Gejza Dohnal, CSc. II. Základy matematické analýzy 1 Matematika I. I. Lineární algebra II. Základy matematické analýzy III. Diferenciální počet IV. Integrální počet 2 Matematika
Stručný přehled učiva
 Stručný přehled učiva TU1M2 Matematika 2 pro LP17, LP18 4. Aplikace diferenciálního počtu 4.1 Rovnice tečny a normály Má-li funkce v bodě vlastní derivaci, pak je to směrnice tečny grafu funkce v tečném
Stručný přehled učiva TU1M2 Matematika 2 pro LP17, LP18 4. Aplikace diferenciálního počtu 4.1 Rovnice tečny a normály Má-li funkce v bodě vlastní derivaci, pak je to směrnice tečny grafu funkce v tečném
Matematika V. Dynamická optimalizace
 Matematika V. Dynamická optimalizace Obsah Kapitola 1. Variační počet 1.1. Derivace funkcí na vektorových prostorech...str. 3 1.2. Derivace integrálu...str. 5 1.3. Formulace základní úlohy P1 var. počtu,
Matematika V. Dynamická optimalizace Obsah Kapitola 1. Variační počet 1.1. Derivace funkcí na vektorových prostorech...str. 3 1.2. Derivace integrálu...str. 5 1.3. Formulace základní úlohy P1 var. počtu,
Derivace vyšších řádů, aplikace derivací
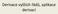 Derivace vyšších řádů, aplikace derivací Značení derivací vyšších řádů Máme funkci f: y = f x f x druhá derivace funkce y = f x f k x k-tá derivace funkce y = f x Derivace vyšších řádů počítáme opakovaným
Derivace vyšších řádů, aplikace derivací Značení derivací vyšších řádů Máme funkci f: y = f x f x druhá derivace funkce y = f x f k x k-tá derivace funkce y = f x Derivace vyšších řádů počítáme opakovaným
fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu (reg. č. CZ.1.07/2.2.00/28.
 Extrémy Vyšší matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu http://akademie.ldf.mendelu.cz/cz
Extrémy Vyšší matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu http://akademie.ldf.mendelu.cz/cz
Úvodní informace. 17. února 2018
 Úvodní informace Funkce více proměnných Přednáška první 17. února 2018 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Limita a spojitost Derivace, diferencovatelnost, diferenciál Úvodní
Úvodní informace Funkce více proměnných Přednáška první 17. února 2018 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Limita a spojitost Derivace, diferencovatelnost, diferenciál Úvodní
Cyklometrické funkce
 Cyklometrické funkce Definice. Cyklometrické funkce jsou funkce arcsin(x) (čteme arkussinus x), arccos(x) (čteme arkuskosinus x), arctg(x) (čteme arkustangens x) a arccotg(x) (čteme arkuskotangens x),
Cyklometrické funkce Definice. Cyklometrické funkce jsou funkce arcsin(x) (čteme arkussinus x), arccos(x) (čteme arkuskosinus x), arctg(x) (čteme arkustangens x) a arccotg(x) (čteme arkuskotangens x),
Integrální počet funkcí jedné proměnné
 Integrální počet funkcí jedné proměnné Neurčité integrály Určité a nevlastní integrály Geometrické aplikace určitého integrálu. p.1/?? Neurčité integrály Příklad 7.1.1 Vhodnou metodou vypočítejte neurčitý
Integrální počet funkcí jedné proměnné Neurčité integrály Určité a nevlastní integrály Geometrické aplikace určitého integrálu. p.1/?? Neurčité integrály Příklad 7.1.1 Vhodnou metodou vypočítejte neurčitý
Vzdělávací materiál. vytvořený v projektu OP VK CZ.1.07/1.5.00/ Anotace. Diferenciální počet VY_32_INOVACE_M0216.
 Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek
Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek
