Matematika 2 Průběh funkce
|
|
|
- Daniela Vítková
- před 6 lety
- Počet zobrazení:
Transkript
1 Matematika 2 Průběh funkce Jiří Fišer KMA, PřF UP Olomouc ZS09 Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 1 / 1
2 Základní věty diferenciálního počtu Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 2 / 1
3 Úvod Věta (Fermatova) - f je definována na M - a nabývá v některém vnitřním bodě x 0 M své největší nebo nejmenší hodnoty. Má-li f v bodě x 0 derivaci, pak f (x 0 )=0. Princip důkazu pro největší hodnotu - Sledujeme znaménko podílu d(x)= f(x) f(x 0) x x 0 - v levém okolí bodu x 0 : d(x) 0 - v pravém okolí bodu x 0 : d(x) 0 Z toho pak plyne f (x 0 )= lim x x0 d(x)=0. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 3 / 1
4 Úvod Fermatovu větu lze vztáhnout na lokální extrém a jeho okolí, má tedy lokální charakter a lze ji formulovat takto: má-li funkce f v bodě x 0 lokální extrém a má v něm derivaci, pak se tato derivace rovná nule. Věta Nutnou podmínkou existence lokálního extrému funkce f v bodě x 0 je, že v něm derivace f (x 0 ) bud neexistuje nebo je rovna nule. Pro diferencovatelnou funkci f je nutnou podmínkou rovnost f (x 0 )=0. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 4 / 1
5 Věty o střední hodnotě Tři věty, Rolleova, Lagrangeova, Cauchyova, jsou obvykle nazývány větami o střední hodnotě diferenciálního počtu. Všechny tři věty o střední hodnotě jsou navzájem ekvivalentní. Jádrem je věta Lagrangeova. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 5 / 1
6 Věty o střední hodnotě Věta (Lagrangeova) Necht funkce f 1) je spojitá na intervalu a, b, 2) má derivaci na intervalu(a, b), Pak existuje bod ξ (a, b) tak, že platí f(b) f(a) b a = f (ξ). Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 6 / 1
7 Věty o střední hodnotě Lagrangeova věta se používá v různých tvarech; některé uvedeme. a=x 0, b=x 0 + x : Pak existuje θ (0, 1) ; f(x 0 + x)=f(x 0 )+f (x 0 + θ x) x. x= x 0 + x : f(x)=f(x 0 )+f (x 0 + θ(x x 0 )) (x x 0 ). Jiný zápis: y= f (x 0 + θ x) x, ukazuje, proč se Lagrangeově větě říká též věta o přírůstku funkce. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 7 / 1
8 Některé důsledky vět o střední hodnotě Nejprve uvedeme dva typické důsledky vět o střední hodnotě; na jednom je založen pojem neurčitého integrálu, druhý umožňuje jednoduchý výpočet limit funkcí. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 8 / 1
9 Některé důsledky vět o střední hodnotě Věta (o konstantní funkci) Funkce f je na intervalu(a, b) konstantní má na(a, b) derivaci a x (a, b) platí f (x)=0. Důsledek Mají-li dvě funkce f, g na(a, b) stejné derivace, tj. f (x)=g (x), pak se na tomto intervalu liší jen o konstantu, tj. C R tak, že na(a, b) je f(x)=g(x)+c. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 9 / 1
10 Některé důsledky vět o střední hodnotě [ ] 0 Následující věta se týká výpočtu limit typu. Podobné tvrzení lze [ 0 vyslovit i pro limity typu a obě pak použít k výpočtu několika ] dalších typů limit. Věta (L Hospitalovo pravidlo) Necht 1) funkce f, g mají derivace v P(a), kde a R, 2) lim x a f(x)=0, lim g(x)=0, x a 3) existuje vlastní nebo nevlastní lim x a f (x) g (x) = K. Pak existuje i f(x) lim x a g(x) a rovná se K. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 10 / 1
11 L Hospitalovo pravidlo Úloha arctg(x 2) Vypočtěte lim x 2 x 2. 4 [ 1 4] Úloha ln x Vypočtěte lim x 1 x 1. [1] Úloha Vypočtěte lim x + 6x 2 + 5x+ 4 3x 3 + 2x [2] Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 11 / 1
12 L Hospitalovo pravidlo L Hospitalovo pravidlo platí i pro jednostranné limity. Úloha ln x Vypočtěte lim x 0+ cotg x. [0] Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 12 / 1
13 L Hospitalovo pravidlo L Hospitalovo pravidlo neplatí naopak a to v tomto smyslu: z existence limity podílu funkcí neplyne existence limity podílu jejich derivací nebo, což je totéž, z neexistence limity podílu derivací ještě neplyne neexistence limity podílu funkcí. sin x Například lim = 1. x 0 x Někdy je potřebné použít l Hospitalovo pravidlo i vícekrát, případně provádět při výpočtu úpravy, které postup zjednoduší. Úloha 1 cos 3x Vypočtěte lim x 0 sin 2 x. [ ] 9 2 Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 13 / 1
14 L Hospitalovo pravidlo Při výpočtu limit typu součin funkcí na podíl f 1 g [0 ] součinu funkcí f g upravíme nebo naopak g 1 f tak, aby to bylo vhodné pro použití l Hospitalova pravidla tedy například funkci logaritmickou je zpravidla nejvhodnější nechat v čitateli. Úloha Vypočtěte lim x ln x. [0] x 0+ Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 14 / 1
15 L Hospitalovo pravidlo Počítáme-li limitu typu[ ] rozdílu funkcí f g, upravíme rozdíl funkcí na podíl: f g= g = 1 f f g fg Úloha Vypočtěte lim (cotg 2 x 1x ) x 0 2. Řešení. 2 ; před použitím l Hospitalova pravidla nejprve získaný zlomek 3 vhodně rozložíme na součin funkcí. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 15 / 1
16 L Hospitalovo pravidlo U limit typu pro funkce [0 0 ],[ 0 ] a[1 ] f g postupujeme tak, že tuto funkci nejprve upravíme na tvar e g ln f(x), limitu přeneseme do exponentu (podle věty o limitě složené funkce) a v exponentu dostaneme limitu typu [0 ]. Úloha Vypočtěte lim x 0+ xsin x. [1] Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 16 / 1
17 Užití diferenciálního počtu Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 17 / 1
18 Monotónnost funkce Věta Při vyšetřování průběhu funkce se také zjišt uje, zda je daná funkce v některém intervalu nebo bodě monotónní. Zjišt ování monotónnosti funkce pomocí derivace funkce. Jestliže existuje okolí U(x 0 ) D(f) a f (x 0 ) > 0, pak f je rostoucí v bodě x 0. Princip důkazu. f (x 0 ) > 0 = v jistém okolí U(x 0 ) je také f(x) f(x 0 ) x x 0 > 0. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 18 / 1
19 Obrázek: Grafy funkcí rostoucích v bodě 0: y= x 3 a y= 2x+ x. Tato věta vyjadřuje jen postačující podmínku, neplatí obráceně. Funkce rostoucí v bodě může mít i nulovou derivaci nebo derivaci nemít (viz obr.). Podobné výsledky platí i pro funkce klesající v bodě a pro zápornou derivaci. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 19 / 1
20 Stacionární bod funkce x 0 je stacionárním bodem funkce f f (x 0 )=0. Ve stacionárním bodě může být funkce rostoucí, klesající nebo v něm nemusí být monotónní. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 20 / 1
21 Věta (o monotónnosti na intervalu) Má-li funkce f derivaci na(a, b), pak platí: 1) Funkce f je na(a, b): neklesající x (a, b) je f (x) 0, nerostoucí x (a, b) je f (x) 0. 2) Funkce f je na(a, b): rostoucí x (a, b) je f (x) 0, klesající x (a, b) je f (x) 0, přičemž neexistuje (α, β) (a, b); x (α, β) f (x)=0. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 21 / 1
22 Úloha Vyšetřete intervaly monotónnosti funkce f: y= x 2 e x. Řešení. D(f)=R. y =(2x x 2 ) e x = x(2 x) e x. intervaly: (1)(, 0 : y 0 (nulová v jediném bodě) = f je klesající, (2) 0, 2 : y 0 (nulová ve dvou bodech) = f je rostoucí, (3) 2,+ ): y 0 (nulová v jediném bodě) = f je klesající. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 22 / 1
23 Obrázek: Grafy funkcí y= x 2 e x a y = x(2 x) e x z úlohy. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 23 / 1
24 Lokální extrémy Řekneme, že funkce f má v bodě x 0 lokální minimum: U(x 0 ), x U(x 0 ): f(x) f(x 0 ), lokální maximum: U(x 0 ), x U(x 0 ): f(x) f(x 0 ). ostré lokální minimum: P(x 0 ), x P(x 0 ): f(x) > f(x 0 ), ostré lokání maximum: P(x 0 ), x P(x 0 ): f(x) < f(x 0 ). Má-li funkce f v bodě x 0 lokální minimum, resp. lokální maximum, říkáme, že f má v bodě x 0 LOKÁLNÍ EXTRÉM. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 24 / 1
25 Nutná podmínka existence lokálního extrému: Má-li funkce f v bodě x 0 lokální extrém a existuje-li f (x 0 ), pak f (x 0 )=0. Funkce tedy může mít extrém jen ve stacionárním bodě nebo v bodě, v němž nemá derivaci (jako tomu je např. u funkce y= x ). Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 25 / 1
26 Postup při určování lokálních extrémů Najdeme body, v nichž může nastat extrém, tj. body, v nichž je derivace funkce rovna nule (body stacionární) nebo v nichž derivace neexistuje; označíme x 0. Další možný postup: (1) Užití monotónnosti v okolí bodu x 0 (2) Užití 1. derivace v okolí bodu x 0 (3) Užití 2. derivace v bodě x 0 Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 26 / 1
27 (1) Užití monotónnosti v okolí bodu x 0 Necht f je spojitá v x 0 a existuje okolí U(x 0 ) D(f). Je-li f rostoucí v P(x 0 ) a klesající v P(x 0 +), má funkce f v bodě x 0 (ostré) lokální maximum. Podobně lze formulovat další případy: - ostré lokální minimum, - neostré extrémy - a případ, kdy extrém neexistuje. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 27 / 1
28 (2) Užití 1. derivace v okolí bodu x 0 f je spojitá v x 0 a existuje okolí P(x 0 ) D(f), v němž má funkce f derivaci. Je-li f (x) > 0 v P(x 0 ) a f (x) < 0 v P(x 0 +), má funkce f v bodě x 0 (ostré) lokální maximum. Podobně lze formulovat další případy. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 28 / 1
29 (3) Užití 2. derivace v bodě x 0 f má derivaci v nějakém okolí U(x 0 ) D(f) a existuje f (x 0 ). Je-li f (x 0 ) < 0, má funkce f v bodě x 0 (ostré) lokální maximum, je-li f (x 0 ) > 0, má funkce f v bodě x 0 (ostré) lokální minimum. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 29 / 1
30 Úloha Zjistěte extrém funkce f: y= x e x. Řešení. y =(1 x) e x y = 0 pro x 0 = 1. y =(x 2) e x. y (1)= e 1 < 0 = f má v bodě 1 lokální maximum. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 30 / 1
31 Obrázek: Graf funkce y= x e x s lokálním maximem v bodě 1. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 31 / 1
32 Pozor: f (x 0 )=0neznamená neexistenci extrému. Jestliže funkce f má derivace v U(x 0 ) a platí(n > 1) f (x 0 )=f (x 0 )= =f (n 1) (x 0 )=0, f (n) (x 0 ) 0, pak (1) pro n sudé existuje v bodě x 0 extrém: lokální maximum pro f (n) (x 0 ) < 0, lokální minimum pro f (n) (x 0 ) > 0. (2) pro n liché lokální extrém v bodě x 0 neexistuje. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 32 / 1
33 Úloha Vyšetřete extrém funkce f: y= x 5. Řešení. Máme y = 5x 4, stacionární bod 0. y = 20x 3, y (0)=0, y = 60x 2, y (0)=0, y (4) = 120x, y (4) (0)=0, y (5) = 120 > 0. První nenulová derivace je lichého řádu, tedy extrém neexistuje. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 33 / 1
34 Obrázek: Graf funkce y= x 5 bez lokálního extrému v bodě 0. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 34 / 1
35 Největší a nejmenší hodnota funkce na intervalu Mějme funkci f definovanou a spojitou na a, b. Podle 2.Weierstrassovy věty nabývá funkce f - v některém bodě c 1 své největší hodnoty - a v některém bodě c 2 své nejmenší hodnoty. Jiné názvy: absolutní extrémy, globální extrémy. Každý z bodů c 1, c 2 přitom může být vnitřním nebo krajním bodem intervalu a, b. Pokud je c i vnitřním bodem, je to současně bod, v němž nastává lokání extrém, - tedy stacionární bod - nebo bod, v němž neexistuje derivace. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 35 / 1
36 Postup při určování největší a nejmenší hodnoty funkce na uzavřeném intervalu a, b (1) Určíme všechny stacionární body a body, v nichž neexistuje derivace a vypočteme v nich funkční hodnoty. (2) Vypočteme funkční hodnoty v bodech a, b. (3) Maximum množiny všech těchto hodnot funkce z (1) a (2) je největší hodnotou funkce na a, b, (4) minimum množiny všech těchto hodnot funkce z (1) a (2) je nejmenší hodnotou funkce na a, b. Tedy: není třeba určovat lokální extrémy. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 36 / 1
37 Úloha Máme určit největší a nejmenší hodnotu funkce f: y= x 3 3x+ 1 na intervalu 0, 2. Řešení. y = 3x 2 3; f má na 0, 2 jediný stacionární bod 1. - f(1)= 1 - f(0)=1, - f(2)=3. Funkce f tedy nabývá největší hodnoty 3 v bodě 2 a nejmenší hodnoty 1 v bodě 1. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 37 / 1
38 Obrázek: Globální extrémy funkce y= x 3 3x+ 1 na intervalu 0, 2. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 38 / 1
39 Konvexnost a konkávnost Věta (1.věta o konvexnosti a konkávnosti) Necht funkce f má na intervalu(a, b) derivaci f. Pak funkce f je na(a, b) konvexní (konkávní) je f na(a, b) rostoucí (klesající) Obrázek: Graf funkce y= x 3 a její první derivace y= 3x 2. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 39 / 1
40 Konvexnost a konkávnost Na funkci f lze nyní použít větu o monotónnosti na intervalu: Věta (2. věta o konvexnosti a konkávnosti) Má-li funkce f druhou derivaci na(a, b), pak tato funkce je na(a, b) konvexní x (a, b) je f (x) 0 ( ) f (x) 0, ( ) konkávní přičemž neexistuje interval (α, β) (a, b) tak, aby x (α, β) bylo f (x)=0. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 40 / 1
41 Inflexe a inflexní body Definice Říkáme, že funkce f má v bodě x 0 inflexi má derivaci f (x 0 ) a je ( ) - v levém okolí U(x 0 ) konvexní konkávní ( ) - a v pravém okolí U(x 0 +) konkávní konvexní. Bod [x 0, f(x 0 )] roviny se nazývá inflexní bod funkce f, resp. grafu funkce f. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 41 / 1
42 Inflexe a inflexní body Obrázek: Graf funkce y= x 3, inflexního bodu(0; 0) a inflexní tečny y 0. V inflexním bodě přechází funkce z konvexního průběhu na konkávní nebo naopak. Inflexní tečna v bodě dotyku graf přechází z jedné poloroviny do druhé. Např. osa x je inflexní tečnou ke grafu funkce y= x 3. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 42 / 1
43 Věta (vztah inflexe a derivace) Má-li funkce f v nějakém okolí U(x 0 ) derivaci f, pak má v bodě x 0 inflexi má f v bodě x 0 lokální extrém. Věta (nutná podmínka existence inflexe) Má-li funkce f v bodě x 0 inflexi a existuje f (x 0 ), je f (x 0 )=0. Důkaz plyne z nutné podmínky existence extrému funkce f. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 43 / 1
44 Vztah inflexe a derivace lze dalšími větami specifikovat pro případ existence druhé resp. i třetí derivace. Věta ((vztah inflexe a druhé derivace) Má-li funkce f v nějakém okolí bodu x 0 derivaci f a má-li tato derivace v P(x 0 ) a P(x 0 +) různá znaménka, má funkce f v bodě x 0 inflexi. Má-li f stejné znaménko v P(x 0 ) a P(x 0 +), pak funkce f v bodě x 0 inflexi nemá. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 44 / 1
45 Věta (vztah inflexe a 3. derivace) Má-li funkce f v nějakém okolí bodu x 0 derivaci f, platí f (x 0 )=0af (x 0 ) 0, pak funkce f má v bodě x 0 inflexi. Tuto větu bychom mohli rozšířit (podobně jako odpovídající pravidlo pro určování lokálního extrému) i na případ, kdy f (x 0 )=f (x 0 )= =f (k 1) (x 0 )=0, f (k) (x 0 ) 0. Pro k liché existuje v bodě x 0 inflexe, pro k sudé nikoli. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 45 / 1
46 Úloha Stanovte konvexnost, konkávnost a inflexi funkce y= x e x. Řešení. Tato funkce má potřebné derivace, vypočteme: y =(1 x) e x, y =(x 2) e x, kde e x > 0. Pro x < 2 je y < 0, funkce je konkávní, pro x > 2 je y > 0, funkce je konvexní. Pro x= 2 má funkce inflexi, inflexní bod je[2; 2 e 2 ]. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 46 / 1
47 Obrázek: Graf funkce y= x e x s inflexním bodem[2; 2 e 2 ]. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 47 / 1
48 Asymptoty Asymptoty jsou přímky, - představujeme si je jako tečny ke grafu funkce v nekonečnu. - Souřadnicové osy jsou asymptotami grafu funkce y = 1/x. Definujeme asymptoty dvou druhů (avšak z geometrického hlediska jde o tentýž jev). Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 48 / 1
49 Asymptoty Obrázek: Asymptoty y= 0 a x= 0 grafu funkce y= 1 x. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 49 / 1
50 Asymptoty Definice Přímka x = c se nazývá vertikální asymptota grafu funkce f funkce f má v bodě c alespoň jednu jednostrannou limitu nevlastní. Definice I nekonečně mnoho: tangens. Kromě toho nejvýše dvě asymptoty s rovnicemi tvaru y= kx+ q. Přímka y = kx + q se nazývá asymptota (se směrnicí) grafu funkce f pro x nebo pro x + je lim[f(x) (kx+ q)]=0. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 50 / 1
51 Asymptoty se směrnicí Věta (o výpočtu asymptot) Přímka y = kx + q je asymptotou grafu funkce f existují limity (pro x nebo pro x + ) lim f(x) x = k a lim[f(x) kx]=q. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 51 / 1
52 Praktický postup v běžných případech 1) Vyšetříme okolí těch hromadných bodů D(f), které leží v R D(f) - (body nespojitosti - zejména izolované body množiny R D(f) nebo krajní body intervalů, jež jsou součástí D(f)). - Zjistíme ve kterém z těchto bodů existují alespoň jednostranné nevlastní limity. 2) Je-li+ nebo hromadným bodem D(f), hledáme lim f(x) x. - Jestliže tato limita (nebo obě) existuje, je to směrnice k asymptot, pokud asymptoty existují. - Dále ještě hledáme lim[f(x) kx] s oním k, jež bylo vypočteno v předchozí limitě. - Existuje-li tato limita, je to q a asymptota existuje. Při výpočtu k= lim f(x) x lze použít l Hospitalova pravidla, z něhož k= lim f (x). Také tento vztah se často využívá k výpočtu směrnice asymptot (ovšem neexistuje-li lim f (x), neznamená to neexistenci asymptot). Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 52 / 1
53 Úloha Určete asymptoty pro funkci y= x + arctg x. 2 Řešení. ( f(x) 1 k= lim = lim x ± x x ± 2 + arctg x ) = 1 x 2. ( x Dále q= lim x ± 2 + arctg x 1 ) 2 x = ± π 2 Existují tedy 2 asymptoty: y= x 2 π 2 y= x 2 + π 2 pro x a pro x +. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 53 / 1
54 Obrázek: Asymptoty y= x 2 π 2 a y=x 2 + π 2 grafu funkce y=x + arctg x. 2 Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 54 / 1
55 Úloha Určete asymptoty pro funkci y= x+ x. Řešení. Zde je nevlastním hromadným bodem D(f) jen+. Počítáme asymptota neexistuje. f(x) k= lim x + x q= lim x + = 1+ lim x + x x = 1, ( x+ x x ) =+, Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 55 / 1
56 Obrázek: Graf funkce y= x+ x je bez asymptot. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 56 / 1
57 Průběh funkce O vyšetřování průběhu funkce lze pojednat dvěma způsoby: uvést věcně, ze kterých činností se vyšetřování průběhu funkce skládá, popsat praktický postup při vyšetřování průběhu funkce. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 57 / 1
58 Věcný výčet činností při vyšetřování PF 1) Definiční obor, body nespojitosti. 2) Funkční obor, omezenost; nulové body funkce; intervaly, kde je funkce kladná, kde je záporná. 3) Funkční vlastnosti funkce: parita, periodičnost. 4) Limity (jednostranné) v bodech nespojitosti funkce, v krajních bodech definičního oboru, resp. v, +. 5) Intervaly monotonnosti (kde funkce roste, kde klesá) nebo konstantnosti. 6) Lokální extrémy funkce. 7) Intervaly konvexnosti a konkávnosti. 8) Inflexe, inflexní body grafu funkce. 9) Asymptoty grafu funkce. 10) Sestrojení grafu funkce. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 58 / 1
59 Praktický postup při vyšetřování PF V běžném případě sleduje i myšlenku správného a přehledného záznamu výsledků a mezivýsledků do tabulky: A. Zjistíme údaje potřebné pro sestavení tabulky, sestavíme tabulku a zaznamenáme do ní dosud známé údaje o funkci, B. postupně zjišt ujeme další vlastnosti funkce a zaznamenáváme je do tabulky, C. doplníme údaje potřebné pro sestrojení grafu a sestrojíme graf funkce. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 59 / 1
60 Doporučené pořadí prací u bodu A. A1. Provedeme 1 (určíme D(f) a body nespojitosti). A2. Provedeme 3 (stanovení parity a periodičnosti), tj. zjistíme, zda bychom mohli zmenšit rozsah vyšetřování funkce tím, že se omezíme např. jen na interval 0,+ ) nebo jen na jednu periodu u funkce periodické. A3. Vypočteme 1.derivaci, položíme ji rovnu 0 a řešením získáme stacionární body. K nim přidáme ty body z D(f), v nichž 1. derivace neexistuje. Má-li funkce lokální extrém, pak nastane v některém z těchto bodů. A4. Vypočteme 2. derivaci, položíme ji rovnu 0 a řešením získáme body, v nichž může mít funkce inflexi. K nim přidáme ty body z D(f ), v nichž 2. derivace neexistuje. A5. Sestavíme tabulku, kde v horizontálním záhlaví zaznamenáme rozčlenění číselné osy s ohledem na A1, A2, A3, A4; ve vertikálním záhlaví jsou řádky pro x, y, y, y, a pro záznam vlastností funkce f. Do tabulky přeneseme údaje již zjištěné. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 60 / 1
61 Doporučené pořadí prací u bodu B. B1. Užitím znaménka 1. derivace určíme 5 (intervaly monotonnosti). B2. Na základě B1 zjistíme 6 (lokální extrémy), včetně funkčních hodnot v těchto bodech. B3. Užitím znaménka 2. derivace určíme 7 (konvexnost a konkávnost). B4. Na základě B3 zjistíme 8 (inflexi), včetně funkčních hodnot v těchto bodech a hodnot 1. derivací. B5. Určíme 9 (asymptoty). B6. Určíme 4 (limity), pokud je to po B5 ještě třeba. B7. Určíme 2 (funkční obor, nulové body, znaménka funkce). Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 61 / 1
62 Doporučené pořadí prací u bodu C. C1. Podle potřeby doplníme např. průsečík grafu funkce s osou y, hodnoty funkce v dalších bodech D(f), případně i hodnoty derivací (připojíme k tabulce jako dodatek). C2. Provedeme bod 10 (sestrojíme graf funkce). Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 62 / 1
63 Úloha Sestavte tabulku pro vyšetření průběhu funkce y=x+ 1 x. Řešení. D(f)=(, 0) (0,+ ), lichá, graf souměrný podle počátku. y = 1 1 ; y = 0 x { 1; 1} (stacionární body); y = 2 0. x 2 x 3 Sestavíme tabulku (např. jen) pro interval 0, + ). x (0, 1) 1 (1, + ) + y n.d y n.d. < 0 0 > 0 + y n.d. > 0 > 0 > 0 n.d. + klesá lok.min. roste + fce asymptota asymptota x=0 konvexní y= x Inflexní body neexistují. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 63 / 1
64 Obrázek: Graf funkce y= x+ 1, vertikální asymptota x= 0 a asymptota se x směrnicí y= x. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 64 / 1
65 Užití extrémů funkcí Na výpočet extrémů vede řada praktických úloh. Úloha Ze čtvercového listu papíru o straně a čtverečků (o straně x objemu. má být po vystřižení ) v rozích složena krabice o maximálním Vypočtěte stranu čtverečků, jež mají být v rozích vystřiženy a rozměry výsledné krabice. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 65 / 1
66 x= 1 6 a a a 2 3 a Obrázek: Budoucí krabice o maximálním objemu Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 66 / 1
67 Řešení. Výsledná krabice má rozměry (a 2x) (a 2x) x. Její objem je tedy: V=(a 2x) 2 x, x ( 0; a ) 2 V = 12x 2 8ax+ a 2 = 0 = x 1 = a 6, x 2= a 2 (x 2 nevyhovuje praktické úloze); rozměry krabice jsou 2 3 a 2 3 a 1 6 a, výška je rovna čtvrtině šířky čtvercového dna. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 67 / 1
68 Užití extrémů funkcí Úloha Pracoviště je v konstantní vzdálenosti a od průmětu světla na vodorovnou rovinu. Při jaké výšce h světla je osvětlení pracoviště maximální? Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 68 / 1
69 r h ϕ a Obrázek: Intenzita osvětlení Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 69 / 1
70 Řešení. Intenzita osvětlení závisí na vstupních podmínkách takto: kde sin ϕ= h r takže I= I(h); po dosazení I= c sinϕ r 2, a r= h I= c( h 2 + a 2). 3 2 h 2 + a 2, I = c a2 2h 2 ( h 2 + a 2) (= 0) = h= a 0, 7a Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 70 / 1
71 Užití extrémů funkcí Úloha Výkon Peltonova kola je P= k u (v u), kde u je obvodová rychlost Peltonova kola a v je rychlost vodního paprsku. Při jaké rychlosti u je výkon Peltonovy turbiny maximální? Řešení. P= P(u), P = kv 2ku(= 0) = u= v 2. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 71 / 1
72 Užití extrémů funkcí Obrázek: Příliš mnoho plechu. Úloha Určete rozměry konzerv tvaru rotačního válce o daném objemu V tak, aby se při jejich výrobě spotřebovalo co nejmenší množství plechu. Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 72 / 1
73 Řešení. Hledá se minimum funkce x je poloměr dna konzervy a v výška konzervy, S= 2πxv+ 2πx2, kde za podmínky, že V= πx 2 v je zadané (tedy konstantní). Po dosazení za v z této podmínky (v= V πx 2 ) máme S= 2V x + 2πx2, odkud S = 2V x 2 + 4πx. Z rovnice S = 0 máme x 0 = 3 V 2π. v 0 = V V πx0 2 = =2 3 2π = 2x 0 Odsud je rovna průměru dna. : výška konzervy je Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 73 / 1
7) Intervaly konvexnosti a konkávnosti. 8) Inflexe, inflexní body grafu funkce. 9) Asymptoty grafu funkce. 10) Sestrojení grafu funkce.
 Přednáška č. 12 Vyšetřování průběhu funkce a užití extrémů funkcí Jiří Fišer 11. prosince 2009 Jiří Fišer (KMA, PřF UP Olomouc) KMA MMAN1 Přednáška č. 12 11. prosince 2009 1 / 18 Průběh funkce O vyšetřování
Přednáška č. 12 Vyšetřování průběhu funkce a užití extrémů funkcí Jiří Fišer 11. prosince 2009 Jiří Fišer (KMA, PřF UP Olomouc) KMA MMAN1 Přednáška č. 12 11. prosince 2009 1 / 18 Průběh funkce O vyšetřování
IX. Vyšetřování průběhu funkce
 IX. Vyšetřování průběhu funkce Úvodní poznámky: Cíl: vyšetřit průběh dané funkce f. Zahrnuje: základní vlastnosti: D(f), spojitost, limity v krajních bodech, průsečíky s osami souřadnic, intervaly, kde
IX. Vyšetřování průběhu funkce Úvodní poznámky: Cíl: vyšetřit průběh dané funkce f. Zahrnuje: základní vlastnosti: D(f), spojitost, limity v krajních bodech, průsečíky s osami souřadnic, intervaly, kde
Diferenciální počet - II. část (Taylorův polynom, L Hospitalovo pravidlo, extrémy
 Diferenciální počet - II. část (Taylorův polynom, L Hospitalovo pravidlo, extrémy funkcí, průběh funkce) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 5. přednáška z AMA1 Michal Fusek (fusekmi@feec.vutbr.cz)
Diferenciální počet - II. část (Taylorův polynom, L Hospitalovo pravidlo, extrémy funkcí, průběh funkce) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 5. přednáška z AMA1 Michal Fusek (fusekmi@feec.vutbr.cz)
Diferenciální počet funkcí jedné proměnné
 Diferenciální počet funkcí jedné proměnné 1 4. Derivace funkce 4.3. Průběh funkce 2 Pro přesné určení průběhu grafu funkce je třeba určit bližší vlastnosti funkce. Monotónnost funkce Funkce monotónní =
Diferenciální počet funkcí jedné proměnné 1 4. Derivace funkce 4.3. Průběh funkce 2 Pro přesné určení průběhu grafu funkce je třeba určit bližší vlastnosti funkce. Monotónnost funkce Funkce monotónní =
Diferenciál funkce. L Hospitalovo pravidlo. 22. a 23. března 2011
 Diferenciál funkce Derivace vyšších řádů L Hospitalovo pravidlo Jiří Fišer 22. a 23. března 2011 Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT2 Přednáška č. 6 22. a 23. března 2011 1 / 18 y ω(h) dy O x Obrázek:
Diferenciál funkce Derivace vyšších řádů L Hospitalovo pravidlo Jiří Fišer 22. a 23. března 2011 Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT2 Přednáška č. 6 22. a 23. března 2011 1 / 18 y ω(h) dy O x Obrázek:
Stručný přehled učiva
 Stručný přehled učiva TU1M2 Matematika 2 pro LP17, LP18 4. Aplikace diferenciálního počtu 4.1 Rovnice tečny a normály Má-li funkce v bodě vlastní derivaci, pak je to směrnice tečny grafu funkce v tečném
Stručný přehled učiva TU1M2 Matematika 2 pro LP17, LP18 4. Aplikace diferenciálního počtu 4.1 Rovnice tečny a normály Má-li funkce v bodě vlastní derivaci, pak je to směrnice tečny grafu funkce v tečném
Funkce jedn e re aln e promˇ enn e Derivace Pˇredn aˇska ˇr ıjna 2015
 Funkce jedné reálné proměnné Derivace Přednáška 2 15. října 2015 Obsah 1 Funkce 2 Limita a spojitost funkce 3 Derivace 4 Průběh funkce Informace Literatura v elektronické verzi (odkazy ze STAGu): 1 Lineární
Funkce jedné reálné proměnné Derivace Přednáška 2 15. října 2015 Obsah 1 Funkce 2 Limita a spojitost funkce 3 Derivace 4 Průběh funkce Informace Literatura v elektronické verzi (odkazy ze STAGu): 1 Lineární
Kapitola 4: Průběh funkce 1/11
 Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
7.1 Extrémy a monotonie
 KAPITOLA 7: Průběh funkce [ZMA13-P38] 7.1 Extrémy a monotonie Řekneme, že funkce f nabývá na množině M Df svého globálního maxima globálního minima A v bodě x 0, jestliže x 0 M, fx 0 = A a pro každé x
KAPITOLA 7: Průběh funkce [ZMA13-P38] 7.1 Extrémy a monotonie Řekneme, že funkce f nabývá na množině M Df svého globálního maxima globálního minima A v bodě x 0, jestliže x 0 M, fx 0 = A a pro každé x
Kapitola 4: Průběh funkce 1/11
 Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
LDF MENDELU. Simona Fišnarová (MENDELU) Průběh funkce ZVMT lesnictví 1 / 21
 Průběh funkce Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Průběh funkce Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Zlín, 23. října 2011
 (. -. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 3. října 0 Postup při vyšetřování průběhu funkce. Definiční obor funkce,
(. -. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 3. října 0 Postup při vyšetřování průběhu funkce. Definiční obor funkce,
Aplikace derivace a průběh funkce
 Aplikace derivace a průběh funkce Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného
Aplikace derivace a průběh funkce Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného
Derivace a monotónnost funkce
 Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je
Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je
Definice derivace v bodě
 Definice derivace v bodě tgϕ = f ( ) f () f () : = tgϕ = lim f f () tgϕ = f f () Obecně: f f f ( ) ( ) : = lim f ( + h) f f : = lim h h Derivace zleva (zprava): f ( ) : = lim f f ( ) f ( ) : = lim + +
Definice derivace v bodě tgϕ = f ( ) f () f () : = tgϕ = lim f f () tgϕ = f f () Obecně: f f f ( ) ( ) : = lim f ( + h) f f : = lim h h Derivace zleva (zprava): f ( ) : = lim f f ( ) f ( ) : = lim + +
Mocninná funkce: Příklad 1
 Mocninná funkce: Příklad 1 Zadání: Vyšetřete průběh mocninné funkce. Řešení: 1. Jako první si určíme definiční obor: D(f)=R. 2. Nyní si spočítáme zda je daná funkce sudá nebo lichá: Daná funkce je lichá.
Mocninná funkce: Příklad 1 Zadání: Vyšetřete průběh mocninné funkce. Řešení: 1. Jako první si určíme definiční obor: D(f)=R. 2. Nyní si spočítáme zda je daná funkce sudá nebo lichá: Daná funkce je lichá.
Základy matematiky pro FEK
 Základy matematiky pro FEK 10. přednáška Blanka Šedivá KMA zimní semestr 016/017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 016/017 1 / 1 Použití derivace pro vyšetřování průběhu funkce
Základy matematiky pro FEK 10. přednáška Blanka Šedivá KMA zimní semestr 016/017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 016/017 1 / 1 Použití derivace pro vyšetřování průběhu funkce
Pavlína Matysová. 5. listopadu 2018
 Soubor řešených úloh Vyšetřování průběhu funkce Pavlína Matysová 5. listopadu 018 1 Soubor řešených úloh Tento text obsahuje 7 úloh na téma vyšetřování průběhu funkce. Každé úloha je řešena dvěma způsoby
Soubor řešených úloh Vyšetřování průběhu funkce Pavlína Matysová 5. listopadu 018 1 Soubor řešených úloh Tento text obsahuje 7 úloh na téma vyšetřování průběhu funkce. Každé úloha je řešena dvěma způsoby
Příklady na konvexnost a inflexní body. Funkce f (x) = x 3 9x. Derivace jsou f (x) = 3x 2 9 a f (x) = 6x. Funkce f je konvexní na intervalu (0, )
 Příklady na konvexnost a inflexní body. Funkce = x 3 9x. Derivace jsou f (x) = 3x 9 a f (x) = 6x. Funkce f je konvexní na intervalu (, ) a konkávní na intervalu (, ). Inflexní bod c =. 3 1 1 y = x 3 9x
Příklady na konvexnost a inflexní body. Funkce = x 3 9x. Derivace jsou f (x) = 3x 9 a f (x) = 6x. Funkce f je konvexní na intervalu (, ) a konkávní na intervalu (, ). Inflexní bod c =. 3 1 1 y = x 3 9x
Průběh funkce 1. Průběh funkce. Při vyšetření grafu funkce budeme postupovat podle následujícího algoritmu:
 Průběh funkce Průběh funkce Při vyšetření grafu funkce budeme postupovat podle následujícího algoritmu:. Určení definičního oboru. 2. Rozhodnutí, jestli je funkce sudá, lichá, periodická nebo nemá ani
Průběh funkce Průběh funkce Při vyšetření grafu funkce budeme postupovat podle následujícího algoritmu:. Určení definičního oboru. 2. Rozhodnutí, jestli je funkce sudá, lichá, periodická nebo nemá ani
Příklad 1 ŘEŠENÉ PŘÍKLADY Z M1A ČÁST 6
 Příklad 1 Vyšetřete průběh funkce: a) = b) = c) = d) =ln1+ e) =ln f) = Poznámka K vyšetřování průběhu funkce použijeme postup uvedený v zadání. Některé kroky nejsou již tak detailní, všechny by ale měly
Příklad 1 Vyšetřete průběh funkce: a) = b) = c) = d) =ln1+ e) =ln f) = Poznámka K vyšetřování průběhu funkce použijeme postup uvedený v zadání. Některé kroky nejsou již tak detailní, všechny by ale měly
Význam a výpočet derivace funkce a její užití
 OPAKOVÁNÍ ZÁKLADŮ MATEMATIKY Metodický list č. 1 Význam a výpočet derivace funkce a její užití 1. dílčí téma: Výpočet derivace přímo z definice a pomocí základních vzorců. K tomuto tématu je třeba zopakovat
OPAKOVÁNÍ ZÁKLADŮ MATEMATIKY Metodický list č. 1 Význam a výpočet derivace funkce a její užití 1. dílčí téma: Výpočet derivace přímo z definice a pomocí základních vzorců. K tomuto tématu je třeba zopakovat
14. Monotonnost, lokální extrémy, globální extrémy a asymptoty funkce
 . Monotonnost, lokální extrém, globální extrém a asmptot funkce Studijní text. Monotonnost, lokální extrém, globální extrém a asmptot funkce A. Rostoucí a klesající funkce Pojm rostoucí, klesající a konstantní
. Monotonnost, lokální extrém, globální extrém a asmptot funkce Studijní text. Monotonnost, lokální extrém, globální extrém a asmptot funkce A. Rostoucí a klesající funkce Pojm rostoucí, klesající a konstantní
Výsledky Př.1. Určete intervaly monotónnosti a lokální extrémy funkce a) ( ) ( ) ( ) Stacionární body:
 Výsledky Př.. Určete intervaly monotónnosti a lokální extrémy funkce a) y < y > y < y > -2 0 3 Funkce je rostoucí v intervalech. Funkce je klesající v intervalech b) y < y > y < - Funkce je rostoucí v
Výsledky Př.. Určete intervaly monotónnosti a lokální extrémy funkce a) y < y > y < y > -2 0 3 Funkce je rostoucí v intervalech. Funkce je klesající v intervalech b) y < y > y < - Funkce je rostoucí v
Označení derivace čárkami, resp. římskými číslicemi, volíme při nižším řádu derivace, jinak užíváme horní index v závorce f (5), f (6),... x c g (x).
 9 Využití derivace 9.1 Derivace vyšších řádů Definice 1. Nechť funkce má derivaci v nějakém okolí bodu c D(f). Nechť funkce ϕ() =f () máderivacivboděc. Pak hodnotu ϕ (c) nazýváme derivací 2. řádu (2. derivací)
9 Využití derivace 9.1 Derivace vyšších řádů Definice 1. Nechť funkce má derivaci v nějakém okolí bodu c D(f). Nechť funkce ϕ() =f () máderivacivboděc. Pak hodnotu ϕ (c) nazýváme derivací 2. řádu (2. derivací)
Derivace funkce. existuje limita lim 0 ) xx xx0. Jestliže tato limita neexistuje nebo pokud funkce ff
 Derivace funkce Derivace je základním pojmem v diferenciálním počtu. Má uplatnění tam, kde se zkoumá povaha funkčních závislostí určitých proměnných (veličin). V matematice, ekonomii, fyzice ale i v jiných
Derivace funkce Derivace je základním pojmem v diferenciálním počtu. Má uplatnění tam, kde se zkoumá povaha funkčních závislostí určitých proměnných (veličin). V matematice, ekonomii, fyzice ale i v jiných
Bakalářská matematika I
 1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
Monotonie a lokální extrémy. Konvexnost, konkávnost a inflexní body. 266 I. Diferenciální počet funkcí jedné proměnné
 66 I. Diferenciální počet funkcí jedné proměnné I. 5. Vyšetřování průběhu funkce Monotonie a lokální etrémy Důsledek. Nechť má funkce f) konečnou derivaci na intervalu I. Je-li f ) > 0 pro každé I, pak
66 I. Diferenciální počet funkcí jedné proměnné I. 5. Vyšetřování průběhu funkce Monotonie a lokální etrémy Důsledek. Nechť má funkce f) konečnou derivaci na intervalu I. Je-li f ) > 0 pro každé I, pak
Matematika B 2. Úvodní informace
 Matematika B 2 MIROSLAV KUČERA Úvodní informace Kontakt miroslav.kucera@vsfs.czvsfs.cz Studijní středisko Kladno IT oddělení 306B (kanceláře studijního oddělení) Konzultační hodiny Po Pá 8:30 15:00 možno
Matematika B 2 MIROSLAV KUČERA Úvodní informace Kontakt miroslav.kucera@vsfs.czvsfs.cz Studijní středisko Kladno IT oddělení 306B (kanceláře studijního oddělení) Konzultační hodiny Po Pá 8:30 15:00 možno
Matematika I A ukázkový test 1 pro 2011/2012. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a
 Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Omezenost funkce. Definice. (shora, zdola) omezená na množině M D(f ) tuto vlastnost. nazývá se (shora, zdola) omezená tuto vlastnost má množina
 Přednáška č. 5 Vlastnosti funkcí Jiří Fišer 22. října 2007 Jiří Fišer (KMA, PřF UP Olomouc) KMA MMAN1 Přednáška č. 4 22. října 2007 1 / 1 Omezenost funkce Definice Funkce f se nazývá (shora, zdola) omezená
Přednáška č. 5 Vlastnosti funkcí Jiří Fišer 22. října 2007 Jiří Fišer (KMA, PřF UP Olomouc) KMA MMAN1 Přednáška č. 4 22. října 2007 1 / 1 Omezenost funkce Definice Funkce f se nazývá (shora, zdola) omezená
Vypracoval: Mgr. Lukáš Bičík TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY
 Vlastnosti funkcí Vypracoval: Mgr. Lukáš Bičík TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY Definiční obor Definiční obor funkce je množina všech čísel,
Vlastnosti funkcí Vypracoval: Mgr. Lukáš Bičík TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY Definiční obor Definiční obor funkce je množina všech čísel,
Matematika I A ukázkový test 1 pro 2014/2015
 Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
1 Množiny, výroky a číselné obory
 1 Množiny, výroky a číselné obory 1.1 Množiny a množinové operace Množinou rozumíme každé shrnutí určitých a navzájem různých objektů (které nazýváme prvky) do jediného celku. Definice. Dvě množiny jsou
1 Množiny, výroky a číselné obory 1.1 Množiny a množinové operace Množinou rozumíme každé shrnutí určitých a navzájem různých objektů (které nazýváme prvky) do jediného celku. Definice. Dvě množiny jsou
MATEMATIKA. Příklady pro 1. ročník bakalářského studia. II. část Diferenciální počet. II.1. Posloupnosti reálných čísel
 MATEMATIKA Příklady pro 1. ročník bakalářského studia II. část II.1. Posloupnosti reálných čísel Rozhodněte, zda posloupnost a n (n = 1, 2, 3,...) je omezená (omezená shora, omezená zdola) resp. monotónní
MATEMATIKA Příklady pro 1. ročník bakalářského studia II. část II.1. Posloupnosti reálných čísel Rozhodněte, zda posloupnost a n (n = 1, 2, 3,...) je omezená (omezená shora, omezená zdola) resp. monotónní
Funkce v ıce promˇ enn ych Extr emy Pˇredn aˇska p at a 12.bˇrezna 2018
 Funkce více proměnných Extrémy Přednáška pátá 12.března 2018 Zdroje informací Diferenciální počet http://homen.vsb.cz/~kre40/esfmat2/fceviceprom.html http://www.studopory.vsb.cz/studijnimaterialy/sbirka_uloh/pdf/7.pdf
Funkce více proměnných Extrémy Přednáška pátá 12.března 2018 Zdroje informací Diferenciální počet http://homen.vsb.cz/~kre40/esfmat2/fceviceprom.html http://www.studopory.vsb.cz/studijnimaterialy/sbirka_uloh/pdf/7.pdf
Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si zopakovat a orientovat se v pojmech: funkce, D(f), g 2 : y =
 0.1 Diferenciální počet Je částí infinitezimálního počtu, což je souhrnný název pro diferenciální a integrální počet. Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si
0.1 Diferenciální počet Je částí infinitezimálního počtu, což je souhrnný název pro diferenciální a integrální počet. Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si
Univerzita Karlova v Praze Pedagogická fakulta
 Univerzita Karlova v Praze Pedagogická akulta DRUHÁ SEMINÁRNÍ PRÁCE Z DIFERENCIÁLNÍHO POČTU PRŮBĚH FUNKCE 000/001 Cirik, M-ZT Zadání: Vyšetřete průběh unkce ( ) : y Vypracování: ( ) : y Předně určíme deiniční
Univerzita Karlova v Praze Pedagogická akulta DRUHÁ SEMINÁRNÍ PRÁCE Z DIFERENCIÁLNÍHO POČTU PRŮBĚH FUNKCE 000/001 Cirik, M-ZT Zadání: Vyšetřete průběh unkce ( ) : y Vypracování: ( ) : y Předně určíme deiniční
5. Lokální, vázané a globální extrémy
 5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
Rolleova věta. Mějme funkci f, která má tyto vlastnosti : má derivaci c) f (a) = f (b). a) je spojitá v a, b b) v každém bodě a,b
 Průběh unkce Rolleova věta Mějme unkci, která má tto vlastnosti : a) je spojitá v a, b b) v každém bodě a,b má derivaci c) (a) = (b). b Potom eistuje v a, alespoň jeden bod c, v němž ( c) : 1, 3 0 1 1
Průběh unkce Rolleova věta Mějme unkci, která má tto vlastnosti : a) je spojitá v a, b b) v každém bodě a,b má derivaci c) (a) = (b). b Potom eistuje v a, alespoň jeden bod c, v němž ( c) : 1, 3 0 1 1
DIFERENCIÁLNÍ POČET SPOJITOST FUNKCE,
 DIFERENCIÁLNÍ POČET SPOJITOST FUNKCE, LIMITA FUNKCE, DERIVACE FUNKCE Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století
DIFERENCIÁLNÍ POČET SPOJITOST FUNKCE, LIMITA FUNKCE, DERIVACE FUNKCE Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století
D(f) =( 1, 1) [ ( 1, 1) [ (1, 1). 2( x)3 ( x) 2 1 = 2(x) 3. (x) 2 1 = f(x) Funkce je lichá, není periodická
 Vyšetříme funkci f(x): f(x) = 2x3.. Stanovme definiční obor funkce D(f) a zjistíme,ve kterých bodech je funkce sojitá D(f) =(, ) [ (, ) [ (, ). 2. Počítáme f( x) = 2( x)3 ( x) 2 = 2(x) 3 (x) 2 = f(x) Funkce
Vyšetříme funkci f(x): f(x) = 2x3.. Stanovme definiční obor funkce D(f) a zjistíme,ve kterých bodech je funkce sojitá D(f) =(, ) [ (, ) [ (, ). 2. Počítáme f( x) = 2( x)3 ( x) 2 = 2(x) 3 (x) 2 = f(x) Funkce
Přednáška 11, 12. prosince Část 5: derivace funkce
 Přednáška 11, 12. prosince 2014 Závěrem pasáže o spojitých funkcích zmíníme jejich podtřídu, lipschitzovské funkce, nazvané podle německého matematika Rudolfa Lipschitze (1832 1903). Fukce f : M R je lipschitzovská,
Přednáška 11, 12. prosince 2014 Závěrem pasáže o spojitých funkcích zmíníme jejich podtřídu, lipschitzovské funkce, nazvané podle německého matematika Rudolfa Lipschitze (1832 1903). Fukce f : M R je lipschitzovská,
22. & 23. & 24. Vlastnosti funkcí a jejich limita a derivace
 22. & 23. & 24. Vlastnosti funkcí a jejich ita a derivace Základní vlastnosti Definiční obor Definiční obor je množina neznámých, pro něž je funkce definována. Obor hodnot Obor hodnot je množina všech
22. & 23. & 24. Vlastnosti funkcí a jejich ita a derivace Základní vlastnosti Definiční obor Definiční obor je množina neznámých, pro něž je funkce definována. Obor hodnot Obor hodnot je množina všech
Definice globální minimum (absolutní minimum) v bodě A D f, jestliže X D f
 Výklad Globální extrémy mají stejný význam jako u funkcí jedné proměnné. Hledáme je bud na celém definičním oboru dané funkce, nebo na předem zadané podmnožině definičního oboru. Definice 6..1. Řekneme,
Výklad Globální extrémy mají stejný význam jako u funkcí jedné proměnné. Hledáme je bud na celém definičním oboru dané funkce, nebo na předem zadané podmnožině definičního oboru. Definice 6..1. Řekneme,
2.7. Průběh funkce. Vyšetřit průběh funkce znamená určit (ne nutně v tomto pořadí): 1) Definiční obor; sudost, lichost; periodičnost
 .7. Průběh unkce Všetřit průběh unkce znamená určit ne nutně v tomto pořadí: deiniční obor; sudost, lichost; periodičnost, interval spojitosti a bod nespojitosti, průsečík grau unkce s osami, interval,
.7. Průběh unkce Všetřit průběh unkce znamená určit ne nutně v tomto pořadí: deiniční obor; sudost, lichost; periodičnost, interval spojitosti a bod nespojitosti, průsečík grau unkce s osami, interval,
Derivace vyšších řádů, aplikace derivací
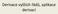 Derivace vyšších řádů, aplikace derivací Značení derivací vyšších řádů Máme funkci f: y = f x f x druhá derivace funkce y = f x f k x k-tá derivace funkce y = f x Derivace vyšších řádů počítáme opakovaným
Derivace vyšších řádů, aplikace derivací Značení derivací vyšších řádů Máme funkci f: y = f x f x druhá derivace funkce y = f x f k x k-tá derivace funkce y = f x Derivace vyšších řádů počítáme opakovaným
Použití derivací L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT. Monotónie. Konvexita. V této části budou uvedena některá použití derivací.
 V této části budou uvedena některá použití derivací. Použití derivací L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT Tvrzení je uvedeno pro jednostrannou itu zprava. Samozřejmě obdobné tvrzení platí pro itu zleva
V této části budou uvedena některá použití derivací. Použití derivací L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT Tvrzení je uvedeno pro jednostrannou itu zprava. Samozřejmě obdobné tvrzení platí pro itu zleva
1.1 Příklad z ekonomického prostředí 1
 1.1 Příklad z ekonomického prostředí 1 Smysl solidního zvládnutí matematiky v bakalářských oborech na Fakultě podnikatelské VUT v Brně je především v aplikační síle matematiky v odborných předmětech a
1.1 Příklad z ekonomického prostředí 1 Smysl solidního zvládnutí matematiky v bakalářských oborech na Fakultě podnikatelské VUT v Brně je především v aplikační síle matematiky v odborných předmětech a
{ } Ox ( 0) 4.2. Konvexnost, konkávnost, inflexe. Definice Obr. 52. Poznámka. nad tečnou
 Konvenost, konkávnost, inflee 4.. Konvenost, konkávnost, inflee Definice 4... Nechť eistuje f ( ), D f. Řekneme, že funkce f ( ) je v bodě konkávní, jestliže eistuje { } O ( ) tak, že platí D : O( )\ f(
Konvenost, konkávnost, inflee 4.. Konvenost, konkávnost, inflee Definice 4... Nechť eistuje f ( ), D f. Řekneme, že funkce f ( ) je v bodě konkávní, jestliže eistuje { } O ( ) tak, že platí D : O( )\ f(
Matematická analýza 1, příklady na procvičení (Josef Tkadlec, )
 Matematická analýza, příklady na procvičení (Josef Tkadlec, 6.. 7) Reálná čísla. Určete maximum, minimum, supremum a infimum následujících množin: Z; b) M = (, ), 5 ; c) M =, Q; d) M = { + n : n N}; e)
Matematická analýza, příklady na procvičení (Josef Tkadlec, 6.. 7) Reálná čísla. Určete maximum, minimum, supremum a infimum následujících množin: Z; b) M = (, ), 5 ; c) M =, Q; d) M = { + n : n N}; e)
, f g jsou elementární funkce.
 Průběh funkce použité definice a věty Definice. Řekneme, že funkce je spojitá na otevřeném intervalu (a, b), jestliže je spojitá v každém vnitřním bodě tohoto intervalu. Řekneme, že funkce je spojitá na
Průběh funkce použité definice a věty Definice. Řekneme, že funkce je spojitá na otevřeném intervalu (a, b), jestliže je spojitá v každém vnitřním bodě tohoto intervalu. Řekneme, že funkce je spojitá na
Použití derivací. V této části budou uvedena některá použití derivací. LEKCE08-PRU. Použití derivací. l Hospital
 V této části budou uvedena některá použití derivací. a derivace a derivace -zbytek L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT Tvrzení je uvedeno pro jednostrannou limitu zprava. Samozřejmě obdobné tvrzení platí
V této části budou uvedena některá použití derivací. a derivace a derivace -zbytek L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT Tvrzení je uvedeno pro jednostrannou limitu zprava. Samozřejmě obdobné tvrzení platí
Přijímací zkouška na navazující magisterské studium 2014
 Přijímací zkouška na navazující magisterské studium 4 Studijní program: Studijní obory: Příklad (5 bodů) Spočtěte Matematika MA, MMIB, MMFT, MSTR, NVM, PMSE, MDU Varianta A M xy dxdy, kde M = {(x, y) R
Přijímací zkouška na navazující magisterské studium 4 Studijní program: Studijní obory: Příklad (5 bodů) Spočtěte Matematika MA, MMIB, MMFT, MSTR, NVM, PMSE, MDU Varianta A M xy dxdy, kde M = {(x, y) R
Aplikační úlohy z diferenciálního počtu jedné proměnné
 Jihočeská univerzita v Českých Budějovicích Fakulta Katedra Bakalářská práce Aplikační úlohy z diferenciálního počtu jedné proměnné Vypracoval: Michaela Jelínková Vedoucí práce: RNDr. Vladimíra Petrášková,
Jihočeská univerzita v Českých Budějovicích Fakulta Katedra Bakalářská práce Aplikační úlohy z diferenciálního počtu jedné proměnné Vypracoval: Michaela Jelínková Vedoucí práce: RNDr. Vladimíra Petrášková,
fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu (reg. č. CZ.1.07/2.2.00/28.
 Extrémy Vyšší matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu http://akademie.ldf.mendelu.cz/cz
Extrémy Vyšší matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu http://akademie.ldf.mendelu.cz/cz
Diferenciální počet 1 1. f(x) = ln arcsin 1 + x 1 x. 1 x 1 a x 1 0. f(x) = (cos x) cosh x + 3x. x 0 je derivace funkce f(x) v bodě x0.
 Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
Derivace funkce DERIVACE A SPOJITOST DERIVACE A KONSTRUKCE FUNKCÍ. Aritmetické operace
 Derivace funkce Derivace je jedním z hlavních nástrojů matematické analýzy. V příští části ukážeme, jak mnoho různorodých aplikací derivace má. Geometricky lze derivaci funkce v nějakém bodě chápat jako
Derivace funkce Derivace je jedním z hlavních nástrojů matematické analýzy. V příští části ukážeme, jak mnoho různorodých aplikací derivace má. Geometricky lze derivaci funkce v nějakém bodě chápat jako
Funkce. RNDR. Yvetta Bartáková. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
 Funkce RNDR. Yvetta Bartáková Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Derivace funkce VY INOVACE_05 0_M Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Definice Mějme funkci f definovanou v okolí bodu 0. Eistuje-li
Funkce RNDR. Yvetta Bartáková Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Derivace funkce VY INOVACE_05 0_M Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Definice Mějme funkci f definovanou v okolí bodu 0. Eistuje-li
Posloupnosti a řady. 28. listopadu 2015
 Posloupnosti a řady Přednáška 5 28. listopadu 205 Obsah Posloupnosti 2 Věty o limitách 3 Řady 4 Kritéria konvergence 5 Absolutní a relativní konvergence 6 Operace s řadami 7 Mocninné a Taylorovy řady Zdroj
Posloupnosti a řady Přednáška 5 28. listopadu 205 Obsah Posloupnosti 2 Věty o limitách 3 Řady 4 Kritéria konvergence 5 Absolutní a relativní konvergence 6 Operace s řadami 7 Mocninné a Taylorovy řady Zdroj
IV. Základní pojmy matematické analýzy IV.1. Rozšíření množiny reálných čísel
 Matematická analýza IV. Základní pojmy matematické analýzy IV.1. Rozšíření množiny reálných čísel na množině R je definováno: velikost (absolutní hodnota), uspořádání, aritmetické operace; znázornění:
Matematická analýza IV. Základní pojmy matematické analýzy IV.1. Rozšíření množiny reálných čísel na množině R je definováno: velikost (absolutní hodnota), uspořádání, aritmetické operace; znázornění:
2. spojitost (7. cvičení) 3. sudost/lichost, periodicita (3. cvičení) 4. první derivace, stacionární body, intervaly monotonie (10.
 MA. cvičení průběh funkce Lukáš Pospíšil,202 Průběh funkce Pod úkolem vyšetřete průběh funkce budeme rozumět nalezení všech kvalitativních vlastností zadané funkce - tedy bude potřeba zjistit o funkci
MA. cvičení průběh funkce Lukáš Pospíšil,202 Průběh funkce Pod úkolem vyšetřete průběh funkce budeme rozumět nalezení všech kvalitativních vlastností zadané funkce - tedy bude potřeba zjistit o funkci
prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. BI-ZMA ZS 2009/2010
 Věty o přírustku funkce prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické
Věty o přírustku funkce prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické
10. cvičení - LS 2017
 10. cvičení - LS 2017 Michal Outrata Příklad 1 Spočtěte následující itu daných posloupností: (a) (b) (c) n 3 +5n 2 n 3 6n 2 +3 n ; n 4 3n 2 6 n 4 + 3n 2 + 6; n 2 15n+2(1 n). 2(n 2) 3 2n 3 Příklad 2 Pro
10. cvičení - LS 2017 Michal Outrata Příklad 1 Spočtěte následující itu daných posloupností: (a) (b) (c) n 3 +5n 2 n 3 6n 2 +3 n ; n 4 3n 2 6 n 4 + 3n 2 + 6; n 2 15n+2(1 n). 2(n 2) 3 2n 3 Příklad 2 Pro
Derivace funkce. Přednáška MATEMATIKA č Jiří Neubauer
 Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
( ) ( ) ( ) ( ) ( ) ( ) Užití derivací. x, x a, b : x x f x f x MATA P12. Funkce rostoucí a klesající: Definice rostoucí a klesající funkce
 MATA P1 Užití derivací Funkce rostoucí a klesající: Deinice rostoucí a klesající unkce Funkce je rostoucí v intervalu (a,b), právě když platí: ( ) ( ) ( ), a, b : 1 1 1 Funkce je klesající v intervalu
MATA P1 Užití derivací Funkce rostoucí a klesající: Deinice rostoucí a klesající unkce Funkce je rostoucí v intervalu (a,b), právě když platí: ( ) ( ) ( ), a, b : 1 1 1 Funkce je klesající v intervalu
Funkce a limita. Petr Hasil. Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
 Funkce a limita Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Funkce a limita Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Přednáška z MA. Michal Tuláček 16. prosince 2004. 1 IV.7 Průběhy funkce 3. 2 Vyšetřování průběhu funkce- KUCHAŘKA 4
 Přednáška z MA Michal Tuláček 6. prosince 004 Obsah IV.7 Průběhy funkce 3 Vyšetřování průběhu funkce- KUCHAŘKA 4 3 Vzorový příklad na průběh funkce ze cvičení 4 4 Příkladynadobumezikapremahusou 7 Definice:
Přednáška z MA Michal Tuláček 6. prosince 004 Obsah IV.7 Průběhy funkce 3 Vyšetřování průběhu funkce- KUCHAŘKA 4 3 Vzorový příklad na průběh funkce ze cvičení 4 4 Příkladynadobumezikapremahusou 7 Definice:
Požadavky k ústní části zkoušky Matematická analýza 1 ZS 2014/15
 Požadavky k ústní části zkoušky Matematická analýza 1 ZS 2014/15 Klíčové pojmy Neznalost některého z klíčových pojmů bude mít za následek ukončení zkoušky se známkou neprospěl(a). supremum infimum limita
Požadavky k ústní části zkoušky Matematická analýza 1 ZS 2014/15 Klíčové pojmy Neznalost některého z klíčových pojmů bude mít za následek ukončení zkoušky se známkou neprospěl(a). supremum infimum limita
Extrémy funkce dvou proměnných
 Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
FUNKCE A JEJICH VLASTNOSTI
 PŘEDNÁŠKA 3 FUNKCE A JEJICH VLASTNOSTI Pojem zobrazení a funkce Uvažujme libovolné neprázdné množiny A, B. Přiřadíme-li každému prvku x A právě jeden prvek y B, dostáváme množinu F uspořádaných dvojic
PŘEDNÁŠKA 3 FUNKCE A JEJICH VLASTNOSTI Pojem zobrazení a funkce Uvažujme libovolné neprázdné množiny A, B. Přiřadíme-li každému prvku x A právě jeden prvek y B, dostáváme množinu F uspořádaných dvojic
MATEMATIKA II - vybrané úlohy ze zkoušek (2015)
 MATEMATIKA II - vybrané úlohy ze zkoušek (2015) doplněné o další úlohy 24. 2. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi (e-mail: Frantisek.Mraz@fs.cvut.cz
MATEMATIKA II - vybrané úlohy ze zkoušek (2015) doplněné o další úlohy 24. 2. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi (e-mail: Frantisek.Mraz@fs.cvut.cz
Funkce a lineární funkce pro studijní obory
 Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
Sbírka úloh z matematiky
 Střední průmyslová škola a Střední odborné učiliště, Trutnov, Školní 101 Sbírka úloh z matematiky v rámci projektu královéhradeckého kraje zavádění inovativních metod výuky pomocí ICT v předmětu matematika
Střední průmyslová škola a Střední odborné učiliště, Trutnov, Školní 101 Sbírka úloh z matematiky v rámci projektu královéhradeckého kraje zavádění inovativních metod výuky pomocí ICT v předmětu matematika
Matematická analýza pro informatiky I. Derivace funkce
 Matematická analýza pro informatiky I. 7. přednáška Derivace funkce Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 31. března 2011 Jan Tomeček, tomecek@inf.upol.cz
Matematická analýza pro informatiky I. 7. přednáška Derivace funkce Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 31. března 2011 Jan Tomeček, tomecek@inf.upol.cz
MATEMATIKA I - vybrané úlohy ze zkoušek v letech
 MATEMATIKA I - vybrané úlohy ze zkoušek v letech 008 0 doplněné o další úlohy. část DIFERENCIÁLNÍ POČET funkcí jedné proměnné Další část ( integrální počet) bude vydána na konci listopadu 9. 9. 0 Případné
MATEMATIKA I - vybrané úlohy ze zkoušek v letech 008 0 doplněné o další úlohy. část DIFERENCIÁLNÍ POČET funkcí jedné proměnné Další část ( integrální počet) bude vydána na konci listopadu 9. 9. 0 Případné
Poznámka: V kurzu rovnice ostatní podrobně probíráme polynomické rovnice a jejich řešení.
 @083 6 Polynomické funkce Poznámka: V kurzu rovnice ostatní podrobně probíráme polynomické rovnice a jejich řešení. Definice: Polynomická funkce n-tého stupně (n N) je dána předpisem n n 1 2 f : y a x
@083 6 Polynomické funkce Poznámka: V kurzu rovnice ostatní podrobně probíráme polynomické rovnice a jejich řešení. Definice: Polynomická funkce n-tého stupně (n N) je dána předpisem n n 1 2 f : y a x
Zimní semestr akademického roku 2014/ prosince 2014
 Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 7. prosince 2014 Předmluva
Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 7. prosince 2014 Předmluva
soubor FUNKCÍ příručka pro studenty
 soubor FUNKCÍ příručka pro studenty 1 Obsah Poznámky 6 lineární funkce mocninné funkce s přirozeným exponentem o sudým o lichým s celým záporným exponentem o sudým o lichým s racionálním exponentem o druhá
soubor FUNKCÍ příručka pro studenty 1 Obsah Poznámky 6 lineární funkce mocninné funkce s přirozeným exponentem o sudým o lichým s celým záporným exponentem o sudým o lichým s racionálním exponentem o druhá
c ÚM FSI VUT v Brně 20. srpna 2007
 20. srpna 2007 1. f = 3 12 2. f = 2 e 3. f = ln Příklad 1. Nakreslete graf funkce f() = 3 12 Příklad 1. f = 3 12 Nejprve je třeba určit definiční obor. Výraz je vždy definován. Příklad 1. f = 3 12 f =
20. srpna 2007 1. f = 3 12 2. f = 2 e 3. f = ln Příklad 1. Nakreslete graf funkce f() = 3 12 Příklad 1. f = 3 12 Nejprve je třeba určit definiční obor. Výraz je vždy definován. Příklad 1. f = 3 12 f =
1. POJMY 1.1. FORMULE VÝROKOVÉHO POČTU
 Obsah 1. Pojmy... 2 1.1. Formule výrokového počtu... 2 1.2. Množina... 3 1.2.1. Operace s množinami... 3 1.2.2. Relace... 3 2. Číselné obory... 5 2.1. Uzavřenost množiny na operaci... 5 2.2. Rozšíření
Obsah 1. Pojmy... 2 1.1. Formule výrokového počtu... 2 1.2. Množina... 3 1.2.1. Operace s množinami... 3 1.2.2. Relace... 3 2. Číselné obory... 5 2.1. Uzavřenost množiny na operaci... 5 2.2. Rozšíření
Matematika I: Pracovní listy do cvičení
 Matematika I: Pracovní listy do cvičení Dagmar Dlouhá, Radka Hamříková, Zuzana Morávková, Michaela Tužilová Pro FAST upravil Petr Volný Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita
Matematika I: Pracovní listy do cvičení Dagmar Dlouhá, Radka Hamříková, Zuzana Morávková, Michaela Tužilová Pro FAST upravil Petr Volný Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita
Matematika I (KX001) Užití derivace v geometrii, ve fyzice 3. října f (x 0 ) (x x 0) Je-li f (x 0 ) = 0, tečna: x = 3, normála: y = 0
 Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Kapitola 1: Reálné funkce 1/13
 Kapitola 1: Reálné funkce 1/13 Číselné množiny 2/13 N = {1, 2, 3, 4,... }... přirozená čísla N 0 = N {0} = {0, 1, 2, 3, 4,... } Z = {..., 2, 1, 0, 1, 2, 3, 4,... }... celá čísla Q = { p q p, q Z}... racionální
Kapitola 1: Reálné funkce 1/13 Číselné množiny 2/13 N = {1, 2, 3, 4,... }... přirozená čísla N 0 = N {0} = {0, 1, 2, 3, 4,... } Z = {..., 2, 1, 0, 1, 2, 3, 4,... }... celá čísla Q = { p q p, q Z}... racionální
PRŮBĚH FUNKCE - CVIČENÍ
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA PRŮBĚH FUNKCE - CVIČENÍ Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA PRŮBĚH FUNKCE - CVIČENÍ Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny
Limita a spojitost funkce
 Přednáška 5 Limita a spojitost funkce V této přednášce se konečně dostaneme k diferenciálnímu počtu funkce jedné reálné proměnné. Diferenciální počet se v podstatě zabývá lokálním chováním funkce v daném
Přednáška 5 Limita a spojitost funkce V této přednášce se konečně dostaneme k diferenciálnímu počtu funkce jedné reálné proměnné. Diferenciální počet se v podstatě zabývá lokálním chováním funkce v daném
Funkce. Limita a spojitost
 Funkce. Limita a spojitost skriptum J. Neustupa text Funkce (úvod) na této web stránce III.2 Fce - základní pojmy 1. Definice, def. obor D(f), obor hodnot H(f), graf 2. Fce složená, omezená, 3. Fce sudá,
Funkce. Limita a spojitost skriptum J. Neustupa text Funkce (úvod) na této web stránce III.2 Fce - základní pojmy 1. Definice, def. obor D(f), obor hodnot H(f), graf 2. Fce složená, omezená, 3. Fce sudá,
Diferenciální počet funkcí více proměnných
 Vysoké učení technické v Brně Fakulta strojního inženýrství Diferenciální počet funkcí více proměnných Doc RNDr Miroslav Doupovec, CSc Neřešené příklady Matematika II OBSAH Obsah I Diferenciální počet
Vysoké učení technické v Brně Fakulta strojního inženýrství Diferenciální počet funkcí více proměnných Doc RNDr Miroslav Doupovec, CSc Neřešené příklady Matematika II OBSAH Obsah I Diferenciální počet
Matematika I. Funkce jedné proměnné. Funkce jedné proměnné Matematika I 1 / 212
 Matematika I Funkce jedné proměnné Funkce jedné proměnné Matematika I 1 / 212 1. Množiny a zobrazení Funkce jedné proměnné Matematika I 2 / 212 Množiny Definice 1.1.1: Množinou rozumíme soubor prvků se
Matematika I Funkce jedné proměnné Funkce jedné proměnné Matematika I 1 / 212 1. Množiny a zobrazení Funkce jedné proměnné Matematika I 2 / 212 Množiny Definice 1.1.1: Množinou rozumíme soubor prvků se
Derivace funkce Otázky
 funkce je jedním z hlavních nástrojů matematické analýzy. V příští části ukážeme, jak mnoho různorodých aplikací derivace má. Geometricky lze derivaci funkce v nějakém bodě chápat jako směrnici tečny grafu
funkce je jedním z hlavních nástrojů matematické analýzy. V příští části ukážeme, jak mnoho různorodých aplikací derivace má. Geometricky lze derivaci funkce v nějakém bodě chápat jako směrnici tečny grafu
Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
MATEMATIKA A Metodický list č. 1
 Metodický list č. 1 Název tématického celku: Lineární algebra I Základním cílem tohoto tématického celku je objasnit některé pojmy lineární algebry a poukázat na jejich vzájemnou souvislost. Posluchači
Metodický list č. 1 Název tématického celku: Lineární algebra I Základním cílem tohoto tématického celku je objasnit některé pojmy lineární algebry a poukázat na jejich vzájemnou souvislost. Posluchači
LOKÁLNÍ A GLOBÁLNÍ EXTRÉMY FUNKCÍ A JEJICH UŽITÍ
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/3.098 IV- Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol LOKÁLNÍ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/3.098 IV- Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol LOKÁLNÍ
Derivace a průběh funkce.
 Derivace a průběh funkce. Robert Mařík 14. října 2008 Obsah 1 Základní myšlenky. 2 2 Přesné věty a definice 10 3 Okolí nevlastních bodů. 16 4 Sestrojení grafu funkce. 19 1 Základní myšlenky. y x Uvažujme
Derivace a průběh funkce. Robert Mařík 14. října 2008 Obsah 1 Základní myšlenky. 2 2 Přesné věty a definice 10 3 Okolí nevlastních bodů. 16 4 Sestrojení grafu funkce. 19 1 Základní myšlenky. y x Uvažujme
f(x) = arccotg x 2 x lim f(x). Určete všechny asymptoty grafu x 2 2 =
 Řešení vzorové písemky z předmětu MAR Poznámky: Řešení úloh ze vzorové písemky jsou formulována dosti podrobně podobným způsobem jako u řešených příkladů ve skriptech U zkoušky lze jednotlivé kroky postupu
Řešení vzorové písemky z předmětu MAR Poznámky: Řešení úloh ze vzorové písemky jsou formulována dosti podrobně podobným způsobem jako u řešených příkladů ve skriptech U zkoušky lze jednotlivé kroky postupu
PRŮBĚH FUNKCE JEDNÉ REÁLNÉ PROMĚNNÉ
 Dierenciální počet unkcí jedné reálné proměnné - 5 - PRŮBĚH FUNKCE JEDNÉ REÁLNÉ PROMĚNNÉ Cílem vyšetřování průběhu unkce je umět nakreslit její gra Obvykle postupujeme tak že nalezneme její maimální deiniční
Dierenciální počet unkcí jedné reálné proměnné - 5 - PRŮBĚH FUNKCE JEDNÉ REÁLNÉ PROMĚNNÉ Cílem vyšetřování průběhu unkce je umět nakreslit její gra Obvykle postupujeme tak že nalezneme její maimální deiniční
2. Ur íme sudost/lichost funkce a pr se íky s osami. 6. Na záv r na rtneme graf vy²et ované funkce. 8x. x 2 +4
 Pr b h funkce V této jednotce si ukáºeme jak postupovat p i vy²et ování pr b hu funkce. P edpokládáme znalost po ítání derivací a limit, které jsou dob e popsány v p edchozích letácích tohoto bloku. P
Pr b h funkce V této jednotce si ukáºeme jak postupovat p i vy²et ování pr b hu funkce. P edpokládáme znalost po ítání derivací a limit, které jsou dob e popsány v p edchozích letácích tohoto bloku. P
Univerzita Karlova v Praze Pedagogická fakulta
 Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z ÚVODU DO MATEMATICKÉ ANLÝZY FUNKCE 999/000 CIFRIK Funkce F a) Zadání: Vyšetřete bez užití limit a derivací funkci : y = { x } f Definice:
Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z ÚVODU DO MATEMATICKÉ ANLÝZY FUNKCE 999/000 CIFRIK Funkce F a) Zadání: Vyšetřete bez užití limit a derivací funkci : y = { x } f Definice:
Digitální učební materiál
 Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/4.080 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/ Inovace a zkvalitnění výuky prostřednictvím
Digitální učební materiál Číslo projektu CZ.1.07/1.5.00/4.080 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/ Inovace a zkvalitnění výuky prostřednictvím
Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
