Pohyb v poli centrální síly

Transkript

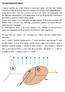
1 K přenášce NUFY8 Teoetická echanika pozatíní čební text, veze 5. Pohyb v poi centání síy Leoš Dvořák, MFF UK Paha, 4 Pohyb v poi centání síy Pohyb hotného bo v poi centání síy se řeší již v úvoní kz kasické echaniky. (Tento pobé bývá označován jako Kepeova úoha.) Vychází se přito ze zákonů zachování oent hybnosti a enegie; řešení vee na integá, jehož výpočet chvíi tvá. Ze si kážee, jak poocí Lagangeových ovnic ospět k tzv. Binetov vzoci, jehož řešení ž be vei jenoché. Znaost pohyb hotného bo v poi centání síy ožňje vyřešit i pohyb vo hotných boů, kteé se přitahjí (nebo opzjí), tey tzv. pobé vo těes. I ten ž znáe z úvoního kz. To, že pohyb vo hotných boů ze převést na pohyb jenoho bo v poi centání síy, však jasně pyne i z Lagangeových ovnic. h. A pávě tí začnee. Pobé vo těes Uvažje va hotné boy o hotnostech,, kteé se navzáje přitahjí nebo opzjí centáníi siai. Poohy těchto boů jso čeny poohovýi vektoy,, viz obázek. Po aší ovození bee potřebovat pooh hotného stře těchto boů + R = + (5.) a pooh vekto, kteý oba boy spojje, =. (5.) Z (5.) a (5.) ůžee zpětně vypočítat = R, = R+. (5.3) + + Zeivjee-i (5.3) poe čas, ostanee anaogické vztahy po ychosti obo boů: = R, = R+. (5.4) + + Kinetická enegie naší sostavy je T = +, (5.5) což po osazení (5.4) a úpavách á T = ( + ) R +. (5.6) + Bývá zvyke označit Napříka se přitahjí gavitačně. Může jít třeba o vojhvěz nebo o sostav Zeě Měsíc (kyž zanebáe působení všech ostatních těes). Nebo ůže jít o eektostatické síy, třeba ezi věa nabitýi kičkai. (V násející kapitoe bee řešit pohyb jáa héia naétajícího na jáo zata, tey tzv. Rthefoův ozpty.) Z (5.4) pyne = = RR + R + ( + ) a = = RR + + R + ( + ), čeny obsahjící R v sočt vypano, pak ž je úpava snaná.

2 K přenášce NUFY8 Teoetická echanika pozatíní čební text, veze 5. Pohyb v poi centání síy Leoš Dvořák, MFF UK Paha, 4 + = M, = µ. (5.7) + M je ceková hotnost sostavy, μ je ekovaná hotnost 3. Výsený vztah po kineticko enegii, T= MR + µ, (5.8) vypaá, jako by šo o pohyb vo jiných hotných boů: jenoho s hotností M, jehož pooh čje vekto R a hého s hotností μ, jehož pooh čje vekto. Potenciání enegie je závisá jen na vzáenosti obo boů =, V = V( ). Lagangián je tey L= T V = M R + µ. (5.9) V( ) Viíe, že agangián se ozpaá na vě nezávisé části opav jako by šo o pohyb vo zcea nezávisých boů o hotnostech M, a μ. R= XYZ,,, je pvní část agangián Označíe-i sožky vekto hotného stře ( ) ( ) ( S ) L = M X + Y + Z a přísšné Lagangeovy ovnice. h ají X = konst., Y = konst., Je tey o pohyb ovnoěný příočaý a ůžee psát: R= R + v t, (5.) ke R a v jso čeny počátečníi poínkai. Rozysete si, jaký á tento výseek fyzikání význa. 4 Poovin pobé áe tey vyřešeno! 5 Spočtee-i, jak se s čase vyvíjí vekto = ( t) pohyb půvoních vo hotných boů ž jenoše číe ze vztahů (5.3). Pobé pohyb sostavy vo hotných boů (tey pobé vo těes) jse převei na pobé pohyb hotného stře (a ten je jenoše án vztahe (5.)) a pohyb hotného bo o hotnosti μ, kteý je chaakteizován agangiáne (viz (5.9)) L = µ V. (5.) Tento agangián popisje pohyb hotného bo o hotnosti μ v poi centání síy (ky siové cent je nehybné), přito V( ) je potenciání enegie tohoto bo v ané poi. ( ), pak Poznaeneje, že v přípaě gavitačního přitahování je (viz (5.7)) Mµ V = κ = κ. 6 (5.) V přípaě vo nabitých boů s náboji q a Q je qq V = 4πε. (5.3) 3 Stejně bya zaveena v úvoní kz kasické echaniky. 4 Je o pohyb hotného stře izoované sostavy hotných boů. Hotný stře takové sostavy se sí pohybovat ovnoěně příočaře v ůsek zákona zachování hybnosti. 5 T ehčí 6 Opav to tey vypaá, jako by se jeen hotný bo o hotnosti μ pohybova v gavitační poi nehybného centa o hotnosti M.

3 K přenášce NUFY8 Teoetická echanika pozatíní čební text, veze 5. Pohyb v poi centání síy Leoš Dvořák, MFF UK Paha, 4 Hotný bo v poi centání síy: agangián ve sféických sořanicích Lagangeovy ovnice po agangián (5.) bee zapisovat ve sféických sořanicích, θ ϕ. Postatné je ozepsat ychost hotného bo poocí zobecněných ychostí, θ a ϕ. Nejjenošší je ozožit vekto ychosti v = o koých sěů poé sořanicových ča 8, v = e + θe + sin( θ) ϕe ϕ. (5.4) θ a 7 = + ( θ) + ( sin( θ) ϕ) Veikost ychosti na ho o je 9 Po osazení o (5.) ostáváe agangián ve tva v. (5.5) ( sin ) ( ) L= µ + θ + θϕ V (5.6) Lagangeovy ovnice a jejich řešení Pohyb hotného bo je án sostavo tří Lagangeových ovnic L L = L L = θ θ L L = ϕ ϕ Po osazení přísšných eivací ostanee konkétní poob ovnic: 7 Mohi bycho je saozřejě zapsat i v katézských sořanicích, ae pak bycho s jejich řešení zcea jistě nehni. Šo by totiž o sostav tří povázaných ifeenciáních ovnic; stačí si věoit, že v kažé z ovnic ( ) ( ) by se objeviy eivace čen V = V x + y + z. Sféické sořanice ná sitaci výazně zjenoší. V Lagangeových ovnicích hého h jse ostatně zvykí pacovat se zobecněnýi sořanicei teď postě za zobecněné sořanice vezee, θ a ϕ. 8 Dobře se to á přestavit na zeěkoi nebo na gobs: e je jenotkový vekto koý k povch Zeě (tj. vekto v aiání sě), e θ jenotkový vekto ve sě poeník, e ϕ jenotkový vekto ve sě ovnoběžky. Rychost v aiání sě je (je ovna časové zěně sořanice ), ychost ve sě poeník je θ (je o pohyb po kžnici pooě, úhová ychost je θ ), ychost ve sě ovnoběžky je sin( θ) ϕ (opět je o pohyb po kžnici, tentokát pooě sinθ, úhová ychost je ϕ ). 9 Stejný výseek bycho ostai, kybycho eivovai poe čas vztahy po přepočet sféických sořanic na katézské ( x = sinθ cosϕ apo.) a sečeti x + y + z. Jeno za život by si čověk ě tento výpočet zksit, je to ae poněk zohavé Rozka o sěů, v nichž osto sořanice, θ a ϕ je opav postatně jenošší a kyž si ho čověk ozysí, á se ěat v postatě z havy. Sybo vnky na L, kteý jse psai v (5.), si ž opstíe. Z (5.6) je L =µ L ϕ = µ sin θϕ a L ϕ =. L = + V, L θ = µ, θ L θ = µ sin θ cos θϕ,, µ ( θ sin θϕ ) 3

4 K přenášce NUFY8 Teoetická echanika pozatíní čební text, veze 5. Pohyb v poi centání síy Leoš Dvořák, MFF UK Paha, 4 V µ µ θ µ θϕ + =, (5.7) ( ) sin ( ) sin cos µ θ µ θ θϕ =, (5.8) Nejjenošší je posení ovnice, (5.9). Z ní okažitě pyne ( sin ) µ θϕ =. (5.9) čii ozn. µ sin θϕ= konst. =, (5.) ϕ µ sin θ = (5.) Poznaeneje, že (5.) á i jasný fyzikání význa zkste si ozyset, jaký. Co s ovnicí (5.8)? Vypaá sožitě a sožité by zřejě byo i její obecné řešení. Naštěstí ovnici není ntno řešit ve zcea obecné přípaě. Je jasné, že pohyb be ovinný. 3 A tto ovin si ůžee zvoit. V naše přípaě be nejjenošší říci, že bo obíhá v ovníkové ovině, tey v ovině 4 π θ =. (5.) V toto přípaě je sin θ =, cos θ = a θ =, takže ovnice (5.8) je spněna ienticky. 5 Zbývá ná vyřešit ž jen ovnici (5.7). Po osazení (5.) a (5.) z ní ostáváe V ( µ ) µ + = µ. (5.3) Je ž o obyčejno ifeenciání ovnici, nezávise poěnno je čas. 6 Kybycho tto ovnici ěi vyřešit, osaii bycho výsené (t) o (5.) a integací čii ϕ ( t). Bohže, ovnici (5.3) jenoše anayticky řešit neíe. Můžee ae něco jiného: spočítat tva tajektoie. Pok jso a θ konstantní, je o pohyb po kžnici s pooěe sin θ, ychost pohyb je sinθϕ. Z toho je viět, že je ovno oent hybnosti (ozysete si, že to je pava) a z úvoního kz kasické echaniky ž víe, že v centání siové poi se oent hybnosti zachovává. Obecně je z-ovo sožko oent hybnosti. 3 Pyne to ze sféické syetie pobé. (Jenoše řečeno, obíhající hotný bo neá žáný ůvo, aby hn z oviny oběh.) Tento výseek také znáe z úvoního kz kasické echaniky, ke se okazje ze zákona zachování oent hybnosti. 4 Můžee to říci i obáceně: Sostav sořanic natočíe tak, aby ovina θ = π spývaa s ovino oběh. Z tohoto vyjáření je viět, že naše voba je bez újy na obecnosti. 5 Há! 6 Deivaci V v konkétních přípaech pře řešení ovnice postě vypočtee z V= V ( ), např. z (5.) nebo (5.3). 4

5 K přenášce NUFY8 Teoetická echanika pozatíní čební text, veze 5. Pohyb v poi centání síy Leoš Dvořák, MFF UK Paha, 4 O časové závisosti k tva tajektoie Tva tajektoie je án závisostí ( ϕ ) vyjáříe eivaci poe čas poocí eivace poe ϕ. Patí (5.): Rovnici (5.3) nejpve pavíe na =. Abycho z (5.3) ostai ovnici po tva tajektoie, ϕ =, tey s vyžití (5.) a ϕ = ϕ =. (5.4) ϕ µ ϕ V µ =. 3 µ Kyž nyní o evé stany osaíe za časové eivace (5.4), ostanee ovnici po tva tajektoie: V 3 = µ ϕ ϕ µ. 7 (5.5) Binetův vzoec Teď ná poůže překvapivý obat: Místo závise poěnné bee žívat poěnno =. (5.6) Je tey =, o V V V = = = ϕ ϕ. Navíc = = ϕ ϕ. Po osazení o (5.5) ostáváe a o po úpavě konečně Tento vztah se nazývá Binetův vzoec. 8 Požití Binetova vzoce v přípaě V = k/ V + = µ ϕ ϕ µ V ϕ + =. (5.7) Ve vei ůežité přípaě, ky potenciání enegie je nepřío úěná vzáenosti 9, k V =, (5.8) V k = k k = =, takže (5.7) á je řešení (5.7) překvapivě jenoché. Je totiž ( ) 7 Tohe vypaá sna ještě sožitěji než (5.3), že? Neěste se, za ao chvíi se to výazně zjenoší. 8 Něky se též při jeho zápis požívá čáka jako sybo eivace poe φ, takže Binetův vzoec á pak tva µ V + =. 9 Viz vztahy (5.) a (5.3) po gavitační přitahování a eektostaticko inteakci. 5

6 K přenášce NUFY8 Teoetická echanika pozatíní čební text, veze 5. Pohyb v poi centání síy Leoš Dvořák, MFF UK Paha, 4 µ k ϕ + =. (5.9) Konkétně po přípa gavitačního přitahování, viz (5.), je κ Mµ ϕ + = (5.3) Jak tto ovnici řešit? Vei jenoše! Je o ineání ifeenciání ovnici hého řá s konstantníi koeficienty. Její obecné řešení ostanee jako sočet ovnice s novo pavo stano, tey ovnice ϕ + = (5.3) a patikáního řešení. To ae ůžee vei jenoše vzít ve tva = κ Mµ. Navíc, ovnice (5.3) ná jistě něco připoíná. Má tva ovnice po ineání haonický osciáto! Její řešení ůžee ovno psát ve tva = Acos( ϕ ϕ ). Obecné řešení ovnice (5.3) je tey κ Mµ = + Acosϕ. (5.3) Tento vztah ž fakticky čje tva tajektoie. Dosaíe-i o něj = a označíe a navíc A = 3 p ε, pyne z (5.3) Toto je již ovnice kžeosečky v poání tva, jak ji znáe z geoetie a také z úvoního kz kasické echaniky. 4 κ Mµ = p p =. (5.33) + ε cos ϕ Závěečná poznáka Binetův vzoec ze požít i v přípaě, že se potenciá iší o závisosti /. 5 Ze o sožitějších pobéů nepůjee ae v příští kapitoe bee získané výseky apikovat na histoicky ůežitý Rthefoův expeient. x + x =, jen ísto čas t ze áe jako nezávise poěnno φ a ísto x áe. Bez újy na obecnosti bee áe bát ϕ =. Voba této konstanty znaená jen vob natočení koe osy z. Konstanta A ůže být ibovoná. Zkste si ho o (5.3) osait a přesvěčit se, že je opav řešení. 3 A bya ibovoná konstanta, takže ná nic nebání vyjářit ji jako sočin /p a jiné ibovoné konstanty ε. 4 Po ε < je o eips (po ε = speciáně o kžnici), po ε = je tajektoií paaboa, po ε > hypeboa. 5 Napříka v obecné teoii eativity vyje po pohyb panety v gavitační poi Snce vztah anaogický Binetov vzoci; z něj ze spočíst posv peihéia Meka. 6