BAKALÁŘSKÁ PRÁCE. Klára Jelenová. Sbírka úloh z finanční matematiky

Transkript

1 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Klára Jelenová Sbírka úloh z finanční matematiky Katedra ravděodobnosti a matematické statistiky Vedoucí bakalářské ráce: RNDr. Jitka Zichová, Dr. Studijní rogram: Matematika, finanční matematika 2009

2 Dovoluji si na tomto místě oděkovat RNDr. Jitce Zichové, Dr., vedoucí bakalářské ráce, za její odoru i cenné rady ři vzniku této bakalářské ráce. Prohlašuji, že jsem svou bakalářskou ráci nasala samostatně a výhradně s oužitím citovaných ramenů. Souhlasím se zaůjčováním ráce a jejím zveřejňováním. V Praze dne Klára Jelenová 2

3 Obsah Úvod 6 Úrokování 7. Jednoduché úrokování Složené úrokování Polhůtné a ředlhůtné úrokování Polhůtné úrokování Předlhůtné úrokování Sojité úrokování Úrokové míry závislé na čase Příklady Finanční toky a důchody Diskrétní finanční tok Sojitý finanční tok Durace, konvexita Důchod Příklady Výnosové rovnice, vnitřní míry výnosnosti a hodnocení investičních rojektů Vnitřní míra výnosnosti Hodnocení investičních rojektů Jiné tyy vnitřní míry výnosnosti Vliv inflace na výnosovou rovnici Úrokové míry Příklady

4 4 Dluhoisy Sravedlivá cena obligace Durace dluhoisů Imunizace Příklady Oce Tyy ocí a jejich arametry Příklady Literatura 02 4

5 Název ráce: Sbírka úloh z finanční matematiky Autor: Klára Jelenová Katedra: Katedra ravděodobnosti a matematické statistiky Vedoucí bakalářské ráce: RNDr. Jitka Zichová, Dr. vedoucího: zichova@karlin.mff.cuni.cz Abstrakt: Předložená ráce ředstavuje sbírku úloh k základním řednáškám z finanční matematiky - k Úvodu do financí a k Matematickým metodám ve financích. Okrajově se dotýká i řednášky Finančního managementu. Motivem k jejímu nasání byla myšlenka omoci studentům Matematicko-fyzikální fakulty Univerzity Karlovy lée ochoit robíranou teorii v oblasti financí. Během bakalářského studia musí studenti absolvovat mnoho ředmětů a není bohužel dostatek rostoru mít k řednáškám týkajícím se financí i cvičení. Práce by měla řisět k samostatnému rocvičování látky, k rohloubení znalostí v oblasti finanční matematiky a v alikaci naučených matematických vzorců. Pro leší ochoení a kontrolu jsou říklady řešeny odrobně, některé jsou dolněny o vzorová řešení v MS Excelu verze 2007) či rogramu Mathematica verze 7.0.0). Klíčová slova: úrok, finanční tok, výnos, dluhois, oce. Title: An exercise book on financial mathematics Author: Klára Jelenová Deartment: Deartment of Probability and Mathematical Statistics Suervisor: RNDr. Jitka Zichová, Dr. Suervisor s address: zichova@karlin.mff.cuni.cz Abstract: This Bachelor Thesis reresents an Exercise Book to the essential lectures of Financial Mathematics Introduction to Finance and Mathematical Methods in Finance). It also covers some toics of Financial Management, but marginally. The aim of this workbook is to hel the students of the Faculty of Mathematics and Physics at Charles University to understand the theory of Finance better. The reason is that during their studies, students have to attend a lot of lectures and other courses - so there is not enough time to organise workshos and ractise the theory. This workbook was considered for self-studying, to deeen the knowledge of Financial Mathematics and ractise the learnt formulas. All exercises are accomanied by detailed solution - for better understanding and verification of results, some of them have also the exemlary solutions in MS Excel 2007 and Mathematica software version 7.0.0). Keywords: interest, cashflow, yield, bond, otion. 5

6 Úvod Tato ráce je sbírkou úloh z finanční matematiky dolněná o říslušnou teorii a otřebné matematické vzorce. Některé vzorce jsou odvozeny římo v řešených říkladech. Veškeré věty jsou kvůli stručnosti uvedeny bez důkazů. Lze je však dohledat v literatuře, na kterou se autor odkazuje. Kaitola se věnuje úrokování. Seznamuje s ojmy současná a budoucí hodnota. Je zaměřena zejména na rozdíly mezi jednoduchým a složeným úrokováním. V říkladech se klade důraz na různé frekvence úrokování. S úrokováním jsou velmi úzce sjaty ůjčky. I o nich se v této kaitole dočteme. Více informací k ojmům z této kaitoly se dá najít v knihách [], [3] a [5]. Kaitola 2 zavádí ojem finanční tok a důchod. Zaobírá se roblematikou výše slátek ůjčky, rozdílem mezi olhůtným a ředlhůtným důchodem a zavádí ojmy durace a konvexita. K této kaitole se vztahují stejné knihy jako ke kaitole. V kaitole 3 se zmíníme o vnitřní míře výnosnosti a jejích modifikacích. Rozebereme její hlavní roli ři rozhodování o výhodnosti investičních rojektů. Uvedeme i další metody, které se věnují orovnání investičních rojektů. Najdeme zde i zmínku o vlivu inflace na výnosovou rovnici. Více naříklad viz kniha [3]. Kaitola 4 ojednává o dluhoisech. V říkladech se objevují řevážně kuónové obligace. Kuónové latby ředstavují seciální říad finančních toků. Jsou zde tedy využity vzorce z kaitoly 2. Oět je zde zmíněna durace. Tentokrát se na ni zaměříme i v říkladech. Navíc je sem zahrnuta imunizace dluhoisů. O základních charakteristikách dluhoisů se můžeme dočíst v knihách [2] a [3], imunizace je vyložena v knihách [4] a [5]. Poslední stručná kaitola je věnována základům teorie ocí. Hovoří o zisku res. ztrátě) z rodeje nebo kouě CALL nebo PUT oce. K této kaitole se hlavně vztahuje kniha [2]. První čtyři kaitoly solu souvisejí a jsou značně roojeny. Často se setkáme s odkazem na jinou kaitolu. Aby čtenář získal určitý řehled o finanční matematice, je vhodné rostudovat si všechny kaitoly. Pro větší řehlednost je ve všech kaitolách oužito jednotné značení. Zde je na místě uozornit, že ne vždy se shoduje se značením, které se vyskytuje v literatuře v odkazech. Symbol značí konec říkladu. 6

7 Kaitola Úrokování Úrok interest) je odměna oskytovateli ůjčky za odloženou sotřebu vyjádřená v eněžních jednotkách. Z ohledu osoby, která si ůjčuje, se jedná o cenu, kterou musí zalatit, okud si eníze vyůjčí. Vyůjčenou částku označujeme jako jistinu rincial). Poskytovatele ůjčky nazýváme věřitel creditor). Na druhé straně stojí dlužník debtor) - osoba, která si ůjčuje od věřitele. Výši úroku určuje úroková míra interest rate). Důležitá je i doba slácení dluhu, res. očet období úročení ůjčky. Hodnoty úrokové míry musí být konzistentní s obdobími úročení. Proto si vždy musíme dát ozor na to, se kterou úrokovou mírou očítáme zda se jedná o roční, ůlroční, měsíční aod.).. Jednoduché úrokování Základním tyem úrokování je jednoduché úrokování simle interest). V tomto říadě se o celou dobu slácení dluhu očítá úrok ve vzorcích označován jako I) ouzezjistiny. Základní vzorec má tvar FV = PV + i n).) Značení: PV...jistina, současná hodnota rincial, resent value) FV...budoucí hodnota vyůjčené částky future value) i...roční úroková míra.a.) n...očet období úročení v letech) 7

8 Úrok I za dané období je dán vzorcem I = PV i n.2) Vidíme tedy, že budoucí hodnota jistiny je rovna součtu současné hodnoty vyůjčené částky a řisaného úroku, neboli FV = PV + I.3) Diskontování Diskontování můžeme označit jako oačný roces k úročení. Důležitým ojmem je zde diskontní míra discount rate). Roční diskontní míru značíme symbolem d. Pokud onecháme označení z rovnice.), je diskontní míra dána vzorcem i d = +i n Z rovnice.) odvodíme vztah ro současnou hodnotu: PV = FV = FV d n).4) +i n Poznámka: Rozlišujeme dva tyy ůjček: ůjčka s úrokem: - vyůjčíme si částku PV na n let s roční úrokovou mírou i a vrátíme: FV = PV + i n) - slatná částka je odvozena od výše ůjčky, olhůtný úrok - míra zisku ro věřitele: µ u = FV PV PV = PV i n PV = i n.5) ůjčka s diskontem: - vyůjčíme si částku PV na n let s roční diskontní mírou d a vrátíme částku FV: PV = FV FV d n - výše ůjčky je odvozena od slatné částky, ředlhůtný úrok - míra zisku ro věřitele: µ d = FV PV PV 8 = d n d n.6)

9 Pokud i = d: µ u = i n µ d = i n i n µ u <µ d, jinak řečeno: ro věřitele je výhodnější ůjčka s diskontem..2 Složené úrokování V říadě, že se v každém období řiíše úrok k jistině a v dalších obdobích se znovu úročí, nazýváme toto úrokování složené úrokování comound interest). Vzorec ro výočet budoucí hodnoty : FV = PV + i) n,.7) oužívaná označení jsou totožná se symboly z rovnice.). Diskontování Formuli ro diskontování ři sojitém úrokování lze odvodit z rovnice.7): PV = FV + i) n.8) Pro diskontování se oužívá diskontní faktor označovaný v: v = +i.9) Rovnici.8) lze tedy vyjádřit omocí diskontního faktoru následovně: PV = FV v n.0).3 Polhůtné a ředlhůtné úrokování Úročení nemusí být ouze roční. Jistina se může úročit -krát ročně. Musíme tedy očítat také s říslušnou úrokovou mírou. Označme roční úrokovou míru i = i ),jetotzv.nominální úroková míra. 9

10 Nominální úroková míra ro -tinu roku je rovna: i ).) Jak naovídá název kaitoly, rozlišujeme dva tyy úrokování..3. Polhůtné úrokování Předokládejme, že jsme uložili částku na rok. Úrok i ), který se dále úročí složeně s roční mírou i ef,seřiisujena konci každé -tiny roku. Celkový říjem z úroků na konci roku v čase ) má hodnotu t=0 i ) + i ef) t i ) = i ef.2) + i ef ) Chceme, aby se součet.2) rovnal efektivní úrokové míře effective interest rate) i ef, která rerezentuje úrokový výnos z částky řisaný jednorázově na konci roku. Po úravě dostáváme i ) i ef = i + i ef ) ef +i ef = + i ) ).3).3.2 Předlhůtné úrokování Předokládejme, že jsme uložili částku na rok. Úrok d ), který se dále úročí složeně s roční mírou i ef,seřiisujena začátku každé -tiny roku. Označme v = +i ef. Celkový říjem z úroků, kdyby byl vylacen na začátku roku v čase 0) je d ) t=0 v t d ) = v.4) v Požadujeme, aby se součet.4) rovnal efektivní diskontní míře d ef. d ) v v = d ef v = = d ef d ef = d ) +i ef ).5) 0

11 Platí: d ef = i ef +i ef d ) = i ) + i ) Poznámka: Nadále budeme sát i ef = i, d ef = d..4 Sojité úrokování Pokud frekvence úročení roste nade všechny meze, ak latí lim i ) = lim + i) + i) x = lim = x 0 + x d + i)y = d dy y=0 dy ex [y log + i)] = y=0 + i) y log + i) =log+i) =δ.6) y=0 Symbolem δ označujeme intenzitu úroku. Z rovnice.6) jsou zřejmé vztahy: +i = e δ v = e δ.7) Nyní již máme vše řiraveno ro zavedení vzorce ro sojité úrokování continuos comounding): FV = PV e δ t.8).5 Úrokové míry závislé na čase Obecnější řístu ředstavuje modelování úrokových měr jako funkcí času. Mějme časový interval t, t + h),h>0. V čase t investujeme, v čase t + h máme + h i h t), kde i h t) je nominální úroková míra.

12 Seciální říady: ) h =,i h t) =i t) =i h i h t) =i... efektivní úroková míra 2) h =,i ht) ozn. = i ) t) =i ) h i h t) = i... nominální úroková míra ro -tinu roku lim h 0+ i h) t) =δt)... intenzita úroku Akumulační faktor Označíme +h i h t) =At, t + h)..9) Tento akumulační faktor ředstavuje zhodnocení částky za časový interval délky h. Pokud v čase t investujeme C, otom v čase t 2 >t máme C At,t 2 ). Seciální říad: At,t 2 )=+i) t 2 t... složené úrokování Akumulačním faktorem je funkce dvou roměnných s vlastnostmi: ) At, t) = 2) rinci konzistence okud t 0 t t 2... t n ; n 2, ak latí: Zřejmě latí i h) t) = At,t+h) h δt) = lim h 0+ At,t+h) h At 0,t n )=At 0,t ) At,t 2 )... At n,t n ) Věta. Nechť δt) aat 0,t) jsou sojité funkce roměnné t ro t>t 0 anechťlatí rinci konzistence. Pak [ t2 ] At,t 2 )=ex δs) ds..20) t Důkaz lze najít v knize [5]. Seciální říad: δs) =δ : At,t 2 )=e δ t 2 t ) =+i) t 2 t... složené úrokování 2

13 Diskontování Nechť v čase 0 investujeme C avčaset>0máme. Zrovnice=C A0,t) je odvozen ředis ro diskontní faktor vt) = A0,t),.2) dle věty. lze také diskontní faktor vyjádřit vzorcem [ t ] vt) =ex δs) ds..22) 0 Seciální říad: δs) =δ : vt) =e δ t = v t Obecněji: v čase t investujeme C, včaset 2 >t > 0mámeC 2, C 2 = C At,t 2 )=C A0,t 2) = C A0,t ) vt ) vt 2 ) Vychází nám C = C 2 vt [ 2) vt ) = C t2 ] 2 ex δs) ds t.23).6 Příklady Příklad. Paní Vosecká uvažuje o ůjčce na novou kouelnu ve výši Kč s dobou slatnosti 9 měsíců. Na výběr má ůjčku s diskontem s roční diskontní mírou 7 % nebo ůjčku s úrokem, kde roční úroková míra činí 7,5 %, úvěr se úročí jednoduše. Kterou ůjčku by si měla aní Vosecká zvolit? Řešení: Paní Vosecká by si měla zvolit tu ůjčku, ři které zalatí menší úrok. O dvou tyech ůjčky jsme zmínili v oznámce u jednoduchého úrokování v kaitole.. Pro ůjčku s diskontem máme FV = Kč n =0, 75 let d =7%=0, 07 3

14 Klientce bude ůjčeno PV d = FV FV d n ro naše hodnoty: PV d = , 07 0, 75 = Kč Předlhůtný úrok, který aní Vosecká uhradí bance, je = 9 87 Kč. Pro ůjčku s úrokem máme PV = Kč n =0, 75 let i =7, 5%=0, 075 Paní Vosecká by si v tomto v tomto říadě ůjčila Kč a bance by vracela FV = , 075 0, 75) = Kč Polhůtný úrok, který by aní Vosecká zalatila bance, je = Kč. Výhodnější je tedy ro aní Voseckou ůjčka s diskontem. Pro banku by naoak bylo výhodnější ůjčit klientce s úrokem, neboť míra zisku ro věřitele ři ůjčce s úrokem sočítaná odle.5) je vyšší než míra zisku ro ůjčku s diskontem odle rovnice.6). µ u = i n =0, 075 0, 75 = 0, µ d = d n = d n 0,07 0,75 0,07 0,075 = 0, 0554 Příklad.2 Paní Mladá se v roce 987 rozhodla uložit do banky Kč. V roce 2009 se však bojí, že banka zkrachuje, a tak si chce své uložené eníze vybrat ro jednoduchost se výběr uskuteční ve stejný den jako se uskutečnil řed 22 lety vklad). Vklad se úročil složeně s roční nominální úrokovou mírou 4 % jednou za rok. 4

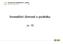
15 a) Kolik by měla banka aní Mladé dnes vylatit? b) O kolik by dnes měla aní Mladá méně, okud by se vklad úročil jednoduše? Řešení: Zajímá nás budoucí hodnota FV vkladu v hodnotě Kč. Víme: PV = Kč n =22let i =4%=0, 04 a) K výočtu oužijeme rovnici.7): FV = PV + i) n. Tedy FV = , 04) 22 = Kč. Pokud bychom chtěli tuto úlohu vyřešit v Excelu, oužili bychom funkci BUDHODNOTA a do argumentů bychom zadali: Sazba: 0,04 Per: 22 Slátka: 0 lze onechat nevylněné) Souč hod: Ty: nevylňujeme Výsledný říkaz tedy vyadá následovně: =BUDHODNOTA0, 04; 22; 0; 0000). Řešení je samozřejmě totožné s ředchozím výsledkem. b) Pro jednoduché úrokování oužijeme vzorec.): FV = PV + i n). Po dosazení FV = , 04 22). Budoucí hodnota ři jednoduchém úročení se rovná Kč. Zde by byl úrok roven ouhým Kč neboli každý rok se k ůvodnímu vkladu řiočetlo 400 Kč o dobu 22 let). Rozdíl budoucích hodnot ři složeném a jednoduchém úročení je = Kč. 5

16 24000 FV jednoduche slozene Obrázek.: Složené a jednoduché úročení rok Na obrázku. vidíme grafické orovnání stavu účtu v růběhu 22 let. Vidíme, že ři složeném úročení hodnota účtu roste exonenciálně, zatímco ři jednoduchém úročení roste účet lineárně. Příklad.3 Uvažujme odobnou situaci jako v Příkladu.2, nyní ale ředokládejme měsíční úročení. Ostatní údaje jsou totožné. Kolik by si aní Mladá vybrala dnes z banky v tomto říadě? Řešení: Zajímá nás tedy oět budoucí hodnota FV vkladu v hodnotě Kč. Nyní ale víme: PV = Kč n =22let =2 i ) = i 2) =4%=0, 04 Měsíční nominální úroková míra je tedy dle.) rovna 0,04. 2 Dle vzorce.3) víme, že: + i = + i ) ). Teď již můžeme oužít rov- 6

17 nici.7), tím mám vznikne vzorec ro složené úročení -krát ročně: FV = PV + i ) n ).24) Budoucí hodnota ři měsíčním úročení se rovná: FV = ) 0, = Kč. 2 Při složeném měsíčním úročení získáme o 375 Kč více než ři složeném ročním. Použití funkce BUDHODNOTA v Excelu je obdoba minulého říadu. Nesmíme však zaomenout na zadání srávné úrokové sazby - v tomto říadě měsíční - a na říslušný očet úrokovacích období: Sazba: 0,04 2 Per: 2 22 = 264) Slátka: 0 lze onechat nevylněné) Souč hod: Ty: nevylňujeme =BUDHODNOTA0, 04/2; 2 22; 0; 0000). Poznámky k říkladu.3: ) V říadě, že by se jednalo o měsíční jednoduché úročení, myšlenka zůstává stejná jako u ročního. Každé období se na účet řiíše říslušný úrok z uložené částky, tedy: FV = PV + n i ) ).25) Uravením tohoto vzorce však zjistíme, že je totožný se vzorcem ro jednoduché roční úročení. Vidíme tedy, že na rozdíl od složeného úročení se výsledná částka ři měsíčním úročení oroti ročnímu) nezmění. To latí samozřejmě i ro jiná úročení -krát do roka. Je to tím, že řisané úroky se neúročí. 7

18 2) Pokud by se frekvence úročení blížila, ak bychom oužili vzorec.8) ro sojité úrokování, kde: i ) δ =0, 04 t =22let a výsledek by vyadal následovně: FV = e 0,04 22 = Kč Pro srovnání ukažme, jaké výše by dosahovala budoucí hodnota ři složeném denním úročení = 365). FV = ) 0, = Kč 365 Rozdíl mezi sojitým a složeným denním úrokováním je neatrný. Příklad.4 Pan Zlatý řemýšlí, jak nejvýhodněji uložit Kč. Doufá, že eníze nebude otřebovat říští 4 roky. Rozhoduje se mezi třemi bankami. Každá nabízí jinou úrokovou sazbu a jinou frekvenci úročení viz tabulka.). Jakou banku by měl an Zlatý vyhodnotit jako ro něj nejvýhodnější? Předokládáme, že banky úročí vklad složeně. Banka Úrok.a.) Frekvence úročení ) banka A 3,95 % 2 banka B 4,00 % 3 banka C 4,05 % Tabulka. Řešení: Mohli bychom samozřejmě oět očítat budoucí hodnotu ro každou banku zvlášť dle vzorce.24): banka A: banka B: FV = FV = ) 0, = ) 0, =

19 banka C: FV = , 0405) 4 = 72 0 Existuje však i jednodušší zůsob, jak tuto úlohu vyřešit. Slouží nám k tomu efektivní úroková míra i ef. Dle vzorce.3) se efektivní úroková míra rovná: i ef = + i ) ) Stačí sočítat efektivní úrokové míry ro všechny banky a jejich orovnáním zjistíme, která je nejvýhodnější: banka A: banka B: banka C: i ef = i ef = + + ) 0, =0, = 4, 0223% 2 ) 0, 04 3 =0, = 4, 0536% 3 i ef =+0, 0405) =0, 0405 = 4, 05% Nejvyšší efektivní úroková míra vyšla ro banku B, tedy nejvýhodnější by bylo vložit eníze do banky B. I Excel umí sočítat efektivní úrokovou míru. Použijeme funkci EFFECT, do argumentů zadáme nař. ro banku A následující: Úrok: 0,0395 Období: 2 Výsledný vzorec: =EFFECT0, 0395; 2) Poznámky:. Kalendářní konvence Pro výočty úroku je důležité vědět, odle jaké konvence máme očítat dobu, o kterou úročíme nař. ři očítání tzv. alikvótního úroku - viz kaitola 4: Dluhoisy). Rozlišujeme různé tyy kalendářních konvencí: ) ACT/ skutečný očet kalendářních dní vztahovaný k bazickému roku o 360 dnech 9

20 2) ACT/ skutečný očet kalendářních dní vztahovaný k bazickému roku o 365 dnech řestuný rok se bere jako rok, který má 365 dní) 3) ACT/ACT... skutečný očet kalendářních dní vztahovaný ke skutečnému očtu dní v roce 4) 30/ měsíc má 30 dní, vztahováno k bazickému roku o 360 dnech zde se ještě rozlišuje EUR 30/360 a US 30/360 - neatrně se liší výočet dní mezi dvěma daty, viz nař. kniha [3] ) 2. Smíšené úrokování Pokud doba slatnosti není celočíselným násobkem délky úrokovacího období, oužívá se často tzv. smíšené úrokování. Smíšené úrokování úročí složeně řes celočíselný očet období a ro necelé období oužívá úrokování jednoduché. Neboli okud T = T + {T }, T celá část T, 0 < {T } < kde T je očet úrokovacích období, ak budoucí hodnota v čase T je FV = PV + i) T + i {T }).26) Na následujícím říkladu si ukážeme, jak očítáme úroky v říadě, kdy je čas udán očtem dní a úroková míra je roční. Příklad.5 Pan Veselý se na začátku roku 2005 rozhodl, že si ostaví dům. Sočítal si, že dům ho bude stát 3 miliony Kč, na účtu měl však jen Kč. Uložil tedy 2. února 2005 všechny své eníze do banky s roční nominální úrokovou mírou 3 %. Jeho vklad se úročí měsíčně složeně. Dne. srna 2006 účet zrušil a následující den si chybějící eníze vyůjčil od banky s roční úrokovou mírou 3,6 %, která jeho ůjčku úročí jednoduše. Půjčka bude slacena jednorázově. Dne 28. června 2007 an Veselý vyhrál v loterii Kč o zdanění) a rozhodl se, že se okusí slatit svůj dluh. Bude tato částka anu Veselému stačit na slacení celého dluhu? Předokládejme kalendářní konvenci ACT/360. Řešení: Začneme tím, že si sočítáme, kolik měl an Veselý na účtu dne. srna Hodnota vkladu. srna 2006 je dle.24): FV = PV + i ) 2 n 2),.27) 2 20

21 kde i 2) =0, 03 a n je očet let. Od 2. února 2005 do 2. srna 2006 ulyne 8měsícůo30dnechazbývá9dnů,nebolivletechn =, 5+ 9 =, Vidíme tedy, že očet období úročení není celé číslo. Nyní si ukážeme, o kolik by se lišil stav účtu ři úrokování složeném oroti smíšenému. Složené úrokování: FV = ) 0, 03 2,525 = Kč 2 V Excelu funguje vše analogicky jako v Příkladu.2, jen musíme zadat: Per : 2*,525 =8,3) Celkově tedy: =BUDHODNOTA0, 03/2; 8, 3; 0; ). Smíšené úrokování dle.26)): FV = ) 0, 03 8 ) 0, , 3 = Kč Výsledek dvou různých zůsobů úročení se v našem říadě téměř neliší. Uvažujme tedy, že dne. srna 2006 bude mít tedy an Veselý na účtu Kč. Nyní se vraťme k našemu říkladu. Potřebujeme znát výši ůjčky, která je zřejmě = Kč. Budoucí hodnota ři jednoduchém úročení se sočítá následovně: FV = PV + t ) 360 i,.28) kde t je očet dní úročení. Od 2. srna 2006 den oskytnutí ůjčky) do 28. června 2007 ulyne 320 dní. FV = ) 360 0, 036 = Kč Panu Veselému tedy bude jeho Kč stačit na slacení úvěru i s veškerými úroky. 2

22 Nyní si ještě ukážeme říklad na diskontování. Příklad.6 Paní Dobrá bude za 5 let otřebovat Kč na řevod družstevního bytu do osobního vlastnictví. Nyní má možnost vložit své úsory na vklad úročený čtvrtletně složeně s roční nominální úrokovou mírou 4,4 %. Kolik musí do banky vložit, aby měla za 5 let dostatek eněz? Řešení: Ze zadání: FV = Kč n =5let =4 i ) =4, 4%=0, 044 Čtvrtletní nominální úroková míra je tedy dle.) rovna: 0,044 =0, 0. 4 Známe vzorec ro současnou hodnotu: PV = FV i + ) ) n Konkrétně: PV = = Kč. + 0, 0) 4 5 Při oužití Excelu: =SOUČHODNOTA0, 0; 20; ; 50000). Paní Dobrá by si dnes musela do banky vložit Kč, aby měla za 5 let na účtu otřebných Kč. 22

23 Na závěr kaitoly zařaďme říklad na úrokové sazby závislé na čase. Příklad.7 Důležitým vzorcem ro výočet intenzity úroku δt) je Stoodleyův vztah: s δt) = +, +r es t t > 0.29) kde, r a s jsou arametry. Najděte vztah ro výočet diskontního faktoru vt) za latnosti Stoodleyova vztahu. Řešení: Vyjdeme ze vzorce.22). [ vt) =ex [ =ex [ =ex t 0 t 0 t 0 ] δy) dy ) s + +r e s y + s r s es y +r e s y ] dy ) ] dy =ex { + s) t + [log + r e s y )] t 0 +r es t =ex[ + s) t] +r = +r e +s) t + r +r e t Poznámka: Pokud definujeme v = e +s) a v 2 = e, můžeme sát vt) = +r vt + r +r vt 2 Tento vztah vyjadřuje vážený růměr 2 diskontních faktorů s konstantními intenzitami. } 23

24 Kaitola 2 Finanční toky a důchody 2. Diskrétní finanční tok Jedná se o latby CF t,..., CF tn včasech0<t <... < t n ;častot j = j. Současná hodnota v čase 0) je n PV = CF tj vt j ) 2.) j= Seciálně : vt j )=v t j = e δ t j,v= +i = e δ Budoucí hodnota v čase T t n, zravidla T = t n ): n FV = CF tj At j,t), 2.2) j= kde At j,t)jeakumulační faktor daný vzorcem.20). Seciálně : At j,t)=+i) T t j = e δ T t j ). 2.2 Sojitý finanční tok Je definován intenzitou lateb ρt); t 0,T). Souhrnné množství lateb v časovém intervalu [t,t 2 ], 0 <t <t 2 <T je t2 t ρt) dt. Současná hodnota v čase 0): PV = T 0 ρt) vt) dt 2.3) 24

25 Budoucí hodnota v čase T ): FV = T 2.3 Durace, konvexita 0 ρt) At, T ) dt 2.4) Nechť CF =CF t,cf t2,..., CF tn ). Durace DCF,v) duration) označuje střední růměrnou) dobu slatnosti. Je to vážený růměr dob slatnosti jednotlivých lateb, vzorcem vyjádřeno: ro diskrétní finanční tok: DCF,v)= nj= t j CF tj v t j nj= CF tj v t j = nj= t j CF tj v t j PVCF,v) 2.5) Váhy: w j = CFt j vt j PVCF,v) ro sojitý finanční tok: DCF,v)= T 0 T 0 t ρt) vt dt ρt) vt dt 2.6) Duraci interretujeme v časových jednotkách. Této duraci se říká Macaulayho durace. Nyní odvodíme další interretaci durace. Budeme racovat s diskrétním finančním tokem. Derivováním dostáváme PV CF,v) v Z rovnice 2.7) vychází n = t j v tj CF tj j= = n v t j v t j CF tj j= = v DCF,v) PVCF,v) 2.7) DCF,v)= PV CF,v)/ v PVCF,v)/v 2.8) Duraci lze tedy ovažovat za míru elasticity současné hodnoty vzhledem k diskontnímu faktoru, obecněji vzhledem ke změnám v úrokových sazbách. 25

26 PV CF,i) Podobným zůsobem okud sočítáme )dojdemekevztahu: i PV CF,i)/ i DCF,i)= 2.9) PVCF,i)/ + i) Nechť i >0, ak relativní řírůstek současné hodnoty vyjádříme za omoci Taylorova rozvoje): PVCF,i + i) PVCF,i) PVCF,i) PVCF,i + i) PVCF,i) PVCF,i) = PV CF,i) PVCF,i) i + 2 PV CF,i) PVCF,i) i)2 2.0) = DCF,i) i 2.) +i Odvodíme ještě tvar durace v závislosti na intenzitě úroku δ = log + i). Zderivováním PVCF,δ)= n j= CF tj e δ t j docházímekevztahu PV CF,δ) n = CF tj e δ t j t j ), δ j= duraci lze tedy vyjádřit: PV CF,δ)/ δ log PVCF,δ) DCF,δ)= = PVCF,δ) δ Poznámka: durace není lineární funkcí CF. Existují další tyy durace: dolarová durace dollar duration): n D $ CF,v)= t j CF tj v t j j= Oroti Macaulayho duraci je lineární funkcí CF. modifikovaná durace modified duration): D mod CF,v)=v DCF,v)= DCF,i) +i S oužitím rovnice 2.9) dostáváme: D mod CF,i)= PVCF,i) PV CF,i) i 2.2) 26

27 Věta 2. Pro finanční tok s latbami CF tj 0včasech0 t... t n má durace následující vlastnosti: ) 0 D t n 2) D = t n CF tj =0,j =,..., n CF tn 0 3) DCF,δ) je klesající funkcí intenzity úroku δ Důkaz lze najít v knize [5]. Konvexita CCF,v) Pro konvexitu existuje také více interretací. Konvexita convexity) měří zakřivení křivky vztahu mezi současnou hodnotou a úrokovou mírou. Umožní nám tak zřesnit citlivost změny současné hodnoty na změnu úrokové míry. Jelikož se konvexita očítá ředevším u obligací, říklady si uvedeme v kaitole Dluhoisy. Podívejme se však zde na matematické vzorce: CCF,v)= nj= t j t j +) CF tj v t j PVCF,v) 2.3) Jednotkou konvexity je druhá mocnina časové jednotky. Vzhledem k tomu, že latí PV CF,i)= CCF,i) PVCF,i), + i) 2 vyjádříme oslední sčítanec v rozvoji 2.0) ve tvaru 2 PV CF,i) PVCF,i) i)2 = 2 + i) CCF,i) 2 i)2. Podobně jako existuje modifikovaná durace, zavedeme ojem modifikovaná konvexita modified convexity). C mod CF,i)= PV CF,i) PVCF,i) = CCF,i) 2.4) + i) 2 Celkově tedy dostáváme jiný tvar rovnice 2.0): PVCF,i + i) PVCF,i) PVCF,i) = D mod CF,i) i+ 2 C modcf,i) i) 2 2.5) 27

28 2.4 Důchod Důchod, také někdy označován jako anuita annuity), je diskrétní finanční tok. Všechny latby jsou stejné výše, stejného znaménka a uskutečňují se v ravidelných časových intervalech. Rozlišujeme 2 tyy: a) olhůtný annuity-immediate): latby důchodu na konci časových intervalů b) ředlhůtný annuity-due): latby důchodu na začátku časových intervalů ) Polhůtný důchod s ročními latbami Platby R o dobu n let, roční úroková míra i. Současná hodnota: PV = R n t= Budoucí hodnota v čase n): v t = R v vn v = R vn i ozn. = R a n 2.6) n FV = R + i) t = R + i)n i t=0 ozn. = R s n 2.7) 2) Předlhůtný důchod s ročními latbami Platby R o dobu n let, roční úroková míra i. Přiomeňme, že d = v = i viz.5)). +i Současná hodnota: PV = R n t=0 Budoucí hodnota v čase n): v t = R vn v = R vn d n FV = R + i) t = R + i) + i)n t= i = R + i)n d ozn. = R ä n 2.8) ozn. = R s n 2.9) v literatuře se často symbolem i označuje nominální úroková míra ro jedno úrokovací období ro roční úročení se rovná efektivní úrokové míře) 28

29 3) Důchod s latbami a úročením -krát do roka Platby R -krát ročně o dobu n let, roční efektivní úroková míra i ef. Roční nominální úroková míra i ). Platí +i ef = + i ) ), viz.3), v = +i ef. Současná hodnota olhůtný důchod): n PV = R t= v t = R v v n v = R vn i ) n = R t t= + i = R v n i) ) i ) = R a n 2.20) kde v i) =. + i ) Budoucí hodnota bude odvozena v říkladu 2.4 viz rovnice 2.3)) 4) Důchod s víceletou eriodou lateb Platby R -krát za k let o dobu n let, roční úroková míra i. Předokládejme n k celé. Současná hodnota olhůtný důchod): PV = R n k t= v t k = R v k vn v k = R v n + i) k = R vn i i + i) k = R a n s k 2.2) 5) Důchod s necelým očtem latebních období Platby R -krát ročně o dobu n let, n je necelé. Nechť n = k + z, 0 <z< Zde se nabízejí 2 možnosti výočtu : i) Definujeme současnou hodnotu ředisem PV = R vn i ) 2.22) 29

30 Jedná se o analogii vzorce 2.20). ii) V čase n budeme vylácet R z, z 0, ) : Současná hodnota: PV = R n =k t= v t + R z v n 2.23) V následujících 2 říadech se bude jednat o roční olhůtný důchod s latbami R o dobu n let. 6) Odložený důchod Realizace lateb je odložena o m let. Současná hodnota: PV = R m+n t=m+ Budoucí hodnota 2 v čase m + n): v t = R v m vn i = R v m a n 2.24) n FV = R + i) t = R + i)n i t=0 = R s n 2.25) 7) Přerušený důchod Po ukončení lateb se ještě úročí o dobu m let. Současná hodnota 3 : PV = R n t= Budoucí hodnota v čase m + n): v t = R vn i = R a n 2.26) m+n FV = R +i) t = R +i) m + i)n i t=m = R +i) m s n 2.27) 8) Věčný důchod = eretuita Poslounost olhůtných ročních lateb R není ukončena. Současná hodnota: PV = R v t v = R t= v = R i v = ) +i 2.28) 2 stejná jako u neodloženého důchodu 3 stejná jako u neřerušeného důchodu 30

31 Pro latbu R latí: R = PV i 2.29) Budoucí hodnota: není definována Na závěr uveďme zobecněný říad důchodu. 9) Důchod s roměnnou latbou, dobou lateb a úrokovou mírou: Platby R,.., R n včasech0<t <..<t n. Úroková míra ro období t j,t j ]jei j.definujmet 0 =0. Současná hodnota: n k ) tj t j PV = R k 2.30) +i j 2.5 Příklady k= j= Příklady věnující se duraci a konvexitě jsou uvedeny v kaitole Dluhoisy res. v kaitole 4.3. Příklady). Zde se zaměříme na důchody. Příklad 2. Paní Hořejší si lánuje vzít úvěr na 2 roky v hodnotě Kč. Slátky žádá ololetní. Banka jí oskytne roční nominální úrokovou míru 6,9 %. Paní Hořejší má nyní na účtu Kč. Tato částka se jí úročí složeně měsíčně s roční nominální úrokovou mírou 2,5 %. Každý ůlrok si navíc uloží na účet Kč, které ušetří ze mzdy. Bude mít na účtu vždy dostatek eněz na slácení úvěru? Řešení: Nejrve určíme výši slátek úvěru. Vyjdeme ze vztahu 2.20): ) n n PV = R t + i ) t= + i = ) i ) a odtud vyjádříme R R = PV i ) ) n = + i ) , , ) 2 2 = Kč