Derivace a průběh funkce.
|
|
|
- Romana Beránková
- před 9 lety
- Počet zobrazení:
Transkript
1 Derivace a průběh funkce. Robert Mařík 14. října 2008 Obsah 1 Základní myšlenky. 2 2 Přesné věty a definice 10 3 Okolí nevlastních bodů Sestrojení grafu funkce. 19
2 1 Základní myšlenky.
3 y x Uvažujme následující funkci.
4 y x Derivace je kladná (= směrnice tečny je kladná) tečna je rostoucí funkce je rostoucí.
5 y x Derivace je záporná (= směrnice tečny je záporná) tečna je klesající funkce je klesající.
6 y x Lokální maximum (bod, v jehož okolí není žádná vyšší funkční hodnota) má spojitá funkce v bodě, kde se mění z rostoucí na klesající. Lokální minimum (bod, v jehož okolí není žádná nižší funkční hodnota) má spojitá funkce v bodě, kde se mění z klesající na rostoucí. Je-li derivace nenulová, funkce nedosahuje lokálního extrému. Je-li v bodě lokální extrém, pak je derivace buď nulová (=: stacionární bod) nebo derivace neexistuje.
7 y x y < 0 (y má zápornou derivaci a tedy klesá) růst se zpomaluje a případně se mění na pokles; pokles se zrychluje funkce je v okolí bodu dotyku pod tečnou (=: konkávní)
8 y x y > 0 (y má kladnou derivaci a tedy roste) růst se zrychluje; pokles zpomaluje a případně se mění na růst funkce je v okolí bodu dotyku nad tečnou (=: konvexní)
9 y x Konvexnost se změní na konkavitu, nebo naopak, (=: funkce má inflexní bod) jedině v bodě, kde se změní znaménko druhé derivace, tj. jedině v bodě, kde je druhá derivace nulová, nebo kde má bod nespojitosti (a potom druhá derivace neexistuje). V inflexním bodě je nárůst nebo pokles funkčních hodnot nejrychlejší nebo nejpomalejší.
10 2 Přesné věty a definice
11 Definice (lokální extrém). Buď f funkce a x 0 Dom(f ). Řekneme, že funkce má v bodě x 0 lokální maximum, jestliže existuje ryzí okolí O(x 0 ), takové, že f (x 0 ) f (x) pro všechna x O(x 0 ). Je-li nerovnost ostrá,říkáme,že funkcef má v boděx 0 ostré lokální maximum. Platí-li opačné nerovnosti, říkáme, že funkce má v bodě x 0 lokální minimum a ostré lokální minimum. Lokální maximum a minimum nazýváme společným názvem lokální extrémy. Ostré lokální maximum a ostré lokální minimum nazýváme společným názvem ostré lokální extrémy.
12 Definice (lokální extrém). Buď f funkce a x 0 Dom(f ). Řekneme, že funkce má v bodě x 0 lokální maximum, jestliže existuje ryzí okolí O(x 0 ), takové, že f (x 0 ) f (x) pro všechna x O(x 0 ). Je-li nerovnost ostrá,říkáme,že funkcef má v boděx 0 ostré lokální maximum. Platí-li opačné nerovnosti, říkáme, že funkce má v bodě x 0 lokální minimum a ostré lokální minimum. Lokální maximum a minimum nazýváme společným názvem lokální extrémy. Ostré lokální maximum a ostré lokální minimum nazýváme společným názvem ostré lokální extrémy.
13 Definice (lokální extrém). Buď f funkce a x 0 Dom(f ). Řekneme, že funkce má v bodě x 0 lokální maximum, jestliže existuje ryzí okolí O(x 0 ), takové, že f (x 0 ) f (x) pro všechna x O(x 0 ). Je-li nerovnost ostrá,říkáme,že funkcef má v boděx 0 ostré lokální maximum. Platí-li opačné nerovnosti, říkáme, že funkce má v bodě x 0 lokální minimum a ostré lokální minimum. Lokální maximum a minimum nazýváme společným názvem lokální extrémy. Ostré lokální maximum a ostré lokální minimum nazýváme společným názvem ostré lokální extrémy.
14 Věta 1 (postačující podmínky pro existenci a neexistenci lokálních extrémů). Buď f funkce definovaná a spojitá v nějakém okolí bodu x 0. Jestliže existuje levé okolí bodu x 0, ve kterém je funkce rostoucí a pravé okolí bodu x 0, ve kterém je funkce klesající, je bod x 0 bodem ostrého lokálního maxima funkce f. Jestliže existuje levé okolí bodu x 0, ve kterém je funkce klesající a pravé okolí bodu x 0, ve kterém je funkce rostoucí, je bod x 0 bodem ostrého lokálního minima funkce f. Jestliže existuje okolí bodu x 0 ve kterém je funkce ryze monotonní, lokální extrém v bodě x 0 nenastává. Poznámka 1. Graficky můžeme předchozí větu ilustrovat následovně. ր MAX ց a min ր b c ր MAX ց d
15 Věta 1 (postačující podmínky pro existenci a neexistenci lokálních extrémů). Buď f funkce definovaná a spojitá v nějakém okolí bodu x 0. Jestliže existuje levé okolí bodu x 0, ve kterém je funkce rostoucí a pravé okolí bodu x 0, ve kterém je funkce klesající, je bod x 0 bodem ostrého lokálního maxima funkce f. Jestliže existuje levé okolí bodu x 0, ve kterém je funkce klesající a pravé okolí bodu x 0, ve kterém je funkce rostoucí, je bod x 0 bodem ostrého lokálního minima funkce f. Jestliže existuje okolí bodu x 0 ve kterém je funkce ryze monotonní, lokální extrém v bodě x 0 nenastává. Poznámka 1. Graficky můžeme předchozí větu ilustrovat následovně. ր MAX ց a min ր b c ր MAX ց d
16 Věta 1 (postačující podmínky pro existenci a neexistenci lokálních extrémů). Buď f funkce definovaná a spojitá v nějakém okolí bodu x 0. Jestliže existuje levé okolí bodu x 0, ve kterém je funkce rostoucí a pravé okolí bodu x 0, ve kterém je funkce klesající, je bod x 0 bodem ostrého lokálního maxima funkce f. Jestliže existuje levé okolí bodu x 0, ve kterém je funkce klesající a pravé okolí bodu x 0, ve kterém je funkce rostoucí, je bod x 0 bodem ostrého lokálního minima funkce f. Jestliže existuje okolí bodu x 0 ve kterém je funkce ryze monotonní, lokální extrém v bodě x 0 nenastává. Poznámka 1. Graficky můžeme předchozí větu ilustrovat následovně. ր MAX ց a min ր b c ր MAX ց d
17 Věta 1 (postačující podmínky pro existenci a neexistenci lokálních extrémů). Buď f funkce definovaná a spojitá v nějakém okolí bodu x 0. Jestliže existuje levé okolí bodu x 0, ve kterém je funkce rostoucí a pravé okolí bodu x 0, ve kterém je funkce klesající, je bod x 0 bodem ostrého lokálního maxima funkce f. Jestliže existuje levé okolí bodu x 0, ve kterém je funkce klesající a pravé okolí bodu x 0, ve kterém je funkce rostoucí, je bod x 0 bodem ostrého lokálního minima funkce f. Jestliže existuje okolí bodu x 0 ve kterém je funkce ryze monotonní, lokální extrém v bodě x 0 nenastává. Poznámka 1. Graficky můžeme předchozí větu ilustrovat následovně. ր MAX ց a min ր b c ր MAX ց d
18 Věta 2 (souvislost derivace a monotonie). Nechť funkce f má derivaci na otevřeném intervalu I. Je-li f (x) > 0 na intervalu I, je funkce f rostoucí na I. Je-li f (x) < 0 na intervalu I, je funkce f klesající na I. Definice (stacionární bod). Řekneme, že bod x 0 je stacionárním bodem funkce f, jestliže funkce f má v bodě x 0 nulovou derivaci, tj. f (x 0 ) = 0. Poznámka 2 (geometrický význam). Geometricky jsou stacionární body body, ve kterých má graf funkce vodorovnou tečnu (proč?). Věta 3 (souvislost derivace a lokálních extrémů). Nechť má funkce v bodě x 0 lokální extrém. Pak funkce f v bodě x 0 buď nemá derivaci, nebo je tato derivace nulová, tj. platí f (x 0 ) = 0 a x 0 je stacionárním bodem funkce f.
19 Věta 2 (souvislost derivace a monotonie). Nechť funkce f má derivaci na otevřeném intervalu I. Je-li f (x) > 0 na intervalu I, je funkce f rostoucí na I. Je-li f (x) < 0 na intervalu I, je funkce f klesající na I. Definice (stacionární bod). Řekneme, že bod x 0 je stacionárním bodem funkce f, jestliže funkce f má v bodě x 0 nulovou derivaci, tj. f (x 0 ) = 0. Poznámka 2 (geometrický význam). Geometricky jsou stacionární body body, ve kterých má graf funkce vodorovnou tečnu (proč?). Věta 3 (souvislost derivace a lokálních extrémů). Nechť má funkce v bodě x 0 lokální extrém. Pak funkce f v bodě x 0 buď nemá derivaci, nebo je tato derivace nulová, tj. platí f (x 0 ) = 0 a x 0 je stacionárním bodem funkce f.
20 Věta 2 (souvislost derivace a monotonie). Nechť funkce f má derivaci na otevřeném intervalu I. Je-li f (x) > 0 na intervalu I, je funkce f rostoucí na I. Je-li f (x) < 0 na intervalu I, je funkce f klesající na I. Definice (stacionární bod). Řekneme, že bod x 0 je stacionárním bodem funkce f, jestliže funkce f má v bodě x 0 nulovou derivaci, tj. f (x 0 ) = 0. Poznámka 2 (geometrický význam). Geometricky jsou stacionární body body, ve kterých má graf funkce vodorovnou tečnu (proč?). Věta 3 (souvislost derivace a lokálních extrémů). Nechť má funkce v bodě x 0 lokální extrém. Pak funkce f v bodě x 0 buď nemá derivaci, nebo je tato derivace nulová, tj. platí f (x 0 ) = 0 a x 0 je stacionárním bodem funkce f.
21 Věta 2 (souvislost derivace a monotonie). Nechť funkce f má derivaci na otevřeném intervalu I. Je-li f (x) > 0 na intervalu I, je funkce f rostoucí na I. Je-li f (x) < 0 na intervalu I, je funkce f klesající na I. Definice (stacionární bod). Řekneme, že bod x 0 je stacionárním bodem funkce f, jestliže funkce f má v bodě x 0 nulovou derivaci, tj. f (x 0 ) = 0. Poznámka 2 (geometrický význam). Geometricky jsou stacionární body body, ve kterých má graf funkce vodorovnou tečnu (proč?). Věta 3 (souvislost derivace a lokálních extrémů). Nechť má funkce v bodě x 0 lokální extrém. Pak funkce f v bodě x 0 buď nemá derivaci, nebo je tato derivace nulová, tj. platí f (x 0 ) = 0 a x 0 je stacionárním bodem funkce f.
22 Definice (konvexnost, konkávnost). Buď f funkce mající derivaci v bodě x 0. Řekneme, že funkce f je v bodě x 0 konvexní (konkávní), jestliže existuje ryzí okolí bodu x 0 takové, že pro všechna x O(x 0 ) leží body grafu funkce nad tečnou (pod tečnou) ke grafu funkcef sestrojenou v boděx 0, tj. platí f (x) > f (x 0 )+f (x 0 )(x x 0 ) ( f (x) < f (x 0 )+f (x 0 )(x x 0 ) ). (1) Řekneme, že funkce je konvexní (konkávní) na otevřeném intervalu I, má-li tuto vlastnost v každém bodě intervalu I. Definice (inflexní bod). Bod ve kterém se mění charakter funkce z konvexní na konkávní nebo naopak nazýváme inflexním bodem funkce f.
23 Věta 4 (souvislost druhé derivace s konvexností a konkávností). Buď f funkce mající druhou derivaci na otevřeném intervalu I. Je-li f (x) > 0 na intervalu I, je funkce f konvexní na I. Je-li f (x) < 0 na intervalu I, je funkce f konkávní na I. Definice (kritický bod). Bod, ve kterém má funkce f nulovou druhou derivaci nazýváme kritickým bodem funkce f. Věta 5 (souvislost inflexních bodů a druhé derivace). Nechť má funkce v bodě x 0 inflexní bod. Pak funkce f v bodě x 0 buď nemá druhou derivaci, nebo je tato druhá derivace nulová, tj. platí f (x 0 ) = 0 a x 0 je kritickým bodem funkce f. Věta 6 (souvislost druhé derivace s lokálními extrémy). Buď f funkce a x 0 stacionární bod funkcef. Je-lif (x 0 ) > 0, nabývá funkce v boděx 0 lokálního minima, je-li f (x 0 ) < 0, nabývá funkce v bodě x 0 lokálního maxima.
24 Věta 4 (souvislost druhé derivace s konvexností a konkávností). Buď f funkce mající druhou derivaci na otevřeném intervalu I. Je-li f (x) > 0 na intervalu I, je funkce f konvexní na I. Je-li f (x) < 0 na intervalu I, je funkce f konkávní na I. Definice (kritický bod). Bod, ve kterém má funkce f nulovou druhou derivaci nazýváme kritickým bodem funkce f. Věta 5 (souvislost inflexních bodů a druhé derivace). Nechť má funkce v bodě x 0 inflexní bod. Pak funkce f v bodě x 0 buď nemá druhou derivaci, nebo je tato druhá derivace nulová, tj. platí f (x 0 ) = 0 a x 0 je kritickým bodem funkce f. Věta 6 (souvislost druhé derivace s lokálními extrémy). Buď f funkce a x 0 stacionární bod funkcef. Je-lif (x 0 ) > 0, nabývá funkce v boděx 0 lokálního minima, je-li f (x 0 ) < 0, nabývá funkce v bodě x 0 lokálního maxima.
25 Věta 4 (souvislost druhé derivace s konvexností a konkávností). Buď f funkce mající druhou derivaci na otevřeném intervalu I. Je-li f (x) > 0 na intervalu I, je funkce f konvexní na I. Je-li f (x) < 0 na intervalu I, je funkce f konkávní na I. Definice (kritický bod). Bod, ve kterém má funkce f nulovou druhou derivaci nazýváme kritickým bodem funkce f. Věta 5 (souvislost inflexních bodů a druhé derivace). Nechť má funkce v bodě x 0 inflexní bod. Pak funkce f v bodě x 0 buď nemá druhou derivaci, nebo je tato druhá derivace nulová, tj. platí f (x 0 ) = 0 a x 0 je kritickým bodem funkce f. Věta 6 (souvislost druhé derivace s lokálními extrémy). Buď f funkce a x 0 stacionární bod funkcef. Je-lif (x 0 ) > 0, nabývá funkce v boděx 0 lokálního minima, je-li f (x 0 ) < 0, nabývá funkce v bodě x 0 lokálního maxima.
26 Věta 4 (souvislost druhé derivace s konvexností a konkávností). Buď f funkce mající druhou derivaci na otevřeném intervalu I. Je-li f (x) > 0 na intervalu I, je funkce f konvexní na I. Je-li f (x) < 0 na intervalu I, je funkce f konkávní na I. Definice (kritický bod). Bod, ve kterém má funkce f nulovou druhou derivaci nazýváme kritickým bodem funkce f. Věta 5 (souvislost inflexních bodů a druhé derivace). Nechť má funkce v bodě x 0 inflexní bod. Pak funkce f v bodě x 0 buď nemá druhou derivaci, nebo je tato druhá derivace nulová, tj. platí f (x 0 ) = 0 a x 0 je kritickým bodem funkce f. Věta 6 (souvislost druhé derivace s lokálními extrémy). Buď f funkce a x 0 stacionární bod funkcef. Je-lif (x 0 ) > 0, nabývá funkce v boděx 0 lokálního minima, je-li f (x 0 ) < 0, nabývá funkce v bodě x 0 lokálního maxima.
27 3 Okolí nevlastních bodů. Již známe dva druhy asymptot. svislá asymptota vodorovná asymptota v+
28 y = f (x) g(x) y = kx +q Definice (asymptota se směrnicí). Buď f funkce definovaná v nějakém okolí bodu. Přímka y = kx +q se nazývá asymptota se směrnicí ke grafu funkce y = f (x), jestliže platí lim kx +q f (x) = 0 x Podobně, zaměníme-li bod za bod, obdržíme definici asymptoty se směrnicí ke grafu funkce f v bodě.
29 y = f (x) g(x) y = kx +q Definice (asymptota se směrnicí). Buď f funkce definovaná v nějakém okolí bodu. Přímka y = kx +q se nazývá asymptota se směrnicí ke grafu funkce y = f (x), jestliže platí lim kx +q f (x) = 0 x Podobně, zaměníme-li bod za bod, obdržíme definici asymptoty se směrnicí ke grafu funkce f v bodě.
30 y = f (x) g(x) y = kx +q Definice (asymptota se směrnicí). Buď f funkce definovaná v nějakém okolí bodu. Přímka y = kx +q se nazývá asymptota se směrnicí ke grafu funkce y = f (x), jestliže platí lim kx +q f (x) = 0 x Podobně, zaměníme-li bod za bod, obdržíme definici asymptoty se směrnicí ke grafu funkce f v bodě.
31 Věta 7 (asymptota se směrnicí). Buď f funkce definovaná v nějakém okolí bodu. Přímka y = kx + q je asymptota se směrnicí ke grafu funkce y = f (x) v bodě + právě tehdy, když existují konečné limity f (x) k := lim x x a q := lim x (f (x) kx). Podobně, zaměníme-li bod za bod, obdržíme asymptotu se směrnicí ke grafu funkce f v bodě. Věta 8 (asymptoty racionální funkce). Asymptoty se směrnicí ke grafu racionální funkce v bodech ± existují současně a jsou stejné. Poznámka 3. Polynom stupně alespoň 2 nemá asymptoty.
32 Věta 7 (asymptota se směrnicí). Buď f funkce definovaná v nějakém okolí bodu. Přímka y = kx + q je asymptota se směrnicí ke grafu funkce y = f (x) v bodě + právě tehdy, když existují konečné limity f (x) k := lim x x a q := lim x (f (x) kx). Podobně, zaměníme-li bod za bod, obdržíme asymptotu se směrnicí ke grafu funkce f v bodě. Věta 8 (asymptoty racionální funkce). Asymptoty se směrnicí ke grafu racionální funkce v bodech ± existují současně a jsou stejné. Poznámka 3. Polynom stupně alespoň 2 nemá asymptoty.
33 4 Sestrojení grafu funkce. 1. Nalezneme definiční obor funkce, zjistíme paritu funkce a její průsečíky s osami, intervaly, kde je funkce kladná a kde záporná. 2. Asymptoty, chování funkce v okolí bodů nespojitosti. 3. První derivace, stacionární body, intervaly růstu a klesání a lokální extrémy. 4. Druhá derivace, kritické body, intervaly konvexnosti a konkávnosti a inflexní body. 5. Asymptoty a charakteristické body (extrémy a inflexní body) zakreslíme do kartézské soustavy souřadnic a načrtneme graf.
34 4 Sestrojení grafu funkce. 1. Nalezneme definiční obor funkce, zjistíme paritu funkce a její průsečíky s osami, intervaly, kde je funkce kladná a kde záporná. 2. Asymptoty, chování funkce v okolí bodů nespojitosti. 3. První derivace, stacionární body, intervaly růstu a klesání a lokální extrémy. 4. Druhá derivace, kritické body, intervaly konvexnosti a konkávnosti a inflexní body. 5. Asymptoty a charakteristické body (extrémy a inflexní body) zakreslíme do kartézské soustavy souřadnic a načrtneme graf.
35 4 Sestrojení grafu funkce. 1. Nalezneme definiční obor funkce, zjistíme paritu funkce a její průsečíky s osami, intervaly, kde je funkce kladná a kde záporná. 2. Asymptoty, chování funkce v okolí bodů nespojitosti. 3. První derivace, stacionární body, intervaly růstu a klesání a lokální extrémy. 4. Druhá derivace, kritické body, intervaly konvexnosti a konkávnosti a inflexní body. 5. Asymptoty a charakteristické body (extrémy a inflexní body) zakreslíme do kartézské soustavy souřadnic a načrtneme graf.
36 4 Sestrojení grafu funkce. 1. Nalezneme definiční obor funkce, zjistíme paritu funkce a její průsečíky s osami, intervaly, kde je funkce kladná a kde záporná. 2. Asymptoty, chování funkce v okolí bodů nespojitosti. 3. První derivace, stacionární body, intervaly růstu a klesání a lokální extrémy. 4. Druhá derivace, kritické body, intervaly konvexnosti a konkávnosti a inflexní body. 5. Asymptoty a charakteristické body (extrémy a inflexní body) zakreslíme do kartézské soustavy souřadnic a načrtneme graf.
37 4 Sestrojení grafu funkce. 1. Nalezneme definiční obor funkce, zjistíme paritu funkce a její průsečíky s osami, intervaly, kde je funkce kladná a kde záporná. 2. Asymptoty, chování funkce v okolí bodů nespojitosti. 3. První derivace, stacionární body, intervaly růstu a klesání a lokální extrémy. 4. Druhá derivace, kritické body, intervaly konvexnosti a konkávnosti a inflexní body. 5. Asymptoty a charakteristické body (extrémy a inflexní body) zakreslíme do kartézské soustavy souřadnic a načrtneme graf.
38 4 Sestrojení grafu funkce. 1. Nalezneme definiční obor funkce, zjistíme paritu funkce a její průsečíky s osami, intervaly, kde je funkce kladná a kde záporná. 2. Asymptoty, chování funkce v okolí bodů nespojitosti. 3. První derivace, stacionární body, intervaly růstu a klesání a lokální extrémy. 4. Druhá derivace, kritické body, intervaly konvexnosti a konkávnosti a inflexní body. 5. Asymptoty a charakteristické body (extrémy a inflexní body) zakreslíme do kartézské soustavy souřadnic a načrtneme graf.
IX. Vyšetřování průběhu funkce
 IX. Vyšetřování průběhu funkce Úvodní poznámky: Cíl: vyšetřit průběh dané funkce f. Zahrnuje: základní vlastnosti: D(f), spojitost, limity v krajních bodech, průsečíky s osami souřadnic, intervaly, kde
IX. Vyšetřování průběhu funkce Úvodní poznámky: Cíl: vyšetřit průběh dané funkce f. Zahrnuje: základní vlastnosti: D(f), spojitost, limity v krajních bodech, průsečíky s osami souřadnic, intervaly, kde
LDF MENDELU. Simona Fišnarová (MENDELU) Průběh funkce ZVMT lesnictví 1 / 21
 Průběh funkce Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Průběh funkce Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Kapitola 4: Průběh funkce 1/11
 Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Kapitola 4: Průběh funkce 1/11
 Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
7.1 Extrémy a monotonie
 KAPITOLA 7: Průběh funkce [ZMA13-P38] 7.1 Extrémy a monotonie Řekneme, že funkce f nabývá na množině M Df svého globálního maxima globálního minima A v bodě x 0, jestliže x 0 M, fx 0 = A a pro každé x
KAPITOLA 7: Průběh funkce [ZMA13-P38] 7.1 Extrémy a monotonie Řekneme, že funkce f nabývá na množině M Df svého globálního maxima globálního minima A v bodě x 0, jestliže x 0 M, fx 0 = A a pro každé x
Aplikace derivace a průběh funkce
 Aplikace derivace a průběh funkce Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného
Aplikace derivace a průběh funkce Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného
Základy matematiky pro FEK
 Základy matematiky pro FEK 10. přednáška Blanka Šedivá KMA zimní semestr 016/017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 016/017 1 / 1 Použití derivace pro vyšetřování průběhu funkce
Základy matematiky pro FEK 10. přednáška Blanka Šedivá KMA zimní semestr 016/017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 016/017 1 / 1 Použití derivace pro vyšetřování průběhu funkce
Pavlína Matysová. 5. listopadu 2018
 Soubor řešených úloh Vyšetřování průběhu funkce Pavlína Matysová 5. listopadu 018 1 Soubor řešených úloh Tento text obsahuje 7 úloh na téma vyšetřování průběhu funkce. Každé úloha je řešena dvěma způsoby
Soubor řešených úloh Vyšetřování průběhu funkce Pavlína Matysová 5. listopadu 018 1 Soubor řešených úloh Tento text obsahuje 7 úloh na téma vyšetřování průběhu funkce. Každé úloha je řešena dvěma způsoby
Diferenciální počet - II. část (Taylorův polynom, L Hospitalovo pravidlo, extrémy
 Diferenciální počet - II. část (Taylorův polynom, L Hospitalovo pravidlo, extrémy funkcí, průběh funkce) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 5. přednáška z AMA1 Michal Fusek (fusekmi@feec.vutbr.cz)
Diferenciální počet - II. část (Taylorův polynom, L Hospitalovo pravidlo, extrémy funkcí, průběh funkce) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 5. přednáška z AMA1 Michal Fusek (fusekmi@feec.vutbr.cz)
Příklady na konvexnost a inflexní body. Funkce f (x) = x 3 9x. Derivace jsou f (x) = 3x 2 9 a f (x) = 6x. Funkce f je konvexní na intervalu (0, )
 Příklady na konvexnost a inflexní body. Funkce = x 3 9x. Derivace jsou f (x) = 3x 9 a f (x) = 6x. Funkce f je konvexní na intervalu (, ) a konkávní na intervalu (, ). Inflexní bod c =. 3 1 1 y = x 3 9x
Příklady na konvexnost a inflexní body. Funkce = x 3 9x. Derivace jsou f (x) = 3x 9 a f (x) = 6x. Funkce f je konvexní na intervalu (, ) a konkávní na intervalu (, ). Inflexní bod c =. 3 1 1 y = x 3 9x
Matematika 1 pro PEF PaE
 Vázané extrémy funkcí více proměnných 1 / 13 Matematika 1 pro PEF PaE 11. Vázané extrémy funkcí více proměnných Přemysl Jedlička Katedra matematiky, TF ČZU Vázané extrémy funkcí více proměnných Vázané
Vázané extrémy funkcí více proměnných 1 / 13 Matematika 1 pro PEF PaE 11. Vázané extrémy funkcí více proměnných Přemysl Jedlička Katedra matematiky, TF ČZU Vázané extrémy funkcí více proměnných Vázané
Funkce jedn e re aln e promˇ enn e Derivace Pˇredn aˇska ˇr ıjna 2015
 Funkce jedné reálné proměnné Derivace Přednáška 2 15. října 2015 Obsah 1 Funkce 2 Limita a spojitost funkce 3 Derivace 4 Průběh funkce Informace Literatura v elektronické verzi (odkazy ze STAGu): 1 Lineární
Funkce jedné reálné proměnné Derivace Přednáška 2 15. října 2015 Obsah 1 Funkce 2 Limita a spojitost funkce 3 Derivace 4 Průběh funkce Informace Literatura v elektronické verzi (odkazy ze STAGu): 1 Lineární
Funkce v ıce promˇ enn ych Extr emy Pˇredn aˇska p at a 12.bˇrezna 2018
 Funkce více proměnných Extrémy Přednáška pátá 12.března 2018 Zdroje informací Diferenciální počet http://homen.vsb.cz/~kre40/esfmat2/fceviceprom.html http://www.studopory.vsb.cz/studijnimaterialy/sbirka_uloh/pdf/7.pdf
Funkce více proměnných Extrémy Přednáška pátá 12.března 2018 Zdroje informací Diferenciální počet http://homen.vsb.cz/~kre40/esfmat2/fceviceprom.html http://www.studopory.vsb.cz/studijnimaterialy/sbirka_uloh/pdf/7.pdf
Derivace a monotónnost funkce
 Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je
Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je
Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si zopakovat a orientovat se v pojmech: funkce, D(f), g 2 : y =
 0.1 Diferenciální počet Je částí infinitezimálního počtu, což je souhrnný název pro diferenciální a integrální počet. Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si
0.1 Diferenciální počet Je částí infinitezimálního počtu, což je souhrnný název pro diferenciální a integrální počet. Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si
Asymptoty grafu funkce
 Asymptoty grafu funkce Lenka Přibylová 8. července 006 Obsah Najděteasymptotygrafufunkce y = 1 x.... 3 Asymptotybezsměrnicekegrafufunkce y = 1 x : D(f) = R {} x + = 0 + = x = 0 = Funkcemáasymptotubezsměrniceajejípřímka
Asymptoty grafu funkce Lenka Přibylová 8. července 006 Obsah Najděteasymptotygrafufunkce y = 1 x.... 3 Asymptotybezsměrnicekegrafufunkce y = 1 x : D(f) = R {} x + = 0 + = x = 0 = Funkcemáasymptotubezsměrniceajejípřímka
Příklad 1 ŘEŠENÉ PŘÍKLADY Z M1A ČÁST 6
 Příklad 1 Vyšetřete průběh funkce: a) = b) = c) = d) =ln1+ e) =ln f) = Poznámka K vyšetřování průběhu funkce použijeme postup uvedený v zadání. Některé kroky nejsou již tak detailní, všechny by ale měly
Příklad 1 Vyšetřete průběh funkce: a) = b) = c) = d) =ln1+ e) =ln f) = Poznámka K vyšetřování průběhu funkce použijeme postup uvedený v zadání. Některé kroky nejsou již tak detailní, všechny by ale měly
http://user.mendelu.cz/marik, kde je dostupný ve formě vhodné pro tisk i ve formě vhodné pro prohlížení na obrazovce a z adresy http://is.mendelu.
 Inženýrská matematika Robert Mařík Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného základu (reg.
Inženýrská matematika Robert Mařík Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného základu (reg.
Zlín, 23. října 2011
 (. -. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 3. října 0 Postup při vyšetřování průběhu funkce. Definiční obor funkce,
(. -. lekce) Sylva Potůčková, Dana Stesková, Lubomír Sedláček Gymnázium a Jazyková škola s právem státní jazykové zkoušky Zlín Zlín, 3. října 0 Postup při vyšetřování průběhu funkce. Definiční obor funkce,
7) Intervaly konvexnosti a konkávnosti. 8) Inflexe, inflexní body grafu funkce. 9) Asymptoty grafu funkce. 10) Sestrojení grafu funkce.
 Přednáška č. 12 Vyšetřování průběhu funkce a užití extrémů funkcí Jiří Fišer 11. prosince 2009 Jiří Fišer (KMA, PřF UP Olomouc) KMA MMAN1 Přednáška č. 12 11. prosince 2009 1 / 18 Průběh funkce O vyšetřování
Přednáška č. 12 Vyšetřování průběhu funkce a užití extrémů funkcí Jiří Fišer 11. prosince 2009 Jiří Fišer (KMA, PřF UP Olomouc) KMA MMAN1 Přednáška č. 12 11. prosince 2009 1 / 18 Průběh funkce O vyšetřování
Diferenciální počet funkcí jedné proměnné
 Diferenciální počet funkcí jedné proměnné 1 4. Derivace funkce 4.3. Průběh funkce 2 Pro přesné určení průběhu grafu funkce je třeba určit bližší vlastnosti funkce. Monotónnost funkce Funkce monotónní =
Diferenciální počet funkcí jedné proměnné 1 4. Derivace funkce 4.3. Průběh funkce 2 Pro přesné určení průběhu grafu funkce je třeba určit bližší vlastnosti funkce. Monotónnost funkce Funkce monotónní =
, f g jsou elementární funkce.
 Průběh funkce použité definice a věty Definice. Řekneme, že funkce je spojitá na otevřeném intervalu (a, b), jestliže je spojitá v každém vnitřním bodě tohoto intervalu. Řekneme, že funkce je spojitá na
Průběh funkce použité definice a věty Definice. Řekneme, že funkce je spojitá na otevřeném intervalu (a, b), jestliže je spojitá v každém vnitřním bodě tohoto intervalu. Řekneme, že funkce je spojitá na
Význam a výpočet derivace funkce a její užití
 OPAKOVÁNÍ ZÁKLADŮ MATEMATIKY Metodický list č. 1 Význam a výpočet derivace funkce a její užití 1. dílčí téma: Výpočet derivace přímo z definice a pomocí základních vzorců. K tomuto tématu je třeba zopakovat
OPAKOVÁNÍ ZÁKLADŮ MATEMATIKY Metodický list č. 1 Význam a výpočet derivace funkce a její užití 1. dílčí téma: Výpočet derivace přímo z definice a pomocí základních vzorců. K tomuto tématu je třeba zopakovat
Definice derivace v bodě
 Definice derivace v bodě tgϕ = f ( ) f () f () : = tgϕ = lim f f () tgϕ = f f () Obecně: f f f ( ) ( ) : = lim f ( + h) f f : = lim h h Derivace zleva (zprava): f ( ) : = lim f f ( ) f ( ) : = lim + +
Definice derivace v bodě tgϕ = f ( ) f () f () : = tgϕ = lim f f () tgϕ = f f () Obecně: f f f ( ) ( ) : = lim f ( + h) f f : = lim h h Derivace zleva (zprava): f ( ) : = lim f f ( ) f ( ) : = lim + +
Použití derivací. V této části budou uvedena některá použití derivací. LEKCE08-PRU. Použití derivací. l Hospital
 V této části budou uvedena některá použití derivací. a derivace a derivace -zbytek L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT Tvrzení je uvedeno pro jednostrannou limitu zprava. Samozřejmě obdobné tvrzení platí
V této části budou uvedena některá použití derivací. a derivace a derivace -zbytek L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT Tvrzení je uvedeno pro jednostrannou limitu zprava. Samozřejmě obdobné tvrzení platí
Derivace funkce. existuje limita lim 0 ) xx xx0. Jestliže tato limita neexistuje nebo pokud funkce ff
 Derivace funkce Derivace je základním pojmem v diferenciálním počtu. Má uplatnění tam, kde se zkoumá povaha funkčních závislostí určitých proměnných (veličin). V matematice, ekonomii, fyzice ale i v jiných
Derivace funkce Derivace je základním pojmem v diferenciálním počtu. Má uplatnění tam, kde se zkoumá povaha funkčních závislostí určitých proměnných (veličin). V matematice, ekonomii, fyzice ale i v jiných
6. F U N K C E 6.1 F U N K C E. Sbírka úloh z matematiky pro SOU a SOŠ RNDr. Milada Hudcová, Mgr. Libuše Kubičíková 181/1 190/24 25
 6. F U N K C E 6.1 F U N K C E Funkce (definice, značení) Způsoby zadání funkce (tabulka, funkční předpis, slovní popis, graf) 181/1 190/24 25 80/1 2 82/3 6.2 D E F I N I Č N Í O B O R, O B O R H O D N
6. F U N K C E 6.1 F U N K C E Funkce (definice, značení) Způsoby zadání funkce (tabulka, funkční předpis, slovní popis, graf) 181/1 190/24 25 80/1 2 82/3 6.2 D E F I N I Č N Í O B O R, O B O R H O D N
Aplikační úlohy z diferenciálního počtu jedné proměnné
 Jihočeská univerzita v Českých Budějovicích Fakulta Katedra Bakalářská práce Aplikační úlohy z diferenciálního počtu jedné proměnné Vypracoval: Michaela Jelínková Vedoucí práce: RNDr. Vladimíra Petrášková,
Jihočeská univerzita v Českých Budějovicích Fakulta Katedra Bakalářská práce Aplikační úlohy z diferenciálního počtu jedné proměnné Vypracoval: Michaela Jelínková Vedoucí práce: RNDr. Vladimíra Petrášková,
Limita posloupnosti, limita funkce, spojitost. May 26, 2018
 Limita posloupnosti, limita funkce, spojitost May 26, 2018 Definice (Okolí bodu) Okolím bodu a R (také ε- okolím) rozumíme množinu U(a, ε) = {x R; x a < ε} = (a ε, a + ε), bod a se nazývá střed okolí a
Limita posloupnosti, limita funkce, spojitost May 26, 2018 Definice (Okolí bodu) Okolím bodu a R (také ε- okolím) rozumíme množinu U(a, ε) = {x R; x a < ε} = (a ε, a + ε), bod a se nazývá střed okolí a
Diferenciální počet 1 1. f(x) = ln arcsin 1 + x 1 x. 1 x 1 a x 1 0. f(x) = (cos x) cosh x + 3x. x 0 je derivace funkce f(x) v bodě x0.
 Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
1 Množiny, výroky a číselné obory
 1 Množiny, výroky a číselné obory 1.1 Množiny a množinové operace Množinou rozumíme každé shrnutí určitých a navzájem různých objektů (které nazýváme prvky) do jediného celku. Definice. Dvě množiny jsou
1 Množiny, výroky a číselné obory 1.1 Množiny a množinové operace Množinou rozumíme každé shrnutí určitých a navzájem různých objektů (které nazýváme prvky) do jediného celku. Definice. Dvě množiny jsou
D(f) =( 1, 1) [ ( 1, 1) [ (1, 1). 2( x)3 ( x) 2 1 = 2(x) 3. (x) 2 1 = f(x) Funkce je lichá, není periodická
 Vyšetříme funkci f(x): f(x) = 2x3.. Stanovme definiční obor funkce D(f) a zjistíme,ve kterých bodech je funkce sojitá D(f) =(, ) [ (, ) [ (, ). 2. Počítáme f( x) = 2( x)3 ( x) 2 = 2(x) 3 (x) 2 = f(x) Funkce
Vyšetříme funkci f(x): f(x) = 2x3.. Stanovme definiční obor funkce D(f) a zjistíme,ve kterých bodech je funkce sojitá D(f) =(, ) [ (, ) [ (, ). 2. Počítáme f( x) = 2( x)3 ( x) 2 = 2(x) 3 (x) 2 = f(x) Funkce
Matematika B 2. Úvodní informace
 Matematika B 2 MIROSLAV KUČERA Úvodní informace Kontakt miroslav.kucera@vsfs.czvsfs.cz Studijní středisko Kladno IT oddělení 306B (kanceláře studijního oddělení) Konzultační hodiny Po Pá 8:30 15:00 možno
Matematika B 2 MIROSLAV KUČERA Úvodní informace Kontakt miroslav.kucera@vsfs.czvsfs.cz Studijní středisko Kladno IT oddělení 306B (kanceláře studijního oddělení) Konzultační hodiny Po Pá 8:30 15:00 možno
Derivace vyšších řádů, aplikace derivací
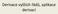 Derivace vyšších řádů, aplikace derivací Značení derivací vyšších řádů Máme funkci f: y = f x f x druhá derivace funkce y = f x f k x k-tá derivace funkce y = f x Derivace vyšších řádů počítáme opakovaným
Derivace vyšších řádů, aplikace derivací Značení derivací vyšších řádů Máme funkci f: y = f x f x druhá derivace funkce y = f x f k x k-tá derivace funkce y = f x Derivace vyšších řádů počítáme opakovaným
Matematika 2 Průběh funkce
 Matematika 2 Průběh funkce Jiří Fišer KMA, PřF UP Olomouc ZS09 Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 1 / 1 Základní věty diferenciálního počtu Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09
Matematika 2 Průběh funkce Jiří Fišer KMA, PřF UP Olomouc ZS09 Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 1 / 1 Základní věty diferenciálního počtu Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09
2. spojitost (7. cvičení) 3. sudost/lichost, periodicita (3. cvičení) 4. první derivace, stacionární body, intervaly monotonie (10.
 MA. cvičení průběh funkce Lukáš Pospíšil,202 Průběh funkce Pod úkolem vyšetřete průběh funkce budeme rozumět nalezení všech kvalitativních vlastností zadané funkce - tedy bude potřeba zjistit o funkci
MA. cvičení průběh funkce Lukáš Pospíšil,202 Průběh funkce Pod úkolem vyšetřete průběh funkce budeme rozumět nalezení všech kvalitativních vlastností zadané funkce - tedy bude potřeba zjistit o funkci
Průběh funkce 1. Průběh funkce. Při vyšetření grafu funkce budeme postupovat podle následujícího algoritmu:
 Průběh funkce Průběh funkce Při vyšetření grafu funkce budeme postupovat podle následujícího algoritmu:. Určení definičního oboru. 2. Rozhodnutí, jestli je funkce sudá, lichá, periodická nebo nemá ani
Průběh funkce Průběh funkce Při vyšetření grafu funkce budeme postupovat podle následujícího algoritmu:. Určení definičního oboru. 2. Rozhodnutí, jestli je funkce sudá, lichá, periodická nebo nemá ani
Matematika I (KX001) Užití derivace v geometrii, ve fyzice 3. října f (x 0 ) (x x 0) Je-li f (x 0 ) = 0, tečna: x = 3, normála: y = 0
 Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Matematika (KMI/PMATE)
 Matematika (KMI/PMATE) Přednáška druhá aneb Úvod do matematické analýzy Limita a spojitost funkce Matematika (KMI/PMATE) 1 / 30 Osnova přednášky lineární funkce y = kx + q definice lineární funkce význam
Matematika (KMI/PMATE) Přednáška druhá aneb Úvod do matematické analýzy Limita a spojitost funkce Matematika (KMI/PMATE) 1 / 30 Osnova přednášky lineární funkce y = kx + q definice lineární funkce význam
MATEMATIKA. Příklady pro 1. ročník bakalářského studia. II. část Diferenciální počet. II.1. Posloupnosti reálných čísel
 MATEMATIKA Příklady pro 1. ročník bakalářského studia II. část II.1. Posloupnosti reálných čísel Rozhodněte, zda posloupnost a n (n = 1, 2, 3,...) je omezená (omezená shora, omezená zdola) resp. monotónní
MATEMATIKA Příklady pro 1. ročník bakalářského studia II. část II.1. Posloupnosti reálných čísel Rozhodněte, zda posloupnost a n (n = 1, 2, 3,...) je omezená (omezená shora, omezená zdola) resp. monotónní
Poznámky z matematiky
 Poznámky z matematiky Verze: 14. dubna 2015 Petr Hasil hasil@mendelu.cz http://user.mendelu.cz/hasil/ Ústav matematiky Lesnická a dřevařská fakulta Mendelova univerzita v Brně Vytvořeno s podporou projektu
Poznámky z matematiky Verze: 14. dubna 2015 Petr Hasil hasil@mendelu.cz http://user.mendelu.cz/hasil/ Ústav matematiky Lesnická a dřevařská fakulta Mendelova univerzita v Brně Vytvořeno s podporou projektu
BAKALÁŘSKÁ PRÁCE. Numerické metody jednorozměrné minimalizace
 UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY BAKALÁŘSKÁ PRÁCE Numerické metody jednorozměrné minimalizace Vedoucí bakalářské práce: RNDr. Horymír
UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY BAKALÁŘSKÁ PRÁCE Numerické metody jednorozměrné minimalizace Vedoucí bakalářské práce: RNDr. Horymír
Přijímací zkouška na navazující magisterské studium 2014
 Přijímací zkouška na navazující magisterské studium 4 Studijní program: Studijní obory: Příklad (5 bodů) Spočtěte Matematika MA, MMIB, MMFT, MSTR, NVM, PMSE, MDU Varianta A M xy dxdy, kde M = {(x, y) R
Přijímací zkouška na navazující magisterské studium 4 Studijní program: Studijní obory: Příklad (5 bodů) Spočtěte Matematika MA, MMIB, MMFT, MSTR, NVM, PMSE, MDU Varianta A M xy dxdy, kde M = {(x, y) R
Výsledky Př.1. Určete intervaly monotónnosti a lokální extrémy funkce a) ( ) ( ) ( ) Stacionární body:
 Výsledky Př.. Určete intervaly monotónnosti a lokální extrémy funkce a) y < y > y < y > -2 0 3 Funkce je rostoucí v intervalech. Funkce je klesající v intervalech b) y < y > y < - Funkce je rostoucí v
Výsledky Př.. Určete intervaly monotónnosti a lokální extrémy funkce a) y < y > y < y > -2 0 3 Funkce je rostoucí v intervalech. Funkce je klesající v intervalech b) y < y > y < - Funkce je rostoucí v
Učební dokument FUNKCE. Vyšetřování průběhu funkce. Mgr. Petra MIHULOVÁ. 4.roč.
 Učební dokument FUNKCE Vyšetřování průběhu funkce Mgr. Petra MIHULOVÁ.roč. Evropský sociální fond Praha a EU Investujeme do vaší budoucnosti Vyš etř ová ní přů be hů fůnkce á šeštřojení její ho gřáfů Určování
Učební dokument FUNKCE Vyšetřování průběhu funkce Mgr. Petra MIHULOVÁ.roč. Evropský sociální fond Praha a EU Investujeme do vaší budoucnosti Vyš etř ová ní přů be hů fůnkce á šeštřojení její ho gřáfů Určování
Metodický list pro první soustředění kombinovaného studia. předmětu MATEMATIKA A
 Metodický list pro první soustředění kombinovaného studia předmětu MATEMATIKA A Název tématického celku: Zobrazení,reálné funkce jedné reálné proměnné,elementární funkce a jejich základní vlastnosti,lineární
Metodický list pro první soustředění kombinovaného studia předmětu MATEMATIKA A Název tématického celku: Zobrazení,reálné funkce jedné reálné proměnné,elementární funkce a jejich základní vlastnosti,lineární
MATEMATIKA. Robert Mařík Ústav matematiky, LDF, MZLU 5. patro, budova B marik@mendelu.cz user.mendelu.cz/marik
 MATEMATIKA Robert Mařík Ústav matematiky, LDF, MZLU 5. patro, budova B marik@mendelu.cz user.mendelu.cz/marik P. Rádl, B. Černá, L. Stará: Základy vyšší matematiky, skriptum MZLU Text přednášky na user.mendelu.cz/marik,
MATEMATIKA Robert Mařík Ústav matematiky, LDF, MZLU 5. patro, budova B marik@mendelu.cz user.mendelu.cz/marik P. Rádl, B. Černá, L. Stará: Základy vyšší matematiky, skriptum MZLU Text přednášky na user.mendelu.cz/marik,
MATEMATICKÁ ANALÝZA A LINEÁRNÍ ALGEBRA PŘÍPRAVA NA ZKOUŠKU PRO SAMOUKY
 MATEMATICKÁ ANALÝZA A LINEÁRNÍ ALGEBRA PŘÍPRAVA NA ZKOUŠKU PRO SAMOUKY POMNĚNKA prase Pomni, abys nezapomněl na Pomněnku MSc. Catherine Morris POMNĚNKA Verze ze dne: 14. října 01 Materiál je v aktuální
MATEMATICKÁ ANALÝZA A LINEÁRNÍ ALGEBRA PŘÍPRAVA NA ZKOUŠKU PRO SAMOUKY POMNĚNKA prase Pomni, abys nezapomněl na Pomněnku MSc. Catherine Morris POMNĚNKA Verze ze dne: 14. října 01 Materiál je v aktuální
Monotonie a lokální extrémy. Konvexnost, konkávnost a inflexní body. 266 I. Diferenciální počet funkcí jedné proměnné
 66 I. Diferenciální počet funkcí jedné proměnné I. 5. Vyšetřování průběhu funkce Monotonie a lokální etrémy Důsledek. Nechť má funkce f) konečnou derivaci na intervalu I. Je-li f ) > 0 pro každé I, pak
66 I. Diferenciální počet funkcí jedné proměnné I. 5. Vyšetřování průběhu funkce Monotonie a lokální etrémy Důsledek. Nechť má funkce f) konečnou derivaci na intervalu I. Je-li f ) > 0 pro každé I, pak
Použití derivací L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT. Monotónie. Konvexita. V této části budou uvedena některá použití derivací.
 V této části budou uvedena některá použití derivací. Použití derivací L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT Tvrzení je uvedeno pro jednostrannou itu zprava. Samozřejmě obdobné tvrzení platí pro itu zleva
V této části budou uvedena některá použití derivací. Použití derivací L HOSPITALOVO PRAVIDLO POČÍTÁNÍ LIMIT Tvrzení je uvedeno pro jednostrannou itu zprava. Samozřejmě obdobné tvrzení platí pro itu zleva
Přijímací zkouška na navazující magisterské studium 2018
 Přijímací zkouška na navazující magisterské studium 2018 Řešení příkladů pečlivě odůvodněte. Příklad 1 (2 bodů) Studijní program: Studijní obory: Varianta A Matematika MMUI Navrhněte deterministický konečný
Přijímací zkouška na navazující magisterské studium 2018 Řešení příkladů pečlivě odůvodněte. Příklad 1 (2 bodů) Studijní program: Studijní obory: Varianta A Matematika MMUI Navrhněte deterministický konečný
DIFERENCIÁLNÍ POČET SPOJITOST FUNKCE,
 DIFERENCIÁLNÍ POČET SPOJITOST FUNKCE, LIMITA FUNKCE, DERIVACE FUNKCE Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století
DIFERENCIÁLNÍ POČET SPOJITOST FUNKCE, LIMITA FUNKCE, DERIVACE FUNKCE Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století
UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA UŽITÍ DERIVACÍ, PRŮBĚH FUNKCE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin
0.1 Úvod do matematické analýzy
 Matematika I (KMI/PMATE) 1 0.1 Úvod do matematické analýzy 0.1.1 Limita a spojitost funkce Lineární funkce Lineární funkce je jedna z nejjednodušších a možná i nejpoužívanějších funkcí. f(x) = kx + q D(f)
Matematika I (KMI/PMATE) 1 0.1 Úvod do matematické analýzy 0.1.1 Limita a spojitost funkce Lineární funkce Lineární funkce je jedna z nejjednodušších a možná i nejpoužívanějších funkcí. f(x) = kx + q D(f)
Vypracoval: Mgr. Lukáš Bičík TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY
 Průběh funkce Vypracoval: Mgr. Lukáš Bičík TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY Průběh funkce Průběhem funkce rozumíme určení vlastností funkce
Průběh funkce Vypracoval: Mgr. Lukáš Bičík TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY Průběh funkce Průběhem funkce rozumíme určení vlastností funkce
Definice globální minimum (absolutní minimum) v bodě A D f, jestliže X D f
 Výklad Globální extrémy mají stejný význam jako u funkcí jedné proměnné. Hledáme je bud na celém definičním oboru dané funkce, nebo na předem zadané podmnožině definičního oboru. Definice 6..1. Řekneme,
Výklad Globální extrémy mají stejný význam jako u funkcí jedné proměnné. Hledáme je bud na celém definičním oboru dané funkce, nebo na předem zadané podmnožině definičního oboru. Definice 6..1. Řekneme,
Kapitola 4: Extrémy funkcí dvou proměnných 1/5
 Kapitola 4: Extrémy funkcí dvou proměnných 1/5 Lokální extrémy Definice: Necht f : M R 2 R a (x 0, y 0 ) M. Říkáme, že fce f má v bodě (x 0, y 0 ) lokální maximum (resp. lokální minimum) jestliže existuje
Kapitola 4: Extrémy funkcí dvou proměnných 1/5 Lokální extrémy Definice: Necht f : M R 2 R a (x 0, y 0 ) M. Říkáme, že fce f má v bodě (x 0, y 0 ) lokální maximum (resp. lokální minimum) jestliže existuje
PRŮBĚH FUNKCE JEDNÉ REÁLNÉ PROMĚNNÉ
 Dierenciální počet unkcí jedné reálné proměnné - 5 - PRŮBĚH FUNKCE JEDNÉ REÁLNÉ PROMĚNNÉ Cílem vyšetřování průběhu unkce je umět nakreslit její gra Obvykle postupujeme tak že nalezneme její maimální deiniční
Dierenciální počet unkcí jedné reálné proměnné - 5 - PRŮBĚH FUNKCE JEDNÉ REÁLNÉ PROMĚNNÉ Cílem vyšetřování průběhu unkce je umět nakreslit její gra Obvykle postupujeme tak že nalezneme její maimální deiniční
Označení derivace čárkami, resp. římskými číslicemi, volíme při nižším řádu derivace, jinak užíváme horní index v závorce f (5), f (6),... x c g (x).
 9 Využití derivace 9.1 Derivace vyšších řádů Definice 1. Nechť funkce má derivaci v nějakém okolí bodu c D(f). Nechť funkce ϕ() =f () máderivacivboděc. Pak hodnotu ϕ (c) nazýváme derivací 2. řádu (2. derivací)
9 Využití derivace 9.1 Derivace vyšších řádů Definice 1. Nechť funkce má derivaci v nějakém okolí bodu c D(f). Nechť funkce ϕ() =f () máderivacivboděc. Pak hodnotu ϕ (c) nazýváme derivací 2. řádu (2. derivací)
Jazyk matematiky. 2.1. Matematická logika. 2.2. Množinové operace. 2.3. Zobrazení. 2.4. Rozšířená číslená osa
 2. Jazyk matematiky 2.1. Matematická logika 2.2. Množinové operace 2.3. Zobrazení 2.4. Rozšířená číslená osa 1 2.1 Matematická logika 2.1.1 Výrokový počet logická operace zapisujeme čteme česky negace
2. Jazyk matematiky 2.1. Matematická logika 2.2. Množinové operace 2.3. Zobrazení 2.4. Rozšířená číslená osa 1 2.1 Matematická logika 2.1.1 Výrokový počet logická operace zapisujeme čteme česky negace
Funkce zadané implicitně
 Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Matematika I A ukázkový test 1 pro 2014/2015
 Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
10. cvičení - LS 2017
 10. cvičení - LS 2017 Michal Outrata Příklad 1 Spočtěte následující itu daných posloupností: (a) (b) (c) n 3 +5n 2 n 3 6n 2 +3 n ; n 4 3n 2 6 n 4 + 3n 2 + 6; n 2 15n+2(1 n). 2(n 2) 3 2n 3 Příklad 2 Pro
10. cvičení - LS 2017 Michal Outrata Příklad 1 Spočtěte následující itu daných posloupností: (a) (b) (c) n 3 +5n 2 n 3 6n 2 +3 n ; n 4 3n 2 6 n 4 + 3n 2 + 6; n 2 15n+2(1 n). 2(n 2) 3 2n 3 Příklad 2 Pro
Stručný přehled učiva
 Stručný přehled učiva TU1M2 Matematika 2 pro LP17, LP18 4. Aplikace diferenciálního počtu 4.1 Rovnice tečny a normály Má-li funkce v bodě vlastní derivaci, pak je to směrnice tečny grafu funkce v tečném
Stručný přehled učiva TU1M2 Matematika 2 pro LP17, LP18 4. Aplikace diferenciálního počtu 4.1 Rovnice tečny a normály Má-li funkce v bodě vlastní derivaci, pak je to směrnice tečny grafu funkce v tečném
Matematika I pracovní listy
 Matematika I pracovní listy Dagmar Dlouhá, Radka Hamříková, Zuzana Morávková, Michaela Tužilová Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Úvod Pracovní listy jsou určeny
Matematika I pracovní listy Dagmar Dlouhá, Radka Hamříková, Zuzana Morávková, Michaela Tužilová Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Úvod Pracovní listy jsou určeny
14. Monotonnost, lokální extrémy, globální extrémy a asymptoty funkce
 . Monotonnost, lokální extrém, globální extrém a asmptot funkce Studijní text. Monotonnost, lokální extrém, globální extrém a asmptot funkce A. Rostoucí a klesající funkce Pojm rostoucí, klesající a konstantní
. Monotonnost, lokální extrém, globální extrém a asmptot funkce Studijní text. Monotonnost, lokální extrém, globální extrém a asmptot funkce A. Rostoucí a klesající funkce Pojm rostoucí, klesající a konstantní
Derivace funkce. Přednáška MATEMATIKA č Jiří Neubauer
 Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
Přijímací zkouška na navazující magisterské studium 2018
 Přijímací zkouška na navazující magisterské studium 208 Studijní program: Studijní obory: Matematika MA, MMIT, MMFT, MSTR, MNVM, MPMSE Varianta A Řešení příkladů pečlivě odůvodněte. Věnujte pozornost ověření
Přijímací zkouška na navazující magisterské studium 208 Studijní program: Studijní obory: Matematika MA, MMIT, MMFT, MSTR, MNVM, MPMSE Varianta A Řešení příkladů pečlivě odůvodněte. Věnujte pozornost ověření
Matematika I A ukázkový test 1 pro 2011/2012. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a
 Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Posloupnosti a řady. 28. listopadu 2015
 Posloupnosti a řady Přednáška 5 28. listopadu 205 Obsah Posloupnosti 2 Věty o limitách 3 Řady 4 Kritéria konvergence 5 Absolutní a relativní konvergence 6 Operace s řadami 7 Mocninné a Taylorovy řady Zdroj
Posloupnosti a řady Přednáška 5 28. listopadu 205 Obsah Posloupnosti 2 Věty o limitách 3 Řady 4 Kritéria konvergence 5 Absolutní a relativní konvergence 6 Operace s řadami 7 Mocninné a Taylorovy řady Zdroj
Základy matematiky pro FEK
 Základy matematiky pro FEK 8. přednáška Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 14 Derivace funkce U lineárních funkcí ve tvaru
Základy matematiky pro FEK 8. přednáška Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 14 Derivace funkce U lineárních funkcí ve tvaru
MATEMATIKA I - vybrané úlohy ze zkoušek v letech
 MATEMATIKA I - vybrané úlohy ze zkoušek v letech 008 0 doplněné o další úlohy. část DIFERENCIÁLNÍ POČET funkcí jedné proměnné Další část ( integrální počet) bude vydána na konci listopadu 9. 9. 0 Případné
MATEMATIKA I - vybrané úlohy ze zkoušek v letech 008 0 doplněné o další úlohy. část DIFERENCIÁLNÍ POČET funkcí jedné proměnné Další část ( integrální počet) bude vydána na konci listopadu 9. 9. 0 Případné
Úvod. Integrování je inverzní proces k derivování Máme zderivovanou funkci a integrací získáme původní funkci kterou jsme derivovali
 NEURČITÝ INTEGRÁL Úvod Integrování je inverzní proces k derivování Máme zderivovanou funkci a integrací získáme původní funkci kterou jsme derivovali Umět pracovat s integrálním počtem Je důležité pro
NEURČITÝ INTEGRÁL Úvod Integrování je inverzní proces k derivování Máme zderivovanou funkci a integrací získáme původní funkci kterou jsme derivovali Umět pracovat s integrálním počtem Je důležité pro
Funkce a limita. Petr Hasil. Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
 Funkce a limita Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Funkce a limita Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Úvodní informace. 17. února 2018
 Úvodní informace Funkce více proměnných Přednáška první 17. února 2018 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Limita a spojitost Derivace, diferencovatelnost, diferenciál Úvodní
Úvodní informace Funkce více proměnných Přednáška první 17. února 2018 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Limita a spojitost Derivace, diferencovatelnost, diferenciál Úvodní
Přednáška 11, 12. prosince Část 5: derivace funkce
 Přednáška 11, 12. prosince 2014 Závěrem pasáže o spojitých funkcích zmíníme jejich podtřídu, lipschitzovské funkce, nazvané podle německého matematika Rudolfa Lipschitze (1832 1903). Fukce f : M R je lipschitzovská,
Přednáška 11, 12. prosince 2014 Závěrem pasáže o spojitých funkcích zmíníme jejich podtřídu, lipschitzovské funkce, nazvané podle německého matematika Rudolfa Lipschitze (1832 1903). Fukce f : M R je lipschitzovská,
Petr Hasil. Prvákoviny c Petr Hasil (MUNI) Úvod do infinitezimálního počtu Prvákoviny / 57
 Úvod do infinitezimálního počtu Petr Hasil Prvákoviny 2015 c Petr Hasil (MUNI) Úvod do infinitezimálního počtu Prvákoviny 2015 1 / 57 Obsah 1 Úvod Funkce Reálná čísla a posloupnosti Limita a spojitost
Úvod do infinitezimálního počtu Petr Hasil Prvákoviny 2015 c Petr Hasil (MUNI) Úvod do infinitezimálního počtu Prvákoviny 2015 1 / 57 Obsah 1 Úvod Funkce Reálná čísla a posloupnosti Limita a spojitost
1.1 Příklad z ekonomického prostředí 1
 1.1 Příklad z ekonomického prostředí 1 Smysl solidního zvládnutí matematiky v bakalářských oborech na Fakultě podnikatelské VUT v Brně je především v aplikační síle matematiky v odborných předmětech a
1.1 Příklad z ekonomického prostředí 1 Smysl solidního zvládnutí matematiky v bakalářských oborech na Fakultě podnikatelské VUT v Brně je především v aplikační síle matematiky v odborných předmětech a
fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu (reg. č. CZ.1.07/2.2.00/28.
 Extrémy Vyšší matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu http://akademie.ldf.mendelu.cz/cz
Extrémy Vyšší matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu http://akademie.ldf.mendelu.cz/cz
Dodatek 2: Funkce dvou proměnných 1/9
 Dodatek 2: Funkce dvou proměnných 1/9 2/9 Funkce dvou proměnných Definice: Reálnou funkcí dvou reálných proměnných, definovanou na množině M R 2, rozumíme předpis f, který každé uspořádané dvojici reálných
Dodatek 2: Funkce dvou proměnných 1/9 2/9 Funkce dvou proměnných Definice: Reálnou funkcí dvou reálných proměnných, definovanou na množině M R 2, rozumíme předpis f, který každé uspořádané dvojici reálných
Funkce dvou a více proměnných
 Funkce dvou a více proměnných. Motivace V praxi nevstačíme s funkcemi jedné proměnné, většina veličin závisí více než na jedné okolnosti, např.: obsah obdélníka: S( ) kinetická energie: Ek = = x mv ekonomika:
Funkce dvou a více proměnných. Motivace V praxi nevstačíme s funkcemi jedné proměnné, většina veličin závisí více než na jedné okolnosti, např.: obsah obdélníka: S( ) kinetická energie: Ek = = x mv ekonomika:
3. ledna list a odevzdejte tento zvláštní list (listy) i všechny ostatní listy, které jste při řešení
 Jméno a příjmení: Písemná část zkoušky z předmětu AN1E 3. ledna 2019 Skutečná písemná práce bude obsahovat 5 příkladů. Zvolte si pořadí, v jakém budete příklady řešit. Vaše řešení nemusí být kulturně zapsané,
Jméno a příjmení: Písemná část zkoušky z předmětu AN1E 3. ledna 2019 Skutečná písemná práce bude obsahovat 5 příkladů. Zvolte si pořadí, v jakém budete příklady řešit. Vaše řešení nemusí být kulturně zapsané,
Matematika I Reálná funkce jedné promìnné
 Matematika I Reálná funkce jedné promìnné RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Reálná funkce Def. Zobrazení f nazveme
Matematika I Reálná funkce jedné promìnné RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Reálná funkce Def. Zobrazení f nazveme
Ten objekt (veličina), který se může svobodně měnit se nazývá nezávislý.
 @001 1. Základní pojmy Funkce funkční? Oč jde? Třeba: jak moc se oblečeme, závisí na venkovní teplotě, jak moc se oblečeme, závisí na našem mládí (stáří) jak jsme staří, závisí na čase jak moc zaplatíme
@001 1. Základní pojmy Funkce funkční? Oč jde? Třeba: jak moc se oblečeme, závisí na venkovní teplotě, jak moc se oblečeme, závisí na našem mládí (stáří) jak jsme staří, závisí na čase jak moc zaplatíme
Spojitost funkcí více proměnných
 Reálné funkce více proměnných Reálnou funkcí n reálných proměnných rozumíme zobrazení, které každé uspořádané n ticireálnýchčíselznějaképodmnožinykartézskéhosoučinur R=R n přiřazuje nějaké reálné číslo.
Reálné funkce více proměnných Reálnou funkcí n reálných proměnných rozumíme zobrazení, které každé uspořádané n ticireálnýchčíselznějaképodmnožinykartézskéhosoučinur R=R n přiřazuje nějaké reálné číslo.
JAK ČTEME Z DERIVACÍ PRŮBĚH PŮVODNÍCH FUNKCÍ? Pozn: veškeré funkce mají ve vnitřních bodech definičního oboru první derivaci. 1.
 JAK ČTEME Z DERIVACÍ PRŮBĚH PŮVODNÍCH FUNKCÍ? Pozn: veškeré funkce mají ve vnitřních bodech definičního oboru první derivaci. 1. Monotonie (1) Dostaneme zadanou např. funkci y = sin x. (2) Když si funkci
JAK ČTEME Z DERIVACÍ PRŮBĚH PŮVODNÍCH FUNKCÍ? Pozn: veškeré funkce mají ve vnitřních bodech definičního oboru první derivaci. 1. Monotonie (1) Dostaneme zadanou např. funkci y = sin x. (2) Když si funkci
Funkce. RNDR. Yvetta Bartáková. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
 Funkce RNDR. Yvetta Bartáková Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Derivace funkce VY INOVACE_05 0_M Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Definice Mějme funkci f definovanou v okolí bodu 0. Eistuje-li
Funkce RNDR. Yvetta Bartáková Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Derivace funkce VY INOVACE_05 0_M Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Definice Mějme funkci f definovanou v okolí bodu 0. Eistuje-li
Limita a spojitost LDF MENDELU
 Limita a spojitost Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Limita a spojitost Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Přednáška z MA. Michal Tuláček 16. prosince 2004. 1 IV.7 Průběhy funkce 3. 2 Vyšetřování průběhu funkce- KUCHAŘKA 4
 Přednáška z MA Michal Tuláček 6. prosince 004 Obsah IV.7 Průběhy funkce 3 Vyšetřování průběhu funkce- KUCHAŘKA 4 3 Vzorový příklad na průběh funkce ze cvičení 4 4 Příkladynadobumezikapremahusou 7 Definice:
Přednáška z MA Michal Tuláček 6. prosince 004 Obsah IV.7 Průběhy funkce 3 Vyšetřování průběhu funkce- KUCHAŘKA 4 3 Vzorový příklad na průběh funkce ze cvičení 4 4 Příkladynadobumezikapremahusou 7 Definice:
c ÚM FSI VUT v Brně 20. srpna 2007
 20. srpna 2007 1. f = 3 12 2. f = 2 e 3. f = ln Příklad 1. Nakreslete graf funkce f() = 3 12 Příklad 1. f = 3 12 Nejprve je třeba určit definiční obor. Výraz je vždy definován. Příklad 1. f = 3 12 f =
20. srpna 2007 1. f = 3 12 2. f = 2 e 3. f = ln Příklad 1. Nakreslete graf funkce f() = 3 12 Příklad 1. f = 3 12 Nejprve je třeba určit definiční obor. Výraz je vždy definován. Příklad 1. f = 3 12 f =
PRŮBĚH FUNKCE - CVIČENÍ
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA PRŮBĚH FUNKCE - CVIČENÍ Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA PRŮBĚH FUNKCE - CVIČENÍ Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny
Přijímací zkouška na navazující magisterské studium 2015
 Přijímací zkouška na navazující magisterské studium 2015 Studijní program: Studijní obory: Matematika MMUI Varianta A Řešení příkladů pečlivě odůvodněte. Příklad 1 (25 bodů Navrhněte deterministický konečný
Přijímací zkouška na navazující magisterské studium 2015 Studijní program: Studijní obory: Matematika MMUI Varianta A Řešení příkladů pečlivě odůvodněte. Příklad 1 (25 bodů Navrhněte deterministický konečný
Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost.
 Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost. Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a
Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost. Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a
5. Lokální, vázané a globální extrémy
 5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
2 Fyzikální aplikace. Předpokládejme, že f (x 0 ) existuje. Je-li f (x 0 ) vlastní, pak rovnice tečny ke grafu funkce f v bodě [x 0, f(x 0 )] je
![2 Fyzikální aplikace. Předpokládejme, že f (x 0 ) existuje. Je-li f (x 0 ) vlastní, pak rovnice tečny ke grafu funkce f v bodě [x 0, f(x 0 )] je 2 Fyzikální aplikace. Předpokládejme, že f (x 0 ) existuje. Je-li f (x 0 ) vlastní, pak rovnice tečny ke grafu funkce f v bodě [x 0, f(x 0 )] je](/thumbs/102/152847701.jpg) Derivace funkce a jej geometrický význam Je dána funkce f) 3 6 + 9 + a naším úkolem je určit směrnici tečny v bodě [; f)] Pro libovolné lze směrnici sečny danou body [; f)] a [; f)] spočítat jako f) f)
Derivace funkce a jej geometrický význam Je dána funkce f) 3 6 + 9 + a naším úkolem je určit směrnici tečny v bodě [; f)] Pro libovolné lze směrnici sečny danou body [; f)] a [; f)] spočítat jako f) f)
I. Úvod. I.1. Množiny. I.2. Výrokový a predikátový počet
 I. Úvod I.1. Množiny Množinou rozumíme každé shrnutí určitých a navzájem různých objektů (které nazýváme prvky) do jediného celku. Značení. Symbol x A značí, že element x je prvkem množiny A. Značení x
I. Úvod I.1. Množiny Množinou rozumíme každé shrnutí určitých a navzájem různých objektů (které nazýváme prvky) do jediného celku. Značení. Symbol x A značí, že element x je prvkem množiny A. Značení x
Matematika pro informatiky
 (FIT ČVUT v Praze) Konvexní analýza 13.týden 1 / 1 Matematika pro informatiky Jaroslav Milota Fakulta informačních technologíı České vysoké učení technické v Praze Letní semestr 2010/11 Extrémy funkce
(FIT ČVUT v Praze) Konvexní analýza 13.týden 1 / 1 Matematika pro informatiky Jaroslav Milota Fakulta informačních technologíı České vysoké učení technické v Praze Letní semestr 2010/11 Extrémy funkce
předmětu MATEMATIKA B 1
 Metodický list pro první soustředění kombinovaného studia předmětu MATEMATIKA B 1 Název tématického celku: Vektorový prostor Cíl: Základním cílem tohoto tematického celku je pochopit, co jsou to vektory
Metodický list pro první soustředění kombinovaného studia předmětu MATEMATIKA B 1 Název tématického celku: Vektorový prostor Cíl: Základním cílem tohoto tematického celku je pochopit, co jsou to vektory
Derivace funkce. prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky BI-ZMA ZS 2009/2010
 Derivace funkce prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Derivace funkce prof. RNDr. Čestmír Burdík DrCs. prof. Ing. Edita Pelantová CSc. Katedra matematiky České vysoké učení technické v Praze c Čestmír Burdík, Edita Pelantová 2009 Základy matematické analýzy
Obsah. Derivace funkce. Petr Hasil. L Hospitalovo pravidlo. Konvexnost, konkávnost a inflexní body Asymptoty
 Petr Hasil Přednáška z Matematické analýzy I c Petr Hasil (MUNI) MA I (M0) / 46 Obsah Základní vlastnosti derivace Geometrický význam derivace Věty o střední hodnotě L Hospitalovo pravidlo 2 Etrémy Konvenost,
Petr Hasil Přednáška z Matematické analýzy I c Petr Hasil (MUNI) MA I (M0) / 46 Obsah Základní vlastnosti derivace Geometrický význam derivace Věty o střední hodnotě L Hospitalovo pravidlo 2 Etrémy Konvenost,
