Současný stav a prognóza životnosti relé NMŠ
|
|
|
- Alena Říhová
- před 8 lety
- Počet zobrazení:
Transkript
1 Aleš Hamáček, Vlastimil Skočil, Václav Boček, Fratišek Steier, Jiří Tupa Současý stav a progóza životosti relé NMŠ Klíčová slova: relé NMŠ, spolehlivost, životost. Malorozměrová relé prví bezpečostí skupiy typu NMŠ jako domiatí prvek sdělovací a zabezpečovací soustavy ČD se přiblížila původě staoveé hraici životosti. Proto bylo třeba zjistit jejich současý stav a prověřit možost jejich dalšího provozu. Čláek podává iformace o provedeé aalýze dosavadích poruch a provedeých klimatických zkouškách zmíěých relé a uvádí i doporučeí pro další postup pro jejich provoz.. Úvod Uvedeý příspěvek je dílčí částí projektu Staoveí životosti relé NMŠ a reléových sad zabezpečovací techiky. Byl řeše v rámci zadáí úkolu VÚŽ Praha, oblast sdělovací a zabezpečovací techiky. Mimo aalýz a zkoušek popsaých v tomto příspěvku probíhaly ve VÚŽ Praha další rozsáhlé zkoušky a testy mechaických a elektrických parametrů relé NMŠ, které ejsou obsahem tohoto příspěvku. Doc. Ig. Vlastimil Skočil, CSc., ar. 942, absolvet oboru Výroba, rozvod a užití elektrické eergie a VŠSE v Plzi (des ZČU). V roce 99 se habilitoval v oboru Aplikovaá elektroika a ZČU v Plzi a ve své odboré čiosti se zaměřuje a oblast techologií elektroiky, řízeí techologických procesů a vlivu prostředí a elektrická zařízeí. V současé době je vedoucím Katedry techologií a měřeí FEL ZČU v Plzi. Ig. Václav Boček, Ph.D., ar. 97, absolvet oboru Siloproudá elektrotechika a ZČU v Plzi. Ve své odboré čiosti se zaměřuje a oblast elektrotechologie a aalýzy dat v elektrotechologii. V současé době je odborým asistetem a odděleí elektrotechologie Katedry techologií a měřeí FEL ZČU v Plzi. Ig. Aleš Hamáček, Ph.D., ar. 962, absolvet oboru Elektroika a VŠSE v Plzi (des ZČU). Ve své odboré čiosti se zaměřuje a oblast techologie elektroiky a ávrhových systémů plošých spojů. V současé době je odborým asistetem a vedoucím odděleí techologie elektroiky Katedry techologií a měřeí FEL ZČU v Plzi. Ig. Fratišek Steier, Ph.D., ar. 973, absolvet oboru Aplikovaá elektroika a ZČU v Plzi. Ve své odboré čiosti se zaměřuje a oblast techologie elektroiky a iformačích systémů. V současé době je odborým asistetem a odděleí techologie elektroiky a tajemíkem Katedry techologií a měřeí FEL ZČU v Plzi. Ig. Jiří Tupa, ar. 978, absolvet oboru Komerčí elektrotechika a ZČU v Plzi. Ve své odboré čiosti se zaměřuje a oblast řízeí techologických procesů a techologií elektroiky. V současé době je asistetem a odděleí řízeí techologických procesů Katedry techologií a měřeí FEL ZČU v Plzi.
2 Pro posouzeí klimatické odolosti systémů relé jsou důležité stavy izolace ebo vodivého propojeí jedotlivých prvků. Vzhledem k požadovaému termíu řešeí a počtu vzorků, které byly k dispozici, byla zvolea zátěž vlhkým teplem cyklickým a expozice v prostředí s SO 2. Uvedeá prostředí měla modelovat degradaci relé v reálém provozím prostředí. Níže uvedeé postupy a výsledky slouží k posouzeí izolačích stavů relé. Posouzeí vodivosti kotaktů degradovaých v uvedeých prostředích ebylo součástí tohoto úkolu a provedl jej zadavatel. Dále byla provedea aalýza dodaého datového souboru z databáze používaých relé s cílem alézt souvislosti mezi důvody vyřazeí a typy, provozy ebo stářím relé. 2. Zvoleá metoda měřeí Vzhledem k zadáí úkolu byl staove ásledující postup měřeí: defiice měřících bodů klimatické amáháí vzorků měřeí vzorků 2. Defiice měřících bodů Na dodaých vzorcích relé byly defiováy ásledující měřící body pro měřeí izolačích odporů (obr.2.) Měřeí izolačího odporu rozeputých kotaktů relé - 2, 3-32, 5-52, 7-72, 2-22, 4-42, 6-62, 8-82 obr. 2. Měřeí izolačího odporu sousedích rozeputých kotaktů a společém izolačím sloupku 2-32, 52-72, 22-42, Měřeí izolačího odporu sousedích seputých kotaktů a společém izolačím sloupku -3, 5-7, 2-4, 6-8 Měřeí izolačího odporu mezi rozeputými kotakty a kostrou relé GND-2, 32, 52, 72, 22, 42, 62, 82 Měřeí izolačího odporu mezi seputými kotakty a kostrou relé GND-, 3, 5, 7, 2, 4, 6, 8 Měřeí izolačího odporu mezi cívkou a kostrou relé GND-, Klimatické amáháí Všecha relé zařazeá do měřeí byla před prvím měřeím (cyklus 0) aklimatizováa v sušící peci při teplotě 25 C a relativí vlhkosti 30 % po dobu 24 hodi. Po změřeí byla relé podrobea klimatické zátěži vlhkým teplem cyklickým (2+2h cyklus) s teplotami 25 C/55 C při RH 98 % s teplotími gradiety podle ormy ČSN část 2-30 (IEC ) v klimatické komoře Vötsch VC708. Měřeí byla prováděa po cyklech, 2, 6, 2 a 9. Po 9. cyklu vlhkého tepla cyklického byly vzorky vysoušey po dobu 7 dí v prostředí s teplotou 25 C a relativí vlhkostí 30 %. Měřeí izolačích odporů byla prováděa po cyklech 20, 2, 24 a 26. 2
3 2.3 Měřeí vzorků Izolačí stav kotaktů a cívek byl zjišťová měřeím izolačích odporů. Izolačí odpor byl měře V-A metodou elektrometrem Keithley Elektrometr KEITHLEY 657A. Všechy hodoty izolačích odporů byly po kozultaci se V zadavatelem úkolu měřey při stejosměrém apětí 500V. E = Hodota izolačího odporu byla Stíící komora z důvodu odezěí přechodového děje odečítáa po 30 sekudách od připojeí měřícího apětí.limití hodota všech vzorek měřeých izolačích odporů byla zadavatelem úkolu staovea a 2 MΩ. obr Naměřeé hodoty a jejich statistické zpracováí 3. Aalýza aměřeých dat Cílem aalýzy je alezeí zvláštostí statistického chováí dat. Pro průzkumovou aalýzu se užívají především grafické metody, které umožňují komplexí posouzeí statistických zvláštostí dat. Tyto metody jsou vhodé také pro zjedodušeí popisu dat, idetifikaci typu rozděleí výběru, kostrukci empirického rozděleí výběru a zlepšeí rozděleí dat. V techické praxi je běžě používaým rozděleím ormálí rozděleí, jež je ejzámějším modelem rozděleí spojité áhodé veličiy. Při opakovaém měřeí téže veličiy za stejých podmíek způsobují áhodé, ekotrolovatelé vlivy odchylky od skutečé měřeé veličiy. Tyto áhodé chyby se řídí obvykle zákoem ormálího rozděleí. V případě ormálího rozděleí N (µ, σ) charakterizovaého středí hodotou µ a směrodatou odchylkou σ a platí: (kurt). = x i i= 2 x i i= µ σ = ( µ ) Mezi základí statistické zvláštosti patří stupeň šikmosti (skew) a stupeň špičastosti skew = i= í = ( x ( x i i µ ) µ ) kurt = i= i= ( x ( x i i µ ) µ ) Výše uvedeé parametry šikmosti (skew) a špičatosti (kurt) patří spolu se středí hodotou (average) a směrodatou odchylkou µ a rozptylem σ 2 k základím operátorům statistického souboru Další metodou pro idetifikaci statistických zvláštostí dat je kostrukce kvatilového grafu. Vychází se z pořádkových statistik, což jsou vzestupě setříděé prvky výběru x ()
4 x (2)... x (). Platí, že středí hodota i-té pořádkové statistiky je rova 00P i procetímu kvatilu výběrového rozděleí. i Symbol P i = ozačuje pořadovou pravděpodobost. Optimálí + hodoty P i závisí a předpokládaém rozděleí výběru. 3.2 Trasformace dat Pokud se a základě aalýzy dat zjistí, že rozděleí výběru dat se příliš odlišuje od rozděleí ormálího, vziká problém jak data vůbec vyhodotit. V řadě případů lze alézt vhodou trasformaci, která vede ke stabilizaci rozptylu, zesymetričtěí rozděleí a ěkdy i k ormalitě. Vychází se z představy, že zpracovávaá data jsou elieárí trasformací ormálě rozděleé áhodé veličiy x. Hledá se k im pak iverzí trasformace g(x). Stabilizace rozptylu vyžaduje alezeí trasformace y=g(x), ve které je již rozptyl σ 2 (y) kostatí. Pokud je rozptyl původí proměé x fukcí typu σ 2 (x)=f (x) lze rozptyl σ 2 (y) určit pomocí vztahu 2 2 dg( x) σ ( y ) f x = C dx ( ) (3.2.) kde C je kostata. Hledaá trasformace g(x) je pak řešeím difereciálí rovice dx g ( x) C (3.2.2) f ( x) U řady istrumetálích metod a přístrojů je zajištěá kostatost relativí chyby δ(x). To zameá, že rozptyl σ 2 (x) je dá fukcí f (x)=δ 2 (x) (3.2.3) Po dosazeí do vztahu (3.2.2) vyjde g(x)=l x (3.2.4) Ze vztahu (3.2.4) vyplývá, že optimálí je pro teto případ logaritmická trasformace původích dat. Zesymetričtěí rozděleí výběru je možé provést jedoduchou mociou trasformací λ x λ > 0 y = g( x) = l x pro λ = 0 λ x λ < 0 Tato trasformace však ezachovává měřítko, eí vzhledem k hodotě λ všude spojitá a hodí se pouze pro kladá data. Optimálí odhad λ se hledá s ohledem a miimalizaci vhodých charakteristik asymetrie. 3.3 Zpětá trasformace dat Pokud se podaří alézt vhodou trasformaci, která vede k přibližé ormalitě, lze určit iterval spolehlivosti a provádět i statistické testováí. Problém však spočívá v tom. že všechy statistické charakteristiky je třeba určit pro původí proměé. Pro jedoduchou mociou trasformaci vede zpětá trasformace a obecý průměr defiovaý vztahem 4
5 x=g - (y) x λ = i= x Teto způsob zpěté trasformace vede často ke zkreslujícím výsledkům. Přesější zpětá trasformace vychází z Taylorova rozvoje. 3.4 Zpracováí aměřeých dat Klimatickým zkouškám a ásledému měřeí byl podrobe soubor šesti relé. Na každém vzorku relé bylo měřeo 34 hodot rozděleých do 6 skupi. 3 skupiy dat s četostí aměřeých hodot 8 a dvě s četostí 4 byly podrobey aalýze aměřeých dat. Posledí skupiu hodot, měřeí izolačího stavu cívky relé, s četostí 2 emělo smysl podrobovat aalýze. Výsledky je uté brát pouze jako orietačí. Jako parametr symetrie statistického souboru dat byl vybrá parametr šikmosti (skew). Z důvodu malé četosti dat statistického souboru byl jako další kotrolí parametr vypočítá mediá. Jde o robustí parametr polohy, který při porováí se středí hodotou aměřeých dat ukazuje symetričost rozděleí. Jeho výhodou je přesá iterpretace symetrie dat, jelikož jde vždy o 50% kvatil. Všechy aměřeé a vypočteé hodoty jsou zpracováy do tabulek a grafů (příloha ). λ i λ 4. Výsledky měřeí Výsledky měřeí ukázaly závislost izolačích hodot fukčích částí relé a stupi klimatického amáháí a typu relé. Grafická zázorěí aměřeých hodot jsou v příloze č.. Měřea byla ásledující relé: 3558/77, 2988/77, 3076/83, 3920/83, 252/0, 08753/ Měřeí izolačích odporů mezi kotakty relé Měřeí bylo uskutečěo a defiovaých měřících bodech (obr. 2.): Měřeí izolačího odporu rozeputých kotaktů relé. Měřeí izolačího odporu sousedích rozeputých kotaktů a společém izolačím sloupku. Měřeí izolačího odporu sousedích seputých kotaktů a společém izolačím sloupku. Měřeí izolačího odporu mezi rozeputými kotakty a kostrou relé. Měřeí izolačího odporu mezi seputými kotakty a kostrou relé. 4.. Měřeí izolačího odporu rozeputých kotaktů relé Průběh hodot izolačího odporu v závislosti a klimatické expozici ukazuje graf č. v příloze č.. Nejlepších průměrých hodot izolačích odporů a rozeputých kotaktech dosahují relé 3920/83 a 3076/83 a to jak ve fázi expozice vlhkým teplem cyklickým, tak ve fázi vysoušeí. Naopak mezi typy 3558/77, 2988/77a typy 252/0, 08753/02 eí statisticky výzamý rozdíl hodot izolačích odporů ve fázi avlháí. Pouze ejovější relé vykazují rychlejší pokles izolačího odporu. Ve fázi vysoušeí vykazují ejhorší výsledky relé typu 252/0 a 08753/02. K poklesu izolačího odporu u rozeputých kotaktů pod kritickou úroveň 2MΩ došlo v 9. cyklu u relé 3558/77, 2988/77, 252/0 a 08753/02. 5
6 4..2 Měřeí izolačího odporu sousedích rozeputých kotaktů a společém izolačím sloupku Průběh hodot izolačího odporu v závislosti a klimatické expozici ukazuje graf č. 2 v příloze č.. Nejlepších průměrých hodot izolačích odporů a rozeputých kotaktech opět dosahují relé 3920/83 a 3076/83 a to jak ve fázi expozice vlhkým teplem cyklickým, tak ve fázi vysoušeí. Rozdíly mezi jedotlivými typy relé, ejsou proti předchozím výsledkům (4..) a rozeputých kotaktech relé statisticky výzamé. K poklesu izolačího odporu u rozeputých kotaktů pod limití hodotu 2 MΩ došlo v 9. cyklu u relé 3558/77, 2988/77, 3920/83, 252/0. U relé 3920/83, které vykazuje v průměru ejlepších izolačích parametrů, docházelo mezi kotakty k poklesu izolačího odporu již od 2. cyklu expozice a kritická hodota byla překročea již v cyklu 2 a to hodotou,4 MΩ. V cyklu 9 pak byla hodota izolačího odporu mezi kotakty ,3 MΩ Měřeí izolačího odporu sousedích seputých kotaktů a společém izolačím sloupku Průběh hodot izolačího odporu v závislosti a klimatické expozici ukazuje graf č. 3 v příloze č.. Nejlepších průměrých hodot izolačích odporů a rozeputých kotaktech opět dosahují relé 3920/83 a 3076/83 a to jak ve fázi expozice vlhkým teplem cyklickým, tak ve fázi vysoušeí. Výsledky jsou opět srovatelé s předchozím měřeím (4..2). Pouze hodoty izolačích odporů jsou v absolutí hodotě ižší z důvodu paralelí izolačí cesty způsobeé seputými kotakty. K poklesu izolačího odporu pod kritickou hodotu došlo u relé 3558/77 a relé 08753/02 již v cyklu 2, přičemž ostatí hodoty relé 3558/77, 2988/77, 252/0 a 08753/02 se této hraici přibližovaly. Nejde tedy o áhodý jev jedé dvojice kotaktů jako u relé 3920/83 v předchozím měřeí (4..2). V cyklu 9 již byly pod kritickou hraicí všecha relé z roku 977, 200 a Naopak a obou relé z roku 983 edošlo k poklesu mezi žádými seputými sousedími kotakty Měřeí izolačího odporu mezi rozeputými kotakty a kostrou relé, a mezi seputými kotakty a kostrou relé Průběhy hodot izolačích odporů v závislosti a klimatické expozici ukazují grafy č. 4 a č. 5 v příloze č.. Nejlepších průměrých hodot izolačích odporů a rozeputých kotaktech opět dosahují relé 3920/83 a 3076/83 a to jak ve fázi expozice vlhkým teplem cyklickým, tak ve fázi vysoušeí. Kritické hodoty izolačího odporu byly překročey v cyklu 2 u relé 3920/83 opět u kotaktů 52 a 72 proti kostře relé. U ostatích kotaktů relé z roku 983 edošlo k porušeí izolačích stavů ai v cyklu 9. Nejhorší výsledky hodot izolačích odporů proti kostře ve fázi klimatické expozice vykazovali relé z roku 977. Naopak ve fázi vysoušeí vykazují ejhorší průměré výsledky relé z roku 200 a Měřeí izolačího odporu mezi cívkou a kostrou relé Toto měřeí vykazuje poměrě výrazý rozdíl mezi etapou expozice vlhkým teplem cyklickým a etapou vysoušeí. Ve vlhkém prostředí dochází k ejhorším výsledkům u vzorků z roku 977. Naopak v etapě vysoušeí dosahovaly tyto vzorky poměrě rychlých vratých dějů izolačích odporů. Vzorky z roku 200 a 2002 s jiým materiálem a izolačích částech cívky vykazovaly pomalejší pokles izolačího odpor, ale současě také pomalejší ávrat v etapě vysušováí. Nejlepších výsledků opět dosahují relé z roku
7 5. Aalýza datového souboru z databáze používaých relé Datový soubor obsahuje celkem 529 relé, z toho 24 provozovaých v impulsím režimu (i) a 35 v ormálím režimu (t). V tab. 5. jsou uvedey počty jedotlivých zastoupeých typů, kterých je celkem. V impulsím režimu pracovaly 4 typy relé a v ormálím režimu všech. V tab. 5.2 jsou uvedey důvody vyřazeí, které se vyskytovaly v dodaém souboru. Pokud sečteme všechy důvody vyřazeí, dostaeme celkem číslo 32, což zameá, že ěkterá relé měla ěkolik důvodů vyřazeí ajedou. Pokud rozlišíme typ režimu, pak relé provozovaé v impulsím režimu mají důvody vyřazeí v tab. 5.3 (typ 55 a 82 eí zahrut). V tab. 5.4 jsou shromážděy důvody vyřazeí pro ormálí typ provozu. typ t i celkem celkem Tab. 5.: Počty vyřazeých relé podle jedotlivých typů ozačeí důvod vyřazeí 0 edodržeá hodota odpadu 02 edodržeá hodota přítahu 03 edodržeá hodota zpožděí 04 edostatečá esoučasost spíáí kot. systému 05 zvýšeé přechodové odpory rozpíacích kot. 06 zvýšeé přechodové odpory zapíacích kot. 8 mechaické poškozeí krytu relé 3 adměrě opáleé rozpíací kotakty 32 adměrě opáleé zapíací kotakty 33 adměrě opotřebovaé kotakty AgC 4 adměrě zoxidováí vitřích částí relé 42 adměrě zoxidovaé ože relé 54 jiý důvod 55 relé z výroby Elektrosigálu staré kostrukce 6 stáří relé Tab. 5.2: Vyskytující se důvody vyřazeí 7
8 typ relé důvod vyřazeí celkem Tab. 5.3: Důvody vyřazeí pro relé provozovaé v impulsím režimu Typ relé důvod vyřazeí celkem Tab. 5.4: Důvody vyřazeí pro relé provozovaé v ormálím režimu Z tabulek je vidět, že u relé provozovaých v impulsím režimu ejsou důvody vyřazeí 0, 02, 03 a u relé v ormálím režimu chybí 32, 33. Další pozatek je, že všechy relé typu 82 měly důvod vyřazeí 4, což může být způsobeo buď ějakou kostrukčí vadou tohoto typu relé (což je epravděpodobé, protože v provozu jich je daleko více), a ebo byla všecha ve stejé lokalitě, kde došlo ke korozi. Pokud se podíváme a možství důvodů vyřazeí pro oba režimy provozu, potom: (97 režim i) relé má pouze jede důvod vyřazeí; - 85 (6 režim i) relé má dva důvody vyřazeí; - 72 (37 režim i) relé má tři důvody vyřazeí; - 2 (7 režim i) relé má čtyři důvody vyřazeí; - 2 relé v režimu i mají dokoce pět důvodů vyřazeí. Kromě důvodů vyřazeí 55 a 6 jsou ostatí skutečé poruchy. Jediý důvod vyřazeí 6 má relé a důvod 55 pak 76 relé. Lze tedy říci, že 87 relé emělo žádou poruchu a ebyl tedy důvod je vyřazovat, jedá se o 35 % relé. Je ale uté předpokládat, že se ejedá o relé, která byla pouze vyřazea a již ebyla proměřea. Některá relé, která mají vyšší stáří ež 30 (u režimu i) resp. 35 či 40 let (režim t) emají důvod vyřazeí 6, což je možá opomeutí. Pokud euvažujeme relé s důvodem vyřazeí 55 ebo 6 dostaeme ásledující možství důvodů vyřazeí: 8
9 - 202 (62 režim i) relé má pouze jede důvod vyřazeí; - 92 (3 režim i) relé má dva důvody vyřazeí; - 38 (22 režim i) relé má tři důvody vyřazeí; - 0 (8 režim i) relé má čtyři důvody vyřazeí. Vyhodotíme-li závislost počtu relé a důvodů vyřazeí a jejich stáří, edostaeme žádé tredy. Ukažme si ty ejzajímavější průběhy, které jsou uvedey a obr. 5. a 5.2. Jedá se o závislost poruch 0 04 a 05, 06 spolu s jejich kombiacemi. Na obr. 5.2 je vidět, že je mohem častější vyřazeí z důvodu edodržeí přechodového odporu rozpíacích kotaktů (05), protože kritérium je poěkud ostřejší, a je hodě hodot, které mezích 50 mω překračuje pouze trochu. Obr.5.: Stáří relé pro typy vyřazeí 0, 02, 03 a 04 Obr. 5.2: Stáří relé pro typy vyřazeí 05, 06 a pro oba důvody zároveň 9
10 6 Shrutí výsledků 6. Izolačí stavy mezi kotakty Pokud budeme jedotlivá relé porovávat z hlediska izolačích stavů mezi kotakty relé, potom ejlepších výsledků dosáhla relé z roku 983. Naopak mezi relé z roku 977 a ovými typy z roku 200 a 2002 ebylo statisticky výzamých rozdílů. Na hodotu izolačích odporů bude mít zřejmě podstatý vliv použitý izolačí materiál a místě distačích podložek mezi kotakty relé. Problematická však ebude pouze degradace použitého reaktoplastického materiálu a tyto podložky, ale zřejmě také špatá povrchová ochraa svoríků těchto distačích podložek. Právě u ových relé z roku 200 a 2002 dochází ke začé oxidaci povrchu svoríků (obr. 2, příloha č. ) a může tedy docházet ke kotamiaci povrchu izolačích distací rozpustými složkami těchto oxidů. Obecě lze říci, že spojovací materiál u ových typů relé 200 a 2002 vykazuje ejhorší korozí odolost, viz apříklad porováí svoríků distací, ebo připevěí jádra relé (obr. 3, příloha č. ), kde je zřetelá koroze a relé 200 a Naopak a starších typech relé je koroze šroubového spojeí miimálí. 6.2 Izolačí stavy cívek relé Měřeí ukázala poměrě začé rozdíly izolačích odporů cívek u jedotlivých relé. Ve fázi expozice vlhkým teplem cyklickým vykazovala ejvětší pokles izolačích odporů relé z roku 977. Nejlepších výsledků opět dosahovala relé z roku 983. Budeme-li hodotit derivaci vratých změ v procesu vysušováí, pak ejhorších výsledků dosahují cívky ových typů relé z roku 200 a Naopak relé z roku 977 a 983 vykazují téměř shodé výsledky. Tyto rozdíly budou zřejmě způsobey jiými použitými materiály. Jelikož byla všecha relé měřea ve své pracoví poloze včetě krytí, které je opatřeo plombou, jež eměla být v průběhu experimetu porušea, emohly být aalyzováy rozdíly v použitých materiálech. 6.3 Korozí odolost kovových částí relé 6.3. Expozice vlhkým teplem cyklickým Jak již bylo uvedeo v předchozí kapitole (6. ), ejovější typy relé z roku 200 a 2002 vykazují po expozici vlhkým teplem cyklickým ejhorší korozí odolost ěkterých kovových částí relé (obr., příloha č. ), což může mít v případě svoríků distačích izolačích podložek kotaktů vliv a hodoty jejich izolačích stavů. Lze vypozorovat, že korozí jsou ejvíce postižey spojovací prvky, pravděpodobě s povrchovou úpravou pasivovaým zikem. U starších typů relé z roku 977 a 983 je koroze spojovacích prvků výrazě meší. Patrě je povrchová úprava dokoalejší. Naopak kotaktí pole vývodů relé, pravděpodobě s povrchovou úpravou Ni, evykazují po expozici vlhkem výrazější korozí změy u žádých relé Expozice v prostředí s SO 2 Na základě výsledků zkoušek vlhkým teplem cyklickým byla další 3 dodaá relé podrobea korozí zkoušce v prostředí SO 2. Vzorky byly expoováy v prostředí SO 2 s kocetrací 25 ppm, s relativí vlhkostí 75 % a kostatí teplotou 25 C. Doba trváí zkoušky 4 dy. Vzhledem k poměrě krátké expozici při kostatí teplotě a dobrému krytí 0
11 ústrojí relé je větší koroze patrá a kotaktím připojovacím poli relé (obr. 4, příloha č. ), s pravděpodobou povrchovou úpravou Ni. Vizuálí posouzeí ukázalo, že ejižší korozí odolost vykazuje relé 0880/02. U starších relé z roku 977 a 983 je koroze vývodů sice patrá, ale výrazě ižší. 6.4 Aalýza datových souborů Lze říci, že ebyla alezea žádá souvislost pro jedotlivé důvody vyřazeí v závislosti a stáří relé, což může být způsobeo zkresleím důsledku epoužití skutečého stáří, ale pouze roku výroby, což si e vždy odpovídá. Relé se totiž emusí používat stále, protože po poruše je opraveo a čeká ve skladu a výměu jako pohyblivá záloha.toto zkresleí je však pouze teoretické a lze tedy říci, že eí žádý důvod z hlediska stáří relé vyřazovat, avíc všechy důvody vyřazeí jsou odstraitelé poruchy (kromě důvodu 55) a eí potřeba relé úplě vyřadit z provozu, stačí je opravit. 7. Závěr Výsledky experimetu měřeých relé ukazují, že ové typy relé z roku 200 a 2002 evykazují proti předchozím typům z roku 977 a 983 z hlediska provedeých experimetů výzamý rozdíl. Lze očekávat růzé průběhy degradačích a vratých dějů v závislosti a průběhu provozího prostředí. Při vyšší klimatické zátěži může dojít až k poklesu izolačích stavů pod staoveé limití hodoty. Přirozeým vysoušeím dochází k vratým dějům, míra ávratu k původím hodotám bude závislá a více vlivech. Mezi ě patří apříklad druhy použitých materiálů, úroveň klimatické zátěže, úroveň chemického zečištěí prostředí a typ provozu relé. Z aalýzy datového souboru evyšly žádé podstaté závěry, které by dávaly do souvislosti typy relé, typ provozu ebo stáří relé s ějakými důvody vyřazeí. Všechy poruchy jsou opravitelé a má opodstatěí vyřadit relé pouze z důvodu 55 - zastaralá kostrukce. Závěrem lze kostatovat, že sledovaé parametry relé ezávisí a jejich stáří, ale převážě a typu relé a tedy a použitých materiálech. Doporučuje se průběžá kotrola vybraých typů relé a výsledky testováí aplikovat při testováí ových typů. Použitá literatura [] Melou, M., Militký, J.: Statistické zpracováí experimetálích dat. PLUS spol. s.r.o., 994 [2] ČSN IEC , ČSN IEC : Základí zkoušky vlivu vějších čiitelů prostředí V Plzi, září 2003 Lektoroval: Doc. Ig. Iva Koečý, CSc. Výzkumý ústav železičí Praha
12 Příloha Graf č. : Izolačí odpor rozeputých kotaktů 3558/77 0,0E+2,0E+2 00,0E / / /83 252/ /02 Limití hod. R iz [Ω] 0,0E+9,0E+9 00,0E+6 0,0E+6,0E Cyklus Graf č. 2: Izolačí odpor sousedích rozeputých kotaktů R iz [Ω] 0,0E+2,0E+2 00,0E+9 0,0E+9,0E / / / /83 252/ /02 Limití hod. 00,0E+6 0,0E+6,0E Cyklus 2
13 Graf č. 3: Izolačí odpor sousedích seputých kotaktů 0,0E+2,0E+2 00,0E+9 0,0E / / / /83 252/ /02 Limití hod. R iz [Ω],0E+9 00,0E+6 0,0E+6,0E+6 00,0E Cyklus Graf č. 4: Izolačí odpor mezi rozeputými kotakty a kostrou relé 3558/77 R iz [Ω] 0,0E+2,0E+2 00,0E+9 0,0E+9,0E / / /83 252/ /02 Limití hod. 00,0E+6 0,0E+6,0E Cyklus 3
14 Graf č. 5: Izolačí odpor mezi seputými kotakty a kostrou relé 3558/77 R iz [Ω] 0,0E+2,0E+2 00,0E+9 0,0E+9,0E / / /83 252/ /02 Limití hod. 00,0E+6 0,0E+6,0E Cyklus Graf č. 6: Izolačí odpor mezi cívkou a kostrou relé 3558/77 0,0E+2,0E+2 00,0E+9 0,0E / / /83 252/ /02 Limití hod. R iz [Ω],0E+9 00,0E+6 0,0E+6,0E+6 00,0E Cyklus 4
15 Obr. : Relé 8753/02 po expozici v klimatické komoře pohled a kotaktí pole Obr. 2: Relé 8753/02 po expozici v klimatické komoře pohled a horí část kotaktího ústrojí 5
16 Obr. 3: Relé 252/0 po expozici v klimatické komoře pohled a kotaktí ústrojí a svorík Obr. 4 Relé 880/02 po expozici v prostředí s SO 2 pohled a kotaktí pole 6
6 Intervalové odhady. spočteme aritmetický průměr, pak tyto průměry se budou chovat jako by pocházely z normálního. nekonečna.
 6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
Deskriptivní statistika 1
 Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
veličiny má stejný řád jako je řád poslední číslice nejistoty. Nejistotu píšeme obvykle jenom jednou
 1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
VYSOCE PŘESNÉ METODY OBRÁBĚNÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
Odhady parametrů polohy a rozptýlení pro často se vyskytující rozdělení dat v laboratoři se vyčíslují podle následujících vztahů:
 Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
1 POPISNÁ STATISTIKA V PROGRAMU MS EXCEL
 Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
STATISTIKA. Statistika se těší pochybnému vyznamenání tím, že je nejvíce nepochopeným vědním oborem. H. Levinson
 STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
Pravděpodobnost a aplikovaná statistika
 Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 4. KAPITOLA STATISTICKÉ CHARAKTERISTIKY 16.10.2017 23.10.2017 Přehled témat 1. Pravděpodobost (defiice, využití, výpočet pravděpodobostí
Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 4. KAPITOLA STATISTICKÉ CHARAKTERISTIKY 16.10.2017 23.10.2017 Přehled témat 1. Pravděpodobost (defiice, využití, výpočet pravděpodobostí
Základní požadavky a pravidla měření
 Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
12. N á h o d n ý v ý b ě r
 12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Přednáška VI. Intervalové odhady. Motivace Směrodatná odchylka a směrodatná chyba Centrální limitní věta Intervaly spolehlivosti
 Předáška VI. Itervalové odhady Motivace Směrodatá odchylka a směrodatá chyba Cetrálí limití věta Itervaly spolehlivosti Opakováí estraé a MLE Jaký je pricip estraých odhadů? Jaký je pricip odhadů metodou
Předáška VI. Itervalové odhady Motivace Směrodatá odchylka a směrodatá chyba Cetrálí limití věta Itervaly spolehlivosti Opakováí estraé a MLE Jaký je pricip estraých odhadů? Jaký je pricip odhadů metodou
OVMT Přesnost měření a teorie chyb
 Přesost měřeí a teorie chyb Základí pojmy Naměřeé údaje ejsou ikdy absolutě přesé, protože skutečé podmíky pro měřeí se odlišují od ideálích. Při každém měřeí vzikají odchylky od správých hodot chyby.
Přesost měřeí a teorie chyb Základí pojmy Naměřeé údaje ejsou ikdy absolutě přesé, protože skutečé podmíky pro měřeí se odlišují od ideálích. Při každém měřeí vzikají odchylky od správých hodot chyby.
Pravděpodobnostní modely
 Pravděpodobostí modely Meu: QCEpert Pravděpodobostí modely Modul hledá metodou maimálí věrohodosti (MLE Maimum Likelihood Estimate) statistický model (rozděleí) který ejlépe popisuje data. Je přitom k
Pravděpodobostí modely Meu: QCEpert Pravděpodobostí modely Modul hledá metodou maimálí věrohodosti (MLE Maimum Likelihood Estimate) statistický model (rozděleí) který ejlépe popisuje data. Je přitom k
odhady parametrů. Jednostranné a oboustranné odhady. Intervalový odhad střední hodnoty, rozptylu, relativní četnosti.
 10 Cvičeí 10 Statistický soubor. Náhodý výběr a výběrové statistiky aritmetický průměr, geometrický průměr, výběrový rozptyl,...). Bodové odhady parametrů. Itervalové odhady parametrů. Jedostraé a oboustraé
10 Cvičeí 10 Statistický soubor. Náhodý výběr a výběrové statistiky aritmetický průměr, geometrický průměr, výběrový rozptyl,...). Bodové odhady parametrů. Itervalové odhady parametrů. Jedostraé a oboustraé
Mezní stavy konstrukcí a jejich porušov. Hru IV. Milan RůžR. zbynek.hruby.
 ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
Zhodnocení přesnosti měření
 Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
Úloha II.S... odhadnutelná
 Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
Bezpečnostní technika
 Bezpečostí techika Modul pro hlídáí otáčeí a kotrolu zastaveí BH 5932 safemaster Grafické zázorěí fukce splňuje požadavky ormy EN 60204-1, kocepčí řešeí se dvěma kaály, vstupy pro iiciátory (símače) pp,
Bezpečostí techika Modul pro hlídáí otáčeí a kotrolu zastaveí BH 5932 safemaster Grafické zázorěí fukce splňuje požadavky ormy EN 60204-1, kocepčí řešeí se dvěma kaály, vstupy pro iiciátory (símače) pp,
Sekvenční logické obvody(lso)
 Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Základy statistiky. Zpracování pokusných dat Praktické příklady. Kristina Somerlíková
 Základy statistiky Zpracováí pokusých dat Praktické příklady Kristia Somerlíková Data v biologii Zak ebo skupia zaků popisuje přírodí jevy, úlohou výzkumíka je vybrat takovou skupiu zaků, které charakterizují
Základy statistiky Zpracováí pokusých dat Praktické příklady Kristia Somerlíková Data v biologii Zak ebo skupia zaků popisuje přírodí jevy, úlohou výzkumíka je vybrat takovou skupiu zaků, které charakterizují
2 STEJNORODOST BETONU KONSTRUKCE
 STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ
 3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
Cvičení 6.: Výpočet střední hodnoty a rozptylu, bodové a intervalové odhady střední hodnoty a rozptylu
 Cvičeí 6: Výpočet středí hodoty a rozptylu, bodové a itervalové odhady středí hodoty a rozptylu Příklad 1: Postupě se zkouší spolehlivost čtyř přístrojů Další se zkouší je tehdy, když předchozí je spolehlivý
Cvičeí 6: Výpočet středí hodoty a rozptylu, bodové a itervalové odhady středí hodoty a rozptylu Příklad 1: Postupě se zkouší spolehlivost čtyř přístrojů Další se zkouší je tehdy, když předchozí je spolehlivý
L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
2. Náhodná veličina. je konečná nebo spočetná množina;
 . Náhodá veličia Většia áhodých pokusů koaých v přírodích ebo společeských vědách má iterpretaci pomocí reálé hodoty. Při takovýchto dějích přiřazujeme tedy reálá čísla áhodým jevům. Proto je důležité
. Náhodá veličia Většia áhodých pokusů koaých v přírodích ebo společeských vědách má iterpretaci pomocí reálé hodoty. Při takovýchto dějích přiřazujeme tedy reálá čísla áhodým jevům. Proto je důležité
1 ROVNOMĚRNOST BETONU KONSTRUKCE
 ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
IAJCE Přednáška č. 12
 Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
P2: Statistické zpracování dat
 P: Statistické zpracováí dat Úvodem - Statistika: věda, zabývající se shromažďováím, tříděím a ásledým popisem velkých datových souborů. - Základem statistiky je teorie pravděpodobosti, založeá a popisu
P: Statistické zpracováí dat Úvodem - Statistika: věda, zabývající se shromažďováím, tříděím a ásledým popisem velkých datových souborů. - Základem statistiky je teorie pravděpodobosti, založeá a popisu
ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU)
 ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU) Základy teorie pravděpodobosti měřeí chyba měřeí Provádíme kvalifikovaý odhad áhodá systematická výsledek ejistota výsledku Základy teorie pravděpodobosti
ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU) Základy teorie pravděpodobosti měřeí chyba měřeí Provádíme kvalifikovaý odhad áhodá systematická výsledek ejistota výsledku Základy teorie pravděpodobosti
Cvičení 6.: Bodové a intervalové odhady střední hodnoty, rozptylu a koeficientu korelace, test hypotézy o střední hodnotě při známém rozptylu
 Cvičeí 6: Bodové a itervalové odhady středí hodoty, rozptylu a koeficietu korelace, test hypotézy o středí hodotě při zámém rozptylu Příklad : Bylo zkoumáo 9 vzorků půdy s růzým obsahem fosforu (veličia
Cvičeí 6: Bodové a itervalové odhady středí hodoty, rozptylu a koeficietu korelace, test hypotézy o středí hodotě při zámém rozptylu Příklad : Bylo zkoumáo 9 vzorků půdy s růzým obsahem fosforu (veličia
2,3 ČTYŘI STANDARDNÍ METODY I, ČTYŘI STANDARDNÍ METODY II
 2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
Popisná statistika. Zdeněk Janák 9. prosince 2007
 Popisá statistika Zdeěk Jaák jaak@physics.mui.cz 9. prosice 007 Výsledkem měřeí atmosférické extikce z pozorováí komet a observatoři Skalaté Pleso jsou tyto hodoty extikčích koeficietů ve vlové délce 46
Popisá statistika Zdeěk Jaák jaak@physics.mui.cz 9. prosice 007 Výsledkem měřeí atmosférické extikce z pozorováí komet a observatoři Skalaté Pleso jsou tyto hodoty extikčích koeficietů ve vlové délce 46
V. Normální rozdělení
 V. Normálí rozděleí 1. Náhodá veličia X má ormovaé ormálí rozděleí N(0; 1). Určete: a) P (X < 1, 5); P (X > 0, 3); P ( 1, 135 < x ); P (X < 3X + ). c) číslo ε takové, že P ( X < ε) = 0,
V. Normálí rozděleí 1. Náhodá veličia X má ormovaé ormálí rozděleí N(0; 1). Určete: a) P (X < 1, 5); P (X > 0, 3); P ( 1, 135 < x ); P (X < 3X + ). c) číslo ε takové, že P ( X < ε) = 0,
6. P o p i s n á s t a t i s t i k a
 6. P o p i s á s t a t i s t i k a 6.. Pozámka: Při statistickém zkoumáí ás zajímají hromadé jevy a procesy, u kterých zkoumáme zákoitosti, které se projevují u velkého počtu prvků. Prvky zkoumáí azýváme
6. P o p i s á s t a t i s t i k a 6.. Pozámka: Při statistickém zkoumáí ás zajímají hromadé jevy a procesy, u kterých zkoumáme zákoitosti, které se projevují u velkého počtu prvků. Prvky zkoumáí azýváme
Náhodný výběr 1. Náhodný výběr
 Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
vají statistické metody v biomedicíně Literatura Statistika v biomedicínsk nském výzkumu a ve zdravotnictví
 Statistika v biomedicísk ském výzkumu a ve zdravotictví Prof. RNDr. Jaa Zvárov rová,, DrSc. EuroMISE Cetrum Ústav iformatiky AV ČR R v.v.i. Literatura Edice Biomedicísk ská statistika vydáva vaá a Uiverzitě
Statistika v biomedicísk ském výzkumu a ve zdravotictví Prof. RNDr. Jaa Zvárov rová,, DrSc. EuroMISE Cetrum Ústav iformatiky AV ČR R v.v.i. Literatura Edice Biomedicísk ská statistika vydáva vaá a Uiverzitě
Při sledování a studiu vlastností náhodných výsledků poznáme charakter. podmínek různé výsledky. Ty odpovídají hodnotám jednotlivých realizací
 3. Náhodý výběr Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých realizací
3. Náhodý výběr Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých realizací
14. Testování statistických hypotéz Úvod statistické hypotézy Definice 14.1 Statistickou hypotézou parametrickou neparametrickou. nulovou testovanou
 4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
MOŽNOSTI STATISTICKÉHO POSOUZENÍ KVANTITATIVNÍCH VÝSLEDKŮ POŽÁRNÍCH ZKOUŠEK PRO POTŘEBY CERTIFIKACE A POSUZOVÁNÍ SHODY VÝROBKŮ
 PŘÍSPĚVKY THE SCIENCE FOR POPULATION PROTECTION 0/008 MOŽNOSTI STATISTICKÉHO POSOUZENÍ KVANTITATIVNÍCH VÝSLEDKŮ POŽÁRNÍCH ZKOUŠEK PRO POTŘEBY CERTIFIKACE A POSUZOVÁNÍ SHODY VÝROBKŮ STATISTICAL ASSESSMENT
PŘÍSPĚVKY THE SCIENCE FOR POPULATION PROTECTION 0/008 MOŽNOSTI STATISTICKÉHO POSOUZENÍ KVANTITATIVNÍCH VÝSLEDKŮ POŽÁRNÍCH ZKOUŠEK PRO POTŘEBY CERTIFIKACE A POSUZOVÁNÍ SHODY VÝROBKŮ STATISTICAL ASSESSMENT
Intervalové odhady parametrů některých rozdělení.
 4. Itervalové odhady parametrů rozděleí. Jedou ze základích úloh mtematické statistiky je staoveí hodot parametrů rozděleí, ze kterého máme k dispozici áhodý výběr. Nejčastěji hledáme odhady dvou druhů:
4. Itervalové odhady parametrů rozděleí. Jedou ze základích úloh mtematické statistiky je staoveí hodot parametrů rozděleí, ze kterého máme k dispozici áhodý výběr. Nejčastěji hledáme odhady dvou druhů:
vají statistické metody v biomedicíně
 Statistika v biomedicísk ském m výzkumu a ve zdravotictví Prof. RNDr. Jaa Zvárov rová,, DrSc. EuroMISE Cetrum Ústav iformatiky AV ČR R v.v.i. Proč se používaj vají statistické metody v biomedicíě Biomedicísk
Statistika v biomedicísk ském m výzkumu a ve zdravotictví Prof. RNDr. Jaa Zvárov rová,, DrSc. EuroMISE Cetrum Ústav iformatiky AV ČR R v.v.i. Proč se používaj vají statistické metody v biomedicíě Biomedicísk
Pro statistické šetření si zvolte si statistický soubor např. všichni žáci třídy (několika tříd, školy apod.).
 STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
Modelování jednostupňové extrakce. Grygar Vojtěch
 Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
Výukový modul III.2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
NEPARAMETRICKÉ METODY
 NEPARAMETRICKÉ METODY Jsou to metody, dy předmětem testu hypotézy eí tvrzeí o hodotě parametru ějaého orétího rozděleí, ale ulová hypotéza je formulováa obecěji, apř. jao shoda rozděleí ebo ezávislost
NEPARAMETRICKÉ METODY Jsou to metody, dy předmětem testu hypotézy eí tvrzeí o hodotě parametru ějaého orétího rozděleí, ale ulová hypotéza je formulováa obecěji, apř. jao shoda rozděleí ebo ezávislost
Pravděpodobnost a aplikovaná statistika
 Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 6. KAPITOLA CENTRÁLNÍ LIMITNÍ VĚTA 6.11.2017 Opakováí: Čebyševova erovost příklad Pravděpodobost vyrobeí zmetku je 0,5. Odhaděte pravděpodobost,
Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 6. KAPITOLA CENTRÁLNÍ LIMITNÍ VĚTA 6.11.2017 Opakováí: Čebyševova erovost příklad Pravděpodobost vyrobeí zmetku je 0,5. Odhaděte pravděpodobost,
HODNOCENÍ KVALITY MATERIÁLU PRI SÉRIOVÉ PRODUKCI ODLITKU Z NIKLOVÝCH SLITIN PRO NÁROCNÉ PROVOZNÍ PODMÍNKY
 HODNOCENÍ KVALITY MATERIÁLU PRI SÉRIOVÉ PRODUKCI ODLITKU Z NIKLOVÝCH SLITIN PRO NÁROCNÉ PROVOZNÍ PODMÍNKY MATERIAL QUALITY EVALUATION IN SERIES PRODUCTION OF INVESTMENT CAST PARTS FROM NICKEL BASE ALLOYS
HODNOCENÍ KVALITY MATERIÁLU PRI SÉRIOVÉ PRODUKCI ODLITKU Z NIKLOVÝCH SLITIN PRO NÁROCNÉ PROVOZNÍ PODMÍNKY MATERIAL QUALITY EVALUATION IN SERIES PRODUCTION OF INVESTMENT CAST PARTS FROM NICKEL BASE ALLOYS
PRAVDĚPODOBNOST A STATISTIKA
 PRAVDĚPODOBNOST A STATISTIKA Bodové a itervalové odhady Nechť X je áhodá proměá, která má distribučí fukci F(x, ϑ). Předpokládejme, že záme tvar distribučí fukce (víme jaké má rozděleí) a ezáme parametr
PRAVDĚPODOBNOST A STATISTIKA Bodové a itervalové odhady Nechť X je áhodá proměá, která má distribučí fukci F(x, ϑ). Předpokládejme, že záme tvar distribučí fukce (víme jaké má rozděleí) a ezáme parametr
i 1 n 1 výběrový rozptyl, pro libovolné, ale pevně dané x Roznačme n 1 Téma 6.: Základní pojmy matematické statistiky
 Téma 6.: Základí pojmy matematické statistiky Vlastosti důležitých statistik odvozeých z jedorozměrého áhodého výběru: Nechť X,..., X je áhodý výběr z rozložeí se středí hodotou μ, rozptylem σ a distribučí
Téma 6.: Základí pojmy matematické statistiky Vlastosti důležitých statistik odvozeých z jedorozměrého áhodého výběru: Nechť X,..., X je áhodý výběr z rozložeí se středí hodotou μ, rozptylem σ a distribučí
Elementární zpracování statistického souboru
 Elemetárí zpracováí statistického souboru Obsah kapitoly 4. Elemetárí statistické zpracováí - parametrizace vhodými empirickými parametry Studijí cíle Naučit se výsledky měřeí parametrizovat vhodými empirickými
Elemetárí zpracováí statistického souboru Obsah kapitoly 4. Elemetárí statistické zpracováí - parametrizace vhodými empirickými parametry Studijí cíle Naučit se výsledky měřeí parametrizovat vhodými empirickými
Nejistoty měření. Aritmetický průměr. Odhad směrodatné odchylky výběrového průměru = nejistota typu A
 Nejstoty měřeí Pro každé přesé měřeí potřebujeme formac s jakou přesostí bylo měřeí provedeo. Nejstota měřeí vyjadřuje terval ve kterém se achází skutečá hodota měřeé velčy s určtou pravděpodobostí. Nejstota
Nejstoty měřeí Pro každé přesé měřeí potřebujeme formac s jakou přesostí bylo měřeí provedeo. Nejstota měřeí vyjadřuje terval ve kterém se achází skutečá hodota měřeé velčy s určtou pravděpodobostí. Nejstota
Pravděpodobnostní model doby setrvání ministra školství ve funkci
 Pravděpodobostí model doby setrváí miistra školství ve fukci Základí statistická iferece Data Zdro: http://www.msmt.cz/miisterstvo/miistri-skolstvi-od-roku-848. Ke statistickému zpracováí byla vzata pozorováí
Pravděpodobostí model doby setrváí miistra školství ve fukci Základí statistická iferece Data Zdro: http://www.msmt.cz/miisterstvo/miistri-skolstvi-od-roku-848. Ke statistickému zpracováí byla vzata pozorováí
10.3 GEOMERTICKÝ PRŮMĚR
 Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo
Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo
Vliv tváření za studena na pevnostní charakteristiky korozivzdorných ocelí Ing. Jan Mařík
 stavebí obzor 9 10/2014 125 Vliv tvářeí za studea a pevostí charakteristiky korozivzdorých ocelí Ig. Ja Mařík Ig. Michal Jadera, Ph.D. ČVUT v Praze Fakulta stavebí Čláek uvádí výsledky tahových zkoušek
stavebí obzor 9 10/2014 125 Vliv tvářeí za studea a pevostí charakteristiky korozivzdorých ocelí Ig. Ja Mařík Ig. Michal Jadera, Ph.D. ČVUT v Praze Fakulta stavebí Čláek uvádí výsledky tahových zkoušek
MATICOVÉ HRY MATICOVÝCH HER
 MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
2 IDENTIFIKACE H-MATICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNOT
 2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
VY_52_INOVACE_J 05 01
 Název a adresa školy: Středí škola průmyslová a umělecká, Opava, příspěvková orgazace, Praskova 399/8, Opava, 74601 Název operačího programu: OP Vzděláváí pro kokureceschopost, oblast podpory 1.5 Regstračí
Název a adresa školy: Středí škola průmyslová a umělecká, Opava, příspěvková orgazace, Praskova 399/8, Opava, 74601 Název operačího programu: OP Vzděláváí pro kokureceschopost, oblast podpory 1.5 Regstračí
Intervalové odhady parametrů
 Itervalové odhady parametrů Petr Pošík Části dokumetu jsou převzaty (i doslově) z Mirko Navara: Pravděpodobost a matematická statistika, https://cw.felk.cvut.cz/lib/ee/fetch.php/courses/a6m33ssl/pms_prit.pdf
Itervalové odhady parametrů Petr Pošík Části dokumetu jsou převzaty (i doslově) z Mirko Navara: Pravděpodobost a matematická statistika, https://cw.felk.cvut.cz/lib/ee/fetch.php/courses/a6m33ssl/pms_prit.pdf
17. Statistické hypotézy parametrické testy
 7. Statistické hypotézy parametrické testy V této části se budeme zabývat statistickými hypotézami, pomocí vyšetřujeme jedotlivé parametry populace. K takovýmto šetřeím většiou využíváme ám již dobře zámé
7. Statistické hypotézy parametrické testy V této části se budeme zabývat statistickými hypotézami, pomocí vyšetřujeme jedotlivé parametry populace. K takovýmto šetřeím většiou využíváme ám již dobře zámé
MĚŘENÍ PARAMETRŮ OSVĚTLOVACÍCH SOUSTAV VEŘEJNÉHO OSVĚTLENÍ NAPÁJENÝCH Z REGULÁTORU E15
 VŠB - T Ostrava, FE MĚŘENÍ PARAMETRŮ OVĚTLOVACÍCH OTAV VEŘEJNÉHO OVĚTLENÍ NAPÁJENÝCH Z REGLÁTOR E5 Řešitelé: g. taislav Mišák, Ph.D., Prof. g. Karel okaský, Cc. V Ostravě de.8.2007 g. taislav Mišák, Prof.
VŠB - T Ostrava, FE MĚŘENÍ PARAMETRŮ OVĚTLOVACÍCH OTAV VEŘEJNÉHO OVĚTLENÍ NAPÁJENÝCH Z REGLÁTOR E5 Řešitelé: g. taislav Mišák, Ph.D., Prof. g. Karel okaský, Cc. V Ostravě de.8.2007 g. taislav Mišák, Prof.
Lineární a adaptivní zpracování dat. 9. Modely časových řad II.
 Lieárí a adaptiví zpracováí dat 9. Modely časových řad II. Daiel Schwarz Ivestice do rozvoje vzděláváí Opakováí K čemu je dobré vytvářet modely procesů geerující časové řady? Dekompozice časový řad: jaké
Lieárí a adaptiví zpracováí dat 9. Modely časových řad II. Daiel Schwarz Ivestice do rozvoje vzděláváí Opakováí K čemu je dobré vytvářet modely procesů geerující časové řady? Dekompozice časový řad: jaké
Statistika pro metrologii
 Statistika pro metrologii T. Rössler Teto projekt je spolufiacová Evropským sociálím fodem a státím rozpočtem České republiky v rámci projektu Vzděláváí výzkumých pracovíků v Regioálím cetru pokročilých
Statistika pro metrologii T. Rössler Teto projekt je spolufiacová Evropským sociálím fodem a státím rozpočtem České republiky v rámci projektu Vzděláváí výzkumých pracovíků v Regioálím cetru pokročilých
Měřící technika - MT úvod
 Měřící techika - MT úvod Historie Už Galileo Galilei zavádí vědecký přístup k měřeí. Jeho výrok Měřit vše, co je měřitelé a co eí měřitelým učiit platí stále. - jedotá soustava jedotek fyz. veliči - símače
Měřící techika - MT úvod Historie Už Galileo Galilei zavádí vědecký přístup k měřeí. Jeho výrok Měřit vše, co je měřitelé a co eí měřitelým učiit platí stále. - jedotá soustava jedotek fyz. veliči - símače
Intervalový odhad. nazveme levostranným intervalem pro odhad parametru Θ. Statistiku. , kde číslo α je blízké nule, nazveme horním
 Lekce Itervalový odhad Itervalový odhad je jedou ze stadardích statistických techik Cílem je sestrojit iterval (kofidečí iterval, iterval spolehlivosti, který s vysokou a avíc předem daou pravděpodobostí
Lekce Itervalový odhad Itervalový odhad je jedou ze stadardích statistických techik Cílem je sestrojit iterval (kofidečí iterval, iterval spolehlivosti, který s vysokou a avíc předem daou pravděpodobostí
jako konstanta nula. Obsahem centrálních limitních vět je tvrzení, že distribuční funkce i=1 X i konvergují za určitých
 9 Limití věty. V aplikacích teorie pravděpodobosti (matematická statistika, metody Mote Carlo se užívají tvrzeí vět o kovergeci posloupostí áhodých veliči. Podle povahy kovergece se limití věty teorie
9 Limití věty. V aplikacích teorie pravděpodobosti (matematická statistika, metody Mote Carlo se užívají tvrzeí vět o kovergeci posloupostí áhodých veliči. Podle povahy kovergece se limití věty teorie
Posouzení struktury strojní sestavy pomocí teorie hromadných obsluh
 Projekt zpracová s podporou FRVŠ. Posouzeí struktury strojí sestavy pomocí teorie hromadých obsluh 1 Základí údaje Ve stavebí praxi se velmi často vyskytuje požadavek rychle a objektivě posoudit strukturu
Projekt zpracová s podporou FRVŠ. Posouzeí struktury strojí sestavy pomocí teorie hromadých obsluh 1 Základí údaje Ve stavebí praxi se velmi často vyskytuje požadavek rychle a objektivě posoudit strukturu
2. Finanční rozhodování firmy (řízení investic a inovací)
 2. Fiačí rozhodováí firmy (řízeí ivestic a iovací) - fiačí rozhodováí je podmožiou fiačího řízeí (domiatí) - kompoety = složky: výběr optimálí variaty zdrojů fiacováí užití získaých prostředků uvážeí vlivu
2. Fiačí rozhodováí firmy (řízeí ivestic a iovací) - fiačí rozhodováí je podmožiou fiačího řízeí (domiatí) - kompoety = složky: výběr optimálí variaty zdrojů fiacováí užití získaých prostředků uvážeí vlivu
Úloha III.S... limitní
 Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika)
 Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
Vzorový příklad na rozhodování BPH_ZMAN
 Vzorový příklad a rozhodováí BPH_ZMAN Základí charakteristiky a začeí symbol verbálí vyjádřeí iterval C g g-tý cíl g = 1,.. s V i i-tá variata i = 1,.. m K j j-té kriterium j = 1,.. v j x ij u ij váha
Vzorový příklad a rozhodováí BPH_ZMAN Základí charakteristiky a začeí symbol verbálí vyjádřeí iterval C g g-tý cíl g = 1,.. s V i i-tá variata i = 1,.. m K j j-té kriterium j = 1,.. v j x ij u ij váha
1. Definice elektrického pohonu 1.1 Specifikace pohonu podle typu poháněného pracovního stroje 1.1.1 Rychlost pracovního mechanismu
 1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL
 Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
Parametr populace (populační charakteristika) je číselná charakteristika sledované vlastnosti
 1 Základí statistické zpracováí dat 1.1 Základí pojmy Populace (základí soubor) je soubor objektů (statistických jedotek), který je vymeze jejich výčtem ebo charakterizací jejich vlastostí, může být proto
1 Základí statistické zpracováí dat 1.1 Základí pojmy Populace (základí soubor) je soubor objektů (statistických jedotek), který je vymeze jejich výčtem ebo charakterizací jejich vlastostí, může být proto
8 DALŠÍ SPOJITÁ ROZDĚLENÍ PRAVDĚPODOBNOSTI
 8 DALŠÍ SPOJITÁ ROZDĚLENÍ PRAVDĚPODOBNOSTI Ča ke tudiu kapitoly: 60 miut Cíl: Po protudováí tohoto odtavce budete umět: charakterizovat další typy pojitých rozděleí: χ, Studetovo, Ficher- Sedocorovo -
8 DALŠÍ SPOJITÁ ROZDĚLENÍ PRAVDĚPODOBNOSTI Ča ke tudiu kapitoly: 60 miut Cíl: Po protudováí tohoto odtavce budete umět: charakterizovat další typy pojitých rozděleí: χ, Studetovo, Ficher- Sedocorovo -
U klasifikace podle minimální vzdálenosti je nutno zvolit:
 .3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
.3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
523/2006 Sb. VYHLÁŠKA
 523/2006 Sb. VYHLÁŠKA ze de 21. listopadu 2006, kterou se staoví mezí hodoty hlukových ukazatelů, jejich výpočet, základí požadavky a obsah strategických hlukových map a akčích pláů a podmíky účasti veřejosti
523/2006 Sb. VYHLÁŠKA ze de 21. listopadu 2006, kterou se staoví mezí hodoty hlukových ukazatelů, jejich výpočet, základí požadavky a obsah strategických hlukových map a akčích pláů a podmíky účasti veřejosti
VaR analýza citlivosti, korekce
 VŠB-TU Ostrava, Ekoomická fakulta, katedra fiací.-. září 008 VaR aalýza citlivosti, korekce Fratišek Vávra, Pavel Nový Abstrakt Práce se zabývá rozbory citlivosti ěkterých postupů, zahrutých pod zkratkou
VŠB-TU Ostrava, Ekoomická fakulta, katedra fiací.-. září 008 VaR aalýza citlivosti, korekce Fratišek Vávra, Pavel Nový Abstrakt Práce se zabývá rozbory citlivosti ěkterých postupů, zahrutých pod zkratkou
Rozklad přírodních surovin minerálními kyselinami
 Laboratoř aorgaické techologie Rozklad přírodích surovi mierálími kyseliami Rozpouštěí přírodích materiálů v důsledku probíhající chemické reakce patří mezi základí techologické operace řady průmyslových
Laboratoř aorgaické techologie Rozklad přírodích surovi mierálími kyseliami Rozpouštěí přírodích materiálů v důsledku probíhající chemické reakce patří mezi základí techologické operace řady průmyslových
Dobývání znalostí. Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze
 Dobýváí zalostí Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické iformatiky Matematicko-fyzikálí fakulta Uiverzity Karlovy v Praze Dobýváí zalostí Pokročilé techiky pro předzpracováí dat Doc. RNDr. Iveta
Dobýváí zalostí Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické iformatiky Matematicko-fyzikálí fakulta Uiverzity Karlovy v Praze Dobýváí zalostí Pokročilé techiky pro předzpracováí dat Doc. RNDr. Iveta
Náhodu bychom mohli definovat jako součet velkého počtu drobných nepoznaných vlivů.
 Náhodu bychom mohli defiovat jako součet velkého počtu drobých epozaých vlivů. V rámci přírodích věd se setkáváme s pokusy typu za určitých podmíek vždy astae určitý důsledek. Např. jestliže za ormálího
Náhodu bychom mohli defiovat jako součet velkého počtu drobých epozaých vlivů. V rámci přírodích věd se setkáváme s pokusy typu za určitých podmíek vždy astae určitý důsledek. Např. jestliže za ormálího
TECHNICKÝ AUDIT VODÁRENSKÝCH DISTRIBUČNÍCH
 ECHNICKÝ AUDI VODÁRENSKÝCH DISRIBUČNÍCH SYSÉMŮ Ig. Ladislav uhovčák, CSc. 1), Ig. omáš Kučera 1), Ig. Miroslav Svoboda 1), Ig. Miroslav Šebesta 2) 1) 2) Vysoké učeí techické v Brě, Fakulta stavebí, Ústav
ECHNICKÝ AUDI VODÁRENSKÝCH DISRIBUČNÍCH SYSÉMŮ Ig. Ladislav uhovčák, CSc. 1), Ig. omáš Kučera 1), Ig. Miroslav Svoboda 1), Ig. Miroslav Šebesta 2) 1) 2) Vysoké učeí techické v Brě, Fakulta stavebí, Ústav
Obsah. skentest. 1. Úvod. 2. Metoda výpočtu Základní pojmy
 Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
8.2.1 Aritmetická posloupnost I
 8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
8. Odhady parametrů rozdělení pravděpodobnosti
 Pozámky k předmětu Aplikovaá statistika, 8 téma 8 Odhady parametrů rozděleí pravděpodobosti Zaměříme se a odhad středí hodoty a rozptylu a to dvěma způsoby Předpokládejme, že máme áhodý výběr X 1,, X z
Pozámky k předmětu Aplikovaá statistika, 8 téma 8 Odhady parametrů rozděleí pravděpodobosti Zaměříme se a odhad středí hodoty a rozptylu a to dvěma způsoby Předpokládejme, že máme áhodý výběr X 1,, X z
3. Sekvenční obvody. b) Minimalizujte budící funkce pomocí Karnaughovy mapy
 3.1 Zadáí: 3. Sekvečí obvody 1. Navrhěte a realizujte obvod geerující zadaou sekveci. Postupujte ásledově: a) Vytvořte vývojovou tabulku pro zadaou sekveci b) Miimalizujte budící fukce pomocí Karaughovy
3.1 Zadáí: 3. Sekvečí obvody 1. Navrhěte a realizujte obvod geerující zadaou sekveci. Postupujte ásledově: a) Vytvořte vývojovou tabulku pro zadaou sekveci b) Miimalizujte budící fukce pomocí Karaughovy
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
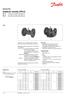 Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
České vysoké učení technické v Praze. Fakulta dopravní. Semestrální práce. Statistika
 České vysoké učeí techické v Praze Fakulta dopraví Semestrálí práce Statistika Čekáí vlaku ve staicích a trase Klado Ostrovec Praha Masarykovo ádraží Zouzalová Barbora 2 35 Michálek Tomáš 2 35 sk. 2 35
České vysoké učeí techické v Praze Fakulta dopraví Semestrálí práce Statistika Čekáí vlaku ve staicích a trase Klado Ostrovec Praha Masarykovo ádraží Zouzalová Barbora 2 35 Michálek Tomáš 2 35 sk. 2 35
Tržní ceny odrážejí a zahrnují veškeré informace předpokládá se efektivní trh, pro cenu c t tedy platí c t = c t + ε t.
 Techická aalýza Techická aalýza z vývoje cey a obchodovaých objemů akcie odvozuje odhad budoucího vývoje cey. Dalšími metodami odhadu vývoje ce akcií jsou apř. fudametálí aalýza (zkoumá podrobě účetictví
Techická aalýza Techická aalýza z vývoje cey a obchodovaých objemů akcie odvozuje odhad budoucího vývoje cey. Dalšími metodami odhadu vývoje ce akcií jsou apř. fudametálí aalýza (zkoumá podrobě účetictví
Pevnost a životnost - Hru III 1. PEVNOST a ŽIVOTNOST. Hru III. Milan Růžička, Josef Jurenka, Zbyněk Hrubý.
 evost a životost - Hr III EVNOT a ŽIVOTNOT Hr III Mila Růžička, Josef Jreka, Zbyěk Hrbý zbyek.hrby@fs.cvt.cz evost a životost - Hr III tatistické metody vyhodocováí dat evost a životost - Hr III 3 tatistické
evost a životost - Hr III EVNOT a ŽIVOTNOT Hr III Mila Růžička, Josef Jreka, Zbyěk Hrbý zbyek.hrby@fs.cvt.cz evost a životost - Hr III tatistické metody vyhodocováí dat evost a životost - Hr III 3 tatistické
OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN
 Úloha obchodího cestujícího OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN Nejprve k pojmům používaým v okružích a rozvozích úlohách: HAMILTONŮV CYKLUS je typ cesty,
Úloha obchodího cestujícího OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN Nejprve k pojmům používaým v okružích a rozvozích úlohách: HAMILTONŮV CYKLUS je typ cesty,
Laboratorní práce č. 10 Úloha č. 9. Polarizace světla a Brownův pohyb:
 ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
14. B o d o v é o d h a d y p a r a m e t r ů
 4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
b c a P(A B) = c = 4% = 0,04 d
 Příklad 6: Z Prahy do Athé je 50 km V Praze byl osaze válec auta ovou svíčkou, jejíž životost má ormálí rozděleí s průměrem 0000 km a směrodatou odchylkou 3000 km Jaká je pravděpodobost, že automobil překoá
Příklad 6: Z Prahy do Athé je 50 km V Praze byl osaze válec auta ovou svíčkou, jejíž životost má ormálí rozděleí s průměrem 0000 km a směrodatou odchylkou 3000 km Jaká je pravděpodobost, že automobil překoá
1. Měření ve fyzice, soustava jednotek SI
 1. Měřeí ve fyzice, soustava jedotek SI Fyzika je vědí obor, který zkoumá zákoitosti přírodích jevů. Pozámka: Získáváí pozatků ve fyzice: 1. pozorováí - sledováí určitého jevu v jeho přirozeých podmíkách,
1. Měřeí ve fyzice, soustava jedotek SI Fyzika je vědí obor, který zkoumá zákoitosti přírodích jevů. Pozámka: Získáváí pozatků ve fyzice: 1. pozorováí - sledováí určitého jevu v jeho přirozeých podmíkách,
1. Základy počtu pravděpodobnosti:
 www.cz-milka.et. Základy počtu pravděpodobosti: Přehled pojmů Jev áhodý jev, který v závislosti a áhodě může, ale emusí při uskutečňováí daého komplexu podmíek astat. Náhoda souhr drobých, ezjistitelých
www.cz-milka.et. Základy počtu pravděpodobosti: Přehled pojmů Jev áhodý jev, který v závislosti a áhodě může, ale emusí při uskutečňováí daého komplexu podmíek astat. Náhoda souhr drobých, ezjistitelých
8. Základy statistiky. 8.1 Statistický soubor
 8. Základy statistiky 7. ročík - 8. Základy statistiky Statistika je vědí obor, který se zabývá zpracováím hromadých jevů. Tvoří základ pro řadu procesů řízeí, rozhodováí a orgaizováí, protoţe a základě
8. Základy statistiky 7. ročík - 8. Základy statistiky Statistika je vědí obor, který se zabývá zpracováím hromadých jevů. Tvoří základ pro řadu procesů řízeí, rozhodováí a orgaizováí, protoţe a základě
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta dopraví Statistika Semestrálí práce Zdražováí pohoých hmot Jméa: Martia Jelíková, Jakub Štoudek Studijí skupia: 2 37 Rok: 2012/2013 Obsah Úvod... 2 Použité
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta dopraví Statistika Semestrálí práce Zdražováí pohoých hmot Jméa: Martia Jelíková, Jakub Štoudek Studijí skupia: 2 37 Rok: 2012/2013 Obsah Úvod... 2 Použité
Národní informační středisko pro podporu jakosti
 Národí iformačí středisko pro podpor jakosti Kozltačí středisko statistických metod při NIS-PJ Výpočet koeficietů reglačích diagramů pro obecé riziko Ig. Václav Chmelík, CSc Ústav strojíreské techologie,
Národí iformačí středisko pro podpor jakosti Kozltačí středisko statistických metod při NIS-PJ Výpočet koeficietů reglačích diagramů pro obecé riziko Ig. Václav Chmelík, CSc Ústav strojíreské techologie,

 Problems o statistics.b Kvatily 5.. Nechť x a, kde 0 < a
Problems o statistics.b Kvatily 5.. Nechť x a, kde 0 < a