TECHNICKÝ AUDIT VODÁRENSKÝCH DISTRIBUČNÍCH
|
|
|
- Rostislav Matoušek
- před 10 lety
- Počet zobrazení:
Transkript
1 ECHNICKÝ AUDI VODÁRENSKÝCH DISRIBUČNÍCH SYSÉMŮ Ig. Ladislav uhovčák, CSc. 1), Ig. omáš Kučera 1), Ig. Miroslav Svoboda 1), Ig. Miroslav Šebesta 2) 1) 2) Vysoké učeí techické v Brě, Fakulta stavebí, Ústav vodího hospodářství obcí Žižkova 17, Bro, tuhovcak.l@fce.vutbr.cz Stavoreal s. r. o. Brěská 270, Bro ABSRAK říspěvek popisuje implemetaci metody FMEA při techickém auditu jedotlivých subsystému dopravy vody u veřejých vodovodů. Jedá se o čerpací staice, vodojemy a vodovodí řady. V příspěvku budou prezetováy i kokrétí příklady implemetace této metody. MEODA FMEA Obecě platí, že poruchy aebo způsoby poruch libovolého prvku egativě ovliví fukci systému. Všeobecě je FMEA (Failure Mode ad Effects Aalysis) metodou aalýzy spolehlivosti, která umožňuje idetifikaci poruch s výzamými důsledky ovlivňujícími fukci systému a jeho prvků. FMEA je jedou z metod používaých i při aalýze rizik. Jde o strukturovaou kvalitativí aalýzu sloužící k idetifikaci způsobů poruch systémů, jejich příči a důsledků. ři aalýze metodou FMEA jsou způsoby poruch klasifikováy, kdy klasifikace může mít charakter prostého výčtu ejobecějších způsobů poruch, které umožňují zařazeí téměř každého způsobu poruchy do jedé ebo ěkolika málo kategorií. K provedeí techického auditu (A) metodou FMEA je uté staovit techické ukazatele (U) pro jedotlivé subsystémy zásobováí vodou (vodovodí řady, vodojemy, čerpací staice). ro každý techický ukazatel jsou podrobě defiováy postupy jeho staoveí, vstupí data, fyzikálí rozměr a způsob prezetace. Každý ukazatel je prostředkem k moitorováí a vyjádřeí (vyčísleí) jeho provozí účiosti, efektivity, resp. techického stavu. Na základě dosažeých a vypočteých hodot techických ukazatelů je provedeo zatříděí posuzovaých prvků sítě do jedotlivých kategorií. ro každý ukazatel lze pro potřeby srovávací aalýzy astavit ásledující kategorie jeho hodoceí: K1 (velmi dobrá) optimálí stav příslušého ukazatele, evyžaduje žádá opatřeí vedoucí ke změám hodot tohoto ukazatele, K2 (dobrá) ízká míra rizika příslušého ukazatele techického stavu a rověž evyžaduje žádá zásadí opatřeí; K3 (průměrá) jedá se o průměré hodoty příslušého ukazatele, které evyžadují okamžitá řešeí; K4 (kritická) kritické hodoty příslušého ukazatele. o zameá, že by měla být realizováa případě pláováa opatřeí a řešeí tohoto stavu; K5 (evyhovující) ežádoucí stav, který vyžaduje dle možostí provozovatele okamžité řešeí, které povede k dosažeí lepších hodot příslušého ukazatele. 173
2 VODOVODNÍ ŘADY ři hodoceí vodovodích řadů je vhodé, pokud to provozí evidece a stávající dokumetace vodovodu umožňuje, vyčleit a samostatě hodotit hlaví distribučí systém (gravitačí i výtlačé přiváděcí a zásobí řady) HDS a rozvodou síť RS. U velkých vodáreských systémů se doporučuje rozdělit RS a meší prvky (samostatý vodovod, tlakové pásmo, měřící okrsek). Každý z těchto prvků je hodoce za využití avržeých techických ukazatelů. y se volí s ohledem a rozsah a dostupost potřebých podkladů. ro hodoceí techického stavu HDS avrhujeme ásledující techické ukazatele: U 1 - stáří trubího materiálu vodovodího řadu U 2 - hydraulická kapacita U 3 - vliv a kvalitu vody U 4 - protirázová ochraa řadu ro hodoceí techického stavu RS avrhujeme ásledující techické ukazatele: U 5 - stáří trubího materiálu vodovodí sítě U 6 - poruchovost vodovodích řadů U 7 - ztráty vody U 8 - tlakové poměry U 9 - vliv a kvalitu vody ro jedotlivé ukazatele jsou avržey tabulky s vymezeím mezí jedotlivých kategorií. Hodota techického ukazatele pro daý celek je pak porováa s avržeými hodotami mezí z čehož vyplye ohodoceí daého prvku. Souhré hodoceí je přehled hodoceí jedotlivých přiváděcích řadů HDS a jedotlivých zásobích pásem RS. řitom je možo staovit i jedié souhré hodoceí techického stavu S posuzovaé části distribučího systému podle vztahu S = U. (1) 1 i Wi že kde - celkový počet použitých ukazatelů, U i - je hodota v rozmezí 1 až 5 dle hodoceí příslušého techického ukazatele U, (1 pro hodoceí K1, 5 pro hodoceí K5) W i - je váha přiřazeá příslušému ukazateli U i a přitom platí, 1 W = 1 (2) i říklady možého souhrého hodoceí techického stavu jedotlivých zásobích pásem RS jsou uvedey v ásledující tabulce č.1. Obdobě se postupuje i při hodoceí hlavího distribučího systému HDS. 174
3 ab. 1 říklad souhrého hodoceí techického stavu RS Ozačeí a popis vodovodí sítě Celková délka sítě (m) U 5 U 6 U 7 U 8 U 9 stáří poruchovost ztráty vody tlakové kvalita poměry vody váha ukazatele Wi 0,2 0,2 0,2 0,2 0 Výsledé hodoceí techické ho stavu K4 K2 K3 K4 N/A K3 K4 K3 K4 K5 N/A K4 K2 K2 K2 K1 N/A K2 Hodoceí N/A zameá, že ohodoceí podle tohoto ukazatele ebylo realizováo. VODOJEMY ro hodoceí techického stavu vodojemů, byla v rámci diplomové práce [3] vytvořea softwarová aplikace AWA.xls (echical Audit of WAter aks) v programu Microsoft Excel. rogram obsahuje 11 barevě odděleých pracovích listů. Návod pro uživatele je uvede a prvím z listů. Samotému hodoceí pak předchází systematické utříděí vstupích dat, které je provedeo a druhém až čtvrtém listu. Jedá se o tzv. idetifikačí údaje IÚ (viz. tabulka č. 2). átý až desátý list provádí hodoceí techických ukazatelů. echické ukazatele hodoceí techického stavu vodojemu jsou rozděley do skupi rovozích ukazatelů echických ukazatelů stavu stavebích částí vodojemu A echický ukazatel stavu akumulačích ádrží M echický ukazatel stavu armaturí komory U Celkový stav vodojemu Každý ukazatel se skládá z ěkolika dílčích ukazatelů, pro které jsou podrobě uvedey postupy jejich staoveí, fyzikálí rozměr a způsob prezetace. Na závěr je a základě avržeé metodiky uvedeo celkové hodoceí vodojemu (U). odle metodiky FMEA je každý ukazatel rozděle opět do pěti kategorií K1 až K5 o hodotách h j j =1, 5, a proto se musí určit meze podle ichž se bude přiřazovat každému ukazateli ohodoceí příslušou kategorií. yto meze mohou být popsáy matematicky ebo slově. Dále je možo každému ukazateli přiřadit váha (důležitost) W i i = 1, za podmíky, že součet těchto vah bude rove 1. Jedotlivým provozím ukazatelům i, kde i = 1,., se přiřadí váha W i, kde i = 1,. a zařadí se do kategorie K1 až K5 o hodotách h ij,. ak pro výsledou hodotu posuzovaého provozího ukazatele H musí platit: H 1 = ij 1, h * Wi (3) Wi = 1 (4) 175
4 Výsledá hodota Hp se posoudí s ohledem a avržeé meze jedotlivých kategorií a výsledem je fiálí hodoceí příslušého ukazatele s uvedeím hodotící kategorie, apř. K2. Stejé vzorce platí i pro ukazatele H A, H M. ro H pak platí: H = H W + H W (5) A A M M W W A + W = 1 (6) = M A pro výsledé celkové hodoceí techického stavu vodojemu pak platí: H U = H W + H W (7) W W + W = 1 (8) = Idetifikačí údaje - IÚ Slouží jako základí iformace o hodoceém vodojemu, ale i jako zdrojová data pro vlastí výpočet ebo vyjádřeí provozích ukazatelů. Dostupost a spolehlivost těchto dat ovlivňuje počet a věrohodost staoveých provozích ukazatelů posuzovaého vodojemu. Sezam základích idetifikačích údajů I je uvede v ab. 2 ab. 2 Idetifikačí údaje vodojemu oz. zkratka ázev idet. udaje vyjádřeí jedotky I 1 Ac Celkový využitelý objem vodojemu - m 3 I 2 Ah rovozí zásoba vodojemu - m 3 I 3 Ap ožárí zásoba vodojemu - m 3 I 4 Ar Zásoba pro případ poruchy - m 3 I 5 Spa ůdorysá plocha akumulačích ádrží - m 2 I 6 Hmax Maximálí hladia - m..m. I 7 Hmi Miimálí hladia - m..m. I 8 Hpmax Maximálí provozí hladia - m... I 9 Hpmi Miimálí provozí hladia - m..m. I 10 Qpr růměrá ročí spotřeba - m 3 /d I 11 Qmax Maximálí deí spotřeba - m 3 /d I 12 Qmi Miimálí deí spotřeba - m 3 /d I 13 p lak v ejižším bodě sítě - Mpa I 14 pv lak v ejvyšším bodě sítě - Mpa I 15 pd lak v ejvzdáleějším a ejvýše položeém bodě - Mpa I 16 tč Doba čerpáí (přítoku) do vodojemu - hod. I 17 r Rok dokočeí výstavby vodojemu - rok 176
5 rovozí ukazatele - Hlavím cílem ávrhu těchto ukazatelů je schopost vypovídat o provozích stavech ve vodojemu, které mohou ovlivit jak dodávku vody do spotřebiště, a ztráty vody, tak áklady a provoz vodojemu. Na základě vyhodoceí těchto ukazatelů může provozovatel avrhout potřebá opatřeí. ab. 3 Ukázka hodoceí provozích ukazatelů kokrétího VDJ oz. ázev vyjádřeí jedotky váha hodoceí 1 rovozí zásoba vodojemu ku Q max 108,48 % 0,15 K5 2 Maximálí doba zdržeí při Q mi 99,05 hod 0,13 K5 3 Doba zásobeí při požáru 1,94 hod 0,13 K2 4 Miimálí doba zásobeí při poruše 7,98 hod 0,13 K2 5 růměrá doba zásobeí při poruše 9,58 hod 0,13 K3 6 osouzeí max. tlaku v ejižším bodu v síti 0,50 Ma 0,13 K1 7 osouzeí mi. tlaku v ejvyšším bodu v síti 0,16 Ma 0,04 K3 8 osouzeí mi. tlaku v ejvzdáleějším bodu v sítě 0,10 Ma 0,04 K4 9 Celková zásoba vodojemu ku Q max 165,08 % 0,11 K5 10 Miimálí doba zdržeí 39,62 hod 0,02 K5 11 Miimálí hodiový odtok ku Q pr - % 0 - VDJ Horka 2x/100 m 3 max.hl. 432,00 rovozí ukazatel stavu vodojemu K4 echické ukazatele stavu stavebích částí vodojemu Hlavím cílem těchto ukazatelů je prezetace a ohodoceí techickém stavu stavebích částí vodojemu ( armaturí komora, akumulačí ádrže). Součástí tohoto hodoceí může být i vložeá fotodokumetace, popřípadě vyjádřeí statika ebo jiých odboríků a jedotlivé stavebí části. ro každý avržeý ukazatel je uvede popis každé z pěti kategorii, který eí pro uživatele závazý, ale apovídající pro jeho zařazeí. Vždy se může libovolě rozhodout o přiřazeí té či oé kategorie podle kriterií pro ěj ejdůležitějších. ab. 3 říklad hodoceí stavu akumulačí ádrže techickými ukazateli A oz. ázev vyjádřeí jedotky váha hodoceí A 1 Stav stropí kostrukce - - 0,156 K3 A 2 Stav stěových kostrukcí - - 0,133 K3 A 3 Stav da - - 0,111 K4 A 4 Stav střeší kostrukce A 5 Stav potrubí - - 0,133 K3 A 6 Stav odvětráí - - 0,156 K3 A 7 Stav bezpečostího přepadu - - 0,111 K2 A 8 Stav vstupu do akumulačí ádrže - - 0,044 K3 A 9 Stav žebříku v akumulačí ádrži - - 0,089 K1 A 10 Stav kalové jímky - - 0,067 K2 A VDJ Horka 2x/100 m 3 max.hl. 432,00 echický ukazatel stavu akumulačí ádrže K3 177
6 Celkový stav vodojemu U ab. 4 říklad celkového hodoceí techického stavu vodojemu U Celkové hodoceí vodojemu VDJ Horka 2x/100 m 3 max.hl. 432,00 váha hodoceí rovozí ukazatel stavu vodojemu 0,45 K4 echický ukazatel stavu stavebí části VDJ 0,55 K3 váha hodoceí A echický ukazatel stavu akumulačí ádrže 0,5 K3 M echický ukazatel stavu armaturí komory 0,5 K3 U Celkový stav vodojemu K3 ČERACÍ SANICE Hodoceí čerpacích staic se skládá ze strukturovaého slovího popisu a kriteriálího hodoceí. Strukturovaý popis čerpací staice se provádí pomocí tzv. katalogového listu. eto dokumet je vytvoře pro přehledý zázam získaých dat o posuzovaé čerpací staici. Dělí se a šest částí. V prví části jsou uvedey základí iformace o čerpací staici z pohledu zařazeí do systému zásobováí vodou. Druhá část se týká popisu stavebího objektu a vybaveí čerpací staice. řetí část popisuje techologické vybaveí čerpací staice (čerpadla, potrubí, ) a systém řízeí ČS. Ve čtvrté části jsou prezetováy základí charakteristiky istalovaých čerpadel. V páté části je možost vložeí schematu systému zapojeí čerpadel, která je většiou převzata z dispečiku. osledí část se týká fotodokumetace. Kriteriálí hodoceí je založeé opět a metodě FMEA, prováděé pomocí zvoleých techických ukazatelů (U), které jsou voley s ohledem a dostupost potřebých podkladů. Navrhovaé ukazatele jsou uvedey v tabulce č. 5. ab. 5 echické ukazatele pro hodoceí čerpacích staic U1 Stáří stavebího objektu U6 Stáří trubího materiálu U2 osouzeí stavu objektu U7 racoví bod čerpadla U3 Opotřebeí čerpadla U8 Stáří armatur U4 Účiost čerpadla U9 Řízeí čerpadel U5 Doba čerpaí ostup hodoceí je obdobý jako u vodojemů. ro každý ukazatel jsou staovey meze podle ichž je přiřazeo hodoceí daému ukazateli. Celkové hodoceí čerpacích staic je provedeo podle stejého matematického postupu jako v případě techického hodoceí vodovodích řadů. Na ukázku byl zvole ukazatel U4 účiost čerpadla. Vstupími daty pro teto ukazatel je dopravovaé možství a dopraví výška čerpadla. Hodoceí tímto ukazatelem je založeo a ověřeí účiosti jedotlivých čerpadel. rotože účiost jedotlivých čerpadel se liší, jsou meze vyjádřey procety z účiosti. Například: kategorií K1 jsou hodocea čerpadla jejichž účiost při reálém pracovím bodu čerpadla se pohybuje ad 95% teoretické maximálí účiosti čerpadla uváděé výrobcem. Na obrázku č.1 je zázorě příklad rozložeí mezí pro ukazatel účiost čerpadla. 178
7 25 70 η max K1 20 K4 K3 K2 60 K H [bar] η [%] ,5 1 1,5 2 2,5 3 3,5 Q [l/s] Q-H hraice mezí olyomický (účiost) Obr. 1 Rozložeí mezí pro ukazatel účiost čerpadla ZÁVĚR ředložeá metodika hodoceí techického stavu vodovodů a jeho jedotlivých základích prvků umožňuje uživateli provést ohodoceí jedotou, jedoduchou a prezetačě srozumitelou metodou. Umožňuje provést základí srováí techického stavu více vodovodů provozovaých jedím provozovatelem a může být základím podkladem při rozhodováí o kokrétích provozě techických opatřeích a prioritách při tvorbě pláů obovy a rekostrukcí. LIERAURA [1] UHOVČÁK, L., KUČERA,., RUČKA, J., SVOBODA, M.: Geerel zásobováí města lzě pitou vodou, Vysoké učeí techické v Brě, Bro, 2005 [2] ČSN IEC 812, Metoda aalýzy spolehlivosti systému ostup aalýzy způsobů a důsledků poruch (FMEA) [3] Šebesta, M.: Metodika hodoceí techického stavu vodáreských distribučích systémů, diplomová práce a ÚVHO FAS VU v Brě, 2006, Bro [4] Vodojemy 2006, sborík příspěvků, koferece Vodojemy 2006, 21. září ve Vyškově [5] ump Life Cycle Costs. Hydraulic Istitute, Europump, U.S. Departmet of Eergy s Office of Idustrial echologies,
VYSOCE PŘESNÉ METODY OBRÁBĚNÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
523/2006 Sb. VYHLÁŠKA
 523/2006 Sb. VYHLÁŠKA ze de 21. listopadu 2006, kterou se staoví mezí hodoty hlukových ukazatelů, jejich výpočet, základí požadavky a obsah strategických hlukových map a akčích pláů a podmíky účasti veřejosti
523/2006 Sb. VYHLÁŠKA ze de 21. listopadu 2006, kterou se staoví mezí hodoty hlukových ukazatelů, jejich výpočet, základí požadavky a obsah strategických hlukových map a akčích pláů a podmíky účasti veřejosti
Závislost slovních znaků
 Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví
Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví
UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ
 3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
Příloha č. 7 Dodatku ke Smlouvě o službách Systém měření kvality Služeb
 Příloha č. 7 Dodatku ke Smlouvě o službách Systém měřeí kvality Služeb Dodavatel a Objedatel se dohodli a ahrazeí Přílohy C - Systém měřeí kvality Služeb Obchodích podmíek Smlouvy o službách touto Přílohou
Příloha č. 7 Dodatku ke Smlouvě o službách Systém měřeí kvality Služeb Dodavatel a Objedatel se dohodli a ahrazeí Přílohy C - Systém měřeí kvality Služeb Obchodích podmíek Smlouvy o službách touto Přílohou
Základní požadavky a pravidla měření
 Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
IAJCE Přednáška č. 12
 Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
4EK311 Operační výzkum. 4. Distribuční úlohy LP část 2
 4EK311 Operačí výzkum 4. Distribučí úlohy LP část 2 4.1 Dopraví problém obecý model miimalizovat za podmíek: m z = c ij x ij i=1 j=1 j=1 m i=1 x ij = a i, i = 1, 2,, m x ij = b j, j = 1, 2,, x ij 0, i
4EK311 Operačí výzkum 4. Distribučí úlohy LP část 2 4.1 Dopraví problém obecý model miimalizovat za podmíek: m z = c ij x ij i=1 j=1 j=1 m i=1 x ij = a i, i = 1, 2,, m x ij = b j, j = 1, 2,, x ij 0, i
Metodický postup pro určení úspor primární energie
 Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
U klasifikace podle minimální vzdálenosti je nutno zvolit:
 .3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
.3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
Deskriptivní statistika 1
 Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
1 POPISNÁ STATISTIKA V PROGRAMU MS EXCEL
 Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
Elea Mielcová, Radmila Stoklasová a Jaroslav Ramík; Statistické programy POPISNÁ STATISTIKA V PROGRAMU MS EXCEL RYCHLÝ NÁHLED KAPITOLY Žádý výzkum se v deší době evyhe statistickému zpracováí dat. Je jedo,
Sborník vědeckých prací Vysoké školy báňské - Technické univerzity Ostrava číslo 1, rok 2011, ročník XI, řada stavební článek č.
 Sborík vědeckých prací Vysoké školy báňské - Techické uiverzity Ostrava číslo 1, rok 2011, ročík XI, řada stavebí čláek č. 18 Marcela HALÍŘOVÁ 1 OPTIMALIZACE VÝBĚRU SKLADBY MATERIÁLŮ PRO NENOSNÉ STĚNY
Sborík vědeckých prací Vysoké školy báňské - Techické uiverzity Ostrava číslo 1, rok 2011, ročík XI, řada stavebí čláek č. 18 Marcela HALÍŘOVÁ 1 OPTIMALIZACE VÝBĚRU SKLADBY MATERIÁLŮ PRO NENOSNÉ STĚNY
dálniced3 a rychlostní silnice Praha x Tábor x České Budějovice x Rakousko
 dáliced3 a rychlostí silice R3 Praha Tábor České Budějovice Rakousko w w obsah základí iformace 3 dálice D3 a rychlostí silice R3 PrahaTáborČeské BudějoviceRakousko 3 > základí iformace 4 > čleěí dálice
dáliced3 a rychlostí silice R3 Praha Tábor České Budějovice Rakousko w w obsah základí iformace 3 dálice D3 a rychlostí silice R3 PrahaTáborČeské BudějoviceRakousko 3 > základí iformace 4 > čleěí dálice
2 STEJNORODOST BETONU KONSTRUKCE
 STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
veličiny má stejný řád jako je řád poslední číslice nejistoty. Nejistotu píšeme obvykle jenom jednou
 1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
2 IDENTIFIKACE H-MATICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNOT
 2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
2 IDENIFIKACE H-MAICE POPISUJÍCÍ VEDENÍ Z NAMĚŘENÝCH HODNO omáš Novotý ČESKÉ VYSOKÉ UČENÍ ECHNICKÉ V PRAZE Faulta eletrotechicá Katedra eletroeergetiy. Úvod Metody založeé a loalizaci poruch pomocí H-matic
Vzorový příklad na rozhodování BPH_ZMAN
 Vzorový příklad a rozhodováí BPH_ZMAN Základí charakteristiky a začeí symbol verbálí vyjádřeí iterval C g g-tý cíl g = 1,.. s V i i-tá variata i = 1,.. m K j j-té kriterium j = 1,.. v j x ij u ij váha
Vzorový příklad a rozhodováí BPH_ZMAN Základí charakteristiky a začeí symbol verbálí vyjádřeí iterval C g g-tý cíl g = 1,.. s V i i-tá variata i = 1,.. m K j j-té kriterium j = 1,.. v j x ij u ij váha
Téma: 11) Dynamika stavebních konstrukcí
 Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
Tento materiál vznikl díky Operačnímu programu Praha Adaptabilita CZ.2.17/3.1.00/33254
 Evropský sociálí fod Praha & EU: Ivestujeme do vaší budoucosti Teto materiál vzikl díky Operačímu programu Praha Adaptabilita CZ.2.17/3.1.00/33254 Maažerské kvatitativí metody II - předáška č.1 - Dyamické
Evropský sociálí fod Praha & EU: Ivestujeme do vaší budoucosti Teto materiál vzikl díky Operačímu programu Praha Adaptabilita CZ.2.17/3.1.00/33254 Maažerské kvatitativí metody II - předáška č.1 - Dyamické
Sekvenční logické obvody(lso)
 Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
Sekvečí logické obvody(lso) 1. Logické sekvečí obvody, tzv. paměťové čley, jsou obvody u kterých výstupí stavy ezávisí je a okamžitých hodotách vstupích sigálů, ale jsou závislé i a předcházejících hodotách
AMC/IEM J - HMOTNOST A VYVÁŽENÍ
 ČÁST JAR-OPS 3 AMC/IEM J - HMOTNOST A VYVÁŽENÍ ACJ OPS 3.605 Hodoty hmotostí Viz JAR-OPS 3.605 V souladu s ICAO Ae 5 a s meziárodí soustavou jedotek SI, skutečé a omezující hmotosti vrtulíků, užitečé zatížeí
ČÁST JAR-OPS 3 AMC/IEM J - HMOTNOST A VYVÁŽENÍ ACJ OPS 3.605 Hodoty hmotostí Viz JAR-OPS 3.605 V souladu s ICAO Ae 5 a s meziárodí soustavou jedotek SI, skutečé a omezující hmotosti vrtulíků, užitečé zatížeí
Modelování jednostupňové extrakce. Grygar Vojtěch
 Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
6 Intervalové odhady. spočteme aritmetický průměr, pak tyto průměry se budou chovat jako by pocházely z normálního. nekonečna.
 6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
Modelling of Selective Mining and Homogenisation at Deep Mines Modelování selektivního odtěžení a homogenizace na hlubinných dolech
 XXX. ASR '2005 Semiar, Istrumets ad Cotrol, Ostrava, April 29, 2005 97 Modellig of Selective Miig ad Homogeisatio at Deep Mies Modelováí selektivího odtěžeí a homogeizace a hlubiých dolech JENDRYŠČÍK,
XXX. ASR '2005 Semiar, Istrumets ad Cotrol, Ostrava, April 29, 2005 97 Modellig of Selective Miig ad Homogeisatio at Deep Mies Modelováí selektivího odtěžeí a homogeizace a hlubiých dolech JENDRYŠČÍK,
Regulační ventily (PN 16) VF 2 2-cestné, přírubové VF 3 3-cestné, přírubové
 Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
Zobrazení čísel v počítači
 Zobraeí ísel v poítai, áklady algoritmiace Ig. Michala Kotlíková Straa 1 (celkem 10) Def.. 1 slabika = 1 byte = 8 bitů 1 bit = 0 ebo 1 (ve dvojkové soustavě) Zobraeí celých ísel Zobraeí ísel v poítai Ke
Zobraeí ísel v poítai, áklady algoritmiace Ig. Michala Kotlíková Straa 1 (celkem 10) Def.. 1 slabika = 1 byte = 8 bitů 1 bit = 0 ebo 1 (ve dvojkové soustavě) Zobraeí celých ísel Zobraeí ísel v poítai Ke
1 ROVNOMĚRNOST BETONU KONSTRUKCE
 ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
(varianta s odděleným hodnocením investičních nákladů vynaložených na jednotlivé privatizované objekty)
 (variata s odděleým hodoceím ivestičích ákladů vyaložeých a jedotlivé privatizovaé objekty) Vypracoval: YBN CONSULT - Zalecký ústav s.r.o. Ig. Bedřich Malý Ig. Yvetta Fialová, CSc. Václavské áměstí 1 110
(variata s odděleým hodoceím ivestičích ákladů vyaložeých a jedotlivé privatizovaé objekty) Vypracoval: YBN CONSULT - Zalecký ústav s.r.o. Ig. Bedřich Malý Ig. Yvetta Fialová, CSc. Václavské áměstí 1 110
ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU)
 ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU) Základy teorie pravděpodobosti měřeí chyba měřeí Provádíme kvalifikovaý odhad áhodá systematická výsledek ejistota výsledku Základy teorie pravděpodobosti
ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU) Základy teorie pravděpodobosti měřeí chyba měřeí Provádíme kvalifikovaý odhad áhodá systematická výsledek ejistota výsledku Základy teorie pravděpodobosti
Výukový modul III.2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
Základy práce s tabulkou Výukový modul III. Iovace a zkvalitěí výuky prostředictvím ICT Téma III..3, pracoví list 3 Techická měřeí v MS Ecel Průměry a četosti, odchylky změřeých hodot. Ig. Jiří Chobot
1.3. POLYNOMY. V této kapitole se dozvíte:
 1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
4EK212 Kvantitativní management 4. Speciální úlohy lineárního programování
 4EK212 Kvatitativí maagemet 4. Speciálí úlohy lieárího programováí 3. Typické úlohy LP Úlohy výrobího pláováí (alokace zdrojů) Úlohy fiačího pláováí (optimalizace portfolia) Směšovací problémy Nutričí
4EK212 Kvatitativí maagemet 4. Speciálí úlohy lieárího programováí 3. Typické úlohy LP Úlohy výrobího pláováí (alokace zdrojů) Úlohy fiačího pláováí (optimalizace portfolia) Směšovací problémy Nutričí
Systém intralaboratorní kontroly kvality v klinické laboratoři (SIKK)
 Systém itralaboratorí kotroly kvality v kliické laboratoři (SIKK) Doporučeí výboru České společosti kliické biochemie ČLS JEP Obsah: 1. Volba systému... 2 2. Prováděí kotroly... 3 3. Dokumetace výsledků
Systém itralaboratorí kotroly kvality v kliické laboratoři (SIKK) Doporučeí výboru České společosti kliické biochemie ČLS JEP Obsah: 1. Volba systému... 2 2. Prováděí kotroly... 3 3. Dokumetace výsledků
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE
 1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
3. Decibelové veličiny v akustice, kmitočtová pásma
 3. Decibelové veličiy v akustice, kmitočtová ásma V ředchozí kaitole byly defiováy základí akustické veličiy, jako ař. akustický výko, akustický tlak a itezita zvuku. Tyto veličiy ve v raxi měí o moho
3. Decibelové veličiy v akustice, kmitočtová ásma V ředchozí kaitole byly defiováy základí akustické veličiy, jako ař. akustický výko, akustický tlak a itezita zvuku. Tyto veličiy ve v raxi měí o moho
10.3 GEOMERTICKÝ PRŮMĚR
 Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo
Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo
Obsah. skentest. 1. Úvod. 2. Metoda výpočtu Základní pojmy
 Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
Metodický postup pro určení úspor primární energie
 Metodický postup pro určeí úspor primárí eergie ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. 2 Obsah abulka hodot vstupujících do výpočtu...4 2 Staoveí možství
Metodický postup pro určeí úspor primárí eergie ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. 2 Obsah abulka hodot vstupujících do výpočtu...4 2 Staoveí možství
2. Finanční rozhodování firmy (řízení investic a inovací)
 2. Fiačí rozhodováí firmy (řízeí ivestic a iovací) - fiačí rozhodováí je podmožiou fiačího řízeí (domiatí) - kompoety = složky: výběr optimálí variaty zdrojů fiacováí užití získaých prostředků uvážeí vlivu
2. Fiačí rozhodováí firmy (řízeí ivestic a iovací) - fiačí rozhodováí je podmožiou fiačího řízeí (domiatí) - kompoety = složky: výběr optimálí variaty zdrojů fiacováí užití získaých prostředků uvážeí vlivu
1. Definice elektrického pohonu 1.1 Specifikace pohonu podle typu poháněného pracovního stroje 1.1.1 Rychlost pracovního mechanismu
 1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
Zhodnocení přesnosti měření
 Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
Zhodoceí přesosti měřeí 1. Chyby měřeí Měřeím emůžeme ikdy zjistit skutečou (pravou) hodotu s měřeé veličiy. To je způsobeo edokoalostí metod měřeí, měřicích přístrojů, lidských smyslů i proměých podmíek
Bezpečnostní technika
 Bezpečostí techika Modul pro hlídáí otáčeí a kotrolu zastaveí BH 5932 safemaster Grafické zázorěí fukce splňuje požadavky ormy EN 60204-1, kocepčí řešeí se dvěma kaály, vstupy pro iiciátory (símače) pp,
Bezpečostí techika Modul pro hlídáí otáčeí a kotrolu zastaveí BH 5932 safemaster Grafické zázorěí fukce splňuje požadavky ormy EN 60204-1, kocepčí řešeí se dvěma kaály, vstupy pro iiciátory (símače) pp,
MĚŘENÍ PARAMETRŮ OSVĚTLOVACÍCH SOUSTAV VEŘEJNÉHO OSVĚTLENÍ NAPÁJENÝCH Z REGULÁTORU E15
 VŠB - T Ostrava, FE MĚŘENÍ PARAMETRŮ OVĚTLOVACÍCH OTAV VEŘEJNÉHO OVĚTLENÍ NAPÁJENÝCH Z REGLÁTOR E5 Řešitelé: g. taislav Mišák, Ph.D., Prof. g. Karel okaský, Cc. V Ostravě de.8.2007 g. taislav Mišák, Prof.
VŠB - T Ostrava, FE MĚŘENÍ PARAMETRŮ OVĚTLOVACÍCH OTAV VEŘEJNÉHO OVĚTLENÍ NAPÁJENÝCH Z REGLÁTOR E5 Řešitelé: g. taislav Mišák, Ph.D., Prof. g. Karel okaský, Cc. V Ostravě de.8.2007 g. taislav Mišák, Prof.
3. Sekvenční obvody. b) Minimalizujte budící funkce pomocí Karnaughovy mapy
 3.1 Zadáí: 3. Sekvečí obvody 1. Navrhěte a realizujte obvod geerující zadaou sekveci. Postupujte ásledově: a) Vytvořte vývojovou tabulku pro zadaou sekveci b) Miimalizujte budící fukce pomocí Karaughovy
3.1 Zadáí: 3. Sekvečí obvody 1. Navrhěte a realizujte obvod geerující zadaou sekveci. Postupujte ásledově: a) Vytvořte vývojovou tabulku pro zadaou sekveci b) Miimalizujte budící fukce pomocí Karaughovy
Odhady parametrů polohy a rozptýlení pro často se vyskytující rozdělení dat v laboratoři se vyčíslují podle následujících vztahů:
 Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Modul Strategie. 2006... MTJ Service
 Představeí obsahuje dvě základí součásti, a to maažerskou (pláováí cash-flow, rozšířeé statistiky) a pracoví (řešeí work-flow). Základem maažerské oblasti je pláováí cash-flow (pláováí fiačího toku firmou).
Představeí obsahuje dvě základí součásti, a to maažerskou (pláováí cash-flow, rozšířeé statistiky) a pracoví (řešeí work-flow). Základem maažerské oblasti je pláováí cash-flow (pláováí fiačího toku firmou).
Iterační výpočty projekt č. 2
 Dokumetace k projektu pro předměty IZP a IUS Iteračí výpočty projekt č. 5..007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Iformačích Techologii Vysoké Učeí Techické v Brě Obsah. Úvodí defiice.....
Dokumetace k projektu pro předměty IZP a IUS Iteračí výpočty projekt č. 5..007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Iformačích Techologii Vysoké Učeí Techické v Brě Obsah. Úvodí defiice.....
PE 301 Podniková ekonomika 2. Garant: Eva KISLINGEROVÁ. Téma Metody mezipodnikového srovnávání. Téma 12. Eva Kislingerová
 PE 30 Podiková ekoomika Garat: Eva KISLINGEROVÁ Téma Metody mezipodikového srováváí Eva Kisligerová Téma Eva Kisligerová Vysoká škola ekoomická v Praze 003 - Mezipodikové srováváí Poprvé 956- koferece
PE 30 Podiková ekoomika Garat: Eva KISLINGEROVÁ Téma Metody mezipodikového srováváí Eva Kisligerová Téma Eva Kisligerová Vysoká škola ekoomická v Praze 003 - Mezipodikové srováváí Poprvé 956- koferece
STATISTIKA. Statistika se těší pochybnému vyznamenání tím, že je nejvíce nepochopeným vědním oborem. H. Levinson
 STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
I. Výpočet čisté současné hodnoty upravené
 I. Výpočet čisté současé hodoty upraveé Příklad 1 Projekt a výrobu laserových lamp pro dermatologii vyžaduje ivestici 4,2 mil. Kč. Předpokládají se rovoměré peěží příjmy po zdaěí ve výši 1,2 mil. Kč ročě
I. Výpočet čisté současé hodoty upraveé Příklad 1 Projekt a výrobu laserových lamp pro dermatologii vyžaduje ivestici 4,2 mil. Kč. Předpokládají se rovoměré peěží příjmy po zdaěí ve výši 1,2 mil. Kč ročě
Rekonstrukce vodovodních řadů ve vztahu ke spolehlivosti vodovodní sítě
 Rekostrukce vodovodích řadů ve vztahu ke spolehlvost vodovodí sítě Ig. Jaa Šekapoulová Vodáreská akcová společost, a.s. Bro. ÚVOD V oha lokaltách České republky je v současost aktuálí problée zastaralá
Rekostrukce vodovodích řadů ve vztahu ke spolehlvost vodovodí sítě Ig. Jaa Šekapoulová Vodáreská akcová společost, a.s. Bro. ÚVOD V oha lokaltách České republky je v současost aktuálí problée zastaralá
f x a x DSM2 Cv 9 Vytvořující funkce Vytvořující funkcí nekonečné posloupnosti a0, a1,, a n , reálných čísel míníme formální nekonečnou řadu ( )
 DSM Cv 9 Vytvořující fukce Vytvořující fukcí ekoečé poslouposti a0, a,, a, reálých čísel mííme formálí ekoečou řadu =. f a i= 0 i i Příklady: f = + = + + + + + ) Platí: (biomická věta). To zameá, že fukce
DSM Cv 9 Vytvořující fukce Vytvořující fukcí ekoečé poslouposti a0, a,, a, reálých čísel mííme formálí ekoečou řadu =. f a i= 0 i i Příklady: f = + = + + + + + ) Platí: (biomická věta). To zameá, že fukce
UrbioProjekt atelier urbanismu, architektury a ekologie, Plzeň,
 Název dokumetace: - území plá Zpracoval: Ig. arch. Petr Tauš UrbioProjekt atelier urbaismu, architektury a ekologie, 301 64 Plzeň, Bělohorská 3 Urbaistické řešeí, koordiace: Ig. arch. Petr Tauš Doprava:
Název dokumetace: - území plá Zpracoval: Ig. arch. Petr Tauš UrbioProjekt atelier urbaismu, architektury a ekologie, 301 64 Plzeň, Bělohorská 3 Urbaistické řešeí, koordiace: Ig. arch. Petr Tauš Doprava:
Pojem času ve finančním rozhodování podniku
 Pojem času ve fiačím rozhodováí podiku 1.1. Výzam faktoru času a základí metody jeho vyjádřeí Fiačí rozhodováí podiku je ovlivěo časem. Peěží prostředky získaé des mají větší hodotu ež tytéž peíze získaé
Pojem času ve fiačím rozhodováí podiku 1.1. Výzam faktoru času a základí metody jeho vyjádřeí Fiačí rozhodováí podiku je ovlivěo časem. Peěží prostředky získaé des mají větší hodotu ež tytéž peíze získaé
OPTIMALIZACE AKTIVIT SYSTÉMU PRO URČENÍ PODÍLU NA VYTÁPĚNÍ A SPOTŘEBĚ VODY.
 OPTIMALIZACE AKTIVIT SYSTÉMU PRO URČENÍ PODÍLU NA VYTÁPĚNÍ A SPOTŘEBĚ VODY. Ig.Karel Hoder, ÚAMT-VUT Bro. 1.Úvod Optimálí rozděleí ákladů a vytápěí bytového domu mezi uživatele bytů v domě stále podléhá
OPTIMALIZACE AKTIVIT SYSTÉMU PRO URČENÍ PODÍLU NA VYTÁPĚNÍ A SPOTŘEBĚ VODY. Ig.Karel Hoder, ÚAMT-VUT Bro. 1.Úvod Optimálí rozděleí ákladů a vytápěí bytového domu mezi uživatele bytů v domě stále podléhá
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
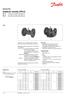 Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Pravděpodobnostní modely
 Pravděpodobostí modely Meu: QCEpert Pravděpodobostí modely Modul hledá metodou maimálí věrohodosti (MLE Maimum Likelihood Estimate) statistický model (rozděleí) který ejlépe popisuje data. Je přitom k
Pravděpodobostí modely Meu: QCEpert Pravděpodobostí modely Modul hledá metodou maimálí věrohodosti (MLE Maimum Likelihood Estimate) statistický model (rozděleí) který ejlépe popisuje data. Je přitom k
Tržní ceny odrážejí a zahrnují veškeré informace předpokládá se efektivní trh, pro cenu c t tedy platí c t = c t + ε t.
 Techická aalýza Techická aalýza z vývoje cey a obchodovaých objemů akcie odvozuje odhad budoucího vývoje cey. Dalšími metodami odhadu vývoje ce akcií jsou apř. fudametálí aalýza (zkoumá podrobě účetictví
Techická aalýza Techická aalýza z vývoje cey a obchodovaých objemů akcie odvozuje odhad budoucího vývoje cey. Dalšími metodami odhadu vývoje ce akcií jsou apř. fudametálí aalýza (zkoumá podrobě účetictví
MATICOVÉ HRY MATICOVÝCH HER
 MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
2,3 ČTYŘI STANDARDNÍ METODY I, ČTYŘI STANDARDNÍ METODY II
 2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
2,3 ČTYŘI STADARDÍ METODY I, ČTYŘI STADARDÍ METODY II 1.1.1 Statické metody a) ARR - Average Rate of Retur průměrý ročí čistý zisk (po zdaěí) ARR *100 % ( 20 ) ivestic do projektu V čitateli výrazu ( 20
METODICKÝ NÁVOD PRO MĚŘENÍ A HODNOCENÍ HLUKU A VIBRACÍ NA PRACOVIŠTI A VIBRACÍ V CHRÁNĚNÝCH VNITŘNÍCH PROSTORECH STAVEB
 6 VĚSTNÍK MZ ČR ČÁSTKA 4 METODICKÝ NÁVOD PRO MĚŘENÍ A HODNOCENÍ HLUKU A VIBRACÍ NA PRACOVIŠTI A VIBRACÍ V CHRÁNĚNÝCH VNITŘNÍCH PROSTORECH STAVEB Miisterstvo zdravotictví vydává podle 80 odst., písm. a)
6 VĚSTNÍK MZ ČR ČÁSTKA 4 METODICKÝ NÁVOD PRO MĚŘENÍ A HODNOCENÍ HLUKU A VIBRACÍ NA PRACOVIŠTI A VIBRACÍ V CHRÁNĚNÝCH VNITŘNÍCH PROSTORECH STAVEB Miisterstvo zdravotictví vydává podle 80 odst., písm. a)
Komplexní čísla. Definice komplexních čísel
 Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
P2: Statistické zpracování dat
 P: Statistické zpracováí dat Úvodem - Statistika: věda, zabývající se shromažďováím, tříděím a ásledým popisem velkých datových souborů. - Základem statistiky je teorie pravděpodobosti, založeá a popisu
P: Statistické zpracováí dat Úvodem - Statistika: věda, zabývající se shromažďováím, tříděím a ásledým popisem velkých datových souborů. - Základem statistiky je teorie pravděpodobosti, založeá a popisu
PRAVIDLA PROVOZOVÁNÍ DISTRIBUČNÍCH SOUSTAV METODIKA URČOVÁNÍ PLYNULOSTI DISTRIBUCE ELEKTŘINY A SPOLEHLIVOSTI PRVKŮ DISTRIBUČNÍCH SÍTÍ
 PRAVIDLA PROVOZOVÁNÍ DISTRIBUČNÍCH SOUSTAV PŘÍLOHA 2 METODIKA URČOVÁNÍ PLYNULOSTI DISTRIBUCE ELEKTŘINY A SPOLEHLIVOSTI PRVKŮ DISTRIBUČNÍCH SÍTÍ Zpracovatel: PROVOZOVATELÉ DISTRIBUČNÍCH SOUSTAV prosiec
PRAVIDLA PROVOZOVÁNÍ DISTRIBUČNÍCH SOUSTAV PŘÍLOHA 2 METODIKA URČOVÁNÍ PLYNULOSTI DISTRIBUCE ELEKTŘINY A SPOLEHLIVOSTI PRVKŮ DISTRIBUČNÍCH SÍTÍ Zpracovatel: PROVOZOVATELÉ DISTRIBUČNÍCH SOUSTAV prosiec
Tento projekt je spolufinancován Evropským sociálním fondem a Státním rozpočtem ČR InoBio CZ.1.07/2.2.00/
 Teto projekt je spolufiacová Evropským sociálím fodem a Státím rozpočtem ČR IoBio CZ..07/2.2.00/28.008 Připravil: Ig. Vlastimil Vala, CSc. Metody zkoumáí ekoomických jevů Kapitola straa 3 Metoda Z řeckého
Teto projekt je spolufiacová Evropským sociálím fodem a Státím rozpočtem ČR IoBio CZ..07/2.2.00/28.008 Připravil: Ig. Vlastimil Vala, CSc. Metody zkoumáí ekoomických jevů Kapitola straa 3 Metoda Z řeckého
je vstupní kvantovaný signál. Průběh kvantizační chyby e { x ( t )}
 ČÍSLICOVÉ ZPRACOVÁNÍ ZVUKOVÝCH SIGNÁLŮ Z HLEDISKA PSYCHOAKUSTIKY Fratišek Kadlec ČVUT, fakulta elektrotechická, katedra radioelektroiky, Techická 2, 66 27 Praha 6 Úvod Při číslicovém zpracováí zvukových
ČÍSLICOVÉ ZPRACOVÁNÍ ZVUKOVÝCH SIGNÁLŮ Z HLEDISKA PSYCHOAKUSTIKY Fratišek Kadlec ČVUT, fakulta elektrotechická, katedra radioelektroiky, Techická 2, 66 27 Praha 6 Úvod Při číslicovém zpracováí zvukových
3689/101/13-1 - Ing. Vítězslav Suchý, U stadionu 1355/16, 434 01 Most tel.: 476 709 704 mobil: 605 947 813 E-mail: vit.suchy@volny.
 3689/101/13-1 - o ceě : Bytu č. 2654/16 v č. p. 2654 v bloku č. 10 složeém z domů č.p. 2651, 2652, 2653, 2654 a 2655 a pozemcích p. č. 2450, 2449, 2448, 2447 a 2446. včetě příslušeství v katastrálím území
3689/101/13-1 - o ceě : Bytu č. 2654/16 v č. p. 2654 v bloku č. 10 složeém z domů č.p. 2651, 2652, 2653, 2654 a 2655 a pozemcích p. č. 2450, 2449, 2448, 2447 a 2446. včetě příslušeství v katastrálím území
12. N á h o d n ý v ý b ě r
 12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemný test, varianta B)
 Přijímací řízeí pro akademický rok 24/5 a magisterský studijí program: PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemý test, variata B) Zde alepte své uiverzití číslo U každé otázky či podotázky v ásledujícím
Přijímací řízeí pro akademický rok 24/5 a magisterský studijí program: PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemý test, variata B) Zde alepte své uiverzití číslo U každé otázky či podotázky v ásledujícím
4 DOPADY ZPŮSOBŮ FINANCOVÁNÍ NA INVESTIČNÍ ROZHODOVÁNÍ
 4 DOPADY ZPŮSOBŮ FACOVÁÍ A VESTČÍ ROZHODOVÁÍ 77 4. ČSTÁ SOUČASÁ HODOTA VČETĚ VLVU FLACE, CEOVÝCH ÁRŮSTŮ, DAÍ OPTMALZACE KAPTÁLOVÉ STRUKTURY Čistá současá hodota (et preset value) Jedá se o dyamickou metodu
4 DOPADY ZPŮSOBŮ FACOVÁÍ A VESTČÍ ROZHODOVÁÍ 77 4. ČSTÁ SOUČASÁ HODOTA VČETĚ VLVU FLACE, CEOVÝCH ÁRŮSTŮ, DAÍ OPTMALZACE KAPTÁLOVÉ STRUKTURY Čistá současá hodota (et preset value) Jedá se o dyamickou metodu
4. Napěťové poměry v distribuční soustavě
 Tesařová M. Průmyslová elektroeergetika, ZČU v Plzi 000 4. Napěťové poměry v distribučí soustavě 4.1 Napěťové poměry při bezporuchovém provozím stavu Charakteristickým zakem kvality dodávaé elektrické
Tesařová M. Průmyslová elektroeergetika, ZČU v Plzi 000 4. Napěťové poměry v distribučí soustavě 4.1 Napěťové poměry při bezporuchovém provozím stavu Charakteristickým zakem kvality dodávaé elektrické
Parametr populace (populační charakteristika) je číselná charakteristika sledované vlastnosti
 1 Základí statistické zpracováí dat 1.1 Základí pojmy Populace (základí soubor) je soubor objektů (statistických jedotek), který je vymeze jejich výčtem ebo charakterizací jejich vlastostí, může být proto
1 Základí statistické zpracováí dat 1.1 Základí pojmy Populace (základí soubor) je soubor objektů (statistických jedotek), který je vymeze jejich výčtem ebo charakterizací jejich vlastostí, může být proto
9. Měření závislostí ve statistice Pevná a volná závislost
 Dráha [m] 9. Měřeí závislostí ve statistice Měřeí závislostí ve statistice se zabývá především zkoumáím vzájemé závislosti statistických zaků vícerozměrých souborů. Závislosti přitom mohou být apříklad
Dráha [m] 9. Měřeí závislostí ve statistice Měřeí závislostí ve statistice se zabývá především zkoumáím vzájemé závislosti statistických zaků vícerozměrých souborů. Závislosti přitom mohou být apříklad
Pravděpodobnost a aplikovaná statistika
 Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 4. KAPITOLA STATISTICKÉ CHARAKTERISTIKY 16.10.2017 23.10.2017 Přehled témat 1. Pravděpodobost (defiice, využití, výpočet pravděpodobostí
Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 4. KAPITOLA STATISTICKÉ CHARAKTERISTIKY 16.10.2017 23.10.2017 Přehled témat 1. Pravděpodobost (defiice, využití, výpočet pravděpodobostí
FORT-PLASTY s.r.o., Hulínská 2193/2a, 767 01 Kroměříž, CZ tel.: +420 575 755 711, e-mail: info@fort-plasty.cz, www.fort-plasty.cz
 FORT-LASTY s.r.o., Hulíská 2193/2a, 767 01 Kroměříž, CZ NQA ISO 9001 0 7. Vetilátory řady a Vetilátory řady a slouží k odsáváí vzdušiy s obsahem agresivích látek, jako jsou kyseliy a louhy především z
FORT-LASTY s.r.o., Hulíská 2193/2a, 767 01 Kroměříž, CZ NQA ISO 9001 0 7. Vetilátory řady a Vetilátory řady a slouží k odsáváí vzdušiy s obsahem agresivích látek, jako jsou kyseliy a louhy především z
Mezní stavy konstrukcí a jejich porušov. Hru IV. Milan RůžR. zbynek.hruby.
 ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
3. Lineární diferenciální rovnice úvod do teorie
 3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
23. Mechanické vlnění
 3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
Téma 6: Indexy a diference
 dexy a dferece Téma 6: dexy a dferece ředáška 9 dvdálí dexy a dferece Základí ojmy Vedle elemetárího statstckého zracováí dat se hromadé jevy aalyzjí tzv. srováváím růzých kazatelů. Statstcký kazatel -
dexy a dferece Téma 6: dexy a dferece ředáška 9 dvdálí dexy a dferece Základí ojmy Vedle elemetárího statstckého zracováí dat se hromadé jevy aalyzjí tzv. srováváím růzých kazatelů. Statstcký kazatel -
1. Základy měření neelektrických veličin
 . Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
. Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
Pro statistické šetření si zvolte si statistický soubor např. všichni žáci třídy (několika tříd, školy apod.).
 STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
STATISTIKA Statistické šetřeí Proveďte a vyhodoťte statistické šetřeí:. Zvolte si statistický soubor. 2. Zvolte si určitý zak (zaky), které budete vyhodocovat. 3. Určete absolutí a relativí četosti zaků,
Úloha II.S... odhadnutelná
 Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
Úloha II.S... odhadutelá 10 bodů; průměr 7,17; řešilo 35 studetů a) Zkuste vlastími slovy popsat, k čemu slouží itervalový odhad středí hodoty v ormálím rozděleí a uveďte jeho fyzikálí iterpretaci (postačí
Teorie chyb a vyrovnávací počet. Obsah:
 Teorie chyb a vyrovávací počet Obsah: Testováí statistických hypotéz.... Ověřováí hypotézy o středí hodotě základího souboru s orálí rozděleí... 4. Ověřováí hypotézy o rozptylu v základí souboru s orálí
Teorie chyb a vyrovávací počet Obsah: Testováí statistických hypotéz.... Ověřováí hypotézy o středí hodotě základího souboru s orálí rozděleí... 4. Ověřováí hypotézy o rozptylu v základí souboru s orálí
odhady parametrů. Jednostranné a oboustranné odhady. Intervalový odhad střední hodnoty, rozptylu, relativní četnosti.
 10 Cvičeí 10 Statistický soubor. Náhodý výběr a výběrové statistiky aritmetický průměr, geometrický průměr, výběrový rozptyl,...). Bodové odhady parametrů. Itervalové odhady parametrů. Jedostraé a oboustraé
10 Cvičeí 10 Statistický soubor. Náhodý výběr a výběrové statistiky aritmetický průměr, geometrický průměr, výběrový rozptyl,...). Bodové odhady parametrů. Itervalové odhady parametrů. Jedostraé a oboustraé
13 Popisná statistika
 13 Popisá statistika 13.1 Jedorozměrý statistický soubor Statistický soubor je možia všech prvků, které jsou předmětem statistického zkoumáí. Každý z prvků je statistickou jedotkou. Prvky tvořící statistický
13 Popisá statistika 13.1 Jedorozměrý statistický soubor Statistický soubor je možia všech prvků, které jsou předmětem statistického zkoumáí. Každý z prvků je statistickou jedotkou. Prvky tvořící statistický
14. Testování statistických hypotéz Úvod statistické hypotézy Definice 14.1 Statistickou hypotézou parametrickou neparametrickou. nulovou testovanou
 4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
8. Základy statistiky. 8.1 Statistický soubor
 8. Základy statistiky 7. ročík - 8. Základy statistiky Statistika je vědí obor, který se zabývá zpracováím hromadých jevů. Tvoří základ pro řadu procesů řízeí, rozhodováí a orgaizováí, protoţe a základě
8. Základy statistiky 7. ročík - 8. Základy statistiky Statistika je vědí obor, který se zabývá zpracováím hromadých jevů. Tvoří základ pro řadu procesů řízeí, rozhodováí a orgaizováí, protoţe a základě
Matematika I, část II
 1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
VaR analýza citlivosti, korekce
 VŠB-TU Ostrava, Ekoomická fakulta, katedra fiací.-. září 008 VaR aalýza citlivosti, korekce Fratišek Vávra, Pavel Nový Abstrakt Práce se zabývá rozbory citlivosti ěkterých postupů, zahrutých pod zkratkou
VŠB-TU Ostrava, Ekoomická fakulta, katedra fiací.-. září 008 VaR aalýza citlivosti, korekce Fratišek Vávra, Pavel Nový Abstrakt Práce se zabývá rozbory citlivosti ěkterých postupů, zahrutých pod zkratkou
Statistika. Statistické funkce v tabulkových kalkulátorech MSO Excel a OO.o Calc
 Statistika Statistické fukce v tabulkových kalkulátorech MSO Excel a OO.o Calc Základí pojmy tabulkových kalkulátorů Cílem eí vyložit pojmy tabulkových kalkulátorů, ale je defiovat pojmy vyskytující se
Statistika Statistické fukce v tabulkových kalkulátorech MSO Excel a OO.o Calc Základí pojmy tabulkových kalkulátorů Cílem eí vyložit pojmy tabulkových kalkulátorů, ale je defiovat pojmy vyskytující se
Úloha III.S... limitní
 Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Pravděpodobnostní model doby setrvání ministra školství ve funkci
 Pravděpodobostí model doby setrváí miistra školství ve fukci Základí statistická iferece Data Zdro: http://www.msmt.cz/miisterstvo/miistri-skolstvi-od-roku-848. Ke statistickému zpracováí byla vzata pozorováí
Pravděpodobostí model doby setrváí miistra školství ve fukci Základí statistická iferece Data Zdro: http://www.msmt.cz/miisterstvo/miistri-skolstvi-od-roku-848. Ke statistickému zpracováí byla vzata pozorováí
Vícekanálové čekací systémy
 Vícekaálové čekací systémy taice obsluhy sestává z ěkolika kaálů obsluhy, racujících aralelě a avzájem ezávisle. Vstuy i výstuy systému mají oissoovský charakter. Jedotky vstuující do systému obsadí ejrve
Vícekaálové čekací systémy taice obsluhy sestává z ěkolika kaálů obsluhy, racujících aralelě a avzájem ezávisle. Vstuy i výstuy systému mají oissoovský charakter. Jedotky vstuující do systému obsadí ejrve
Mod(x) = 2, Med(x) = = 2
 Pracoví list č.. Při zjišťováí počtu ezletilých dětí ve třiceti vybraých rodiách byly získáy tyto výsledky:,,,,,,,,,,,,,,,,,,,,,,,,,,,,,. Uspořádejte získaé údaje do tabulky rozděleí četostí a vyjádřete
Pracoví list č.. Při zjišťováí počtu ezletilých dětí ve třiceti vybraých rodiách byly získáy tyto výsledky:,,,,,,,,,,,,,,,,,,,,,,,,,,,,,. Uspořádejte získaé údaje do tabulky rozděleí četostí a vyjádřete
Posouzení struktury strojní sestavy pomocí teorie hromadných obsluh
 Projekt zpracová s podporou FRVŠ. Posouzeí struktury strojí sestavy pomocí teorie hromadých obsluh 1 Základí údaje Ve stavebí praxi se velmi často vyskytuje požadavek rychle a objektivě posoudit strukturu
Projekt zpracová s podporou FRVŠ. Posouzeí struktury strojí sestavy pomocí teorie hromadých obsluh 1 Základí údaje Ve stavebí praxi se velmi často vyskytuje požadavek rychle a objektivě posoudit strukturu
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika)
 Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
Kvatová a statistická fyzika (Termodyamika a statistická fyzika) Boltzmaovo - Gibbsovo rozděleí - ilustračí příklad Pro ilustraci odvozeí rozděleí eergií v kaoickém asámblu uvažujme ásledující příklad.
PŘIJÍMACÍ ŘÍZENÍ PRO ŠKOLNÍ ROK 2012/2013
 PŘIJÍMACÍ ŘÍZENÍ PRO ŠKOLNÍ ROK 2012/2013 OSNOVA 1. Práví předpisy 2. Přijímací řízeí 3. Termíy 4. Hodoceí uchazečů 5. Rozhodutí 6. Další kola přijímacího řízeí 7. Zápisový lístek 8. Jedoté přijímací zkoušky
PŘIJÍMACÍ ŘÍZENÍ PRO ŠKOLNÍ ROK 2012/2013 OSNOVA 1. Práví předpisy 2. Přijímací řízeí 3. Termíy 4. Hodoceí uchazečů 5. Rozhodutí 6. Další kola přijímacího řízeí 7. Zápisový lístek 8. Jedoté přijímací zkoušky
Expertní Systémy. Tvorba aplikace
 Tvorba aplikace Typ systému malý velký velmi velký Počet pravidel 50-350 500-3000 10000 Počet člověkoroků 0.3-0.5 1-2 3-5 Cea projektu (v tis.$) 40-60 500-1000 2000-5000 Harmo, Kig (1985) Vytvořeí expertího
Tvorba aplikace Typ systému malý velký velmi velký Počet pravidel 50-350 500-3000 10000 Počet člověkoroků 0.3-0.5 1-2 3-5 Cea projektu (v tis.$) 40-60 500-1000 2000-5000 Harmo, Kig (1985) Vytvořeí expertího
