Implementace a testování SVM Implementation and testing of SVM

Transkript

1 VŠB Technická univerzita Ostrava Fakulta elektrotechniky a informatiky Katedra aplikované matematiky Implementace a testování SVM Implementation and testing of SVM 2011 Ondřej Zjevík

2 Prohlašuji, že jsem tuto bakalářskou práci vypracoval samostatně. Uvedl jsem všechny literární prameny a publikace, ze kterých jsem čerpal. V Ostravě

3 Rád bych na tomto místě poděkoval především Prof. RNDs. Zdeňku Dostálovi, DrSc. za pomoc a vedení mé bakalářské práce, jakož i Ing. Oldřichu Vlachovi, Ph.D. za poskytnutí cenných rad.

4 Abstrakt Tato práce se zabývá problémy spojeni s SVM, definicí primární optimalizační úlohy a jak ji pomocí Lagrangeových multiplikátorů převést na konvexní duální úlohu kvadratického programování. Dále vysvětluje princip SVM a aplikuje algoritmy pro řešení duální úlohy vycházející z metody sdružených gradientů v Matlabu. Zabývá se implementací rozšíření jako volný okraj a použití různých kernel funkcí při řešení duální minimalizační úlohy. Díky těmto rozšířením se dá SVM použít pro nelineární klasifikaci nebo pro klasifikaci dat, která jsou zatížena chybou a nelze je úspěšně separovat libovolnou funkcí. Klíčová slova: support vector machines, volný okraj, primární a duální optimalizační úloha, kernel funkce, metoda sdružených gradientů, Polyakův algoritmus Abstract This bachelor thesis helps to understand problems related with the SVM, definition of primary optimalization task, and explain how it convert to convex dual optimalization task of quadratic programming. The thesis shows algorithm based on conjugate gradients method to solve convex dual problem and describes how to implement extensions like Soft margin and different kernel function. Due to this methods the SVM can classify non linear datasets or classify error loaded datasets which can t be successfully separated by any function. Keywords: support vector machines, soft margin, primal and dual optimalization task, kernel function, conjugate gradient method, Polyak s algorithm

5 Seznam použitých zkratek a symbolů SVM Support vector machines SMO Sequential Minimal Optimisation N množina všech přirozených čísel R množina všech reálných čísel R n n-dimenzionální eukleidovský prostor, n N e Eulerovo číslo Eukleidovská norma vektoru l počet prvků trénikové sady x reálný vektor α Larangeovy multiplikátory x, z skalární součin vektorů x a z x T transpozice vektoru

6 1 Obsah 1 Úvod 5 2 Binární klasifikace 6 3 Formalizace Primární úloha Duální úloha Další rozšíření SVM Volný okraj Používání kernel funkcí Algoritmy Metoda sdružených gradientů Polyakův algoritmus SVM v Matlabu Numerické experimenty 31 7 Závěr 32 8 Reference 33 Přílohy 33 A Numerické experimenty 34 B Zdrojové kódy 39 B.1 Polyakův algoritmus B.2 Implementace SVM

7 2 Seznam tabulek 1 Úspěšnost klasifikace datového souboru

8 3 Seznam obrázků 1 Ukázka separace bodů Ukázka separace bodů s maximální vzdáleností přímky od bodů Mapování do lineárního prostoru nám značně zjednodušší klasifikaci Ukázka špatné separace bodů Ukázka volného okraje Grafické znázornění volných proměnných Aplikační rozhraní Ukázky Lineárního kernelu s volným okrajem a různým parametrem C Ukázky Polynomiálního kernelu druhého stupně s volným okrajem a různým parametrem C Ukázky RBF kernelu s volným okrajem, kde γ = 2 2 a parametr C je různý Ukázky různých kernel funkcí bez volného okraje

9 4 Seznam výpisů zdrojového kódu 1 Příklad implementace metody sdružených gradientů v Matlabu Příklad implementace Polyakova algoritmu v pseudokódu Definice kernel funkce a tvorba Hessovy matice Volání minimalizačních funkcí a rozpoznávání support vektorů Implementace Polyakova algoritmu pro obecné řešení SVM Implementace SVM v Matlabu

10 5 1 Úvod Princip metody SVM, která se využívá ke klasifikaci bodů v n rozměrném prostoru, je prostý. Data jsou ve formě n-rozměrných vektorů obsažených ve cvičné sadě a testovacích dat ve formě bodů. U každého takového bodu máme navíc informaci, která určuje do jaké kategorie tento bod patří 1. Cvičná sada bodů by měla co možná nejlépe charakterizovat rozložení bodů různých kategorií v testovacích datech. Pouze z těchto bodů se určuje vhodná volba parametrů klasifikační funkce, tato funkce body separuje do různých kategorií. Pro každou vhodnou kombinaci parametrů se určí úspěšnost klasifikace na bodech z testovací sady, které nebyly použity pro určení klasifikační funkce. Kombinace s nejvyšší úspěšností na testovacích datech je poté použita pro další klasifikaci nových bodů, jež je třeba klasifikovat. Tato práce se zabývá implementací algoritmů pro řešení duální optimalizační úlohy k nalezení funkce, která nejlépe odděluje množinu bodů dvou kategorií. Zjistíme, že řešení pro množinu bodů, které se dají dokonale oddělit 2 je jednodušší. Primární minimalizační úlohu lze přeformulovat na duální a naopak, přičemž si uvedeme výhody i nevýhody řešení jednotlivých úloh. Zjistíme, jak postupovat, když dané rozložení dat nelze rozdělit lineární funkcí. V tomto případě využijeme tzv. kernel funkci, jež nám dovolí používat i nelineární klasifikační funkci. Tomuto tématu se věnuje Kapitola 4.2. Pokud danou cvičnou sadu bodů nelze dokonale oddělit ani libovolnou nelineární funkcí, použijeme tu funkci, jež bude data oddělovat co možná nejlépe. Tento postup je označován jako použití volného okraje, v originále Soft margin a seznámíme se s ním v Kapitole 4.1.Například pokud sledujeme stav elektrického obvodu v závislosti na velikosti proudu procházejícího jističem, jistě musí existovat přesná hodnota proudu, kdy jistič obvod rozpojí. Pokud bychom prováděli laboratorní měření, tuto přesnou hodnotu nezjistíme. Kolem této hodnoty budou rozptýleny body, kdy již jistič rozpojil obvod a kdy ještě ne. Většina dat pocházejících z reálného měření, je zatížena chybou a může se stát, že nejde dokonale oddělit. Použitím volného okraje můžeme problémovým bodům, které jsou nejspíše špatně klasifikovány, přiřadit penalizaci, díky které algoritmus nalezne řešení tak, aby byla celková hodnota funkce minimální. Penalizace se určuje pomocí vzdálenosti daného bodu od dělící funkce jak můžeme vidět na Obrázku 6. V této práci se věnuji převážně tomu, jak správně úlohu formulovat, implementovat úlohu s volným okrajem a vypočítat duální minimalizační úlohu, nebot toto jsou hlavní problémy, se kterými se setkáváme v SVM. V příloze můžeme nalézt vytvořené programy pro aplikaci většiny algoritmů v práci popsaných v programu Matlab a vyzkoušet si je. 1 Nejpoužívanější je binární klasifikace dat, kdy máme pouze dvě kategorie. 2 O dokonalé oddělení se jedná tehdy, pokud lze rovinu rozdělit na dvě poloroviny tak, že v každé budou body z právě jedné kategorie.

11 6 2 Binární klasifikace SVM jsou používány výhradně pro klasifikaci dat dvou kategorií tzn. binární klasifikaci. Tato vlastnost je omezující, ale neznamená to, že se SVM nedají použít pro klasifikaci dat do více množin, jen se musí prvek porovnat s více kategoriemi. Zařazování je velmi podobné jako vyhledávání v binárním stromu. Touto metodou se ale zabývat nebudeme, jelikož existují jiné rychlejší metody pro zařazování dat do více kategorií než je SVM. Dále se ve své práci věnuji jen klasifikaci do dvou kategorií. Předpokládejme, že máme zadány body z R n, kde n N, u kterých víme, do které kategorie patří. Množinu kategorií si označme Y = { 1, 1}. Pro příklad si představme, že jsou body z R 2 a navíc jsou dokonale oddělitelné. Potom máme několik možností, jak je můžeme oddělit viz Obrázek 1. Vidíme, že všechny přímky dokonale oddělují body stejné kategorie (body jsou rozděleny do kategorií podle barvy), ale přímky p 1 a p 3 mají větší vzdálenost od červeného bodu než od zeleného. Normálu přímky označme w = [x 1, x 2 ]. Pro přímky p 1, p 2 a p 3 z Obrázku 1 můžeme zapsat obecnou rovnici přímky p i : w i x i b i = 0, kde i {1, 2, 3}. My ale chceme nalézt takovou přímku, která nejlépe odděluje dané množiny bodů tzn. její vzdálenost od nejbližšího bodu z každé kategorie je největší. Necht má tato přímka rovnici p : w x b = 0, tj. hledáme w, x a b. Přímky, které jsou s touto přímkou rovnoběžné a prochází nejbližším bodem z každé kategorie 3, budou mít rovnici p : w x b = y, kde y Y, {, +} a x, x + označují support vektory vždy z jedné kategorie. Označení přímek můžeme vidět na Obrázku 2. Vzdálenost V budeme nazývat okraj 4. Pokud sada bodů půjde oddělit funkcí, budeme požadovat, aby byl okraj maximální. Tuto klasifikaci nazývejme klasifikace s maximálním okrajem. Okraj vypočítáme z rovnic přímek procházejících support vektory (Definice 3.9) w x + b = 1 w x b = 1 w x + b 1 = w x b + 1 w x + w x = 2 w (x + x ) = 2 x + x 2 w. Pokud požadujeme, aby odhad vzdálenosti x + x byl co největší, znamená to, že 2 w má být maximální, neboli w má být minimální. 3 Bodům, jež leží na těchto dvou přímkách, říkáme support vektory. 4 V anglických textech je tato vzdálenost označována jako margin.

12 7 Obrázek 1: Ukázka separace bodů Obrázek 2: Ukázka separace bodů s maximální vzdáleností přímky od bodů

13 8 3 Formalizace V této kapitole se pokusím formulovat optimalizační úlohu pro nalezení řešení klasifikace s maximálním okrajem. Pokusím se převést optimalizační úlohu se dvěmi parametry pomocí Lagrangeových multiplikátorů na úlohu s jedním parametrem (duální úloha). Některé použité věty a definice vycházejí nebo jsou převzaty z [1]. Definice 3.1 Nadrovinou daného prostoru dimenze n rozumíme jakýkoliv jeho n 1 dimenzionální afinní podprostor. Poznámka 3.1 Nadrovinou k rovině tedy prostoru R 2, je každá přímka, která leží v této rovině. V prostoru R 3 je nadrovinou každá rovina, která leží v tomto prostoru. Platí, že nadrovinu prostoru R n můžeme zapsat pomocí lineární rovnice o n neznámých, např. obecná rovnice přímky nebo obecná rovnice roviny. Definice 3.2 Označme X vstupní prostor, ze kterého jsou body jež chceme oddělit nadrovinou, a Y označme výstupní doménu. Obvykle platí, že X R n a v případě binární klasifikace Y { 1, 1}. Definice 3.3 Cvičná sada je soubor bodů, kde u každého bodu víme, do které kategorie patří. Každý bod můžeme zapsat jako uspořádanou dvojici (x i, y i ), kde x i X, y i Y a i = 1,..., l. Někdy tuto sadu označujeme jako tréninková data. Velikost tréninkové sady počet bodů, označme l. Definice 3.4 Definujeme (funkční) okraj bodu (x i, y i ) od nadroviny (w, b) jako kde i {1,..., l}. γ i = y i ( w x i + b), Definice 3.5 Okraj nadroviny definujeme jako minimum z funkčních okrajů všech bodů vzhledem k příslušné nadrovině. Můžeme jej tedy zapsat jako kde i {1,..., l}. min γ i, Definice 3.6 Pojmem okraj tréninkové sady označujeme maximum ze všech okrajů nadrovin. Nadrovinu, která má tento maximální okraj, nazýváme nadrovina s maximálním okrajem. 5 Definice 3.7 Kernel je funkce K : R n n R a pro všechna x, z X platí K(x, z) = φ(x), φ(z), kde φ : X F je nelineární funkce, která mapuje prostor X do obecně jiného prostoru F. Poznámka 3.2 Pokud chceme body oddělit nelineární funkcí, rozdělíme postup na dva kroky. V prvním převedeme body pomocí funkce φ do prostoru F. Poté můžeme nalézt lineární funkci v F, která body odděluje. Příklad můžeme vidět na Obrázku 3.

14 9 Obrázek 3: Mapování do lineárního prostoru nám značně zjednodušší klasifikaci Definice 3.8 Mějme f : X R n R, x X, n N. Potom přiřadíme bodu x = (x 1,..., x n ) T kladnou kategorii, pokud platí nerovnost f (x) 0. Zápornou kategorii, pokud tato nerovnost neplatí. Pokud máme zadány dokonale oddělitelné body z prostoru R 2, můžeme funkci, která je odděluje, zapsat jako f (x) = w x b, kde w je normálový vektor přímky a b je vzdálenost přímky od počátku. Definice 3.9 Definujme support vektory jako takové testovací body, pro které platí y i (w x i b) = 1. Poznámka 3.3 Support vektory můžeme vidět na Obrázku 2 jako body, jež leží na přímkách s rovnicemi w x b = 1, w x + b = Primární úloha Definice 3.10 Optimalizační úlohu definujeme jako min f (w), w Ω za podmínek g i (w) 0, i = 0,..., k, h i (w) = 0, i = 0,..., m, (1) kde f (w) je minimalizovaná funkce a funkce g i a h i jsou definovány na množině Ω. Optimalizační úlohy, se kterými budeme pracovat, jsou úlohy s omezením. Ve většině případů bude toto omezení dáno jednou nebo dvěma nerovnostníma funkcema. 5 Z anglického označení maximal margin hyperplane.

15 10 Poznámka 3.4 Všimněme si, že úlohu na hledání minima funkce f (w), lze převést na úlohu hledání maxima funkce f (w) a naopak. Nadrovina (w,b) je řešením minimalizační úlohy, kterou definujeme jako min w,b w, za podmínek y i (w x i b) 1, (2) kde i {1,..., l} je nadrovinou s maximálním okrajem Duální úloha Každou primární optimalizační úlohu můžeme převést na duální. Zkusme pomocí Lagrangeových multiplikátorů nalézt duální optimalizační úlohu k (2). Budeme postupovat souběžně s literaturou [1]. Definice 3.11 Obecná duální minimalizační úloha má tvar 1 min x 2 xt Ax x T b, za podmínek g i (x) 0, i = 0,..., k, h i (x) = 0, i = 0,..., m, kde A je čtvercová matice rozměru n a b je sloupcový vektor délky n. Věta 3.1 Pokud je daná funkce f konvexní na celém definičním oboru Ω, v bodě x 0 diferencovatelná a gradient je nulový, pak je bod x 0 globálním minimem. Věta 3.2 Minimum jakékoliv funkce se nezmění, pokud funkci složíme s libovolnou rostoucí funkcí. Důkaz. Dokažme si, že minimum jakékoliv funkce se nezmění, pokud funkci složíme s libovolnou rostoucí funkcí. Necht f : R n R, g : R R, kde n N, g je funkce rostoucí a funkce f má globální minimum v bobě x. Označme D f a D g po řadě definiční obory funkcí f a g. Obor hodnot funkce f označme H f. Předpokládejme, že substitucí y 1 = f (x ), y 2 = f (x) dojdeme k což je vztah, který jsme chtěli dokázat. x D f, x x : f (x ) < f (x), H f = D g, y 1, y 2 D g, y 1 < y 2 : g(y 1 ) < g(y 2 ), g( f (x )) < g( f (x)), 6 Tento vztah jsme si odvodili v Kapitole 2.

16 11 Věta 3.3 V primární úloze nezáleží na tom, jestli minimalizujeme w nebo 1 2 w 2. Důkaz. Definice Eukleidovy normy je w = w w w2 n, pokud w = (w 1, w 2,..., w n ). Všimněme si, že výraz pod odmocninou je součet kvadrátů vektorových složek. Součet těchto kvadrátů musí být číslo nezáporné a také si připomeňme, že druhá mocnina je na R + funkcí rostoucí. Z Věty 3.2 a omezení oboru hodnot odmocniny vyplývá, že se minimum nezmění, pokud místo funkce f (w) = w minimalizujeme funkci g(w) = 1 2 w 2. Pomocí Věty 3.3 můžeme primární úlohu (2) také zapsat jako kde i {1,..., l}. min w 1 2 w 2, za podmínek y i (w x i b) 1, (3) Definice 3.12 Necht je dána primární minimalizační úloha z Definice 3.10, tedy Definujeme Lagrangeovu funkci jako min f (w), w Ω za podmínek g i (w) 0, i = 0,..., k, h i (w) = 0, i = 0,..., m. L(w, α, β) = f (w) + k α ig i (w) + m β ih i (w) = f (w) + αg(w) + βh(w). Definice 3.13 Lagrangeův duální problém vzhledem k Definici 3.10 má tvar kde θ(α, β) = inf w Ω L(w, α, β). max θ(α, β), za podmínek α 0, Věta 3.4 Necht w Ω splňuje podmínky primárního optimalizačního problému z Definice 3.10 a (α, β ) splňuje podmínky duálního problému z Definice 3.13, potom platí f (w) θ(α, β). Důkaz. Důkaz vychází z Definice 3.13, tedy platí θ(α, β) = inf w Ω L(w, α, β), θ(α, β) = inf L(w, α, β) L(w, α, β) = f (w) + αg(w) + βh(w) f (w). w Ω Pokud w Ω, pak platí nerovnice g(w) 0, rovnice h(w) = 0 a také α 0. Z Věty 3.4 vyplývají dva podstatné vztahy, které si ted ukážeme.

17 12 Poznámka 3.5 Hodnota duálního Lagrangeového problému je shora ohraničena hodnotou primární úlohy sup{θ(α, β) : α 0} inf{f(w) : g(w) 0, h(w) = 0}. Věta 3.5 Pokud w řeší primární úlohu (3) a (α, β ) řeší optimalizační úlohu z Definice 3.13, pak platí α i g i(w ) = 0, (4) pro i = 1,..., n. [1] Důkaz. Tento důkaz můžeme nalézt také v [1]. Necht w je řešením primární úlohy z Definice 3.10, (α, β ) je řešením duálního Lagrangeova problému z Definice Z Definic 3.12 a 3.13 vyplývá, že α 0, g(w ) 0 a h(w ) = 0. Duální úlohu můžeme upravit θ(α, β ) = L(w, α, β ) = f (w ) + α g(w ) + β h(w ) = f (w ) + α g(w ). Všimněme si, že výraz α g(w ) je vždy menší nebo roven nule, nebot platí α 0 a g(w ) 0. Dále, uplatníme podmínku f (w ) = θ(α, β ) na upravenou duální úlohu θ(α, β ) = f (w ) + α g(w ) f (w ) = f (w ) + α g(w ) f (w ) f (w ) = α g(w ) 0 = α g(w ). Abychom mohli dokázat, že platí Věta 3.5, musíme dokázat, že řešení primární a duální úlohy si jsou rovna. Pokud si jsou primární a duální optimalizační úlohy rovny, mluvíme o tzv. silné podmínce duality. Tato podmínka není vždy splněna, ale pokud je primární úloha (1) konvexní a funkce g 1 (w),..., g k (w) jsou také konvexní, obvykle splněna je. Tyto podmínky nazýváme tzv. podmínky regularity a jednou z nich je například Slaterova podmínka: w Ω : g i (w) < 0, i {1,..., k}, h i (w) = 0, i {1,..., m}. Tato podmínka je jistě v našich primárních optimalizačních úlohách vztahujících se k SVM splněna. Úlohu (3) převedeme na hledání sedlového bodu Lagrangeovy funkce (viz [1]) L(w, b, α) = 1 2 w 2 α i yi (w x i b) 1, kde α i 0 jsou Lagrangeovy multiplikátory. Minimum této funkce je určeno vzhledem k w a b. Nalezneme jej, pokud parciální derivace položíme rovny nule L(w, b, α ) w = w α i y i x i = 0,

18 13 L(w, b, α ) b = α i y i = 0. (5) Upravíme minimalizační úlohu s Lagrangeovými multiplikátory a dosadíme vypočítané hodnoty z parciálních derivací L(w, b, α) = 1 2 w 2 α i yi (w x i b) 1 = 1 2 w, w α i y i (w x i b) + = 1 2 = 1 2 = 1 2 α i α j y i y j x i, x j i,j=1 α i α j y i y j x i, x j i,j=1 α i α j y i y j x i, x j + α i y i w, x i + b α i y i + α i α j y i y j x i, x j + i,j=1 i,j=1 α i. α i α i α i L(w, b, α) = 1 2 α i α j y i y j x i, x j + i,j=1 α i (6) Tímto postupem jsme primární úlohu (3) upravili na optimalizační úlohu vzhledem k proměnné α. Z (5) můžeme pozorovat, že výsledné řešení je lineární kombinací bodů. Duální optimalizační úloha vzhledem k primární bude vypadat takto max α za podmínek 1 α i α j y i y j x i, x j + 2 i,j=1 n y iα i = 0, α i 0, i = 1,..., n. α i, Skalární násobení vektorů x i a x j můžeme nahradit kernel funkcí definovanou jako (7) K(x i, x j ) = x i, x j. V Kapitole 4.2 si ukážeme, jaké má tato funkce další využití. Poznámka 3.6 Při hledání maxima duální úlohy se jednotlivé Lagrangeovy multiplikátory, které nejsou příslušné k support vektorům, během procesu optimalizace vynulují. Naopak ty, které jsou příslušné k support vektorům, jsou nenulové 7. Již po pár iteracích optimalizačního algoritmu můžeme pozorovat, které body nejsou jistě support vektory. Tím se nám množina bodů značně zredukuje. Dosavadní implementace SVM řeší tento problém pomocí různých metod jako Chunking, Dekompozičních nebo SMO algoritmů [2]. Valná 7 Vzácně se stává, že nenulové L. multiplikátory mají i body, jejichž funkční hodnota klasifikační funkce f (x) není o moc větší než funkční hodnota support vektorů.

19 část algoritmů využívá pro výpočet řešení duální úlohy algoritmus sdružených gradientů, který většinou není nijak upraven. Stále je otevřená otázka, jestli se nedá více optimalizovat samotná optimalizační úloha pro hledání klasifikační funkce. Pro určení výsledné funkce jsou totiž důležité jen support vektory a těch může být oproti celé množině bodů jen nepatrné množství. 14

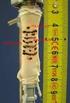
20 15 4 Další rozšíření SVM V této kapitole se podíváme blíže praktickému použití SVM pro klasifikaci bodů. Ukážeme si, jak postupovat, pokud data nejsou lineárně separovatelná a také jak postupovat, pokud jsou zatížená chybou, např. při měření reálných hodnot. Dále se pokusíme nahlédnout do problematiky kernel matic, jak se využívají, sestavují a k čemu slouží. 4.1 Volný okraj V roce 1995 Corrina Cortes a Vladimir Vapnik navrhli modifikaci Maximum margin algoritmu tak, aby mohl oddělovat i data zatížená chybou. [3] Pokud jako vstup byla data, která se nedala oddělit zvolenou funkcí, tak výsledek optimalizace dopadl špatně, nebot v duální úloze se hodnota příslušného Lagrangeova multiplikátoru blížila nekonečnu. V důsledku to znamenalo, že pokud tréninkovou sadu nebylo možné separovat lineární nadrovinou, funkce se nenalezla, nebo nalezená nadrovina data špatně klasifikovala. Příklad takového výsledku můžeme vidět na Obrázku 4. Můžeme pozorovat, že špatně klasifikovaných bodů je 7 z 15. Úspěšnost této klasifikační je pouze 53,3%, což je skoro nejhorší možné oddělení. Z rozdělení bodů můžeme ale vidět, že pokud bychom dělicí přímku posunuli doleva a otočili, aby oddělovala většinu bodů, počet špatně klasifikovaných bodů klesne na jeden. Všimněme si, že na Obrázku 5 jsou body takto odděleny. 8 Zde byla použita technika volného okraje, což znamená 93,3% úspěšnost. Ukažme si, jak sestrojíme takovouto úlohu. Nejprve si zopakujme, jak vypadá primární minimalizační úloha: min 1 2 w 2, za podmínek y i (w x i b) 1. (8) Pokud požadujeme, aby nerovnostní podmínka mohla být porušena, musíme zavést tzv. volné proměnné ξ i, aby minimalizační úloha vypadala takto min 1 2 w 2 + C ξ i, za podmínek y i (w x i b) 1 ξ i, ξ i 0. Parametr C R + určuje váhu chyby jednoho bodu. Pokud by se parametr C blížil nekonečnu, optimalizační úloha by se přibližovala obyčejné úloze bez volného okraje. Tuto úlohu můžeme převést na úlohu nalezení sedlového bodu Lagrangeovy funkce L(w, b, ξ, α, β) = 1 2 w 2 + C ξ i α i yi (w x i b) 1 + ξ i β i ξ i, 8 Support vektory jsou znázorněny bílým kolečkem.

21 16 Obrázek 4: Ukázka špatné separace bodů kde α i 0 a β i 0 jsou Lagrangeovy multiplikátory. Vypočteme parciální derivace vzhledem k w, ξ a b L(w, b, ξ, α, β) w = w n α iy i x i, L(w, b, ξ, α, β) ξ i = C α i β i, L(w, b, ξ, α, β) b = n α iy i. Minimum Lagrangeovy funkce nalezneme, pokud jednotlivé parciální derivace budou rovny nule, tzn. w = α i y i x i C = α i + β i α i y i = 0.

22 17 Obrázek 5: Ukázka volného okraje Duální úlohu nalezneme, pokud dosadíme vztahy získané z parciálních derivací zpět do Lagrangeovy funkce L(w, b, ξ, α, β) = 1 2 w 2 + C ξ i α i yi (w x i b) 1 + ξ i β i ξ i = 1 2 w w + C ξ i = 1 2 = 1 2 = 1 2 = 1 2 α i y i (w x i b) + α i α j y i y j x i, x j + b i,j=1 α i α j y i y j x i, x j + i,j=1 α i α j y i y j x i, x j + i,j=1 α i α j y i y j x i, x j + i,j=1 α i y i + C α i ξ i + (α i + β i )ξ i + α i ξ i + α i. α i ξ i α i α i β i ξ i + β i ξ i α i ξ i α i ξ i α i β i ξ i α i ξ i β i ξ i β i ξ i L(w, b, ξ, α, β) = 1 2 α i α j y i y j x i, x j + i,j=1 α i (9)

23 18 Obrázek 6: Grafické znázornění volných proměnných Jistě nám neuniklo, že Lagrangeova funkce pro volný okraj (9) je identická jako Lagrangeova funkce (6). Jediný rozdíl je v omezující podmínce C α i β i = 0, kterou musíme dodržet. Vzhledem k tomu, že β i 0, musí také platit α i C ξ i 0 a α i = C β i = 0. Z Věty 3.5 vyplývají tyto podmínky α i [y i (w x i b) 1 + ξ i ] = 0, i = 1,..., n, (10) ξ i (C α i ) = 0, i = 1,..., n. (11) Všimněme si, že pro splnění podmínky (11), musí být příslušná volná proměnná ξ i rovna nule nebo α i = C. Body, které mají příslušné ξ i nenulové, jsou těmi body, které jsou špatně klasifikované a musí u nich platit, že α i = C. Naopak, pokud α i < C, volná proměnná ξ i musí být rovna nule (viz Obrázek 6). Pokud je daný bod dobře klasifikován, tedy platí ξ i = 0, tak podmínka (10) přechází na (8). (viz [1]) Definice 4.1 Duální minimalizační úlohu s volným okrajem definujeme jako max α za podmínek 1 α i α j y i y j x i x j + 2 i,j=1 y i α i = 0, C α i 0, i = 1,..., l. α i, (12)

24 Používání kernel funkcí Původně bylo SVM vynalezeno pro lineární klasifikaci a nepředpokládalo se, že by se data mohla klasifikovat také pomocí nelineární funkce. Toto omezení bylo ale v devadesátých letech odstraněno. Již se nemusely zavádět nové speciální parametry, které by se musely volit a ztěžovaly by tak nalezení klasifikační funkce. Řešení pomocí kernel funkcí bylo poprvé představeno v [4]. Reprezentace dat pomocí kernelů nám nabízí alternativní řešení, jak data mapovat do prostoru vyšší dimenze, kde mohou být lépe oddělena lineární funkcí. Používání duální úlohy k nalezení nelineární funkce nám výpočet ještě zjednodušuje. Uvnitř duální úlohy se tréninkové body nevyskytují osamoceny, ale vždy ve formě skalárního součinu s dalším bodem. Výhoda používání duálního přístupu vyplývá z toho, že pokud změníme kernel funkci, omezující podmínky zůstanou zachovány. Pokud nahradíme skalární součin vhodně zvolenou kernel funkcí, která poskytne nelineární mapování do vyššího prostoru, výpočet úlohy se tím nijak neztíží. Dokonce nalezená funkce bude tréninková data oddělovat v původním prostoru nelineárně. Ukážeme si, že technika založená na kernel funkcích, je důležitou částí SVM. V dnešní době se SVM těší tak velké oblibě z velké míry díky kernel funkcím. Díky naprosté separaci kernel funkcí od řešení duálních úloh můžeme aplikovat jakýkoliv algoritmus na řešení duální úlohy s omezením jak pro lineární, tak nelineární klasifikační funkce. Definice 4.2 Definujme funkci φ : X F, x = (x 1,..., x n ) φ(x) = (φ 1 (x),..., φ n (x)), kde F = {φ(x) x X} a φ je nelineární funkce mapující body ze vstupního prostoru do prostoru stejné nebo vyšší dimenze. Definice 4.3 Definujme matici K, i, j {1,..., l} 2 takovou, že platí K i,j = K(x i, x j ), kde K je kernel funkce z Definice 3.7. Matici K nazýváme kernel matice nebo také Grammova matice. Pokud chceme data separovat nelineární funkcí f (x), musíme nejprve takovou vhodnou funkci nalézt. Funkci, která bude dané body separovat, pak budeme hledat ve tvaru (viz [1]) f (x) = w φ(x) b. Toto řešení by znamenalo, že bychom museli nalézt danou mapující funkci a poté zjišt ovat, jestli jsou body v novém prostoru F lineárně separovatelné. Pokud se ale podíváme na definici duální úlohy, vidíme, že v maximalizační úloze se již nevyskytují body, ale jen jejich skalární součiny. Pokud bychom tedy měli body transformované do prostoru F, bude optimalizovaná funkce z (7) vypadat f (x) = 1 2 α i α j y i y j φ(x i ), φ(x j ) + i,j=1 α i.

25 20 Pokud by existoval způsob, jak vypočítat tento skalární součin přímo jako kernel funkci K ze vstupního prostoru bez znalosti funkce φ, znamenalo by to, že bychom byli schopni výpočet nelineárního SVM provést v jednom kroku. Tím bychom nemuseli hledat funkci φ a poté sestavit kernel matici jako skalární součin dvou funkčních hodnot K(x i, x j ) = φ(x i ), φ(x j ). Tento výpočet je většinou náročný a např. pro nekonečně dimenzionální prostory nemusí být řešitelný. Ukážeme si, že takové kernel funkce K existují. Výpočet kernel funkce nemusí být nutně závislý na tom, kolika rozměrný je prostor do kterého mapujeme dané body. To znamená, že rychlost výpočtu bude přibližně stejná, at už použijeme lineární separaci nadrovinou v původním prostoru, nebo dané body transformujeme do jiného prostoru a oddělíme je nadrovinou tam. Příklad 4.1 Necht x, z R n a kernel funkce Tuto kernel funkci můžeme také zapsat jako K(x, z) = K(x, z) = (x T z) 2. (13) = = x i z i x j z j j=1 x i x j z i z j j=1 (x i x j )(z i z j ) i,j=1 = φ(x), φ(z), kde k této kernel funkci existuje mapující funkce φ z Definice 4.2 taková, že (pro n = 2) platí x 1 x 1 x φ(x) = 1 x 2. (14) x 2 x 1 x 2 x 2 Toto je příklad polynomiálního kernelu druhého stupně, který prochází počátkem. Můžeme pozorovat, že výpočet funkce φ (14) má složitost O(n 2 ), ale výpočet kernel funkce (13) má složitost pouze O(n). Bežněji se ale používá pro polynomiální kernely obecný vztah K(x, z) = (x T z + c) d,

26 21 kde d značí stupeň polynomu a konstanta c určuje relativní váhu mezi prvky x i (prvního řádu) a ostatními prvky obecně vyšších řádů nejvyšší řád je stupně d. 9 U této kernel funkce nemusí hledaná funkce f (x) procházet počátkem jako v Příkladu 4.1. Pro úplnost si ukažme, jak vypadá funkce φ(x) pro obecný polynomiální kernel druhého řádu, kde x R 2 x 1 x 1 x 1 x 2 x φ(x) = 2 x 1. x 2 x 2 c x 1 c x 2 Pokud sada bodů {x i, i = 1,..., l} má tu vlastnost, že její těžiště je blízko 0, tak s určitým přiblížením můžeme na kernel funkci pohlížet jako na funkci, která nám určuje, jak jsou od sebe body x a z v prostoru F vzdáleny. Pokud jsou body blízko sebe, očekáváme hodnotu kernel funkce velkou, a pokud jsou si body vzdáleny, je hodnota kernel funkce malá. Vzhledem k takovému přístupu si můžeme např. zvolit kernel funkci K(x, z) = e γ x z 2, kde γ > 0. Tato funkce bude mít hodnotu 1, pokud x = z, a blízkou nule, čím víc budou vektory x a z odlišné. Ale existuje k této kernel funkci mapující funkce φ? 10 Věta 4.1 Funkce je platnou kernel funkcí. K(x, z) = e γ x z 2 Důkaz. Ukažme si nástin důkazu pro x, z R 1. Důkaz je založen na tom, že můžeme nalézt takovou funkci φ, jejíž skalární součin bude roven kernel funkci. Necht γ > 0, pak platí K(x, z) = e γ x z 2 = e γ(x z)2 = e γx2 +2γxz γz 2. Tento výraz můžeme dále rozložit pomocí Taylorova polynomu a upravit na skalární součin dvou funkcí φ 9 Uvědomme si, že pokud d = 1, máme také platný kernel pro lineární funkci. Konstanta c se obvykle volí jako c = Tento kernel je nazýván Gaussian nebo Radial Basis Function RBF a koresponduje s prostorem F o nekonečném počtu dimenzí a do něj mapující funkcí φ(x).

27 22 e γx2 +2γxz γz 2 = e γx2 γz 2 +2γxz e γx2 +2γxz γz 2 = e γx2 γz γxz + (2γxz)2 + 1! 2! = e γx2 γz 2 2γ 1 + 1! x 2γ 1! z + (2γ) 2 2! x 2 (2γ) 2 2! z 2 + = φ(x), φ(z), e 2γxz kde mapující funkce φ je definována jako 1 φ(x) = e γx2 2γ 1! x (2γ) 2 2! (2γ) 3 Pro prokázání platnosti RBF kernelu pro více rozměrný vstupní prostor můžeme použít stejný postup. 3!. x 2 x 3. Věta 4.2 (Mercerova) Necht je dána funkce K : R n R n R. Potom funkce K je platným (Mercerovým) kernelem (tj. existuje k ní odpovídající φ) právě tehdy, když odpovídající kernel matice je symetrická a pozitivně semidefinitní. (viz [1]) Důkaz. Předpokládejme, že funkce K je platná kernel funkce, tedy existuje k ní příslušná mapující funkce φ. Platí K i,j = K(x i, z j ) = φ(x i ), φ(z j ) = φ(z j ), φ(x i ) =K(z j, x i ) = K j,i, kde K j,i je prvek matice K se souřadnicemi i a j. Kernel matice tedy musí být symetrická. Navíc si označme φ k (x) k-tou složku vektoru φ(x). Potom pro libovolný vektor z platí

28 23 z Kz = = = = = z i K ij z j i j i j i j k i z i φ(xi ) T φ(x j ) z j z i φk (x i )φ k (x j ) z j k z i φ k (x i )φ k (x j )z j z i φ k (x i ) k 0, i j tedy, že kernel matice je pozitivně semidefinitní. Druhou stranu ekvivalence můžeme dokázat na základě singulárního rozkladu matice, kde ke každé pozitivně semidefinitní matici můžeme nalézt funkci φ. 2

29 24 5 Algoritmy Budeme implementovat řešení pomocí duální optimalizační úlohy, protože je to úloha s jednoduchým omezením a dají se zde lehce aplikovat vlastnosti jako volný okraj nebo různé kernel funkce bez změny výpočetní náročnosti úlohy. Oproti primární úloze má toto řešení jedinou nevýhodu, a tou je nutnost sestavit kernel matici, která je bohužel plná a její rozměr je závislý na počtu prvků v tréninkové sadě. Stejné výpočty, jako při sestavování kernel matice, se musí provést při řešení primární úlohy. Nevýhodou zůstává, že musí být sestavena v celku. Právě zde přichází na řadu tradiční optimalizace ve formě SMO nebo chunking algoritmů. Těmito algoritmy se z důvodu rozsahu tato práce nezabývá, ale ukážeme si, jak řešit obecné duální optimalizační úlohy. Jedním z nejvhodnějších algoritmů k hledání řešení soustavy lineárních rovnic je metoda sdružených gradientů. V krátkosti si ji popíšeme a implementujeme do této metody omezující podmínku, abychom ji mohli použít pro řešení duální úlohy (12). 11 Pro implementaci SVM jsem vytvořil aplikaci v jazyce Matlab. Tato aplikace využívá mnou vytvořenou implementaci Polyakova algoritmu. Nalezené řešení optimalizační úlohy je porovnáváno s výpočtem pomocí integrované funkce quadprog, která řeší řeší duální minimalizační úlohu s omezením. 5.1 Metoda sdružených gradientů Tato metoda slouží pro hledání minima kvadratické funkce ve tvaru f (x) = 1 2 xt Ax x T b, (15) kde A je symetrická pozitivně definitní matice a x, b jsou vektory. Tato funkce bude mít minimum v bodě, kde bude gradient funkce f (x) nulový, f (x) = Ax b. Metoda sdružených gradientů je iterační metodou. Byla odvozena z metody největšího spádu, kdy jednotlivé kroky jsou na sebe A-ortogonální. Pokud počítáme bez zaokrouhlovacích chyb, potom v jednom iteračním kroku dochází k nalezení minima alespoň v jednom směru tedy maximální počet kroků je roven velikosti matice. Označme x i postupnost vektorů, pro kterou platí x i x, kde x je minimem (15). Vektory posloupnosti budeme konstruovat jako x i+1 = x i α i v i, kde v i jsou vektory A-ortogonální báze, pro které platí Av i, v j = 0, pro i j, Av i, v i 0, pro i {0, 1,..., n}. (16) 11 Metodu sdružených gradientů s omezením využívá např. Polyakův algoritmus, který si představíme.

30 25 Dále α i je koeficient, který vypočteme jako α i = ri, v i v i, Av i. Označmě r i reziduum a necht r i = (Ax i b). A-ortogonální vektory v i vytvoříme z reziduí procesem A-ortogonalizace kde v 0 = r i a koeficient β i 1 vypočteme jako v i = r i β i 1 v i 1, β i 1 = ri, Av i 1 Av i 1, v i 1. Chyba pro x i je rovna normě rezidua, tedy r i. Algoritmus nalezne řešení s chybou ϵ, právě tehdy, když r i ϵ. Více o metodě sdružených gradientů můžeme nalézt např. v [5] Implementace Ukažme si tedy, jak by mohla vypadat implementace v jazyce Matlab. Necht matice A a vektor b jsou zadány a proměnná e určuje požadovanou přesnost řešení. x = zeros(length(b),1); r = (A x b); v = r ; while (norm(r) > e) z = A v; alpha = (r v) /( v z); x = x + alpha v; r = r alpha z; bet = (r z) /( v z); v = r + bet v; Výpis 1: Příklad implementace metody sdružených gradientů v Matlabu 5.2 Polyakův algoritmus Tento algoritmus můžeme nalézt v [6]. Metoda sdružených gradientů řeší úlohu (15) bez omezení, která vyplývají z definice duální úlohy SVM. Abychom tedy podmínku nezápornosti x i mohli dodržet, musíme metodu sdružených gradientů upravit. 12 Necht máme zadanou tuto optimalizační úlohu max x 1 2 xt Ax + x T b, za podmínek x k, (17) 12 Aplikací omezením shora můžeme implementovat řešení úlohy s volným okrajem.

31 26 kde x Ω. Předpokládejme, že úloha má právě jedno řešení, matice A je pozitivně semidefinitní čtvercová matice o rozměrech n n a vektory b a k mají délku n. Definujme množinu N = {1, 2,..., l} a dvě množiny. Aktivní množinu A a množinu F A(x) = {i N : x i = k i } F (x) = {i N : x i k i }, jež nazýváme volnou. Definujme také vektorové funkce ϕ a β, které definujeme po složkách jako ϕ i (x) = r i, pro i F (x), β i (x) = 0, pro i F (x), ϕ i (x) = 0, pro i A(x), β i (x) = min{r i, 0}, pro i A(x), funkce ϕ značí gradient volných směrů. Tento gradient je v dané složce nenulový pouze, pokud vektor x je v dané složce větší než limit k i. Naopak funkce β je nulová v těch směrech, které jsou volné. V těch směrech, které jsou v aktivní množině, nenabývá hodnoty 0 ale r i, pokud je r i < 0. Projektovaný gradient označme jako g P (x) = ϕ(x) + β(x). Uvědomme si rozdíl Polyakova algoritmu a metody sdružených gradientů. Polyakův algoritmus využívá projekce gradientu residua tak, aby jednotlivé složky hledaného řešení x nebyly menší než k. Pokud by byl krok sdružených gradientů tak velký, že by jedna složka přesáhla hodnotu k, velikost kroku se omezí na tzv. zkrácený krok. Pokud se provede zkrácený krok, tak x i = k i a příslušná složka gradientu se přesune z volné množiny směrů do aktivní. Tento směr se z aktivní množiny může dostat zpět do volné jedině tehdy, pokud je již norma volného gradientu menší než numerická chyba ϵ a norma projektovaného gradientu je stále velká. Poté se provede krok ve směru projektovaného gradientu. Některé složky gradientu se odpoutají z aktivní množiny a přesunou se do volné. Polyakův algoritmus nalezne přesné řešení úlohy právě tehdy, pokud platí g P (x) = 0. Jelikož ale počítač nepočítá v přesné aritmetice, označíme iteraci x i za řešení úlohy (17), pokud platí g P (x) ϵ, kde ϵ je velmi malé, řádově Implementace Ukažeme si implementaci Polyakova algoritmu v pseudokódu. Optimalizovanou implementaci v Matlabu můžeme nalézt v příloze B.1 i s horním omezením pro x. Necht x 0 Ω, potom

32 27 % Inicializace g = (Ax 0 b), p = g P (x 0 ), i = 0 while g P (x i ) e if ϕ(x i ) er % Vypočtení délky kroku sdružených gradientů a zkráceného kroku α CG = (g p)/(p Ap); y = x i α CG p; α f =max α : x i αp = min (x i k j j)/p j : p j > 0) if α CG α f % provedeme krok sdružených gradientů x k = y, g = g α CG Ap; β = (ϕ(y) Ap)/(p Ap), p = ϕ(y) βp; else % provedeme zkrácený krok x i+1 = x i α f p, g = g α f Ap, p = ϕ(x i+1 ); else % v tomto kroku uvolníme některé prvky z aktivní množiny d = β(x i ), α CG = (g d)/(d Ad); x i+1 = x i α CG d, g = g α CG Ad, p = ϕ(x i+1 ) i = i + 1; x = x i ; Výpis 2: Příklad implementace Polyakova algoritmu v pseudokódu Výsledný algoritmus vrátí výsledek optimalizační úlohy (17) jako x. 5.3 SVM v Matlabu Mnou vytvořená grafická aplikace v Matlabu je obsažena na přiloženém CD v adresáři Matlab. Spustíme jí příkazem gui. Po spuštění vidíme, že můžeme volit mezi různými druhy kernelu, kde máme na výběr mezi lineárním, polynomiálním a RBF kernelem. Pokud zvolíme polynomiální kernel, musíme také zvolit stupěň polynomu. Pokud zvolíme RBF kernel, musíme zvolit hodnotu parametru γ. Tuto hodnotu volíme jako číslo 2 n, kde n je z rozsahu 15 až 3. [7] Body můžeme zadávat pomocí polohy kurzoru. Pravým a levým tlačítkem myši umístíme bod bud jedné, nebo druhé kategorie na polohu kurzoru. Po spustění klasifikace se zvýrazní Support vektory bílým kolečkem a vrstevnice klasifikační funkce f (x) = ±1, jsou zvýrazněny čárkovaně. Po spuštění klasifikačního procesu se vypíše číslo podmíněnosti matice. 13 Např. pro úlohu na Obrázku 7 je číslo podmíněnosti 6, Toto číslo zmačí poměr mezi největším a nejmenším vlastním číslem matice. Číslo podmíněnosti také značí, jak rychle konvergují gradientní metody hledání minima kvadratické funkce. Čím je toto číslo větší, tím hůře je soustava podmíněna a je vhodné zvolit některé předpodmínění.

33 28 Obrázek 7: Aplikační rozhraní Aplikace také vypíše relativní rozdíl řešení Polyakova algoritmu, který nalezne řešení s přesností na 10 6 nebo se ukončí po 2000 iteracích, od řešení pomocí funkce guadprog. Tento rozdíl je menší než 10 6, pokud oba algoritmy dokonvergují k přesnému řešení. Pokud je úloha velká a navíc špatně podmíněná, algoritmy neskončí na základě normy rezidua, ale kvůli omezení na maximální počet iterací. Program také vypíše kolik kroků provedl Polyakův algoritmus a kolik integrovaná funkce quadprog. Již bylo v textu zmíněno, že maximální počet iterací Polyakova algoritmu je rovnen velikosti kernel matice, tedy počtu bodů. Díky zaokrouhlovacím chybám a relativně velké požadované přesnosti řešení nepočítáme v přesné aritmetice, proto se musí Polyakův algoritmus někdy i několikrát restartovat, tedy uvolnit některé složky z aktivní množiny do volné. Díky tomuto kroku může být, a ve většině případů také je, počet iterací větší než velikost sady. Pokud potřebujeme aplikovat SVM na data, kde nevíme, jaká volba kernelu bude nejlepší, je třeba vždy nalézt vhodný kernel i s parametry, které naleznou nejlepší hledanou funkci. Ve většině případů musíme navíc použít úlohu s volným okrajem, nebot data nejdou separovat nadrovinou v původním prostoru. Proces hledání těchto atributů se anglicky nazývá cross validation, v této práci bude nazýván křížová validace. Křížová validace probíhá tak, že na cvičné sadě bodů vyzkoušíme všechny možné kombinace kernel funkcí. Pro každou nalezenou funkci určíme, jak dobře klasifikuje testovací data ze stejného zdroje, u kterých ale také víme, do jaké kategorie patří. Díky porovnání úspěšnosti klasifikace mezi různými kernely můžeme určit, který kernel a s jakými

34 29 parametry je nejvhodnější. Křížová validace je nejlepší způsob, jak nalézt vhodný kernel i s parametry. Díky tomu, že musíme porovnávat všechny možnosti, je ale časově i výpočetně nejnáročnější operací. Polyakův algoritmus nalezne řešení jen pro pozitivně definitní matice. Pro implementaci lineárního kernelu byl proto použit polynomiální kernel stupně jedna, nebot Grammova matice lineárního kernelu je podmíněně pozitivně definitní. [8] Lineární kernel, který jsem implementoval, tedy vypadá K(x, z) = (x T z + 1). Do algoritmu jako vstupní parametry vystupují souřadnice bodů 14, druh kernelu, který se má použít, parametr γ pro RBF kernel, dva parametry pro limitní hodnoty zobrazované části plochy grafu a hodnota parametru C, která představuje horní omezení v aplikaci úlohy s volným okrajem Implementace Zde budou popsány podstatné části implementace algoritmu pro SVM v Matlabu, jenž spolupracuje také s GUI, které jsem vytvořil. Jako první vstupní proměnou points rozdělíme na proměnné X a d. Proměnná X obsahuje souřadnice jednotlivých bodů a proměnná d obsahuje kategorie těchto bodů. Vytvoříme anonymní funkci, která nám bude reprezentovat zvolený kernel, a sestavíme Hessovu matici. function [ uspesnost ] = SVM( points, kernel, deg, gama, XLim, YLim, C ) X = points (:,1:2) ; %souřadnice bodů d = points (:,3) ; %karegorie bodů [p, n] = size(x); %p značí počet bodů, n počet složek H = zeros(p,p); switch kernel case lin K x z +1; case poly K (x z +1)ˆdeg; case rbf K ( exp( gama sum((x z).ˆ2) )); %lineární kernel %polynomiální kernel %RBF kernel for :p for j=1:p H(i, j ) = d(i ) d(j ) K(X(i,:),X(j,:) ) ; %tvorba Hessovy matice Výpis 3: Definice kernel funkce a tvorba Hessovy matice Poznámka 5.1 Zde se nabízí místo pro aplikaci předpodmínění pro Hessovu matici. Různými druhy předpodmínění se tato práce nezabývá kvůli rozsahu. 14 Implemetován je algoritmus pro body z R 2, ale úprava na více rozměrné prostory je triviální.

35 30 Poznámka 5.2 Pro lineární kernel použijeme jako kernel funkci K(x, z) = x, z + 1, nebot při implementaci duální optimalizační úlohy nemusíme uplatnit rovnostní podmínku y i α i = 0. Tato podmínka je začleněna přímo do mapující funkce φ. Ani u ostatních kernelů tuto podmínku nemusím aplikovat, jelikož je také v φ. [1] Můžeme zavolat obě minimalizační metody Polyakův algoritmus, jež je uveden v příloze B.1, a také Matlabovskou funkci quadprog a můžeme porovnat výsledky obou minimalizačních algoritmů. Ukažme si, jak poznáme, jaký bod je support vektor. b = ones(p, 1); lb = zeros(p,1); ub = C. ones(p,1); x0 = zeros(length(b),1); %dolní limit pro hledané řešení %horní limit pro hledané řešení %počáteční poloha ze které začínáme minimalizovat funkci options = optimset( quadprog ); options = optimset( MaxIter,300); [ reseniquad,fval,exitflag,output ] = quadprog(h, b, [], [], [], [], lb, ub,x0,options); [ resenipolyak,k,estep,cstep ] = PolyakSVM(H,b,zeros(p,1),C); for i = 1:p if resenipolyak(i) > 10ˆ 5 %pokud je příslušná složka nulová, tak je support vektor plot(x(i,1),x(i,2), wo, LineWidth,2); %tento bod vyznačíme v grafu Výpis 4: Volání minimalizačních funkcí a rozpoznávání support vektorů Celý tento algoritmus můžeme nalézt jako přílohu B.2.

36 31 6 Numerické experimenty Díky algorimu v Kapitole 5.3 si můžeme ukázat, jaký vliv má zvolení správné kernel funkce na tvar klasifikační funkce. Na Obrázku 11 můžeme vidět, jak se změní funkce při použití různých kernelů. Vidíme, že RBF kernel je při malé hodnotě γ velmi podobný lineárnímu kernelu. Při zvětšování γ se vytvářejí shluky podobně, jako tomu je při použití KNN algoritmů (viz [9]). Velikost těchto shluků závisí právě na správně voleném atributu γ u RFB kernelu. Na Obrázku 8 můžeme vidět, jak ovlivňuje různá volba parametru C výslednou funkci u bodů, jež nelze separovat nadrovinou, pokud aplikujeme lineární kernel. Ukázka použití volného okraje u polynomiálního kernelu druhého řádu je na Obrázku 9. Můžeme pozorovat, že bez použití omezení pro atribut α, tedy bez aplikace volného okraje, je úspěšnost pouze 31,0%. Tato hodnota velmi rychle roste už při použítí velkého omezení pro α i. U RBF kernelu byl zvolen parametr γ = 2 2, nebot úspěšnost funkce byla minimální. Můžeme pozorovat, jaký nárůst úspěšnosti má použití volného okraje i u RBF kernelu. Pro použití Polyakova algoritmu na úlohy, které jsou více rozměrné a jejichž zadání je ve speciálním formátu, který můžeme nalézt třeba na stránkách projektu LIBSVM, byl vytvořit skript. Tento skript data v určeném formátu načte a zjistí, jak dobře klasifikuje nalezená funkce testovací sadu dat, která se také dají stáhnout na těchto stránkách. Pro mé testy jsem zvolil soubor splice. Sbírka bodů splice obsahuje 1000 bodů pro naučení a dalších 2175 bodů pro kontrolu, každý bod je klasifikován do jedné ze dvou kategorií a má 60 atributů. V Tabulce 1 můžeme vidět počty iterací algoritmů, časy řešení a také, jak se mění úspěšnost klasifikace v závislosti na zvolené kernel funkci a jejích parametrech. Vidíme, že vyzkoušení všech parametrizací je důležité, protože rozdíly jsou i v rámci jediného kernelu veliké. Hodnota N/A značí, že algoritmus nedoiteroval ke správnému řešení, ale zastavil se po maximálním počtu kroků. Test probíhal pod operačním systémem Windows s taktem procesoru 2,67 GHz bez paralelizace. Pozorujeme, že počet iterací Polyakova algoritmu i na tak velkou úlohu není příliš rozdílný od integrovaného algoritmu quadprog. Existují i jiné iterační metody, jež konvergují rychleji k přesnému řešení, než Polyakův algoritmus. Některé z těchto algoritmů můžeme nalézt v poblikaci [6].

37 32 7 Závěr Tato práce čtenáře seznámila s pojmem Support Vector Machines. Popsaný matematický základ poskytuje čtenáři úvodní seznámení s optimalizačními úlohami a dále popisuje, jak se vytvoří primární minimalizační úloha SVM. Pro aplikaci rozšíření, jako hledání nelineární klasifikační funkce a volba volného okraje, byla popsána duální úloha, jež byla odvozena pomocí Lagrangeových multiplikátorů. Ukazuje se, že při řešení duální úlohy se Lagrangeovy multiplikátory příslušné k bodům, jež nejsou support vektory, vynulují. Této vlastnosti se jistě může využít pro optimalizaci řešení duální úlohy. Zavedení kernel funkcí do duální optimalizační úlohy umožňuje body jednoduše separovat nelineární funkcí. Optimalizace v SVM je možna ve dvou směrech. Tím prvním je hledání takové kernel funkce, která by měla co nejméně parametrů. Nemusela by se zkoušet úspěšnost klasifikace pro každou volbu parametru, ale jen pro úzkou množinu hodnot. Druhým směrem je hledání algoritmu pro řešení duální optimalizační úlohy. Tato úloha má tak specifický tvar, že již dnes existují algoritmy, které jsou lepší než standardní iterační metody. Nutno podotknout, že většina takových algoritmů používá různých heuristických metod a uživatel musí mít určitou znalost vstupních dat. Součástí této práce je také aplikace v jazyce Matlab, která umožňuje graficky znázornit klasifikační funkci v rovině. Implementována jsou také rozšíření, jako např. různé kernel funkce a úloha s volným okrajem.

38 33 8 Reference [1] CRISTIANINI, Nello; SHAWE-TAYLOR, John. An Introduction to Support Vector Machines., Cambridge (USA) : Cambridge University Press, xiii, 189 s. ISBN [2] PLATT, john C. Fast training of support vector machines using sequential minimal optimization, Cambridge (USA) : Cambridge University Press, xx, 185 s. ISBN [3] CORTES, Corinna; VAPNIK, Vladimir. Support-vector networks. Machine Learning , č. 20, s ISSN [4] BOSER, Bernhard E.; GUYON, Isabelle M.; VAPNIK, Vladimir N. A training algorithm for optimal margin classifiers. A training algorithm for optimal margin classifiers. 1992, č. 1, s ISBN X. [5] SHEWCHUK, Jonathan Richard. An Introduction to the Conjugate Gradient Method Without the Agonizing Pain [online]. Pittsburg : [s.n.], [cit ]. Dostupné z WWW: quake-papers/painless-conjugategradient.pdf. [6] DOSTÁL, Zdeněk. Optimal Quadratic Programing Algorithms. New York : Springer, Bound Constrained Minimalization, s ISBN [7] Support vector machine. In Wikipedia : the free encyclopedia [online]. St. Petersburg (Florida) : Wikipedia Foundation, 27 July 2002, last modified on 29 April 2011 [cit ]. Dostupné z WWW: vectormachine. [8] KECMAN, V. Real World Applications of Computational Intelligence. Springer Berlin / Heidelberg : Springer, Basics of Machine Learning by Support Vector Machines, s [9] BEYER, Kevin; GOLDSTEIN, Jonathan; RAMAKRISHNAN, Raghu; SHAFT, Uri. Database Theory ICDT 99 Springer Berlin / Heidelberg : Springer, When Is Nearest Neighbor Meaningful?, s

39 34 A Numerické experimenty (a) C = +, úspěšnost je 34,0% (b) C = 2 4, úspěšnost je 66,0% (c) C = 2 2, úspěšnost je 80,9% (d) C = 2 0, úspěšnost je 85,1% (e) C = 2 2, úspěšnost je 87,2% (f) C = 2 4, úspěšnost je 87,2% (g) C = 2 6, úspěšnost je 89,4% (h) C = 2 8, úspěšnost je 89,4% (i) C = 2 14, úspěšnost je 89,4% Obrázek 8: Ukázky Lineárního kernelu s volným okrajem a různým parametrem C

40 35 (a) C = +, úspěšnost je 31,0% (b) C = 2 4, úspěšnost je 69,0% (c) C = 2 2, úspěšnost je 69,0% (d) C = 2 0, úspěšnost je 69,0% (e) C = 2 2, úspěšnost je 95,2% (f) C = 2 4, úspěšnost je 95,2% (g) C = 2 6, úspěšnost je 95,2% (h) C = 2 8, úspěšnost je 95,2% (i) C = 2 14, úspěšnost je 95,2% Obrázek 9: Ukázky Polynomiálního kernelu druhého stupně s volným okrajem a různým parametrem C

41 36 (a) C = +, úspěšnost je 55,6% (b) C = 2 4, úspěšnost je 82,7% (c) C = 2 2, úspěšnost je 84,0% (d) C = 2 0, úspěšnost je 84,0% (e) C = 2 2, úspěšnost je 86,4% (f) C = 2 4, úspěšnost je 85,2% (g) C = 2 6, úspěšnost je 85,2% (h) C = 2 8, úspěšnost je 85,2% (i) C = 2 14, úspěšnost je 86,4% Obrázek 10: Ukázky RBF kernelu s volným okrajem, kde γ = 2 2 a parametr C je různý

42 37 (a) Lineární kernel (b) Polynomiální řádu 2 (c) Polynomiální řádu 3 (d) Polynomiální řádu 4 (e) RBF, γ = 2 15 (f) RBF, γ = 2 12 (g) RBF, γ = 2 10 (h) RBF, γ = 2 8 (i) RBF, γ = 2 7 (j) RBF, γ = 2 6 (k) RBF, γ = 2 5 (l) RBF, γ = 2 4 (m) RBF, γ = 2 3 (n) RBF, γ = 2 2 (o) RBF, γ = 2 1 Obrázek 11: Ukázky různých kernel funkcí bez volného okraje