množina, na které je zavedena určitá struktura. Zejména, součet každých dvou prvků X = [x 1,..., x n ] R n,

Transkript

1 Náplní předmětu bude klkulus R n R (přípdně R m ). Proč se zbývt funkcemi více proměnných? V prxi je čsto třeb uvžovt veličiny, které závisejí n více než jedné proměnné, npř. objem rotčního kužele závisí n poloměru podstvy r výšce h, teplot v kovovém prutu může záviset n místě x čse t, hustot těles se může měnit v závislosti n bodu X o souřdnicích [x, y, z], vektor síly f = (f 1, f 2 ) v rovině může záviset n souřdnicích bodu v rovině (tj. máme f = (f 1 (x, y), f 2 (x, y))) pod. Výše uvedené nznčuje, že nám půjde o geometricko fyzikální popis situce. Připomeňme, že v SA1 jsme množinu R chápli nejenom jko množinu nějkých prvků (reálných čísel), le byl zde jsně dán lgebrická struktur (sčítání, násobení, R je vybven relcí uspořádání, klíčový byl tké xiom o suprému). Podobně, R n := R R R nebude chápán pouze jko množin uspořádných n-tic, le jko }{{} n krát množin, n které je zveden určitá struktur. Zejmén, součet kždých dvou prvků X = [,..., x n ] R n, Y = [y 1,..., y 2 ] R n je definován jko X + Y = [ + y 1,..., x n + y n ] R n násobek libovolným sklárem c R je pro kždé X R n definován jko cx = [c,..., cx n ] R n. Lze ukázt, že R n s tkto definovnými opercemi tvoří vektorový prostor dimenze n (viz lineární lgebr). Prvky R n budeme nzývt buď body, nebo vektory (podle situce). Interpretujeme-li prvky X Y jko body, pk rozdíl Y X bude chápán jko vektor (to je v souldu s tím, co známe z nlytické geometrie). Dlší podsttnou vlstností je, že v R n umíme měřit vzdálenosti bodů, viz úvodní kpitol. 1 Metrické prostory Definice 1.1 (metriky metrického prostoru). Buď M libovolná množin ρ : M M 0, ) zobrzení, které pro všechn x, y, z M splňuje (m1) ρ(x, y) = 0 x = y (xiom totožnosti), (m2) ρ(x, y) = ρ(y, x) (xiom symetrie), (m3) ρ(x, y) ρ(x, z) + ρ(z, y) (trojúhelníková nerovnost) Zobrzení ρ nzýváme metrik n M, prvky množiny M nzýváme body metrického prostoru (M, ρ), číslo ρ(x, y) nzýváme vzdálenost bodů x, y. { 1 pro x y Příkld Je-li M libovolná množin ρ(x, y) =, pk (M, ρ) je metrický prostor 0 pro x = y (nzývá se diskrétní). 2. Je-li M = R, pk ρ(x, y) = x y je metrik. 3. Je-li M = R n, x = (,,..., x n ), y = (y 1, y 2,..., y n ) R n, pk ρ 1 (x, y) = y 1 + y x n y n, ρ 2 (x, y) = ( y 1 ) 2 + ( y 2 ) (x n y n ) 2, ρ (x, y) = mx{ y 1, y 2,..., x n y n } jsou metriky. Metrik ρ 1 se nzývá součtová (mnhttnská, txíkářská), metrik ρ 2 se nzývá eukleidovská 1, metrik ρ se nzývá mximální (šchovnicová, Čebyševov 2 ). Axiomy (m1), (m2) zřejmě pltí. Ověřme (m3). ρ 1 : ρ 1 (x, z) + ρ 1 (z, y) = x i z i + x i z i + z i y i = ρ 1 (x, y). ρ 2 : Vyjdeme z nerovnosti z i y i = ( x i z i + z i y i ) u i v i n u 2 i n vi 2 (Cuchyov Buňkovského 3 Schwrzov 4 ). 1 Eukleidés 3. stol. př.n.l., Řek žijící v Alexndrii v Egyptě 2 Pfnutij Lvovič Čebyšev , Rus 1

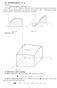
2 Položme u i = p i + q i, v i = q i. Potom u i = p i, v i = p i + q i, potom máme (p i + q i )q i n (p i + q i ) 2 n qi 2. Pokud nopk p i (p i + q i ) n p 2 i n (p i + q i ) 2. Sečtením pk (p i + q i ) 2 n (p i + q i ) 2 n p 2 i + n q 2 i, tj. n (p i + q i ) 2 n p 2 i + n qi 2 (Minkowského nerovnost 5 ). Doszením p i = x i z i, q i = z i y i máme n (x i y i ) 2 n (x i z i ) 2 + n (z i y i ) 2, tj. ρ 2 (x, y) ρ 2 (x, z) + ρ 2 (z, y). ρ : Oznčme j, resp. k, resp. l, ten index, pro který nstne mximum z hodnot x i z i, resp. z i y i, resp. x i y i, tj. ρ (x, z) = mx{ x i z i : i = 1, 2,..., n} = x j z j, ρ (z, y) = mx{ z i y i : i = 1, 2,..., n} = z k y k, ρ (x, y) = mx{ x i y i : i = 1, 2,..., n} = x l z l. Potom ρ (x, z) + ρ (z, y) = x j z j + z k y k x l z l + z l y l x l z l + z l y l = x l y l = ρ (x, y), tedy ρ (x, z) + ρ (z, y) ρ (x, y). 4. Je-li M = C(, b ) (množin všech funkcí spojitých n, b ), pk ρ C (f, g) = mx{ f(x) g(x) : x, b } (metrik stejnoměrné konvergence), ρ I (f, g) = b f(x) g(x) dx (integrální metrik) jsou metriky. Ověření xiomů (m1) (m2) je opět triviální. Axiom (m3) lze v přípdě ρ C podobně jko v přípdě ρ n R n. V přípdě ρ I máme lze ověřit ρ I (f, g) = f(x) g(x) dx = f(x) h(x) + h(x) g(x) dx ˆ ( ) b f(x) h(x) + h(x) g(x) dx = f(x) h(x) dx + = ρ I (f, h) + ρ I (h, f), h(x) g(x) dx kde jsme využili trojúhelníkovou nerovnost pro bsolutní hodnotu, monotonii vzhledem k integrovným funkcím (viz vět v SA1) ditivitu integrálu (integrál součtu je součet integrálů, viz vět z SA1). 5. Je-li M = l (množin všech ohrničených posloupností), pk ρ ({ n }, {b n }) = sup{ n b n : n N} je metrik. Splnění xiomů (m1), (m2) je opět zřejmé. Axiom (m3) by se dokázl nlogicky jko u ρ n R n. Definice 1.3 (otevřené uzvřené koule, okolí). Nechť (M, ρ) je metrický prostor, M, r R +. Pk množin B r () := {x M : ρ(, x) < r} se nzývá otevřená koule se středem poloměrem r ( bll ) množin B r [] := {x M : ρ(, x) r} se nzývá uzvřená koule se středem poloměrem r. Speciálně: O ε () := B ε () se nzývá (epsilonové) okolí bodu O ε() := O ε () \ {} se nzývá ryzí (epsilonové) okolí bodu. Poznámk. Pltí: ε δ O ε O δ. Není-li podsttná velikost poloměru ε, budeme psát stručně O(). Příkld 1.4. Nčrtněte O ε () v R 2 s metrikmi ρ 1, ρ 2 ρ. Viz obrázek 1 (voleno = (0, 0) ε = 1). 1 Viktor Jkovlevič Buňkovskij , Rus 2 Krl Hermnn Amndus Schwrz , Němec 3 Hermnn Minkowski , německý Žid 2

3 0 0 0 Obrázek 1: Jednotková koule (se středem v počátku) v R 2 s metrikou ρ 1, resp. ρ 2, resp. ρ Poznámk. Metriku n R n lze (obecněji) zvést pro libovolné p 1, ) vzthem ( n ) 1/p ρ p (x, y) = x i y i p. Jednotková kružnice se středem v počátku pro přípd n = 2 (tj. množin všech bodů mjící jednotkovou vzdálenost od počátku v metrice ρ p ) je nčrtnut pro několik hodnot prmetru p n obrázku 2. Z tohoto obrázku je pk zřejmé, proč se mximální metrik znčí indexem. 0 p = 10 p = 2.5 p = 4 p = 1.5 Obrázek 2: Jednotkové kružnice v R 2 se středem v počátku pro p = 1.5, p = 2.5, p = 4 p = 10 Pozor, pro p < 1 výše uvedená funkce ρ p nepředstvuje metriku! Definice 1.5 (vzdálenosti dvou množin průměru množiny). Nechť (M, ρ) je metrický prostor. Pro neprázdné A, B M definujeme: ρ(a, B) := inf{ρ(, b) : A, b B} vzdálenost množin A, B, d(a) := sup{ρ(x, y) : x, y A} průměr množiny A. Jestliže množin {ρ(x, y) : x, y A} není shor ohrničená, kldeme d(a) =. Vzdálenost bodu x od množiny A definujeme jko ρ(x, A) := ρ({x}, A). Poznámk. Je-li A B, pk zřejmě ρ(a, B) = 0 (vzdálenost všk může být nulová i pro A, B disjunktní). Je-li lespoň jedn z množin A, B prázdná, pk kldeme jejich vzdálenost rovnu. Nopk průměr prázdné množiny kldeme nulový, tj. d( ) = 0. Definice 1.6. Buď (M, ρ) metrický prostor, A M. Řekneme, že A je ohrničená, jestliže d(a) <. Poznámk. Množin A je zřejmě ohrničená, jestliže existuje bod číslo r > 0 tk, že A B r (). 3

4 2 Podmnožiny metrického prostoru Definice 2.1 (význčných bodů v metrickém prostoru). Nechť (M, ρ) je metrický prostor A M. Bod M se nzývá vnitřní bod množiny A, jestliže existuje ε > 0 tkové, že O ε () A, hrniční bod množiny A, jestliže pro kždé ε > 0 pltí O ε () A zároveň O ε () (M \ A), bod uzávěru množiny A, jestliže ρ(, A) = 0, hromdný bod množiny A, jestliže pro kždé ε > 0 pltí O ε() A, izolovný bod množiny A, jestliže existuje ε > 0 tkové, že O ε () A = {}. Definice 2.2 (vnitřku, hrnice, uzávěru derivce množiny). Nechť (M, ρ) je metrický prostor A M. 1. Množin všech vnitřních bodů množiny A se nzývá vnitřek množiny A znčí se A (někdy inta interior), 2. Množin všech hrničních bodů množiny A se nzývá hrnice množiny A znčí se A (někdy fra frontier), 3. Množin všech bodů uzávěru množiny A se nzývá uzávěr množiny A znčí se A (někdy cla), 4. Množin všech hromdných bodů množiny A se nzývá derivce množiny A znčí se A. Příkld 2.3. Uvžujte R s metrikou ρ(x, y) = x y množiny ) A = (0, 1), b) A = 0, 1) Q, c) A = 0, 1 {2}. Npište A, A, A A. d ) A = A = (0, 1), A = {0, 1}, A = 0, 1, A = 0, 1. d b) A =, A = 0, 1, A = 0, 1, A = 0, 1. d c) A = A = (0, 1), A = {0, 1, 2}, A = 0, 1 {2}, A = 0, 1. Definice 2.4 (otevřené uzvřené množiny v metrickém prostoru). Buď (M, ρ) metrický prostor, A M. Množin A se nzývá otevřená, jestliže A = A, množin A se nzývá uzvřená, jestliže A = A. Vět 2.5. Buď (M, ρ) metrický prostor, A M. Množin A je otevřená M \ A je uzvřená. Množin A je uzvřená M \ A je otevřená. Důkz. Ukžme nejprve, že pro kždou A M pltí A = M \ M \ A. Skutečně, x M \ M \ A x / M \ A ε := ρ(x, M \ A) > 0 (y M \ A)(ρ(x, y) ε) O ε (x) (M \ A) = O ε (x) A x A. Nechť A je otevřená, tj. A = A. Podle výše dokázného tedy pltí A = M \ M \ A. Odtud plyne, že M \ A = M \ (M \ M \ A). Protože pro kždou podmnožinu B M pltí M \ (M \ B) = B, pltí z předchozí rovnosti, že M \ A = M \ A, tj. M \ A je uzvřená. Nechť nopk M \ A je uzvřená, tj. M \ A = M \ A. Pk podle první části máme A = M \ M \ A = M \ (M \ A) = A. Pltnost druhého tvrzení by se ukázl nlogicky. Poznámk. ) Lze ukázt, že v kždém metrickém prostoru (M, ρ) pro libovolnou A M pltí (A ) = A, A = A, tedy A je vždy otevřená A je vždy uzvřená. b) Obecně B r () B r [], npř. je-li (M, ρ) diskrétní, M, r = 1, potom B 1 () = {} tedy B 1 () = {}, všk B 1 [] = M. c) Pltí =, = tedy je v jkémkoliv metrickém prostoru otevřená i uzvřená zároveň. Podle předchozí věty je pk celá M tké otevřená i uzvřená zároveň. 3 Konvergence v metrickém prostoru Definice 3.1 (konvergentní posloupnosti v metrickém prostoru). Buď (M, ρ) metrický prostor {x n } n=1 posloupnost bodů z M (tj. zobrzení N M). Řekneme, že posloupnost {x n } n=1 konverguje k bodu x M (je konvergentní v M), jestliže lim n ρ(x n, x) = 0 (zpisujeme lim n x n = x, stručně lim x n = x nebo x n x). Příkld (M, ρ) diskrétní (viz příkld 1.2.1): x n x ( n 0 N)(n n 0 x n = x). 2. (R 2, ρ 1 ) (viz příkld 1.2.3): (x n, y n ) (x, y) x n x, y n y v R s metrikou ρ(x, y) = x y. Důkz. 0 = lim( x n x + y n y ) = lim x n x +lim y n y. Protože, le lim x n x 0, lim y n y 0, musí být lim x n x = 0, lim y n y = 0. Anlogické tvrzení pltí pro všechny metrické prostory z příkldu (C(, b ), ρ C ) (viz příkld 1.2.4): f n f ( ε > 0)( n 0 N)( n n 0 )( x, b ) : f n (x) f(x) < ε. Má-li posloupnost funkcí definovných n intervlu, b vlstnost uvedenou n prvé strně ekvivlence, řekneme, že posloupnost funkcí {f n } n=1 konverguje stejnoměrně n, b k funkci f. Důkz. Konvergence f n f v (C(, b ), ρ C ) znmená: 4

5 ( ε > 0)( n 0 N)( n n 0 ) : ρ C (f n, f) < ε ( ε > 0)( n 0 N)( n n 0 ) : mx{ f n (x) f(x) : x, b } < ε ( ε > 0)( n 0 N)( n n 0 )( x, b ) : f n (x) f(x) < ε. Definice 3.3 (ohrničenosti posloupnosti). Buď (M, ρ) metrický prostor {x n } n=1 posloupnost bodů z M. Řekneme, že posloupnost {x n } n=1 je ohrničená, jestliže množin {x n : n N} je ohrničená ve smyslu definice 1.6. Vět 3.4. Buď (M, ρ) metrický prostor. Pk pltí 1. Kždá posloupnost {x n } M má nejvýše jednu limitu v M. 2. Posloupnost konvergentní v (M, ρ) je ohrničená v (M, ρ). 3. lim n x n = x M pro kždou posloupnost {x nk } vybrnou z {x n } pltí lim k x nk = x. Důkz. Plyne z příslušných tvrzení v kpitole o posloupnostech, viz SA1. Definice 3.5 (cuchyovské posloupnosti). Buď (M, ρ) metrický prostor {x n } n=1 posloupnost bodů z M. Řekneme, že posloupnost {x n } n=1 je cuchyovská, jestliže ke kždému ε > 0 existuje n 0 N tkové, že pro všechn m, n n 0 je ρ(x m, x n ) < ε. Vět 3.6. Nechť (M, ρ) je metrický prostor {x n } n=1 posloupnost bodů z M. Je-li {x n } n=1 konvergentní v (M, ρ), pk je cuchyovská. ZK Důkz. Nechť x n x ε > 0 je libovolné. K ε 2 existuje n 0 N tkové, že pro všechn n n 0 je ρ(x n, x) < ε 2. Pro libovolné m n 0 libovolné n n 0 tedy s využitím trojúhelníkové nerovnosti pltí ρ(x m, x n ) ρ(x m, x)+ ρ(x n, x) < ε 2 + ε 2 = ε. Poznámk. Obrácené tvrzení obecně nepltí. Npř. pro M = (0, 1), ρ(x, y) = x y, {x n } n=1 = {1/n} n=1 je cuchyovská, le není konvergentní (protože 0 / M). Vět 3.7. Nechť (M, ρ) je metrický prostor A M. Množin A je uzvřená v (M, ρ) pro kždou konvergentní posloupnost {x n } A tkovou, že x n x, pltí x A. Důkz. Nechť A je uzvřená, tj. A = A nechť {x n } je libovolná posloupnost konvergující k x M. Kdyby x / A, pk by ε := ρ(x, A) > 0 tedy pro kždé x n by pltilo ρ(x n, x) ε, což by bylo ve sporu s x n x. Nechť pro kždou posloupnost {x n } A, pro kterou x n x, pltí x A. Buď y A libovolný bod, tj. pltí ρ(y, A) = 0. Ke kždému 1 n > 0 existuje x n A tkové, že ρ(x n, y) < 1 n. To znmená, že pro tkto vytvořenou posloupnost {x n } pltí lim ρ(x n, y) = 0, tj. x n y. Z podmínky plyne, že y A. Tedy A A. Protože všk tké A A, máme A = A, tj. A je uzvřená. Definice 3.8 (ekvivlentních metrik). Nechť M je množin ρ, σ metriky n M. Řekneme, že ρ σ jsou ekvivlentní metriky n M, jestliže pro kždou posloupnost {x n } n=1 M pltí: x n x v (M, ρ) x n x v (M, σ). Příkld 3.9. ) Metriky ρ 1, ρ 2 ρ n R n jsou ekvivlentní, protože pro kždou z těchto metrik pltí, že x k x x k i x i v (R, x y ). To znmená, že x k x v (R n, ρ j ), kde j {1, 2, } ( ε > 0)( k 0 N)( k k 0 )( i {1, 2,..., n}) : x k i x i < ε. b) Metriky ρ I ρ C n C(, b ) nejsou ekvivlentní. Poznámk. Jsou-li ρ, σ ekvivlentní metriky n M, pk množin A M je uzvřená v (M, ρ) je uzvřená v (M, σ) je otevřená v (M, ρ) je otevřená v (M, σ). Vět Buďte ρ, σ metriky n M. Jestliže existují kldné konstnty, b tkové, že pro všechny dvojice bodů (x, y) M 2 je σ(x, y) ρ(x, y) bσ(x, y), pk jsou metriky ekvivlentní. ZK Důkz. Nechť je splněn podmínk věty, x M, nechť {x n } M je tková posloupnost, že lim σ(x n, x) = 0. Pk σ(x n, x) ρ(x n, x) bσ(x n, x) z věty o 3 posloupnostech (viz SA1) plyne lim ρ(x n, x) = 0. Pokud bychom vyšli z posloupnosti, pro kterou lim ρ(x n, x) = 0, pk se důkz provede stejně s využitím nerovnosti 1 b ρ(x, y) σ(x, y) 1 ρ(x, y), která je ekvivlentní s nerovností v podmínce věty. Definice 3.11 (indukovné metriky metrického podprostoru). Nechť (M, ρ) je metrický prostor A M. Metriku ρ A, definovnou jko ρ A (x, y) = ρ(x, y) pro x, y A, nzýváme metrikou indukovnou n množině A metrikou ρ. Metrický prostor (A, ρ A ) nzýváme podprostorem metrického prostoru (M, ρ). Píšeme (A, ρ A ) (M, ρ). Příkld Uvžujeme-li R jko podmnožinu R 2 (tj. reálná čísl ztotožníme s dvojicemi (, 0)), pk kždá z metrik ρ i, i = 1, 2,, n R 2 indukuje metriku ρ(x, y) = x y n R. 5

6 4 Úplné kompktní metrické prostory Definice 4.1 (úplného metrického prostoru). Metrický prostor (M, ρ) se nzývá úplný, jestliže v něm kždá cuchyovská posloupnost má limitu. Příkld Prostor R s metrikou ρ(x, y) = x y je úplný. Důkz. Tvrzení plyne ihned z Cuchyov Bolznov kritéri konvergence, viz vět 7.27 v SA1. 2. Prostory (R n, ρ 1 ), (R n, ρ 2 ), (R n, ρ ) jsou úplné. Důkz. V přípdě (R n, ρ 1 ) cuchyovskost znmená, že pro k, m k 0 je n xk i xm i < ε, z čehož plyne, že x k i xm i < ε i {1, 2,..., n} tedy kždá {xk i }, i = 1, 2,..., n, je cuchyovská v (R, ρ 1). Podle Cuchyho Bolznov kritéri konvergence je všk kždá {x k i } tké konvergentní, tj. lim xk i = x i, i = 1, 2,..., n. Odtud plyne, že lim k x k = x = (,,..., x n ) R n. Protože metriky ρ 1, ρ 2 ρ jsou ekvivlentní, jsou úplné tké prostory (R n, ρ 2 ) (R n, ρ ). 3. Q s metrikou ρ(x, y) = x y není úplný. Npř. {(1 + 1 n )} je cuchyovská, le konverguje k e / Q. 4. Lze ukázt, že (C(, b ), ρ C ) je úplný, le (C(, b ), ρ I ) úplný není. Stčí vzít npř. posloupnost funkcí 1 pro x 1, 1/n), f n (x) = nx pro x 1/n, 1/n, 1 pro x (1/n, 1. Posloupnost {f n } je cuchyovská v (C(, b ), ρ I ), le limit není spojitá funkce tedy neptří do C(, b ). Vět 4.3. Je-li metrický prostor (M, ρ) úplný množin A M je uzvřená, pk metrický prostor (A, ρ A ) (ρ A je metrik indukovná metrikou ρ) je úplný. Důkz. Buď {x n } A libovolná cuchyovská posloupnost. Poněvdž (M, ρ) je úplný, existuje lim x n = x M. n Podle věty 3.7 je všk x A. Definice 4.4 (kompktního metrického prostoru kompktní množiny v metrickém prostoru). Řekneme, že metrický prostor (M, ρ) je kompktní, jestliže z kždé posloupnosti jeho bodů lze vybrt posloupnost konvergentní. Řekneme, že množin A M je kompktní, jestliže podprostor (A, ρ A ) je kompktní. Vět 4.5. Je-li A kompktní množin v metrickém prostoru (M, ρ), pk je A uzvřená ohrničená. Důkz. Uzvřenost sporem: Připusťme, že A není uzvřená, tj. A A, tedy že existuje x A \ A. Protože ρ(x, A) = 0, existuje posloupnost {x n } A tk, že ρ(x n, x) 0, neboli x n x. Pro kždou vybrnou posloupnost {x nk } z posloupnosti {x n } je podle věty lim k x nk = x / A, což je spor s kompktností A. Ohrničenost sporem: Připusťme, že A není ohrničená, tj. d(a) =. Sestrojme posloupnost {x n } tkto. Bod A vybereme libovolně nechť A je tkové, že ρ(, ) 1 (tkové jistě existuje, protože A je neohrničená). Bod x 3 A vybereme tk, by jeho vzdálenost od obou byl větší nebo rovn 1 (tento bod opět existuje z důvodu neohrničenosti). Pokrčujeme tk, by bod x n měl vzdálenost větší nebo rovnu jedn o všech předchozích bodů. Posloupnost {x n } i kždá posloupnost z ní vybrná není cuchuovská, neboť ρ(x n, x m ) > 1 pro m, n N, m n, tedy podle věty 3.6 nemůže být konvergentní. To je le spor s kompktností A. Vět 4.6. V prostorech (R n, ρ i ), kde i = 1, 2,, pltí i opčné tvrzení. Máme tedy: A R n je kompktní je v tomto prostoru uzvřená ohrničená. Důkz. Nutnost podmínky plyne z věty 4.5. Dokžme její dosttečnost. Uvžujme nejprve metriku ρ 1. Buď {x k } k=1 = {(xk 1, x k 2,..., x k n)} k=1 libovolná posloupnost bodů z A. Poněvdž A je ohrničená, je kždá z číselných posloupností {x k i } k=1, i = 1, 2,..., n tké ohrničená, tedy lze z kždé z nich vybrt konvergentní podposloupnost {x k l i i } l konvergující k x0 i R, i = 1, 2,..., n (viz vět 7.22 v SA1). To znmená, že kždá posloupnost {x k } k=1 A má podvýběr konvergující k bodu x0 = (x 0 1, x 0 2,..., x 0 n) R. Protože všk A je uzvřená, musí podle věty 3.7 být x 0 A. Jink řečeno, kždá posloupnost z A obshuje konvergentní podposloupnost s limitou v A, což je poždvek v definici kompktnosti. Z ekvivlence metrik ρ 1, ρ 2 ρ plyne tvrzení i pro prostory (R n, ρ 2 ) (R n, ρ ). Vět 4.7. Je-li metrický prostor (M, ρ) kompktní, pk je úplný. Důkz. Buď {x n } libovolná cuchyovská posloupnost v (M, ρ). Poněvdž (M, ρ) je kompktní, existuje posloupnost {x nk } vybrná z {x n } tková, že lim k x nk = x M. Ukžme, že x = lim n x n. Buď ε > 0 libovolné. Posloupnost {x nk } konverguje k x, což znmená, že k ε 2 existuje k 0 N tkové, že pro k k 0 je ρ(x nk, x) < ε 2. Protože {x n } je cuchyovská, k ε 2 > 0 existuje n 1 N tkové, že pro n, m n 1 pltí ρ(x n, x m ) < ε 2. Položme 6

7 n 0 = mx{n 1, n k0 } nechť n n 0 k k 0 jsou libovolná čísl. Pk tké n k n 0. S využitím trojúhelníkové nerovnosti dostneme ρ(x n, x) ρ(x n, x nk ) + ρ(x nk, x) < ε 2 + ε 2 = ε, což znmená, že lim n x n = x. 7