Úvod do numerické matematiky. Přednáška pro posluchače informatiky. Zimní resp. Letní semestr 2/2
|
|
|
- Bedřich Musil
- před 8 lety
- Počet zobrazení:
Transkript
1 Úvod do numerické mtemtiky Přednášk pro posluchče informtiky Zimní resp Letní semestr 2/2 Ivo Mrek, Petr Myer Bohuslv Sekerk 1 Úvodní poznámky Vymezení problemtiky vystihuje následující chrkteristik Numerická (výpočtová) mtemtik je relizce mtemtických modelů n výpočetní technice Numerická mtemtik je tedy součástí mtemtiky Je to všk součást mjící oproti teoretické mtemtice jeden význmný nedosttek Ten spočívá v tom, že čistě teoretické mtemtické modely podsttným způsobem operují s relnými čísly ztímco numerická mtemtik je závislá n výpočetní technice tudíž se musí bez tohoto prostředku obejít Typickým projevem této skutečnosti jsou zokrouhlovcí chyby, což vede ve svých důsledcích k numerické nestbilitě Zdroj numerické nestbility všk nemusí být výhrdně chyby ze zokrouhlení Numerická nestbilit může být zpřičiněn též vlstnostmi mtemtických modelů smých, n př relizce mtemtického šptně podmíněného modelu n počítči je přirozeným zdrojem numerické nestbility Zde použitý pojem šptně podmíněný model je chrkterizován nespojitou závislostí výstupní informce n informcích vstupních Příkld 11 Buď [ 11 A = kde jk jsou reálná čísl Symbolem h(a) oznčme hodnost mtice A Sndno si uvědomíme, že h není spojitou funkcí prvků jk Abychom si tuto okolnost uvědomili, stčí položiti A 0 = [ ], ], 11 0, 1
2 tkže n jedné strně h(a 0 ) = 1, všk, n strně druhé, pro libovolné reálné b 0 h(a(b)) = 2, kde A(b) = [ b ] Předchozí příkld ukzuje jednk nespojitost hodnosti mtice jkožto funkce jejích prvků jednk dlší pozoruhodnou vlstnost hodnosti T je obshem následující věty Vět 11 Hodnost mtice je zdol polospojitou funkcí jejích prvků Definice 11 Sklární reálná funkce f se nzývá zdol polospojitou v bodě s 0, jestliže množin {s : f(s) > f(s 0 )} je otevřená, t j existuje δ > 0 tkové, že pro s (s 0 δ, s 0 + δ) f(s) f(s 0 ) ɛ Dlším příkldem uvedeme numerickou nestbilitu popltnou chybám ze zokrouhlení Příkld 12 Určeme hodnoty integrálů (11) pro n = 1, 2, I n = 1 e 1 0 t n e t dt Užitím metody per prtes zjistíme, že (12) při čemž (13) Zřejmě pltí (14) jkož i (15) I n = 1 ni n 1 I 0 = e 1 e 0 I n I n 1 1 lim I n = 0 n 2
3 Výpočet n počítči se relizuje nikoliv v termínech zvedených veličin I n všk v termínech veličin počítných Ĩn Vzhledem k zokrouhlovcím chybám zjistíme, že existují indexy n 1 n 2 tk, že (16) Ĩ n1 < 0 (17) Ĩ n2 > 1 Vidíme tedy, že vzthy (14) nepltí pro veličiny Ĩn Důvodem pro pltnost vzthů (16) (17) je skutečnost vyjádřená rovnostmi z nichž plyne, že Ĩ n = I n + δ n, n = 1, 2, δ n = nδ n 1, odkud je ptrné, že chyb se n kždém kroku výpočtu násobí indexem kroku Toto zesílení chyby je velikosti fktoriálu, což znčí, že destrukce se explicitně projeví po p krocích, kde p znčí počet cifer používných v průběhu výpočtu 2 Diferenční rovnice Připomeňme si pojem obyčejné diferenciální rovnice Buď f = f(s, y, z) sklární reálná funkce, při čemž (21) s I = (, b), y S 1, z S 2, kde S 1 R, S 2 R, při stndrtním znčení množiny reálných čísel symbolem R Úlohu nlézti funkci x = x(s), s I tkovou,že jednk (22) x(s) S 1, x (s) S 2 jednk (23) f(s, x(s), x (s)) = 0, se nzývá obyčejnou diferenciální rovnicí 1 řádu Příkld 21 Položme f(s, y, z) = z αy Sndno se přesvědčíme, že x(s) = Cexp{αs} 3
4 je pro s [0, T ), kde T > 0, řešením diferenciální rovnice x = αx splňující počáteční podmínku x(0) = C Příkld 22 Nechť I = (, + ), S 0 = S 1 = [ 1, 1] f(s, y, z) = z 2 (1 y 2 ) Pk máme co do činění s diferenciální rovnicí jejíž řešení jsou dán formulí kde R je libovolné x 2 = 1 x 2, x(s) = sin(s ), Dále si připomeňme pojem diferenciální rovnice N-tého řádu Buď f = f(s, y 0, y 1,, y N ) sklární reálná funkce definovná pro s I R y 0,, y N ležící v podmnožinách reálných čísel S 0, S N Problém nlézt funkci x = x(s) definovnou pro s I, mjící N derivcí n I splňující relce (24) x (k) (s) S k k = 0, 1,, N (25) f(s, x(s), x (s),, x (N) (s)) = 0 pro všechn s I, se nzývá obyčejnou diferenciální rovnicí řádu N; symbolicky píšeme f(s, x(s), x (s),, x (N) ) = 0 Příkld 23 Nechť N = 2 I = S 0 = S 2 = R Nechť dále Potom kždá funkce x tvru f(s, y 0, y 1, y 2 ) = y 0 + y 2 x(s) = Acoss + Bsins, kde A B jsou konstnty, je řešením odpovídjící diferenciální rovnice x + x = 0 4
5 Nyní přistoupíme k úlohám podobným diferenciálním rovnicím Anlogie bude zřejmá z definice Budeme se zbývti diferenčními rovnicemi Uveďme npřed pojem diferenční rovnice 1 řádu Budiž dán soustv f = {f n (y, z)}, kde f n = f n (y, z), n = 1, 2,, jsou sklární reálné funkce definovné n množině I Z, při čemž Z znčí množinu celých čísel y, z S R Úloh nlézt posloupnost {x n } R, n I, splňující (26) (27) x n S, x n 1 S f n (x n, x n 1 ) = 0 se nzývá diferenční rovnice 1 řádu Kždá posloupnost {x n } splňující (26) (27) se nzývá řešením diferenční rovnice (27) Příkld 24 Buď I množin celých čísel Potom vede k diferenční rovnici Její řešení mjí tvr kde c R je libovolné Podobně f n (y, z) = y z 1 x n x n 1 = 1, x n = n + c, Příkld 25 Nechť I je množin nezáporných celých čísel tkže nše diferenční rovnice má tvr f n (y, z) = y z n, x n x n 1 = n Jejím řešením je posloupnost {x n }, kde x n = n(n 1) 2 Příkld 26 Buď I množin všech celých čísel f n (y, z) = y qz, Není obtížné ukázt, že řešení splňující x 0 = 1 odpovídjící rovnice má tvr x n = qx n 1 x n = q n 5
6 Nyní přistoupíme k vyšetřování diferenčních rovnic řádu N 1 Buď f = {f n (y 0, y 1,, y N )} posloupnost funkcí definovných n množině I Z, př čemž y j S j R, j = 0, 1,, N Úlohu nlézt posloupnost {x n }, n I splňující následují poždvky (28) x n S n, x n 1 S n 1, x n N S n N (29) f n (x n, x n 1,, X n N ) = 0 Posloupnost {x n } splňující (28) (29) se nzývá řešení diferenční rovnice (29) Příkld 27 Nechť I = Z f n (y 0, y 1, y 2 ) = y 0 2cosφy 1 + y 2, kde φ R Řešení tkto vzniklé diferenční rovnice x n 2cosφ x n 1 + x n 2 = 0 je dáno formulí x n = cosnφ Podobně jko v teorii diferenciálních rovnic se pro některé třídy úloh jednoznčné řešitelnosti dociluje vhodnou volbou počátečních podmínek Důležitým přípdem diferenčních rovnic jsou diferenční rovnice lineární V tom pǐpdě (210) f n (y 0, y 1,, y N ) = 0n y 0 + 1n y A Nn y N + b n, kde jn, b n R, j = 0, 1,, N, n = 0, 1, Příkld 28 Všechny diferenční rovnice uvedené v příkldech jsou lineární Podobně diferenční rovnice x n + 5nx n 1 + n 2 x n 2 = 2 je lineární, ztímco je nelineární x n 1 2x 2 n 1 = 0 6
7 Anlogicky jko v teorii diferenciálních rovnic, obecné řešení diferenčních rovnic umíme plně chrkterizovt pro přípd diferenčních rovnic lineárních Zbývejme se úlohou (nlytického) sestrojení řešení diferenčních rovnic 1 řádu Tedy, řešme rovnici (211) x n = n x n 1 + b n, n I Z +, n 0, kde Z + znčí množinu všech nezáporných celých čísel Vyšetřujme nejprve homogenní diferenční rovnici (212) x n = n x n 1 Sndno zsjistíme, že řešení splňující podmínku (213) je dáno výrzem (214) kde (215) x 0 = c x n = cπ n, n π 0 = 1, π n = k, n = 1, 2, k=1 K určení řešení nehomogenní rovnice (212) splňující x 0 = c, použijeme metody známé z teorie lineárních diferenciálních rovnic pod názvem metod vrice konstnty Položme (216) kde {c n } podléhá určení Z rovností vidíme, že x n = c n π n, x 0 = c 0 π 0 = c 0, c 0 = c Po doszení (216) do (211) zjistíme, že c n π n = n c n 1 π n 1 + b n = c n 1 π n + b n Z předpokldu n 0 plyne, že též π n 0 Předchozí vzthy implikují rovnost c n = c n 1 + b n π n 7
8 dále pk rovnosti c n = c 0 + n (c k c k 1 ) = c + k=1 n k=1 b k π k Výsledek shrneme ve tvru věty Vět 21 Nechť n 0, n = 1, 2, Řešení diferenční rovnice x n = n x n 1 + b n, splňující x 0 = c, je dáno výrzem ) n b k (217) x n = π n (c +, n = 01, π k k=1 při čemž n π 0 = 1, π n = k k=1 Příkld 29 Buď I množin nezáporných čísel, f n (y 0, y 1, y 2 ) = y 0 y 1 y 2 Odpovídjící diferenční rovnice (218) x n x n 1 x n 2 = 0 definuje Fiboncciov čísl (x 0 = 0, x 1 = 1) Podobně jko v problemtice diferenciálních rovnic je jedním z možných způsobů řešení lineárních rovnic řádu N jejich převod n soustvy lineárních rovnic 1 řádu Ukážeme si zmíněný postup n příkldě rovnice (218) Nechť X n = ( xn x n 1 ) ( 1, X 0 = 0 ), n = 1, 2, A = ( ) 8
9 Sndno nhlédneme, že rovnici (218) lze vyjádřiti ve tvru ( ) 1 (219) X n = AX n 1, X 0 = 0 Podobně jko v přípdě lineární diferenční rovnice 1 řádu, řešení rovnice (219) má tvr X n = A n X 0 Odtud plyne pltnost zjímvého vzthu x n lim = n x n 1 2 Vidíme tedy, že limitní poměr veličin x n x n 1 je dán číslem chrkterizujícím t zv zltý řez Protože rovnice (218) má vskutku zjímvou biologickou interpretci, můžeme ve výše uvedeném výsledku sptřovti úkz estetiky projevující se v některých oblstech život n nší plnetě Model popisující jistý způsob rozmnožování králíků pochází ze 13 století; jeho utorem je právě Fiboncci (r 1228) Zcel jinou plikcí lineárních diferenčních rovnic je následující úloh Buď n p n (x) = b k x n k, b 0 0, n = 0, 1,, N k=0 položme si úlohu stnovit hodnotu p n (z), kde z je dný bod n reálné ose Nším cílem je pokud možno minimlitovt při tom počet ritmetických opercí ve snze snížit riziko numerické nestbility Algoritmus 21 Počítejme veličiny x 0, x 1,, x N rekurentně pomocí relcí (220) x 0 = b 0, x n = zx n 1 + b n, n = 1,, N Posloupnost {x n } dná v (220) je řešení diferenční rovnice (211) splňující podmínku x 0 = b 0, kde n = z pro n = 1, 2,, V tomto přípdě π n = z n 9
10 tudíž, n zákldě věty 21,, speciálně pro n = N, Pltí tedy n x n = b k z k k=0 N x N = b k z k = p N (z) k=0 Vět 22 Veličiny x n tvořené pomocí lgoritmu 21 jsou hodnoty polynomů p n definovných pomocí v bodě x = z p n (x) = n b k x k, n = 0, 1,, N k=0 Algoritmus 21 se nzývá Hornerovým schémtem Nyní si ukážeme jk lze uvedený lgoritmus zobecnit pro výpočet hodnot derivcí polynomu p n v bodě x = z Opět je nutné zdůrznit, že přímá plikce stndrdních prvidel derivování člen po členu není vhodná lgoritmy typu Hornerov jsou dleko stbilnější jednodušší z hledisk teorie složitosti Vyjdeme ze známých vzthů kde (221) N p(x) = p(z + h) = c k h N k, k=0 c N k = 1 k! p(k) (z), k = 0, 1,, N Algoritmus 22 Oznčme prvky tvořené pomocí lgoritmu 21 symboly {x n (0) } Pro k = 1, 2,, N tvořme posloupnosti {x n (k) } rekurzivně pomocí diferenčních schémt (222) x (k) 0 = x (k 1) 0, x (k) n = zx (k) n 1 + x(k 1) n, n = 0, 1,, N k Vět 23 Oznčuje-li p n polynom p n (x) = n b k x n k, n = 0, 1,, N, k=0 10
11 x (0) 0 x (0) 1 x (0) 2 x (0) 3 x (0) 4 x (1) 0 x (1) 1 x (1) 2 x (1) 3 x (2) 0 x (2) 1 x (2) 2 x (3) 0 x (3) 1 x (4) 0 Figure 1: Obrázek č 21 pk veličiny určovné lgoritmem 22 splňují (223) x (k) n = 1 k! p(k) n+k (z), n = 1,,, N, k = 0,, N n Tudíž koeficienty c N k poždovné ve formuli (221) jsou právě ty, jež se nlézjí v dolní digonále n obrázku 21 pro N = 4 v posloupnosti veličin tvořených lgoritmem 22 3 Iterční metody řešení nelineárních rovnic jejich soustv 31 Postupné proximce Zčněme příkldem úlohy njít kořen funkce g, t j nlézt tkový bod ˆx I = [, b], < b < +, tk, by g(ˆx) = 0 z předpokldu, že g je dná spojitá funkce zobrzující I = I 1 do I 2 R Speciálně, g může být polynom A již v tomto speciálním přípdě si můžeme uvědomit několik důležitých skutečností Tk především, obecně nemusí v I existovt kořen funkce g Ale i když tkový kořen existuje, nemusí existovt nlytické vyjádření tohoto kořene pomocí prmetrů chrkterizujících g (n př koeficienty polynomu); tkové formule jsou známy pro přípd polynomů stupňů nepřevyšujících 4 A jk víme, cen tkových formulí je sporná, protože tkové formule jsou mnohdy prkticky nepoužitelné (t zv csus irreducibilis) Důsledky těchto skutečností jsou zřejmé: Nději, že se podří nlézt kořen g mjí spíše numerické než nlytické metody Mezi numerickými metodmi se z důvodů sndné lgoritmické relizovtelnosti prosdily metody iterční to nvzdory jejich neuniversálnosti pohříchu poměrně pomlé konvergenci Právě uvedený nedosttek dl podnět k rozvoji metod urychlování konvergence obecných posloupností, jmenovitě pk tkových 11
12 generovných iterčními procesy Zákldním iterčním postupem jsou postupné proximce Jsou určeny k sestrojování proximcí řešení rovnic typu (31) s = f(s), kde f je dná funkce, tedy, g(s) = s f(s) Algoritmus 31 Zvolme x 0 pomocí relce (32) libovolně tvořme posloupnost {x n } rekurzívně x n = f(x n 1 ) Všímněme si, že k tomu, bychom mohli prováděti jednotlivé kroky dle (32) musí f kromě spojitosti míti ještě dlší vhodné vlstnosti Budeme předpokládt, že obor hodnot funkce f ptří do I 1 ; k tomu stčí, by I 2 I 1 V tkovém přípdě spojitost f nejen zručuje neomezenou proveditelnost procesu (32) le též existenci hledného kořene v I 1 Abychom to ozřejmili, položme tkže g(s) = s f(s), s b, g() 0, g(b) 0 Ze spojitosti f plyne spojitost g odtud pk skutečnost, že g nbývá všech hodnot z intervlu [g(), g(b)] = I 3 I 1 Existuje tedy lespoň jeden bod ŝ tkový, g(ŝ) = 0 To znčí, že ŝ je námi hledný kořen ŝ = f(ŝ) Obecně, množin M všech smodružných bodů funkce f, t j M = {s I 1 : s = f(s)} má mohutnost moh M 1 Jednoznčnosti se dociluje pomocí dlších předpokldů I R do R že existuje kon- Definice 31 Předpokládejme, že f zobrzuje stnt L tková, že nerovnost (33) f(s) f(t) L s t pltí pro libovolná s, t I V tkovém přípdě se f nzývá lipschitzovskou konstnt L Lipschitzovou konstntou funkce f 12
13 Všímněme si, že funkce lipschitzovská n I je nutně spojitá n I Je - li f diferencovtelná n I pltí sup { f (s) : s I} L, kde L > 0 je konstnt, pk je f n I lipschitzovská L je Lipschitzovou konstntou funkce f Předpokládejme, že Lipschitzov konstnt L splňuje nerovnost (34) 0 < L < 1 Sndno nhlédneme, že pro s 1, s 2 M pltí tudíž s 1 s 2 = f(s 1 ) f(s 2 ) L s 1 s 2 s 1 = s 2 Můžeme přistoupit k formulci zákldního výsledku o konvergenci postupných proximcí Vět 31 Buď I = [, b] uzvřený konečný intervl nechť funkce f splňuje následující podmínky (i) (iii) (i) f(s) I pro s I (ii) f je lipschitzovská s Lipschitzovou konstntou L < 1 Potom pro libovolné nulové přiblížení x 0 I posloupnost {x n } definovná pomocí lgoritmu 31 konverguje k (jedinému) řešení rovnice s = f(s) Důkz Z předchozích úvh již víme, že existuje lespoň jedno řešení rovnice s = f(s) v I že, díky předpokldu o L, toto řešení je určeno jednoznčně Stčí tedy dokázti konvergenci posloupnosti {x n } Nechť ˆx = f(ˆx) Zřejmě x n ˆx = f(x n 1 ) f(ˆx), tkže tudíž (35) Protože obdržíme žádný výsledek x n ˆx L x n 1 ˆx x n ˆx L n x 0 ˆx lim n Ln = 0, lim x n ˆx = 0 n 13
14 Příkld 31 Pomocí postupných proximcí hledejme řešení rovnice s = e s Protože e s > 0 pro s (, + ) s > 1 e s pro s > 1, stčí omezit se n intervl [0, 1] Sndno si uvědomíme, že obor hodnot funkce f(s) = e s pro s [0, 1] leží v intervlu [e 1, 1] [0, 1] že pro s 1 s 2 [0, 1] pltí při čemž Protože f(s 1 ) f(s 2 ) = f ( s) s 1 s 2, f ( s) = e s, s [s 1, s 2 ] mx { f (s) : s [0, 1]} = 1, Lipschitzov konstnt pro f n [0, 1] je rovn 1, což k pltnosti věty 31 nestčí Avšk zvolíme-li z I intervl [ 1 2, log 2], sndno zjistíme, že pro 1 2 s log 2, 1 2 = e log2 e s e 1 2 < log 2 tudíž [ 1 2, log 2] = I [0, 1] Nvíc první derivce funkce f, kde f(s) = e s, je klesjící, tkže mx { f (s) : s I} = f ( 1 ) 0, < 1 2 Iterční proces (32) pro funkci f(s) = e s je tedy konvergentní v I Odhd (35) nemá bezprostřední prktický význm, závisí totiž n znlosti hledného řešení V prxi jsme totiž vždy nuceni omezit se n určitý konečný počet itercí x n v (32) Rádi bychom proto znli nějký relistický odhd chyby po n - tém kroku Všímněme si, že pro libovolné k 1 pltí vzthy x k+1 x k = f(x k ) f(x k 1 ) L x k x k 1 L k x 1 x 0 Buď n zfixováno pevně nechť m = n + p > n Potom p 1 x m x n = (x k+1 x k ) k=n 14
15 Po plikci trojúhelníkové nerovnosti obdržíme vzthy x m x n n+p 1 k=n L k x 1 x 0 = L n p 1 k=0 Lk x 1 x 0 L n k=0 Lk x 1 x 0 = L n (1 L) 1 x 1 x 0 Protože pro m plyne, že x m ˆx, tedy též p, pltí (36) x n ˆx Ln 1 L x 1 x 0 Důsledek 31 Při splnění předpokldů věty 31 je odhd chyby po n krocích postupných proximcí definovných pomocí lgoritmu 31 dán výrzem (36) Zkoumejme blíže chování posloupnosti {x n } z předpokldů věty 31 doplněných o předpokld následující Nechť f je spojitě diferencovtelná nechť v celém intervlu I je tto derivce nenulová To znmená, že f buď klesá nebo roste v I Je-li x 0 ˆx = f(ˆx), pk f(x n ) ˆx pro libovolné n = 1, 2, Abychom to nhlédli, stčí si uvědomit, že kdyby při čemž x n = x n 1, pk kde ξ leží mezi x n 1 x n, tj x n = f(x n 1 ) = f(x n ), 0 = f(x n 1 ) f(x n ) = f (ξ) (x n 1 x n ), (x n 1 ξ) (ξ x n ) < 0 Protože x n 1 x n 0, musí být f (ξ) = 0, le to je ve sporu s předpokldem Odtud vyplývá, že chyb d n = x n ˆx není pro žádné n 0 nulová Existuje limit když no, pk čemu je rovn? d n+1 lim n d n 15
16 Sndno zjistíme, že d n+1 = x n+1 ˆx = f(x n ) f(ˆx) = f(ˆx + d n ) f(ˆx) = f (ˆx + θ n d n ) d n, kde 0 < θ n < 1 Definujme ε n pomocí relce f (ˆx + θ n d n ) = f (ˆx) + ε n Potom (37) d n+1 = (f (ˆx) + ε n )d n tudíž, ježto ε n 0 pro n plyne n zákldě spojitosti f rovnost (38) d n+1 lim n d n = f (ˆx) Lze této skutečnosti využít pro prktické účely? Veličinu ˆx tudíž i f (ˆx) neznáme Ukážeme, že explicitní znlost uvedených veličin není nutná k tomu, bychom rovnosti (38) efektivně využili k sestrojení lgoritmu, který poskytne proximce konvergující k hlednému řešení ˆx rychleji než posloupnost {x n } Předpokládejme n okmžik, že ve formuli (37) ε n = 0 pro nějké pevné n 1 Nechť f (ˆx) = A, tkže tkže Sndno zjistíme, že x n+1 ˆx = A (x n ˆx), x n+2 ˆx = A (x n+1 ˆx) A = x n+2 x n+1 x n+1 x n, ˆx = 1 1 A (x n+1 Ax n ) = x n A (x n+1 x n ) = x n (x n+1 x n ) 2 x n+2 2x n+1 + x n Vidíme tedy, že z předpokldu, že ε n = 0, pro nějké n 1, lze přesné řešení ˆx obdržeti použitím tří po sobě jdoucích itercí To všk je dost kdemická situce Ačkoliv veličiny ε n 0, lze očekávt, že ve srovnání s modulem f (ˆx) jsou mlé 16
17 (39) Pro velká n tk posloupnost skýtá pro ˆx lepší proximci než x n Má tedy smysl vyšetřovt (x n+1 x n ) 2 y n = x n x n+2 2x n+1 + x n Algoritmus 32 Buď {x n} libovolná posloupnost nechť y n je tvořeno pomocí (39) Zveďme oznčení x n = x n+1 x n, n = 0, 1, N př k+1 x n = ( k x n ), k 1 2 x n = (x n+1 x n ) (310) Formuli (39) lze pk psát ve tvru = x n+2 2x n+1 + x n y n = x n ( x n) 2 2 x n Posloupnost {y n } tvořená pomocí lgoritmu 32 definuje t zv Aitkenův urychlovcí 2 - proces Jest n místě zdůrznit, že Aitkenův proces je definován pro posloupnosti ne nutně generovné pomocí lgoritmu 31 Pro tkto obecný proces pltí poměrně silné tvrzení Vět 32 Buď {x n} dná posloupnost tková, že Nechť (311) (312) kde A je konstnt tková, že ˆx = lim n x n d n = x n ˆx = 0 n = 0, 1, d n+1 = (A + ε n ) d n, A < 1 ε n 0 pro n 17
18 Potom posloupnost {y n } tvořená pomocí (39) v lgoritmu 32 je dobře definovná pro dosttečně velká n nvíc (313) y n ˆx lim n x n ˆx = 0, což znčí, že posloupnost {y n } konverguje k ˆx rychleji než posloupnost {x n } tkže kde Důkz Použitím formule (312) obdržíme d n+2 = (A + ε n+1 ) (A + ε n ) d n, 2 x n = x n+2 2x n+1 + x n = d n+2 2d n+1 + d n = [ (A 1) 2 + ε n] dn, ε n = A[ε n + ε n+1 ] 2ε n + ε n ε n+1 Z podmínky ε n 0 pro n plyne, že (314) ε n 0 pro n Odtud dostáváme, (A 1) 2 + ε n = 0 pro dosttečně velká n, řekněme pro n > n 0 Tudíž 2 x n = 0 pro n > n 0 Dále pk tudíž x n = d n = (A 1 + ε n ) d n y n ˆx = d n ( x n) 2 2 x n Z ε n 0 pro n (314) plyne, že = d n (A 1 + ε n) 2 d n (A 1) 2 + ε n y n ˆx d n což jsme měli dokázti = ε n 2(A 1) ε n ε 2 n (A 1) 2 + ε n 0, Důsledek 32 Předpokládejme, že f splňuje podmínky věty 31 nvíc, že f má spojitou 1 derivci n I f (s) 0 pro s I Pro x 0 = ˆx posloupnost {x n } vyhovuje předpokldům věty 32, tkže lgoritmus 32 poskytuje urychlení konvergence 18
19 Důkz Zřejmě stčí ověřit pltnost vzthu (312) To všk je vzth (37) odvozený z obecnějších předpokldů Zbývá tudíž ověřit poždvek A < 1 Pltnost tohoto vzthu všk plyne odtud, že proces postupných proximcí je konvergentní Tímto konsttováním můžeme důkz ukončit Znovu připomeňme širší plikbilitu urychlovcího Aitkenov 2 - procesu i mimo oblst metody postupných proximcí 32 Kvdrtická konvergence Newtonov metod V předchozím odstvci jsme předpokládli, že f (s) 0 pro s I obdrželi jsme tk chrkteristiku rychlosti konvergence dnou pomocí (312), t zv lineární konvergenci Dá se říci, že v tkovém přípdě počet pltných cifer je lineární funkcí indexu itercí Učiňme nyní předpokld (315) f (ˆx) = 0 Tento předpokld je poměrně velmi silný zbezpečuje splnění některých předpokldů věty 31 Vět 33 Buď I (, + ), (nikoliv nutně ohrničený intervl) nechť f je definovná n I přitom pltí (i) f f jsou spojité n I (ii) Rovnice s = f(s) má řešení ˆx I tkové, že pltí (315) Potom existuje δ > 0 tkové, že lgoritmus 31 poskytuje posloupnost {x n } konvergující k ˆx pro všechn x 0 ˆx δ Důkz Oznčme I δ = [ˆx δ, ˆx + δ] Pro dosttečně mlá δ 1 > 0, I δ1 I Buď 0 < L < 1 Potom existuje δ 0 > 0 L > 0 tkové, že f (s) L pro s I δ0 Nechť δ = min{δ 0, δ 1 } Podle věty o střední hodnotě, f(s) ˆx = f(s) f(ˆx) f (ξ) s ˆx L s ˆx < δ Tudíž obor hodnot funkce f je obsžen v I δ lgoritmus 31 vede ke konvergenci podle věty 31 Zesilme nše poždvky n hldkost funkce f předpokldem existence spojité druhé derivce f n I δ její nenulovosti Podobně jko v předchozích úvhách předpokld x 0 ˆx implikuje pltnost vzthů x n ˆx, n = 1, 2, Postupné proximce nemohou tedy poskytnout 19
20 přesné řešení v konečném počtu kroků Užitím Tylorov rozvoje se zbytkem, obdržíme vzthy kde 0 < θ n < 1 Z nšich předpokldů plyne, že d n+1 = x n+1 ˆx = f(x n ) f(ˆx) = f (ˆx)d n f (ˆx + θ n d n )d 2 n, (316) d n+1 = 1 2 f (ˆx + θ n d n )d 2 n Protože d n 0, n = 1, 2, d n 0 pro n, odvodíme, že (317) d n+1 lim n d 2 = 1 n 2 f (ˆx) To je pozoruhodný vzth, podle něhož chyb po (1+n)- tém kroku je úměrná čtverci chyby po n - tém kroku Tto skutečnost se oznčuje jko kvdrtická konvergenvce Počet pltných cifer se zdvojuje po kždém iterčním kroku Příkld 32 Buď > 0 nechť f(s) = (1/2)[s + (/s)] pro s > 0 Rovnice s = f(s) má řešení Zřejmě f ( ) = 0 f (s) > 0 pro s > 0 f ( ) = 1 ) Tudíž x n+1 = 1 ( x n + ) (318) 2 x n konverguje k kvdrticky pro x 0 dosttečně blízká k Později ukážeme, že tento proces konverguje pro libovolné výchozí přiblížení x 0 > 0 Nyní přistoupíme k snd nejpoužívnější metodě přibližného řešení nelineárních rovnic lze říci, že nejen rovnic le nelineárních úloh - k metodě Newtonově V předchozích úvhách jsme dospěli ke kvdrtické konvergenci z výrzně kdemického předpokldu nulovosti první derivce v přesném řešení Ani se nechce věřit, že tento kdemismus má tk nádherné upltnění, k jehož výkldu teď přistupujeme Buď F definovná dvkrát spojitě diferencovtelná n intervlu I = [, b] R nechť F (s) 0 pro s I Dále nechť rovnice (319) F (s) = 0 má řešení ˆx (, b) (nikoliv nutně jediné) Dá se ukázt, že toto řešení lze nlézt pomocí postupných proximcí s funkcí f(s) = s + MF (s), 20
21 kde M je konstnt splňující určité podmínky, n př M = (α + β)/2, kde I = [0, 1], F (0) < 0 < F (1) 0 < α F (s) β Víme též, že genericky obdržíme lineární konvergenci Jk to tedy zřídit, bychom sestrojili lgoritmus poskytující kvdrtickou konvergenci? Což připustit místo konstntního fktoru M vhodnou funkci, tedy snžit se sestrojit f ve tvru f(s) = s + h(s)f (s), kde hodnoty funkce h se sndno počítjí Snžme se tedy splnit tyto poždvky: To nás vede k relcím tudíž ježto F (ˆx) = 0, ˆx = f(ˆx) f (ˆx) = 0, f (s) = 1 + h (s)f (s) + h(s)f (s) h (ˆx)F (ˆx) + h(ˆx)f (ˆx) = 1 h(s) = 1 F (s) Dospěli jsme tedy k následujícímu lgoritmu Algoritmus 33 Volme x 0 určeme posloupnost {x n } pomocí vzthů (320) x n+1 = x n 1 F (x n ) F (x n), n = 0, 1, Algoritmus 33 nese název Newtonov metod, či metod Newtonov - Rphsonov Z předchozího výkldu již víme, že, ježto f(s) = (1/F (s))f (s), f (ˆx) = 0, tkže přípdná konvergence posloupnosti {x n } je kvdrtická Jednotlivé kroky Newtonovy metody mjí velice názornou interpretci V bodě x n proximuje grf funkce F pomocí tečny ke grfu F v tomto bodě Průsečík této tečny s osou x určuje dlší proximci x n+1 Umíme si sndno předstvit grfy funkce F, pro něž Newtonův proces diverguje (To je velice hezké cvičení) Podobně jko pro všechny iterční metody typu postupných proximcí, slbin Newtonovy metody spočívá mimo jiné též v silné závislosti n volbě počátečního přiblížení Ukážeme si jk lze zbezpečit globální konvergenci; poždujeme vyšší hldkost F - totiž znménkovou stálost druhé derivce F 21
22 Vět 34 Předpokládejme, že funkce F je definovná dvkrát spojitě diferencovtelná v I = [, b] nechť splňuje tyto poždvky (i) F ()F (b) < 0; (ii) F (s) 0 pro s I; (iii) Buď F (s) 0 s I nebo F (s) 0, s I; (iv) Nechť (α) c = jestliže Dále nechť (β) c = b, jestliže F () F (b), F (b) F () F (c) F (c) b Potom Newtonov metod konverguje pro libovolné výchozí přiblížení x 0 k jedinému řešení rovnice F (s) = 0 Poznámky Podmínk (i) zřejmě zručuje existenci kořene díky spojitosti F Z (ii) plyne jednoznčnost kořene v I Podmínk (iii) říká, že F je buď konkávní nebo konvexní v I Posléze (iv) zjišťuje, by tečn ke křivce y = F (x) v koncovém bodě, kde F (x) je menší, protínl osu x v intervlu I Důkz věty 34 Vět 34 zhrnuje tyto čtyři odlišné situce () F () < 0, F (b) > 0, F (s) 0 (c = b), (b) F () > 0, F (b) < 0, F (s) 0 (c = b), (c) F () < 0, F (b) > 0, F (s) 0 (c = ), (d) F () > 0, F (b) < 0, F (s) 0 (c = ) Přípdy (b) (d) se sndno redukují n () (c) volbou F n místě F (Tto úprv nemění dokonce ni prvky posloupnosti {x n }) Přípd (c) se převede n () volbou x x (V tomto přípdě obdržíme místo {x n } { x n } Stčí se tedy zbývti přípdem () Máme pk co do činění s grfem rostoucí konkávní funkce F tkové,že F () < 0 < F (b) Buď ˆx jediný kořen rovnice F (s) = 0 Npřed předpokládejme, že x 0 ˆx Potom, n zákldě předpokldu, že F (x 0 ) 0, Indukcí lze ukázti, že x 1 = x 0 F (x 0) F (x 0 ) x 0 (321) x 0 x 1 x n ˆx 22
23 Indukční krok je relizován tkto Z věty o střední hodnotě, F (x n ) = F (ˆx) F (x n ) = F (ξ)(ˆx x n ) přitom x n ξ n ˆx Z podmínky F (s) 0 plyne, že F je nerostoucí tudíž F (ξ n ) F (x n ), tkže tedy F (x n ) F (x n )(ˆx x n ) x n+1 = x n F (x n) F (x n ) x n + (ˆx x n ) = ˆx Aplikcí F k oběm strnám nerovnosti obdržíme (F je neklesjící), že F (x n+1 ) 0 tudíž x n+2 = x n+1 F (x n+1) F (x n+1 ) x n+1 Tedy pltí (321) N tomto místě plikujeme jednu z fundmentálních vět mtemtické nlýzy: Kždá ohrničená monotonní posloupnost reálných čísel je konvergentní Oznčme tedy x = lim n x n Z (321) plyne, že x ˆx N druhé strně z definice posloupnosti {x n } obdržíme při rovnost x = x F ( x) F ( x) tedy F ( x) = 0 Z jednoznčnosti pk x = ˆx Tím je dokázáno tvrzení věty 34 pro přípd x 0 ˆx Dále vyšetřujme pŕípd x 0 ˆx Opět použitím věty o střední hodnotě F (x 0 ) = F (x 0 ) F (ˆx) = F (ξ 0 )(x 0 ˆx), kde ˆx ξ 0 x 0 díky monotonii F, F (x 0 ) F (x 0 )(x 0 ˆx) Sndno zjistíme, že x 1 = x 0 F (x 0) F (x 0 ) x 0 (x 0 ˆx) = ˆx tudíž F (x 0 ) F (b) (b x 0 )F (b) N zákldě podmínky (iv) obdržíme, že pltí x 1 = x 0 F (x 0) F (x 0 ) x 0 F (x 0) F (b) 23
24 x 0 F (b) F (b) + b x 0 = x 0 (b ) + b x 0 = Tudíž x 1 ˆx Tím jsme se dostli do situce, již jsme vyšetřovli v předchozí části důkzu s tím rozdílem, že n místě x 0 vystupuje x 1 Podle již dokázného, {x n } konverguje k ˆx Tím je důkz věty 34 proveden Vrťme se ještě k příkldu 32 O procesu v něm vyšetřovném již víme, že je konvergentní pro počáteční přiblížení dosttečně blízká k přesnému řešení, t j k c, kde c > 0 je dné kldné číslo, jehož odmocninu hledáme Položme tedy F (s) = s 2 c Sndno zjistíme, že f(s) = s F (s) F (s) F (s) = 2s > 0, F (s) = 2 > 0 tudíž nstává v tomto přípdě situce (c) popsná v důkzu věty 34 kždém intervlu (, b), kde 0 < < c < b, pltí, že F () F = c 2 b, () 2 pro kždé b splňující nerovnost b 1 ( + c/) 2 Z věty 34 plyne konvergence posloupnosti x n+1 = 1 ( x n + c ) c 2 x n pro libovolné x 0 > 0 Zvlášť výhodné je použití metody Newtonovy k hledání nulových bodů polynomů V tom přípdě využijeme té skutečnosti, že umíme efektivně stnoviti jk hodnoty p(z) tk p (z), kde p je dný mnohočlen z je dná veličin V 24
25 Buď tedy pk pomocí vzthů (322) (323) obdržíme rovnosti p(z) = N k z k, k=0 b 0 = 0, b n = zb n 1 + n, n = 1, 2,, N; c 0 = b 0, c n = zc n 1 + b n, n = 1, 2,, N 1, b N = p(z) c n 1 = p (z) Schémticky postupujeme jk znázorněno níže N 1 N b 0 b 1 b 2 b N 1 b N c 0 c 1 c 2 c N 1 při čemž znmená sčítání násobení fktorem z sčítání Buď nyní z kořen polynomu p Pk kde q je polynom stupně N 1, Tudíž Sndno zjistíme, že při čemž neboli, (324) q(x) = p(x) = (x z)q(x), N 1 k=0 b k x N k 1, b N = 0 0 = b 0 n 1 = b n z + b n, n = 1,, N 1 N k x N k = k=0 N 1 k=0 N 1 b k x N k z n = b n zb n 1, b n = n + zb n 1 k=0 Vidíme, že jsme obdrželi vzthy (220) lgoritmu 21 Pltí tedy b k x N k 1, 25
26 Vět 35 Je-li z kořen polynomu p, kde p(x) = N k x N k, 0 = 0, k=0 koeficienty b 0,, b N 1 se počítjí podle formule (324), pk q(x) = (x z) 1 p(x) = N 1 k=0 b k x N k, b 0 = 0 Mohlo by se zdát, že je výhodné hledt dlší kořeny polynomu p jkožto nulové body polynomu nižšího stupně q Ukzuje se všk, že tková procedur je numericky nestbilní je tudíž vhodnější počítt všechny kořeny polynomu pomocí původního polynomu p nikoliv modifikovného polynomu q Cvičení 31 Anlyzujte způsobem obdobným nlýze Newtonovy metody metodu následující, metodu regul flsi, definovnou předpisem x n+1 = x n (x n x n 1 )F (x n ) F (x n ) F (x n 1 ), kde F je funkce, jejíž kořeny hledáme, t j F (x) = 0 Cvičení 32 Jké vlstnosti má Newtonov metod v přípdě, kdy F (x ) = 0, kde F (x ) = 0 (Whittkerovu - Robin- Cvičení 33 Anlyzujte modifikovnou Newtonovu sonovu) metodu dnou předpisem x n+1 = x n 1 m F (x n), kde m je pevně zvolená konstnt, n př m = F (x 0 ) 4 Iterční metody řešení soustv nelineárních rovnic 41 Vět o kontrkci Předmětem nšeho studi bude vyšetřování následující úlohy Nlézt prvek x R N tkový, že x 1 = f 1 (x 1,, x N ), x 2 = f 2 (x 1,, x N ), (41) x N = f N (x 1,, x N ), 26
27 neboli, psáno vektorově, (42) x = f(x), kde x = (x 1,, x N ) T f = (f 1,, f N ) T Příkld 41 Nechť N = 2 f 1 (x 1, x 2 ) = x x 2 2, f 2 (x 1, x 2 ) = x 2 1 x 2 2Potom má (41) tvr x 1 = x x 2 2, x 2 = x 2 1 x 2 2 Výrz x x 2 2 x 1 = 0 je rovnicí kružnice se středem v bodě (1/2, 0) x 2 1 x 2 2 x 2 = 0 je rovnicí hyperboly se středem v bodě (0, 1/2) Obě tyto křivky procházejí počátkem, což znčí, že jedním z nulových bodů je x 1 = 0, x 2 = 0 Pomocí grfů pro (x 1 1/2) 2 + x 2 2 = 1/4 (x 2 + 1/2) 2 x 2 1 = 1/4 sndno nhlédneme, že v okolí bodu x 1 = 0, 8, x 2 = 0, 4 leží dlší (netriviální) nulový bod soustvy (41) Při nlýze důkzů konvergence metod studovných v předchozí kpitole zjistíme, že význmným důkzovým prostředkem byly vlstnosti bsolutní hodnoty reálných čísel: x = 0 x = 0; pro c, x y R cx = c x ; x + y x + y V souvislosti s prostory R N dimenze N 2, to vede k nutnosti zobecnit pojem bsolutní hodnoty Mtemtik n přelomu století dospěl při tomto zobecňování k pojmu normy normovného prostoru Definice 41 Buď E lineární prostor nd tělesem reálných čísel Funkce ν : E R+ 1 se nzývá normou n E, jestliže pltí následující relce: (i) ν(x) = 0 x = 0; (ii) ν(cx) = c ν(x) x E, c R 1 ; (iii) ν(x + y) ν(x) + ν(y), x, y E Existuje-li n E norm, tk se prostor E se nzývá normovným Poznámk Obvykle se norm n E oznčuje symbolem Je-li zpotřebí zvýrznit, že norm je brán n prostoru E, pk se znčí následovně E Definice 42 Posloupnost {x n }, x n E se nzývá konvergentní k x E x její limitou, jestliže pltí lim n x n x = 0 27
28 Definice 43 Posloupnost {x n }, x n E, se nzývá cuchyovskou, jestliže pro kždé ε > 0 existuje N 0 tkové, že x n+p x n < ε pro n N 0 p 1 Normovný prostor E se nzývá Bnchovým prostorem je-li v něm kždá cuchyovská posloupnost konvergentní Příkld 42 Nechť E = R N () ( N 1/p x p = x k ), 1 p < +, (b) Všímněme si, že pro N = 1 k=1 x = mx { x k : k = 1,, N} x = x, tkže bsolutní hodnot v R 1 je norm Dále nechť C = (c jk ) je regulární mtice typu NxN Potom výrz x C = Cx R N je norm n R N Speciálně nechť E = (R N, 2 ) C = (c jk ), detc = 0 Dále nechť N (x, y) = x k y k Položme B = C T C k=1 x 2 2,B = (Bx, x) Sndno se ukáže, že 2,B je norm n R N Vrťme se všk k vyšetřování soustv nelineárních rovnic v R N Metod postupných proximcí je definován podobně jko pro přípd jedné rovnice Algoritmus 41 Zvolme prvek x E počítejme posloupnost vektorů {x n } rekurzívně pomocí formule (43) x n+1 = f(x n ), n = 1,, Opět si kldeme otázku, zd je proces (43) konvergentní jké vlstnosti má přípdná limit; zřejmě se nbízí řešení rovnice (42) Odpovědi n položené otázky jsou obshem následujícího tvrzení 28
29 Vět 41 Nechť I = N j=1 I j, kde I j = [ j, b j ], j = 1,, N, nechť funkce f 1, f N vyhovují následujícím podmínkám: (i) f 1,, f N jsou definovány jsou spojité n I; (ii) Pro kždý prvek x I též vektor f(x) I; (iii) Existuje konstnt L, 0 < L < 1, tková, že pro libovolná x 1, x 2 I pltí (44) f(x 1 ) f(x 2 ) L x 1 x 2 Potom pltí následující výroky () Rovnice (42) má právě jedno řevsení x I (b) Pro libovolný výchozí prvek x 0 I posloupnost {x n } určená v lgoritmu 41 je definován pro kždé n konverguje k x (c) Pro libovolné n 1 pltí odhd (45) x n x Ln 1 L x 1 x 0 Definice 44 Konstnt L, poždovná v (44) se nzývá Lipschitzovou konstntou (vzhledem k normě ) vektorové funkce f Vzth (44) se nzývá Lipschitzovou podmínkou pro f vzhledem k normě Poznámky Podmínky kldené ve větě 41 n Lipschitzovu konstntu L npovídjí interpretci metody Vzdálenost obrzů je při tkovém zobrzení f ostře mjorizován vzdáleností vzorů, což dává tkovému zobrzení jméno : kontrktivní zobrzení, čili kontrkce Je n místě podotknout, že tvrzení () je v přípdě N 2 dleko hlubším výrokem než je tomu pro N = 1, kdy existenci řešení lze nhlédnout n př vyšetřením grfu zkoumné funkce Tvrzení (b) vypovídá o konvergenci lgoritmu, ztímco v (c) je dán horní odhd chyby Důkz věty 41 Z poždvku (ii) plyne, že posloupnost {x n } je definován pro kždé n 1 x 0 I N zákldě (iii) odvodíme sndno, že (46) x n+1 x n L n x 1 x 0, n = 0, 1, Fixujme n pevně vezměme m > n, m = n + p, p 1 Vidíme, že p x m x n = (x n+k x n+k 1 ), k=1 tedy, p x m x n x n+k x n+k 1 k=1 29
30 Použitím (46) obdržíme vzthy (47) x m x n p k=1 Ln+k 1 x 1 x 0 Ln 1 L x 1 x 0 Protože E = R N je úplný (Bnchův) prostor, plyne odtud konvergence posloupnosti {x n } Nechť ˆx = lim n x n, což je totéž co lim n x n ˆx = 0 Vzhledem ke spojitosti funkcí f 1,, f N obdržíme z (47) tudíž lim f(x n) = f(ˆx) n ˆx = lim n x n+1 = lim n f(x n) = f(ˆx), tk ˆx = x je řešením soustvy rovnic (42) Jednoznčnost se dokzuje zcel nlogicky jko v přípdě N = 1 Nechť x 1 x 2 jsou dvě řešení soustvy (42) Potom, n zákldě (44) x 1 x 2 = f(x 1) f(x 2 ) L x 1 x 2, což je možné pouze když x 1 = x 2 Pltnost (45) plyne z (47) pro p : x n x = lim x n x n+p Ln n 1 L x 1 x 0 Tím je důkz věty 41 proveden 42 Kvdrtická konvergence Newtonov metod pro soustvy Zbývejme se otázkou explicitního vyjádření vektoru chyby d n = x n x při n Předpokládejme, že f splňuje předpokldy věty 41 nvíc, že funkce f 1,, f N mjí v I spojité prcální derivce ž do řádu 2 včetně Aplikcí Tylorovy věty pro funkce N proměnných zjistíme, že d n+1 = x n+1 x = f(x n ) f(x ) = f(x +d n ) f(x n ) = J (x )d n +O( d n 2 ), (48) 30
31 kde (49) J (x) = (f 1) x1 (x 1,, x N ) (f 1 ) xn (x 1,, x N ) (f N ) x1 (x 1,, x N ) (f N ) xn (x 1,, x N ) O( d 2 n ) znčí výrzy mjící mjorntu tvru c d n 2, při čemž c je konstnt nezávislá jk n n tk n x I Definice 45 Mtice definovná v (49) se nzývá Jcobiovou mticí soustvy (41) resp (42) Všímněme si toho, že vzth (48) je N-dimenzionálním nlogem vzthu (312) Je-li J (x ) nenulová mtice, pk (48) říká, že vektor chyby se v kždém iterčním kroku násobí Jcobiovou mticí (49), což odpovídá lineární konvergenci Je-li J (x ) = 0, je z (48) ptrné, že chyb po 1+n- tém kroku je úměrná čtverci chyby po n-tém kroku - v tom přípdě máme co do činění s kvdrtickou konvergencí Opět můžeme formulovt nlog věty 33 pro N > 1 Vět 42 Nechť funkce f 1,, f N definovné n I splňují n I tyto poždvky: (i) Existují spojité derivce f j x l, 1 j, l N; (ii) Soustv (41) má uvnitř I řešení x tkové, že J (x ) = 0 Potom existuje číslo δ > 0 tkové, že posloupnost definovná pomocí lgoritmu 41 konverguje k x pro libovolný strtovcí vektor x 0, pro nějž x 0 x < δ Tedy opět, jko pro N = 1, je-li výchozí přiblížení dosttečně blízké přesnému řešení, dochází ke konvergenci Globální konvergence je pro vícerozměrný přípd problém principiálně komplikovnější než pro N = 1 (konvexit ev konkvit řešení se jeví pro N = 1 dost kdemicky) Podmínky zručující globální konvergenci jsou dost složité jejich nlýz ptří mezi speciální prtie numerických metod Hledejme řešení soustvy (410) F(x) = 0, kde F = (F 1,, F N ) T 31
32 Algoritmus 42 (Newtonov metod pro soustvy) Volme x 0 I sestrojme posloupnost {x n } podle schemtu (411) x n+1 = x n h n, kde h n = (h 0 1,, h 0 N )T je řešením soustvy (412) J (x n )h n = F(x n ) J = F 1 F 1 x N x 1 F N x N F N x N Jk je ptrné z (411) při provádění lgoritmu 42 musíme při kždém iterčním kroku řešiti soustvu lineárních lgebrických rovnic (412) Jest proto přirozené poždovti (413) detj (x n ) 0, n = 0, 1, Cvičení 41 Nlezněte mtici H = H(x) tk, by užití postupných proximcí n rovnici x = x H(x)F (x) poskytlo kvdrtickou konvergenci Rozhodněte, zd se vždy obdrží Newtonov metod 5 Řešení soustv lineárních lgebrických rovnic 51 Obecné soustvy řešení ve smyslu nejmenších čtverců Budeme se zbývt řešením soustv typu (51) Ax = b, kde x R N, b R M, A = ( jk ), 1 j M, 1 k N Poznámk Je zřejmé, že lze vždy docílit situce, kdy M = N to rozšířením mtice A o vhodný počet nulových sloupců pro přípd N < M či řádků pro přípd N > M Řešitelnost soustvy v klsickém smyslu t j kdy vzth (51) je chápán jko soustv rovností N jk x k = b j, j = 1,, M, k=1 32
33 nelze vyždovt Jko příkld může sloužit čstý přípd, kdy soustv (51) representuje nějký model v němž některé z prvků jk b j se obdrží měřením Obecně nelze vyloučit, by odpovídjící soustv pro pro dvě různá měření byl v jednom pŕípdě řešitelná v druhém nikoliv V prktických plikcích se ukzuje potřeb následujícího tvrzení Kždá soustv typu (51) má právě jedno řešení Tkové tvrzení nemůže pltit pro klsické řešení (podmínk o hodnostech) Aby poždovné tvrzení pltilo, musíme vhodným způsobem zobecnit pojem řešení Proto zvedeme zobecněné řešení Buďte (, ) M (, ) N sklární součiny n R M R N Definujme (52) hledejme x R N tk, by F (x, x) = (Ax b, Ax b) M (53) F (x) = min{f (x) : x R N } Vět 51 Existuje lespoň jeden vektor x R N tkový, že pltí (53) Důkz Sndno ověříme, že pltí relce (54) R M = rngea kera (55) R N = rngea kera, kde A je definován pomocí vzthu A v = y, při čemž pro libovolná x R N v R M (Ax, v) M = (x, y) N Existence i jednoznčnost y je důsledkem Rieszovy věty o reprezentci spojitého lineárního funkcionálu n Hilbertově prostoru (R N, (, ) N ) N zákldě (54) (55) obdržíme, že pltí x = A u + v, Av = 0, Odtud pk b = Ac + d, A d = 0 F (x) = (Au Ac, Au Ac) M + (d, d) M 33
34 tkže (56) Vzhledem k tomu, že d je pevný vektor, stčí tedy položiti Tím je vět 51 dokázán x = u = c, F ( x) = (d, d) M = min{f (x) : x R N } Poznámk Protože (56) je hodnot globálního minim kvdrtické funkce F, je veličin (56) táž pro všechn eventuální zobecněná řešení x soustvy Ax = b Tto hodnot se nzývá cenou uvedené úlohy njít zobecněné řešení, neboli cenou zobecněného řešení Všímněme si té skutečnosti, že cen zobecněného řešdení x je nulová právě když x je řešení klsické Nechť M = {x R N : F (x) = (d, d) M } Z věty 51 plyne, že M = ze spojitosti F pk, že M je uzvřená Díky subditivitě normy sndno nhlédneme, že M je konvexní Existuje tedy jediný prvek x M tkový, že x N = min{ x N : x M} Zobecněné řešení x se nzývá normálním řešením soustvy (51) Vět 52 Existuje právě jedno normální řešení libovolné soustvy Ax = b Vidíme tedy, že námi poždovné tvrzení uvedené n počátku této kpitoly, pltí pro námi zvedené zobecněné řešení Poznámk Zobecněná řešení tedy též normální řešení jsou podsttně závislá n sklárních součinech (, ) M (, ) N (57) Volíme-li speciálně (u, v) M = M (u) j (v) j, j=1 kde (u) j znčí j-tou komponentu vektoru u R M, obdržíme funkci F ve tvru F (x) = [ M N ] 2 jk (x) k (b) j j=1 k=1 Odtud získlo zobecněné řešení tkto zvedené název řešení ve smyslu nejmenších čtverců Řešení ve smyslu nejmenších čtverců ptří mezi nejrozšířenější Toto zobecněné řešení bylo zvedeno velmi zevrubně plikováno již Gussem Zobecněné inverzní operátory 34
35 Buď A mtice typu M N Vyšetřujme soustvu relcí (i)axa = A, (ii)xax = X, (iii) (AX) = AX, (iv) (XA) = XA Příkld Nechť M = N deta 0 Položme X = A 1 Splnění vzthů (i) - (iv) s X = A 1 je očividné Npřed si ukážeme, že mtice X typu N N splňující vzthy (i) - (iv) existuje nejvýše jedn Buďte tedy X 1 X 2 dvě tkové mtice Jest potom N druhé strně, tkže X 1 = X 1 AX 1 = X 1 (AX 1 ) = X 1 (AX 2 AX 1 ) = X 1 (AX 1 ) (AX 2 ) = X 1 AX 1 AX 2 = X 1 AX 2 = (X 1 A) X 2 AX 2 = (X 1 A) (X 2 A) X 2 (X 2 AX 1 A) X 2 = X 1 AX 2 AX 2 = (X 1 A) (X 2 A) X 2, X 1 = (X 1 AX 2 A) X 2 = X 2 AX 2 = X 2 Již víme, že v přípdě M = N deta 0 jediným řešením soustvy vzthů (i) - (iv) je inverzní mtice A 1 Existuje řešení v obecném přípdě? Ano! Položme T = A A Sndno nhlédneme, že mtice T je typu N N, je symetrická též je pozitivně semidefinitní, t j (T x, x) N 0 Existují tedy projekce P j, j = 1, s, s N tkové, že pltí vzthy (58) T = s λ k P k, T P 0 = 0, k=1 35
36 při čemž (59) dále pk (510) (511) P j P k = P k P j = δ jk P k, P j = P j, Položme s P k = I P 0, j, k = 0, 1,, N k=1 (T λ j )P j = 0, λ j > 0, j = j,, N, λ 0 = 0 Z = N j=1 λ 1 j P j A Vět 53 Ke kždé mtici A typu M N existuje právě jedn mtice typu N M tková, že pro ni pltí vzthy (i) - (iv) Definice 51 Mtice, jejíž existenci jednoznčnost zručuje vět 53, se nzývá (Mooreovou - Penroseovou) pseudoinverzní mticí oznčuje se symbolem A + Důkz Důkz jednoznčnosti je elementární lze jej přenecht čtenáři N zákldě (511) (58) sndno zjistíme, že AZA = A N j=1 λ 1 j P j A A = A Z tohoto vyjádření pomocí (59) odvodíme, že tkže N N j=1 k=1 AZA = A(I P 0 ) Buď x RN Podle předpokldu (58) pltí, že Protože x je libovolný, plyne odtud, že λ 1 j λ k P j P k 0 = (T P 0 x, P 0 x) N = (AP 0 x, AP 0 x) N, AP 0 x = 0 AP 0 = 0 Dokázli jsme tk, že, díky (512), mtice Z splňuje vzth (i) Pltnost zbývjících vzthů (ii) - (iv) lze dokázt nlogicky, což přenecháme čtenáři pokládáme tím větu 53 z dokáznou s tím, že A + = Z, při čemž Z je definován v (511) Položme (512) x + = A + b Dokážeme, že pltí 36
37 Vět 54 Buďte A mtice typu M N b RM, b = b 1 +b 2, b 1 rnge(a), b 2 ker(a) Potom pltí rovnost (513) x + = x Důkz Zřejmě F (x ) = (Ax + b, Ax + b) M = (AA + b b, AA + b b) M = ((I P 0 )b b, (I P 0 )b b) M = (b 2, b 2 ) M Stčí tedy ukázti, že x + R(A ) To všk plyne odtud, že P 0 x + = 0 tudíž, x + = (I P 0 )x +, čímž je tvrzení dokázáno Vyšetřujme opět soustvu Ax = b, kde A je M N mtice b R N b = b 1 + b 2, při čemž b 1 rnge(a) tj b 1 = Ac 1, dále pk A b 2 = 0 Sndno zjistíme, že pltí A Ax = A b = A b 1, kterážto soustv se nzývá normální soustvou Tto soustv má vždy klsické řešení To vyplývá odtud, že (A A) = A A pro kždé řešení y homogenní soustvy A Ay = 0 pltí vzthy (y, A b) N = (y, A Ac 1 ) N ) = (A Ay, c 1 ) N = 0 Hledt řešení normální soustvy rovnic je numericky velmi náročné, protože číslo podmíněnosti κ(a A) = s mx s min, kde smx = A A 1/2 2 s min je odmocnin nejmenší kldné vlstní hodnoty mtice A A, je zprvidl velmi veliké; v přípdě čtvercové mtice A je rovno čtverci čísl podmíněnosti mtice A Připomeňme, že číslo podmíněnosti čtvercoivé mtice A je definováno jkožto výrz A A 1 Normální řešení je tedy (klsické) řešení normální soustvy ležící v rnge(a + ) Dále pltí Lemm 51 Kždé zobecněné řešení x M má tvr (514) kde x = x + + y, Ay = 0 37
38 Proof Buď x dlší řešení soustvy Ax = b nechť Potom pltí, že x = 1 + 2, 1 = A c 1, A 2 = 0 x x = x y 2 Protože A 1 = b 1, odvodíme, že pltí vzthy Jest tudíž A(x + 1 ) = AA + b 1 b 1 = 0 A + b 1 A c 1 2 = (A b1 A + c 1 ) N = ( b 1 c 1, A[(x + 1 ) M = 0, kde A + b 1 = A b 1 tedy x = x = x + Protože x x ker(a), tvrzení lemmtu je dokázáno 52 Pomocné prostředky ke konstrukci speciálních reprezentcí mtic Nejprve si zopkujme některé pojmy, jež se ukáží jko vhodné pro konstrukci vyšetřování určitých lgoritmů Předpokládáme, že všechny mtice v tomto článku jsou obecně komplexní typu N N Mtice A je hermiteovsky združená, jestliže při čemž Je-li mtice A reálná, t j je-li A H = A, A H = ( jk) jk = ā kj, j, k = 1,, N ā jk = jk nzýváme mtici hermiteovskou symetrickou Jest totiž A T = A, A T = ( T jk), T jk = kj, j, k = 1,, N Permutční mtice P = (p jk ) splňuje vzthy { 0 N p jk = 1, N p jk = p kj = 1, k=1 detp 0 k=1 38
39 Zřejmě P H = P T = P 1 Projekční mticí či projekcí se nzývá mtice splňující P 2 = P Speciálně tedy, I 2 = I 0 2 = 0 Permutční mtice, která relizuje záměnu l - té k - té složky vektorůz R N, se nzývá elementární permutční mticí neboli trnspoziční mticí Tková elementární permutční mtice má tvr k l k l při její plikci pltí vzthy y = P x, při čemž y j = X j, j = k, l, ztímco y k = x l y l = x k Unitární mtice U je definová n vzthy což pro reálnou mtici V znčí, že UU H = U H U = I, V V T = V T V = I V tkovém pří pdě hovoříme o mtici ortogonální Pro involutorní mtici B pltí B 2 = I 39
40 Tedy speciálně I 2 = I Buďte x RN y R M Definujeme mtici kldouce Jinými slovy, y v [y v] = (x, v) N y y v = y v T Ntice E k se nzývá elementární dolní trojúhelníkovou indexu k, jestliže přitom To znčí, že E k = 1 E k = I N v e k e T j v = 0, j = 1,, k 1 v k+1 1 v N 1 Sndno prověříme, že y v splňuje následující relci tkže, je - li (y, v) N = 0, tedy, [y v] 2 x = (y, v) N [y v] x [y v] 2 = 0 σ(y v) = {0} neboli, y v je nilpotentní mtice V přípdě elementární mtice E k vidíme, že (e k, v) N = 0, tkže pltí Vět 55 Buď E k = I N v k e k, při čemž (v k, e j ) N = 0, j = k, k + 1,, N Potom existuje inverzní mtice E 1 k pltí E 1 k = I N + v k e k 40
41 Vět 56 Nechť x T = (ξ 1,, ξ N ) nechť 0 ξ k = e T k x Potom existuje jednoznčně určená elementární dolní trojúhelníková mtice indexu k E k tková, že Důkz Hledejme E k ve tvru E k x = (ξ 1,, ξ k, 0,, 0) T E k = I N v k e k Z poždvku elementrity E k plyne, že (515) kde Dále pk protože žádáme, by (516) ν 1 = = ν k = 0, vk T = (ν 1,, ν N ) E k x = x (x, e k ) N v = x ξ k v ξ j ξ k ν j = 0, j = k + 1,, N, z předpokldu ξ k 0 odvodíme vzthy (517) ν j = ξ j ξ k, j = k + 1,, N Tedy, E k existuje je vzthy (515), (516), (517) určen jednoznčně Householderovu mtici zvedeme pomocí vzthů H = I 2ww H, w H w = 1, kde w je (obecně komplexní) sloupcový vektor w H odpovídjící vektor řádkový Zřejmě Householderov mtice je hermiteovsky združená H H = H též unitární, neboť H H H = H 2 = (I 2ww H ) 2 = I Všímněme si, že pro x C N y = Hx pltí, že y = x 2w H xw, tkže y H y = (y, y) = (Hx, Hx) = (H H Hx, x) = (x, x) (x, y) = (y, x) 41
42 Lemm 52 K dnému vektoru v 0 existuje ortogonální mtice Q tková, že (518) kde σ = Qv = σ v e 1, { +1 pro v1 = (v, e 1 ) 0 1 pro v 1 < 0 Důkz Nechť u = v + σ (v, v)e 1 Zřejmě Dále pk Avšk Q = I 2 uuh u u H u Q H = I 2 uuh u H u = Q Q H Q = Q 2 = I Qv = Qu σ v Qe 1 Qu = u Odtud plyne, že Qe 1 = e 1 2σ v u(u) 1 1 (u, u) Qv = u σ v oe 1 + 2σ 2 v 2 (u) 1 (u, u) u, protože (u) 1 = (v) 1 + σ v no, zjistíme, že Tedy u + 2σ v (v) 1 + σ v (u, u) = 1 { 2σ 2 (v, v) 2σ v (v) 1 + 2σ 2 v 2 } + 2σ v (v) 1 = 0 (u, u) Qv = σ v e 1 42
43 Mtice H = (h jk ) tková, že h jk = 0 pro j k > 2 j 3, se nzývá horní Hessenbergov Názorně je ptrno rozmístění prvků n následujícím schémtu Lemm 53 Ke kždé mtici A existuje unitární mtice T, tková, že kde mtice H je horní Hessenbergov A = T HT H, Čtvercová mtice A = ( jk ) jk R j, k = 1,, N, se nzývá slbě digonálně dominntní, jestliže pltí (519) N k=1,k j jk jj, j = 1,, N, při čemž existuje lespoň jeden index j 0, 1 j 0 N, tk, že (520) N k=1,k j 0 j0 k < j0 j 0 Nstne-li v (519) ostrá nerovnost pro všechny indexy j = 1,, N, pk se mtice A nzývá digonálně dominntní Vět 57 (Geršgorinov) Buď A = ( jk) mtice N N, při čemž jk jsou komlexní čísl Dále buď λ vlstní hodnot mtice A Potom existuje index j 0, 1 j 0 N tkový, že pltí vzthy (521) λ j0 j 0 N k=1,k j 0 j0 k Důkz Buď x RN i R N vlstní vektor odpovídjící vlstní hodnotě λ Tedy, Ax = λx, x = 0 43
44 Položme x j0 = mx{ x j : j = 1,, N} Jest potom λ j0 N k=1, j 0 j0 k x k x j0 N k=1, j 0 j0 k Je tk dokázán pltnost relce (521) tím i vět 57 Důsledek 51 Kždá digonálně dominntní mtice A je regulární Důkz Stčı si uvědomit, že čtvercová mtice je regulární právě když 0 není její vlstní hodnotou To, že 0 není vlstní hodnotou dné čtvercové mtice všk je bezprostředním důsledkem digonální dominnce Kdyby totiž 0 byl vlstní hodnotou mtice A, pltily by vzthy (521) pro λ = 0, j0j 0 = λ j0j 0 Tento spor dokzuje pltnost tvrzení N k=1,k j 0 j0 k < j0 j 0 Vět 58 Buď 0 = A = ( jk), digonálně dominntní buď E 1 = I N v 1 e 1 elementární dolní trojúhelníková mtice indexu 1, kde 0 21 / 11 v 1 = N1 / 11 Potom je též digonálně dominntní A (1) = E 1 A DůkzVyšetřujme výrz 1 jk rovný dle definice, 1 jk = jk j1 11 1k, 1,, N 44
45 Jest tedy, 1 jj N k=2, k j 1 jk jj 1 11 j1 1j N k=2, k j jk 1 11 N k=2, k j j1 1k = jj N k=2, k j jk 1 11 N k=1, k j j1 1k jj N k=1, k =j jk 0, j = 2,, N Čtvercová mtice A = ( jk ) nd tělesem komplexních čísel se nzývá pozitivně definitní, jestliže existuje konstnt κ > 0 tková, že (Ax, x) N κ(x, x) N rm pro všechny vektoryx C Jsou - li jk R, pk nvíc poždujeme, by A = A T 53 Přímé metody řešení soustv lineárních lgebrických rovnic Pod přímými metodmi řešení soustv lineárních lgebrických rovnic rozumíme tkové metody, které jsou zloženy n lgoritmech, jež poskytují přesné řešení po provedení jistého konečného počtu ritmetických opercí Je zřejmé, že pro soustvy, jejichž mtice jsou trojúhelníkové - horní či dolní - se nbízejí přirozené přímé metody Jsou to t zv zpětná přímé doszení Vyšetřujme soustvy (522) Ly = c, (523) kde U = Ux = b, l 11 0 L = l 21 0 l N1 l NN u 11 u 12 u 1N 0 u 22 u 2N 0 0 u NN 45
46 Nechť l jj = 0, j = 1,, N u jj 0, j = 1,, N Potom (524) (525) podobně y 1 = c 1 l 11 y k = c k 1 k l kj c j, k = 2,, N, l kk l j=1 jj l kk (526) (527) x N k = b N k u N k,n k x N = N j=k+1 b N u NN, u N k,j b j u N k,n k u jj, k = 1,, N 1 Nejznámější přitom nejdůležitější přímou metodou řešení soustv linárních lgebrických rovnic je Gussov eliminční metod Její zákldní myšlenk spočívá v trnsformci původní soustvy s mticí A n soustvu s trojúhelníkovou mticí à Mtici à lze získt postupným eliminováním, jež lze reprezentovt elementárními eliminčními mticemi popsnými v odstvci 52 Buď tedy A = ( jk) dná regulární mtice s 11 0 E 1 = I v 1 e 1 elementární dolní trojúhelníková mtice indexu 1, kde 0 12 v 1 = 1 11 N1 Jest tedy A (0) = A N A (1) = N 1N N N1 NN 1N 11 N1 46
3. ROVNICE A NEROVNICE 85. 3.1. Lineární rovnice 85. 3.2. Kvadratické rovnice 86. 3.3. Rovnice s absolutní hodnotou 88. 3.4. Iracionální rovnice 90
 ROVNICE A NEROVNICE 8 Lineární rovnice 8 Kvdrtické rovnice 8 Rovnice s bsolutní hodnotou 88 Ircionální rovnice 90 Eponenciální rovnice 9 Logritmické rovnice 9 7 Goniometrické rovnice 98 8 Nerovnice 0 Úlohy
ROVNICE A NEROVNICE 8 Lineární rovnice 8 Kvdrtické rovnice 8 Rovnice s bsolutní hodnotou 88 Ircionální rovnice 90 Eponenciální rovnice 9 Logritmické rovnice 9 7 Goniometrické rovnice 98 8 Nerovnice 0 Úlohy
2.3. DETERMINANTY MATIC
 2.3. DETERMINANTY MATIC V této kpitole se dozvíte: definici determinntu čtvercové mtice; co je to subdeterminnt nebo-li minor; zákldní vlstnosti determinntů, používné v mnoh prktických úlohách; výpočetní
2.3. DETERMINANTY MATIC V této kpitole se dozvíte: definici determinntu čtvercové mtice; co je to subdeterminnt nebo-li minor; zákldní vlstnosti determinntů, používné v mnoh prktických úlohách; výpočetní
4. přednáška 22. října Úplné metrické prostory. Metrický prostor (M, d) je úplný, když každá cauchyovská posloupnost bodů v M konverguje.
 4. přednášk 22. říjn 2007 Úplné metrické prostory. Metrický prostor (M, d) je úplný, když kždá cuchyovská posloupnost bodů v M konverguje. Příkldy. 1. Euklidovský prostor R je úplný, kždá cuchyovská posloupnost
4. přednášk 22. říjn 2007 Úplné metrické prostory. Metrický prostor (M, d) je úplný, když kždá cuchyovská posloupnost bodů v M konverguje. Příkldy. 1. Euklidovský prostor R je úplný, kždá cuchyovská posloupnost
Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech.
 Kapitola 9 Skalární součin Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech. Definice 9.1 Je-li x = (x 1,..., x n ) T R n 1 reálný
Kapitola 9 Skalární součin Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech. Definice 9.1 Je-li x = (x 1,..., x n ) T R n 1 reálný
LINEÁRNÍ DIFERENCIÁLNÍ ROVNICE 2.ŘÁDU
 LINEÁRNÍ DIFERENCIÁLNÍ ROVNICE 2.ŘÁDU ZDENĚK ŠIBRAVA 1. Obecné řešení lin. dif. rovnice 2.řádu s konstntními koeficienty 1.1. Vrice konstnt. Příkld 1.1. Njděme obecné řešení diferenciální rovnice (1) y
LINEÁRNÍ DIFERENCIÁLNÍ ROVNICE 2.ŘÁDU ZDENĚK ŠIBRAVA 1. Obecné řešení lin. dif. rovnice 2.řádu s konstntními koeficienty 1.1. Vrice konstnt. Příkld 1.1. Njděme obecné řešení diferenciální rovnice (1) y
Masarykova univerzita. Základy konvexní analýzy a optimalizace v R n.
 Masarykova univerzita Ondřej Došlý Základy konvexní analýzy a optimalizace v R n. První vydání Brno 2004 Došlý Ondřej Název knihy c prof. RNDr. Ondřej Došlý, DrSc., 2005 Největší životní umění je neoptimalizovat
Masarykova univerzita Ondřej Došlý Základy konvexní analýzy a optimalizace v R n. První vydání Brno 2004 Došlý Ondřej Název knihy c prof. RNDr. Ondřej Došlý, DrSc., 2005 Největší životní umění je neoptimalizovat
VIII. Primitivní funkce a Riemannův integrál
 VIII. Primitivní funkce Riemnnův integrál VIII.2. Riemnnův integrál opkování Vět. Nechť f je spojitá funkce n intervlu, b nechť c, b. Oznčíme-li F (x) = x (, b), pk F (x) = f(x) pro kždé x (, b). VIII.3.
VIII. Primitivní funkce Riemnnův integrál VIII.2. Riemnnův integrál opkování Vět. Nechť f je spojitá funkce n intervlu, b nechť c, b. Oznčíme-li F (x) = x (, b), pk F (x) = f(x) pro kždé x (, b). VIII.3.
TEORIE MATIC. Tomáš Vondra
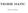 TEORIE MATIC Tomáš Vondra 2 Obsah 1 Opakování 5 1.1 Základní operace s maticemi..................... 5 1.2 Determinant matice......................... 7 1.2.1 Cauchyův-Binedův vzorec..................
TEORIE MATIC Tomáš Vondra 2 Obsah 1 Opakování 5 1.1 Základní operace s maticemi..................... 5 1.2 Determinant matice......................... 7 1.2.1 Cauchyův-Binedův vzorec..................
( 5 ) 6 ( ) 6 ( ) Přijímací řízení ak. r. 2010/11 Kompletní znění testových otázek - matematický přehled
 řijímcí řízení k. r. / Kompletní znění testových otázek - mtemtický přehled Koš Znění otázky Odpověď ) Odpověď b) Odpověď c) Odpověď d) Správná odpověď. Které číslo doplníte místo otzníku? 8?. Které číslo
řijímcí řízení k. r. / Kompletní znění testových otázek - mtemtický přehled Koš Znění otázky Odpověď ) Odpověď b) Odpověď c) Odpověď d) Správná odpověď. Které číslo doplníte místo otzníku? 8?. Které číslo
13. Soustava lineárních rovnic a matice
 @9. Soustv lineárních rovnic mtice Definice: Mtice je tbulk reálných čísel. U mtice rozlišujeme řádky (i=,..n), sloupce (j=,..m) říkáme, že mtice je typu (n x m). Oznčíme-li mtici písmenem A, její prvky
@9. Soustv lineárních rovnic mtice Definice: Mtice je tbulk reálných čísel. U mtice rozlišujeme řádky (i=,..n), sloupce (j=,..m) říkáme, že mtice je typu (n x m). Oznčíme-li mtici písmenem A, její prvky
2. Funkční řady Studijní text. V předcházející kapitole jsme uvažovali řady, jejichž členy byla reálná čísla. Nyní se budeme zabývat studiem
 2. Funkční řd Studijní text 2. Funkční řd V předcházející kpitole jsme uvžovli řd, jejichž člen bl reálná čísl. Nní se budeme zbývt studiem obecnějšího přípdu, kd člen řd tvoří reálné funkce. Definice
2. Funkční řd Studijní text 2. Funkční řd V předcházející kpitole jsme uvžovli řd, jejichž člen bl reálná čísl. Nní se budeme zbývt studiem obecnějšího přípdu, kd člen řd tvoří reálné funkce. Definice
1 i= VLIV ZMĚN FYZIKÁLNÍCH PARAMETRŮ FLUIDNÍCH VRSTEV NA CHARAKTERISTIKY TLAKOVÝCH FLUKTUACÍ. OTAKAR TRNKA a MILOSLAV HARTMAN. i M
 Chem. Listy, 55 53 (7) VLIV ZMĚN FYZIKÁLNÍCH PARAMETRŮ FLUIDNÍCH VRSTEV NA CHARAKTERISTIKY TLAKOVÝCH FLUKTUACÍ OTAKAR TRNKA MILOSLAV HARTMAN Ústv chemických procesů, AV ČR, Rozvojová 35, 65 Prh 6 trnk@icpf.cs.cz
Chem. Listy, 55 53 (7) VLIV ZMĚN FYZIKÁLNÍCH PARAMETRŮ FLUIDNÍCH VRSTEV NA CHARAKTERISTIKY TLAKOVÝCH FLUKTUACÍ OTAKAR TRNKA MILOSLAV HARTMAN Ústv chemických procesů, AV ČR, Rozvojová 35, 65 Prh 6 trnk@icpf.cs.cz
Součin matice A a čísla α definujeme jako matici αa = (d ij ) typu m n, kde d ij = αa ij pro libovolné indexy i, j.
 Kapitola 3 Počítání s maticemi Matice stejného typu můžeme sčítat a násobit reálným číslem podobně jako vektory téže dimenze. Definice 3.1 Jsou-li A (a ij ) a B (b ij ) dvě matice stejného typu m n, pak
Kapitola 3 Počítání s maticemi Matice stejného typu můžeme sčítat a násobit reálným číslem podobně jako vektory téže dimenze. Definice 3.1 Jsou-li A (a ij ) a B (b ij ) dvě matice stejného typu m n, pak
FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ MATEMATIKA 1
 FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ MATEMATIKA 1 Grnt předmětu: Prof. RNDr. Josef DIBLÍK, DrSc. (do 31.8.00) Prof. RNDr. Jn CHVALINA, DrSc. (od 1.9.00) Autoři
FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ MATEMATIKA 1 Grnt předmětu: Prof. RNDr. Josef DIBLÍK, DrSc. (do 31.8.00) Prof. RNDr. Jn CHVALINA, DrSc. (od 1.9.00) Autoři
Konzultace z předmětu MATEMATIKA pro první ročník dálkového studia
 - - Konzultce z předmětu MATEMATIKA pro první ročník dálkového studi ) Číselné obor ) Zákldní početní operce procentový počet ) Absolutní hodnot reálného čísl ) Intervl množinové operce ) Mocnin ) Odmocnin
- - Konzultce z předmětu MATEMATIKA pro první ročník dálkového studi ) Číselné obor ) Zákldní početní operce procentový počet ) Absolutní hodnot reálného čísl ) Intervl množinové operce ) Mocnin ) Odmocnin
Jazyk matematiky. 2.1. Matematická logika. 2.2. Množinové operace. 2.3. Zobrazení. 2.4. Rozšířená číslená osa
 2. Jazyk matematiky 2.1. Matematická logika 2.2. Množinové operace 2.3. Zobrazení 2.4. Rozšířená číslená osa 1 2.1 Matematická logika 2.1.1 Výrokový počet logická operace zapisujeme čteme česky negace
2. Jazyk matematiky 2.1. Matematická logika 2.2. Množinové operace 2.3. Zobrazení 2.4. Rozšířená číslená osa 1 2.1 Matematická logika 2.1.1 Výrokový počet logická operace zapisujeme čteme česky negace
26. listopadu a 10.prosince 2016
 Integrální počet Přednášk 4 5 26. listopdu 10.prosince 2016 Obsh 1 Neurčitý integrál Tbulkové integrály Substituční metod Metod per-prtes 2 Určitý integrál Geometrické plikce Fyzikální plikce K čemu integrální
Integrální počet Přednášk 4 5 26. listopdu 10.prosince 2016 Obsh 1 Neurčitý integrál Tbulkové integrály Substituční metod Metod per-prtes 2 Určitý integrál Geometrické plikce Fyzikální plikce K čemu integrální
Západočeská univerzita v Plzni. Fakulta aplikovaných věd Katedra matematiky. Geometrie pro FST 1. Pomocný učební text
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky Geometrie pro FST 1 Pomocný učební text František Ježek, Marta Míková, Světlana Tomiczková Plzeň 29. srpna 2005 verze 1.0 Předmluva
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky Geometrie pro FST 1 Pomocný učební text František Ježek, Marta Míková, Světlana Tomiczková Plzeň 29. srpna 2005 verze 1.0 Předmluva
Komplexní čísla tedy násobíme jako dvojčleny s tím, že použijeme vztah i 2 = 1. = (a 1 + ia 2 )(b 1 ib 2 ) b 2 1 + b2 2.
 7 Komplexní čísl 71 Komplexní číslo je uspořádná dvojice reálných čísel Komplexní číslo = 1, ) zprvidl zpisujeme v tzv lgebrickém tvru = 1 + i, kde i je imginární jednotk, pro kterou pltí i = 1 Číslo 1
7 Komplexní čísl 71 Komplexní číslo je uspořádná dvojice reálných čísel Komplexní číslo = 1, ) zprvidl zpisujeme v tzv lgebrickém tvru = 1 + i, kde i je imginární jednotk, pro kterou pltí i = 1 Číslo 1
Obecně: K dané funkci f hledáme funkci ϕ z dané množiny funkcí M, pro kterou v daných bodech x 0 < x 1 <... < x n. (δ ij... Kroneckerovo delta) (4)
 KAPITOLA 13: Numerická integrce interpolce [MA1-18:P13.1] 13.1 Interpolce Obecně: K dné funkci f hledáme funkci ϕ z dné množiny funkcí M, pro kterou v dných bodech x 0 < x 1
KAPITOLA 13: Numerická integrce interpolce [MA1-18:P13.1] 13.1 Interpolce Obecně: K dné funkci f hledáme funkci ϕ z dné množiny funkcí M, pro kterou v dných bodech x 0 < x 1
Funkce zadané implicitně
 Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Kapitola 1. Tenzorový součin matic
 Kapitola 1 Tenzorový součin matic Definice 1.1. Buď F komutativní těleso. Pro matice A F m n a B F r s definujeme tenzorový součin A B jako matici o rozměru mr ns zapsanou blokově: A 11 B A 12 B A 1n B
Kapitola 1 Tenzorový součin matic Definice 1.1. Buď F komutativní těleso. Pro matice A F m n a B F r s definujeme tenzorový součin A B jako matici o rozměru mr ns zapsanou blokově: A 11 B A 12 B A 1n B
VIII. Primitivní funkce a Riemannův integrál
 VIII. Primitivní funkce Riemnnův integrál VIII.2. Primitivní funkce Definice. Nechť funkce f je definován n neprázdném otevřeném intervlu I. Řekneme, že funkce F : I R je primitivní funkce k f n intervlu
VIII. Primitivní funkce Riemnnův integrál VIII.2. Primitivní funkce Definice. Nechť funkce f je definován n neprázdném otevřeném intervlu I. Řekneme, že funkce F : I R je primitivní funkce k f n intervlu
Determinant. Definice determinantu. Permutace. Permutace, vlastnosti. Definice: Necht A = (a i,j ) R n,n je čtvercová matice.
 [] Definice determinantu BI-LIN, determinant, 9, P Olšák [2] Determinant je číslo jistým způsobem charakterizující čtvercovou matici det A 0 pro singulární matici, det A 0 pro regulární matici používá
[] Definice determinantu BI-LIN, determinant, 9, P Olšák [2] Determinant je číslo jistým způsobem charakterizující čtvercovou matici det A 0 pro singulární matici, det A 0 pro regulární matici používá
u, v, w nazýváme číslo u.( v w). Chyba! Chybné propojení.,
 Def: Vetorovým součiem vetorů u =(u, u, u 3 ) v = (v, v, v 3 ) zýváme vetor u v = (u v 3 u 3 v, u 3 v u v 3, u v u v ) Vět: Pro vetory i, j, ortoormálí báze pltí i i = j = i, i = j Vět: Nechť u v, w, jsou
Def: Vetorovým součiem vetorů u =(u, u, u 3 ) v = (v, v, v 3 ) zýváme vetor u v = (u v 3 u 3 v, u 3 v u v 3, u v u v ) Vět: Pro vetory i, j, ortoormálí báze pltí i i = j = i, i = j Vět: Nechť u v, w, jsou
OBECNÝ URČITÝ INTEGRÁL
 OBECNÝ URČITÝ INTEGRÁL Zobecnění Newtonov nebo Riemnnov integrálu se definují různým způsobem dostnou se někdy různé, někdy stejné pojmy. V tomto textu bude postup volen jko zobecnění Newtonov integrálu,
OBECNÝ URČITÝ INTEGRÁL Zobecnění Newtonov nebo Riemnnov integrálu se definují různým způsobem dostnou se někdy různé, někdy stejné pojmy. V tomto textu bude postup volen jko zobecnění Newtonov integrálu,
Obsah rovinného obrazce
 Osh rovinného orzce Nejjednodušší plikcí určitého integrálu je výpočet oshu rovinného orzce. Zčneme větou. Vět : Je-li funkce f spojitá nezáporná n n orázku níže roven f ( ) d. ;, je osh rovinného orzce
Osh rovinného orzce Nejjednodušší plikcí určitého integrálu je výpočet oshu rovinného orzce. Zčneme větou. Vět : Je-li funkce f spojitá nezáporná n n orázku níže roven f ( ) d. ;, je osh rovinného orzce
Lineární algebra II. Adam Liška. 9. února 2015. Zápisky z přednášek Jiřího Fialy na MFF UK, letní semestr, ak. rok 2007/2008
 Lineární algebra II Zápisky z přednášek Jiřího Fialy na MFF UK, letní semestr, ak rok 2007/2008 Adam Liška 9 února 2015 http://kammffcunicz/~fiala http://wwwadliskacom 1 Obsah 10 Permutace 3 11 Determinant
Lineární algebra II Zápisky z přednášek Jiřího Fialy na MFF UK, letní semestr, ak rok 2007/2008 Adam Liška 9 února 2015 http://kammffcunicz/~fiala http://wwwadliskacom 1 Obsah 10 Permutace 3 11 Determinant
1.1 Numerické integrování
 1.1 Numerické integrování 1.1.1 Úvodní úvhy Nším cílem bude přibližný numerický výpočet určitého integrálu I = f(x)dx. (1.1) Je-li znám k integrovné funkci f primitivní funkce F (F (x) = f(x)), můžeme
1.1 Numerické integrování 1.1.1 Úvodní úvhy Nším cílem bude přibližný numerický výpočet určitého integrálu I = f(x)dx. (1.1) Je-li znám k integrovné funkci f primitivní funkce F (F (x) = f(x)), můžeme
Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava email: dalibor.lukas@vsb.cz http://www.am.vsb.cz/lukas/la1
 Lineární algebra 10. přednáška: Ortogonalita II Dalibor Lukáš Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava email: dalibor.lukas@vsb.cz http://www.am.vsb.cz/lukas/la1 Text byl vytvořen
Lineární algebra 10. přednáška: Ortogonalita II Dalibor Lukáš Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava email: dalibor.lukas@vsb.cz http://www.am.vsb.cz/lukas/la1 Text byl vytvořen
Regulární matice. Věnujeme dále pozornost zejména čtvercovým maticím.
 Regulární matice Věnujeme dále pozornost zejména čtvercovým maticím. Věta. Pro každou čtvercovou matici A = (a ij ) řádu n nad tělesem (T, +, ) jsou následující podmínky ekvivalentní: (i) Řádky matice
Regulární matice Věnujeme dále pozornost zejména čtvercovým maticím. Věta. Pro každou čtvercovou matici A = (a ij ) řádu n nad tělesem (T, +, ) jsou následující podmínky ekvivalentní: (i) Řádky matice
NEWTONŮV INTEGRÁL. V předchozích kapitolách byla popsána inverzní operace k derivování. Zatím nebylo jasné, k čemu tento nástroj slouží.
 NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování. Ztím nebylo jsné, k čemu tento nástroj slouží. Uvžujme trmvj, která je poháněn elektřinou při brždění vyrábí dynmem elektřinu:
NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování. Ztím nebylo jsné, k čemu tento nástroj slouží. Uvžujme trmvj, která je poháněn elektřinou při brždění vyrábí dynmem elektřinu:
V předchozích kapitolách byla popsána inverzní operace k derivování. Zatím nebylo jasné, k čemu tento nástroj slouží.
 NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování Ztím nebylo jsné, k čemu tento nástroj slouží Uvžujme trmvj, která je poháněn elektřinou při brždění vyrábí dynmem elektřinu:
NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování Ztím nebylo jsné, k čemu tento nástroj slouží Uvžujme trmvj, která je poháněn elektřinou při brždění vyrábí dynmem elektřinu:
x + F F x F (x, f(x)).
 I. Funkce dvou více reálných proměnných 8. Implicitně dné funkce. Budeme se zbývt úlohou, kdy funkce není zdná přímo předpisem, který vyjdřuje závislost její hodnoty n hodnotách proměnných. Jeden z možných
I. Funkce dvou více reálných proměnných 8. Implicitně dné funkce. Budeme se zbývt úlohou, kdy funkce není zdná přímo předpisem, který vyjdřuje závislost její hodnoty n hodnotách proměnných. Jeden z možných
6. Určitý integrál a jeho výpočet, aplikace
 Aplikovná mtemtik 1, NMAF071 6. Určitý integrál výpočet, plikce T. Slč, MÚ MFF UK ZS 2017/18 ZS 2017/18) Aplikovná mtemtik 1, NMAF071 6. Určitý integrál 1 / 13 6.1 Newtonův integrál Definice 6.1 Řekneme,
Aplikovná mtemtik 1, NMAF071 6. Určitý integrál výpočet, plikce T. Slč, MÚ MFF UK ZS 2017/18 ZS 2017/18) Aplikovná mtemtik 1, NMAF071 6. Určitý integrál 1 / 13 6.1 Newtonův integrál Definice 6.1 Řekneme,
BAKALÁŘSKÁ PRÁCE. Numerické metody jednorozměrné minimalizace
 UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY BAKALÁŘSKÁ PRÁCE Numerické metody jednorozměrné minimalizace Vedoucí bakalářské práce: RNDr. Horymír
UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY BAKALÁŘSKÁ PRÁCE Numerické metody jednorozměrné minimalizace Vedoucí bakalářské práce: RNDr. Horymír
Matematika II: Testy
 Mtemtik II: Testy Petr Schreiberová Ktedr mtemtiky deskriptivní geometrie VŠB - Technická univerzit Ostrv Mtemtik II - testy 69. Řy 9 - Test Ktedr mtemtiky deskriptivní geometrie, VŠB - Technická univerzit
Mtemtik II: Testy Petr Schreiberová Ktedr mtemtiky deskriptivní geometrie VŠB - Technická univerzit Ostrv Mtemtik II - testy 69. Řy 9 - Test Ktedr mtemtiky deskriptivní geometrie, VŠB - Technická univerzit
Matice. a B =...,...,...,...,..., prvků z tělesa T (tímto. Definice: Soubor A = ( a. ...,..., ra
 Definice: Soubor A ( i j ) Mtice 11 12 1n 21 22 2n m 1 m2 prvků z těles T (tímto tělesem T bude v nší prxi nejčstěji těleso reálných čísel R resp těleso rcionálních čísel Q či těleso komplexních čísel
Definice: Soubor A ( i j ) Mtice 11 12 1n 21 22 2n m 1 m2 prvků z těles T (tímto tělesem T bude v nší prxi nejčstěji těleso reálných čísel R resp těleso rcionálních čísel Q či těleso komplexních čísel
Učební texty k státní bakalářské zkoušce Matematika Matice. študenti MFF 15. augusta 2008
 Učební texty k státní bakalářské zkoušce Matematika Matice študenti MFF 15. augusta 2008 1 12 Matice Požadavky Matice a jejich hodnost Operace s maticemi a jejich vlastnosti Inversní matice Regulární matice,
Učební texty k státní bakalářské zkoušce Matematika Matice študenti MFF 15. augusta 2008 1 12 Matice Požadavky Matice a jejich hodnost Operace s maticemi a jejich vlastnosti Inversní matice Regulární matice,
2.1 - ( ) ( ) (020201) [ ] [ ]
![2.1 - ( ) ( ) (020201) [ ] [ ] 2.1 - ( ) ( ) (020201) [ ] [ ]](/thumbs/102/155984102.jpg) - FUNKCE A ROVNICE Následující zákldní znlosti je nezbytně nutné umět od okmžiku probrání ž do konce studi mtemtiky n gymnáziu. Vyždováno bude porozumění schopnost plikovt ne pouze mechnicky zopkovt. Některé
- FUNKCE A ROVNICE Následující zákldní znlosti je nezbytně nutné umět od okmžiku probrání ž do konce studi mtemtiky n gymnáziu. Vyždováno bude porozumění schopnost plikovt ne pouze mechnicky zopkovt. Některé
je jedna z orientací určena jeho parametrizací. Je to ta, pro kterou je počátečním bodem bod ϕ(a). Im k.b.(c ) ( C ) (C ) Obr Obr. 3.5.
 10. Komplexní funkce reálné proměnné. Křivky. Je-li f : (, b) C, pk lze funkci f povžovt z dvojici (u, v), kde u = Re f v = Im f. Rozdíl proti vektorovému poli je v tom, že jsou pro komplexní čísl definovány
10. Komplexní funkce reálné proměnné. Křivky. Je-li f : (, b) C, pk lze funkci f povžovt z dvojici (u, v), kde u = Re f v = Im f. Rozdíl proti vektorovému poli je v tom, že jsou pro komplexní čísl definovány
Jak již bylo uvedeno v předcházející kapitole, můžeme při výpočtu určitých integrálů ze složitějších funkcí postupovat v zásadě dvěma způsoby:
 .. Substituční metod pro určité integrály.. Substituční metod pro určité integrály Cíle Seznámíte se s použitím substituční metody při výpočtu určitých integrálů. Zákldní typy integrálů, které lze touto
.. Substituční metod pro určité integrály.. Substituční metod pro určité integrály Cíle Seznámíte se s použitím substituční metody při výpočtu určitých integrálů. Zákldní typy integrálů, které lze touto
MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z. Obsah. 1. Parciální diferenciální rovnice obecně. 2. Kvaazilineární rovnice prvního řádu
 MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Parciální diferenciální rovnice obecně 1. Kvaazilineární rovnice prvního řádu 1 3. Lineární rovnice druhého řádu
MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Parciální diferenciální rovnice obecně 1. Kvaazilineární rovnice prvního řádu 1 3. Lineární rovnice druhého řádu
4. cvičení z Matematiky 2
 4. cvičení z Mtemtiky 2 14.-18. březn 2016 4.1 Njděte ity (i (ii (iii (iv 2 +(y 1 2 +1 1 2 +(y 1 2 z 2 y 2 z yz 1 2 y 2 (,y (0,0 2 +y 2 2 y 2 (,y (0,0 2 +y 3 (i Pro funkci f(, y = 2 +(y 1 2 +1 1 2 +(y
4. cvičení z Mtemtiky 2 14.-18. březn 2016 4.1 Njděte ity (i (ii (iii (iv 2 +(y 1 2 +1 1 2 +(y 1 2 z 2 y 2 z yz 1 2 y 2 (,y (0,0 2 +y 2 2 y 2 (,y (0,0 2 +y 3 (i Pro funkci f(, y = 2 +(y 1 2 +1 1 2 +(y
Integrální počet - IV. část (aplikace na určitý vlastní integrál, nevlastní integrál)
 Integrální počet - IV. část (plikce n určitý vlstní integrál, nevlstní integrál) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 9. přednášk z AMA Michl Fusek (fusekmi@feec.vutbr.cz) / 4 Obsh
Integrální počet - IV. část (plikce n určitý vlstní integrál, nevlstní integrál) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 9. přednášk z AMA Michl Fusek (fusekmi@feec.vutbr.cz) / 4 Obsh
c 2 b 2 a 2 2.8.20 Důkazy Pythagorovy věty Předpoklady: 020819
 .8.0 Důkzy Pythgorovy věty Předpokldy: 00819 Pedgogická poznámk: V řešení kždého příkldu jsou uvedeny rdy, které dávám postupně žákům, bych jim pomohl. Pedgogická poznámk: Diskuse o následujícím příkldu
.8.0 Důkzy Pythgorovy věty Předpokldy: 00819 Pedgogická poznámk: V řešení kždého příkldu jsou uvedeny rdy, které dávám postupně žákům, bych jim pomohl. Pedgogická poznámk: Diskuse o následujícím příkldu
Integrální počet - II. část (určitý integrál a jeho aplikace)
 Integrální počet - II. část (určitý integrál jeho plikce) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 7. přednášk z ESMAT Michl Fusek (fusekmi@feec.vutbr.cz) 1 / 23 Obsh 1 Určitý vlstní (Riemnnův)
Integrální počet - II. část (určitý integrál jeho plikce) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 7. přednášk z ESMAT Michl Fusek (fusekmi@feec.vutbr.cz) 1 / 23 Obsh 1 Určitý vlstní (Riemnnův)
R n výběr reprezentantů. Řekneme, že funkce f je Riemannovsky integrovatelná na
 Mtemtik II. Určitý integrál.1. Pojem Riemnnov určitého integrálu Definice.1.1. Říkáme, že funkce f( x ) je n intervlu integrovtelná (schopná integrce), je-li n něm ohrničená spoň po částech spojitá.
Mtemtik II. Určitý integrál.1. Pojem Riemnnov určitého integrálu Definice.1.1. Říkáme, že funkce f( x ) je n intervlu integrovtelná (schopná integrce), je-li n něm ohrničená spoň po částech spojitá.
Seriál XXVII.III Aplikační
 Seriál XXVII.III Aplikční Seriál: Aplikční Tento díl seriálu bude tk trochu plikční. Minule jsme si pověděli úvod k vričním metodám ve fyzice, nyní bychom rádi nbyté znlosti plikovli n tři speciální přípdy.
Seriál XXVII.III Aplikční Seriál: Aplikční Tento díl seriálu bude tk trochu plikční. Minule jsme si pověděli úvod k vričním metodám ve fyzice, nyní bychom rádi nbyté znlosti plikovli n tři speciální přípdy.
FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ. Matematika 3. RNDr. Břetislav Fajmon, PhD. Autoři textu:
 FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Matematika 3 Garant předmětu: RNDr. Břetislav Fajmon, PhD Autoři textu: Mgr. Irena Růžičková RNDr. Břetislav Fajmon, PhD
FAKULTA ELEKTROTECHNIKY A KOMUNIKAČNÍCH TECHNOLOGIÍ VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Matematika 3 Garant předmětu: RNDr. Břetislav Fajmon, PhD Autoři textu: Mgr. Irena Růžičková RNDr. Břetislav Fajmon, PhD
množina, na které je zavedena určitá struktura. Zejména, součet každých dvou prvků X = [x 1,..., x n ] R n,
![množina, na které je zavedena určitá struktura. Zejména, součet každých dvou prvků X = [x 1,..., x n ] R n, množina, na které je zavedena určitá struktura. Zejména, součet každých dvou prvků X = [x 1,..., x n ] R n,](/thumbs/99/140214707.jpg) Náplní předmětu bude klkulus R n R (přípdně R m ). Proč se zbývt funkcemi více proměnných? V prxi je čsto třeb uvžovt veličiny, které závisejí n více než jedné proměnné, npř. objem rotčního kužele závisí
Náplní předmětu bude klkulus R n R (přípdně R m ). Proč se zbývt funkcemi více proměnných? V prxi je čsto třeb uvžovt veličiny, které závisejí n více než jedné proměnné, npř. objem rotčního kužele závisí
Několik poznámek na téma lineární algebry pro studenty fyzikální chemie
 Několik poznámek na téma lineární algebry pro studenty fyzikální chemie Jiří Kolafa Vektory. Vektorový prostor Vektor je často zaveden jako n-tice čísel, (v,..., v n ), v i R (pro reálný vektorový prostor);
Několik poznámek na téma lineární algebry pro studenty fyzikální chemie Jiří Kolafa Vektory. Vektorový prostor Vektor je často zaveden jako n-tice čísel, (v,..., v n ), v i R (pro reálný vektorový prostor);
2002 Katedra obecné elektrotechniky FEI VŠB-TU Ostrava Ing.Stanislav Kocman
 STEJNOSĚRNÉ STROJE 1. Princip činnosti stejnosměrného stroje 2. Rekce kotvy komutce stejnosměrných strojů 3. Rozdělení stejnosměrných strojů 4. Stejnosměrné generátory 5. Stejnosměrné motory 2002 Ktedr
STEJNOSĚRNÉ STROJE 1. Princip činnosti stejnosměrného stroje 2. Rekce kotvy komutce stejnosměrných strojů 3. Rozdělení stejnosměrných strojů 4. Stejnosměrné generátory 5. Stejnosměrné motory 2002 Ktedr
Definice. Nechť k 0 celé, a < b R. Definujeme. x < 1. ϕ(x) 0 v R. Lemma [Slabá formulace diferenciální rovnice.] x 2 1
![Definice. Nechť k 0 celé, a < b R. Definujeme. x < 1. ϕ(x) 0 v R. Lemma [Slabá formulace diferenciální rovnice.] x 2 1 Definice. Nechť k 0 celé, a < b R. Definujeme. x < 1. ϕ(x) 0 v R. Lemma [Slabá formulace diferenciální rovnice.] x 2 1](/thumbs/103/161289080.jpg) 9. Vriční počet. Definice. Nechť k 0 celé, < b R. Definujeme C k ([, b]) = { ỹ [,b] : ỹ C k (R) } ; C 0 ([, b]) = { y C ([, b]) : y() = y(b) = 0 }. Důležitá konstrukce. Shlzovcí funkce (molifiér, bump
9. Vriční počet. Definice. Nechť k 0 celé, < b R. Definujeme C k ([, b]) = { ỹ [,b] : ỹ C k (R) } ; C 0 ([, b]) = { y C ([, b]) : y() = y(b) = 0 }. Důležitá konstrukce. Shlzovcí funkce (molifiér, bump
56. ročník Matematické olympiády. b 1,2 = 27 ± c 2 25
 56. ročník Mtemtické olympiády Úlohy domácí části I. kol ktegorie 1. Njděte všechny dvojice (, ) celých čísel, jež vyhovují rovnici + 7 + 6 + 5 + 4 + = 0. Řešení. Rovnici řešíme jko kvdrtickou s neznámou
56. ročník Mtemtické olympiády Úlohy domácí části I. kol ktegorie 1. Njděte všechny dvojice (, ) celých čísel, jež vyhovují rovnici + 7 + 6 + 5 + 4 + = 0. Řešení. Rovnici řešíme jko kvdrtickou s neznámou
ROTAČNÍ KVADRIKY. Definice, základní vlastnosti, tečné roviny a řezy, průsečíky přímky s rotační kvadrikou
 ROTAČNÍ KVADRIKY Definice, základní vlastnosti, tečné roviny a řezy, průsečíky přímky s rotační kvadrikou Rotační kvadriky jsou rotační plochy, které vzniknou rotací kuželosečky kolem některé její osy.
ROTAČNÍ KVADRIKY Definice, základní vlastnosti, tečné roviny a řezy, průsečíky přímky s rotační kvadrikou Rotační kvadriky jsou rotační plochy, které vzniknou rotací kuželosečky kolem některé její osy.
10 Určitý integrál Riemannův integrál. Definice. Konečnou posloupnost {x j } n j=0 nazýváme dělením intervalu [a,b], jestliže platí
![10 Určitý integrál Riemannův integrál. Definice. Konečnou posloupnost {x j } n j=0 nazýváme dělením intervalu [a,b], jestliže platí 10 Určitý integrál Riemannův integrál. Definice. Konečnou posloupnost {x j } n j=0 nazýváme dělením intervalu [a,b], jestliže platí](/thumbs/54/33422824.jpg) 10 Určitý integrál 10.1 Riemnnův integrál Definice. Konečnou posloupnost {x j } n j=0 nzýváme dělením intervlu [,b], jestliže pltí = x 0 < x 1 < < x n = b. Body x 0,...,x n nzýváme dělícími body. Normou
10 Určitý integrál 10.1 Riemnnův integrál Definice. Konečnou posloupnost {x j } n j=0 nzýváme dělením intervlu [,b], jestliže pltí = x 0 < x 1 < < x n = b. Body x 0,...,x n nzýváme dělícími body. Normou
Větu o spojitosti a jejich užití
 0..7 Větu o spojitosti jejich užití Předpokldy: 706, 78, 006 Pedgogická poznámk: Při proírání této hodiny je tře mít n pměti, že všechny věty, které studentům sdělujete z jejich pohledu neuvěřitelně složitě
0..7 Větu o spojitosti jejich užití Předpokldy: 706, 78, 006 Pedgogická poznámk: Při proírání této hodiny je tře mít n pměti, že všechny věty, které studentům sdělujete z jejich pohledu neuvěřitelně složitě
Mgr. Karel Pazourek. online prostředí, Operační program Praha Adaptabilita, registrační číslo CZ.2.17/3.1.00/31165.
 Mnohočleny z různých stran Mgr. Karel Pazourek Kurz vznikl v rámci projektu Rozvoj systému vzdělávacích příležitostí pro nadané žáky a studenty v přírodních vědách a matematice s využitím online prostředí,
Mnohočleny z různých stran Mgr. Karel Pazourek Kurz vznikl v rámci projektu Rozvoj systému vzdělávacích příležitostí pro nadané žáky a studenty v přírodních vědách a matematice s využitím online prostředí,
Soustavy lineárních rovnic
 7 Matice. Determinant Soustavy lineárních rovnic 7.1 Matice Definice 1. Matice typu (m, n) jesoustavam n reálných čísel uspořádaných do m řádků a n sloupců a 11, a 12, a 13,..., a 1n a 21, a 22, a 23,...,
7 Matice. Determinant Soustavy lineárních rovnic 7.1 Matice Definice 1. Matice typu (m, n) jesoustavam n reálných čísel uspořádaných do m řádků a n sloupců a 11, a 12, a 13,..., a 1n a 21, a 22, a 23,...,
integrovat. Obecně lze ale říct, že pokud existuje určitý integrál funkce podle různých definic, má pro všechny takové definice stejnou hodnotu.
 Přednášk 1 Určitý integrál V této přednášce se budeme zbývt určitým integrálem. Eistuje několik definic určitého integrálu funkce jedné reálné proměnné. Jednotlivé integrály se liší v tom, jké funkce lze
Přednášk 1 Určitý integrál V této přednášce se budeme zbývt určitým integrálem. Eistuje několik definic určitého integrálu funkce jedné reálné proměnné. Jednotlivé integrály se liší v tom, jké funkce lze
3. Polynomy Verze 338.
 3. Polynomy Verze 338. V této kapitole se věnujeme vlastnostem polynomů. Definujeme základní pojmy, které se k nim váží, definujeme algebraické operace s polynomy. Diskutujeme dělitelnost polynomů, existenci
3. Polynomy Verze 338. V této kapitole se věnujeme vlastnostem polynomů. Definujeme základní pojmy, které se k nim váží, definujeme algebraické operace s polynomy. Diskutujeme dělitelnost polynomů, existenci
17 Křivky v rovině a prostoru
 17 Křivky v rovině prostoru Definice 17.1 (rovinné křivky souvisejících pojmů). 1. Nechť F (t) [ϕ(t), ψ(t)] je 2-funkce spojitá n, b. Rovinnou křivkou nzveme množinu : {F (t) : t, b } R 2. 2-funkce F [ϕ,
17 Křivky v rovině prostoru Definice 17.1 (rovinné křivky souvisejících pojmů). 1. Nechť F (t) [ϕ(t), ψ(t)] je 2-funkce spojitá n, b. Rovinnou křivkou nzveme množinu : {F (t) : t, b } R 2. 2-funkce F [ϕ,
5. Maticová algebra, typy matic, inverzní matice, determinant.
 5. Maticová algebra, typy matic, inverzní matice, determinant. Matice Matice typu m,n je matice složená z n*m (m >= 1, n >= 1) reálných (komplexních) čísel uspořádaných do m řádků a n sloupců: R m,n (resp.
5. Maticová algebra, typy matic, inverzní matice, determinant. Matice Matice typu m,n je matice složená z n*m (m >= 1, n >= 1) reálných (komplexních) čísel uspořádaných do m řádků a n sloupců: R m,n (resp.
Úvod do optimalizace
 Přednáška Ú-Opt, February 19, 2006:1324 Petr Lachout 1 Úvod do optimalizace Prof. RNDr. Jitka Dupačová, DrSc. Doc. RNDr. Petr Lachout, CSc. KPMS MFF UK Verze 19. února 2006 2 Obsah 1 Úvod 5 2 Optimalizace
Přednáška Ú-Opt, February 19, 2006:1324 Petr Lachout 1 Úvod do optimalizace Prof. RNDr. Jitka Dupačová, DrSc. Doc. RNDr. Petr Lachout, CSc. KPMS MFF UK Verze 19. února 2006 2 Obsah 1 Úvod 5 2 Optimalizace
Maticový a tenzorový počet
 Maticový a tenzorový počet Doc. RNDr. Martin Kovár, Ph.D. Ústav matematiky Fakulta elektrotechniky a komunikačních technologií VUT v Brně Obsah. Test vstupních znalostí............................. 5 Matice
Maticový a tenzorový počet Doc. RNDr. Martin Kovár, Ph.D. Ústav matematiky Fakulta elektrotechniky a komunikačních technologií VUT v Brně Obsah. Test vstupních znalostí............................. 5 Matice
Exponenciála matice a její užití. fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu
 1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
7. Integrální počet Primitivní funkce, Neurčitý integrál
 7. Integrální počet 7.. Primitivní funkce, Neurčitý integrál Definice 7. Říkáme, že F (x) je v intervlu (, b) (přitom může být tké =, b = + ) primitivní funkcí k finkci f(x), jestliže pro všechn x (, b)
7. Integrální počet 7.. Primitivní funkce, Neurčitý integrál Definice 7. Říkáme, že F (x) je v intervlu (, b) (přitom může být tké =, b = + ) primitivní funkcí k finkci f(x), jestliže pro všechn x (, b)
Spojitost funkce v bodě, spojitost funkce v intervalu
 10.1.6 Spojitost funkce v bodě, spojitost funkce v intervlu Předpokldy: 10104, 10105 Př. 1: Nkresli, jk funkce f ( x ) dná grfem zobrzí vyznčené okolí bodu n ose x n osu y. Poté nkresli n osu x vzor okolí
10.1.6 Spojitost funkce v bodě, spojitost funkce v intervlu Předpokldy: 10104, 10105 Př. 1: Nkresli, jk funkce f ( x ) dná grfem zobrzí vyznčené okolí bodu n ose x n osu y. Poté nkresli n osu x vzor okolí
Numerická realizace metod. lineárního a kvadratického
 Matematicko-fyzikální fakulta Univerzita Karlova Praha Numerická realizace metod vnitřního bodu pro řešení úloh lineárního a kvadratického programování Věra Koubková Diplomová práce Praha 1997 Studijní
Matematicko-fyzikální fakulta Univerzita Karlova Praha Numerická realizace metod vnitřního bodu pro řešení úloh lineárního a kvadratického programování Věra Koubková Diplomová práce Praha 1997 Studijní
Křivkový integrál funkce
 Kpitol 6 Křivkový integrál funkce efinice způsob výpočtu Hlvním motivem pro definici určitého integrálu funkce jedné proměnné byl úloh stnovit obsh oblsti omezené grfem dné funkce intervlem n ose x. Řd
Kpitol 6 Křivkový integrál funkce efinice způsob výpočtu Hlvním motivem pro definici určitého integrálu funkce jedné proměnné byl úloh stnovit obsh oblsti omezené grfem dné funkce intervlem n ose x. Řd
ZÁKLADY. y 1 + y 2 dx a. kde y je hledanou funkcí proměnné x.
 VARIAČNÍ POČET ZÁKLADY V prxi se čsto hledjí křivky nebo plochy, které minimlizují nebo mximlizují jisté hodnoty. Npř. se hledá nejkrtší spojnice dvou bodů n dné ploše, nebo tvr zvěšeného ln (má minimální
VARIAČNÍ POČET ZÁKLADY V prxi se čsto hledjí křivky nebo plochy, které minimlizují nebo mximlizují jisté hodnoty. Npř. se hledá nejkrtší spojnice dvou bodů n dné ploše, nebo tvr zvěšeného ln (má minimální
Až dosud jsme se zabývali většinou reálnými posloupnostmi, tedy zobrazeními s definičním
 Limit funkce. Zákldní pojmy Až dosud jsme se zbývli většinou reálnými posloupnostmi, tedy zobrzeními s definičním oborem N. Nyní obrátíme svou pozornost n širší třídu zobrzení. Definice.. Zobrzení f, jehož
Limit funkce. Zákldní pojmy Až dosud jsme se zbývli většinou reálnými posloupnostmi, tedy zobrzeními s definičním oborem N. Nyní obrátíme svou pozornost n širší třídu zobrzení. Definice.. Zobrzení f, jehož
Petr Hasil. Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
 Určitý integrál Petr Hsil Přednášk z mtemtiky Podpořeno projektem Průřezová inovce studijních progrmů Lesnické dřevřské fkulty MENDELU v Brně (LDF) s ohledem n discipĺıny společného zákldu (reg. č. CZ.1.07/2.2.00/28.0021)
Určitý integrál Petr Hsil Přednášk z mtemtiky Podpořeno projektem Průřezová inovce studijních progrmů Lesnické dřevřské fkulty MENDELU v Brně (LDF) s ohledem n discipĺıny společného zákldu (reg. č. CZ.1.07/2.2.00/28.0021)
Skalár- veličina určená jedním číselným údajem čas, hmotnost (porovnej životní úroveň, hospodaření firmy, naše poloha podle GPS )
 LINEÁRNÍ ALGEBRA Úvod vektor Skalár- veličina určená jedním číselným údajem čas, hmotnost (porovnej životní úroveň, hospodaření firmy, naše poloha podle GPS ) Kartézský souřadnicový systém -je taková soustava
LINEÁRNÍ ALGEBRA Úvod vektor Skalár- veličina určená jedním číselným údajem čas, hmotnost (porovnej životní úroveň, hospodaření firmy, naše poloha podle GPS ) Kartézský souřadnicový systém -je taková soustava
NMAF061, ZS Písemná část zkoušky 25. leden 2018
 Jednotlivé kroky při výpočtech stručně, le co nejpřesněji odůvodněte. Pokud používáte nějké tvrzení, nezpomeňte ověřit splnění předpokldů. Jméno příjmení: Skupin: Příkld 3 4 5 6 Celkem bodů Bodů 6 6 4
Jednotlivé kroky při výpočtech stručně, le co nejpřesněji odůvodněte. Pokud používáte nějké tvrzení, nezpomeňte ověřit splnění předpokldů. Jméno příjmení: Skupin: Příkld 3 4 5 6 Celkem bodů Bodů 6 6 4
+ c. n x ( ) ( ) f x dx ln f x c ) a. x x. dx = cotgx + c. A x. A x A arctgx + A x A c
 ) INTEGRÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem neurčitého integrálu Je dán funkce Pltí všk tké F tk, y pltilo F ( ) f ( ) Zřejmě F ( ), protože pltí, 5,, oecně c, kde c je liovolná kon- stnt f ( ) nším
) INTEGRÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem neurčitého integrálu Je dán funkce Pltí všk tké F tk, y pltilo F ( ) f ( ) Zřejmě F ( ), protože pltí, 5,, oecně c, kde c je liovolná kon- stnt f ( ) nším
rovnice 8.1 Úvod Kapitola 8
 Kpitol 8 Zobecněné lineární diferenciální rovnice 8.1 Úvod Všechny integrály v této kpitole jsou KS-integrály, jejichž definice je rozšířen ve smyslu odstvce 6.8 n mticové funkce (tj. funkce zobrzující
Kpitol 8 Zobecněné lineární diferenciální rovnice 8.1 Úvod Všechny integrály v této kpitole jsou KS-integrály, jejichž definice je rozšířen ve smyslu odstvce 6.8 n mticové funkce (tj. funkce zobrzující
Definice limit I
 08 Definice limit I Předpokld: 006 Pedgogická poznámk: N úvod je třeb upozornit, že tto hodin je ze strn studentů snd nejvíce sbotovnou látkou z celé studium (podle rekcí 4B009) Jejich ochot brát n vědomí
08 Definice limit I Předpokld: 006 Pedgogická poznámk: N úvod je třeb upozornit, že tto hodin je ze strn studentů snd nejvíce sbotovnou látkou z celé studium (podle rekcí 4B009) Jejich ochot brát n vědomí
1. Pravděpodobnost a statistika (MP leden 2010)
 1. Pravděpodobnost a statistika (MP leden 2010) Pravděpodobnost pojmy 1. Diskrétní pravděpodobnostní prostor(definice, vlastnosti, příklad). Diskrétní pravděpodobnostní prostor je trojice(ω, A, P), kde
1. Pravděpodobnost a statistika (MP leden 2010) Pravděpodobnost pojmy 1. Diskrétní pravděpodobnostní prostor(definice, vlastnosti, příklad). Diskrétní pravděpodobnostní prostor je trojice(ω, A, P), kde
a n (z z 0 ) n, z C, (1) n=0
 Mocniné řady Nechť 0, a 0, a, a 2,... jsou konečná komplexní čísla. Pak řadu funkcí a n ( 0 ) n, C, () naýváme mocninou řadou. Číslo 0 koeficienty mocniné řady. Onačme dále: se naývá střed mocniné řady,
Mocniné řady Nechť 0, a 0, a, a 2,... jsou konečná komplexní čísla. Pak řadu funkcí a n ( 0 ) n, C, () naýváme mocninou řadou. Číslo 0 koeficienty mocniné řady. Onačme dále: se naývá střed mocniné řady,
1. Alternativní rozdělení A(p) (Bernoulli) je diskrétní rozdělení, kdy. p(0) = P (X = 0) = 1 p, p(1) = P (X = 1) = p, 0 < p < 1.
 2. Některá důležitá rozdělení Diskrétní rozdělení. Alternativní rozdělení Ap) Bernoulli) je diskrétní rozdělení, kdy náhodná veličina X nabývá pouze dvou hodnot a a pro její pravděpodobnostní funkci platí:
2. Některá důležitá rozdělení Diskrétní rozdělení. Alternativní rozdělení Ap) Bernoulli) je diskrétní rozdělení, kdy náhodná veličina X nabývá pouze dvou hodnot a a pro její pravděpodobnostní funkci platí:
Základy teorie matic
 Zákldy teorie mtic 1. Pojem mtice nd číselným tělesem In: Otkr Borůvk (uthor): Zákldy teorie mtic. (Czech). Prh: Acdemi, 1971. pp. 9--12. Persistent URL: http://dml.cz/dmlcz/401328 Terms of use: Akdemie
Zákldy teorie mtic 1. Pojem mtice nd číselným tělesem In: Otkr Borůvk (uthor): Zákldy teorie mtic. (Czech). Prh: Acdemi, 1971. pp. 9--12. Persistent URL: http://dml.cz/dmlcz/401328 Terms of use: Akdemie
Zavedení a vlastnosti reálných čísel PŘIROZENÁ, CELÁ A RACIONÁLNÍ ČÍSLA
 Zvedení vlstnosti reálných čísel Reálná čísl jsou zákldním kmenem mtemtické nlýzy. Konstrukce reálných čísel sice není náplní mtemtické nlýzy, le množin reálných čísel R je pro mtemtickou nlýzu zákldním
Zvedení vlstnosti reálných čísel Reálná čísl jsou zákldním kmenem mtemtické nlýzy. Konstrukce reálných čísel sice není náplní mtemtické nlýzy, le množin reálných čísel R je pro mtemtickou nlýzu zákldním
6. T e s t o v á n í h y p o t é z
 6. T e s t o v á n í h y p o t é z Na základě hodnot z realizace náhodného výběru činíme rozhodnutí o platnosti hypotézy o hodnotách parametrů rozdělení nebo o jeho vlastnostech. Používáme k tomu vhodně
6. T e s t o v á n í h y p o t é z Na základě hodnot z realizace náhodného výběru činíme rozhodnutí o platnosti hypotézy o hodnotách parametrů rozdělení nebo o jeho vlastnostech. Používáme k tomu vhodně
Poznámky z matematiky
 Poznámky z matematiky Verze: 14. dubna 2015 Petr Hasil hasil@mendelu.cz http://user.mendelu.cz/hasil/ Ústav matematiky Lesnická a dřevařská fakulta Mendelova univerzita v Brně Vytvořeno s podporou projektu
Poznámky z matematiky Verze: 14. dubna 2015 Petr Hasil hasil@mendelu.cz http://user.mendelu.cz/hasil/ Ústav matematiky Lesnická a dřevařská fakulta Mendelova univerzita v Brně Vytvořeno s podporou projektu
Přijímací řízení akademický rok 2014/2015 Bc. studium Kompletní znění testových otázek matematika
 Přijímcí řízení kemický rok 0/0 Bc. stuium Kompletní znění testových otázek mtemtik Koš Znění otázky Opověď ) Opověď ) Opověď c) Opověď ) Správná opověď. Které číslo oplníte místo otzníku? 9 7?. Které
Přijímcí řízení kemický rok 0/0 Bc. stuium Kompletní znění testových otázek mtemtik Koš Znění otázky Opověď ) Opověď ) Opověď c) Opověď ) Správná opověď. Které číslo oplníte místo otzníku? 9 7?. Které
0. Lineární rekurence Martin Mareš, 2010-07-04
 0 Lineární rekurence Martin Mareš, 2010-07-04 V tomto krátkém textu se budeme zabývat lineárními rekurencemi, tj posloupnostmi definovanými rekurentní rovnicí typu A n+k = c 0 A n + c 1 A n+1 + + c k 1
0 Lineární rekurence Martin Mareš, 2010-07-04 V tomto krátkém textu se budeme zabývat lineárními rekurencemi, tj posloupnostmi definovanými rekurentní rovnicí typu A n+k = c 0 A n + c 1 A n+1 + + c k 1
Souhrn základních výpočetních postupů v Excelu probíraných v AVT 04-05 listopad 2004. r r. . b = A
 Souhrn zákldních výpočetních postupů v Ecelu probírných v AVT 04-05 listopd 2004. Řešení soustv lineárních rovnic Soustv lineárních rovnic ve tvru r r A. = b tj. npř. pro 3 rovnice o 3 neznámých 2 3 Hodnoty
Souhrn zákldních výpočetních postupů v Ecelu probírných v AVT 04-05 listopd 2004. Řešení soustv lineárních rovnic Soustv lineárních rovnic ve tvru r r A. = b tj. npř. pro 3 rovnice o 3 neznámých 2 3 Hodnoty
Úřední věstník Evropské unie 25.6.2004 ÚŘEDNÍ VĚSTNÍK EVROPSKÉ UNIE
 03/sv. 45 75 32004R0854 25.6.2004 ÚŘEDNÍ VĚSTNÍK EVROPSKÉ UNIE L 226/83 NAŘÍZENÍ EVROPSKÉHO PARLAMENTU A RADY (ES) č. 854/2004 ze dne 29. dubn 2004, kterým se stnoví zvláštní prvidl pro orgnizci úředních
03/sv. 45 75 32004R0854 25.6.2004 ÚŘEDNÍ VĚSTNÍK EVROPSKÉ UNIE L 226/83 NAŘÍZENÍ EVROPSKÉHO PARLAMENTU A RADY (ES) č. 854/2004 ze dne 29. dubn 2004, kterým se stnoví zvláštní prvidl pro orgnizci úředních
ZÁKLADY MATEMATIKY 2. 1. SÉRIE: URƒITÝ INTEGRÁL, APLIKACE
 ZÁKLADY MATEMATIKY 2. SÉRIE: URƒITÝ INTEGRÁL, APLIKACE I. P íprvní úlohy. V této sérii pot ebujete znlost výpo t následujících úloh - otestujte si ji:. Vypo ítejte neur ité integrály: ) (x 2 x + ) 2 dx
ZÁKLADY MATEMATIKY 2. SÉRIE: URƒITÝ INTEGRÁL, APLIKACE I. P íprvní úlohy. V této sérii pot ebujete znlost výpo t následujících úloh - otestujte si ji:. Vypo ítejte neur ité integrály: ) (x 2 x + ) 2 dx
Elektrotechnická fakulta
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Elektrotechnická fakulta OPTIMÁLNÍ ROZHODOVÁNÍ A ŘÍZENÍ Jan Štecha Katedra řídicí techniky 1999 Předmluva Toto skriptum je určeno posluchačům 4. ročníku oboru technická
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Elektrotechnická fakulta OPTIMÁLNÍ ROZHODOVÁNÍ A ŘÍZENÍ Jan Štecha Katedra řídicí techniky 1999 Předmluva Toto skriptum je určeno posluchačům 4. ročníku oboru technická
Lineární algebra a analytická geometrie sbírka úloh a ř ešených př íkladů
 Lineární algebra a analytická geometrie sbírka úloh a ř ešených př íkladů Linear algebra and analytic geometry problems and solved examples Klára Javornická Bakalářská práce 2010 UTB ve Zlíně, Fakulta
Lineární algebra a analytická geometrie sbírka úloh a ř ešených př íkladů Linear algebra and analytic geometry problems and solved examples Klára Javornická Bakalářská práce 2010 UTB ve Zlíně, Fakulta
2. Pokud nedojde k nejasnostem, budeme horní a dolní součty značit pouze
 8. Určitý integrál 8.1. Newtonův integrál Definice 8.1 Buďte,b R. Řekneme,žeNewtonůvintegrálzfunkce fnintervlu(,b) existuje(znčímejej(n) f(x)dx),jestliže 1.existuje primitivní funkce F k f n intervlu(,
8. Určitý integrál 8.1. Newtonův integrál Definice 8.1 Buďte,b R. Řekneme,žeNewtonůvintegrálzfunkce fnintervlu(,b) existuje(znčímejej(n) f(x)dx),jestliže 1.existuje primitivní funkce F k f n intervlu(,
Přímé metody výpočtu charakteristických čísel matic
 Masarykova Univerzita v Brně Přírodovědecká fakulta Přímé metody výpočtu charakteristických čísel matic Bakalářská práce Vedoucí bakalářské práce RNDr. Ladislav Adamec, CSc. Brno 2007 Roman Melichar Prohlašuji,
Masarykova Univerzita v Brně Přírodovědecká fakulta Přímé metody výpočtu charakteristických čísel matic Bakalářská práce Vedoucí bakalářské práce RNDr. Ladislav Adamec, CSc. Brno 2007 Roman Melichar Prohlašuji,
Integrální počet - III. část (určitý vlastní integrál)
 Integrální počet - III. část (určitý vlstní integrál) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 8. přednášk z AMA1 Michl Fusek (fusekmi@feec.vutbr.cz) 1 / 18 Obsh 1 Určitý vlstní (Riemnnův)
Integrální počet - III. část (určitý vlstní integrál) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 8. přednášk z AMA1 Michl Fusek (fusekmi@feec.vutbr.cz) 1 / 18 Obsh 1 Určitý vlstní (Riemnnův)
Přednáška 6, 6. listopadu 2013
 Přednáška 6, 6. listopadu 2013 Kapitola 2. Posloupnosti a řady funkcí. V dalším jsou f, f n : M R, n = 1, 2,..., reálné funkce jedné reálné proměnné definované na (neprázdné) množině M R. Co to znamená,
Přednáška 6, 6. listopadu 2013 Kapitola 2. Posloupnosti a řady funkcí. V dalším jsou f, f n : M R, n = 1, 2,..., reálné funkce jedné reálné proměnné definované na (neprázdné) množině M R. Co to znamená,
FAKULTA STAVEBNÍ MATEMATIKA II MODUL 2 STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ MATEMATIKA II MODUL KŘIVKOVÉ INTEGRÁLY STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Typeset by L A TEX ε c Josef Daněček, Oldřich Dlouhý,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ MATEMATIKA II MODUL KŘIVKOVÉ INTEGRÁLY STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Typeset by L A TEX ε c Josef Daněček, Oldřich Dlouhý,
2. Matice, soustavy lineárních rovnic
 Matice, soustavy lineárních rovnic Tento učební text byl podpořen z Operačního programu Praha- Adaptabilita Irena Sýkorová Některé vlastnosti matic Uvažujmečtvercovoumatici A=(a ij ) n n Matice Asenazývásymetrická,jestližeplatí
Matice, soustavy lineárních rovnic Tento učební text byl podpořen z Operačního programu Praha- Adaptabilita Irena Sýkorová Některé vlastnosti matic Uvažujmečtvercovoumatici A=(a ij ) n n Matice Asenazývásymetrická,jestližeplatí
Úlohy krajského kola kategorie A
 67. ročník mtemtické olympiády Úlohy krjského kol ktegorie A 1. Pvel střídvě vpisuje křížky kolečk do políček tbulky (zčíná křížkem). Když je tbulk celá vyplněná, výsledné skóre spočítá jko rozdíl X O,
67. ročník mtemtické olympiády Úlohy krjského kol ktegorie A 1. Pvel střídvě vpisuje křížky kolečk do políček tbulky (zčíná křížkem). Když je tbulk celá vyplněná, výsledné skóre spočítá jko rozdíl X O,
