1 Ohyb nosníků - mindlinovské řešení
|
|
|
- Zbyněk Vítek
- před 8 lety
- Počet zobrazení:
Transkript
1 1 OHYB NOSNÍKŮ - MNDLNOVSKÉ ŘEŠENÍ 1 1 Ohyb nosníků - mindlinovské řešení Předpoklady o přemístění průřezů Zatížení působí v rovině xz, která je i rovinou symetrie Ω v(x) = 0 m Průhyb se po výšce mění málo (vzhledem k hodnotě průhybu) w(x) = w(x) Průřez zůstává i po deformaci rovinný, ne však nezbytně kolmý k deformované střednici u(x) = u(x, z) = ϕ y (x)z Navrženy nezávisle Timošenkem [6], Reissnerem [5] a Mindlinem [4].
2 2 GEOMETRCKÉ ROVNCE 2 2 Geometrické rovnice Kinematika přemístění průřezu nenulové složky vektoru deformace ε x (x) = u(x) x γ zx (x) = w(x) x = x (ϕ y(x)z)) = dϕ y(x) z = κ y(x)z + u(x) = dw(x) z + z (ϕ y(x)z) = dw(x) kde κ y označuje pseudokřivost ohybové čáry. + ϕ y(x), Bernoulli-Navier [7, kap..2] Mindlin Obor platnosti h/l < 1/10 h/l < 1/3 Průřez Rovinný, kolmý Rovinný γ zx 0 0 (vliv smyku) Neznámé w(x) w(x), ϕ y (x) ϕ y (x) = dw(x) nezávislé
3 3 FYZKÁLNÍ ROVNCE 3 3 Fyzikální rovnice Pro jednoduchost zanedbáme vliv ε 0 σ x (x, z) = E(x)ε x (x, z) = E(x)κ y (x)z ( dw(x) τ zx (x) = G(x)γ zx (x) = G(x) ) + ϕ y(x) Nenulové vnitřní síly M y (x) = σ x (x, z)z dy dz = E(x)κ y (x) A(x) A(x) z 2 dy dz = E(x) y (x)κ y (x) = E(x) y (x) dϕ y(x) ( ) dw(x) Q c z(x) = τ zx (x) dy dz = G(x) A(x) + ϕ y(x) A(x) ( ) dw(x) = G(x)A(x) + ϕ y(x) (1) dy dz
4 3 FYZKÁLNÍ ROVNCE 4 Rozložení smykových napětí τ zx po obdélníkovém průřezu Bernoulli-Navier Mindlin Konstitutivní rce: τ = Gγ 0 konstantní Podmínky rovnováhy kvadratické? [7, kap..2.5] Modifikujeme vztah pro posouvající sílu tak, aby podmínka rovnováhy byla splněna alespoň ve smyslu průměrné energie smykových členů ( ) dw(x) Q z (x) = k(x)q c z(x) = k(x)g(x)a(x) + ϕ y(x) (2) Součinitel k(x) závisí na tvaru průřezu, pro obdélník uvažujeme k = 5/6. Domací úkol 1. k = 2 y/(a A S 2 y (z) b 2 (z) da) Odvoďte obecný vztah pro korekční součinitel
5 4 PODMÍNKY ROVNOVÁHY 5 4 Podmínky rovnováhy (a) (b) Podmínka rovnováhy svislých sil (a) dq z (x) Momentová podmínka rovnováhy (b) dm y (x) + f z (x) = 0 (3) Q z (x) = 0 (4) Podrobné odvození viz domácí úkol č. 1, přednáška 1
6 5 ŘÍDCÍ ROVNCE 6 5 Řídicí rovnice d d ( E(x) y (x) dϕ y(x) ( ( dw(x) k(x)g(x)a(x) ) k(x)g(x)a(x) )) + ϕ y(x) + f z (x) = 0 (5) ( ) dw(x) + ϕ y(x) = 0 (6) 5.1 Kinematické okrajové podmínky: x u Kloub w = 0 Vetknutí w = 0, ϕ y = Statické okrajové podmínky x p Q z (x) = Q z (x) M y (x) = M y (x)
7 6 SLABÉ ŘEŠENÍ 7 6 Slabé řešení Pro zkrácení zápisu budeme používat rovnice (3) (4) namísto (5) (6) Rovnici (3) zvážíme δw(x), rovnici (4) δϕ y (x) a zintegrujeme přes. Dostáváme ( ) dqz (x) 0 = δw(x) + f z (x) ( ) dmy (x) 0 = δϕ y (x) Q z (x) pro všechna δw(x) a δϕ y (x) splňující kinematické okrajové podmínky. ntegrace per partes 0 = [δw(x)q z (x)] b a 0 = [δϕ y (x)m y (x)] b a d(δw(x)) Q z (x) + d(δϕ y (x)) M y (x) δw(x)f z (x) δϕ y (x)q z (x)
8 6 SLABÉ ŘEŠENÍ 8 Vyjádření hraničních členů z okrajových podmínek 0 = [ δw(x)q z (x) ] d(δw(x)) p Q z (x) + δw(x)f z (x) 0 = [ δϕ y (x)m y (x) ] d(δϕ y (x)) p M y (x) δϕ y (x)q z (x) Slabé formulace podmínek rovnováhy (dosazení za V z z (2) a za ohybový moment M y z (1)) ( d(δw(x)) dw(x) k(x)g(x)a(x) [ δw(x)qz (x) ] p + ) + ϕ y(x) = δw(x)f z (x) (7)
9 6 SLABÉ ŘEŠENÍ 9 d(δϕ y (x)) E(x) y (x) dϕ y(x) + (8) ( ) dw(x) δϕ y (x)k(x)g(x)a(x) + ϕ y(x) = [ δϕ y (x)m y (x) ] p
10 7 DSKRETZACE MKP 10 7 Diskretizace MKP Konstrukci nahradíme n uzlovými body a (n 1) prvky V každém uzlu zavádíme průhyb w i a pootočení ϕ yi Neznámé jsou vektory uzlových průhybů r w a pootočení r ϕ Diskretizace deformačních neznámých w(x) N w (x)r w ϕ y (x) N ϕ (x)r ϕ Diskretizace váhových funkcí δw(x) N w (x)δr w δϕ y (x) N ϕ (x)δr ϕ dw(x) B w (x)r w dϕ y (x) B ϕ (x)r ϕ d(δw(x)) B w (x)δr w d(δϕ y (x)) B ϕ (x)δr ϕ
11 7 DSKRETZACE MKP 11 Soustava podmínek rovnováhy K ww r w + K wϕ r ϕ = R w K ϕw r w + K ϕϕ r ϕ = R ϕ Kompaktní zápis K ww K ϕw K wϕ K ϕϕ r w r ϕ = R w R ϕ K (2n 2n) r (2n 1) = R (2n 1) K ϕw = K wϕ T matice K je opět symetrická díky členům (δw(x)) kga(x)ϕ y (x) v (7) a δϕ y (x)kga(x)w (x) v (8)
12 7 DSKRETZACE MKP 12 Domací úkol 2. Odvoďte vztahy pro matice K ww, K wϕ, K ϕw, K ϕϕ a vektory R w, R ϕ.
13 8 SMYKOVÉ ZAMKNUTÍ 13 8 Smykové zamknutí Pro h/l 0 by se výsledky mindlinovského prvku měly blížit klasickému bernoulli-navierovskému řešení (zanedbatelný vliv smyku). Pokud ale volíme funkce N w a N ϕ lineární, výsledek je pro štíhlé nosníky příliš tuhý přílišný vliv smyku, tzv. smykové zamknutí (shear locking). 8.1 Statické zdůvodnění ( dw(x) Posouvající síla: Q z (x) = k(x)g(x)a(x) Ohybový moment: M y (x) = E(x) y (x) dϕ y(x) Hrubý rozpor se Schwedlerovou větou dm y (x) Q z (x) = 0 ) + ϕ y(x) konstantní lineární
14 8 SMYKOVÉ ZAMKNUTÍ Kinematické zdůvodnění Aby přibližné řešení poskytovalo správnou odpověď, musí být správně schopno popsat případ čistého ohybu (viz např. [3, Kapitola 3.1]): κ y (x) = dϕ y(x) Pro zvolenou diskretizaci ( w(x) w 1 1 x ) L ( ϕ y (x) ϕ 1 1 x ) L = κ = konst γ zx (x) = dw(x) + ϕ y(x) = 0 + w 2 x L + ϕ 2 x L dw(x) 1 L (w 2 w 1 ) dϕ y (x) 1 L (ϕ 2 ϕ 1 )
15 9 SELEKTVNÍ NTEGRACE 15 Požadavek nulového smykového zkosení γ zx (x) 1 L (w 2 w 1 ) + ϕ 1 + x L (ϕ 2 ϕ 1 ) = 0 Předchozí výraz nesmí záviset na souřadnici x ϕ 2 ϕ 1 = 0 κ y 1 L (ϕ 2 ϕ 1 ) = 0 κ 9 Selektivní integrace Smykové zkosení je uvažováno konstantní po celém prvku, jeho hodnota odpovídá hodnotě uprostřed intervalu γ zx (x) 1 L (w 2 w 1 ) + ϕ (ϕ 2 ϕ 1 ) = 1 L (w 2 w 1 ) (ϕ 1 + ϕ 2 ) Kinematika: prvek je v pořádku, umožňuje popsat čistý ohyb Statické hledisko: Q z (x) = k(x)g(x)a(x)γ xz (x) konstantní, M y zůstává konstantní Schwedlerova věta není hrubě porušena
16 10 BUBLNOVÁ (HERARCHCKÁ) FUNKCE Bublinová (hierarchická) funkce Z kinematické analýzy vyplývá, že zamknutí je způsobeno nedostatečným stupněm aproximace průhybu w(x) Přidáme kvadratický člen k aproximaci w(x): ( w(x) w 1 1 x ) x + w 2 + αx(x L) L L Požadavek čistého ohybu γ zx (x) = dw(x) + ϕ y(x) 1 L (w 2 w 1 ) + α(2x L) + ϕ 1 + x L (ϕ 2 ϕ 1 ) = 1 L (w 2 w 1 ) αl + ϕ 1 + x L (ϕ 2 ϕ 1 + 2αL) = 0
17 10 BUBLNOVÁ (HERARCHCKÁ) FUNKCE 17 Nezávislost na x Výsledné aproximace w(x) w 1 ( α = 1 2L (ϕ 1 ϕ 2 ) ) 1 x L ) ϕ y (x) ϕ 1 ( 1 x L x + w 2 L + 1 2L (ϕ 1 ϕ 2 ) x(x L) x + ϕ 2 L Ze statického hlediska se prvek chová podobně jako předchozí formulace Q z je konstantní, M y je též konstantní Průhyby aproximovány jak pomocí uzlových posunů, tak i pootočení [2] tzv. spojená interpolace (linked interpolation) J. Bernoulli J.-L. Lagrange C.-L. Navier R.-D. Mindlin B. F. de Veubeke
18 11 METODA LANGRANGEOVÝCH SOUČNTELŮ Metoda Langrangeových součinitelů Připomeňme slabou momentovou podmínku rovnováhy (8) pro konstrukci s M y = 0, konstantním E, G a obdélníkovým průřezem: 0 = E y = E bh d(δϕ y (x)) d(δϕ y (x)) E 2(1 + ν) bh dϕ y (x) d(δϕ y (x)) dϕ y (x) ( dw(x) δϕ y (x) ν h 2 dϕ y (x) + kga ) + ϕ y(x) ( dw(x) δϕ y (x) ( dw(x) δϕ y (x) / 12 Ebh 3 ) + ϕ y(x) ) + ϕ y(x) = 0 Podmínka nulového smykového zkosení pro h 0 tzv. penalizační metoda
19 11 METODA LANGRANGEOVÝCH SOUČNTELŮ 19 Pro štíhlé nosníky a lineárně-lineární aproximaci způsobuje smykové zamknutí, jelikož {}}{ 1 h 2 libovolné {}}{ δϕ y (x) musí 0 pro všechna x {( }} ){ dw(x) + ϕ y(x) = 0 Pokud zavedeme novou nezávislou proměnnou pro zajištění podmínky γ xz = 0 pro h 0, odstraníme vliv aproximace w(x) a ϕ y (x) Ke slabým podmínkám rovnováhy (7) (8) přidáme podmínku ( δλ(x) γ zx (x) dw(x) ) ϕ y(x) = 0, (9) kde γ zx (x) je nyní nezávislá proměnná a δλ(x) je další váhová funkce. Konstitutivní rovnice pro posouvající sílu se zjednoduší na Q z (x) = k(x)g(x)a(x)γ xz (x)
20 11 METODA LANGRANGEOVÝCH SOUČNTELŮ 20 Slabé podmínky rovnováhy mají nyní tvar 0 = d(δw(x)) k(x)g(x)a(x)γ zx (x) [ δw(x)q z (x) ] p δw(x)f z (x) 0 = + 0 = d(δϕ y (x)) E(x) y (x) dϕ y(x) δϕ y (x)k(x)g(x)a(x)γ zx (x) [ δϕ y (x)m y (x) ] p ( δλ(x) γ zx (x) dw(x) ) ϕ y(x) Abychom nakonec získali symetrickou matici tuhosti, volíme váhovu funkci δλ(x) ve tvaru δλ(x) = k(x)g(x)a(x)δγ xz (x)
21 11 METODA LANGRANGEOVÝCH SOUČNTELŮ 21 Poslední rovnice se po těchto úpravách změní na ( 0 = δγ xz (x)k(x)g(x)a(x) γ zx (x) dw(x) Nyní stačí zvolit aproximace ) ϕ y(x) γ xz (x) N γ (x)r γ a dosadit do jednotlivých rovnic. Po standardních úpravách získáváme K ww K wϕ K wγ r w R w K ϕw K ϕϕ K ϕγ r ϕ = R ϕ K γw K γϕ K γγ r γ 0 Soustava rovnic vyplývající z této metody je větší pouze zdánlivě. Proměnné r γ jsou vnitřní a lze je eliminovat (vyjádřit v závislosti na proměnných r w a r ϕ ), viz [1, str ]
22 11 METODA LANGRANGEOVÝCH SOUČNTELŮ 22 Tato formulace funguje i pro lineární aproximaci w(x) a ϕ y (x), pokud volíme aproximaci γ jako konstantní po prvku. Kinematika: Smykové zamknutí ošetřeno podmínkou (9) Statika: Posouvající síla je konstantní díky zvolené aproximaci, ohybový moment je opět konstantní Domací úkol 3. Odvoďte matici tuhosti ohýbaného prvku založenou na Lagrangeových součinitelích. Uvažujte lineární průběh průhybů w(x), lineární průběh pootočení ϕ y (x) a konstantní hodnotu γ xz na daném prvku. Ukažte, že po eliminaci γ xz získáte stejnou matici tuhosti jako u předchozích formulací. Prosba. V případě, že v textu objevíte nějakou chybu nebo budete mít námět na jeho vylepšení, ozvěte se prosím na zemanj@cml.fsv.cvut.cz.
23 11 METODA LANGRANGEOVÝCH SOUČNTELŮ 23 Opravy verze -001: str. 1, škrtnuto jedno mění, str. 2. v posledním řádku tabulky připsáno a škrtnuto ϕy (x), str. 5, 6, 13, 18, 20: jazykové úpravy, str. 15: přehozeni vědátoři podle věku, (na chyby upozornil J. Šejnoha), str. 9: připsána δ u váhy ϕy, str : prohození indexů u w 1 w 2 a ϕ 1 ϕ 2, (na chyby upozornila A. Kučerová), str. 5: prohození obrázků, str. 6, opraven člen Mz (opravy po přednášce) Opravy verze 000: str. 5, opraven vzorec v domácím úkolu (na chybu upozornila A. Somolová) str. 2: opraveno předmístění na přemístění, opraven člen x na z, str. 10: opravena matrice na matice (na chyby upozornil M. Wierer) Opravy verze 001: str. 2: opraven termín křivost na pseudokřivost (na chybu upozornil M. Kozel) Opravy verze 002: str. 3: nahrazeno v průměru výrazem ve smyslu průměrné energie smykových členů (vylepšení navrhl R. Valenta), str. 13: opraveno se na je (na chybu upozornil J. Skoček), str. 9: připsány členy δ u derivací váhových funkcí, str. 14: oprava obrázku (opravy po přednášce), str. 18: zpřesněn výraz pro váhovou funkci δλ Opravy verze 003: Nová formátovací makra, označeny důležité vztahy, opraveno označení pro řádkové matice z A na A. Doplněny opravy po předkladu do angličtiny, str. 2: smazáno jedno mění (na chybu upozornil M. Jandera), v celé přednášce zaměněno ztuhnutí na zamknutí (na chyby upozornil R. Pekař). Opravy verze 004: str. 14: opraven překlep v bernoulli-navierovském řešení (na chybu upozornil P. Hlaváček). Verze 005
24 REFERENCE 24 Reference [1] Z. Bittnar and J. Šejnoha, Numerické metody mechaniky, vol., ES ČVUT, Praha, [2] B. F. de Veubeke, Displacement and equilibrium models in the finite element method, nternational Journal for Numerical Methods in Engineering 52 (2001), , ediční řada Classic Reprints Series, původně publikováno v Stress Analysis (O. C. Zienkiewicz and G. S. Holister, editořı), John Wiley & Sons, [3] A. brahimbegović and F. Frey, Finite element analysis of linear and non-linear planar deformations of elastic initially curved beams, nternational Journal for Numerical Methods in Engineering 36 (1993), [4] R. D. Mindlin, nfluence of rotatory inertia and shear in flexural motions of isotropic elastic plates, Journal of Applied Mechanics 18 (1951),
25 REFERENCE 25 [5] E. Reissner, The effect of transverse shear deformation on the bending of elastic plates, Journal of Applied Mechanics 12 (1945), [6] S. Timoshenko, On the correction for shear of the differential equation for transverse vibrations of prismatic bars, Philosophical Magazine 41 (1921), [7] J. Šejnoha and J. Bittnarová, Pružnost a pevnost 10, Vydavatelství ČVUT, Praha, 1997.
1 Ohyb desek - mindlinovské řešení
 1 OHYB DESEK - MINDLINOVSKÉ ŘEŠENÍ 1 1 Ohyb desek - mindlinovské řešení Kinematika přemístění Posun w se po tloušťce desky mění málo (vzhledem k hodnotě průhybu) w(x, y, z) = w(x, y) Normály ke střednicové
1 OHYB DESEK - MINDLINOVSKÉ ŘEŠENÍ 1 1 Ohyb desek - mindlinovské řešení Kinematika přemístění Posun w se po tloušťce desky mění málo (vzhledem k hodnotě průhybu) w(x, y, z) = w(x, y) Normály ke střednicové
1 Stabilita prutových konstrukcí
 1 STABLTA PRUTOVÝCH KONSTRUKCÍ 1 1 Stabilita prutových konstrukcí Pod účinky tlakových sil dochází u štíhlých prutů k vybočení stabilitní problém Posuny ve směru střednice u a rotace ϕ y zůstávají malé,
1 STABLTA PRUTOVÝCH KONSTRUKCÍ 1 1 Stabilita prutových konstrukcí Pod účinky tlakových sil dochází u štíhlých prutů k vybočení stabilitní problém Posuny ve směru střednice u a rotace ϕ y zůstávají malé,
ROVINNÁ ÚLOHA. Všechny veličiny (geometrie, materiálové vlastnosti, zatížení) jsou nezávislé na jedné prostorové proměnné
 ROVINNÁ ÚLOHA Rovinná úloha Všechny veličiny (geometrie, materiálové vlastnosti, zatížení) jsou nezávislé na jedné prostorové proměnné Rovinná napjatost Rovinná deformace Rotačně symetrická úloha Rovinná
ROVINNÁ ÚLOHA Rovinná úloha Všechny veličiny (geometrie, materiálové vlastnosti, zatížení) jsou nezávislé na jedné prostorové proměnné Rovinná napjatost Rovinná deformace Rotačně symetrická úloha Rovinná
1 Modelování pružného podloží
 1 MODELOVÁNÍ PRUŽNÉHO PODLOŽÍ 1 1 Modelování pružného podloží Úloha mechaniky zemin Modely pružného podloží interakce podloží se základovými konstrukcemi Boussinesqův model (pružný poloprostor) [2]: homogenní
1 MODELOVÁNÍ PRUŽNÉHO PODLOŽÍ 1 1 Modelování pružného podloží Úloha mechaniky zemin Modely pružného podloží interakce podloží se základovými konstrukcemi Boussinesqův model (pružný poloprostor) [2]: homogenní
TENSOR NAPĚTÍ A DEFORMACE. Obrázek 1: Volba souřadnicového systému
 TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
Nosné desky. 1. Kirchhoffova teorie ohybu tenkých desek (h/l < 1/10) 3. Mindlinova teorie pro tlusté desky (h/l < 1/5)
 Nosné desky Deska je těleso, které má jeden rozměr mnohem menší než rozměry zbývající. Zatížení desky je orientováno výhradně kolmo k její střednicové rovině. 1. Kirchhoffova teorie ohybu tenkých desek
Nosné desky Deska je těleso, které má jeden rozměr mnohem menší než rozměry zbývající. Zatížení desky je orientováno výhradně kolmo k její střednicové rovině. 1. Kirchhoffova teorie ohybu tenkých desek
Rovinná úloha v MKP. (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v. prostorové úlohy: u, v, w
 Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
1 Přesnost metody konečných prvků
 1 PŘESNOST METODY KONEČNÝCH PRVKŮ 1 1 Přesnost metody konečných prvků Metoda konečných prvků je založena na diskretizaci původní spojité konstrukce soustavou prvků (nebo obecněji na diskretizaci slabé
1 PŘESNOST METODY KONEČNÝCH PRVKŮ 1 1 Přesnost metody konečných prvků Metoda konečných prvků je založena na diskretizaci původní spojité konstrukce soustavou prvků (nebo obecněji na diskretizaci slabé
Platnost Bernoulli Navierovy hypotézy
 Přednáška 03 Diferenciální rovnice ohybu prutu Platnost Bernoulli Navierovy hypotézy Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Příklady Copyright (c) 011 Vít Šmilauer
Přednáška 03 Diferenciální rovnice ohybu prutu Platnost Bernoulli Navierovy hypotézy Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Příklady Copyright (c) 011 Vít Šmilauer
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6
 OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
Dvě varianty rovinného problému: rovinná napjatost. rovinná deformace
 Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
1 Vedení tepla stacionární úloha
 1 VEDENÍ TEPLA STACIONÁRNÍ ÚLOHA 1 1 Vedení tepla stacionární úloha Typický představitel transportních jevů Obdobným způsobem možno řešit například Fyzikální jev Neznámá Difuze koncentrace [3] Deformace
1 VEDENÍ TEPLA STACIONÁRNÍ ÚLOHA 1 1 Vedení tepla stacionární úloha Typický představitel transportních jevů Obdobným způsobem možno řešit například Fyzikální jev Neznámá Difuze koncentrace [3] Deformace
FAKULTA STAVEBNÍ. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků
 Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 Obsah Variační principy
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 Obsah Variační principy
Platnost Bernoulli Navierovy hypotézy
 Přednáška 0 Platnost Bernoulli Navierovy hypotézy Diferenciální rovnice ohybu prutu Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Vliv teploty na průhyb a křivost prutu Příklady
Přednáška 0 Platnost Bernoulli Navierovy hypotézy Diferenciální rovnice ohybu prutu Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Vliv teploty na průhyb a křivost prutu Příklady
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady. Část 1 - Test
 Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Zjednodušená deformační metoda (2):
 Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA Bakalářské studium, 4. ročník Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA Bakalářské studium, 4. ročník Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
Lineární stabilita a teorie II. řádu
 Lineární stabilita a teorie II. řádu Sestavení podmínek rovnováhy na deformované konstrukci Konstrukce s a bez počáteční imperfekce Výpočet s malými vs. s velkými deformacemi ANKC-C 1 Zatěžovacídráhy [Šejnoha,
Lineární stabilita a teorie II. řádu Sestavení podmínek rovnováhy na deformované konstrukci Konstrukce s a bez počáteční imperfekce Výpočet s malými vs. s velkými deformacemi ANKC-C 1 Zatěžovacídráhy [Šejnoha,
Základy matematické teorie pružnosti Tenzor napětí a tenzor deformace Statické (Cauchyho) rovnice. Geometrické rovnice
 Přednáška 1 Základy matematické teorie pružnosti Tenzor napětí a tenzor deformace Statické (Cauchyho) rovnice Rozšířený Hookův zákon Geometrické rovnice Ondřej Jiroušek Ústav mechaniky a materiálů Fakulta
Přednáška 1 Základy matematické teorie pružnosti Tenzor napětí a tenzor deformace Statické (Cauchyho) rovnice Rozšířený Hookův zákon Geometrické rovnice Ondřej Jiroušek Ústav mechaniky a materiálů Fakulta
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
Vícerozměrné úlohy pružnosti
 Přednáška 07 Rovinná napjatost nosné stěny Rovinná deformace Hlavní napětí Mohrova kružnice Metoda konečných prvků pro rovinnou napjatost Laméovy rovnice Příklady Copyright (c) 011 Vít Šmilauer Czech Technical
Přednáška 07 Rovinná napjatost nosné stěny Rovinná deformace Hlavní napětí Mohrova kružnice Metoda konečných prvků pro rovinnou napjatost Laméovy rovnice Příklady Copyright (c) 011 Vít Šmilauer Czech Technical
FAKULTA STAVEBNÍ. Stavební statika. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Přednáška 2 pro kombinované studium Jiří Brožovský Kancelář: LP C 303/1 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Přednáška 2 pro kombinované studium Jiří Brožovský Kancelář: LP C 303/1 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
ÚVOD DO MODELOVÁNÍ V MECHANICE
 ÚVO O MOELOVÁNÍ V MECHNICE MECHNIK KOMPOZITNÍCH MTERIÁLŮ 2 Přednáška č. 7 Robert Zemčík 1 Zebry normální Zebry zdeformované 2 Zebry normální Zebry zdeformované 3 Zebry normální 4 Zebry zdeformované protažené?
ÚVO O MOELOVÁNÍ V MECHNICE MECHNIK KOMPOZITNÍCH MTERIÁLŮ 2 Přednáška č. 7 Robert Zemčík 1 Zebry normální Zebry zdeformované 2 Zebry normální Zebry zdeformované 3 Zebry normální 4 Zebry zdeformované protažené?
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady.
 Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
Rozdíly mezi MKP a MHP, oblasti jejich využití.
 Rozdíly mezi, oblasti jejich využití. Obě metody jsou vhodné pro určitou oblast problémů. základě MKP vyžaduje rozdělení těles na vhodný počet prvků, jejichž analýza je poměrně snadná a pro většinu částí
Rozdíly mezi, oblasti jejich využití. Obě metody jsou vhodné pro určitou oblast problémů. základě MKP vyžaduje rozdělení těles na vhodný počet prvků, jejichž analýza je poměrně snadná a pro většinu částí
PRUŽNOST A PEVNOST II
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ PRUŽNOST A PEVNOST II Navazující magisterské studium, 1. ročník Alois Materna (přednášky) Jiří Brožovský (cvičení) Kancelář: LP C 303/1
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ PRUŽNOST A PEVNOST II Navazující magisterské studium, 1. ročník Alois Materna (přednášky) Jiří Brožovský (cvičení) Kancelář: LP C 303/1
NOSNÍK NA PRUŽNÉM PODLOŽÍ (WINKLEROVSKÉM)
 NOSNÍK NA PRUŽNÉ PODLOŽÍ (WINKLEROVSKÉ) Uvažujeme spojitý nosník na pružných podporách. Pružná podpora - odpor je úměrný zatlačení. Pružné podpory velmi blízko sebe - jejich účinek lze nahradit spojitou
NOSNÍK NA PRUŽNÉ PODLOŽÍ (WINKLEROVSKÉ) Uvažujeme spojitý nosník na pružných podporách. Pružná podpora - odpor je úměrný zatlačení. Pružné podpory velmi blízko sebe - jejich účinek lze nahradit spojitou
OHYB (Napjatost) M A M + qc a + b + c ) M A = 2M qc a + b + c )
 3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
Martin NESLÁDEK. 14. listopadu 2017
 Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Přednáška 08. Obecná trojosá napjatost. Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův zákon Příklad zemní tlak v klidu
 Přednáška 08 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův ákon Příklad emní tlak v klidu Copyright (c) 2011 Vít Šmilauer Cech Technical University in
Přednáška 08 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův ákon Příklad emní tlak v klidu Copyright (c) 2011 Vít Šmilauer Cech Technical University in
Stavební mechanika 3 132SM3 Přednášky. Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků.
 Stavební mechanika 12SM Přednášky Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků. Porovnání ODM a ZDM Příklad 1: (viz předchozí přednáška)
Stavební mechanika 12SM Přednášky Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků. Porovnání ODM a ZDM Příklad 1: (viz předchozí přednáška)
ÚVOD DO MODELOVÁNÍ V MECHANICE
 ÚVOD DO MODELOVÁNÍ V MECHANICE PRUŽNOST A PEVNOST Přednáška č. 5 Prof. Ing. Vladislav Laš. CSc. MECHANIKA PODDAJNÝCH TĚLES Úkolem PP z inženýrského hlediska je navrhnout součásti nebo konstrukce, které
ÚVOD DO MODELOVÁNÍ V MECHANICE PRUŽNOST A PEVNOST Přednáška č. 5 Prof. Ing. Vladislav Laš. CSc. MECHANIKA PODDAJNÝCH TĚLES Úkolem PP z inženýrského hlediska je navrhnout součásti nebo konstrukce, které
Přednáška č. 5: Jednorozměrné ustálené vedení tepla
 Přednáška č. 5: Jednorozměrné ustálené vedení tepla Motivace Diferenciální rovnice problému Gradient teploty Energetická bilance Fourierův zákon Diferenciální rovnice vedení tepla Slabé řešení Diskretizace
Přednáška č. 5: Jednorozměrné ustálené vedení tepla Motivace Diferenciální rovnice problému Gradient teploty Energetická bilance Fourierův zákon Diferenciální rovnice vedení tepla Slabé řešení Diskretizace
Přednáška 10. Kroucení prutů
 Přednáška 10 Kroucení prutů 1) Kroucení prutu s kruhovým průřezem 2) Volné kroucení prutu s průřezem a) Masivním b) Tenkostěnným otevřeným, střed smyku c) Tenkostěnným uzavřeným 3) Ohybové (vázané) kroucení
Přednáška 10 Kroucení prutů 1) Kroucení prutu s kruhovým průřezem 2) Volné kroucení prutu s průřezem a) Masivním b) Tenkostěnným otevřeným, střed smyku c) Tenkostěnným uzavřeným 3) Ohybové (vázané) kroucení
Rekapitulace princip virtuálních sil pro tah/tlak
 SMA Přednáška Doplňková virtuální práce momentů Metody integrace dvou spojitých funkcí Doplňková virtuální práce posouvajících sil Vliv rovnoměrné a nerovnoměrné teploty Formulace principu virtuálních
SMA Přednáška Doplňková virtuální práce momentů Metody integrace dvou spojitých funkcí Doplňková virtuální práce posouvajících sil Vliv rovnoměrné a nerovnoměrné teploty Formulace principu virtuálních
Přednáška 08. Obecná trojosá napjatost
 Přednáška 8 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův zákon Objemový modul pružnosti Oedometrický modul pružnosti Hlavní napětí, hlavní deformace
Přednáška 8 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův zákon Objemový modul pružnosti Oedometrický modul pružnosti Hlavní napětí, hlavní deformace
Betonové konstrukce (S) Přednáška 3
 Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Princip virtuálních posunutí (obecný princip rovnováhy)
 SMA2 Přednáška 05 Princip virtuálních posunutí Deformační metoda Matice tuhosti prutu pro tah/tlak Matice tuhosti prutu pro ohyb Program EduBeam Příklady Copyright (c) 2012 Vít Šmilauer Czech Technical
SMA2 Přednáška 05 Princip virtuálních posunutí Deformační metoda Matice tuhosti prutu pro tah/tlak Matice tuhosti prutu pro ohyb Program EduBeam Příklady Copyright (c) 2012 Vít Šmilauer Czech Technical
Pružnost a pevnost. 2. přednáška, 10. října 2016
 Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění )
 1 Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění ) 1. Rozšířený Hookeův zákon pro jednoosou napjatost Základním materiálovým vztahem lineární teorie pružnosti
1 Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění ) 1. Rozšířený Hookeův zákon pro jednoosou napjatost Základním materiálovým vztahem lineární teorie pružnosti
PRUŽNOST A PLASTICITA I
 Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
12. Prostý krut Definice
 p12 1 12. Prostý krut 12.1. Definice Prostý krut je označení pro namáhání přímého prizmatického prutu, jestliže jsou splněny prutové předpoklady, příčné průřezy se nedeformují, pouze se vzájemně natáčejí
p12 1 12. Prostý krut 12.1. Definice Prostý krut je označení pro namáhání přímého prizmatického prutu, jestliže jsou splněny prutové předpoklady, příčné průřezy se nedeformují, pouze se vzájemně natáčejí
Princip virtuálních prací (PVP)
 Zatěžujme pružinu o tuhosti k silou F k ū F Princip virtuálních prací (PVP) 1 ū u Energie pružné deformace W ext (skalár) je definována jako součin konstantní síly a posunu. Protože se zde síla během posunu
Zatěžujme pružinu o tuhosti k silou F k ū F Princip virtuálních prací (PVP) 1 ū u Energie pružné deformace W ext (skalár) je definována jako součin konstantní síly a posunu. Protože se zde síla během posunu
Téma 12, modely podloží
 Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Optimalizace vláknového kompozitu
 Optimalizace vláknového kompozitu Bc. Jan Toman Vedoucí práce: doc. Ing. Tomáš Mareš, Ph.D. Abstrakt Optimalizace trubkového profilu z vláknového kompozitu při využití Timošenkovy hypotézy. Hledání optimálního
Optimalizace vláknového kompozitu Bc. Jan Toman Vedoucí práce: doc. Ing. Tomáš Mareš, Ph.D. Abstrakt Optimalizace trubkového profilu z vláknového kompozitu při využití Timošenkovy hypotézy. Hledání optimálního
DIPLOMOVÁ PRÁCE. České vysoké učení technické v Praze Fakulta stavební. Prvky pro analýzu deskových a skořepinových konstrukcí.
 České vysoké učení technické v Praze Fakulta stavební katedra mechaniky DIPLOMOVÁ PRÁCE Prvky pro analýzu deskových a skořepinových konstrukcí Autor: Bc. Edita Dvořáková Vedoucí práce: Prof. Dr. Ing. Bořek
České vysoké učení technické v Praze Fakulta stavební katedra mechaniky DIPLOMOVÁ PRÁCE Prvky pro analýzu deskových a skořepinových konstrukcí Autor: Bc. Edita Dvořáková Vedoucí práce: Prof. Dr. Ing. Bořek
13. Prostý ohyb Definice
 p13 1 13. Prostý ohyb 13.1. Definice Prostý ohyb je označení pro namáhání přímého prizmatického prutu, jestliže jsou splněny prutové předpoklady, příčné průřezy se vzájemně natáčejí kolem osy ležící v
p13 1 13. Prostý ohyb 13.1. Definice Prostý ohyb je označení pro namáhání přímého prizmatického prutu, jestliže jsou splněny prutové předpoklady, příčné průřezy se vzájemně natáčejí kolem osy ležící v
Princip virtuálních posunutí (obecný princip rovnováhy)
 SMA Přednáška 5 Princip virtuálních posunutí Deformační metoda Matice tuhosti prutu pro tahtlak Matice tuhosti prutu pro ohyb Program EduBeam Příklady Copyright (c) Vít Šmilauer Czech Technical University
SMA Přednáška 5 Princip virtuálních posunutí Deformační metoda Matice tuhosti prutu pro tahtlak Matice tuhosti prutu pro ohyb Program EduBeam Příklady Copyright (c) Vít Šmilauer Czech Technical University
písemky (3 příklady) Výsledná známka je stanovena zkoušejícím na základě celkového počtu bodů ze semestru, ze vstupního testu a z písemky.
 POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy
![Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy](/thumbs/97/130835283.jpg) Aproimace posuvů Pro každý prvek se musí nalézt vztahy kde jsou prozatím neznámé transformační matice. Neznámé funkce posuvů se obvykle aproimují ve formě mnohočlenů kartézských souřadnic. Například 1.
Aproimace posuvů Pro každý prvek se musí nalézt vztahy kde jsou prozatím neznámé transformační matice. Neznámé funkce posuvů se obvykle aproimují ve formě mnohočlenů kartézských souřadnic. Například 1.
Katedra geotechniky a podzemního stavitelství
 Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Náhradní ohybová tuhost nosníku
 Náhradní ohybová tuhost nosníku Autoři: Doc. Ing. Jiří PODEŠVA, Ph.D., Katedra mechaniky, Fakulta strojní, VŠB - Technická univerzita Ostrava, e-mail: jiri.podesva@vsb.cz Anotace: Výpočty ocelových výztuží
Náhradní ohybová tuhost nosníku Autoři: Doc. Ing. Jiří PODEŠVA, Ph.D., Katedra mechaniky, Fakulta strojní, VŠB - Technická univerzita Ostrava, e-mail: jiri.podesva@vsb.cz Anotace: Výpočty ocelových výztuží
Pružnost a plasticita II CD03
 Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
ANALÝZA KONSTRUKCÍ. 5. přednáška
 ANALÝZA KONSTRUKCÍ 5. přednáška Nosné stěny rovinná napjatost Způsoby výpočtu napjatosti: Deformační metodou Primární neznámé: posuny u(,y), v(,y) Výchozí rovnice: statické Silovou metodou Primární neznámá:
ANALÝZA KONSTRUKCÍ 5. přednáška Nosné stěny rovinná napjatost Způsoby výpočtu napjatosti: Deformační metodou Primární neznámé: posuny u(,y), v(,y) Výchozí rovnice: statické Silovou metodou Primární neznámá:
Pružnost a pevnost. zimní semestr 2013/14
 Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil
 Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Vliv okrajových podmínek na tvar ohybové čáry
 Vliv okrajových podmínek na tvar ohybové čáry Petr Havlásek 213 1 Co budeme zkoumat? Tvar deformované střednice při zatížení osamělou silou v polovině rozpětí o prostě podepřeného nosníku (KK) o oboustranně
Vliv okrajových podmínek na tvar ohybové čáry Petr Havlásek 213 1 Co budeme zkoumat? Tvar deformované střednice při zatížení osamělou silou v polovině rozpětí o prostě podepřeného nosníku (KK) o oboustranně
Projevy dotvarování na konstrukcích (na úrovni průřezových modelů)
 PŘEDNÁŠKY Projevy dotvarování na konstrukcích (na úrovni průřezových modelů) Volné dotvarování Vázané dotvarování Dotvarování a geometrická nelinearita Volné dotvarování Vývoj deformací není omezován staticky
PŘEDNÁŠKY Projevy dotvarování na konstrukcích (na úrovni průřezových modelů) Volné dotvarování Vázané dotvarování Dotvarování a geometrická nelinearita Volné dotvarování Vývoj deformací není omezován staticky
Vlastnosti a zkoušení materiálů. Přednáška č.4 Úvod do pružnosti a pevnosti
 Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
16. Matematický popis napjatosti
 p16 1 16. Matematický popis napjatosti Napjatost v bodě tělesa jsme definovali jako množinu obecných napětí ve všech řezech, které lze daným bodem tělesa vést. Pro jednoznačný matematický popis napjatosti
p16 1 16. Matematický popis napjatosti Napjatost v bodě tělesa jsme definovali jako množinu obecných napětí ve všech řezech, které lze daným bodem tělesa vést. Pro jednoznačný matematický popis napjatosti
Konstrukční systémy vícepodlažních budov Přednáška 5 Stěnové systémy Doc. Ing. Hana Gattermayerová,CSc Obsah
 Konstrukční systémy vícepodlažních budov Přednáška 5 Doc. Ing. Hana Gattermayerová,CSc gatter@fsv.cvut.cz Literatura Obsah Rojík: Konstrukční systémy vícepodlažních budov, CVUT 1979, předběžné a podrobné
Konstrukční systémy vícepodlažních budov Přednáška 5 Doc. Ing. Hana Gattermayerová,CSc gatter@fsv.cvut.cz Literatura Obsah Rojík: Konstrukční systémy vícepodlažních budov, CVUT 1979, předběžné a podrobné
Prostorové konstrukce. neznámé parametry: u, v w. (prvky se středostranovými uzly)
 Konečné prvk pro řešení 3D úloh Prostorové konstrukce neznámé parametr: u, v w volba různého počtu uzlů a neznámých v uzlech možnost zakřivených hran prvků (prvk se středostranovými uzl) Opakování: Geometrické
Konečné prvk pro řešení 3D úloh Prostorové konstrukce neznámé parametr: u, v w volba různého počtu uzlů a neznámých v uzlech možnost zakřivených hran prvků (prvk se středostranovými uzl) Opakování: Geometrické
1 Zatížení konstrukcí teplotou
 1 ZATÍŽENÍ KONSTRUKCÍ TEPLOTOU 1 1 Zatížení konstrukcí teplotou Časově proměnné nepřímé zatížení Klimatické vlivy, zatížení stavebních konstrukcí požárem Účinky zatížení plynou z rozšířeného Hookeova zákona
1 ZATÍŽENÍ KONSTRUKCÍ TEPLOTOU 1 1 Zatížení konstrukcí teplotou Časově proměnné nepřímé zatížení Klimatické vlivy, zatížení stavebních konstrukcí požárem Účinky zatížení plynou z rozšířeného Hookeova zákona
Příklad 7 Průhyb nosníku - složitější případ
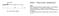 Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
vztažný systém obecné napětí předchozí OBSAH další
 p05 1 5. Deformace těles S deformací jako složkou mechanického pohybu jste se setkali už ve statice. Běžně je chápána jako změna rozměrů a tvaru tělesa. Lze ji popsat změnami vzdáleností různých dvou bodů
p05 1 5. Deformace těles S deformací jako složkou mechanického pohybu jste se setkali už ve statice. Běžně je chápána jako změna rozměrů a tvaru tělesa. Lze ji popsat změnami vzdáleností různých dvou bodů
Kˇriv e pruty Martin Fiˇser Martin Fiˇ ser Kˇ riv e pruty
 Obsah Dimenzování křivého tenkého prutu zde Deformace v daném místě prutu zde Castiglianova věta zde Dimenzování křivého tenkého prutu Mějme obecný křivý prut z homogeního izotropního materiálu. Obrázek:
Obsah Dimenzování křivého tenkého prutu zde Deformace v daném místě prutu zde Castiglianova věta zde Dimenzování křivého tenkého prutu Mějme obecný křivý prut z homogeního izotropního materiálu. Obrázek:
7. Základní formulace lineární PP
 p07 1 7. Základní formulace lineární PP Podle tvaru závislosti mezi vnějšími silami a deformačně napěťovými parametry tělesa dělíme pružnost a pevnost na lineární a nelineární. Lineární pružnost vyšetřuje
p07 1 7. Základní formulace lineární PP Podle tvaru závislosti mezi vnějšími silami a deformačně napěťovými parametry tělesa dělíme pružnost a pevnost na lineární a nelineární. Lineární pružnost vyšetřuje
Teorie tkaní. Modely vazného bodu. M. Bílek
 Teorie tkaní Modely vazného bodu M. Bílek 2016 Základní strukturální jednotkou tkaniny je vazný bod, tj. oblast v okolí jednoho zakřížení osnovní a útkové nitě. Proces tkaní tedy spočívá v tvorbě vazných
Teorie tkaní Modely vazného bodu M. Bílek 2016 Základní strukturální jednotkou tkaniny je vazný bod, tj. oblast v okolí jednoho zakřížení osnovní a útkové nitě. Proces tkaní tedy spočívá v tvorbě vazných
Obr. 0.1: Nosník se spojitým zatížením.
 Každý test obsahuje jeden příklad podobný níže uvedeným tpovým příkladům a několik otázek vbraných z níže uvedených testových otázek. Za příklad je možno získat maimálně bodů, celkový počet bodů z testu
Každý test obsahuje jeden příklad podobný níže uvedeným tpovým příkladům a několik otázek vbraných z níže uvedených testových otázek. Za příklad je možno získat maimálně bodů, celkový počet bodů z testu
Pružnost a pevnost I
 Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
Přednáška 10. Kroucení prutů
 Přednáška 1 Kroucení prutů 1) Kroucení prutu s kruhovým průřezem ) Volné kroucení prutu s průřezem a) Masivním b) Tenkostěnným otevřeným c) Tenkostěnným uzavřeným ) Ohybové (vázané) kroucení Příklady Copyright
Přednáška 1 Kroucení prutů 1) Kroucení prutu s kruhovým průřezem ) Volné kroucení prutu s průřezem a) Masivním b) Tenkostěnným otevřeným c) Tenkostěnným uzavřeným ) Ohybové (vázané) kroucení Příklady Copyright
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí
 Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
Ztráta stability tenkých přímých prutů - vzpěr
 Ztráta stability tenkých přímých prutů - vzpěr Motivace štíhlé pruty namáhané tlakem mohou vybočit ze svého původně přímého tvaru a může dojít ke ztrátě stability a zhroucení konstrukce dříve, než je dosaženo
Ztráta stability tenkých přímých prutů - vzpěr Motivace štíhlé pruty namáhané tlakem mohou vybočit ze svého původně přímého tvaru a může dojít ke ztrátě stability a zhroucení konstrukce dříve, než je dosaženo
STAVEBNÍ MECHANIKA 3 - SM 3
 STAVEBNÍ MECHANIKA 3 - SM 3 Základní předměty vyučované na katedrě mechaniky a jejich vzájemná vazba SM1, SM2 - výpočet reakcí na staticky určitých konstrukcích, výpočet průběhů vnitřních sil na staticky
STAVEBNÍ MECHANIKA 3 - SM 3 Základní předměty vyučované na katedrě mechaniky a jejich vzájemná vazba SM1, SM2 - výpočet reakcí na staticky určitých konstrukcích, výpočet průběhů vnitřních sil na staticky
Desky. Petr Kabele. Pružnost a pevnost 132PRPE Přednášky. Deska/stěna/skořepina, desky základní předpoklady, proměnné a rovnice
 Pružnost a pevnost 13PRPE Přednášk Desk Deska/stěna/skořepina, desk ákladní předpoklad, proměnné a rovnice Petr Kabele České vsoké učení technické v Prae Fakulta stavební Úvod Přemístění, deformaci a napjatost
Pružnost a pevnost 13PRPE Přednášk Desk Deska/stěna/skořepina, desk ákladní předpoklad, proměnné a rovnice Petr Kabele České vsoké učení technické v Prae Fakulta stavební Úvod Přemístění, deformaci a napjatost
2 Odvození pomocí rovnováhy sil
 Řetězovka Abstrakt: Ukážeme si, že řetěz pověšený mezi dvěma body v homogenním gravitačním poli se prohne ve tvaru grafu funkce hyperbolický kosinus. Odvození provedeme dvojím způsobem: pomocí rovnováhy
Řetězovka Abstrakt: Ukážeme si, že řetěz pověšený mezi dvěma body v homogenním gravitačním poli se prohne ve tvaru grafu funkce hyperbolický kosinus. Odvození provedeme dvojím způsobem: pomocí rovnováhy
POŽADAVKY KE ZKOUŠCE Z PP I
 POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze o vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze o vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
Statika 1. Vnitřní síly na prutech. Miroslav Vokáč 11. dubna ČVUT v Praze, Fakulta architektury. Statika 1. M.
 Definování 4. přednáška prutech iroslav okáč miroslav.vokac@cvut.cz ČUT v Praze, Fakulta architektury 11. dubna 2016 prutech nitřní síly síly působící uvnitř tělesa (desky, prutu), které vznikají působením
Definování 4. přednáška prutech iroslav okáč miroslav.vokac@cvut.cz ČUT v Praze, Fakulta architektury 11. dubna 2016 prutech nitřní síly síly působící uvnitř tělesa (desky, prutu), které vznikají působením
Nauka o materiálu. Přednáška č.4 Úvod do pružnosti a pevnosti
 Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
3. kapitola. Průběhy vnitřních sil na lomeném nosníku. Janek Faltýnek SI J (43) Teoretická část: Příkladová část: Stavební mechanika 2
 3. kapitola Stavební mechanika Janek Faltýnek SI J (43) Průběhy vnitřních sil na lomeném nosníku Teoretická část: Naším úkolem je v tomto příkladu vyšetřit průběh vnitřních sil na lomeném rovinném nosníku
3. kapitola Stavební mechanika Janek Faltýnek SI J (43) Průběhy vnitřních sil na lomeném nosníku Teoretická část: Naším úkolem je v tomto příkladu vyšetřit průběh vnitřních sil na lomeném rovinném nosníku
Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření
 Pružnost a plasticita, 2.ročník kombinovaného studia Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření Základní pojmy, výchozí předpoklady Vztahy mezi vnitřními silami a napětími v průřezu
Pružnost a plasticita, 2.ročník kombinovaného studia Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření Základní pojmy, výchozí předpoklady Vztahy mezi vnitřními silami a napětími v průřezu
6. Statika rovnováha vázaného tělesa
 6. Statika rovnováha vázaného tělesa 6.1 Rovnováha vázaného tělesa Těleso je vystaveno působení vnějších sil akčních, kterými mohou být osamělé síly, spojité zatížení a momenty silových dvojic. Akční síly
6. Statika rovnováha vázaného tělesa 6.1 Rovnováha vázaného tělesa Těleso je vystaveno působení vnějších sil akčních, kterými mohou být osamělé síly, spojité zatížení a momenty silových dvojic. Akční síly
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Metoda konečných prvků 2
 Nelineární analýza materiálů a konstrukcí (V-132YNAK) Metoda konečných prvků 2 Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 1 Obsah Gaussova numerická integrace
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Metoda konečných prvků 2 Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 1 Obsah Gaussova numerická integrace
Statika soustavy těles.
 Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
Kontraktantní/dilatantní
 Kontraktantní/dilatantní plasticita - úhel dilatance směr přírůstku plastické deformace Na základě experimentálního měření dospěl St. Venant k závěru, že směry hlavních napětí jsou totožné se směry přírůstku
Kontraktantní/dilatantní plasticita - úhel dilatance směr přírůstku plastické deformace Na základě experimentálního měření dospěl St. Venant k závěru, že směry hlavních napětí jsou totožné se směry přírůstku
1 ÚVOD 1. Odolání vlivům se prokazuje statickým resp. dynamickým výpočtem.
 1 ÚVOD 1 1 Úvod Stavební konstrukce musí být navržena (a provedena) tak, aby vyhovovala požadovanému účelu a odolala vlivům, které se mohou vyskytnout během její životnosti. Odolání vlivům se prokazuje
1 ÚVOD 1 1 Úvod Stavební konstrukce musí být navržena (a provedena) tak, aby vyhovovala požadovanému účelu a odolala vlivům, které se mohou vyskytnout během její životnosti. Odolání vlivům se prokazuje
Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření
 Pružnost a plasticita, 2.ročník kombinovaného studia Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření Základní pojmy, výchozí předpoklady Vztahy mezi vnitřními silami a napětími v průřezu
Pružnost a plasticita, 2.ročník kombinovaného studia Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření Základní pojmy, výchozí předpoklady Vztahy mezi vnitřními silami a napětími v průřezu
Stavební mechanika přednáška, 10. dubna 2017
 Stavební mechanika 3 7. přednáška, 10. dubna 2017 Stavební mechanika 3 7. přednáška, 10. dubna 2017 Obecná deformační metoda 8) poznámky k využití symetrie 9) využití výpočetních programů 10) kontrola
Stavební mechanika 3 7. přednáška, 10. dubna 2017 Stavební mechanika 3 7. přednáška, 10. dubna 2017 Obecná deformační metoda 8) poznámky k využití symetrie 9) využití výpočetních programů 10) kontrola
8. Okrajový problém pro LODR2
 8. Okrajový problém pro LODR2 A. Základní poznatky o soustavách ODR1 V kapitole 6 jsme zavedli pojem lineární diferenciální rovnice n-tého řádu, která je pro n = 2 tvaru A 2 (x)y + A 1 (x)y + A 0 (x)y
8. Okrajový problém pro LODR2 A. Základní poznatky o soustavách ODR1 V kapitole 6 jsme zavedli pojem lineární diferenciální rovnice n-tého řádu, která je pro n = 2 tvaru A 2 (x)y + A 1 (x)y + A 0 (x)y
Jednoosá tahová zkouška betonářské oceli
 Přednáška 06 Nepružné chování materiálu Ideálně pružnoplastický model Plastická analýza průřezu ohýbaného prutu Mezní plastický stav konstrukce Plastický kloub Interakční diagram N, M Příklady Copyright
Přednáška 06 Nepružné chování materiálu Ideálně pružnoplastický model Plastická analýza průřezu ohýbaného prutu Mezní plastický stav konstrukce Plastický kloub Interakční diagram N, M Příklady Copyright
Vícerozměrné úlohy pružnosti
 Přednáška 07 Víceroměrné úlohy Rovinná napjatost a deformace Hlavní napětí Mohrova kružnice Metoda konečných prvků pro úlohu rovinné napjatosti Příklady Copyright (c) 0 Vít Šmilauer Cech Technical University
Přednáška 07 Víceroměrné úlohy Rovinná napjatost a deformace Hlavní napětí Mohrova kružnice Metoda konečných prvků pro úlohu rovinné napjatosti Příklady Copyright (c) 0 Vít Šmilauer Cech Technical University
Přednáška 1 Obecná deformační metoda, podstata DM
 Statika stavebních konstrukcí II., 3.ročník bakalářského studia Přednáška 1 Obecná deformační metoda, podstata DM Základní informace o výuce předmětu SSK II Metody řešení staticky neurčitých konstrukcí
Statika stavebních konstrukcí II., 3.ročník bakalářského studia Přednáška 1 Obecná deformační metoda, podstata DM Základní informace o výuce předmětu SSK II Metody řešení staticky neurčitých konstrukcí
Přetvořené ose nosníku říkáme ohybová čára. Je to rovinná křivka.
 OHYBOVÁ ČÁRA ZA PROSTÉHO OHYBU - rovinné průřez zůstávají po deformaci rovinnými, avšak natáčejí se. - při prostém ohbu hlavní centrální osa setrvačnosti všech průřezů leží v rovině vnějších sil, která
OHYBOVÁ ČÁRA ZA PROSTÉHO OHYBU - rovinné průřez zůstávají po deformaci rovinnými, avšak natáčejí se. - při prostém ohbu hlavní centrální osa setrvačnosti všech průřezů leží v rovině vnějších sil, která
OTÁZKY VSTUPNÍHO TESTU PP I LS 2010/2011
 OTÁZKY VSTUPNÍHO TESTU PP I LS 010/011 Pomocí Thumovy definice, s využitím vrubové citlivosti q je definován vztah mezi součiniteli vrubu a tvaru jako: Součinitel tvaru α je podle obrázku definován jako:
OTÁZKY VSTUPNÍHO TESTU PP I LS 010/011 Pomocí Thumovy definice, s využitím vrubové citlivosti q je definován vztah mezi součiniteli vrubu a tvaru jako: Součinitel tvaru α je podle obrázku definován jako:
Definujte poměrné protažení (schematicky nakreslete a uved te jednotky) Napište hlavní kroky postupu při posouzení prutu na vzpěrný tlak.
 00001 Definujte mechanické napětí a uved te jednotky. 00002 Definujte normálové napětí a uved te jednotky. 00003 Definujte tečné (tangenciální, smykové) napětí a uved te jednotky. 00004 Definujte absolutní
00001 Definujte mechanické napětí a uved te jednotky. 00002 Definujte normálové napětí a uved te jednotky. 00003 Definujte tečné (tangenciální, smykové) napětí a uved te jednotky. 00004 Definujte absolutní
3.2.2 Navierova-Bernoulliho hypotéza
 3.. JEDNODUCHÝ OHYB 57 3.. Navierova-Bernoulliho hypotéza V předchozím článku jsme vyslovili hypotézu o zachování rovinnosti průřezu, která umožnila pracovat s představou pootočení průřezu a definovat
3.. JEDNODUCHÝ OHYB 57 3.. Navierova-Bernoulliho hypotéza V předchozím článku jsme vyslovili hypotézu o zachování rovinnosti průřezu, která umožnila pracovat s představou pootočení průřezu a definovat
Kinematická metoda výpočtu reakcí staticky určitých soustav
 Kinematická metoda výpočtu reakcí staticky určitých soustav 1) Uvolnění jednoho stupně volnosti odpovídající reakci, kterou chceme určit (vytvoření kinematického mechanismu o jednom stupni volnosti). Zavedení
Kinematická metoda výpočtu reakcí staticky určitých soustav 1) Uvolnění jednoho stupně volnosti odpovídající reakci, kterou chceme určit (vytvoření kinematického mechanismu o jednom stupni volnosti). Zavedení
Mechanika kontinua. Mechanika elastických těles Mechanika kapalin
 Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
TA Sanace tunelů - technologie, materiály a metodické postupy Zesilování Optimalizace
 Jaroslav Lacina, Martin Zlámal SANACE TUNELŮ TECHNOLOGIE A MATERIÁLY, SPÁROVACÍ HMOTY PRO OSTĚNÍ TA03030851 Sanace tunelů - technologie, materiály a metodické postupy Zesilování Optimalizace Petr ŠTĚPÁNEK,
Jaroslav Lacina, Martin Zlámal SANACE TUNELŮ TECHNOLOGIE A MATERIÁLY, SPÁROVACÍ HMOTY PRO OSTĚNÍ TA03030851 Sanace tunelů - technologie, materiály a metodické postupy Zesilování Optimalizace Petr ŠTĚPÁNEK,
