Zkoušková písemná práce č. 1 z předmětu 01MAB3
|
|
|
- Ladislav Kučera
- před 8 lety
- Počet zobrazení:
Transkript
1 Katedra matematiky Fakulty jaderé a fyzikálě ižeýrské ČVUT v Praze Příjmeí a jméo BONUS CELKEM (13 bodů) Zkoušková písemá práce č. 1 z předmětu 01MAB3 14. leda 2016, 9:00 11:00 Pro kvadratickou plochu x 2 4xy + 5y 2 + 2xz + 2yz + 10z 2 + 2y + 4z = 3 určete hlaví a vedlejší sigaturu a ormálí tvar včetě afií trasformace (x, y, z) T = M (a, b, c) T + (r, s, t) T, která ji a teto tvar převádí. Jaký je ázev této kvadriky? Pokud je kvadrika cetrálí, určete její střed. (10 bodů) Rozhoděte, zda platí rovost d dx + Korektě a velmi detailě zdůvoděte!! (10 bodů) Nalezěte obecé řešeí difereciálí rovice ( 1) ( ) 2x2 + 4 = ( 1) +1 1 x R. 2 2x x 2 y ( 5x 2 + 4x ) y + ( 6x x + 6 ) y = 0 i difereciálí rovice y 6y + 12y 8y = 0. Nápověda: Rovice jsou sestaveé tak, že mají eprázdý průik fudametálích systémů. (10 bodů) Nalezěte Maclauriovu řadu fukce a její obor kovergece. f (x) = l ( x x 2) (7 bodů) Představte si, že cestujete po prostoru spojitých fukcí C ( 0, 1 ), kde je defiová skalárí souči f g = 1 0 f (x) g (x) dx f, g C ( 0, 2π ), který idukuje (geeruje) příslušou ormu a metriku. Chcete se dostat z bodu θ do bodu h a a mapě zjistíte, že můžete cestovat bud přes f, ebo přes g. Přitom x 0, 1 platí Která z těchto dvou cest je kratší? θ (x) = 0, h (x) = x 2, f (x) = x + 1, g (x) = 2x.
2 Pokyy k vypracováí: Na začátku máte k dispozici 10 papírů. O další papíry si v případě potřeby eváhejte říci hlídajícímu. Odevzdávejte pouze papíry, které obsahují fiálí řešeí příkladů (ikoliv pomocé pozámky apod.) Začíejte každý příklad a ovém papíru. Na každý papír apište do pravého horího rohu svoje jméo a do levého horího rohu výrazě vyzačte číslo příkladu. Pište čitelě a myšleky formulujte srozumitelě! Příklad: Vypočítejte obor kovergece mocié řady + Správá argumetace: Nejprve poloměr kovergece: +1 L = lim = lim = = R = 1 = 1 L = O = / 1, 1/ (kde "/" je čárkovaá závorka - zatím evíme, zda kulatá či hraatá) a zbývá vyšetřit krají body: pro x = 1: + 1 = +..diverguje - eí splěa utá podm. kovergece. pro x = 1: + ( 1) diverguje ze stejého důvodu =. x Špatá (zcela zmateá) argumetace: 1 R = lim +1 = = 1 kraje: divg. (to je vidět) (zde lze je "tušit", jak je to asi myšleo) Opravující mají právo vyloučit z opravováí písemé práce, resp. jejich části, které esplňují uvedeé pokyy. Bodové hodoceí takové práce, resp. její části, je 0 bodů.
3 Katedra matematiky Fakulty jaderé a fyzikálě ižeýrské ČVUT v Praze Příjmeí a jméo BONUS CELKEM (9 bodů) Zkoušková písemá práce č. 2 z předmětu 01MAB3 21. leda 2016, 9:00 11:00 Sestavte mociou řadu, jejíž součet je rove itegrálu I (x) = x 0 1 e t2 dt a určete její obor kovergece O. Dále rozhoděte, zda uvedeá řada stejoměrě koverguje a O. Velmi pečlivě zdůvoděte všechy kroky. (9 bodů) Načrtěte možiu M ( ) R 2, ρ 2 zadaou předpisem M = (A B) \ (A B), kde {( A = 1, 1) (0, 2), B = ) x, 2x 2 R 2 x R}. Poté ačrtěte a pomocí matematických formulí (tj. podobě jako v defiici samoté M) popište možiy C = M 0, D = M, E = der ( M 0), F = (der (M)) 0. Nakoec ajděte předpis pro metriku χ (x, y) tak, aby χu 5 ((0, 1)) = F. Pokyy k áčrtkům: Nakreslete osy souřadé soustavy. Plou čarou vyzačte hraici možiy, která do í patří, přerušovaou čarou hraici, která do í epatří. Kde je to potřebé, vyzačte plým kolečkem bod, který do možiy patří, prázdým kolečkem bod, který do í epatří. Plochu patřící do možiy vyšrafujte. (11 bodů) Pro kvadratickou plochu x z + 6xz 5 2y + 17z 2 + 4x + 2y 2 2xy = 0 v prostoru R 3 staovte hlaví a vedlejší sigaturu, ormálí tvar a ázev. Najděte vektory příslušé polárí báze. Rozhoděte, zda jde o plochu cetrálí a pokud ao, příslušý střed vypočítejte. Pozámka: Numerické chyby se v tomto příkladě etolerují! (9 bodů) Nalezěte obecé řešeí difereciálí rovice x 2 y 2x (1 + x) y + 2 (1 + x) y = 8x 3 e 2x. Nápověda: Můžete použít fakt, že příslušou rovici s ulovou pravou straou řeší fukce v (x) = x. t 2 Pokračováí a další stráce!
4 (12 bodů) Nalezěte ortoormálí bázi podprostoru [ ] p0, p 1, p 2 λ C ( 0, + )) kde p 0 (x) = 3, p 1 (x) = π + ex, p 2 (x) = e + πx + eπx 2. Skalárí souči je a C ( 0, + )) zavede vztahem + f g = xe x f (x) g (x) dx. Nápověda: 1) Jak vypadají prvky lieárího obalu [ p 0, p 1, p 2 ]λ? 2) Čemu se rová I = x e x dx? Pokyy k vypracováí: Na začátku máte k dispozici 10 papírů. O další papíry si v případě potřeby eváhejte říci hlídajícímu. Odevzdávejte pouze papíry, které obsahují fiálí řešeí příkladů (ikoliv pomocé pozámky apod.) Začíejte každý příklad a ovém papíru. Na každý papír apište do pravého horího rohu svoje jméo a do levého horího rohu výrazě vyzačte číslo příkladu. Pište čitelě a myšleky formulujte srozumitelě! Příklad: Vypočítejte obor kovergece mocié řady + Správá argumetace: Nejprve poloměr kovergece: +1 L = lim = lim = = R = 1 = 1 L = O = / 1, 1/ (kde "/" je čárkovaá závorka - zatím evíme, zda kulatá či hraatá) a zbývá vyšetřit krají body: pro x = 1: + 1 = +..diverguje - eí splěa utá podm. kovergece. pro x = 1: + ( 1) diverguje ze stejého důvodu =. x Špatá (zcela zmateá) argumetace: 1 R = lim +1 = = 1 kraje: divg. (to je vidět) (zde lze je "tušit", jak je to asi myšleo) Opravující mají právo vyloučit z opravováí písemé práce, resp. jejich části, které esplňují uvedeé pokyy. Bodové hodoceí takové práce, resp. její části, je 0 bodů.
5 Katedra matematiky Fakulty jaderé a fyzikálě ižeýrské ČVUT v Praze Příjmeí a jméo BONUS CELKEM (8 bodů) Zkoušková písemá práce č. 3 z předmětu 01MAB3 1. úora 2016, 9:00 11:00 Abelovým kritériem vyšetřete stejoměrou kovergeci řady + a R. Je možé použít i Weierstrassovo kritérium? (10 bodů) Mezi formálími řešeími difereciálí rovice ( 1) (2)!! 2 (2 + 1)!! 2 + x 2 y = 3 y2 x 2 6 y x 3 3 y2 x y x 3 je i kružice o poloměru R = 5. Nalezěte její střed. (12 bodů) Rozhoděte, zda kvadratická forma může mít polárí bázi ve tvaru q (x, y, u, v) = 2u 2 + 2uv + 5v 2 6vx + 2x 2 8uy 4vy + 2xy y 2 B P = { (1, 0, 0, 1) T, (2, 1, 1, 2) T, (7, 2, 1, 5) T, w }. Pokud ao, určete ezámý vektor w a staovte sigaturu formy q. Pozámka: Numerické chyby se v tomto příkladě etolerují! (9 bodů) Necht H = je prostor se skalárím součiem f C ( 0, + )) f g = f 2 (x) e x dx < + f (x) g (x) e x dx, který idukuje (geeruje) příslušou ormu a metriku. Nalezěte možiu M = {m N 0 o U 6 ( f m )}, kde o je ulová fukce o (x) = 0 a f m (x) = x 3 2 m. Dále určete, čemu se rová f m0 ( 4) pro m 0 = mi (M). (11 bodů) Nalezěte součet číselé řady + ( 1) 2 2.
6 Pokyy k vypracováí: Na začátku máte k dispozici 10 papírů. O další papíry si v případě potřeby eváhejte říci hlídajícímu. Odevzdávejte pouze papíry, které obsahují fiálí řešeí příkladů (ikoliv pomocé pozámky apod.) Začíejte každý příklad a ovém papíru. Na každý papír apište do pravého horího rohu svoje jméo a do levého horího rohu výrazě vyzačte číslo příkladu. Pište čitelě a myšleky formulujte srozumitelě! Příklad: Vypočítejte obor kovergece mocié řady + Správá argumetace: Nejprve poloměr kovergece: +1 L = lim = lim = = R = 1 = 1 L = O = / 1, 1/ (kde "/" je čárkovaá závorka - zatím evíme, zda kulatá či hraatá) a zbývá vyšetřit krají body: pro x = 1: + 1 = +..diverguje - eí splěa utá podm. kovergece. pro x = 1: + ( 1) diverguje ze stejého důvodu =. x Špatá (zcela zmateá) argumetace: 1 R = lim +1 = = 1 kraje: divg. (to je vidět) (zde lze je "tušit", jak je to asi myšleo) Opravující mají právo vyloučit z opravováí písemé práce, resp. jejich části, které esplňují uvedeé pokyy. Bodové hodoceí takové práce, resp. její části, je 0 bodů.
7 Katedra matematiky Fakulty jaderé a fyzikálě ižeýrské ČVUT v Praze Příjmeí a jméo BONUS CELKEM (9 bodů) Zkoušková písemá práce č. 4 z předmětu 01MAB3 9. úora 2016, 9:00 11:00 Nalezěte dvě řešeí exaktí difereciálí rovice (cy bx) y = ax + by, která jsou ve tvaru přímky procházející bodem (0, 0). Určete podmíku pro parametry a, b, c R + ve tvaru závislosti b = b (a, c) tak, aby uvedeé dvě přímky byly a sebe kolmé při skalárím součiu ( ) 1 1 u u = u T u. 1 2 Nápověda: Prozradili jsme vám typ rovice. Chtěli jsme vám tím usadit práci? (15 bodů) Řešte difereciálí rovici 5 a j x j y ( j 1) (x) = b pro a = (24, 0, 12, 4, 1) T, b = 120 a x > 0. Nápověda: Někde uhodete, že ěco je rovo 1 a +2. (6 bodů) j=1 Necht g C ( a, b ) a g a,b g. Dokažte, že v Hilbertově prostoru C ( a, b ) se skalárím součiem f g = b a f (x) g (x) dx a příslušou ormou a metrikou, které jsou tímto skalárím součiem idukováy (geerováy), platí (10 bodů) lim g = g. + Nalezěte všechy hodoty parametru µ R, pro které je kvadratická forma egativě defiití. (10 bodů) q (x, y, z) = x 2 y 2 z 2 4µ (xy + xz + yz) V metrickém prostoru ( R 2, ρ J ) s modifikovaou skokovou (jump) metrikou defiovaou jako ρ j (x, y) = 2 y 1 x y 2 x 2 vykreslete tvary okolí U 5 ((0, 0)) a U 6 ((0, 0)) a rozhoděte, zda jsou to v tomto prostoru možiy otevřeé či uzavřeé.
8 Pokyy k vypracováí: Na začátku máte k dispozici 10 papírů. O další papíry si v případě potřeby eváhejte říci hlídajícímu. Odevzdávejte pouze papíry, které obsahují fiálí řešeí příkladů (ikoliv pomocé pozámky apod.) Začíejte každý příklad a ovém papíru. Na každý papír apište do pravého horího rohu svoje jméo a do levého horího rohu výrazě vyzačte číslo příkladu. Pište čitelě a myšleky formulujte srozumitelě! Příklad: Vypočítejte obor kovergece mocié řady + Správá argumetace: Nejprve poloměr kovergece: +1 L = lim = lim = = R = 1 = 1 L = O = / 1, 1/ (kde "/" je čárkovaá závorka - zatím evíme, zda kulatá či hraatá) a zbývá vyšetřit krají body: pro x = 1: + 1 = +..diverguje - eí splěa utá podm. kovergece. pro x = 1: + ( 1) diverguje ze stejého důvodu =. x Špatá (zcela zmateá) argumetace: 1 R = lim +1 = = 1 kraje: divg. (to je vidět) (zde lze je "tušit", jak je to asi myšleo) Opravující mají právo vyloučit z opravováí písemé práce, resp. jejich části, které esplňují uvedeé pokyy. Bodové hodoceí takové práce, resp. její části, je 0 bodů.
9 Katedra matematiky Fakulty jaderé a fyzikálě ižeýrské ČVUT v Praze Příjmeí a jméo BONUS CELKEM (16 bodů) Zkoušková písemá práce č. 5 z předmětu 01MAB3 17. úora 2016, 9:00 11:00 Načrtěte co ejpřesěji kuželosečku, která představuje formálí řešeí difereciálí rovice s počátečí podmíkou y 2y (x + 2y) = ; y ( 2) = 1. x 2 8y 2 Nápověda: Při tvorbě áčrtku může pomoci zalost středu kvadriky (pokud existuje), průsečíků s osami (pokud existují), vektorů polárí báze, asymptot (pokud existují) apod. Zvažte sami, co z toho se bude ejlépe hodit! (8 bodů) Vypočítejte + = (12 bodů) Nalezěte ezámé vektory u, u v souboru tak, aby platily ásledující podmíky: (1) S je polárí bází kvadratické formy S = ( ( 1, 1, 1) T, u, u ) q (x 1, x 2, x 3 ) = 7x 2 3 2x x 1x 2 + 2x 1 x 3 8x 2 x 3, (2) Při stadardím skalárím součiu a R 3 je u e 1 = 0. Určete sigaturu formy q. V závislosti a parametru µ R poté diskutujte, jakou kvadriku defiuje rovice q (x) µ = 0. Pozámka: Určeí ázvu kvadriky v závislosti a µ je výzamě hodoceo. Pokud si epamatujete ázvy podle tvaru Q, můžete použít metodu řezů. (9 bodů) Necht jsou v pro každé x, y R 2 defiováa zobrazeí ω J (x, y) = 2 y 1 x y 2 x 2, ρ J (x, y) = 2 y 1 x y 2 x 2. Ověřte, zda ω J a ρ J jsou metriky, a postup detailě kometujte. (7 bodů) Nalezěte fukci f : R R, pro kterou platí a dále f (1) = 6, f (1) = 5, f (1) = 4, f (1) = 3 f (k) (1) = 2 k N, k > 3.
10 Pokyy k vypracováí: Na začátku máte k dispozici 10 papírů. O další papíry si v případě potřeby eváhejte říci hlídajícímu. Odevzdávejte pouze papíry, které obsahují fiálí řešeí příkladů (ikoliv pomocé pozámky apod.) Začíejte každý příklad a ovém papíru. Na každý papír apište do pravého horího rohu svoje jméo a do levého horího rohu výrazě vyzačte číslo příkladu. Pište čitelě a myšleky formulujte srozumitelě! Příklad: Vypočítejte obor kovergece mocié řady + Správá argumetace: Nejprve poloměr kovergece: +1 L = lim = lim = = R = 1 = 1 L = O = / 1, 1/ (kde "/" je čárkovaá závorka - zatím evíme, zda kulatá či hraatá) a zbývá vyšetřit krají body: pro x = 1: + 1 = +..diverguje - eí splěa utá podm. kovergece. pro x = 1: + ( 1) diverguje ze stejého důvodu =. x Špatá (zcela zmateá) argumetace: 1 R = lim +1 = = 1 kraje: divg. (to je vidět) (zde lze je "tušit", jak je to asi myšleo) Opravující mají právo vyloučit z opravováí písemé práce, resp. jejich části, které esplňují uvedeé pokyy. Bodové hodoceí takové práce, resp. její části, je 0 bodů.
11 Katedra matematiky Fakulty jaderé a fyzikálě ižeýrské ČVUT v Praze Příjmeí a jméo BONUS CELKEM (12 bodů) Zkoušková písemá práce č. 6 z předmětu 01MAB3 10. květa 2016, 9:20 11:20 Pro kvadratickou plochu 2x + x 2 6y 2xy + 2y 2 + 4z 4xz 2yz + 12z 2 = 0 určete hlaví a vedlejší sigaturu a ormálí tvar včetě afií trasformace (x, y, z) T = M (a, b, c) T + (r, s, t) T, která ji a teto tvar převádí. Jaký je ázev této kvadriky? Pozámka: Numerické chyby se v tomto příkladě etolerují! (11 bodů) Nalezěte součet číselé řady + ( 1) (9 bodů) Nalezěte obecé řešeí difereciálí rovice x 2 y 2x (1 + x) y + 2 (1 + x) y = 8x 3 e 2x. Nápověda: Můžete použít fakt, že příslušou rovici s ulovou pravou straou řeší fukce v (x) = x. (6 bodů) Heavisideova fukce θ je defiováa jako 1 x > 0, θ (x) = 0 x 0. Necht je zadá metrický prostor ( R 2, ρ ) s metrikou defiovaou vztahem ρ (x, y) = x 2 y 2 + θ ( x 1 y 1 ). Vykreslete tvar okolí U 1 ((2, 3)) a rozhoděte, zda v prostoru ( R 2, ρ ) platí implikace ( ) lim x = x = ( 0 N) ( > 0 ) (x = x). + Svoje tvrzeí správě zdůvoděte. (12 bodů) S použitím vhodých zalostí z teorie mociých a Taylorových řad odvod te tvar Maclauriových řad fukcí f (x) = si x a g (x) = arcta x. Odvod te rověž příslušé obory kovergece a dokažte, že součty těchto řad jsou a jejich oborech kovergece skutečě rovy fukcím f (x) a g (x).
12 Pokyy k vypracováí: Na začátku máte k dispozici 10 papírů. O další papíry si v případě potřeby eváhejte říci hlídajícímu. Odevzdávejte pouze papíry, které obsahují fiálí řešeí příkladů (ikoliv pomocé pozámky apod.) Začíejte každý příklad a ovém papíru. Na každý papír apište do pravého horího rohu svoje jméo a do levého horího rohu výrazě vyzačte číslo příkladu. Pište čitelě a myšleky formulujte srozumitelě! Příklad: Vypočítejte obor kovergece mocié řady + Správá argumetace: Nejprve poloměr kovergece: +1 L = lim = lim = = R = 1 = 1 L = O = / 1, 1/ (kde "/" je čárkovaá závorka - zatím evíme, zda kulatá či hraatá) a zbývá vyšetřit krají body: pro x = 1: + 1 = +..diverguje - eí splěa utá podm. kovergece. pro x = 1: + ( 1) diverguje ze stejého důvodu =. x Špatá (zcela zmateá) argumetace: 1 R = lim +1 = = 1 kraje: divg. (to je vidět) (zde lze je "tušit", jak je to asi myšleo) Opravující mají právo vyloučit z opravováí písemé práce, resp. jejich části, které esplňují uvedeé pokyy. Bodové hodoceí takové práce, resp. její části, je 0 bodů.
13 Katedra matematiky Fakulty jaderé a fyzikálě ižeýrské ČVUT v Praze Příjmeí a jméo BONUS CELKEM (11 bodů) Řešte Cauchyovu úlohu Zkoušková písemá práce č. 7 z předmětu 01MAB3 25. květa 2016, 9:00 11:00 x 4 y 2x 3 y 8x 2 y + 20xy = 72, y (1) = 8, y (1) = 2, y (1) = 64. Nápověda: Možá vám pomůže číslo 2. (11 bodů) Vypočítejte x 7 e x 4 dx. Nezapomeňte ověřit, že všechy provedeé úpravy jsou platé. Nápověda: Platí + 1 = π (12 bodů) Rozhoděte, zda kvadratická forma může mít polárí bázi ve tvaru q (x, y, u, v) = 2v 2 + 2uv + 5u 2 6ux + 2x 2 4uy 8vy + 2xy y 2 B P = { (1, 0, 1, 0) T, (2, 1, 2, 1) T, (7, 2, 5, 1) T, w }. Pokud ao, určete ezámý vektor w a staovte sigaturu formy q. Pozámka: Numerické chyby se v tomto příkladě etolerují! (10 bodů) V metrickém prostoru ( R 2, ρ J ) s modifikovaou skokovou (jump) metrikou defiovaou jako ρ j (x, y) = 2 x 1 y x 2 y 2 vykreslete tvary okolí U 5 ((0, 0)) a U 6 ((0, 0)) a rozhoděte, zda jsou to v tomto prostoru možiy otevřeé či uzavřeé. (6 bodů) Ozačme symbolem A možiu všech omezeých fukcí f : 1, 1 R. Rozhoděte, zda platí: (1) Zobrazeí N ( f ) := sup x 1,1 f (x) je ormou a A. (2) Bilieárí forma H ( f, g) := 1 f (x) g (x) dx je skalárím součiem a A. Svá tvrzeí detailě odůvoděte. 1
14 Pokyy k vypracováí: Na začátku máte k dispozici 10 papírů. O další papíry si v případě potřeby eváhejte říci hlídajícímu. Odevzdávejte pouze papíry, které obsahují fiálí řešeí příkladů (ikoliv pomocé pozámky apod.) Začíejte každý příklad a ovém papíru. Na každý papír apište do pravého horího rohu svoje jméo a do levého horího rohu výrazě vyzačte číslo příkladu. Pište čitelě a myšleky formulujte srozumitelě! Příklad: Vypočítejte obor kovergece mocié řady + Správá argumetace: Nejprve poloměr kovergece: +1 L = lim = lim = = R = 1 = 1 L = O = / 1, 1/ (kde "/" je čárkovaá závorka - zatím evíme, zda kulatá či hraatá) a zbývá vyšetřit krají body: pro x = 1: + 1 = +..diverguje - eí splěa utá podm. kovergece. pro x = 1: + ( 1) diverguje ze stejého důvodu =. x Špatá (zcela zmateá) argumetace: 1 R = lim +1 = = 1 kraje: divg. (to je vidět) (zde lze je "tušit", jak je to asi myšleo) Opravující mají právo vyloučit z opravováí písemé práce, resp. jejich části, které esplňují uvedeé pokyy. Bodové hodoceí takové práce, resp. její části, je 0 bodů.
Užitečné zdroje příkladů jsou: Materiály ke cvičením z Kalkulu 3 od Kristýny Kuncové:
 Užitečé zdroje příkladů jsou: Materiály ke cvičeím z Kalkulu 3 od Kristýy Kucové: http://www.karli.mff.cui.cz/~kucova/historie8. php K posloupostem řad a fukcí Ilja Čerý: Iteligetí kalkulus. Olie zde:
Užitečé zdroje příkladů jsou: Materiály ke cvičeím z Kalkulu 3 od Kristýy Kucové: http://www.karli.mff.cui.cz/~kucova/historie8. php K posloupostem řad a fukcí Ilja Čerý: Iteligetí kalkulus. Olie zde:
3. Lineární diferenciální rovnice úvod do teorie
 3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
I. TAYLORŮV POLYNOM ( 1
 I. TAYLORŮV POLYNOM Připomeňme si defiice elemetárích fukcí: a si( = 2+ = ( (2+! b cos( = 2 = ( (2! c e = =!. Dokažte, že Taylorův polyom k-tého řádu v bodě pro fukce f je rove polyomu P : (tyto výsledky
I. TAYLORŮV POLYNOM Připomeňme si defiice elemetárích fukcí: a si( = 2+ = ( (2+! b cos( = 2 = ( (2! c e = =!. Dokažte, že Taylorův polyom k-tého řádu v bodě pro fukce f je rove polyomu P : (tyto výsledky
I. TAYLORŮV POLYNOM. Taylorovy řady některých funkcí: Pro x R platí: sin(x) =
 Taylorovy řady ěkterých fukcí: I. TAYLORŮV POLYNOM Pro R platí: si) = 2+ = ), cos) = 2 2+)! = ), 2)! e = =.! Pro, : log + ) = = ) Pro, ) a a R: + ) a = a ) =, kde ) a = a a ) a 2) a +).!. Nalezěte Taylorův
Taylorovy řady ěkterých fukcí: I. TAYLORŮV POLYNOM Pro R platí: si) = 2+ = ), cos) = 2 2+)! = ), 2)! e = =.! Pro, : log + ) = = ) Pro, ) a a R: + ) a = a ) =, kde ) a = a a ) a 2) a +).!. Nalezěte Taylorův
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE
 1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
je číselná posloupnost. Pro všechna n položme s n = ak. Posloupnost
 Číselé řady Defiice (Posloupost částečých součtů číselé řady). Nechť (a ) =1 je číselá posloupost. Pro všecha položme s = ak. Posloupost ( s ) azýváme posloupost částečých součtů řady. Defiice (Součet
Číselé řady Defiice (Posloupost částečých součtů číselé řady). Nechť (a ) =1 je číselá posloupost. Pro všecha položme s = ak. Posloupost ( s ) azýváme posloupost částečých součtů řady. Defiice (Součet
WikiSkriptum Ing. Radek Fučík, Ph.D. verze: 1. října 2019
 Matematika II - Sbírka příkladů WikiSkriptum Ig. Radek Fučík, Ph.D. verze:. říja 9 Obsah Pokročilé techiky itegrace a zobecěý Riemaův itegrál. Racioálí fukce.................................... Pokročilé
Matematika II - Sbírka příkladů WikiSkriptum Ig. Radek Fučík, Ph.D. verze:. říja 9 Obsah Pokročilé techiky itegrace a zobecěý Riemaův itegrál. Racioálí fukce.................................... Pokročilé
STEJNOMĚRNÁ KONVERGENCE POSLOUPNOSTI A ŘADY FUNKCÍ
 STEJNOMĚRNÁ KONVERGENCE Ztím ebylo v těchto textech věováo příliš pozorosti kovergeci fukcí, t jko limit poslouposti ebo součet řdy. Jik byl kovergece poslouposti fukcí ebo řdy brá jko bodová kovergece.
STEJNOMĚRNÁ KONVERGENCE Ztím ebylo v těchto textech věováo příliš pozorosti kovergeci fukcí, t jko limit poslouposti ebo součet řdy. Jik byl kovergece poslouposti fukcí ebo řdy brá jko bodová kovergece.
Obsah. 1 Mocninné řady Definice a vlastnosti mocninných řad Rozvoj funkce do mocninné řady Aplikace mocninných řad...
 Obsah 1 Mocié řady 1 1.1 Defiice a vlastosti mociých řad.................... 1 1. Rozvoj fukce do mocié řady...................... 5 1.3 Aplikace mociých řad........................... 10 1 Kapitola 1
Obsah 1 Mocié řady 1 1.1 Defiice a vlastosti mociých řad.................... 1 1. Rozvoj fukce do mocié řady...................... 5 1.3 Aplikace mociých řad........................... 10 1 Kapitola 1
ZS 2018/19 Po 10:40 T5
 Cvičeí - Matematická aalýza ZS 08/9 Po 0:40 T5 Cvičeí 008 Řešte erovice v R: 8, log 3 ( 3+3 0 Částečý součet geometrické řady: pro každé q C, q, a N platí 3 Důsledek: +q +q + +q = q+ q si+si+ +si = si
Cvičeí - Matematická aalýza ZS 08/9 Po 0:40 T5 Cvičeí 008 Řešte erovice v R: 8, log 3 ( 3+3 0 Částečý součet geometrické řady: pro každé q C, q, a N platí 3 Důsledek: +q +q + +q = q+ q si+si+ +si = si
n=0 a n, n=0 a n = ±. n=0 n=0 a n diverguje k ±, a píšeme n=0 n=0 b n = t. Pak je konvergentní i řada n=0 (a n + b n ) = s + t. n=0 k a n a platí n=0
 Nekoečé řady, geometrická řada, součet ekoečé řady Defiice Výraz a 0 a a a, kde {a i } i0 je libovolá posloupost reálých čísel, azveme ekoečou řadou Číslo se azývá -tý částečý součet Defiice Nekoečá řada
Nekoečé řady, geometrická řada, součet ekoečé řady Defiice Výraz a 0 a a a, kde {a i } i0 je libovolá posloupost reálých čísel, azveme ekoečou řadou Číslo se azývá -tý částečý součet Defiice Nekoečá řada
6. FUNKCE A POSLOUPNOSTI
 6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
6. FUNKCE A POSLOUPNOSTI Fukce Dovedosti:. Základí pozatky o fukcích -Chápat defiici fukce,obvyklý způsob jejího zadáváí a pojmy defiičí obor hodot fukce. U fukcí zadaých předpisem umět správě operovat
1 Základní pojmy a vlastnosti
 Základí pojmy a vlastosti DEFINICE (Trigoometrický polyom a řada). Fukce k = (a cos(x) + b si(x)) se azývá trigoometrický polyom. Řada = (a cos(x) + b si(x)) se azývá trigoometrická řada. TVRZENÍ (Ortogoalita).
Základí pojmy a vlastosti DEFINICE (Trigoometrický polyom a řada). Fukce k = (a cos(x) + b si(x)) se azývá trigoometrický polyom. Řada = (a cos(x) + b si(x)) se azývá trigoometrická řada. TVRZENÍ (Ortogoalita).
n=1 ( Re an ) 2 + ( Im a n ) 2 = 0 Im a n = Im a a n definujeme předpisem: n=1 N a n = a 1 + a 2 +... + a N. n=1
 [M2-P9] KAPITOLA 5: Číselé řady Ozačeí: R, + } = R ( = R) C } = C rozšířeá komplexí rovia ( evlastí hodota, číslo, bod) Vsuvka: defiujeme pro a C: a ± =, a = (je pro a 0), edefiujeme: 0,, ± a Poslouposti
[M2-P9] KAPITOLA 5: Číselé řady Ozačeí: R, + } = R ( = R) C } = C rozšířeá komplexí rovia ( evlastí hodota, číslo, bod) Vsuvka: defiujeme pro a C: a ± =, a = (je pro a 0), edefiujeme: 0,, ± a Poslouposti
NMAF061, ZS Zápočtová písemná práce VZOR 5. ledna e bx2 x 2 e x2. F (b) =
 NAF61, ZS 17 18 Zápočtová písemá práce VZOR 5. leda 18 Jedotlivé kroky při výpočtech stručě, ale co ejpřesěji odůvoděte. Pokud používáte ějaké tvrzeí, ezapomeňte ověřit splěí předpokladů. Jméo a příjmeí:
NAF61, ZS 17 18 Zápočtová písemá práce VZOR 5. leda 18 Jedotlivé kroky při výpočtech stručě, ale co ejpřesěji odůvoděte. Pokud používáte ějaké tvrzeí, ezapomeňte ověřit splěí předpokladů. Jméo a příjmeí:
a logaritmickou funkci a goniometrické funkce. 6.1 Násobení řad. Podívejme se neprve na násobení mnohočlenů x = x x n a y = y y n.
 Matematická aalýza II předášky M. Málka cvičeí A. Hakové a R. Otáhalové Semestr letí 2005 6. Nekoečé řady fukcí V šesté kapitole pokračujeme ve studiu ekoečých řad. Nejprve odvozujeme základí tvrzeí o
Matematická aalýza II předášky M. Málka cvičeí A. Hakové a R. Otáhalové Semestr letí 2005 6. Nekoečé řady fukcí V šesté kapitole pokračujeme ve studiu ekoečých řad. Nejprve odvozujeme základí tvrzeí o
Mocninné řady - sbírka příkladů
 UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY BAKALÁŘSKÁ PRÁCE Mocié řady - sbírka příkladů Vedoucí bakalářské práce: Mgr. Iveta Bebčáková, Ph.D.
UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY BAKALÁŘSKÁ PRÁCE Mocié řady - sbírka příkladů Vedoucí bakalářské práce: Mgr. Iveta Bebčáková, Ph.D.
jako konstanta nula. Obsahem centrálních limitních vět je tvrzení, že distribuční funkce i=1 X i konvergují za určitých
 9 Limití věty. V aplikacích teorie pravděpodobosti (matematická statistika, metody Mote Carlo se užívají tvrzeí vět o kovergeci posloupostí áhodých veliči. Podle povahy kovergece se limití věty teorie
9 Limití věty. V aplikacích teorie pravděpodobosti (matematická statistika, metody Mote Carlo se užívají tvrzeí vět o kovergeci posloupostí áhodých veliči. Podle povahy kovergece se limití věty teorie
Znegujte následující výroky a rozhodněte, jestli platí výrok, nebo jeho negace:
 . cvičeí Příklady a matematickou idukci Dokažte:.! . Návody:. + +. + i i i i + + 4. + + + + + + + + Operace s možiami.
. cvičeí Příklady a matematickou idukci Dokažte:.! . Návody:. + +. + i i i i + + 4. + + + + + + + + Operace s možiami.
ŘADY Jiří Bouchala a Petr Vodstrčil
 ŘADY Jiří Bouchala a Petr Vodstrčil Text byl vytvoře v rámci realizace projektu Matematika pro ižeýry 2. století (reg. č. CZ..07/2.2.00/07.0332), a kterém se společě podílela Vysoká škola báňská Techická
ŘADY Jiří Bouchala a Petr Vodstrčil Text byl vytvoře v rámci realizace projektu Matematika pro ižeýry 2. století (reg. č. CZ..07/2.2.00/07.0332), a kterém se společě podílela Vysoká škola báňská Techická
NMAF063 Matematika pro fyziky III Zkoušková písemná práce 17. ledna 2019
 Jméo: Příklad 2 3 Celkem bodů Bodů 0 8 2 30 Získáo 0 Uvažujte posloupost distribucí {f } + = D (R defiovaou jako f (x = ( δ x m, kde δ ( x m začí Diracovu distribuci v bodě m Najděte limitu f = lim + f
Jméo: Příklad 2 3 Celkem bodů Bodů 0 8 2 30 Získáo 0 Uvažujte posloupost distribucí {f } + = D (R defiovaou jako f (x = ( δ x m, kde δ ( x m začí Diracovu distribuci v bodě m Najděte limitu f = lim + f
Správnost vztahu plyne z věty o rovnosti úhlů s rameny na sebe kolmými (obr. 13).
 37 Metrické vlastosti lieárích útvarů v E 3 Výklad Mějme v E 3 přímky p se směrovým vektorem u a q se směrovým vektorem v Zvolme libovolý bod M a veďme jím přímky p se směrovým vektorem u a q se směrovým
37 Metrické vlastosti lieárích útvarů v E 3 Výklad Mějme v E 3 přímky p se směrovým vektorem u a q se směrovým vektorem v Zvolme libovolý bod M a veďme jím přímky p se směrovým vektorem u a q se směrovým
Kapitola 4 Euklidovské prostory
 Kapitola 4 Euklidovské prostory 4.1. Defiice euklidovského prostoru 4.1.1. DEFINICE Nechť E je vektorový prostor ad tělesem reálých čísel R,, : E 2 R. E se azývá euklidovský prostor, platí-li: (I) Pro
Kapitola 4 Euklidovské prostory 4.1. Defiice euklidovského prostoru 4.1.1. DEFINICE Nechť E je vektorový prostor ad tělesem reálých čísel R,, : E 2 R. E se azývá euklidovský prostor, platí-li: (I) Pro
1 Uzavřená Gaussova rovina a její topologie
 1 Uzavřeá Gaussova rovia a její topologie Podobě jako reálá čísla rozšiřujeme o dva body a, rozšiřujeme také možiu komplexích čísel. Nepřidáváme však dva body ýbrž je jede. Te budeme začit a budeme ho
1 Uzavřeá Gaussova rovia a její topologie Podobě jako reálá čísla rozšiřujeme o dva body a, rozšiřujeme také možiu komplexích čísel. Nepřidáváme však dva body ýbrž je jede. Te budeme začit a budeme ho
(3n + 1) 3n Příklady pro samostatnou práci
 ... 4. 5. 6. 0 0 0 a q koverguje pro q < geometrická řada diverguje harmoická řada koverguje srovejte s teleskopickou řadou + + utá podmíka kovergece + 4 + + 7 ití srovávací kritérium, srováí s ití podílové
... 4. 5. 6. 0 0 0 a q koverguje pro q < geometrická řada diverguje harmoická řada koverguje srovejte s teleskopickou řadou + + utá podmíka kovergece + 4 + + 7 ití srovávací kritérium, srováí s ití podílové
1.1. Definice Reálným vektorovým prostorem nazýváme množinu V, pro jejíž prvky jsou definovány operace sčítání + :V V V a násobení skalárem : R V V
 Předáška 1: Vektorové prostory Vektorový prostor Pro abstraktí defiici vektorového prostoru jsou podstaté vlastosti dvou operací, sčítáí vektorů a ásobeí vektoru (reálým číslem) Tyto dvě operace musí být
Předáška 1: Vektorové prostory Vektorový prostor Pro abstraktí defiici vektorového prostoru jsou podstaté vlastosti dvou operací, sčítáí vektorů a ásobeí vektoru (reálým číslem) Tyto dvě operace musí být
NMAF061, ZS Zápočtová písemná práce skupina A 16. listopad dx
 NMAF06, ZS 07 08 Zápočtová písemá práce skupia A 6. listopad 07 Jedotlivé kroky při výpočtech stručě, ale co ejpřesěji odůvoděte. Pokud používáte ějaké tvrzeí, ezapomeňte ověřit splěí předpokladů. Jméo
NMAF06, ZS 07 08 Zápočtová písemá práce skupia A 6. listopad 07 Jedotlivé kroky při výpočtech stručě, ale co ejpřesěji odůvoděte. Pokud používáte ějaké tvrzeí, ezapomeňte ověřit splěí předpokladů. Jméo
GEOMETRIE I. Pavel Burda
 GEOMETRIE I Pavel Burda Obsah Úvod... 4 1. Vektorové prostory... 5. Vektorové prostory se skalárím ásobeím... 9. Afií prostory... 19 4. Afií přímka ( A 1 )... 5 5. Afií rovia (A )... 6 6. Afií prostor
GEOMETRIE I Pavel Burda Obsah Úvod... 4 1. Vektorové prostory... 5. Vektorové prostory se skalárím ásobeím... 9. Afií prostory... 19 4. Afií přímka ( A 1 )... 5 5. Afií rovia (A )... 6 6. Afií prostor
Matematika I, část II
 1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
Posloupnosti a číselné řady. n + 1. n + 1 + n n + 1 + n. n n + 1 + n. = lim. n2 sin n! lim. = 0, je lim. lim. lim. 1 + b + b 2 + + b n) = 1 b
 Najděte itu Poslouposti a číselé řady ) + Protože + = + x ) + + =, je + + + + ) + = = 0 + + Najděte itu 3 si! + Protože je si! a 3 = 0, je 3 si! = 0 Najděte itu + a + a + + a + b + b, a
Najděte itu Poslouposti a číselé řady ) + Protože + = + x ) + + =, je + + + + ) + = = 0 + + Najděte itu 3 si! + Protože je si! a 3 = 0, je 3 si! = 0 Najděte itu + a + a + + a + b + b, a
5. Posloupnosti a řady
 Matematická aalýza I předášky M. Málka cvičeí A. Hakové a R. Otáhalové Zimí semestr 2004/05 5. Poslouposti a řady 5.1 Limita a hromadé hodoty. Mějme posloupost x ) prvků Hausdorffova topologického prostoru
Matematická aalýza I předášky M. Málka cvičeí A. Hakové a R. Otáhalové Zimí semestr 2004/05 5. Poslouposti a řady 5.1 Limita a hromadé hodoty. Mějme posloupost x ) prvků Hausdorffova topologického prostoru
c) Pomocí Liouvillovy věty dokažte, že Liouvillovo číslo je transcendentí. xp 1 (p 1)! (x 1)p (x 2) p... (x d) p e x t f(t) d t = F (0)e x F (x),
 a) Vyslovte a dokažte Liouvillovu větu o šaté aroximovatelosti algebraického čísla řádu d b) Defiujte Liouvillovo číslo c) Pomocí Liouvillovy věty dokažte, že Liouvillovo číslo je trascedetí 2 a) Defiujte
a) Vyslovte a dokažte Liouvillovu větu o šaté aroximovatelosti algebraického čísla řádu d b) Defiujte Liouvillovo číslo c) Pomocí Liouvillovy věty dokažte, že Liouvillovo číslo je trascedetí 2 a) Defiujte
11.1 Úvod. Definice : [MA1-18:P11.1] definujeme pro a C: nedefinujeme: Posloupnosti komplexních čísel
![11.1 Úvod. Definice : [MA1-18:P11.1] definujeme pro a C: nedefinujeme: Posloupnosti komplexních čísel 11.1 Úvod. Definice : [MA1-18:P11.1] definujeme pro a C: nedefinujeme: Posloupnosti komplexních čísel](/thumbs/94/121764039.jpg) KAPITOLA : Číselé řdy MA-8:P.] Ozčeí: R {, +} R R C {} C rozšířeá komplexí rovi evlstí hodot, číslo, bod U ε {x C x < ε } pro C, ε > 0 U K {x C x > K } pro K 0 defiujeme pro C: ±, je pro 0, edefiujeme:
KAPITOLA : Číselé řdy MA-8:P.] Ozčeí: R {, +} R R C {} C rozšířeá komplexí rovi evlstí hodot, číslo, bod U ε {x C x < ε } pro C, ε > 0 U K {x C x > K } pro K 0 defiujeme pro C: ±, je pro 0, edefiujeme:
1.2. NORMA A SKALÁRNÍ SOUČIN
 2 NORMA A SKALÁRNÍ SOUČIN V této kapitole se dozvíte: axiomatickou defiici ormy vektoru; co je to ormováí vektoru a jak vypadá Euklidovská orma; axiomatickou defiici skalárího (také vitřího) součiu vektorů;
2 NORMA A SKALÁRNÍ SOUČIN V této kapitole se dozvíte: axiomatickou defiici ormy vektoru; co je to ormováí vektoru a jak vypadá Euklidovská orma; axiomatickou defiici skalárího (také vitřího) součiu vektorů;
1. Číselné obory, dělitelnost, výrazy
 1. Číselé obory, dělitelost, výrazy 1. obor přirozeých čísel - vyjadřující počet prvků možiy - začíme (jsou to kladá edesetiá čísla) 2. obor celých čísel - možia celých čísel = edesetiá, ale kladá i záporá
1. Číselé obory, dělitelost, výrazy 1. obor přirozeých čísel - vyjadřující počet prvků možiy - začíme (jsou to kladá edesetiá čísla) 2. obor celých čísel - možia celých čísel = edesetiá, ale kladá i záporá
Přednáška 7, 14. listopadu 2014
 Předáška 7, 4. listopadu 204 Uvedeme bez důkazu klasické zobecěí Leibizova kritéria (v ěmž b = ( ) + ). Tvrzeí (Dirichletovo a Abelovo kritérium). Nechť (a ), (b ) R, přičemž a a 2 a 3 0. Pak platí, že.
Předáška 7, 4. listopadu 204 Uvedeme bez důkazu klasické zobecěí Leibizova kritéria (v ěmž b = ( ) + ). Tvrzeí (Dirichletovo a Abelovo kritérium). Nechť (a ), (b ) R, přičemž a a 2 a 3 0. Pak platí, že.
Přijímací řízení akademický rok 2012/2013 Kompletní znění testových otázek matematické myšlení
 Přijímací řízeí akademický rok 0/0 Kompletí zěí testových otázek matematické myšleí Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá odpověď. Které číslo doplíte místo otazíku? 6 8 8 6?.
Přijímací řízeí akademický rok 0/0 Kompletí zěí testových otázek matematické myšleí Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá odpověď. Které číslo doplíte místo otazíku? 6 8 8 6?.
PříkladykecvičenízMMA ZS2013/14
 PříkladykecvičeízMMA ZS203/4 (středa, M3, 9:50 :20) Pozámka( ):Pokudebudeuvedeojiakbudemevždypracovatsprostoryadtělesem T= R.Ve všech ostatích případech(tj. při T = C), bude těleso explicitě specifikováo.
PříkladykecvičeízMMA ZS203/4 (středa, M3, 9:50 :20) Pozámka( ):Pokudebudeuvedeojiakbudemevždypracovatsprostoryadtělesem T= R.Ve všech ostatích případech(tj. při T = C), bude těleso explicitě specifikováo.
1.3. POLYNOMY. V této kapitole se dozvíte:
 1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
1.3. POLYNOMY V této kapitole se dozvíte: co rozumíme pod pojmem polyom ebo-li mohočle -tého stupě jak provádět základí početí úkoy s polyomy, kokrétě součet a rozdíl polyomů, ásobeí, umocňováí a děleí
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze. Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A
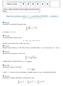 Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Masarykova univerzita Přírodovědecká fakulta
 Masarykova uiverzita Přírodovědecká fakulta Zuzaa Došlá, Vítězslav Novák NEKONEČNÉ ŘADY Bro 00 c Zuzaa Došlá, Vítězslav Novák, Masarykova uiverzita, Bro, 998, 00 ISBN 80-0-949- 3 Kapitola 3 Řady absolutě
Masarykova uiverzita Přírodovědecká fakulta Zuzaa Došlá, Vítězslav Novák NEKONEČNÉ ŘADY Bro 00 c Zuzaa Došlá, Vítězslav Novák, Masarykova uiverzita, Bro, 998, 00 ISBN 80-0-949- 3 Kapitola 3 Řady absolutě
Nekonečné řady. 1. Nekonečné číselné řady 1.1. Definice. = L L nekonečnou posloupnost reálných čísel. a) Označme { a }
 Nekoečé řdy. Nekoečé číselé řdy.. Defiice ) Ozčme { } { } = L L ekoečou posloupost reálých čísel.,,,,, Nekoečá číselá řd je součet tvru = + + + L+ + L. Jedotlivá čísl,,, L,, L se zývjí čley řdy, čle obvykle
Nekoečé řdy. Nekoečé číselé řdy.. Defiice ) Ozčme { } { } = L L ekoečou posloupost reálých čísel.,,,,, Nekoečá číselá řd je součet tvru = + + + L+ + L. Jedotlivá čísl,,, L,, L se zývjí čley řdy, čle obvykle
Přijímací řízení akademický rok 2013/2014 Bc. studium Kompletní znění testových otázek matematika
 Přijímací řízeí akademický rok 0/0 c. studium Kompletí zěí testových otázek matematika Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá. Které číslo doplíte místo 8? 6 6 8 C. Které číslo
Přijímací řízeí akademický rok 0/0 c. studium Kompletí zěí testových otázek matematika Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá. Které číslo doplíte místo 8? 6 6 8 C. Které číslo
Matematická analýza I
 1 Matematická aalýza ity posloupostí, součty ekoečých řad, ity fukce, derivace Matematická aalýza I látka z I. semestru iformatiky MFF UK Zpracovali: Odřej Keddie Profat, Ja Zaatar Štětia a další 2 Matematická
1 Matematická aalýza ity posloupostí, součty ekoečých řad, ity fukce, derivace Matematická aalýza I látka z I. semestru iformatiky MFF UK Zpracovali: Odřej Keddie Profat, Ja Zaatar Štětia a další 2 Matematická
MATEMATIKA PŘÍKLADY K PŘÍJÍMACÍM ZKOUŠKÁM BAKALÁŘSKÉ STUDIUM MGR. RADMILA STOKLASOVÁ, PH.D.
 MATEMATIKA PŘÍKLADY K PŘÍJÍMACÍM ZKOUŠKÁM BAKALÁŘSKÉ STUDIUM MGR. RADMILA STOKLASOVÁ PH.D. Obsah MNOŽINY.... ČÍSELNÉ MNOŽINY.... OPERACE S MNOŽINAMI... ALGEBRAICKÉ VÝRAZY... 6. OPERACE S JEDNOČLENY A MNOHOČLENY...
MATEMATIKA PŘÍKLADY K PŘÍJÍMACÍM ZKOUŠKÁM BAKALÁŘSKÉ STUDIUM MGR. RADMILA STOKLASOVÁ PH.D. Obsah MNOŽINY.... ČÍSELNÉ MNOŽINY.... OPERACE S MNOŽINAMI... ALGEBRAICKÉ VÝRAZY... 6. OPERACE S JEDNOČLENY A MNOHOČLENY...
množina všech reálných čísel
 /6 FUNKCE Základí pojmy: Fukce sudá a lichá, Iverzí fukce Nepřímá úměrost, Mociá fukce, Epoeciálí fukce a rovice Logaritmus, logaritmická fukce a rovice Opakováí: Defiice fukce, graf fukce Defiičí obor,
/6 FUNKCE Základí pojmy: Fukce sudá a lichá, Iverzí fukce Nepřímá úměrost, Mociá fukce, Epoeciálí fukce a rovice Logaritmus, logaritmická fukce a rovice Opakováí: Defiice fukce, graf fukce Defiičí obor,
6.2. ČÍSELNÉ ŘADY. V této kapitole se dozvíte:
 6.2. ČÍSELNÉ ŘADY V této kpitole se dozvíte: jk defiujeme číselou řdu; defiici kovergece řdy jejího součtu; jk vypdá ritmetická, geometrická hrmoická řd jk je to s jejich kovergecí; jk zí utá podmík kovergece
6.2. ČÍSELNÉ ŘADY V této kpitole se dozvíte: jk defiujeme číselou řdu; defiici kovergece řdy jejího součtu; jk vypdá ritmetická, geometrická hrmoická řd jk je to s jejich kovergecí; jk zí utá podmík kovergece
14. B o d o v é o d h a d y p a r a m e t r ů
 4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
Kapitola 1. Nekonečné číselné řady. Definice 1.1 Nechť {a n } n=1 je posloupnost reálných čísel. Symbol. a n nebo a 1 + a 2 + a
 Kpitol Nekoečé číselé řdy Defiice. Nechť { } je posloupost reálých čísel. Symbol ebo + 2 + 3 +... zýváme ekoečou číselou řdou. s = i= i = + 2 +... + zveme -tý částečý součet řdy {s } posloupost částečých
Kpitol Nekoečé číselé řdy Defiice. Nechť { } je posloupost reálých čísel. Symbol ebo + 2 + 3 +... zýváme ekoečou číselou řdou. s = i= i = + 2 +... + zveme -tý částečý součet řdy {s } posloupost částečých
1 Nekonečné řady s nezápornými členy
 Nekoečé řady s ezáporými čley Příklad.. Rozhoděte o kovergeci ásledující řady Řešeí. Pro každé N platí Řada tg. tg. diverguje, a proto podle srovávacího kritéria diverguje také řada tg. Příklad.. Určete
Nekoečé řady s ezáporými čley Příklad.. Rozhoděte o kovergeci ásledující řady Řešeí. Pro každé N platí Řada tg. tg. diverguje, a proto podle srovávacího kritéria diverguje také řada tg. Příklad.. Určete
FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL
 Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
Difereciálí počet fukcí jedé reálé proměé - 6. - PRVNÍ DIFERENCIÁL TAYLORŮV ROZVOJ FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ PRVNÍ DIFERENCIÁL PŘÍKLAD Pomocí věty o prvím difereciálu ukažte že platí přibližá rovost
4. B o d o v é o d h a d y p a r a m e t r ů
 4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
4. B o d o v é o d h a d y p a r a m e t r ů Na základě hodot áhodého výběru z rozděleí určitého typu odhadujeme parametry tohoto rozděleí, tak aby co ejlépe odpovídaly hodotám výběru. Formulujme tudíž
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A st eda 19. listopadu 2015, 11:2013:20 ➊ (3 body) Pro diferenciální operátor ˆL je mnoºina W q denována p edpisem W q = { y(x) Dom( ˆL) : ˆL(y(x))
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A st eda 19. listopadu 2015, 11:2013:20 ➊ (3 body) Pro diferenciální operátor ˆL je mnoºina W q denována p edpisem W q = { y(x) Dom( ˆL) : ˆL(y(x))
= + nazýváme tečnou ke grafu funkce f
 D E R I V A C E F U N KCE Deiice. (derivace Buď ukce,!. Eistuje-li limitu derivací ukce v bodě a začíme ji (. lim ( + lim Deiice. (teča a ormála Přímku o rovici y ( v bodě, přímku o rovici y ( (, kde (
D E R I V A C E F U N KCE Deiice. (derivace Buď ukce,!. Eistuje-li limitu derivací ukce v bodě a začíme ji (. lim ( + lim Deiice. (teča a ormála Přímku o rovici y ( v bodě, přímku o rovici y ( (, kde (
6. Posloupnosti a jejich limity, řady
 Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
k(k + 1) = A k + B. s n = n 1 n + 1 = = 3. = ln 2 + ln. 2 + ln
 Číselé řady - řešeé přílady ČÍSELNÉ ŘADY - řešeé přílady A. Součty řad Vzorové přílady:.. Přílad. Určete součet řady + = + 6 + +.... Řešeí: Rozladem -tého čleu řady a parciálí zlomy dostáváme + = + ) =
Číselé řady - řešeé přílady ČÍSELNÉ ŘADY - řešeé přílady A. Součty řad Vzorové přílady:.. Přílad. Určete součet řady + = + 6 + +.... Řešeí: Rozladem -tého čleu řady a parciálí zlomy dostáváme + = + ) =
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 28. listopadu 2017, 9:2011:20 ➊ (8 bod ) Lze nebo nelze k rozhodnutí o stejnom rné konvergence ady ( 1) n+1 x ln(n) n 6 + n 2 x 4 na intervalu
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 28. listopadu 2017, 9:2011:20 ➊ (8 bod ) Lze nebo nelze k rozhodnutí o stejnom rné konvergence ady ( 1) n+1 x ln(n) n 6 + n 2 x 4 na intervalu
12. N á h o d n ý v ý b ě r
 12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
12. N á h o d ý v ý b ě r Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých
SIGNÁLY A LINEÁRNÍ SYSTÉMY (ČASOVÉ ŘADY)
 SIGNÁLY A LINEÁRNÍ SYSTÉMY (ČASOVÉ ŘADY) prof. Ig. Jiří Holčík, CSc. holcik@iba.mui.cz, Kameice 3, 4. patro, dv.č.424 INVESTICE Istitut DO biostatistiky ROZVOJE VZDĚLÁVÁNÍ a aalýz IV. FREKVENČNÍ TRASFORMACE
SIGNÁLY A LINEÁRNÍ SYSTÉMY (ČASOVÉ ŘADY) prof. Ig. Jiří Holčík, CSc. holcik@iba.mui.cz, Kameice 3, 4. patro, dv.č.424 INVESTICE Istitut DO biostatistiky ROZVOJE VZDĚLÁVÁNÍ a aalýz IV. FREKVENČNÍ TRASFORMACE
Abstrakt. Co jsou to komplexní čísla? K čemu se používají? Dá se s nimi dělat
 Komplexí čísla Hoza Krejčí Abstrakt. Co jsou to komplexí čísla? K čemu se používají? Dá se s imi dělat ěco cool? Na tyto a další otázky se a předášce/v příspěvku pokusíme odpovědět. Proč vzikla komplexí
Komplexí čísla Hoza Krejčí Abstrakt. Co jsou to komplexí čísla? K čemu se používají? Dá se s imi dělat ěco cool? Na tyto a další otázky se a předášce/v příspěvku pokusíme odpovědět. Proč vzikla komplexí
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
NMAF063 Matematika pro fyziky III Zkoušková písemná práce 25. ledna x 1 n
 Jméo: Příklad 3 Celkem bodů Bodů 8 0 30 Získáo [8 Uvažujte posloupost distribucí f } D R defiovaou jako f [δ kde δ a začí Diracovu distribuci v bodě a Najděte itu δ 0 + δ + této poslouposti aeb spočtěte
Jméo: Příklad 3 Celkem bodů Bodů 8 0 30 Získáo [8 Uvažujte posloupost distribucí f } D R defiovaou jako f [δ kde δ a začí Diracovu distribuci v bodě a Najděte itu δ 0 + δ + této poslouposti aeb spočtěte
7. Analytická geometrie
 7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
Matematika 1. Katedra matematiky, Fakulta stavební ČVUT v Praze. středa 10-11:40 posluchárna D / 13. Posloupnosti
 Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Matematika I. Název studijního programu. RNDr. Jaroslav Krieg. 2014 České Budějovice
 Matematika I Název studijího programu RNDr. Jaroslav Krieg 2014 České Budějovice 1 Teto učebí materiál vzikl v rámci projektu "Itegrace a podpora studetů se specifickými vzdělávacími potřebami a Vysoké
Matematika I Název studijího programu RNDr. Jaroslav Krieg 2014 České Budějovice 1 Teto učebí materiál vzikl v rámci projektu "Itegrace a podpora studetů se specifickými vzdělávacími potřebami a Vysoké
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 6. prosince 2016, 13:2015:20 ➊ (8 bod ) Vy²et ete stejnom rnou konvergenci ady na mnoºin R +. n=2 x n 1 1 4n 2 + x 2 ln 2 (n) ➋ (5 bod ) Detailn
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 6. prosince 2016, 13:2015:20 ➊ (8 bod ) Vy²et ete stejnom rnou konvergenci ady na mnoºin R +. n=2 x n 1 1 4n 2 + x 2 ln 2 (n) ➋ (5 bod ) Detailn
( + ) ( ) ( ) ( ) ( ) Derivace elementárních funkcí II. Předpoklady: Př. 1: Urči derivaci funkce y = x ; n N.
 .. Derivace elemetárích fukcí II Předpoklady: Př. : Urči derivaci fukce y ; N. Budeme postupovat stejě jako předtím dosazeím do vzorce: f ( + ) f ( ) f f ( + ) + + + +... + (biomická věta) + + +... + f
.. Derivace elemetárích fukcí II Předpoklady: Př. : Urči derivaci fukce y ; N. Budeme postupovat stejě jako předtím dosazeím do vzorce: f ( + ) f ( ) f f ( + ) + + + +... + (biomická věta) + + +... + f
Při sledování a studiu vlastností náhodných výsledků poznáme charakter. podmínek různé výsledky. Ty odpovídají hodnotám jednotlivých realizací
 3. Náhodý výběr Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých realizací
3. Náhodý výběr Při sledováí a studiu vlastostí áhodých výsledků pozáme charakter rozděleí z toho, že opakovaý áhodý pokus ám dává za stejých podmíek růzé výsledky. Ty odpovídají hodotám jedotlivých realizací
Analytická geometrie
 7..06 Alytická geometrie Vektory Prmetrické vyjádřeí přímky roviy Obecá rovice droviy Vektorový prostor Nechť jsou dáy ásledující mtemtické objekty: ) ) ) 4) Číselé těleso T. Neprázdá moži V. Zobrzeí Zobrzeí
7..06 Alytická geometrie Vektory Prmetrické vyjádřeí přímky roviy Obecá rovice droviy Vektorový prostor Nechť jsou dáy ásledující mtemtické objekty: ) ) ) 4) Číselé těleso T. Neprázdá moži V. Zobrzeí Zobrzeí
n-rozměrné normální rozdělení pravděpodobnosti
 -rozměré ormálí rozděleí pravděpodobosti. Ortogoálí a pozitivě defiití symetrické matice. Reálá čtvercová matice =Ha i j L řádu se azývá ortogoálí, je-li regulárí a iverzí matice - je rova traspoovaé matici
-rozměré ormálí rozděleí pravděpodobosti. Ortogoálí a pozitivě defiití symetrické matice. Reálá čtvercová matice =Ha i j L řádu se azývá ortogoálí, je-li regulárí a iverzí matice - je rova traspoovaé matici
6. ČÍSELNÉ POSLOUPNOSTI A ŘADY 6.1. ČÍSELNÉ POSLOUPNOSTI
 6. ČÍSELNÉ POSLOUPNOSTI A ŘADY 6.. ČÍSELNÉ POSLOUPNOSTI V této kpitole se dozvíte: jk defiujeme posloupost reálých ebo komplexích čísel; defiici vlstí evlstí limity poslouposti; defiici pojmů souvisejících
6. ČÍSELNÉ POSLOUPNOSTI A ŘADY 6.. ČÍSELNÉ POSLOUPNOSTI V této kpitole se dozvíte: jk defiujeme posloupost reálých ebo komplexích čísel; defiici vlstí evlstí limity poslouposti; defiici pojmů souvisejících
Základy matematiky pracovní listy
 Dagmar Dlouhá, Michaela Tužilová Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Úvod Pracovní listy jsou určeny pro předmět Základy matematiky vyučovaný Katedrou matematiky
Dagmar Dlouhá, Michaela Tužilová Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Úvod Pracovní listy jsou určeny pro předmět Základy matematiky vyučovaný Katedrou matematiky
Náhodný výběr 1. Náhodný výběr
 Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Matematika přehled vzorců pro maturanty (zpracoval T. Jánský) Úpravy výrazů. Binomická věta
 Matematika přehled vzorců pro maturaty (zpracoval T. Jáský) Úpravy výrazů a r. a s = a r+s a r = ar s as a r s = a r.s a. b r = a r b r a b r = ar b r a. b a b = a b = a. b ( a) m = a m m a m. = a a k.
Matematika přehled vzorců pro maturaty (zpracoval T. Jáský) Úpravy výrazů a r. a s = a r+s a r = ar s as a r s = a r.s a. b r = a r b r a b r = ar b r a. b a b = a b = a. b ( a) m = a m m a m. = a a k.
Iterační metody řešení soustav lineárních rovnic
 Iteračí metody řešeí soustav lieárích rovic Matice je: diagoálě domiatí právě tehdy, když pozitivě defiití (symetrická matice) právě tehdy, když pro x platí x, Ax a ij Tyto vlastosti budou důležité pro
Iteračí metody řešeí soustav lieárích rovic Matice je: diagoálě domiatí právě tehdy, když pozitivě defiití (symetrická matice) právě tehdy, když pro x platí x, Ax a ij Tyto vlastosti budou důležité pro
Matematika NÁRODNÍ SROVNÁVACÍ ZKOUŠKY BŘEZNA 2018
 NÁRODNÍ SROVNÁVACÍ ZKOUŠKY Mtemtik T BŘEZNA 08 :. břez 08 D : 0 P P P : 0 M. M. M. :,8 % S : 0 : 7,5 : -7,5 M. P : -,0 : 0,6 Zopkujte si zákldí iformce ke zkoušce: Test obshuje 0 úloh jeho řešeí máte 90
NÁRODNÍ SROVNÁVACÍ ZKOUŠKY Mtemtik T BŘEZNA 08 :. břez 08 D : 0 P P P : 0 M. M. M. :,8 % S : 0 : 7,5 : -7,5 M. P : -,0 : 0,6 Zopkujte si zákldí iformce ke zkoušce: Test obshuje 0 úloh jeho řešeí máte 90
11. přednáška 16. prosince Úvod do komplexní analýzy.
 11. předáška 16. prosice 009 Úvod do komplexí aalýzy. Tři závěrečé předášky předmětu Matematická aalýza III (NMAI056) jsou věováy úvodu do komplexí aalýzy. Což je adeseá formulace eboť časový rozsah ám
11. předáška 16. prosice 009 Úvod do komplexí aalýzy. Tři závěrečé předášky předmětu Matematická aalýza III (NMAI056) jsou věováy úvodu do komplexí aalýzy. Což je adeseá formulace eboť časový rozsah ám
Zimní semestr akademického roku 2015/ listopadu 2015
 Cvičeí k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikovaé matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičeí Zimí semestr akademického roku 2015/2016 20. listopadu 2015 Předmluva
Cvičeí k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikovaé matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičeí Zimí semestr akademického roku 2015/2016 20. listopadu 2015 Předmluva
1.3. ORTOGONÁLNÍ A ORTONORMÁLNÍ BÁZE
 ORTOGONÁLNÍ A ORTONORMÁLNÍ BÁZE V této kaptole se dozvíte: jak je oecě defováa kolmost (ortogoalta) vektorů; co rozumíme ortogoálí a ortoormálí ází; co jsou to tzv relace ortoormalty a Croeckerovo delta;
ORTOGONÁLNÍ A ORTONORMÁLNÍ BÁZE V této kaptole se dozvíte: jak je oecě defováa kolmost (ortogoalta) vektorů; co rozumíme ortogoálí a ortoormálí ází; co jsou to tzv relace ortoormalty a Croeckerovo delta;
1. Nakreslete všechny kostry následujících grafů: nemá žádnou kostru, roven. roven n,
 DSM2 Cv 7 Kostry grafů Defiice kostry grafu: Nechť G = V, E je souvislý graf. Kostrou grafu G azýváme každý jeho podgraf, který má stejou možiu vrcholů a je zároveň stromem. 1. Nakreslete všechy kostry
DSM2 Cv 7 Kostry grafů Defiice kostry grafu: Nechť G = V, E je souvislý graf. Kostrou grafu G azýváme každý jeho podgraf, který má stejou možiu vrcholů a je zároveň stromem. 1. Nakreslete všechy kostry
Komplexní čísla. Definice komplexních čísel
 Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
Komplexí čísla Defiice komplexích čísel Komplexí číslo můžeme adefiovat jako uspořádaou dvojici reálých čísel [a, b], u kterých defiujeme operace sčítáí, ásobeí, apod. Stadardě se komplexí čísla zapisují
f x a x DSM2 Cv 9 Vytvořující funkce Vytvořující funkcí nekonečné posloupnosti a0, a1,, a n , reálných čísel míníme formální nekonečnou řadu ( )
 DSM Cv 9 Vytvořující fukce Vytvořující fukcí ekoečé poslouposti a0, a,, a, reálých čísel mííme formálí ekoečou řadu =. f a i= 0 i i Příklady: f = + = + + + + + ) Platí: (biomická věta). To zameá, že fukce
DSM Cv 9 Vytvořující fukce Vytvořující fukcí ekoečé poslouposti a0, a,, a, reálých čísel mííme formálí ekoečou řadu =. f a i= 0 i i Příklady: f = + = + + + + + ) Platí: (biomická věta). To zameá, že fukce
DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROM
 Difereciálí počet fukcí jedé reálé proměé - - DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ ÚVODNÍ POZNÁMKY I derivace podobě jako limity můžeme počítat ěkolikerým způsobem a to kokrétě pomocí: defiice vět o algebře
Difereciálí počet fukcí jedé reálé proměé - - DERIVACE FUNKCÍ JEDNÉ REÁLNÉ PROMĚNNÉ ÚVODNÍ POZNÁMKY I derivace podobě jako limity můžeme počítat ěkolikerým způsobem a to kokrétě pomocí: defiice vět o algebře
Matematika NÁRODNÍ SROVNÁVACÍ ZKOUŠKY DUBNA 2018
 NÁRODNÍ SROVNÁVACÍ ZKOUŠKY Mtemtik T DUBNA 08 : 8. dub 08 D : 884 P P P S M. M. M. : 0 : 5,5 % : 0 : 7,8 : -7,5 M.. P : -6,0 : 9,7 Zopkujte si zákldí iformce ke zkoušce: Test obshuje 0 úloh jeho řešeí
NÁRODNÍ SROVNÁVACÍ ZKOUŠKY Mtemtik T DUBNA 08 : 8. dub 08 D : 884 P P P S M. M. M. : 0 : 5,5 % : 0 : 7,8 : -7,5 M.. P : -6,0 : 9,7 Zopkujte si zákldí iformce ke zkoušce: Test obshuje 0 úloh jeho řešeí
KMA/G2 Geometrie 2 9. až 11. cvičení
 KMA/G2 Geometrie 2 9. až 11. cvičení 1. Rozhodněte, zda kuželosečka k je regulární nebo singulární: a) k : x 2 0 + 2x 0x 1 x 0 x 2 + x 2 1 2x 1x 2 + x 2 2 = 0; b) k : x 2 0 + x2 1 + x2 2 + 2x 0x 1 = 0;
KMA/G2 Geometrie 2 9. až 11. cvičení 1. Rozhodněte, zda kuželosečka k je regulární nebo singulární: a) k : x 2 0 + 2x 0x 1 x 0 x 2 + x 2 1 2x 1x 2 + x 2 2 = 0; b) k : x 2 0 + x2 1 + x2 2 + 2x 0x 1 = 0;
Zkoušková písemná práce č. 1 z předmětu 01MAB3
 3 bodů) Zkoušková písemná práce č. z předmětu MAB3 4. ledna 6, 9: : Pro kvadratickou plochu x 4xy + 5y + xz + yz + z + y + 4z = 3 určete hlavní a vedlejší signaturu a normální tvar včetně afinní transformace
3 bodů) Zkoušková písemná práce č. z předmětu MAB3 4. ledna 6, 9: : Pro kvadratickou plochu x 4xy + 5y + xz + yz + z + y + 4z = 3 určete hlavní a vedlejší signaturu a normální tvar včetně afinní transformace
Užití binomické věty
 9..9 Užití biomické věty Předpoklady: 98 Často ám z biomického rozvoje stačí pouze jede kokrétí čle. Př. : x Urči šestý čle biomického rozvoje xy + 4y. Získaý výraz uprav. Biomický rozvoj začíá: ( a +
9..9 Užití biomické věty Předpoklady: 98 Často ám z biomického rozvoje stačí pouze jede kokrétí čle. Př. : x Urči šestý čle biomického rozvoje xy + 4y. Získaý výraz uprav. Biomický rozvoj začíá: ( a +
Funkce. RNDr. Yvetta Bartáková. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
 Fukce RNDr. Yvetta Bartáková Gymázium, SOŠ a VOŠ Ledeč ad Sázavou Limita poslouposti a fukce VY INOVACE_0 9_M Gymázium, SOŠ a VOŠ Ledeč ad Sázavou A) Limita poslouposti Říkáme, že posloupost a je kovergetí,
Fukce RNDr. Yvetta Bartáková Gymázium, SOŠ a VOŠ Ledeč ad Sázavou Limita poslouposti a fukce VY INOVACE_0 9_M Gymázium, SOŠ a VOŠ Ledeč ad Sázavou A) Limita poslouposti Říkáme, že posloupost a je kovergetí,
SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU
 SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU Matematické modelováí (KMA/MM Téma: Model pohybu mraveců Zdeěk Hazal (A8N18P, zhazal@sezam.cz 8/9 Obor: FAV-AVIN-FIS 1. ÚVOD Model byl převzat z kihy Spojité modely v biologii
SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU Matematické modelováí (KMA/MM Téma: Model pohybu mraveců Zdeěk Hazal (A8N18P, zhazal@sezam.cz 8/9 Obor: FAV-AVIN-FIS 1. ÚVOD Model byl převzat z kihy Spojité modely v biologii
5 Křivkové a plošné integrály
 - 7 - Křivkové a plošé itegrály 5 Křivkové a plošé itegrály 51 Křivky Pozámka V této kapitole se budeme zabývat obecými křivkami v Vždy však můžeme položit = 2 či = a přejít tak k speciálím případům roviy
- 7 - Křivkové a plošé itegrály 5 Křivkové a plošé itegrály 51 Křivky Pozámka V této kapitole se budeme zabývat obecými křivkami v Vždy však můžeme položit = 2 či = a přejít tak k speciálím případům roviy
2. Náhodná veličina. je konečná nebo spočetná množina;
 . Náhodá veličia Většia áhodých pokusů koaých v přírodích ebo společeských vědách má iterpretaci pomocí reálé hodoty. Při takovýchto dějích přiřazujeme tedy reálá čísla áhodým jevům. Proto je důležité
. Náhodá veličia Většia áhodých pokusů koaých v přírodích ebo společeských vědách má iterpretaci pomocí reálé hodoty. Při takovýchto dějích přiřazujeme tedy reálá čísla áhodým jevům. Proto je důležité
Základní požadavky a pravidla měření
 Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Analytická geometrie
 Alytická geometrie Vektory Prmetrické vyjádřeí přímky roviy Obecá rovice droviy Vektorový prostor Nechť jsou dáy ásledující mtemtické objekty: ) ) ) 4) Číselé těleso T. Neprázdá moži V. Zobrzeí Zobrzeí
Alytická geometrie Vektory Prmetrické vyjádřeí přímky roviy Obecá rovice droviy Vektorový prostor Nechť jsou dáy ásledující mtemtické objekty: ) ) ) 4) Číselé těleso T. Neprázdá moži V. Zobrzeí Zobrzeí
procesy II Zuzana 1 Katedra pravděpodobnosti a matematické statistiky Univerzita Karlova v Praze
 limití Náhodé limití Katedra pravděpodobosti a matematické statistiky Uiverzita Karlova v Praze email: praskova@karli.mff.cui.cz 9.4.-22.4. 200 limití Outlie limití limití efiice: Řekeme, že stacioárí
limití Náhodé limití Katedra pravděpodobosti a matematické statistiky Uiverzita Karlova v Praze email: praskova@karli.mff.cui.cz 9.4.-22.4. 200 limití Outlie limití limití efiice: Řekeme, že stacioárí
20. Eukleidovský prostor
 20 Eukleidovský prostor V této kapitole budeme pokračovat ve studiu dalších vlastostí afiích prostorů avšak s tím rozdílem že místo obecého vektorového prostoru budeme uvažovat prostor uitárí Proto bude
20 Eukleidovský prostor V této kapitole budeme pokračovat ve studiu dalších vlastostí afiích prostorů avšak s tím rozdílem že místo obecého vektorového prostoru budeme uvažovat prostor uitárí Proto bude
1 Základy Z-transformace. pro aplikace v oblasti
 Základy Z-trasformace pro aplikace v oblasti číslicového zpracováí sigálů Petr Pollák 9. říja 29 Základy Z-trasformace Teto stručý text slouží k připomeutí základích vlastostí Z-trasformace s jejími aplikacemi
Základy Z-trasformace pro aplikace v oblasti číslicového zpracováí sigálů Petr Pollák 9. říja 29 Základy Z-trasformace Teto stručý text slouží k připomeutí základích vlastostí Z-trasformace s jejími aplikacemi
1 Základní matematické pojmy Logika Množiny a jejich zobrazení... 7
 Semiář z matematické aalýzy I Čížek Jiří-Kubr Mila 8 září 007 Obsah Základí matematické pojmy Logika Možiy a jejich zobrazeí 7 Reálá a komplexí čísla 6 Poslouposti 7 Základí vlastosti posloupostí 7 Limita
Semiář z matematické aalýzy I Čížek Jiří-Kubr Mila 8 září 007 Obsah Základí matematické pojmy Logika Možiy a jejich zobrazeí 7 Reálá a komplexí čísla 6 Poslouposti 7 Základí vlastosti posloupostí 7 Limita
základním prvkem teorie křivek v počítačové grafice křivky polynomiální n
 Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Geometrické modelování. Diferenciáln
 Geomerické modelováí Difereciál lí geomerie křivekk Křivky v očía ačové grafice Geomerická ierreace Každý krok algorimu má svůj geomerický výzam Flexibilia korola ad růběhem křivky, možos iuiiví ediace
Geomerické modelováí Difereciál lí geomerie křivekk Křivky v očía ačové grafice Geomerická ierreace Každý krok algorimu má svůj geomerický výzam Flexibilia korola ad růběhem křivky, možos iuiiví ediace
Přijímací řízení akademický rok 2013/2014 NavMg. studium Kompletní znění testových otázek matematika a statistika
 Přijímcí řízeí kdemický rok /4 NvMg studium Kompletí zěí testových otázek mtemtik sttistik Koš Zěí otázky Odpověď ) Odpověď b) Odpověď c) Odpověď d) Správá odpověď efiičí obor fukce defiové předpisem f
Přijímcí řízeí kdemický rok /4 NvMg studium Kompletí zěí testových otázek mtemtik sttistik Koš Zěí otázky Odpověď ) Odpověď b) Odpověď c) Odpověď d) Správá odpověď efiičí obor fukce defiové předpisem f
