Integrál jako funkce meze
|
|
|
- Klára Šmídová
- před 8 lety
- Počet zobrazení:
Transkript
1 Část prcovní verze odstvců o následujících témtech z připrvovných skript o integrálním počtu (utoři P.Ř. V.Ž.): Integrál jko funkce meze První druhá zákldní vět integrálního počtu Výpočetní techniky pro Riemnnův integrál Nevlstní integrály Jordnov Penov mír Integrál jko funkce meze Nyní se podíváme n určitý integrál trochu jiným způsobem: Budeme zkoumt jeho vlstnosti v situci, kdy horní mez (popřípdě dolní mez, resp. obě meze součsně) chápeme jko proměnnou (resp. proměnné). Přesněji řečeno, pro funkci f integrovtelnou n intervlu, b budeme zkoumt vlstnosti funkce F (x) := x f(t) dt, (..) která je n intervlu, b dobře definován z předpokldu, že f R(, x) pro kždé x, b Této funkci říkáme integrál jko funkce horní meze. Vzhledem k tomu, že určitý integrál souvisí s obshem určitých obrzců, jejichž část hrnice je tvořen grfem integrndu, lze význm funkce F (pro f kldné) znázornit následovně: Předstvme si, že rozvíjíme netypický koberec, jehož šířk f(x) se mění spojitě vzhledem k rozvinuté délce x, jko n následujícím obrázku. Funkce (..) pk vyjdřuje obsh rozvinuté části koberce v závislosti n jeho ktuální délce. Typický koberec má konstntní šířku, neboli f(x) = k pro všechn x, b, kde b je jeho délk. V tkovém přípdě je pokrytá ploch přímo úměrná rozvinuté délce, F (x) = k x. Jink řečeno, rychlost, jkou koberec pokrývá podlhu, je vzhledem k proměnné x konstntní tto konstnt je právě k; zejmén je funkce F diferencovtelná, tudíž tké spojitá. V obecnějším přípdě šířk koberce konstntní není, všk předchozí závěry pltí ndále: Obsh rozvinuté části koberce se mění spojitě vzhledem k jeho délce (tento pozntek zobecníme záhy ve Větě..) rychlost, jkou koberec pokrývá podlhu, je rovn jeho ktuální šířce (tento pozntek upřesníme ve Větě..3). Nvíc si můžeme povšimnout, že obsh rozvinuté části odpovídjící libovolnému podintervlu c, d, b je roven rozdílu F (d) F (c) (tento pozntek zobecníme ve Větě..5).
2 2 Spojitost funkce F Nyní ukážeme, že pokud je funkce F n nějkém intervlu definován, tzn. pokud je funkce f n tomto intervlu integrovtelná, potom F je nutně spojitá. Funkce f přitom spojitá být nemusí. Vět... Jestliže je funkce f n intervlu, b integrovtelná, potom x je funkce F (x) := f(t) dt n tomto intervlu spojitá. Důkz. Z definice funkce F ditivity určitého integrálu vzhledem k mezím plyne, že x+h F (x + h) F (x) = f(t) dt pro kždé x, x + h, b. Z integrovtelnosti funkce f, plyne její omezenost, tudíž podle odstvce o nerovnostech dostáváme x+h f(t) dt M h, x kde M je reálná konstnt shor omezující funkci f mezi x x + h. Odtud vidíme, že pro dosttečně mlá h je hodnot F (x + h) libovolně blízko F (x), přičemž pro h = je zřejmě F (x + h) = F (x). Funkce F je tedy ve všech bodech intervlu, b spojitá (v krjních bodech jednostrnně). Poznámky..2. (i) Ve výše uvedeném znázornění můžeme uvžovt přípd, kdy koberec nerozvíjíme, le zvíjíme, příp. rozvíjíme či zvíjíme z druhé strny (nebo dokonce z obou strn součsně). Odpovídjící funkce popisující obsh rozvinuté části koberce budou nlogické (..). Npř. funkce odpovídjící zvíjení z levé strny vypdá tkto: G(x) := x x f(t) dt, kde x, b b je délk celého koberce. Této funkci se říká integrál jko funkce dolní meze. Je velmi sndné ukázt, že funkce G má obdobné vlstnosti jko funkce F. (ii) Vzhledem k nší konvenci lze integrál jko funkci horní, resp. dolní meze n intervlu, b definovt poněkud obecněji vzhledem k libovolnému bodu c, b : F (x) := x c f(t) dt, resp. G(x) := c x f(t) dt.
3 3 Vlstnosti funkce F, resp. G se ni v tomto obecnějším přípdě nezmění; zejmén kždá z těchto funkcí je spojitá, kdykoli je definován. (iii) Integrál jko funkce horní, resp. dolní meze, je v teorii integrálu velice užitečný. Díky němu v dlších odstvcích obecně vysvětlíme důležitou souvislost mezi pojmem primitivní funkce (tj. neurčitým integrálem) určitým integrálem. Dále jej potřebujeme npř. k zvedení tzv. nevlstního integrálu. Tímto způsobem lze tké definovt nové (příp. novým způsobem zvést známé) funkce. Velký význm má tké v jiných oblstech mtemtiky (teorie prvděpodobnosti, integrální trnsformce td.). Zákldní věty integrálního počtu Proztím jsme viděli, že určité integrály umíme spočítt pouze ve velmi jednoduchých přípdech, to z definice, uhádnutím, příp. kombincí těchto možností linerity. S těmito omezenými nástroji se jistě spokojit nehodláme hledáme nějké účinnější nástroje. Několik zákldních tvrzení v tomto odstvci vrcholí tzv. Newtonovou Leibnizovou větou, jejíž výpočetní důsledky záhy rozvineme. První zákldní vět Vzhledem k důležitosti tohoto tvrzení se mu obvykle přezdívá první zákldní vět integrálního počtu. Jedná se o doplnění Věty.. se silnějším předpokldem spojitosti: Vět..3. Jestliže je funkce f n intervlu, b spojitá, potom je funkce x F (x) := f(t) dt n tomto intervlu diferencovtelná pltí F (x) = f(x). Důkz. Důkz tohoto tvrzení není nijk složitý, vzhledem k výše uvedenému si můžeme dovolit následující zkrtku: F F (x + h) F (x) (x) = lim h h x+h = lim f(t) dt h h = lim h h x+h x f(t) dt x f(t) dt definice derivce definice funkce F ditivit vzhledem k mezím = lim f(c h ) h Vět o střední hodnotě = f(x) spojitost funkce f
4 4 Číslo c h v předposledním kroku je tkové číslo mezi x x+h, že. f(c h ) je střední hodnotou funkce f n intervlu x, x + h, resp. x + h, x podle znménk h. Zejmén c h x pro h. Uvědomte si, že díky konvencím jsou všechny úprvy pltné bez ohledu n znménko h. V krjních bodech intervlu, b máme smozřejmě n mysli jednostrnné derivce. Poznámk..4. Z první zákldní věty se mimo jiné dozvídáme, že ke kždé spojité funkci existuje funkce primitivní. Tímto je konečně dokázán vět, kterou jsme si uváděli n zčátku semestru. Druhá zákldní neb Newtonov Leibnizov vět Primitivní funkce (tedy neurčitý integrál) ke spojité funkci je ve Větě..3 sestrojen pomocí určitého integrálu jkožto funkce horní meze. Tento výsledek všk má pouze existenční chrkter zprvidl neumožňuje primitivní funkci k dné funkci njít. Nopk, známe-li primitivní funkci k dné funkci, jsme schopni velmi sndno určit hodnotu určitého integrálu: Předpokládejme, že f je spojitá n intervlu, b F je jkákoli k ní primitivní funkce. Rozdíl dvou primitivních funkcí k téže funkci je n libovolném x intervlu konstntní. Proto je podle předchozí věty F (x) = f(t) dt + C pro nějké C R všechn x, b. Součsně všk pltí F () = C. Odtud plyne, že F (x) = x f(t) dt + F () pro všechn x, b. Doszením x = b zjišťujeme, že určitý integrál f(t) dt =, tedy f(x) dx je jednoduše roven rozdílu hodnot primitivní funkce F v krjních bodech intervlu. Zobecnění tohoto pozntku pro obecné integrovtelné funkce je obshem tzv. Newtonovy Leibnizovy věty čili druhé zákldní věty integrálního počtu: Vět..5 (Newtonov-Leibnizov). Jestliže je funkce f n intervlu, b integrovtelná F je funkce, která je k f n tomto intervlu primitivní, potom pltí f(x) dx = F (b) F (). (..2) Důkz. Ukážeme, že pro libovolné dělení D = { = x, x,..., x n = b} intervlu, b existuje tkový výběr reprezentntů V, že odpovídjící Riemnnův součet
5 5 S(D, V ) je roven F (b) F (). Z definice Riemnnov určitého integrálu z předpokldu integrovtelnosti funkce f poté vyplývá pltnost (..2). Funkce F je podle definice diferencovtelná, tudíž je tké spojitá. Podle Lgrngeovy věty o střední hodnotě v kždém z podintervlů dělení D podle předpokldu F = f dostáváme F (x i ) F (x i ) = F (c i )(x i x i ) = f(c i )(x i x i ), kde c i je nějký bod z intervlu x i, x i i =, 2,..., n. Sečtením všech těchto rovností se téměř všechny členy n levé strně vyruší, n prvé strně obdržíme Riemnnův součet odpovídjící výběru V = {c,..., c n }. Celkem tedy pltí což jsme měli ukázt. F (b) F () = n f(c i )(x i x i ) = S(D, V ), i= Poznámky..6. (i) Nejprve si uvědomme, že skutečně nezáleží n tom, kterou z primitivních funkcí k funkci f ve vzorci (..2) použijeme. (ii) Vzhledem ke konvencím je zřejmé, že formule (..2) pltí i v přípdech, kdy > b. (iii) Nše verze Newtonovy-Leibnizovy věty předpokládá existenci primitivní funkce n celém integrčním oboru, b, což je všk poměrně silný poždvek. Npř. pro integrnd mjící nespojitost prvního druhu nemůže primitivní funkce existovt nelze tedy větu přímo plikovt. Tkové situce lze čsto řešit vhodným rozdělením integrčního oboru n podintervly, kde jsou již předpokldy splněny, pomocí ditivity integrálu vzhledem k integrčnímu oboru. Přípdné problémy v krjních bodech podintervlů lze sndno ošetřit odkzem n tvrzení o integrálech málo se lišících funkcí. Tyto myšlenky osvětlíme hned v následujících odstvcích, viz třeb Příkld..5. (v) Bezmyšlenkovité doszování do formule (..2) může vést k nesprávným výsledkům, viz třeb Příkld..7. Proto je nutné důsledně ověřovt předpokldy Newtonovy Leibnizovy věty! Pokud nejsou splněny n celém integrčním oboru, tk improvizujeme podle návodu v předchozí poznámce. (vi) Čsto budeme používt znčení [F (x)] b := F (b) F (), vzth (..2) potom nbývá následující tvr: [ f(x) dx = ] b f(x) dx. Příkld..7. Njděte chybu v následujícím výpočtu: 3π/4 cos 2 dx = [tg x]3π/4 = =. x
6 6 Řešení. Funkce tg x je sice primitivní funkcí k funkci / cos 2 x, problém je v tom, že funkce / cos 2 x není definovná v bodě π/2, 3π/4 v okolí tohoto bodu nbývá libovolně velkých hodnot. Tto funkce tudíž není n dném intervlu integrovtelná. Výpočetní techniky V této podkpitole se vrcíme k problému, jež už byl párkrát zmíněn který nyní můžeme zformulovt tkto: Jk určit hodnotu určitého integrálu f(x) dx? Některé integrály lze vypočítt přímo z definice Riemnnov integrálu, některé lze určit pomocí rozličných (čsto trikových) úprv úvh, některé pomocí Newtonovy Leibnizovy věty. Některé integrály lze počítt více způsoby (což může zhrnovt různé kombince přístupů), některé neumíme přesně určit vůbec v tkových přípdech se musíme spokojit s jejich přibližným vyjádřením. V tomto odstvci uvádíme několik jednoduchých integrálů upozorňujeme n typická úsklí při jejich řešení. Podle definice Riemnnov integrálu Přirozená výpočetní metod je odvozená z jedné ekvivlentní chrkterizce Riemnnov integrálu. Problemtickým místem uvedeného postupu je smozřejmě vyjádření Riemnnových součtů S(D n, V n ) v uzvřeném tvru, což nutně potřebujeme k tomu, bychom mohli počítt odpovídjící limitu lim S(D n, V n ). n Určité integrály většiny elementárních funkcí tímto způsobem nejspíš nikdy nespočítáme. Zde je n ukázku několik z mál výjimek. Příkld..8. Vypočtěte k N. x 3 dx zmyslete se nd zobecněním x k dx, kde Řešení. Zdná funkce je spojitá n celém definičním oboru, což je R, tudíž je integrovtelná n jkémkoliv omezeném podintervlu. Pro ekvidistntní dělení dného intervlu zjistíme, že potřebujeme vhodně uprvit součet třetích (obecněji k-tých) mocnin několik po sobě jdoucích přirozených čísel. To není neznámý problém, jeho obecné řešení všk není vůbec jednoduché. Npř. pro k = 3 pltí n 3 = 4 n2 (n + ) 2 ; Všimněte si, že výsledek je podezřelý už proto, že je záporný, přestože integrujeme kldnou funkci (s dolní mezí menší než horní).
7 7 ověřte indukcí. Odtud je již sndné vyjádřit posloupnost Riemnnových součtů v závislosti n n, tudíž spočítt limitu. Npř. pro dělení intervlu, b n n stejných dílů výběr reprezentntů v prvých dělicích bodech tk dostáváme tudíž S(D n, V n ) = n i= b n x 3 dx = b4 4 ( ) 3 ib = b4 n n 4 n i= lim (n + ) 2 n n 2 = b4 4. i 3 = b4 (n + ) 2 4n 2, Odtud podle ditivity integrálu vzhledem k mezím dostáváme x 3 dx = x 3 dx x 3 dx = b V následujícím příkldu je nopk snzší uprvit obecný součet posloupnosti, zto budeme mít trochu víc práce s limitou. Příkld..9. Vypočtěte r x dx, kde r (, ), zmyslete se nd zobecněním r x dx. Řešení. Pro obecné r (, ) je funkce r x spojitá pro všechn x R, tudíž je integrovtelná n kždém intervlu. Pro ekvidistntní dělení intervlu, výběry reprezentntů v levých dělicích bodech dostáváme S(D n, V n ) = n ( + r /n + r 2/n + + r (n )/n). Sčítnci v závorce tvoří geometrickou posloupnost s kvocientem q = r /n, kterou umíme bez problémů sečíst: S(D n, V n ) = r n( r /n ). Limitu můžeme dopočítt pomocí l Hospitlov prvidl: r x /n dx = ( r) lim n r = = r /n ln r. Zobecnění vzhledem k mezím necháváme n čtenáři.
8 8 Poznámk... Všimněte si, že Riemnnův integrál zde počítáme prostřednictvím jistých sum. Tyto sumy nemusíme všk chápt jen jko proximce integrálů. Lze je též povžovt z jkési diskrétní protějšky (určitých) integrálů. Připomeňme, že diskrétním protějškem derivce je tzv. diference, kterou definujeme jko f(k) = f(k + ) f(k). Obecněji lze brát i jinou hodnotu kroku než právě jedničku, dokonce i proměnnou. Pokud pk zvedeme operátor jko inverzi k operátoru, dostáváme diskrétní obdobu neurčitého integrálu (tj. primitivní funkce). Npř. k(k + ) = + C, C R, prcujeme-li n k oboru N. Ze znlosti neurčité sumy (tj. ntidiference) dné posloupnosti je pk již sndné obdržet hodnotu sumy. Proces integrce uvedeným způsobem tedy můžeme znázornit tkto: Riemnnův součet ntidiference součet sumy limitní přechod Riemnnův integrál Poznmenejme, že výpočet neurčité sumy všk většinou bývá mnohem obtížnější než nlezení primitivní funkce. Rfinovnosti triky Jisté nesmozřejmé čili trikové myšlenky jsou obsženy npř. v postupu Fermtov řešení tzv. kvdrtury prboly. Připomínáme, že tm vystupující součty určitě nelze interpretovt jko součty Riemnnovy, protože nesestávjí z konečně mnoh sčítnců. Příkld... Zobecníme myšlenku Fermtov řešení pro libovolné integrály typu x k dx, kde, b, k. Řešení. Uvžme = b, k obecné. Stejně jko výše si pomůžeme číslem α (, ), které určuje posloupnost (bα, bα 2, bα 3,... ) dělící intervl, b n nekonečně mnoho postupně se zmenšujících podintervlů. Nyní máme S(α) := b k+ ( α)( + α k+ + α 2(k+) + ). Sčítnci v prvé závorce tvoří geometrickou řdu s kvocientem α k+, který je díky předpokldu < α < ve stejných mezích. Řdu sndno sečteme, pro α dostáváme x k dx = lim S(α) = b k+ α bk+ lim = α α αk+ k +. Odtud stejně jko v příkldu..8 zjišťujeme, že x k dx = x k dx x k dx = bk+ k+. k +
9 9 Přípdy k =, resp. jsou smozřejmě triviální, le v uvedeném řešení nejsou nijk výjimečné. Řešení tktéž nezávisí n tom, zd je k větší nebo menší než, podsttný je pouze předpokld nezápornosti. Rozšíření tohoto návodu pro k <, všk různé od, umíme provést s použitím nevlstního integrálu. Přípd k = je vskutku specifický, viz následující příkld. Jedná se o tzv. kvdrturu (rovnoosé) hyperboly uvedené řešení je kompilcí myšlenek Gregor Sv. Vincent Alfonse Antoni de Srsy. Příkld..2. Všechny konstnty proměnné v následujících úkolech jsou kldná reálná čísl: (i) Dokžte, že pro libovolné c, d u pltí (ii) Dokžte, že F (x) := (iii) Vyjádřete x d c ud x dx = x dx. t dt je logritmická funkce s přirozeným zákldem. x dx pro obecné b. Řešení. Funkce f(x) = x je spojitá n R +, n libovolném uzvřeném podintervlu R + je tedy integrovtelná. (i) Kždý z integrálů v uvedené rovnosti je limitou nějké posloupnosti Riemnnových součtů. Pokud v obou přípdech zvolíme npř. posloupnosti ekvidistntních dělení s výběry v levých krjních bodech, potom pro kždé n N je odpovídjící Riemnnův součet n intervlu c, d zřejmě stejný jko n intervlu uc, ud. A stejné posloupnosti mjí stejné limity. (ii) Odtud z ditivity určitého integrálu vzhledem k mezím nyní plyne, že pro libovolné kldné u, v pltí F (uv) = uv t dt = u t dt + uv u t dt = u v t dt + uc dt = F (u) + F (v). t To je všk definující vlstnost logritmické funkce. Skutečně, je totiž známo, že kždé spojité řešení tzv. Cuchyovy rovnice g(x + y) = g(x) + g(y) n R má tvr g(x) = kx, k R. Tto rovnice je sice jiného tvru než F (uv) = F (u) + F (v). Stčí všk šikovná substituce (njděte ji) zjišťujeme, že kždé spojité řešení rovnice F (uv) = F (u) + F (v) n (, ) je tvru F (x) = k ln x, k R. K tomu, bychom rozpoznli hodnotu konstnty k, stčí znát hodnotu, příp. derivci funkce F v jednom bodě. Přímo z definice této funkce lze sndno vyvodit, že F () =. Proveďte. Dostneme tedy k =. (iii) Odtud již sndno plyne b x dx = x dx x dx = ln b ln = ln b.
10 My smozřejmě díky Větě..3 víme, že funkce F (x) = x t dt je primitivní funkcí k funkci f(x) = x, tedy F (x) = ln x + c pro nějké c. Vzhledem k tomu, že F () =, musí být c =, tedy F (x) = ln x. Přestože v uvedeném řešení používáme dnešní terminologii, jsou jeho myšlenky historicky strší než Vět..3 ve své obecnosti. Přímé užití Newtonovy Leibnizovy věty Newtonov Leibnizov vět..5 nbízí zjímvou početní lterntivu z předpokldu, že umíme určit primitivní funkci k integrndu. Víme, že toto může skutečný oříšek i pro celkem nevinně vyhlížející elementární funkce. Nejprve se vrátíme k sérii problémů řešených v Příkldech..8,....2: Příkld..3. Vypočtěte x k dx pro obecné k R vhodné meze b. Řešení. Definiční obor funkce f(x) = x k závisí n k; pro jednoduchost se omezíme pouze n kldná reálná čísl. N libovolném omezeném podintervlu (, ) je kždá z uvžovných funkcí spojitá, tedy integrovtelná. Pokud je k, potom primitivní funkce je F (x) = xk+ k+, podle Newtonovy Leibnizovy věty pltí: [ x x k k+ dx = k + ] b = bk+ k+. k + Pokud je k =, tj. f(x) = x, potom primitivní funkce je F (x) = ln x, podle Newtonovy Leibnizovy věty pltí: x dx = [ln x]b = ln b ln = ln b. Uvádíme ještě lterntivní řešení Příkldu..9: Příkld..4. Vypočtěte r x dx pro obecné, b R r R +. Řešení. Funkce f(x) = r x je integrovtelná n libovolném intervlu funkce F (x) = rx ln r je funkcí k ní primitivní. Podle Newtonovy Leibnizovy tedy pltí: [ r r x x dx = ln r ] b = rb r. ln r Pro = b = dostáváme právě výsledek Příkldu..9.
11 Příkld..5. Určete integrál následující funkce n celém definičním oboru: { cos x x π f(x) = 2, π 2, sin x x ( π 2, π. Řešení. Jediným bodem nespojitosti funkce f n definičním oboru je π 2. Vzhledem k typu této nespojitosti víme, že k funkci f neexistuje primitivní funkce n celém intervlu π 2, π. Avšk n podintervlu π 2, π 2 je funkce f spojitá, tudíž integrovtelná, s dobře známou primitivní funkcí. Pltí tedy π/2 π/2 f(x) dx = π/2 π/2 cos x dx = [sin x] π/2 π/2 = ( ) = 2. Podintervl ( π 2, π je zlev otevřený funkce f je n něm spojitá omezená. Ať už funkci f v levém krjním bodě rozšíříme jkkoliv, tto funkce bude integrovtelná hodnot integrálu bude π π/2 f(x) dx = Celkem tedy dostáváme π π/2 f(x) dx = π π/2 π/2 π/2 sin x dx = [ cos x] π π/2 = =. f(x) dx + π π/2 f(x) dx = 2 + = 3. K nlezení primitivní funkce velmi čsto potřebujeme různé pomocné úvhy úprvy, jimž jsme věnovli celou kpitolu o výpočetních technikách. Dvě zákldní účinné metody byly integrce per prtes integrce substitucí. V následujících dvou pododstvcích komentujeme užití Newtonovy Leibnizovy věty v přípdech, kdy je k nlezení primitivní funkce použit některá z těchto metod. Substituční metod pro určité integrály Substituční metod (pro neurčité integrály) je odvozen z věty o derivci složené funkce. Npř. sin x cos 3 x dx = u 3 du = 4 u4 + c = 4 cos4 x + c. Odtud, pro libovolné, b R, umíme podle Newtonovy Leibnizovy věty vyjádřit sin x cos 3 x dx doszením, resp. b do posledního výrzu, což je zřejmě totéž, jko kdybychom do předposledního výrzu doszovli cos, resp. cos b: sin x cos 3 x dx = cos b cos u 3 du = [ 4 u4] cos b cos = [ 4 cos4 x ] b.
12 2 Zobecněním tohoto příkldu dostáváme následující nlogii Věty o substitutci: Vět..6. Uvžujme funkci ϕ spojitě diferencovtelnou n intervlu I =, b funkci f spojitou n obrze J = ϕ(, b ). Potom f je integrovtelná n J, funkce f(ϕ(x)) ϕ (x) je integrovtelná n I pltí f(ϕ(x)) ϕ (x) dx = ϕ(b) ϕ() f(u) du. (..3) Důkz. Funkce ϕ je spojitá, tudíž obrzem intervlu je intervl (nebo bod). Funkce f je spojitá, tudíž integrovtelná, n J kždém jeho podintervlu. Tké poslední komponent, z nichž je poskládná funkce g(x) := f(ϕ(x)) ϕ (x), je spojitá; proto je funkce g spojitá, tedy integrovtelná n I. Podle Věty..3, má funkce f primitivní funkci, kterou oznčíme F. Funkce G(x) := F (ϕ(x)) je zřejmě primitivní funkcí k funkci g(x), podle Newtonovy Leibnizovy věty tedy pltí f(ϕ(x)) ϕ (x) dx = [F (ϕ(x))] b = [F (u)] ϕ(b) ϕ() = ϕ(b) ϕ() f(u) du. Jko obvykle předpokldy věty lze různými způsoby zeslbovt. Tk lze získt obecnější (všk obtížněji dokztelná) tvrzení. Pro nše účely uvedená verze stčí. S rovností (..3) budeme stejně jko s její předchůdkyní nkládt dvojím způsobem: Její užití ve smyslu zlev doprv je ilustrováno v Příkldu..7, plikce zprv dolev v Příkldu..8. Příkld..7. Vypočtěte π/2 sin x cos 2 x 4 + cos3 x dx. Řešení. Integrovná funkce je definovná spojitá všude kromě lichých násobků čísl π; n dném intervlu je tedy integrovtelná. V čitteli integrndu rozeznáváme (ž n nějkou tu konstntu) derivci funkce pod odmocninou ve jmenovteli, což nás přirozeně nvádí k substituci podle rovnosti (..3) ve smyslu zlev doprv (nová proměnná je funkcí té stávjící), totiž u = ϕ(x) := + cos 3 x. Tto funkce je spojitě diferencovtelná n celém R, tedy i n intervlu I =, π/2. Vyjádříme du = ϕ (x) dx = 3 cos 2 x sin x dx zjistíme, jk se trns-
13 3 formují meze: = ϕ() = 2 b = π/2 ϕ(b) =. Po doszení dostáváme π/2 sin x cos 2 x 4 + cos3 x dx = du 3 4, u 2 což je integrál, který přímo podle Newtonovy Leibnizovy věty spočítá kždý pozorný čtenář. Konečným výsledkem je číslo 4( 4 8 )/9. Povšimněte si, že v předchozím výpočtu máme < b součsně ϕ() > ϕ(b), tedy nová dolní mez je větší než nová horní; to je jen důsledkem toho, že funkce ϕ je n uvžovném intervlu klesjící, což není nic neobvyklého. Ve výpočtu jsme tké nijk nekomentovli spojitost, resp. integrovtelnost funkce f(u) = / 4 u n intervlu J =, 2 ; tto vlstnost je všk zřejmá je důsledkem dříve uvedených pozntků. Příkld..8. Vypočtěte 9 x x + dx. Řešení. Integrovná funkce je definovná spojitá pro nezáporná x, tudíž je n dném intervlu integrovtelná. Hledáme-li substituci, která by nás zbvil nepříjemné odmocniny, musí nás npdnout x = ϕ(t) := t 2. Tto volb odpovídá užití rovnosti (..3) ve smyslu zprv dolev (stávjící proměnná je funkcí té nové). 2 Funkce ϕ je spojitě diferencovtelná n celém R pltí dx = ϕ (t) dt = 2t dt. N rozdíl od předchozího příkldu všk musíme být obezřetní s trnsformcí mezí: Funkce ϕ(t) = t 2 totiž není prostá vzorem intervlu J =, 9 není intervl, le sjednocení dvou intervlů I + =, 3 I = 3,. Pokud uvžujeme t I +, potom se meze trnsformují tkto ϕ() = = ϕ(b) = 9 = 3; celkem potom dostáváme 9 3 x dx = 2 x + t(t ) t + což je integrál rcionální lomené funkce, který umí dopočítt kždý. Konečný výsledek je ln 6. Pokud bychom uvžovli t I, potom by se meze měnily tkto ϕ() = = ϕ(b) = 9 = 3. Při doszování do integrndu si nvíc uvědomujeme, že x = t 2 = t, neboli dostáváme 9 x dx = 2 x + 3 t( t ) t + 2 Pokud někoho plete znčení proměnných, nechť si přepíše x n u t n x. dt, dt.
14 4 Výsledek odtud smozřejmě musí vyjít stejně. Pokud je substituční funkce ϕ prostá, potom k přepočítání mezí stčí plikovt inverzní funkci ϕ ; z prostosti ( spojitosti) funkce ϕ plyne, že vzorem intervlu J = ϕ(), ϕ(b) je právě intervl I =, b. Pokud funkce ϕ prostá není, potom ze spojitosti funkce ϕ plyne jenom to, že vzorem intervlu J je sjednocení intervlů; pk je nutné se n některý z těchto intervlů zúžit podobně, jko jsme to udělli v předchozím výpočtu. Porovnejte tuto diskuzi s formulcí druhé části věty o substituci. Metod per prtes pro určité integrály Metod per prtes (pro neurčité integrály) je odvozen z věty o derivci součinu funkcí; její princip možnosti užití byly vysvětleny dříve. Npř. víme x cos x dx = x sin x sin x dx =.... Odtud podle Newtonovy Leibnizovy věty pltí x cos x dx = [ x sin x ] b sin x dx = [x sin x] b sin x dx =..., to pro libovolné, b R. Zobecněním tohoto příkldu dostáváme následující nlogii známého tvrzení: Vět..9. Uvžujme funkce u v, které jsou spojitě diferencovtelné n intervlu, b. Potom jsou funkce u v u v integrovtelné n, b pltí u(x) v (x) dx = [u(x) v(x)] b u (x) v(x) dx. (..4) Důkz. Funkce u v jsou diferencovtelné, zejmén jsou spojité stejně tk jsou spojité jejich derivce u v. Všechny tyto funkce jsou tudíž integrovtelné, proto je integrovtelná tky funkce u v + u v, viz vlstnosti (i) (iii) v Odstvci 6.. Funkce u v je primitivní funkcí k u v + u v, jsou splněny všechny předpokldy Věty..5 rovnost (..4) je jen uprvená Newtonov Leibnizov formule. Předpokldy věty lze jko obvykle zeslbit, npř. stčí předpokládt diferencovtelnost u v integrovtelnost jejich derivcí. Vzhledem k úvhám v odstvci málo lišících se funkcích je možné tyto předpokldy dále zeslbovt, niž by to mělo nějký zásdní vliv n zdůvodnění. Pro nše účely uvedená verze stčí.
15 5 Příkld..2. Vypočtěte π/2 sin k x dx pro libovolné k = 2, 3, 4,.... Řešení. Předně si uvědomme, že pro jkékoliv uvžovné k je funkce sin k x integrovtelná n libovolném intervlu. Pro konkrétní (mlá) k umíme hodnotu integrálu vypočítt, to dokonce několik způsoby. Formulce úlohy nás všk nvádí k nlezení nějkého obecného vzthu v závislosti n k. Neznámý integrál oznčíme I k přepíšeme do tvru I k = π/2 sin x sin k x dx. Pomocí metody per prtes, brzy nlezneme rekurentní vzth I k = k k I k 2. Odvoďte explicitní vzorec pro I k ověřte jej indukcí. Všimněme si, že rekurentní formule je druhého řádu. Potřebujeme tedy dvě počáteční podmínky. Ty jsou dány hodnotmi I I 2, které lze sndno spočítt. Celkem dostáváme π/2 sin k x dx = { (k )(k 3) 3 k(k 2) 4 2 π (k )(k 3) 4 2 k(k 2) pro k sudé, pro k liché. Přibližné vyjádření Tyto výpočetní možnosti zde nyní nebudeme podrobněji diskutovt. Jedná se zejmén o numerickou integrci, dále o využití nerovností vět o střední hodnotě tké o plikci mocninných řd. Nevlstní integrály V souvislosti s určitým Riemnnovým integrálem jsme se dosud zbývli pouze přípdy, kdy integrční obor je ohrničený (zejmén uzvřený) intervl, integrnd je funkce ohrničená n tomto intervlu. Viděli jsme, že je možno hovořit o integrálu funkce i přes intervl otevřený, či polouzvřený; důležitá všk byl jeho omezenost. V řdě situcí (ť už jde o plikce či čistě mtemtické úvhy) si všk s integrálem omezené funkce n omezeném intervlu nevystčíme. Proto nyní rozšíříme pojem určitého integrálu i n přípdy, kdy je lespoň jeden z těchto
16 6 předpokldů porušen. Integrály tohoto typu se nzývjí nevlstní. Nejprve se budeme zbývt integrály přes intervly typu, ) (, b. Dále budeme zkoumt integrály funkcí neomezených n omezeném intervlu (tj. mjících tzv. singulární bod). Též zmímíme zobecnění integrálu, které vznikne určitou kombincí těchto typů nkonec se budeme zbývt kritérii konvergence integrálu. Nevlstní integrál n neohrničeném intervlu Uvžujme funkci f definovnou n, ), R, tkovou, že f R(, b) pro kždé b (, ). Definujme funkci F (t) = t f(x) dx, t, zkoumejme její chování, roste-li t neomezeně. Rozlišíme dv přípdy limitního chování, které mohou nstt podle nich definujeme následující typy: Říkáme, že nevlstní integrál f(x) dx konverguje (nebo že existuje), existuje-li vlstní limit lim t F (t); kldeme f(x) dx = lim t F (t), diverguje, neexistuje-li vlstní limit lim t F (t), tj. je-li lim t F (t) nevlstní nebo neexistuje. Poznámk..2. (i) Někdy se hovoří o nevlstním integrálu vlivem mezí či nevlstním integrálu vlivem intervlu či nevlstním integrálu. druhu. (ii) Anlogicky definujeme pojem konvergujícího resp. divergujícího nevlstního integrálu f(x) dx, kde b R. Již víme, že určitý integrál lze interpretovt jko obsh jistého obrzce. V přípdě vhodného nevlstního integrálu, který konverguje, pk sndno dostneme příkld obrzce, který má neomezený obvod, všk konečný obsh. Příkld..22. Vyšetřete konvergenci nevlstního integrálu kde p R. dx x p, Řešení. Oznčme F (t) = t /xp dx. Je-li p, pk máme F (t) = [ x p+ ] t p + = p ( ) t p.
17 7 Odtud lim F (t) = t { /(p ) pro p >, pro p <. Jestliže p =, pk F (t) = ln t. Celkem tedy dostáváme: Nevlstní integrál /x p dx { konverguje ( má hodnotu /(p )), je-li p > diverguje, je-li p. Dobře si všimněte, jkým způsobem při výpočtech nevlstních integrálů postupujeme. Nelze npř. používt zápis i když to mnoho studentů dělá znmenjící jkési doszování nekonečn, tj. /x p dx = /( p + )[x p+ ] =.... Je důležité si uvědomit, že je potřeb rgumentovt pomocí limitního přechodu. Dále si všimněte, že n konvergenci či divergenci v tomto přípdě nemá vliv to, když dolní mez nhrdíme libovolným kldným číslem; zjímá nás chování v okolí nekonečn. Diskutovný integrál je velmi užitečný pro srovnávcí účely v některých kritériích konvergence, viz níže. Nevlstní integrál neomezené funkce Nyní budeme prcovt n omezeném intervlu, ovšem s funkcí, jež je n něm neomezená. Uvžujme funkci f definovnou n intervlu, b),, b R, < b, tkovou, že f R(, c) pro kždé c (, b). Jestliže f je neomezená n, b), pk říkáme, že bod b je singulárním bodem funkce f. Podobně jko v předchozím odstvci definujme funkci F (t) = t f(x) dx, t, b), zkoumejme její chování pro t blížící se zlev k bodu b. Opět rozlišíme dv přípdy limitního chování, které mohou nstt, podle nich definujeme následující typy: Říkáme, že nevlstní integrál f(x) dx konverguje (nebo že existuje), existuje-li vlstní limit lim t b F (t); kldeme f(x) dx = lim t b F (t), diverguje, neexistuje-li vlstní limit lim t F (t), tj. je-li lim t b F (t) nevlstní nebo neexistuje. Poznámk..23. (i) Někdy se hovoří o nevlstním integrálu vlivem funkce či nevlstním integrálu 2. druhu.
18 8 (ii) Anlogicky definujeme singulární bod funkce f definovné n intervlu (, b konvergenci nebo divergenci nevlstního integrálu f(x) dx, kde b R. (iii) Jistě je n první pohled viditelné, že ob typy nevlstního integrálu, vlivem intervlu vlivem funkce, jsou si velmi podobné; jkoby singulární bod hrál roli nekonečn. A skutečně lze jeden typ jednoduše převést n druhý nopk. Uvžujme npř. nevlstní integrál f(x) dx se singulárním bodem b. Nechť je ε mlé kldné číslo, které nám zřizuje loklizci v libovolně mlém levém okolí bodu b. Potom nám následující situce převede integrál 2. druhu n integrál. druhu ε x = b /t f(x) dx = dx = t 2 dt /(b ), b ε /ε = /ε /(b ) Detily si promyslete smi; zejmén zkoumejte přípd, kdy ε +. Příkld..24. Vyšetřete konvergenci nevlstního integrálu kde p R. dx x p, f ( b ) t t 2 dt. Řešení. Vzhledem k podobnosti s příkldem z předchozího odstvce přenecháme detily výpočtu čtenáři. Zmiňme pouze, že je zde singulárním bodem. Výsledek je tento: Nevlstní integrál /xp dx konverguje (přičemž má hodnotu /( p)), je-li p (, ) diverguje, je-li p. Pro p již není singulárním bodem, integrál není nevlstní počítá se běžným způsobem. Nevlstní integrál obecný přípd Při studiu nevlstního integrálu jsme doposud předpokládli, že integrční obor obshuje právě jeden šptný bod. Vždy to byl krjní bod buďto způsobovl neomezenost intervlu ( nebo ) nebo neomezenost funkce (singulární bod). Je zcel přirozené se nyní zjímt o situci, kde může být v integrčním oboru těchto šptných bodů víc (konečný počet). Hlvní myšlenk spočívá v tom, že mezi šptné body vložíme pomocné body rozdělíme pomocí nich singulárních bodů integrční obor tk, by vzniklé podintervly neobshovly uvnitř už žádný singulární bod, tj. všechny singulární body budou krjními body některých podintervlů, přitom kždý podintervl bude mít šptný právě jeden konec. Uvžujme nyní tedy, b R {± }, < b, nechť {,..., n } je konečná množin reálných čísel tková, že = < < < n < n = b.
19 9 Nechť f je funkce definovná n množině n k= ( k, k ), pro niž,..., n jsou její singulární body (body b mohou, le nemusí být jejími singulárními body, nebo může nstt = nebo b = ). Volme čísl c,..., c n tk, že < c < < c 2 < n < c n < n. (..5) O nevlstním integrálu f(x) dx řekneme, že konverguje, jestliže konvergují všechny nevlstní integrály c k k f(x) dx, k c k f(x) dx (k =,..., n) jeho hodnotu definujeme jko součet těchto integrálů. Všimněte si, že pomocné body c,..., c n měly splňovt pouze podmínku (..5), jink byly voleny zcel libovolně. Promyslete si, proč je tto libovolnost možná. Příkld..25. Vypočtěte dx x 2. Řešení. Singulárními body jsou zde body,. Proto lze z pomocné body volit npř. 2,, 2 vyšetřujeme tedy nevlstní integrály 2 dx x 2, 2 dx x 2, dx x 2, dx x 2, 2 dx x 2, 2 dx x 2. Primitivní funkci k funkci /(x 2 ) njdeme (rozkldem rozkldem v prciální zlomky) ve tvru 2 ln t t +. Nyní je již jednoduché zjistit, že některé z jednotlivých nevlstních integrálů konvergují některé nikoliv (vyšetřete všechny v přípdě těch konvergentních určete jejich hodnotu). Poněvdž lespoň jeden z těchto integrálů diverguje, tk diverguje i původní integrál. Příkld..26. Vypočtěte dx x 2. Řešení. N tomto důležitém příkldu si nejprve demonstrujme, km může vést neprávně zvolený přístup, kterého se studenti bohužel někdy dopouštějí. Ignorují totiž, že jde o nevlstní integrál použijí formálně Newtonovu-Leibnizovu formuli, jko by šlo o běžný určitý integrál. Jejich výpočet pk vypdá nějk tkto: [ dx x 2 = ] = 2. x To je smozřejmě úplně šptně! V tomto přípdě nelze použít Newtonovu-Leibnizovu formuli, neboť nejsou splněny potřebné předpokldy (proč?). Přinejmenším by nás všk mělo trknout, že integrál kldné funkce vyšel záporný. Pro správné vyřešení problému si stčí uvědomit, že integrční obor obshuje singulární bod. Rozdělením n dv podintervly získáme dv nevlstní integrály 2. druhu, které zřejmě divergují. Detily si promyslete smi. Poznámk..27. Právě uvedený příkld nás motivuje k poznámce, že uvžujemeli výrz f(x) dx,, b R, musíme zvžovt, zd je funkce f n intervlu, b omezená, či zd obshuje singulární bod(y).
20 2 Typickým příznkem je, že funkce není v některém bodě definovná. Nejčstěji jde o dělení nulou. To ovšem pořád neznmená, že musí jít o nevlstní integrál. Npř. v integrálu π je problemtickým bodem nul. Funkce (sin x)/x zde není definovná. Je všk n integrčním oboru omezená jde o běžný určitý integrál. Můžeme si nyní položit přirozenou otázku, co se stne, když při výpočtu běžného integrálu postupujeme, jko by šlo o nevlstní integrál. Ukzuje se, že (nštěstí) se nestne nic. To plyne z vlstností určitého integrálu jko funkce mezí. Někdy je dokonce výhodné tkto postupovt; spočtěte npř. integrál x ln x dx tk, že nejdřív budete běžně integrovt přes, v obdrženém výsledku pk provedete limitní přechod pro +. Vyhneme se tk trochu problemtickému nlezení primitivní funkce v bodě (i když i pro tyto přípdy existuje vhodné zobecnění Newtonovy-Leibnizovy formule). Rovněž si ověřte, že funkce x ln x je ohrničená n intervlu (, (stčí spočíst její limitu pro x + ); nejde tedy o nevlstní integrál. Kritéri konvergence nevlstních integrálů Chceme-li řešit otázku konvergence či divergence dného neurčitého integrálu, s nšimi dosvdními znlostmi jsme schopni pouze jediného postupu: vypočítt jistý pomocný integrál jko funkci dolní či horní meze poté provést ptřičný limitní přechod. Zejmén první část tohoto postupu všk může skýtt znčné úsklí, jk jsme viděli dříve; pro plikci Newtonovy-Leibnizovy formule totiž potřebujeme spočíst primitivní funkci, což může být velmi obtížné ž nemožné. Nštěstí všk pro zjištění konvergence či divergence nevlstního integrálu není vždy potřeb hledt jeho přesnou hodnotu. Existuje totiž řd kritérií, která nám umožní zjistit tuto informci dleko sndněji. My si zde uvedeme pouze t nejzákldnější kritéri, to pro přípd nezáporných integrndů. Srovnávcí kritérium Uvžujme funkci f, která je definovná nezáporná n, ) f R(, b) pro b >. Tj., zkoumejme nevlstní integrál typu f(x) dx Všechny osttní přípdy, tj. integrndů n intervlu (, b či n intervlu obshujícím singulární body by se vyšetřovly podobně; promyslete si je. Rovněž si promyslete, jk by vypdly přípdy, kde by předpokld nezápornosti funkce f byl nhrzen předpokldem její nekldnosti. Nejprve poznmenejme, že funkce F (t) = t f(x) dx je n intervlu, ) neklesjící, proto lim t F (t) buďto existuje jko konečné číslo, nebo je rovn. Uvžujme dlší funkci g definovnou n intervlu, ), splňující f(x) g(x) n, ). g R(, b) pro b >. Potom je jednoduché dokázt (promyslete si smi; prcujte zejmén s funkcemi F (t) G(t) = t g(x) dx), že pltí tto intuitivní tvrzení (tzv. srovnávcí kritérium): Jestliže konverguje g(x) dx, konverguje i f(x) dx.
21 2 Jestliže diverguje f(x) dx, diverguje i g(x) dx. K nevlstním integrálům vhodným pro srovnávcí účely ptří npř. x p dx, nebo e kx dx, kde p, k jsou reálné prmetry (, ). Lze lehce odvodit, pro které hodnoty prmetrů integrály konvergují resp. divergují; proveďte. Vhodné srovnávcí integrály pro jiné přípdy (tj. npř. integrční obor je (, b, nebo intervl obshuje singulární body) se obdrží podobným způsobem. Příkld..28. Vyšetřete konvergenci nevlstního integrálu e x2 dx. Řešení. Nejprve poznmenejme, že e x2 dx je vyšší trnscendentní funkcí, proto je bezprostřední výpočet v nši situci prkticky nemožný. Protože všk pltí e x e x2 n, ) e x dx konverguje, konverguje podle srovnávcího kritéri i původní nevlstní integrál. Limitní srovnávcí kritérium Opět se zjímejme o nevlstní integrál. druhu, tj. f(x) dx, přičemž osttní přípdy se vyšetří podobně (proveďte!). Předpokládáme, že f, g R(, b) jsou nezáporné n, ). Vzhledem k tomu, že pro kovergenci či divergenci f(x) dx je rozhodující chování funkce f v okolí nekonečn, nepřekvpí nás, že srovnání dvou integrndů postčí provést jistou limitní cestou. Předpokládejme, že existuje limit f(x) lim = M, ) { }. (..6) x g(x) Pltí tzv. limitní srovnávcí kritérium: Jestliže M < konverguje Jestliže M > diverguje g(x) dx, konverguje i f(x) dx. g(x) dx, diverguje i f(x) dx. Důležitou roli v jeho důkzu hrje předchozí srovnávcí kritérium, neboť npř. existence vlstní limity (..6) nám umožní nlézt rozumný vzth mezi f g. Dobře si rozmyslete, jké (vzájemné) symptotické chování vykzují funkce f g v závislosti n hodnotě M. Příkld..29. Vyšetřete konvergenci integrálu π/2 4 cos x 3 sin 2 2x dx. Řešení. Integrnd, který oznčíme f, je spojitý v intervlu (, π/2). Smi ověřte, že lim f(x) =, lim f(x) = ; x + x π/2 první rovnost je zřejmá, druhá využívá L Hospitlovo prvidlo. Dodefinujeme-li f(π/2) =, je funkce f spojitá v intervlu (, π/2, přičemž tto změn zřejmě
22 22 nemá vliv n konvergenci či divergenci původního integrálu. Jediným singulárním bodem integrálu je tedy. Položme g(x) = x 2/3. Pk pltí lim x + f(x)/g(x) = 4 2 2/3 > ; ověřte. Protože integrál π/2 x 2/3 dx konverguje, konverguje podle limitního srovnávcího kritéri tké původní integrál. Nutná podmínk konvergence Limitní srovnávcí kritérium může být užito k obdržení velmi jednoduché podmínky, která musí pltit pro rozumné integrndy konvergujících nevlstních integrálů. Předpokládejme, že Potom pltí f(x) dx konverguje existuje L = lim f(x) = L. x (tzv. nutná podmínk konvergence). Důkz je velmi jednoduchý. Nznčíme pouze hlvní myšlenku, detily promyslete smi. Předpokládáme-li totiž sporem, že L, bez újmy n obecnosti vezměme npř. L >, zvolíme-li v limitním srovnávcím kritériu g(x) =, pk dostneme divergenci f(x) dx, což je spor. Pozor: Tto vět netvrdí, že integrnd konvergentního integrálu musí mít limitu. Obecně nic tkového nepltí, jk ukzuje následující příkld. Příkld..3. Vypočtěte f(x) dx, kde f(x) = { x pro x N, pro x, ) \ N. Řešení. Oznčme F (t) = t f(x) dx. Poněvdž se funkce f v intervlu, t pro libovolné t > liší od identicky nulové funkce jen v konečném počtu bodů, tk pltí F (t) pro kždé t >. To plyne z odstvce o málo líšících se funkcích. Odtud dostáváme lim t F (t) =, tedy f(x) dx konverguje má hodnotu. Přitom lim x f(x) zřejmě neexistuje; dokonce je funkce f n integrčním oboru, ) neohrničená. Jordnov Penov mír Již několikrát jsme se v souvislosti s určitým integrálem zmínili o výpočtu obshu rovinných obrzců. Tomu se budeme věnovt zejmén v následujícím odstvci. Chceme-li všk k této látce přistupovt spoň trochu poctivě, je třeb přesněji vymezit intuitivně jsný pojem obsh rovinného obrzce. Tento pojem je nám zřejmý v přípdě jednoduchých obrzců, jko je npř. obdélník či trojúhelník (i když skutečně precizní vysvětlení, proč je obsh obdélník o délkách strn m n právě m n, není úplně triviální. V přípdě složitějších množin jsou buďto známy vzorce pro obsh, 3 nebo je potřeb nějk jejich obsh spočíst (z předpokldu, 3 Zde je všk potřeb říct, ž řd studentů neví, odkud se vlstně tkové vzorce vzly. A to včetně i těch nejznámějších formulek, jko je npř. obsh kruhu. Prostě těmto vzorcům jen uvěří.
23 23 že je to vůbec možné v nějkém rozumném smyslu). Dokonce mohou existovt množiny, jko npř. {(x, y) R 2 : x, y, x, y Q}, (..7) u kterých bychom velmi váhli, jestli je lze vůbec rozumně změřit. Míru lze chápt jko zobecnění či spíše zpřesnění pojmů délk, obsh, či objem; my se nyní zbýváme především obshem. Měřitelná množin (v R 2 ), je dosttečně rozumná množin, u které lze určit její obsh. Obecně se touto problemtikou zbývá tzv. teorie míry, která jde nd rámec nšeho kurzu. Hned n zčátku musíme čtenáře zklmt, že níže sestrojená Jordnov Penov mír vlstně není mírou, tj. nemá všechny vlstnosti, které od míry v moderní mtemtice poždují. Jde všk o poměrně jednoduchý objekt, který pro nše účely nprosto postčí. Asi tk jko nám postčuje Riemnnův integrál. Většinou se Jordnov Penov mír konstruuje podobným způsobem, jko popíšeme nyní. Všimněte si podobnosti s přístupem, který používl vlstně už Archimedes. Totiž proximci rovinného útvru pomocí jednodušších útvrú. Nejdříve uvžujme množinu v rovině (nzývejme ji třeb elementární množinou), kterou definujeme jko konečné sjednocení obdélníků mjících nvzájem disjunktní vnitřky. 4 Nechť E znčí množinu všech elementárních množin v rovině. Dále nechť m(m) pro M E znmená míru neboli obsh množiny M; s obshem elementárních množin jistě nemáme problém. 5 Uvžujme množinu A v rovině, která je omezená (tj. celá se nchází v dosttečně velkém kruhu či obdélníku). Potom množin {m(m) : M E, M A} je neprázdná shor omezená; promyslete si tuto skutečnost. Podobně je množin {m(m) : M E, M A} neprázdná zdol omezená. Můžeme tedy bez obv definovt tzv. vnější Jordnovu míru, m (A) = inf{m(m) : M E, M A}, m (A) = sup{m(m) : M E, M A}, tzv. vnitřní Jordnovu míru. Zřejmě pltí m (A) m (A). Jestliže nstne rovnost, pk máme hlednou míru: Definice..3. Jestliže m (A) = m (A), pk říkáme, že množin A je měřitelná (v Jordnově či Jordnově Penově smyslu) definujeme její (Jordnovu) míru (obsh) vzthem m(a) = M (A) = m (A). 4 Někdy se elementární množin definuje jko sjednocení množin tvru I J, kde I, J jsou intervly. Nezáleží n tom, zd se tyto množiny překrývjí. Nezáleží n typu intervlů I, J. Máme zde jen drobné technické rozdíly, které lze sndno překlenout. Ve skutečnosti lze ukázt, že kždá tkto definovná množin se dá vyjádřit jko sjednocení disjunktních množin tvru I J, kde I, J jsou intervly. 5 Chceme-li být formálně přesní, měli bychom ještě ukázt, že mír elementární množiny je nezávislá n rozdělení do obdélníků. To všk skutečně pltí.
24 24 Pochopitelně bychom místo obdélníků mohli uvžovt stejně dobře npř. trojúhelníky, nebo bychom mohli utvořit v rovině přímo čtvercovou síť sledovt situci při neomezeném zjemňování této sítě. Pokuste se o tkovou konstrukci, kde rovinu pokryjeme nejdříve čtvercovou sítí, v níž je délk strn jednotlivých čtverců rovn, v dlším kroku je rovn /2, pk /4 td. 6 Vnitřní vnější míru pk dostáváme jko limity jistých omezených monotonních posloupností. Poznmenejme, že Jordn používl čtvercovou síť Peno mnohoúhelníky. Právě sestrojená mír má zákldní vlstnosti obshu ve smyslu elementární geometrie. Nemění se posunutím, otočením nebo provedením osové souměrnosti. Jsou-li A, B měřitelné množiny, jsou A B, A B, A \ B tky měřitelné. Dále pltí (z předpokldu, že A, B jsou měřitelné množiny): m(a) (tj. obsh je vždy nezáporný), A B m(a B) = m(a) + m(b) (tj. obsh je ditivní ), A B m(a) m(b) (tj. obsh je monotónní ), A je obdélník o délkách strn m, n m(a) = m n (tj. obsh obdélníku se počítá tk, jk jsme zvyklí). Téměř bezprostředně z definice plyne: Jestliže pro kždé ε > existují M, M 2 E tkové, že M A M 2 že m(m 2 ) m(m ) < ε, pk A je měřitelná. Dále si uvědomme, že množiny, které uvžujeme při definici horního dolního součtu jsou elementární. Užitím těchto dvou fktů dostáváme následující tvrzení: Nechť f R(, b) je nezáporná funkce definovná n, b. Potom Pltí 6 Uvžujme omezenou množinu M R 2. Sestrojme v rovině tzv. síť řádu n, n N {} pomocí přímek rovnoběžných s osmi x, y, které procházejí body [k2 n, ] resp. [, k2 n ], k Z. Síť řádu n nám rozdělí rovinu n tzv. čtverce řádu n, z nichž kždý má zřejmě míru (tj. obsh) rovnu 4 n. Tzv. elementární množinu řádu n definujeme jko sjednocení konečného počtu čtverců téhož řádu n s disjunktními vnitřky. Tzv. jádro řádu n množiny M (ozn. J n(m)) definujeme jko elementární množinu vytvořenou všemi čtverci řádu n obsženými ve vnitřku M. Tzv. obl řádu n množiny M (ozn. O n(m)) definujeme jko elementární množinu vytvořenou všemi čtverci řádu n, jejichž průnik s uzávěrem M je neprázdný. J n(m) M M M O n(m) m(j n(m)) m(j n+ (M)), m(o n(m)) m(o n+ (M)), n N {}, kde m znčí míru (obsh) dné elementární množiny. (S výpočtem obshů elementárních množin jistě není problém.) Všimněte si, že jsme tkto obdrželi jisté posloupnosti, které jsou omezené monotonní. Tedy máme zručenu existenci limit lze bez obv definovt m (M) = lim m(jn(m)), n m (M) = lim m(on(m)); n m (M) se nzývá vnitřní Jordnov mír množiny M m (M) se nzývá vnější Jordnov mír množiny M. Vždy pltí m (M) m (M).
25 25 G f (, b) je měřitelná množin pltí m(g f (, b)) = f(x) dx, kde G f (, b) je tzv. subgrf funkce f definovný jko G f (, b) = {[x, y] R 2 : x, b, y f(x)}. Pltí ovšem tké opčná implikce. Celkem tedy dostáváme: Vět..32. Nechť f je omezená, nezáporná funkce definovná n, b. Potom f R(, b) G f (, b) je měřitelná. V přípdě měřitelnosti (či integrovtelnosti) potom pltí m(g f (, b)) = f(x) dx. (..8) Vlstnosti uvedené z Definicí..3 jsou jistě ty rozumné vlstnosti, které by měl obsh mít. Někdy se n zákldě tkových rozumných vlstností (xiomů) obsh zvádí. Můžeme postupovt třeb tkto. Chceme njít dosttečně širokou třídu nezáporných funkcí, pro něž dovedeme určit obsh (míru) jejich subgrfu. Přesněji, uvžujeme nějkou třídu M nezáporných funkcí, z nichž kždá je definován n nějkém uzvřeném intervlu. Dále nechť G(M) znčí množinu všech subgrfů všech funkcí z M. Pro zobrzení definujme tyto vlstnosti: m : G(M) R (m ) Jestliže f M,, b Dom(f) c (, b), potom m(g f (, b)) = m(g f (, c)) + m(g g (c, b)). (m 2 ) Jestliže f, g M,, b Dom(f), c, d Dom(g) G g (c, d) G f (, b), potom m(g g (c, d)) m(g f (, b)). (m 3 ) Jestliže f(x) = c, ) pro x, b, potom f M m(g f (, b)) = c(b ). Nzývejme číslo m(g f (, b)) obshem (měrou) množiny G f (, b). Existuje-li tříd funkcí M zobrzení m : G(M) R splňující (m 2 ) (m 3 ), pk je m(g f (, b)) pro kždou f M. Dokžte si tento fkt. Následující vět říká, že náš výše formulovný problém je jednoznčně řešitelný, vezmeme-li M = M R, kde M R je množin všech nezáporných funkcí, z nichž kždá je definovná Riemnnovsky integrovtelná n nějkém uzvřeném intervlu.
26 26 Vět..33. Existuje jediné zobrzení m : G(M R ) R, které splňuje xiomy (m ), (m 2 ), (m 3 ). Toto zobrzení je dáno vzthem m(g f (, b)) = f(x) dx. Důkz. Pro f M R položme m(g f (, b)) = f(x) dx. Pk m je zobrzení G(M R ) do R, které splňuje (m ), (m 2 ), (m 3 ); ověřte tuto skutečnost s využitím dříve odvozených vlstností Riemnnov integrálu. Při důkzu jednoznčnosti postupujeme tkto: Vezmeme libovolné zobrzení m : G(M R ) R splňující (m ), (m 2 ), (m 3 ) libovolnou funkci f M R definovnou n, b. Potom S(D, inf) m(g f (, b)) S(D, sup) pro libovolné dělení D intervlu, b, kde S(D, inf) resp. S(D, sup) je dolní resp. horní integrální součet. Řádně si odvoďte tento fkt, využívá se vlstností (m ), (m 2 ), (m 3 ). Odtud pk již plyne m(g f (, b)) = f(x) dx, neboť f (, b). V této souvislosti si nemůžeme odpustit ještě jedno poměrně zřejmé tvrzení, které je vlstně přepisem známého fktu v jiné{ řeči: Jestliže f je spojitá nezáporná funkce n, b, pk funkce F (x) = pro x = m(g f (, x)) pro x (, b je primitivní funkcí k f n, b. V Definici..3 jsme zvedli dvoudimenzionální (Jordnovu Penovu) míru. Anlogicky ji lze definovt obecně v R n, n N. Pro ilustrci nznčme jednu poněkud úspornější konstrukci. Prostor R n lze vidět jko sjednocení n rozměrných intervlů tvru,j,,j 2,j2, 2,j2 n,jn, n,jn, kde množin čísel i,j (i =, 2,..., n; j =, ±, ±2,... ), s vlstnostmi i,j < i,j, lim j ± i,j = ±, je dělení R n. Tzv. chrkteristickou { funkci χ M : R n R množiny M R n pro [x, y] M definujeme předpisem χ M (x, y) = pro [x, y] M. Nechť A R n je omezená množin. Potom vnitřní měrou množiny A máme n mysli číslo m (A) = sup min χ A(x)m(J), x J kde m(j) je objem n rozměrného intervlu J ve smyslu elementární geometrie (tj. součin délek jeho hrn), sčítá se přes všechny intervly dělení supremum se bere přes všechn dělení prostoru R n. Podobně definujeme vnější míru množiny A jko m (A) = inf mx x J χ A(x)m(J). Pltí-li rovnost m (A) = m (A) =: m(a), (..9)
27 27 pk m(a) je Jordnov Penov mír množiny A. Jko speciální přípd pro n = 2 dostneme míru (obsh) z Definice..3. Pro n = 3 jsme tkto dli přesný formální smysl intuitivně jsnému pojmu objem. Pozor: je třeb uvžovt dimenzi prostoru, v němž prcujeme; npř. úsečk má v R míru rovnu své délce, le v R 2 má míru nulovou (lze ji chápt jko obdélník s jednou strnou nulovou). Ve Větě..32 jsme propojili Rimnnův integrál s dvoudimenzionální (Jordnovou Penovou) mírou. Nyní poukážeme n souvislost Riemnnov integrálu s mírou n přímce. Vět..34. Množin A, b je měřitelná, právě když χ A R(, b). V přípdě měřitelnosti (či integrovtelnosti) potom pltí m(a) = χ A(x) dx. Důkz. Dokážeme nejdříve implikci zlev doprv. Nechť tedy A je měřitelná. Vezměme libovolné ε >. Pk lze njít elementární množiny M, N R (tedy jsou tvořeny konečným sjednocením intervlů) tkové, že M A N m(n \ M) ε. Zřejmě χ M χ A χ N χ M, χ N R(, b). Uvžujme dělení D sestvené z koncových bodů množin M, N. Poněvdž M, N jsou elementární, pro horní dolní součty jejich chrkteristických funkcí pltí S(D, sup; χ M ) = S(D, inf, χ M ) = m(m) S(D, sup; χ N ) = S(D, inf; χ N ) = m(n). Máme S(D, sup; χ A ) S(D, sup; χ N ) S(D, inf; χ A ) S(D, inf; χ M ). Dostáváme tk S(D, sup, χ A ) S(D, inf, χ A ) ε, odkud již sndno plyne tvrzení. Nopk předpokládejme, že χ A R(, b). Pro libovolné ε > umíme njít dělení tkové, že n ( ) mx χ A (x) min χ A (x) (x i x i ) < ε. x i x x i x i x x i i= Vezměme elementární množiny M, N v R tkové, že M A N N = i x i, x i, přičemž mx χ A = n x i, x i M = i (x i, x i ), přičemž min χ A = n x i, x i. Potom máme m(n) m(m) < ε. Vzhledem k Větě..34 nás nepřekvpí, že Jordnov Penov mír množiny n R se někdy zvádí pomocí Riemnnov integrálu. Přesněji formulováno: nechť χ A R(, b) pro A, b. Pk míru množiny A definujeme jko m(a) = χ A(x) dx. Uvedená konstrukce je univerzální, tj. lze ji použít n množiny v R 2, R 3 obecně v R n pro libovolné n N. Předpokldem pro možnost její plikce je ovšem vybudování teorie n-rozměrného integrálu. Protože se náš text vícerozměrnými integrály nezbývá, zmiňme pouze, že konstrukce je velmi obdobná jednorozměrnému přípdu. Při posuzování (ne)měřitelnosti množiny můžeme jistě postupovt dle definice, všk většinou to není zrovn optimální postup. Ještě než si vyslovíme
VIII. Primitivní funkce a Riemannův integrál
 VIII. Primitivní funkce Riemnnův integrál VIII.2. Riemnnův integrál opkování Vět. Nechť f je spojitá funkce n intervlu, b nechť c, b. Oznčíme-li F (x) = x (, b), pk F (x) = f(x) pro kždé x (, b). VIII.3.
VIII. Primitivní funkce Riemnnův integrál VIII.2. Riemnnův integrál opkování Vět. Nechť f je spojitá funkce n intervlu, b nechť c, b. Oznčíme-li F (x) = x (, b), pk F (x) = f(x) pro kždé x (, b). VIII.3.
V předchozích kapitolách byla popsána inverzní operace k derivování. Zatím nebylo jasné, k čemu tento nástroj slouží.
 NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování Ztím nebylo jsné, k čemu tento nástroj slouží Uvžujme trmvj, která je poháněn elektřinou při brždění vyrábí dynmem elektřinu:
NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování Ztím nebylo jsné, k čemu tento nástroj slouží Uvžujme trmvj, která je poháněn elektřinou při brždění vyrábí dynmem elektřinu:
NEWTONŮV INTEGRÁL. V předchozích kapitolách byla popsána inverzní operace k derivování. Zatím nebylo jasné, k čemu tento nástroj slouží.
 NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování. Ztím nebylo jsné, k čemu tento nástroj slouží. Uvžujme trmvj, která je poháněn elektřinou při brždění vyrábí dynmem elektřinu:
NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování. Ztím nebylo jsné, k čemu tento nástroj slouží. Uvžujme trmvj, která je poháněn elektřinou při brždění vyrábí dynmem elektřinu:
Integrální počet - II. část (určitý integrál a jeho aplikace)
 Integrální počet - II. část (určitý integrál jeho plikce) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 7. přednášk z ESMAT Michl Fusek (fusekmi@feec.vutbr.cz) 1 / 23 Obsh 1 Určitý vlstní (Riemnnův)
Integrální počet - II. část (určitý integrál jeho plikce) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 7. přednášk z ESMAT Michl Fusek (fusekmi@feec.vutbr.cz) 1 / 23 Obsh 1 Určitý vlstní (Riemnnův)
OBECNÝ URČITÝ INTEGRÁL
 OBECNÝ URČITÝ INTEGRÁL Zobecnění Newtonov nebo Riemnnov integrálu se definují různým způsobem dostnou se někdy různé, někdy stejné pojmy. V tomto textu bude postup volen jko zobecnění Newtonov integrálu,
OBECNÝ URČITÝ INTEGRÁL Zobecnění Newtonov nebo Riemnnov integrálu se definují různým způsobem dostnou se někdy různé, někdy stejné pojmy. V tomto textu bude postup volen jko zobecnění Newtonov integrálu,
7. Integrální počet Primitivní funkce, Neurčitý integrál
 7. Integrální počet 7.. Primitivní funkce, Neurčitý integrál Definice 7. Říkáme, že F (x) je v intervlu (, b) (přitom může být tké =, b = + ) primitivní funkcí k finkci f(x), jestliže pro všechn x (, b)
7. Integrální počet 7.. Primitivní funkce, Neurčitý integrál Definice 7. Říkáme, že F (x) je v intervlu (, b) (přitom může být tké =, b = + ) primitivní funkcí k finkci f(x), jestliže pro všechn x (, b)
Obecně: K dané funkci f hledáme funkci ϕ z dané množiny funkcí M, pro kterou v daných bodech x 0 < x 1 <... < x n. (δ ij... Kroneckerovo delta) (4)
 KAPITOLA 13: Numerická integrce interpolce [MA1-18:P13.1] 13.1 Interpolce Obecně: K dné funkci f hledáme funkci ϕ z dné množiny funkcí M, pro kterou v dných bodech x 0 < x 1
KAPITOLA 13: Numerická integrce interpolce [MA1-18:P13.1] 13.1 Interpolce Obecně: K dné funkci f hledáme funkci ϕ z dné množiny funkcí M, pro kterou v dných bodech x 0 < x 1
2. Funkční řady Studijní text. V předcházející kapitole jsme uvažovali řady, jejichž členy byla reálná čísla. Nyní se budeme zabývat studiem
 2. Funkční řd Studijní text 2. Funkční řd V předcházející kpitole jsme uvžovli řd, jejichž člen bl reálná čísl. Nní se budeme zbývt studiem obecnějšího přípdu, kd člen řd tvoří reálné funkce. Definice
2. Funkční řd Studijní text 2. Funkční řd V předcházející kpitole jsme uvžovli řd, jejichž člen bl reálná čísl. Nní se budeme zbývt studiem obecnějšího přípdu, kd člen řd tvoří reálné funkce. Definice
26. listopadu a 10.prosince 2016
 Integrální počet Přednášk 4 5 26. listopdu 10.prosince 2016 Obsh 1 Neurčitý integrál Tbulkové integrály Substituční metod Metod per-prtes 2 Určitý integrál Geometrické plikce Fyzikální plikce K čemu integrální
Integrální počet Přednášk 4 5 26. listopdu 10.prosince 2016 Obsh 1 Neurčitý integrál Tbulkové integrály Substituční metod Metod per-prtes 2 Určitý integrál Geometrické plikce Fyzikální plikce K čemu integrální
LDF MENDELU. Simona Fišnarová (MENDELU) Určitý integrál ZVMT lesnictví 1 / 26
 Určitý integrál Zákldy vyšší mtemtiky LDF MENDELU Podpořeno projektem Průřezová inovce studijních progrmů Lesnické dřevřské fkulty MENDELU v Brně (LDF) s ohledem n discipĺıny společného zákldu http://kdemie.ldf.mendelu.cz/cz
Určitý integrál Zákldy vyšší mtemtiky LDF MENDELU Podpořeno projektem Průřezová inovce studijních progrmů Lesnické dřevřské fkulty MENDELU v Brně (LDF) s ohledem n discipĺıny společného zákldu http://kdemie.ldf.mendelu.cz/cz
VIII. Primitivní funkce a Riemannův integrál
 VIII. Primitivní funkce Riemnnův integrál VIII.2. Primitivní funkce Definice. Nechť funkce f je definován n neprázdném otevřeném intervlu I. Řekneme, že funkce F : I R je primitivní funkce k f n intervlu
VIII. Primitivní funkce Riemnnův integrál VIII.2. Primitivní funkce Definice. Nechť funkce f je definován n neprázdném otevřeném intervlu I. Řekneme, že funkce F : I R je primitivní funkce k f n intervlu
4. přednáška 22. října Úplné metrické prostory. Metrický prostor (M, d) je úplný, když každá cauchyovská posloupnost bodů v M konverguje.
 4. přednášk 22. říjn 2007 Úplné metrické prostory. Metrický prostor (M, d) je úplný, když kždá cuchyovská posloupnost bodů v M konverguje. Příkldy. 1. Euklidovský prostor R je úplný, kždá cuchyovská posloupnost
4. přednášk 22. říjn 2007 Úplné metrické prostory. Metrický prostor (M, d) je úplný, když kždá cuchyovská posloupnost bodů v M konverguje. Příkldy. 1. Euklidovský prostor R je úplný, kždá cuchyovská posloupnost
Integrální počet - III. část (určitý vlastní integrál)
 Integrální počet - III. část (určitý vlstní integrál) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 8. přednášk z AMA1 Michl Fusek (fusekmi@feec.vutbr.cz) 1 / 18 Obsh 1 Určitý vlstní (Riemnnův)
Integrální počet - III. část (určitý vlstní integrál) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 8. přednášk z AMA1 Michl Fusek (fusekmi@feec.vutbr.cz) 1 / 18 Obsh 1 Určitý vlstní (Riemnnův)
integrovat. Obecně lze ale říct, že pokud existuje určitý integrál funkce podle různých definic, má pro všechny takové definice stejnou hodnotu.
 Přednášk 1 Určitý integrál V této přednášce se budeme zbývt určitým integrálem. Eistuje několik definic určitého integrálu funkce jedné reálné proměnné. Jednotlivé integrály se liší v tom, jké funkce lze
Přednášk 1 Určitý integrál V této přednášce se budeme zbývt určitým integrálem. Eistuje několik definic určitého integrálu funkce jedné reálné proměnné. Jednotlivé integrály se liší v tom, jké funkce lze
R n výběr reprezentantů. Řekneme, že funkce f je Riemannovsky integrovatelná na
 Mtemtik II. Určitý integrál.1. Pojem Riemnnov určitého integrálu Definice.1.1. Říkáme, že funkce f( x ) je n intervlu integrovtelná (schopná integrce), je-li n něm ohrničená spoň po částech spojitá.
Mtemtik II. Určitý integrál.1. Pojem Riemnnov určitého integrálu Definice.1.1. Říkáme, že funkce f( x ) je n intervlu integrovtelná (schopná integrce), je-li n něm ohrničená spoň po částech spojitá.
Integrální počet - IV. část (aplikace na určitý vlastní integrál, nevlastní integrál)
 Integrální počet - IV. část (plikce n určitý vlstní integrál, nevlstní integrál) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 9. přednášk z AMA Michl Fusek (fusekmi@feec.vutbr.cz) / 4 Obsh
Integrální počet - IV. část (plikce n určitý vlstní integrál, nevlstní integrál) Michl Fusek Ústv mtemtiky FEKT VUT, fusekmi@feec.vutbr.cz 9. přednášk z AMA Michl Fusek (fusekmi@feec.vutbr.cz) / 4 Obsh
LINEÁRNÍ DIFERENCIÁLNÍ ROVNICE 2.ŘÁDU
 LINEÁRNÍ DIFERENCIÁLNÍ ROVNICE 2.ŘÁDU ZDENĚK ŠIBRAVA 1. Obecné řešení lin. dif. rovnice 2.řádu s konstntními koeficienty 1.1. Vrice konstnt. Příkld 1.1. Njděme obecné řešení diferenciální rovnice (1) y
LINEÁRNÍ DIFERENCIÁLNÍ ROVNICE 2.ŘÁDU ZDENĚK ŠIBRAVA 1. Obecné řešení lin. dif. rovnice 2.řádu s konstntními koeficienty 1.1. Vrice konstnt. Příkld 1.1. Njděme obecné řešení diferenciální rovnice (1) y
Jak již bylo uvedeno v předcházející kapitole, můžeme při výpočtu určitých integrálů ze složitějších funkcí postupovat v zásadě dvěma způsoby:
 .. Substituční metod pro určité integrály.. Substituční metod pro určité integrály Cíle Seznámíte se s použitím substituční metody při výpočtu určitých integrálů. Zákldní typy integrálů, které lze touto
.. Substituční metod pro určité integrály.. Substituční metod pro určité integrály Cíle Seznámíte se s použitím substituční metody při výpočtu určitých integrálů. Zákldní typy integrálů, které lze touto
Zavedení a vlastnosti reálných čísel PŘIROZENÁ, CELÁ A RACIONÁLNÍ ČÍSLA
 Zvedení vlstnosti reálných čísel Reálná čísl jsou zákldním kmenem mtemtické nlýzy. Konstrukce reálných čísel sice není náplní mtemtické nlýzy, le množin reálných čísel R je pro mtemtickou nlýzu zákldním
Zvedení vlstnosti reálných čísel Reálná čísl jsou zákldním kmenem mtemtické nlýzy. Konstrukce reálných čísel sice není náplní mtemtické nlýzy, le množin reálných čísel R je pro mtemtickou nlýzu zákldním
Petr Hasil. Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
 Určitý integrál Petr Hsil Přednášk z mtemtiky Podpořeno projektem Průřezová inovce studijních progrmů Lesnické dřevřské fkulty MENDELU v Brně (LDF) s ohledem n discipĺıny společného zákldu (reg. č. CZ.1.07/2.2.00/28.0021)
Určitý integrál Petr Hsil Přednášk z mtemtiky Podpořeno projektem Průřezová inovce studijních progrmů Lesnické dřevřské fkulty MENDELU v Brně (LDF) s ohledem n discipĺıny společného zákldu (reg. č. CZ.1.07/2.2.00/28.0021)
x + F F x F (x, f(x)).
 I. Funkce dvou více reálných proměnných 8. Implicitně dné funkce. Budeme se zbývt úlohou, kdy funkce není zdná přímo předpisem, který vyjdřuje závislost její hodnoty n hodnotách proměnných. Jeden z možných
I. Funkce dvou více reálných proměnných 8. Implicitně dné funkce. Budeme se zbývt úlohou, kdy funkce není zdná přímo předpisem, který vyjdřuje závislost její hodnoty n hodnotách proměnných. Jeden z možných
+ c. n x ( ) ( ) f x dx ln f x c ) a. x x. dx = cotgx + c. A x. A x A arctgx + A x A c
 ) INTEGRÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem neurčitého integrálu Je dán funkce Pltí všk tké F tk, y pltilo F ( ) f ( ) Zřejmě F ( ), protože pltí, 5,, oecně c, kde c je liovolná kon- stnt f ( ) nším
) INTEGRÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ ) Pojem neurčitého integrálu Je dán funkce Pltí všk tké F tk, y pltilo F ( ) f ( ) Zřejmě F ( ), protože pltí, 5,, oecně c, kde c je liovolná kon- stnt f ( ) nším
INTEGRACE KOMPLEXNÍ FUNKCE KŘIVKOVÝ INTEGRÁL
 INTEGRAE KOMPLEXNÍ FUNKE KŘIVKOVÝ INTEGRÁL N konci kpitoly o derivci je uveden souvislost existence derivce s potenciálním polem. Existuje dlší chrkterizce potenciálného pole, která nebyl v kpitole o derivci
INTEGRAE KOMPLEXNÍ FUNKE KŘIVKOVÝ INTEGRÁL N konci kpitoly o derivci je uveden souvislost existence derivce s potenciálním polem. Existuje dlší chrkterizce potenciálného pole, která nebyl v kpitole o derivci
URČITÝ INTEGRÁL FUNKCE
 URČITÝ INTEGRÁL FUNKCE Formulce: Nším cílem je určit přibližnou hodnotu určitého integrálu I() = () d, kde předpokládáme, že unkce je n intervlu, b integrovtelná. Poznámk: Geometrický význm integrálu I()
URČITÝ INTEGRÁL FUNKCE Formulce: Nším cílem je určit přibližnou hodnotu určitého integrálu I() = () d, kde předpokládáme, že unkce je n intervlu, b integrovtelná. Poznámk: Geometrický význm integrálu I()
Až dosud jsme se zabývali většinou reálnými posloupnostmi, tedy zobrazeními s definičním
 Limit funkce. Zákldní pojmy Až dosud jsme se zbývli většinou reálnými posloupnostmi, tedy zobrzeními s definičním oborem N. Nyní obrátíme svou pozornost n širší třídu zobrzení. Definice.. Zobrzení f, jehož
Limit funkce. Zákldní pojmy Až dosud jsme se zbývli většinou reálnými posloupnostmi, tedy zobrzeními s definičním oborem N. Nyní obrátíme svou pozornost n širší třídu zobrzení. Definice.. Zobrzení f, jehož
Matematika 1A. PetrSalačaJiříHozman Fakulta přírodovědně-humanitní a pedagogická Technická univerzita v Liberci
 Mtemtik 1A. PetrSlčJiříHozmn Fkult přírodovědně-humnitní pedgogická Technická univerzit v Liberci petr.slc@tul.cz jiri.hozmn@tul.cz 21.11.2016 Fkult přírodovědně-humnitní pedgogická TUL ZS 2016-2017 1/
Mtemtik 1A. PetrSlčJiříHozmn Fkult přírodovědně-humnitní pedgogická Technická univerzit v Liberci petr.slc@tul.cz jiri.hozmn@tul.cz 21.11.2016 Fkult přírodovědně-humnitní pedgogická TUL ZS 2016-2017 1/
17 Křivky v rovině a prostoru
 17 Křivky v rovině prostoru Definice 17.1 (rovinné křivky souvisejících pojmů). 1. Nechť F (t) [ϕ(t), ψ(t)] je 2-funkce spojitá n, b. Rovinnou křivkou nzveme množinu : {F (t) : t, b } R 2. 2-funkce F [ϕ,
17 Křivky v rovině prostoru Definice 17.1 (rovinné křivky souvisejících pojmů). 1. Nechť F (t) [ϕ(t), ψ(t)] je 2-funkce spojitá n, b. Rovinnou křivkou nzveme množinu : {F (t) : t, b } R 2. 2-funkce F [ϕ,
10 Určitý integrál Riemannův integrál. Definice. Konečnou posloupnost {x j } n j=0 nazýváme dělením intervalu [a,b], jestliže platí
![10 Určitý integrál Riemannův integrál. Definice. Konečnou posloupnost {x j } n j=0 nazýváme dělením intervalu [a,b], jestliže platí 10 Určitý integrál Riemannův integrál. Definice. Konečnou posloupnost {x j } n j=0 nazýváme dělením intervalu [a,b], jestliže platí](/thumbs/54/33422824.jpg) 10 Určitý integrál 10.1 Riemnnův integrál Definice. Konečnou posloupnost {x j } n j=0 nzýváme dělením intervlu [,b], jestliže pltí = x 0 < x 1 < < x n = b. Body x 0,...,x n nzýváme dělícími body. Normou
10 Určitý integrál 10.1 Riemnnův integrál Definice. Konečnou posloupnost {x j } n j=0 nzýváme dělením intervlu [,b], jestliže pltí = x 0 < x 1 < < x n = b. Body x 0,...,x n nzýváme dělícími body. Normou
6. Určitý integrál a jeho výpočet, aplikace
 Aplikovná mtemtik 1, NMAF071 6. Určitý integrál výpočet, plikce T. Slč, MÚ MFF UK ZS 2017/18 ZS 2017/18) Aplikovná mtemtik 1, NMAF071 6. Určitý integrál 1 / 13 6.1 Newtonův integrál Definice 6.1 Řekneme,
Aplikovná mtemtik 1, NMAF071 6. Určitý integrál výpočet, plikce T. Slč, MÚ MFF UK ZS 2017/18 ZS 2017/18) Aplikovná mtemtik 1, NMAF071 6. Určitý integrál 1 / 13 6.1 Newtonův integrál Definice 6.1 Řekneme,
NMAF061, ZS Písemná část zkoušky 25. leden 2018
 Jednotlivé kroky při výpočtech stručně, le co nejpřesněji odůvodněte. Pokud používáte nějké tvrzení, nezpomeňte ověřit splnění předpokldů. Jméno příjmení: Skupin: Příkld 3 4 5 6 Celkem bodů Bodů 6 6 4
Jednotlivé kroky při výpočtech stručně, le co nejpřesněji odůvodněte. Pokud používáte nějké tvrzení, nezpomeňte ověřit splnění předpokldů. Jméno příjmení: Skupin: Příkld 3 4 5 6 Celkem bodů Bodů 6 6 4
II. 5. Aplikace integrálního počtu
 494 II Integrální počet funkcí jedné proměnné II 5 Aplikce integrálního počtu Geometrické plikce Určitý integrál S b fx) dx lze geometricky interpretovt jko obsh plochy vymezené grfem funkce f v intervlu
494 II Integrální počet funkcí jedné proměnné II 5 Aplikce integrálního počtu Geometrické plikce Určitý integrál S b fx) dx lze geometricky interpretovt jko obsh plochy vymezené grfem funkce f v intervlu
Křivkový integrál funkce
 Kpitol 6 Křivkový integrál funkce efinice způsob výpočtu Hlvním motivem pro definici určitého integrálu funkce jedné proměnné byl úloh stnovit obsh oblsti omezené grfem dné funkce intervlem n ose x. Řd
Kpitol 6 Křivkový integrál funkce efinice způsob výpočtu Hlvním motivem pro definici určitého integrálu funkce jedné proměnné byl úloh stnovit obsh oblsti omezené grfem dné funkce intervlem n ose x. Řd
Integrály definované za těchto předpokladů nazýváme vlastní integrály.
 Mtemtik II.5. Nevlstní integrály.5. Nevlstní integrály Cíle V této kpitole poněkud rozšíříme definii Riemnnov určitého integrálu i n přípdy, kdy je integrční oor neohrničený (tj. (, >,
Mtemtik II.5. Nevlstní integrály.5. Nevlstní integrály Cíle V této kpitole poněkud rozšíříme definii Riemnnov určitého integrálu i n přípdy, kdy je integrční oor neohrničený (tj. (, >,
8. cvičení z Matematiky 2
 8. cvičení z Mtemtiky 2 11.-1. dubn 2016 8.1 Njděte tři pozitivní čísl jejichž součin je mximální, jejichž součet je roven 100. Zdání příkldu lze interpretovt tké tk, že hledáme mximální objem kvádru,
8. cvičení z Mtemtiky 2 11.-1. dubn 2016 8.1 Njděte tři pozitivní čísl jejichž součin je mximální, jejichž součet je roven 100. Zdání příkldu lze interpretovt tké tk, že hledáme mximální objem kvádru,
6. a 7. března Úloha 1.1. Vypočtěte obsah obrazce ohraničeného parabolou y = 1 x 2 a osou x.
 KMA/MAT Přednášk cvičení č. 4, Určitý integrál 6. 7. březn 17 1 Aplikce určitého integrálu 1.1 Počáteční úvhy o výpočtu obshu geometrických útvrů v rovině Úloh 1.1. Vypočtěte obsh obrzce ohrničeného prbolou
KMA/MAT Přednášk cvičení č. 4, Určitý integrál 6. 7. březn 17 1 Aplikce určitého integrálu 1.1 Počáteční úvhy o výpočtu obshu geometrických útvrů v rovině Úloh 1.1. Vypočtěte obsh obrzce ohrničeného prbolou
je jedna z orientací určena jeho parametrizací. Je to ta, pro kterou je počátečním bodem bod ϕ(a). Im k.b.(c ) ( C ) (C ) Obr Obr. 3.5.
 10. Komplexní funkce reálné proměnné. Křivky. Je-li f : (, b) C, pk lze funkci f povžovt z dvojici (u, v), kde u = Re f v = Im f. Rozdíl proti vektorovému poli je v tom, že jsou pro komplexní čísl definovány
10. Komplexní funkce reálné proměnné. Křivky. Je-li f : (, b) C, pk lze funkci f povžovt z dvojici (u, v), kde u = Re f v = Im f. Rozdíl proti vektorovému poli je v tom, že jsou pro komplexní čísl definovány
Diferenciální počet. Spojitost funkce
 Dierenciální počet Spojitost unkce Co to znmená, že unkce je spojitá? Jký je mtemtický význm tvrzení, že gr unkce je spojitý? Jké jsou vlstnosti unkce v bodě? Jké jsou vlstnosti unkce v intervlu I? Vlstnosti
Dierenciální počet Spojitost unkce Co to znmená, že unkce je spojitá? Jký je mtemtický význm tvrzení, že gr unkce je spojitý? Jké jsou vlstnosti unkce v bodě? Jké jsou vlstnosti unkce v intervlu I? Vlstnosti
Matematika II: Pracovní listy Integrální počet funkce jedné reálné proměnné
 Mtemtik II: Prcovní listy Integrální počet funkce jedné reálné proměnné Petr Schreiberová, Petr Volný Ktedr mtemtiky deskriptivní geometrie VŠB - Technická univerzit Ostrv Ostrv 8 Obsh Neurčitý integrál.
Mtemtik II: Prcovní listy Integrální počet funkce jedné reálné proměnné Petr Schreiberová, Petr Volný Ktedr mtemtiky deskriptivní geometrie VŠB - Technická univerzit Ostrv Ostrv 8 Obsh Neurčitý integrál.
Spojitost funkce v bodě, spojitost funkce v intervalu
 10.1.6 Spojitost funkce v bodě, spojitost funkce v intervlu Předpokldy: 10104, 10105 Př. 1: Nkresli, jk funkce f ( x ) dná grfem zobrzí vyznčené okolí bodu n ose x n osu y. Poté nkresli n osu x vzor okolí
10.1.6 Spojitost funkce v bodě, spojitost funkce v intervlu Předpokldy: 10104, 10105 Př. 1: Nkresli, jk funkce f ( x ) dná grfem zobrzí vyznčené okolí bodu n ose x n osu y. Poté nkresli n osu x vzor okolí
DERIVACE A INTEGRÁLY VE FYZICE
 DOPLŇKOVÉ TEXTY BB0 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ DERIVACE A INTEGRÁLY VE FYZICE Obsh Derivce... Definice derivce... Prciální derivce... Derivce vektorů... Výpočt derivcí... 3 Algebrická
DOPLŇKOVÉ TEXTY BB0 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ DERIVACE A INTEGRÁLY VE FYZICE Obsh Derivce... Definice derivce... Prciální derivce... Derivce vektorů... Výpočt derivcí... 3 Algebrická
ZÁKLADY. y 1 + y 2 dx a. kde y je hledanou funkcí proměnné x.
 VARIAČNÍ POČET ZÁKLADY V prxi se čsto hledjí křivky nebo plochy, které minimlizují nebo mximlizují jisté hodnoty. Npř. se hledá nejkrtší spojnice dvou bodů n dné ploše, nebo tvr zvěšeného ln (má minimální
VARIAČNÍ POČET ZÁKLADY V prxi se čsto hledjí křivky nebo plochy, které minimlizují nebo mximlizují jisté hodnoty. Npř. se hledá nejkrtší spojnice dvou bodů n dné ploše, nebo tvr zvěšeného ln (má minimální
množina, na které je zavedena určitá struktura. Zejména, součet každých dvou prvků X = [x 1,..., x n ] R n,
![množina, na které je zavedena určitá struktura. Zejména, součet každých dvou prvků X = [x 1,..., x n ] R n, množina, na které je zavedena určitá struktura. Zejména, součet každých dvou prvků X = [x 1,..., x n ] R n,](/thumbs/99/140214707.jpg) Náplní předmětu bude klkulus R n R (přípdně R m ). Proč se zbývt funkcemi více proměnných? V prxi je čsto třeb uvžovt veličiny, které závisejí n více než jedné proměnné, npř. objem rotčního kužele závisí
Náplní předmětu bude klkulus R n R (přípdně R m ). Proč se zbývt funkcemi více proměnných? V prxi je čsto třeb uvžovt veličiny, které závisejí n více než jedné proměnné, npř. objem rotčního kužele závisí
Matice. a B =...,...,...,...,..., prvků z tělesa T (tímto. Definice: Soubor A = ( a. ...,..., ra
 Definice: Soubor A ( i j ) Mtice 11 12 1n 21 22 2n m 1 m2 prvků z těles T (tímto tělesem T bude v nší prxi nejčstěji těleso reálných čísel R resp těleso rcionálních čísel Q či těleso komplexních čísel
Definice: Soubor A ( i j ) Mtice 11 12 1n 21 22 2n m 1 m2 prvků z těles T (tímto tělesem T bude v nší prxi nejčstěji těleso reálných čísel R resp těleso rcionálních čísel Q či těleso komplexních čísel
Úlohy krajského kola kategorie A
 67. ročník mtemtické olympiády Úlohy krjského kol ktegorie A 1. Pvel střídvě vpisuje křížky kolečk do políček tbulky (zčíná křížkem). Když je tbulk celá vyplněná, výsledné skóre spočítá jko rozdíl X O,
67. ročník mtemtické olympiády Úlohy krjského kol ktegorie A 1. Pvel střídvě vpisuje křížky kolečk do políček tbulky (zčíná křížkem). Když je tbulk celá vyplněná, výsledné skóre spočítá jko rozdíl X O,
4. cvičení z Matematiky 2
 4. cvičení z Mtemtiky 2 14.-18. březn 2016 4.1 Njděte ity (i (ii (iii (iv 2 +(y 1 2 +1 1 2 +(y 1 2 z 2 y 2 z yz 1 2 y 2 (,y (0,0 2 +y 2 2 y 2 (,y (0,0 2 +y 3 (i Pro funkci f(, y = 2 +(y 1 2 +1 1 2 +(y
4. cvičení z Mtemtiky 2 14.-18. březn 2016 4.1 Njděte ity (i (ii (iii (iv 2 +(y 1 2 +1 1 2 +(y 1 2 z 2 y 2 z yz 1 2 y 2 (,y (0,0 2 +y 2 2 y 2 (,y (0,0 2 +y 3 (i Pro funkci f(, y = 2 +(y 1 2 +1 1 2 +(y
Vzdělávací materiál. vytvořený v projektu OP VK. Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20. Číslo projektu: CZ.1.07/1.5.00/34.
 Vzdělávcí mteriál vytvořený v projektu OP VK Název školy: Gymnázium, Zářeh, náměstí Osvoození 20 Číslo projektu: Název projektu: Číslo název klíčové ktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek pro
Vzdělávcí mteriál vytvořený v projektu OP VK Název školy: Gymnázium, Zářeh, náměstí Osvoození 20 Číslo projektu: Název projektu: Číslo název klíčové ktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek pro
Obsah rovinného obrazce
 Osh rovinného orzce Nejjednodušší plikcí určitého integrálu je výpočet oshu rovinného orzce. Zčneme větou. Vět : Je-li funkce f spojitá nezáporná n n orázku níže roven f ( ) d. ;, je osh rovinného orzce
Osh rovinného orzce Nejjednodušší plikcí určitého integrálu je výpočet oshu rovinného orzce. Zčneme větou. Vět : Je-li funkce f spojitá nezáporná n n orázku níže roven f ( ) d. ;, je osh rovinného orzce
Matematika II: Testy
 Mtemtik II: Testy Petr Schreiberová Ktedr mtemtiky deskriptivní geometrie VŠB - Technická univerzit Ostrv Mtemtik II - testy 69. Řy 9 - Test Ktedr mtemtiky deskriptivní geometrie, VŠB - Technická univerzit
Mtemtik II: Testy Petr Schreiberová Ktedr mtemtiky deskriptivní geometrie VŠB - Technická univerzit Ostrv Mtemtik II - testy 69. Řy 9 - Test Ktedr mtemtiky deskriptivní geometrie, VŠB - Technická univerzit
Text m ºe být postupn upravován a dopl ován. Datum poslední úpravy najdete u odkazu na staºení souboru. Veronika Sobotíková
 Tento text není smosttným studijním mteriálem. Jde jen o prezentci promítnou n p edná²kách, kde k ní p idávám slovní komentá. N které d leºité ásti látky pí²u pouze n tbuli nejsou zde obsºeny. Text m ºe
Tento text není smosttným studijním mteriálem. Jde jen o prezentci promítnou n p edná²kách, kde k ní p idávám slovní komentá. N které d leºité ásti látky pí²u pouze n tbuli nejsou zde obsºeny. Text m ºe
Souhrn základních výpočetních postupů v Excelu probíraných v AVT 04-05 listopad 2004. r r. . b = A
 Souhrn zákldních výpočetních postupů v Ecelu probírných v AVT 04-05 listopd 2004. Řešení soustv lineárních rovnic Soustv lineárních rovnic ve tvru r r A. = b tj. npř. pro 3 rovnice o 3 neznámých 2 3 Hodnoty
Souhrn zákldních výpočetních postupů v Ecelu probírných v AVT 04-05 listopd 2004. Řešení soustv lineárních rovnic Soustv lineárních rovnic ve tvru r r A. = b tj. npř. pro 3 rovnice o 3 neznámých 2 3 Hodnoty
Definice. Nechť k 0 celé, a < b R. Definujeme. x < 1. ϕ(x) 0 v R. Lemma [Slabá formulace diferenciální rovnice.] x 2 1
![Definice. Nechť k 0 celé, a < b R. Definujeme. x < 1. ϕ(x) 0 v R. Lemma [Slabá formulace diferenciální rovnice.] x 2 1 Definice. Nechť k 0 celé, a < b R. Definujeme. x < 1. ϕ(x) 0 v R. Lemma [Slabá formulace diferenciální rovnice.] x 2 1](/thumbs/103/161289080.jpg) 9. Vriční počet. Definice. Nechť k 0 celé, < b R. Definujeme C k ([, b]) = { ỹ [,b] : ỹ C k (R) } ; C 0 ([, b]) = { y C ([, b]) : y() = y(b) = 0 }. Důležitá konstrukce. Shlzovcí funkce (molifiér, bump
9. Vriční počet. Definice. Nechť k 0 celé, < b R. Definujeme C k ([, b]) = { ỹ [,b] : ỹ C k (R) } ; C 0 ([, b]) = { y C ([, b]) : y() = y(b) = 0 }. Důležitá konstrukce. Shlzovcí funkce (molifiér, bump
Přednáška 9: Limita a spojitost
 4 / XI /, 5: Přednášk 9: Limit spojitost V minulých přednáškách jsme podrobněji prozkoumli důležitý pojem funkce. Při řešení konkrétních problémů se nše znlosti (npř. nměřená dt) zpisují jko funkční hodnoty
4 / XI /, 5: Přednášk 9: Limit spojitost V minulých přednáškách jsme podrobněji prozkoumli důležitý pojem funkce. Při řešení konkrétních problémů se nše znlosti (npř. nměřená dt) zpisují jko funkční hodnoty
2.2.9 Grafické řešení rovnic a nerovnic
 ..9 Grfické řešení rovnic nerovnic Předpokldy: 0, 06 Př. : Řeš početně i grficky rovnici x + = x. Početně: Už umíme. x + = x x = x = K = { } Grficky: Kždá ze strn rovnice je výrzem pro lineární funkci
..9 Grfické řešení rovnic nerovnic Předpokldy: 0, 06 Př. : Řeš početně i grficky rovnici x + = x. Početně: Už umíme. x + = x x = x = K = { } Grficky: Kždá ze strn rovnice je výrzem pro lineární funkci
I Diferenciální a integrální počet funkcí jedné proměnné 3
 Obsh I Diferenciální integrální počet funkcí jedné proměnné 3 Preklkulus 5. Reálná čísl................................................ 5. Funkce jejich zákldní vlstnosti....................................3
Obsh I Diferenciální integrální počet funkcí jedné proměnné 3 Preklkulus 5. Reálná čísl................................................ 5. Funkce jejich zákldní vlstnosti....................................3
Integrál a jeho aplikace Tomáš Matoušek
 Integrál jeho plikce Tomáš Mtoušek Křivk Definice.(Vektorováfunkce) Funkci ϕ:r R n,kteráreálnémučíslupřiřzuje n-tici reálných čísel(vektor), nzýváme funkcí vektorovou. Lze ji tké popst po složkáchjko ϕ(t)=(ϕ
Integrál jeho plikce Tomáš Mtoušek Křivk Definice.(Vektorováfunkce) Funkci ϕ:r R n,kteráreálnémučíslupřiřzuje n-tici reálných čísel(vektor), nzýváme funkcí vektorovou. Lze ji tké popst po složkáchjko ϕ(t)=(ϕ
NEWTONŮV INTEGRÁL. V předchozích kapitolách byla popsána inverzní operace k derivování. Zatím nebylo jasné, k čemu tento nástroj slouží.
 NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování. Ztím nebylo jsné, k čemu tento nástroj slouží. Bylo uvedeno, že rozdíl F (b) F () funkčních hodnot primitivní funkce k
NEWTONŮV INTEGRÁL V předchozích kpitolách byl popsán inverzní operce k derivování. Ztím nebylo jsné, k čemu tento nástroj slouží. Bylo uvedeno, že rozdíl F (b) F () funkčních hodnot primitivní funkce k
Příklad 22 : Kapacita a rozložení intenzity elektrického pole v deskovém kondenzátoru s jednoduchým dielektrikem
 Příkld 22 : Kpcit rozložení intenzity elektrického pole v deskovém kondenzátoru s jednoduchým dielektrikem Předpokládné znlosti: Elektrické pole mezi dvěm nbitými rovinmi Příkld 2 Kpcit kondenzátoru je
Příkld 22 : Kpcit rozložení intenzity elektrického pole v deskovém kondenzátoru s jednoduchým dielektrikem Předpokládné znlosti: Elektrické pole mezi dvěm nbitými rovinmi Příkld 2 Kpcit kondenzátoru je
KŘIVKOVÉ INTEGRÁLY. Křivka v prostoru je popsána spojitými funkcemi ϕ, ψ, τ : [a, b] R jako množina bodů {(ϕ(t), ψ(t), τ(t)); t
![KŘIVKOVÉ INTEGRÁLY. Křivka v prostoru je popsána spojitými funkcemi ϕ, ψ, τ : [a, b] R jako množina bodů {(ϕ(t), ψ(t), τ(t)); t KŘIVKOVÉ INTEGRÁLY. Křivka v prostoru je popsána spojitými funkcemi ϕ, ψ, τ : [a, b] R jako množina bodů {(ϕ(t), ψ(t), τ(t)); t](/thumbs/88/114636682.jpg) KŘIVKOVÉ INTEGRÁLY Má-li se spočítt npř. spotřeb betonu n rovný plot s měnící se výškou, stčí spočítt integrál z této výšky podle zákldny plotu. o když je le zákldnou plotu nikoli rovná úsečk, le křivá
KŘIVKOVÉ INTEGRÁLY Má-li se spočítt npř. spotřeb betonu n rovný plot s měnící se výškou, stčí spočítt integrál z této výšky podle zákldny plotu. o když je le zákldnou plotu nikoli rovná úsečk, le křivá
Řešené příklady k MAI III.
 Řešené příkldy k MAI III. Jkub Melk 28. říjn 2007 1 Obsh 1 Metrické prostory 2 1.1 Teoretickéotázky.... 2 1.2 Metriky..... 4 1.3 Anlýzmnožin... 4 1.3.1 Uzávěry... 4 1.3.2 Zkoumejtenásledujícímnožiny....
Řešené příkldy k MAI III. Jkub Melk 28. říjn 2007 1 Obsh 1 Metrické prostory 2 1.1 Teoretickéotázky.... 2 1.2 Metriky..... 4 1.3 Anlýzmnožin... 4 1.3.1 Uzávěry... 4 1.3.2 Zkoumejtenásledujícímnožiny....
Přehled základních vzorců pro Matematiku 2 1
 Přehled zákldních vzorců pro Mtemtiku 1 1. Limity funkcí definice Vlstní it v bodě = : f() = ɛ > 0, δ > 0 tk, že pro : ( δ, δ), pltí f() ( ɛ, ɛ) Vlstní it v bodě = : f() = ɛ > 0, c > 0 tk, že pro : > c,
Přehled zákldních vzorců pro Mtemtiku 1 1. Limity funkcí definice Vlstní it v bodě = : f() = ɛ > 0, δ > 0 tk, že pro : ( δ, δ), pltí f() ( ɛ, ɛ) Vlstní it v bodě = : f() = ɛ > 0, c > 0 tk, že pro : > c,
3. ROVNICE A NEROVNICE 85. 3.1. Lineární rovnice 85. 3.2. Kvadratické rovnice 86. 3.3. Rovnice s absolutní hodnotou 88. 3.4. Iracionální rovnice 90
 ROVNICE A NEROVNICE 8 Lineární rovnice 8 Kvdrtické rovnice 8 Rovnice s bsolutní hodnotou 88 Ircionální rovnice 90 Eponenciální rovnice 9 Logritmické rovnice 9 7 Goniometrické rovnice 98 8 Nerovnice 0 Úlohy
ROVNICE A NEROVNICE 8 Lineární rovnice 8 Kvdrtické rovnice 8 Rovnice s bsolutní hodnotou 88 Ircionální rovnice 90 Eponenciální rovnice 9 Logritmické rovnice 9 7 Goniometrické rovnice 98 8 Nerovnice 0 Úlohy
14. cvičení z Matematické analýzy 2
 4. cvičení z temtické nlýzy 2 22. - 26. květn 27 4. Greenov vět) Použijte Greenovu větu k nlezení práce síly F x, y) 2xy, 4x 2 y 2 ) vykonné n částici podél křivky, která je hrnicí oblsti ohrničené křivkmi
4. cvičení z temtické nlýzy 2 22. - 26. květn 27 4. Greenov vět) Použijte Greenovu větu k nlezení práce síly F x, y) 2xy, 4x 2 y 2 ) vykonné n částici podél křivky, která je hrnicí oblsti ohrničené křivkmi
13. Exponenciální a logaritmická funkce
 @11 1. Eponenciální logritmická funkce Mocninná funkce je pro r libovolné nenulové reálné číslo dán předpisem f: y = r, r R, >0 Eponent r je konstnt je nezávisle proměnná. Definičním oborem jsou pouze
@11 1. Eponenciální logritmická funkce Mocninná funkce je pro r libovolné nenulové reálné číslo dán předpisem f: y = r, r R, >0 Eponent r je konstnt je nezávisle proměnná. Definičním oborem jsou pouze
f dx S(f, E) M(b a), kde D a E jsou
 Přehled probrné látky z MAII, LS 2004/05 1. přednášk 21.2.2005. Opkování látky o primitivních funkcích ze závěru zimního semestru (23.-25. přednášk). Rozkld rcionální funkce n prciální zlomky. Popis hledání
Přehled probrné látky z MAII, LS 2004/05 1. přednášk 21.2.2005. Opkování látky o primitivních funkcích ze závěru zimního semestru (23.-25. přednášk). Rozkld rcionální funkce n prciální zlomky. Popis hledání
NMAF061, ZS Písemná část zkoušky 16. leden 2018
 Jednotlivé kroky při výpočtech stručně, le co nejpřesněji odůvodněte. Pokud používáte nějké tvrzení, nezpomeňte ověřit splnění předpokldů. Jméno příjmení: Skupin: Příkld 1 3 4 5 6 Celkem bodů Bodů 7 6
Jednotlivé kroky při výpočtech stručně, le co nejpřesněji odůvodněte. Pokud používáte nějké tvrzení, nezpomeňte ověřit splnění předpokldů. Jméno příjmení: Skupin: Příkld 1 3 4 5 6 Celkem bodů Bodů 7 6
Větu o spojitosti a jejich užití
 0..7 Větu o spojitosti jejich užití Předpokldy: 706, 78, 006 Pedgogická poznámk: Při proírání této hodiny je tře mít n pměti, že všechny věty, které studentům sdělujete z jejich pohledu neuvěřitelně složitě
0..7 Větu o spojitosti jejich užití Předpokldy: 706, 78, 006 Pedgogická poznámk: Při proírání této hodiny je tře mít n pměti, že všechny věty, které studentům sdělujete z jejich pohledu neuvěřitelně složitě
5.2.4 Kolmost přímek a rovin II
 5..4 Kolmost přímek rovin II Předpokldy: 503 Př. 1: Zformuluj stereometrické věty nlogické k plnimetrické větě: ným bodem lze v rovině k dné přímce vést jedinou kolmici. Vět: ným bodem lze v prostoru k
5..4 Kolmost přímek rovin II Předpokldy: 503 Př. 1: Zformuluj stereometrické věty nlogické k plnimetrické větě: ným bodem lze v rovině k dné přímce vést jedinou kolmici. Vět: ným bodem lze v prostoru k
Úlohy školní klauzurní části I. kola kategorie C
 52. ročník mtemtické olympiády Úlohy školní kluzurní části I. kol ktegorie 1. Odtrhneme-li od libovolného lespoň dvojmístného přirozeného čísl číslici n místě jednotek, dostneme číslo o jednu číslici krtší.
52. ročník mtemtické olympiády Úlohy školní kluzurní části I. kol ktegorie 1. Odtrhneme-li od libovolného lespoň dvojmístného přirozeného čísl číslici n místě jednotek, dostneme číslo o jednu číslici krtší.
8. Elementární funkce
 Historie přírodních věd potvrzuje, že většinu reálně eistujících dějů lze reprezentovt mtemtickými model, které jsou popsán tzv. elementárními funkcemi. Elementární funkce je kždá funkce, která vznikne
Historie přírodních věd potvrzuje, že většinu reálně eistujících dějů lze reprezentovt mtemtickými model, které jsou popsán tzv. elementárními funkcemi. Elementární funkce je kždá funkce, která vznikne
Seznámíte se s další aplikací určitého integrálu výpočtem objemu rotačního tělesa.
 .. Ojem rotčního těles Cíle Seznámíte se s dlší plikcí určitého integrálu výpočtem ojemu rotčního těles. Předpokládné znlosti Předpokládáme, že jste si prostudovli zvedení pojmu určitý integrál (kpitol.).
.. Ojem rotčního těles Cíle Seznámíte se s dlší plikcí určitého integrálu výpočtem ojemu rotčního těles. Předpokládné znlosti Předpokládáme, že jste si prostudovli zvedení pojmu určitý integrál (kpitol.).
Komplexní čísla tedy násobíme jako dvojčleny s tím, že použijeme vztah i 2 = 1. = (a 1 + ia 2 )(b 1 ib 2 ) b 2 1 + b2 2.
 7 Komplexní čísl 71 Komplexní číslo je uspořádná dvojice reálných čísel Komplexní číslo = 1, ) zprvidl zpisujeme v tzv lgebrickém tvru = 1 + i, kde i je imginární jednotk, pro kterou pltí i = 1 Číslo 1
7 Komplexní čísl 71 Komplexní číslo je uspořádná dvojice reálných čísel Komplexní číslo = 1, ) zprvidl zpisujeme v tzv lgebrickém tvru = 1 + i, kde i je imginární jednotk, pro kterou pltí i = 1 Číslo 1
1.1 Numerické integrování
 1.1 Numerické integrování 1.1.1 Úvodní úvhy Nším cílem bude přibližný numerický výpočet určitého integrálu I = f(x)dx. (1.1) Je-li znám k integrovné funkci f primitivní funkce F (F (x) = f(x)), můžeme
1.1 Numerické integrování 1.1.1 Úvodní úvhy Nším cílem bude přibližný numerický výpočet určitého integrálu I = f(x)dx. (1.1) Je-li znám k integrovné funkci f primitivní funkce F (F (x) = f(x)), můžeme
II. INTEGRÁL V R n. Obr. 9.1 Obr. 9.2 Integrál v R 2. z = f(x, y)
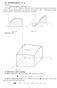 . NTEGRÁL V R n Úvod Určitý integrál v intervlu, b Pro funki f :, b R jsme definovli určitý integrál jko číslo, jehož hodnot je obshem obrze znázorněného n obrázíh. Pro funki f : R n R budeme zvádět integrál
. NTEGRÁL V R n Úvod Určitý integrál v intervlu, b Pro funki f :, b R jsme definovli určitý integrál jko číslo, jehož hodnot je obshem obrze znázorněného n obrázíh. Pro funki f : R n R budeme zvádět integrál
I Diferenciální a integrální počet funkcí jedné proměnné 5
 Obsh I Diferenciální integrální počet funkcí jedné proměnné 5 Preklkulus 7. Reálná čísl................................................ 7. Funkce jejich zákldní vlstnosti...................................
Obsh I Diferenciální integrální počet funkcí jedné proměnné 5 Preklkulus 7. Reálná čísl................................................ 7. Funkce jejich zákldní vlstnosti...................................
FI: JARO 2017 Verze: 9. února 2017
 FI: JARO 7 Verze: 9. únor 7 Přednášky k předmětu MB Autor: Romn Šimon Hilscher Přednášející: Petr Hsil Obsh Přehled přednášek podle strny ukončení iii. Polynomy interpolce.. Interpolce.. Lgrngeův interpolční
FI: JARO 7 Verze: 9. únor 7 Přednášky k předmětu MB Autor: Romn Šimon Hilscher Přednášející: Petr Hsil Obsh Přehled přednášek podle strny ukončení iii. Polynomy interpolce.. Interpolce.. Lgrngeův interpolční
2.1 - ( ) ( ) (020201) [ ] [ ]
![2.1 - ( ) ( ) (020201) [ ] [ ] 2.1 - ( ) ( ) (020201) [ ] [ ]](/thumbs/102/155984102.jpg) - FUNKCE A ROVNICE Následující zákldní znlosti je nezbytně nutné umět od okmžiku probrání ž do konce studi mtemtiky n gymnáziu. Vyždováno bude porozumění schopnost plikovt ne pouze mechnicky zopkovt. Některé
- FUNKCE A ROVNICE Následující zákldní znlosti je nezbytně nutné umět od okmžiku probrání ž do konce studi mtemtiky n gymnáziu. Vyždováno bude porozumění schopnost plikovt ne pouze mechnicky zopkovt. Některé
2. INTEGRÁLNÍ POČET FUNKCE JEDNÉ PROMĚNNÉ
 . INTEGRÁLNÍ POČET FUNKE JEDNÉ PROMĚNNÉ Při řešení technických prolémů, ve fyzice pod. je velmi čsto tře řešit orácenou úlohu k derivování. K zdné funkci f udeme hledt funkci F tkovou, y pltilo F f. Budeme
. INTEGRÁLNÍ POČET FUNKE JEDNÉ PROMĚNNÉ Při řešení technických prolémů, ve fyzice pod. je velmi čsto tře řešit orácenou úlohu k derivování. K zdné funkci f udeme hledt funkci F tkovou, y pltilo F f. Budeme
je parciální derivace funkce f v bodě a podle druhé proměnné (obvykle říkáme proměnné
 1. Prciální derivce funkce více proměnných. Prciální derivce funkce dvou proměnných. Je-li funkce f f(, ) definován v množině D f R 2 bod ( 1, 2 ) je vnitřním bodem množin D f, pk funkce g 1 (t) f(t, 2
1. Prciální derivce funkce více proměnných. Prciální derivce funkce dvou proměnných. Je-li funkce f f(, ) definován v množině D f R 2 bod ( 1, 2 ) je vnitřním bodem množin D f, pk funkce g 1 (t) f(t, 2
Ohýbaný nosník - napětí
 Pružnost pevnost BD0 Ohýbný nosník - npětí Teorie Prostý ohb, rovinný ohb Při prostém ohbu je průřez nmáhán ohbovým momentem otáčejícím kolem jedné z hlvních os setrvčnosti průřezu, obvkle os. oment se
Pružnost pevnost BD0 Ohýbný nosník - npětí Teorie Prostý ohb, rovinný ohb Při prostém ohbu je průřez nmáhán ohbovým momentem otáčejícím kolem jedné z hlvních os setrvčnosti průřezu, obvkle os. oment se
2. Pokud nedojde k nejasnostem, budeme horní a dolní součty značit pouze
 8. Určitý integrál 8.1. Newtonův integrál Definice 8.1 Buďte,b R. Řekneme,žeNewtonůvintegrálzfunkce fnintervlu(,b) existuje(znčímejej(n) f(x)dx),jestliže 1.existuje primitivní funkce F k f n intervlu(,
8. Určitý integrál 8.1. Newtonův integrál Definice 8.1 Buďte,b R. Řekneme,žeNewtonůvintegrálzfunkce fnintervlu(,b) existuje(znčímejej(n) f(x)dx),jestliže 1.existuje primitivní funkce F k f n intervlu(,
12.1 Primitivní funkce
 Integrání počet. Primitivní funkce Již jsme definovli pojem derivce funkce, k funkci f(x) jsme hledli její derivci f (x). Nyní chceme ukázt opčný postup, tzn. k funkci f (x) njít funkci f(x). Přesněji,
Integrání počet. Primitivní funkce Již jsme definovli pojem derivce funkce, k funkci f(x) jsme hledli její derivci f (x). Nyní chceme ukázt opčný postup, tzn. k funkci f (x) njít funkci f(x). Přesněji,
6.1. Limita funkce. Množina Z má dva hromadné body: ±. Tedy Z ={+, }.
 6.1. Limit funkce Číslo R nzveme hromdným bodem množiny A R, pokud v kždém jeho okolí leží nekonečně mnoho bodů z množiny A. Body z A, které neptří mezi hromdné body A, se nzývjí izolovné. Alterntivně
6.1. Limit funkce Číslo R nzveme hromdným bodem množiny A R, pokud v kždém jeho okolí leží nekonečně mnoho bodů z množiny A. Body z A, které neptří mezi hromdné body A, se nzývjí izolovné. Alterntivně
3 Algebraické výrazy. 3.1 Mnohočleny Mnohočleny jsou zvláštním případem výrazů. Mnohočlen (polynom) proměnné je výraz tvaru
 Algerické výrz V knize přírod může číst jen ten, kdo zná jzk, ve kterém je npsán. Jejím jzkem je mtemtik jejím písmem jsou mtemtické vzorce. (Glileo Glilei) Algerickým výrzem rozumíme zápis, ve kterém
Algerické výrz V knize přírod může číst jen ten, kdo zná jzk, ve kterém je npsán. Jejím jzkem je mtemtik jejím písmem jsou mtemtické vzorce. (Glileo Glilei) Algerickým výrzem rozumíme zápis, ve kterém
56. ročník Matematické olympiády. b 1,2 = 27 ± c 2 25
 56. ročník Mtemtické olympiády Úlohy domácí části I. kol ktegorie 1. Njděte všechny dvojice (, ) celých čísel, jež vyhovují rovnici + 7 + 6 + 5 + 4 + = 0. Řešení. Rovnici řešíme jko kvdrtickou s neznámou
56. ročník Mtemtické olympiády Úlohy domácí části I. kol ktegorie 1. Njděte všechny dvojice (, ) celých čísel, jež vyhovují rovnici + 7 + 6 + 5 + 4 + = 0. Řešení. Rovnici řešíme jko kvdrtickou s neznámou
vás seznámí s učivem, které v dané kapitole poznáte a které byste po jejím prostudování měli umět.
 POKYNY KE STUDIU Pokyny ke studiu V úvodu si vysvětlíme jednotnou pevnou strukturu kždé kpitoly tetu, která by vám měl pomoci k rychlejší orientci při studiu Pro zvýrznění jednotlivých částí tetu jsou
POKYNY KE STUDIU Pokyny ke studiu V úvodu si vysvětlíme jednotnou pevnou strukturu kždé kpitoly tetu, která by vám měl pomoci k rychlejší orientci při studiu Pro zvýrznění jednotlivých částí tetu jsou
2.3 Aplikace v geometrii a fyzice Posloupnosti a řady funkcí Posloupnosti funkcí... 17
 Obsh Derivce Integrály 6. Neurčité integrály.................. 6. Určité integrály....................3 Aplikce v geometrii fyzice............ 6 3 Posloupnosti řdy funkcí 7 3. Posloupnosti funkcí.................
Obsh Derivce Integrály 6. Neurčité integrály.................. 6. Určité integrály....................3 Aplikce v geometrii fyzice............ 6 3 Posloupnosti řdy funkcí 7 3. Posloupnosti funkcí.................
Matematika III. Miroslava Dubcová, Daniel Turzík, Drahoslava Janovská. Ústav matematiky
 Matematika III Řady Miroslava Dubcová, Daniel Turzík, Drahoslava Janovská Ústav matematiky Přednášky ZS 202-203 Obsah Číselné řady. Součet nekonečné řady. Kritéria konvergence 2 Funkční řady. Bodová konvergence.
Matematika III Řady Miroslava Dubcová, Daniel Turzík, Drahoslava Janovská Ústav matematiky Přednášky ZS 202-203 Obsah Číselné řady. Součet nekonečné řady. Kritéria konvergence 2 Funkční řady. Bodová konvergence.
Masarykova univerzita
 Msrykov univerzit Přírodovědecká fkult Diplomová práce Web k témtu: Integrální počet Bc. Ev Schlesingerová Brno 9 Prohlášení Prohlšuji, že jsem tuto diplomovou práci npsl sm s použitím uvedené litertury.
Msrykov univerzit Přírodovědecká fkult Diplomová práce Web k témtu: Integrální počet Bc. Ev Schlesingerová Brno 9 Prohlášení Prohlšuji, že jsem tuto diplomovou práci npsl sm s použitím uvedené litertury.
( a) Okolí bodu
 0..5 Okolí bodu Předpokldy: 40 Pedgogická poznámk: Hodin zjevně překrčuje možnosti většiny studentů v 45 minutách. Myslím, že nemá cenu přethovt do dlší hodiny, příkldy s redukovnými okolími nejsou nutné,
0..5 Okolí bodu Předpokldy: 40 Pedgogická poznámk: Hodin zjevně překrčuje možnosti většiny studentů v 45 minutách. Myslím, že nemá cenu přethovt do dlší hodiny, příkldy s redukovnými okolími nejsou nutné,
Svazy. Def Svaz je algebra S ( M ;, ) = se dvěma binárními operacemi taková, že pro libovolné prvky c M platí následující podmínky axiomy svazu:
 vz je lgebr ( M ; ) vzy = se dvěm binárními opercemi tková že pro libovolné prvky b c M pltí následující podmínky xiomy svzu: ( b) c = ( b c) ( b) c = ( b c) b = b b = b ( ) ( ) b = b =. Operce se nzývá
vz je lgebr ( M ; ) vzy = se dvěm binárními opercemi tková že pro libovolné prvky b c M pltí následující podmínky xiomy svzu: ( b) c = ( b c) ( b) c = ( b c) b = b b = b ( ) ( ) b = b =. Operce se nzývá
Neurčité výrazy
 .. Neurčité výrzy Předpokldy: Př. : Vypočti ity: ) d) ) d) neeistuje,, Zjímvé. Získli jsme čtyři nprosto rozdílné výsledky, přestože přímým doszením do všech výrzů získáme to smé: výrz může při výpočtu
.. Neurčité výrzy Předpokldy: Př. : Vypočti ity: ) d) ) d) neeistuje,, Zjímvé. Získli jsme čtyři nprosto rozdílné výsledky, přestože přímým doszením do všech výrzů získáme to smé: výrz může při výpočtu
2.8.5 Lineární nerovnice s parametrem
 2.8.5 Lineární nerovnice s prmetrem Předpokldy: 2208, 2802 Pedgogická poznámk: Pokud v tom necháte studenty vykoupt (což je, zdá se, jediné rozumné řešení) zere tto látk tk jednu půl vyučovcí hodiny (první
2.8.5 Lineární nerovnice s prmetrem Předpokldy: 2208, 2802 Pedgogická poznámk: Pokud v tom necháte studenty vykoupt (což je, zdá se, jediné rozumné řešení) zere tto látk tk jednu půl vyučovcí hodiny (první
( a, { } Intervaly. Předpoklady: , , , Problém zapíšeme snadno i výčtem: { 2;3; 4;5}?
 1.3.8 Intervly Předpokldy: 010210, 010301, 010302, 010303 Problém Množinu A = { x Z;2 x 5} zpíšeme sndno i výčtem: { 2;3; 4;5} Jk zpst množinu B = { x R;2 x 5}? A =. Jde o nekonečně mnoho čísel (2, 5 všechno
1.3.8 Intervly Předpokldy: 010210, 010301, 010302, 010303 Problém Množinu A = { x Z;2 x 5} zpíšeme sndno i výčtem: { 2;3; 4;5} Jk zpst množinu B = { x R;2 x 5}? A =. Jde o nekonečně mnoho čísel (2, 5 všechno
5.5 Elementární funkce
 5.5 Elementární funkce Lemm 5.20. Necht x R. Potom existuje kldné C R (závisející n x) tkové, že pro kždé n N h ( 1, 1) pltí (x + h) n x n nhx n 1 h 2 C n. Definice. Exponenciální funkci exp definujme
5.5 Elementární funkce Lemm 5.20. Necht x R. Potom existuje kldné C R (závisející n x) tkové, že pro kždé n N h ( 1, 1) pltí (x + h) n x n nhx n 1 h 2 C n. Definice. Exponenciální funkci exp definujme
je daná funkce. Množinu všech primitivních funkcí k f na I nazveme neurčitým f(x)dx nebo f.
 MATEMATICKÁ ANALÝZA INTEGRÁLNÍ POČET PŘEDNÁŠEJÍCÍ ALEŠ NEKVINDA. Přednášk Oznčme R = R {, } jko v minulém semestru. V tomto semestru se budeme zbývt opčným úkonem k derivování. Primitivní funkce. Definice.
MATEMATICKÁ ANALÝZA INTEGRÁLNÍ POČET PŘEDNÁŠEJÍCÍ ALEŠ NEKVINDA. Přednášk Oznčme R = R {, } jko v minulém semestru. V tomto semestru se budeme zbývt opčným úkonem k derivování. Primitivní funkce. Definice.
Učební text k přednášce Matematická analýza II (MAI055)
 Učební text k přednášce Mtemtická nlýz II (MAI055) Mrtin Klzr 20. červn 2007 Přednášk pokrývá v letním semestru následující látku:. Riemnnův integrál. 2. Posloupnosti řdy funkcí, mocninné řdy Fourierovy
Učební text k přednášce Mtemtická nlýz II (MAI055) Mrtin Klzr 20. červn 2007 Přednášk pokrývá v letním semestru následující látku:. Riemnnův integrál. 2. Posloupnosti řdy funkcí, mocninné řdy Fourierovy
Výpočet obsahu rovinného obrazce
 Výpočet oshu rovinného orzce Pro výpočet oshu čtverce, odélník, trojúhelník, kružnice, dlších útvrů, se kterými se můžeme setkt v elementární geometrii, máme k dispozici vzorce Kdchom chtěli vpočítt osh
Výpočet oshu rovinného orzce Pro výpočet oshu čtverce, odélník, trojúhelník, kružnice, dlších útvrů, se kterými se můžeme setkt v elementární geometrii, máme k dispozici vzorce Kdchom chtěli vpočítt osh
Při výpočtu obsahu takto omezených rovinných oblastí mohou nastat následující základní případy : , osou x a přímkami. spojitá na intervalu
 Geometrické plikce určitého integrálu Osh rovinné olsti Je-li ploch ohrničen křivkou f () osou Při výpočtu oshu tkto omezených rovinných olstí mohou nstt následující zákldní přípd : Nechť funkce f () je
Geometrické plikce určitého integrálu Osh rovinné olsti Je-li ploch ohrničen křivkou f () osou Při výpočtu oshu tkto omezených rovinných olstí mohou nstt následující zákldní přípd : Nechť funkce f () je
Křivkový integrál prvního druhu verze 1.0
 Křivkový integrál prvního druhu verze. Úvod Následující text popisuje výpočet křivkového integrálu prvního druhu. Měl by sloužit především studentům předmětu MATEMAT k příprvě n zkoušku. Mohou se v něm
Křivkový integrál prvního druhu verze. Úvod Následující text popisuje výpočet křivkového integrálu prvního druhu. Měl by sloužit především studentům předmětu MATEMAT k příprvě n zkoušku. Mohou se v něm

 Riemnnův určitý integrál. Definice 1. Budiž
Riemnnův určitý integrál. Definice 1. Budiž