UNIVERZITA PALACKÉHO V OLOMOUCI
|
|
|
- Helena Hrušková
- před 8 lety
- Počet zobrazení:
Transkript
1 UNIVERZITA PALACKÉHO V OLOOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA ATEATICKÉ ANALÝZY A APLIKACÍ ATEATIKY BAKALÁŘSKÁ PRÁCE Dvojný integrál princip řešení a sbírka příkladů Vedoucí bakalářské práce: gr. Iveta Bebčáková, Ph.D. Rok odevzdání: Vypracovala: artina Šušková E, III. ročník
2 Prohlášení Prohlašuji, že jsem bakalářskou práci zpracovala samostatně pod vedením paní gr. Ivety Bebčákové, Ph.D. s použitím uvedené literatury. V Olomouci dne. března
3 Poděkování Ráda bych poděkovala vedoucí bakalářské práce paní gr. Ivetě Bebčákové, Ph.D. za spolupráci i za čas, který mi věnovala při konzultacích.
4 Obsah Úvod 4 Seznam použitého značení 5 Integrální počet. Dvojný Riemannův) Integrál otivace Základní věty a definice Integrální počet funkce jedné proměnné Základní věty a definice Přehled základních vzorců Dvojný integrál na obdélníkové oblasti Dvojný integrál na elementárních množinách 4 Transformace do polárních souřadnic 5 5 Geometrická aplikace obsahy ploch 79 Geometrická aplikace objemy těles 9 7 Zadávání dvojných integrálů do programu Wolfram athematica Závěr 8 Literatura 9
5 Úvod Téma mé bakalářské práce je Dvojný integrál - sbírka příkladů. Tato práce by měla sloužit studentům prvního ročníku oboru atematika - ekonomie se zaměřením na bankovnictví a pojišťovnictví jako učební pomůcka v předmětu atematika. Doufám tedy, že pro ně bude přínosná a dokážou díky ní lépe pochopit počítání dvojných integrálů. Bakalářská práce je psaná s předpokladem, že čtenář má již základní znalost z předmětu atematika. V první kapitole je uvedena motivace dvojného integrálu a základní vzorce, definice a věty, bez jejichž znalostí by počítání integrálů nešlo. Dále je celá práce rozdělena do pěti kapitol řešených příkladů kapitoly - ), kde se postupně čtenář naučí řešit různé typy příkladů týkajících se řešení dvojných integrálů. Začínáme nejjednodušší kapitolou - dvojný integrál na obdélníkové oblasti, pokračujeme trochu složitější částí - dvojný integrál na elementárních množinách, po které následují příklady řešené transformací do polárních souřadnic. Čtenář se také naučí i něco z geometrické aplikace, jako jsou výpočty obsahu ploch a objemu těles pomocí dvojných integrálů. V této kapitole je zahrnuto i odvození vzorců pro výpočty objemů těles. V poslední, sedmé kapitole, si navíc ukážeme, jak používat program Wolfram athematica při řešení dvojných integrálů. Důvod, proč jsem si toto téma vybrala, byl ten, že se mi ze všech vypsaných prací téma Dvojný integrál líbilo nejvíce. Co mě ale zaujalo možná ještě více je fakt, že moje bakalářská práce může v budoucnu někomu posloužit a neskončí jen její obhajobou. 4
6 Seznam použitého značení R N Z R n a, b A B A B fx, y)dxdy R) množina reálných čísel množina přirozených čísel množina celých čísel kartézský součin R R R }{{} n uzavřený interval od a do b kartézský součin množin A a B sjednocení množin A a B dvojný integrál funkce dvou proměnných na množině množina všech funkcí Riemannovsky integrovatelných na množině 5
7 . Integrální počet.. Dvojný Riemannův) Integrál V práci se budu zabývat dvojným integrálem, který je definován a podrobně rozebrán v [4], [5], []. Kvůli náročnosti definice a kvůli zaměření této práce zde nebudu tuto definici uvádět, ale zaměřím se pouze na tvrzení, která nám pomáhají s výpočtem dvojného integrálu.... otivace Na začátek si zavedeme geometrickou motivaci dvojného integrálu. Tou je úloha, kdy chceme určit objem tělesa s podstavou v rovině xy) a horní stěnou, která je tvořená částí grafu nezáporné omezené funkce f definované na množině. Integračním oborem u dvojného integrálu může být např. čtverec, obdélník, trojúhelník, kruh, lichoběžník atd. Tím se liší od jednorozměrného integrálu, kde je integračním oborem vždy interval. Nejprve se budeme zabývat dvojným integrálem na obdélníku, tudíž množina bude obdélníkového tvaru. Podobným postupem bychom mohli počítat také n-rozměrný integrál, kde n N. Například pro n bychom integrovali přes kvádr. Budeme uvažovat uzavřený obdélník R, kde je kartézský součin uzavřených intervalů a, b na ose x a c, d na ose y, tj. a, b c, d. Existuje-li dvojný Riemannův integrál funkce f na, říkáme, že funkce f je Riemannovsky integrovatelná na obdélníku. nožinu všech funkcí Riemannovsky integrovatelných na značíme jako R). Dvojný integrál funkce dvou proměnných na množině budeme značit fx, y)dxdy.
8 ... Základní věty a definice Věta Fubiniova pro obdélník) Nechť funkce f je spojitá na uzavřeném obdélníku a, b c, d. Potom platí fx, y) dx dy b a d c ) fx, y) dy dx d c b a ) fx, y) dx dy Definice Elementární množina vzhledem k proměnné x je množina tvaru {x, y) R ; x a, b, gx) y hx)}, kde g a h jsou funkce jedné reálné proměnné spojité na a, b takové, že pro všechna x a, b platí gx) < hx). Definice Elementární množina vzhledem k proměnné y je množina tvaru {x, y) R ; y c, d, ϕy) x ψy)}, kde ϕ a ψ jsou funkce jedné reálné proměnné spojité na c, d takové, že pro všechna y c, d platí ϕy) < ψy). Definice Elementární množina je uzavřená množina, kterou lze vyjádřit jako sjednocení konečně mnoha disjunktních elementárních množin vzhledem k x nebo y. Věta Fubiniova pro elementární množinu) Nechť je funkce f spojitá na uzavřené elementární množině vzhledem k proměnné x, tj. {x, y) R ; a x b, gx) y hx)}. Potom platí fx, y) dx dy b a gx) ) hx) fx, y) dy dx 7
9 Nechť je funkce f spojitá na uzavřené elementární množině vzhledem k proměnné y, tj. {x, y) R ; c y d, ϕy) x ψy)}. Potom platí fx, y) dx dy d c ϕy) ) ψy) fx, y) dx dy Věta Transformace souřadnic ve dvojném integrálu) Nechť se uzavřená omezená množina N R proměnných u, v) zobrazí pomocí soustavy rovnic x gu, v) a y hu, v) vzájemně jednoznačně na uzavřenou omezenou množinu R proměnných x, y), přičemž funkce g a h jsou v N spojité spolu se svými parciálními derivacemi g, g, h a h u v u v a pro tzv. Jacobiův determinant jakobián) platí J g u h u g v h v ve všech bodech množiny N. Dále nechť funkce f fx, y) je spojitá na. Potom platí fx, y) dx dy fgu, v), hu, v)) J du dv, N kde J je absolutní hodnota jakobiánu. 8
10 .. Integrální počet funkce jedné proměnné Výše jsme viděli, že dvojný integrál převádíme na integrál dvojnásobný a při výpočtu dvojných integrálů tedy používáme metody známé z integrálního počtu funkce jedné proměnné. Proto si zde nyní nejdůležitější z nich uvedeme. Integrál funkce jedné proměnné je podrobně rozebrán v [], [], [].... Základní věty a definice Věta 4 etoda per partes) Nechť funkce ux) a vx) mají na intervalu I derivace u x) a v x). Existuje-li na I primitivní funkce k jedné z funkcí u x)vx), ux)v x), existuje i k druhé z nich a platí ux)v x) dx ux)vx) u x)vx) dx Věta 5 Substituční metoda) Nechť funkce ft) je spojitá na intervalu a, b), nechť funkce ϕx) má na intervalu α, β) spojitou derivaci a nechť ϕx) a, b) pro každé x α, β). Potom na intervalu α, β) platí ft) dt fϕx)) ϕ x) dx, kde t ϕx). Věta Newton Leibnizův vzorec) Nechť funkce f R a, b ) a F je primitivní funkce k f na a, b. Potom platí b a fx) dx [F x)] b a F b) F a) 9
11 ... Přehled základních vzorců a dx ax + c a R, x R x n dx x α dx xn+ n+ + c n N, x R xα+ α+ + c α R \ { }, x R+ x dx ln x + c x R \ {} e x dx e x + c x R a x dx ax ln a + c a R+ \ {}, x R sin x dx cos x + c x R cos x dx sin x + c x R dx cotg x + c x R \ {k, k Z} sin x dx tg x + c x R \ { + k, k Z} cos x dx arctg x + c x R +x x dx arcsin x + c x, ), kde c R Při výpočtech integrálů používáme následující pravidla: c fx) dx c fx) dx, kde c R je libovolná konstanta fx) ± gx)) dx fx) dx ± gx) dx
12 . Dvojný integrál na obdélníkové oblasti V následující kapitole se budeme zabývat počítáním integrálů na obdélníkové oblasti. Naučíme se dvojný integrál převádět na dvojnásobný, tj. využívat Fubiniovu větu, a dále počítat podle vět uvedených na začátku práce. Vypočítejte daný integrál pro danou množinu.. x y dxdy, 5, Řešení: Dvojný integrál můžeme přepsat na integrál dvojnásobný, protože je zde splněna podmínka Fubiniho věty pro obdélník. Kartézský součin nám udává, jaké budou integrační meze. 5 x y dy dx Nejprve budeme funkci integrovat podle proměnné y a proto budeme x považovat za konstantu, kterou můžeme vytknout před integrál. Zintegrujeme tedy funkci y. 5 [ y x ] dx V dalším kroku využijeme Newton Leibnizův vzorec. 5 x 7 dx Získáváme tak určitý integrál funkce jedné proměnné x. Nejprve vytkneme konstantu 7 před integrál a nalezneme primitivní funkci k funkci x. 7 [ x ] 5 Potom opět použijeme Newton Leibnizův vzorec, pomocí kterého dojdeme ke konečnému výsledku.
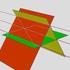
13 7 5 ) Poznámka: V tomto případě nezáleží na pořadí proměnných, podle kterých integrujeme. ohli bychom tedy postupovat i tak, že bychom začali v prvním kroku integrovat podle proměnné x, takže bychom proměnnou y považovali za konstantu a vytkli ji před integrál. Dále bychom postupovali úplně stejně, jako v předchozím řešení. Pořadí proměnných, podle kterých integrujeme, volíme vždy tak, aby bylo pro nás snadnější integrál vypočítat. Výsledek příkladu můžeme interpretovat jako objem tělesa s dolní podstavou, 5, v rovině xy) a horní stěnou, která je tvořená částí grafu funkce fx, y) x y definované na množině viz obrázek ). Obrázek : Těleso, jehož objem počítáme pomocí integrálu x y dxdy na množině, 5,
14 . 4xy e xy dxdy {x, y) R ; x ; y } Řešení: Protože je zde splněna podmínka Fubiniho věty pro obdélník, přepíšeme dvojný integrál na dvojnásobný. Budeme integrovat nejprve podle proměnné x, tudíž y budeme považovat za konstantu. 4xy e xy dx dy 4y xe xy dx dy V dalším kroku zavedeme substituci, kde x y položíme rovno t, abychom mohli snadno zintegrovat funkci xe xy. Důsledkem této substituce dostáváme i nové integrační meze. Novou funkci proměnné t tedy zintegrujeme podle t a dále postupujeme stejně, jako u předchozího příkladu, tj. použijeme Newton Leibnizův vzorec. t x y dt xydx y x t y e t dt dy x t y y e y ) dy ye y dy ydy y [ e t ] y ) dy Dále použijeme Per partes, neboli integrujeme po částech podle známého vzorce z věty 4. Poté použijeme opět Newton Leibnizův vzorec a dopočítáme integrál. u y u v e y v e y [yey ] e y [ y ] [ye y ] [ey ] [ y ] e e + + Další příklady této kapitoly již nebudou tak podrobně komentované. Řeší se obdobně, jako ty vzorové, takže budou okomentovány vždy jen nějaké nové postupy nebo úpravy, které se ještě dříve nevyskytly.
15 . x dxdy,, y Řešení: x y dy dx + [ x ] [ x ] dx x y + ) dx 4. lnxy )dxdy, e, e Řešení: e e e e e lnxy )dy dx e e [x ln x x] e dy + e [e e) )] dy + dy + e ln xdx dy + e [ y ln y y ] e dx e e ln y dy dx [e e) )] dx dx [y] e + [x]e e + e e e ) Poznámka: Integrál e e druhém kroku, vypočítáme následovně: ln y dy t y dt ydy ) ln y dy dx, který jsme potřebovali spočítat ve ln t t dt ln t t t tdt t ln t y ln y y + c 4 u ln t v t t u v t t t t dt t ln t t
16 5. x y sin x + y ) dxdy sin, sin, Řešení: Zde si musíme nejprve uvědomit, že hraniční body intervalu, jejichž kartézský součin tvoří množinu, jsou čísla a tudíž jde opět o integraci přes obdélník. sin sin x y sin x + y ) dy dx t x + y dt ydy y t x y t x + x [ cos t] x+ x dx x cos xdx x+ x x y sin x + y ) dy dx x sin tdt dx x cos x cos x + )) dx x cos x + ) dx [ x sin x + x cos x sin x ] [ x sin x + ) + x cos x + ) sin x + ) ] 4 sin + 4 cos sin ) 4 sin + 4 cos sin ) ) ) ) 4 4) + 4 Poznámka: Integrály, které potřebujeme spočítat ve čtvrtém řádku výpočtu, si zintegrujeme zvlášť následujícím způsobem s využitím substituce. x cos xdx u x v cos x u x v sin x x sin x x sin xdx 5
17 u x v sin x u v cos x x sin x + x cos x x sin x + x cos x sin x + c cos xdx x cos x + ) dx u x v cos x + ) u x v sin x + ) x sin x + ) x sin x + ) dx u x v sin x + ) u v cos x + ) x sin x + ) + x cos x + ) cos x + ) dx x sin x + ) + x cos x + ) sin x + ) + c. x + y 4) dxdy cos, 4 cos, 4 log Řešení: Stejně jako u předchozího příkladu je zde nezvykle zadaná množina, a to pomocí známých funkčních hodnot elementárních funkcí. usíme si tudíž uvědomit, jaké hodnoty tyto zápisy vyjadřují. 4log 4 cos 4 4 x + y 4) dx dy x + y 4) dx dy cos t x + y 4 dt dx x t y 4 x 4 t y y dy+ u du y y 4 y 4 dy t dt dy 4 [ ] y dy t y 4 u y v y 4 du dy y u 4 ; dv dy y v y 4 u y 4 v 8 v dv [ln u ] 4 + [ln v ]8 ln ln 4) + ln 8 ln ) ln 8 + ln 4 ln ln )
18 ) 8 4 ln ) ln ) 8 ln 5 7. y cos x dxdy,, Řešení: y cos x dy dx 9 tg tg ) 9 cos x [ y ) ] dx 9 cos x dx 9 [tg x] 8. e x cos xdxdy sin, sin, sin Řešení: sin sin sin e x cos xdy dx e x cos x dx u ex u e x u ex u e x e x cos xdy dx v cos x v sin x [ex sin x] v sin x v cos x [ex sin x] + [e x cos x] e x cos x [y] dx e x sin xdx e x cos xdx Nyní budeme pokračovat v řešení příkladu pomocí rekurence, protože jsme se dostali do situace, kdy nám vyšlo, že integrál funkce jedné proměnné ex cos xdx, který dostáváme na začátku druhého řádku výpočtu, je roven [e x sin x] + [e x cos x] ex cos xdx. Proto budeme řešit následující rovnici: 7
19 e x cos xdx [e x sin x] + [e x cos x] e x cos xdx e x cos xdx [e x sin x] + [e x cos x] e x cos xdx [ex sin x] + [ex cos x] e sin e sin ) + e e e ) + e ) e e ) cos e cos ) 9. 9x 5x dxdy, 4, x x 4x + 4 Řešení: Tento příklad budeme řešit rozkladem na parciální zlomky. Nejprve si upravíme jmenovatele na součinový tvar. x x 4x + 4 x x ) 4 x ) x ) x 4) x ) x + ) x ) Nyní již můžeme integrál upravit do tvaru: 4 9x 5x 4 x x 4x + 4 dy dx 9x 5x x ) x + ) x ) dy dx 4 4 x + x ) dy dx x x + x ) [y] x dx [ ln x + ln x ln x ] 4 8
20 [ ln + ln + 4 ln ) ln + ln ln )] ) 9 ln 9 + ln + ln ln 4 ln 5 ln 4 5 ln Poznámka: Při výpočtu jsme použili rozklad racionální lomené funkce na parciální zlomky, což konkrétně v tomto příkladu vypadá takto: 9x 5x x ) x + ) x ) A x + B x + + C x / x ) x + ) x ) 9x 5x A x + ) x ) + B x ) x ) + C x ) x + ) 9x 5x Ax 4A + Bx Bx + B + Cx + Cx C 9x 5x x A + B + C) + x B + C) + x 4A + B C) Dále jsme řešili soustavu tří rovnic o třech neznámých. A + B + C 9 B + C 5 4A + B C Řešením soustavy jsou A, B a C 4.. x + 7 dxdy, log cos, ln e x 7x + Řešení: Stejně jako v předchozím příkladu použijeme rozklad racionální lomené funkce na parciální zlomky. Také si musíme uvědomit, že množina je opět obdélník, i když to tak na první pohled nevypadá. x 7x + x ) x 5) log ln e x + 7 x ) x 5) dy dx cos A x + B ) dy dx x 5 9 x + 7 x ) x 5) dy dx x + 4 ) dy dx x 5
21 4 x 5 ) x [y] dx 4 x 5 ) ) dx x 4 x 5 ) dx [4 ln x 5 ln x ] x [4 ln 5 ln ) 4 ln 5 ln )] ln ln ln ln 5 4) ) 54 ln 5 4 ln 8 ) 8 ln ln 4 9. x x + 8 y dxdy,, 4 x x x + Řešení: Příklad opět řešíme rozkladem racionální lomené funkce na parciální zlomky. Platí totiž vztah: x x x + x x ) x ) x ) x ) x ) x 4) x + 4) 4 x x + 8 x x x + ydy dx x x + 8 x ) x 4) x + 4) ydy dx x x + 8 x ) x 4) x + 4) A x + B x 4 + [ y ] 4 dx C ) dx x + 4 x + x 4 + ) dx x + 4
22 8 [ ln x + ln x 4 + ln x + 4 ] 8 [ ln + ln + ln 5 + ln 4 ln ln ] 8 ln 9 + ln 5 + ln 4 ln ln ) 8 ln ln 5
23 . Dvojný integrál na elementárních množinách V této kapitole se naučíme řešit dvojné integrály na elementárních množinách. To znamená, že integrační množina již nebude zadaná kartézským součinem dvou intervalů, jako tomu bylo doposud, ale bude dána funkcemi. Abychom mohli určit integrační meze, budeme si vždy muset v prvé řadě danou množinu nakreslit. Jakmile určíme integrační meze, postup výpočtu je již obdobný, jako u dvojného integrálu na obdélníku.. e y dxdy {x, y) R ; x 5; y ln x} Řešení: Nejprve si namalujeme obrázek - danou množinu, přes kterou budeme integrovat. nožina je dána nerovnicemi x 5 a y ln x. Na základě obrázku určíme integrační meze. Obrázek : {x, y) R ; x 5; y ln x} Dále přepíšeme dvojný integrál na dvojnásobný pomocí věty Fubiniova pro elementární množinu). Daná integrační množina je elementární vzhledem k proměnné x.
24 5 ln x e y dy dx Protože je integrační množina elementární vzhledem k proměnné x, budeme nejprve integrovat podle proměnné y. 5 [e y ] ln x dx Využitím Newton Leibnizova vzorce a postupným dosazením dostaneme jednoduchý integrál funkce proměnné x. 5 e ln x e ) dx 5 x ) dx Vypočítaný integrál dále řešíme opět Newton-Leibnizovým vzorcem. Po jeho použití dojdeme ke konečnému výsledku. [ ] x 5 x
25 . x y dxdy {x, y) R ; x + y 9; y + x } Řešení: Stejně jako v předchozím příkladu si nejprve namalujeme danou množinu, přes kterou budeme integrovat. nožina je dána dvěma nerovnicemi. Nerovnice x + y 9 popisuje kruh se středem v bodě [, ] a poloměrem a y + x popisuje polorovinu. Na základě obrázku určíme integrační meze. Tentokrát je množina elementární vzhledem k proměnné y. Obrázek : {x, y) R ; x + y 9; y + x } Dvojný integrál si přepíšeme na dvojnásobný, opět pomocí věty Fubiniova pro elementární množinu). 9 y x y dx dy y Jak již bylo řečeno, množina je elementární vzhledem k proměnné y a budeme tedy integrovat nejprve podle proměnné x, tzn. y budeme považovat 4
26 za konstantu. [ ] x y 9 y dy y Dále využijeme Newton Leibnizův vzorec. ] [ 9 y y ) y) dy y 9 y ) dy y y) dy Dostali jsme rozdíl dvou integrálů, které nejsme schopni vypočítat podle vzorce, ale musíme si je vypočítat každý zvlášť. Nejdříve si spočítáme jen primitivní funkci. Integrál y 9 y ) dy budeme počítat pomocí dvou substitucí. Nejprve zavedeme první z nich, kde y nahradíme t. y 9 y ) dy t y dt ydy t9 t) dt V dalším kroku zavedeme substituci s 9 t a upravíme, aby se nám lépe integrovalo. s 9 t ds dt s 5 9s ) ds 9 s) s ds s 9) s ds Nyní již můžeme integrovat podle vzorce x n dx xn+ n+ a postupnými matematickými úpravami integrál dopočítáme. s s s s t) t) y ) y ) 5 Ještě si musíme zvlášť vypočítat integrál y y) dy. Nejprve 5
27 roznásobíme závorku pomocí vzorce a b) a a b+ab b a poté ještě vynásobíme výrazem y. Dále počítáme postupně jednotlivé integrály. y y) dy y 7 7y + 9y y ) dy 7y 7y 4 + 9y 5 y ) dy 7 4 y4 7 5 y5 + 9 y y7 7 Nyní již můžeme pokračovat ve výpočtu samotného integrálu. Využijeme Newton Leibnizův vzorec a postupnými úpravami dojdeme ke konečnému výsledku [ 9 y ) 7 7 [ 9 9) 7 7 [ y ) ) ] [ 7 4 y4 7 5 y5 + 9 y y7 7 ] 5 87 ] ] Další příklady této kapitoly již nebudou tak podrobně komentované. Řeší se obdobně, jako ty vzorové, takže budou okomentovány vždy jen nějaké nové postupy nebo úpravy, které se ještě dříve nevyskytly.
28 4. ln 9 x ) dxdy je uzavřený trojúhelník s vrcholy v bodech A [, ]; B [, ]; C [, ] Řešení: Obrázek 4: nožina daná body A [, ]; B [, ]; C [, ] V tomto příkladu je množina zadaná jinak, než v dosud komentovaných příkladech. Nemáme zde dány funkce, ale pouze body určující plochu, proto si tyto funkce musíme určit sami. Po nakreslení daného trojúhelníku vidíme, že podle proměnné x budeme integrovat na intervalu, a y máme od do funkce y x. x ln 9 x ) dy dx t 9 x dt xdx x t 9 x t ln 9 x ) [y] x dx ln tdt 9 ln ln 5 + 5) 9 5 ln 9 x ) xdx ln tdt [t ln t t]9 5 ) ln ln
29 5. x y dxdy { x, y) R ; x 5; x y x} Řešení: 5 5 x x Obrázek 5: { x, y) R ; x 5; x y x} x y dy dx 5 [ x ] x y ) [ x + x x 4 dx 4 x ) x ] 5 dx 5 [ x 4 x 5 4 x ) x + x dx ] 5 8
30 . x 5y ) dxdy {x, y) R ; y ; y x ; x + y } Řešení: Obrázek : {x, y) R ; y ; y x ; x + y } Tento příklad musíme řešit jako součet dvou integrálů, tj. dělením dané množiny na dvě množiny. Je to tím, že na intervalu, je plocha shora omezená funkcí y x a na intervalu, je omezená funkcí y x. Proto musíme vypočítat každý integrál zvlášť a následně je sečíst. + x x 5y ) dy dx + ] x [x y 5y dx + x x 5y ) dy dx ] x [x y 5y dx x x ) 5 ) x x + ) dx + x x) 5 9 x + ) x ) dx 9
31 x x 5 x + 5x 5 ) dx+ x x x 5 ) x dx [ x 4 4 x 5x + 5x 5x ] + [x x x + 5 x 5 x [ ) )] + [ ) 8 )] ] 7. x + y) dxdy {x, y) R ; y x ; y x 9 } Řešení: Obrázek 7: {x, y) R ; y x ; y x 9 } x+9 x + y) dy dx x+9 x + y) dy dx x + x +
32 [ xy + y ] x+9 x + dx [ x x + 9) + x + 9) x x + ) x + ) ] dx x + 8x + x + 54x + 4 x x x 4 8x 7 ) dx x + x x x 4 + x ) dx [ x + x x4 ] 5 x5 + x ) + ) Poznámka: V tomto příkladu jsme si museli integrační meze vypočítat, a to jako průniky dvou křivek. Zavedli jsme tedy rovnici x + x+9 a jejím vyřešením jsme dostali kořeny x, x, což jsou naše integrační meze.
33 8. xydxdy { x, y) R ; y 4; y x; y x} Řešení: x Obrázek 8: { x, y) R ; y 4; y x; y x} xydy x dx+ 4 xydy x x 4x 9 ) x dx + 4x 9 x ) dx + [x 4 + [8 44 ] 9 x4 4 dx + [8x ) x [ y ] x x dx+ x 9 ) x dx x 9 x ) dx ] 9 x4 [ )] ) x [ y ] 4 x dx ] +
34 9. ln xdxdy {x, y) R ; y x ; y x} Řešení: x x Obrázek 9: {x, y) R ; y x ; y x} ln xdy dx x ln xdx ln x) [y] x x dx x ln x x ln x ) dx [ ] x ln xdx x 4 ln x 9 x x x ln x + 9 ) ) 9 Poznámka: Integrály x ln xdx a x ln xdx, které se vyskytly na začátku druhého řádku výpočtu, jsou zintegrovány zvlášť v této poznámce. Vypočítáme si zde jen primitivní funkce. x u ln x v x ln xdx u v x x x ln x x x dx x xdx ln x x 4 ln x 9 x + c
35 x ln xdx u ln x v x u v x x x ln x x ln x x x dx x dx x ln x x x x ln x 9 + c. 5x dxdy { x, y) R ; y x + 4x; y 4 x; x } Řešení: Obrázek : { x, y) R ; y x + 4x; y 4 x; x } x +4x 5x dy 4 x dx 5x [y] x +4x 4 dx x 5x x + 4x 4 ) x dx [ 5 x x x x4 ] 8 ) 5x 5x 4 + x ) x dx ) 8 4
36 . 4ydxdy {x, y) R ; xy ; x + y 5 } Řešení: Obrázek : {x, y) R ; xy ; x + y 5 } 5 x x 4ydy dx [ 5 x + 4x ) 8x ] dx [ 5x x + 8 x + 8 x [ ] [ y 5 x dx 5 x) 4 ] dx x x ] 5 4x + 8x 8 ) dx x ) ) 5
37 . Řešení: xydxdy { x, y) R ; y x; y x; y 4 x; x } Obrázek : { x, y) R ; y x; y x; y 4 x; x } x 4 x xydy dx+ x xydy x dx [ y x ] x 4 x dx+ [ y x ] x dx x x x + 8x x ) dx + x x + 8x x ) dx + x x 9 ) x dx x 9 x ) dx [ 4 x4 8x + 8 x ] 4 x4 + [ 4 x4 ] x4 [ ) )] [ ) )]
38 . x + y) dxdy je trojúhelník s vrcholy A [, 4], B [, ], C [4, 4] Řešení: Obrázek : nožina dána body A [, 4], B [, ], C [4, 4] 4 x + y) dy dx x + y) dy dx x [ xy + ] 4 4 y dx + 4 x x 4 [ xy + y ] 4 x 4 dx [ x 4 + x 4 x) ] 4 x) dx + [ x 4 + x x 4) ] x 4) dx 8x + 4 8x + 4x )) x + 4x dx + 7
39 x + 4 4x + 8x 4x x + )) dx 4 + 4x 4 + 4x x ) dx + x + 4 4x x + 4x 4 ) dx 4x x ) dx + 4 4x x ) dx [ 4 x ] [ 4 x + x ] 4 x 4 ) ) 9 8
40 4. Řešení: sin x + y ) dxdy { x, y) R ; y x; y ; x } x Obrázek 4: { x, y) R ; y x; y ; x } sin x + y ) x+ sin t) dt 5 x t x + y dy dx dt dy y x t x + x 5x y t x + dx cos x + ) dx + [cos t)] x+ 5 x dx ) 5 cos x dx u x + v 5 du dx x x u ; dv 5 dx x u x v 5 x v 5 9
41 4 5 5 sin 5 sin 5 cos u) du ) 5 sin ) ) cos v) dv 4 5 [sin v)] 5 [sin u)] 5 ) sin ) 5 ) ) sin ) + sin x dxdy {x, y) R ; y x ; y x + } Řešení: Obrázek 5: {x, y) R ; y x ; y x + } V tomto příkladu musíme uvažovat dvě situace, a to případ, kdy je výraz v absolutní hodnotě kladný, a případ, kdy je záporný. Proto zde máme dvoubarevný obrázek, modrá polovina znázorňuje případ, kdy x a integrál vypočítáme klasickým způsobem. Zelená plocha znázorňuje případ, 4
42 kdy x, a proto při výpočtu integrálu musíme otočit znaménko integrované funkce. Oba vypočtené integrály nakonec sečteme, čímž dojdeme k výsledku. a) x x+ x xdy dx x x + x + ) dx x [y] x+ x dx x + 7x x ) dx [ 4x + x x 4] b) x x+ x xdy dx x + 7x x ) dx [ 4x + x x 4] 4 8) x dxdy
43 . xy dxdy {x, y) R ; y x + ; y x } Řešení: Obrázek : {x, y) R ; y x + ; y x } xy x y ) a) x y ) b) xy x y ) c) x y ) d) a) x y x xydy dx x x + x 4) dx [ x 4 x4 + x ] x [ ] y x dx 4 x x + x 5) dx + )
44 b) x y x xydy dx x [ ] y dx x x x x ) dx [ 4 x4 x ] x x x x ) dx 4 + ) 4 c) x y x xydy dx x x + x + ) dx [ 4 x4 + x + x ] x xydy dx x + x + x ) dx ) 7 4 x x 5 4 xydy dx x x xydy dx x [ x + x + ) x + x 4)] dx x x + x x 4) dx [ 4 x4 + x x ] x [ ] y x dx x x + x x 5) dx [ + ) 4 + )] 4
45 d) x y x xydy dx x [ y ] x dx x x + x 5) dx + ) x xydy dx x x + x 4) dx [ x 4 x4 + ] x xy dxdy
46 7. Řešení: xydxdy { x, y) R ; y x, y x +, y x } 4 Obrázek 7: 4 + x x xydy dx + { x, y) R ; y x, y x +, y x } x [ y ] x dx + x 4 x x+ x xydy dx + x [ y ] x+ dx + x 4 x + ) 4 x4 x + 4x 4 dx + x x + 4x + 4 x + 4x 4 ) dx + x x xydy dx x [ y ] x dx x 45
47 + x 4 x + ) 4 x4 x + 4x 4 dx x 4x x + 4 ) x4 dx+ x 8xdx+ x 4x x + 4 ) x4 dx 4 4 4x x + 4 ) x5 dx+ [ 4 x 4 x4 + ] 4 x + [ 8 4 [ + 4 ) ) x 4 4 8x dx+ 4x x + 4 x5 ) dx ] + [ 4 x 4 x4 + 4 x )] ) + ] )
48 8. x 5 x + dxdy {x, y) R ; y x; x ; x 4} x x Řešení: 4 4 x Obrázek 8: {x, y) R ; y x; x ; x 4} x 5 x + x x dy dx 4 x 5 x + x x 4 [y] x dx x 5 x + 4 ) dx x + dx x x ) x + ) 4 [ x 4 4 x + A x + B ) 4 dx x + x + x ) dx x + ] 4 + ln x ln x ) ln 7 ln 5 + ln 7 + ln 5 x 5 x + x x ) xdx + ln ln 5 4 ln + ln 4 + ln
49 9. y cos xdxdy {x, y) R ; y x; y ; x } Řešení: x Obrázek 9: {x, y) R ; y x; y ; x } u x u x u x u x u x u + y cos xdy dx sin xdx v cos x v sin x cos x [ y ] x dx [ x sin x ] v sin x v cos x [ x sin x ] v cos x v sin x [ x sin x ] [ x sin x ] + [ x cos x ] +[ x cos x ] + [ x cos x ] x cos xdx x sin xdx [x sin x] x cos xdx [x sin x] + [cos x] 8 sin sin + 4 cos cos 4 sin + sin cos + cos ) 48
50 4 + + ) ln x dxdy {x, y) R ; y x; y x; x e} Řešení: e x x Obrázek : {x, y) R ; y x; y x; x e} ln x dy dx u ln x u x x x [ x ln x ] e e e e ln x [y] x x dx [ v x x v x [ x xdx ln x ] e ln x 4 x ln x dx ] e e [ x ] e x x dx e ln e ln 4 e + 4 e 4 e e 4 e + 4 e + ) 4 49
51 . y ln xdxdy {x, y) R ; y x; y ; x } Řešení: Obrázek : {x, y) R ; y x; y ; x } x y ln xdy dx [ y ln x ] x ) 9 ln x x dx 9 x ln xdx ln xdx 9 ln xdx x ln xdx u ln x v x u v x 9 x [x ln x x] [ ] x ln x + + x x dx 9 [x ln x x] [ x ln x ] + [ ] x 9 ln ln + ) 7 ln ln ) + 7 ) 8 5
52 9 7 ln 7 ) ln ln 7 ) 9 ln ln ln ln ln ln 9 9 ln ln
53 4. Transformace do polárních souřadnic V této kapitole budeme integrály počítat transformací do polárních souřadnic. Polární souřadnice používáme u příkladů, které neumíme integrovat v kartézských souřadnicích, ve kterých jsme počítali doposud. V polárních souřadnicích je každý bod popsán svou vzdáleností od počátku souřadnicového systému značíme r) a orientovaným úhlem, který svírá jeho průvodič s kladným směrem osy x značíme α). Na začátek si zavedeme následující transformaci: x r cos α, y r sin α Poté vypočítáme Jakobián podle věty Transformace souřadnic ve dvojném integrálu). J cos α sin α r sin α r cos α r cos α + sin α ) r Dále přepíšeme výraz x + y do polárních souřadnic. x + y r cos α + r sin α r cos α + sin α ) r Poté si určíme integrační meze a dále již můžeme začít s integrováním. Budeme postupovat podle věty Transformace souřadnic ve dvojném integrálu). Ta nám říká, že platí následující vzorec. fx, y) dx dy fgu, v), hu, v)) J du dv, kde J je absolutní hodnota jakobiánu. 5
54 . x +y dxdy {x, y) R ; x + y 9; x ; y } Řešení: V některých případech je potřeba využít transformaci do polárních souřadnic. Nejprve si opět nakreslíme danou množinu, přes kterou budeme integrovat. Tou je zde čtvrtina kruhu o poloměru. Obrázek : {x, y) R ; x + y 9; x ; y } Zavedeme si následující transformaci: x r cos α, y r sin α, kde r vyjadřuje vzdálenost bodu x, y) od počátku a α je orientovaný úhel, který svírá průvodič bodu s kladným směrem osy x. Z předchozího již víme, že platí x + y r a J r. Než začneme intergál počítat, musíme si ještě určit integrační meze. V tomto případě je určujeme přímo z obrázku. Na něm vidíme, že poloměr je jednotky, tudíž r se bude pohybovat na množině, a sevřený úhel se mění od do 9, takže α,. Nyní již můžeme začít počítat samotný integrál funkce dvou proměnných, kterými jsou r a α. Nejprve si přepíšeme dvojný integrál na dvojnásobný 5
55 podle věty Fubiniho pro elementární množinu). Integrovat budeme nejprve podle proměnné r a α budeme považovat za konstantu. x +y dxdy r rdr dα Zavedeme substituci t r, čímž se nám změní integrační meze uvnitř integrálu. t r dt rdr r t r t 9 9 t dt dα Zintegrujeme tedy funkci podle proměnné t a dopočítáme podle Newton Leibnizova vzorce. [ t ln ] 9 dα 9 ln ) dα ln Dále zde máme už jen integrál jedné proměnné, kterou je α, který vypočítáme a upravíme opět podle Newton Leibnizova vzorce. 9 ln [α] 4 9 ln Poznámka: U některých příkladů je možné integrovat nejdříve podle proměnné α a až poté podle r. Je to ovšem individuální a závisí to na zadání příkladu. Vždy se rozhodujeme, které proměnné dáme přednost podle toho, co je pro výpočet integrálu jednodušší. 54
56 . x + y dxdy { x, y) R ; x ) + y 4; x + y ; y x; y } Řešení: V tomto příkladě opět využijeme transformaci do polárních souřadnic. Nejprve si nakreslíme integrační množinu. Tentokrát už má složitější tvar, a proto nebudeme schopni podle obrázku určit integrační meze, ale budeme si je muset vypočítat. Obrázek : { x, y) R ; x ) + y 4; x + y ; y x; y } Zavedeme opět následující transformaci: x r cos α, y r sin α a zároveň víme, že platí x + y r a J r. Nejprve určíme integrační meze pro proměnnou r, a to tak, že ze zadaných nerovnic x ) + y 4 a x + y, které popisují kruhy a určují nám poloměr, uděláme rovnice, u obou dosadíme za x r cos α a za y r sin α a dopočítáme r. 55
57 x ) + y 4 x + y x 4x + y r r cos α 4r cos α + r sin α r r 4r cos α r r r 4 cos α) r r 4 cos α r 4 cos α V prvním sloupci nám zde vyšly kořeny pro r, ale protože žádný bod, kterému by odpovídal poloměr r, se nevyskytuje v zadané množině, nepočítáme s ním a bereme pouze druhý výsledek. Podle proměnné r budeme tedy integrovat na množině, 4 cos α. Dále musíme určit i integrační meze pro proměnnou α. To uděláme tak, že obě další zadané nerovnosti změníme za rovnosti, budeme tedy mít dvě rovnice: y x a y. Přímky, které jsou těmito rovnicemi popsány, svírají úhel s osou x, a proto udávají úhel α. Budeme počítat arkustangens směrnice, který tyto dvě přímky svírají s osou x. } y x α arctg 4 α y α arctg 4 Na množině, 4 budeme tedy integrovat podle proměnné α. Nyní již můžeme přistoupit k samotnému integrování. Dvojný integrál si nejprve přepíšeme na dvojnásobný podle věty Fubiniho pro elementární množinu). x + y dxdy 4 4cos α r rdr dα Nejprve budeme integrovat podle proměnné r a α budeme považovat za konstantu. 4 [r] 4 cos α dα 5
58 Dále využijeme Newton Leibnizův vzorec a dosazením dostaneme jednoduchý integrál funkce proměnné α. 4 4 cos α ) dα Integrál vypočítáme a opět použijeme Newton Leibnizův vzorec, pomocí něhož dojdeme ke konečnému výsledku. [4 sin α α] 4 [4 sin 4 ] 4 4 sin + ) Dále již nebudou příklady komentované, protože se počítají pomocí stejných principů, které byly vysvětleny výše. 57
59 4. Řešení: e x +y ) x + y ) dxdy { x, y) R ; x + y ; x + y ; y } x Obrázek 4: { x, y) R ; x + y ; x + y ; y } x x r cos α y r sin α x + y r cos α + r sin α r cos α + sin α ) r x + y x + y r r r r 4 r ± r ±4 y x, odtud α arctg y x, odtud α arctg r 4 ) 5 } α 5 58
60 5 5 e x +y ) x + y ) dxdy e r ) r rdr dα t r 4 e r4 r dr dα dt 4r dr r t r 4 t e t 4 dt dα [ ] e t 5 dα 4 e 5 e ) dα 4 4 e e 55 ) [α] 5 4 e e 55 ) 4 e e 55 ) e e 55 ) 5 ) 59
61 5. x + y + dxdy {x, y) R ; x + y ; x + y 4} Řešení: Obrázek 5: {x, y) R ; x + y ; x + y 4} x r cos α y r sin α x + y r cos α + r sin α r cos α + sin α ) r x + y x + y 4 r r 4 r r r ± r ± r α x + y + dxdy t r + r + rdr dα dt rdr r t r t
62 tdt dα ) [α] [ t ] dα ) ) dα
63 . xy x + y dxdy {x, y) R ; x + y 4x; x + y x; y x; y x} Řešení: Obrázek : {x, y) R ; x + y 4x; x + y x; y x; y x} x r cos α y r sin α x + y r cos α + r sin α r cos α + sin α ) r 4x x + y x y x α arctg 4 4r cos α r r cos α y x α arctg ) 4 α cos α r cos α 4 4 xy x + y dxdy cos α 4 cos α 4 4 cos α 4 cos α sin α cos α rdr dα r sin α cos α r 4 4 rdr dα sin α cos α [ r ] cos α 4 cos α dα
64 4 sin α cos α cos α cos α ) d 4 sin α cos αdα 4 t cos α 4 dt sin α sin α cos αdα α 4 4 t α t 4 [ ] ) t ) t dt
65 7. Řešení: ln x + y ) ln [ x + y ) ]dxdy {x, y) R ; x + y y; x + y 4y} Obrázek 7: {x, y) R ; x + y y; x + y 4y} x r cos α y r sin α x + y r cos α + r sin α r cos α + sin α ) r y x + y 4y r sin α r 4r sin α sin α r 4 sin α α ln x + y ) ln [ x + y ) ]dxdy 4 sin α sin α 4 sin α sin α ln r 4 ln r rdr dα ln r ln r rdr dα 4 [ r ] 4 sin α sin α dα 4
66 4 sin α 4 sin α ) dα sin αdα [α sin α cos α] sin cos + sin cos ) ) + ) Poznámka: Integrál, který potřebujeme vypočítat na konci třetího řádku výpočtu, si zintegrujeme zvlášť v této poznámce. Využijeme zde rekurenci, která již byla vysvětlena dříve. sin αdα cos α ) dα dα cos αdα dα u cos α v cos α u sin α v sin α ) dα sin α cos α sin αdα α sin α cos α sin αdα sin αdα α sin α cos α sin αdα α sin α cos α) 5
67 8. Řešení: x y dxdy { x, y) R ; x + y ; x + y 4; y x ; y x } Obrázek 8: { x, y) R ; x + y ; x + y 4; y x ; y x } x r cos α y r sin α x + y r cos α + r sin α r cos α + sin α ) r r y x α arctg y x α arctg } α x y dxdy t r dt rdr x t 5 x t 5 r rdr dα tdt dα [ t ] 5 dα
68 5 ) dα ) [α] ) ) ) 7
69 9. Řešení: x + y dxdy {x, y) R ; x + y y; x + y 4; y x} Obrázek 9: {x, y) R ; x + y y; x + y 4; y x} x r cos α y r sin α x + y r cos α + r sin α r cos α + sin α ) r Tento příklad musíme vypočítat ve dvou krocích. V prvním z nich budeme uvažovat pouze plochu, která je popsaná úhlem α, 4, a vypočítáme si poloměr pro tento úhel. V dalším kroku vypočítáme integrál pro plochu popsanou úhlem α, a opět musíme vypočítat i poloměr platný 4 pro tento úhel. Oba vypočtené integrály nakonec sečteme. 8
70 a) α 4 x + y y x + y 4 r r sin α r 4 sin α r r sin α r 4 rdr dα r 4 dr dα 4 sin α) dα sin α sin α [α + cos α] cos 4 cos + + b) α r 4 rdr dα r dr dα 4 4 dα [α] x + y dxdy
71 4. Řešení: x + y dxdy {x, y) R ; 4 x + y 9; x } Obrázek : {x, y) R ; 4 x + y 9; x } x r cos α y r sin α x + y r cos α + r sin α r cos α + sin α ) r r α x + y dxdy r rdr dα r dr dα [ln r ] dα ln ln ) dα ln dα ln [α] ln + ) ln 7
72 4. ln x + y ) dxdy {x, y) R ; x + y ; y } Řešení: Obrázek : {x, y) R ; x + y ; y } x r cos α, y r sin α x + y r cos α + r sin α r cos α + sin α ) r r 4 α ln x + y ) dxdy [ r 4 ln r rdr dα ] 4 r ln r dα 8 ln ln + ) dα 4 ) 8 ln 4 5 ) dα ln ln 4 5) ln r rdr dα [α] ln 4 5 ) 4
73 Poznámka: Integrál ln r rdr, který máme na konci prvního řádku výpočtu, vypočítáme takto. r ln rdr u ln r v r u v r r r ln r r r dr r ln r r 4 + c 4. ln x + y ) x + y dxdy {x, y) R ; x + y 4; y x; y ; x } Řešení: Obrázek : {x, y) R ; x + y 4; y x; y ; x } x r cos α, y r sin α, x + y r r α ln x + y ) x + y dxdy ln r rdr dα r ln rdr dα
74 [r ln r r] dα 5 4 ln ln + ) dα ln ) dα ln ) [α] 5 4 ln ) 4 ln ) ln ) ) x + y x + y dxdy {x, y) R ; x x + y 4x; x } Řešení: Obrázek : {x, y) R ; x x + y 4x; x } x r cos α y r sin α x + y r a) x x + y 4x r cos α r 4r cos α cos α r 4 cos α α 7
75 4cos α cos α [sin α] r rdr dα r sin sin 4 cos α cos α ) dr dα ) cos αdα b) cos α r α cos α cos α cos α r rdr dα r cos α cos α dr dα [ ln sin α + cos α ) ln cos α sin α )] ) ) ) cos α cos α dα [sin α] ln sin + cos ln cos sin [ ln sin ) + cos )] [ + ln cos ) sin )] sin + sin ) ) + ln ) + + ) + ln ln ) + + ln ) ln ln ln + ln ln ln ln + ln ) ln ln ln ln ) ln ln ) ln ln 7 74
76 c) x x + y 4x α r cos α r 4r cos α cos α r 4 cos α 4cos α r rdr dα cos α r [sin α] sin ) sin 4 cos α cos α dr dα cos αdα )) ) ) x + y dxdy + ln 7 + ln 7 x + y 75
77 44. Řešení: x ln ydxdy { x, y) R ; x + y ; y x; x } Obrázek 4: { x, y) R ; x + y ; y x; x } x r cos α y r sin α x + y r r α x ln ydxdy r cos α ln r sin α) rdr dα r cos α ln r + ln sin α) dr dα 7
78 cos α r cos α ln rdr dα + r ln rdr dα + 7 ln 5 ) cos αdα ln 5 ) [sin α] 9 7 ln ln ) r cos α ln sin α) dr dα cos α ln sin α) + 5 sin sin ) [ r cos α ln sin α) r dr dα ] cos α ln sin α) dα + 5 ) ) 5 ln 5 5 ln ln 4 9 ln )5 dα ln ) ln ln 4 9 Poznámka: Integrály r ln rdr a r ln rdr u ln r v r u v r [ln r r r cos α ln sin α) dα vypočítáme takto. ] r r dr [ ] [ ] ln r r r ln ln ln 5 9 t sin α cos α ln sin α) dα dt cos αdα α t α t ln tdt [t ln t t] ln ln + ln 77
79 45. Řešení: x y dxdy { x, y) R ; x + y 4; y x; y x } Obrázek 5: { x, y) R ; x + y 4; y x; y x } x r cos α y r sin α x + y r r y x α arctg ) } y x α arctg ) 4 α 4 4 x y dxdy [ln t ] ) 4 cos α sin α dα ln ln ln r cos α r sin α rdr dα 4 cos α sin α t sin α dt cos α α t α t 4 ) ln ln ln 78 [ r ] t dt ln dα )
80 5. Geometrická aplikace obsahy ploch Dvojný integrál má různá využití a jedním z nich je i to, že s jeho použitím umíme spočítat obsahy různých ploch. Obsah plochy R ohraničené několika křivkami budeme počítat pomocí vztahu S dxdy, kde označuje plochu. 4. Pomocí dvojného integrálu určete obsah plochy ohraničené křivkami: y x ; y x ; y 4 Řešení: Nejprve si nakreslíme dané křivky do grafu a pomocí nich určíme integrační meze. Obrázek : Plocha ohraničená křivkami y x ; y x ; y 4 Vidíme, že obrázek je symetrický podle osy y, proto můžeme vypočítat integrál jen pro např. pravou půlku plochy a vynásobit dvěma. nožina, přes kterou integrujeme, je elementární vzhledem k proměnné x i vzhledem k proměnné y. Nezáleží zde tedy na pořadí proměnných, podle kterých budeme integrovat, ukážeme si to oběma způsoby. 79
81 Nejprve budeme integrovat podle proměnné y a x budeme považovat za konstantu. S 4 dy dx x Zintegrujeme tedy podle y a upravíme za použití Newton Leibnizova vzorce. [y] 4 x dx 4 x ) dx Dále integrujeme podle x a opět upravíme podle Newton Leibnizova vzorce a dopočítáme. [4x x ln ] 8 4 ln + ) 8 ) ln ln ln Druhý způsob bude velmi obdobný, rozdíl bude jen v tom, že budeme integrovat nejprve podle proměnné x a y budeme považovat za konstantu. Vypočteme vnitřní integrál podle proměnné x a upravíme podle Newton Leibnizova vzorce. 4 log y S dx dy 4 [x] log y dy Dále počítáme jednoduchý integrál proměnné y. usíme použít metodu Per partes z věty 4 a potom opět upravit podle Newton Leibnizova vzorce. u log y v 4 u v y [y log y] 4 y ln 4 log 4 log ) ln dy ln [y]4 ln Obsah plochy na obrázku je ln jednotek čtverečních. 8
82 47. Pomocí dvojného integrálu určete obsah plochy ohraničené křivkami: y x x; y 4x x Řešení: Nejprve si nakreslíme dané křivky do grafu, abychom mohli určit integrační meze. Plocha, jejíž obsah počítáme, je ohraničena dvěma parabolami. Obrázek 7: Plocha ohraničená křivkami y x x; y 4x x Budeme integrovat nejprve podle proměnné y a x budeme považovat za konstantu. S 4x x x x dy dx [y] 4x x x x dx Nyní integrál upravíme podle Newton Leibnizova vzorce. 4x x x + x ) dx x x ) dx Na závěr vypočteme integrál jedné proměnné x a pomocí Newton Leibnizova vzorce opět upravíme. 8
83 [ x ] x Obsah plochy na obrázku 7 je 9 jednotek čtverečních. 48. Pomocí dvojného integrálu určete obsah plochy dané množinou. { } x, y) R ; y sin x; y cos x; y ; x Řešení: Obrázek 8: { x, y) R ; y sin x; y cos x; y ; x } Tento příklad jde vypočítat čtyřmi způsoby. Plocha je souměrná podle osy x, tudíž si ji můžeme rozdělit na dvě poloviny a vypočítat integrál 4 pouze jedné poloviny plochy a výsledek vynásobit dvěma. ůžeme také počítat dva integrály a ty potom sečíst. Další možností je udělat z plochy plochu elementární vzhledem k y a vypočítat takto. Ukážeme si zde pro názornost všechny čtyři způsoby.. způsob: S 4 sin x dy dx 4 sin xdx [ cos x] 4 cos ) ) 4 + cos + 8
84 . způsob: S cos x dy dx cos xdx [sin x] 4 sin sin ) 4 4 ) 4. způsob: S 4 sin x dy dx + 4 cos x dy dx 4 sin xdx + 4 cos xdx [ cos x] 4 + [sin x] cos ) cos + sin sin ) ) ) způsob: S arccos y arcsin y dx dy arccos y arcsin y) dy [ y arccos y y y arcsin y ] y 4 ) 4 ) Poznámka: Integrály arcsin ydy a arccos ydy vypočítáme takto. u arcsin y v arcsin ydy u y v y y arcsin y y dy y t y dt ydy y arcsin y + y + c 8
85 u arccos y v arccos ydy u y v y y arccos y + t y dt ydy y arccos y y + c y y dy Obsah plochy na obrázku 8 je jednotek čtverečních. 49. Pomocí dvojného integrálu určete obsah plochy. { x, y) R ; y x ; y sin x; x } Řešení: S Obrázek 9: { x, y) R ; y x ; y sin x; x } x sin x dy dx 4 4 cos + cos + x ) [ ] + sin x dx 4 x cos x Obsah plochy na obrázku 9 je jednotek čtverečních. 84
86 5. Pomocí dvojného integrálu určete obsah plochy. { x, y) R ; y 4 x ; y 5 x} Řešení: S 4 Obrázek 4: { x, y) R ; y 4 x ; y 5 x} 5 x 4 x dy dx ln x 4 ) ] 4 dx [5x x 4 ln x x + 4 ln ln 4 ln 44 5 ln 5 Obsah plochy na obrázku 4 je 5 ln 5 jednotek čtverečních. 85
87 5. Pomocí dvojného integrálu určete obsah plochy. { } x, y) R ; y x; y x ; x 4 Řešení: S 4 Obrázek 4: x x 4 4 dy dx { x, y) R ; y x; y x 4 ; x } ) [ ] x x x 4 dx 4 x Obsah plochy na obrázku 4 je 9 4 jednotek čtverečních. 8
88 5. Pomocí dvojného integrálu určete obsah plochy. { } x, y) R ; y x ; y x; x Řešení: { x, y) R ; y x ; y x; x, } Obrázek 4: nožina z příkladu č. 5 Tento obsah vypočítáme jako součet dvou integrálů, protože v počátku souřadnic se nám mění integrační meze. x S dy dx + x dy dx x ) x x dx + [ x 4 8 x ] + x ) x x dx ] [x x Obsah plochy na obrázku 4 je 8 jednotek čtverečních. 87
89 5. Pomocí dvojného integrálu určete obsah plochy. {x, y) R ; y x ; y 4 x ; y } Řešení: Obrázek 4: {x, y) R ; y x ; y 4 x ; y } S 4 x dy dx + 4 x dy dx x ) 4 x dx + 4 x + x ) dx ] ) [4x x + [x] ) Obsah plochy na obrázku 4 je 8 jednotek čtverečních. 88
90 54. Pomocí dvojného integrálu určete obsah plochy. {x, y) R ; y x; x 4; y } Řešení: Obrázek 44: {x, y) R ; y x; x 4; y } S 4 x dy dx 4 + x ) dx [ x + x ] Obsah plochy na obrázku 44 je 5 jednotek čtverečních. 89
91 55. Pomocí dvojného integrálu určete obsah plochy. { } x, y) R ; x 4 Řešení: S 4 tg x Obrázek 45: { x, y) R ; x 4 dy dx 4 tg xdx 4 sin x cos x dx t dt [ln t ] ln + ln ln } t cos x dt sin xdx x t x t 4 Obsah plochy na obrázku 45 je ln jednotek čtverečních. 9
92 5. Pomocí dvojného integrálu určete obsah plochy. {x, y) R ; x + y ; y ; x } Řešení: S Obrázek 4: {x, y) R ; x + y ; y ; x } x dy dx sin t cos tdt [t + sin t cos t] x sin t x dx dx cos tdt x t x t cos t cos tdt ) + 4 cos tdt Obsah plochy na obrázku 4 je 4 jednotek čtverečních. Poznámka: Integrál cos tdt, který se vyskytuje na konci druhého řádku ve výpočtu obsahu plochy, počítáme takto. cos tdt sin t ) dt dt sin tdt dt u sin t v sin t u cos t v cos t t + sin t cos t cos tdt 9
93 cos tdt t + sin t cos t + c cos tdt t + sin t cos t) + c 57. Pomocí dvojného integrálu určete obsah plochy. {x, y) R ; y sin x; y sin x; x } {x, y) R ; y sin x; y sin x; x } Řešení: Obrázek 47: nožina z příkladu č. 57 S sin x dy dx sin x sin x) dx sin xdx sin x [cos x] ) 4 Obsah plochy na obrázku 47 jsou 4 jednotky čtverečné. 9
94 58. Pomocí dvojného integrálu určete obsah plochy. { } x, y) R ; y cos x; y cos x; x { x, y) R ; y cos x; y cos x; x } { x, y) R ; y cos x; y cos x; x } Řešení: Obrázek 48: nožina z příkladu č. 58 S cos x dy dx + cos x dy dx + cos x dy dx cos x cos x cos x cos xdx cos xdx + cos xdx [sin x] [sin x] + [sin x] ) ) + )) 4 Obsah plochy na obrázku 48 je 4 jednotek čtverečních. 9
95 59. Pomocí dvojného integrálu určete obsah plochy. { } x, y) R ; y x ; y x ; y Řešení: S Obrázek 49: x x { x, y) R ; y x ; y x ; y } dy dx + ) x x dx + [ ] x x + 9 [ ) + 9 [x x 9 x dy dx ) x ] ) )] 8 dx Obsah plochy na obrázku 49 je 8 jednotek čtverečních. 94
96 . Pomocí dvojného integrálu určete obsah plochy. {x, y) R ; y x; y x ; x } Řešení: Obrázek 5: {x, y) R ; y x; y x ; x } S x x dy dx ) [ x + x x dx + x ] Obsah plochy na obrázku 5 je 4 jednotek čtverečních. 95
97 . Geometrická aplikace objemy těles Dvojné integrály můžeme využít například i k odvození nám známých vzorečků pro objem některých těles. Také pomocí nich můžeme přímo objem těles vypočítat. Výpočet objemů těles i postup pro odvození vzorečků si ukážeme v této kapitole. Objemy těles s podstavou, která je dána množinou v rovině xy) ohraničené shora částí grafu funkce f, budeme počítat pomocí vzorce V fx, y)dxdy. Pomocí dvojného integrálu spočítejte objem kvádru s podstavou o rozměrech 4 cm a výškou 5 cm. Řešení: Nejdříve si nakreslíme obrázek zadaného kvádru. Podle něho určíme integrační meze pro x a y. Obrázek 5: Zadaný kvádr 9
98 Nyní začneme počítat objem kvádru podle vzorce V fx, y)dxdy. Dvojný integrál si přepíšeme na dvojnásobný podle věty Fubiniova pro obdélník) a fx, y) je v tomto případě konstantní funkce, jejíž graf leží ve výšce pěti jednotek nad rovinou xy), tj. fx, y) 5. V tomto případě záleží na nás, podle které proměnné začneme integrovat, zvolíme tedy např. vnitřní integrál podle y a vnější podle x. V 4 5dy dx Funkci tedy zintegrujeme podle proměnné y a následně použijeme Newton Leibnizův vzorec. 5 [y] 4 dx dx Poté vypočítáme jednoduchý integrál podle proměnné x a za pomocí Newton Leibnizova vzorce dopočteme námi požadovaný objem kvádru. [x] cm Objem kvádru na obrázku 5 je cm. Pro ověření výsledku si objem kvádru můžeme vypočítat i pomocí známého vzorce V a b c, kde a, b, c R jsou délky jeho hran. V a b c 4 5 cm. 97
99 . Pomocí dvojného integrálu spočítejte objem válce s podstavou o poloměru cm a výškou 4 cm. Řešení: Než začneme počítat, nakreslíme si dva obrázky, a to válec i jeho podstavu, pomocí nichž určíme integrační meze. Podstavou bude kruh o poloměru. Obrázek 5: Vlevo: zadaný válec, vpravo: podstava válce Podle obrázku 5 vlevo určíme, že funkce fx, y) 4, protože je to výška válce. Z obrázku 5 vpravo vidíme, že integrační množina bude následující: { x, y) R ; x ; x y x }. Nyní již známe integrační meze a můžeme začít počítat objem válce pomocí dvojného integrálu. Námi určená množina je elementární vzhledem k proměnné x a z toho důvodu budeme nejprve integrovat podle proměnné y a x 98
100 budeme považovat za konstantu. Nejprve si však dvojný integrál přepíšeme na dvojnásobný. V x x 4dy dx Zintegrujeme podle y a upravíme pomocí Newton Leibnizova vzorce. 4 [y] x x 4 x dx Dále zavedeme substituci x sin t, čímž se nám následně změní integrační meze. x sin t dx cos tdt x t 8 x t sin t cos tdt 8 cos tdt Vypočteme jednoduchý integrál proměnné t a pomocí Newton Leibnizova vzorce dojdeme ke konečnému výsledku. 8 [t + sin t cos t] 4 + ) ) ) 4 cm Objem válce na obrázku 5 je 4 cm. Pro ověření výsledku si objem válce můžeme vypočítat i pomocí známého vzorce V r v, kde r R je poloměr podstavy válce a v R je výška válce. V r v 4 4 cm. 99
101 . Pomocí dvojného integrálu spočítejte objem krychle o délce hrany a cm. Řešení: Výpočet objemu krychle pomocí dvojného integrálu bude velmi obdobný, jako výpočet objemu kvádru. Pro znázornění si nejprve nakreslíme obrázek. Obrázek 5: Zadaná krychle Budeme integrovat na množině {x, y) R ; x ; ; y }. Za funkci fx, y) budeme považovat výšku krychle, neboli délku hrany a, tedy cm. Opět nezáleží na pořadí proměnných, podle kterých budeme integrovat, zkusíme to tedy naopak, než jak jsme počítali objem kvádru. Budeme nejprve integrovat podle x a následně podle y. Dvojný integrál si přepíšeme na dvojnásobný podle věty Fubiniova pro obdélník). V dx dy Zintegrujeme podle x a použijeme Newton Leibnizův vzorec pro úpravu.
102 [x] dy 9dy Na závěr vypočteme jednoduchý integrál proměnné y a upravíme podle Newton Leibnizova vzorce. Tím dojdeme ke konečnému výsledku. 9 [y] 7 cm Objem krychle na obrázku 5 je 7 cm. Pro ověření výsledku si objem krychle můžeme vypočítat i pomocí známého vzorce V a, kde a R je délka hrany krychle. V a 7 cm. Poznámka: Pomocí dvojného integrálu můžeme také odvodit objem krychle o jakékoli délce hrany a: V a a ady dx a a [y] a dx a a dx a [x] a a
103 7. Zadávání dvojných integrálů do programu Wolfram athematica V této kapitole si ukážeme, jak používat program athematica od společnosti Wolfram Research na výpočet dvojných integrálů. To nám velmi usnadní jejich počítání. Navážeme na příklady, které jsme si již vypočítali v předchozích kapitolách, čímž si také ověříme, že jsme počítali správně. Abychom mohli program athematica používat, musíme vlastnit licenci, kterou je možno zakoupit na stránkách výrobce [8] a pro studenty je dostupná na některých školách zdarma. Také je možné využít zkušební verzi programu zdarma, která je opět dostupná ke stažení na stránkách výrobce [8]. Po zapnutí programu se nám objeví následující okno - obrázek 54. Obrázek 54: Úvodní okno při zapnutí programu Zde klikneme na tlačítko Create New Notebook a tím otevřeme naši pracovní plochu obrázek 55), do které budeme zadávat příkazy.
104 Obrázek 55: Pracovní plocha programu Jednoduché i dvojné integrály zadáváme do programu příkazem Integrate. Dále píšeme do hranatých závorek funkci, kterou chceme vypočítat, a zadané integrační meze. Ty zapisujeme do složených závorek. Vždy napíšeme do složené závorky proměnnou, podle které integrujeme a meze, pak i druhou proměnnou a opět její integrační meze. Vše od sebe oddělujeme čárkami. Nakonec zmáčkneme kombinaci kláves Shift+Enter a zobrazí se nám výsledek jako výstup Out. Nejprve si zadáme do programu athematica příklad 5 z kapitoly, a to následujícím způsobem:
105 Na zadání příkladu si ukážeme, že athematica zvládá vypočítat i dvojné integrály na elementárních množinách. Integrační meze si ovšem musíme určit sami, nestačí zadat integrační množinu, kterou dostaneme v zadání příkladu. Nejdřív si tedy vypočítáme integrační meze a poté zadáme integrál do programu takto: Vidíme, že výsledky jsou v obou příkladech stejné, jako ty, které jsme vypočítali výše, tudíž máme ověřenu jejich správnost. Dále je nutno říci, že goniometrické funkce zadáváme do programu athematica příkazy Sin, Cos, Tan, Cot a jejich argumenty píšeme do hranatých závorek přímo za ně. Symbol píšeme příkazem Pi, přirozený logaritmus příkazem Log, dekadický logaritmus Log a odmocninu zapíšeme jako Sqrt. Jejich argumenty budou také vždy v hranatých závorkách. Absolutní hodnotu píšeme příkazem Abs a její argument zadáváme opět do hranaté závorky. Všechny grafy, které jsou obsaženy v této bakalářské práci, byly vykresleny také pomocí programu athematica. Proto si zde ukážeme i návod na jejich vytvoření, a to na příkladu 44. Integrační množinu tohoto příkladu nám athematica vykreslí, když do ní zadáme tento příkaz: 4
106 Začínáme nadefinováním funkcí, které potřebujeme vykreslit. Potom si vykreslíme grafy těchto funkcí příkazem Plot. Do hranaté závorky píšeme vlastnosti grafu, například příkaz PlotRange určuje, v jakém intervalu se bude pohybovat graf na ose y. Do příkazu PlotStyle vepisujeme do hranaté závorky parametry, jako například barvu nebo tloušťku grafu funkce. Protože si zde definujeme grafy funkcí, a to g, g a g, vykreslí se nám všechny, každý do zvláštního obrázku - Out[], Out[4], Out[5]. Příkazem Show potom vykreslíme všechny grafy do jednoho obrázku a máme celou naši integrační množinu. Tu nám znázorňuje poslední, čtvrtý obrázek - Out[]. Za příkaz Show píšeme do hranaté závorky parametry, které nám určují vlastnosti posledního grafu - Out[]. Těmi jsou například tloušťka os, velikost popisků os a další. 5
Substituce ve vícenásobném integrálu verze 1.1
 Úvod Substituce ve vícenásobném integrálu verze. Následující text popisuje výpočet vícenásobných integrálů pomocí věty o substituci. ěl by sloužit především studentům předmětu ATEAT k přípravě na zkoušku.
Úvod Substituce ve vícenásobném integrálu verze. Následující text popisuje výpočet vícenásobných integrálů pomocí věty o substituci. ěl by sloužit především studentům předmětu ATEAT k přípravě na zkoušku.
Dvojné a trojné integrály příklad 3. x 2 y dx dy,
 Spočtěte = { x, y) ; 4x + y 4 }. Dvojné a trojné integrály příklad 3 x y dx dy, Řešení: Protože obor integrace je symetrický vzhledem k ose x, tj. vzhledem k substituci [x; y] [x; y], a funkce fx, y) je
Spočtěte = { x, y) ; 4x + y 4 }. Dvojné a trojné integrály příklad 3 x y dx dy, Řešení: Protože obor integrace je symetrický vzhledem k ose x, tj. vzhledem k substituci [x; y] [x; y], a funkce fx, y) je
Kapitola 7: Neurčitý integrál. 1/14
 Kapitola 7: Neurčitý integrál. 1/14 Neurčitý integrál 2/14 Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní
Kapitola 7: Neurčitý integrál. 1/14 Neurčitý integrál 2/14 Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní
Obsah. Aplikovaná matematika I. Gottfried Wilhelm Leibniz. Základní vlastnosti a vzorce
 Neurčitý integrál Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah Primitivní funkce, neurčitý integrál Základní vlastnosti a vzorce Základní integrační metody Úpravy integrandu Integrace racionálních
Neurčitý integrál Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah Primitivní funkce, neurčitý integrál Základní vlastnosti a vzorce Základní integrační metody Úpravy integrandu Integrace racionálních
10. cvičení z Matematické analýzy 2
 . cvičení z Matematické analýzy 3. - 7. prosince 8. (dvojný integrál - Fubiniho věta Vhodným způsobem integrace spočítejte daný integrál a načrtněte oblast integrace (a (b (c y ds, kde : y & y 4. e ma{,y
. cvičení z Matematické analýzy 3. - 7. prosince 8. (dvojný integrál - Fubiniho věta Vhodným způsobem integrace spočítejte daný integrál a načrtněte oblast integrace (a (b (c y ds, kde : y & y 4. e ma{,y
Kapitola 7: Integrál.
 Kapitola 7: Integrál. Neurčitý integrál. Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f(x) x I nazýváme primitivní funkcí k funkci
Kapitola 7: Integrál. Neurčitý integrál. Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f(x) x I nazýváme primitivní funkcí k funkci
11. cvičení z Matematické analýzy 2
 11. cvičení z Matematické analýzy 11. - 15. prosince 17 11.1 (trojný integrál - Fubiniho věta) Vypočtěte (i) xyz dv, kde je ohraničeno plochami y x, x y, z xy a z. (ii) y dv, kde je ohraničeno shora rovinou
11. cvičení z Matematické analýzy 11. - 15. prosince 17 11.1 (trojný integrál - Fubiniho věta) Vypočtěte (i) xyz dv, kde je ohraničeno plochami y x, x y, z xy a z. (ii) y dv, kde je ohraničeno shora rovinou
V. Riemannův(dvojný) integrál
 V. Riemannův(dvojný) integrál Obsah 1 Základní pojmy a definice 2 2 Podmínky existence dvojného integrálu 4 3 Vlastnosti dvojného integrálu 4 4 Výpočet dvojného integrálu; převod na dvojnásobný integrál
V. Riemannův(dvojný) integrál Obsah 1 Základní pojmy a definice 2 2 Podmínky existence dvojného integrálu 4 3 Vlastnosti dvojného integrálu 4 4 Výpočet dvojného integrálu; převod na dvojnásobný integrál
Kapitola 7: Integrál. 1/17
 Kapitola 7: Integrál. 1/17 Neurčitý integrál - Motivační příklad 2/17 Příklad: Necht se bod pohybuje po přímce rychlostí a) v(t) = 3 [m/s] (rovnoměrný přímočarý pohyb), b) v(t) = 2t [m/s] (rovnoměrně zrychlený
Kapitola 7: Integrál. 1/17 Neurčitý integrál - Motivační příklad 2/17 Příklad: Necht se bod pohybuje po přímce rychlostí a) v(t) = 3 [m/s] (rovnoměrný přímočarý pohyb), b) v(t) = 2t [m/s] (rovnoměrně zrychlený
= 0,1 1,3. je oblast ohraničená přímkami =, =, =0 :0 1, : =2, =, =1
 ŘEŠENÉ PŘÍKLADY Z MB ČÁST Příklad 1 Vypočtěte integrály a) b) c) d) e) f) g) h) i) j),, = 0,1 1,3 je oblast ohraničená přímkami =,=,=0 1+, :=0,=1,=1,= +3, :=0,=,=0,=1 sin+, 3,,,, :=0,=,= : + 4 : =4+,+3=0
ŘEŠENÉ PŘÍKLADY Z MB ČÁST Příklad 1 Vypočtěte integrály a) b) c) d) e) f) g) h) i) j),, = 0,1 1,3 je oblast ohraničená přímkami =,=,=0 1+, :=0,=1,=1,= +3, :=0,=,=0,=1 sin+, 3,,,, :=0,=,= : + 4 : =4+,+3=0
Petr Hasil. Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
 Neurčitý integrál Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Neurčitý integrál Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Kapitola 8: Dvojný integrál 1/26
 Kapitola 8: vojný integrál 1/26 vojný integrál - osnova kapitoly 2/26 dvojný integrál přes obdélník definice výpočet (Fubiniova věta pro obdélník) dvojný integrál přes standardní množinu definice výpočet
Kapitola 8: vojný integrál 1/26 vojný integrál - osnova kapitoly 2/26 dvojný integrál přes obdélník definice výpočet (Fubiniova věta pro obdélník) dvojný integrál přes standardní množinu definice výpočet
PŘEDNÁŠKA 6 INTEGRACE POMOCÍ SUBSTITUCE
 PŘEDNÁŠKA 6 INTEGRACE POMOCÍ SUBSTITUCE Příklad Představme si, že máme vypočítat integrál I = f(, y) d dy, M kde M = {(, y) R 2 1 < 2 + y 2 < 4}. y M je mezikruží mezi kružnicemi o poloměru 1 a 2 a se
PŘEDNÁŠKA 6 INTEGRACE POMOCÍ SUBSTITUCE Příklad Představme si, že máme vypočítat integrál I = f(, y) d dy, M kde M = {(, y) R 2 1 < 2 + y 2 < 4}. y M je mezikruží mezi kružnicemi o poloměru 1 a 2 a se
Příklady pro předmět Aplikovaná matematika (AMA) část 1
 Příklady pro předmět plikovaná matematika (M) část 1 1. Lokální extrémy funkcí dvou a tří proměnných Nalezněte lokální extrémy funkcí: (a) f 1 : f 1 (x, y) = x 3 3x + y 2 + 2y (b) f 2 : f 2 (x, y) = 1
Příklady pro předmět plikovaná matematika (M) část 1 1. Lokální extrémy funkcí dvou a tří proměnných Nalezněte lokální extrémy funkcí: (a) f 1 : f 1 (x, y) = x 3 3x + y 2 + 2y (b) f 2 : f 2 (x, y) = 1
Funkce jedné reálné proměnné. lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou
 Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
1. Několik základních pojmů ze středoškolské matematiky. Na začátku si připomeneme následující pojmy:
 Opakování středoškolské matematiky Slovo úvodem: Tato pomůcka je určena zejména těm studentům presenčního i kombinovaného studia na VŠFS, kteří na středních školách neprošli dostatečnou průpravou z matematiky
Opakování středoškolské matematiky Slovo úvodem: Tato pomůcka je určena zejména těm studentům presenčního i kombinovaného studia na VŠFS, kteří na středních školách neprošli dostatečnou průpravou z matematiky
arcsin x 2 dx. x dx 4 x 2 ln 2 x + 24 x ln 2 x + 9x dx.
 Neurčitý integrál arcsin. Integrál najdeme integrací per partes. Pomocí této metody dostaneme arcsin = arcsin 4 = arcsin + 4 + C, (,. ln + 4 ln + 9. Tento integrál lze převést substitucí ln = y na integrál
Neurčitý integrál arcsin. Integrál najdeme integrací per partes. Pomocí této metody dostaneme arcsin = arcsin 4 = arcsin + 4 + C, (,. ln + 4 ln + 9. Tento integrál lze převést substitucí ln = y na integrál
Neurčitý integrál. Robert Mařík. 4. března 2012
 Neurčitý integrál Robert Mařík 4. března 0 V tomto souboru jsou vysvětleny a na příkladech s postupným řešením demonstrovány základní integrační metody. Ikonka za integrálem načte integrál do online aplikace
Neurčitý integrál Robert Mařík 4. března 0 V tomto souboru jsou vysvětleny a na příkladech s postupným řešením demonstrovány základní integrační metody. Ikonka za integrálem načte integrál do online aplikace
PŘÍKLADY K MATEMATICE 3 - VÍCENÁSOBNÉ INTEGRÁLY. x 2. 3+y 2
 PŘÍKLADY K ATEATICE 3 - VÍCENÁSOBNÉ INTEGRÁLY ZDENĚK ŠIBRAVA.. Dvojné integrály.. Vícenásobné intergrály Příklad.. Vypočítejme dvojný integrál x 3 + y da, kde =, 3,. Řešení: Funkce f(x, y) = x je na obdélníku
PŘÍKLADY K ATEATICE 3 - VÍCENÁSOBNÉ INTEGRÁLY ZDENĚK ŠIBRAVA.. Dvojné integrály.. Vícenásobné intergrály Příklad.. Vypočítejme dvojný integrál x 3 + y da, kde =, 3,. Řešení: Funkce f(x, y) = x je na obdélníku
1 Integrální počet. 1.1 Neurčitý integrál. 1.2 Metody výpočtů neurčitých integrálů
 Integrální počet. Neurčitý integrál Neurčitým integrálem k dané funkci f() nazýváme takovou funkci F (), pro kterou platí, že f() = F (). Neboli integrálem funkce f() je taková funkce F (), ze které bychom
Integrální počet. Neurčitý integrál Neurčitým integrálem k dané funkci f() nazýváme takovou funkci F (), pro kterou platí, že f() = F (). Neboli integrálem funkce f() je taková funkce F (), ze které bychom
Příklad 1. Řešení 1a Máme určit obsah rovinné plochy ohraničené křivkami: ŘEŠENÉ PŘÍKLADY Z M1A ČÁST 14. a) =0, = 1, = b) =4, =0
 Příklad Určete obsah rovinné plochy ohraničené křivkami: a) =0,=,= b) =4,=0 c) =,=,=3,=0 d) =+, =0 e) + )=,= f) = +4,+= g) =arcsin,=0,= h) =sin,=0, 0; i) =,=,=4,=0 j) =,= k) = 6,= +5 4 l) =4,+=5 m) = +
Příklad Určete obsah rovinné plochy ohraničené křivkami: a) =0,=,= b) =4,=0 c) =,=,=3,=0 d) =+, =0 e) + )=,= f) = +4,+= g) =arcsin,=0,= h) =sin,=0, 0; i) =,=,=4,=0 j) =,= k) = 6,= +5 4 l) =4,+=5 m) = +
Určete a graficky znázorněte definiční obor funkce
 Určete a grafick znázorněte definiční obor funkce Příklad. z = ln( + ) Řešení: Vpíšeme omezující podmínk pro jednotlivé části funkce. Jmenovatel zlomku musí být 0, logaritmická funkce je definovaná pro
Určete a grafick znázorněte definiční obor funkce Příklad. z = ln( + ) Řešení: Vpíšeme omezující podmínk pro jednotlivé části funkce. Jmenovatel zlomku musí být 0, logaritmická funkce je definovaná pro
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
II. 3. Speciální integrační metody
 48 II. Integrální počet funkcí jedné proměnné II.. Speciální integrační metody Integrály typu f ( x, r x, r x,..., r k x ), tj. integrály obsahující proměnnou x pod odmocninou, kde k N a r,..., r k jsou
48 II. Integrální počet funkcí jedné proměnné II.. Speciální integrační metody Integrály typu f ( x, r x, r x,..., r k x ), tj. integrály obsahující proměnnou x pod odmocninou, kde k N a r,..., r k jsou
Matematika II: Pracovní listy do cvičení
 Matematika II: Pracovní listy do cvičení Radomír Paláček, Petra Schreiberová, Petr Volný Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Příklady Integrální počet funkcí
Matematika II: Pracovní listy do cvičení Radomír Paláček, Petra Schreiberová, Petr Volný Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Příklady Integrální počet funkcí
Úvod. Integrování je inverzní proces k derivování Máme zderivovanou funkci a integrací získáme původní funkci kterou jsme derivovali
 NEURČITÝ INTEGRÁL Úvod Integrování je inverzní proces k derivování Máme zderivovanou funkci a integrací získáme původní funkci kterou jsme derivovali Umět pracovat s integrálním počtem Je důležité pro
NEURČITÝ INTEGRÁL Úvod Integrování je inverzní proces k derivování Máme zderivovanou funkci a integrací získáme původní funkci kterou jsme derivovali Umět pracovat s integrálním počtem Je důležité pro
Diferenciální rovnice 1
 Diferenciální rovnice 1 Základní pojmy Diferenciální rovnice n-tého řádu v implicitním tvaru je obecně rovnice ve tvaru,,,, = Řád diferenciální rovnice odpovídá nejvyššímu stupni derivace v rovnici použitému.
Diferenciální rovnice 1 Základní pojmy Diferenciální rovnice n-tého řádu v implicitním tvaru je obecně rovnice ve tvaru,,,, = Řád diferenciální rovnice odpovídá nejvyššímu stupni derivace v rovnici použitému.
, = , = , = , = Pokud primitivní funkci pro proměnnou nevidíme, pomůžeme si v tuto chvíli jednoduchou substitucí = +2 +1, =2 1 = 1 2 1
 ŘEŠENÉ PŘÍKLADY Z MB ČÁST 7 Příklad 1 a) Vypočtěte hmotnost oblasti ohraničené přímkami =1,=3,=1,= jestliže její hustota je dána funkcí 1,= ++1 b) Vypočtěte statický moment čtverce ohraničeného přímkami
ŘEŠENÉ PŘÍKLADY Z MB ČÁST 7 Příklad 1 a) Vypočtěte hmotnost oblasti ohraničené přímkami =1,=3,=1,= jestliže její hustota je dána funkcí 1,= ++1 b) Vypočtěte statický moment čtverce ohraničeného přímkami
1. Náhodný vektor (X, Y ) má diskrétní rozdělení s pravděpodobnostní funkcí p, kde. p(x, y) = a(x + y + 1), x, y {0, 1, 2}.
 VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
má spojité parciální derivace druhého řádu ve všech bodech této množiny. Výpočtem postupně dostaneme: y = 9xy2 + 2,
 4. Parciální derivace a diferenciál. řádu 0-a3b/4dvr.tex Příklad. Určete parciální derivace druhého řádu funkce f v obecném bodě a v daných bodech. Napište obecný tvar. diferenciálu, jeho hodnotu v daných
4. Parciální derivace a diferenciál. řádu 0-a3b/4dvr.tex Příklad. Určete parciální derivace druhého řádu funkce f v obecném bodě a v daných bodech. Napište obecný tvar. diferenciálu, jeho hodnotu v daných
( ) ( ) Vzorce pro dvojnásobný úhel. π z hodnot goniometrických funkcí. Předpoklady: Začneme příkladem.
 Vzorce pro dvojnásobný úhel Předpoklady: 0 Začneme příkladem Př : Pomocí součtových vzorců odvoď vzorec pro sin x sin x sin x + x sin x cos x + cos x sin x sin x cos x Př : Pomocí součtových vzorců odvoď
Vzorce pro dvojnásobný úhel Předpoklady: 0 Začneme příkladem Př : Pomocí součtových vzorců odvoď vzorec pro sin x sin x sin x + x sin x cos x + cos x sin x sin x cos x Př : Pomocí součtových vzorců odvoď
Diferenciální počet funkcí více proměnných
 Vysoké učení technické v Brně Fakulta strojního inženýrství Diferenciální počet funkcí více proměnných Doc RNDr Miroslav Doupovec, CSc Neřešené příklady Matematika II OBSAH Obsah I Diferenciální počet
Vysoké učení technické v Brně Fakulta strojního inženýrství Diferenciální počet funkcí více proměnných Doc RNDr Miroslav Doupovec, CSc Neřešené příklady Matematika II OBSAH Obsah I Diferenciální počet
Matematika vzorce. Ing. Petr Šídlo. verze
 Matematika vzorce Ing. Petr Šídlo verze 0050409 Obsah Jazyk matematiky 3. Výrokový počet.......................... 3.. Logické spojky...................... 3.. Tautologie výrokového počtu...............
Matematika vzorce Ing. Petr Šídlo verze 0050409 Obsah Jazyk matematiky 3. Výrokový počet.......................... 3.. Logické spojky...................... 3.. Tautologie výrokového počtu...............
Obsah Obyčejné diferenciální rovnice
 Obsah 1 Obyčejné diferenciální rovnice 3 1.1 Základní pojmy............................................ 3 1.2 Obyčejné diferenciální rovnice 1. řádu................................ 5 1.3 Exaktní rovnice............................................
Obsah 1 Obyčejné diferenciální rovnice 3 1.1 Základní pojmy............................................ 3 1.2 Obyčejné diferenciální rovnice 1. řádu................................ 5 1.3 Exaktní rovnice............................................
VKM/IM /2015. Zintegrujte. f (x, y) dx dy = f (x, y) = (y x) 2, Ω : x 2 + y 2 4, x 0.
 VKM/IM - 4/5 Zintegrujte f, y) d dy pro f, y) y ), : + y 4,. Řešení: S využitím postupů a výsledků použitých při řešení příkladů z předchozí části věnované dvojnému integrálu, se můžeme bez obav pustit
VKM/IM - 4/5 Zintegrujte f, y) d dy pro f, y) y ), : + y 4,. Řešení: S využitím postupů a výsledků použitých při řešení příkladů z předchozí části věnované dvojnému integrálu, se můžeme bez obav pustit
Integrální počet - I. část (neurčitý integrál a základní integrační metody)
 Integrální počet - I. část (neurčitý integrál a základní integrační metody) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 6. přednáška z AMA Michal Fusek (fusekmi@feec.vutbr.cz) / 23 Obsah
Integrální počet - I. část (neurčitý integrál a základní integrační metody) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 6. přednáška z AMA Michal Fusek (fusekmi@feec.vutbr.cz) / 23 Obsah
MATEMATIKA II V PŘÍKLADECH
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ MATEMATIKA II V PŘÍKLADECH CVIČENÍ Č. Ing. Petra Schreiberová, Ph.D. Ostrava 0 Ing. Petra Schreiberová, Ph.D. Vysoká škola báňská Technická
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ MATEMATIKA II V PŘÍKLADECH CVIČENÍ Č. Ing. Petra Schreiberová, Ph.D. Ostrava 0 Ing. Petra Schreiberová, Ph.D. Vysoká škola báňská Technická
CVIČNÝ TEST 10. OBSAH I. Cvičný test 2. Mgr. Renáta Koubková. II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19
 CVIČNÝ TEST 10 Mgr. Renáta Koubková OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Pro x R řešte rovnici: 5 x 1 + 5 x + 5 x + 3 = 3 155. 2 Za předpokladu
CVIČNÝ TEST 10 Mgr. Renáta Koubková OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Pro x R řešte rovnici: 5 x 1 + 5 x + 5 x + 3 = 3 155. 2 Za předpokladu
CVIČNÝ TEST 15. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C)
 VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
1 Neurčitý integrál 1.1 NEURČITÝ INTEGRÁL
 1 Neurčitý integrál 1.1 NEURČITÝ INTEGRÁL V předchozím semestru jsme se seznámili s derivováním funkcí. Nyní se přesuneme k integrování funkce, což je vlastně zpětný proces k derivaci. Ukážeme si, jakým
1 Neurčitý integrál 1.1 NEURČITÝ INTEGRÁL V předchozím semestru jsme se seznámili s derivováním funkcí. Nyní se přesuneme k integrování funkce, což je vlastně zpětný proces k derivaci. Ukážeme si, jakým
2. DVOJROZMĚRNÝ (DVOJNÝ) INTEGRÁL
 . VOJROZMĚRNÝ (VOJNÝ) INTEGRÁL Úvodem připomenutí základních integračních vzorců, bez nichž se neobejdete: [.] d = C [.] d = + C n+ n [.] d = + C n + [4.] d = ln + C [5.] sin d = cos + C [6.] cos d = sin
. VOJROZMĚRNÝ (VOJNÝ) INTEGRÁL Úvodem připomenutí základních integračních vzorců, bez nichž se neobejdete: [.] d = C [.] d = + C n+ n [.] d = + C n + [4.] d = ln + C [5.] sin d = cos + C [6.] cos d = sin
KOMPLEXNÍ ČÍSLA INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ
 KOMPLEXNÍ ČÍSLA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu INVESTICE
KOMPLEXNÍ ČÍSLA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu INVESTICE
INTEGRÁLY S PARAMETREM
 INTEGRÁLY S PARAMETREM b a V kapitole o integraci funkcí více proměnných byla potřeba funkce g(x) = f(x, y) dy proměnné x. Spojitost funkce g(x) = b a f(x, y) dy proměnné x znamená vlastně prohození limity
INTEGRÁLY S PARAMETREM b a V kapitole o integraci funkcí více proměnných byla potřeba funkce g(x) = f(x, y) dy proměnné x. Spojitost funkce g(x) = b a f(x, y) dy proměnné x znamená vlastně prohození limity
Úvodní informace. 17. února 2018
 Úvodní informace Funkce více proměnných Přednáška první 17. února 2018 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Limita a spojitost Derivace, diferencovatelnost, diferenciál Úvodní
Úvodní informace Funkce více proměnných Přednáška první 17. února 2018 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Limita a spojitost Derivace, diferencovatelnost, diferenciál Úvodní
Diferenciální počet 1 1. f(x) = ln arcsin 1 + x 1 x. 1 x 1 a x 1 0. f(x) = (cos x) cosh x + 3x. x 0 je derivace funkce f(x) v bodě x0.
 Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
Nalezněte definiční obor funkce Diferenciální počet f = ln arcsin + Definiční obor funkce f je určen vztahy Z těchto nerovností plyne < + ln arcsin + je tedy D f =, Určete definiční obor funkce arcsin
7. Integrál přes n-rozměrný interval
 7. Integrál přes n-rozměrný interval Studijní text 7. Integrál přes n-rozměrný interval Definice 7.1. Buď A = a 1, b 1 a n, b n R n n-rozměrný uzavřený interval a f : R n R funkce ohraničená na A Df. Definujme
7. Integrál přes n-rozměrný interval Studijní text 7. Integrál přes n-rozměrný interval Definice 7.1. Buď A = a 1, b 1 a n, b n R n n-rozměrný uzavřený interval a f : R n R funkce ohraničená na A Df. Definujme
Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
7. Derivace složené funkce. Budeme uvažovat složenou funkci F = f(g), kde některá z jejich součástí
 202-m3b2/cvic/7slf.tex 7. Derivace složené funkce. Budeme uvažovat složenou funkci F = fg, kde některá z jejich součástí může být funkcí více proměnných. Předpokládáme, že uvažujeme funkce, které mají
202-m3b2/cvic/7slf.tex 7. Derivace složené funkce. Budeme uvažovat složenou funkci F = fg, kde některá z jejich součástí může být funkcí více proměnných. Předpokládáme, že uvažujeme funkce, které mají
Hledáme lokální extrémy funkce vzhledem k množině, která je popsána jednou či několika rovnicemi, vazebními podmínkami. Pokud jsou podmínky
 6. Vázané a absolutní extrémy. 01-a3b/6abs.tex Hledáme lokální extrémy funkce vzhledem k množině, která je popsána jednou či několika rovnicemi, vazebními podmínkami. Pokud jsou podmínky jednoduché, vyřešíme
6. Vázané a absolutní extrémy. 01-a3b/6abs.tex Hledáme lokální extrémy funkce vzhledem k množině, která je popsána jednou či několika rovnicemi, vazebními podmínkami. Pokud jsou podmínky jednoduché, vyřešíme
Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
4.3.3 Goniometrické nerovnice
 4 Goniometrické nerovnice Předpoklady: 40 Pedagogická poznámka: Nerovnice je stejně jako rovnice možné řešit grafem i jednotkovou kružnicí Oba způsoby mají své výhody i nevýhody a jsou v podstatě rovnocenné
4 Goniometrické nerovnice Předpoklady: 40 Pedagogická poznámka: Nerovnice je stejně jako rovnice možné řešit grafem i jednotkovou kružnicí Oba způsoby mají své výhody i nevýhody a jsou v podstatě rovnocenné
[obrázek γ nepotřebujeme, interval t, zřejmý, integrací polynomu a per partes vyjde: (e2 + e) + 2 ln 2. (e ln t = t) ] + y2
![[obrázek γ nepotřebujeme, interval t, zřejmý, integrací polynomu a per partes vyjde: (e2 + e) + 2 ln 2. (e ln t = t) ] + y2 [obrázek γ nepotřebujeme, interval t, zřejmý, integrací polynomu a per partes vyjde: (e2 + e) + 2 ln 2. (e ln t = t) ] + y2](/thumbs/102/153207878.jpg) 4.1 Křivkový integrál ve vektrovém poli přímým výpočtem 4.1 Spočítejte práci síly F = y i + z j + x k při pohybu hmotného bodu po orientované křivce, která je dána jako oblouk ABC na průnikové křivce ploch
4.1 Křivkový integrál ve vektrovém poli přímým výpočtem 4.1 Spočítejte práci síly F = y i + z j + x k při pohybu hmotného bodu po orientované křivce, která je dána jako oblouk ABC na průnikové křivce ploch
Obecná rovnice kvadratické funkce : y = ax 2 + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených funkcí je množina reálných čísel.
 5. Funkce 9. ročník 5. Funkce ZOPAKUJTE SI : 8. ROČNÍK KAPITOLA. Funkce. 5.. Kvadratická funkce Obecná rovnice kvadratické funkce : y = ax + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených
5. Funkce 9. ročník 5. Funkce ZOPAKUJTE SI : 8. ROČNÍK KAPITOLA. Funkce. 5.. Kvadratická funkce Obecná rovnice kvadratické funkce : y = ax + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených
Vzdělávací materiál. vytvořený v projektu OP VK CZ.1.07/1.5.00/34.0211. Anotace. Integrální počet VY_32_INOVACE_M0308. Matematika
 Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 0 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ..07/.5.00/3.0 Zlepšení podmínek pro
Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 0 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ..07/.5.00/3.0 Zlepšení podmínek pro
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU
 PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
Q(y) dy = P(x) dx + C.
 Cíle Naše nejbližší cíle spočívají v odpovědích na základní otázky, které si klademe v souvislosti s diferenciálními rovnicemi: 1. Má rovnice řešení? 2. Kolik je řešení a jakého jsou typu? 3. Jak se tato
Cíle Naše nejbližší cíle spočívají v odpovědích na základní otázky, které si klademe v souvislosti s diferenciálními rovnicemi: 1. Má rovnice řešení? 2. Kolik je řešení a jakého jsou typu? 3. Jak se tato
1. a) Určete parciální derivace prvního řádu funkce z = z(x, y) dané rovnicí z 3 3xy 8 = 0 v
 . a) Určete parciální derivace prvního řádu funkce z = z(x, y) dané rovnicí z xy 8 = v bodě A =, ]. b) e grafu funkce f najděte tečnou rovinu, která je rovnoběžná s rovinou ϱ. f(x, y) = x + y x, ϱ : x
. a) Určete parciální derivace prvního řádu funkce z = z(x, y) dané rovnicí z xy 8 = v bodě A =, ]. b) e grafu funkce f najděte tečnou rovinu, která je rovnoběžná s rovinou ϱ. f(x, y) = x + y x, ϱ : x
MATEMATIKA III. Olga Majlingová. Učební text pro prezenční studium. Předběžná verze
 Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
PRIMITIVNÍ FUNKCE. Primitivní funkce primitivní funkce. geometrický popis integrály 1 integrály 2 spojité funkce konstrukce prim.
 PRIMITIVNÍ FUNKCE V předchozích částech byly zkoumány derivace funkcí a hlavním tématem byly funkce, které derivace mají. V této kapitole se budou zkoumat funkce, které naopak jsou derivacemi jiných funkcí
PRIMITIVNÍ FUNKCE V předchozích částech byly zkoumány derivace funkcí a hlavním tématem byly funkce, které derivace mají. V této kapitole se budou zkoumat funkce, které naopak jsou derivacemi jiných funkcí
Definice Řekneme, že funkce z = f(x,y) je v bodě A = [x 0,y 0 ] diferencovatelná, nebo. z f(x 0 + h,y 0 + k) f(x 0,y 0 ) = Ah + Bk + ρτ(h,k),
![Definice Řekneme, že funkce z = f(x,y) je v bodě A = [x 0,y 0 ] diferencovatelná, nebo. z f(x 0 + h,y 0 + k) f(x 0,y 0 ) = Ah + Bk + ρτ(h,k), Definice Řekneme, že funkce z = f(x,y) je v bodě A = [x 0,y 0 ] diferencovatelná, nebo. z f(x 0 + h,y 0 + k) f(x 0,y 0 ) = Ah + Bk + ρτ(h,k),](/thumbs/62/47835194.jpg) Definice 5.2.1. Řekneme, že funkce z = f(x,y) je v bodě A = [x 0,y 0 ] diferencovatelná, nebo má v tomto bodě totální diferenciál, jestliže je možné její přírůstek z na nějakém okolí bodu A vyjádřit jako
Definice 5.2.1. Řekneme, že funkce z = f(x,y) je v bodě A = [x 0,y 0 ] diferencovatelná, nebo má v tomto bodě totální diferenciál, jestliže je možné její přírůstek z na nějakém okolí bodu A vyjádřit jako
12 Trojný integrál - Transformace integrálů
 Trojný integrál transformace integrálů) - řešené příklady 8 Trojný integrál - Transformace integrálů. Příklad Spočtěte x + y dxdydz, kde : z, x + y. Řešení Integrační obor určený vztahy z, x + y je válec.
Trojný integrál transformace integrálů) - řešené příklady 8 Trojný integrál - Transformace integrálů. Příklad Spočtěte x + y dxdydz, kde : z, x + y. Řešení Integrační obor určený vztahy z, x + y je válec.
Integrální počet - II. část (další integrační postupy pro některé typy funkcí)
 Integrální počet - II. část (další integrační postupy pro některé typy funkcí) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 7. přednáška z AMA1 Michal Fusek (fusekmi@feec.vutbr.cz) 1 /
Integrální počet - II. část (další integrační postupy pro některé typy funkcí) Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 7. přednáška z AMA1 Michal Fusek (fusekmi@feec.vutbr.cz) 1 /
PRIMITIVNÍ FUNKCE DEFINICE A MOTIVACE
 PIMITIVNÍ FUNKCE V předchozích částech byly zkoumány derivace funkcí a hlavním tématem byly funkce, které derivace mají. V této kapitole se budou zkoumat funkce, které naopak jsou derivacemi jiných funkcí
PIMITIVNÍ FUNKCE V předchozích částech byly zkoumány derivace funkcí a hlavním tématem byly funkce, které derivace mají. V této kapitole se budou zkoumat funkce, které naopak jsou derivacemi jiných funkcí
Matematická analýza III.
 2. Parciální derivace Miroslav Hušek, Lucie Loukotová UJEP 2010 Parciální derivace jsou zobecněním derivace funkce jedné proměnné. V této kapitole poznáme jejich základní vlastnosti a využití. Co bychom
2. Parciální derivace Miroslav Hušek, Lucie Loukotová UJEP 2010 Parciální derivace jsou zobecněním derivace funkce jedné proměnné. V této kapitole poznáme jejich základní vlastnosti a využití. Co bychom
4 Integrální počet funkcí více reálných proměnných
 Dvojné integrály - 61-4 ntegrální počet funkcí více reálných proměnných 4.1 Dvojné a dvojnásobné integrály Dvojné a dvojnásobné integrály na intervalech z Pod uzavřeným intervalem z rozumíme kartézský
Dvojné integrály - 61-4 ntegrální počet funkcí více reálných proměnných 4.1 Dvojné a dvojnásobné integrály Dvojné a dvojnásobné integrály na intervalech z Pod uzavřeným intervalem z rozumíme kartézský
Derivace funkcí více proměnných
 Derivace funkcí více proměnných Pro studenty FP TUL Martina Šimůnková 16. května 019 1. Derivace podle vektoru jako funkce vektoru. Pro pevně zvolenou funkci f : R d R n a bod a R d budeme zkoumat zobrazení,
Derivace funkcí více proměnných Pro studenty FP TUL Martina Šimůnková 16. května 019 1. Derivace podle vektoru jako funkce vektoru. Pro pevně zvolenou funkci f : R d R n a bod a R d budeme zkoumat zobrazení,
Přijímací zkouška na navazující magisterské studium 2018
 Přijímací zkouška na navazující magisterské studium 208 Studijní program: Studijní obory: Matematika MA, MMIT, MMFT, MSTR, MNVM, MPMSE Varianta A Řešení příkladů pečlivě odůvodněte. Věnujte pozornost ověření
Přijímací zkouška na navazující magisterské studium 208 Studijní program: Studijní obory: Matematika MA, MMIT, MMFT, MSTR, MNVM, MPMSE Varianta A Řešení příkladů pečlivě odůvodněte. Věnujte pozornost ověření
2 Fyzikální aplikace. Předpokládejme, že f (x 0 ) existuje. Je-li f (x 0 ) vlastní, pak rovnice tečny ke grafu funkce f v bodě [x 0, f(x 0 )] je
![2 Fyzikální aplikace. Předpokládejme, že f (x 0 ) existuje. Je-li f (x 0 ) vlastní, pak rovnice tečny ke grafu funkce f v bodě [x 0, f(x 0 )] je 2 Fyzikální aplikace. Předpokládejme, že f (x 0 ) existuje. Je-li f (x 0 ) vlastní, pak rovnice tečny ke grafu funkce f v bodě [x 0, f(x 0 )] je](/thumbs/102/152847701.jpg) Derivace funkce a jej geometrický význam Je dána funkce f) 3 6 + 9 + a naším úkolem je určit směrnici tečny v bodě [; f)] Pro libovolné lze směrnici sečny danou body [; f)] a [; f)] spočítat jako f) f)
Derivace funkce a jej geometrický význam Je dána funkce f) 3 6 + 9 + a naším úkolem je určit směrnici tečny v bodě [; f)] Pro libovolné lze směrnici sečny danou body [; f)] a [; f)] spočítat jako f) f)
Příklad 1. Řešení 1a Máme vyšetřit lichost či sudost funkce ŘEŠENÉ PŘÍKLADY Z M1A ČÁST 3
 Příklad 1 Zjistěte, zda jsou dané funkce sudé nebo liché, případně ani sudé ani liché: a) =ln b) = c) = d) =4 +1 e) =sin cos f) =sin3+ cos+ Poznámka Všechny tyto úlohy řešíme tak, že argument funkce nahradíme
Příklad 1 Zjistěte, zda jsou dané funkce sudé nebo liché, případně ani sudé ani liché: a) =ln b) = c) = d) =4 +1 e) =sin cos f) =sin3+ cos+ Poznámka Všechny tyto úlohy řešíme tak, že argument funkce nahradíme
PROGRAMU 2. Obvod D je dán součtem velikostí všech tří stran D=a+b+c= =23.07
 VZOROVÉ ŘEŠENÍ A VYSVĚTLENÍ PROGRAMU. Ing. Marek Nikodým Ph.D. Katedra matematiky a deskriptívní geometrie VŠB-TU Ostrava 1 Výpočty v trojúhelníku Je dán trojúhelník ABC v prostoru A[, 3, 3], B[4, 5, ],
VZOROVÉ ŘEŠENÍ A VYSVĚTLENÍ PROGRAMU. Ing. Marek Nikodým Ph.D. Katedra matematiky a deskriptívní geometrie VŠB-TU Ostrava 1 Výpočty v trojúhelníku Je dán trojúhelník ABC v prostoru A[, 3, 3], B[4, 5, ],
i=1 Přímka a úsečka. Body, které leží na přímce procházející body a a b můžeme zapsat pomocí parametrické rovnice
 I. Funkce dvou a více reálných proměnných 1. Úvod Značení: V textu budeme používat označení: N pro množinu všech přirozených čísel; R pro množinu všech reálných čísel; R n pro množinu všech uspořádaných
I. Funkce dvou a více reálných proměnných 1. Úvod Značení: V textu budeme používat označení: N pro množinu všech přirozených čísel; R pro množinu všech reálných čísel; R n pro množinu všech uspořádaných
Zimní semestr akademického roku 2014/ prosince 2014
 Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 24/25 2. prosince 24 Předmluva iii
Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 24/25 2. prosince 24 Předmluva iii
Derivace funkce. Přednáška MATEMATIKA č Jiří Neubauer
 Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
5.3. Implicitní funkce a její derivace
 Výklad Podívejme se na následující problém. Uvažujme množinu M bodů [x,y] R 2, které splňují rovnici F(x, y) = 0, M = {[x,y] D F F(x,y) = 0}, kde z = F(x,y) je nějaká funkce dvou proměnných. Je-li F(x,y)
Výklad Podívejme se na následující problém. Uvažujme množinu M bodů [x,y] R 2, které splňují rovnici F(x, y) = 0, M = {[x,y] D F F(x,y) = 0}, kde z = F(x,y) je nějaká funkce dvou proměnných. Je-li F(x,y)
Extrémy funkce dvou proměnných
 Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
1 1 x 2. Jedná se o diferenciální rovnici se separovanými proměnnými, která má smysl pro x ±1 a
 . Řešené úlohy Příklad. (separace proměnných). Řešte počáteční úlohu y 2 + yy ( 2 ) = 0, y(0) = 2. Řešení. Rovnici přepíšeme do tvaru y 2 = yy ( 2 ) y = y2 y 2. Jedná se o diferenciální rovnici se separovanými
. Řešené úlohy Příklad. (separace proměnných). Řešte počáteční úlohu y 2 + yy ( 2 ) = 0, y(0) = 2. Řešení. Rovnici přepíšeme do tvaru y 2 = yy ( 2 ) y = y2 y 2. Jedná se o diferenciální rovnici se separovanými
Derivace a monotónnost funkce
 Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je
Derivace a monotónnost funkce Věta : Uvažujme funkci f (x), která má na intervalu I derivaci f (x). Pak platí: je-li f (x) > 0 x I, funkce f je na intervalu I rostoucí. je-li f (x) < 0 x I, funkce f je
4. OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE
 FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
FBI VŠB-TUO 28. března 2014 4.1. Základní pojmy Definice 4.1. Rovnice tvaru F (x, y, y, y,..., y (n) ) = 0 se nazývá obyčejná diferenciální rovnice n-tého řádu a vyjadřuje vztah mezi neznámou funkcí y
Management rekreace a sportu. 10. Derivace
 Derivace Derivace Před mnoha lety se matematici snažily o obecné vyřešení úlohy, jak sestrojit tečnu k dané křivce a také yzici zápolili s problémem určení rychlosti nerovnoměrného pohybu K zásadnímu obratu
Derivace Derivace Před mnoha lety se matematici snažily o obecné vyřešení úlohy, jak sestrojit tečnu k dané křivce a také yzici zápolili s problémem určení rychlosti nerovnoměrného pohybu K zásadnímu obratu
Teorie. Hinty. kunck6am
 kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
y = 1 x (y2 y), dy dx = 1 x (y2 y) dy y 2 = dx dy y 2 y y(y 4) = A y + B 5 = A(y 1) + By, tj. A = 1, B = 1. dy y 1
 ODR - řešené příkla 20 5 ANALYTICKÉ A NUMERICKÉ METODY ŘEŠENÍ ODR A. Analtické meto řešení Vzorové příkla: 5.. Příklad. Řešte diferenciální rovnici = 2. Řešení: Přepišme danou rovnici na tvar = (2 ), což
ODR - řešené příkla 20 5 ANALYTICKÉ A NUMERICKÉ METODY ŘEŠENÍ ODR A. Analtické meto řešení Vzorové příkla: 5.. Příklad. Řešte diferenciální rovnici = 2. Řešení: Přepišme danou rovnici na tvar = (2 ), což
Matematika 1 pro PEF PaE
 Derivace funkcí jedné proměnné / 9 Matematika pro PEF PaE 4. Derivace funkcí jedné proměnné Přemysl Jedlička Katedra matematiky, TF ČZU Derivace funkcí jedné proměnné Nejjednodušší derivace 2 / 9 Derivace
Derivace funkcí jedné proměnné / 9 Matematika pro PEF PaE 4. Derivace funkcí jedné proměnné Přemysl Jedlička Katedra matematiky, TF ČZU Derivace funkcí jedné proměnné Nejjednodušší derivace 2 / 9 Derivace
sin(x) x lim. pomocí mocninné řady pro funkci sin(x) se středem x 0 = 0. Víme, že ( ) k=0 e x2 dx.
 Použití mocniných řad Nejprve si ukážeme dvě jednoduchá použití Taylorových řad. Příklad Spočtěte následující limitu: ( ) sin(x) lim. x x ( ) Najdeme lim sin(x) x x pomocí mocninné řady pro funkci sin(x)
Použití mocniných řad Nejprve si ukážeme dvě jednoduchá použití Taylorových řad. Příklad Spočtěte následující limitu: ( ) sin(x) lim. x x ( ) Najdeme lim sin(x) x x pomocí mocninné řady pro funkci sin(x)
R β α. Obrázek 1: Zadání - profil složený ze třech elementárních obrazců: 1 - rovnoramenný pravoúhlý trojúhelník, 2 - čtverec, 3 - kruhová díra
 Zadání: Vypočtěte polohu těžiště, momenty setrvačnosti a deviační moment k centrálním osám a dále určete hlavní centrální momenty setrvačnosti, poloměry setrvačnosti a natočení hlavních centrálních os
Zadání: Vypočtěte polohu těžiště, momenty setrvačnosti a deviační moment k centrálním osám a dále určete hlavní centrální momenty setrvačnosti, poloměry setrvačnosti a natočení hlavních centrálních os
ˇ EDNA SˇKA 9 DALS ˇ I METODY INTEGRACE
 PŘEDNÁŠKA 9 DALŠÍ METODY INTEGRACE 1 9.1. Věta o substituci Věta 1 (O substituci) Necht je ϕ(x) prosté regulární zobrazení otevřené množiny X R n na množinu Y R n. Necht je M X, f(y) funkce definovaná
PŘEDNÁŠKA 9 DALŠÍ METODY INTEGRACE 1 9.1. Věta o substituci Věta 1 (O substituci) Necht je ϕ(x) prosté regulární zobrazení otevřené množiny X R n na množinu Y R n. Necht je M X, f(y) funkce definovaná
SPECIÁLNÍCH PRIMITIVNÍCH FUNKCÍ INTEGRACE RACIONÁLNÍCH FUNKCÍ
 VÝPOČET PEIÁLNÍH PRIMITIVNÍH FUNKÍ Obecně nelze zadat algoritmus, který by vždy vedl k výpočtu primitivní funkce. Nicméně eistují jisté třídy funkcí, pro které eistuje algoritmus, který vždy vede k výpočtu
VÝPOČET PEIÁLNÍH PRIMITIVNÍH FUNKÍ Obecně nelze zadat algoritmus, který by vždy vedl k výpočtu primitivní funkce. Nicméně eistují jisté třídy funkcí, pro které eistuje algoritmus, který vždy vede k výpočtu
ANALYTICKÁ GEOMETRIE V ROVINĚ
 ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
Analytická geometrie kvadratických útvarů v rovině
 Analytická geometrie kvadratických útvarů v rovině V následujícím textu se budeme postupně zabývat kružnicí, elipsou, hyperbolou a parabolou, které souhrnně označujeme jako kuželosečky. Současně budeme
Analytická geometrie kvadratických útvarů v rovině V následujícím textu se budeme postupně zabývat kružnicí, elipsou, hyperbolou a parabolou, které souhrnně označujeme jako kuželosečky. Současně budeme
4.3.2 Goniometrické nerovnice
 4 Goniometrické nerovnice Předpoklady: 40 Pedagogická poznámka: Nerovnice je stejně jako rovnice možné řešit grafem i jednotkovou kružnicí Oba způsoby mají své výhody i nevýhody a jsou v podstatě rovnocenné
4 Goniometrické nerovnice Předpoklady: 40 Pedagogická poznámka: Nerovnice je stejně jako rovnice možné řešit grafem i jednotkovou kružnicí Oba způsoby mají své výhody i nevýhody a jsou v podstatě rovnocenné
( x) ( ) ( ) { } Vzorce pro dvojnásobný úhel II. Předpoklady: Urči definiční obor výrazů a zjednoduš je. 2. x x x
 9 Vzorce pro dvojnásobný úhel II Předpoklady: 08 Př : Urči definiční obor výrazů a zjednoduš je a) ( sin cos ) sin x + cos x sin x x + x sin x b) cos x + cos x + sin x + cos x sin x a) x R sin x + cos
9 Vzorce pro dvojnásobný úhel II Předpoklady: 08 Př : Urči definiční obor výrazů a zjednoduš je a) ( sin cos ) sin x + cos x sin x x + x sin x b) cos x + cos x + sin x + cos x sin x a) x R sin x + cos
Příklad 1 ŘEŠENÉ PŘÍKLADY Z M1B ČÁST 2. Určete a načrtněte definiční obory funkcí více proměnných: a) (, ) = b) (, ) = 3. c) (, ) = d) (, ) =
 Příklad 1 Určete a načrtněte definiční obory funkcí více proměnných: a) (, ) = b) (, ) = 3 c) (, ) = d) (, ) = e) (, ) = ln f) (, ) = 1 +1 g) (, ) = arcsin( + ) Poznámka V těchto úlohách máme nalézt největší
Příklad 1 Určete a načrtněte definiční obory funkcí více proměnných: a) (, ) = b) (, ) = 3 c) (, ) = d) (, ) = e) (, ) = ln f) (, ) = 1 +1 g) (, ) = arcsin( + ) Poznámka V těchto úlohách máme nalézt největší
y ds, z T = 1 z ds, kde S = S
 Plošné integrály příklad 5 Určete souřadnice těžiště části roviny xy z =, která leží v prvním oktantu x >, y >, z >. Řešení: ouřadnice těžiště x T, y T a z T homogenní plochy lze určit pomocí plošných
Plošné integrály příklad 5 Určete souřadnice těžiště části roviny xy z =, která leží v prvním oktantu x >, y >, z >. Řešení: ouřadnice těžiště x T, y T a z T homogenní plochy lze určit pomocí plošných
Lineární funkce, rovnice a nerovnice 3 Soustavy lineárních rovnic
 Lineární funkce, rovnice a nerovnice Soustavy lineárních rovnic motivace Využívají se napřklad při analytickém vyšetřování vzájemné polohy dvou přímek v rovině a prostoru. Při řešení některých slovních
Lineární funkce, rovnice a nerovnice Soustavy lineárních rovnic motivace Využívají se napřklad při analytickém vyšetřování vzájemné polohy dvou přímek v rovině a prostoru. Při řešení některých slovních
Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých
 Obyčejné diferenciální rovnice Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých se vyskytují derivace neznámé funkce jedné reálné proměnné. Příklad. Bud dána funkce f : R R.
Obyčejné diferenciální rovnice Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých se vyskytují derivace neznámé funkce jedné reálné proměnné. Příklad. Bud dána funkce f : R R.
Funkce pro studijní obory
 Variace 1 Funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce Funkce je přiřazení,
Variace 1 Funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce Funkce je přiřazení,
Nerovnice, grafy, monotonie a spojitost
 Nerovnice, grafy, monotonie a spojitost text pro studenty Fakulty přírodovědně-humanitní a pedagogické TU v Liberci vzniklý za podpory fondu F Martina Šimůnková 29. prosince 2016 1 Úvod Na druhém stupni
Nerovnice, grafy, monotonie a spojitost text pro studenty Fakulty přírodovědně-humanitní a pedagogické TU v Liberci vzniklý za podpory fondu F Martina Šimůnková 29. prosince 2016 1 Úvod Na druhém stupni
analytické geometrie v prostoru s počátkem 18. stol.
 4.. Funkce více proměnných, definice, vlastnosti Funkce více proměnných Funkce více proměnných se v matematice začal používat v rámci rozvoje analtické geometrie v prostoru s počátkem 8. stol. I v sami
4.. Funkce více proměnných, definice, vlastnosti Funkce více proměnných Funkce více proměnných se v matematice začal používat v rámci rozvoje analtické geometrie v prostoru s počátkem 8. stol. I v sami
Zkouška ze Aplikované matematiky pro Arboristy (AMPA), LDF, minut. Součet Koeficient Body. 4. [10 bodů] Integrální počet. 5.
![Zkouška ze Aplikované matematiky pro Arboristy (AMPA), LDF, minut. Součet Koeficient Body. 4. [10 bodů] Integrální počet. 5. Zkouška ze Aplikované matematiky pro Arboristy (AMPA), LDF, minut. Součet Koeficient Body. 4. [10 bodů] Integrální počet. 5.](/thumbs/92/109752097.jpg) Zkouška ze Aplikované matematiky pro Arboristy (AMPA), LDF, 6.2.204 60 minut 2 3 4 5 6 Jméno:................................... Součet Koeficient Body. [2 bodů] V následující tabulce do každého z šesti
Zkouška ze Aplikované matematiky pro Arboristy (AMPA), LDF, 6.2.204 60 minut 2 3 4 5 6 Jméno:................................... Součet Koeficient Body. [2 bodů] V následující tabulce do každého z šesti
